Automatic Stomatal Segmentation Based on Delaunay-Rayleigh Frequency Distance
Abstract
:1. Introduction
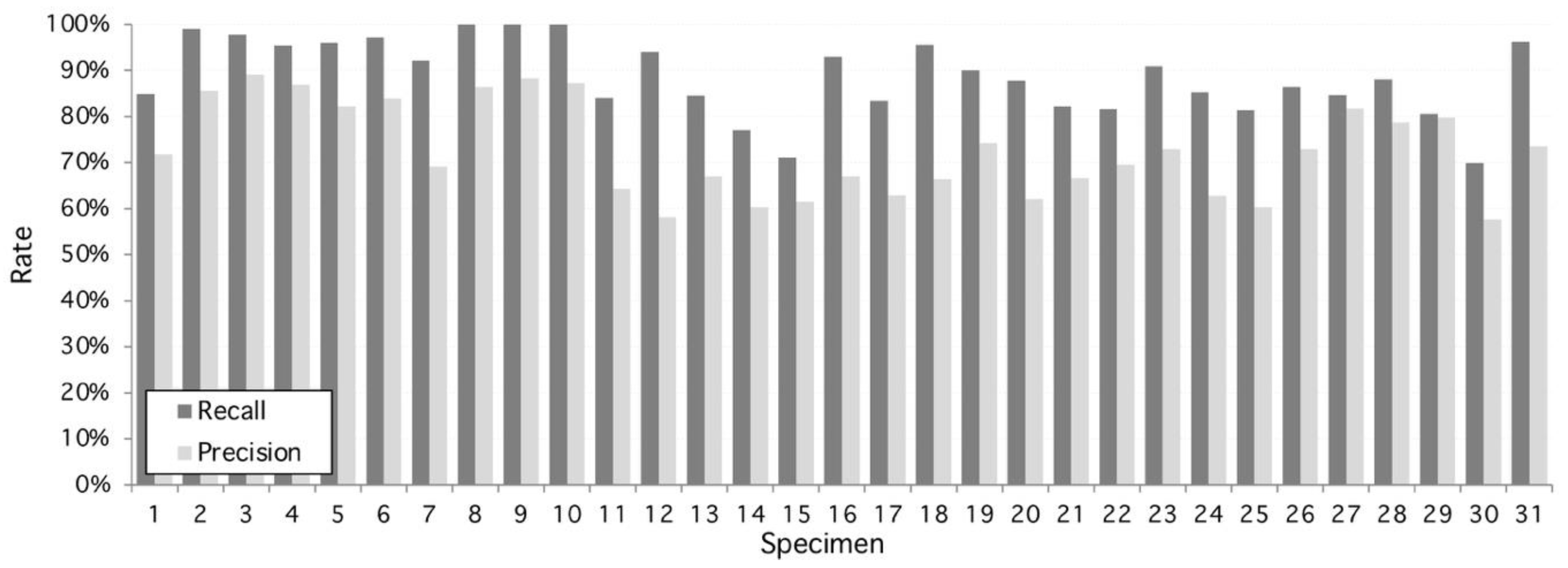
2. Results
3. Discussion
3.1. Manual Segmentation
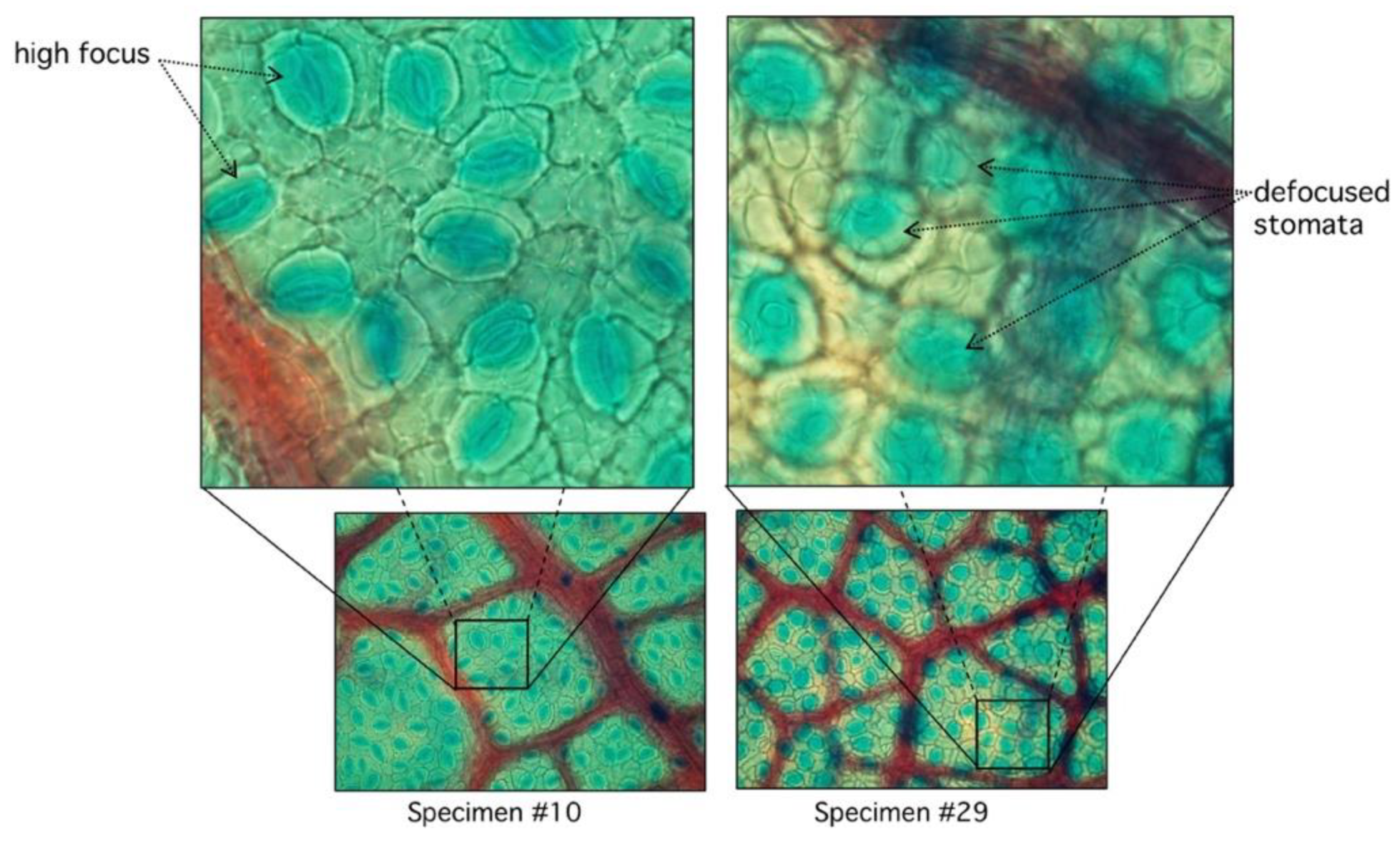
3.2. Defocus Stomata in Automatic Mode
3.3. Main Advantages and Disadvantages
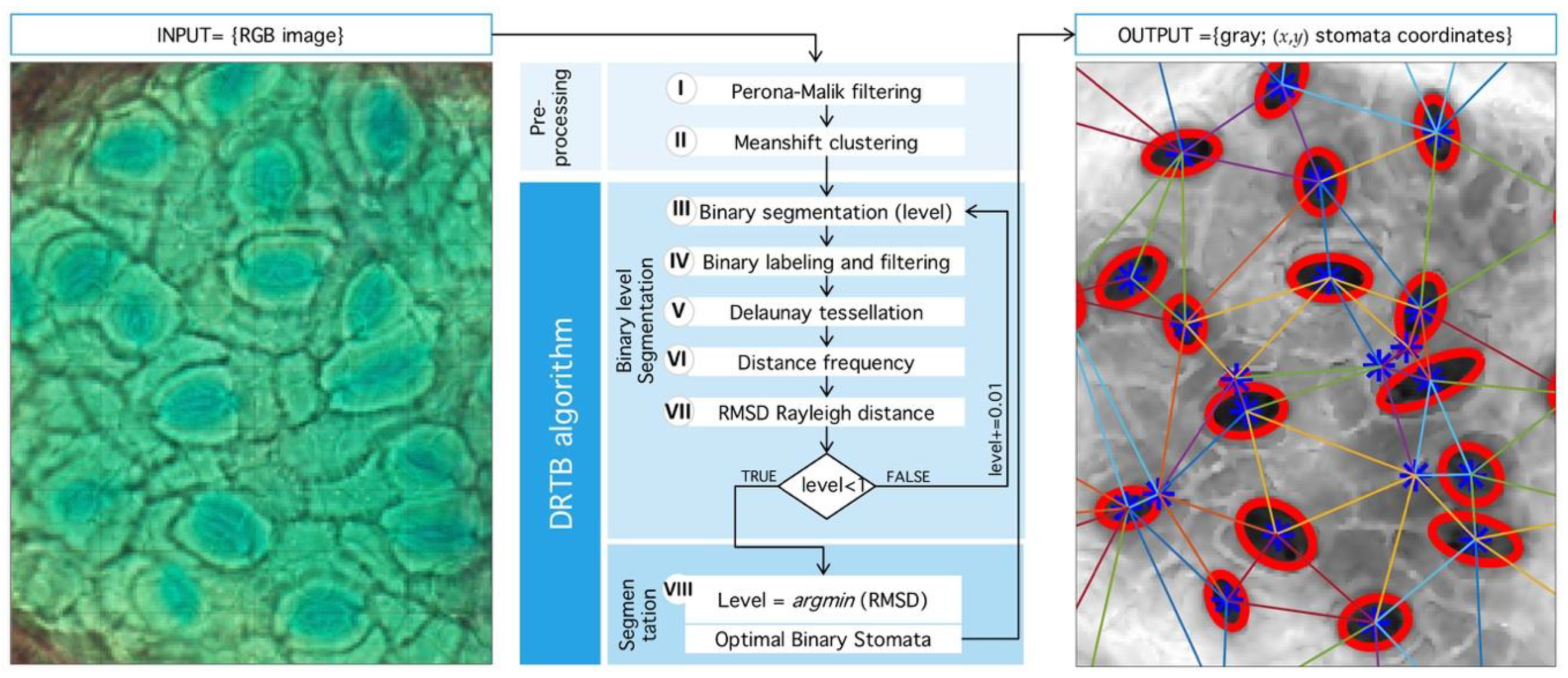
4. Materials and Methods
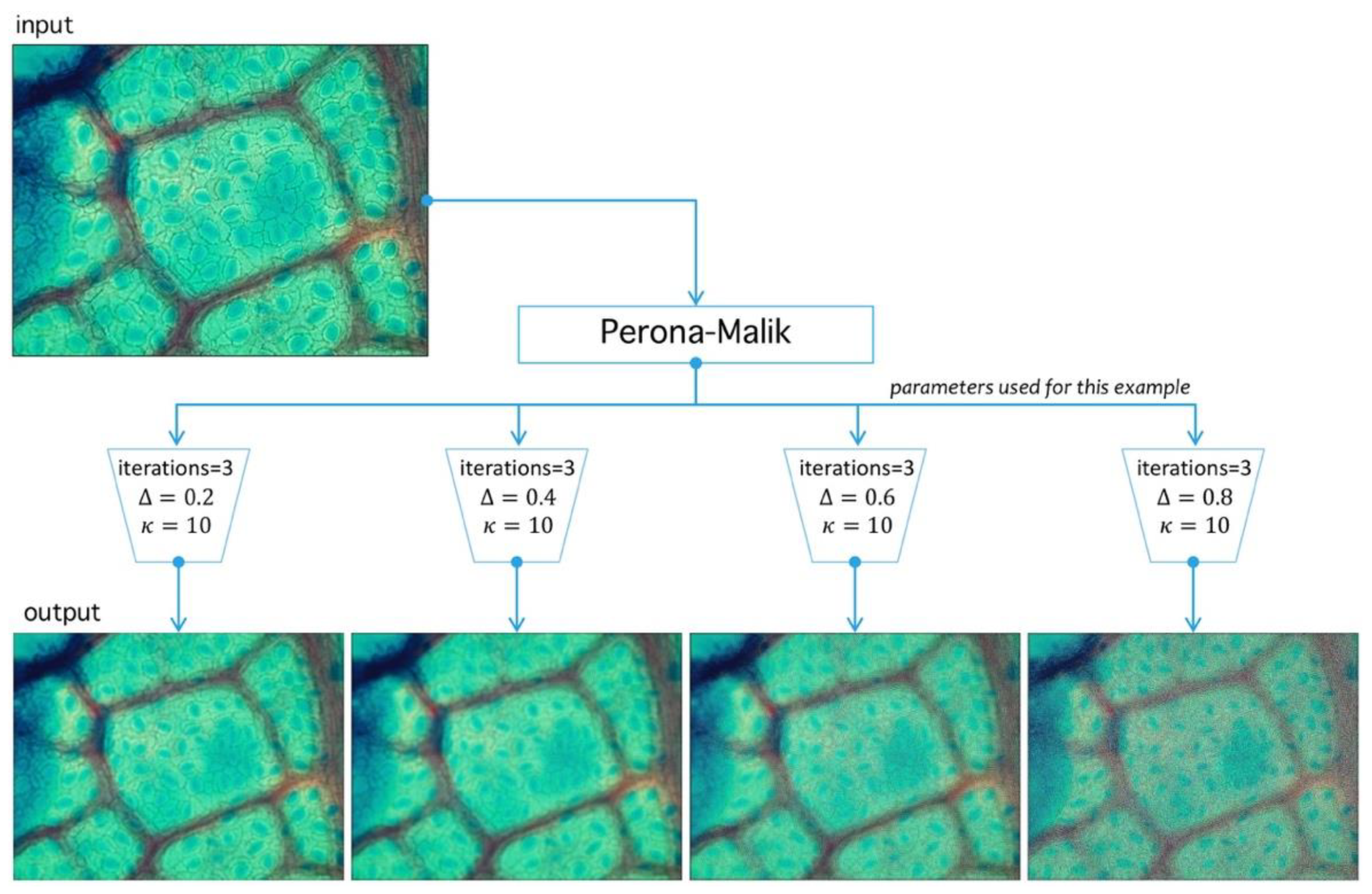
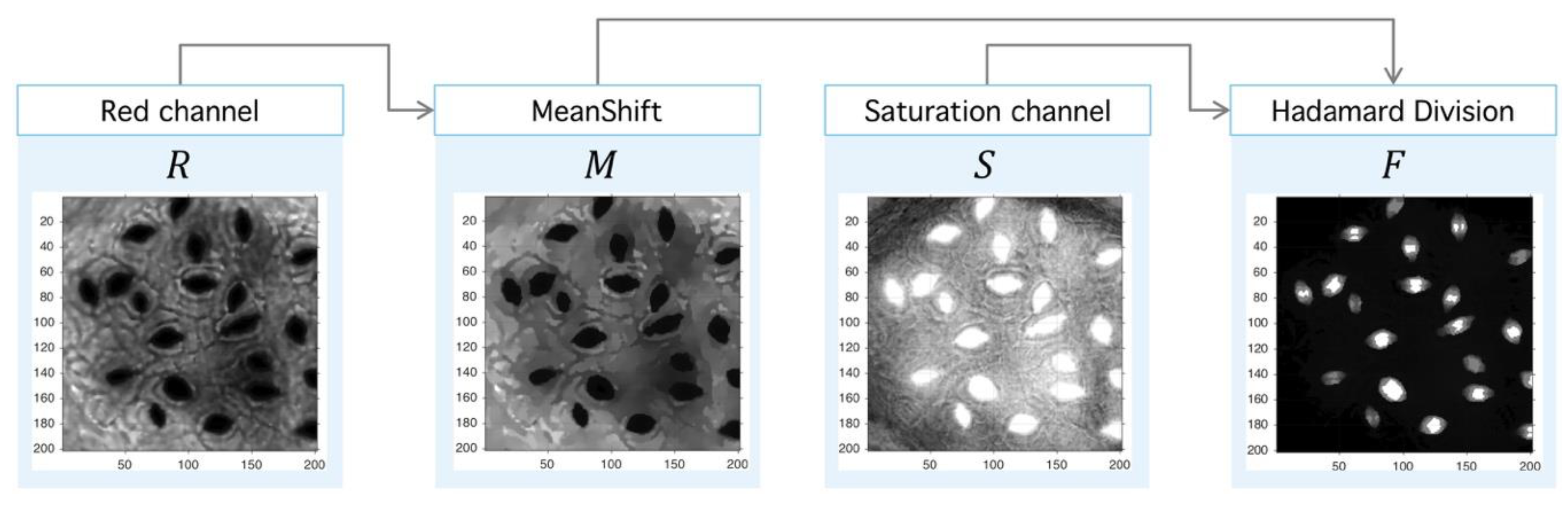
4.1. Preprocessing
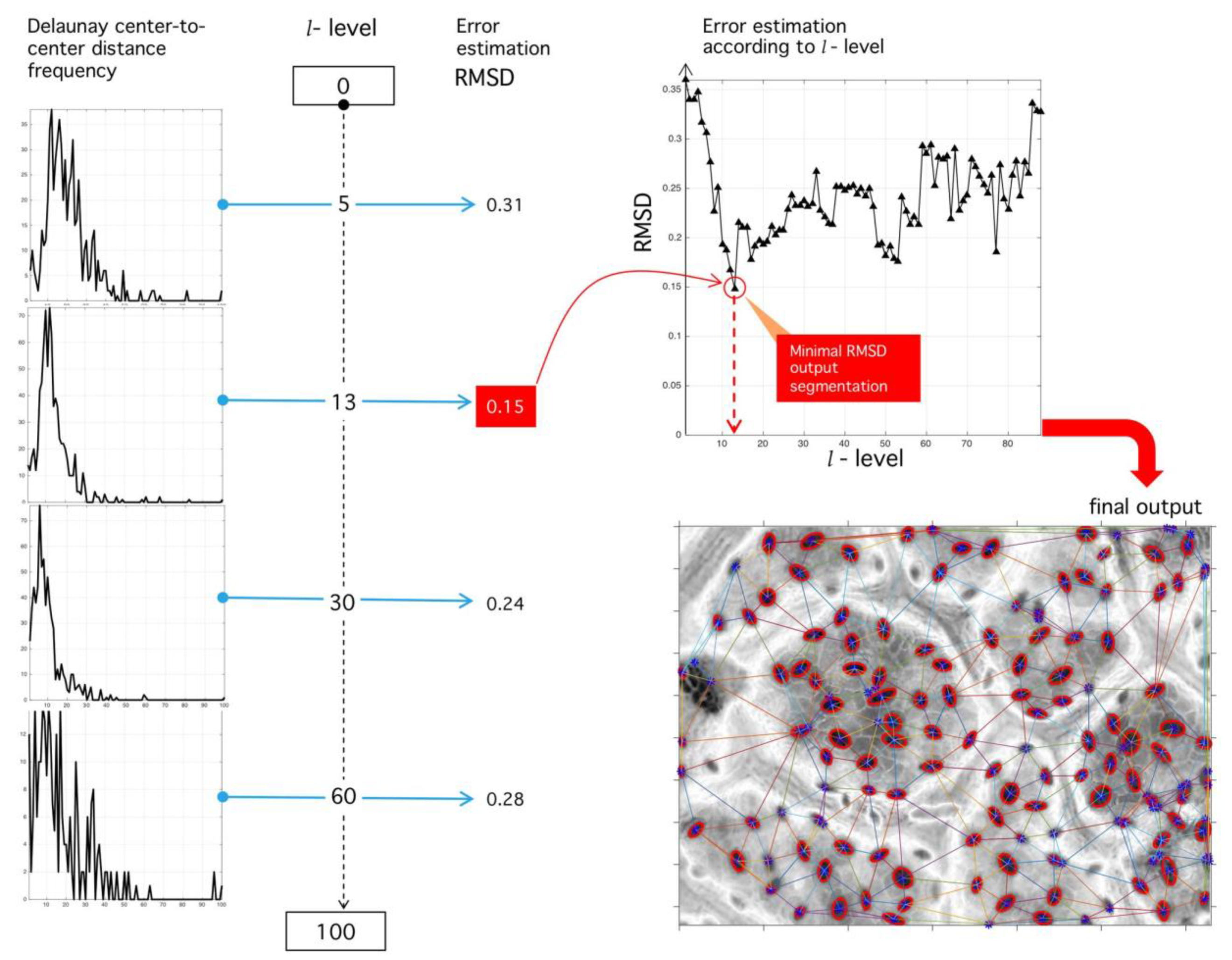
4.2. Delaunay-Rayleigh Threshold Binarization (DRTB Algorithm)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Fanourakis, D.; Nikoloudakis, N.; Pappi, P.; Markakis, E.; Doupis, G.; Charova, S.; Delis, C.; Tsaniklidis, G. The Role of Proteases in Determining Stomatal Development and Tuning Pore Aperture: A Review. Plants 2020, 9, 340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fanourakis, D.; Aliniaeifard, S.; Sellin, A.; Giday, H.; Körner, O.; Nejad, A.R.; Delis, C.; Bouranis, D.; Koubouris, G.; Kambourakis, E.; et al. Stomatal behavior following mid- or long-term exposure to high relative air humidity: A review. Plant Physiol. Biochem. 2020, 153, 92–105. [Google Scholar] [CrossRef] [PubMed]
- Pillitteri, L.J.; Torii, K.U. Mechanisms of Stomatal Development. Annu. Rev. Plant Biol. 2012, 63, 591–614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Franks, P.J.; Drake, P.L.; Beerling, D.J. Plasticity in maximum stomatal conductance constrained by negative correlation between stomatal size and density: An analysis usingEucalyptus globulus. Plant Cell Environ. 2009, 32, 1737–1748. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L.; Zhao, H.; Jiang, Z.; Cai, J. Differences in Near Isohydric and Anisohydric Behavior of Contrasting Poplar Hybrids (I-101 (Populus alba L.) × 84K (Populus alba L. × Populus glandulosa Uyeki)) under Drought-Rehydration Treatments. Forests 2020, 11, 402. [Google Scholar] [CrossRef] [Green Version]
- Fanourakis, D.; Hyldgaard, B.; Giday, H.; Aulik, I.; Bouranis, D.; Körner, O.; Ottosen, C.-O. Stomatal anatomy and closing ability is affected by supplementary light intensity in rose (Rosa hybrida L.). Hortic. Sci. 2019, 46, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Niu, Y.; Ahammed, G.J.; Tang, C.; Guo, L.; Yu, J. Physiological and Transcriptome Responses to Combinations of Elevated CO2 and Magnesium in Arabidopsis thaliana. PLoS ONE 2016, 11, e0149301. [Google Scholar] [CrossRef] [Green Version]
- Croxdale, J.L. Stomatal patterning in angiosperms. Am. J. Bot. 2000, 87, 1069–1080. [Google Scholar] [CrossRef]
- Franks, P.J.; Beerling, D.J. Maximum leaf conductance driven by CO2 effects on stomatal size and density over geologic time. Proc. Natl. Acad. Sci. USA 2009, 106, 10343–10347. [Google Scholar] [CrossRef] [Green Version]
- Dow, G.J.; Berry, J.A.; Bergmann, D.C. The physiological importance of developmental mechanisms that enforce proper stomatal spacing inArabidopsis thaliana. New Phytol. 2014, 201, 1205–1217. [Google Scholar] [CrossRef]
- Li, K.; Huang, J.; Song, W.; Wang, J.; Lv, S.; Wang, X. Automatic segmentation and measurement methods of living stomata of plants based on the CV model. Plant Methods 2019, 15, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, W.; Li, J.; Li, K.; Chen, J.; Huang, J. An Automatic Method for Stomatal Pore Detection and Measurement in Microscope Images of Plant Leaf Based on a Convolutional Neural Network Model. Forests 2020, 11, 954. [Google Scholar] [CrossRef]
- Naulin, P.I.; Valenzuela, G.; Estay, S.A. Size matters: Point pattern analysis biases the estimation of spatial properties of stomata distribution. New Phytol. 2016, 213, 1956–1960. [Google Scholar] [CrossRef] [PubMed]
- Bhaiswar, N.; Dixit, D.V.V.; Student, P.G. A Review: Methods of Automatic Stomata Detection and Counting Through Microscopic Images of a Leaf. IJIRSET 2007, 5, 6. [Google Scholar]
- Da Silva, N.R.; Oliveira, M.W.D.S.; Filho, H.A.D.A.; Pinheiro, L.F.S.; Rossatto, D.R.; Kolb, R.M.; Bruno, O.M. Leaf epidermis images for robust identification of plants. Sci. Rep. 2016, 6, 25994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jayakody, H.; Liu, S.; Whitty, M.; Petrie, P. Microscope image based fully automated stomata detection and pore measurement method for grapevines. Plant Methods 2017, 13, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Florindo, J.B.; Landini, G.; Filho, H.A.; Bruno, O.M. Analysis of Stomata Distribution Patterns for Quantification of the Foliar Plasticity of Tradescantia Zebrina. J. Phys. Conf. Ser. 2015, 633, 012113. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Yu, Q.; Xu, C.; Li, J.; Qin, G. Rapid Estimation of Stomatal Density and Stomatal Area of Plant Leaves Based on Object-Oriented Classification and Its Ecological Trade-Off Strategy Analysis. Forests 2018, 9, 616. [Google Scholar] [CrossRef] [Green Version]
- Fetter, K.C.; Eberhardt, S.; Barclay, R.S.; Wing, S.; Keller, S.R. StomataCounter: A neural network for automatic stomata identification and counting. New Phytol. 2019, 223, 1671–1681. [Google Scholar] [CrossRef]
- Toda, Y.; Toh, S.; Bourdais, G.; Robatzek, S.; MacLean, D.; Kinoshita, T. DeepStomata: Facial Recognition Technology for Automated Stomatal Aperture Measurement. Bioinformatics 2018, 365098. [Google Scholar] [CrossRef] [Green Version]
- Casado-García, A.; Del-Canto, A.; Sanz-Saez, A.; Pérez-López, U.; Bilbao-Kareaga, A.; Fritschi, F.B.; Miranda-Apodaca, J.; Muñoz-Rueda, A.; Sillero-Martínez, A.; Yoldi-Achalandabaso, A.; et al. LabelStoma: A tool for stomata detection based on the YOLO algorithm. Comput. Electron. Agric. 2020, 178, 105751. [Google Scholar] [CrossRef]
- García Álvarez, S.; Morla Juaristi, C.; Solana Gutiérrez, J.; García-Amorena, I. Taxonomic differences between Pinus sylvestris and P. uncinata revealed in the stomata and cuticle characters for use in the study of fossil material. Rev. Palaeobot. Palynol. 2009, 155, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Sweeney, C.A. A key for the identification of stomata of the native conifers of Scandinavia. Rev. Palaeobot. Palynol. 2004, 128, 281–290. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, Y.; Guo, X. Conifer stomata analysis in paleoecological studies on the Loess Plateau: An example from Tianchi Lake, Liupan Mountains. J. Arid. Environ. 2011, 75, 1209–1213. [Google Scholar] [CrossRef]
- Camargo, M.A.B.; Marenco, R.A. Density, size and distribution of stomata in 35 rainforest tree species in Central Amazonia. Acta Amaz. 2011, 41, 205–212. [Google Scholar] [CrossRef] [Green Version]
- Eisele, J.F.; Fäßler, F.; Bürgel, P.F.; Chaban, C. A Rapid and Simple Method for Microscopy-Based Stomata Analyses. PLoS ONE 2016, 11, e0164576. [Google Scholar] [CrossRef]
- Shapiro, B.E.; Jönsson, H.; Sahlin, P.; Heisler, M.; Roeder, A.; Burl, M.; Meyerowitz, E.M.; Mjolsness, E.D. Tessellations and Pattern Formation in Plant Growth and Development. In Tessellations in the Sciences: Virtues, Techniques and Applications of Geometric Tilings; van de Weijgaert, R., Vegter, G., Ritzerveld, J., Icke, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Karabourniotis, G.; Tzobanoglou, D.; Nikolopoulos, D.; Liakopoulos, G. Epicuticular Phenolics Over Guard Cells: Exploitation for in situ Stomatal Counting by Fluorescence Microscopy and Combined Image Analysis. Ann. Bot. 2001, 87, 631–639. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Bala, G.; Caldeira, K.; Nemani, R.; Ban-Weiss, G. Importance of carbon dioxide physiological forcing to future climate change. Proc. Natl. Acad. Sci. USA 2010, 107, 9513–9518. [Google Scholar] [CrossRef] [Green Version]
- Konrad, W.; Roth-Nebelsick, A.; Grein, M. Modelling of stomatal density response to atmospheric. J. Theor. Biol. 2008, 253, 638–658. [Google Scholar] [CrossRef] [PubMed]
- Chater, C.; Peng, K.; Movahedi, M.; Dunn, J.A.; Walker, H.J.; Liang, Y.-K.; McLachlan, D.H.; Casson, S.A.; Isner, J.C.; Wilson, I.D.; et al. Elevated CO2 -Induced Responses in Stomata Require ABA and ABA Signaling. Curr. Biol. 2015, 25, 2709–2716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tomimatsu, H.; Tang, Y. Effects of high CO2 levels on dynamic photosynthesis: Carbon gain, mechanisms, and environmental interactions. J. Plant Res. 2016, 129, 365–377. [Google Scholar] [CrossRef] [PubMed]
- Franklin, G.L. Preparation of Thin Sections of Synthetic Resins and Wood-Resin Composites, and a New Macerating Method for Wood. Nat. Cell Biol. 1945, 155, 51. [Google Scholar] [CrossRef]
- Peat, H.J.; Fitter, A.H. A comparative study of the distribution and density of stomata in the British flora. Biol. J. Linn. Soc. 1994, 52, 377–393. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Xu, M.; Hou, R.; Shen, R.; Qiu, S.; Ouyang, Z. Effects of experimental warming on stomatal traits in leaves of maize (Zea may L.). Ecol. Evol. 2013, 3, 3095–3111. [Google Scholar] [CrossRef] [PubMed]
- Fanourakis, D.; Heuvelink, E.; Carvalho, S.M.P. Spatial heterogeneity in stomatal features during leaf elongation: An analysis using Rosa hybrida. Funct. Plant Biol. 2015, 42, 737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gan, Y.; Zhou, L.; Shen, Z.-J.; Shen, Z.-X.; Zhang, Y.-Q.; Wang, G.-X. Stomatal clustering, a new marker for environmental perception and adaptation in terrestrial plants. Bot. Stud. 2010, 51, 12. [Google Scholar]
- Weickert, J. Anisotropic Diffusion in Image Processing; Teubner, B.G., Ed.; European Consortium for Mathematics in Industry: Stuttgart, Germany, 1998. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A Review of Image Denoising Algorithms, with a New One. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Liu, K.; Tan, J.; Ai, L. Hybrid regularizers-based adaptive anisotropic diffusion for image denoising. SpringerPlus 2016, 5, 404. [Google Scholar] [CrossRef] [Green Version]
- Staff, L.; Hurd, P.; Reale, L.; Seoighe, C.; Rockwood, A.; Gehring, C. The Hidden Geometries of the Arabidopsis thaliana Epidermis. PLoS ONE 2012, 7, e43546. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Aw, W.Y.; Devenport, D.; Torquato, S. Structural Characterization and Statistical-Mechanical Model of Epidermal Patterns. Biophys. J. 2016, 111, 2534–2545. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kamalaveni, V.; Rajalakshmi, R.A.; Narayanankutty, K. Image Denoising Using Variations of Perona-Malik Model with Different Edge Stopping Functions. Procedia Comput. Sci. 2015, 58, 673–682. [Google Scholar] [CrossRef] [Green Version]
- Tschumperlé, D.; Deriche, R. Anisotropic Diffusion Partial Differential Equations in MultiChannel Image Processing: Framework and Applications; Advances in Imaging and Electron Physics (AIEP); Academic Press: Cambridge, MA, USA, 2007; pp. 145–209. [Google Scholar]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Fashing, M.; Tomasi, C. Mean shift is a bound optimization. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 471–474. [Google Scholar] [CrossRef] [PubMed]
- Reams, R. Hadamard inverses, square roots and products of almost semidefinite matrices. Linear Algebra Appl. 1999, 288, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Leys, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef] [Green Version]
- Grimmett, G.; Stirzaker, D. Probability and Random Processes; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Vanselow, R. About Delaunay Triangulations and Discrete Maximum Principles for the Linear Conforming FEM Applied to the Poisson Equation. Appl. Math. 2001, 46, 13–28. [Google Scholar] [CrossRef] [Green Version]


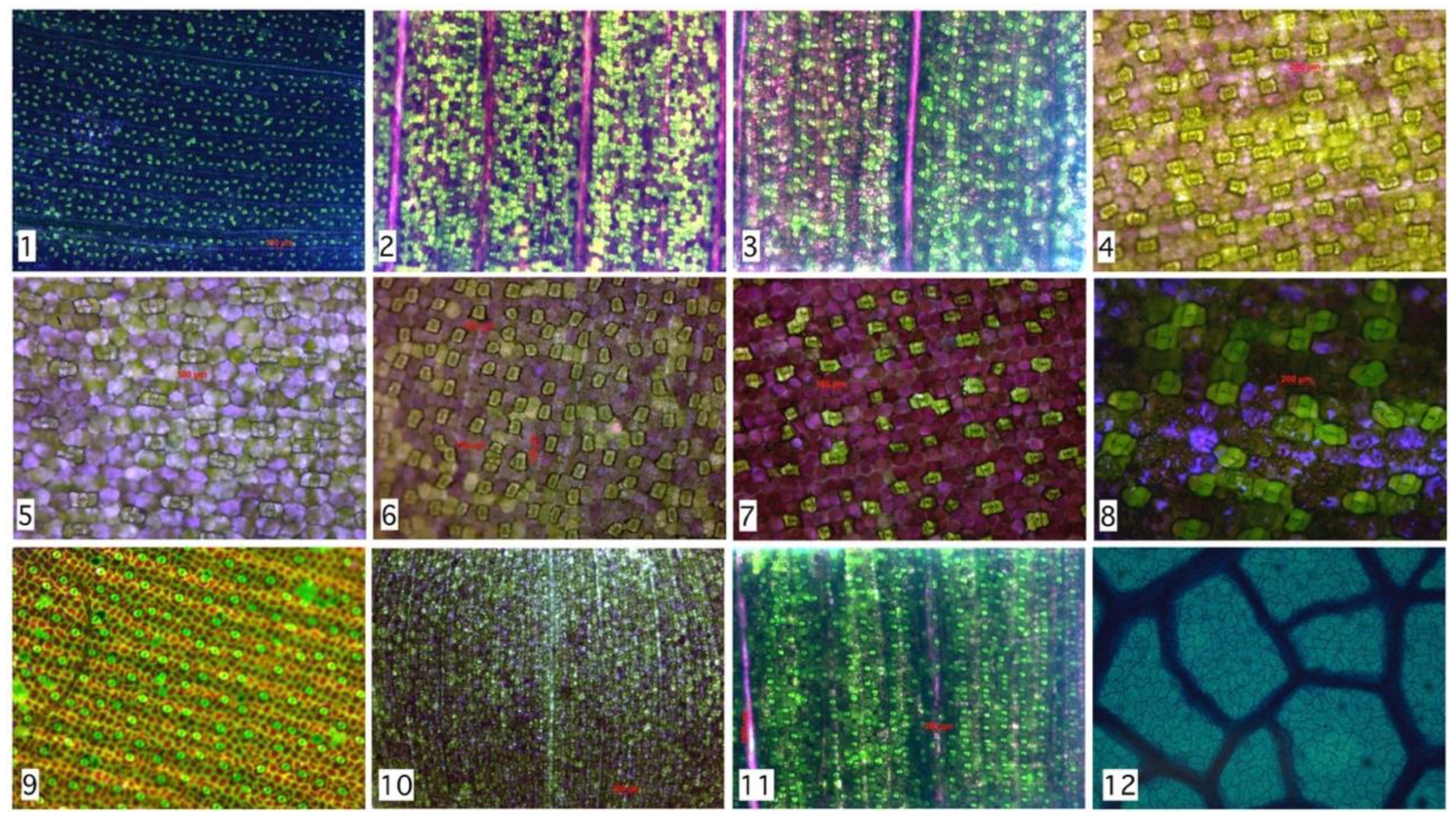





| # | Species Analyzed | Stomata’s Number | RMSD | Rayleigh Parameter | Group | Family |
|---|---|---|---|---|---|---|
| 1 | Tradescantia Zebrina | 753 | 0.00832 | 3.3 | Monocot | C |
| 2 | Tradescantia Pallida—under 24 h of light | 394 | 0.00983 | 3.6 | Monocot | C |
| 3 | Tradescantia Pallida—in natural condition | 245 | 0.03327 | 7.1 | Monocot | C |
| 4 | Callisia reppens | 65 | 0.05358 | 8.8 | Monocot | C |
| 5 | Callisia reppens | 29 | 0.12969 | 9.7 | Monocot | C |
| 6 | Callisia reppens | 104 | 0.02037 | 4.3 | Monocot | C |
| 7 | Tradescantia Zebrina | 69 | 0.05905 | 8.3 | Monocot | C |
| 8 | Tradescantia Pallid | 25 | 0.13832 | 11.1 | Monocot | C |
| 9 | Ctenanthe Oppenheimiana | 138 | 0.02531 | 7.1 | Monocot | M |
| 10 | Calisia reppens—using stereoscope 15× | 586 | 0.01578 | 3.3 | Monocot | C |
| 11 | Tradescantia Pallida using stereoscope 15× | 295 | 0.01902 | 5.4 | Monocot | C |
| 12 | Hymenaea Courbaril | 139 | 0.02420 | 6.1 | Dicot | F |
| Total Regions | 2842 | μ = 0.04473 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, M.; Toledo, P.A.; Velázquez, R.; Bruno, O.M. Automatic Stomatal Segmentation Based on Delaunay-Rayleigh Frequency Distance. Plants 2020, 9, 1613. https://doi.org/10.3390/plants9111613
Carrasco M, Toledo PA, Velázquez R, Bruno OM. Automatic Stomatal Segmentation Based on Delaunay-Rayleigh Frequency Distance. Plants. 2020; 9(11):1613. https://doi.org/10.3390/plants9111613
Chicago/Turabian StyleCarrasco, Miguel, Patricio A. Toledo, Ramiro Velázquez, and Odemir M. Bruno. 2020. "Automatic Stomatal Segmentation Based on Delaunay-Rayleigh Frequency Distance" Plants 9, no. 11: 1613. https://doi.org/10.3390/plants9111613
APA StyleCarrasco, M., Toledo, P. A., Velázquez, R., & Bruno, O. M. (2020). Automatic Stomatal Segmentation Based on Delaunay-Rayleigh Frequency Distance. Plants, 9(11), 1613. https://doi.org/10.3390/plants9111613







