Analysis of Snow Cover in the Sibillini Mountains in Central Italy
Abstract
:1. Introduction
1.1. Aim of the Study and State of the Art
1.2. Geographical Framework
2. Materials and Methods
- = previous data
- = following data
- = time series of data
- and are data values at time and , respectively.
- = primary variable
- = location α1
- = location α2
- = kriging weight for the α primary data sample
- = estimated value
- = observed value
- = sample size
- = variance
- = standard deviation
3. Results
3.1. Correlation of Snow between Different Weather Stations
3.2. Trend Test for the Period 1991–2020
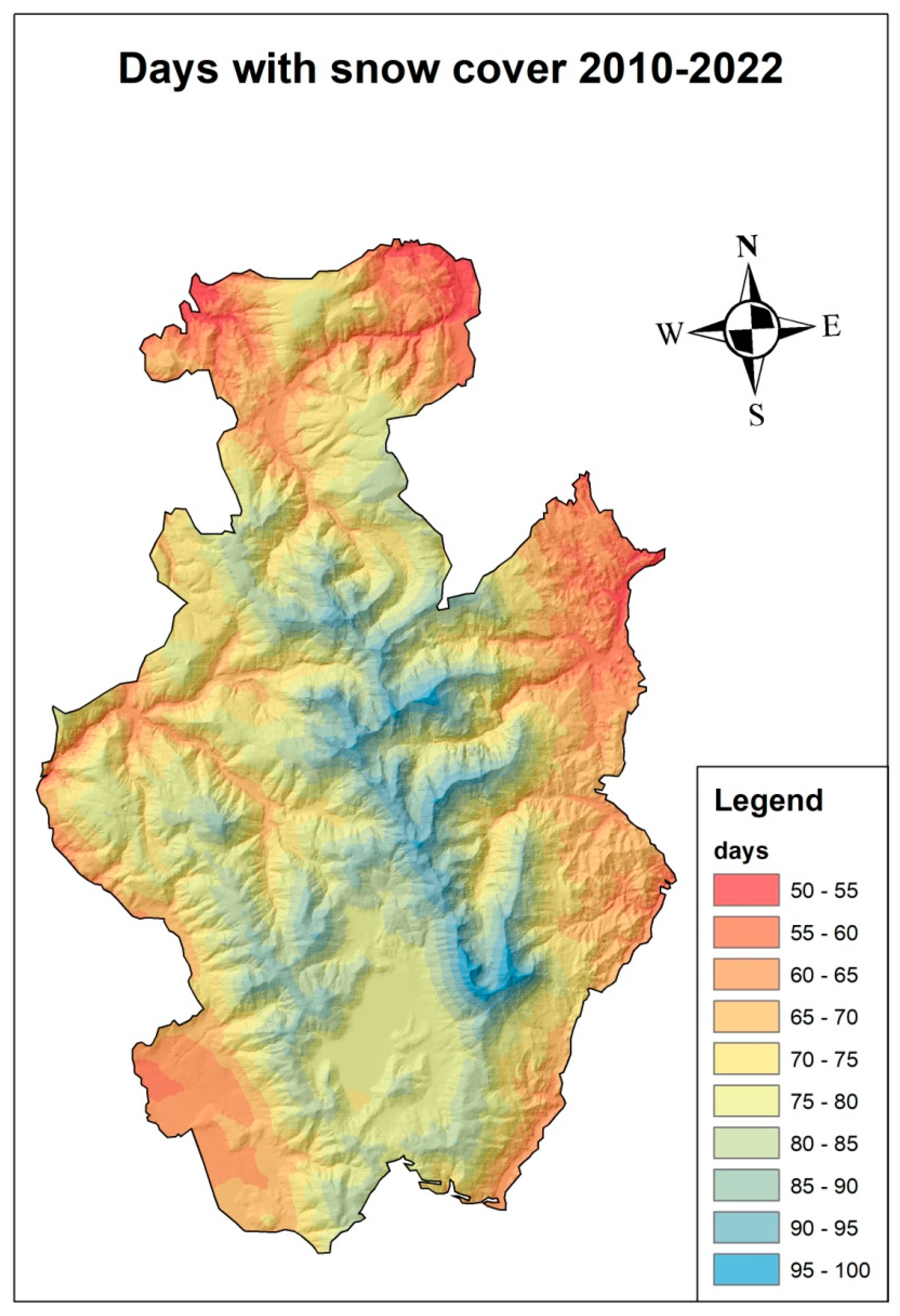
3.3. Interpolation of Snow Cover Variables for the Period 2010–2022
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Drescher, M.; Thomas, S.C. Snow cover manipulations alter survival of early life stages of cold-temperate tree species. Oikos 2013, 122, 541–554. [Google Scholar] [CrossRef]
- Milbau, A.; Graae, B.J.; Shevtsova, A.; Nijs, I. Effects of a warmer climate on seed germination in the subarctic. Ann. Bot. 2009, 104, 287–296. [Google Scholar] [CrossRef] [Green Version]
- Gentilucci, M.; Barbieri, M.; Burt, P. Climate and territorial suitability for the Vineyards developed using GIS techniques. In Exploring the Nexus of Geoecology, Geography, Geoarcheology and Geotourism: Advances and Applications for Sustainable Development in Environmental Sciences and Agroforestry Research, Proceedings of the 1st Springer Conference of the Arabian Journal of Geosciences (CAJG-1), Hammamet, Tunisia, 12–15 November 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 11–13. [Google Scholar]
- Dong, C. Remote sensing, hydrological modeling and in situ observations in snow cover research: A review. J. Hydrol. 2018, 561, 573–583. [Google Scholar] [CrossRef]
- Dressler, K.A.; Leavesley, G.H.; Bales, R.C.; Fassnacht, S.R. Evaluation of gridded snow water equivalent and satellite snow cover products for mountain basins in a hydrologic model. Hydrol. Process. 2006, 20, 673–688. [Google Scholar] [CrossRef]
- Matsuura, S.; Okamoto, T.; Asano, S.; Osawa, H.; Shibasaki, T. Influences of the snow cover on landslide displacement in winter period: A case study in a heavy snowfall area of Japan. Environ. Earth Sci. 2017, 76, 362. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Dalei, N.N.; Gentilucci, E. Management and Creation of a New Tourist Route in the National Park of the Sibillini Mountains using GIS Software, for Economic Development. In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management, Crete, Greece, 3–5 May 2019; pp. 183–188. [Google Scholar]
- Zhu, L.; Ma, G.; Zhang, Y.; Wang, J.; Tian, W.; Kan, X. Accelerated decline of snow cover in China from 1979 to 2018 observed from space. Sci. Total. Environ. 2022, 814, 152491. [Google Scholar] [CrossRef]
- Olefs, M.; Koch, R.; Schöner, W.; Marke, T. Changes in Snow Depth, Snow Cover Duration, and Potential Snowmaking Conditions in Austria, 1961–2020—A Model Based Approach. Atmosphere 2020, 11, 1330. [Google Scholar] [CrossRef]
- Martínez-Ibarra, E.; Serrano-Montes, J.; Arias-García, J. Reconstruction and analysis of 1900–2017 snowfall events on the southeast coast of Spain. Clim. Res. 2019, 78, 41–50. [Google Scholar] [CrossRef]
- Eccel, E.; Cau, P.; Ranzi, R. Data reconstruction and homogenization for reducing uncertainties in high-resolution climate analysis in Alpine regions. Theor. Appl. Clim. 2012, 110, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Gentilucci, M.; Barbieri, M.; Pambianchi, G. Reliability of the IMERG product through reference rain gauges in Central Italy. Atmospheric Res. 2022, 278, 106340. [Google Scholar] [CrossRef]
- Jeoung, H.; Shi, S.; Liu, G. A Novel Approach to Validate Satellite Snowfall Retrievals by Ground-Based Point Measurements. Remote. Sens. 2022, 14, 434. [Google Scholar] [CrossRef]
- Gentilucci, M.; Pambianchi, G. Rainy Day Prediction Model with Climate Covariates Using Artificial Neural Network MLP, Pilot Area: Central Italy. Climate 2022, 10, 120. [Google Scholar] [CrossRef]
- Panahi, M.; Behrangi, A. Comparative Analysis of Snowfall Accumulation and Gauge Undercatch Correction Factors from Diverse Data Sets: In Situ, Satellite, and Reanalysis. Asia-Pacific J. Atmospheric Sci. 2020, 56, 615–628. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Grossi, G.; Lendvai, A.; Peretti, G.; Ranzi, R. Snow Precipitation Measured by Gauges: Systematic Error Estimation and Data Series Correction in the Central Italian Alps. Water 2017, 9, 461. [Google Scholar] [CrossRef] [Green Version]
- Allamano, P.; Claps, P. Precipitation measurement errors at high-elevation sites in the Italian Alps. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 2–7 May 2010; p. 11287. [Google Scholar]
- Pelak, N.; Sohrabi, M.; Safeeq, M.; Conklin, M. Improving snow water equivalent simulations in an alpine basin by blending precipitation gauge and snow pillow measurements. Hydrol. Process. 2023, 37, e14796. [Google Scholar] [CrossRef]
- Gascoin, S.; Lhermitte, S.; Kinnard, C.; Bortels, K.; Liston, G.E. Wind effects on snow cover in Pascua-Lama, Dry Andes of Chile. Adv. Water Resour. 2013, 55, 25–39. [Google Scholar] [CrossRef] [Green Version]
- Raparelli, E.; Tuccella, P.; Colaiuda, V.; Marzano, F.S. Snow cover prediction in the Italian central Apennines using weather forecast and land surface numerical models. Cryosphere 2023, 17, 519–538. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Abyaneh, H.Z.; Sharifi, M.R. Comparison of artificial neural network and combined models in estimating spatial distribution of snow depth and snow water equivalent in Samsami basin of Iran. Neural Comput. Appl. 2010, 19, 625–635. [Google Scholar] [CrossRef]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial neural network-based techniques for the re-trieval of SWE and snow depth from SSM/I data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Goovaerts, P. Ordinary Cokriging Revisited. J. Int. Assoc. Math. Geol. 1998, 30, 21–42. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Peters-Lidard, C.D.; Kumar, S.; Foster, J.L.; Shaw, M.; Tian, Y.; Fall, G.M. Assimilating satellite-based snow depth and snow cover products for improving snow predictions in Alaska. Adv. Water Resour. 2013, 54, 208–227. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Buisán, S.T.; Earle, M.E.; Collado, J.L.; Kochendorfer, J.; Alastrué, J.; Wolff, M.; López-Moreno, J.I. Assessment of snowfall accumulation underestimation by tipping bucket gauges in the Spanish operational network. Atmos. Meas. Tech. 2017, 10, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Valt, M.; Cianfarra, P. Recent snow cover variability in the Italian Alps. Cold Reg. Sci. Technol. 2010, 64, 146–157. [Google Scholar] [CrossRef]
- Bulygina, O.N.; Razuvaev, V.N.; Korshunova, N.N. Changes in snow cover over Northern Eurasia in the last few decades. Environ. Res. Lett. 2009, 4, 045026. [Google Scholar] [CrossRef]
- Onuchin, A.; Kofman, G.; Zubareva, O.; Danilova, I. Using an Urban Snow Cover Composition-Based Cluster Analysis to Zone Krasnoyarsk Town (Russia) by Pollution Level. Pol. J. Environ. Stud. 2020, 29, 4257–4267. [Google Scholar] [CrossRef]
- Hong, H.P.; Ye, W. Analysis of extreme ground snow loads for Canada using snow depth records. Nat. Hazards 2014, 73, 355–371. [Google Scholar] [CrossRef]
- Gentilucci, M.; Bufalini, M.; Materazzi, M.; Barbieri, M.; Aringoli, D.; Farabollini, P.; Pambianchi, G. Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy. Geosciences 2021, 11, 348. [Google Scholar] [CrossRef]
- Uno, F.; Kawase, H.; Ishizaki, N.N.; Yoshikane, T.; Hara, M.; Kimura, F.; Iyobe, T.; Kawashima, K. Analysis of Regional Difference in Altitude Dependence of Snow Depth Using High Resolve Numerical Experiments. Sola 2014, 10, 19–22. [Google Scholar] [CrossRef] [Green Version]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from Earth observation data: Validation and statistical measures. J. Appl. Remote. Sens. 2012, 6, 063557. [Google Scholar] [CrossRef]
- Harshburger, B.J.; Humes, K.S.; Walden, V.P.; Blandford, T.R.; Moore, B.C.; Dezzani, R.J. Spatial interpolation of snow water equivalency using surface observations and remotely sensed images of snow-covered area. Hydrol. Process. 2010, 24, 1285–1295. [Google Scholar] [CrossRef]
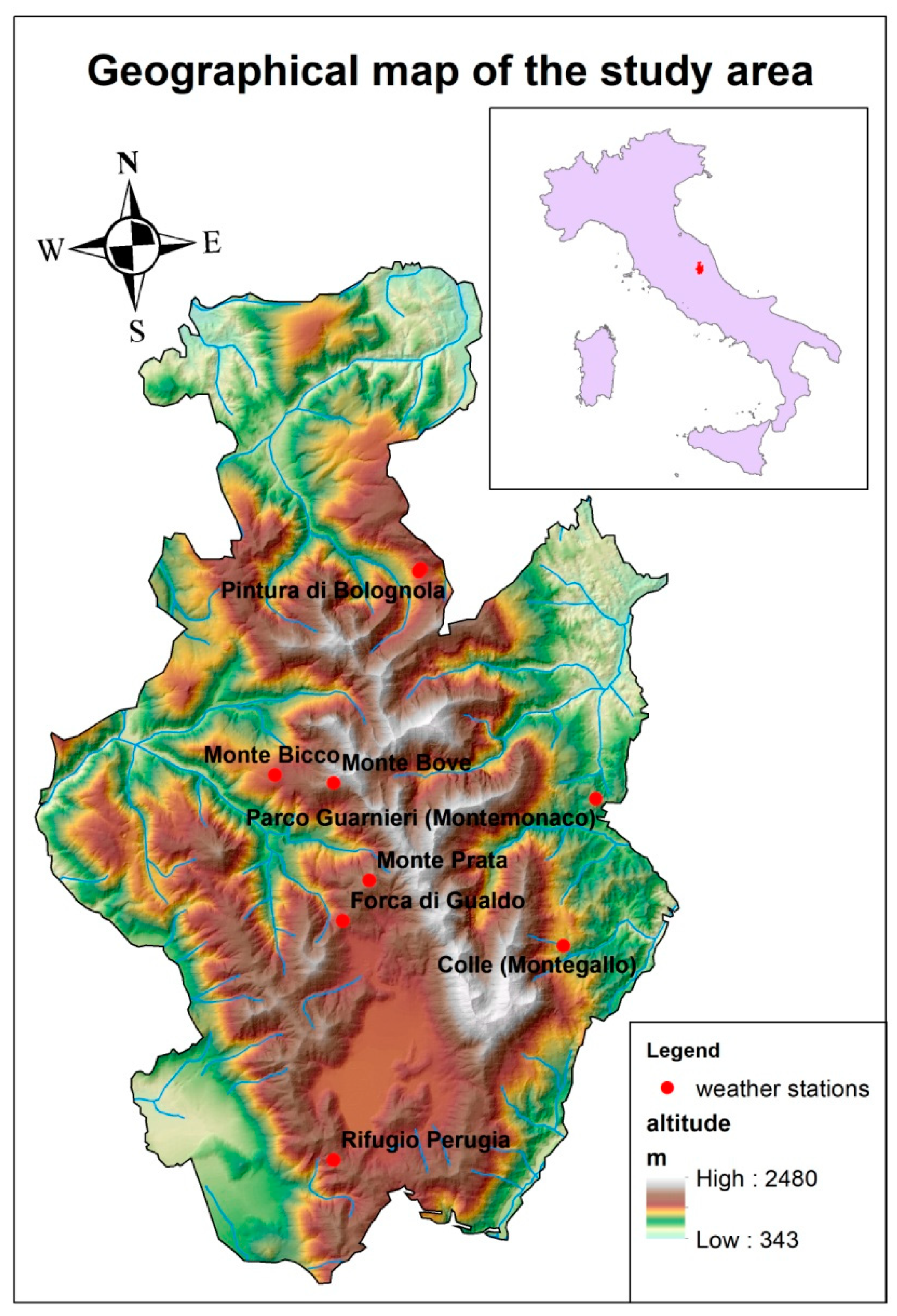
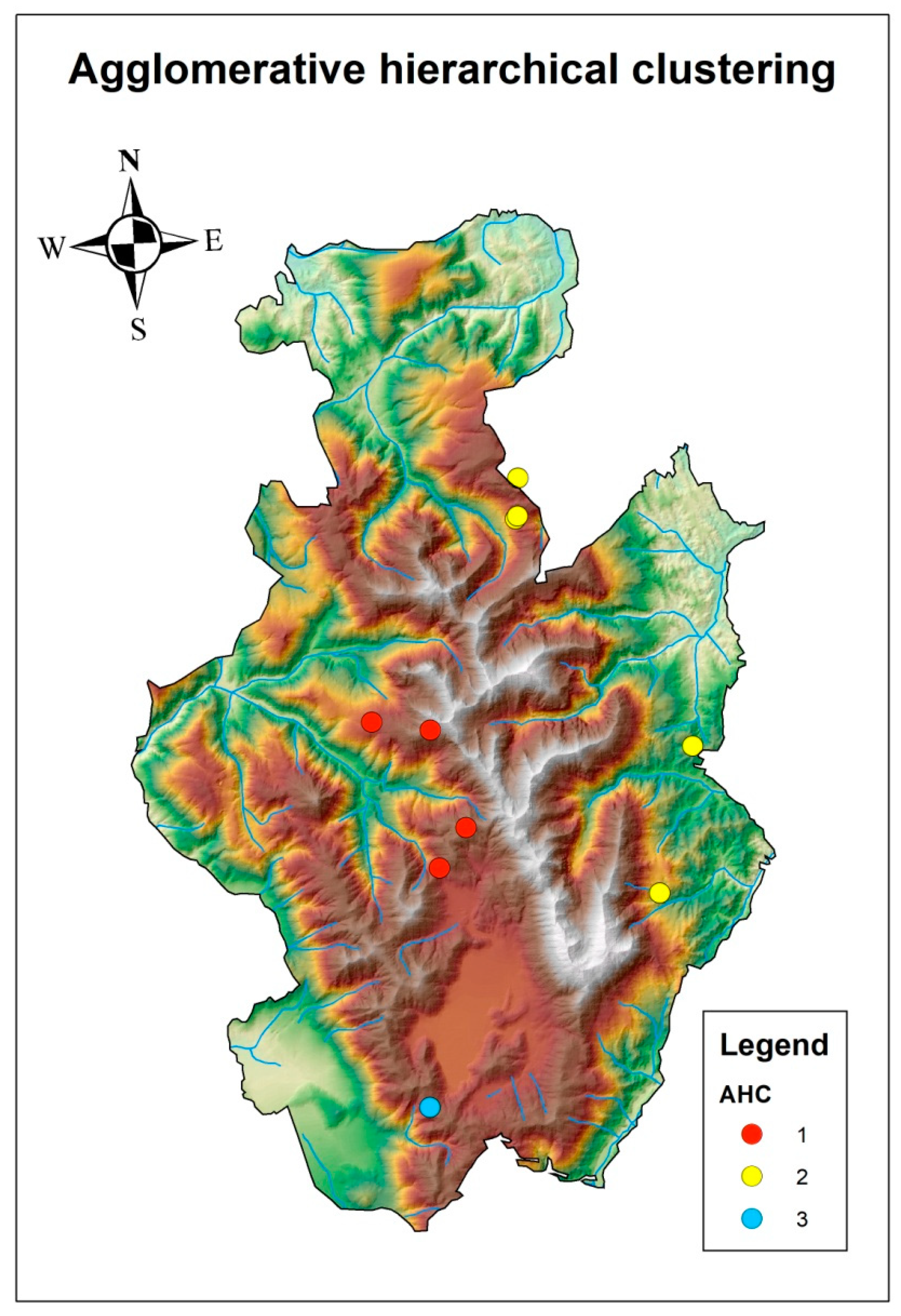
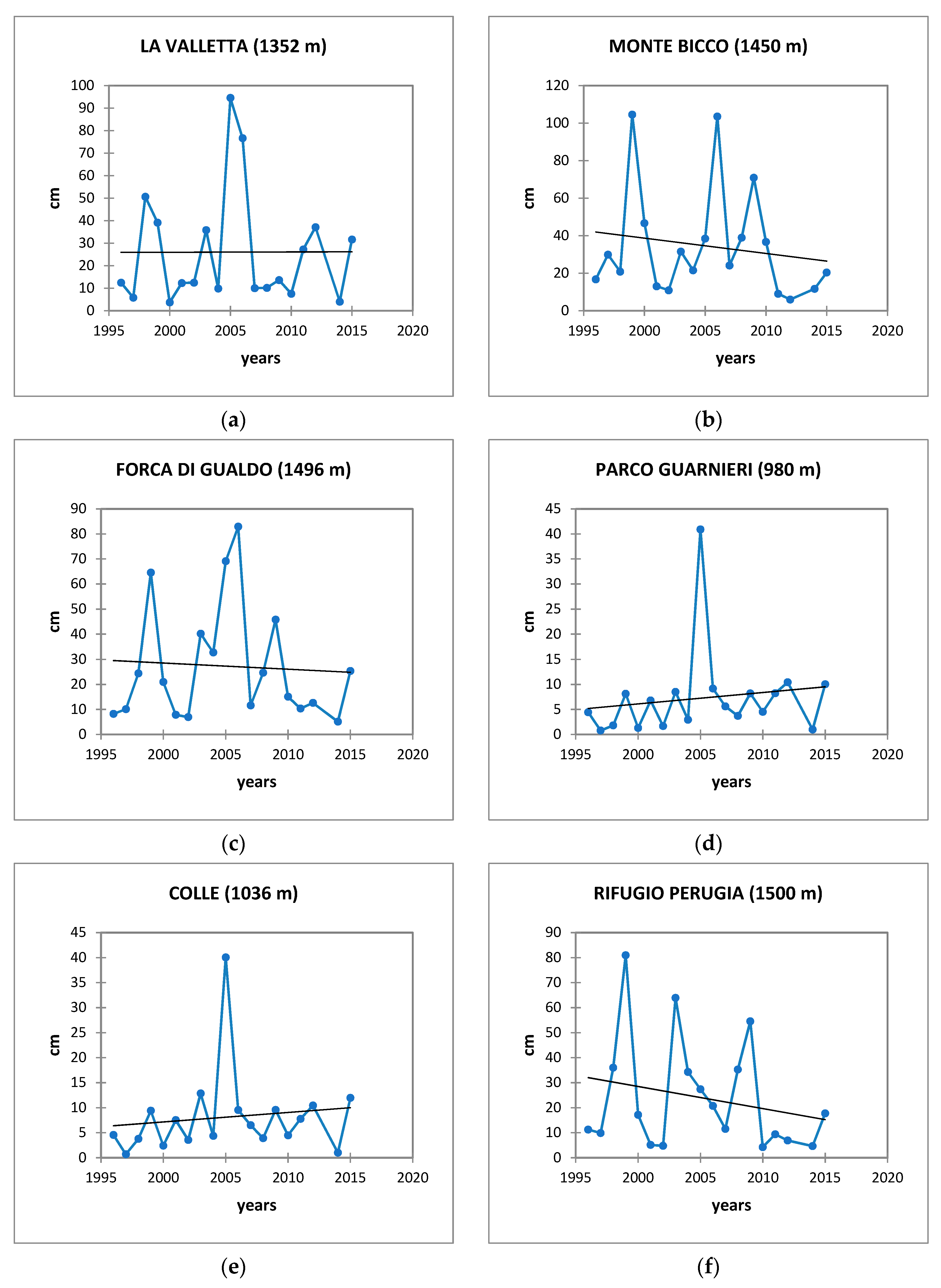


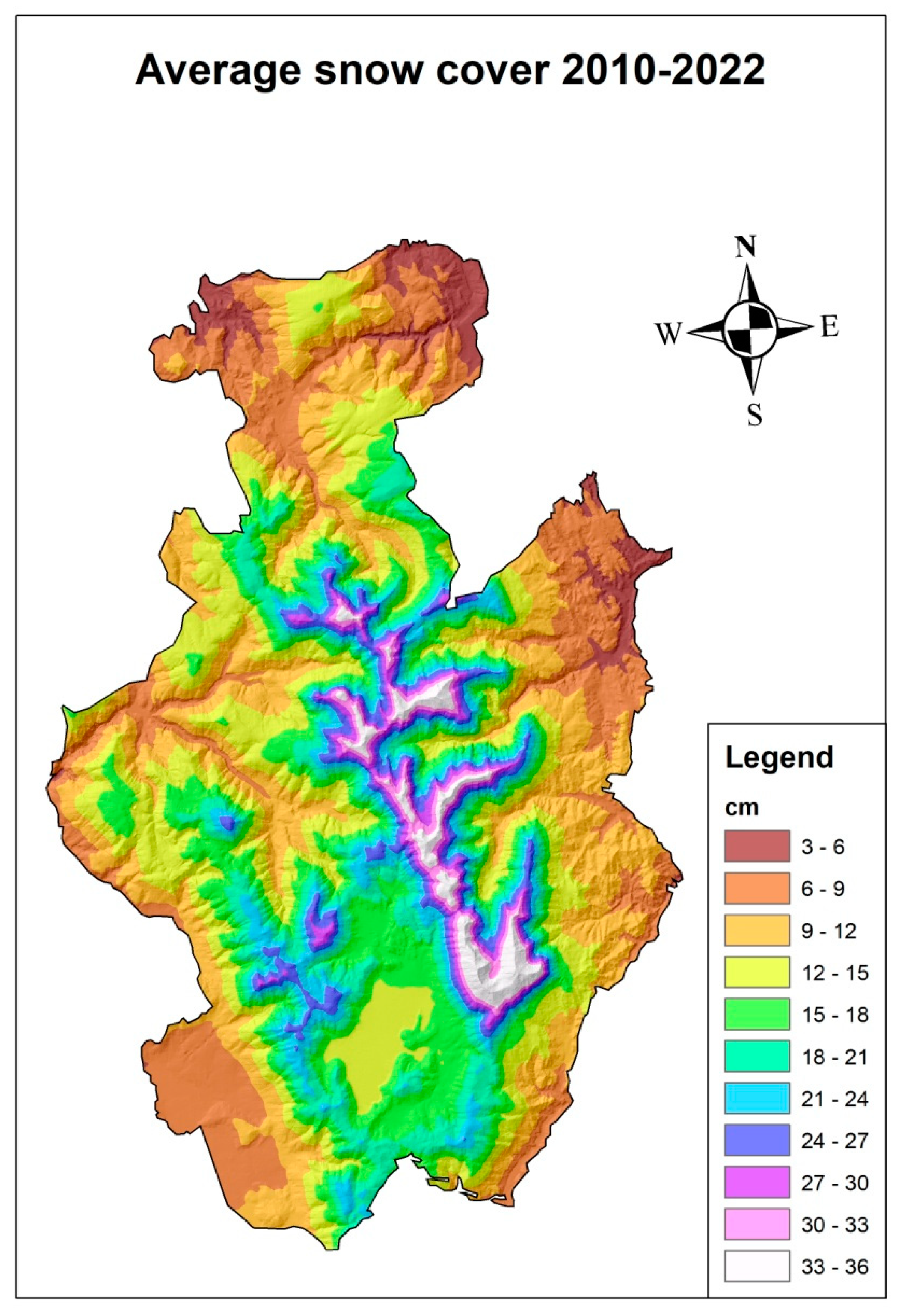

| Name | Alt. | Lon. | Lat. | 1991–2020 | 2010–2022 |
|---|---|---|---|---|---|
| Colle | 1036 | 13.30 | 42.84 | X | X |
| Forca di Gualdo | 1496 | 13.19 | 42.86 | X | X |
| La Valletta | 1352 | 13.24 | 42.99 | X | X |
| Monte Bicco | 1450 | 13.16 | 42.92 | X | X |
| Monte Bove | 1917 | 13.19 | 42.91 | X | |
| Monte Prata | 1813 | 13.21 | 42.87 | X | |
| Parco Guarnieri | 980 | 13.33 | 42.90 | X | X |
| Pintura di Bolognola | 1360 | 13.24 | 42.99 | X | |
| Rifugio Perugia | 1500 | 13.18 | 42.77 | X | X |
| Sassotetto | 1365 | 13.24 | 43.01 | X |
| Name | M. Prata | F. di Gualdo | M. Bove | M. Bicco | P. di Bolognola | La Valletta | Sassotetto | Rif. Perugia | P. Guarnieri | Colle |
|---|---|---|---|---|---|---|---|---|---|---|
| M. Prata | 1.00 | 0.53 | 0.83 | 0.80 | 0.17 | 0.00 | 0.14 | 0.55 | −0.06 | −0.05 |
| F. di Gualdo | 0.53 | 1.00 | 0.73 | 0.70 | 0.39 | 0.44 | 0.44 | 0.66 | 0.02 | 0.05 |
| M. Bove | 0.83 | 0.73 | 1.00 | 0.82 | 0.32 | 0.23 | 0.24 | 0.59 | −0.09 | −0.08 |
| M. Bicco | 0.80 | 0.70 | 0.82 | 1.00 | 0.00 | 0.01 | 0.11 | 0.24 | −0.32 | −0.34 |
| P. di Bolognola | 0.17 | 0.39 | 0.32 | 0.00 | 1.00 | 0.86 | 0.68 | 0.53 | 0.76 | 0.78 |
| La Valletta | 0.00 | 0.44 | 0.23 | 0.01 | 0.86 | 1.00 | 0.59 | 0.52 | 0.74 | 0.76 |
| Sassotetto | 0.14 | 0.44 | 0.24 | 0.11 | 0.68 | 0.59 | 1.00 | 0.26 | 0.41 | 0.45 |
| Rif. Perugia | 0.55 | 0.66 | 0.59 | 0.24 | 0.53 | 0.52 | 0.26 | 1.00 | 0.19 | 0.25 |
| P. Guarnieri | −0.06 | 0.02 | −0.09 | −0.32 | 0.76 | 0.74 | 0.41 | 0.19 | 1.00 | 0.96 |
| Colle | −0.05 | 0.05 | −0.08 | −0.34 | 0.78 | 0.76 | 0.45 | 0.25 | 0.96 | 1.00 |
| Name | M. Prata | F. di Gualdo | M. Bove | M. Bicco | P. di Bolognola | La Valletta | Sassotetto | Rif. Perugia | P. Guarnieri | Colle |
|---|---|---|---|---|---|---|---|---|---|---|
| M. Prata | 1.00 | 0.33 | 0.62 | 0.61 | 0.16 | 0.02 | 0.21 | 0.31 | 0.04 | 0.00 |
| F. di Gualdo | 0.33 | 1.00 | 0.52 | 0.51 | 0.29 | 0.38 | 0.32 | 0.41 | 0.11 | 0.12 |
| M. Bove | 0.62 | 0.52 | 1.00 | 0.63 | 0.26 | 0.19 | 0.32 | 0.34 | −0.05 | −0.05 |
| M. Bicco | 0.61 | 0.51 | 0.63 | 1.00 | 0.08 | 0.09 | 0.20 | 0.16 | −0.16 | −0.18 |
| P. di Bolognola | 0.16 | 0.29 | 0.26 | 0.08 | 1.00 | 0.64 | 0.67 | 0.35 | 0.51 | 0.55 |
| La Valletta | 0.02 | 0.38 | 0.19 | 0.09 | 0.64 | 1.00 | 0.67 | 0.36 | 0.45 | 0.50 |
| Sassotetto | 0.21 | 0.32 | 0.32 | 0.20 | 0.67 | 0.67 | 1.00 | 0.34 | 0.45 | 0.48 |
| Rif. Perugia | 0.31 | 0.41 | 0.34 | 0.16 | 0.35 | 0.36 | 0.34 | 1.00 | 0.13 | 0.20 |
| P. Guarnieri | 0.04 | 0.11 | −0.05 | −0.16 | 0.51 | 0.45 | 0.45 | 0.13 | 1.00 | 0.80 |
| Colle | 0.00 | 0.12 | −0.05 | −0.18 | 0.55 | 0.50 | 0.48 | 0.20 | 0.80 | 1.00 |
| Statistical Index | Average Snow Cover | Maximum Snow Cover | Days with Snow Cover on the Ground |
|---|---|---|---|
| ASE (cm) | 12.09 | 24.76 | 21.46 |
| MSE | 0.32 | 0.25 | 0.27 |
| RMSE (cm) | 8.98 | 23.17 | 21.04 |
| RMSSE | 0.85 | 0.98 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gentilucci, M.; Catorci, A.; Panichella, T.; Moscatelli, S.; Hamed, Y.; Missaoui, R.; Pambianchi, G. Analysis of Snow Cover in the Sibillini Mountains in Central Italy. Climate 2023, 11, 72. https://doi.org/10.3390/cli11030072
Gentilucci M, Catorci A, Panichella T, Moscatelli S, Hamed Y, Missaoui R, Pambianchi G. Analysis of Snow Cover in the Sibillini Mountains in Central Italy. Climate. 2023; 11(3):72. https://doi.org/10.3390/cli11030072
Chicago/Turabian StyleGentilucci, Matteo, Andrea Catorci, Tiziana Panichella, Sara Moscatelli, Younes Hamed, Rim Missaoui, and Gilberto Pambianchi. 2023. "Analysis of Snow Cover in the Sibillini Mountains in Central Italy" Climate 11, no. 3: 72. https://doi.org/10.3390/cli11030072
APA StyleGentilucci, M., Catorci, A., Panichella, T., Moscatelli, S., Hamed, Y., Missaoui, R., & Pambianchi, G. (2023). Analysis of Snow Cover in the Sibillini Mountains in Central Italy. Climate, 11(3), 72. https://doi.org/10.3390/cli11030072









