A Weather-Pattern-Based Evaluation of the Performance of CMIP5 Models over Mexico
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. CMIP5 Output and Reference Data
2.3. Weather Pattern Identification
2.4. Evaluation Method
3. Results
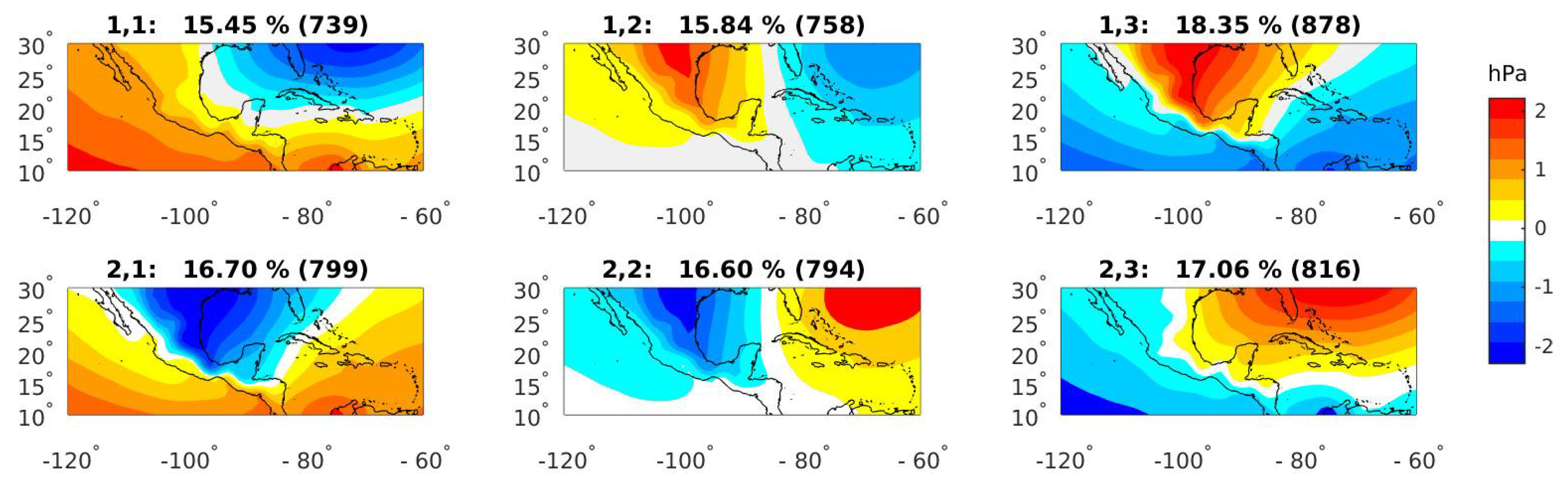
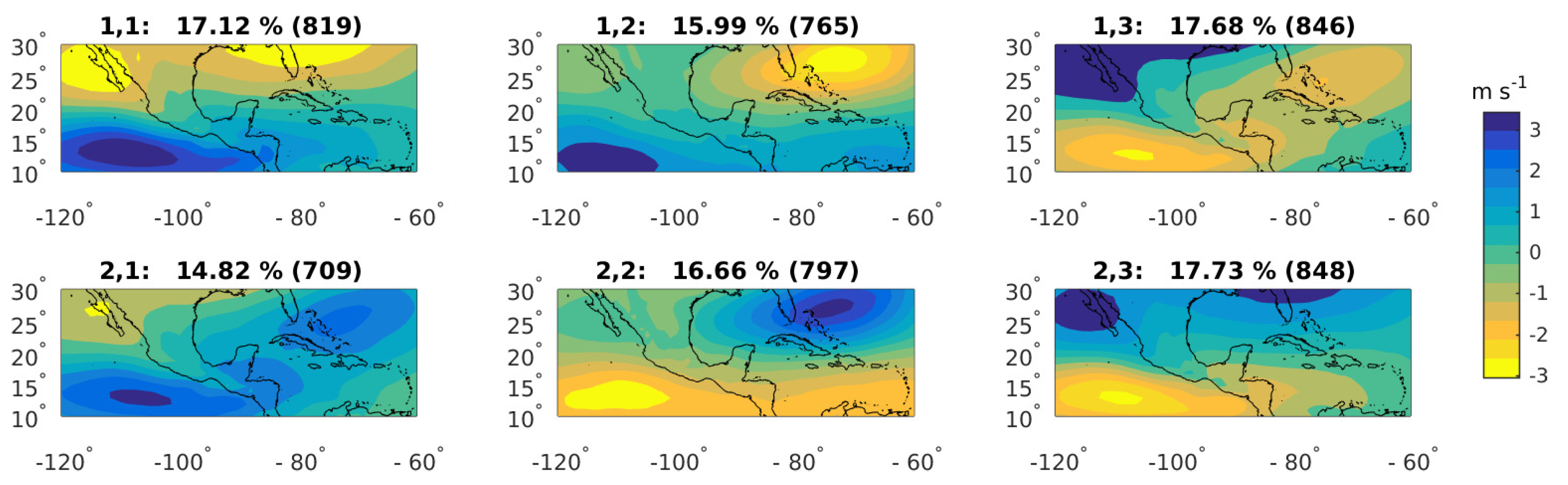
3.1. Weather Patterns from ERA-Interim
3.2. Comparison between CMIP5 and ERA-Interim Patterns
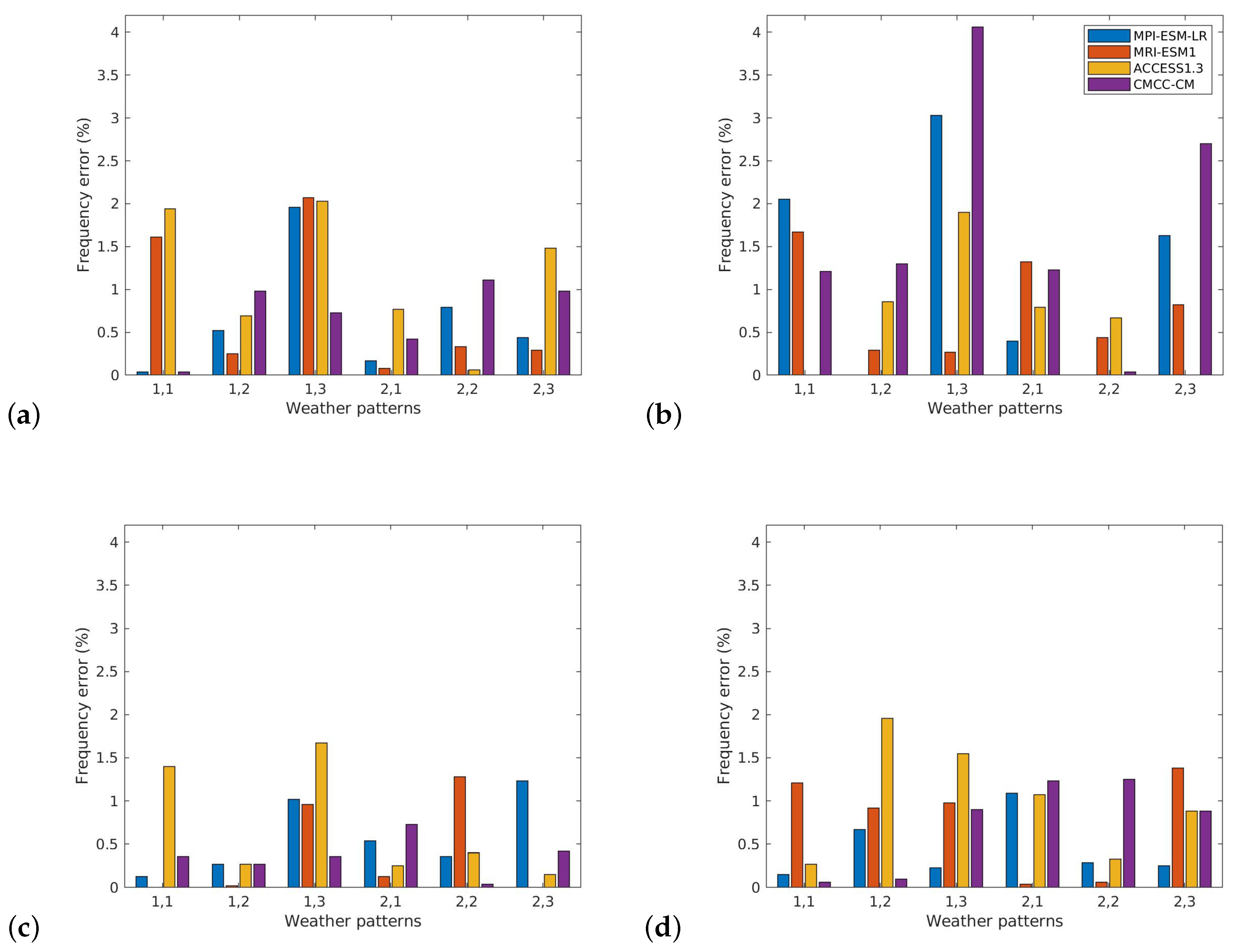
3.3. Comparison between Frequencies of Occurrence
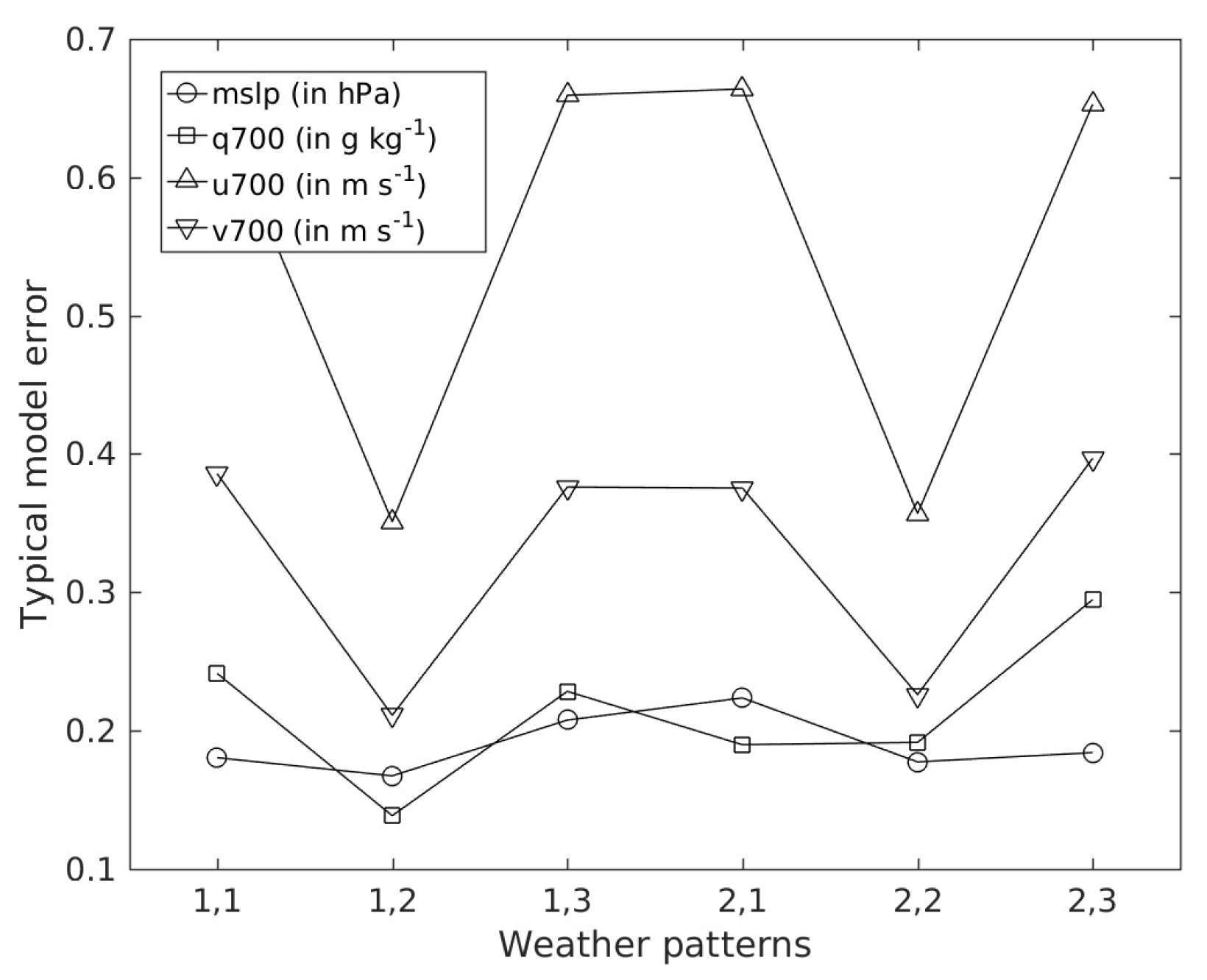
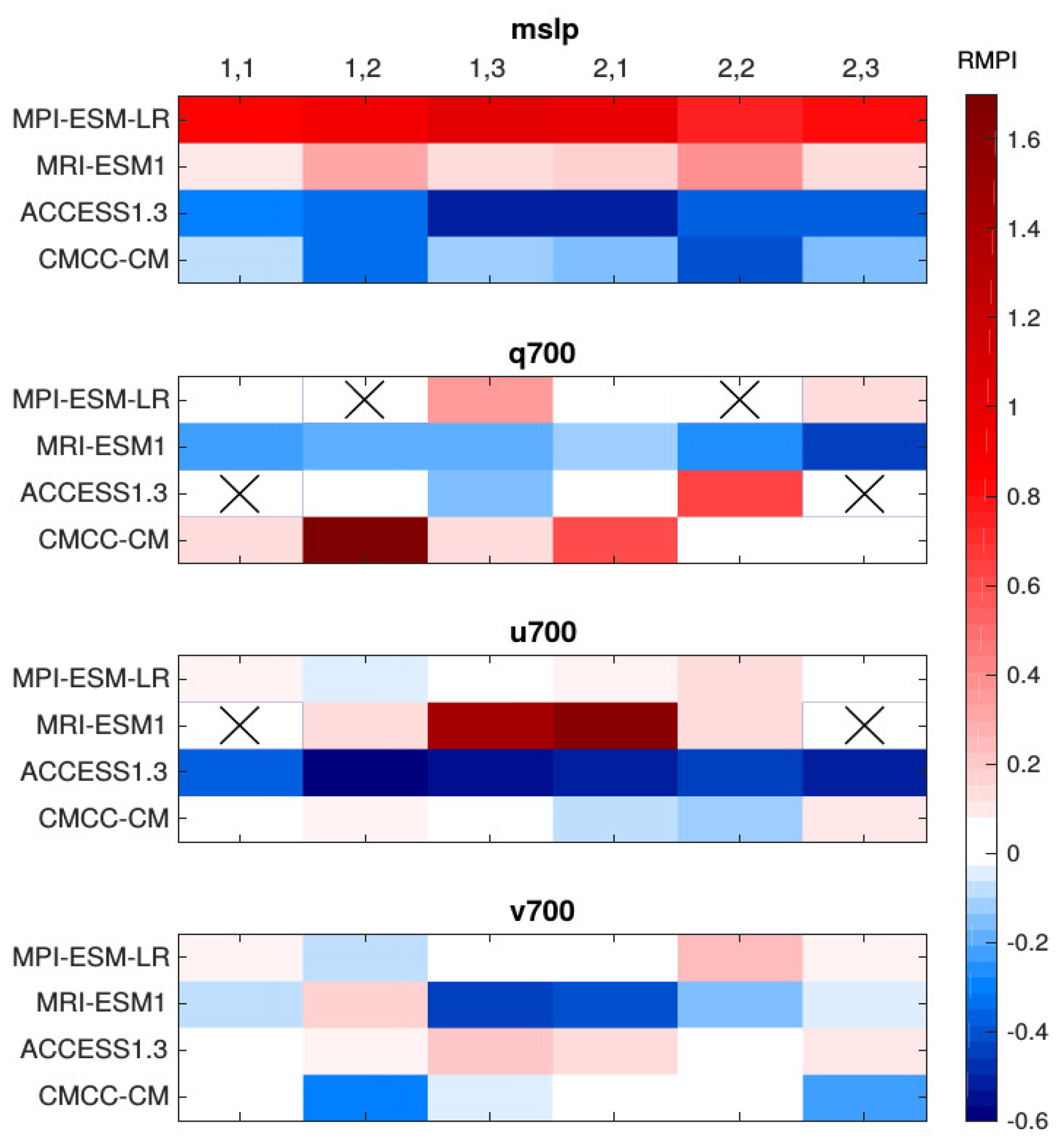
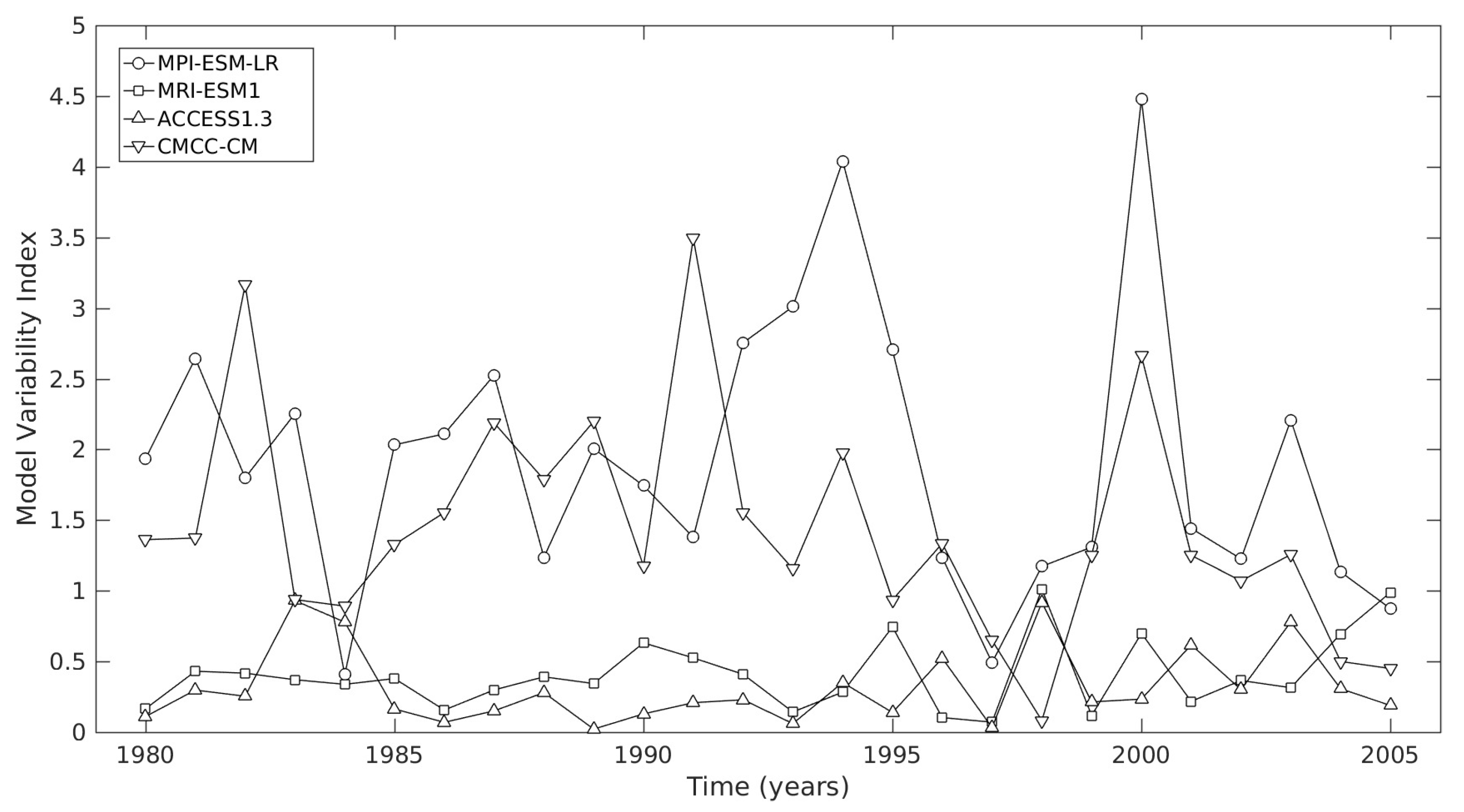
3.4. Characterization of Model Performance
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Chapter Evaluation of Climate Models; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 485–498. [Google Scholar] [CrossRef]
- Kim, H.; Webster, P.; Curry, J. Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys. Res. Lett. 2012, 39, L10701. [Google Scholar] [CrossRef]
- Knutti, R.; Sedláček, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Chang. 2013, 3, 369–373. [Google Scholar] [CrossRef]
- Neelin, J.; Langenbrunner, B.; Meyerson, J.; Hall, A.; Berg, N. California winter precipitation change under global warming in the coupled model intercomparison project phase 5 ensemble. J. Clim. 2013, 26. [Google Scholar] [CrossRef]
- Polade, S.; Gershunov, A.; Cayan, D.; Dettinger, M.; Pierce, D. Natural climate variability and teleconnections to precipitation over the Pacific-North American region in CMIP3 and CMIP5 models. Geophys. Res. Lett. 2013, 40, 2296–2301. [Google Scholar] [CrossRef]
- Zappa, G.; Shaffrey, L.; Hodges, K. The Ability of CMIP5 Models to Simulate North Atlantic Extratropical Cyclones. J. Clim. 2013, 26, 5379–5396. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble:Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Maloney, E.D.; Camargo, S.J.; Chang, E.; Colle, B.; Fu, R.; Geil, K.L.; Hu, Q.; Jiang, X.; Johnson, N.; Karnauskas, K.B.; et al. North American Climate in CMIP5 Experiments: Part III: Assessment of Twenty-First-Century Projections. J. Clim. 2014, 27, 2230–2270. [Google Scholar] [CrossRef]
- Thibeault, J.; Seth, A. A Framework for Evaluating Model Credibility for Warm-Season Precipitation in Northeastern North America: A Case Study of CMIP5 Simulations and Projections. J. Clim. 2014, 27, 493–510. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A.; Phillips, T. Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations. J. Geophys. Res. Atmos. 2014, 119, 1695–1707. [Google Scholar] [CrossRef]
- Grainger, S.; Frederiksen, C.S.; Zheng, X. Assessment of Modes of Interannual Variability of Southern Hemisphere Atmospheric Circulation in CMIP5 Models. J. Clim. 2014, 27, 8107–8125. [Google Scholar] [CrossRef]
- Elguindi, N.; Giorgi, F.; Turuncoglu, U. Assessment of CMIP5 global model simulations over the subset of CORDEX domains used in the Phase I CREMA. Clim. Chang. 2014, 125, 7–21. [Google Scholar] [CrossRef]
- Elguindi, N.; Grundstein, A.; Bernardes, S.; Turuncoglu, U.; Feddema, J. Assessment of CMIP5 global model simulations and climate change projections for the 21st century using a modified Thornthwaite climate classification. Clim. Chang. 2014, 122, 523–538. [Google Scholar] [CrossRef]
- Stanfield, R.E.; Dong, X.; Xi, B.; Kennedy, A.; Del Genio, A.; Minnins, P.; Jiang, J.H. Assessment of NASA GISS CMIP5 and Post-CMIP5 Simulated Clouds and TOA Radiation Budgets Using Satellite Observations. Part I: Cloud Fraction and Properties. J. Clim. 2014, 27, 4189–4208. [Google Scholar] [CrossRef]
- Stanfield, R.E.; Dong, X.; Xi, B.; Del Genio, A.; Minnis, P.; Doelling, D.; Loeb, N. Assessment of NASA GISS CMIP5 and Post-CMIP5 Simulated Clouds and TOA Radiation Budgets Using Satellite Observations. Part II: TOA Radiation Budget and CREs. J. Clim. 2015, 28, 1842–1864. [Google Scholar] [CrossRef]
- Koutroulis, A.; Grillakis, M.G.; Tsanis, I.K.; Papadimitriou, L. Evaluation of precipitation and temperature simulation performance of the CMIP3 and CMIP5 historical experiments. Clim.Dyn. 2016, 47, 1881–1898. [Google Scholar] [CrossRef]
- Ning, L.; Bradley, R.S. NAO and PNA influences on winter temperature and precipitation over the eastern United States in CMIP5 GCMs. Clim. Dyn. 2016, 46, 1257–1276. [Google Scholar] [CrossRef]
- Masato, G.; Woollings, T.; Williams, P.; Hoskins, B.; Lee, R. A regime analysis of Atlantic winter jet variability applied to evaluate HadGEM3-GC2. Q. J. R. Meteorol. Soc. 2016, 142, 3162–3170. [Google Scholar] [CrossRef]
- Parsons, L.; Loope, G.; Overpeck, J.; Ault, T.; Stouffer, R.; Cole, J. Temperature and Precipitation Variance in CMIP5 Simulations and Paleoclimate Records of the Last Millennium. J. Clim. 2017, 30, 8885–8912. [Google Scholar] [CrossRef]
- Sheffield, J.; Barrett, A.P.; Colle, B.; Nelun Fernando, D.; Fu, R.; Geil, K.L.; Hu, Q.; Kinter, J.; Kumar, S.; Langenbrunner, B. North American Climate in CMIP5 Experiments. Part I: Evaluation of Historical Simulations of Continental and Regional Climatology. J. Clim. 2013, 26, 9209–9245. [Google Scholar] [CrossRef]
- Carvalho, L.; Jones, C. CMIP5 Simulations of Low-Level Tropospheric Temperature and Moisture over the Tropical Americas. J. Clim. 2013, 26, 6257–6286. [Google Scholar] [CrossRef]
- Stanfield, R.E.; Jiang, J.H.; Dong, X.; Xi, B.; Su, H.; Donner, L.; Rotstayn, L.; Wu, T.; Cole, J.; Shindo, E. A quantitative assessment of precipitation associated with the ITCZ in the CMIP5 GCM simulations. Clim. Dyn. 2016, 47, 1863–1880. [Google Scholar] [CrossRef]
- Grose, M.R.; Brown, J.N.; Narsey, S.; Brown, J.R.; Murphy, B.F.; Langlais, C.; Sen Gupta, A.; Moise, A.F.; Irving, D.B. Assessment of the CMIP5 global climate model simulations of the western tropical Pacific climate system and comparison to CMIP3. Int. J. Climatol. 2014, 34, 3382–3399. [Google Scholar] [CrossRef]
- Sheffield, J.; Camargo, S.J.; Fu, R.; Hu, Q.; Jiang, X.; Johnson, N.; Karnauskas, K.B.; Kim, S.T.; Kinter, J.; Kumar, S.; et al. North American Climate in CMIP5 Experiments. Part II: Evaluation of Historical Simulations of Intraseasonal to Decadal Variability. J. Clim. 2013, 26, 9247–9290. [Google Scholar] [CrossRef]
- Langenbrunner, B.; Neelin, J. Analyzing ENSO teleconnections in CMIP models as a measure of model fidelity in simulating precipitation. J. Clim. 2013, 26, 4431–4446. [Google Scholar] [CrossRef]
- Geil, K.L.; Serra, Y.L.; Zeng, X. Assessment of CMIP5 Model Simulations of the North American Monsoon System. J. Clim. 2013, 26, 8787–8801. [Google Scholar] [CrossRef]
- Hidalgo, H.; Alfaro, E. Skill of CMIP5 climate models in reproducing 20th century basic climate features in Central America. Int. J. Climatol. 2015, 35, 3397–3421. [Google Scholar] [CrossRef]
- Simon Wang, S.Y.; Huang, W.R.; Yoon, J.H. The North American winter ‘dipole’ and extremes activity: A CMIP5 assessment. Atmos. Sci. Lett. 2015, 16, 338–345. [Google Scholar] [CrossRef]
- Fuentes-Franco, R.; Giorgi, F.; Coppola, E.; Kucharski, F. The role of ENSO and PDO in variability of winter precipitation over North America from twenty first century CMIP5 projections. Clima. Dyn. 2016, 46, 3259–3277. [Google Scholar] [CrossRef]
- Nigro, M.; Cassano, J.; Seefeldt, M. A Weather-Pattern-Based Approach to Evaluate the Antarctic Mesoscale Prediction System (AMPS) Forecasts: Comparison to Automatic Weather Station Observations. Weather Forecast. 2011, 26, 184–198. [Google Scholar] [CrossRef]
- Schuenemann, K.; Cassano, J. Changes in synoptic weather patterns and Greenland precipitation in the 20th and 21st centuries: 1. Evaluation of late 20th century simulations from IPCC models. J. Geophys. Res. 2009, 114, D20113. [Google Scholar] [CrossRef]
- Finnis, J.; Cassano, J.; Holland, M.; Serrezed, M.; Uotila, P. Synoptically forced hydroclimatology of major Arctic watersheds in general circulation models; Part 1: The Mackenzie River Basin. Int. J. Climatol. 2009, 29, 1226–1243. [Google Scholar] [CrossRef]
- Radić, V.; Clarke, G. Evaluation of IPCC Models’ Performance in Simulating Late-Twentieth-Century Climatologies and Weather Patterns over North America. J. Clim. 2011, 24, 5257–5274. [Google Scholar] [CrossRef]
- Perez, J.; Menendez, M.; Mendez, F.J.; Losada, I.J. Evaluating the performance of CMIP3 and CMIP5 global climate models over the north-east Atlantic region. Clim. Dyn. 2014, 43, 2663–2680. [Google Scholar] [CrossRef]
- Muñoz, A.G.; Yang, X.; Vecchi, G.A.; Robertson, A.W.; Cooke, W.F. A Weather-Type-Based Cross-Time-Scale Diagnostic Framework for Coupled Circulation Models. J. Clim. 2017, 30, 8951–8972. [Google Scholar] [CrossRef]
- Frederiksen, C.S.; Ying, K.; Grainger, S.; Zheng, X. Modes of interannual variability in northern hemisphere winter atmospheric circulation in CMIP5 models: Evaluation, projection and role of external forcing. Clim. Dyn. 2018, 1–21. [Google Scholar] [CrossRef]
- Brigode, P.; Gérardin, M.; Bernardara, P.; Gailhard, J.; Ribstein, P. Changes in French weather pattern seasonal frequencies projected by a CMIP5 ensemble. Int. J. Climatol. 2018, 38, 3991–4006. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.; Kennedy, A.; Hagenhoff, B.; Xi, B. A Regime-Based Evaluation of Southern and Northern Great Plains Warm-Season Precipitation Events in WRF. Weather Forecast. 2019, 34, 805–831. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Díaz-Esteban, Y.; Raga, G. Weather regimes associated with summer rainfall variability over southern Mexico. Int. J. Climatol. 2018, 38, 169–186. [Google Scholar] [CrossRef]
- Méndez, M.; Magaña, V. Regional aspects of prolonged meteorological droughts over Mexico and Central America. J. Clim. 2010, 23, 1175–1188. [Google Scholar] [CrossRef]
- Curtis, S. Daily precipitation distributions over the intra-Americas seas and their inter-annual variability. Atmósfera 2013, 26, 243–259. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Glecker, P.; Taylor, K.; Doutriaux, C. Performance metrics for climate models. J. Geophys. Res. 2008, 113, L06711. [Google Scholar] [CrossRef]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Elghazel, H.; Benabdeslem, K. Different aspects of clustering the self-organizing maps. Neural Process. Lett. 2014, 39, 97–114. [Google Scholar] [CrossRef]
- Romero-Centeno, R.; Zavala-Hidalgo, J.; Raga, G.B. Midsummer Gap Winds and Low-Level Circulation over the Eastern Tropical Pacific. J. Clim. 2007, 20, 3768–3784. [Google Scholar] [CrossRef]
- Wang, C. Variability of the Caribbean low-level jet and itsrelations to climate. Clim. Dyn. 2007, 29, 411–422. [Google Scholar] [CrossRef]
- Wang, C.; Lee, S. Atlantic warm pool, Caribbean low-level jet, and their potential impact on Atlantic hurricanes. Geophys. Res. Lett. 2007, 34, L02703. [Google Scholar] [CrossRef]
- Colbert, A.J.; Soden, B.J. Climatological Variations in North Atlantic Tropical Cyclone Tracks. J. Clim. 2012, 25, 657–673. [Google Scholar] [CrossRef]
- Amador, J.A. The intra-Americas sea low-level jet, overview and future research. Ann. N. Y. Acad. Sci. 2008, 1146, 153–188. [Google Scholar] [CrossRef]
- Cook, K.H.; Vizy, E.K. Hydrodynamics of the Caribbean Low-Level Jet and Its Relationship to Precipitation. J. Clim. 2010, 23, 1477–1494. [Google Scholar] [CrossRef]
- Magaña, V.; Amador, J.; Medina, S. The midsummer drought over Mexico and Central America. J. Clim. 1999, 12, 1577–1588. [Google Scholar] [CrossRef]
- Muñoz, E.; Busalacchi, A.; Nigam, S.; Ruiz-Barradas, A. Winter and summer structure of the Caribbean low-level jet. J. Clim. 2008, 21, 1260–1276. [Google Scholar] [CrossRef]
- Whyte, F.; Taylor, M.; Stephenson, T.; Campbell, J. Features of the Caribbean low level jet. Int. J. Climatol. 2008, 28, 119–128. [Google Scholar] [CrossRef]
- Martin, E.R.; Schumacher, C. The Caribbean Low-Level Jet and Its Relationship with Precipitation in IPCC AR4 Models. J. Clim. 2011, 24, 5935–5950. [Google Scholar] [CrossRef]





| Model | Institution | Spatial Resolution (Lat × Lon) | Temporal Resolution |
|---|---|---|---|
| MPI-ESM-LR | Max Planck Institute for Meteorology | 1.87° × 1.88° | Daily |
| MRI-ESM1 | Meteorological Research Institute | 1.12° × 1.13° | Daily |
| ACCESS1.3 | CSIRO (Commonwealth Scientific and Industrial Research Organization, Australia), and BOM (Bureau of Meteorology, Australia) | 1.25° × 1.88° | Daily |
| CMCC-CM | Centro Euro-Mediterraneo per I Cambiamenti Climatici | 0.75° × 0.75° | Daily |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Esteban, Y.; Raga, G.B.; Díaz Rodríguez, O.O. A Weather-Pattern-Based Evaluation of the Performance of CMIP5 Models over Mexico. Climate 2020, 8, 5. https://doi.org/10.3390/cli8010005
Díaz-Esteban Y, Raga GB, Díaz Rodríguez OO. A Weather-Pattern-Based Evaluation of the Performance of CMIP5 Models over Mexico. Climate. 2020; 8(1):5. https://doi.org/10.3390/cli8010005
Chicago/Turabian StyleDíaz-Esteban, Yanet, Graciela B. Raga, and Oscar Onoe Díaz Rodríguez. 2020. "A Weather-Pattern-Based Evaluation of the Performance of CMIP5 Models over Mexico" Climate 8, no. 1: 5. https://doi.org/10.3390/cli8010005
APA StyleDíaz-Esteban, Y., Raga, G. B., & Díaz Rodríguez, O. O. (2020). A Weather-Pattern-Based Evaluation of the Performance of CMIP5 Models over Mexico. Climate, 8(1), 5. https://doi.org/10.3390/cli8010005





