An Extension Algorithm of Regional Eigenvalue Assignment Controller Design for Nonlinear Systems
Abstract
:1. Introduction
- 1.
- We extended the rEA that had been proposed for linear systems in [7] to the state-dependent rEA for controlling the “frozen” nonlinear systems.
- 2.
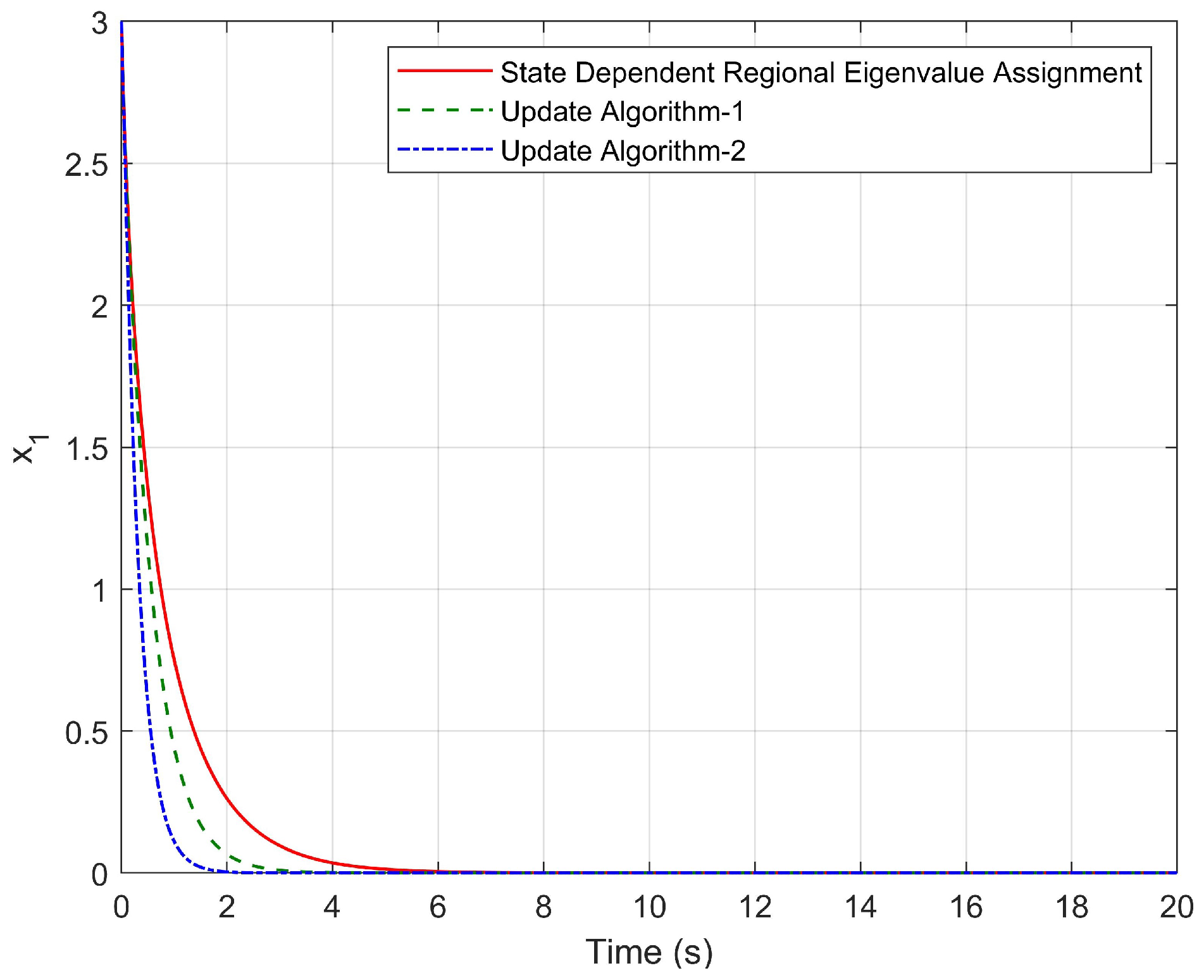
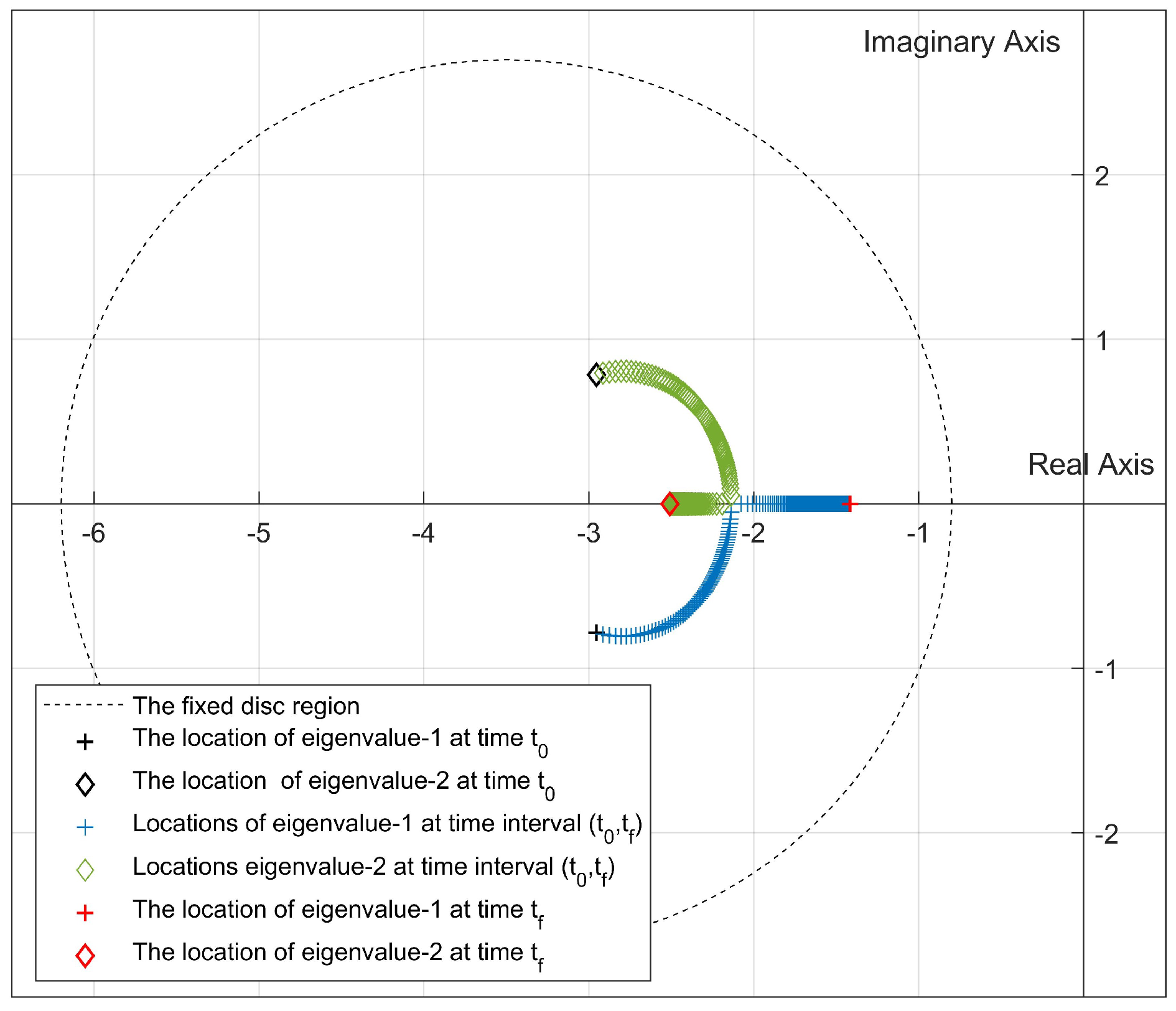
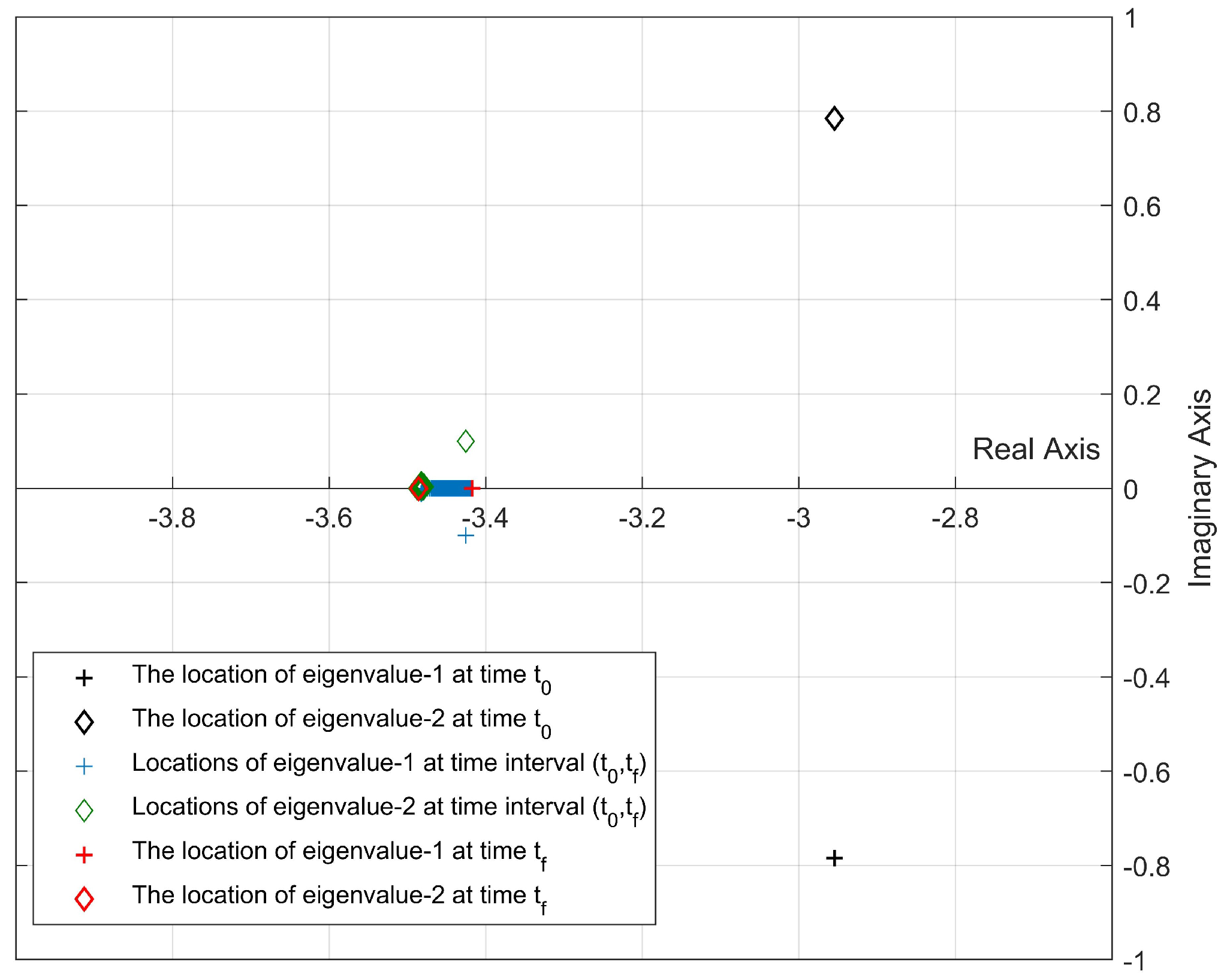
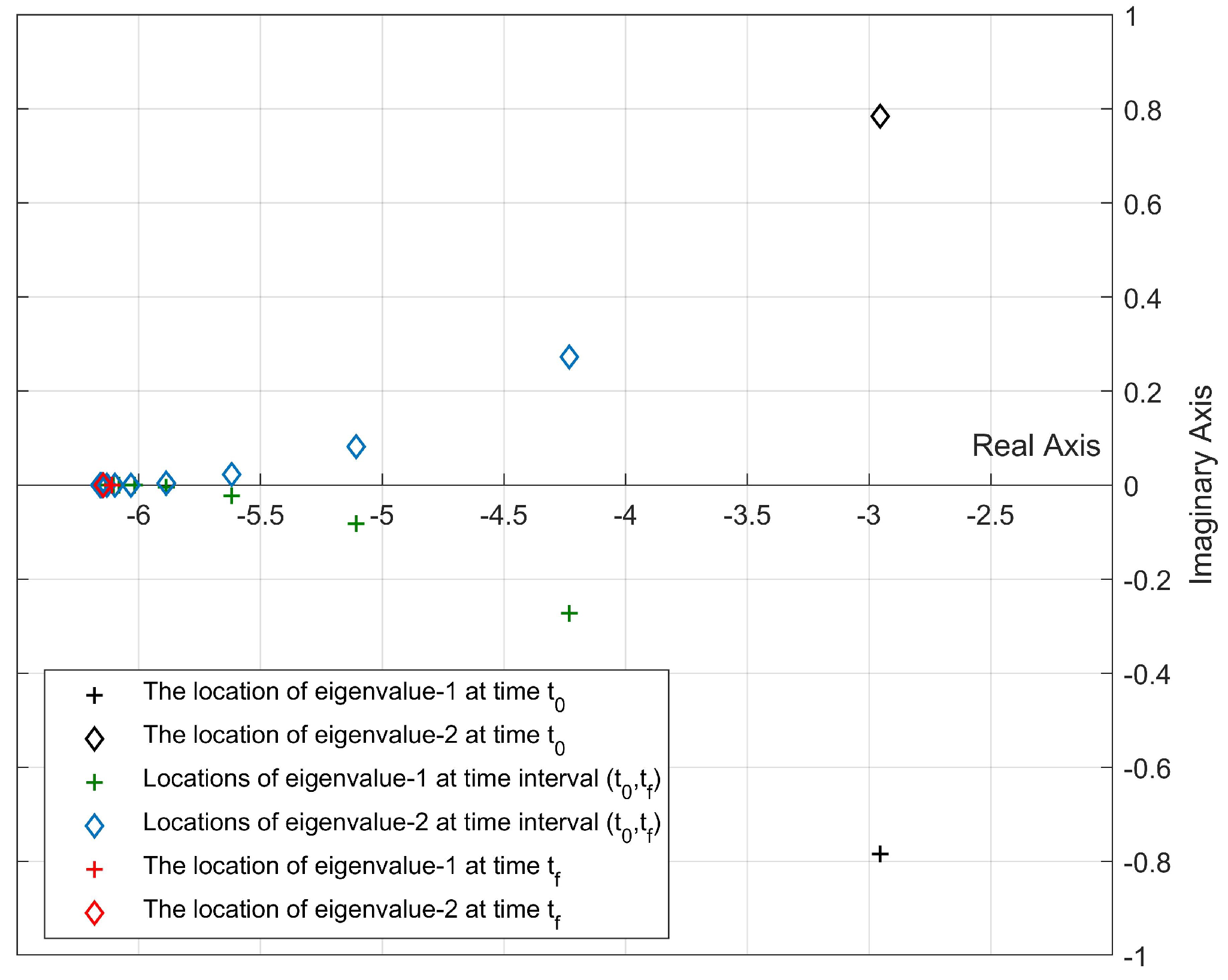
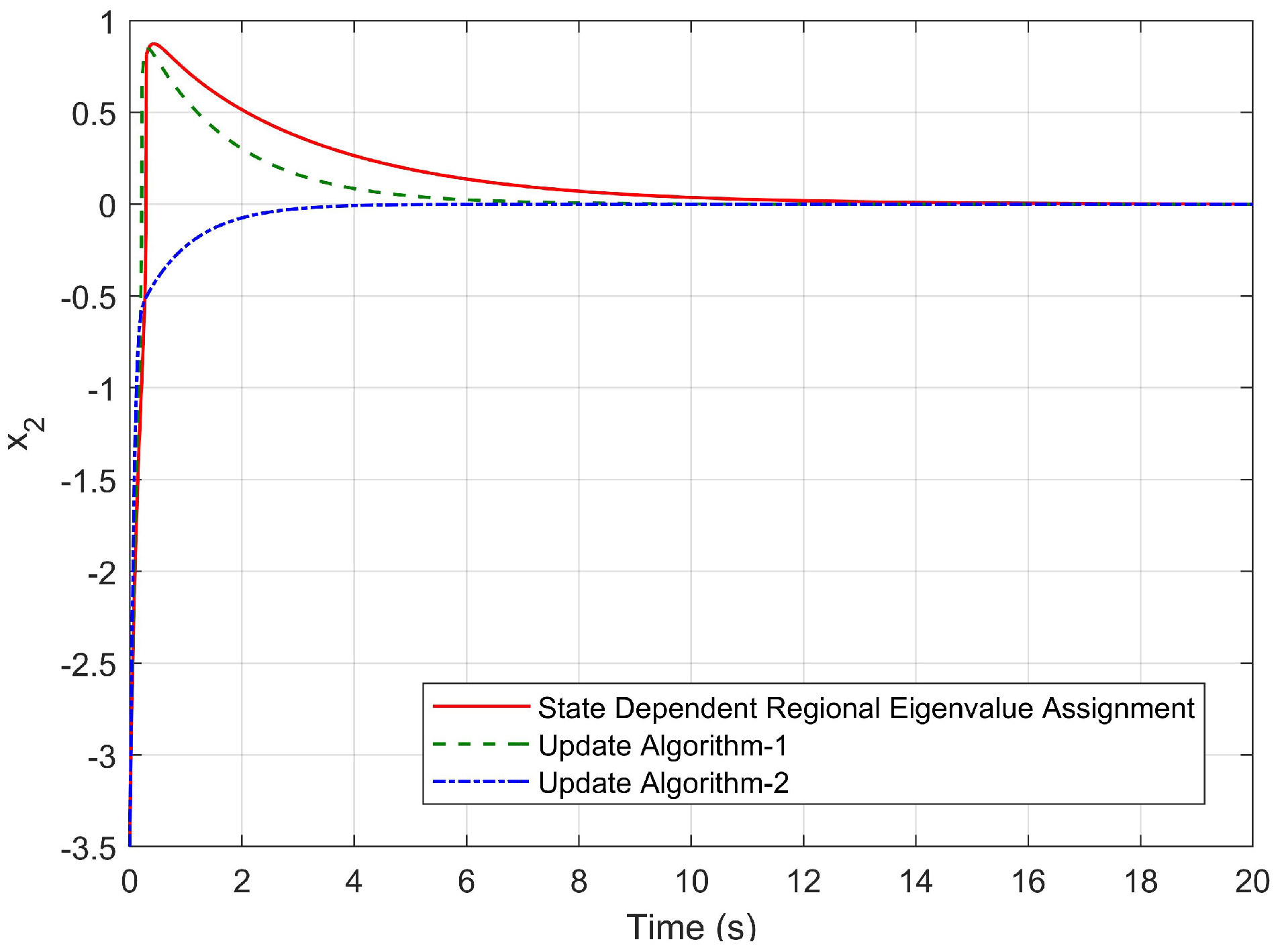
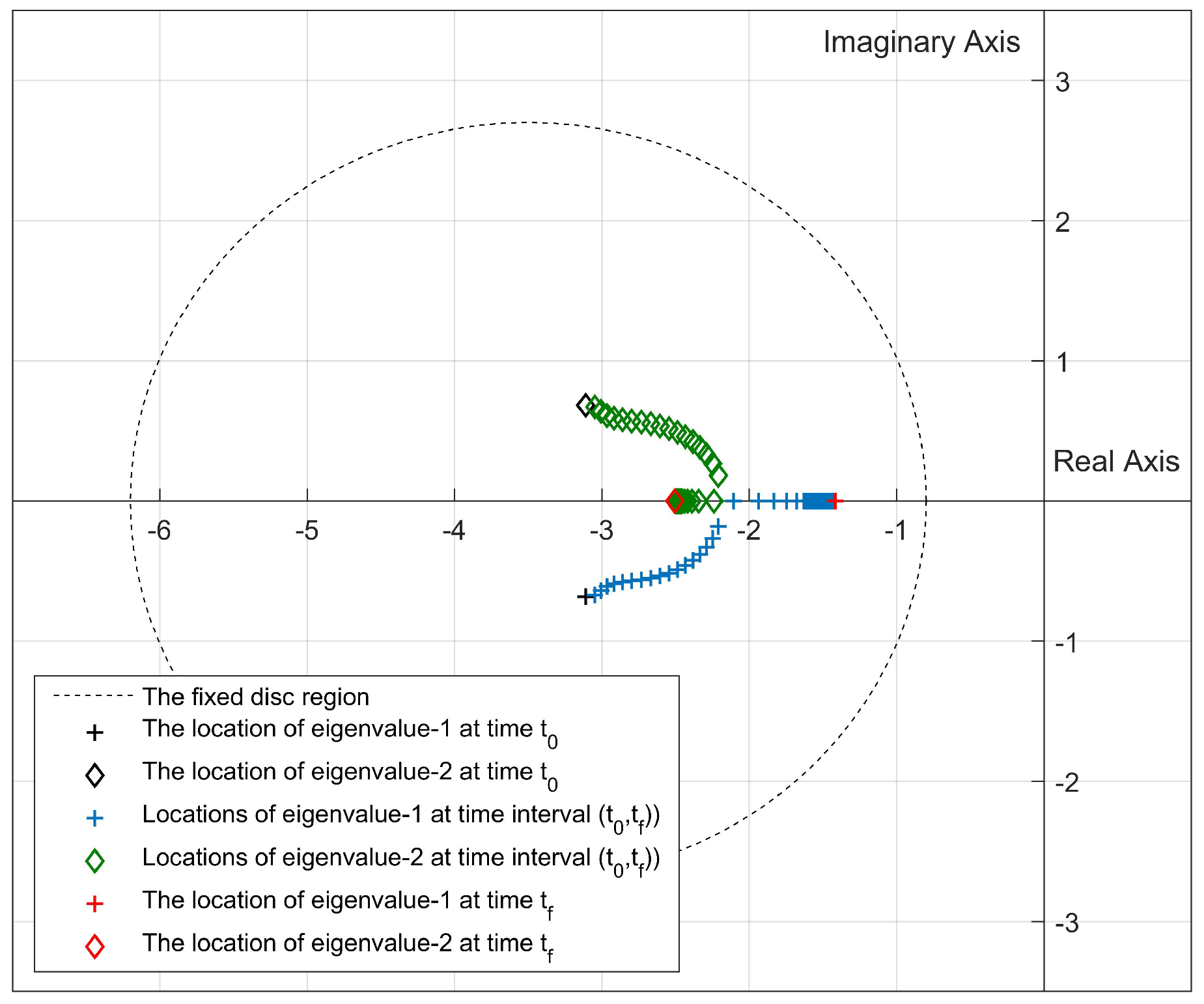
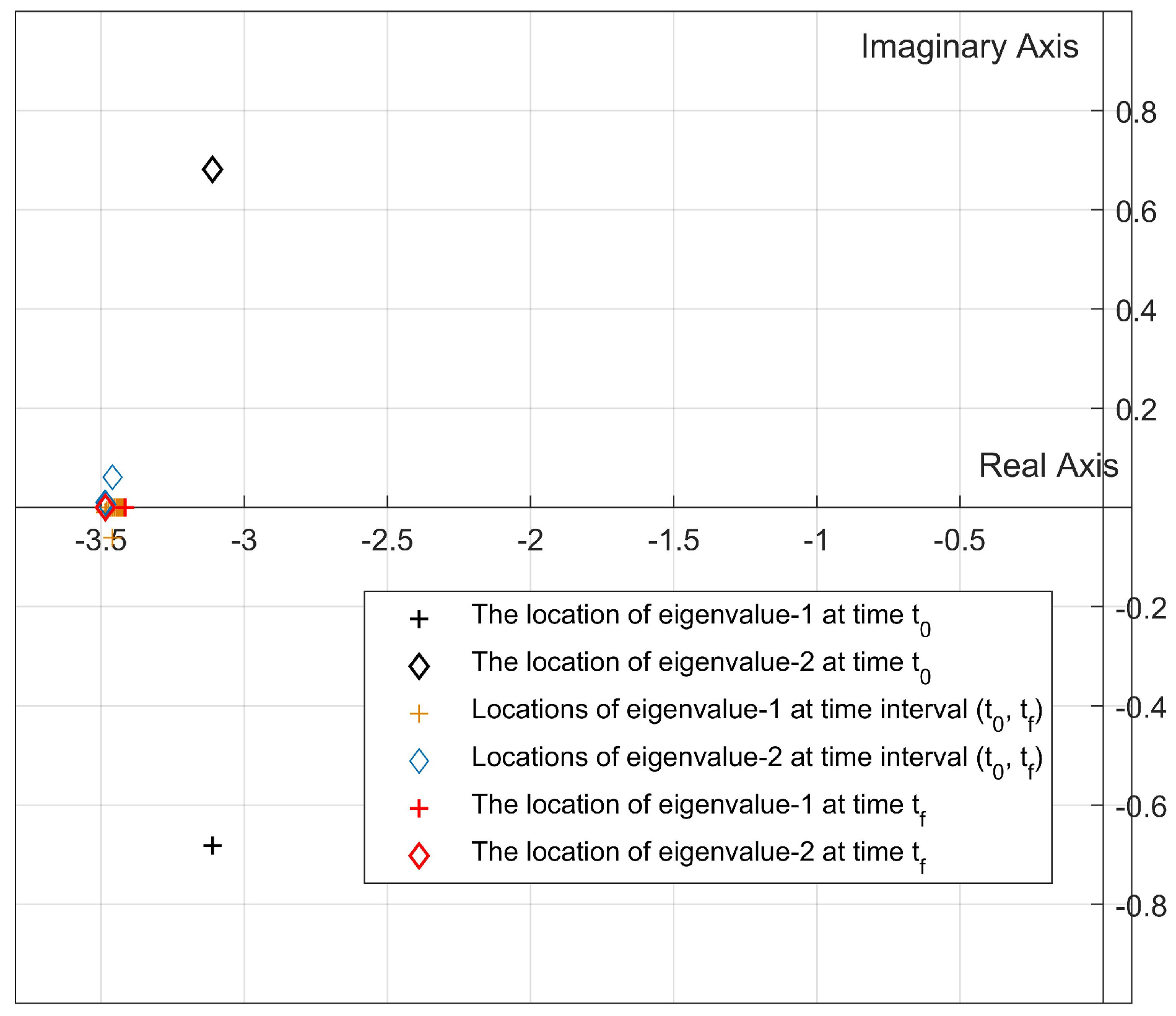
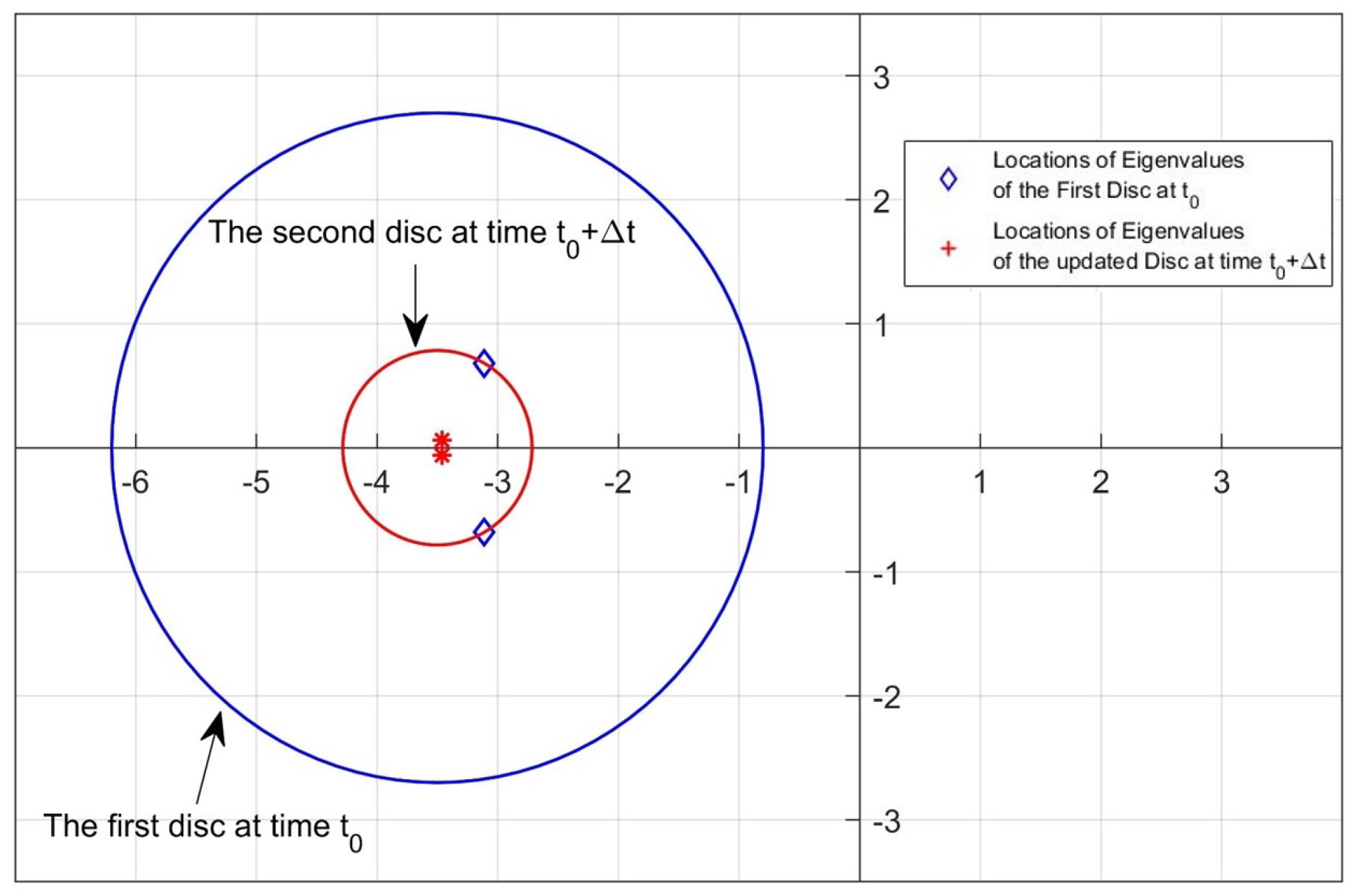
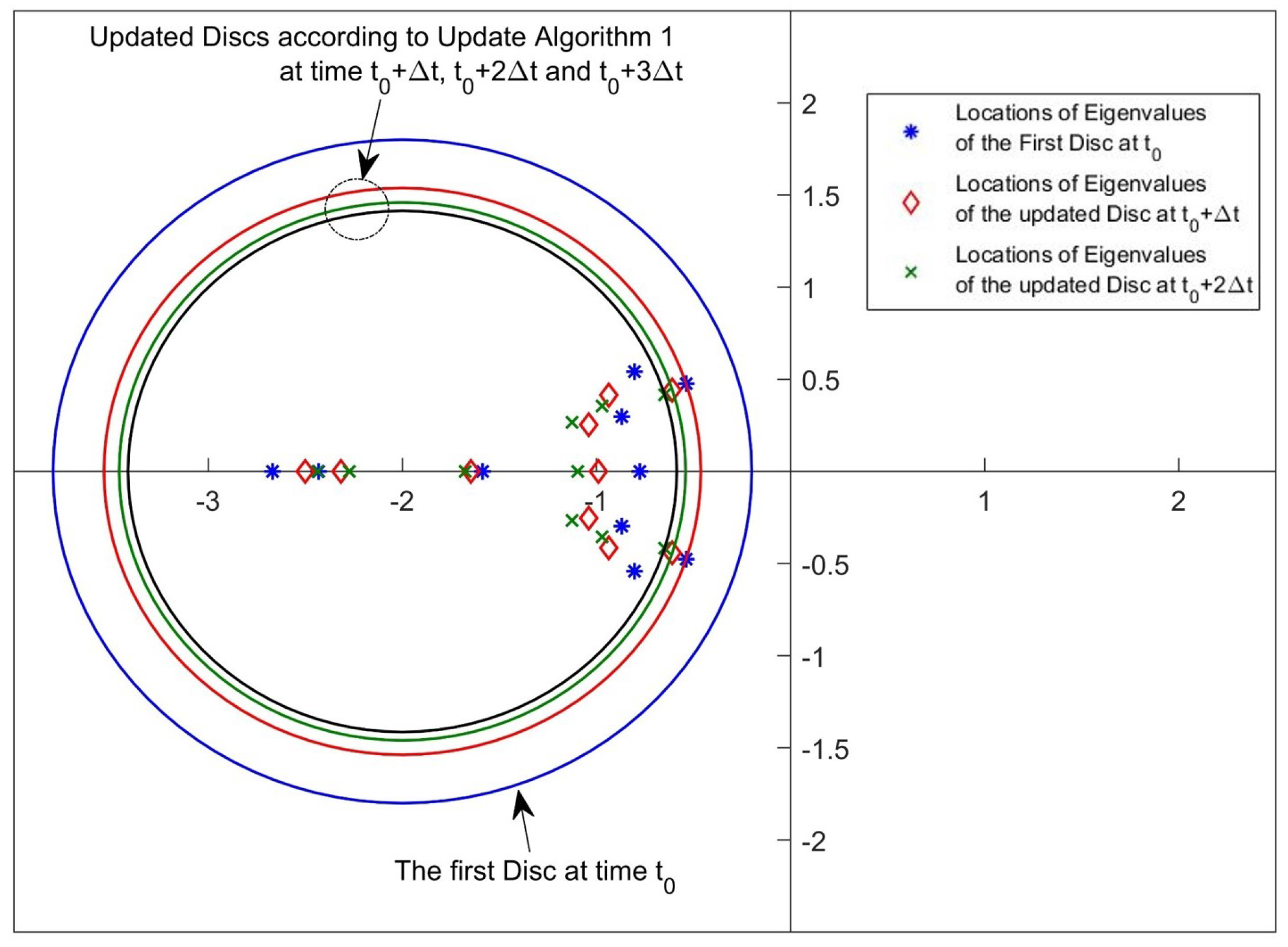
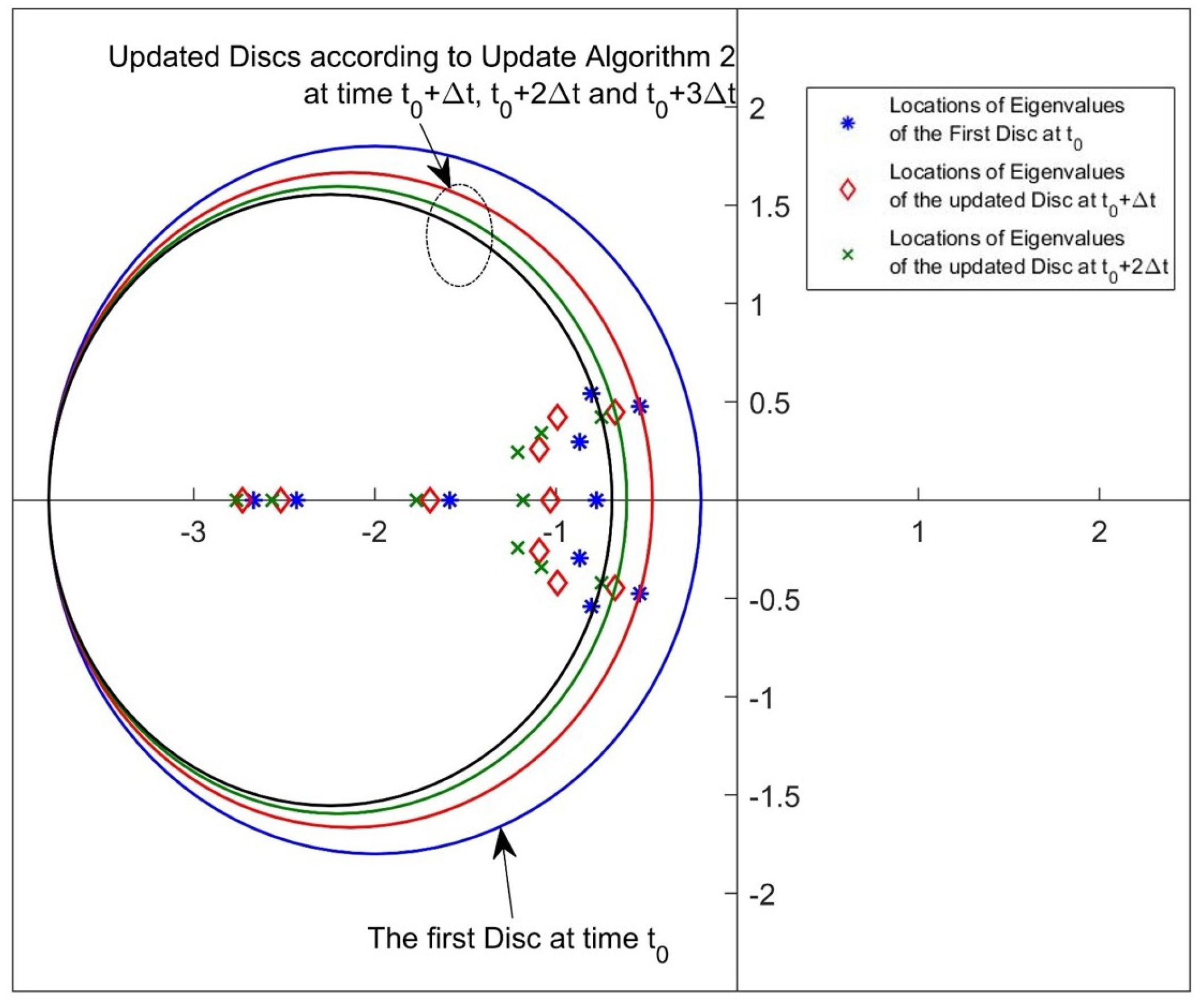
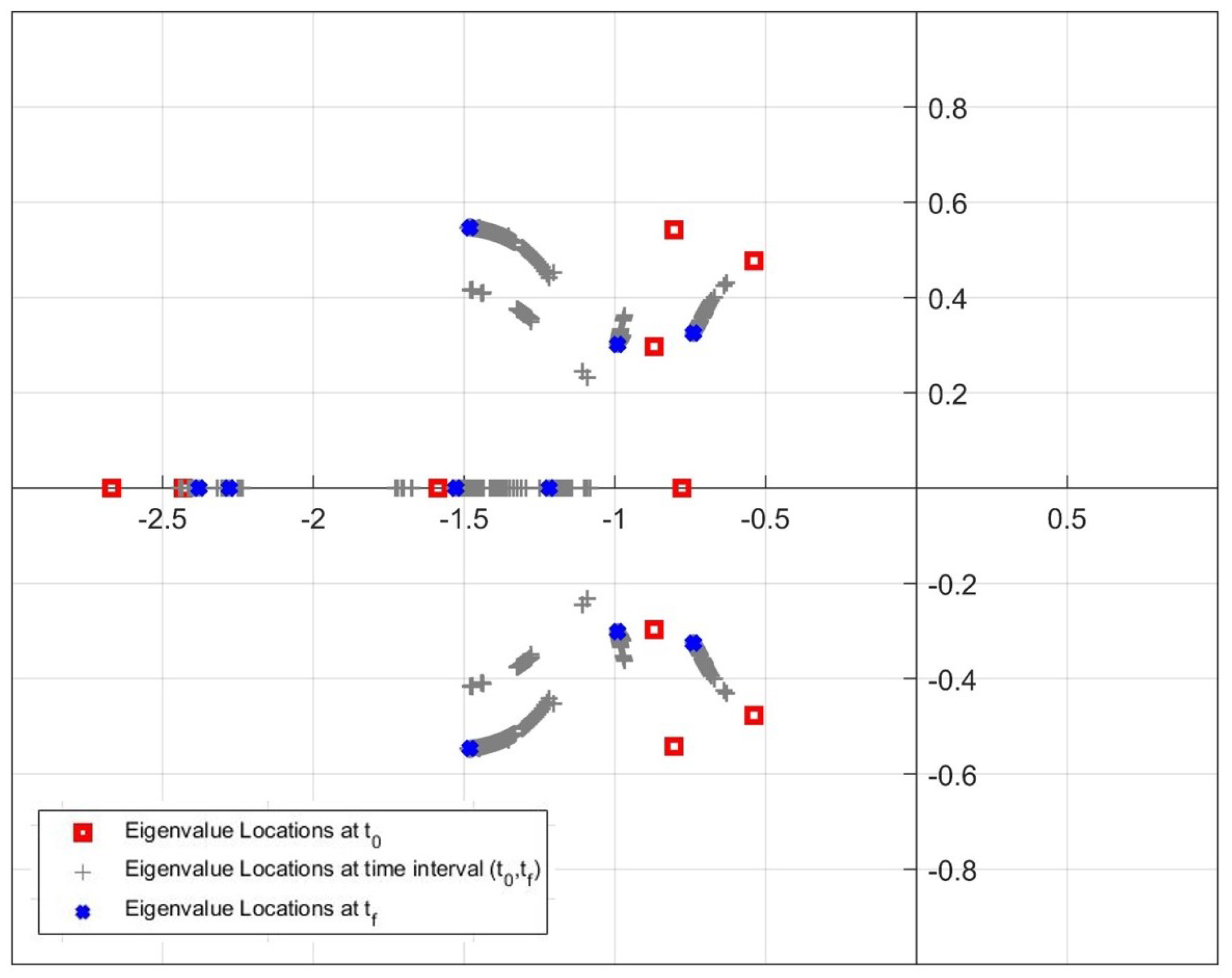
- In our previous studies [31,32], all pointwise eigenvalues of the “frozen” closed-loop system of the nonlinear systems were located in the desired fixed disc region at each time step by using the state-dependent rEA. In this study, we propose two new algorithms that are used to update the disc parameters depending on the locations of the pointwise eigenvalues at the current time for improving the stability and response characteristics according to the design criteria.
2. Methodology
2.1. State-Dependent Regional Eigenvalue Assignment for Control of Nonlinear Systems
- Given a bounded open set , is a continuously differentiable vector-valued function; that is, .
- Given a bounded open set , the origin is an equilibrium point of the system (1) with ; that is, .
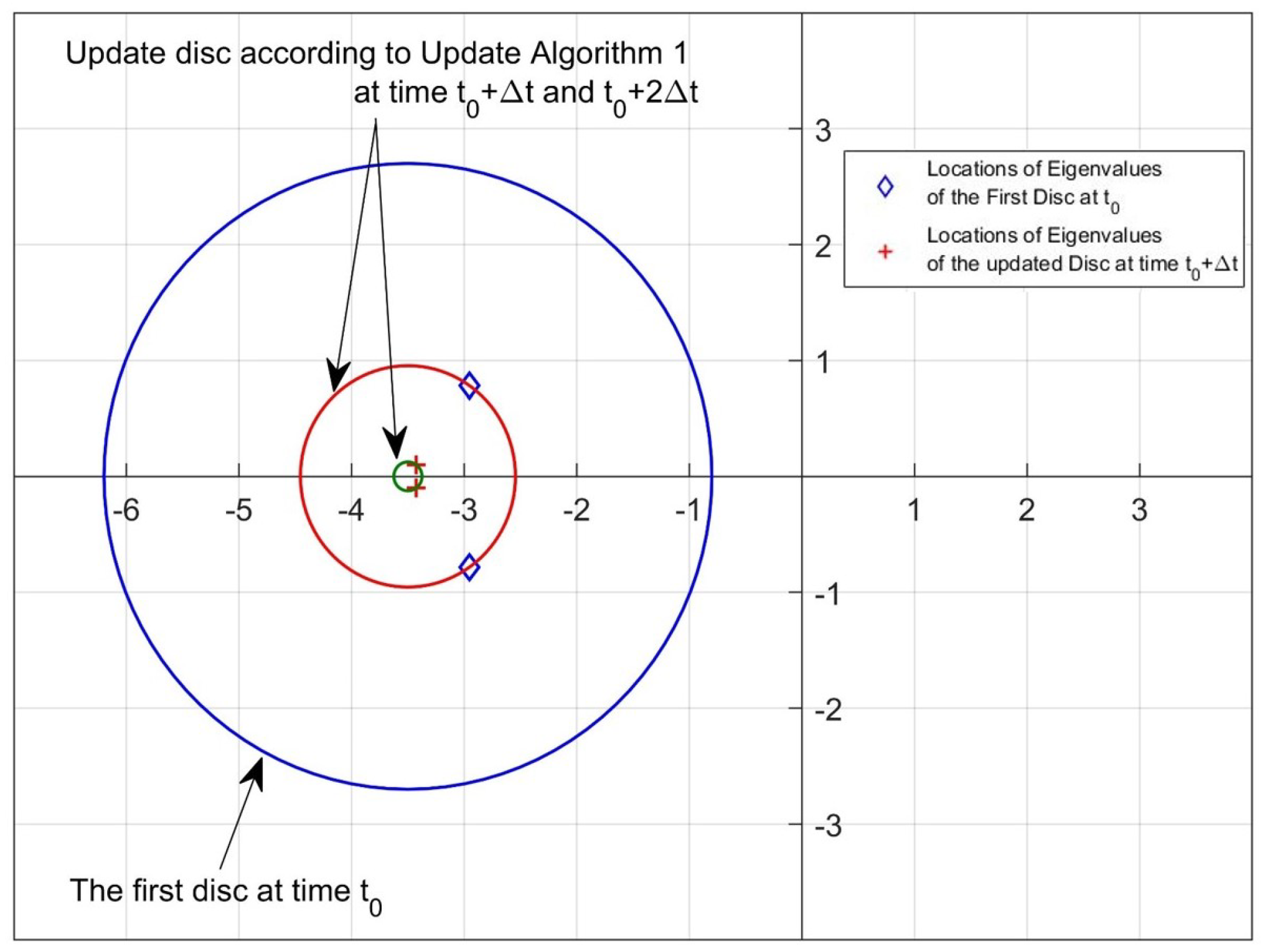
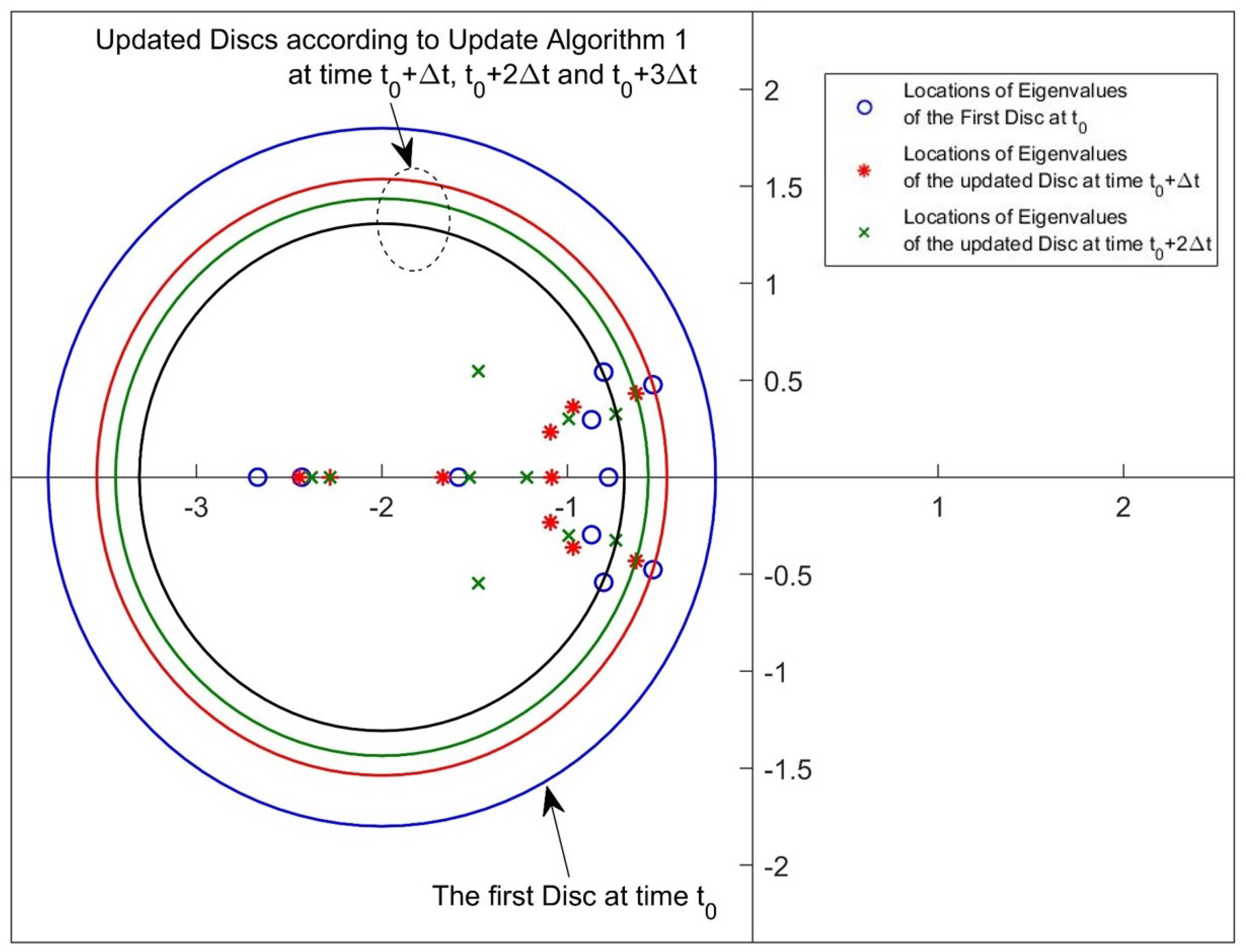
2.2. Update Algorithm 1
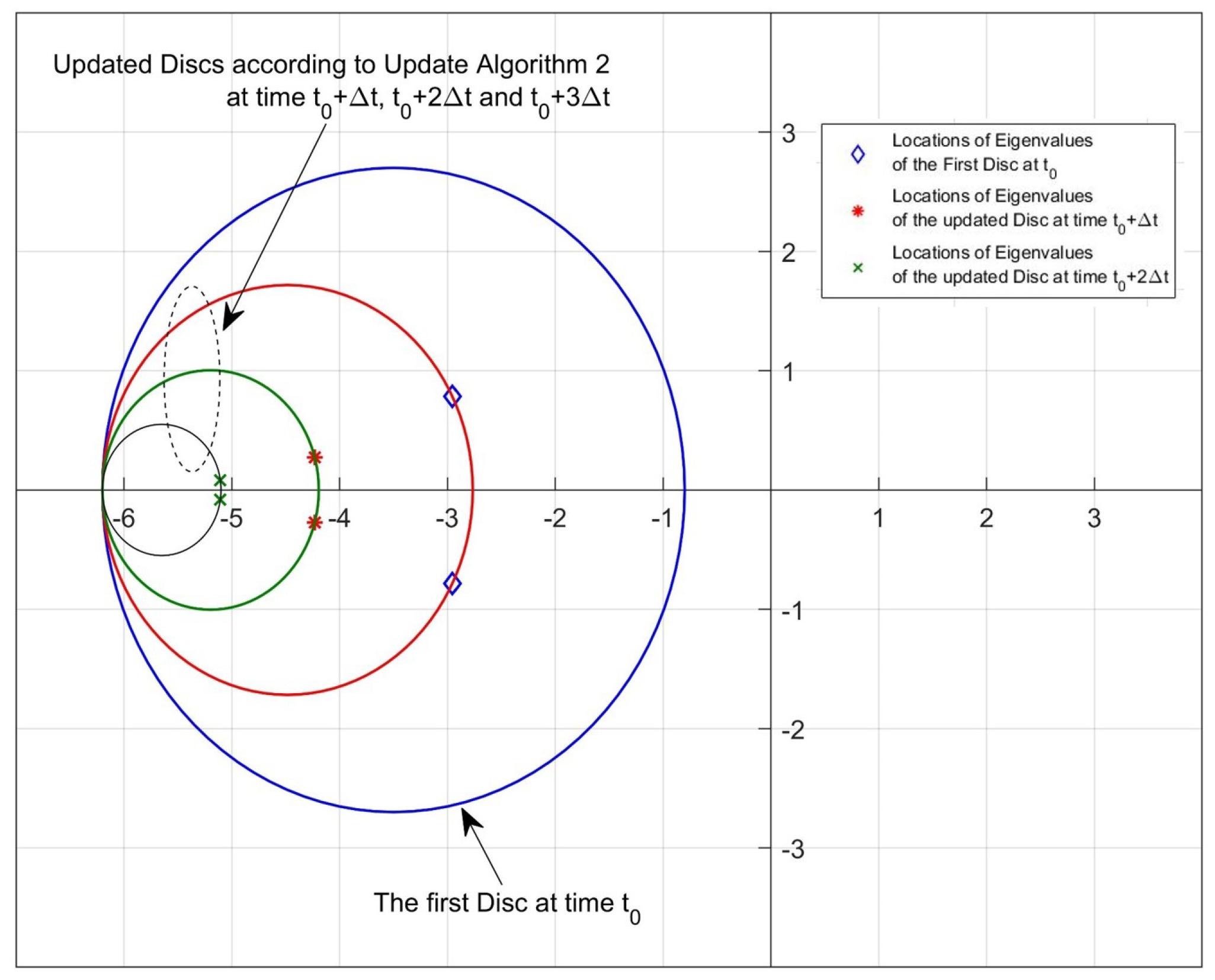
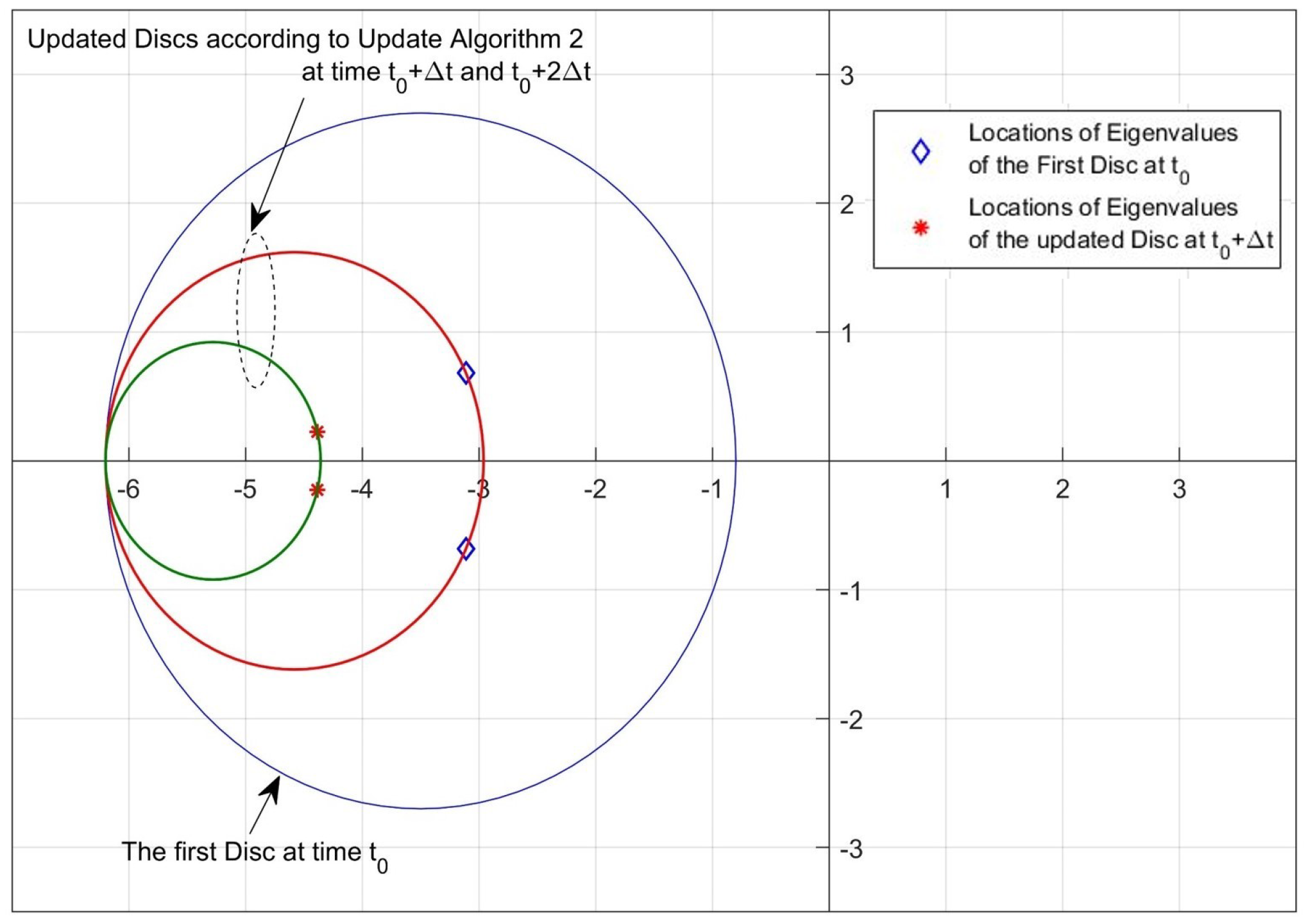
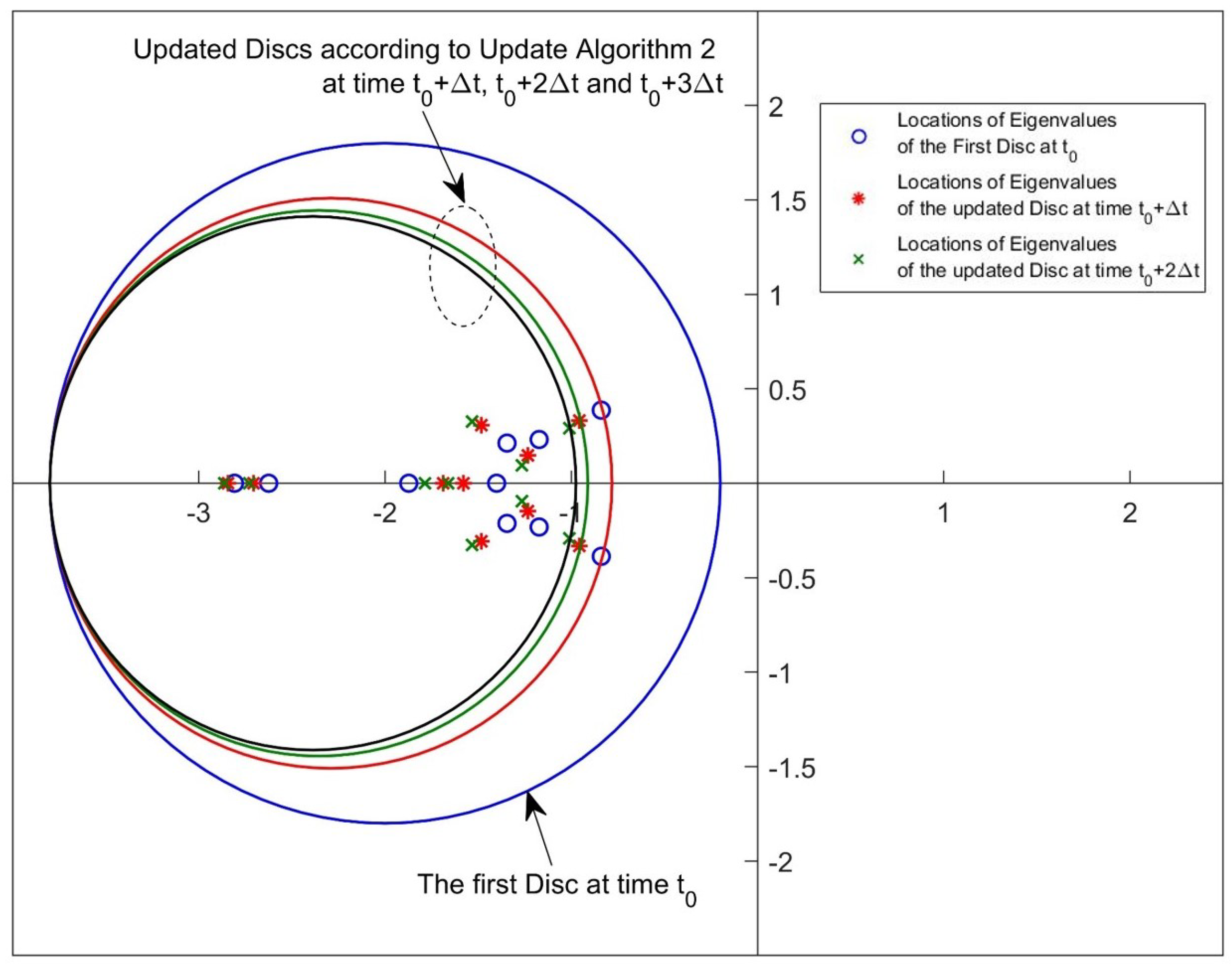
2.3. Update Algorithm 2
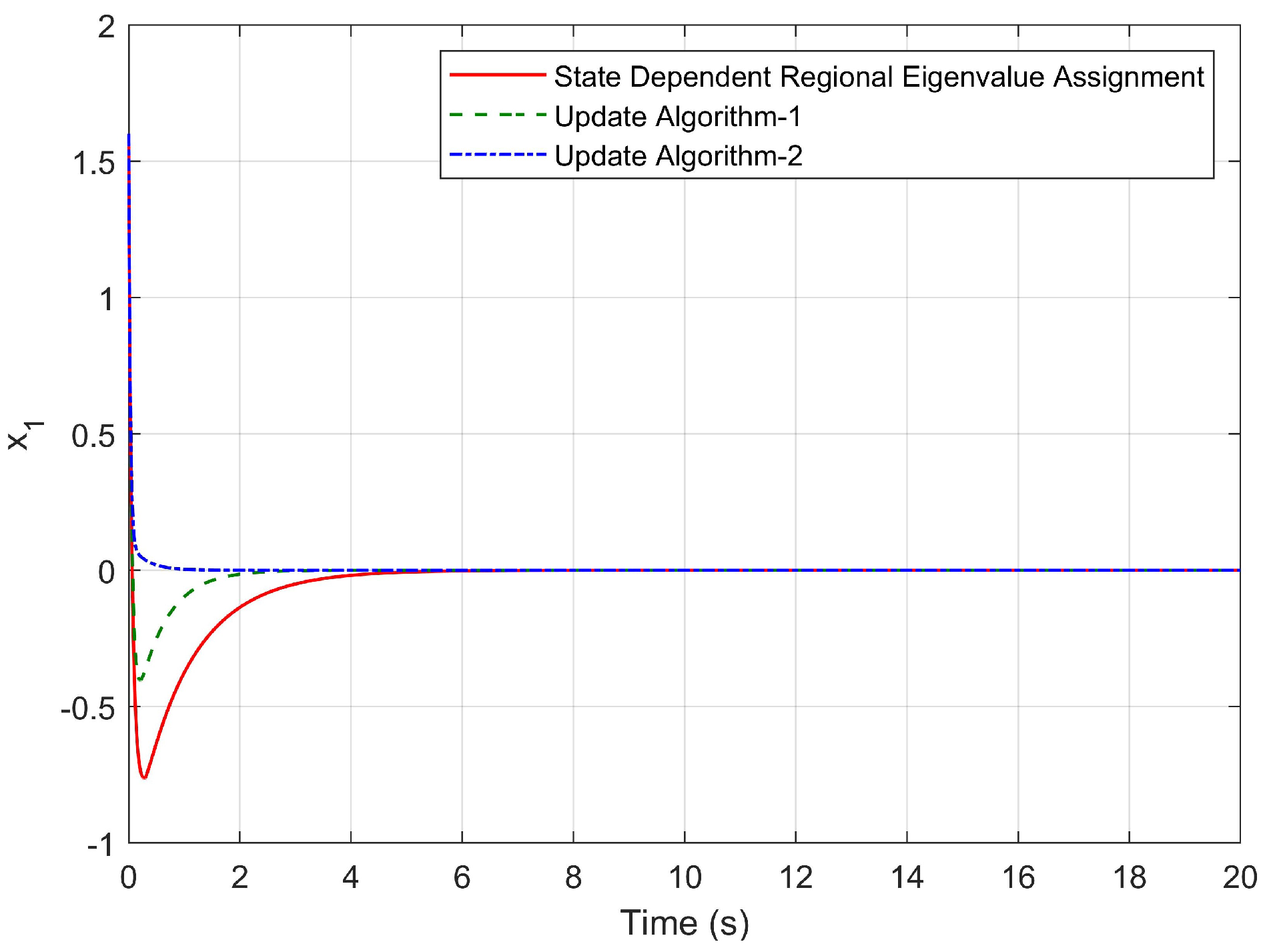
3. A Simulation Study
4. Application
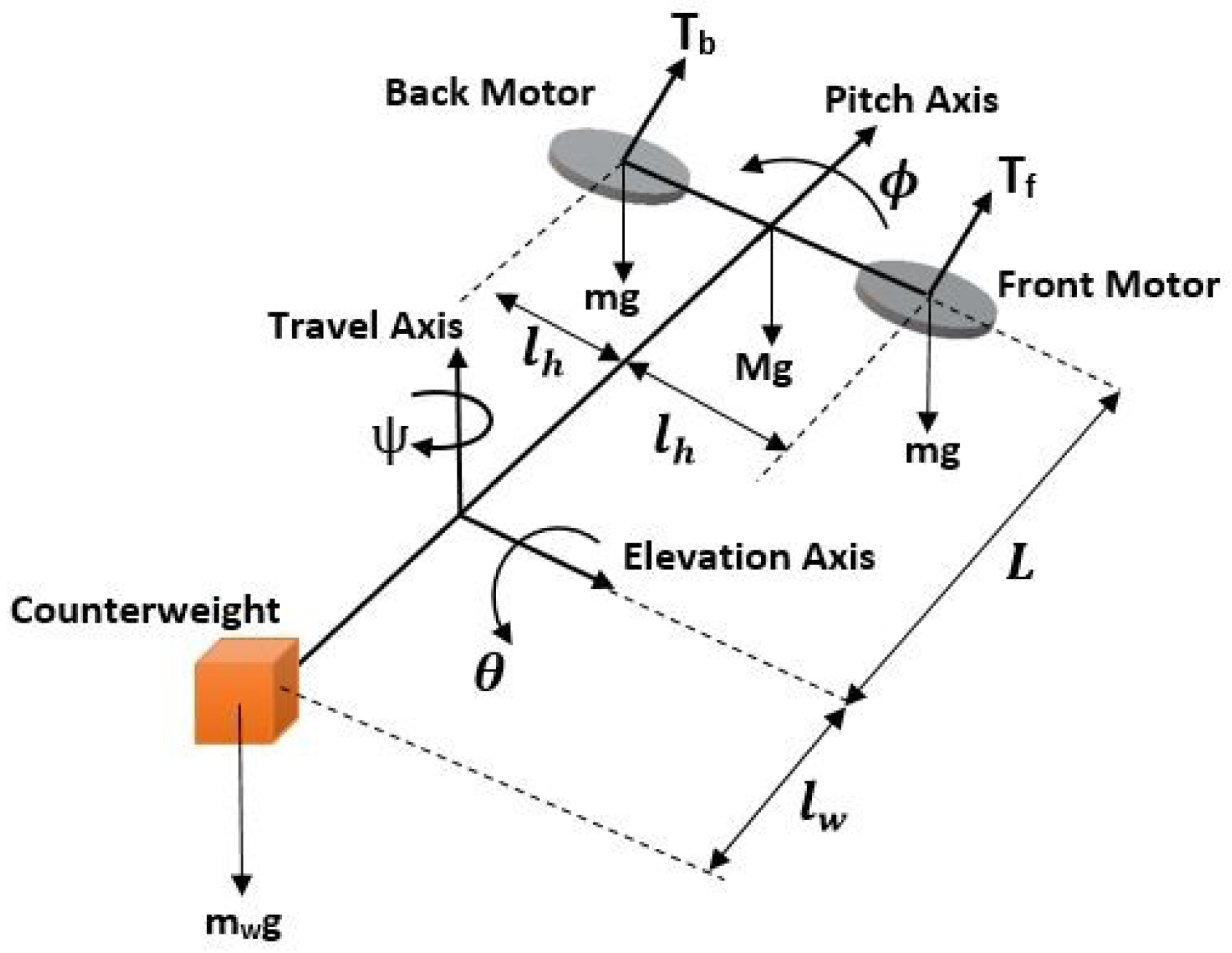
4.1. Mathematical Model of the 3-DOF Helicopter
4.2. Controller Design
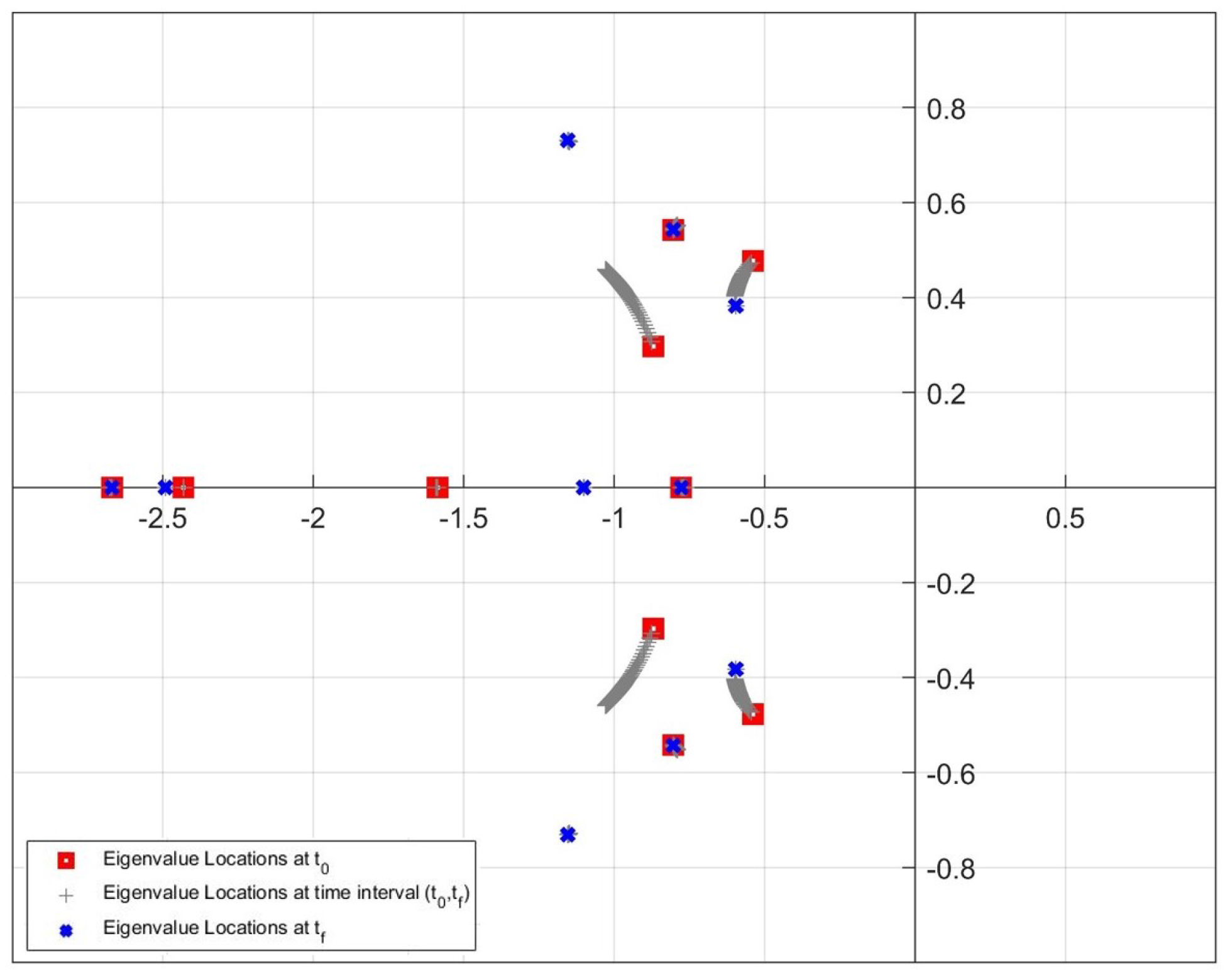
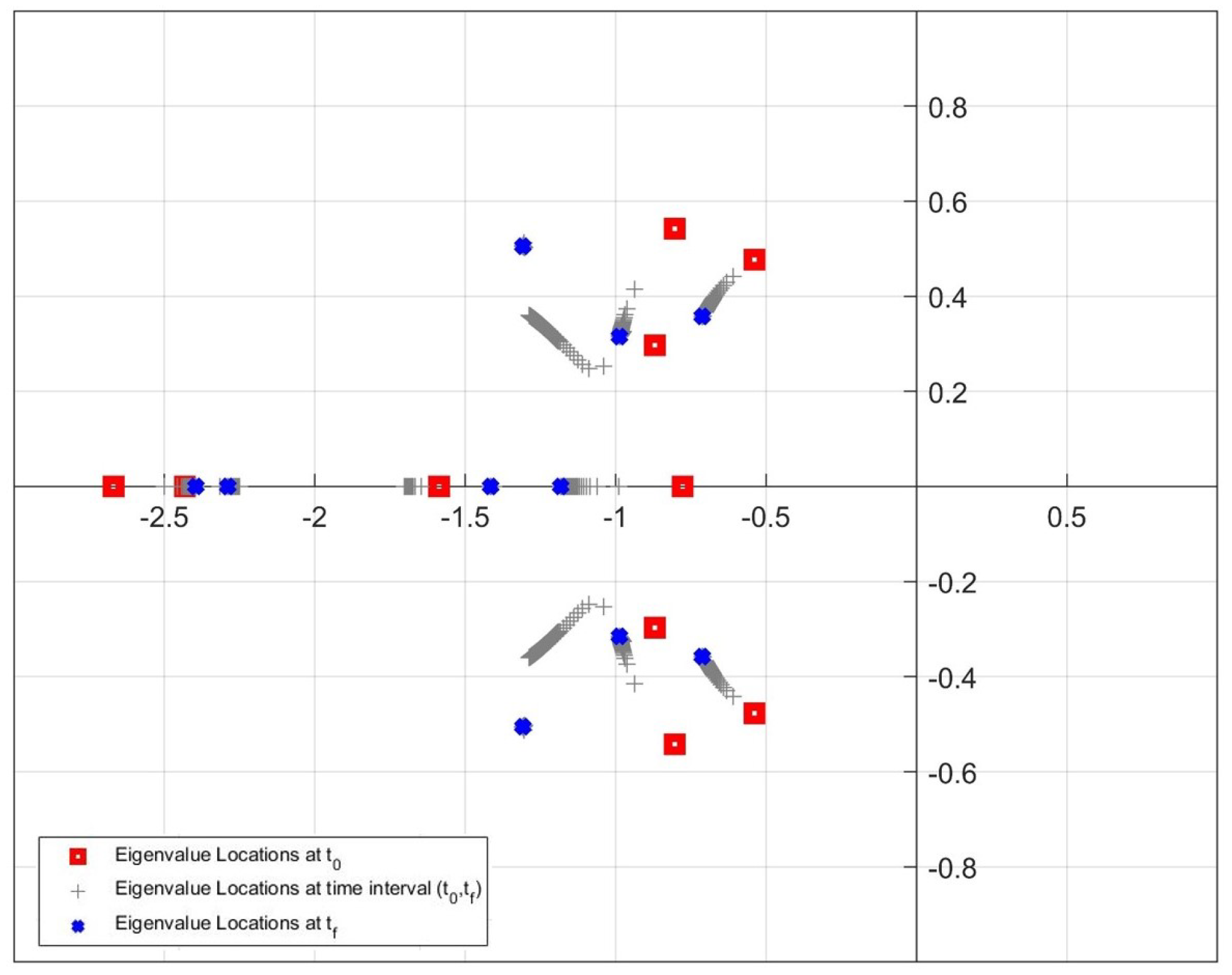
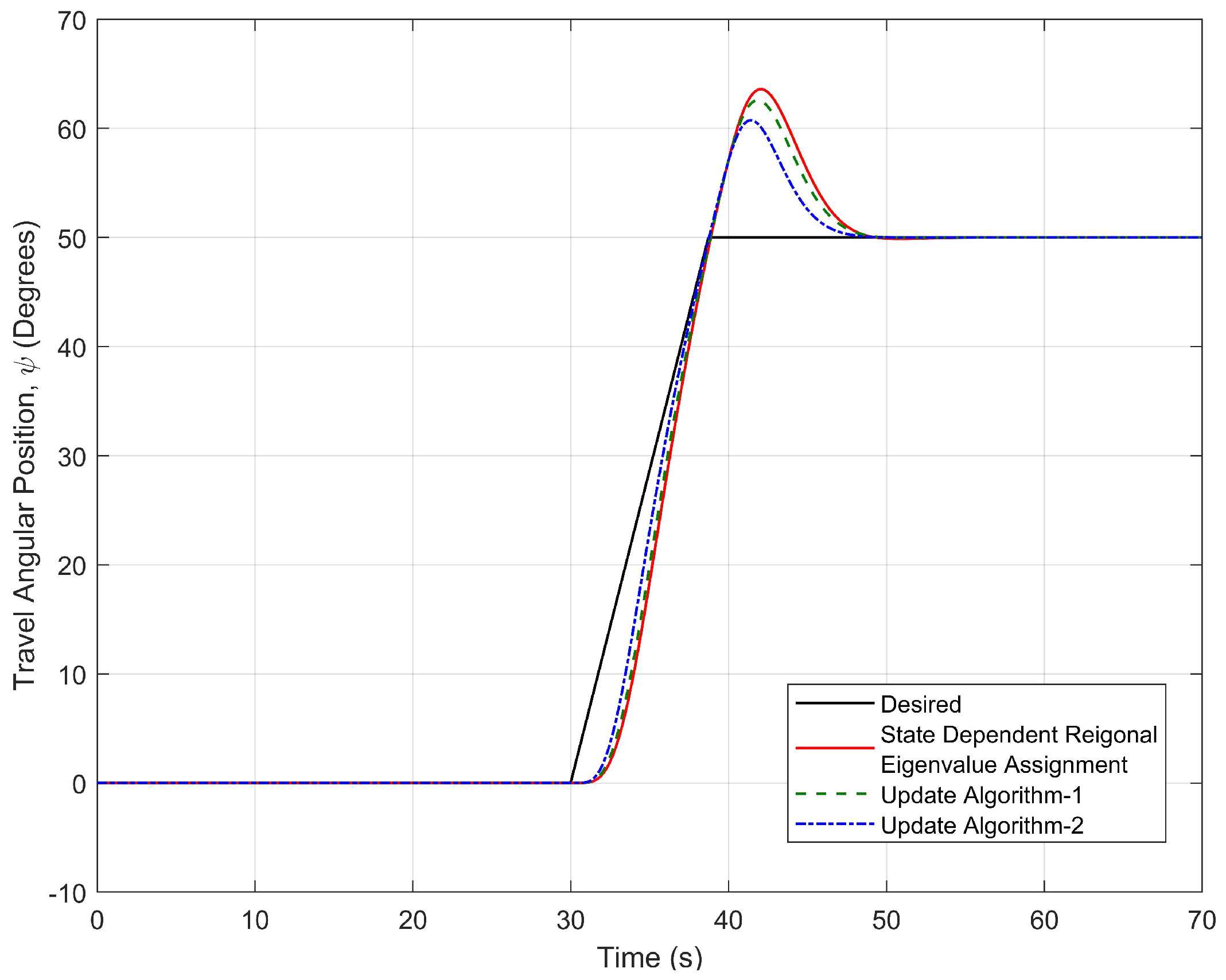
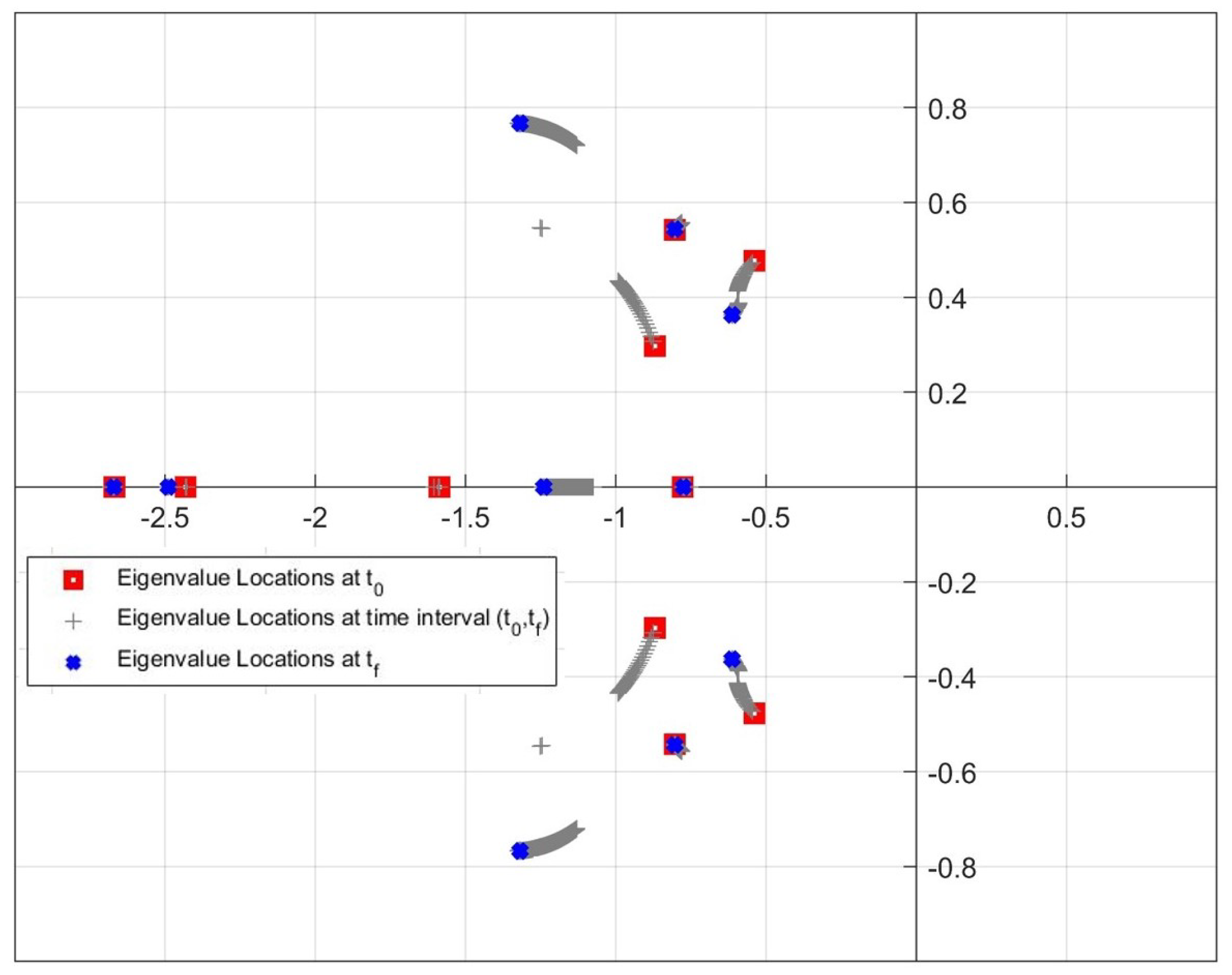
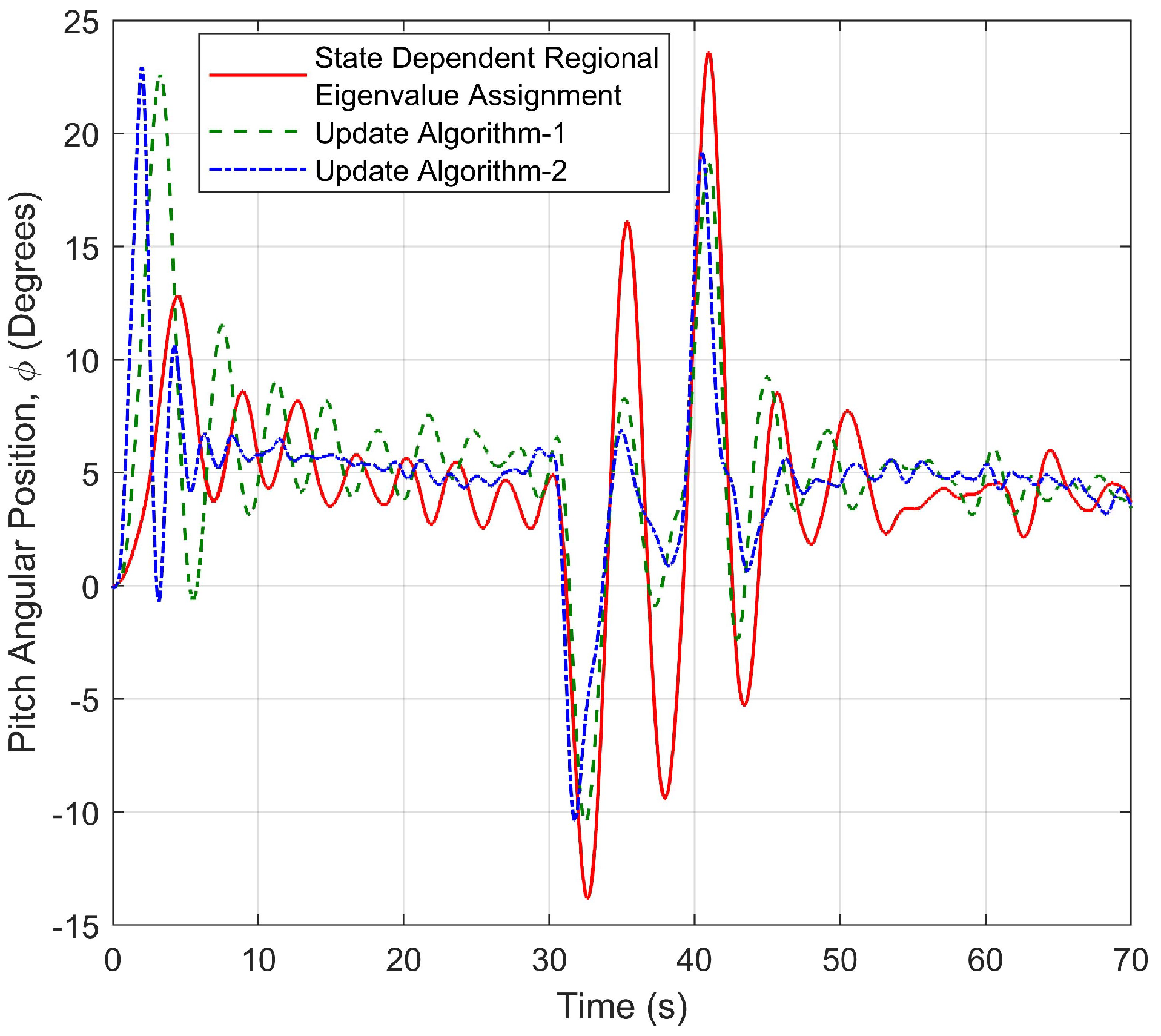
4.3. Simulation Results
4.4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, C.H.; Shin, M.H.; Chung, M.J. A design of gain-scheduled control for a linear parameter varying system: An application to flight control. Control Eng. Pract. 2001, 9, 11–21. [Google Scholar] [CrossRef]
- Ma, T. Eigenvalue assignment enabled control law for multivariable nonlinear systems with mismatched uncertainties. Eur. J. Control 2020, 56, 154–166. [Google Scholar] [CrossRef]
- Yi, S.; Nelson, P.W.; Ulsoy, A.G. Proportional-Integral Control of First-Order Time-Delay Systems via Eigenvalue Assignment. IEEE Trans. Control Syst. Technol. 2013, 21, 1586–1594. [Google Scholar]
- Carotenuto, L.; Franzé, G. A general formula for eigenvalue assignment by static output feedback with application to robust design. Syst. Control Lett. 2003, 49, 175–190. [Google Scholar] [CrossRef]
- Koru, A.T.; Sarsılmaz, S.B.; Yucelen, T.; Muse, J.A.; Lewis, F.L.; Açıkmeşe, B. Regional Eigenvalue Assignment in Cooperative Linear Output Regulation. IEEE Trans. Autom. Control 2023, 68, 4265–4272. [Google Scholar] [CrossRef]
- Haddad, W.M.; Bernstein, D.S. Controller design with regional pole constraints. IEEE Trans. Autom. Control 1992, 37, 54–69. [Google Scholar] [CrossRef]
- Furuta, K.; Kim, S. Pole assignment in a specified disk. IEEE Trans. Autom. Control 1987, 32, 423–427. [Google Scholar] [CrossRef]
- Yaz, E.; Skelton, R.; Grigoriadis, K. Robust regional pole assignment with output feedback. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993. [Google Scholar]
- Garcia, G.; Bernussour, J. Pole assignment for uncertain systems in a specified disk by state feedback. IEEE Trans. Autom. Control 1995, 40, 184–190. [Google Scholar] [CrossRef]
- Garcia, G.; Daafouz, J.; Bernussour, J. Output feedback disk pole assignment for systems with positive real uncertainty. IEEE Trans. Autom. Control 1996, 41, 1385–1391. [Google Scholar] [CrossRef]
- Kim, H.S.; Han, H.S.; Lee, J.G. Pole placement of uncertain discrete systems in the smallest disk by state feedback. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996. [Google Scholar]
- Chou, J.-H. Pole-assignment robustness in a specified disk. Syst. Control Lett. 1991, 16, 41–44. [Google Scholar] [CrossRef]
- Schuchert, P.; Karimi, A. A convex set of robust D—Stabilizing controllers using Cauchy’s argument principle. IFAC-PapersOnLine 2022, 55, 49–54. [Google Scholar] [CrossRef]
- Ling, B. State-feedback regional pole placement via LMI optimization. In Proceedings of the 2001 American Control Conference, Arlington, VA, USA, 25–27 June 2001. [Google Scholar]
- Soliman, H.; Dabroum, A.; Mahmoud, M.; Soliman, M. Guaranteed-cost reliable control with regional pole placement of a power system. J. Frankl. Inst. 2011, 348, 884–898. [Google Scholar] [CrossRef]
- Wisniewski, V.; Maddalena, E.; Godoy, R. Discrete-time regional pole-placement using convex approximations: Theory and application to a boost converter. J. Control Eng. Pract. 2019, 91, 104102. [Google Scholar] [CrossRef]
- Almeida, M.O.; Araújo, J.M. Partial Eigenvalue Assignment for LTI Systems with D-Stability and LMI. J. Control Autom. Electr. Syst. 2019, 30, 301–310. [Google Scholar] [CrossRef]
- Baker, W.A.; Schneider, S.C.; Yaz, E.E. Robust regional eigenvalue assignment by dynamic state-feedback control for nonlinear continuous-time systems. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015. [Google Scholar]
- Xiong, S.; Chen, M.; Wei, Z. Tracking flight control of UAV based on multiple regions pole assignment method. Aerosp. Sci. Technol. 2022, 129, 107848. [Google Scholar] [CrossRef]
- Chilali, M.; Gahinet, P.; Apkarian, P. Robust pole placement in LMI regions. IEEE Trans. Autom. Control 1999, 44, 2257–2270. [Google Scholar] [CrossRef]
- Leite, V.J.; Peres, P.L. An improved LMI condition for robust D-stability of uncertain polytopic systems. IEEE Trans. Autom. Control 2003, 48, 500–504. [Google Scholar] [CrossRef]
- Satoh, A.; Sugimoto, K. An LMI approach to gain parameter design for regional eigenvalue/eigenstructure assignment. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Sahoo, P.R.; Goyal, J.K.; Ghosh, S.; Naskar, A.K. New results on restricted static output feedback controller design with regional pole placement. IET Control Theory Appl. 2019, 13, 1095–1104. [Google Scholar] [CrossRef]
- Richiedei, D.; Tamellin, I. Active control of linear vibrating systems for antiresonance assignment with regional pole placement. J. Sound Vib. 2021, 494, 115858. [Google Scholar] [CrossRef]
- Zhai, J.; Gao, L.; Li, S. Robust pole assignment in a specified union region using harmony search algorithm. Neurocomputing 2015, 155, 12–21. [Google Scholar] [CrossRef]
- Rosinová, D.; Veselý, V.; Hypiusová, M. Novel robust gain scheduled PID controller design using DR regions. Asian J. Control 2021, 24, 2062–2073. [Google Scholar] [CrossRef]
- Veselý, V.; Körösi, L. Robust PI-D Controller Design for Uncertain Linear Polytopic Systems Using LMI Regions and H2 Performance. IEEE Trans. Ind. Appl. 2019, 55, 5353–5359. [Google Scholar] [CrossRef]
- Singh, H.; Naidu, D.S.; Moore, K.L. On regional pole assignment in discrete-time systems using linear quadratic regulator theory. In Proceedings of the 1994 American Control Conference—ACC ’94, Baltimore, MD, USA, 29 June–1 July 1994. [Google Scholar]
- Mori, Y.; Shimemura, Y. On a design method for feedback control law to locate the eigenvalues in a specified region. SICE 1980, 16, 462–463. [Google Scholar]
- Bogachev, A.V.; Grigorev, V.V.; Drozdov, V.N.; Korovyakov, A.N. Analytic design of controls from root indicators. Autom. Remote Control 1979, 40, 1118–1123. [Google Scholar]
- Arıcan, A.Ç.; Çopur, E.H.; Inalhan, G.; Salamci, M.U. State Dependent Regional Pole Assignment Controller Design for a 3-DOF Helicopter Model. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023. [Google Scholar]
- Arıcan, A.Ç.; Çopur, E.H.; Inalhan, G.; Salamci, M.U. Sliding Mode Control of a 3-DOF Helicopter with State Dependent Regional Pole Placement. In Proceedings of the 2023 24th International Carpathian Control Conference (ICCC), Miskolc-Szilvásvárad, Hungary, 27–30 May 2023. [Google Scholar]
- Cimen, T. Systematic and effective design of nonlinear feedback controllers via the state-dependent Riccati equation (SDRE) method. Ann. Rev. Control 2010, 34, 32–51. [Google Scholar] [CrossRef]
- Ozcan, S.; Çopur, E.H.; Arican, A.C.; Salamci, M.U. A Modified SDRE-based Sub-optimal Hypersurface Design in SMC. IFAC-PapersOnLine 2020, 53, 6250–6255. [Google Scholar] [CrossRef]
- Copur, E.H.; Arican, A.C.; Ozcan, S.; Salamci, M.U. An update algorithm design using moving Region of Attraction for SDRE based control law. J. Frankl. Inst. 2019, 356, 8388–8413. [Google Scholar] [CrossRef]
- Kocagil, B.M.; Ozcan, S.; Arican, A.C.; Guzey, U.M.; Copur, E.H.; Salamci, M.U. MRAC of a 3-DoF Helicopter with Nonlinear Reference Model. In Proceedings of the 2018 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018. [Google Scholar]
- Arıcan, A.Ç.; Ozcan, S.; Kocagil, B.M.; Guzey, Ü.M.; Salamci, M.U. Suboptimal control of a 3 dof helicopter with state dependent riccati Equations. In Proceedings of the XXVI International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 26–28 October 2017. [Google Scholar]
- Kara, F.; Salamci, M.U. Controller Design for a Nonlinear 3 DOF Helicopter Model Using Adaptive Sliding Surfaces. In Proceedings of the 2019 XXVII International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 20–23 October 2019. [Google Scholar]
- Perk, B.E.; Inalhan, G. Safe Motion Planning and Learning for Unmanned Aerial Systems. Aerospace 2022, 9, 56. [Google Scholar] [CrossRef]
- Chaoui, H.; Yadav, S.; Ahmadi, R.S.; Bouzid, A.E.M. Adaptive Interval Type-2 Fuzzy Logic Control of a Three Degree-of-Freedom Helicopter. Robotics 2020, 9, 59. [Google Scholar] [CrossRef]
- Peng, H.; Wei, L.; Zhu, X.; Xu, W.; Zhang, S. Aggressive maneuver oriented integrated fault-tolerant control of a 3-DOF helicopter with experimental validation. Aerosp. Sci. Technol. 2022, 120, 107265. [Google Scholar] [CrossRef]
- Ishutkina, M. Design and Implimentation of a Supervisory Safety Controller for a 3DOF Helicopter. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]










| States | Algorithms | ISE | IAE | ITAE | ITSE |
|---|---|---|---|---|---|
| SDREAM-FDR | 2.913 | 2.238 | 2.023 | 1.153 | |
| Algorithm 1 | 2.313 | 1.561 | 0.815 | 0.597 | |
| Algorithm 2 | 1.518 | 0.958 | 0.282 | 0.224 | |
| SDREAM-FDR | 2.896 | 3.970 | 11.279 | 3.677 | |
| Algorithm 1 | 2.526 | 2.817 | 4.423 | 1.962 | |
| Algorithm 2 | 2.127 | 1.962 | 1.754 | 0.966 |
| States | Algorithms | ISE | IAE | ITAE | ITSE |
|---|---|---|---|---|---|
| SDREAM-FDR | 0.440 | 0.951 | 1.011 | 0.251 | |
| Algorithm 1 | 0.118 | 0.321 | 0.175 | 0.026 | |
| Algorithm 2 | 0.059 | 0.084 | 0.010 | 9.551 × | |
| SDREAM-FDR | 2.298 | 3.233 | 9.046 | 3.711 × | |
| Algorithm 1 | 1.537 | 1.852 | 2.674 | 2.280 × | |
| Algorithm 2 | 0.833 | 0.827 | 0.567 | 0.119 × |
| Variables | Units |
|---|---|
| radian | |
| radian | |
| radian | |
| radian/s | |
| radian/s | |
| radian/s | |
| voltage | |
| voltage |
| Parameter | Constant Coefficient |
|---|---|
| 0.2517 | |
| 0.2105 | |
| 0.3290 | |
| 1.5664 | |
| 16.200 | |
| 7.3200 | |
| 1.000 | |
| 0.1011 | |
| 0.5040 | |
| 1.3400 | |
| 6.1600 | |
| 1.000 | |
| 4.000 |
| States | Algorithms | ISE | IAE | ITAE | ITSE |
|---|---|---|---|---|---|
| SDREAM-FDR | 256.695 | 33.875 | 84.218 | 344.201 | |
| Elevation Motion | Algorithm 1 | 228.111 | 30.576 | 70.882 | 269.844 |
| Algorithm 2 | 182.148 | 24.618 | 47.330 | 168.824 | |
| SDREAM-FDR | 1334.8 | 134.334 | 5150.8 | 50,763 | |
| Travel Motion | Algorithm 1 | 1103 | 120.303 | 4590.41 | 41,716 |
| Algorithm 2 | 713.817 | 92.053 | 3472.6 | 26,673 |
| States | Algorithms | ISE | IAE | ITAE | ITSE |
|---|---|---|---|---|---|
| SDREAM-FDR | 735.023 | 88.734 | 585.259 | 1981 | |
| Elevation Motion | Algorithm 1 | 483.564 | 62.43 | 387.902 | 897.356 |
| Algorithm 2 | 196.272 | 27.179 | 163.415 | 142.37 | |
| SDREAM-FDR | 755.611 | 129.584 | 4552.8 | 27,696 | |
| Travel Motion | Algorithm 1 | 745.19 | 122.759 | 4474.6 | 25,689 |
| Algorithm 2 | 369.362 | 74.125 | 2418.9 | 12,845 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arıcan, A.Ç.; Çopur, E.H.; Inalhan, G.; Salamci, M.U. An Extension Algorithm of Regional Eigenvalue Assignment Controller Design for Nonlinear Systems. Aerospace 2023, 10, 893. https://doi.org/10.3390/aerospace10100893
Arıcan AÇ, Çopur EH, Inalhan G, Salamci MU. An Extension Algorithm of Regional Eigenvalue Assignment Controller Design for Nonlinear Systems. Aerospace. 2023; 10(10):893. https://doi.org/10.3390/aerospace10100893
Chicago/Turabian StyleArıcan, Ahmet Çağrı, Engin Hasan Çopur, Gokhan Inalhan, and Metin Uymaz Salamci. 2023. "An Extension Algorithm of Regional Eigenvalue Assignment Controller Design for Nonlinear Systems" Aerospace 10, no. 10: 893. https://doi.org/10.3390/aerospace10100893
APA StyleArıcan, A. Ç., Çopur, E. H., Inalhan, G., & Salamci, M. U. (2023). An Extension Algorithm of Regional Eigenvalue Assignment Controller Design for Nonlinear Systems. Aerospace, 10(10), 893. https://doi.org/10.3390/aerospace10100893








