A Methodology for Assessing Capacity of the Terminal Maneuvering Area Based on Service Resource Equilibrium
Abstract
:1. Introduction
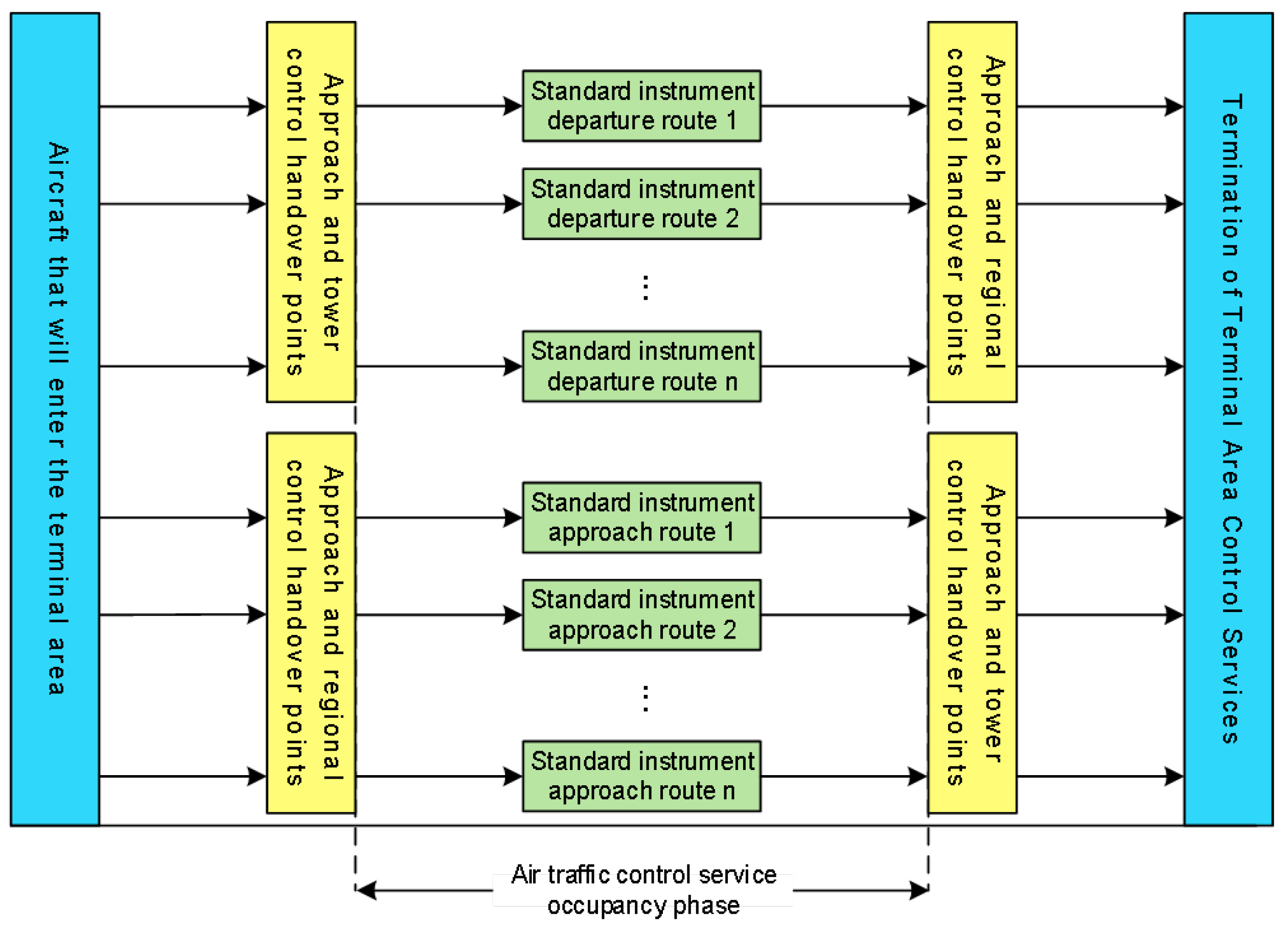
2. Capacity and Service Resource Analysis of Terminal Areas
3. Mathematical Modeling
3.1. Model Assumptions
- Any two arriving or departing aircraft are equipped with a minimum flight separation greater than that used in the control area where they are located.
- In the terminal area, if the service for an aircraft has already started and has not yet finished, the service for another aircraft cannot begin.
- Aircraft service requests in the terminal area are continuous, and the number of aircraft being served in the terminal area does not exceed the safe handling capacity.
- Each aircraft flies according to its planned route and will not deviate from or change the planned route.
- Each aircraft of the same type experiences the same flight time on the same air route.
- To simplify the modeling, the arrival and departure routes are assumed to have sufficient vertical separation by altitude, as implemented in real-world air traffic management, which ensures arrival and departure flows do not interfere, allowing their traffic capacities to be analyzed independently without conflicts.
3.2. Model Formulation
3.2.1. Demand Model
3.2.2. Supply Model
3.2.3. Capacity Calculation Model
4. Empirical Analysis of the Proposed Model
4.1. Model Implementation Using ZBLA Airport Data
- Under normal conditions, air traffic controllers at the terminal area of Hulunbuir Hailar Airport (ZBLA) can safely handle up to four aircraft at peak workload periods. Therefore, the supply model parameter is set to 4, and the calculation time is 1 h. The continuous working time is calculated as
- Considering that the average workload of air traffic controllers in China should not exceed 70% of the maximum workload threshold, the utilization coefficient u is set to 0.7 for this calculation.
- When the utilization coefficient is unconstrained, the mathematical model can be expressed as
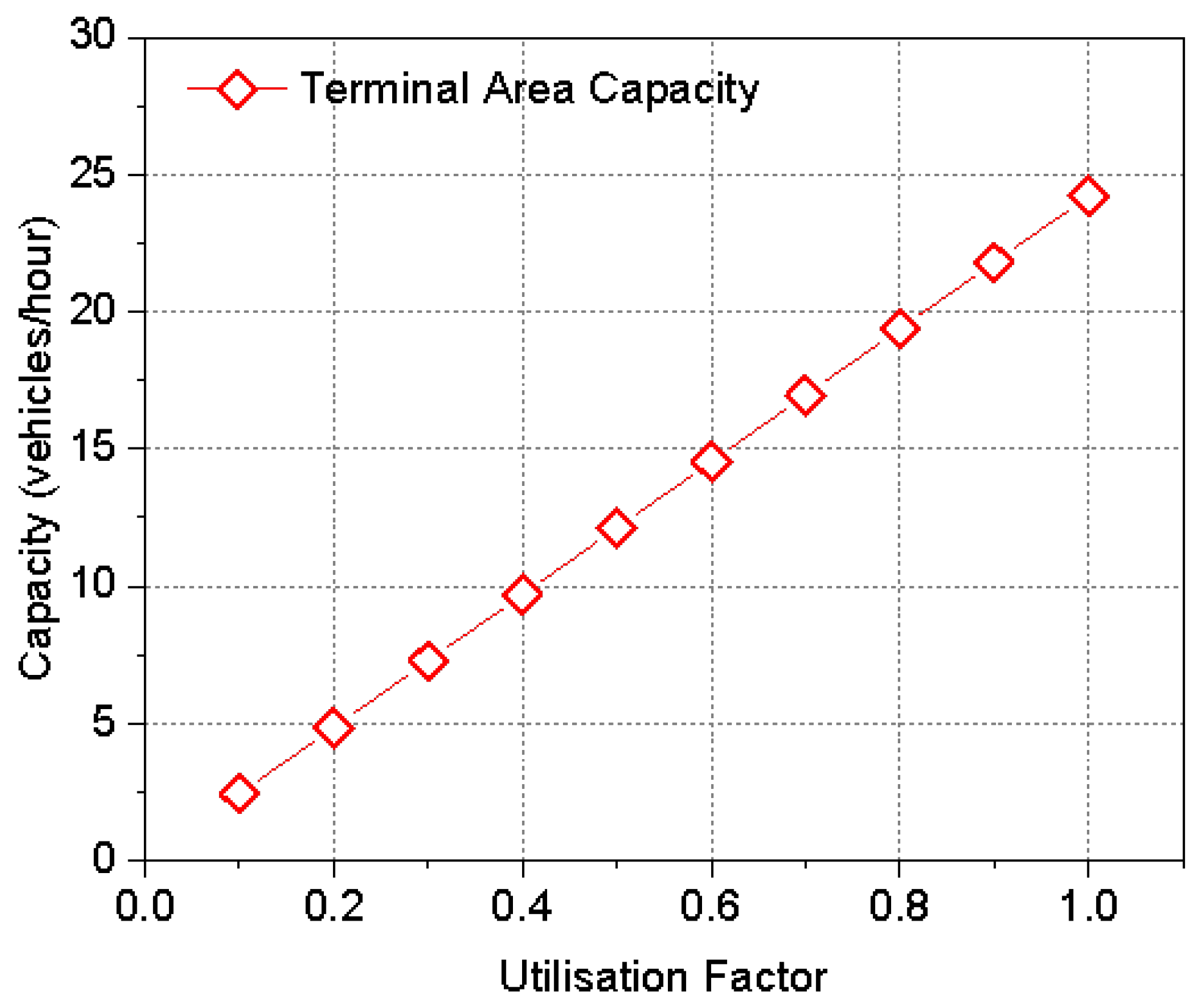
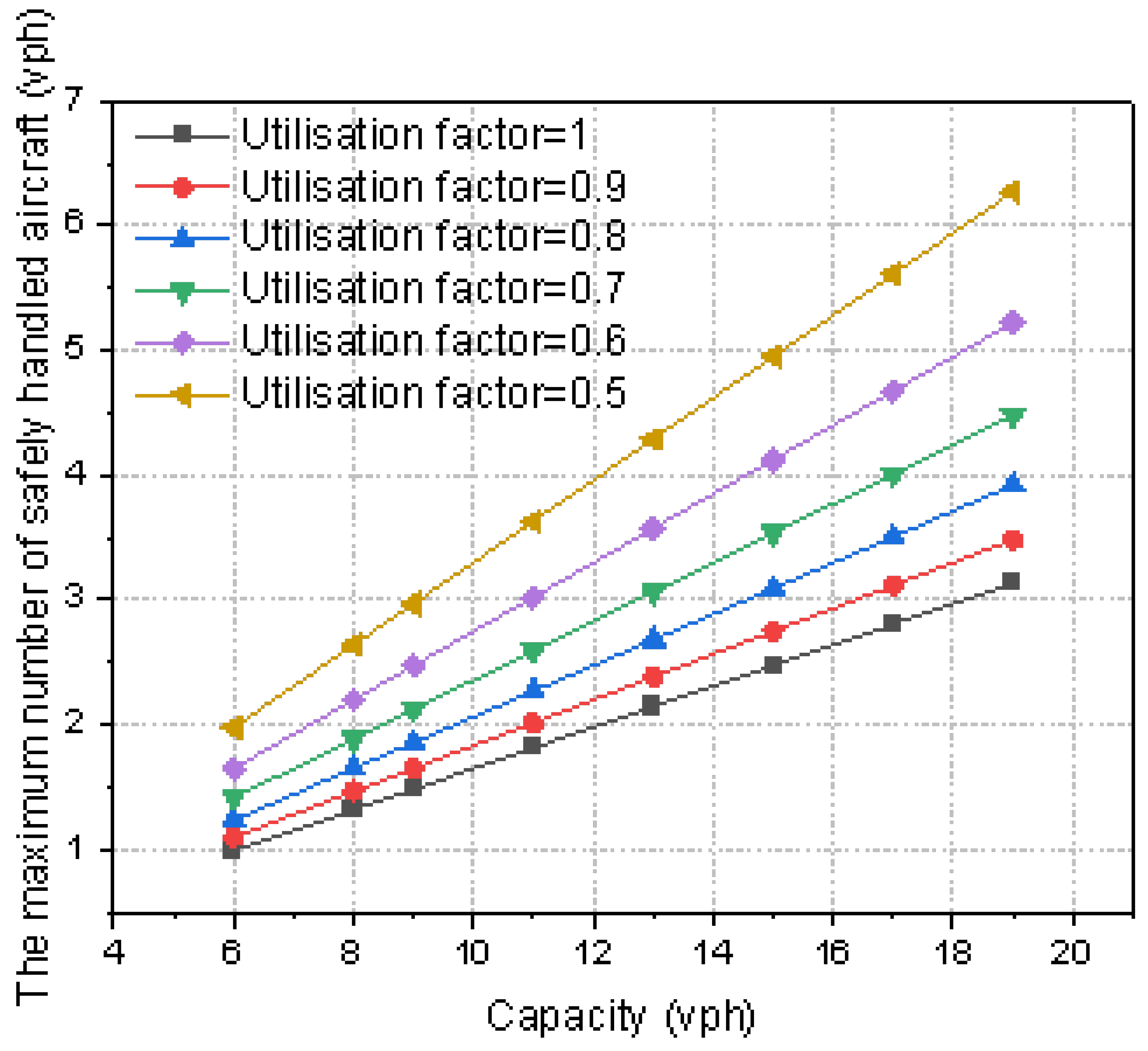
- When the utilization coefficient u assumes different values between 0.1 and 1, the workload and estimated terminal airspace capacity results vary accordingly. A higher u indicates a greater workload for air traffic controllers; thus, as shown in Figure 3, the increases as u increases. The relationship can be expressed as a linear equation approximately equal to . In this study, a utilization coefficient of 0.7 is selected to represent a busy workload scenario for terminal airspace controllers at Hulunbuir Hailar Airport (ZBLA). Consequently, the calculated recommended operational capacity is 17 aircraft movements per hour.
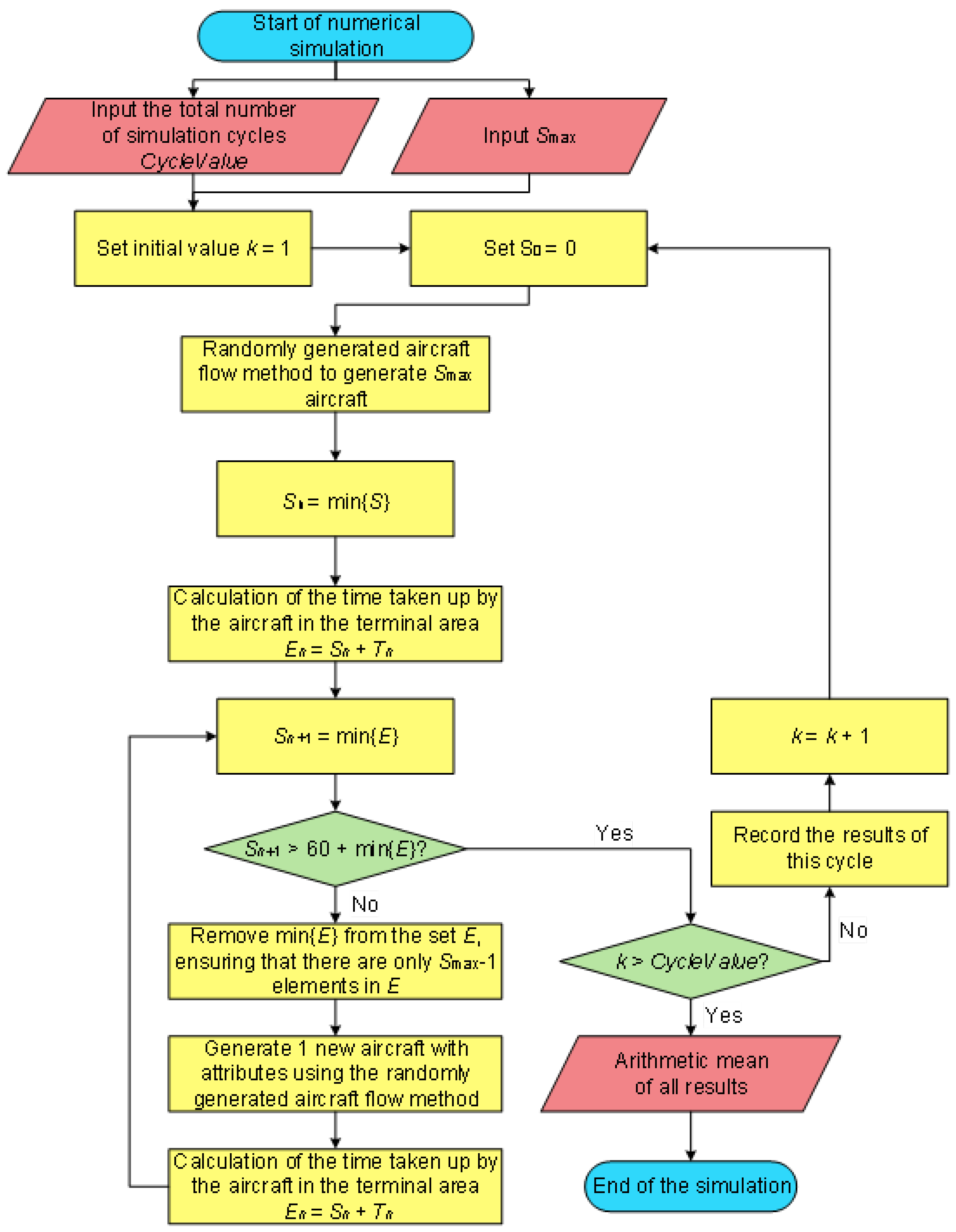
4.2. Model Validation by Monte Carlo Simulation
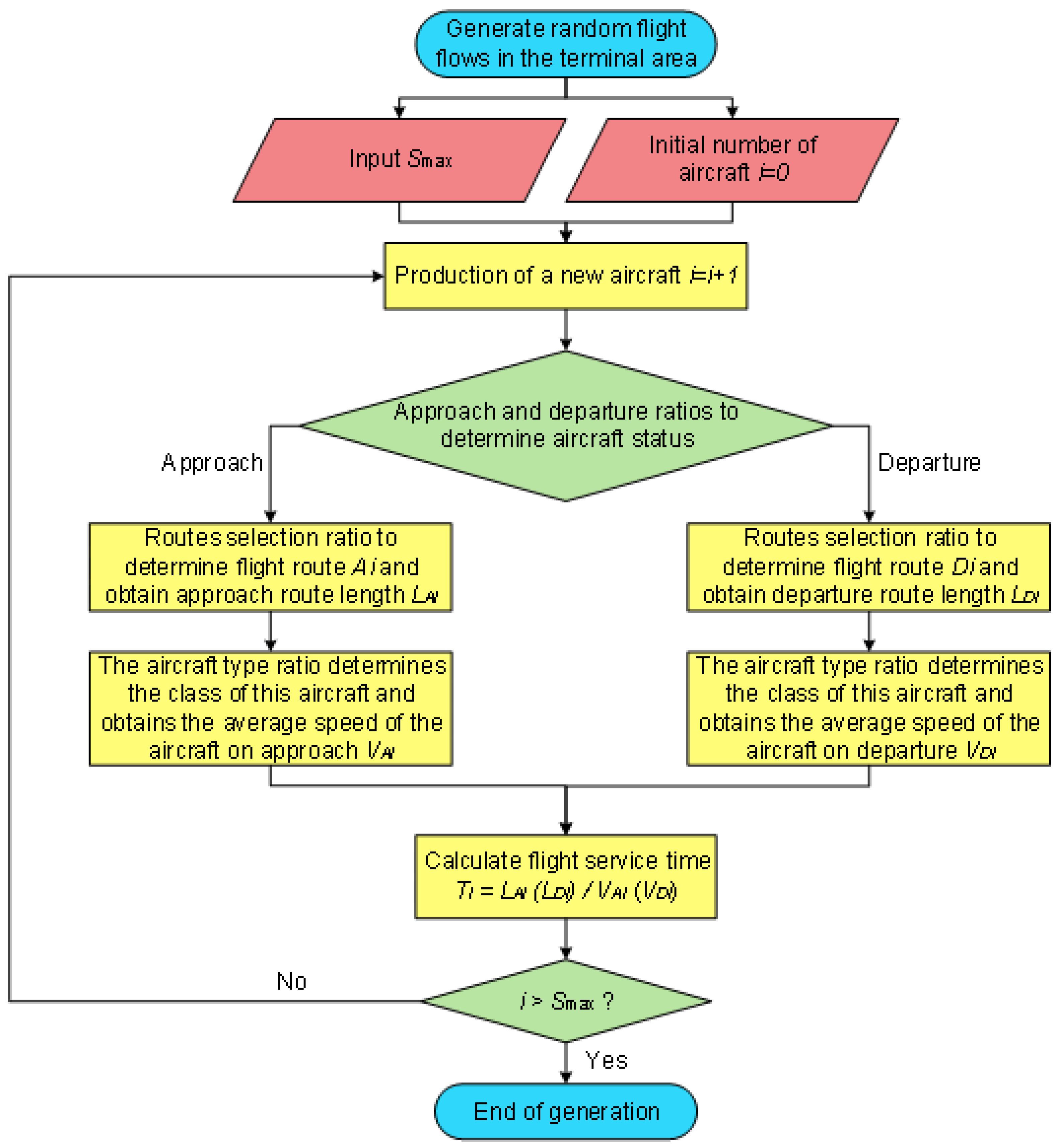
- Random aircraft generation within the terminal area In the simulation, each aircraft needs to be randomly generated to operate in the airspace based on the take-off and landing ratios, the percentages of approach and departure procedures, and the percentages of aircraft types for different approach and departure procedures. The flight distance and speed are determined based on the selected approach, departure procedure, and aircraft type, resulting in the flight time for that aircraft. In each cycle, n aircraft are first generated to meet the condition that no more than n aircraft are under ATC control at the same time, which means n aircraft sorties in the terminal area are maintained as the limit case.
- Confirmation upon aircraft’s proceeding out of the terminal area in the simulation progresses, aircraft fly along the selected approach and departure procedures until one of the aircraft reaches the endpoint. The timing starts from aircraft’s proceeding out of the first aircraft until the cumulative time reaches 1 h. The endpoints in this simulation are the points where arriving aircraft hand over control to the tower (for landing aircraft) or the approach control (for departing aircraft). In this simulation, the endpoints are the transfer points where aircraft in the approach control zone transfer control to the control zone (for landing aircraft) or the Area Control Center (for departing aircraft).
- Defining the iteration rules: When an aircraft proceeds out of the endpoint, an aircraft is generated randomly in the scenario. This constantly maintains n aircraft being operated within the terminal control area. Steps 2 and 3 are repeated until the cumulative time reaches 1 h. After counting the total number of aircraft present in this iteration, aircraft generation was ceased for this iteration.
- Defining the integrated iteration rules: Repeat Steps 1 through 3 until reaching the preset number of iterations. Take the arithmetic mean of the results as the numerical simulation capacity of the terminal area. The total number of iterations k is set to 1000. The approach and departure traffic distribution data, terminal area route selection ratios, and flight durations used in this simulation are the same as those in the previous model. The arithmetic mean of the results from these 1000 computational loops is used to determine the limit capacity of the terminal area. The final results are presented in Figure 6.
4.3. Quantitative Assessment and Extrapolation
5. Conclusions
- This study validates the computed results by using a Monte Carlo-based numerical simulation method, which demonstrates a close similarity between the simulated and actual results. The computation and simulation results show that the difference between estimated and amended capacities was within 0.3 flights per hour, aligned with historical data, proving the robustness of the proposed approach. This confirms the reliability of the capacity computations obtained through the proposed model. The findings indicate that the model can accurately and reasonably estimate the terminal maneuvering area’s capacity, providing theoretical support for traffic management methods at airports and terminal maneuvering areas and offering an innovative approach to evaluating the capacity of certain airspace.
- By incorporating service resources and traffic alert operations, and examining the relationship between the maximum safe number of aircraft handled during peak periods and the capacity, this study broadens the utility of the mathematical model. It enables the prediction of the maximum safe number of aircraft that controllers can handle during peak periods based on the determined terminal maneuvering area capacity, offering guidance for shift scheduling of air traffic controllers and traffic flow management at Air Traffic Control (ATC) facilities. The model outputs can also inform flight scheduling and air traffic control departments on optimizing arrival and departure efficiency.
- This study has some limitations. First, the case study only selected the terminal maneuvering area of Hulunbuir Hailar Airport, which has limited sample representativeness. Second, human factors like fatigue also negatively impact the study, beyond the consideration of workload. Moreover, as the research is based on a single case analysis, the findings may not be directly generalizable to other terminal maneuvering areas or scenarios. The current model only considers the balance of service resource supply and demand, while stochastic factors like meteorological elements such as extreme adverse weather are not yet incorporated. In summary, the results and model need validation in more extensive samples and scenarios. This requires further refinement of the model to achieve higher fidelity to authentic operational circumstances. Future research should consider these factors from a more comprehensive perspective to enrich the applicability of the model.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, B.; Hu, M.; Tian, Y.; Huang, W. Simulation method of airspace capacity eval-uation at terminal area. J. Traffic Transp. Eng. 2003, 1, 97–100. [Google Scholar] [CrossRef]
- Pan, W.; Kang, R. Multi-airports Coordination Optimizing Model Based on Key Points Air Traffic Flow Limitation. J. Sichuan Univ. Eng. Sci. Ed. 2013, 45, 106–111. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J. Arriving and leaving aircraft scheduling model based on dynamic optimize. J. Sichuan Univ. Nat. Sci. Ed. 2012, 49, 90–96. [Google Scholar] [CrossRef]
- Mitchell, J.; Polishchuk, V.; Krozel, J. Airspace throughput analysis considering stochastic weather. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, Colorado, 21–24 August 2006; p. 6770. [Google Scholar] [CrossRef]
- Janic, M. Modeling effects of different air traffic control operational procedures, separation rules, and service disciplines on runway landing capacity. J. Adv. Transp. 2014, 48, 556–574. [Google Scholar] [CrossRef]
- Volf, P. NAS-wide simulation of air traffic with ATC behavior model. In Proceedings of the 2015 Integrated Communication, Navigation and Surveillance Conference (ICNS), Herndon, VA, USA, 21–23 April 2015; p. O3-1. Available online: https://www.researchgate.net/publication/299853129_NAS-wide_simulation_of_air_traffic_with_ATC_behavior_model (accessed on 14 October 2023).
- Kicinger, R.; Chen, J.T.; Steiner, M.; Pinto, J. Airport capacity prediction with explicit consideration of weather forecast uncertainty. J. Air Transp. 2016, 24, 18–28. [Google Scholar] [CrossRef]
- Kageyama, K. ATC Procedures Modeling for Capacity Estimation of Japanese Airspace. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, Y.; Wang, J.; Song, H.; Liu, D. Tree-based airspace capacity estimation. In Proceedings of the 2020 Integrated Communications Navigation and Surveillance Conference (ICNS), Herndon, VA, USA, 8–10 September 2020; pp. 5C1-1–5C1-8. [Google Scholar] [CrossRef]
- Zamarreño Suárez, M.; Arnaldo Valdes, R.M.; Pérez Moreno, F.; Delgado-Aguilera Jurado, R.; López de Frutos, P.M.; Gomez Comendador, V.F. How much workload is workload? A human neurophysiological and affective-cognitive performance measurement methodology for ATCOs. Aircr. Eng. Aerosp. Technol. 2022, 94, 1525–1536. [Google Scholar] [CrossRef]
- Chu, M.; Yang, Y.; Fang, J.; Cai, K. An Adaptive Capacity Estimation Method for Terminal Airspace Operation. In Proceedings of the 2022 Integrated Communication, Navigation and Surveillance Conference (ICNS), Dulles, VA, USA, 5–7 April 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Dong, X.; Hu, M.; Su, J. Terminal Capacity Assessment Based on Workload of ATC. Aeronaut. Comput. Tech. 2011, 41, 5–8+13. [Google Scholar] [CrossRef]
- Li, Y.; Hu, M.; Peng, Y.; Wang, H. Effect Mechanism of Multi-scenarios Terminal Capacity Based on Flow Decomposition Barrier. J. Southwest Jiaotong Univ. 2014, 49, 928–934. [Google Scholar] [CrossRef]
- Shen, L.; Xie, P.; Fu, C. Terminal Area Capacity Assessment Based on Certain Delay Level. Informatiz. Res. 2017, 43, 24–27+36. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKibYlV5Vjs7iAEhECQAQ9aTiC5BjCgn0Rj41MJcFXPushonbYEMvaP7kA1m32PiOQOeoUjqE9Erw&uniplatform=NZKPT&src=copy (accessed on 14 October 2023).
- Huang, H.; Gan, X.; Ding, L.; Sun, J. Study on capacity assessment method of terminal area under the influence of military activities. Adv. Aeronaut. Sci. Eng. 2020, 11, 344–352. [Google Scholar] [CrossRef]
- Ying, P.E.N.G.; Hong, W.A.N.G.; Limin, M.A.O.; Peng, W.A.N.G. Terminal Traffic Flow Prediction Method Under Convective Weather Using Deep Learning Approaches. Trans. Nanjing Univ. Aeronaut. Astronaut. 2021, 38, 634–645. [Google Scholar] [CrossRef]
- Mao, L.; Peng, Y.; Li, J.; Guo, C.; Kang, B.; Cao, Z. Random-forest based terminal capacity prediction under convective weather. Syst. Eng.—Theory Pract. 2021, 41, 2125–2136. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H.; Xiong, Y. An improved evaluation model of en route dynamic capacity. J. Sichuan Univ. Nat. Sci. Ed. 2007, 44, 1005–1008. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Wang, L. Terminal area capacity evaluation method based on following stability. Syst. Eng.—Theory Pract. 2009, 29, 173–179. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, Z. A Model for Dynamic Terminal Airspace Capacity Estimation Considering Hazardous Weather. Sci. Technol. Eng. 2015, 346, 53–59+71. [Google Scholar] [CrossRef]
- Liu, J.X.; Li, C.C. Assessment of Capacity Based on Air Traffic Controllers’ Workload Simulated on Airtop. Aeronaut. Comput. Tech. 2018, 48, 8–12. [Google Scholar] [CrossRef]
- Zhao, Z. Research on Airspace Capacity Assessment and Forecast. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CDFDLAST2016&filename=1016751873.nh (accessed on 14 October 2023).
- Civil Aviation Administration of China. Civil Aviation Air Traffic Management Rules (CCAR-93TM-R5). 21 December 2017. Available online: http://www.caac.gov.cn/XXGK/XXGK/MHGZ/201712/P020171221370496163543.pdf (accessed on 14 October 2023).
- Xie, C.; Wang, X. Terminal Area Capacity Calculation Based on Monte-Carlo Simulation Method. Aeronaut. Comput. Tech. 2009, 39, 1–4. [Google Scholar] [CrossRef]
- Bowen, E.G.; Pearcey, T. Delays in the flow of air traffic. Aeronaut. J. 1948, 52, 251–258. [Google Scholar] [CrossRef]
- Blumstein, A. An Analytical Investigation of Airport Capacity; Technical Report; Cornell Aeronautical LAB Inc.: Buffalo, NY, USA, 1960; Available online: https://www.researchgate.net/publication/235022981_AN_ANALYTICAL_INVESTIGATION_OF_AIRPORT_CAPACITY (accessed on 14 October 2023).
- Zhao, Y.; Chen, K.; Liu, G.; Yue, R. A New Flow Alert Index for Sector Congestion and Its Application. China Saf. Sci. J. 2009, 19, 103–107. [Google Scholar] [CrossRef]
- Mou, Q.; Zhang, L.; Feng, X.; Li, M.; Wang, R. 一种基于服务资源供需平衡的机场终端区容量预测方法. China Patent No. CN114758528B, 21 April 2023. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1x1h0gj0f00y0cc0sr4u06k0me444570 (accessed on 14 October 2023).
- Mou, Q.; Zhang, L.; Fang, C.; Li, M.; Feng, X. Airport Terminal Area Capacity Calculation Based on Supply and Demand Balance of Service Resources. Preprint 2022. [Google Scholar] [CrossRef]
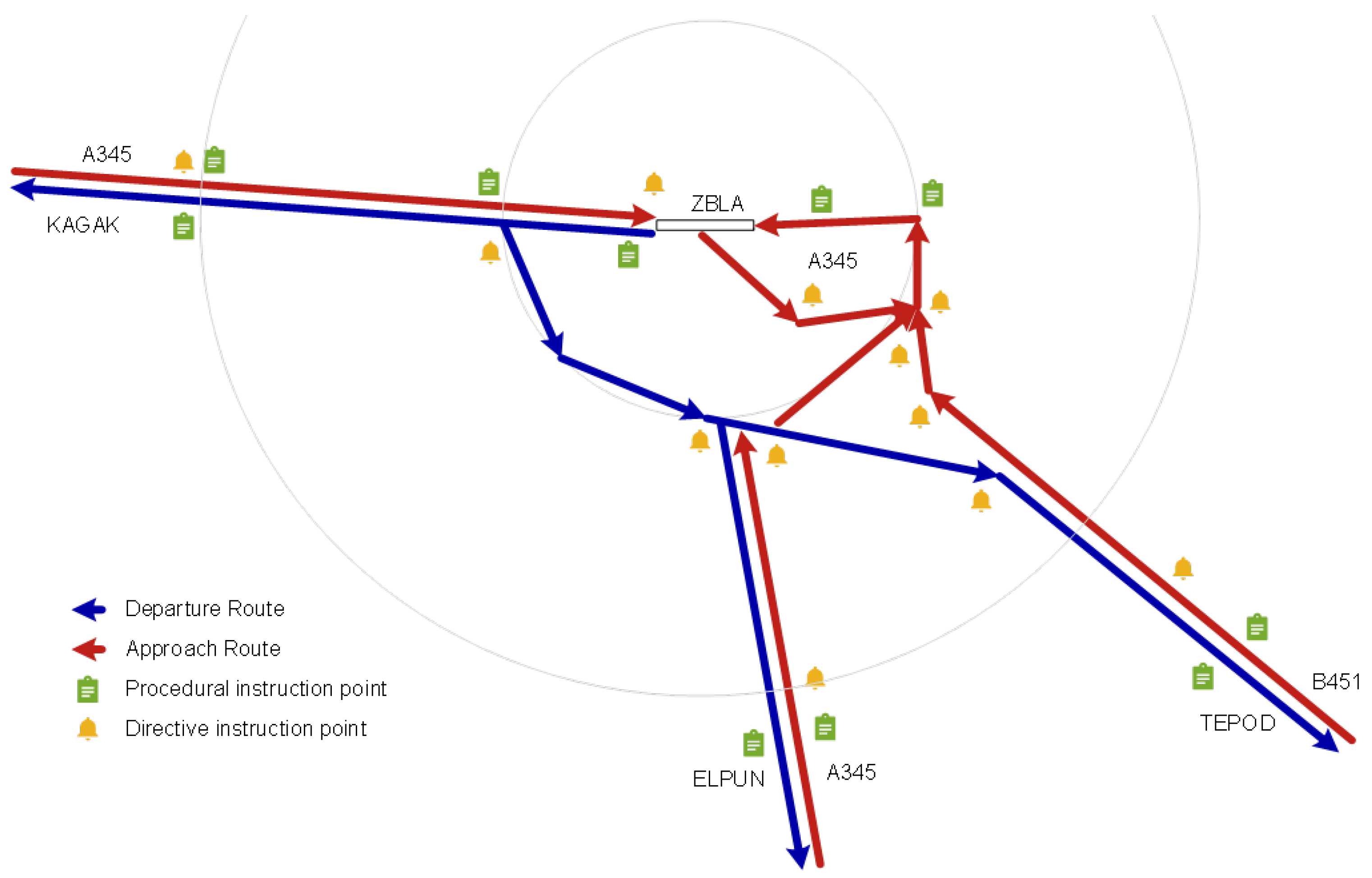


| Legend | Explanation | |||
| Flight mission | The purpose of the flight (departure or approach) | |||
| Procedure | The specific approach or departure procedure used, typically represented by a five-letter code known as a waypoint which is designated locations along an aircraft’s flight path, established according to the standards set by the ICAO | |||
| Aircraft Type | The type of aircraft | |||
| Proportion (%) | The percentage of aircraft for each procedure | |||
| Mean time (min) | The average flight time for each aircraft type during the procedure | |||
| Flight Mission | Procedure | Aircraft Type | Proportion (%) | Mean Time (min) |
| Departure | KAGAK | A320, B738 | 53% | 6.5 |
| E190, CRJ, RRJ | 30% | 8 | ||
| ATR, Y12 | 17% | 7 | ||
| ELPUN | A320, B738 | 85% | 11.2 | |
| E190, CRJ, RRJ | 15% | 14.4 | ||
| ATR, Y12 | 0% | 20.2 | ||
| TEPOD | A320, B738 | 84% | 9 | |
| E190, CRJ, RRJ | 16% | 11.5 | ||
| ATR, Y12 | 0% | 16.2 | ||
| Approach | KAGAK | A320, B738 | 53% | 12.3 |
| E190, CRJ, RRJ | 30% | 15.8 | ||
| ATR, Y12 | 17% | 22.2 | ||
| ELPUN | A320, B738 | 85% | 7.8 | |
| E190, CRJ, RRJ | 15% | 10.1 | ||
| ATR, Y12 | 0% | 14.2 | ||
| TEPOD | A320, B738 | 84% | 6 | |
| E190, CRJ, RRJ | 16% | 7.7 | ||
| ATR, Y12 | 0% | 10.8 | ||
| Assessment Models | Ultimate Capacity (fph) | Corrected Capacity (fph) |
|---|---|---|
| Mathematical modeling | 24.230 | 16.961 |
| Numerical simulation | 23.939 | 16.757 |
| ATC simulator experiment | - | 17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, Q.; Yang, Z.; Zhang, L. A Methodology for Assessing Capacity of the Terminal Maneuvering Area Based on Service Resource Equilibrium. Aerospace 2023, 10, 894. https://doi.org/10.3390/aerospace10100894
Mou Q, Yang Z, Zhang L. A Methodology for Assessing Capacity of the Terminal Maneuvering Area Based on Service Resource Equilibrium. Aerospace. 2023; 10(10):894. https://doi.org/10.3390/aerospace10100894
Chicago/Turabian StyleMou, Qifeng, Ze Yang, and Liming Zhang. 2023. "A Methodology for Assessing Capacity of the Terminal Maneuvering Area Based on Service Resource Equilibrium" Aerospace 10, no. 10: 894. https://doi.org/10.3390/aerospace10100894
APA StyleMou, Q., Yang, Z., & Zhang, L. (2023). A Methodology for Assessing Capacity of the Terminal Maneuvering Area Based on Service Resource Equilibrium. Aerospace, 10(10), 894. https://doi.org/10.3390/aerospace10100894







