Learning to Predict 3D Rotational Dynamics from Images of a Rigid Body with Unknown Mass Distribution
Abstract
:1. Introduction
2. Related Work
3. Background
3.1. The Parameterization of 3D Rotation Group SO(3)
3.2. 3D Rotating Rigid-Body Kinematics
3.3. 3D Rigid-Body Dynamics in Hamiltonian Form
4. Materials and Methods
4.1. Notation
4.2. Embedding Images to an SO(3) Latent Space
4.3. Computing Dynamics in the Latent Space
| Algorithm 1: An algorithm to calculate the body angular velocity given two sequential orientation matrices and the time step in between them. |
 |
4.4. Decoding SO(3) Latent States to Images
4.5. Training Methodology
4.5.1. Reconstruction Losses
4.5.2. Latent Losses
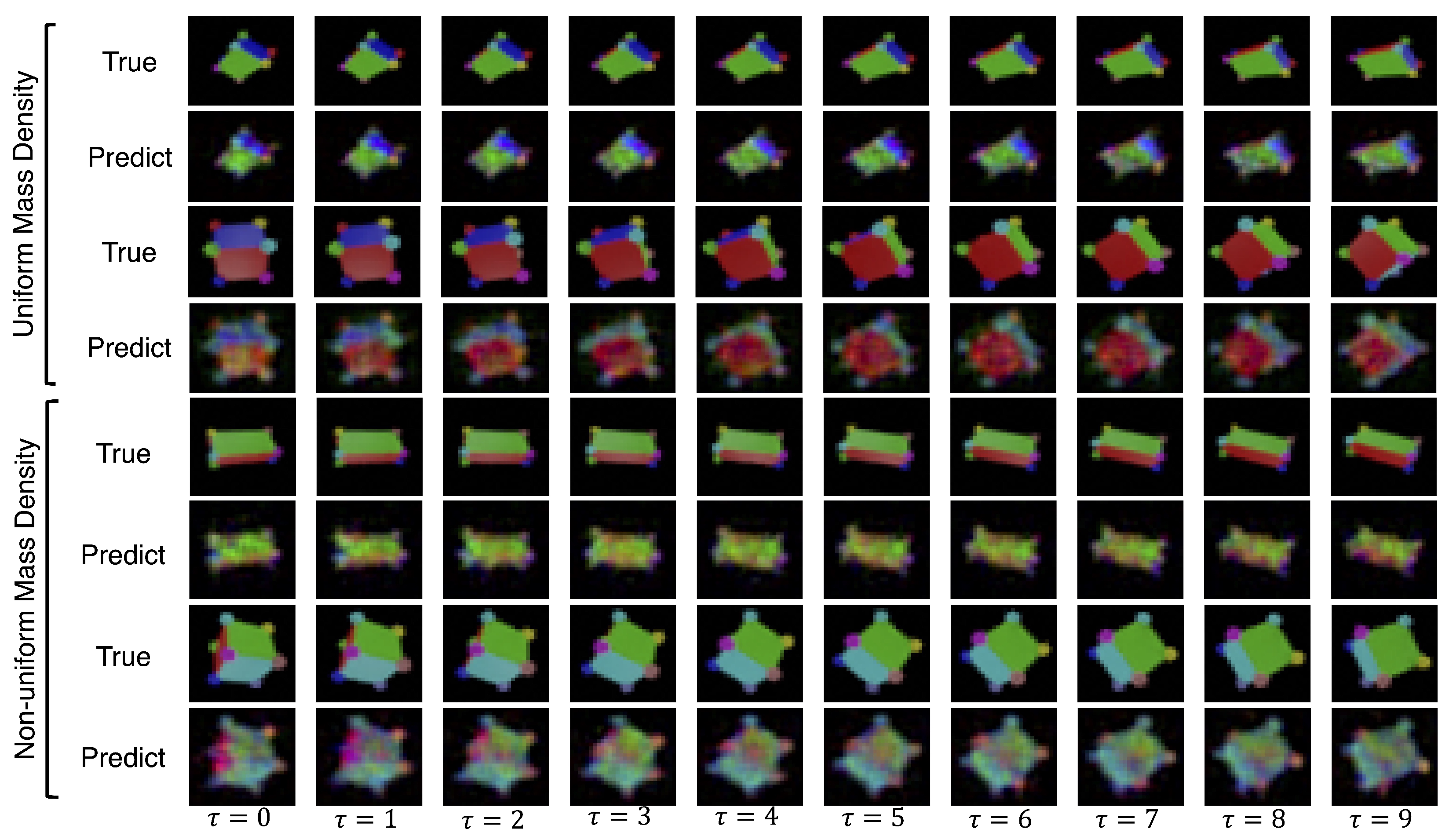
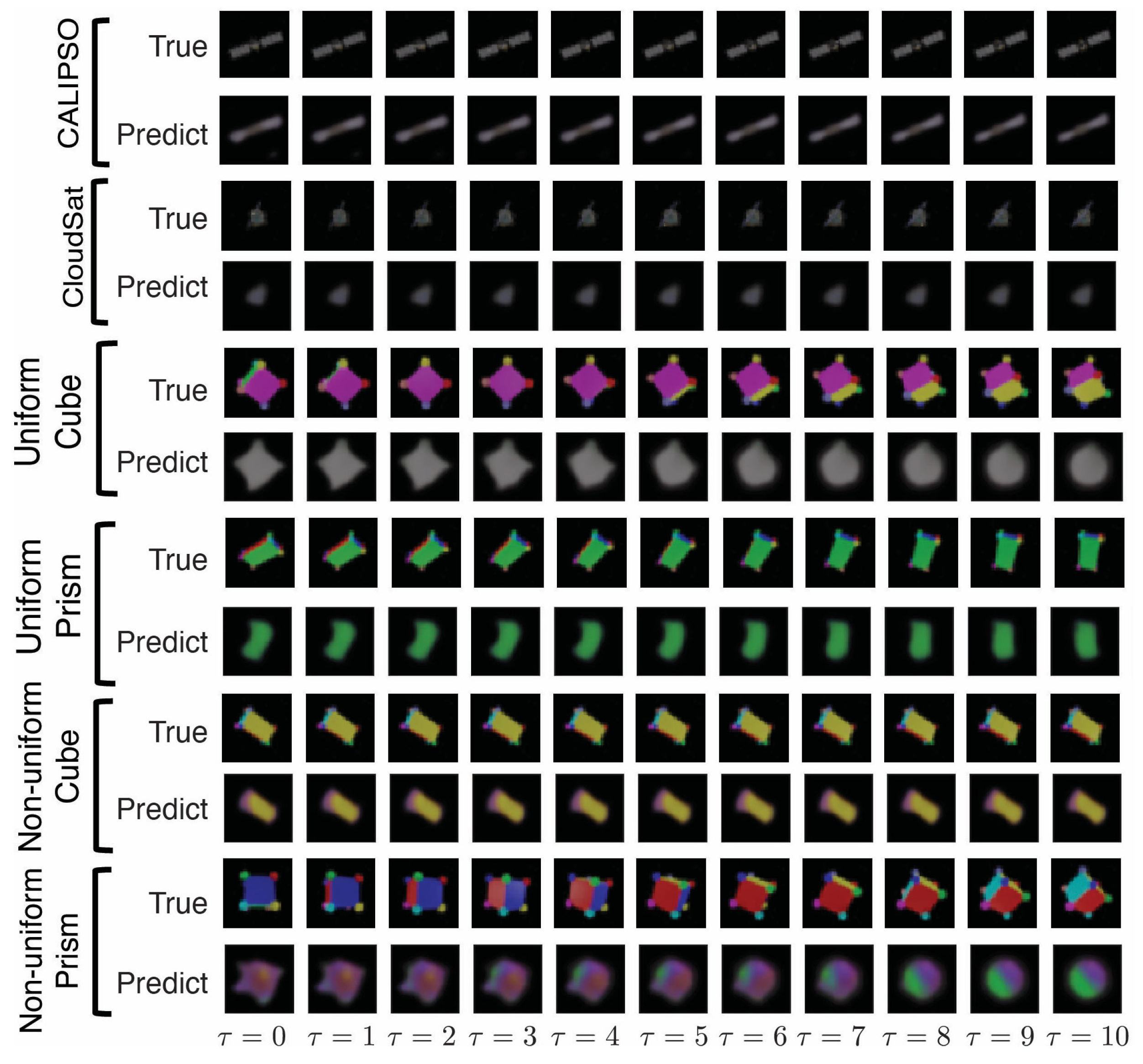
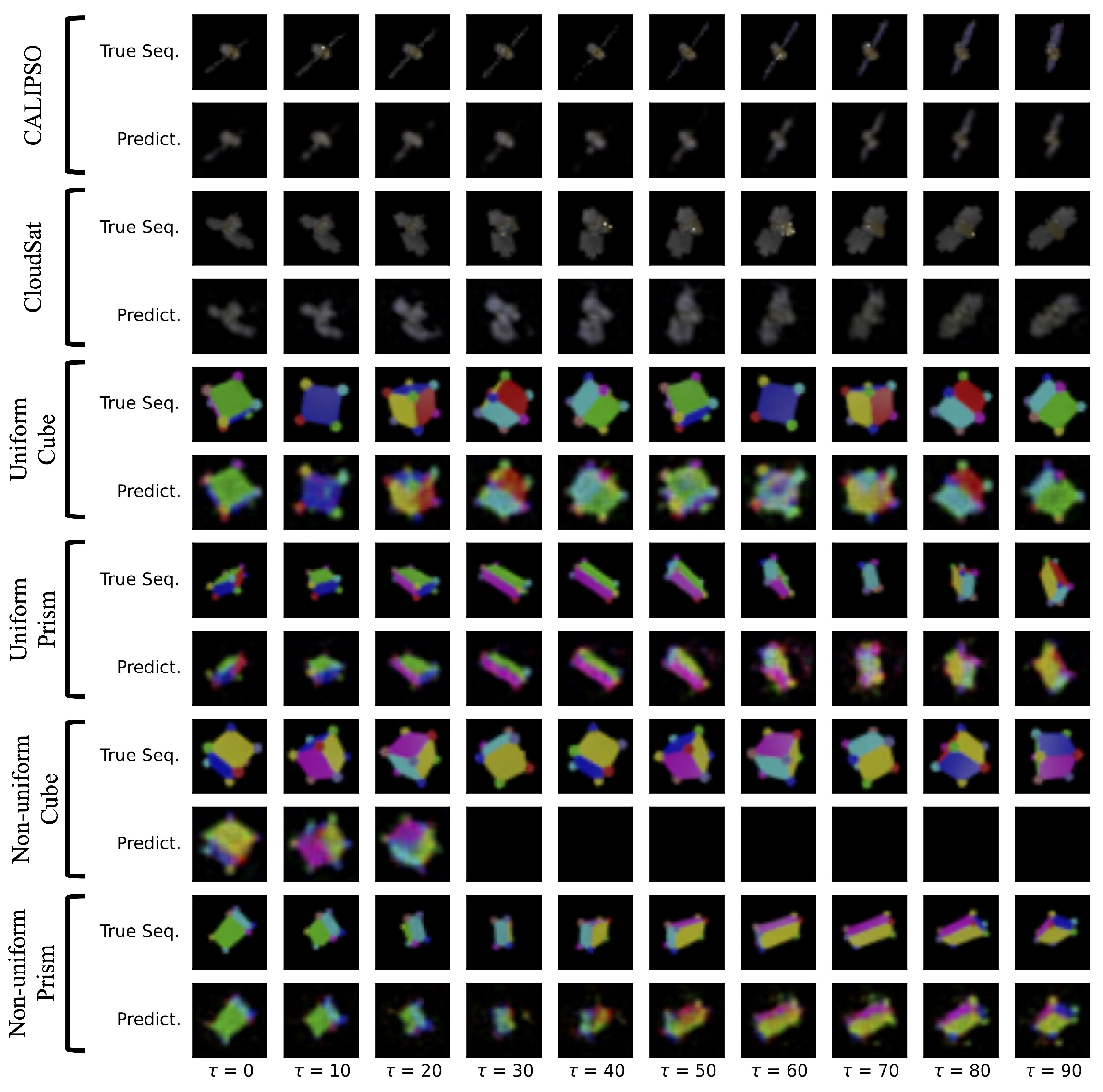
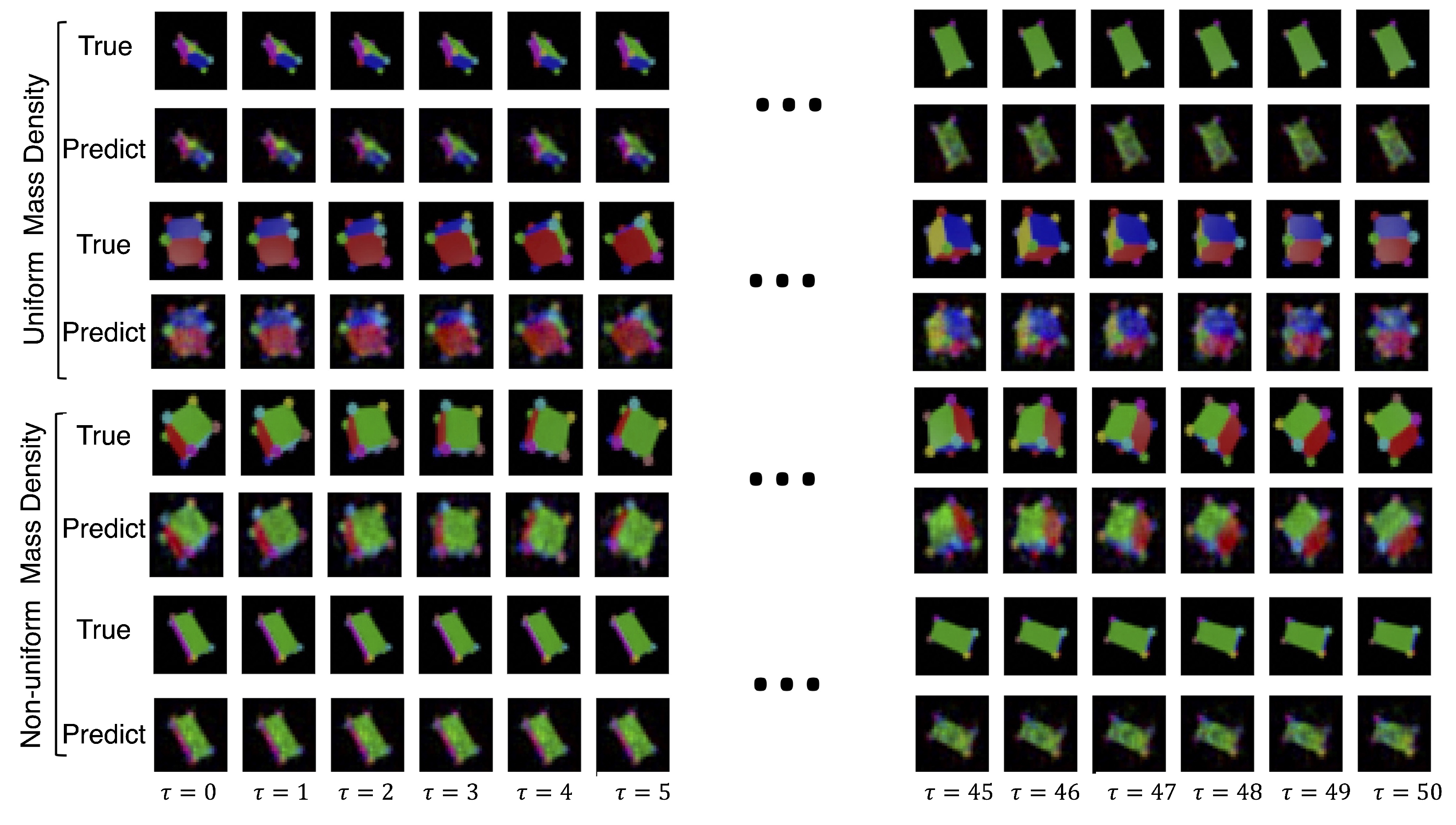
4.6. 3D Rotating Rigid-Body Datasets
- Uniform mass density cube: a multi-colored cube of uniform mass density;
- Uniform mass density prism: a multi-colored rectangular prism with uniform mass density;
- Non-uniform mass density cube: a multi-colored cube with non-uniform mass density;
- Non-uniform mass density prism: a multi-colored prism with non-uniform mass density;
- Uniform density synthetic-satellites: renderings of CALIPSO and CloudSat satellites with uniform mass density.
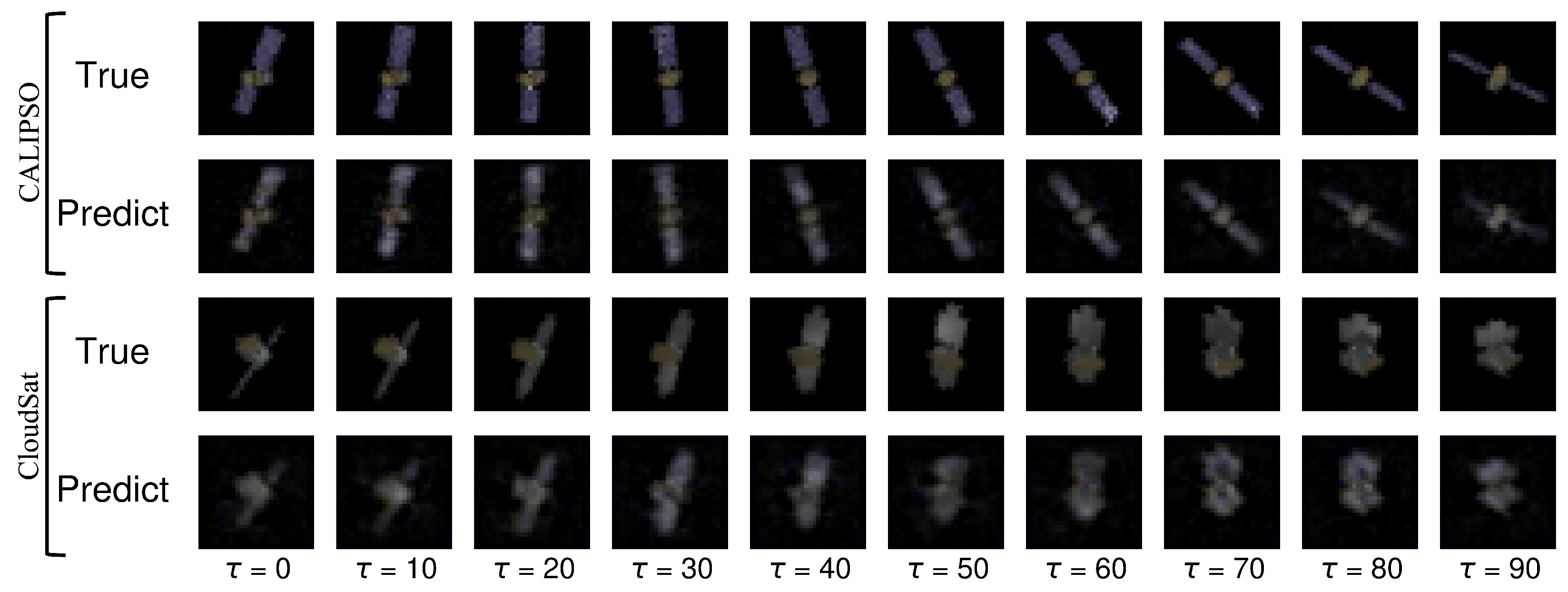
5. Results
6. Summary and Conclusions
6.1. Summary
6.2. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Rigid Body Rotational Dynamics and Stability
Appendix A.2. Dataset Generation Parameters
Appendix A.2.1. Uniform Mass Density Cube
| Object | Moment-of-Inertia Tensor | Inverse Moment-of-Inertia Tensor | Principal Axes |
|---|---|---|---|
| Uniform Cube | |||
| Uniform Prism | |||
| Non-uniform Cube | |||
| Non-uniform Prism | |||
| CALIPSO | |||
| CloudSat |
Appendix A.2.2. Uniform Mass Density Prism
Appendix A.2.3. Non-Uniform Mass Density Cube
Appendix A.2.4. Non-Uniform Mass Density Prism
Appendix A.2.5. CALIPSO
Appendix A.2.6. CloudSat
Appendix A.3. Hyperparameters
| Experiment Hyperparameters | |
|---|---|
| Parameter Name | Value |
| Random seed | 0 |
| Test dataset split | 0.2 |
| Validation dataset split | 0.1 |
| Number of epochs | 1000 |
| Batch size | 256 |
| Autoencoder learning rate | |
| Dynamics learning rate | |
| Sequence length | 10 |
| Time step | |
Appendix A.4. Performance of Baseline Models
Appendix A.4.1. LSTM-Baseline

Appendix A.4.2. Neural ODE [33]-Baseline
Appendix A.4.3. Hamiltonian Generative Network (HGN)
Appendix A.5. Ablation Studies

| Dataset | total | dyn | dyn + ae | dyn + latent | ||||
|---|---|---|---|---|---|---|---|---|
| TRAIN | TEST | TRAIN | TEST | TRAIN | TEST | TRAIN | TEST | |
| Uniform Prism | 3.03 ± 1.26 | 3.05 ± 1.21 | 3.99 ± 1.21 | 3.74 ± 0.93 | 3.99 ± 1.50 | 3.85 ± 1.45 | 4.82 ± 1.32 | 5.09 ± 1.53 |
| Uniform Cube | 4.13 ± 2.14 | 4.62 ± 2.02 | 5.73 ± 0.51 | 5.87 ± 0.56 | 7.11 ± 2.63 | 6.95 ± 2.41 | 2.80 ± 0.18 | 2.80 ± 0.20 |
| Non-uniform Prism | 4.98 ± 1.26 | 7.07 ± 1.88 | 4.27 ± 1.28 | 3.89 ± 1.10 | 3.86 ± 1.38 | 3.66 ± 1.27 | 4.16 ± 1.27 | 5.09 ± 1.53 |
| Non-uniform Cube | 7.27 ± 1.06 | 5.65 ± 1.50 | 6.23 ± 0.88 | 5.93 ± 0.85 | - | - | 8.78 ± 0.93 | 8.64 ± 1.14 |
| CALIPSO | 1.18 ± 0.43 | 1.19 ± 0.63 | 2.00 ± 0.78 | 1.85 ± 0.58 | 1.73 ± 0.73 | 1.62 ± 0.50 | 0.49 ± 0.07 | 0.54 ± 0.18 |
| CloudSat | 1.32 ± 0.74 | 1.56 ± 1.01 | 0.96 ± 0.17 | 1.39 ± 0.48 | 0.87 ± 0.29 | 1.40 ± 0.40 | 0.28 ± 0.06 | 0.28 ± 0.06 |

References
- Williams, B.; Antreasian, P.; Carranza, E.; Jackman, C.; Leonard, J.; Nelson, D.; Page, B.; Stanbridge, D.; Wibben, D.; Williams, K.; et al. OSIRIS-REx Flight Dynamics and Navigation Design. Space Sci. Rev. 2018, 214, 69. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Mark, C.P.; Kamath, S. Review of active space debris removal methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Zhong, Y.D.; Leonard, N.E. Unsupervised Learning of Lagrangian Dynamics from Images for Prediction and Control. In Proceedings of the Conference on Neural Information Processing Systems 2020, Virtual, 6–12 December 2020. [Google Scholar]
- Toth, P.; Rezende, D.J.; Jaegle, A.; Racanière, S.; Botev, A.; Higgins, I. Hamiltonian Generative Networks. In Proceedings of the International Conference on Learning Representations 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Allen-Blanchette, C.; Veer, S.; Majumdar, A.; Leonard, N.E. LagNetViP: A Lagrangian Neural Network for Video Prediction. arXiv 2020, arXiv:2010.12932. [Google Scholar]
- Byravan, A.; Fox, D. SE3-nets: Learning Rigid Body Motion Using Deep Neural Networks. In Proceedings of the International Conference on Robotics and Automation 2017, Singapore, 29 May–3 June 2017. [Google Scholar]
- Peretroukhin, V.; Giamou, M.; Rosen, D.M.; Greene, W.N.; Roy, N.; Kelly, J. A Smooth Representation of Belief over SO(3) for Deep Rotation Learning with Uncertainty. arXiv 2020, arXiv:2006.01031. [Google Scholar]
- Duong, T.; Atanasov, N. Hamiltonian-based Neural ODE Networks on the SE(3) Manifold For Dynamics Learning and Control. In Proceedings of the Robotics: Science and Systems, Virtual, 12–16 July 2021. [Google Scholar]
- Greydanus, S.; Dzamba, M.; Yosinski, J. Hamiltonian Neural Networks. In Proceedings of the Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Chen, Z.; Zhang, J.; Arjovsky, M.; Bottou, L. Symplectic Recurrent Neural Networks. In Proceedings of the International Conference on Learning Representations 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Cranmer, M.; Greydanus, S.; Hoyer, S.; Battaglia, P.W.; Spergel, D.N.; Ho, S. Lagrangian Neural Networks. In Proceedings of the International Conference on Learning Representations 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Falorsi, L.; de Haan, P.; Davidson, T.R.; Cao, N.D.; Weiler, M.; Forré, P.; Cohen, T.S. Explorations in Homeomorphic Variational Auto-Encoding. In Proceedings of the International Conference of Machine Learning Workshop on Theoretical Foundations and Application of Deep Generative Models, Stockholm, Sweden, 14–15 July 2018. [Google Scholar]
- Levinson, J.; Esteves, C.; Chen, K.; Snavely, N.; Kanazawa, A.; Rostamizadeh, A.; Makadia, A. An analysis of svd for deep rotation estimation. Adv. Neural Inf. Process. Syst. 2020, 33, 22554–22565. [Google Scholar]
- Brégier, R. Deep regression on manifolds: A 3D rotation case study. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 166–174. [Google Scholar]
- Zhou, Y.; Barnes, C.; Lu, J.; Yang, J.; Li, H. On the Continuity of Rotation Representations in Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5738–5746. [Google Scholar]
- Andrle, M.S.; Crassidis, J.L. Geometric Integration of Quaternions. AIAA J. Guid. Control 2013, 36, 1762–1772. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics; Addison Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Zhong, Y.D.; Dey, B.; Chakraborty, A. Symplectic ODE-Net: Learning Hamiltonian Dynamics with Control. In Proceedings of the International Conference on Learning Representations 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Zhong, Y.D.; Dey, B.; Chakraborty, A. Dissipative SymODEN: Encoding Hamiltonian Dynamics with Dissipation and Control into Deep Learning. In Proceedings of the ICLR 2020 Workshop on Integration of Deep Neural Models and Differential Equations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Finzi, M.; Wang, K.A.; Wilson, A.G. Simplifying Hamiltonian and Lagrangian Neural Networks via Explicit Constraints. Conf. Neural Inf. Process. Syst. 2020, 33, 13. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Global Formulations of Lagrangian and Hamiltonian Dynamics on Manifolds; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry; Texts in Applied Mathematics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Lin, Z. Riemannian Geometry of Symmetric Positive Definite Matrices via Cholesky Decomposition. SIAM J. Matrix Anal. Appl. 2019, 40, 1353–1370. [Google Scholar] [CrossRef]
- Atkinson, K.A. An Introduction to Numerical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Markley, F.L. Unit quaternion from rotation matrix. AIAA J. Guid. Control 2008, 31, 440–442. [Google Scholar] [CrossRef]
- Kisantal, M.; Sharma, S.; Park, T.H.; Izzo, D.; Martens, M.; D’Amico, S. Satellite Pose Estimation Challenge: Dataset, Competition Design, and Results. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4083–4098. [Google Scholar] [CrossRef]
- Sharma, S.; Beierle, C.; D’Amico, S. Pose estimation for non-cooperative spacecraft rendezvous using convolutional neural networks. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–12. [Google Scholar] [CrossRef]
- Park, T.H.; Märtens, M.; Lecuyer, G.; Izzo, D.; D’Amico, S. SPEED+: Next-Generation Dataset for Spacecraft Pose Estimation across Domain Gap. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–15. [Google Scholar] [CrossRef]
- Proença, P.F.; Gao, Y. Deep Learning for Spacecraft Pose Estimation from Photorealistic Rendering. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 6007–6013. [Google Scholar] [CrossRef]
- Community, B.O. Blender—A 3D Modelling and Rendering Package; Blender Foundation, Stichting Blender Foundation: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Chen, R.T.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D.K. Neural ordinary differential equations. Adv. Neural Inf. Process. Syst. 2018, 31, 1–13. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Balsells Rodas, C.; Canal Anton, O.; Taschin, F. [Re] Hamiltonian Generative Networks. ReScience C 2021, 7. [Google Scholar] [CrossRef]
- Watter, M.; Springenberg, J.T.; Boedecker, J.; Riedmiller, M. Embed to control: A locally linear latent dynamics model for control from raw images. Adv. Neural Inf. Process. Syst. 2015, 27, 1–9. [Google Scholar]


| Dataset | Ours | LSTM-Baseline | Neural ODE-Baseline | HGN | ||||
|---|---|---|---|---|---|---|---|---|
| TRAIN | TEST | TRAIN | TEST | TRAIN | TEST | TRAIN | TEST | |
| Uniform Prism | 2.66 ± 0.10 | 2.71 ± 0.08 | 3.46 ± 0.59 | 3.47 ± 0.61 | 3.96 ± 0.68 | 4.00 ± 0.68 | 4.18 ± 0.0 | 7.80 ± 0.30 |
| Uniform Cube | 3.54 ± 0.17 | 3.97 ± 0.16 | 21.55 ± 1.98 | 21.64 ± 2.12 | 9.48 ± 1.19 | 9.43 ± 1.20 | 17.43 ± 0.00 | 18.69 ± 0.12 |
| Non-uniform Prism | 4.27 ± 0.18 | 6.61 ± 0.88 | 4.50 ± 1.31 | 4.52 ± 1.34 | 4.67 ± 0.58 | 4.75 ± 0.59 | 6.16 ± 0.08 | 8.33 ± 0.26 |
| Non-uniform Cube | 6.24 ± 0.29 | 4.85 ± 0.35 | 7.47 ± 0.51 | 7.51 ± 0.50 | 7.89 ± 1.50 | 7.94 ± 1.59 | 14.11 ± 0.13 | 18.14 ± 0.36 |
| CALIPSO | 0.79 ± 0.53 | 0.87 ± 0.50 | 0.62 ± 0.21 | 0.65 ± 0.22 | 0.69 ± 0.26 | 0.71 ± 0.27 | 1.18 ± 0.02 | 1.34 ± 0.05 |
| CloudSat | 0.64 ± 0.45 | 0.65 ± 0.29 | 0.89 ± 0.36 | 0.93 ± 0.43 | 0.65 ± 0.22 | 0.66 ± 0.25 | 1.48 ± 0.04 | 1.66 ± 0.11 |
| Number of Parameters | 6 | 52,400 | 11,400 | - | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mason, J.J.; Allen-Blanchette, C.; Zolman, N.; Davison, E.; Leonard, N.E. Learning to Predict 3D Rotational Dynamics from Images of a Rigid Body with Unknown Mass Distribution. Aerospace 2023, 10, 921. https://doi.org/10.3390/aerospace10110921
Mason JJ, Allen-Blanchette C, Zolman N, Davison E, Leonard NE. Learning to Predict 3D Rotational Dynamics from Images of a Rigid Body with Unknown Mass Distribution. Aerospace. 2023; 10(11):921. https://doi.org/10.3390/aerospace10110921
Chicago/Turabian StyleMason, Justice J., Christine Allen-Blanchette, Nicholas Zolman, Elizabeth Davison, and Naomi Ehrich Leonard. 2023. "Learning to Predict 3D Rotational Dynamics from Images of a Rigid Body with Unknown Mass Distribution" Aerospace 10, no. 11: 921. https://doi.org/10.3390/aerospace10110921
APA StyleMason, J. J., Allen-Blanchette, C., Zolman, N., Davison, E., & Leonard, N. E. (2023). Learning to Predict 3D Rotational Dynamics from Images of a Rigid Body with Unknown Mass Distribution. Aerospace, 10(11), 921. https://doi.org/10.3390/aerospace10110921





