Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net
Abstract
1. Introduction
2. Dynamic Model of the Rectangular Tether-Net
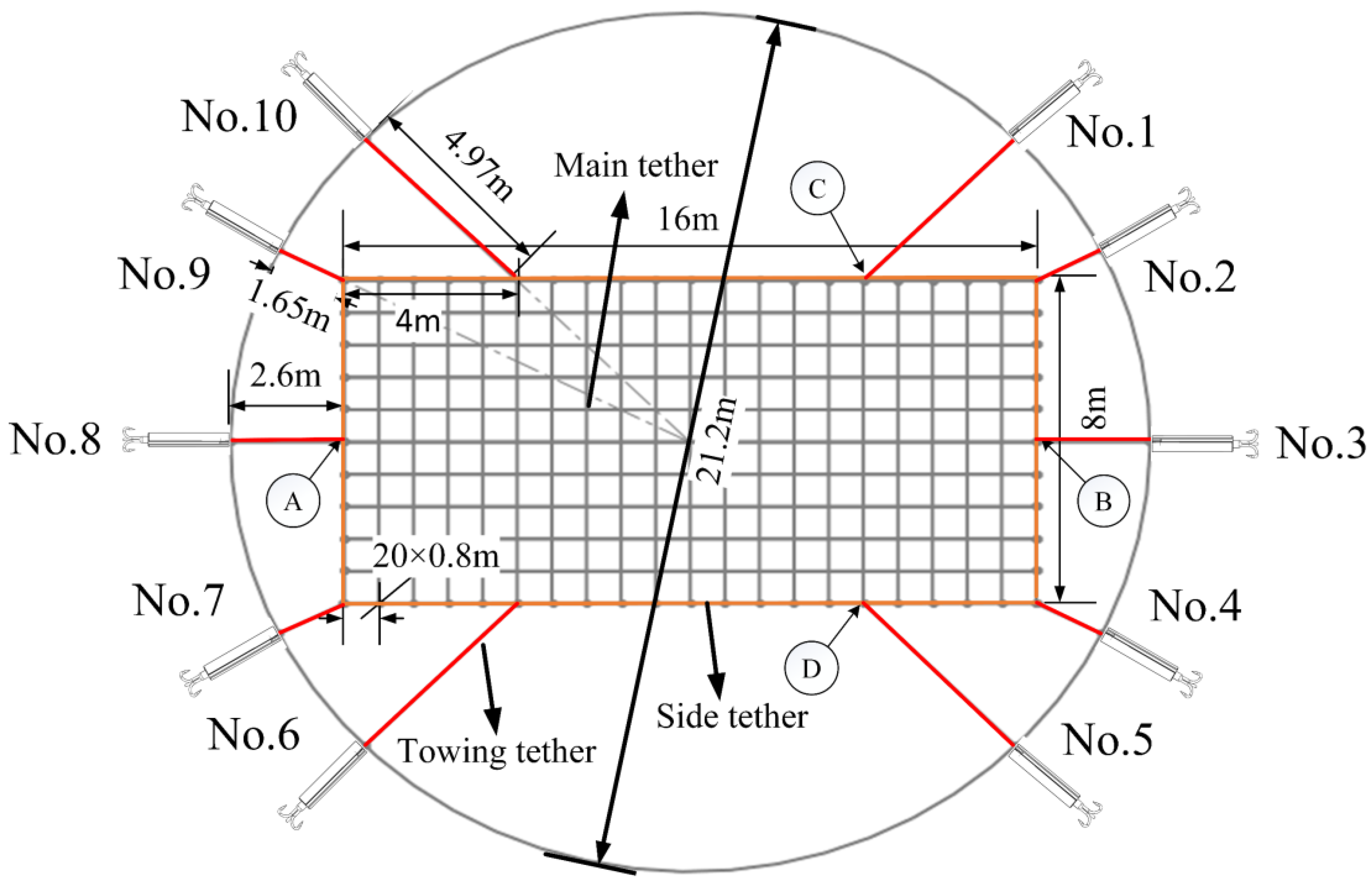
2.1. Overview of the Rectangular Tether-Net
2.2. Model Description
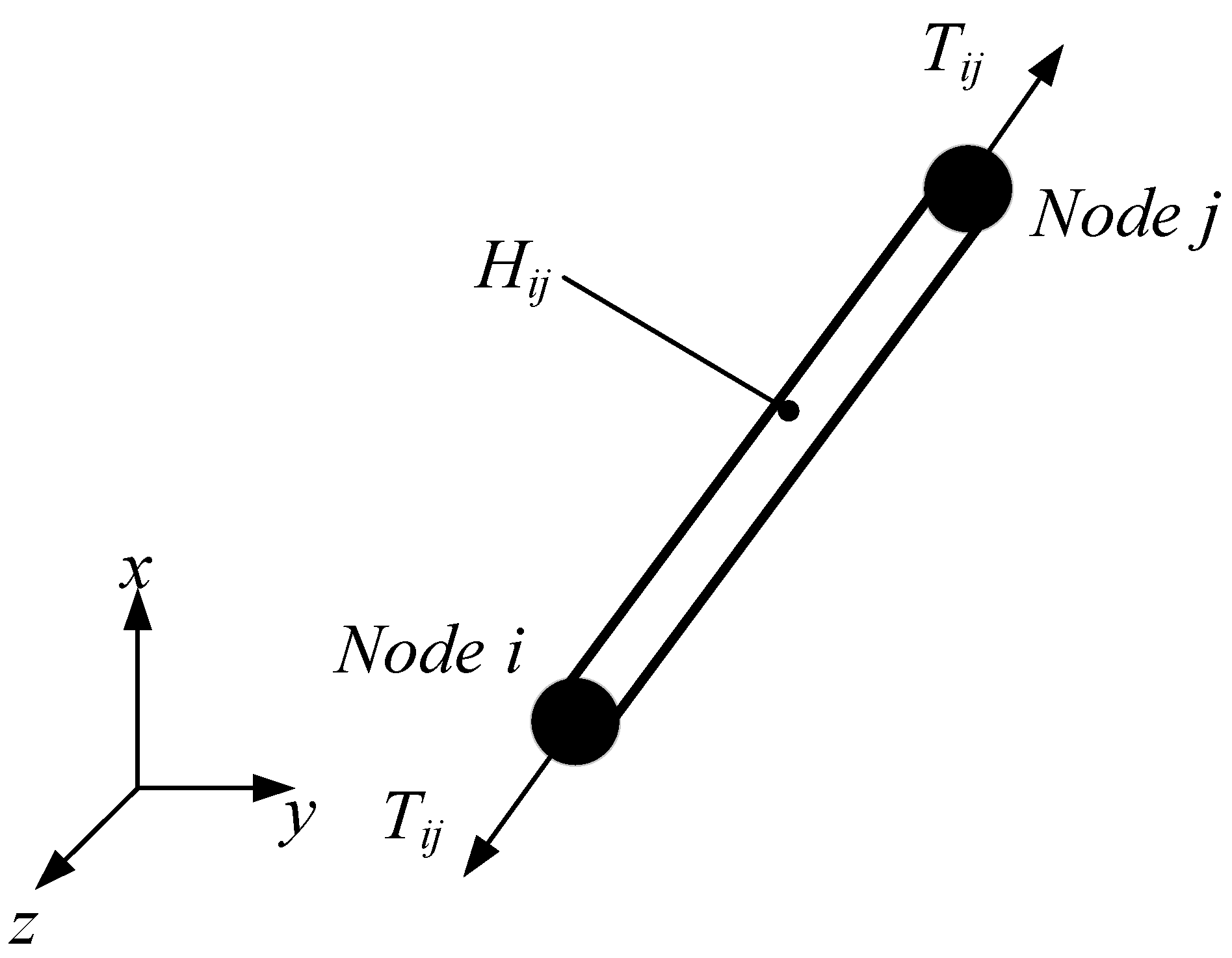
2.3. Establishment of the Tether-Net Dynamic Model
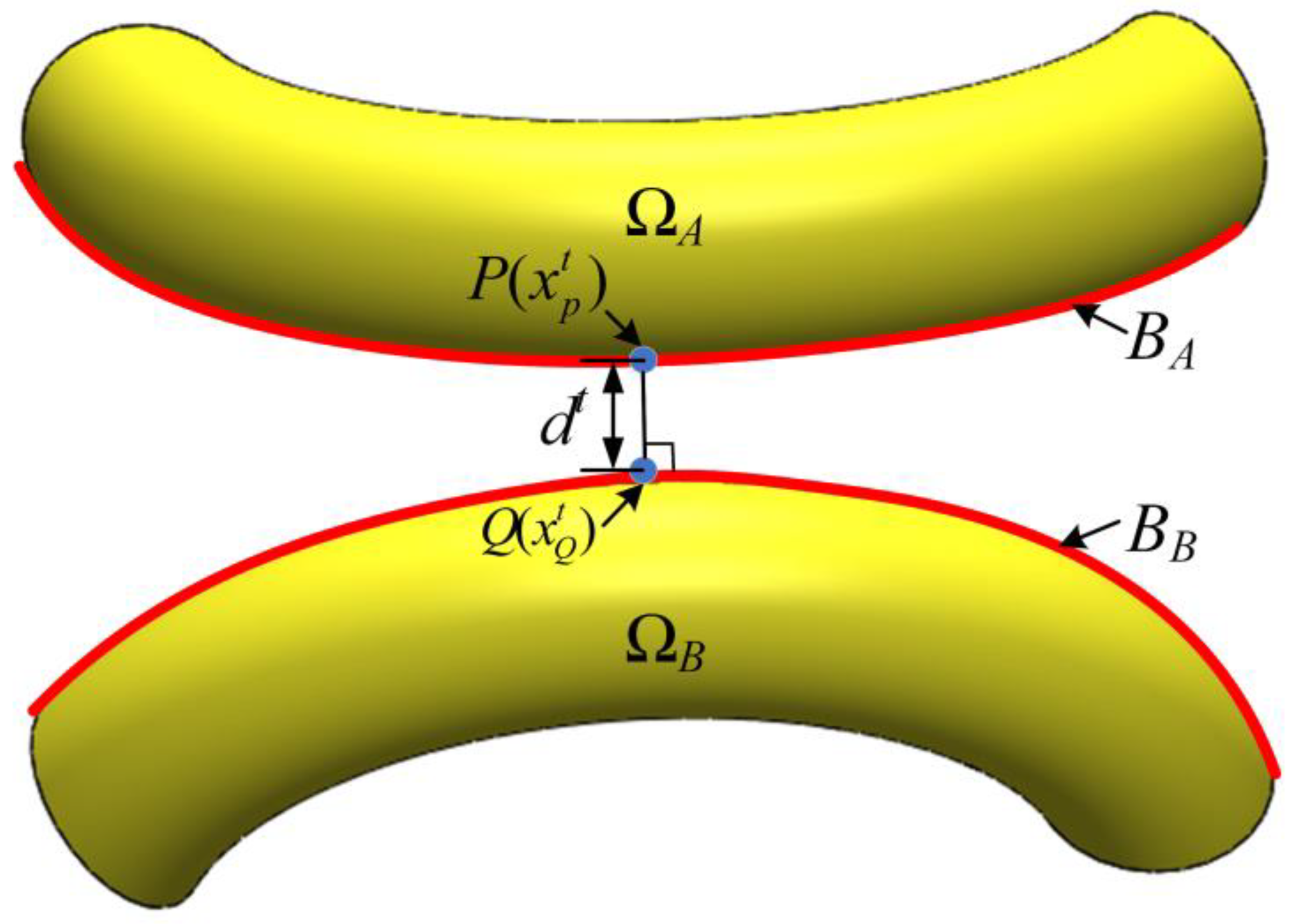
2.4. Contact between Net Tethers
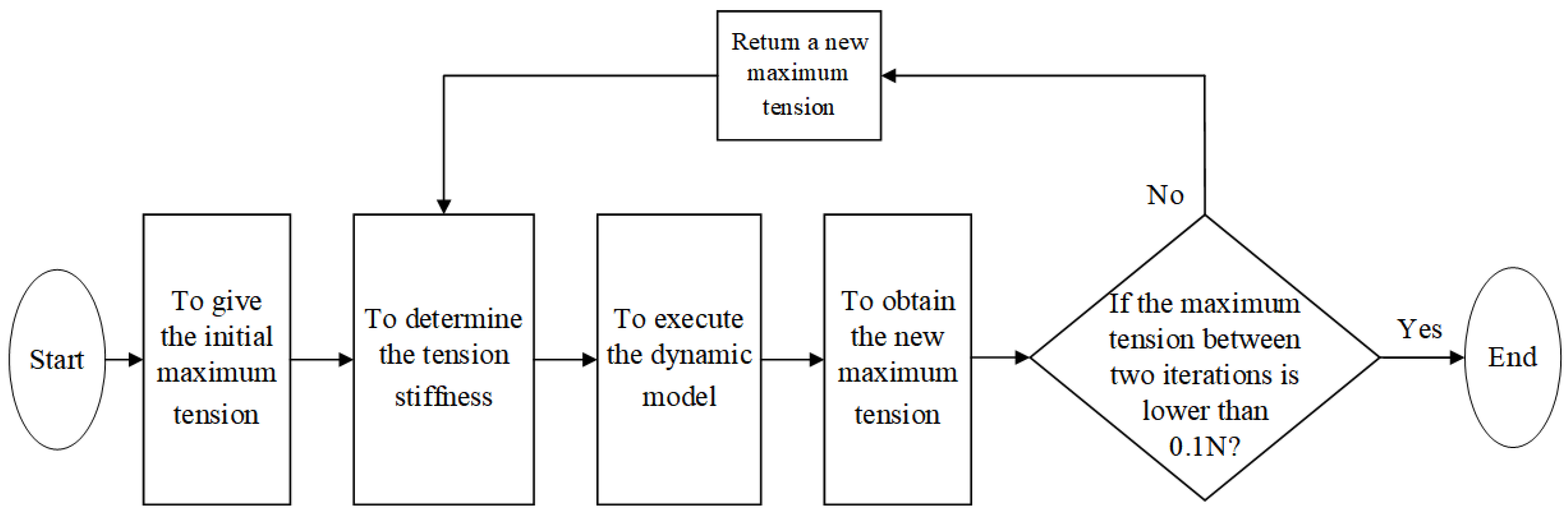
2.5. Solution of the Tether-Net Dynamic Model
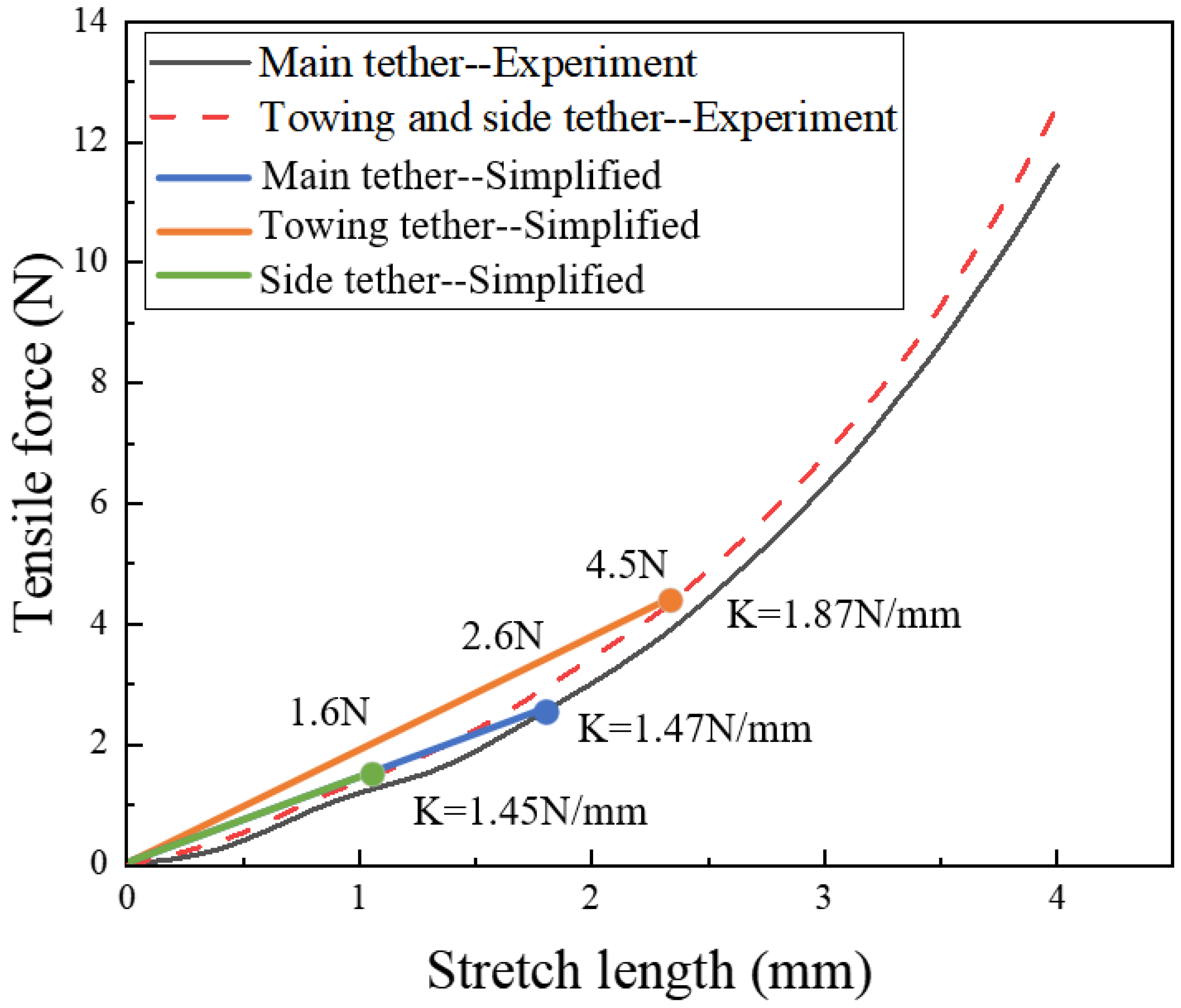
2.6. Elastic Moduli of Net Tethers
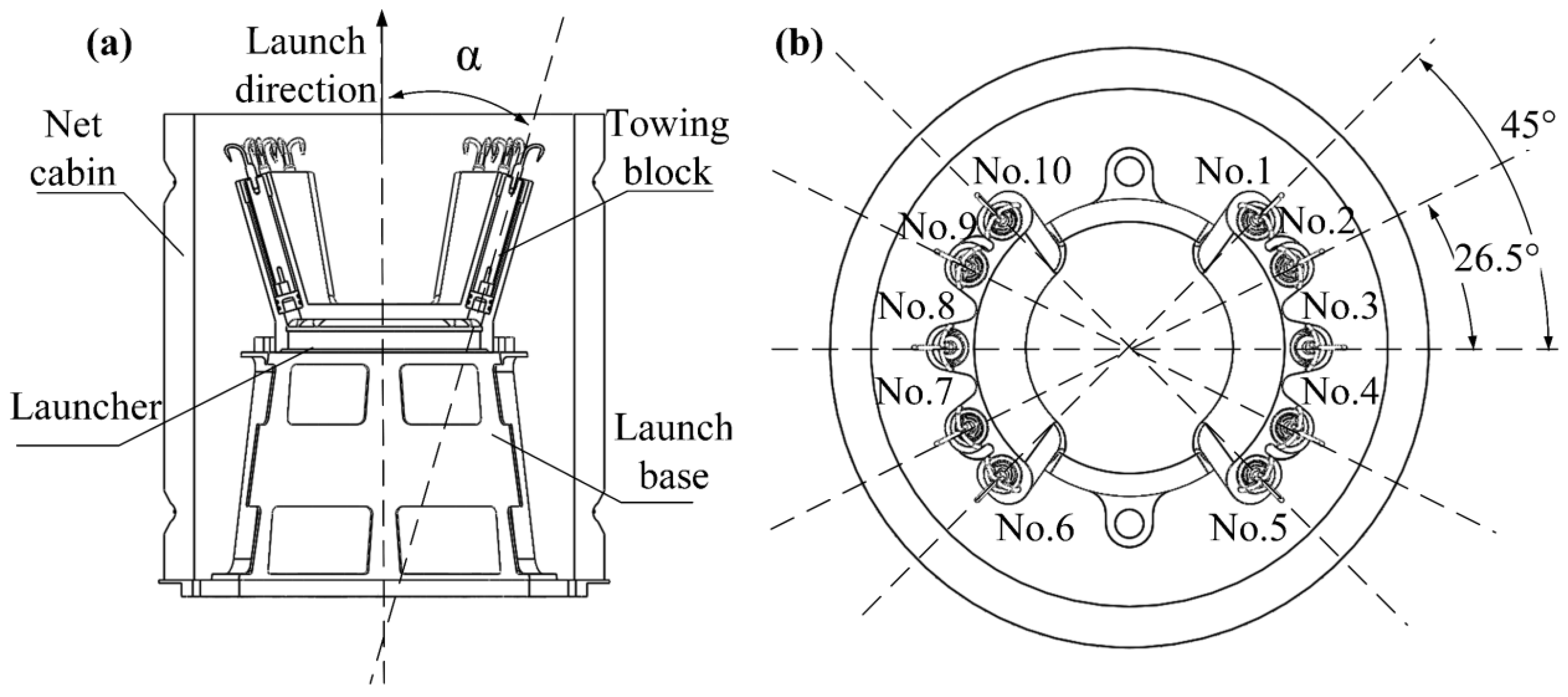
2.7. Interior Ballistics of the Tether-Net System
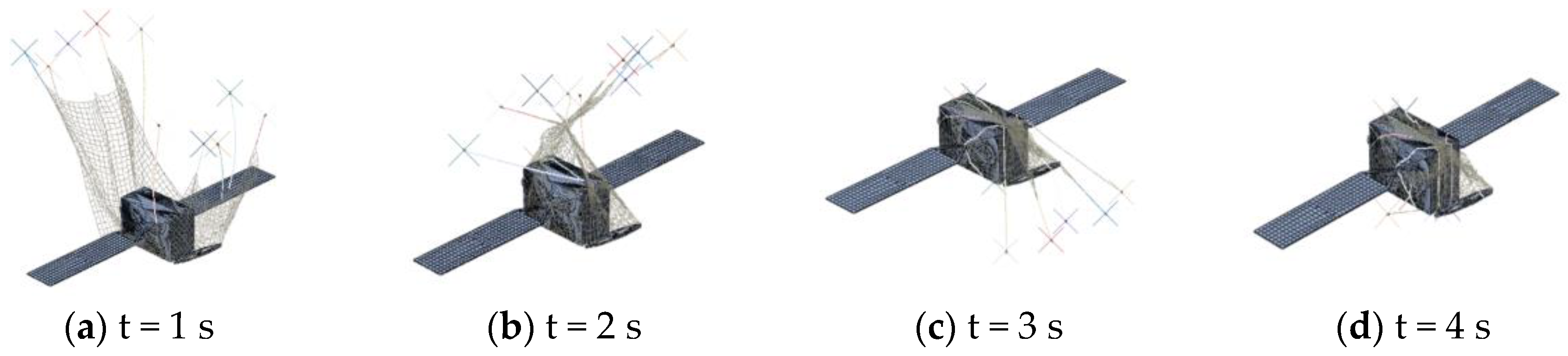
3. Experimental Validation
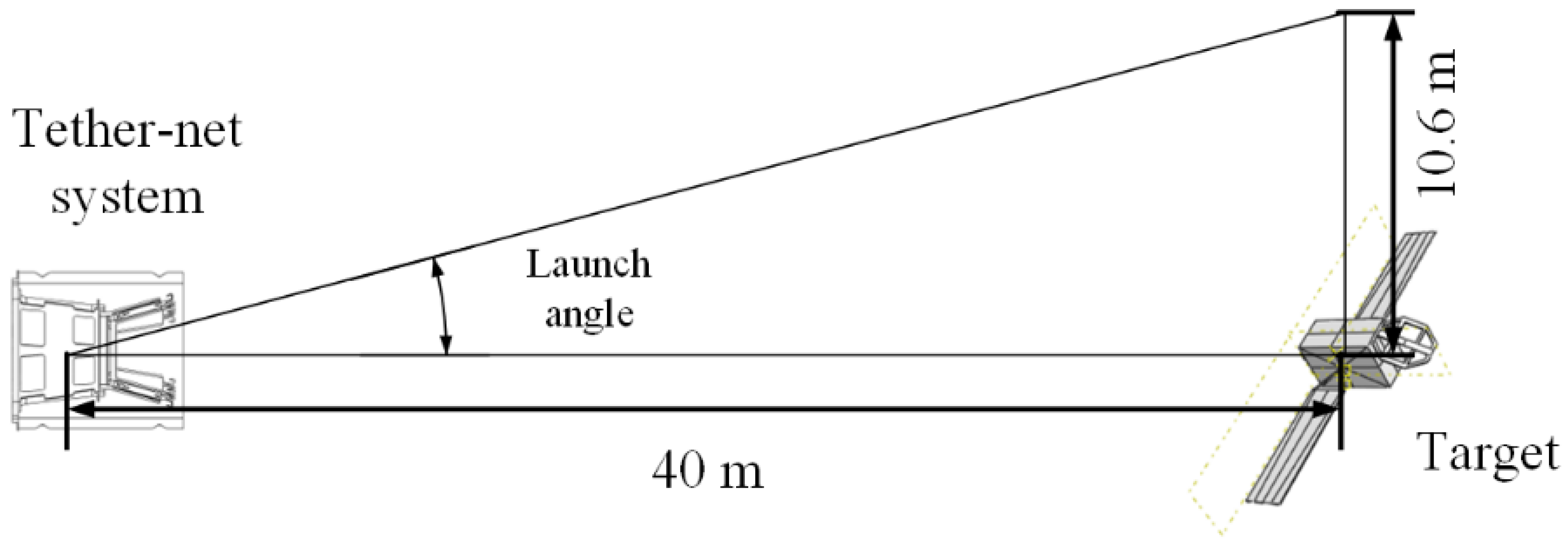
3.1. Prototype Design
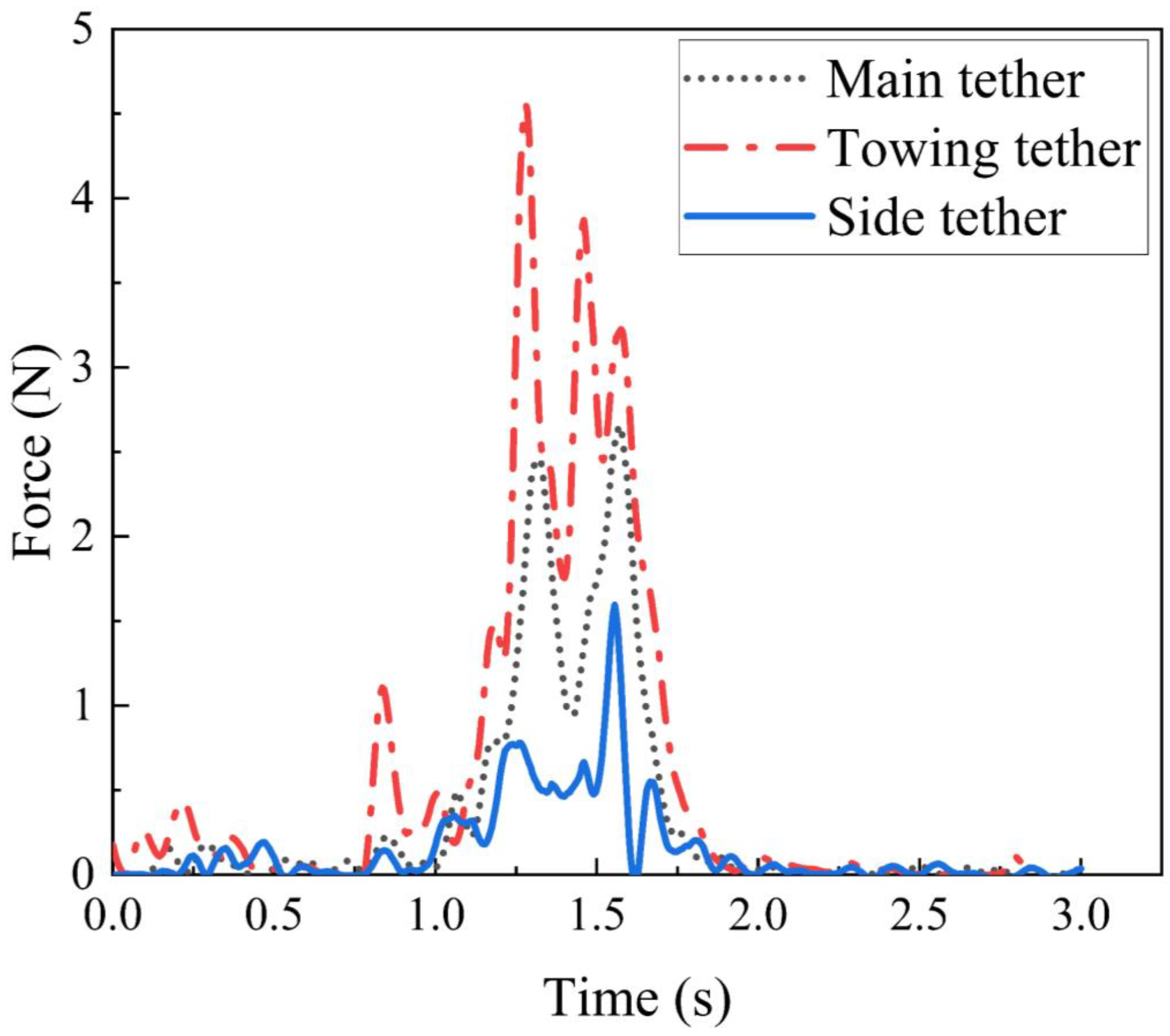
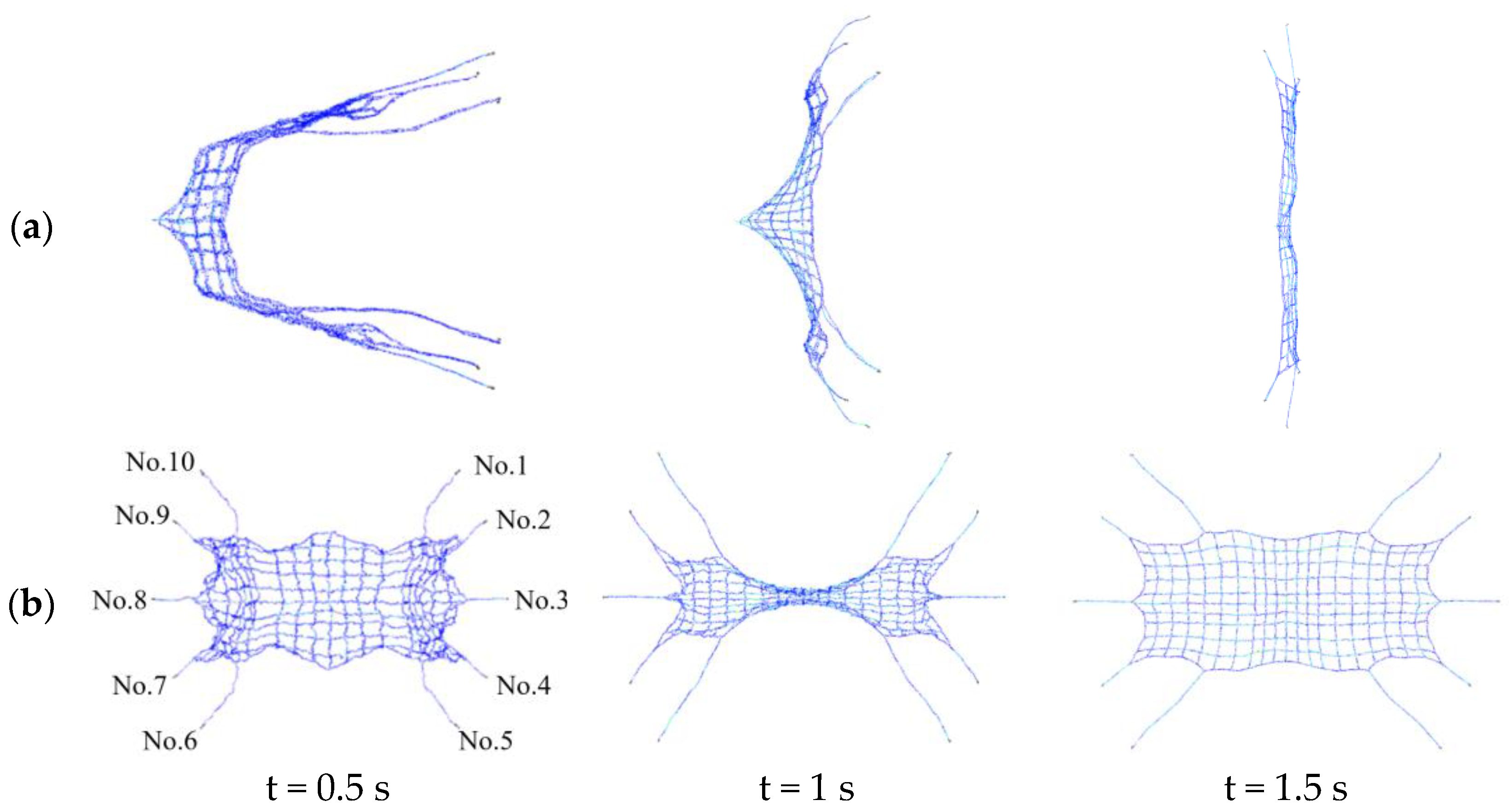
3.2. Comparison of Simulations and Experiments
4. Parameter Analysis of the Rectangular Tether-Net
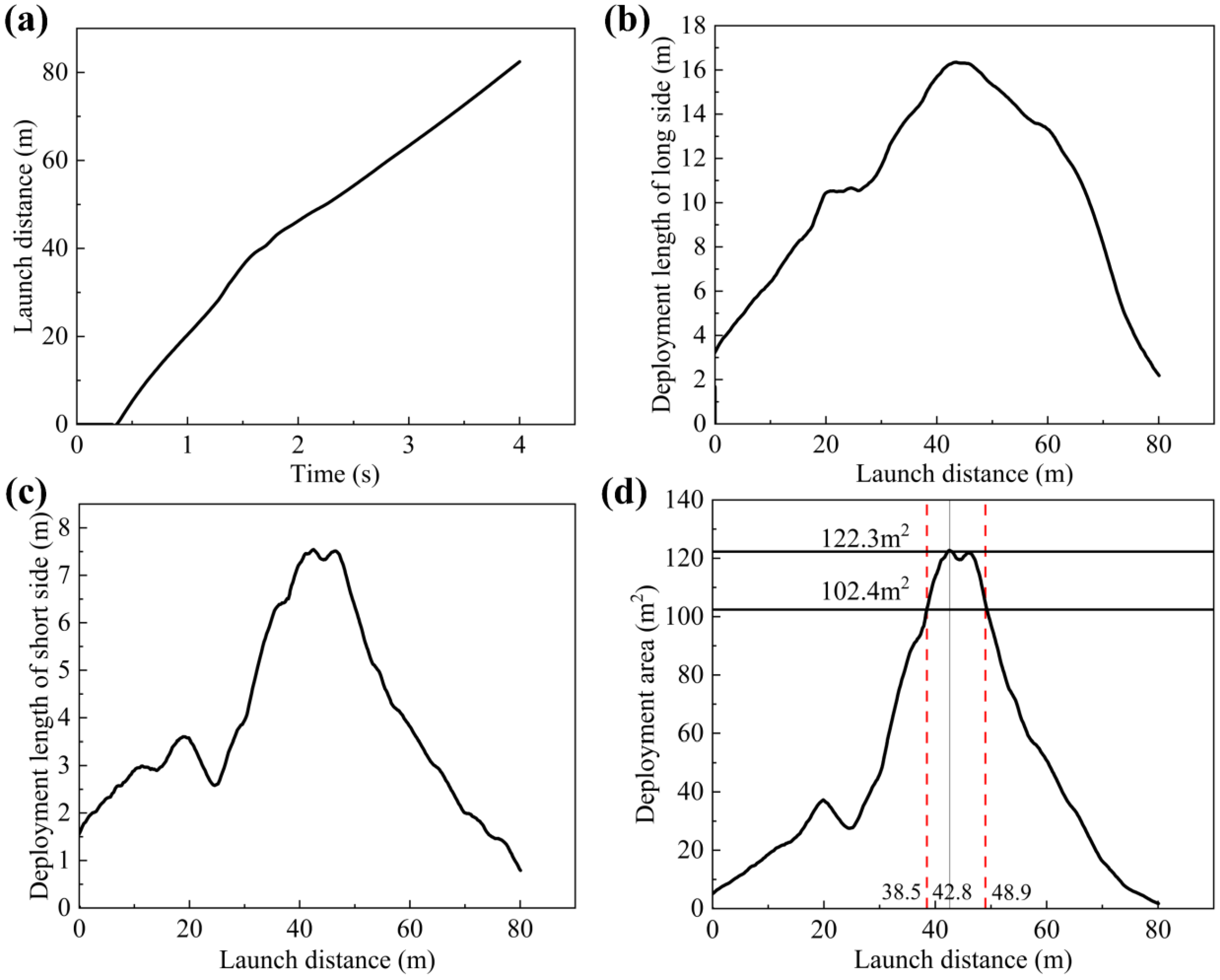
4.1. Deployment Performance of the Rectangular Tether-Net
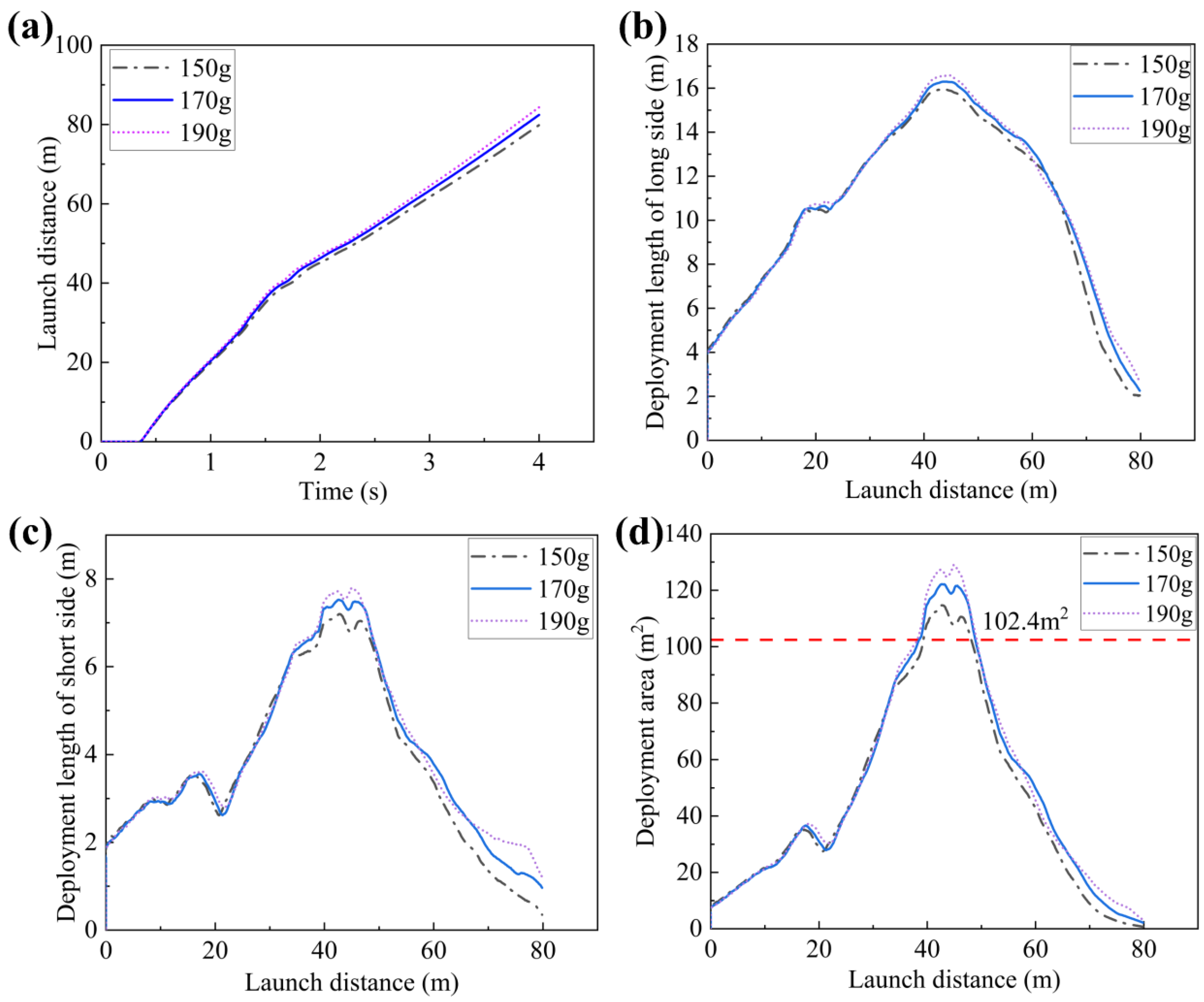
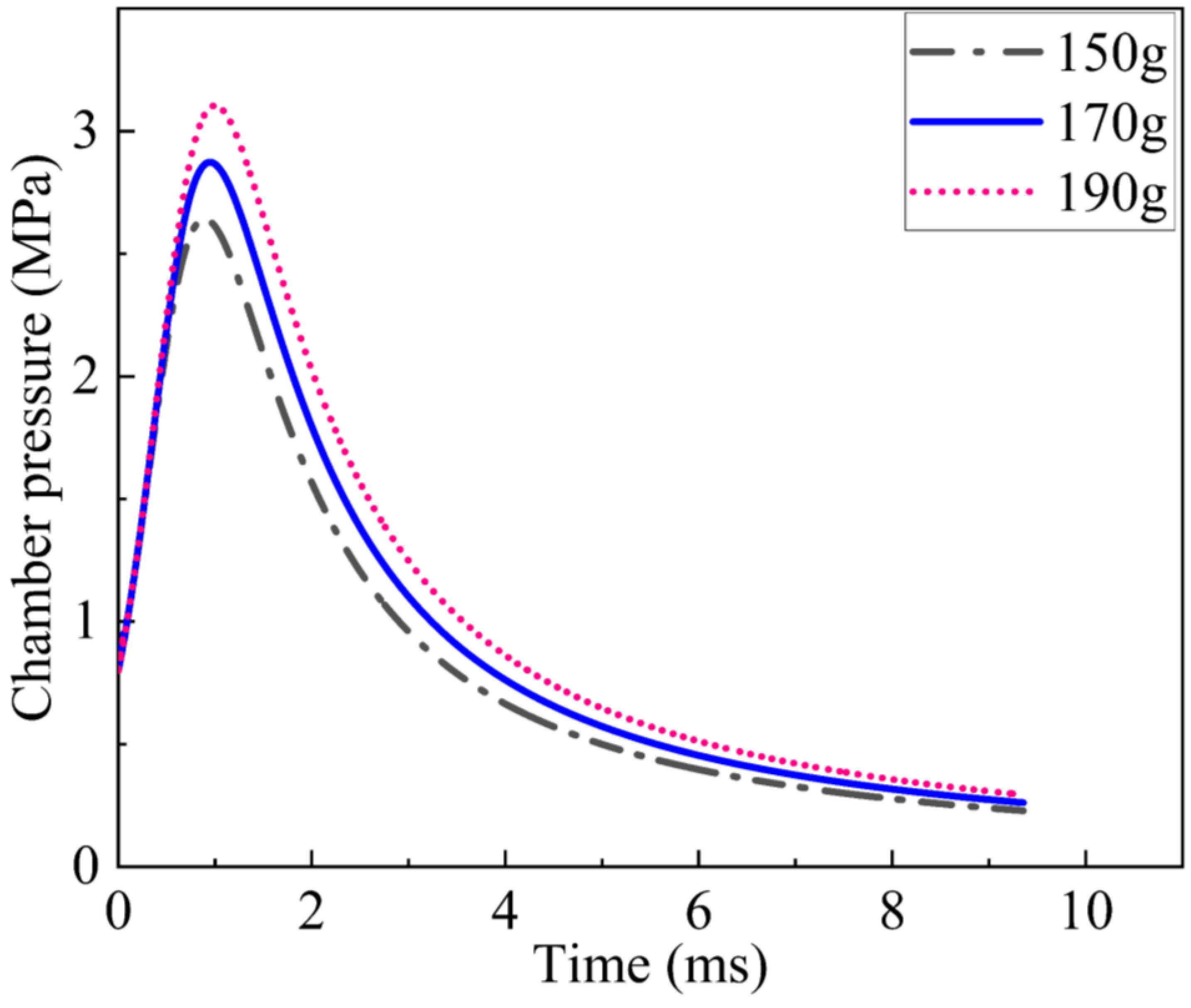
4.2. Influence of the Mass of Towing Blocks
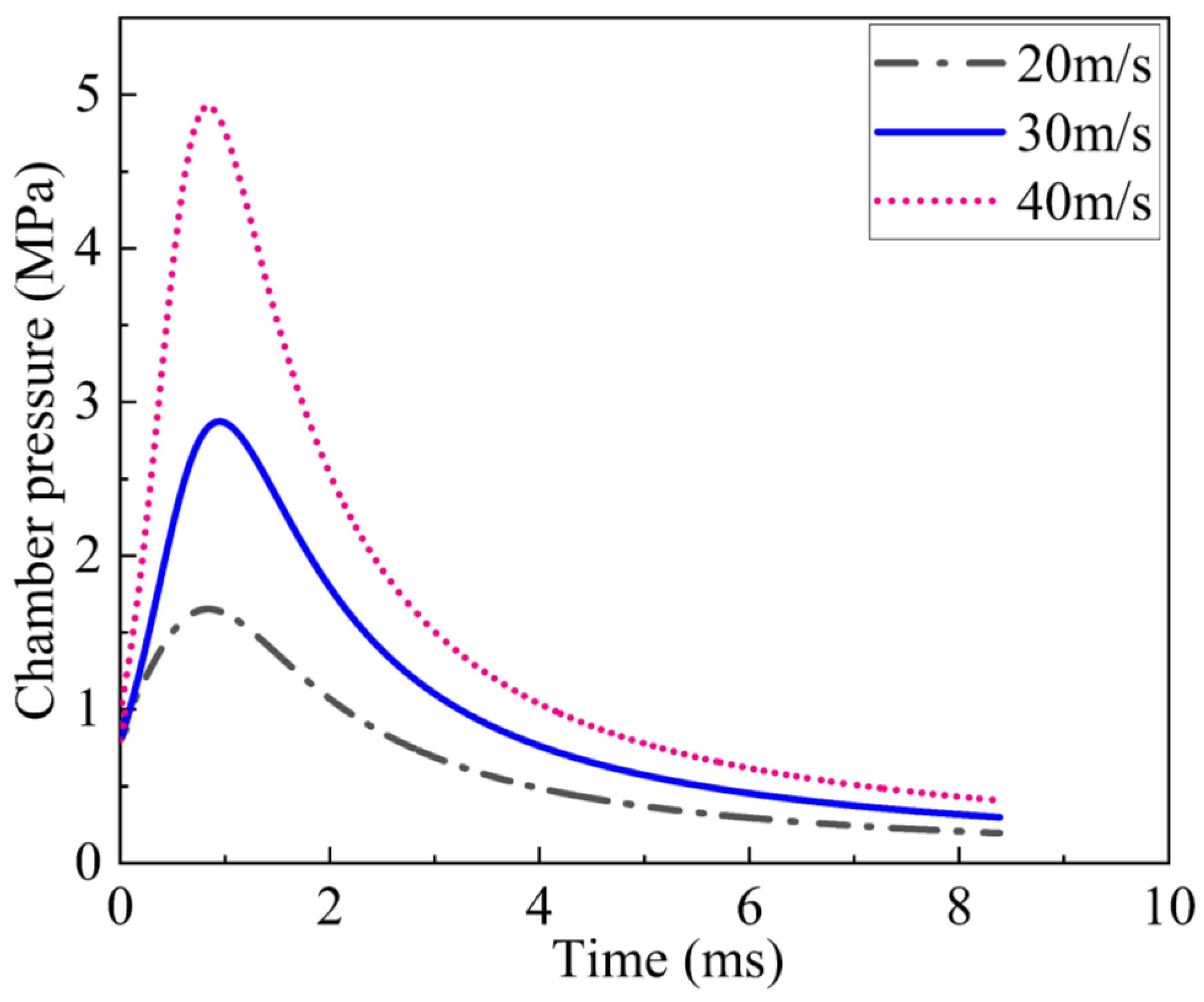
4.3. Influence of the Launch Speed of Towing Blocks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, B.; Li, K.; Tang, H.-W. The latest development of foreign space debris. Int. Space 2021, 5, 14–19. [Google Scholar] [CrossRef]
- Mark, C.P.; Kamath, S. Review of Active Space Debris Removal Methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Huang, P.F.; Zhang, F.; Cai, J.; Wang, D.K.; Meng, Z.J.; Guo, J. Dexterous Tethered Space Robot: Design, Measurement, Control and Experiment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1452–1468. [Google Scholar] [CrossRef]
- Cyril, X.; Jaar, G.J.; Misra, A.K. Dynamical modelling and control of a spacecraft-mounted manipulator capturing a spinning satellite. Acta Astronaut. 1995, 35, 167–174. [Google Scholar] [CrossRef]
- Golebiowski, W.; Michalczyka, R.; Dyrekb, M.; Battistac, U.; Wormnes, K. Validated simulator for space debris removal with nets and other flexible tethers applications. Acta Astronaut. 2016, 129, 229–240. [Google Scholar] [CrossRef]
- Yang, J.-K.; Ren, C.W.; Yang, C.H.; Wang, Y.Y.; Wan, S.-M.; Kang, R.J. Design of a Flexible Capture Mechanism Inspired by Sea Anemone for Non-cooperative Targets. Chin. J. Mech. Eng. 2021, 34, 77. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, Q.; Liu, Y.-W.; Xie, Z.W.; Jin, M.H.; Liu, H. A survey of non-cooperative target capturing methods. J. Natl. Univ. Def. Technol. 2020, 42, 74–90. [Google Scholar] [CrossRef]
- Chen, T.; Wen, H. Autonomous assembly with collision avoidance of a fleet of flexible spacecraft based on disturbance observer. Acta Astronaut. 2018, 147, 86–96. [Google Scholar] [CrossRef]
- Gao, Q.Y.; Zhang, Q.B.; Peng, W.Y.; Tang, Q.G.; Feng, Z.W. Dynamic modelling and ground test of space nets. In Proceedings of the 2016 7th International Conference on Mechanical and Aerospace Engineering (ICMAE), London, UK, 18–20 July 2016; IEEE: London, UK, 2016; pp. 587–591. [Google Scholar] [CrossRef]
- Shan, M.H.; Guo, J.; Gill, E. Deployment Dynamics of Tethered-Net for Space Debris Removal. Acta Astronaut. 2017, 132, 293–302. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Contact dynamics modeling and simulation of tether nets for space-debris capture. J. Guid. Control Dyn. 2017, 40, 110–123. [Google Scholar] [CrossRef]
- Bridson, R.; Fedkiw, R.; Anderson, J. Robust treatment of collisions, contact and friction for cloth animation. ACM Trans. Graph. 2002, 21, 594–603. [Google Scholar] [CrossRef]
- Harmon, D.; Vouga, E.; Tamstorf, R.; Grinspun, E. Robust treatment of simultaneous collisions. In ACM SIGGRAPH 2008 Papers, Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference, Los Angeles, CA, USA, 11–15 August 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Si, J.Y.; Pang, Z.J.; Du, Z.H.; Cheng, C. Dynamic modeling and simulation of self-collision of tether-net for space debris removal. Adv. Space Res. 2019, 64, 1675–1687. [Google Scholar] [CrossRef]
- Yu, Y.; Baoyin, H.X.; Li, J.F. Dynamic modeling and Simulation of space flying net projectile deployment. J. Astronaut. 2010, 31, 1289–1296. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K.; Teichmann, M. On the simulation of tether-nets for space debris capture with vortex dynamics. Acta Astronaut. 2016, 123, 91–102. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Energy and Momentum Analysis of the Deployment Dynamics of Nets in Space. Acta Astronaut. 2017, 140, 554–564. [Google Scholar] [CrossRef]
- Li, J.Y.; Yu, Y.; Baoyin, H.X.; Li, J.F. Comparative study on two dynamic models of space flying net. Chin. J. Theor. Appl. Mech. 2011, 43, 542–550. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, P.F. Releasing Dynamics and Stability Control of Maneuverable Tethered Space Net. IEEE/ASME Trans. Mechatron. 2017, 22, 983–993. [Google Scholar] [CrossRef]
- Benvenuto, R.; Lavagna, M.; Salvi, S. Multibody dynamics driving GNC and system design in tethered nets for active debris removal. Adv. Space Res. 2016, 58, 45–63. [Google Scholar] [CrossRef]
- Sharf, I.; Thomsen, B.; Botta, E.M.; Misra, A.K. Experiments and simulation of a net closing mechanism for tether-net capture of space debris. Acta Astronaut. 2017, 139, 332–343. [Google Scholar] [CrossRef]
- Yu, Y.; Baoyin, H.X.; Li, J.F. Dynamic modeling method of space tether-net system. In Proceedings of the 16th Annual Meeting of Beijing Society of Mechanics; Beijing Society of Theoretical and Applied Mechanics: Beijing, China, 2010; pp. 164–166. [Google Scholar]
- Liu, H.T.; Zhang, Q.B.; Yang, L.P.; Zhu, Y.W. The deployment dynamic characteristics analysis of space web system. J. Natl. Univ. Def. Technol. 2015, 37, 68–77. [Google Scholar] [CrossRef]
- Wang, X.C.; Shao, M. Basic Principle and Numerical Method of Finite Element Method; Tsinghua Press: Beijing, China, 1997. [Google Scholar]
- Zhuang, Z.; You, X.C.; Liao, J.H. Based on ABAQUS Finite Element Analysis and Application; Tsinghua Press: Beijing, China, 2009. [Google Scholar]
- Wang, Y.L.; Yu, Y.; Wang, C.Y.; Zhou, G.; Aminreza, K.; Zhao, W.Z. On the out-of-plane ballistic performances of hexagonal, reentrant, square, triangular and circular honeycomb panels. Int. J. Mech. Sci. 2020, 173, 105402. [Google Scholar] [CrossRef]
- Yue, S.; Titurus, B.; Nie, H.; Zhang, M. Liquid spring damper for vertical landing Reusable Launch Vehicle under impact conditions. Mech. Syst. Signal Process. 2019, 121, 579–599. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Net size, m2 | 16 × 8 |
| Net mesh, m2 | 0.8 × 0.8 |
| Diameter of main tethers, mm | 0.5 |
| Diameter of side tethers, mm | 2 |
| Diameter of towing tethers, mm | 2 |
| Towing block mass, g | 170 |
| Launch speed, m/s | 30 |
| Launch angle, ° | 16 |
| Tether Type | Elastic Modulus |
|---|---|
| Main tether | 748.7 MPa |
| Towing tether | 59.5 MPa |
| Side tether | 46.2 MPa |
| Parameter | Value |
|---|---|
| Maximum deployment length of the long side, m | 16.3 |
| Maximum deployment length of the short side, m | 7.5 |
| Maximum deployment area, m2 | 122.3 |
| Deployment distance, m | 42.8 |
| Shape-preserving distance, m~m | 38.5~48.9 |
| Parameter | 150 g | 170 g | 190 g |
|---|---|---|---|
| Maximum deployment length of the long side, m | 16 | 16.3 | 16.6 |
| Maximum deployment length of the short side, m | 7.2 | 7.5 | 7.8 |
| Maximum deployment area, m2 | 114.3 | 122.3 | 128.7 |
| Deployment distance, m | 42.8 | 42.8 | 45 |
| Shape-preserving distance, m~m | 39.3~48.2 | 38.5~48.9 | 38.7~48.9 |
| Parameter | 20 m/s | 30 m/s | 40 m/s |
|---|---|---|---|
| Maximum deployment length of the long side, m | 13.8 | 16.3 | 17 |
| Maximum deployment length of the short side, m | 5.8 | 7.5 | 8 |
| Maximum deployment area, m2 | 80 | 122.3 | 135 |
| Deployment distance, m | 42.8 | 42.8 | 45 |
| Shape-preserving distance, m~m | 38.5~48.9 | 37.8~52.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, S.; Li, M.; Zhao, Z.; Du, Z.; Wu, C.; Zhang, Q. Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net. Aerospace 2023, 10, 115. https://doi.org/10.3390/aerospace10020115
Yue S, Li M, Zhao Z, Du Z, Wu C, Zhang Q. Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net. Aerospace. 2023; 10(2):115. https://doi.org/10.3390/aerospace10020115
Chicago/Turabian StyleYue, Shuai, Mengsheng Li, Zhen Zhao, Zhonghua Du, Chunbo Wu, and Qingzhan Zhang. 2023. "Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net" Aerospace 10, no. 2: 115. https://doi.org/10.3390/aerospace10020115
APA StyleYue, S., Li, M., Zhao, Z., Du, Z., Wu, C., & Zhang, Q. (2023). Parameter Analysis and Experiment Validation of Deployment Characteristics of a Rectangular Tether-Net. Aerospace, 10(2), 115. https://doi.org/10.3390/aerospace10020115







