Numerical Study on Buoyancy-Driven Görtler Vortices above Horizontal Heated Flat Plate
Abstract
:1. Introduction
2. CFD Methods and Validation
2.1. Turbulence Model
2.2. Validation of CFD Result
2.2.1. Experimental Setup/Model
2.2.2. Computation Setup/Model
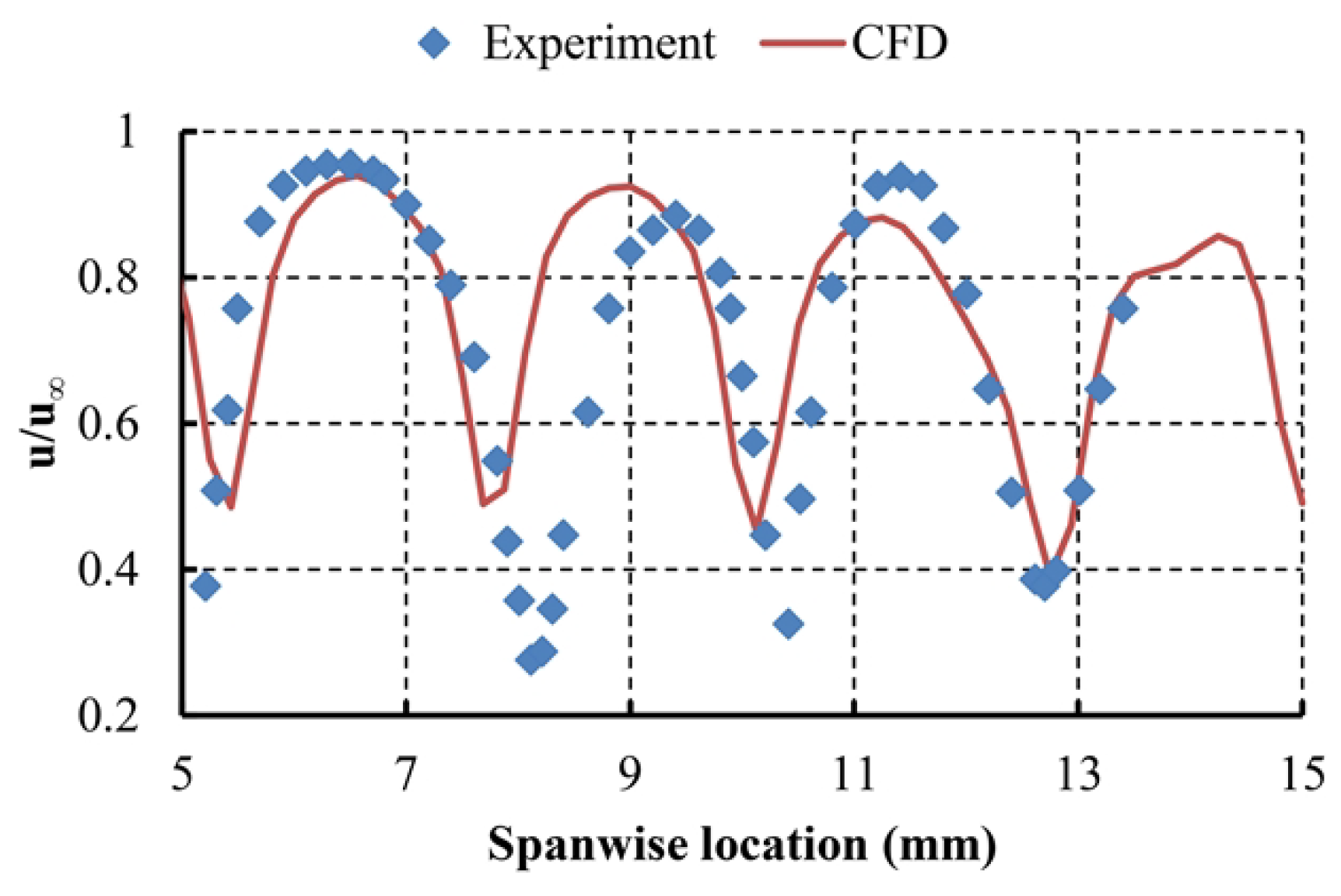
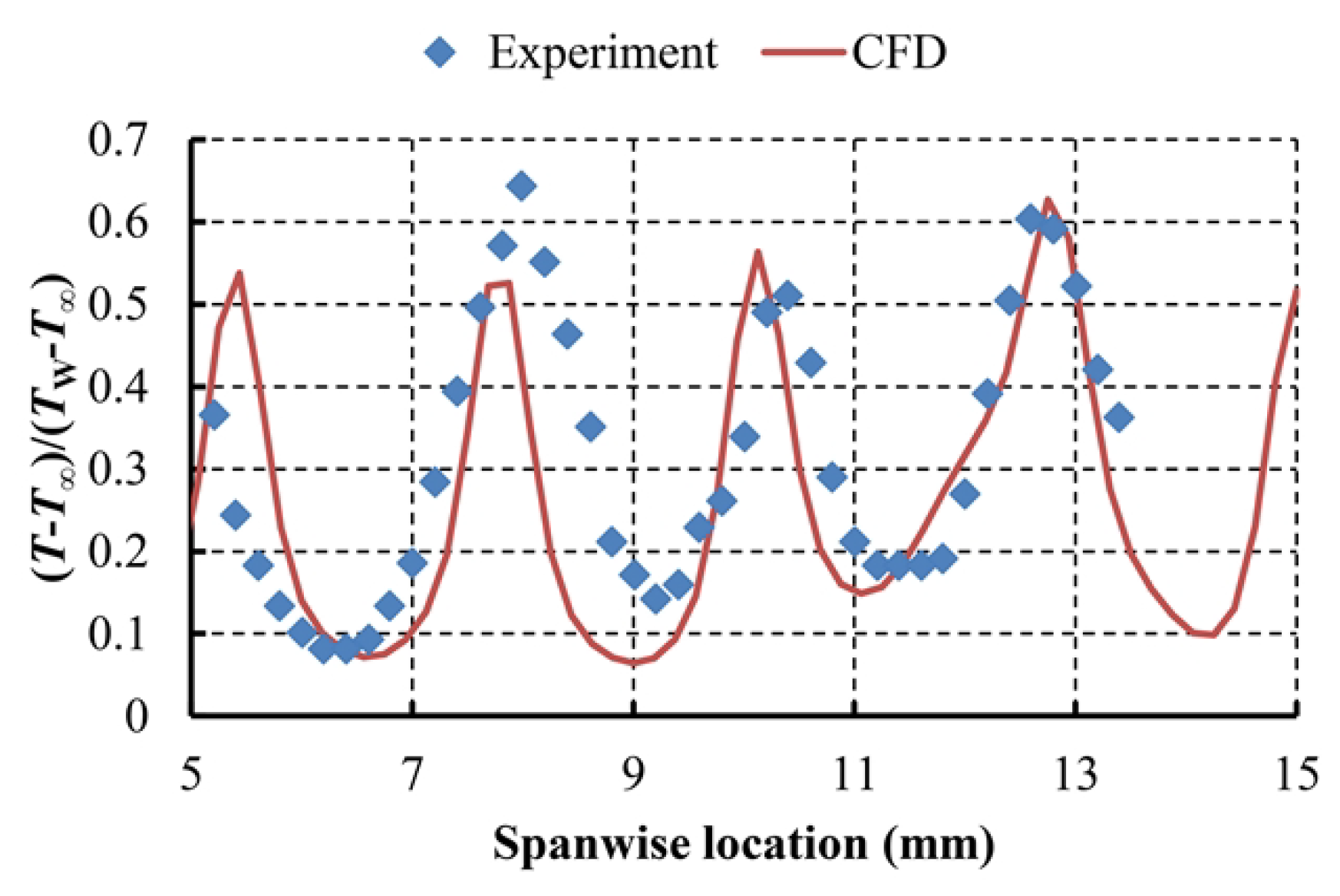
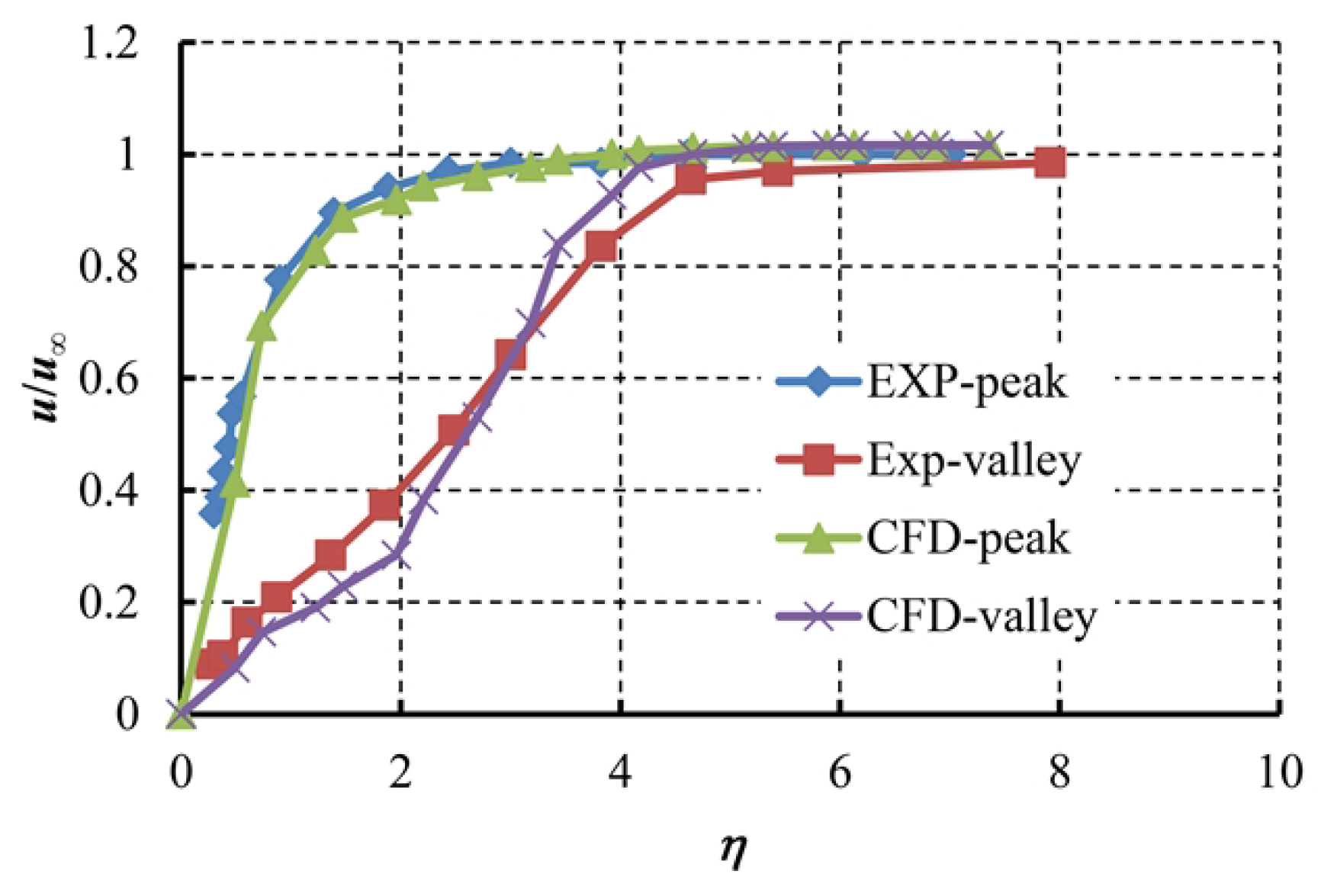
2.2.3. Comparison of Computational and Experimental Results
3. Results and Discussion
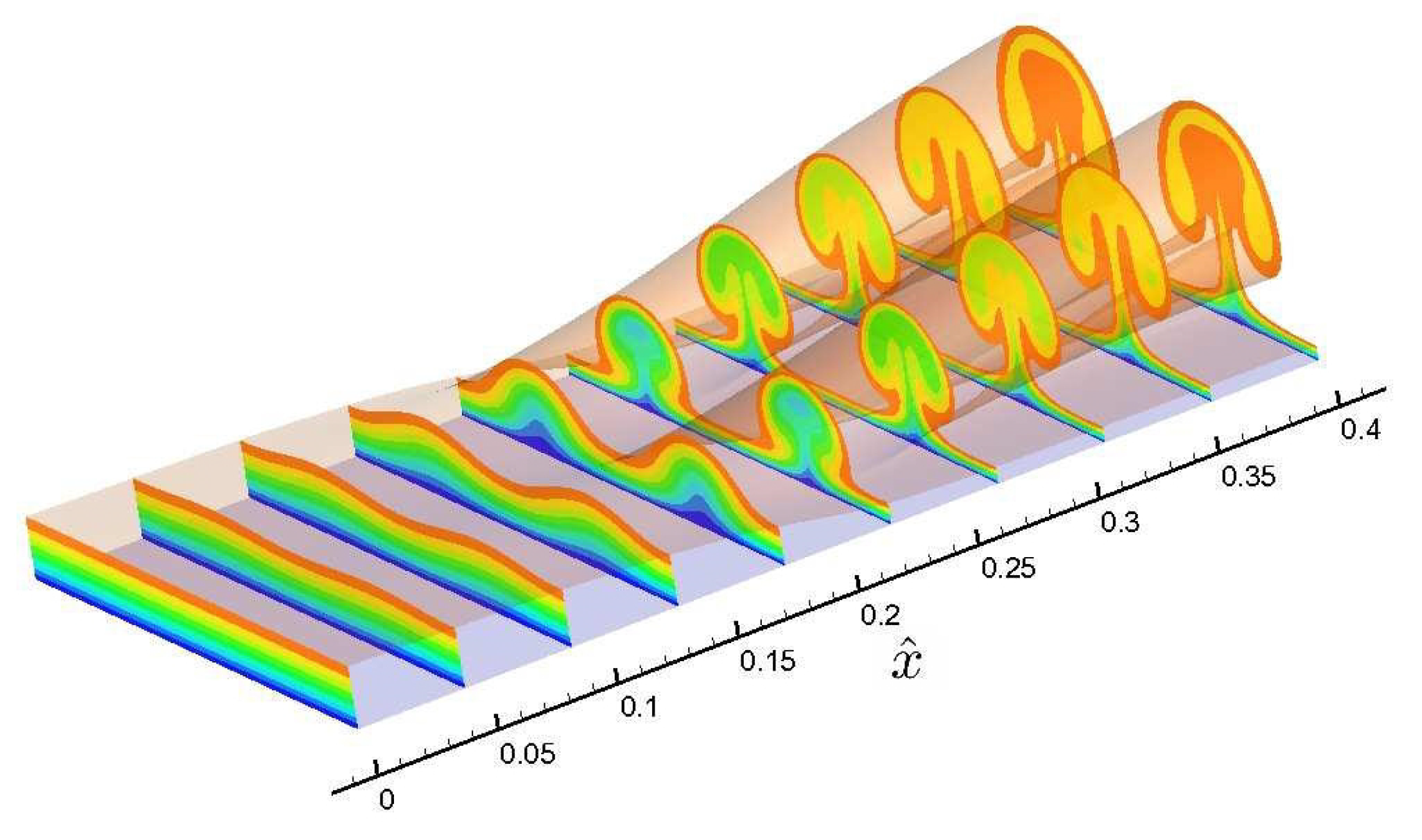
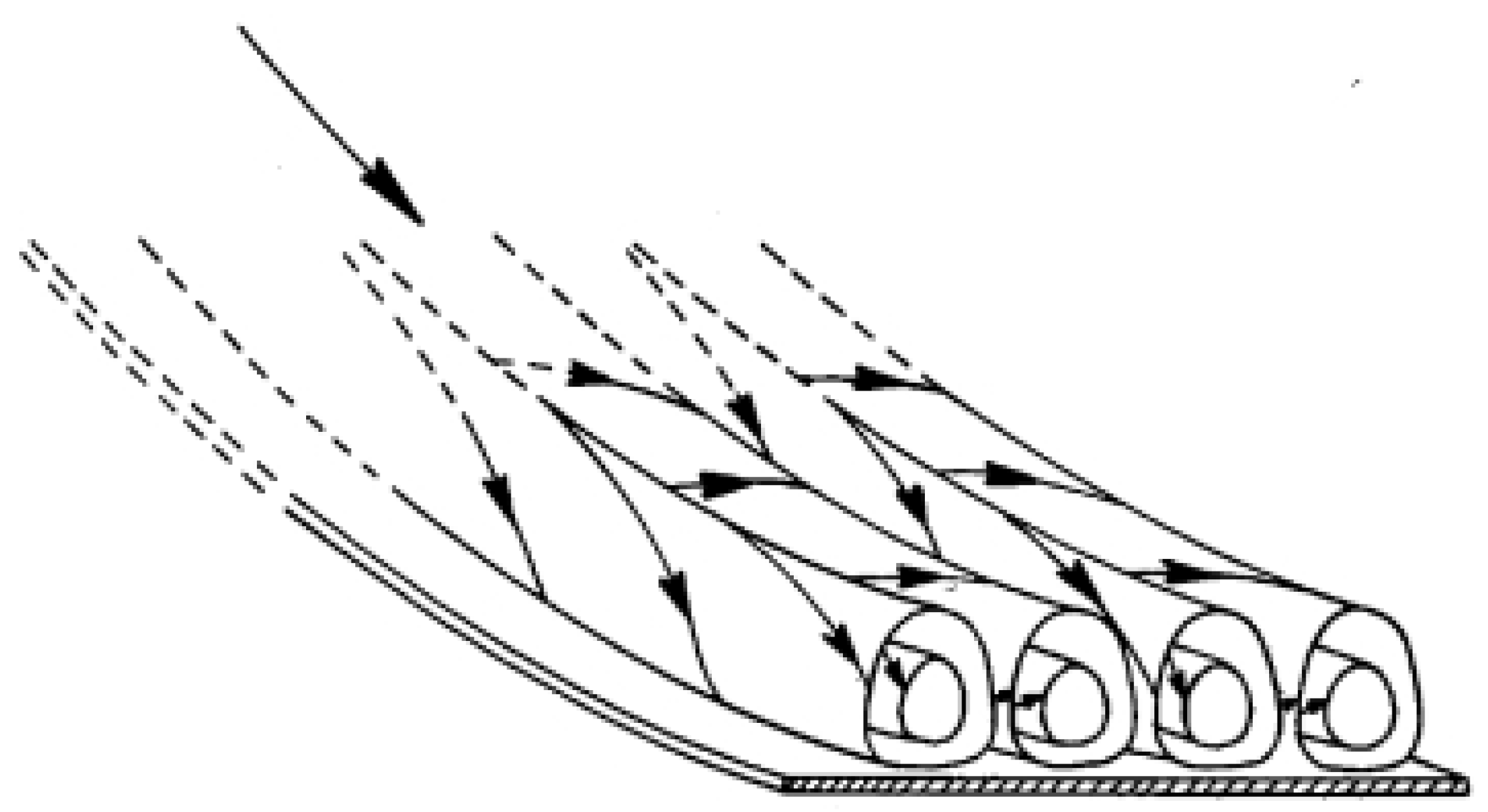
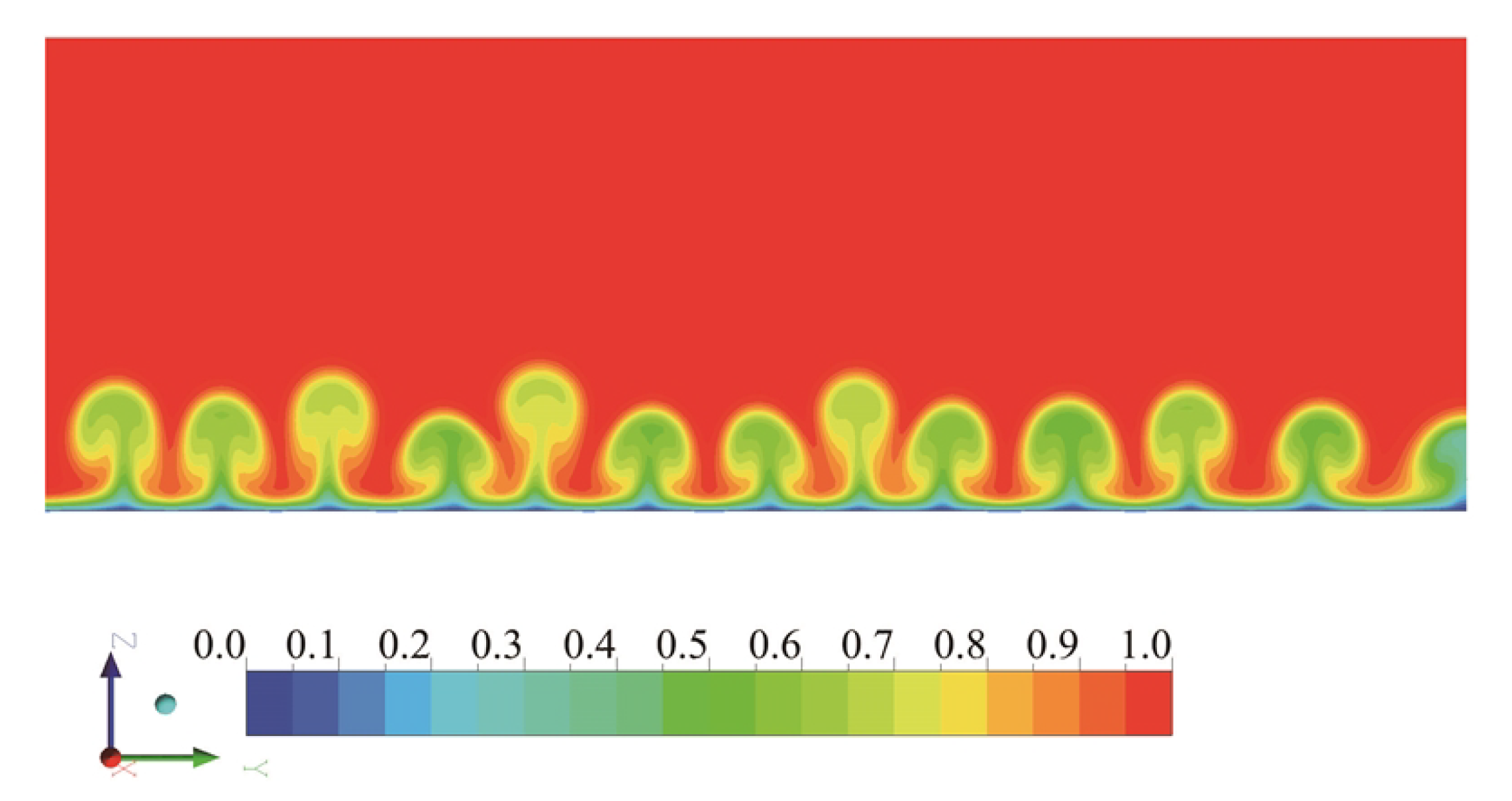
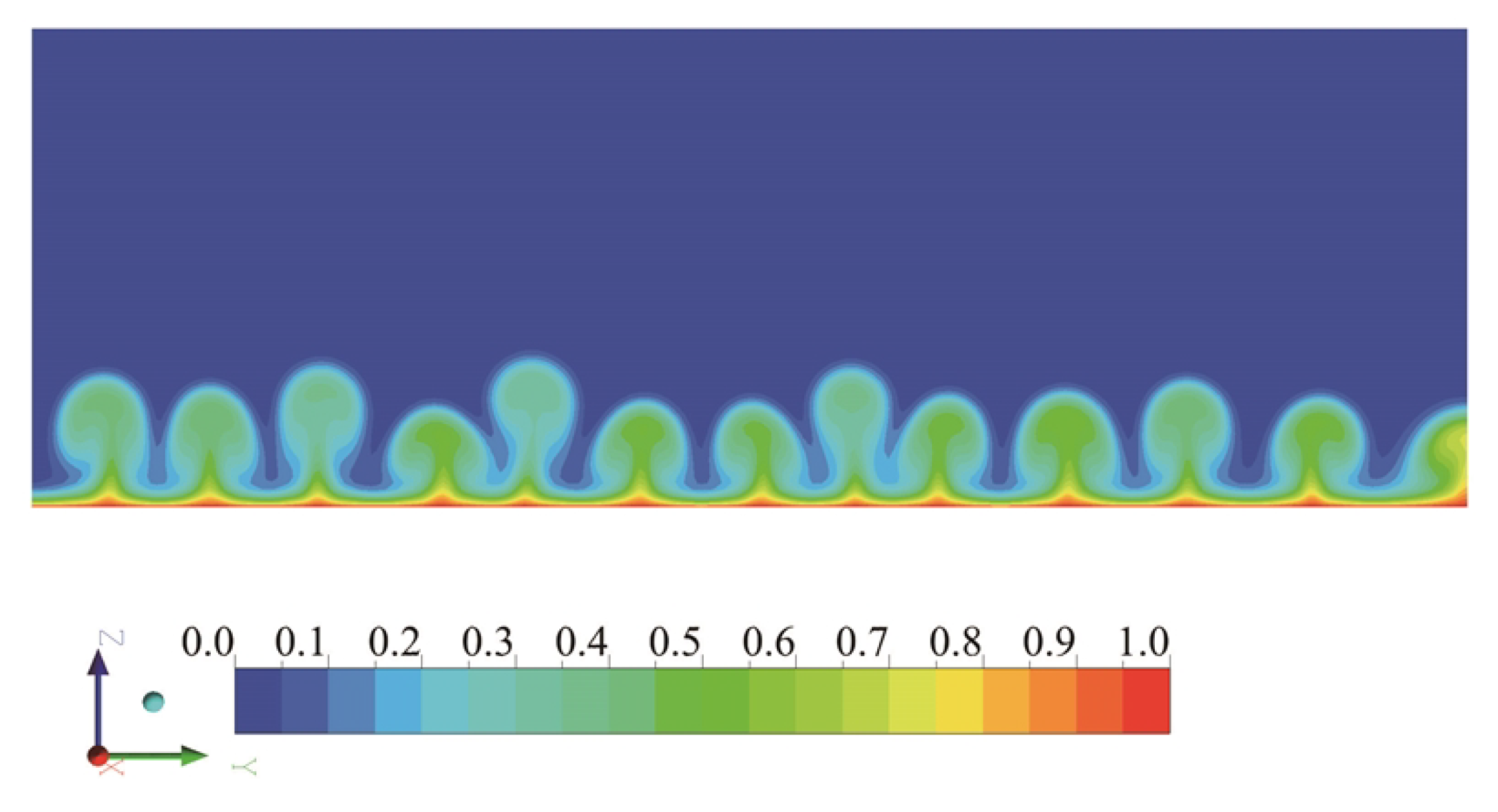
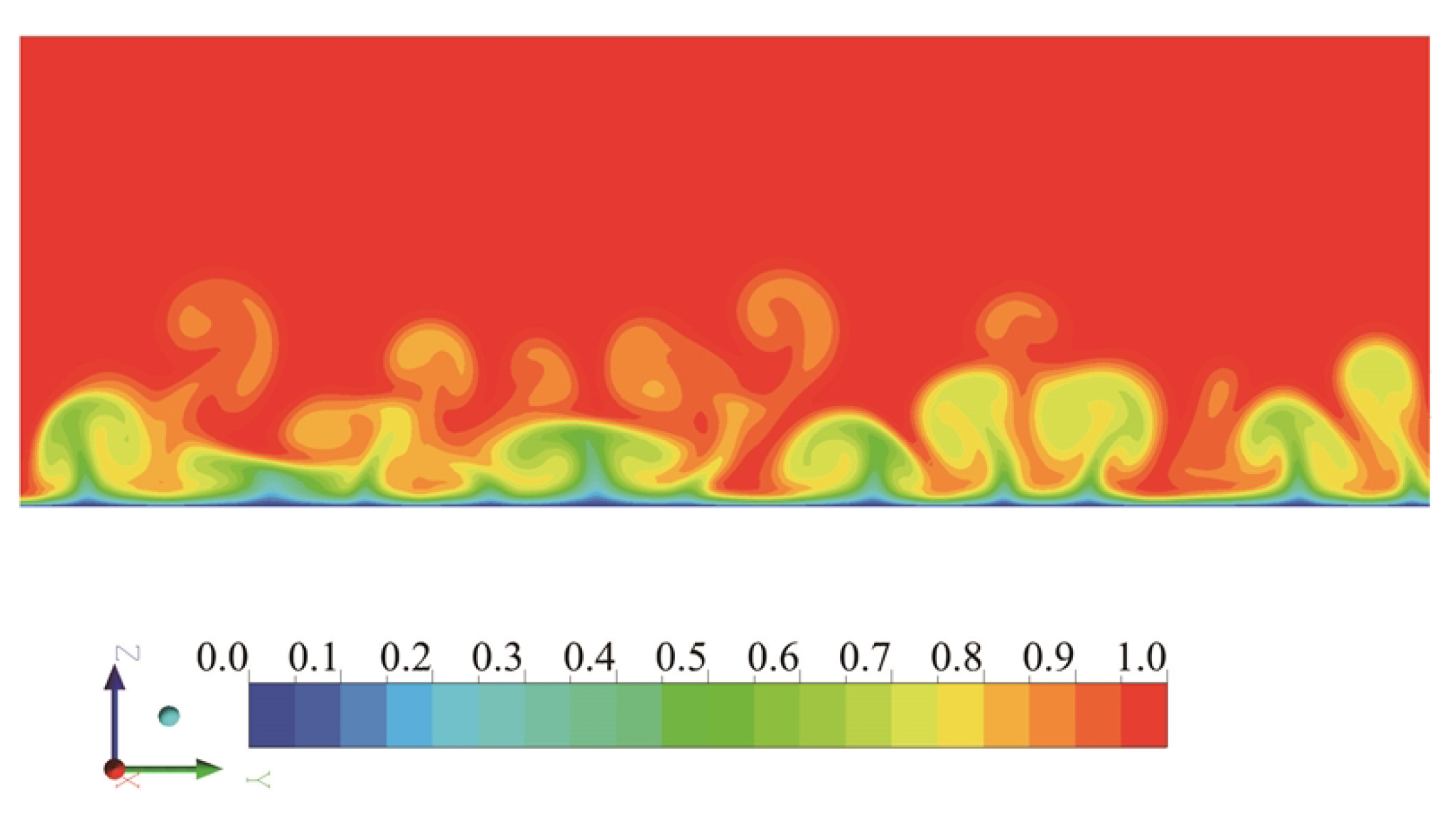
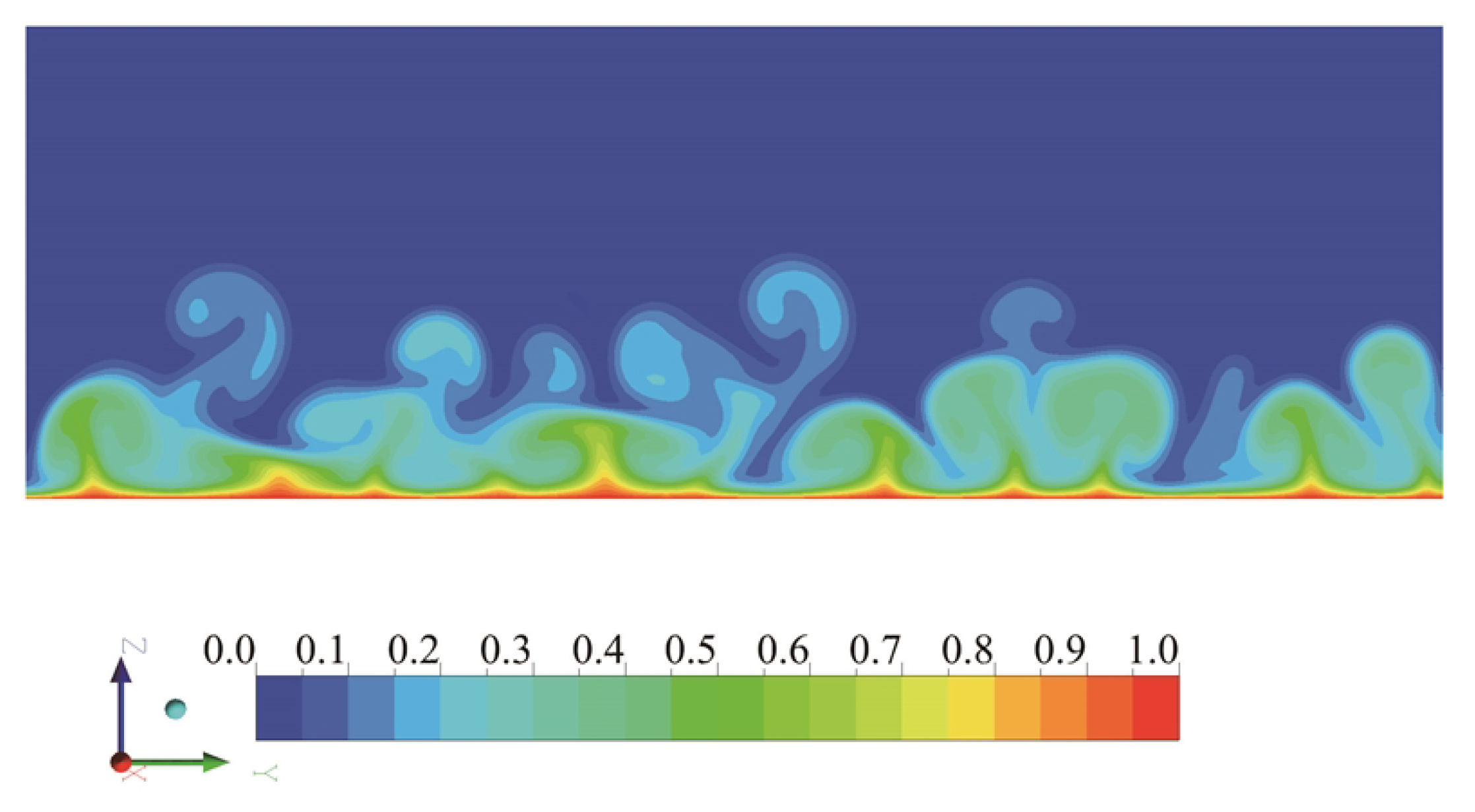
3.1. Flow Visualization
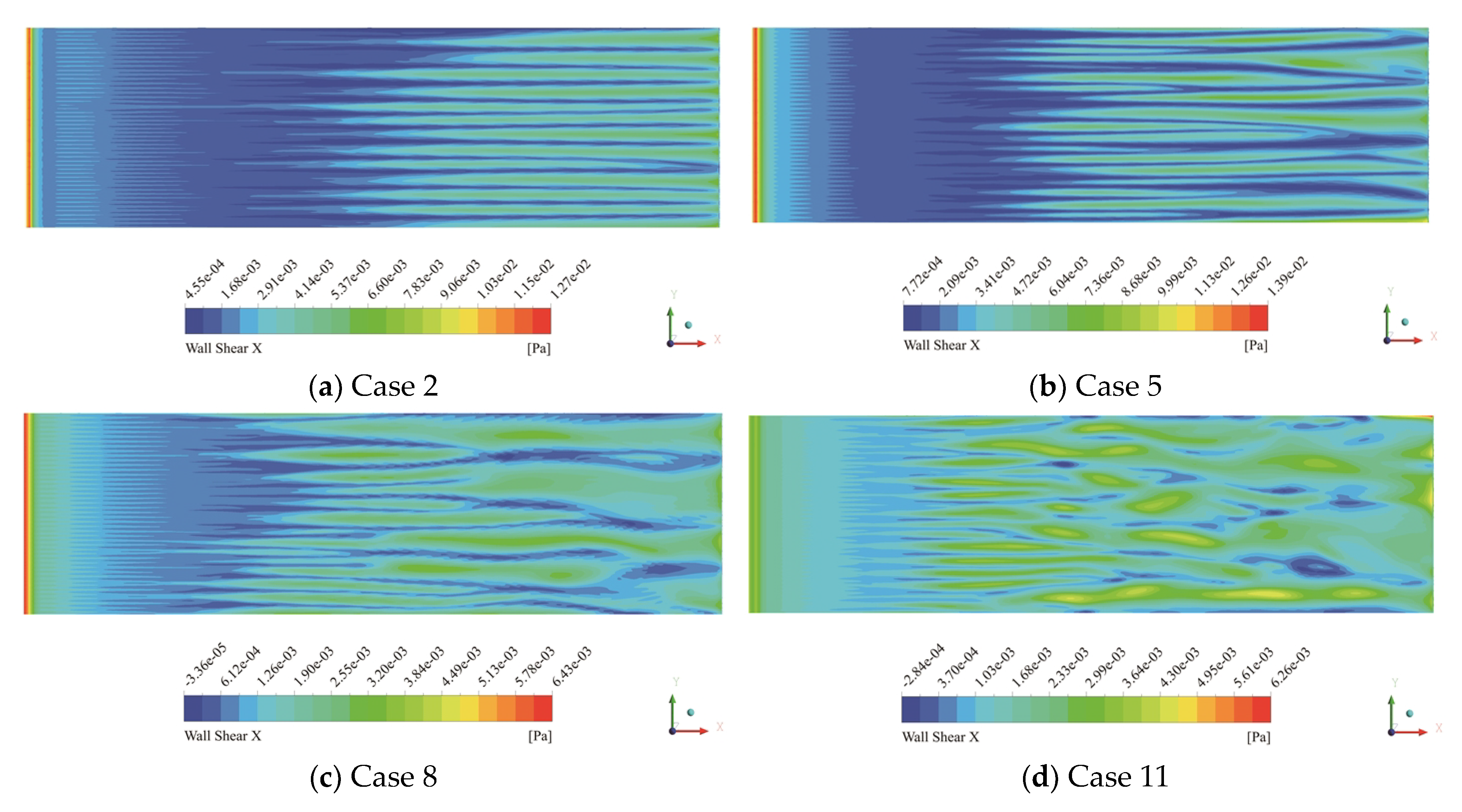
3.2. Wall Shear
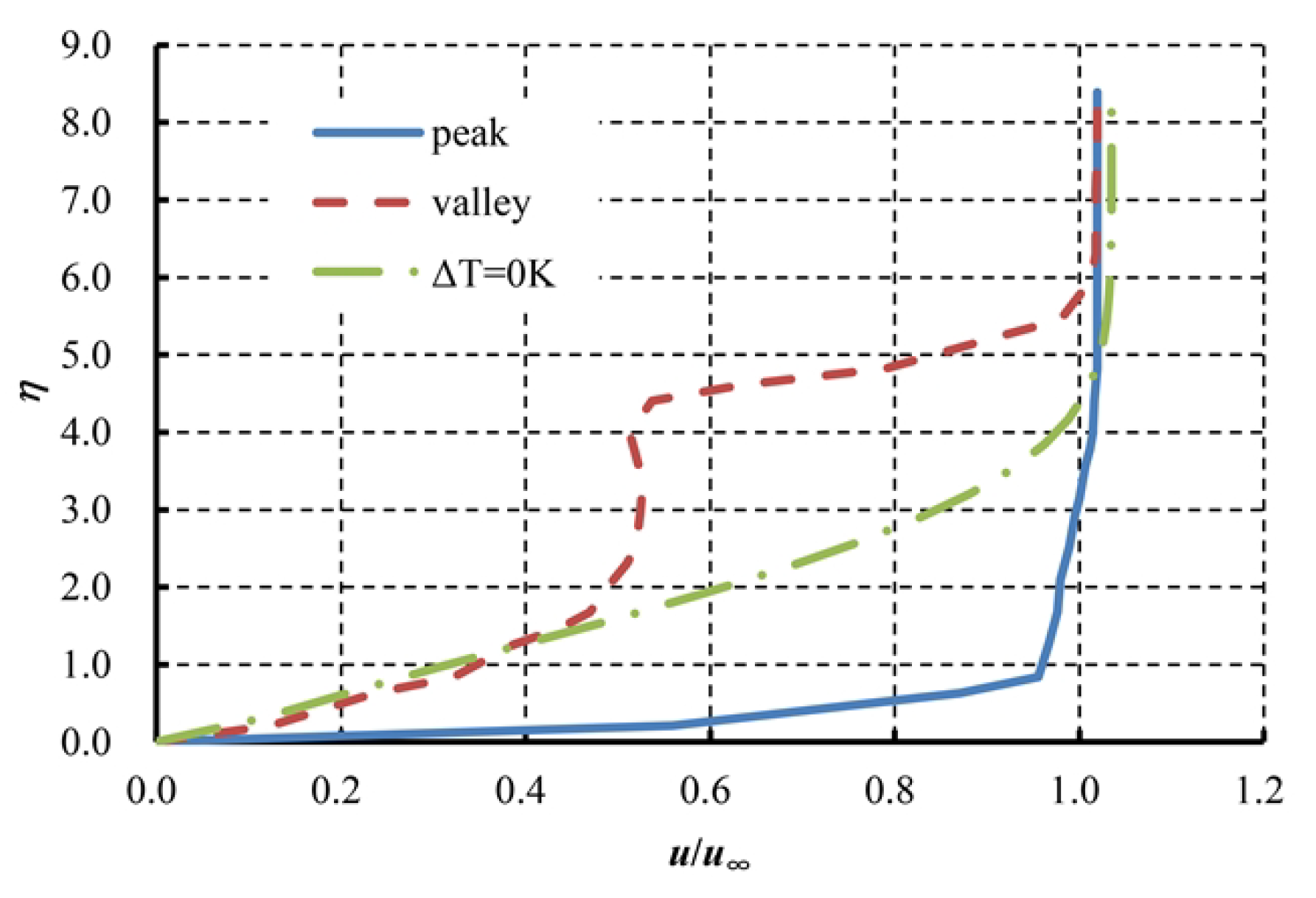
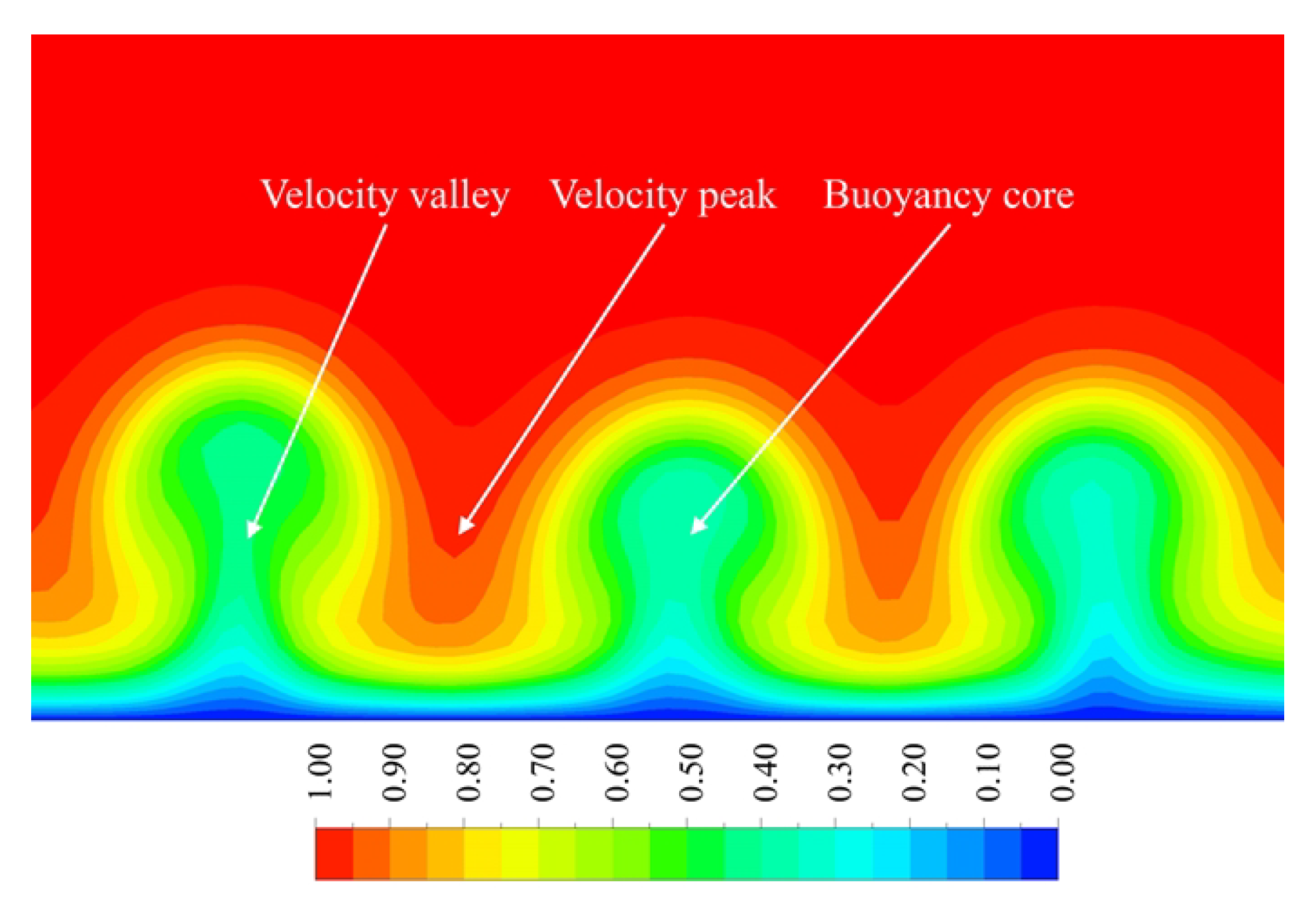
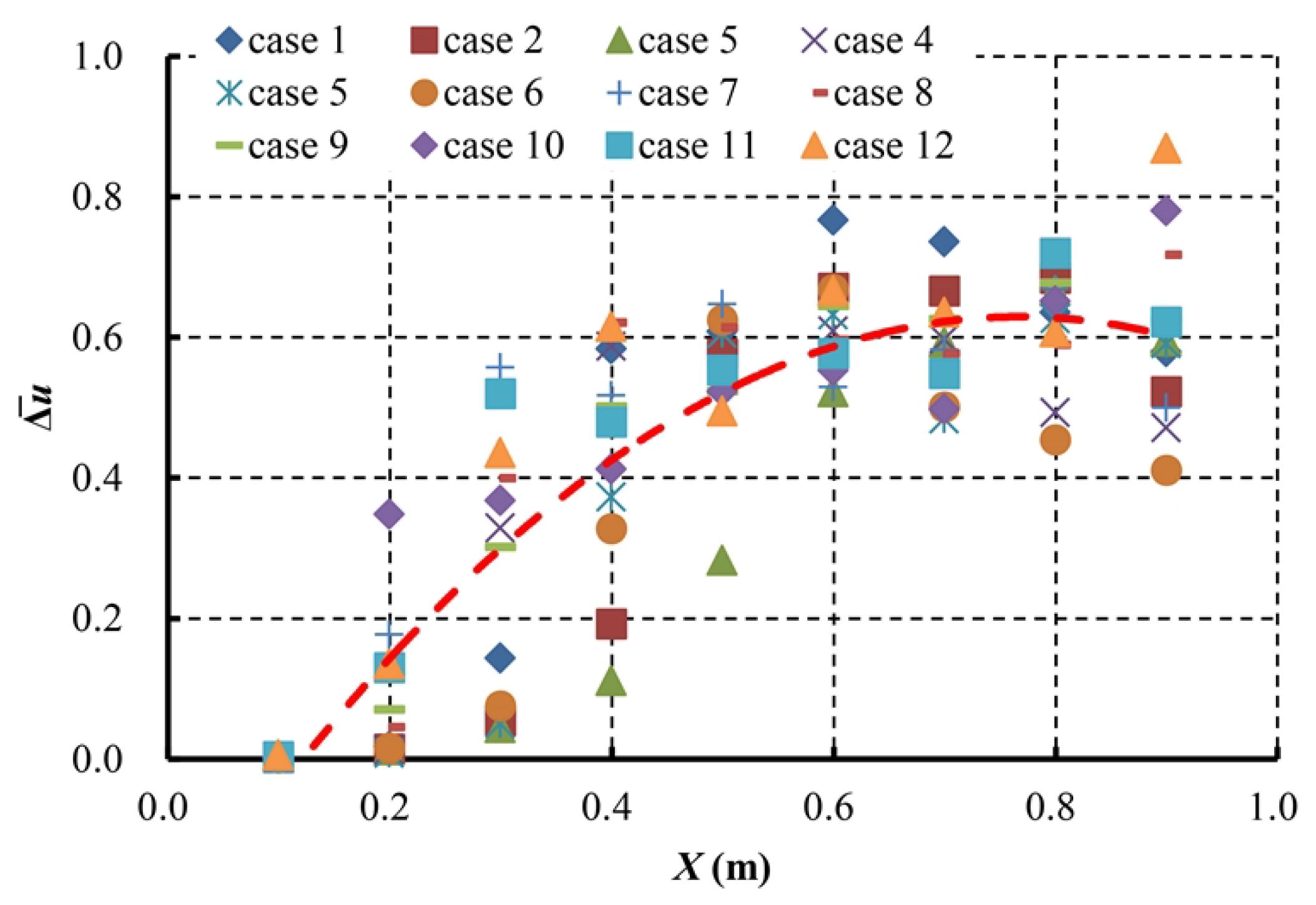
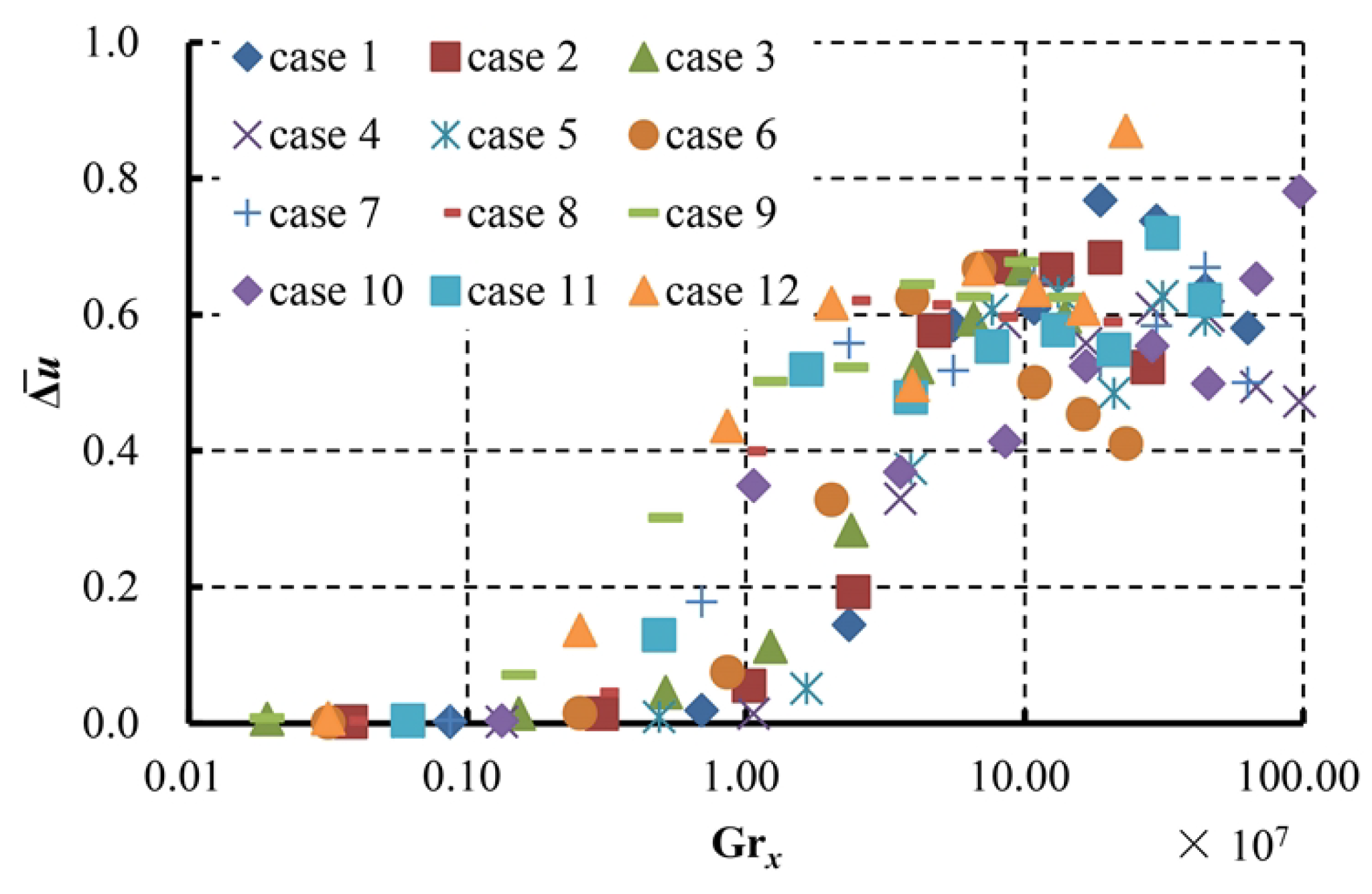
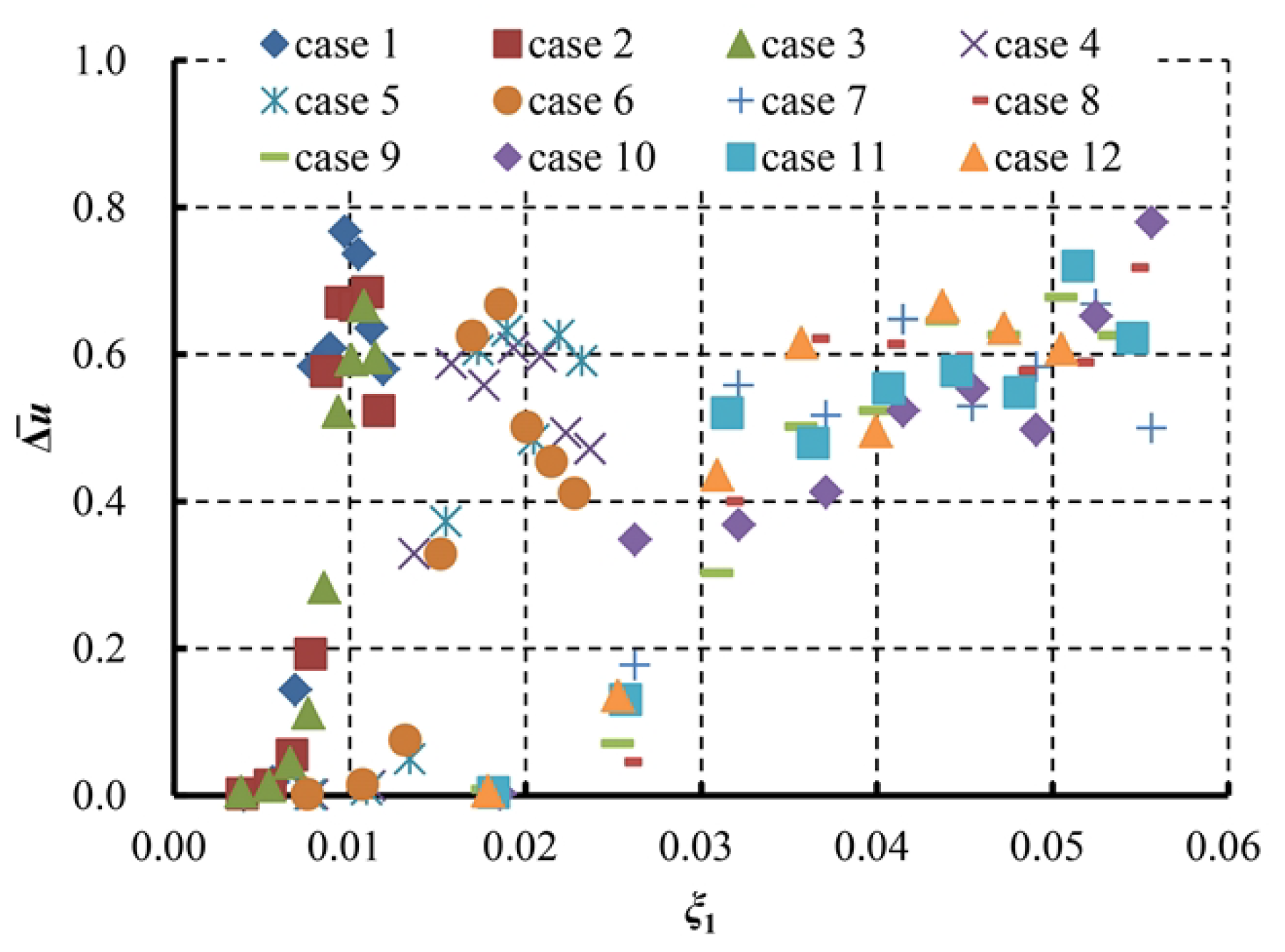
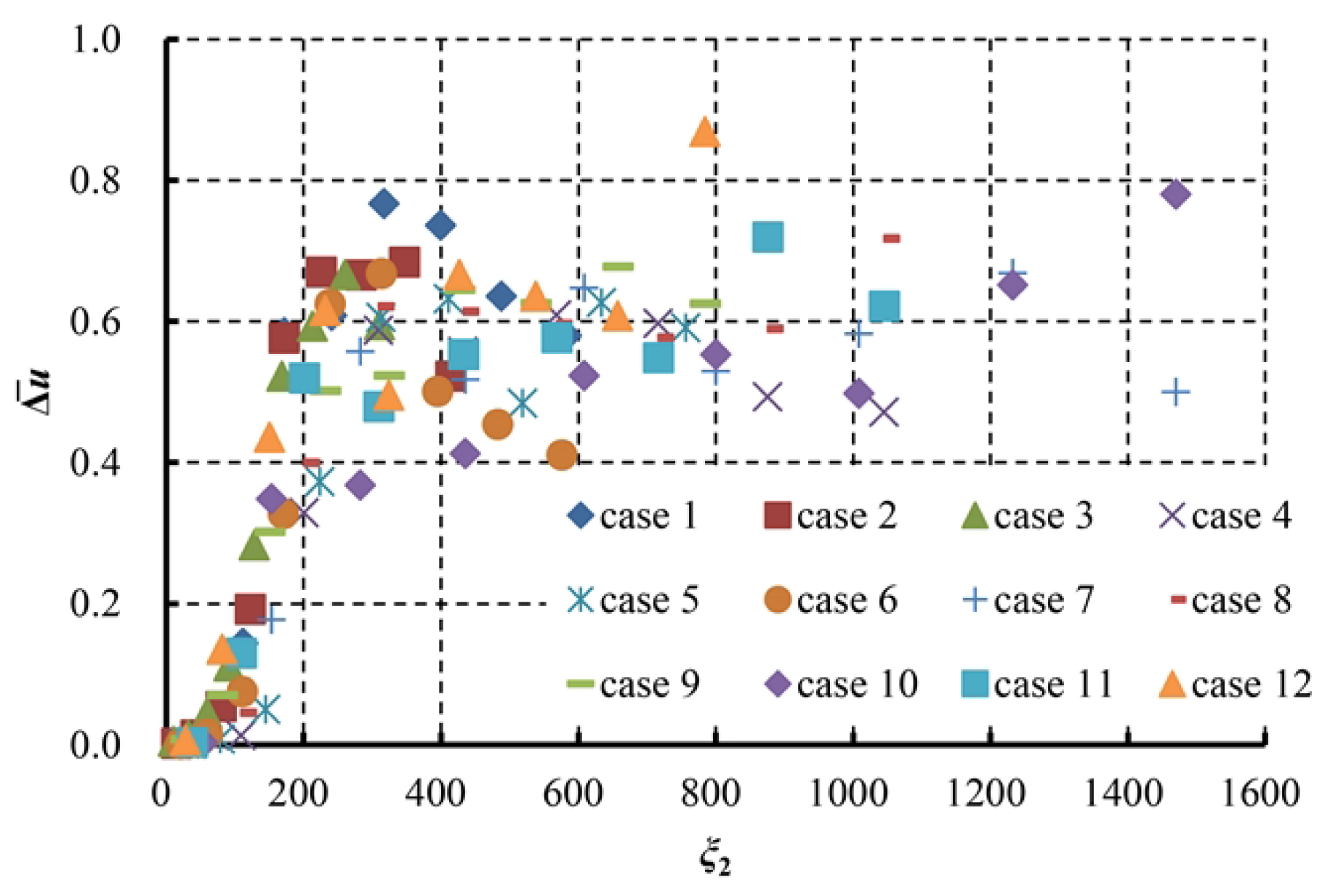
3.3. Buoyancy Parameter
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, D.L.; Zhang, L.; Yang, M.Q.; Xia, X.; Wang, S. Review of Key Technologies of Ultra-Long-Endurance Solar Powered Unmanned Aerial Vehicle. Acta Aeronaut. Astronaut. Sin. 2020, 41, 623418. (In Chinese) [Google Scholar] [CrossRef]
- Lun, Y.; Yao, P.; Wang, Y. Trajectory Optimization of SUAV for Marine Vessels Communication Relay Mission. IEEE Syst. J. 2020, 14, 5014–5024. [Google Scholar] [CrossRef]
- Noll, T.E.; Ishmael, S.D.; Henwood, B.; Perez-Davis, M.E.; Tiffany, G.C.; Madura, J.; Gaier, M.; Brown, J.M.; Wierzbanowski, T. Technical Findings, Lessons Learned, and Recommendations Resulting from the Helios Prototype Vehicle Mishap. In Proceedings of the NATO/RTO AVT-145 Workshop on Design Concepts, Processes and Criteria for UAV Structural Integrity, Florence, Italy, 1 January 2007. [Google Scholar]
- Rapinett, A. Zephyr: A High Altitude Long Endurance Unmanned Air Vehicle. Master’s Thesis, University of Surrey, Guildford Surrey, UK, 2009. [Google Scholar]
- Qian, Y. Aerodynamics, 1st ed.; Beihang University Press: Beijing, China, 2004; pp. 15–25. (In Chinese) [Google Scholar]
- Vinnichenko, N.A.; Uvarov, A.V.; Znamenskaya, I.A.; Ay, H.; Wang, T.-H. Solar car aerodynamic design for optimal cooling and high efficiency. Sol. Energy 2014, 103, 183–190. [Google Scholar] [CrossRef]
- Zhang, J. Preliminary Study and Experiments on Energy Management of Solar Powered Aircraft. Master’s Thesis, Tsinghua University, Beijing, China, 2005. (In Chinese). [Google Scholar]
- Natarajan, S.K.; Mallick, T.K.; Katz, M.; Weingaertner, S. Numerical investigations of solar cell temperature for photovoltaic concentrator system with and without passive cooling arrangements. Int. J. Therm. Sci. 2011, 50, 2514–2521. [Google Scholar] [CrossRef]
- Görtler, H. On the Three-Dimensional Instability of Laminar Boundary Layers on Concave Walls; National Advisory Commitee for Aeronautics: Edwards, CA, USA, 1954.
- Floryan, J.M.; Saric, W.S. Stability of Gortler Vortices in Boundary Layers. AIAA J. 1982, 20, 316–324. [Google Scholar] [CrossRef]
- Mitsudharmadi, H.; Winoto, S.H.; Shah, D.A. Development of most amplified wavelength Görtler vortices. Phys. Fluids 2006, 18, 14101. [Google Scholar] [CrossRef]
- Mitsudharmadi, H.; Winoto, S.H.; Shah, D.A. Secondary instability in forced wavelength Görtler vortices. Phys. Fluids 2005, 17, 74101–74104. [Google Scholar] [CrossRef]
- Mitsudharmadi, H.; Winoto, S.H.; Shah, D.A. Splitting and merging of Görtler vortices. Phys. Fluids 2005, 17, 124101–124102. [Google Scholar] [CrossRef]
- Winoto, S.H.; Mitsudharmadi, H.; Shah, D.A. Visualizing Görtler vortices. J. Vis. 2005, 8, 315–322. [Google Scholar] [CrossRef]
- Tandiono; Winoto, S.H.; Shah, D.A. On the linear and nonlinear development of Görtler vortices. Phys. Fluids 2008, 20, 94101–94103. [Google Scholar] [CrossRef]
- Tandiono; Winoto, S.H.; Shah, D.A. Wall shear stress in Görtler vortex boundary layer flow. Phys. Fluids 2009, 21, 84101–84106. [Google Scholar] [CrossRef]
- Tandiono, T.; Winoto, S.H.; Shah, D.A. Spanwise Velocity Component in Nonlinear Region of Görtler Vortices. Phys. Fluids 2013, 25, 104101–104104. [Google Scholar] [CrossRef]
- Rogenski, J.K.; de Souza, L.F.; Floryan, J.M. Influence of Pressure Gradients on the Evolution of the Görtler Instability. AIAA J. 2016, 54, 2916–2921. [Google Scholar] [CrossRef]
- Kahawita, R.; Meroney, R. The Influence of Heating on the Stability of Laminar Boundary Layers Along Concave Curved Walls. J. Appl. Mech. 1977, 44, 11–17. [Google Scholar] [CrossRef]
- Imura, H.; Gilpin, R.R.; Cheng, K.C. An Experimental Investigation of Heat Transfer and Buoyancy Induced Transition from Laminar Forced Convection to Turbulent Free Convection over a Horizontal Isothermally Heated Plate. J. Heat Transf. 1978, 100, 429–434. [Google Scholar] [CrossRef]
- Moutsoglou, A.; Chen, T.S.; Cheng, K.C. Vortex Instability of Mixed Convection Flow over a Horizontal Flat Plate. J. Heat Transf. 1981, 103, 257–261. [Google Scholar] [CrossRef]
- Momayez, L.; Dupont, P.; Peerhossaini, H. Effects of vortex organization on heat transfer enhancement by Görtler instability. Int. J. Therm. Sci. 2004, 43, 753–760. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P. Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 2010, 22, 85101–85105. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. In Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003. [Google Scholar]
- Moharreri, S.S.; Armaly, B.F.; Chen, T.S. Measurements in the Transition Vortex Flow Regime of Mixed Convection Above a Horizontal Heated Plate. J. Heat Transf. 1988, 110, 358–365. [Google Scholar] [CrossRef]







| Case No. | Airflow Velocity (m/s) | Airflow Temperature (K) | Temperature Difference (K) | Reynolds Number |
|---|---|---|---|---|
| Case 1 | 0.63 | 238 | 30 | 5.44 × 104 |
| Case 2 | 288 | 3.95 × 104 | ||
| Case 3 | 338 | 3.02 × 104 | ||
| Case 4 | 238 | 60 | 4.91 × 104 | |
| Case 5 | 288 | 3.62 × 104 | ||
| Case 6 | 338 | 2.81 × 104 | ||
| Case 7 | 0.34 | 238 | 30 | 2.94 × 104 |
| Case 8 | 288 | 2.13 × 104 | ||
| Case 9 | 338 | 1.63 × 104 | ||
| Case 10 | 238 | 60 | 2.65 × 104 | |
| Case 11 | 288 | 1.96 × 104 | ||
| Case 12 | 338 | 1.52 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Ma, D.; Zhang, L. Numerical Study on Buoyancy-Driven Görtler Vortices above Horizontal Heated Flat Plate. Aerospace 2023, 10, 685. https://doi.org/10.3390/aerospace10080685
Yang M, Ma D, Zhang L. Numerical Study on Buoyancy-Driven Görtler Vortices above Horizontal Heated Flat Plate. Aerospace. 2023; 10(8):685. https://doi.org/10.3390/aerospace10080685
Chicago/Turabian StyleYang, Muqing, Dongli Ma, and Liang Zhang. 2023. "Numerical Study on Buoyancy-Driven Görtler Vortices above Horizontal Heated Flat Plate" Aerospace 10, no. 8: 685. https://doi.org/10.3390/aerospace10080685




