Vibration Qualification Campaign on Main Landing Gear System for High-Speed Compound Helicopter
Abstract
:1. Introduction
1.1. Vibration Characterization in Aerospace Field
1.2. RACER Main Landing Gear
1.3. Scope of the Research
2. Materials and Methods
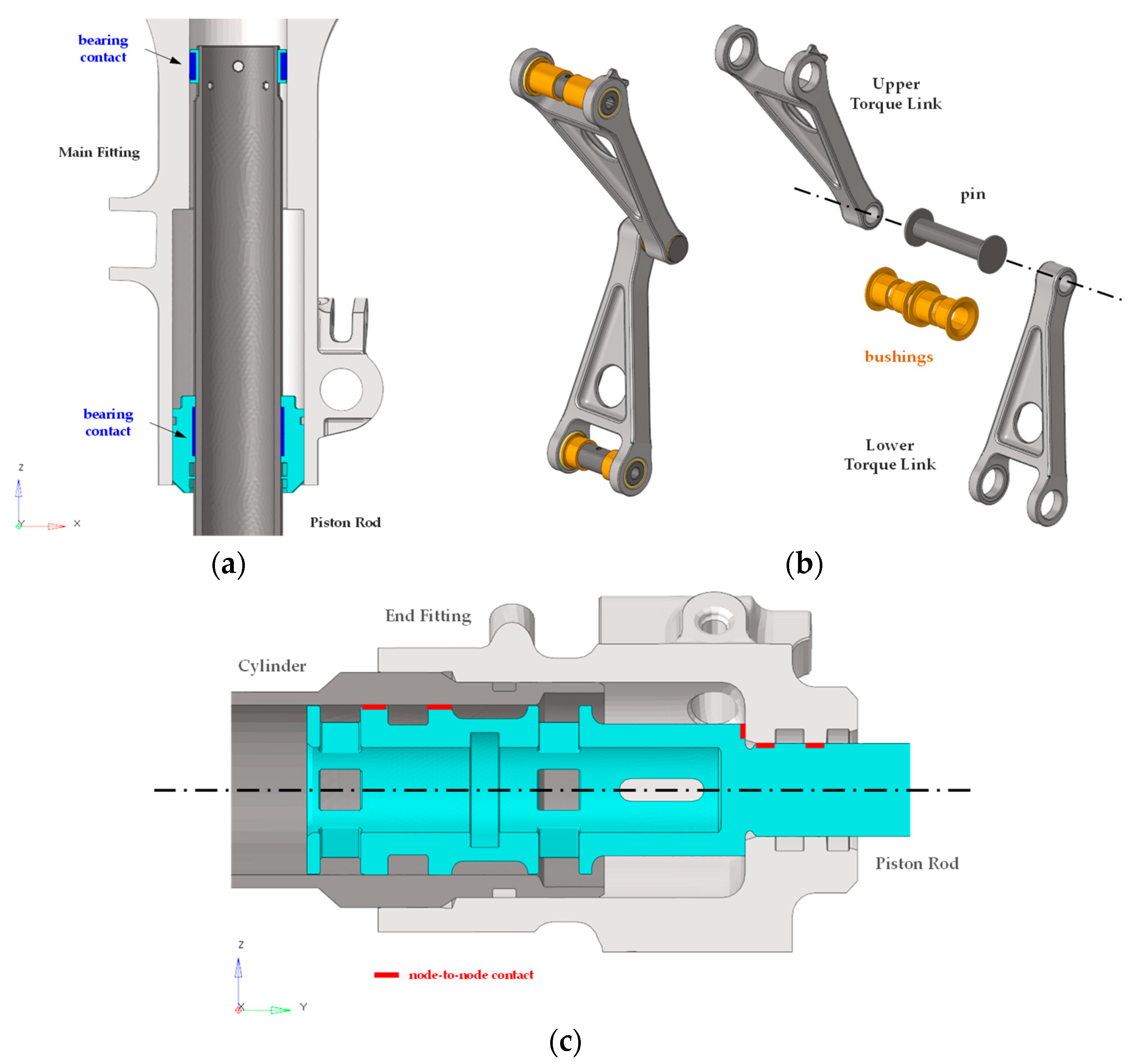
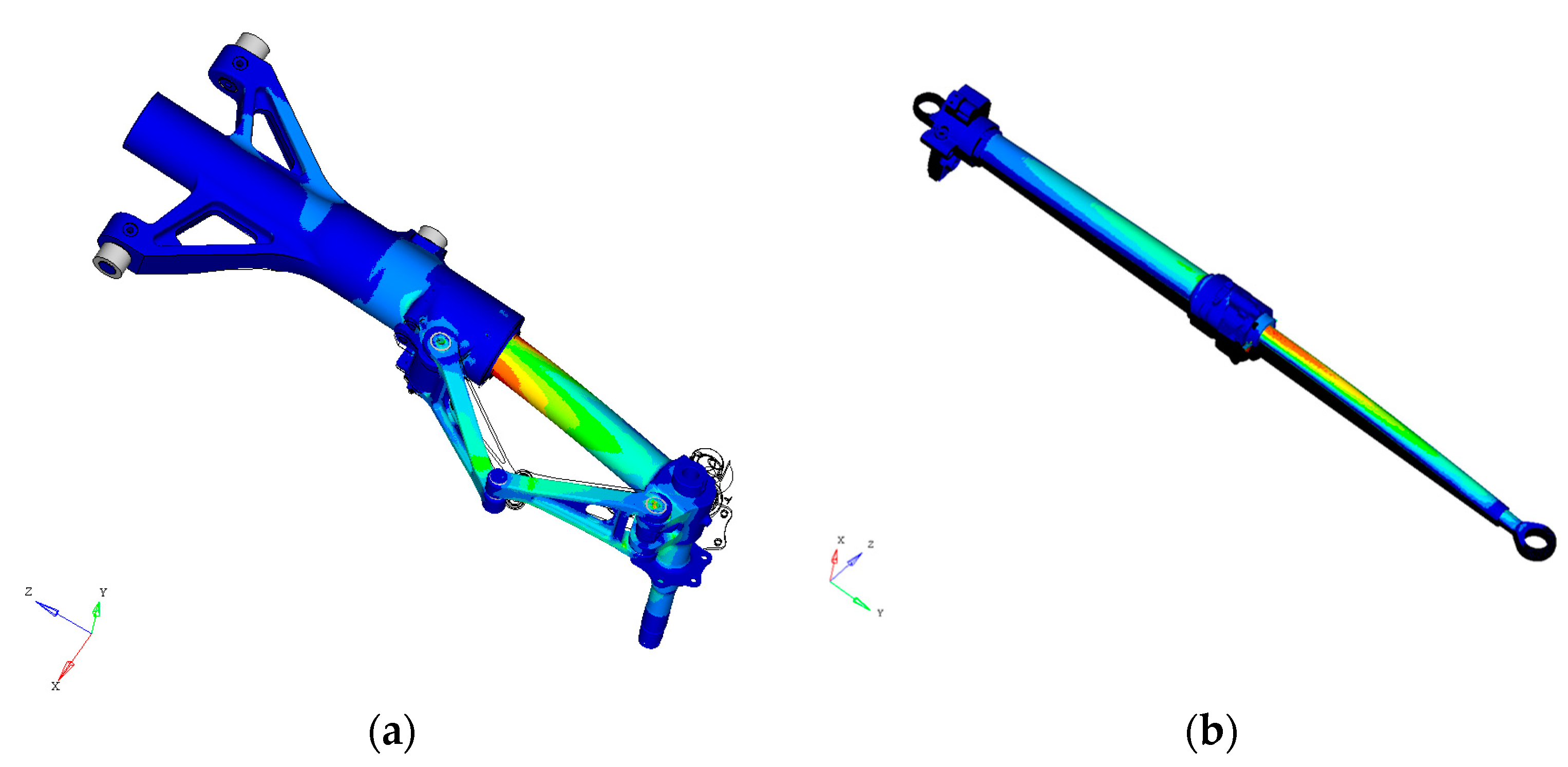
2.1. Numerical Model Design
2.2. FEM Boundary Conditions
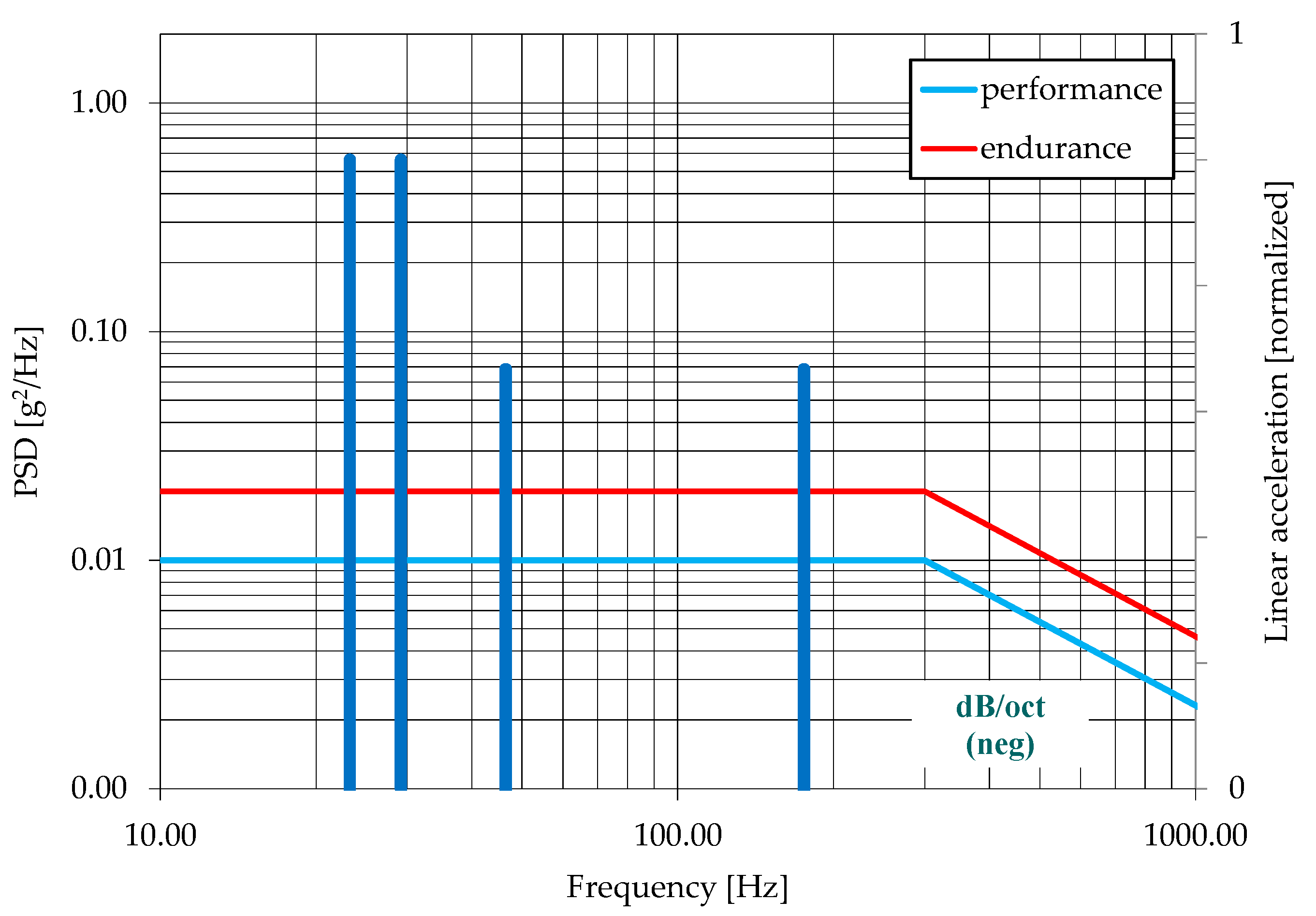
2.3. Sine-on-Random Loading Conditions
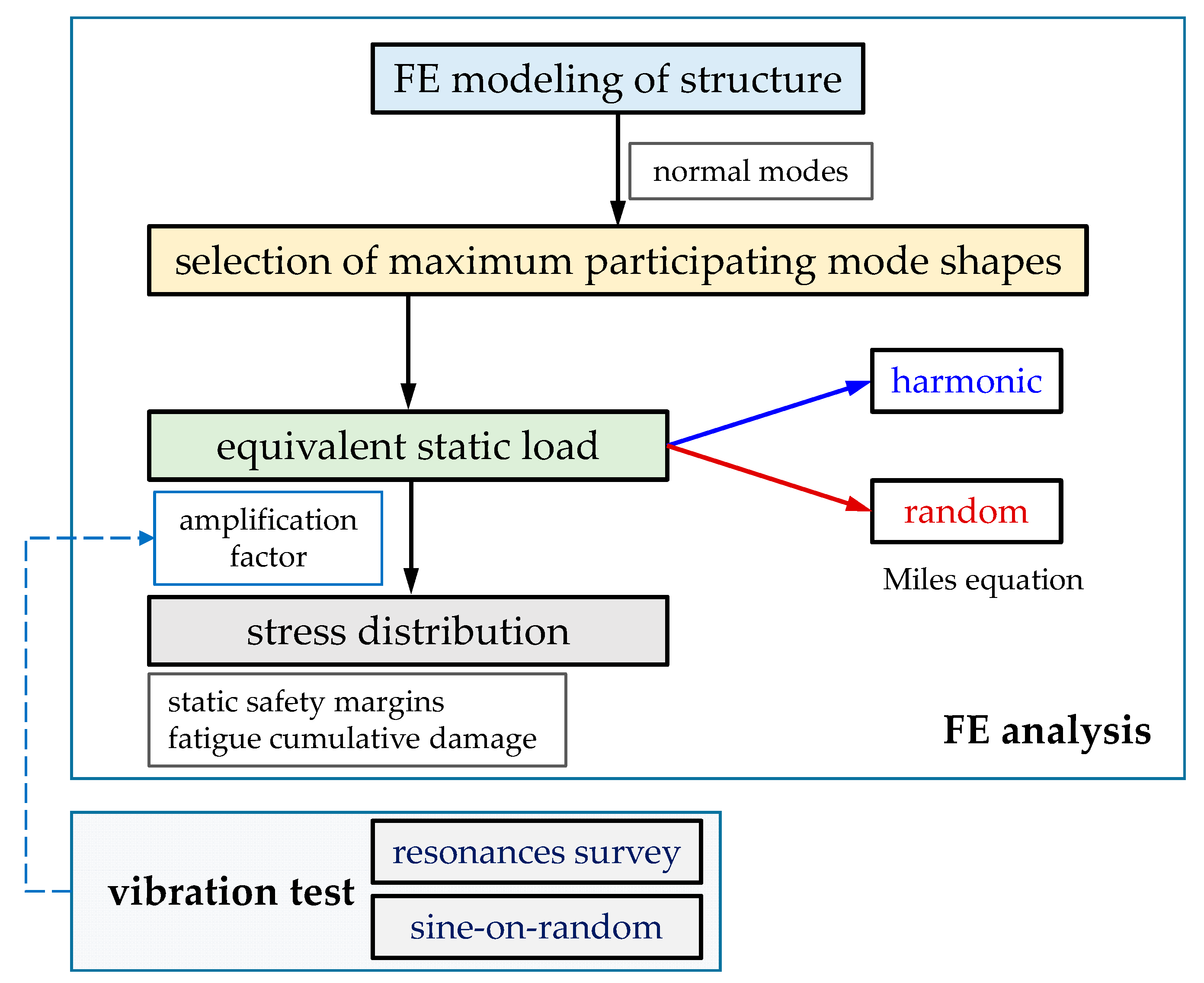
2.4. Computational Methodology for Dynamic Loads
- The harmonic sinusoidal load can be introduced as a factor of gravitational acceleration (ain):
- 2.
- The random load to be applied is approximated by means of the Miles equation [43]:
3. Numerical Results
3.1. MLG Normal Mode Analysis
3.2. Model Validation against Experiment
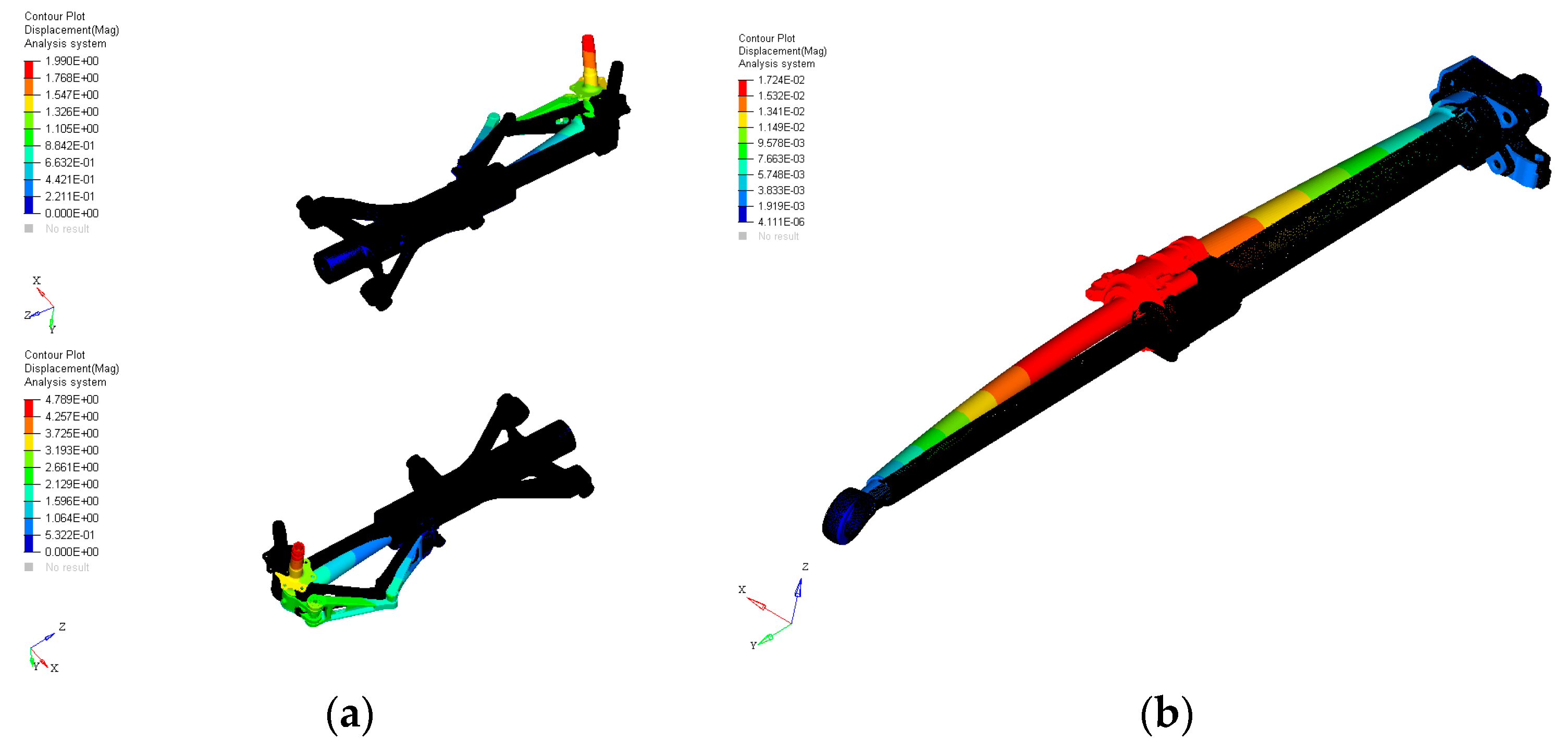
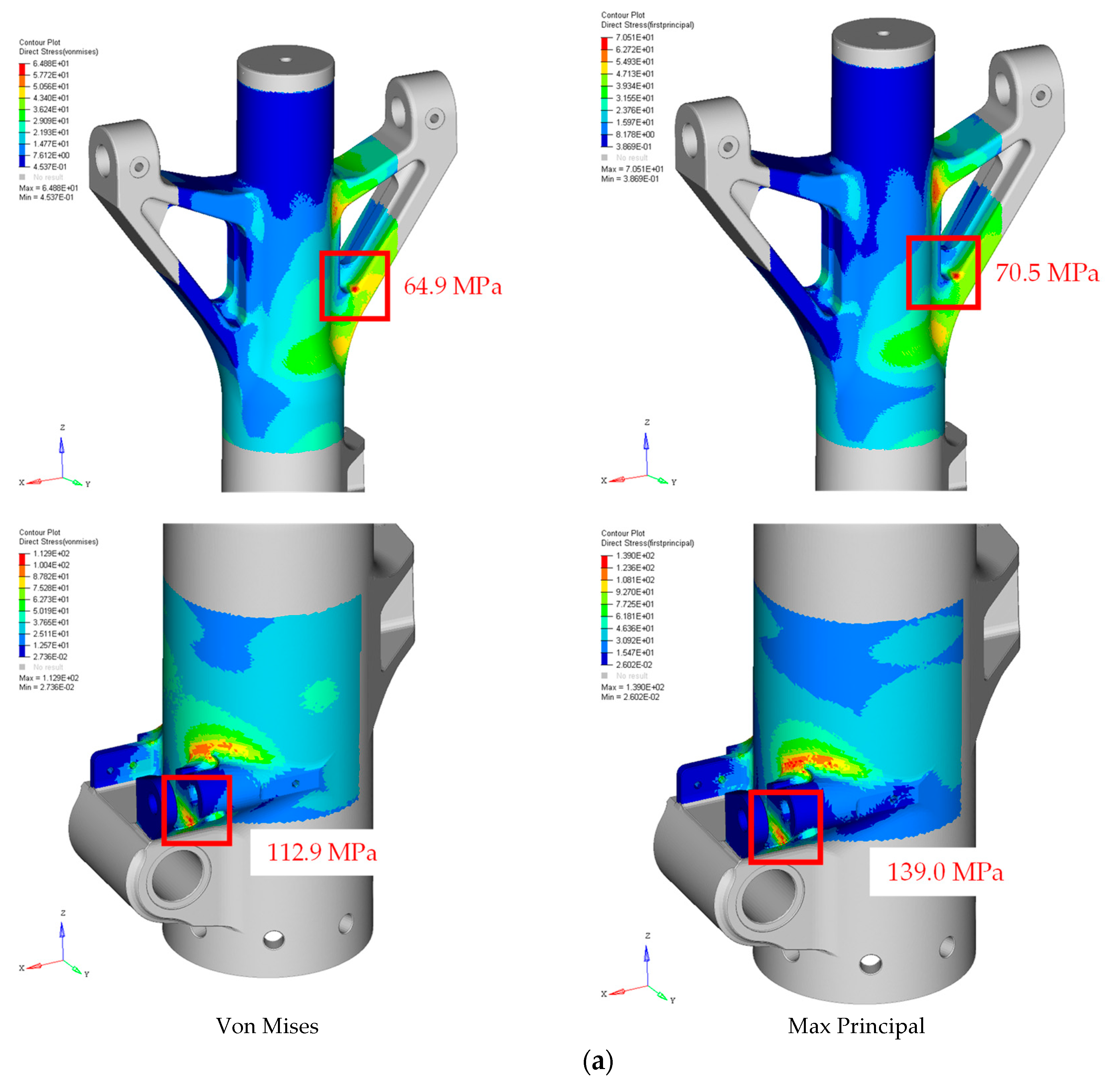
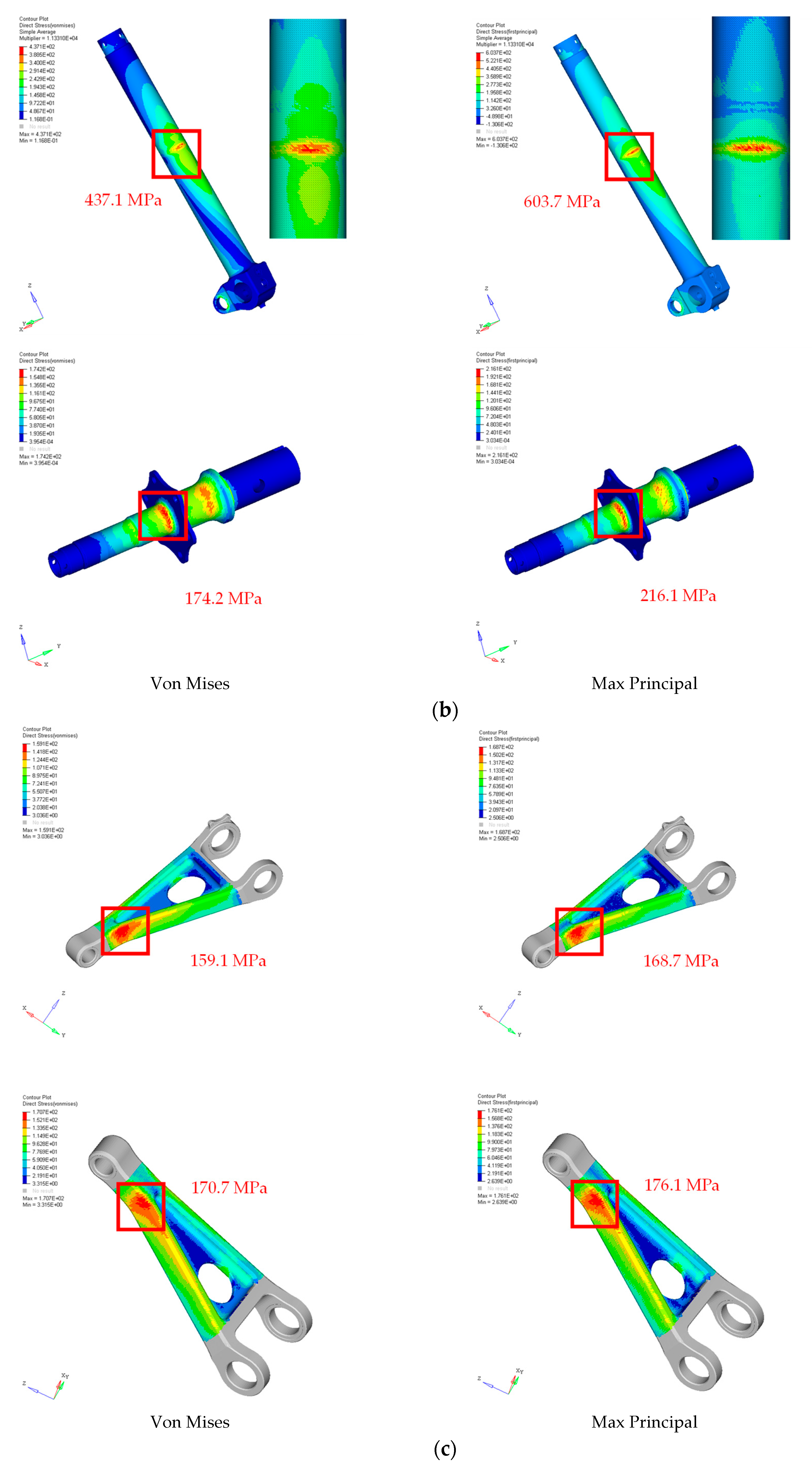
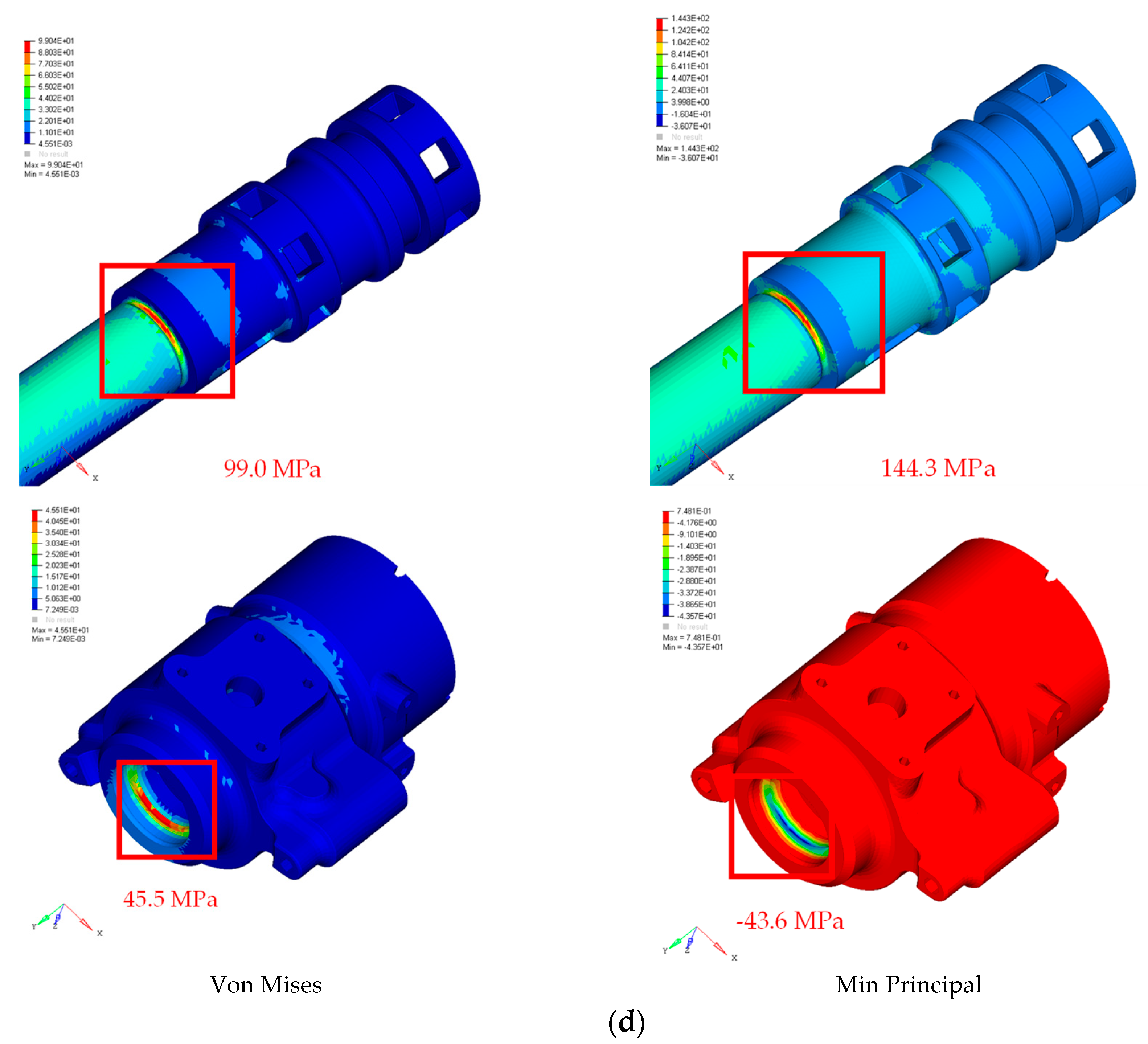
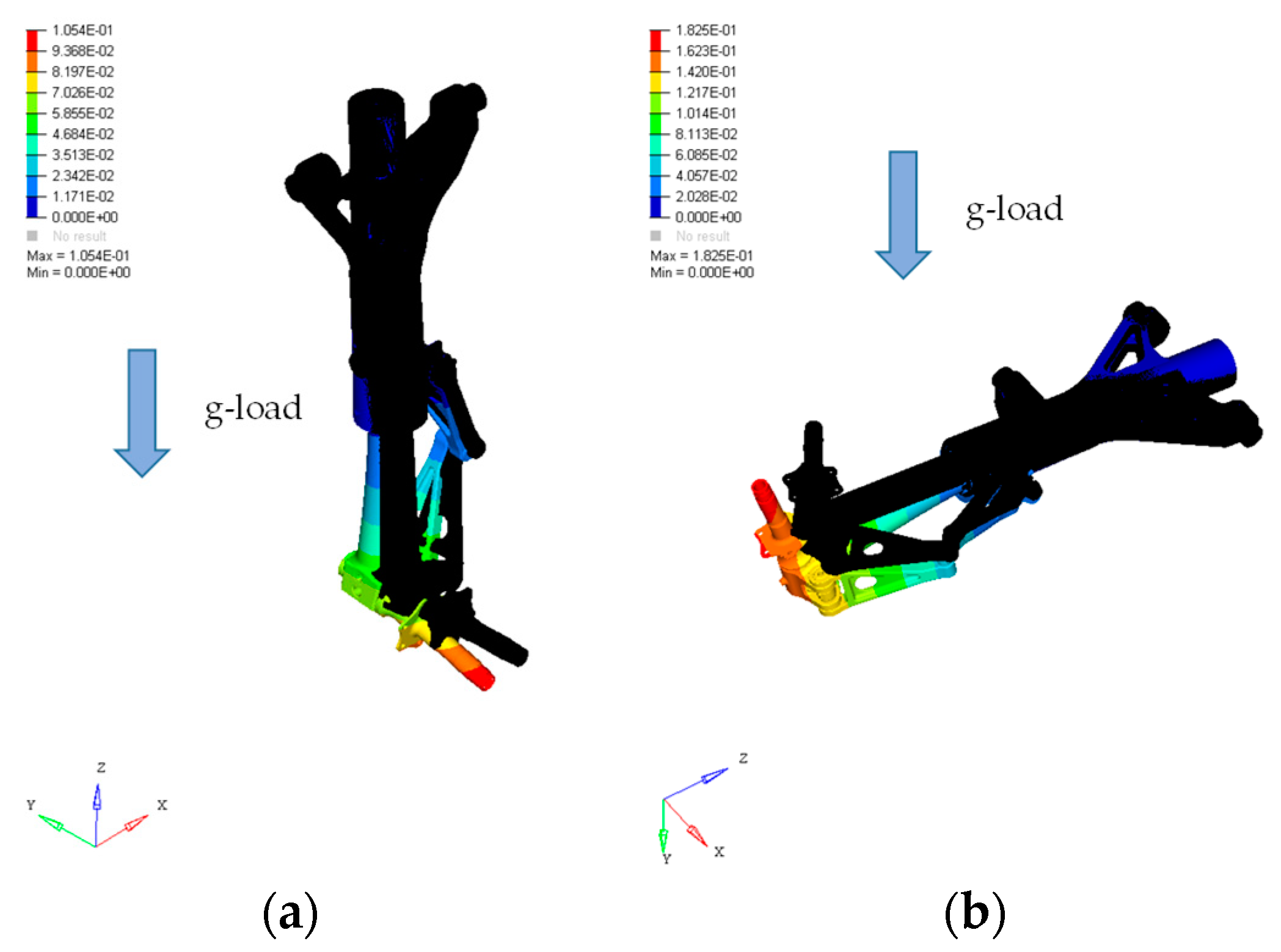
3.3. FE Calculation of Quasi-Steady Structural Loads
- αx = 0.98; αy = 1.00; αz = 0.68; for the first MLG mode shape;
- αx = 1.00; αy = 0.68; αz = 0.48; for the second MLG mode shape;
- αx = 1.00; αy = 0.00; αz = 0.00; for the actuator first mode shape.
3.4. Vibration Preliminary Fatigue Analysis
4. Vibration Qualification Process
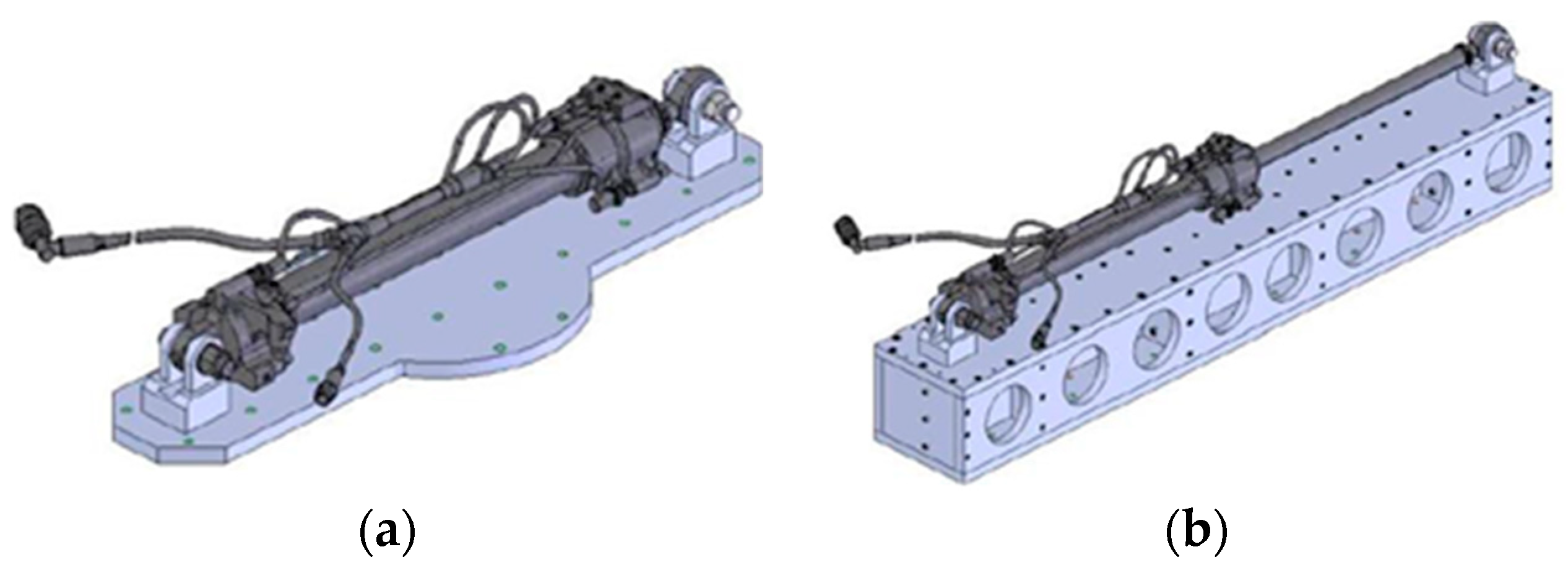
4.1. Equipment under Test
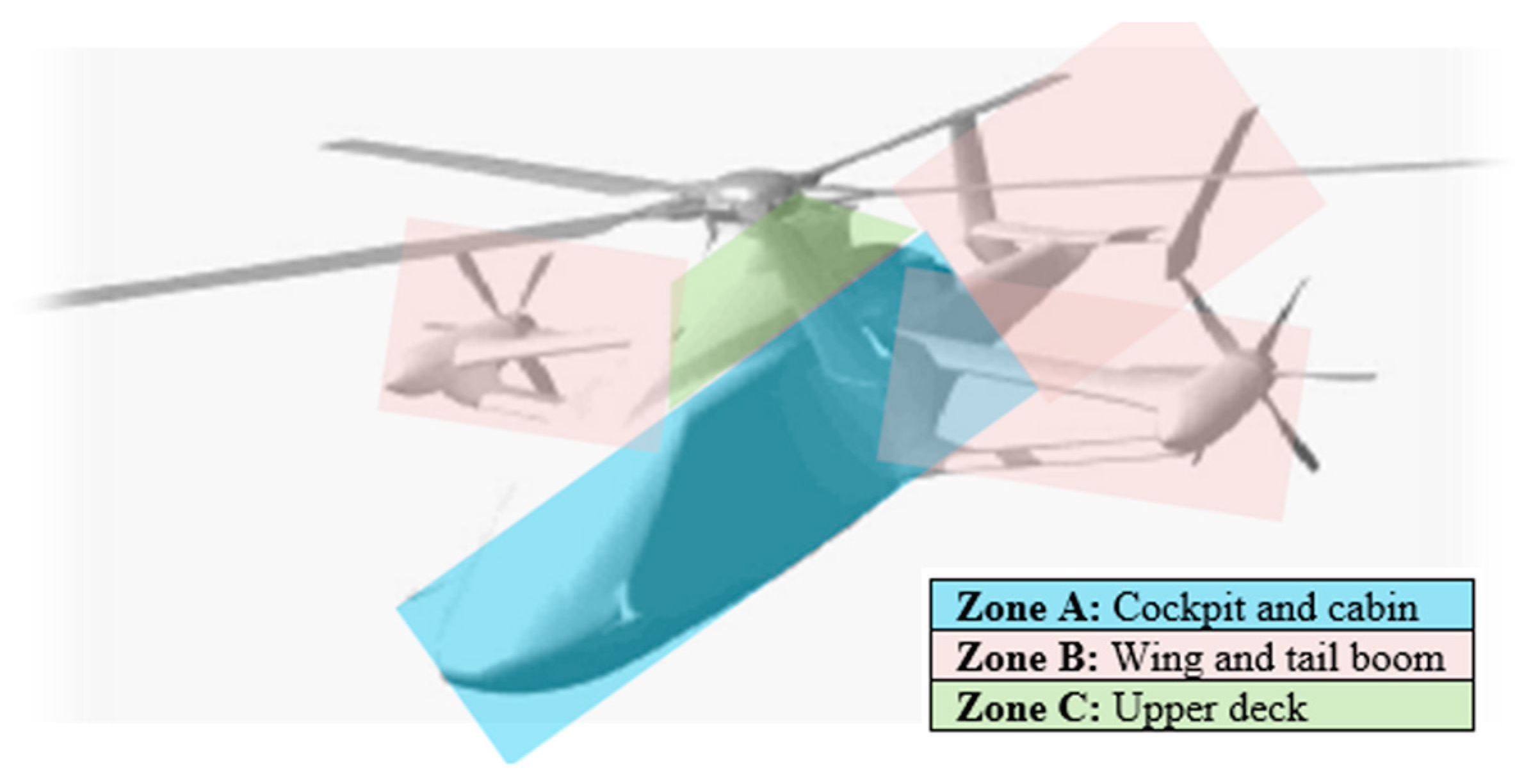
4.2. Test Specification Tailoring
- NLG and DBA are placed under the cockpit and therefore belong to area A;
- MLG and SBA are placed under the wing and therefore belong to zone B.
- sine sweep at 0.5 g from 10 Hz to 2000 Hz at 1 octave/min;
- sine-on-random performance test level for a minimum of 10 min;
- sine-on-random endurance test level for a minimum of 20 min;
- repeat performance test level for a minimum of 10 min;
- repeat sine sweep at 0.5 g from 10 Hz to 2000 Hz at 1 octave/min.
4.3. Test Setup
4.3.1. Test Setup: MLG
4.3.2. Test Setup: SBA in Extended Configuration
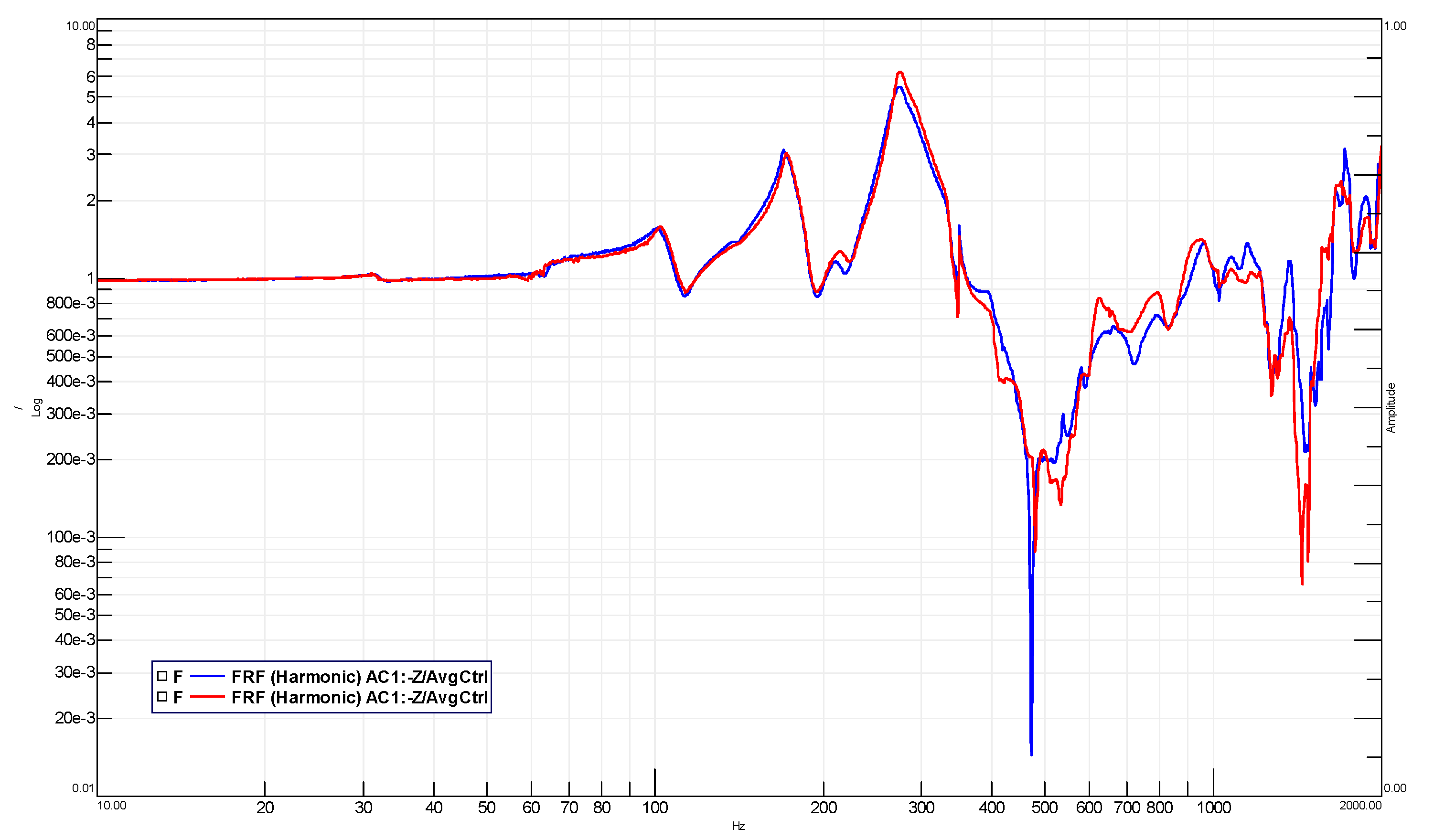
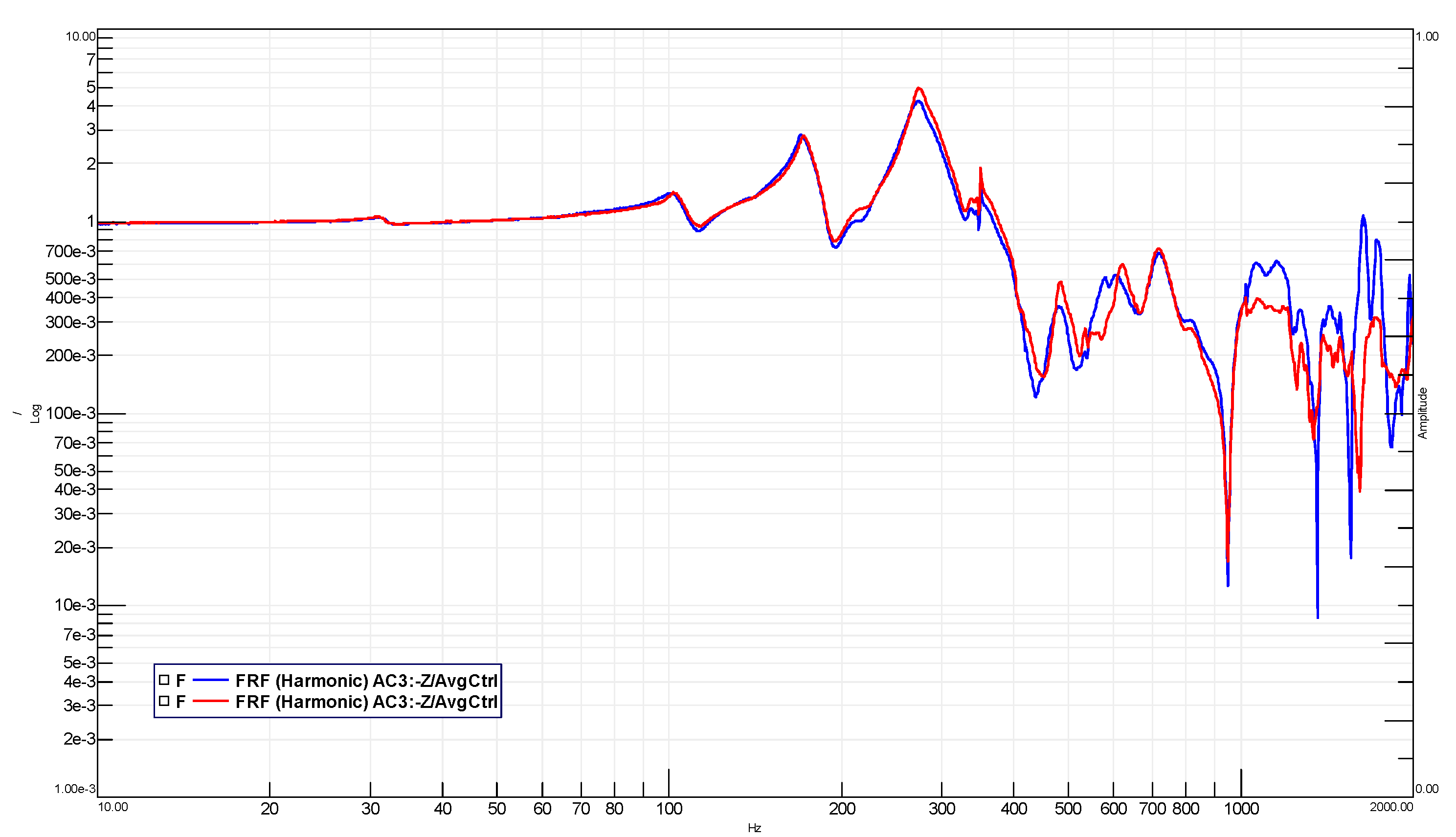
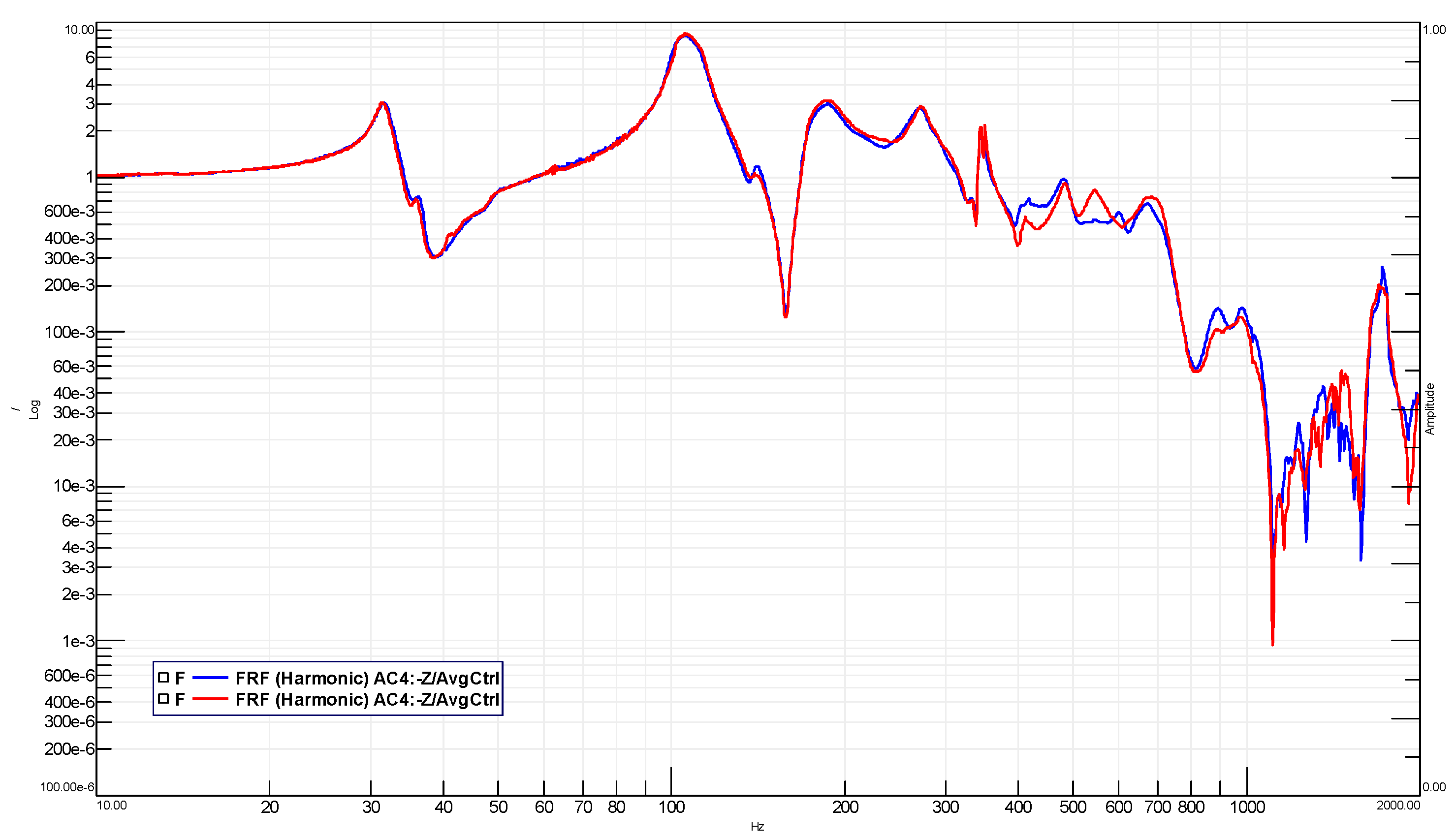
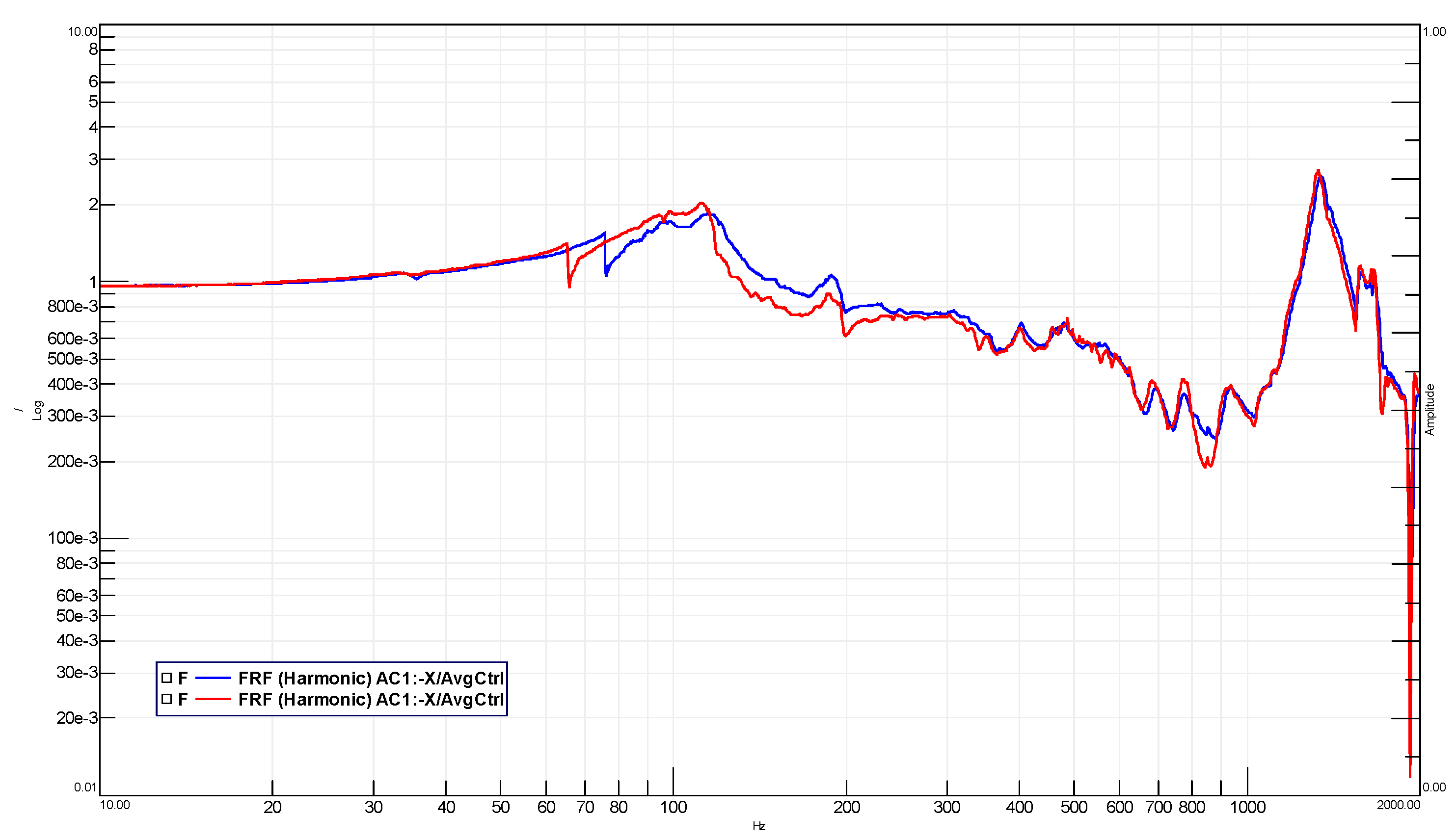
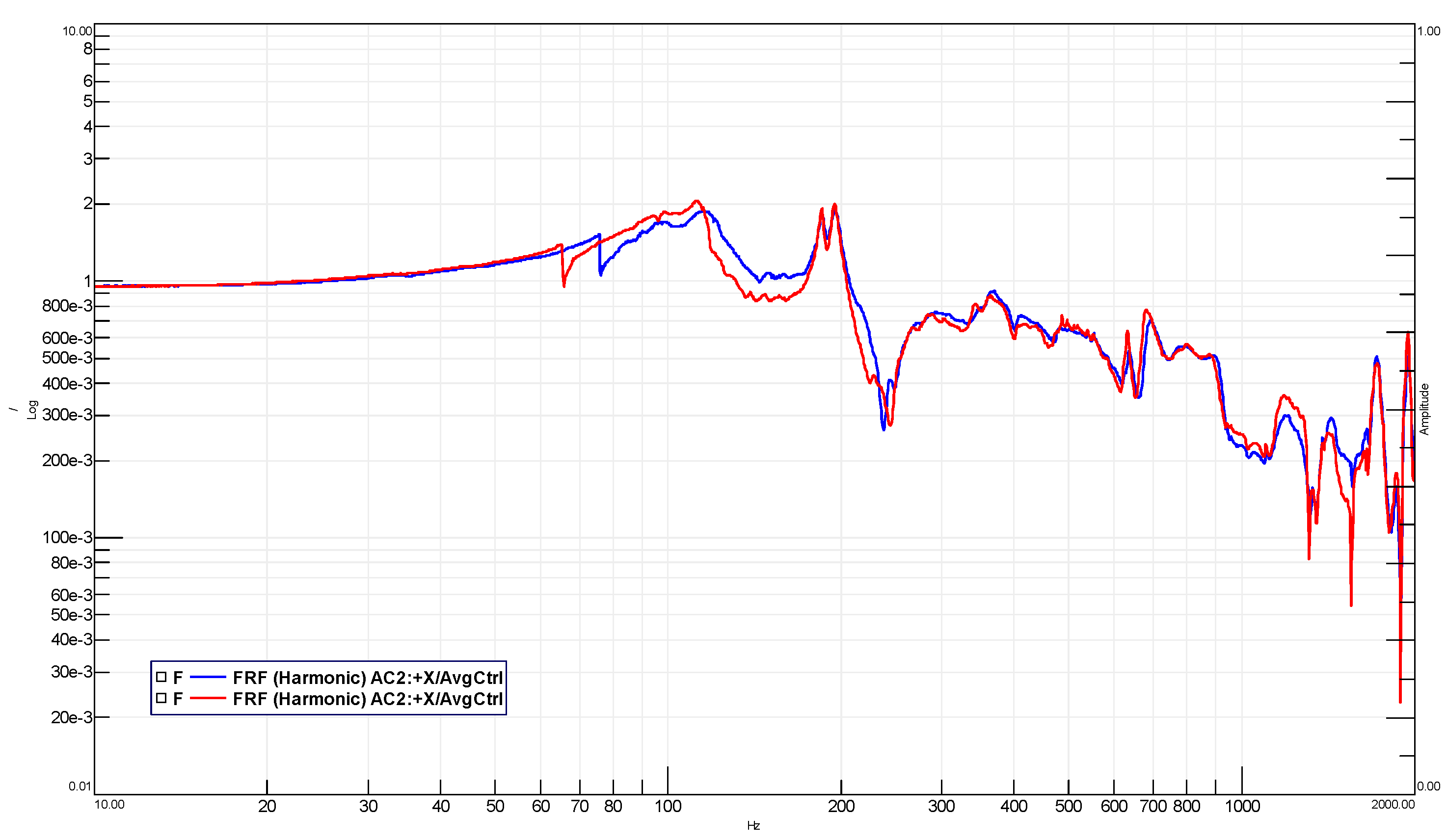
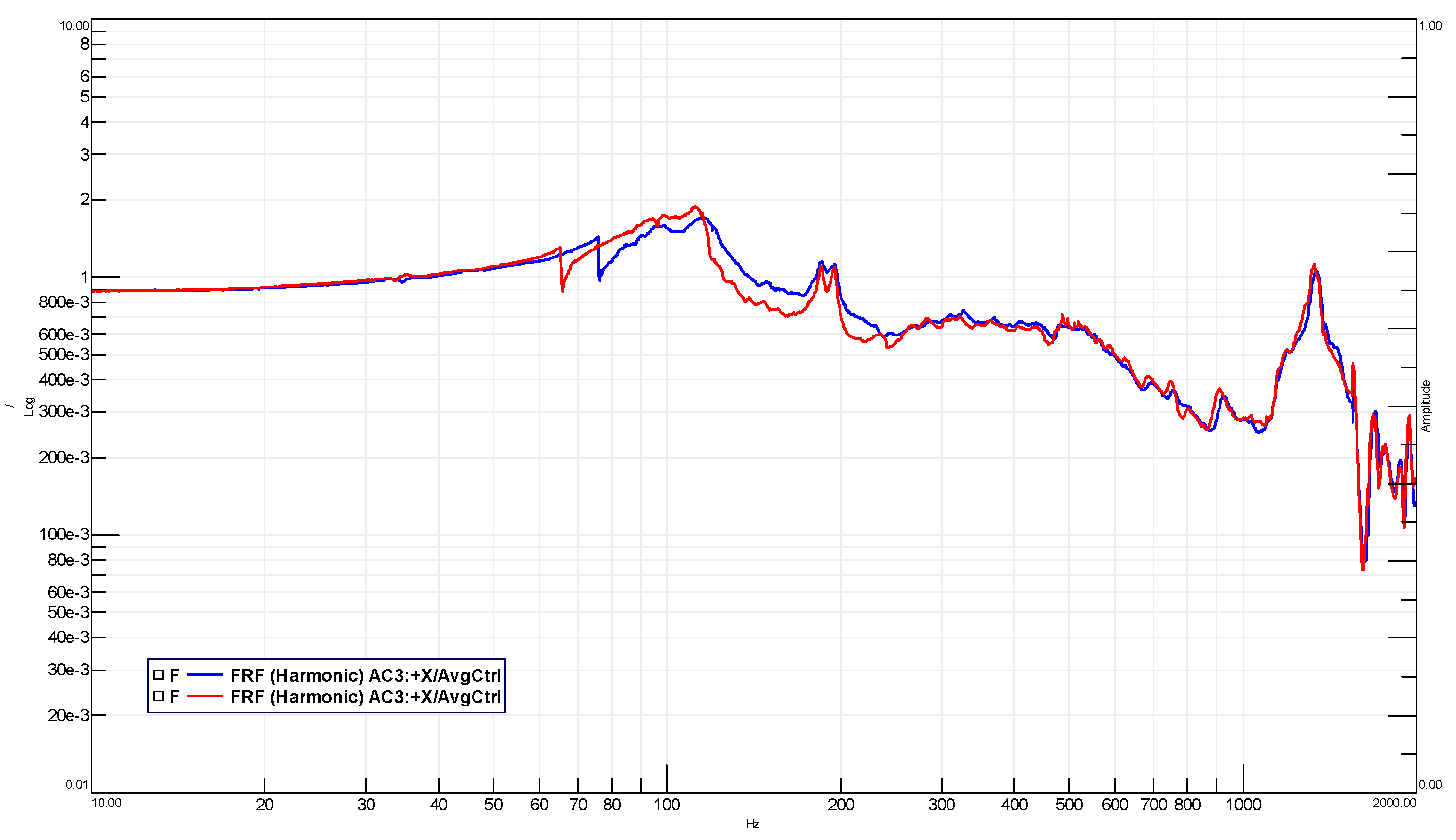
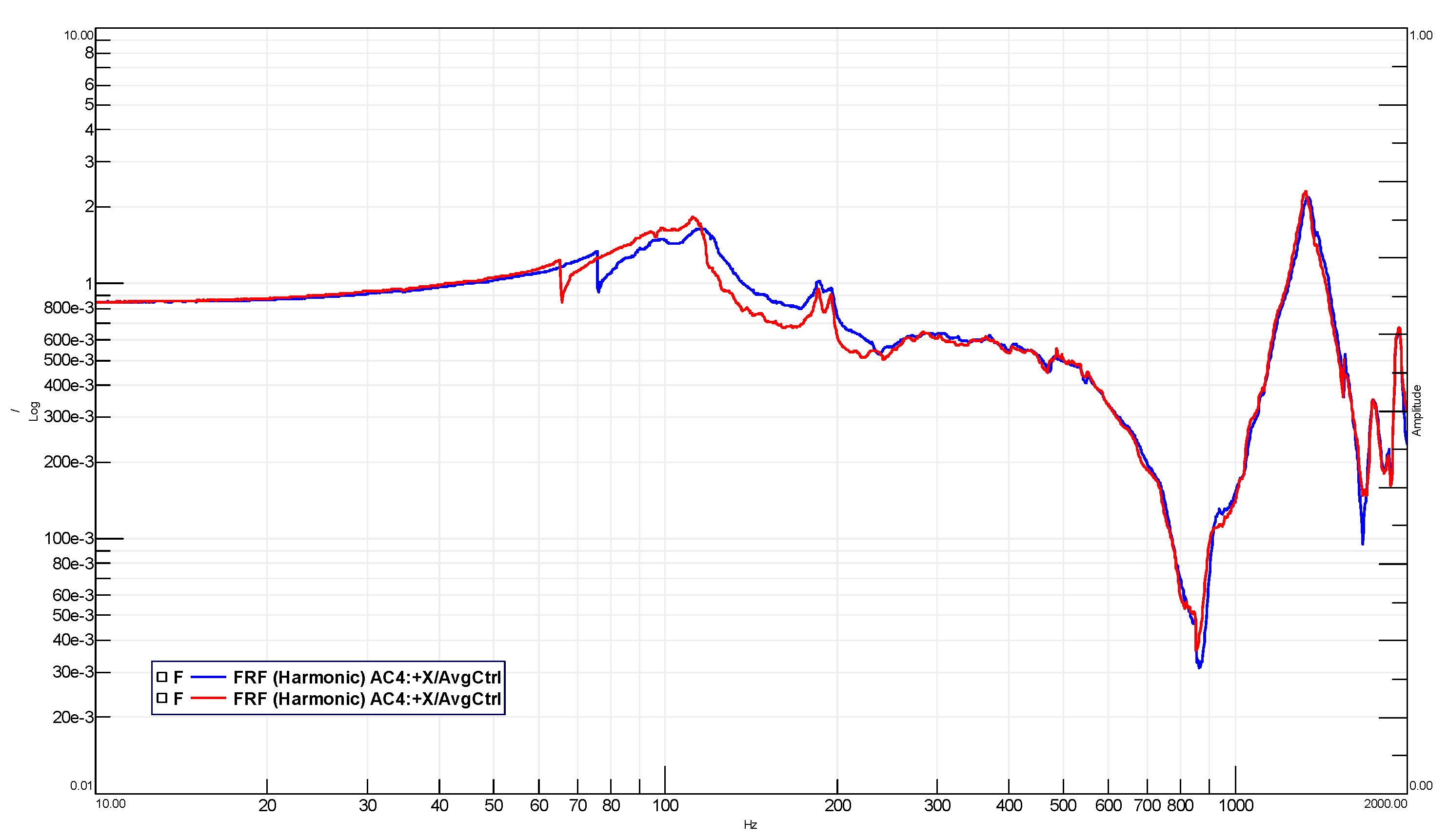
5. Test Results
- AC4 for the MLG;
- AC2 for the SBA.
- less than 5% in frequency shift;
- less than 20% in amplitude shift.
6. Conclusions and Future Activities
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kehoe, M.W. Aircraft Ground Vibration Testing at NASA Ames–Dryden Flight Research Facility; NASA TM–88272; National Aeronautics and Space Administration, AMES Research Center, Dryden Flight Research Facility: Edwards, CA, USA, 1987. [Google Scholar]
- Kehoe, M.W.; Voracek, D.F. Ground Vibration Test Results of a JetStar Airplane Using Impulsive Sine Excitation; NASA TM–100448; National Aeronautics and Space Administration, AMES Research Center, Dryden Flight Research Facility: Edwards, CA, USA, 1994. [Google Scholar]
- Cox, T.H.; Gilyard, G.B. Ground Vibration Test Results for Drones for Aerodynamic and Structural Testing (DAST)/Aeroelastic Research Wing (ARW–1R) Aircraft; NASA TM–85906; National Aeronautics and Space Administration, AMES Research Center, Dryden Flight Research Facility: Edwards, CA, USA, 1986. [Google Scholar]
- Afonso, F.; Vale, J.; Oliveira, É.; Lau, F.; Suleman, A. A review on non-linear aeroelasticity of high aspect-ratio wings. Prog. Aerosp. Sci. 2017, 89, 40–57. [Google Scholar] [CrossRef]
- Gao, Y.; An, G.; Zhi, C. Chapter 9–Airworthiness verification test of the flight control system. In Test Techniques for Flight Control Systems of Large Transport Aircraft; Gao, Y., An, G., Zhi, C., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 631–672. [Google Scholar]
- Chang, C.; Hodges, D. Modeling of Ground Vibration Testing for Highly Flexible Aircraft. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006. [Google Scholar]
- Göge, D.; Böswald, M.; Füllekrug, U.; Lubrina, P. Ground vibration testing of large aircraft-state-of-the-art and future perspectives. In Proceedings of the 25th International Modal Analysis Conference (IMAC XXV), Orlando, FL, USA, 19–22 January 2007. [Google Scholar]
- Füllekrug, U.; Gloth, G.; Sinapius, M.; Fargette, P.; Levadoux, B.; Lubina, P.; Schaak, H. Tasks for improvement in ground vibration testing of large aircraft. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD 2001), Madrid, Spain, 5–7 June 2001. [Google Scholar]
- Pickrel, C.R.; Foss, G.C.; Phillips, A.; Allemang, R.J.; Brown, D.L. New concepts GVT. In Proceedings of the 24th International Modal Analysis Conference (IMAC XXIV), St. Louis, MO, USA, 30 January–2 February 2006. [Google Scholar]
- Lubrina, P. Ground vibration experiments on large civil aircraft for engine imbalance purpose. In Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD 2003), Amsterdam, The Netherlands, 4–6 June 2003. [Google Scholar]
- Gloth, G.; Degener, M.; Füllekrug, U.; Gschwilm, J.; Sinapius, M.; Fargette, P.; Levadoux, B.; Lubrina, P. Experimental investigation of new GVT concepts for large aircraft. Sound Vib. 2001, 35, 14–18. [Google Scholar]
- Simsiriwong, J.; Sullivan, R.W. Experimental Vibration Analysis of a Composite UAV Wing. Mech. Adv. Mater. Struct. 2012, 19, 196–206. [Google Scholar] [CrossRef]
- Sullivan, R.; Rais-Rohani, M.; Lacy, T.; Alday, N. Structural testing of an ultralight UAV composite wing. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006. [Google Scholar]
- Sullivan, R.W.; Hwang, Y.; Rais-Rohani, M.; Lacy, T. Structure analysis and testing of an ultralight UAV carbon composite wing. J. Aircr. 2009, 46, 814–820. [Google Scholar] [CrossRef]
- Simsiriwong, J.; Sullivan, R. Vibration testing of a carbon composite fuselage. In Proceedings of the 23rd American Society for Composites Conference, Memphis, TN, USA, 9–11 September 2008. [Google Scholar]
- Gupta, A.; Seiler, P.; Danowsky, B. Ground vibration tests on a flexible flying wing aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, AIAA SciTech, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-1753. [Google Scholar]
- Kerschen, G.; Peeters, M.; Golinval, J.C.; Stéphan, C. Nonlinear Modal Analysis of a Full-Scale Aircraft. J. Aircr. 2013, 50, 1409–1419. [Google Scholar] [CrossRef]
- Ahlquist, J.; Carreño, J.; Climent, H.; de Diego, R.; de Alba, J. Assessment of nonlinear structural response in A400M GVT. In Proceedings of the 28th International Modal Analysis Conference (IMAC XXVIII), Jacksonville, FL, USA, 1–4 February 2010. [Google Scholar]
- Goege, D. Fast Identification and Characterization of Nonlinearities in Experimental Modal Analysis of Large Aircraft. J. Aircr. 2007, 44, 399–409. [Google Scholar] [CrossRef]
- Pritchard, J. Overview of Landing Gear Dynamics. J. Aircr. 2001, 38, 130–137. [Google Scholar] [CrossRef]
- Somieski, G. Shimmy analysis of a simple aircraft nose landing gear model using different mathematical methods. Aerosp. Sci. Technol. 1997, 1, 545–555. [Google Scholar] [CrossRef]
- Esmailzadeh, E.; Farzaneh, K. Shimmy Vibration Analysis of Aircraft Landing Gears. J. Vib. Control 1999, 5, 45–56. [Google Scholar] [CrossRef]
- Feng, F.; Nie, H.; Zhang, M.; Peng, Y. Effect of Torsional Damping on Aircraft Nose Landing-Gear Shimmy. J. Aircr. 2015, 52, 561–568. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Interaction of torque link freeplay and Coulomb friction nonlinearities in nose landing gear shimmy scenarios. Int. J. Non-Linear Mech. 2020, 119, 103338. [Google Scholar] [CrossRef]
- Du, X.; Xu, Y.; Liu, Q.; Liu, C.; Yue, X.; Liu, X.; Kurths, J. Shimmy dynamics in a dual-wheel nose landing gear with freeplay under stochastic wind disturbances. Nonlinear Dyn. 2024, 112, 2477–2499. [Google Scholar] [CrossRef]
- Li, Y.; Howcroft, C.; Neild, S.A.; Jiang, J.Z. Using Continuation Analysis to Identify Shimmy-Suppression Devices for an Aircraft Main Landing Gear. J. Sound Vib. 2017, 408, 234–251. [Google Scholar] [CrossRef]
- Orlando, C.; Alaimo, A. A Robust Active Control System for Shimmy Damping in the Presence of Free Play and Uncertainties. Mech. Syst. Signal Process. 2017, 84, 551–569. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Parametric study of a novel nose landing gear shimmy damper concept. J. Sound Vib. 2019, 457, 299–313. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. On the effectiveness of shimmy dampers in stabilizing nose landing gears. Aerosp. Sci. Technol. 2019, 91, 272–286. [Google Scholar] [CrossRef]
- Mustashin, M.S.; Rahmani, M.; Behdinan, K. Experimental characterization of a novel nose landing gear shimmy damper using a small-scale test rig. Aerosp. Sci. Technol. 2021, 112, 106625. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y. Amplitude reduction optimization of time delay semi-active control for aircraft landing gear shimmy. J. Phys. Conf. Ser. 2022, 2230, 012009. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Structural design and optimization of a novel shimmy damper for nose landing gears. Struct. Multidiscip. Optim. 2020, 62, 2783–2803. [Google Scholar] [CrossRef]
- Biehl, F.A. Aircraft Landing Gear Brake Squeal and Strut Chatter Investigation. In The Shock and Vibration Bulletin; Naval Research Laboratory: Washington, DC, USA, 1969. [Google Scholar]
- Travis, M.H. Predicting Landing Gear Carbon Brake Vibration and Performance via Subscale Test and Analysis; SAE Technical Paper 2005-01-3437; SAE International: Warrendale, PA, USA, 2005. [Google Scholar] [CrossRef]
- Yin, Q.; Jiang, J.Z.; Neild, S.A.; Nie, H. Investigation of gear walk suppression while maintaining braking performance in a main landing gear. Aerosp. Sci. Technol. 2019, 91, 122–135. [Google Scholar] [CrossRef]
- Jiao, Z.; Bai, N.; Liu, J.; Li, Y.; Wang, Z.; Sun, D.; Qi, P.; Shang, Y. Aircraft anti-skid braking control technology: A review. Acta Aeronaut. Astronaut. Sin. 2022, 43, 1–27. [Google Scholar]
- Sinou, J.-J.; Dereure, O.; Mazet, G.-B.; Thouverez, F.; Jezequel, L. Friction-induced vibration for an aircraft brake system—Part 1: Experimental approach and stability analysis. Int. J. Mech. Sci. 2006, 48, 536–554. [Google Scholar] [CrossRef]
- Arena, M.; Chiariello, A.; Castaldo, M.; Di Palma, L. Vibration Response Aspects of a Main Landing Gear Composite Door Designed for High-Speed Rotorcraft. Aerospace 2021, 8, 52. [Google Scholar] [CrossRef]
- Liu, R.; Li, Z.; Xu, W.; Yang, X.; Zhang, D.; Yao, Z.; Yang, K. Dynamic Analysis and Experiment of a Space Mirror Based on a Linear State Space Expression. Appl. Sci. 2021, 11, 5379. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, H. A time finite element method for structural dynamics. Appl. Math. Model. 2017, 41, 445–461. [Google Scholar] [CrossRef]
- MSC Nastran®. Quick Reference Guide 2021; MSC Software: Newport Beach, CA, USA, 2021. [Google Scholar]
- MMPDS-16; Metallic Materials Properties Development and Standardization. Battelle Memorial Institute: Columbus, OH, USA, 2021.
- Wijker, J. Miles’ Equation in Random Vibrations; Solid Mechanics and Its Applications; Springer: Cham, Switzerland, 2018; Volume 248. [Google Scholar] [CrossRef]
- Vince, A.; Abraham, A. Building Better Products with Finite Element Analysis; Onward Press: Santa Fe, NM, USA, 1999. [Google Scholar]
- Budynas, R.; Nisbett, K. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Lee, Y.-L. Stress-Based Fatigue Analysis and Design. In Fatigue Testing and Analysis; Elsevier: Oxford, UK, 2005. [Google Scholar]
- RACER Compound Helicopter. Clean Aviation. Available online: https://www.clean-aviation.eu/racer-compound-helicopter (accessed on 1 December 2023).
- Clean Sky 2–ANGELA. Available online: https://www.maregroup.it/cleansky2/portfolio/angela/ (accessed on 1 December 2023).
- CIRA. ANGELA Project, Vibrational Qualification Campaign of the RACER Compound Helicopter Landing Gears Completed. Available online: https://www.cira.it/en/competences/strutture-e-materiali/progetto-angela-superati-i-test-di-qualifica-vibrazionale-per-i-carrelli-d’atterraggio-del-racer-compound-helicopter (accessed on 1 December 2023).
- RTCA-DO-160-F; Environmental Conditions and Test Procedures for Airborne Equipment. RTCA, Inc.: Washington, DC, USA, 2007.
- Shaker Fixture Design. Vibration Research. Available online: https://vibrationresearch.com/blog/shaker-fixtures-and-fixture-design (accessed on 1 December 2023).
- ECSS-E-ST-10-03C; Space Engineering: Testing. ECSS: Noordwijk, The Netherlands, 2012.
- Orefice, M.; Bruno, G.; Tartaglia, C.C.; Di Caprio, F.; Menichino, A.; Quaranta, V.; Belardo, M. Vibration test campaign on ALM flanges of bladder fuel tanks for Tiltrotor application. In Proceedings of the 2022 IEEE 9th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 27–29 June 2022; pp. 38–42. [Google Scholar]


















| Item | Component | Material | Specification |
|---|---|---|---|
| [-] | [-] | [-] | [-] |
| MLG Leg | Main Fitting | Al 7050-T7452 | AMS 4108 |
| Sliding Rod—Wheel Axle | Steel 300M | AMS 6257 | |
| Torque Links | Ti-6Al-4V | AMS 4928 | |
| Actuator | End Cap—End Fitting | Ti-6Al-4V | AMS 4928 |
| Cylinder—Piston Rod | Steel 15-5PH | AMS 5659 |
| FE Entity | Number |
|---|---|
| Nodes | 1,384,642 |
| 3D elements, ctet4 | 6,270,015 |
| 1D elements, cgap contact | 32,785 |
| 0D elements, conm2 | 1 |
| Rigid elements, rbe | 36 |
| Mass, m | 19.5 | [kg] |  |
| Inertia moment, xy Ixx = Iyy | 0.229 | [kgm2] | |
| Inertia moment, z Izz | 0.331 | [kgm2] |
| Frequency Band | Amplitude | Description |
|---|---|---|
| [Hz] | [g, linear], [g2/Hz, Random] | [-] |
| 23.3 | ±1.0 | 5/rev MR |
| 29.2 | ±1.0 | 1/rev LR |
| 46.5 | ±0.67 | 10/rev MR |
| 175.2 | ±0.67 | 6/rev LR |
| 10–2000 | 0.01 (10; 300 Hz), 0.001 (f ≤ 2000) | performance Grms = 2.75 g |
| 0.02 (10; 300 Hz), 0.002 (f ≤ 2000) | endurance Grms = 3.89 g |
| Frequency | Modal Mass | Description |
|---|---|---|
| [Hz] | [kg] | [-] |
| 33.2 | 41.1 | MLG leg first bending |
| 34.8 | 27.8 | MLG leg second bending |
| 35.5 | 8.0 | Actuator first bending |
| Axis | First Numerical Frequency [Hz] | First Experimental Frequency [Hz] | Numerical Q Factor | Experimental Q Factor |
|---|---|---|---|---|
| X | 33.2 | 27.24 | 20 | 1.86 |
| Y | 30.28 | 10.84 | ||
| Z | 31.23 | 11.45 |
| Axis | First Numerical Frequency [Hz] | First Experimental Frequency [Hz] | Numerical Q Factor | Experimental Q Factor |
|---|---|---|---|---|
| X | 35.5 | No resonance up to 200 Hz | 20 | n/a |
| Y | 29.03 | 7.03 | ||
| Z | 27.39 | 3.31 |
| Assy | Component | Stress Component | Yield Strength | Load Case |
|---|---|---|---|---|
| [-] | [-] | [MPa] | [MPa] | [-] |
| MLG leg | Main Fitting | 139.0 (Max P) | 400.0 | x direction |
| Sliding Rod | 603.7 (Max P) | 1586.0 | x direction | |
| Wheel Axle | 216.9 (Max P) | 1586.0 | z direction | |
| Upper Torque Link | 168.7 (Max P) | 792.0 | x direction | |
| Lower Torque Link | 176.1 (Max P) | 792.0 | x direction | |
| Actuator | End Cap | <40.0 | 806.0 | x direction (SBA reference frame) |
| End Fitting | (−)43.6 (Max P) | 806.0 | ||
| Cylinder | <40.0 | 1000.0 | ||
| Piston Rod | 144.3 (Max P) | 1000.0 |
| Test | Duration | Cycles Required, ni | |
|---|---|---|---|
| [-] | [min] | [–] | |
| MLG | Actuator | ||
| Performance | 10.0 | 19,920 | 21,283 |
| Endurance | 20.0 | 39,840 | 42,566 |
| Performance | 10.0 | 19,920 | 21,283 |
| Assy | Component | Max Principal (Performance/Endurance) | Cycles to Failure, Ni | Damage, D |
|---|---|---|---|---|
| [-] | [-] | [MPa] | [-] | |
| MLG leg | Main Fitting | (39.4; 55.5) | 1.0 × 107 | 0.000 |
| Sliding Rod | (184.1; 259.6) | 1.0 × 106 | 0.415 | |
| Wheel Axle | (45.0; 63.4) | 1.0 × 107 | 0.000 | |
| Upper Torque Link | (47.7; 67.3) | 1.0 × 107 | 0.000 | |
| Lower Torque Link | (49.8; 70.3) | 1.0 × 107 | 0.000 | |
| Actuator | End Cap | <40 MPa | 1.0 × 107 | 0.000 |
| End Fitting | <40 MPa | 1.0 × 107 | 0.000 | |
| Cylinder | <40 MPa | 1.0 × 107 | 0.000 | |
| Piston Rod | (118.1; 144.0) | 1.0 × 107 | 0.004 |
| Description | Serial Number | Length [mm] | EUT Mass [kg] |
|---|---|---|---|
| MLG | TS100-G1033-00 | 1065.4 | 62.0 |
| SBA | TS100-A1051-00 | EXTENDED: 1326.7 RETRACTED: 810.8 | 14.0 |
| Sine-on-Random PERFORMANCE (600 s) | Sine-on-Random ENDURANCE (1200 s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Background Random | Background Random | ||||||||
| Frequency [Hz] | ASD [g2/Hz] | Frequency [Hz] | ASD [g2/Hz] | ||||||
| 10 | 0.01 | 10 | 0.02 | ||||||
| 300 | 0.01 | 300 | 0.02 | ||||||
| 2000 | 0.001 | 2000 | 0.002 | ||||||
| Sweeping Sine Tones | Sweeping Sine Tones | ||||||||
| Item | Frequency [Hz] | 23.25 | 29.20 | 46.50 | 175.20 | 23.25 | 29.20 | 46.50 | 175.20 |
| MLG | X-Axis [g] * | 1.00 | 0.67 | 0.67 | 0.67 | 1.00 | 0.67 | 0.67 | 0.67 |
| Y-Axis [g] * | 1.00 | 0.67 | 0.67 | 0.67 | 1.00 | 0.67 | 0.67 | 0.67 | |
| Z-Axis [g] * | 1.00 | 0.19 | 0.19 | 0.19 | 1.00 | 0.33 | 0.33 | 0.33 | |
| SBA Retracted | X-Axis [g] * | 1.00 | 0.67 | 0.67 | 0.67 | 1.00 | 0.67 | 0.67 | 0.67 |
| Y-Axis [g] * | 1.00 | 0.67 | 0.67 | 0.67 | 1.00 | 0.67 | 0.67 | 0.67 | |
| Z-Axis [g] * | 1.00 | 0.19 | 0.19 | 0.19 | 1.00 | 0.33 | 0.33 | 0.33 | |
| SBA Extended | X-Axis [g] * | 1.00 | 0.67 | 0.67 | 0.67 | 1.00 | 0.67 | 0.67 | 0.67 |
| Y-Axis [g] * | 0.88 | 0.75 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Z-Axis [g] * | 0.88 | 0.75 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Resonance ID | Frequency Shift [%] | Amplitude Shift [%] |
|---|---|---|
| 1 | 0.29 | 0.00 |
| 2 | −1.11 | 2.54 |
| 3 | 0.83 | −3.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiariello, A.; Carandente Tartaglia, C.; Arena, M.; Quaranta, V.; Bruno, G.; Belardo, M.; Castaldo, M. Vibration Qualification Campaign on Main Landing Gear System for High-Speed Compound Helicopter. Aerospace 2024, 11, 130. https://doi.org/10.3390/aerospace11020130
Chiariello A, Carandente Tartaglia C, Arena M, Quaranta V, Bruno G, Belardo M, Castaldo M. Vibration Qualification Campaign on Main Landing Gear System for High-Speed Compound Helicopter. Aerospace. 2024; 11(2):130. https://doi.org/10.3390/aerospace11020130
Chicago/Turabian StyleChiariello, Antonio, Carmine Carandente Tartaglia, Maurizio Arena, Vincenzo Quaranta, Giovanni Bruno, Marika Belardo, and Martina Castaldo. 2024. "Vibration Qualification Campaign on Main Landing Gear System for High-Speed Compound Helicopter" Aerospace 11, no. 2: 130. https://doi.org/10.3390/aerospace11020130
APA StyleChiariello, A., Carandente Tartaglia, C., Arena, M., Quaranta, V., Bruno, G., Belardo, M., & Castaldo, M. (2024). Vibration Qualification Campaign on Main Landing Gear System for High-Speed Compound Helicopter. Aerospace, 11(2), 130. https://doi.org/10.3390/aerospace11020130








