Conceptual Design of Layered Distributed Propulsion System to Improve Power-Saving Benefit of Boundary-Layer Ingestion
Abstract
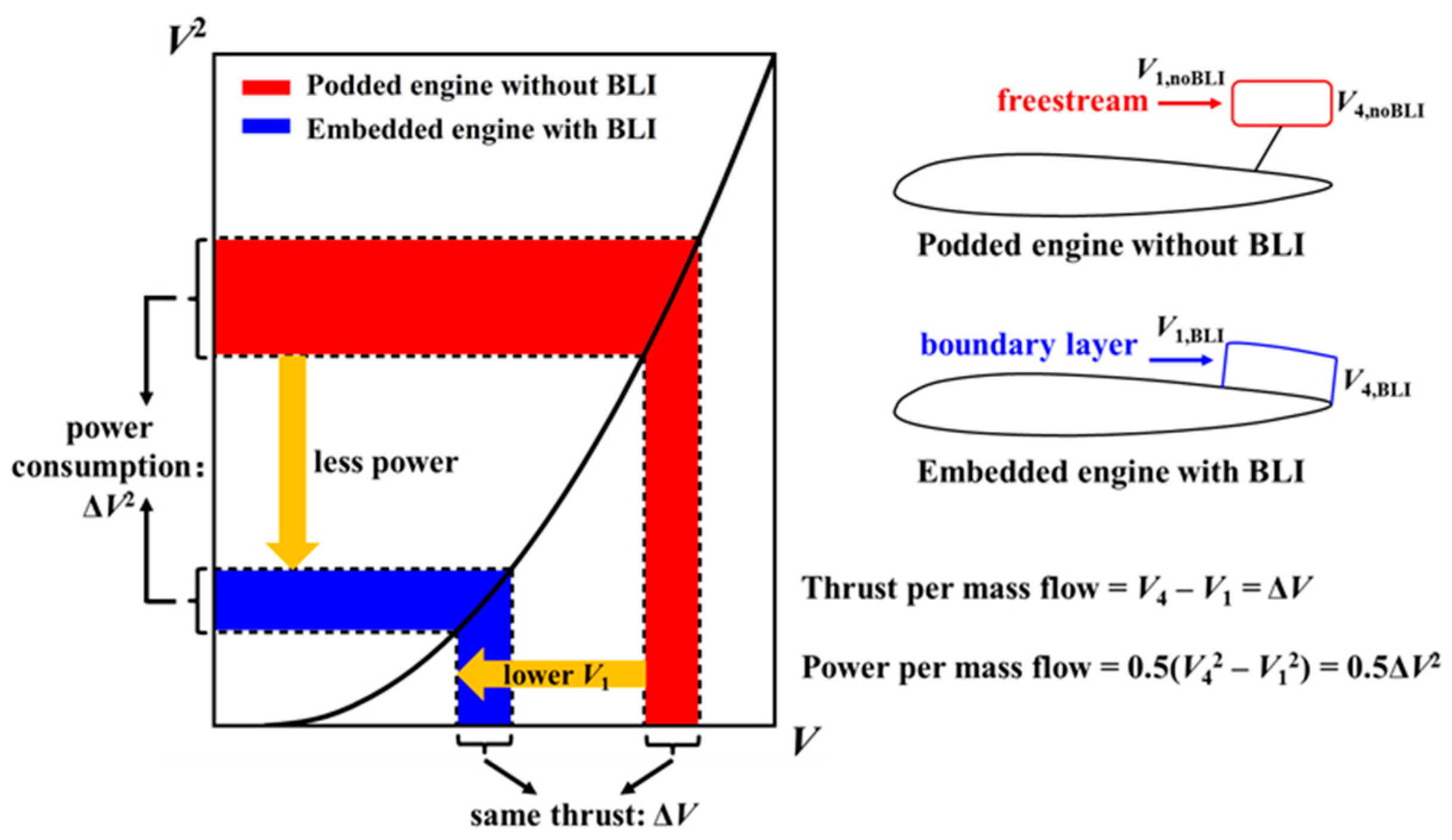
:1. Introduction
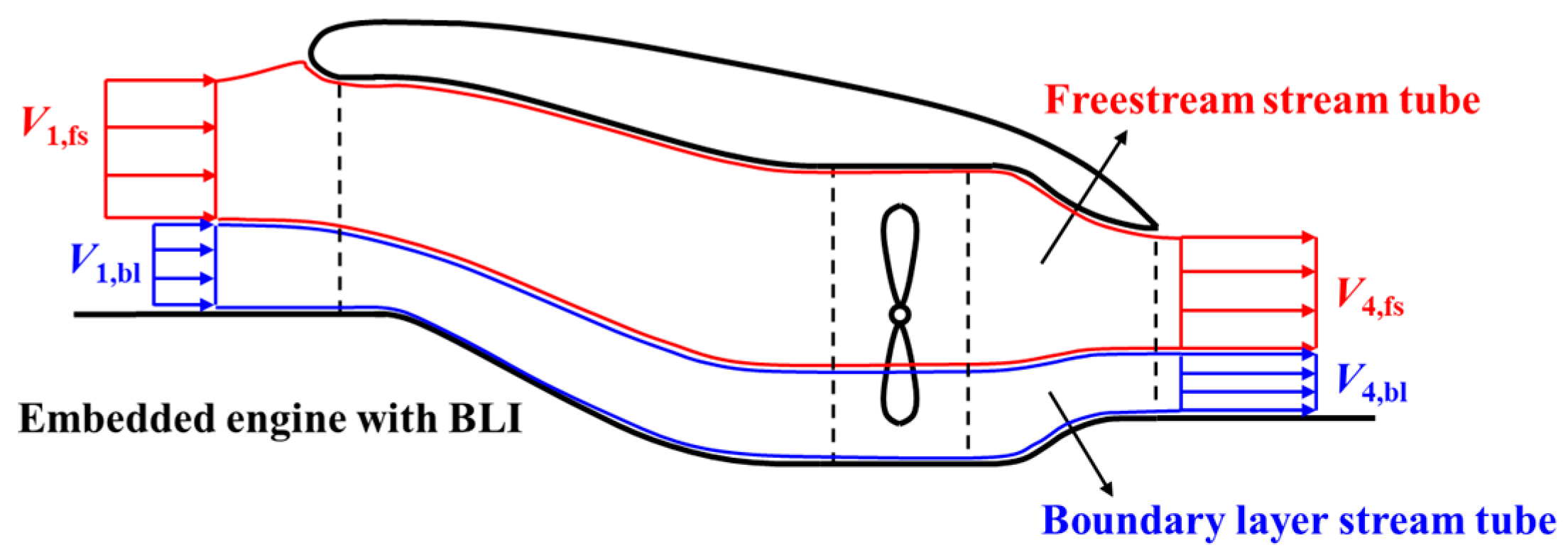
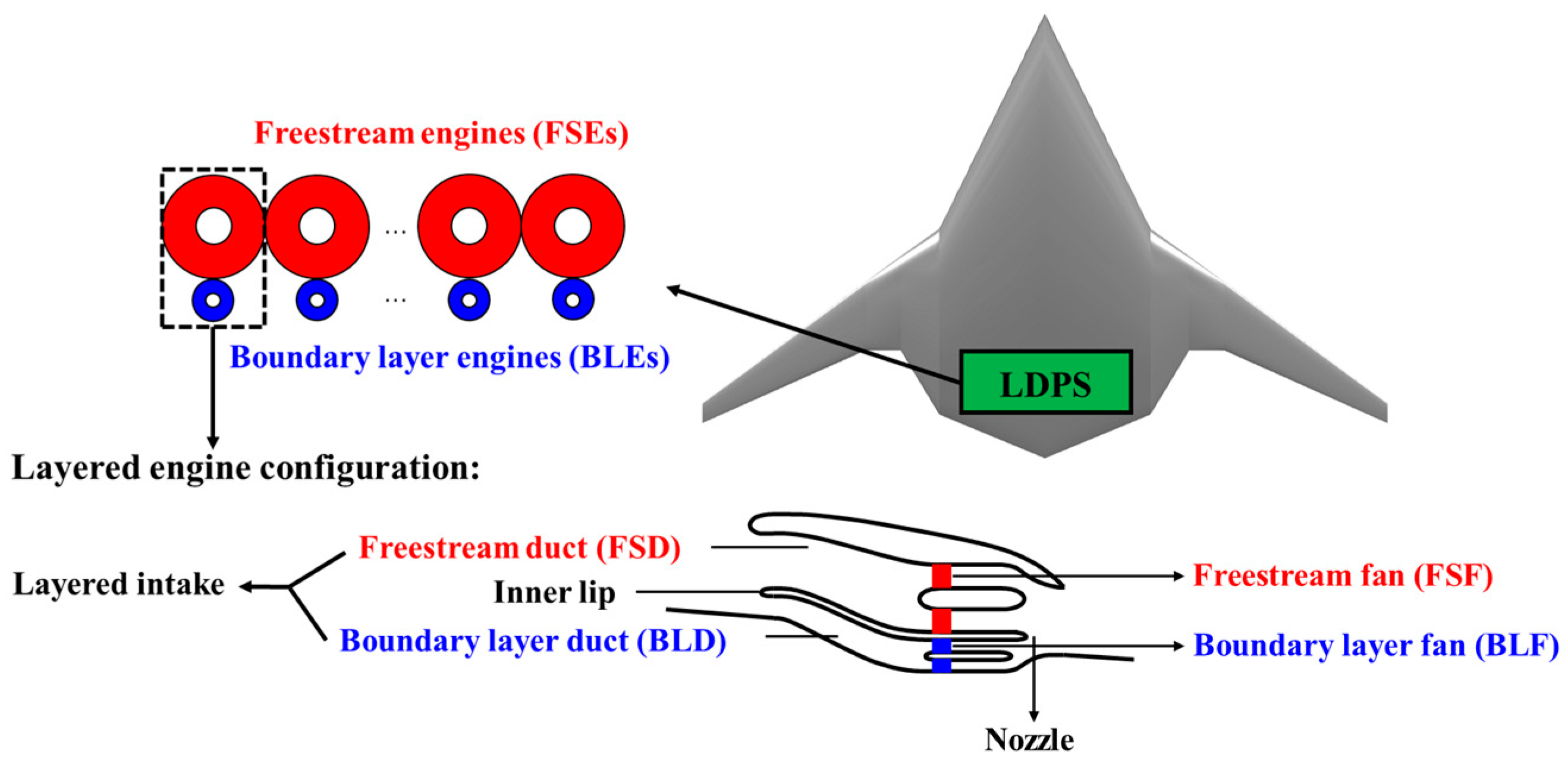
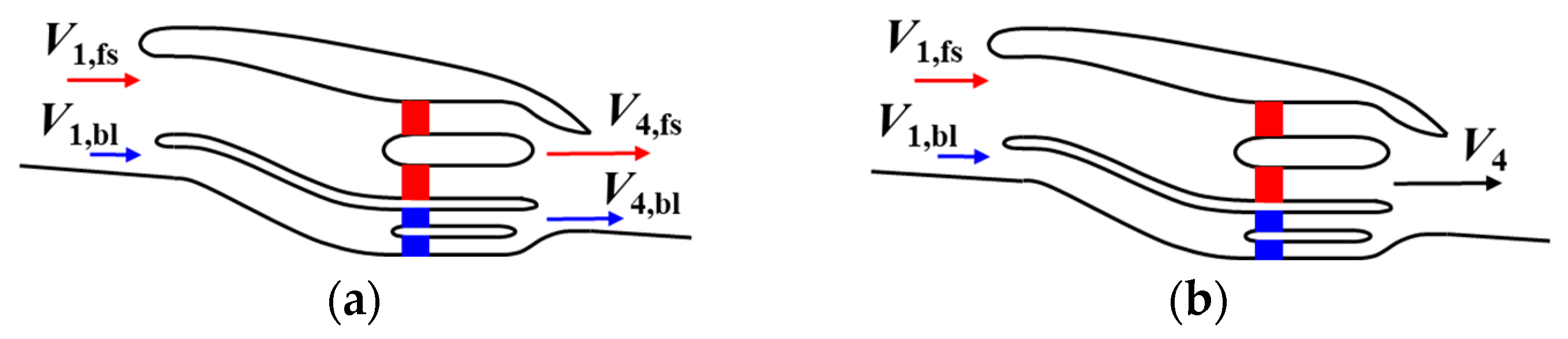
2. Concept Descriptions of LDPS
- Possible increased weight from two fan arrays of LDPS;
- Possible increased drag due to a larger wetted area needed for the nacelle;
- Design of the layered intake to split the freestream and boundary layer;
- Design of the BLF since it is only ingesting the boundary layer;
- Coupling effect between FSE and BLE, especially at off-design conditions;
- Design of the control laws of FSF and BLF to match the incoming flow conditions.
3. Studied Case and Modeling Methods
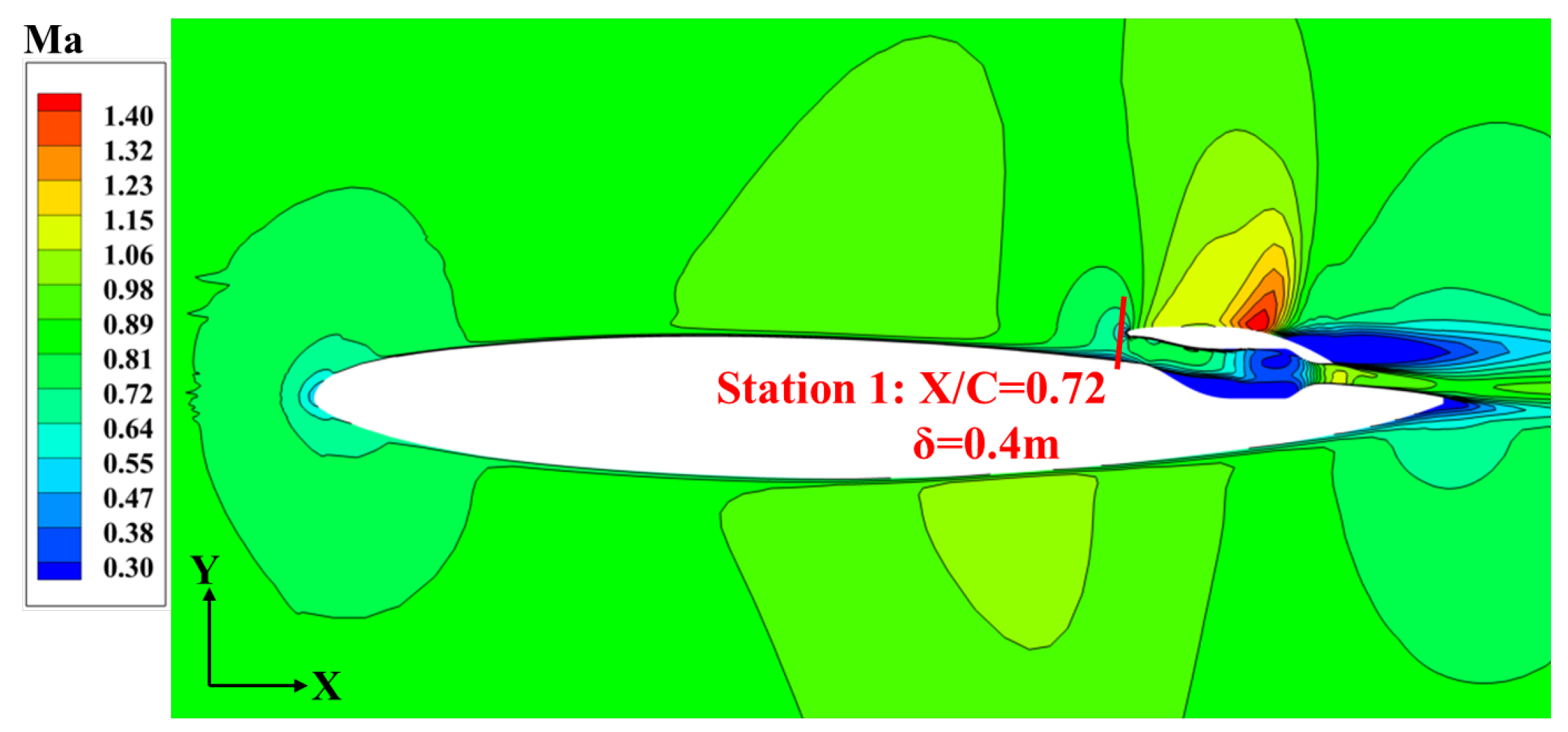
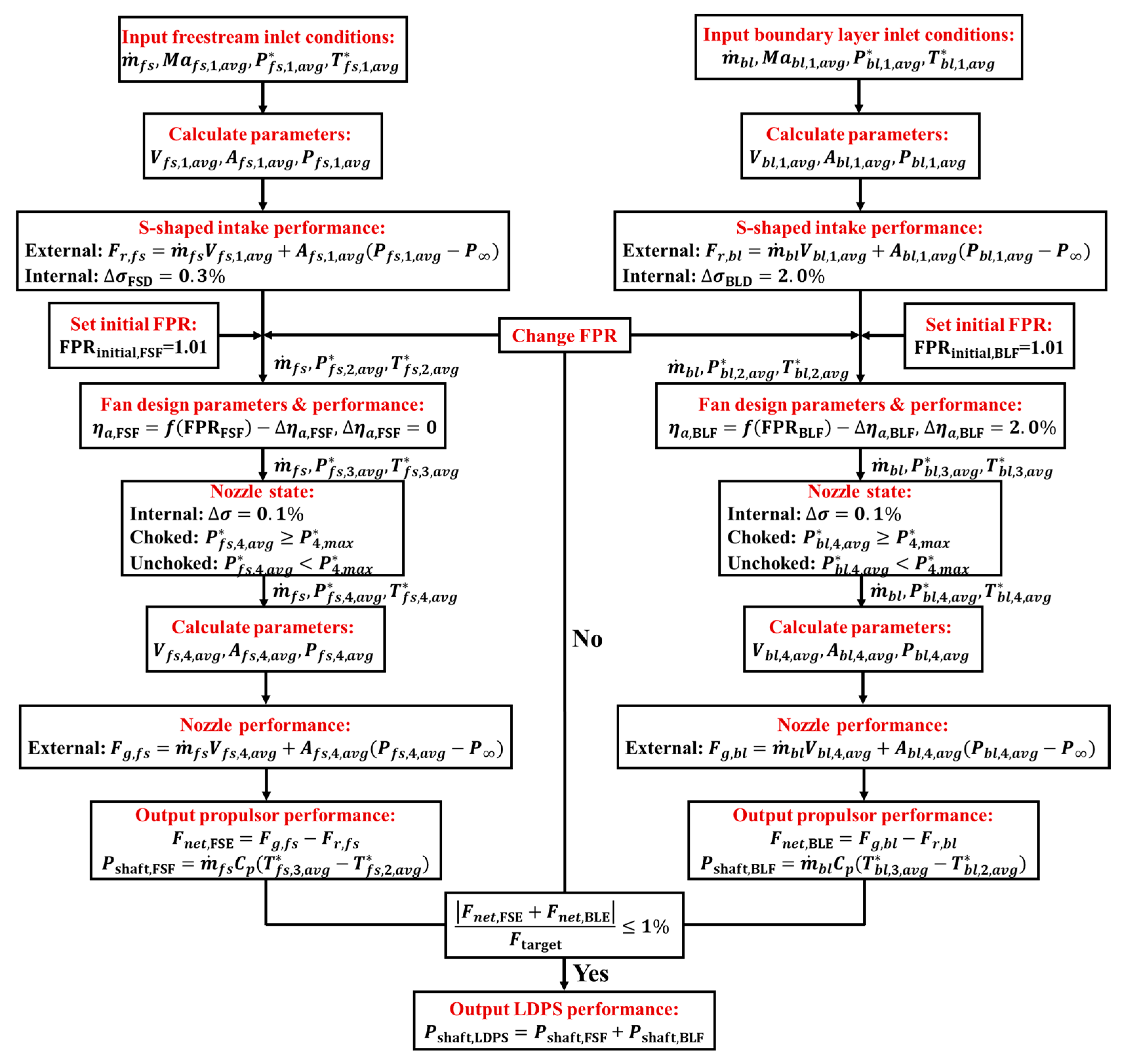
3.1. Modeling Methods
3.2. Performance Metrics
4. Results
4.1. Design-Parameters Analysis
4.2. Propulsion-System Performance Analysis
5. Conclusions
- (1)
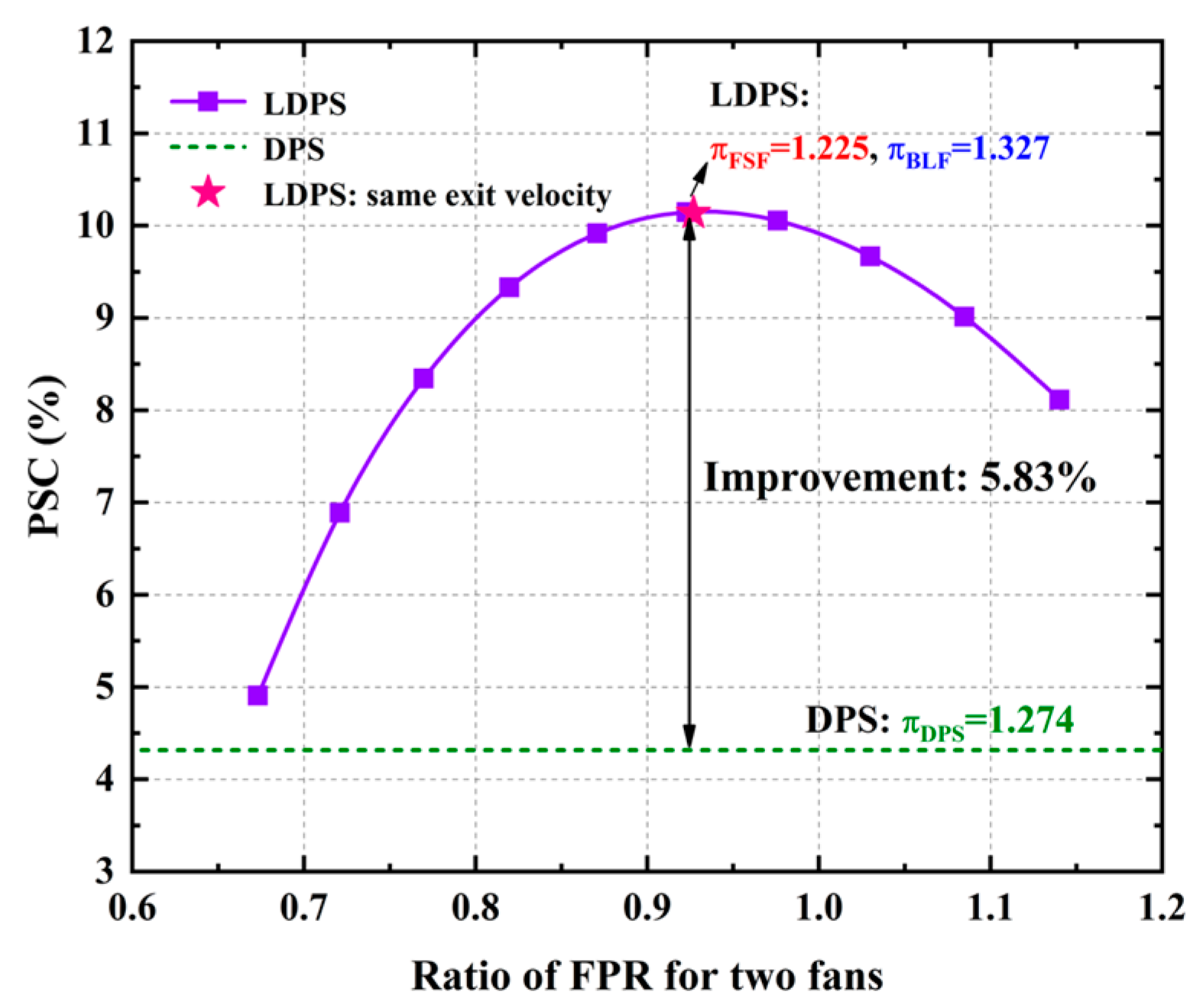
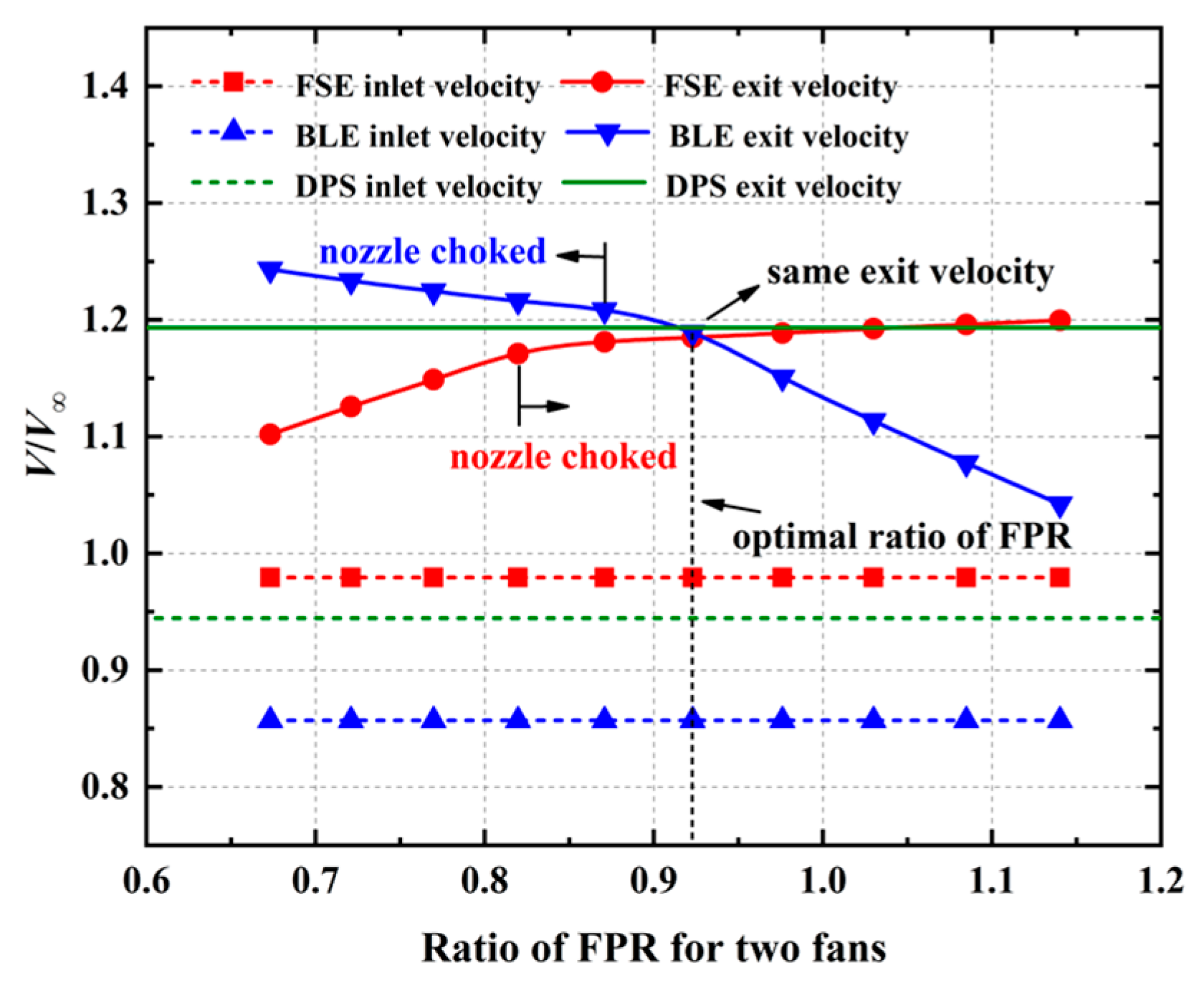
- There is an optimal ratio of FPR for two fans that maximizes the PSC of LDPS. Under this optimal ratio of FPR, the FPR of BLE is higher than that of FSE, indicating that the fan should add more energy to the boundary layer than to the freestream to improve the power-saving benefit. In addition, the FSE and BLE have the same exit velocity under the optimal ratio of FPR. By analyzing the ideal LDPS, the required mechanical power to produce the same thrust is least when the FSE and the BLE of LDPS have the same exit velocity, and this minimum mechanical power also corresponds to the minimum fan-shaft power. Therefore, the same exit velocity of FSE and BLE can be used as the principle to determine the optimal ratio of FPR, which maximizes the PSC of LDPS;
- (2)
- Under the optimal ratio of FPR, the PSC of LDPS is improved by 5.83% compared to DPS when the same component performance penalties due to BLI are considered. On the one hand, the ingesting boundary-layer flow alone can further lower the inlet velocity of BLE and thus improve the PSC of LDPS by 1.3% compared to DPS. On the other hand, the additional power loss of LDPS, which offsets the power-saving benefit of BLI, is reduced by 39.2% compared to DPS, when the component performance penalties due to BLI occur only in BLE. In addition, when various component performance penalties are considered, the LDPS can effectively reduce the sensitivity of PSC to the component performance penalties due to BLI, thus improving the power-saving benefit of BLI.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AAM | Advanced air mobility |
| ADP | Aerodynamic design point |
| AIP | Aerodynamic interface plane |
| ASDL | Aerospace system design laboratory |
| BLI | Boundary-layer ingestion |
| BLE | Boundary-layer engine |
| BLD | Boundary-layer duct |
| BLF | Boundary-layer fan |
| BWB | Blended-wing body |
| CFD | Computational fluid dynamics |
| DPS | Distributed propulsion system |
| FSE | Freestream engine |
| FSD | Freestream duct |
| FSF | Freestream fan |
| FPR | Fan pressure ratio |
| ISA | International standard atmosphere |
| LDPS | Layered distributed propulsion system |
| PSC | Power-saving coefficient |
| RTO | Rolling takeoff |
| SAX | Silent aircraft eXperiment |
| TPR | Thrust-to-power ratio |
| Variables | |
| A | Flow area |
| Chord length | |
| Specific heat capacity at constant pressure | |
| Thrust | |
| Fg | Gross thrust |
| Fnet | Net thrust |
| Fr | Ram Drag |
| Total enthalpy change | |
| Mass flow | |
| Mach number | |
| Mechanical power | |
| Lost power | |
| Fan-shaft power | |
| P | Static pressure |
| Total pressure | |
| Excess mechanical power | |
| Ideal gas constant | |
| Total entropy change | |
| Total temperature | |
| Velocity | |
| Lost work | |
| Chord-wise position | |
| Propulsion efficiency | |
| Fan adiabatic efficiency | |
| Fan adiabatic efficiency penalty | |
| Fan pressure ratio | |
| Total pressure recovery | |
| Total pressure-recovery penalty | |
| Subscripts | |
| 1 | Propulsion system inlet |
| 4 | Propulsion system exit |
| avg | Mass averaged |
| bl | Boundary-layer stream tube |
| BLI | BLI inlet condition |
| uniform | Uniform inlet condition |
| d | Different exit velocity |
| fs | Freestream stream tube |
| i | Irreversible process |
| n | Begin of irreversible process |
| n + 1 | End of irreversible process |
| s | Same exit velocity |
| ∞ | Far upstream |
References
- Betz, A. Introduction to the Theory of Flow Machines, 1st ed.; Section 59; Pergamon: New York, NY, USA, 1966; pp. 215–217. [Google Scholar]
- Freuler, P.N. Boundary Layer Ingesting Inlet Design for a Silent Aircraft. Ph.D. Thesis, Massachusetts Institute of Technology, Department of Aeronautics and Astronautics, Cambridge, MA, USA, January 2005. [Google Scholar]
- Seitz, A.; Habermann, A.L.; Peter, F.; Troeltsch, F.; Pardo, A.C.; Corte, B.D.; Sluis, M.V.; Goraj, Z.; Kowalski, M.; Zhao, X.; et al. Proof of Concept Study for Fuselage Boundary Layer Ingesting Propulsion. Aerospace 2021, 8, 16. [Google Scholar] [CrossRef]
- Gray, J.S.; Mader, C.A.; Kenway, G.K.W.; Martins, J.R.R.A. Modeling Boundary Layer Ingestion using a Coupled Aeropropulsive Analysis. J. Aircr. 2019, 55, 1191–1199. [Google Scholar] [CrossRef]
- Uranga, A.; Drela, M.; Greitzer, E.M.; Hall, D.K.; Titchener, N.A.; Lieu, M.K.; Siu, M.N.; Casses, C.; Huang, A.C.; Gatlin, G.M.; et al. Boundary Layer Ingestion Benefit of the D8 Transport Aircraft. AIAA J. 2017, 55, 3693–3708. [Google Scholar] [CrossRef]
- Felder, J.L.; Kim, H.D.; Brown, G.V.; Chu, J. An Examination of the Effect of Boundary Layer Ingestion on Turboelectric Distributed Propulsion Systems. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. Paper No. AIAA-2011-300. [Google Scholar]
- Mantič-Lugo, V.; Doulgeris, G.; Singh, R. Computational Analysis of the Effects of a Boundary Layer Ingesting Propulsion System in Transonic Flow. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 227, 1215–1232. [Google Scholar] [CrossRef]
- Goldberg, C.; Nalianda, D.; MacManus, D.; Pilidis, P.; Felder, J. Method for Simulating the Performance of a Boundary Layer Ingesting Propulsion System at Design and Off-design. Aerosp. Sci. Technol. 2018, 78, 312–319. [Google Scholar] [CrossRef]
- Smith, A.M.O.; Roberts, H.E. The Jet Airplane Utilizing Boundary Layer Air for Propulsion. J. Aerosol Sci. 1947, 14, 97–109. [Google Scholar] [CrossRef]
- Smith, L.H. Wake Ingestion Propulsion Benefit. J. Propuls. Power 1993, 9, 74–82. [Google Scholar] [CrossRef]
- Liou, M.S.; Kim, H.; Liou, M.F. Challenges and Progress in Aerodynamic Design of Hybrid Wingbody Aircraft with Embedded Engines; Technical Memorandum NASA/TM-2016-218309; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2016. [Google Scholar]
- de la Rosa Blanco, E.; Hall, C.; Crichton, D. Challenges in the Silent Aircraft Engine Design. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Hathaway, M.D.; Rosario, R.D.; Madavan, N.K. NASA Fixed Wing Project Propulsion Research and Technology Development Activities to Reduce Thrust Specific Energy Consumption; Technical Memorandum NASA/TM-2013-216548; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2013. [Google Scholar]
- Berrier, B.L.; Carter, M.B.; Allan, B.G. High Reynolds Number Investigation of a Flush-Mounted, S-Duct Inlet with Large Amounts of Boundary Layer Ingestion; Technical Publication NASA/TP-2005-213766; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2005. [Google Scholar]
- Ferrar, A.M.; O’Brien, W.F. Fan Response to Total Pressure Distortions Produced by Boundary Layer Ingesting Serpentine Inlets. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. Paper No. AIAA-2012-3996. [Google Scholar]
- Giuliani, J.E.; Chen, J.P. Fan Response to Boundary-Layer Ingesting Inlet Distortions. AIAA J. 2016, 54, 3232–3243. [Google Scholar] [CrossRef]
- Plas, A.P.; Sargeant, M.A.; Madani, V.; Crichton, D.; Greitzer, E.M.; Hynes, T.P.; Hall, C.A. Performance of a Boundary Layer Ingesting (BLI) Propulsion System. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. Paper No. AIAA-2007-450. [Google Scholar]
- Geiselhart, K.A.; Daggett, D.L.; Kawai, R.; Friedman, D. Blended Wing Body Systems Studies: Boundary Layer Ingestion Inlets with Active Flow Control; Contractor Report NASA/CR-2003-212670; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2003. [Google Scholar]
- Kawai, R.; Friedman, D.; Serrano, L. Blended Wing Body (BWB) Boundary Layer Ingestion (BLI) Inlet Configuration and System Studies; Contractor Report NASA/CR-2006-21453; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2006. [Google Scholar]
- Rodriguez, D.L. Multidisciplinary Optimization Method for Designing Boundary-Layer-Ingesting Inlets. J. Aircr. 2009, 46, 883–894. [Google Scholar] [CrossRef]
- Hardin, L.W.; Tillman, G.; Sharma, O.P.; Berton, J.; Arend, D.J. Aircraft System Study of Boundary Layer Ingesting Propulsion. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. Paper No. AIAA-2012-3993. [Google Scholar]
- Li, Z.P.; Zhang, Y.F.; Pan, T.Y.; Zhang, J.; Shang, Y.H. Study on the Aerodynamic Performance of Boundary-layer-ingesting Inlet with Various Geometries. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 60–71. [Google Scholar] [CrossRef]
- Chiang, C.; Koo, D.; Zingg, D.W. Aerodynamic Shape Optimization of an S-Duct Duct for a Boundary Layer Ingesting Engine. J. Aircr. 2022, 59, 725–741. [Google Scholar] [CrossRef]
- Lee, B.J.; Liou, M.S.; Kim, C. Optimizing a Boundary-Layer-Ingestion Offset Inlet by Discrete Adjoint Approach. AIAA J. 2010, 48, 2008–2016. [Google Scholar] [CrossRef]
- Owens, L.R.; Allan, B.G.; Gorton, S.A. Boundary-Layer-Ingesting Inlet Flow Control. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. Paper No. AIAA 2006-839. [Google Scholar]
- Allan, B.G.; Owens, L.R.; Berrier, B.L. Numerical Modeling of Active Flow Control in a Boundary Layer Ingesting Offset Inlet. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. Paper No. AIAA2004-2318. [Google Scholar]
- Gunn, E.J.; Tooze, S.E.; Hall, C.A.; Colin, Y. An Experimental Study of Loss Sources in a Fan Operating with Continuous Inlet Stagnation Pressure Distortion. J. Turbomach. 2013, 135, 051002. [Google Scholar] [CrossRef]
- Fidalgo, V.J.; Hall, C.A.; Colin, Y. A Study of Fan-Distortion Interaction Within the NASA Rotor 67 Transonic Stage. J. Turbomach. 2012, 134, 051011. [Google Scholar] [CrossRef]
- Castillo Pardo, A.; Hall, C.A. Aerodynamics of Boundary Layer Ingesting Fuselage Fans. J. Turbomach. 2021, 143, 041007. [Google Scholar] [CrossRef]
- Hall, D.K.; Greitzer, E.M.; Tan, C.S. Analysis of Fan Stage Conceptual Design Attributes for Boundary Layer Ingestion. J. Turbomach. 2017, 139, 071012. [Google Scholar] [CrossRef]
- Cui, R.; Li, Q.S.; Pan, T.Y.; Zhang, J. Streamwise-body-force-model for rapid simulation combining internal and external flow fields. Chin. J. Aeronaut. 2016, 29, 1205–1212. [Google Scholar] [CrossRef]
- Li, Z.P.; Zhang, Y.F.; Pan, T.Y.; Zhang, J. A modified streamwise body force model of fan with distorted inflow for rapid propulsion-airframe integrated simulation. Chin. J. Aeronaut. 2023, 36, 202–213. [Google Scholar] [CrossRef]
- Guynn, M.D.; Berton, J.J.; Fisher, K.L.; Haller, W.J.; Tong, M.T.; Thurman, D.R. Engine Concept Study for an Advance Single-Aisle Transport; Technical Memorandum NASA/TM-2009-215784; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2009. [Google Scholar]
- Greitzer, E.M.; Tan, C.S.; Graf, M.B. Internal Flow: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]




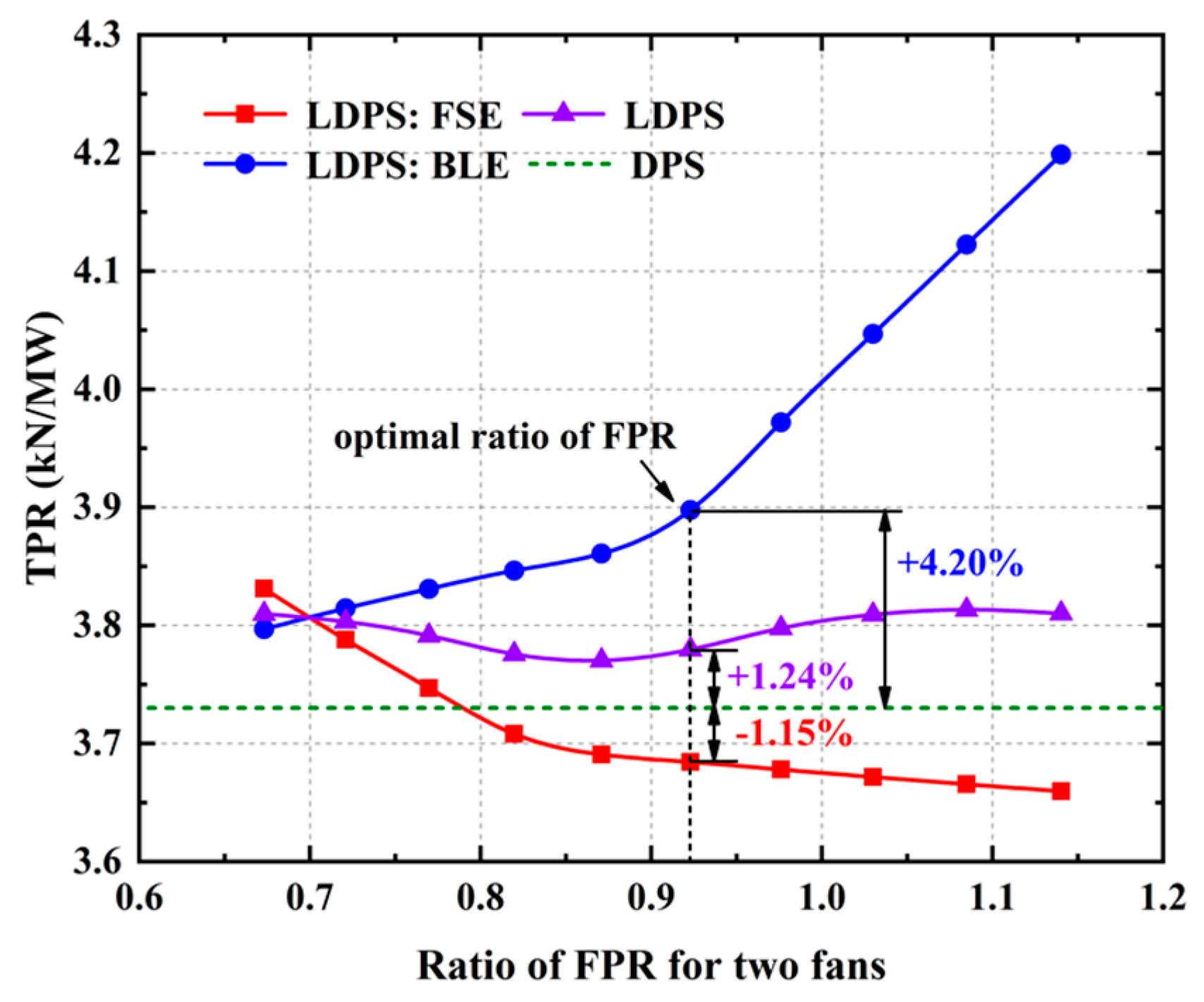
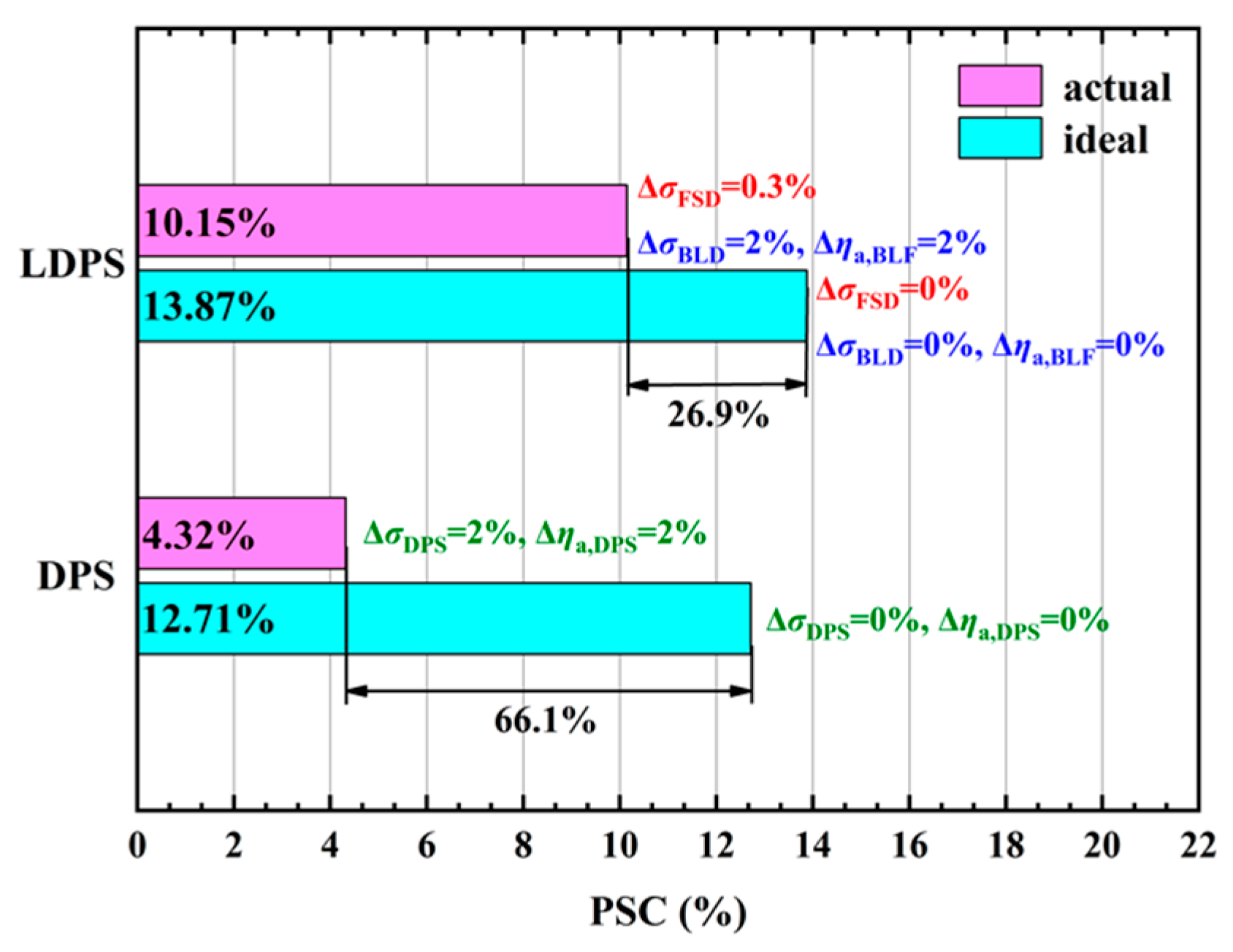
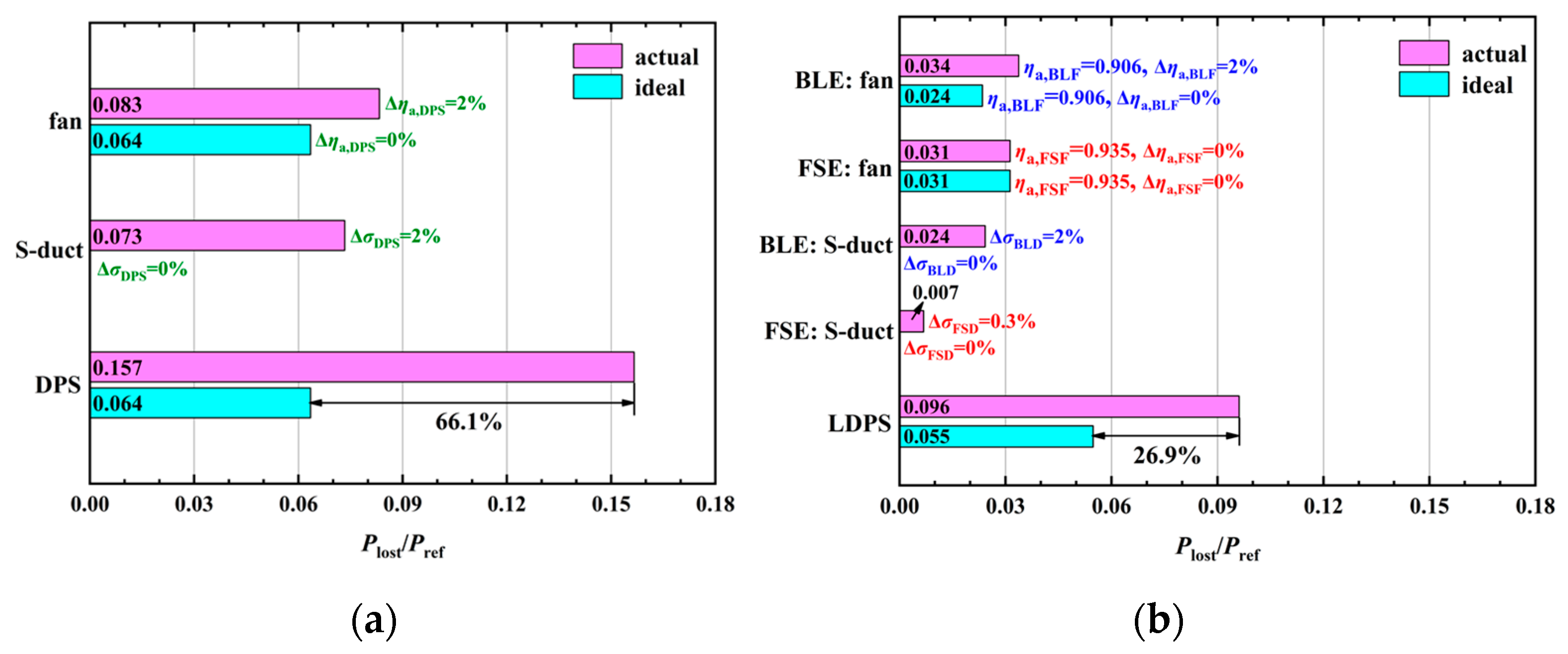
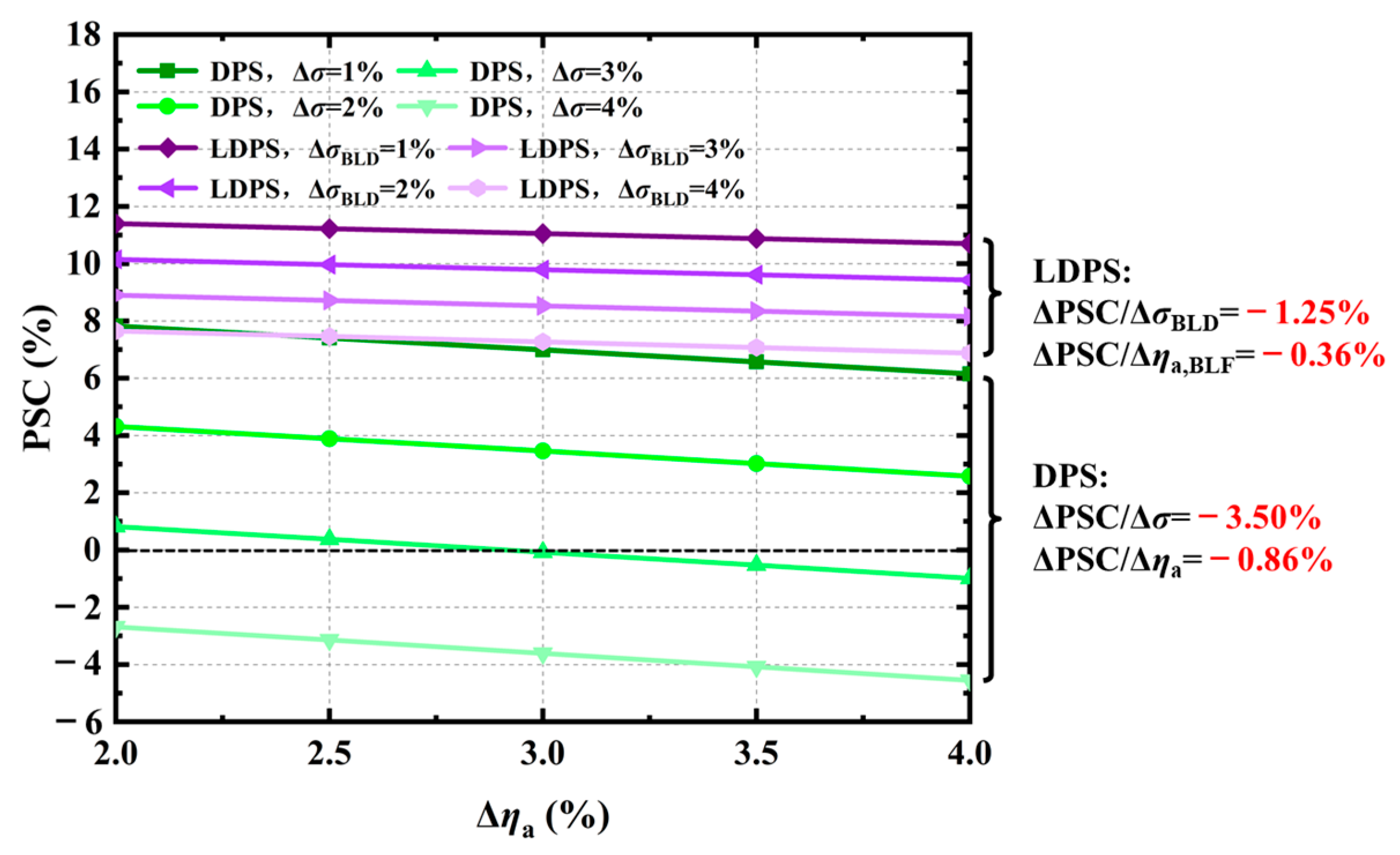
| Flight Condition | Minimum Thrust Requirements |
|---|---|
| Aerodynamic Design Point (ADP) (11,000 m/Ma∞ 0.85/ISA) | 112.78 kN |
| Rolling Takeoff (RTO) (Sea level/Ma∞ 0.265/ISA + 50K) | 598.21 kN |
| Engine Type | (kg/s) | |||
|---|---|---|---|---|
| DPS | 180.2 | 0.937 | 0.967 | 1 |
| FSE | 125.6 | 0.976 | 1 | 1 |
| BLE | 54.6 | 0.841 | 0.895 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, Y.; Pan, T. Conceptual Design of Layered Distributed Propulsion System to Improve Power-Saving Benefit of Boundary-Layer Ingestion. Aerospace 2024, 11, 141. https://doi.org/10.3390/aerospace11020141
Li Z, Lu Y, Pan T. Conceptual Design of Layered Distributed Propulsion System to Improve Power-Saving Benefit of Boundary-Layer Ingestion. Aerospace. 2024; 11(2):141. https://doi.org/10.3390/aerospace11020141
Chicago/Turabian StyleLi, Zhiping, Yujiang Lu, and Tianyu Pan. 2024. "Conceptual Design of Layered Distributed Propulsion System to Improve Power-Saving Benefit of Boundary-Layer Ingestion" Aerospace 11, no. 2: 141. https://doi.org/10.3390/aerospace11020141
APA StyleLi, Z., Lu, Y., & Pan, T. (2024). Conceptual Design of Layered Distributed Propulsion System to Improve Power-Saving Benefit of Boundary-Layer Ingestion. Aerospace, 11(2), 141. https://doi.org/10.3390/aerospace11020141






