Computational Study of Fluidic-Valve Injectors for Detonation Engines
Abstract
:1. Introduction
2. Numerical Method and Physical Model
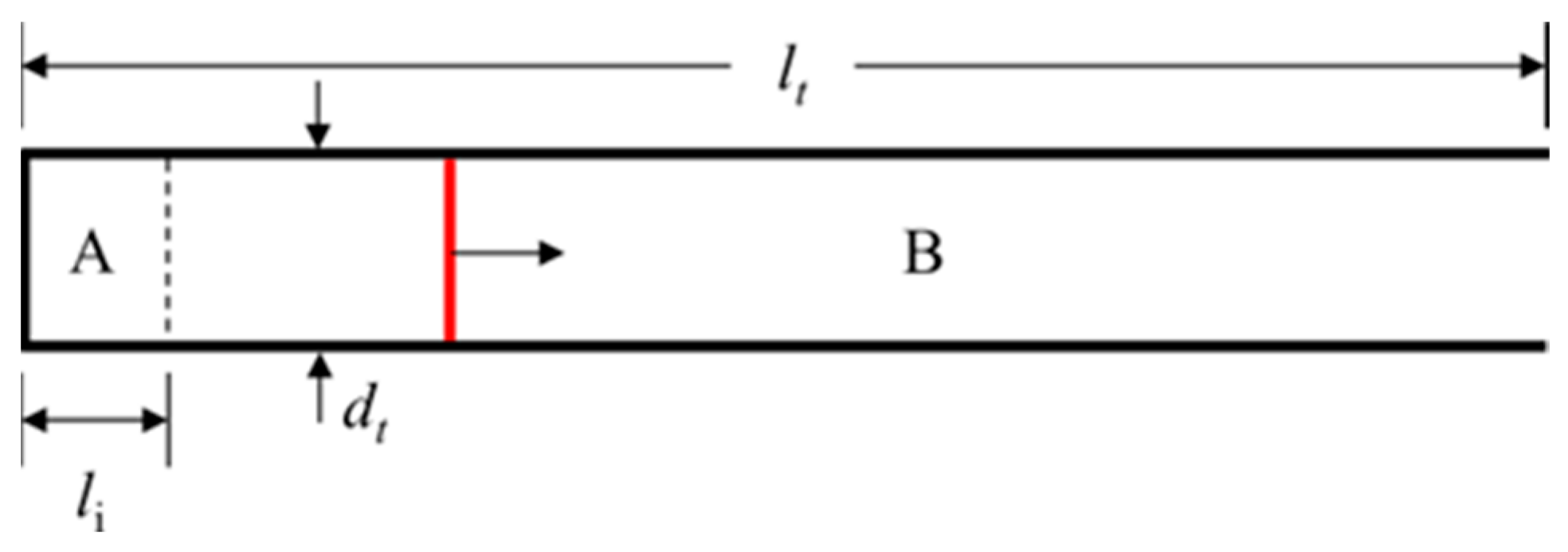
2.1. Case Descriptions
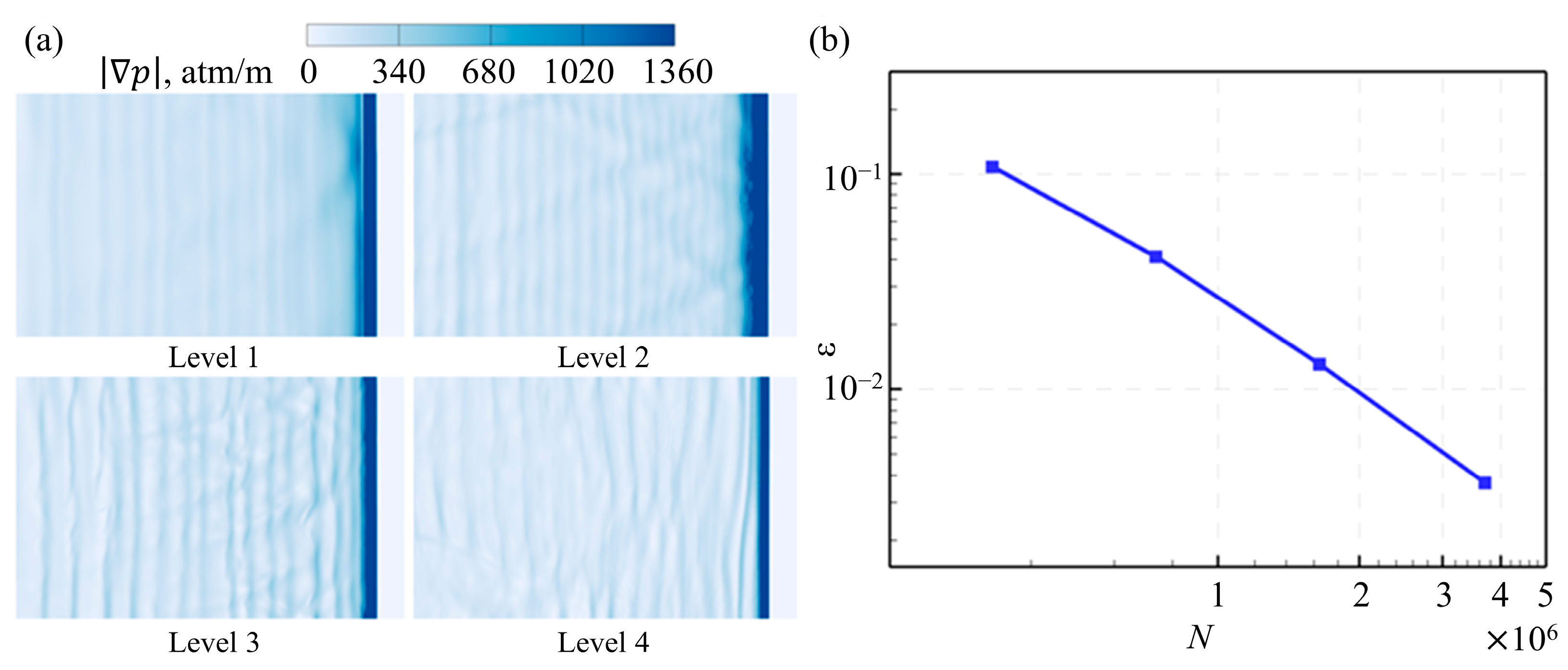
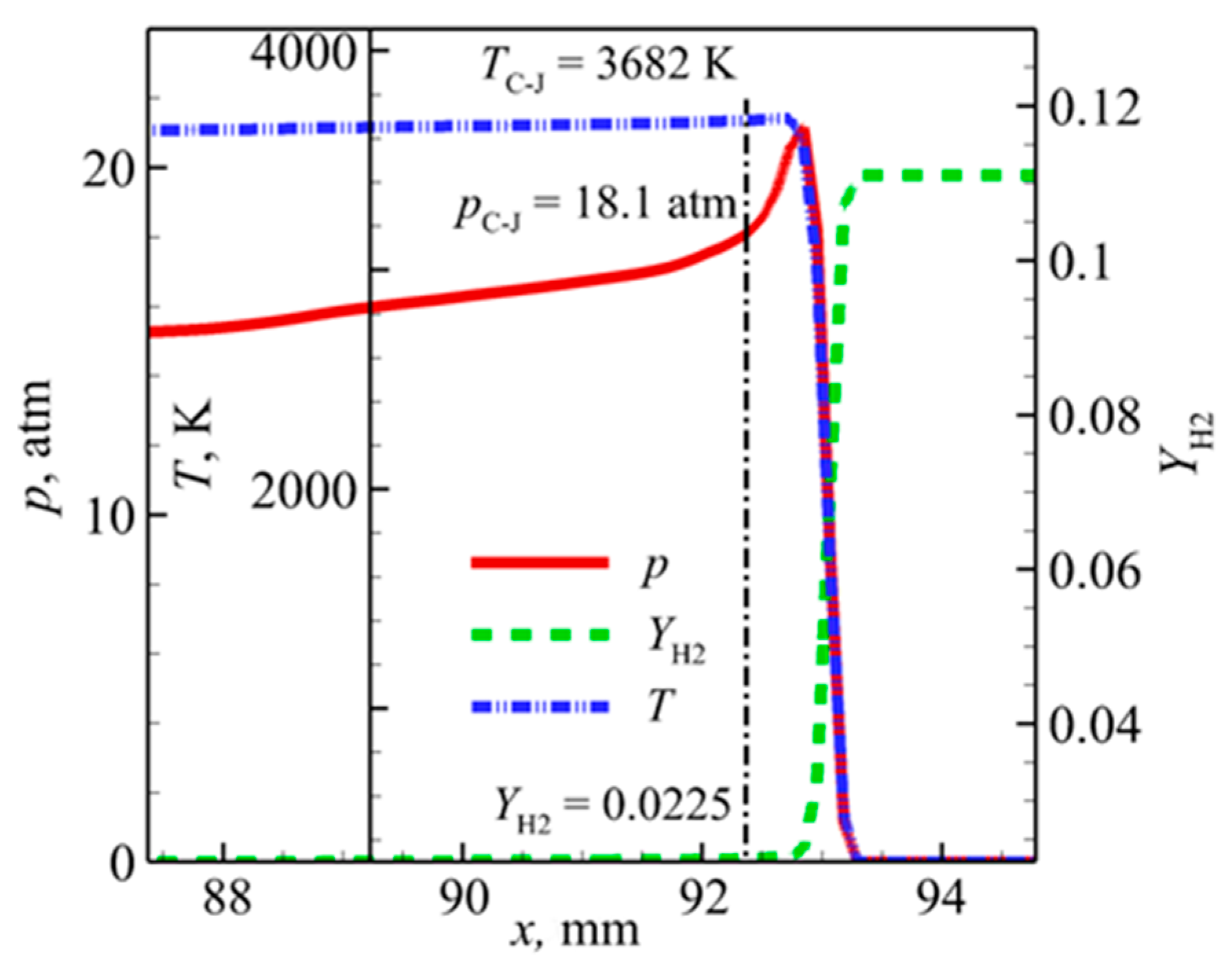
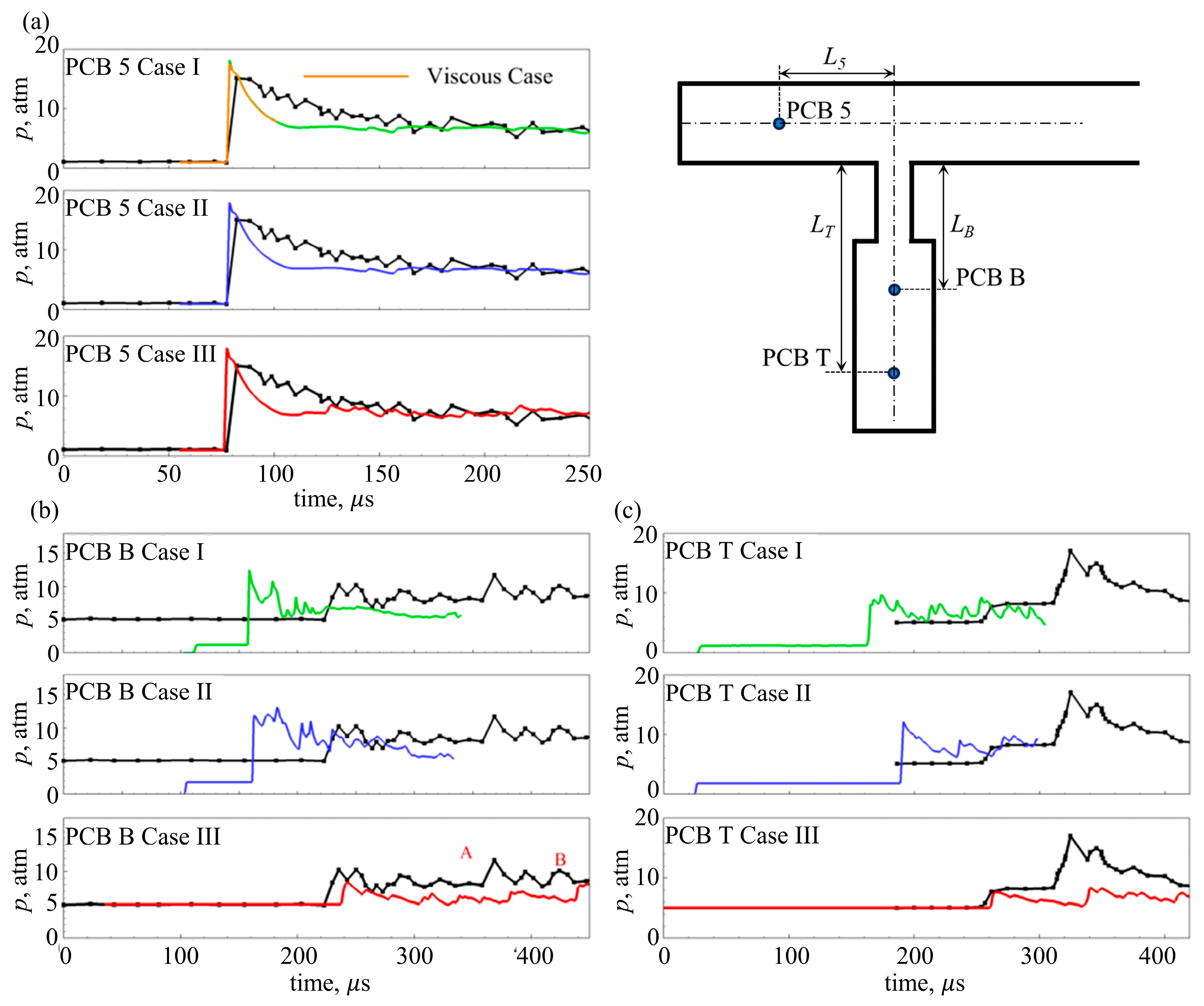
2.2. Model Validation and Verification
3. Results and Discussion
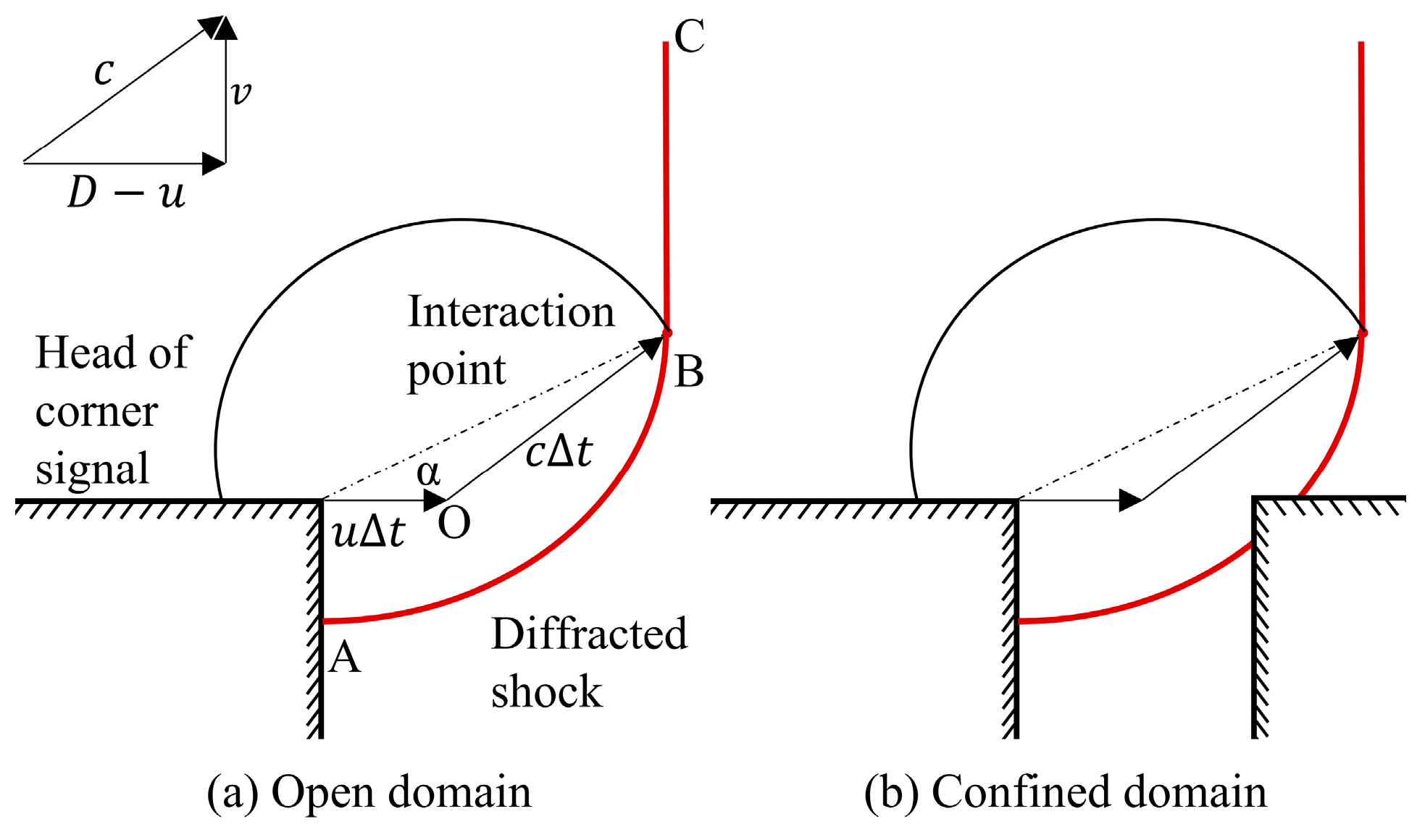
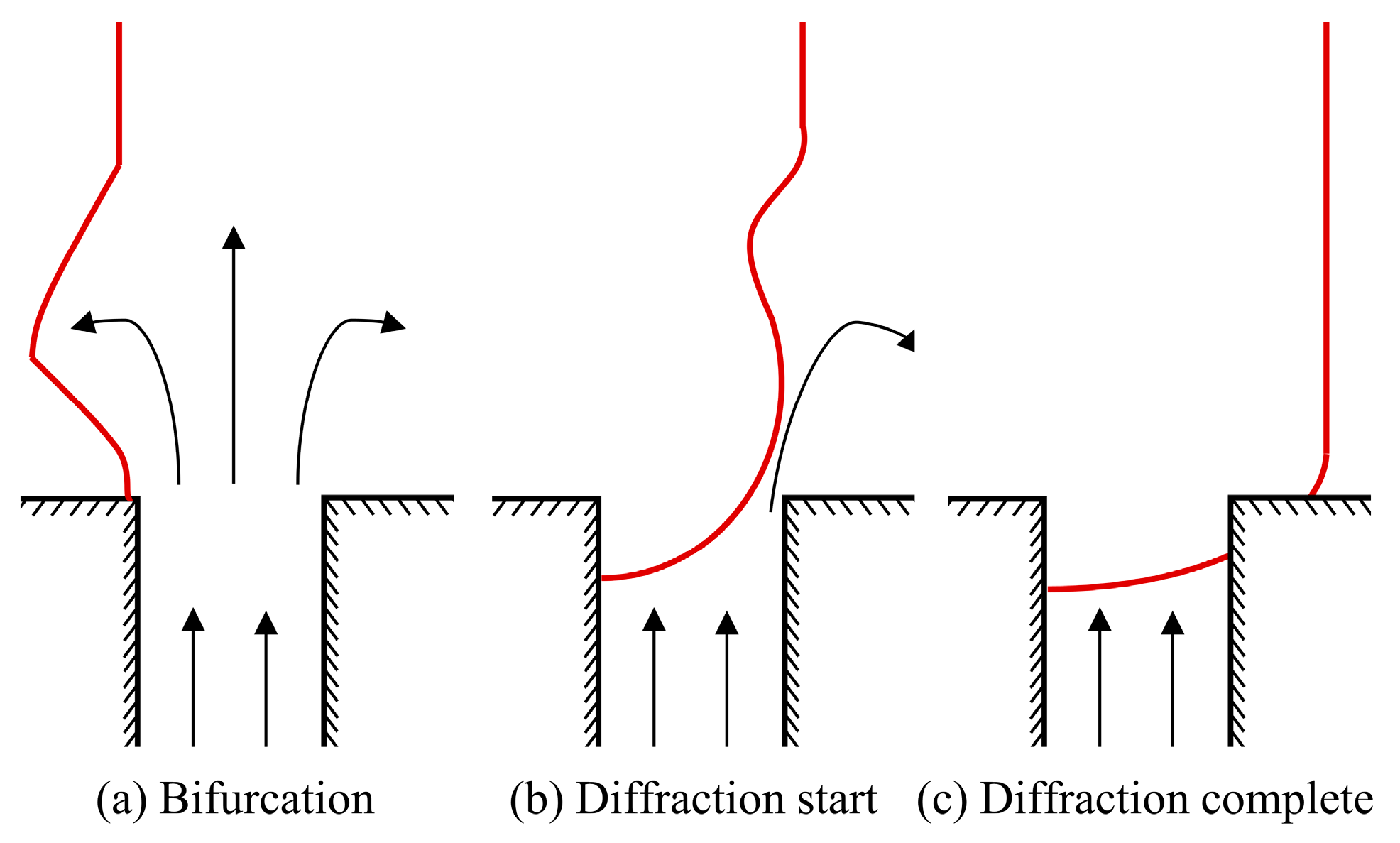
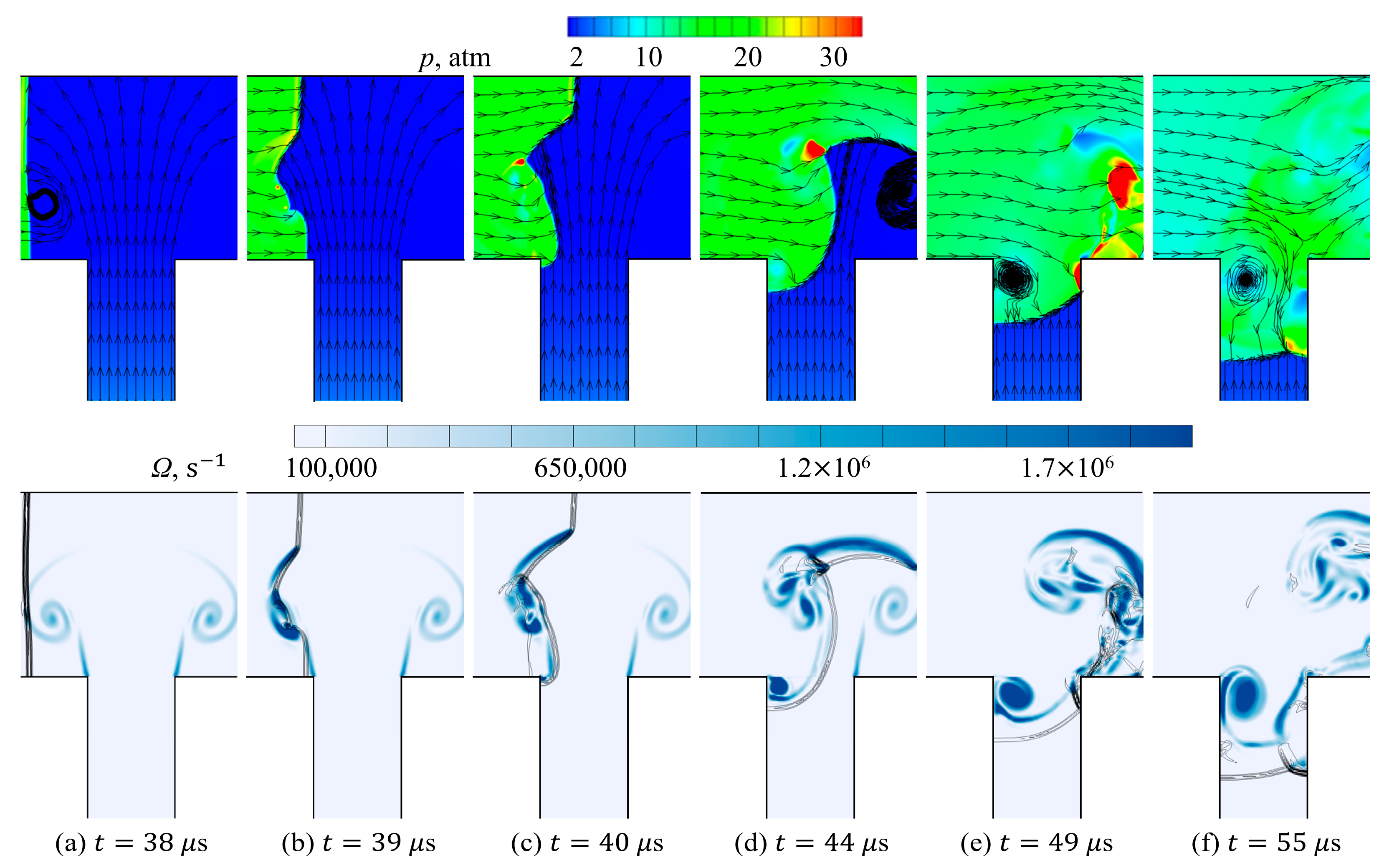
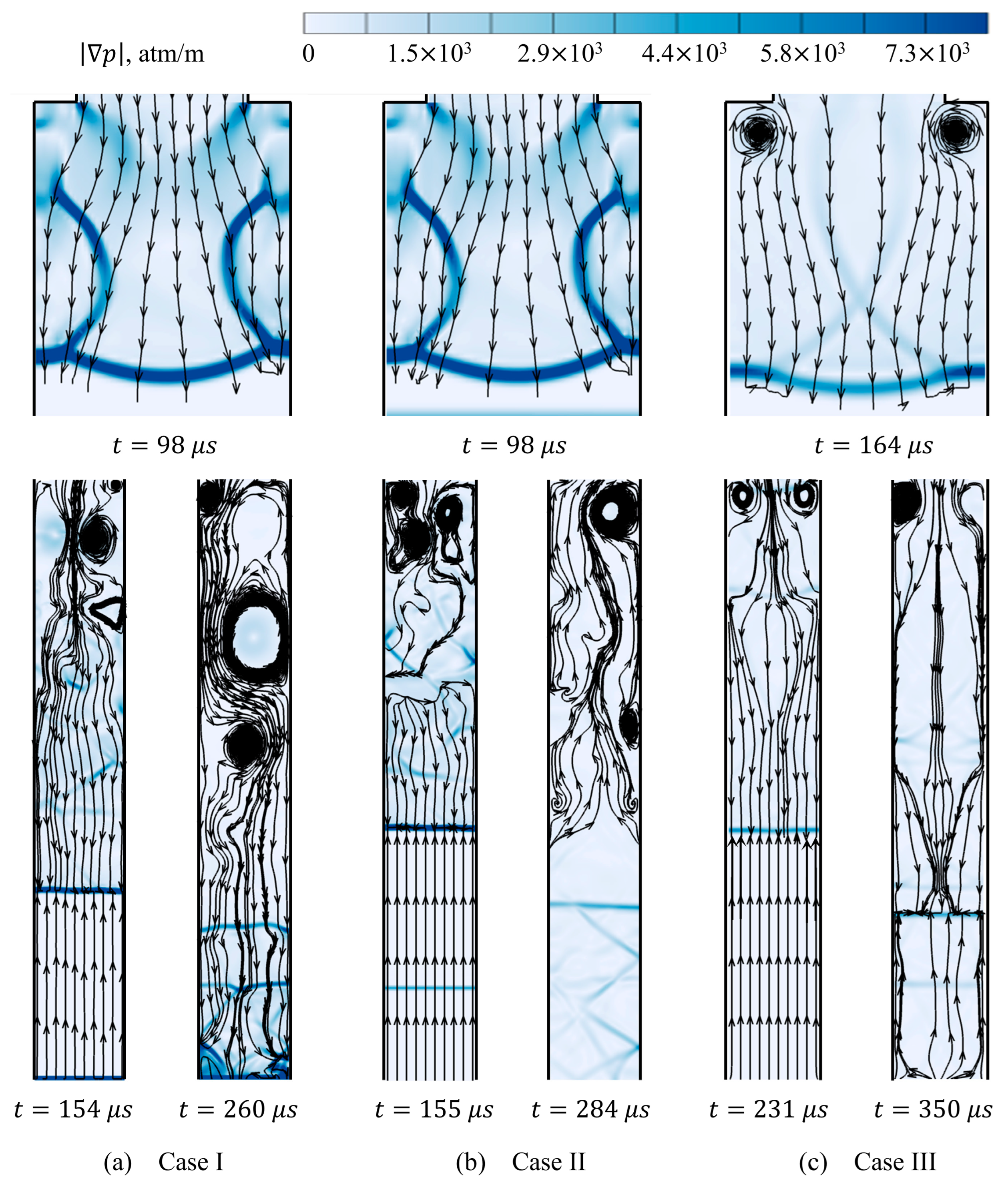
3.1. Detonation Wave Diffraction at the Injector Orifice
3.2. Shock Wave Dynamics Inside the Cavity
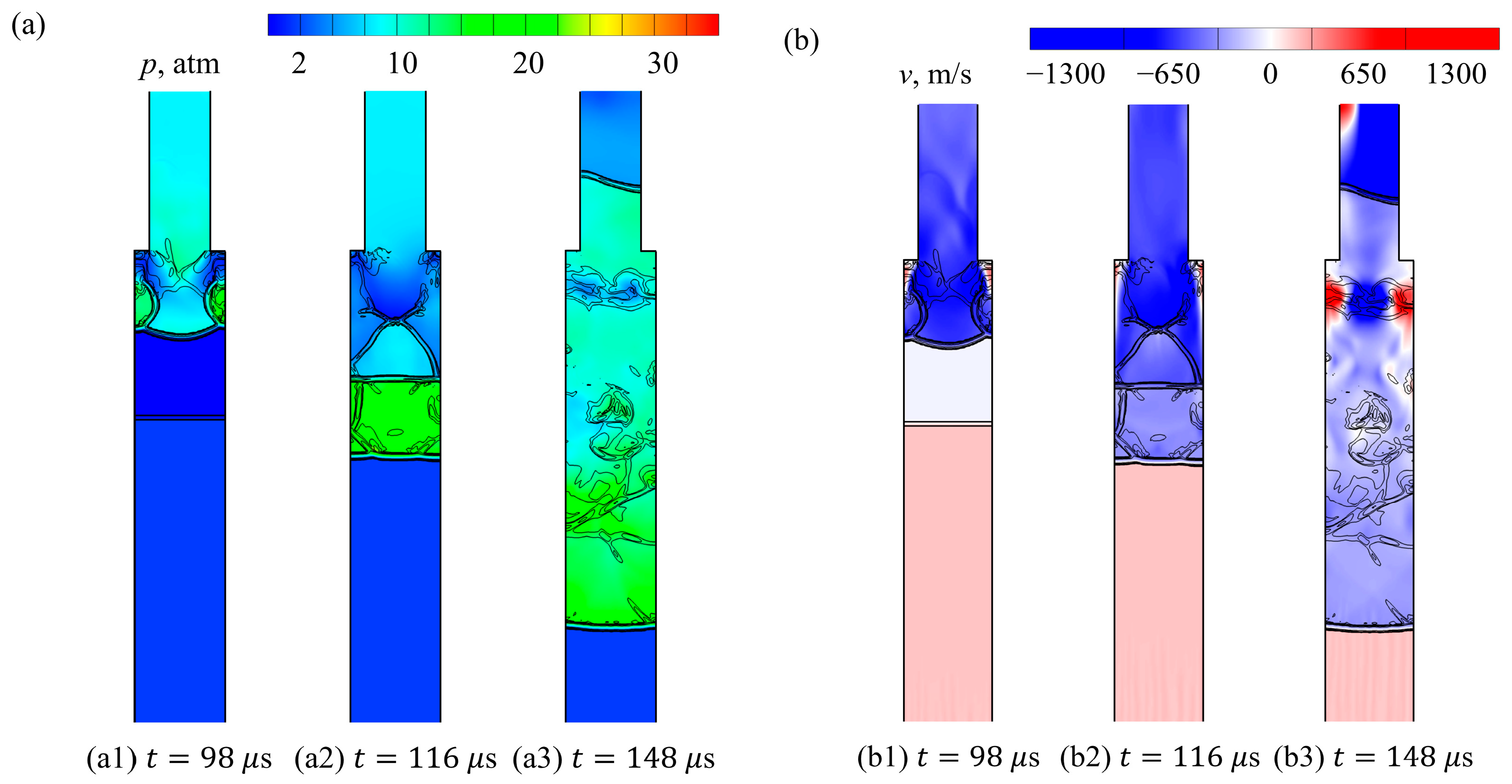
3.3. Evolution of Contact Surfaces
3.4. Potential for Reinitiation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| A | preexponential factor |
| c | speed of sound |
| D | detonation wave speed |
| d | diameter |
| Ea | activation energy |
| et | specific total energy |
| FS | convergence factor of safety |
| f | flow property |
| l | length |
| M | Mach number |
| N | number of cells |
| ns | number of species |
| p | pressure |
| universal gas constant | |
| r | grid refinement ratio |
| T | temperature |
| t | time |
| u, v | velocity components |
| x, y | spatial coordinates |
| Y | mass fraction |
| α | angle between disturbance trajectory and detonation wave normal |
| ε | relative error |
| Π | order of convergence |
| ρ | density |
| Ω | vorticity magnitude |
| mass production rate of reactants | |
| Subscripts | |
| c | property of cavity |
| C-J | Chapman-Jouguet condition |
| i | index of nominal species |
| i | property of injector |
| o | property of orifice |
| t | property of detonation tube |
References
- Kailasanath, K. Review of Propulsion Applications of Detonation Waves. AIAA J. 2000, 38, 1698–1708. [Google Scholar] [CrossRef]
- Lu, F.K.; Braun, E.M. Rotating Detonation Wave Propulsion: Experimental Challenges, Modeling, and Engine Concepts. J. Propuls. Power 2014, 30, 1125–1142. [Google Scholar] [CrossRef]
- Pandey, K.M.; Debnath, P. Review on Recent Advances in Pulse Detonation Engines. J. Combust. 2016, 2016, 4193034. [Google Scholar] [CrossRef]
- Roy, G.D.; Frolov, S.M.; Borizov, A.A.; Netzer, D.W. Pulse Detonation Propulsion: Challenges, Current Status, and Future Perspective. Prog. Energy Combust. Sci. 2004, 30, 545–672. [Google Scholar] [CrossRef]
- Gejji, R.M.; Buschhagen, T.; Slabaugh, C.D. Occurrence of Rotating Detonation Waves in a Jet Stabilized Combustor with Premixed Injection. J. Propuls. Power 2021, 37, 645–649. [Google Scholar] [CrossRef]
- Schwer, D.A.; Kailasanath, K. Towards Non-Premixed Injection Modeling of Rotating Detonation Engines. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar]
- Fan, L.Z.; Shi, Q.; Zhi, Y.; Nie, W.S.; Lin, W. Experimental and Numerical Study on Multi-Wave Modes of H2/O2 Rotating Detonation Combustor. Int. J. Hydrogen Energy 2022, 47, 13121–13133. [Google Scholar] [CrossRef]
- Han, J.; Bai, Q.; Zhang, S.; Wu, M.; Cui, S.; Chen, H.; Weng, C. Experimental Study of H2/Air Rotating Detonation Wave Propagation Characteristics at Low Injection Pressure. Aerosp. Sci. Technol. 2022, 126, 107628. [Google Scholar] [CrossRef]
- Braun, E.M.; Balcazar, T.S.; Wilson, D.R.; Lu, F.K. Experimental Study of a High-Frequency Fluidic Valve Fuel Injector. J. Propuls. Power 2012, 28, 1121–1125. [Google Scholar] [CrossRef]
- Lu, F.K.; Jensen, D. Potential Viability of a Fast-Acting Micro-Solenoid Valve for Pulsed Detonation Fuel Injection. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Peace, J.T.; Joshi, D.D.; Lu, F.K. Experimental Study of High-Frequency Fluidic Valve Injectors for Detonation Engine Applications. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MA, USA, 13–17 January 2014. [Google Scholar]
- Fujii, J.; Kumazawa, Y.; Matsuo, A.; Nakagami, S.; Matsuoka, K.; Kasahara, J. Numerical Investigation on Detonation Velocity in Rotating Detonation Engine Chamber. Proc. Combust. Inst. 2017, 36, 2665–2672. [Google Scholar] [CrossRef]
- Sato, T.; Chacon, F.; White, L.; Raman, V.; Gamba, M. Mixing and Detonation Structure in a Rotating Detonation Engine with an Axial Air Inlet. Proc. Combust. Inst. 2021, 38, 3769–3776. [Google Scholar] [CrossRef]
- Redhal, S.C.; Burr, J.R.; Yu, K. Injector Flowfield-Detonation Wave Interaction in Unwrapped RDE Channel. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Goto, K.; Nishimura, J.; Kawasaki, A.; Matsuoka, K.; Kasahara, J.; Matsuo, A.; Funaki, I.; Nakata, D.; Uchiumi, M.; Higashino, K. Propulsive Performance and Heating Environment of Rotating Detonation Engine with Various Nozzles. J. Propuls. Power 2019, 35, 213–223. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and Validation in Computational Fluid Dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]
- Chapman, D.R.; Mark, H.; Pirtle, M.W. Computers vs. Wind Tunnels for Aerodynamic Flow Simulations. Astronaut. Aeronaut. 1975, 13, 12–35. [Google Scholar]
- Smith, B.L. The difference between traditional experiments and CFD validation benchmark experiments. Nucl. Eng. Des. 2017, 312, 42–47. [Google Scholar] [CrossRef]
- Ma, F.; Choi, J.Y.; Yang, V. Thrust Chamber Dynamics and Propulsive Performance of Single-Tube Pulse Detonation Engines. J. Propuls. Power 2005, 21, 512–526. [Google Scholar] [CrossRef]
- Oran, E.S.; Weber, J.W., Jr.; Stefaniw, E.I.; Lefebvre, M.H.; Anderson, J.D., Jr. A Numerical Study of a Two-Dimensional H2-O2-Ar Detonation Using a Detailed Chemical Reaction Model. Combust. Flame 1998, 113, 147–163. [Google Scholar] [CrossRef]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamics Properties of Individual Species; NASA-TP-2002-211556; NASA: Washington, DC, USA, 2002.
- Jachimowski, C.J. An Analytical Study of the Hydrogen-Air Reaction Mechanism with Application to Scramjet Combustion; NASA TP-2791; Langley Research Center: Hampton, VA, USA, 1988. [Google Scholar]
- Meng, Q.; Zhao, N.; Zheng, H.; Yang, J.; Qi, L. Numerical Investigation of the Effect of Inlet Mass Flow Rates on H2/Air Non-Premixed Rotating Detonation Wave. Int. J. Hydrogen Energy 2018, 43, 13618–13631. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, J.; Liu, S.; Lin, Z.; Cai, J. Effects of Injection Nozzle Exit Width on Rotating Detonation Engine. Acta Astronaut. 2017, 140, 388–401. [Google Scholar] [CrossRef]
- Denisov, Y.N. Structure of Gaseous Detonation in Tubes. J. Tech. Phys. 1960, 30, 450–459. [Google Scholar]
- Kaneshige, M.; Shepherd, J.E. Detonation Database; Technical Report FM97-8; California Institute of Technology: Pasadena, CA, USA, 1997. [Google Scholar]
- Prakash, S.; Fiévet, R.; Raman, V.; Burr, J.; Yu, K.H. Analysis of the Detonation Wave Structure in a Linearized Rotating Detonation Engine. AIAA J. 2020, 58, 5063–5077. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Arienti, M. A Numerical and Analytical Study of Detonation Diffraction; California Institute of Technology: Pasadena, CA, USA, 2003. [Google Scholar]
- Skews, B.W. The Shape of a Diffracting Shock Wave. J. Fluid Mech. 1967, 29, 297–304. [Google Scholar] [CrossRef]
- Guo, C.; Wang, C.; Xu, S.; Zhang, H. Cellular Pattern Evolution in Gaseous Detonation Diffraction in a 90°-Branched Channel. Combust. Flame 2007, 148, 89–99. [Google Scholar] [CrossRef]
- Wang, C.J.; Xu, S.L.; Guo, C.M. Gaseous Detonation Propagation in a Bifurcated Tube. J. Fluid Mech. 2008, 599, 81–110. [Google Scholar] [CrossRef]
- Bedick, C.; Ferguson, D.; Strakey, P. Characterization of Rotating Detonation Engine Injector Response Using Laser-Induced Fluorescence. J. Propuls. Power 2019, 35, 827–838. [Google Scholar] [CrossRef]
- Peraldi, O.; Knystautas, R.; Lee, J.H. Criteria for Transition to Detonation in Tubes. Symp. (Int.) Combust. 1988, 21, 1629–1637. [Google Scholar] [CrossRef]
- Radulescu, M.I.; Mével, R.; Xiao, Q.; Gallier, S. On the Self-Similarity of Diffracting Gaseous Detonations and the Critical Channel Width Problem. Phys. Fluids 2021, 33, 066106. [Google Scholar] [CrossRef]
- Li, H.; Han, W.; Li, J.; Fan, W. Influences of Incoming Flow on Re-Initiation of Cellular Detonations. Combust. Flame 2021, 229, 111376. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Chen, H. Diffraction of Weakly Unstable Detonation Through an Obstacle with Different Sizes and Shapes. Phys. Rev. Fluids 2021, 6, 043201. [Google Scholar] [CrossRef]
- Kawasaki, A.; Kasahara, J. A Novel Characteristic Length of Detonation Relevant to Supercritical Diffraction. Shock Waves 2020, 30, 1–12. [Google Scholar] [CrossRef]
- Sun, H.; Kawasaki, A.; Matsuoka, K.; Kasahara, J. A Study on Detonation-Diffraction Reflection Point Distances in H2/O2, C2H2/O2, and C2H4/O2 Systems. Proc. Combust. Inst. 2021, 38, 3605–3613. [Google Scholar] [CrossRef]




| Case | Initial Condition | Boundary Condition for Propellant Supply |
|---|---|---|
| I | oxygen, 1.0 atm | velocity inlet, 325 m/s |
| II | oxygen, 1.0 atm | pressure inlet, static pressure = 5.1 atm |
| III | oxygen, 5.1 atm | pressure inlet, total pressure = 5.1 atm |
| Level 1 | Level 2 | Level 3 | Level 4 | |
|---|---|---|---|---|
| number of cells, N | 330,000 | 737,550 | 1,648,128 | 3,708,288 |
| average cell size, in mm | 0.25 | 0.17 | 0.11 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Small, J.C.; Zhang, L. Computational Study of Fluidic-Valve Injectors for Detonation Engines. Aerospace 2024, 11, 171. https://doi.org/10.3390/aerospace11030171
Small JC, Zhang L. Computational Study of Fluidic-Valve Injectors for Detonation Engines. Aerospace. 2024; 11(3):171. https://doi.org/10.3390/aerospace11030171
Chicago/Turabian StyleSmall, Jayson Craig, and Liwei Zhang. 2024. "Computational Study of Fluidic-Valve Injectors for Detonation Engines" Aerospace 11, no. 3: 171. https://doi.org/10.3390/aerospace11030171
APA StyleSmall, J. C., & Zhang, L. (2024). Computational Study of Fluidic-Valve Injectors for Detonation Engines. Aerospace, 11(3), 171. https://doi.org/10.3390/aerospace11030171





