Experimental Study of the Effect of the Initial Droplet Diameter on the Evaporation Characteristics of Unsymmetrical Dimethylhydrazine Droplets in a Subcritical Environment
Abstract
:1. Introduction
2. Experimental Apparatus and Methods
2.1. Experimental Apparatus
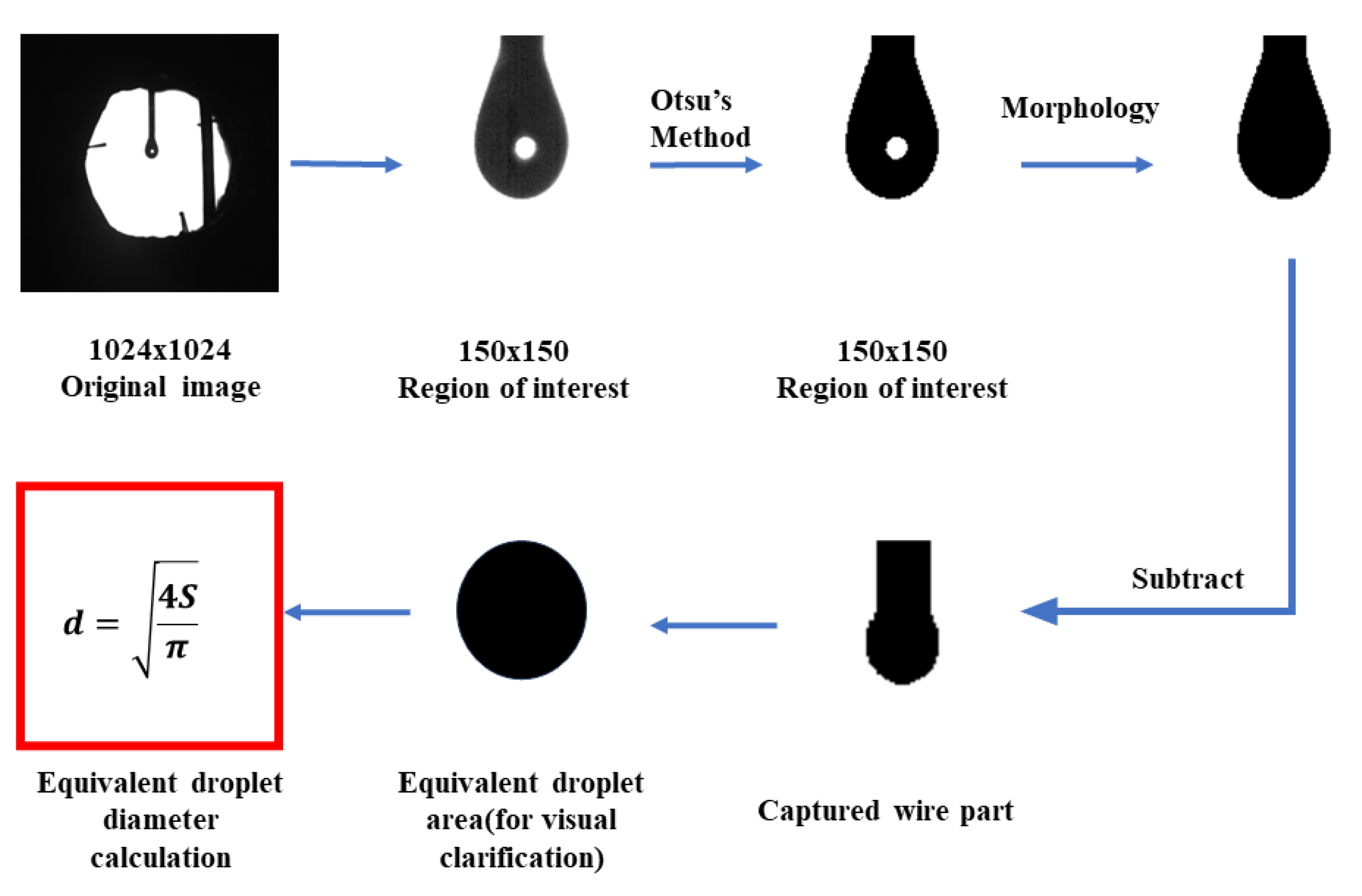
2.2. Data Processing Methods
3. Results and Discussion
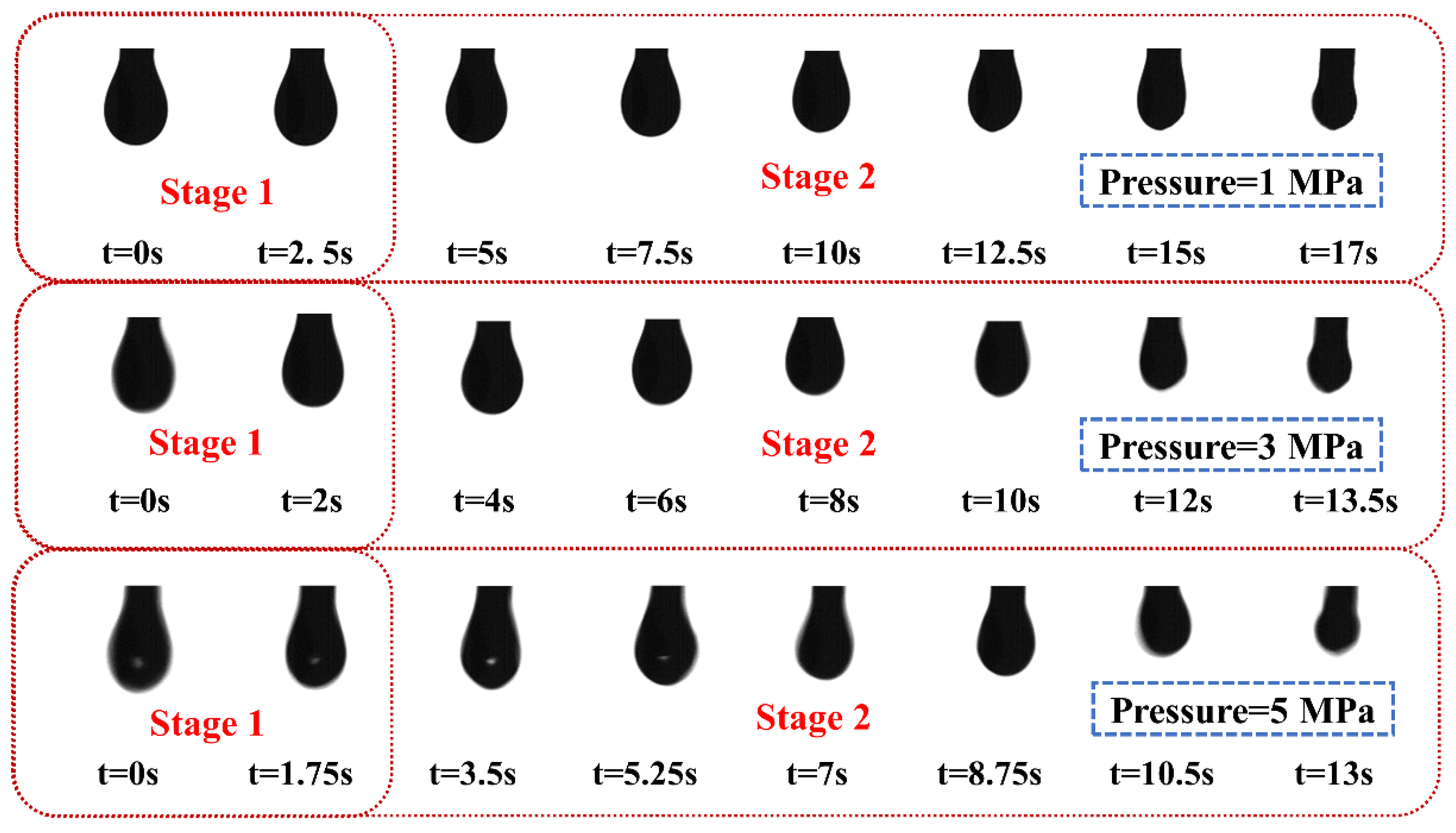
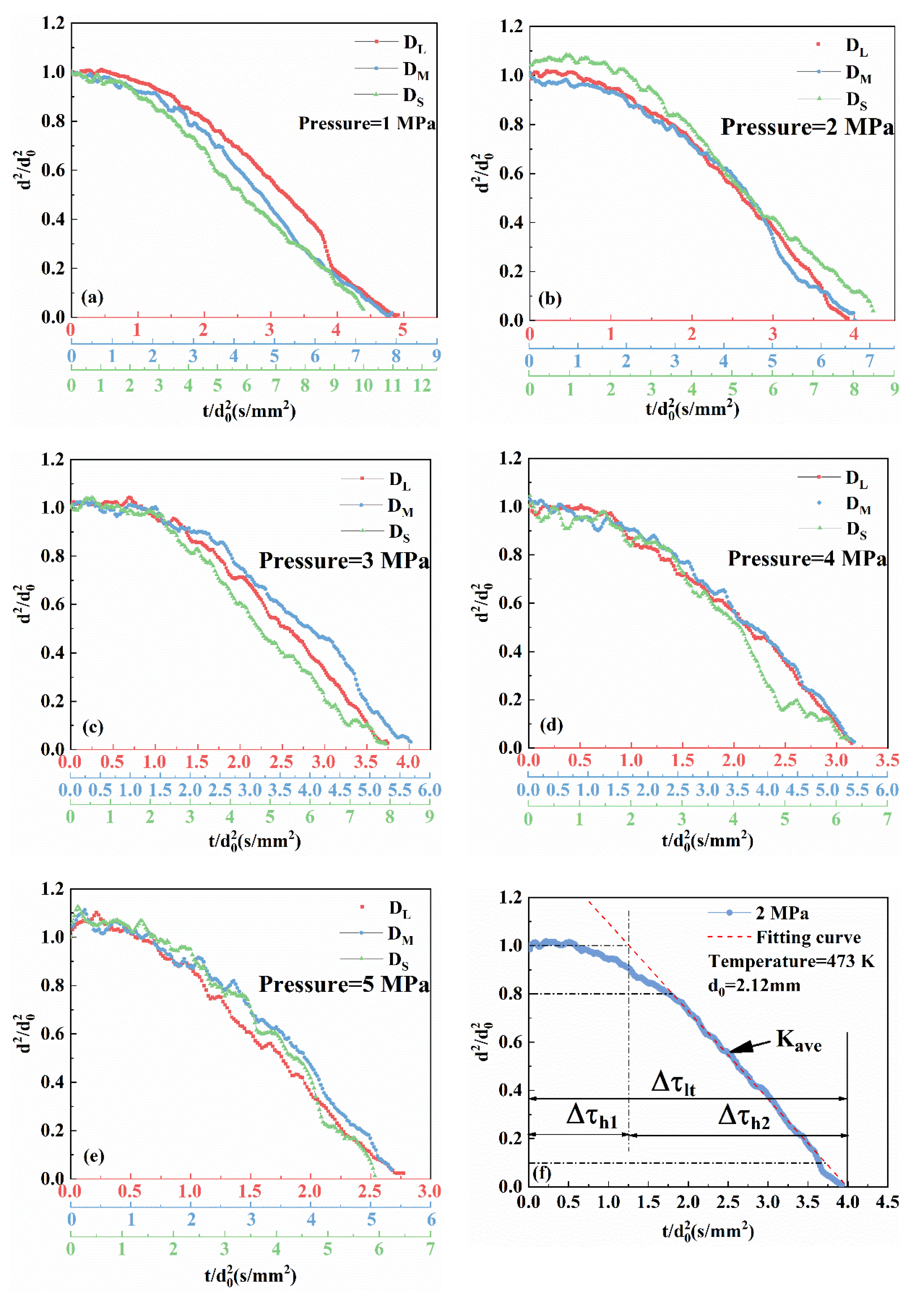
3.1. Evaporation Properties of Liquid Droplets
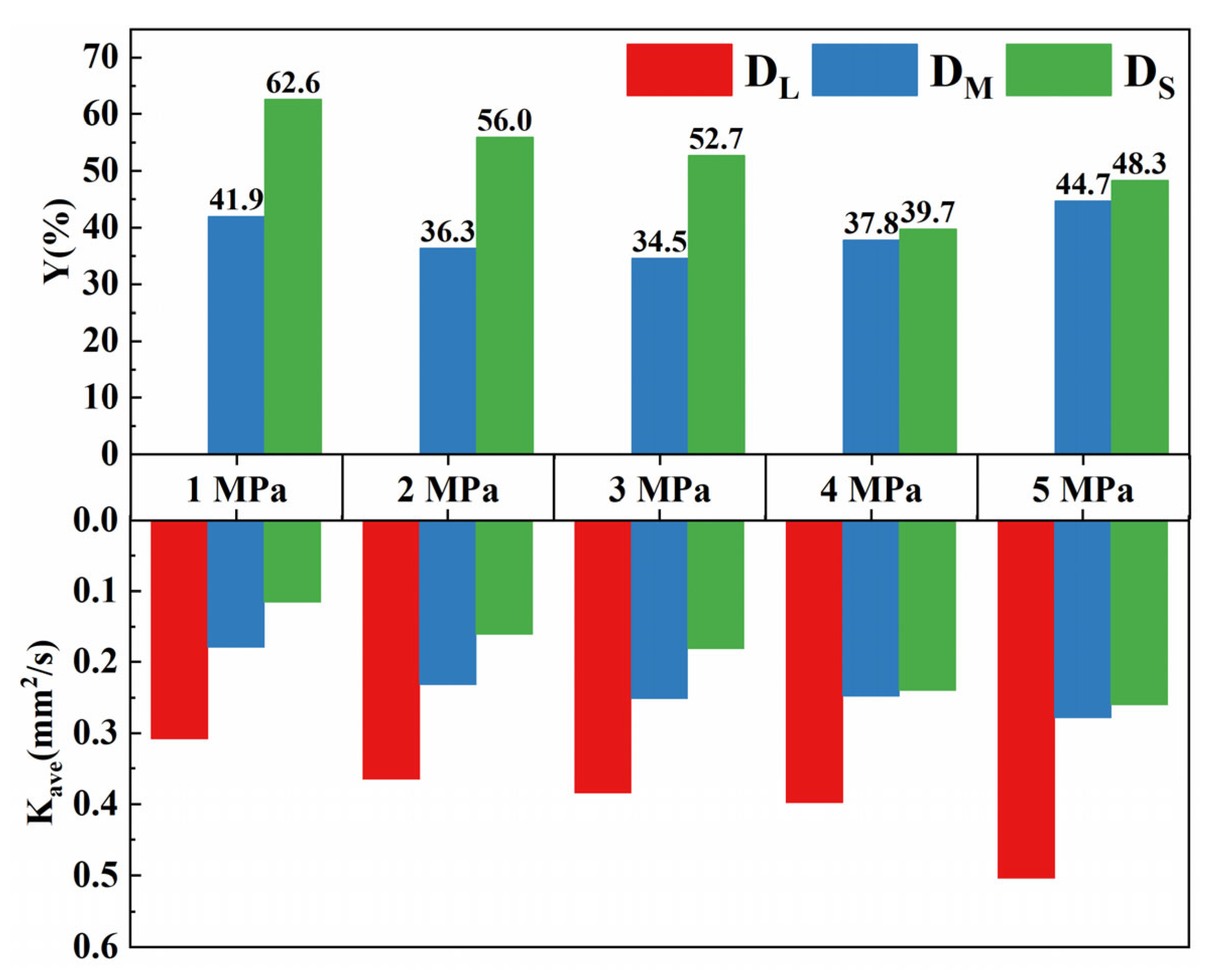
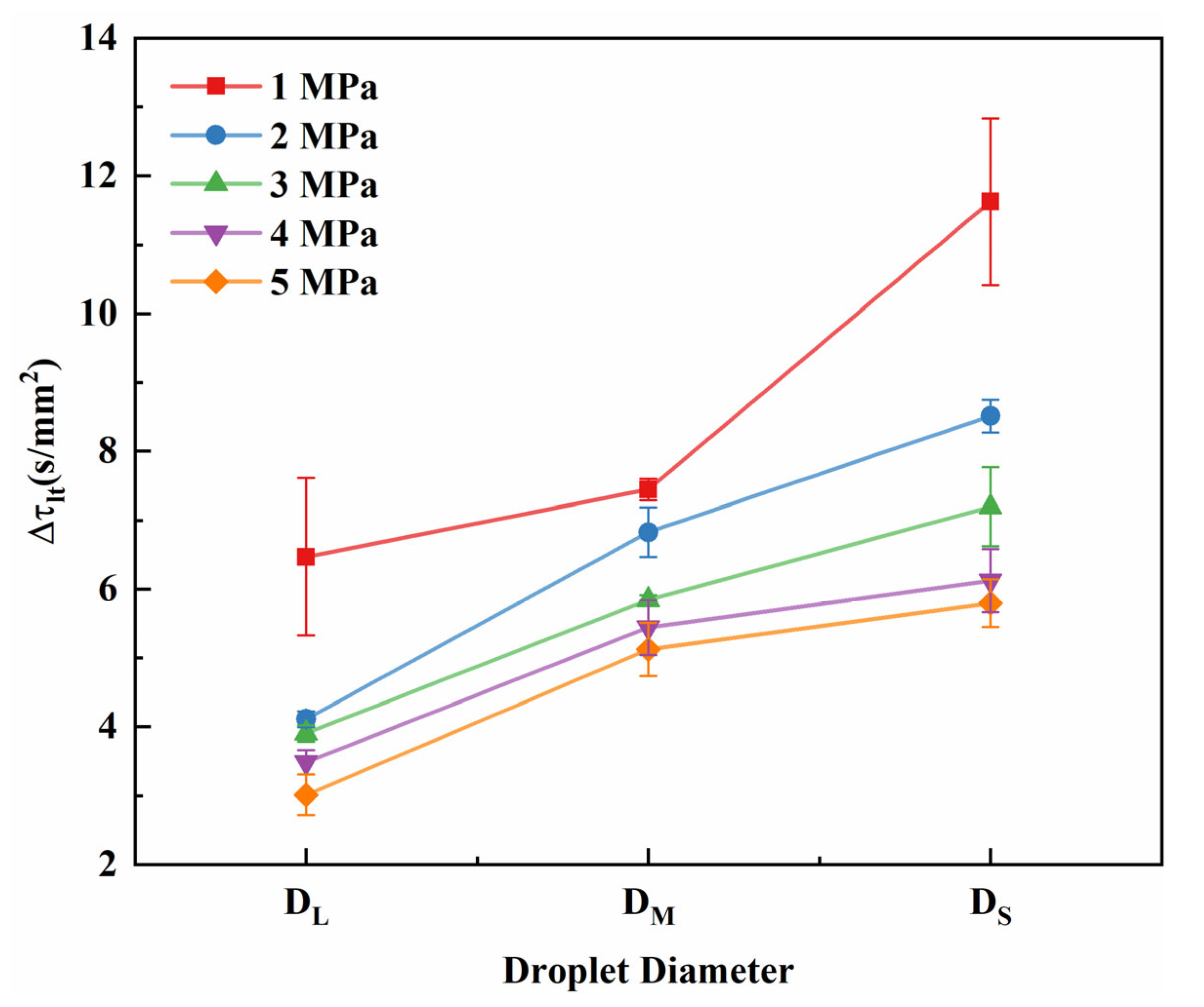
3.2. Effect of Initial Droplet Diameter on Evaporation Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sánchez, A.L.; Urzay, J.; Liñán, A. The role of separation of scales in the description of spray combustion. Proc. Combust. Inst. 2015, 35, 1549–1577. [Google Scholar] [CrossRef]
- Chigier, N.A. The atomization and burning of liquid fuel sprays. Prog. Energy Combust. Sci. 1976, 2, 97–114. [Google Scholar] [CrossRef]
- Fei, L.; Qin, F.; Wang, G.; Luo, K.H.; Derome, D.; Carmeliet, J. Droplet evaporation in finite-size systems: Theoretical analysis and mesoscopic modeling. Phys. Rev. E 2022, 105, 025101. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Chen, S.-Y.; Zhu, D.-Q.; Xue, S.-Q.; Li, S.-Y.; Zhou, Z.-F.; Liu, B. Experimental investigation on evaporation characteristics of RP-3 aviation kerosene droplet above the critical temperature under various pressure conditions. Aerosp. Sci. Technol. 2023, 140, 108463. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, H.; He, Y.; Zhu, Y.; Wang, Z. Evaporation, Autoignition and Micro-Explosion Characteristics of RP-3 Kerosene Droplets under Sub-Atmospheric Pressure and Elevated Temperature. Energies 2022, 15, 7172. [Google Scholar] [CrossRef]
- Katre, P.; Balusamy, S.; Banerjee, S.; Chandrala, L.D.; Sahu, K.C. Evaporation Dynamics of a Sessile Droplet of Binary Mixture Laden with Nanoparticles. Langmuir ACS J. Surf. Colloids 2021, 37, 6311–6321. [Google Scholar] [CrossRef] [PubMed]
- Xiao, G.; Luo, K.H.; Ma, X.; Shuai, S. A molecular dynamics study of fuel droplet evaporation in sub- and supercritical conditions. Proc. Combust. Inst. 2019, 37, 3219–3227. [Google Scholar] [CrossRef]
- Strizhak, P.A.; Volkov, R.; Misyura, S.Y.; Lezhnin, S.; Morozov, V.S. The role of convection in gas and liquid phases at droplet evaporation. Int. J. Therm. Sci. 2018, 134, 421–439. [Google Scholar] [CrossRef]
- Fan, D.; Wang, H.; Cui, C.; Wang, Y. Predictive simulation of evaporation and diffusion pattern of unsymmetrical dimethylhydrazine in natural environment. Comput. Simul. 2017, 34, 6. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, X.; Ping, Y.; Wang, X. Evaporation Characteristic of Unsymmetrical Dimethylhydrazine Propellant in Storage. Missiles Space Veh. 2011, 30, 58–61. [Google Scholar] [CrossRef]
- Huang, Z.; Luo, F.; Shi, H. Numerical Simulation of Diffusion of Unsymmetrical Dimethylhrazine Under Storage Condition. Sci. Technol. Rev. 2011, 29, 67–70. [Google Scholar] [CrossRef]
- Yin, T. Experimental study on the droplet evaporation process and influence factors. In Proceedings of the AIAA 2014-3570, 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- Faeth, G.M. Mixing, transport and combustion in sprays. Prog. Energy Combust. Sci. 1987, 13, 293–345. [Google Scholar] [CrossRef]
- Szekely, G.A.; Faeth, G.M. Effects of envelope flames on drop gasification rates in turbulent diffusion flames. Combust. Flame 1983, 49, 255–259. [Google Scholar] [CrossRef]
- Ju, D.; Zhang, T.; Xiao, J.; Qiao, X.; Huang, Z. Effect of droplet sizes on evaporation of a bi-component droplet at DME (dimethyl ether)/n-heptane-fueled engine conditions. Energy 2015, 86, 257–266. [Google Scholar] [CrossRef]
- Brenn, G.; Deviprasath, L.J.; Durst, F.; Fink, C. Evaporation of acoustically levitated multi-component liquid droplets. Int. J. Heat Mass Transf. 2007, 50, 5073–5086. [Google Scholar] [CrossRef]
- Abramzon, B.; Sirignano, W.A. Droplet vaporization model for spray combustion calculations. In Proceedings of the 26th Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1988. [Google Scholar]
- Miller, R.S.; Harstad, K.G.; Bellan, J. Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations. Int. J. Multiph. Flow 1998, 24, 1025–1055. [Google Scholar] [CrossRef]
- Verwey, C.; Birouk, M. Experimental investigation of the effect of natural convection on the evaporation characteristics of small fuel droplets at moderately elevated temperature and pressure. Int. J. Heat Mass Transf. 2018, 118, 1046–1055. [Google Scholar] [CrossRef]
- Dgheim, J.; Abdallah, M.; Nasr, N.B. Enhanced Evaporation of Droplet of Ternary Component Under the Effect of Thermo-physical and Transport Properties Variability. Arab. J. Sci. Eng. 2018, 43, 2181–2194. [Google Scholar] [CrossRef]
- Liu, L.; Bi, Q.-C.; Liu, W.-M.; Qi, F.-C.; Bi, X.-G. Experimental and Theoretical Investigation on Rapid Evaporation of Ethanol Droplets and Kerosene Droplets During Depressurization. Microgravity Sci. Technol. 2011, 23, 89–97. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.F.; Mi, M.; Wang, Z.; Jiang, L. Evaporation of a bicomponent droplet during depressurization. Int. J. Heat Mass Transf. 2016, 100, 615–626. [Google Scholar] [CrossRef]
- Lorenzini, G.; Conti, A.; De Wrachien, D. Computational Fluid Dynamics (CFD) Picture of Water Droplet Evaporation in Air. Irrig. Drain. Syst. Eng. 2012, 1, 1000101. [Google Scholar] [CrossRef]
- Ruan, Y.; Chen, L.; Liu, X.; Chen, S.; Hou, Y. Numerical Study of Evaporation and Motion Characteristics of Liquid Nitrogen Droplet in High-Speed Gas Flow. IOP Conf. Ser. Mater. Sci. Eng. 2017, 278, 012130. [Google Scholar] [CrossRef]
- Stagni, A.; Calabria, R.; Frassoldati, A.; Cuoci, A.; Faravelli, T.; Chiariello, F.; Massoli, P. Kinetic Modeling of the Ignition of Droplets of Fast Pyrolysis Bio-oil: Effect of Initial Diameter and Fuel Composition. Ind. Eng. Chem. Res. 2021, 60, 6719–6729. [Google Scholar] [CrossRef] [PubMed]
- Verwey, C. An Experimental Investigation of the Effect of Fuel Droplet Size on the Vaporization Process in a Turbulent Environment at Elevated Temperature and Pressure. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2017. [Google Scholar]
- Verwey, C.; Birouk, M. Experimental investigation of the effect of droplet size on the vaporization process in ambient turbulence. Combust. Flame 2017, 182, 288–297. [Google Scholar] [CrossRef]
- Birouk, M.; Toth, S.L. Vaporization and Combustion of a Soybean Biodiesel Droplet in Turbulent Environment at Elevated Ambient Pressure. Combust. Sci. Technol. 2015, 187, 937–952. [Google Scholar] [CrossRef]
- Wu, G.; Wang, Z.; Yang, C.; Wang, H.; Nie, W. Experimental study of the evaporation characteristics of unsymmetrical dimethylhydrazine in a sub-supercritical environment. Phys. Fluids 2024, 36, 023321. [Google Scholar] [CrossRef]
- Han, K.; Zhao, C.L.; Fu, G.; Zhang, F.J.; Pang, S.P.; Li, Y.C. Evaporation characteristics of dual component droplet of benzyl azides-hexadecane mixtures at elevated temperatures. Fuel 2015, 157, 270–278. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Nie, W.; Yang, C.; Zhou, S.; Wang, H. Experimental Study of the Effect of the Initial Droplet Diameter on the Evaporation Characteristics of Unsymmetrical Dimethylhydrazine Droplets in a Subcritical Environment. Aerospace 2024, 11, 297. https://doi.org/10.3390/aerospace11040297
Wu G, Nie W, Yang C, Zhou S, Wang H. Experimental Study of the Effect of the Initial Droplet Diameter on the Evaporation Characteristics of Unsymmetrical Dimethylhydrazine Droplets in a Subcritical Environment. Aerospace. 2024; 11(4):297. https://doi.org/10.3390/aerospace11040297
Chicago/Turabian StyleWu, Gangqiang, Wansheng Nie, Congling Yang, Siyin Zhou, and Hui Wang. 2024. "Experimental Study of the Effect of the Initial Droplet Diameter on the Evaporation Characteristics of Unsymmetrical Dimethylhydrazine Droplets in a Subcritical Environment" Aerospace 11, no. 4: 297. https://doi.org/10.3390/aerospace11040297
APA StyleWu, G., Nie, W., Yang, C., Zhou, S., & Wang, H. (2024). Experimental Study of the Effect of the Initial Droplet Diameter on the Evaporation Characteristics of Unsymmetrical Dimethylhydrazine Droplets in a Subcritical Environment. Aerospace, 11(4), 297. https://doi.org/10.3390/aerospace11040297





