Investigation of the Internal Flow Characteristics of a Tiltrotor Aircraft Engine Inlet in a Gust Environment
Abstract
:1. Introduction
2. Theory and Methodology
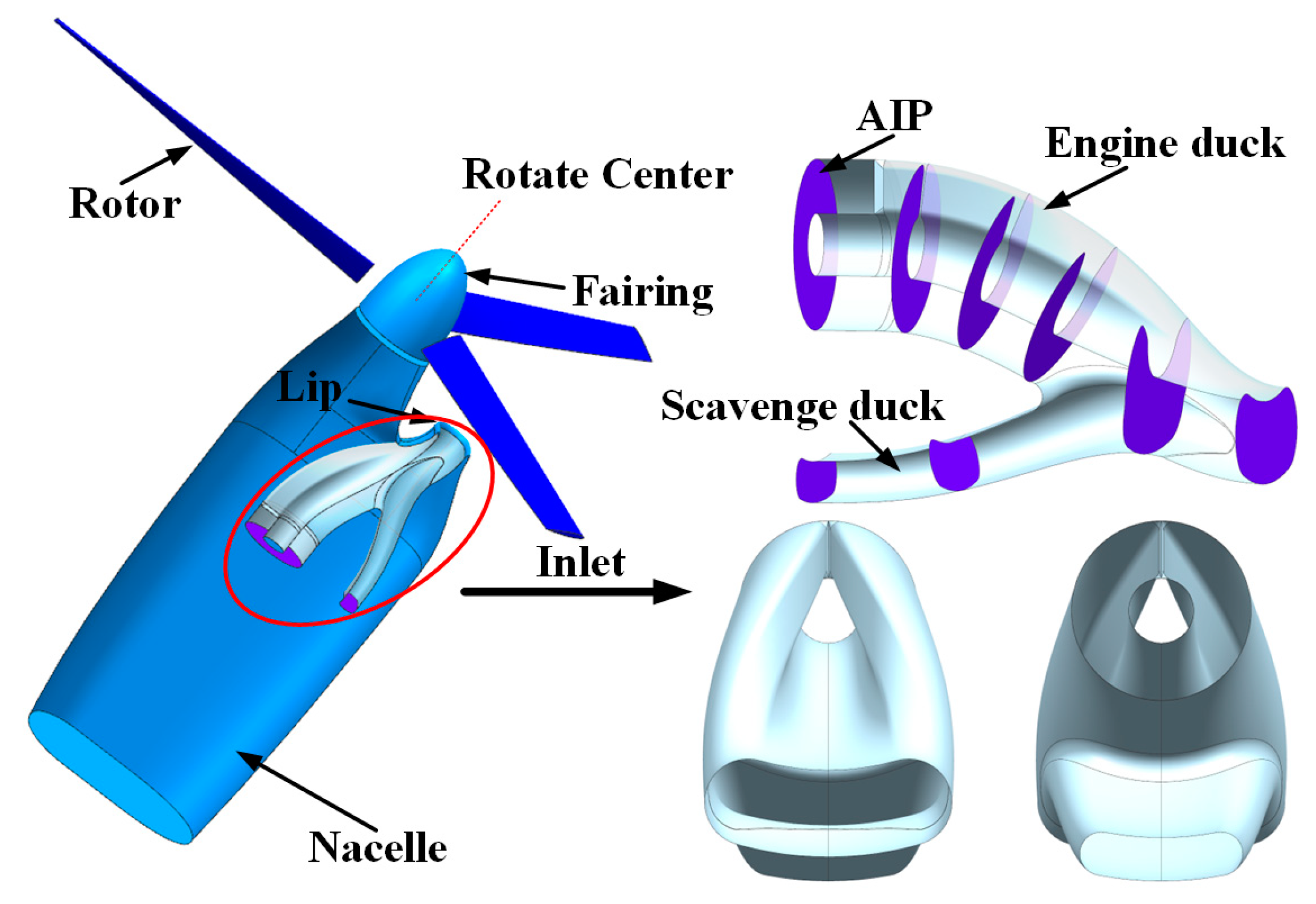
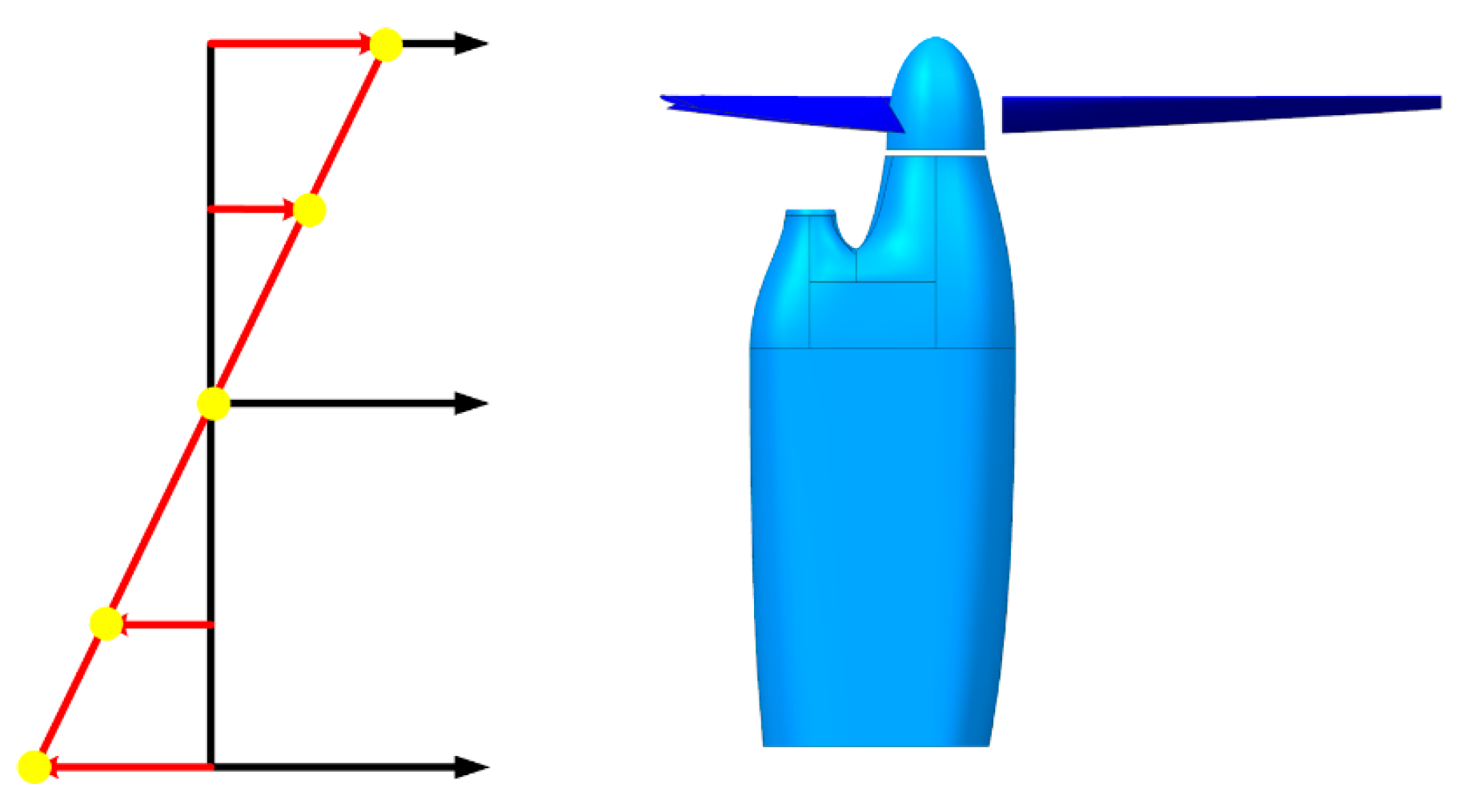
2.1. Model Introduction
2.2. Performance Parameter Definitions
- (1)
- is defined aswhere is the total pressure of the freestream, and is the mass flow weighted average total pressure at the AIP.
- (2)
- is defined aswhere is the minimum value of the mass flow weighted average total pressure over any 60° sector around the center of the AIP, and is the mass flow weighted average dynamic pressure at the AIP.
- (3)
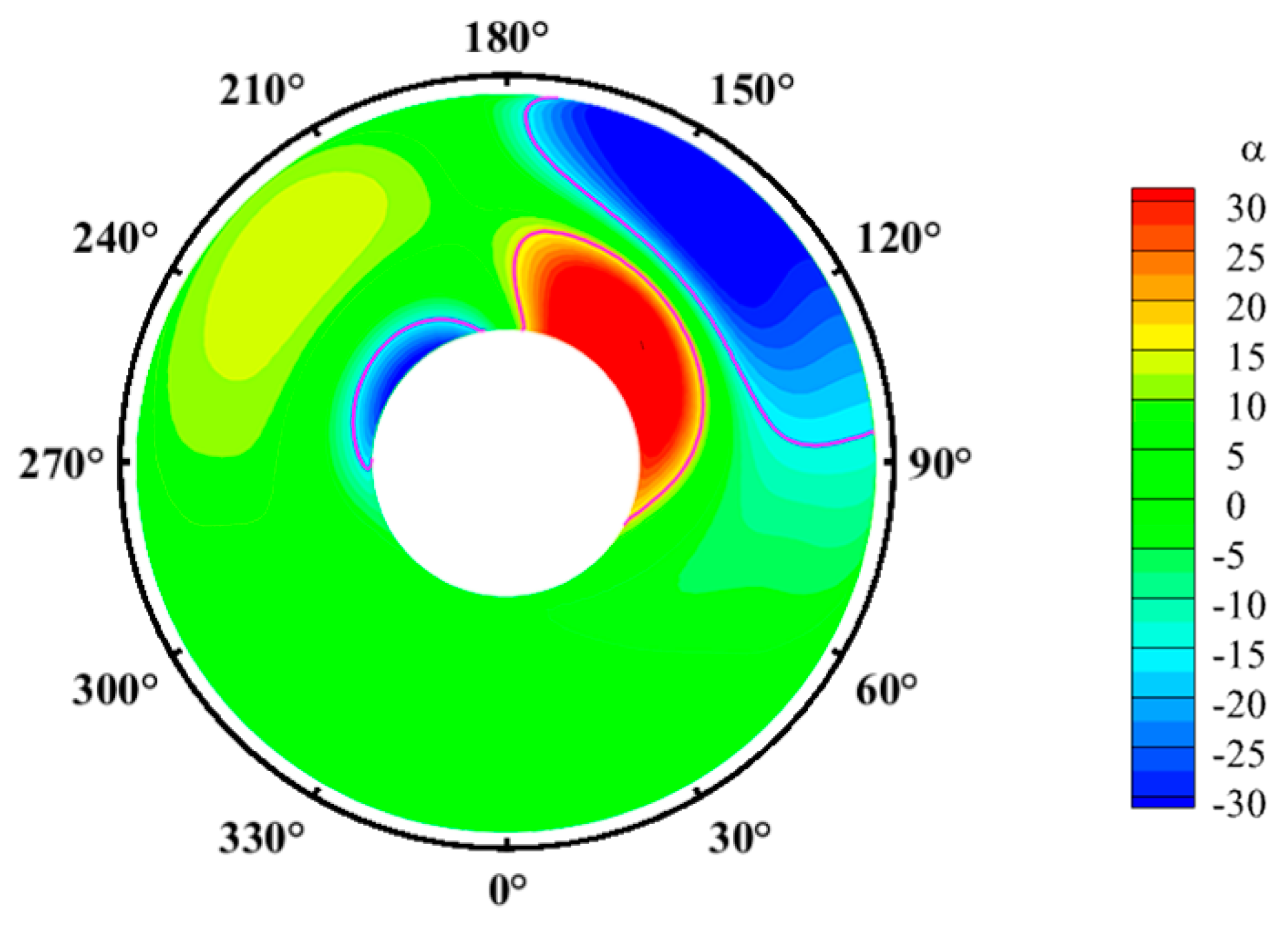
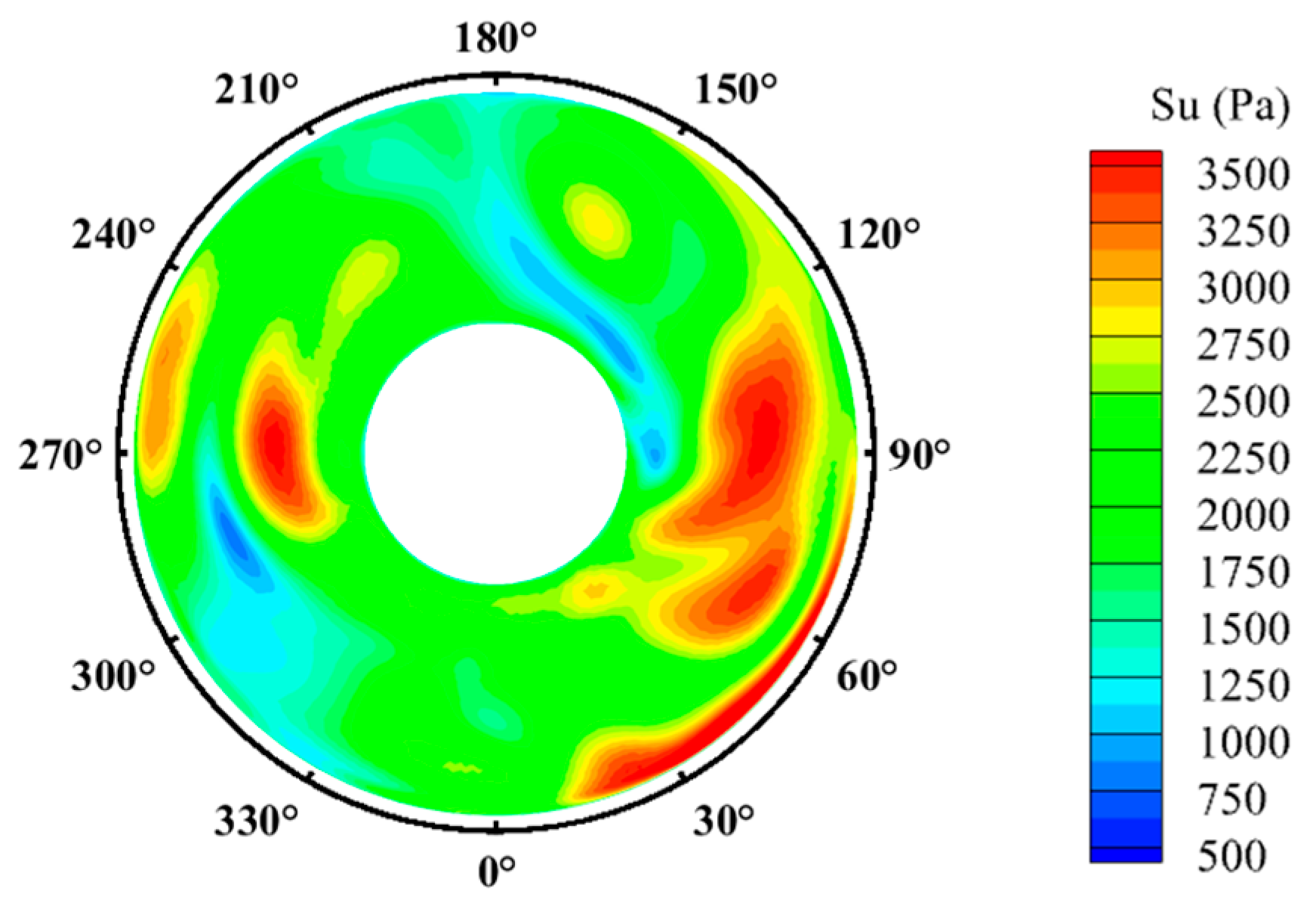
- The swirl angle used in this study follows the definition and swirl index system specified in the AUR5686 standard [27] for swirl distortion parameters. The expression is given as follows:where is the circumferential velocity at the measurement point on the AIP, and is the axial velocity at the same point. To better quantify the swirl intensity at the AIP, the absolute value of the swirl angle is integrated over the section to obtain the swirl angle flux , which quantifies the degree of swirl distortion at the AIP [28]. Additionally, since engineering applications are primarily concerned with areas and proportions where the swirl angle exceeds ±15° [29], we employed ηα15 to characterize the proportion of the area where || exceeds 15° to the AIP. The formula is as follows:
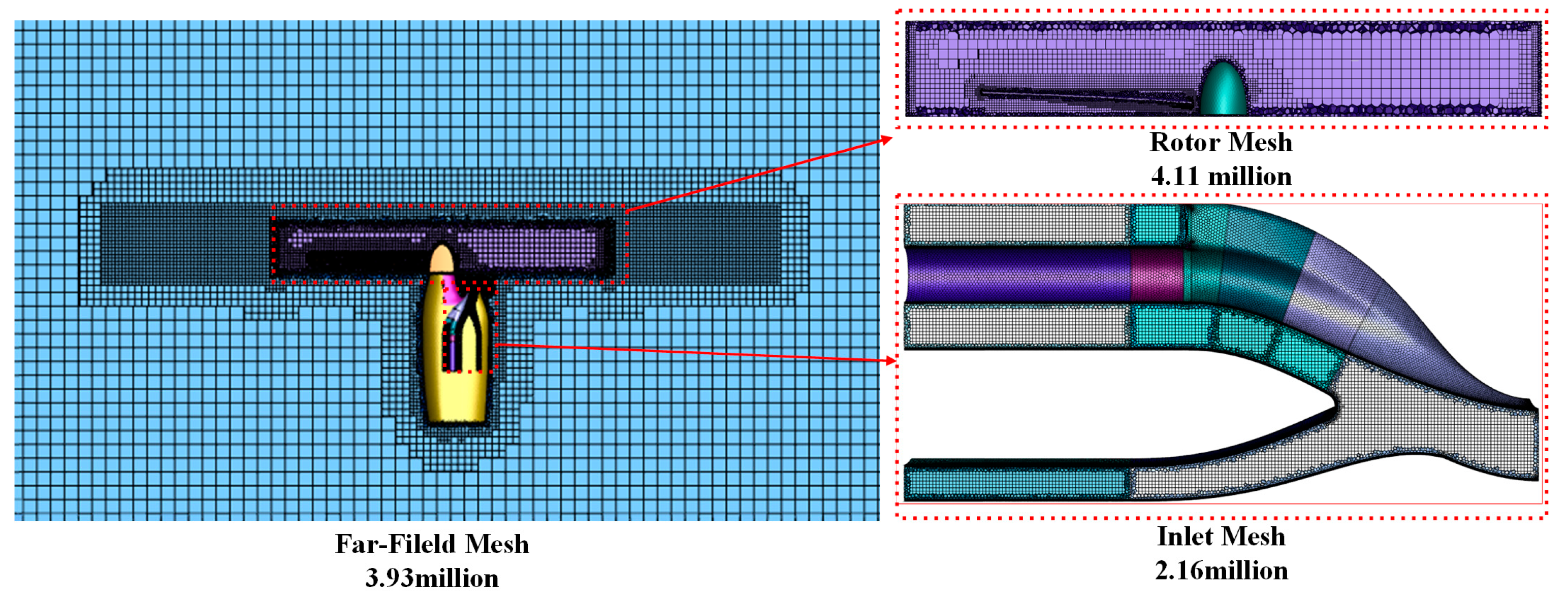
2.3. Numerical Methods
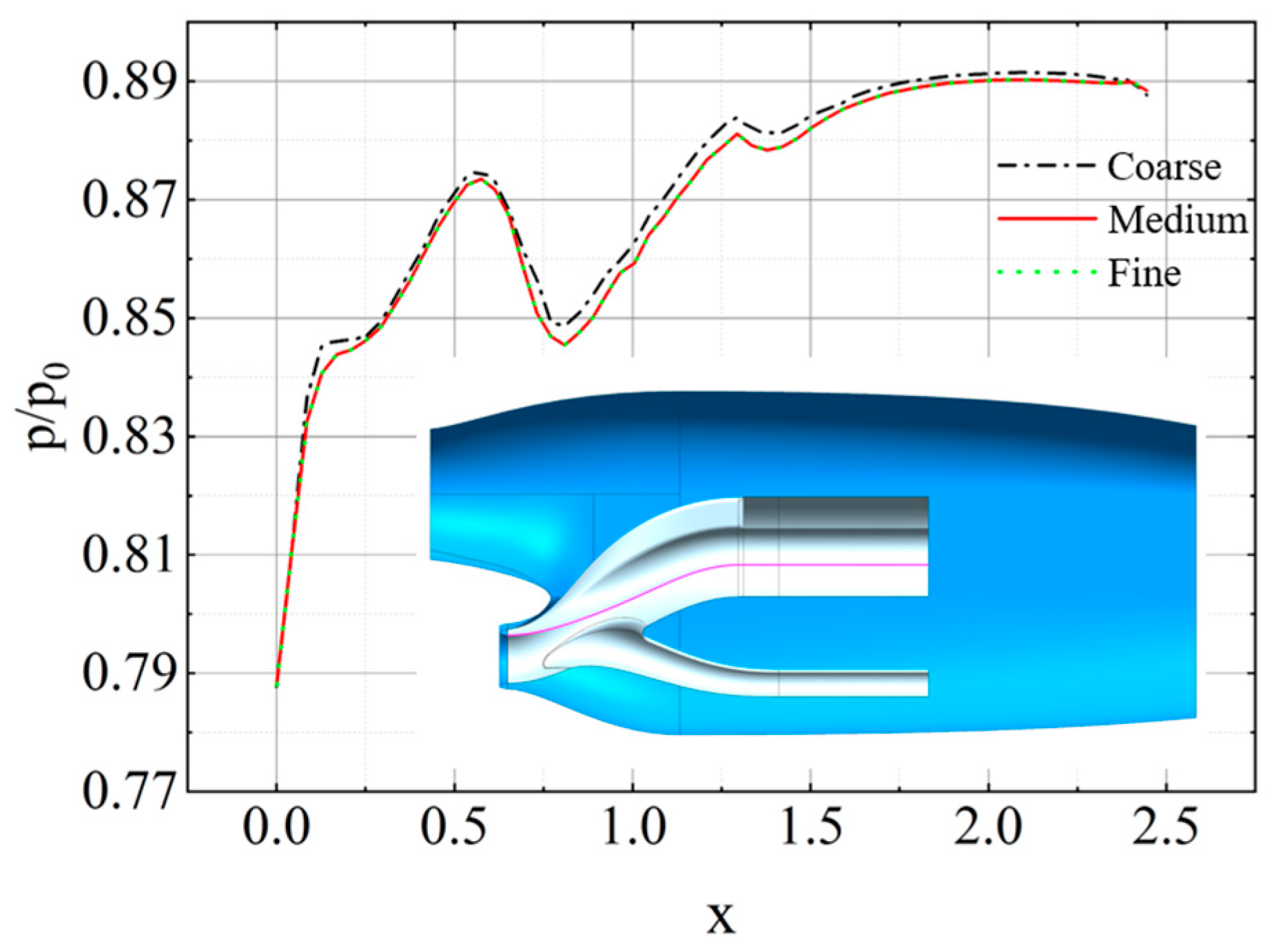
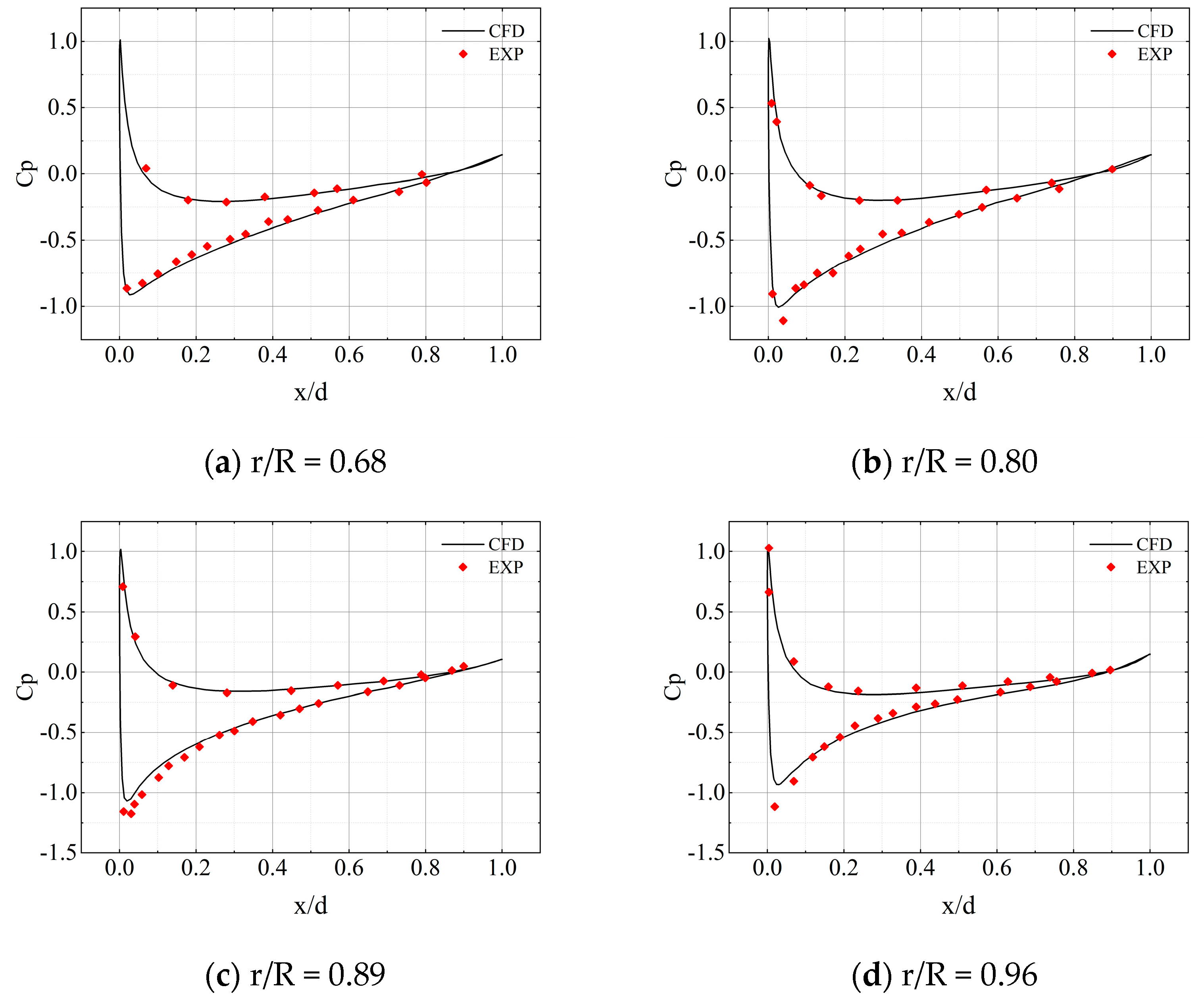
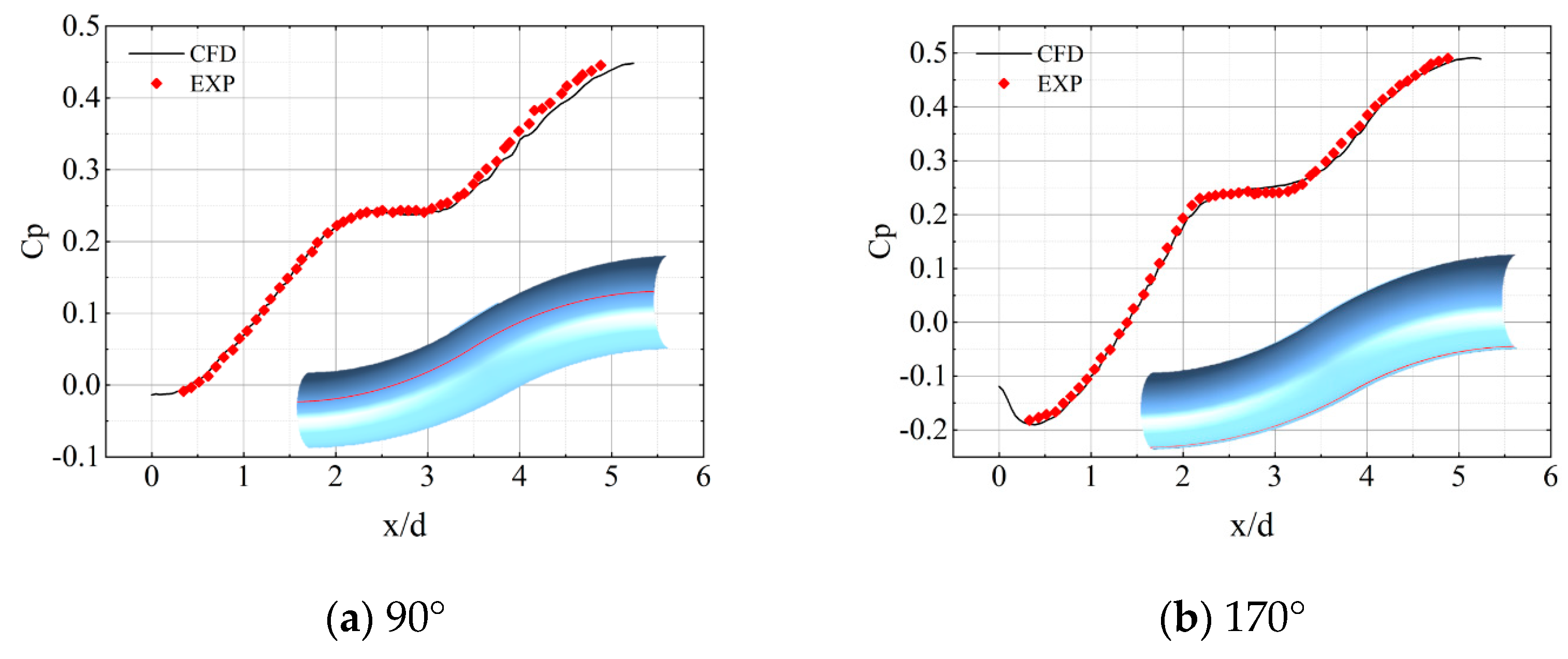
2.4. Numerical Validation
3. Results and Discussion
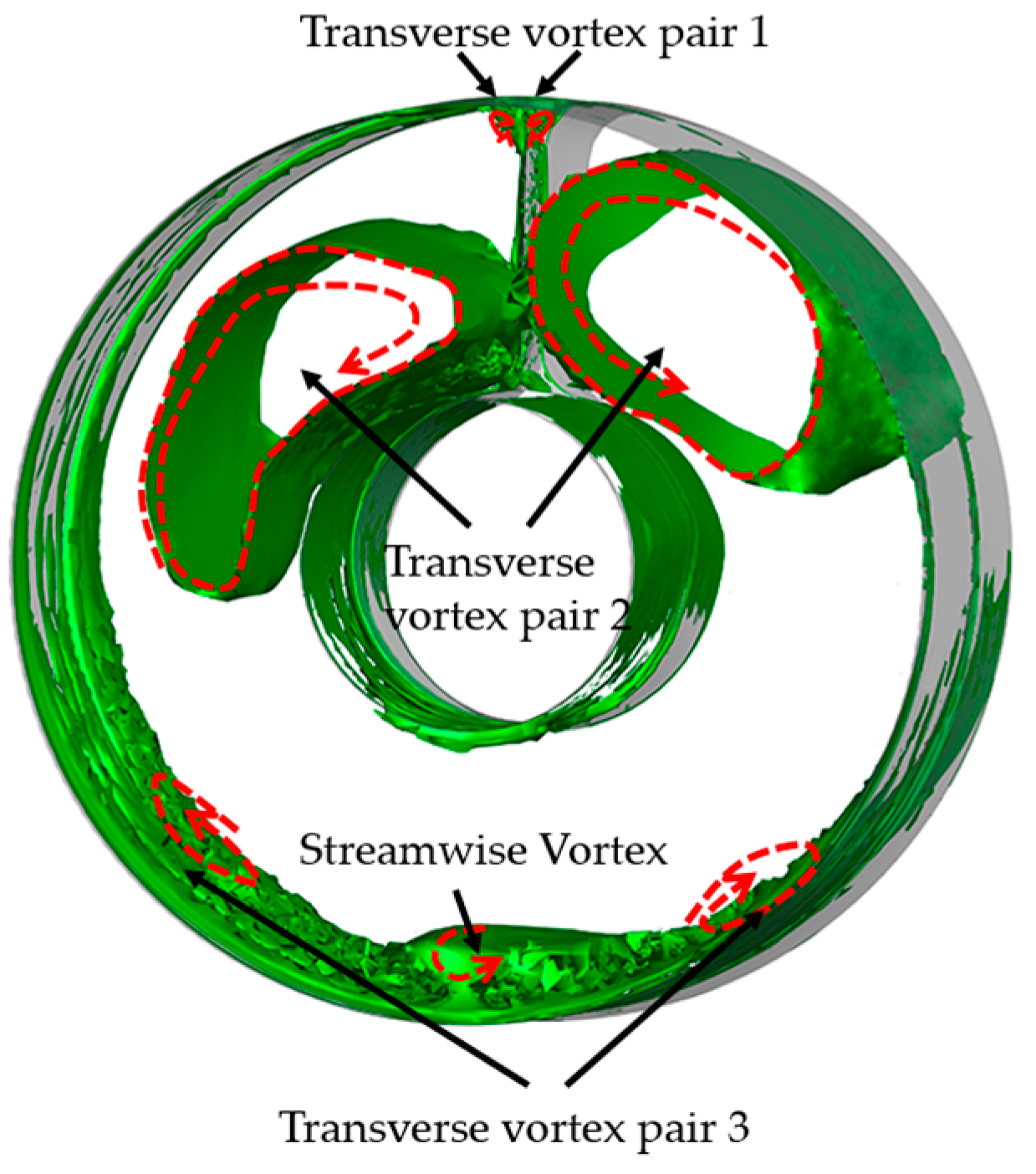
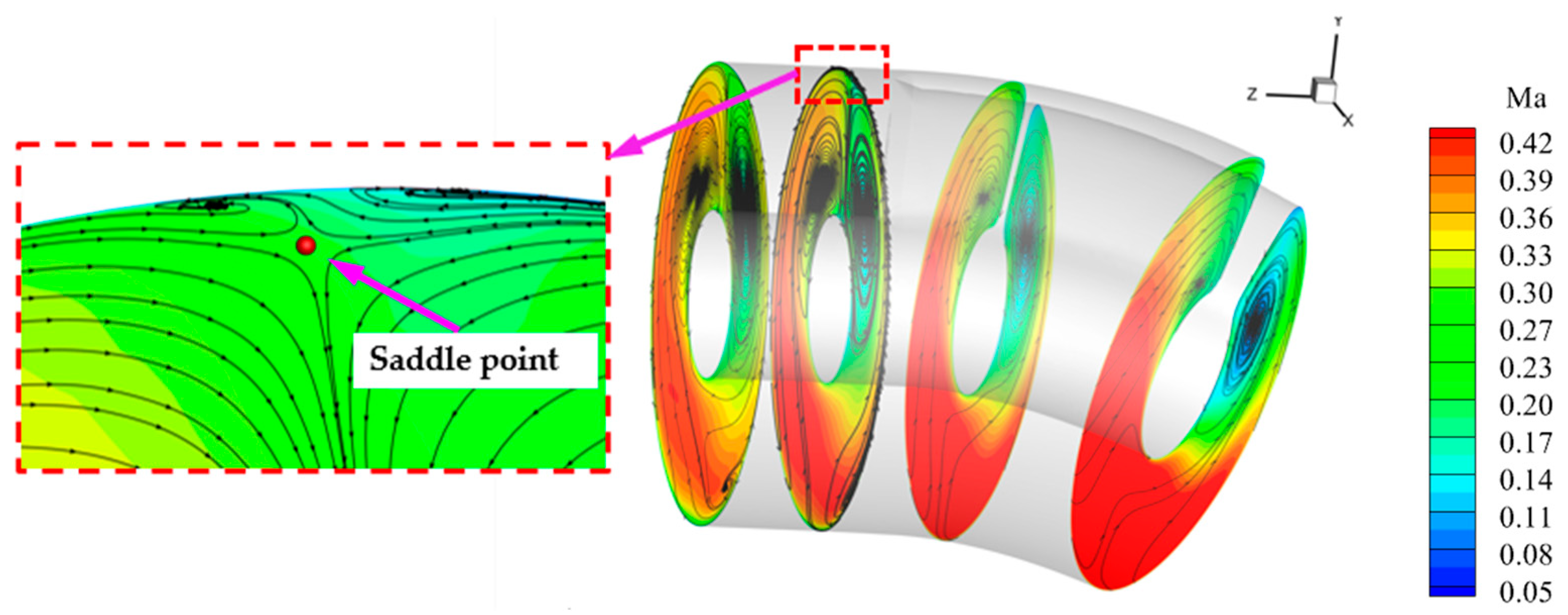
3.1. Time-Averaged Internal Flow Field Analysis of Gust-Free Inlet
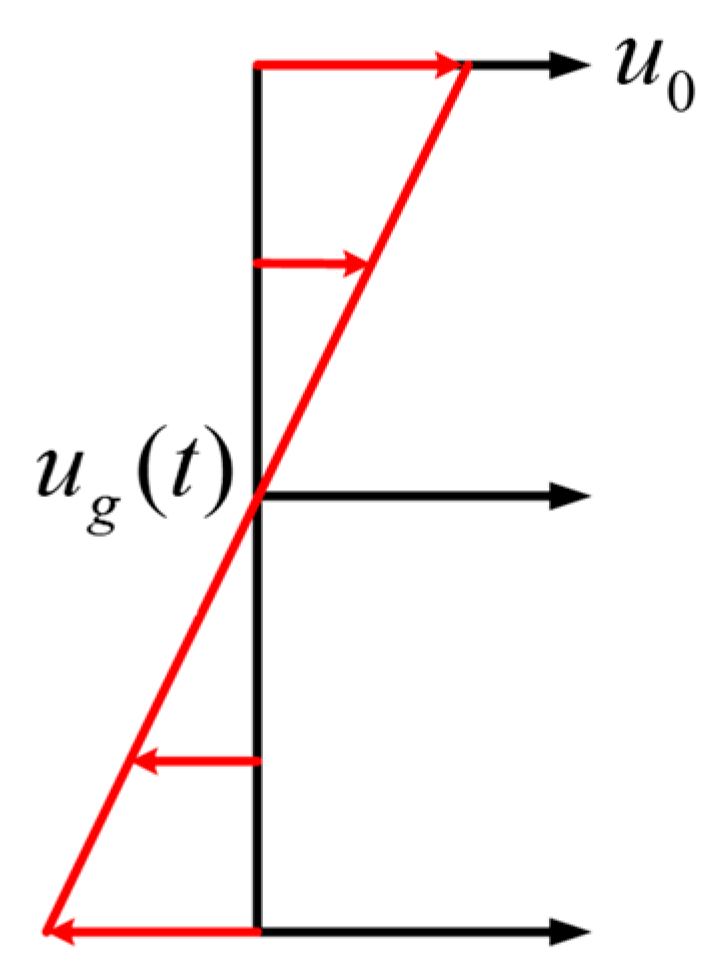
3.2. Gust Model and Simulation Condition
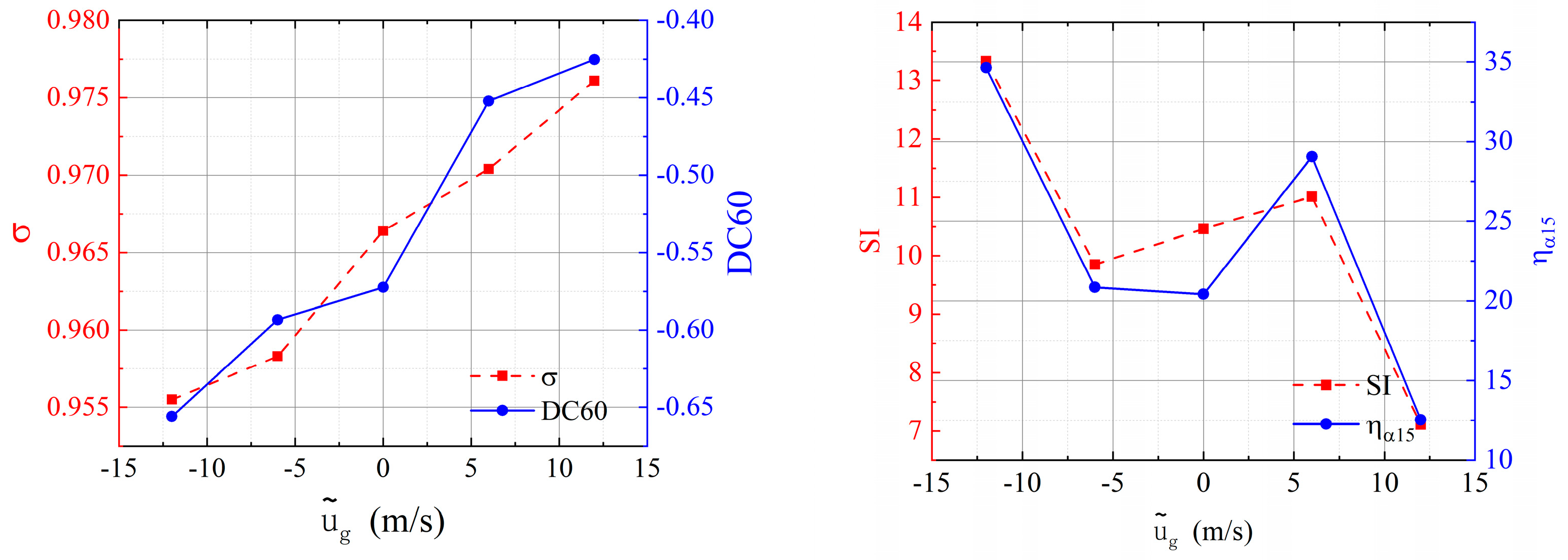
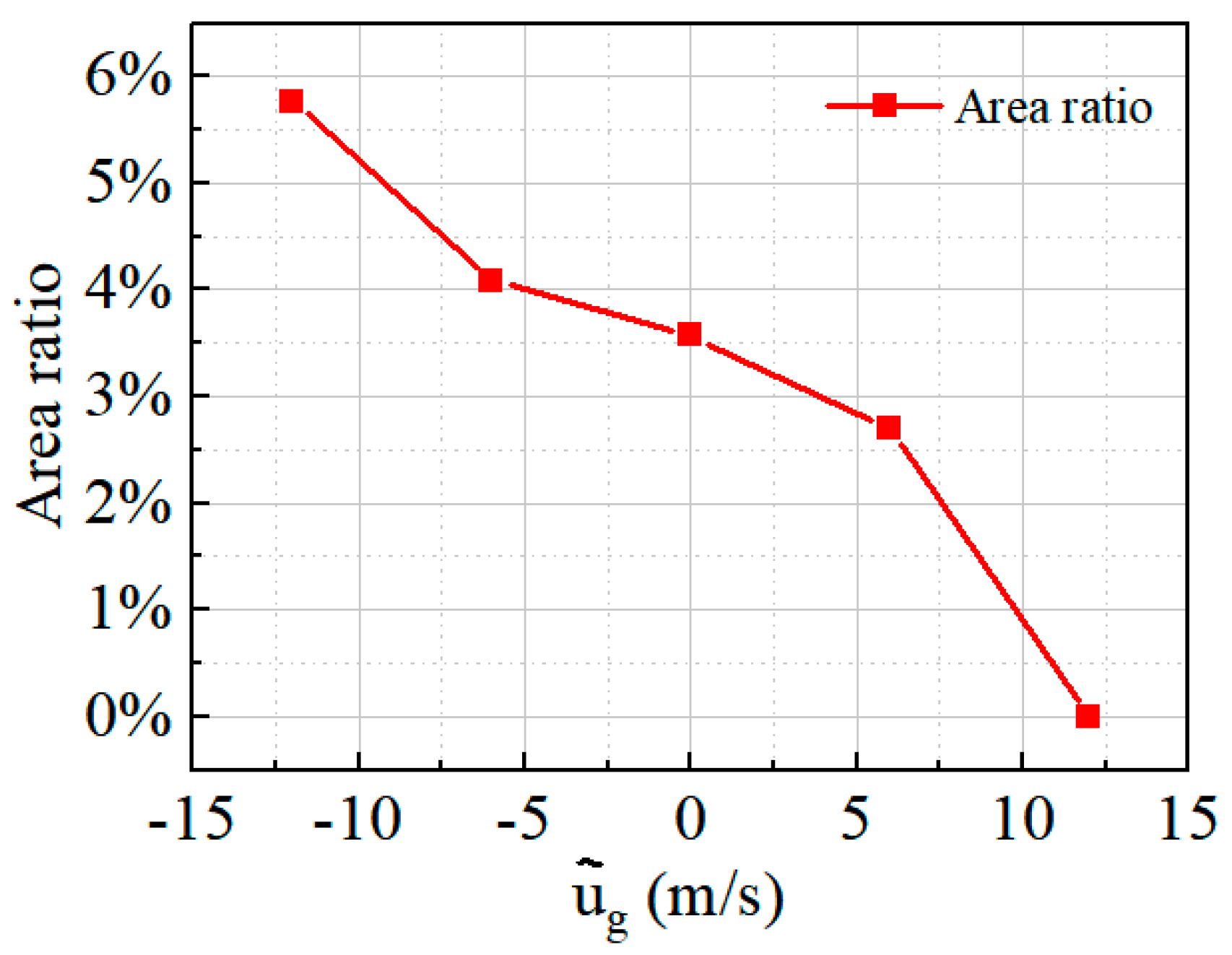
3.3. Effect of Head-On Gusts on the Time-Averaged Performance of the Inlet
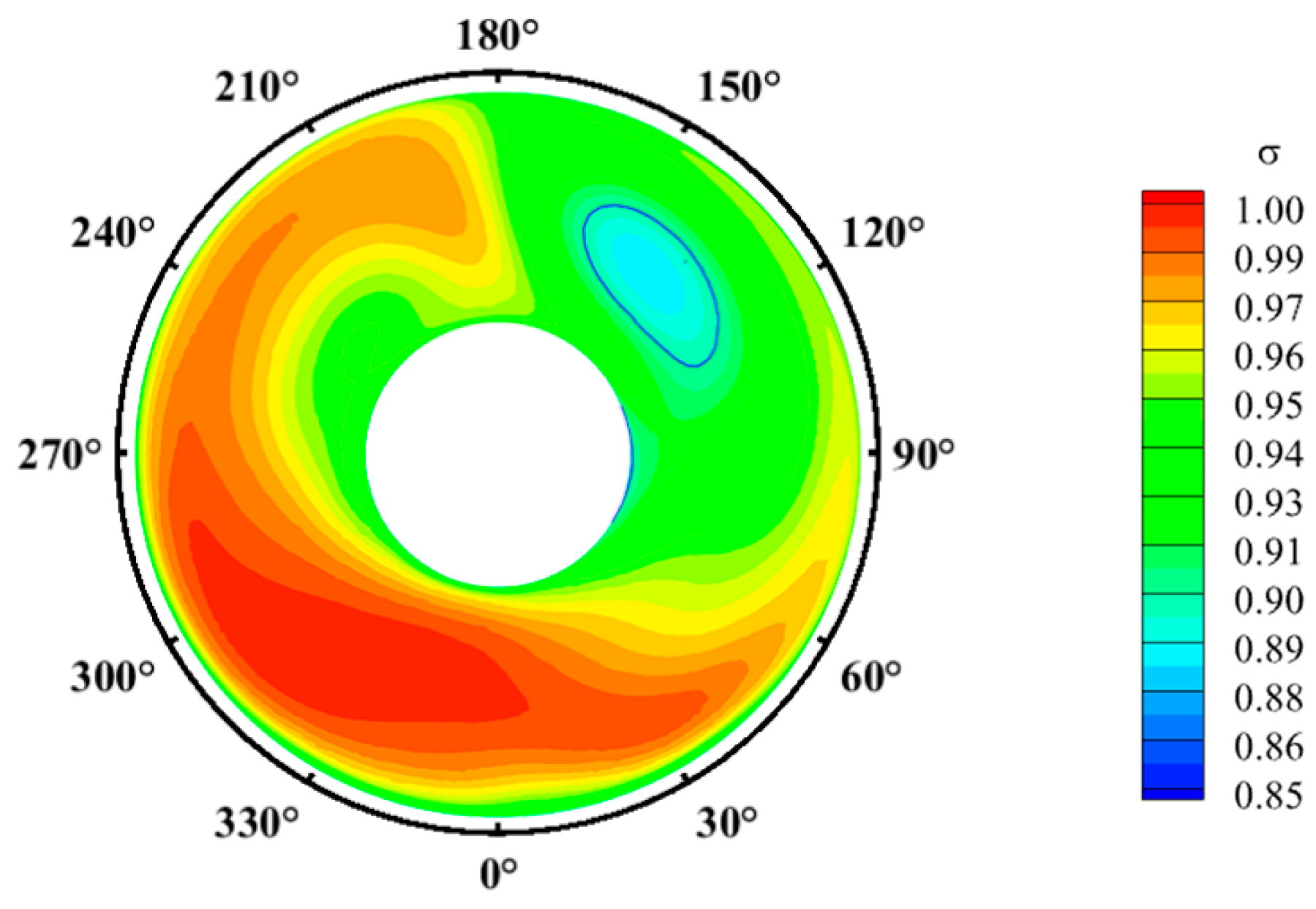
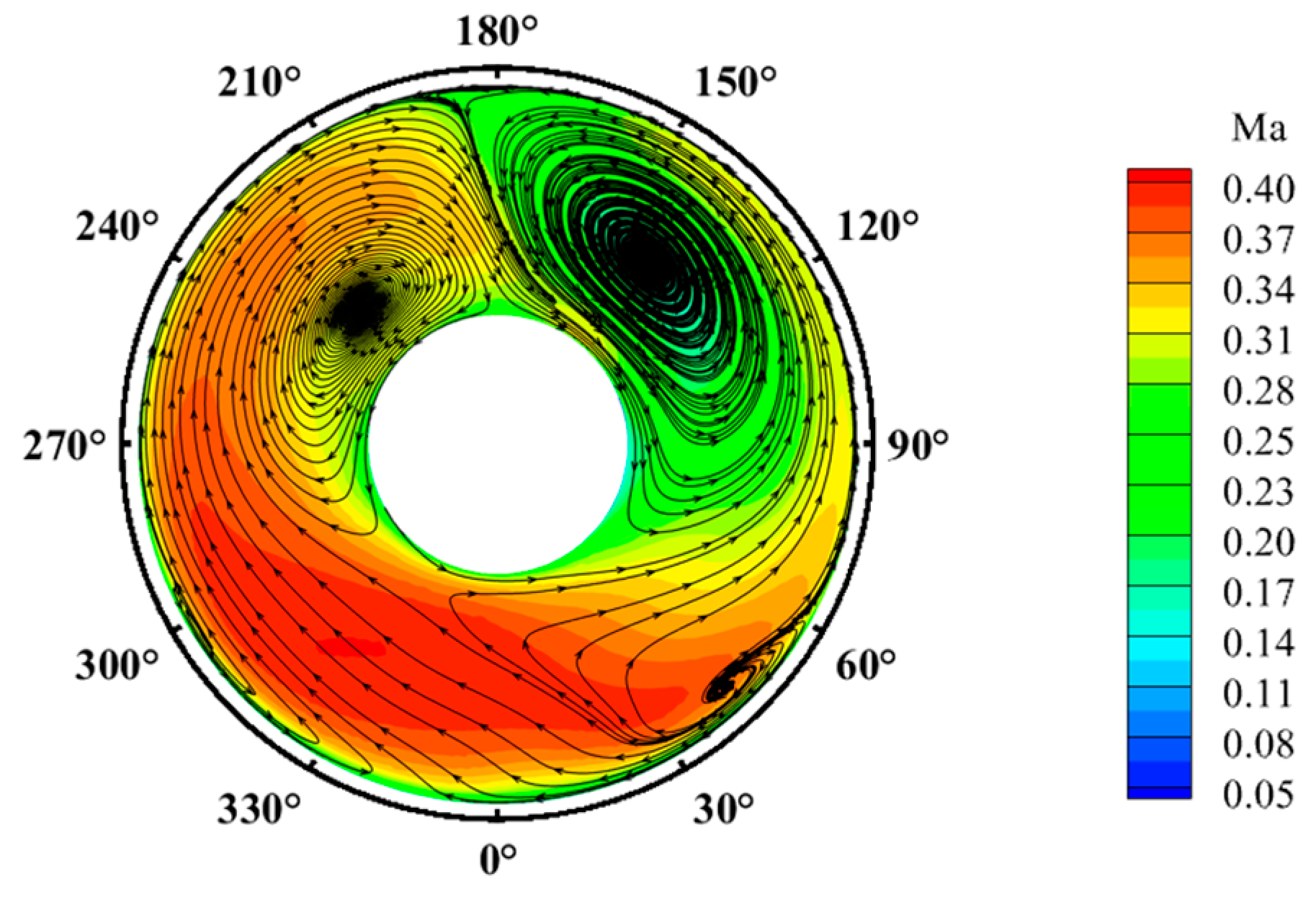
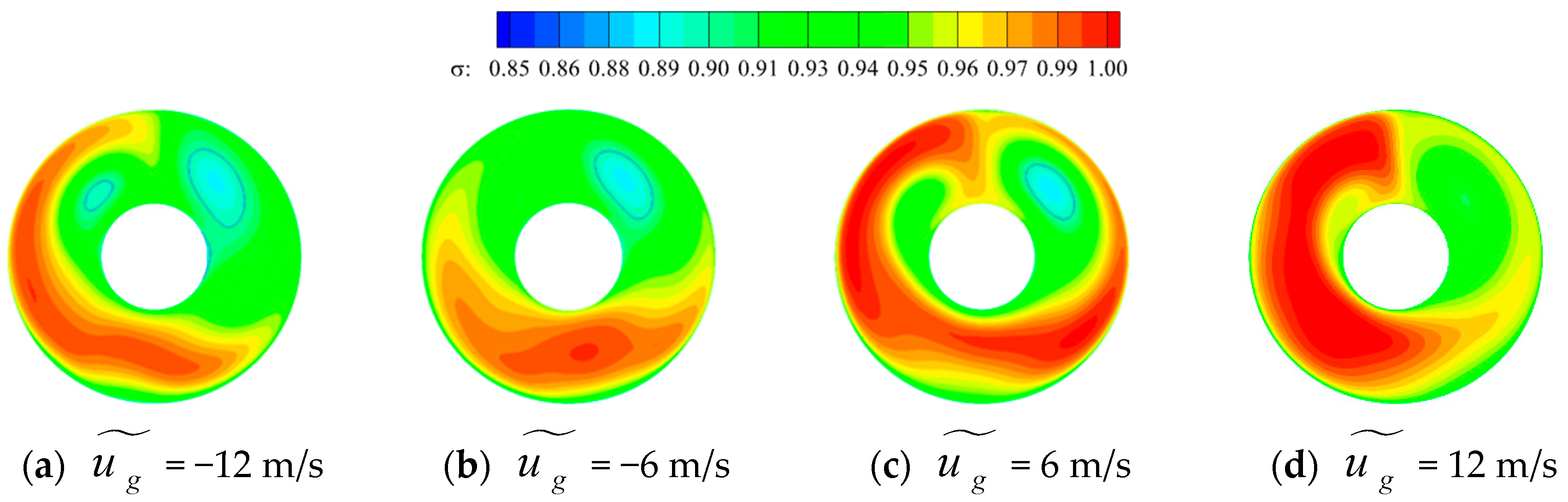
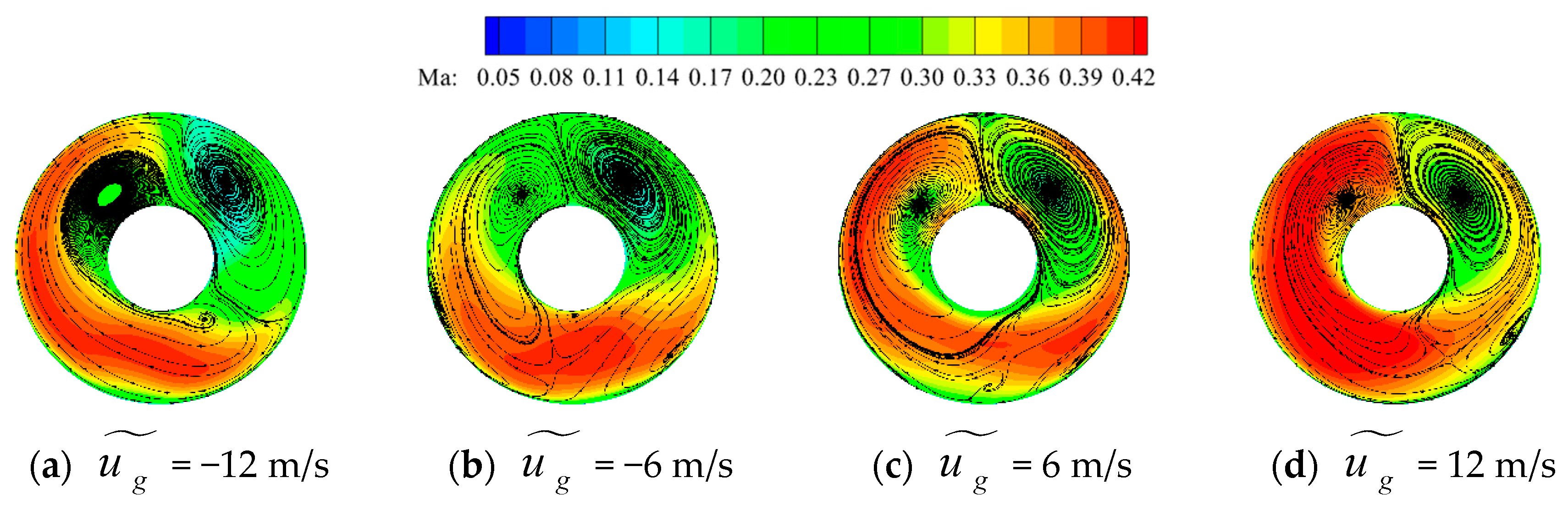
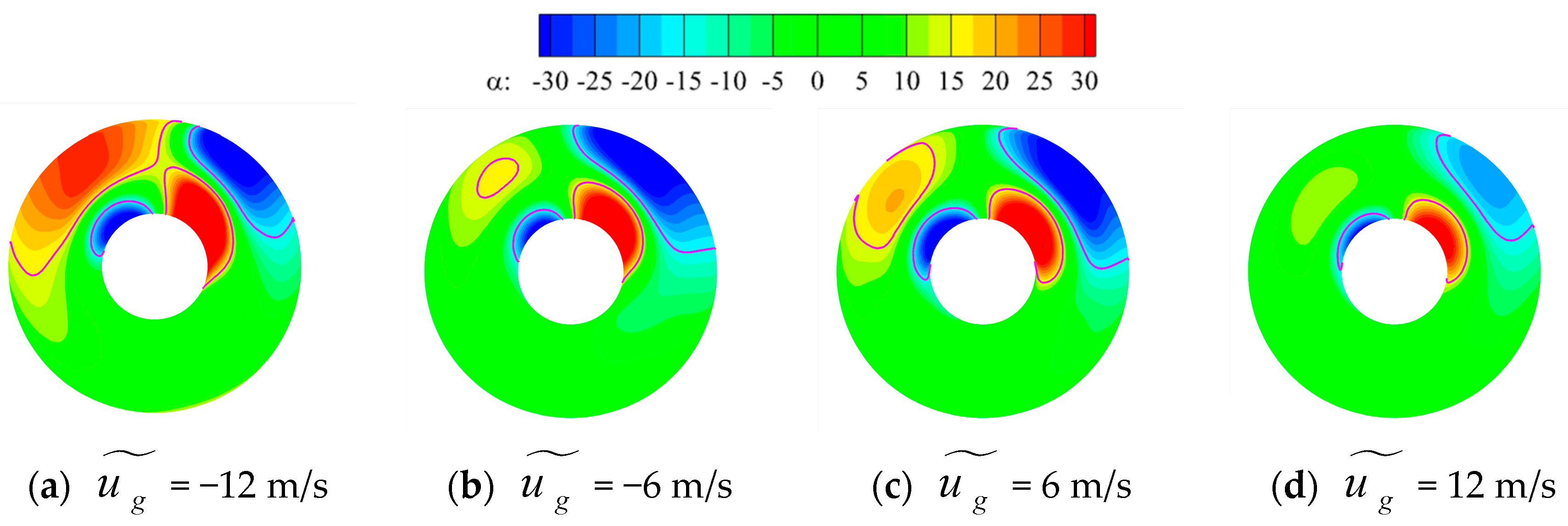
3.4. Effect of Head-On Gusts on the Time-Averaged Flow Field Characteristics of the Inlet
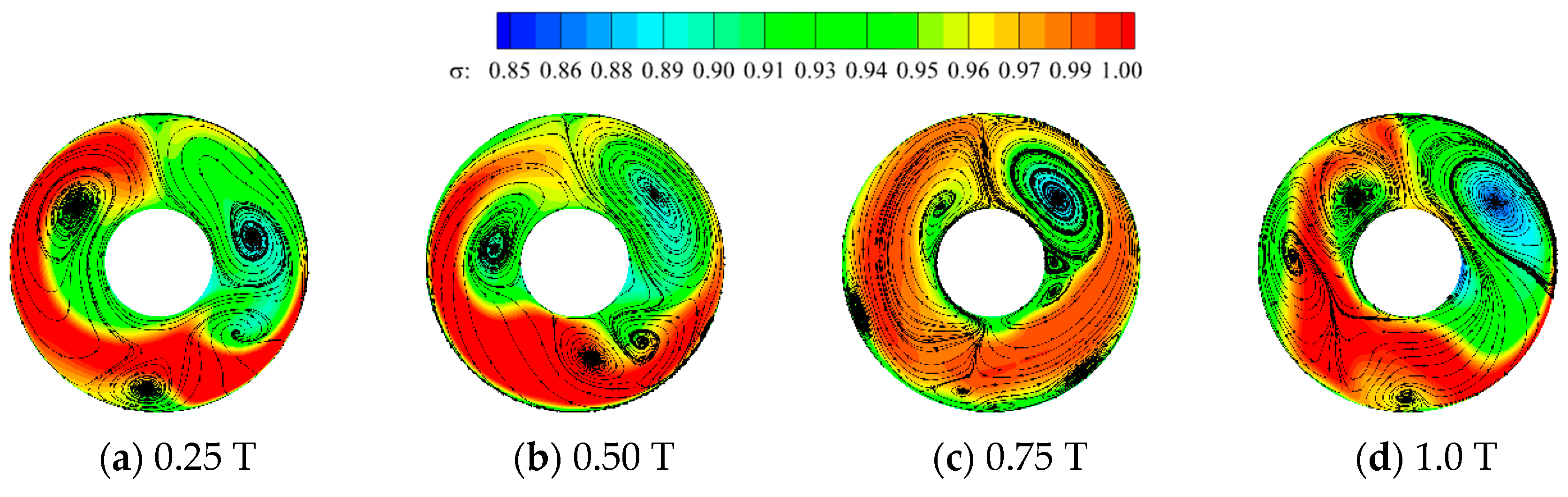
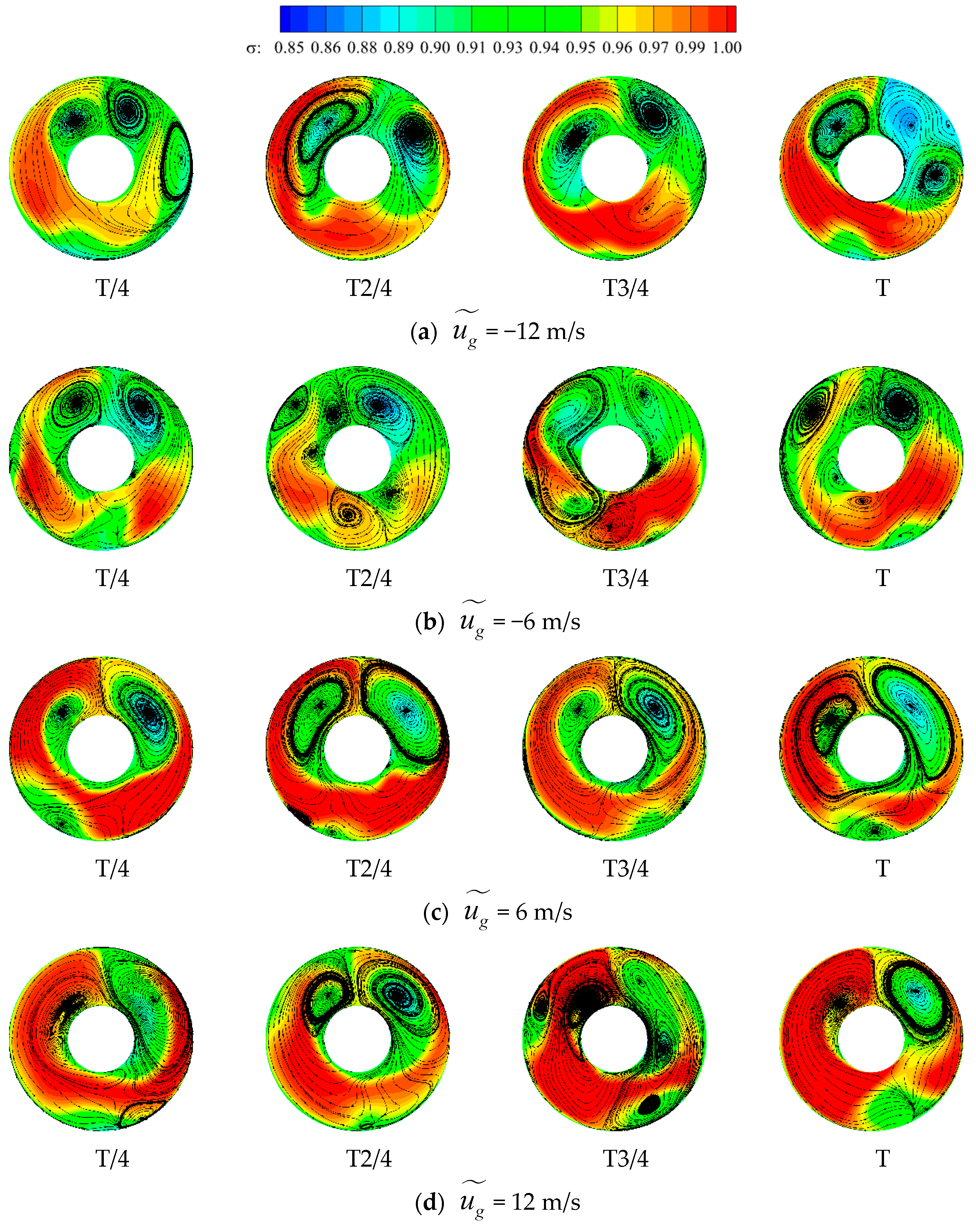
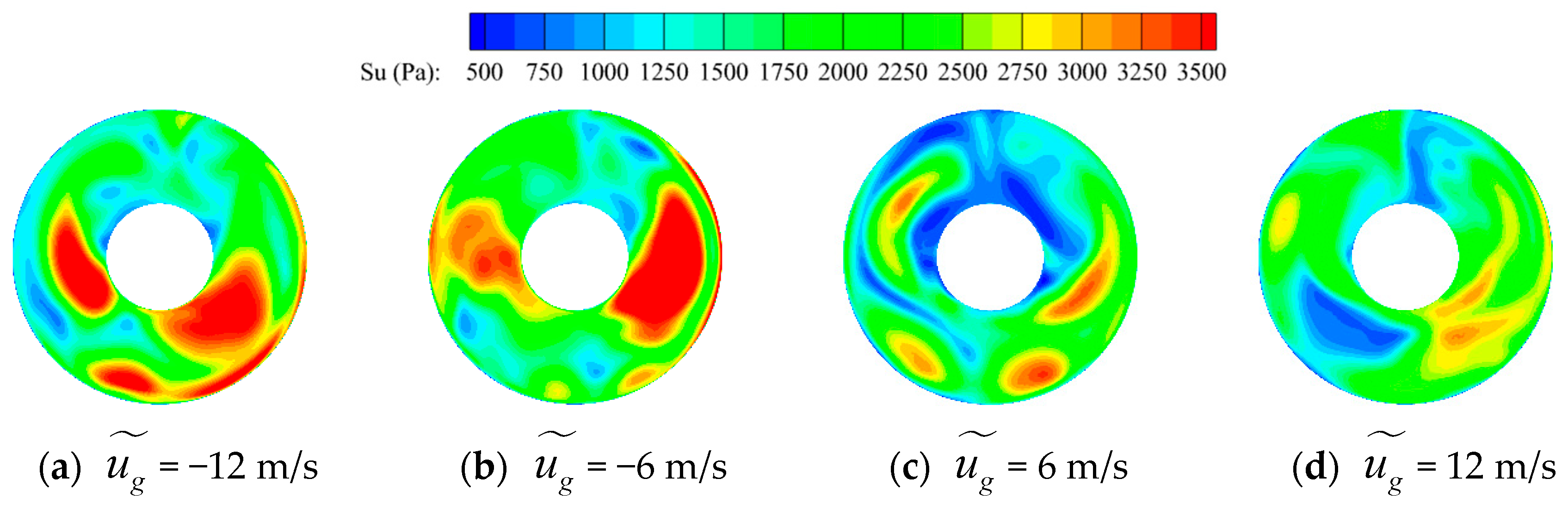
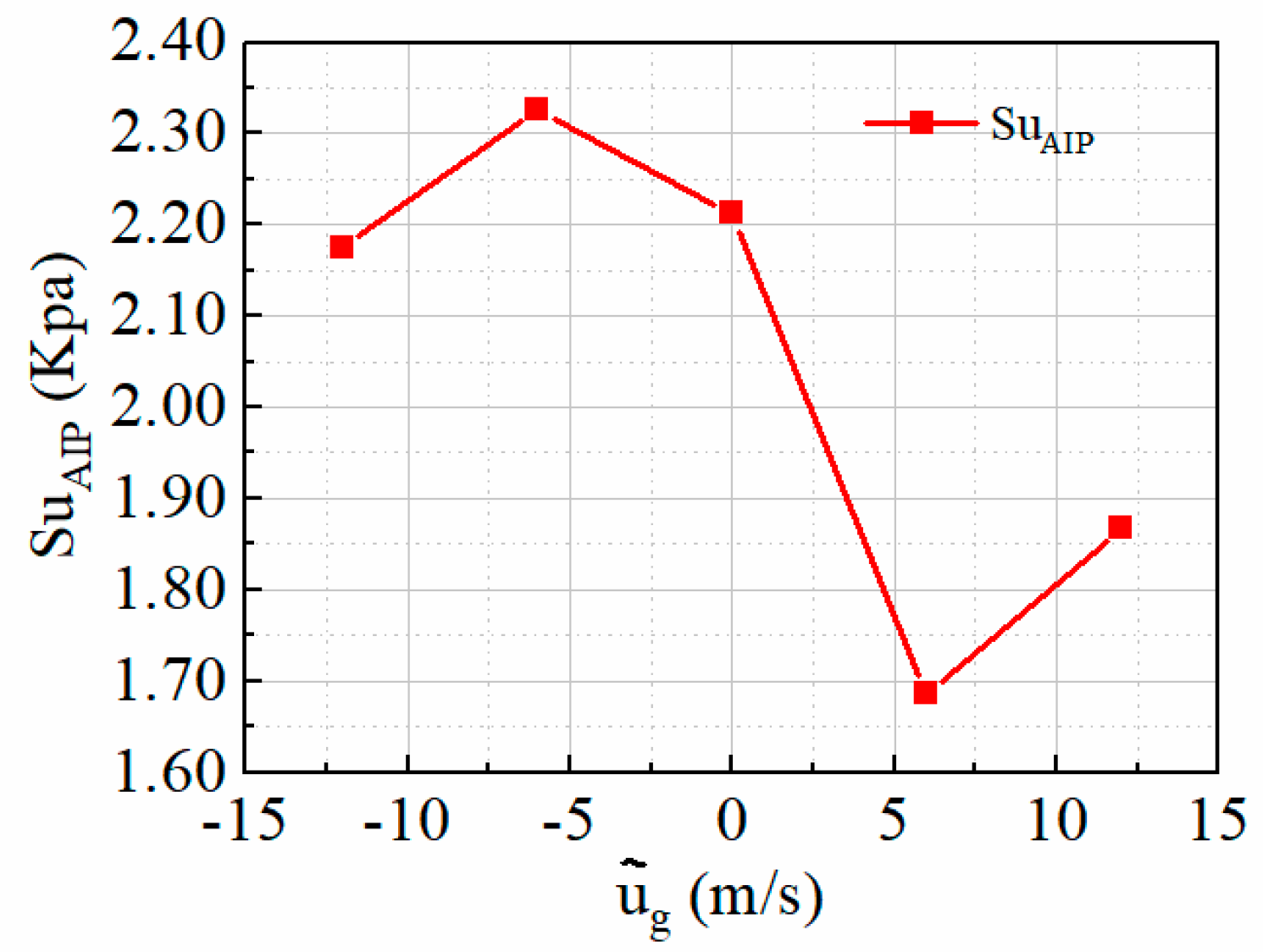
3.5. Effect of Head-On Gusts on the Unsteady Characteristics of the Flow Field within the Inlet
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| VTOL | vertical take-off and landing |
| AIP | aerodynamic interface plane |
| CFD | Computational Fluid Dynamics |
| total pressure of the freestream | |
| mass flow weighted average total pressure at the AIP | |
| total pressure recovery coefficient | |
| minimum value of the mass flow weighted average total pressure over any 60° sector around the center AIP | |
| mass flow weighted average dynamic pressure at the AIP | |
| circumferential distortion index | |
| swirl angle | |
| circumferential velocity at the measurement point on the AIP | |
| axial velocity at the measurement point on the AIP | |
| SI | swirl angle flux |
| proportion of the area where || exceeds 15° to the AIP | |
| Cp | pressure coefficient |
| RPM | revolutions per minute |
| instantaneous wind velocity | |
| mean wind velocity | |
| gust velocity | |
| maximum gust velocity | |
| Su | unsteady intensity |
| flux of unsteady intensity |
References
- Zanotti, A.; Savino, A.; Palazzi, M.; Tugnoli, M.; Muscarello, V. Assessment of a Mid-Fidelity Numerical Approach for the Investigation of Tiltrotor Aerodynamics. Appl. Sci. 2021, 11, 3385. [Google Scholar] [CrossRef]
- Wen, J.; Song, Y.; Wang, H.; Han, D.; Yang, C. Hybrid Adaptive Control for Tiltrotor Aircraft Flight Control Law Reconfiguration. Aerospace 2023, 10, 1001. [Google Scholar] [CrossRef]
- Garcia, A.J.; Barakos, G.N. Numerical Simulations on the ERICA Tiltrotor. Aerosp. Sci. Technol. 2017, 64, 171–191. [Google Scholar] [CrossRef]
- Hwa, V. Test and Evaluation of an Inlet Barrier Filter to Increase Engine Time-on-Wing for the Bell Boeing V-22 Osprey Tiltrotor; The University of Texas at Arlington: Arlington, TX, USA, 2015. [Google Scholar]
- Maisel, M.D.; Giulianetti, D.J.; Dugan, D.C. The History of the XV-15 Tilt Rotor Research Aircraft: From Concept to Flight, The NASA History; Series No. 17; National Aeronautics and Space Administration, Office of Policy and Plans, NASA History Division: Washington, DC, USA, 2000. [Google Scholar]
- Droandi, G.; Zanotti, A.; Gibertini, G.; Grassi, D.; Campanardi, G. Experimental Investigation of the Rotor-Wing Aerodynamic Interaction in a Tiltwing Aircraft in Hover. Aeronaut. J. 2015, 119, 591–612. [Google Scholar] [CrossRef]
- Wu, Z.L.; Li, C.; Cao, Y.H. Numerical Simulation of Rotor–Wing Transient Interaction for a Tiltrotor in the Transition Mode. Mathematics 2019, 7, 116. [Google Scholar] [CrossRef]
- Meakin, R. Unsteady Simulation of the Viscous Flow about a V-22 Rotor and Wing in Hover. In Proceedings of the 20th Atmospheric Flight Mechanics Conference, Baltimore, MD, USA, 7–15 August 1995; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1995. [Google Scholar]
- Bao, W.; Wang, W.; Chen, X.; Zhang, H.; Zhao, Q. Numerical Analyses of Aeroacoustic Characteristics of Tiltrotor Considering the Aerodynamic Interaction by the Fuselage in Hover. Aerosp. Sci. Technol. 2023, 141, 108558. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, Y.; Yang, S.; Zhu, X.; Dong, J. Numerical Simulation of Aerodynamic Interaction for a Tilt Rotor Aircraft in Helicopter Mode. Chin. J. Aeronaut. 2016, 29, 843–854. [Google Scholar] [CrossRef]
- Narducci, R.P.; Liu, J.; Wells, A.J.; Mobley, F.J.; Mayer, R.J. CFD Simulations of a Hovering Tiltrotor in Ground Effect. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Desopper, A.; Routhieau, V.; Roth, G. Study of the low speed characteristics of a tiltrotor. In Proceedings of the 28th European Rotorcraft Forum, Bristol, UK, 17–20 September 2002. [Google Scholar]
- Lakshminarayan, V.K.; Kalra, T.S.; Baeder, J.D. Detailed Computational Investigation of a Hovering Microscale Rotor in Ground Effect. AIAA J. 2013, 51, 893–909. [Google Scholar] [CrossRef]
- Houbolt, J.C. Atmospheric Turbulence. AIAA J. 1973, 11, 421–437. [Google Scholar] [CrossRef]
- Etkin, B. Turbulent Wind and Its Effect on Flight. J. Aircr. 1981, 18, 327–345. [Google Scholar] [CrossRef]
- Yang, C.; Qiu, Q.; Zhou, Y.; Wu, Z. Review of Aircraft Gust Alleviation Technology. Acta Aeronaut. Astronaut. Sin. 2022, 43, 527350. (In Chinese) [Google Scholar]
- Hunsaker, J.C.; Wilson, E.B. Report on Behavior of Aeroplanes in Gusts; NACA-TR-1: Washington, DC, USA, 1917. [Google Scholar]
- Wu, Z.; Cao, Y.; Ismail, M. Gust Loads on Aircraft. Aeronaut. J. 2019, 123, 1216–1274. [Google Scholar] [CrossRef]
- Seddon, J.; Goldsmith, E.L. Intake Aerodynamics: An Account of the Mechanics of Flow in and around the Air Intake of Turbine-Engined and Ramjet Aircraft and Missiles; Collins Professional and Technical: London, UK, 1985. [Google Scholar]
- Paynter, G.; Koncsek, J.; Turczeniuk, B.; Dvorak, F.A. Extension of CFD Technology Used to Design the JVX Inlet. In Proceedings of the 21st Joint Propulsion Conference, Monterey, CA, USA, 8–10 July 1985.
- Garavello, A.; Benini, E.; Ponza, R.; Scandroglio, A.; Saporiti, A. Aerodynamic Optimization of the ERICA Tilt-Rotor Intake and Exhaust System. In Proceedings of the 37th European Rotorcraft Forum, Ticino Park, Italy, 13–15 September 2011. [Google Scholar]
- Gibertini, G.; Auteri, F.; Colaiuda, L.; Ermacora, M.; Grassi, D.; Zanotti, A. Optimized ERICA Engine Intake Wind Tunnel Test. In Proceedings of the 41st European Rotorcraft Forum, Munich, Germany, 1–4 September 2015. [Google Scholar]
- Gibertini, G.; Zanotti, A.; Campanardi, G.; Auteri, F.; Zagaglia, D.; Crosta, G. Wind-tunnel tests of the ERICA tiltrotor optimised air-intake. Aeronaut. J. 2018, 122, 821–837. [Google Scholar] [CrossRef]
- Soemarwoto, B.; Habing, R.; Pecoraro, M. Adaptive Design Method for a Tilt-Rotor Engine Inlet Duct Optimization. In Proceedings of the AIAA AVIATION 2022 Forum, Virtual, 27 June 2022; American Institute of Aeronautics and Astronautics: Chicago, IL, USA. [Google Scholar]
- Sun, S.; Wu, Z.; Huang, H.; Bangga, G.; Tan, H. Aerodynamic Response of a Serpentine Inlet to Horizontal Periodic Gusts. Aerospace 2022, 9, 824. [Google Scholar] [CrossRef]
- Felker, F.F.; Betzina, M.D.; Signor, D.B. Performance and Loads Data from a Hover Test of a Full-Scale XV-15 Rotor; Technical Report; NASA Ames Research Center: Moffett Field, CA, USA, 1985. [Google Scholar]
- Turbine Engine Inlet Flow Distortion Committee. A Methodology for Assessing Inlet Swirl Distortion; Report No. AIR5686; Society of Automotive Engineers: Warrendale, PA, USA, 2007. [Google Scholar]
- Zheng, G.J.; He, X.M.; Li, D.P.; Tan, H.J.; Wang, K.; Wu, Z.L.; Wang, D.P. Double 90-Degree Deflection Inlet/Volute Coupling Flow Characteristics of Tail Powered UAV. Acta Aeronaut. Astronaut. Sin. 2023, 44, 128782. (In Chinese) [Google Scholar]
- Xu, Z.L.; Da, X.Y.; Fang, Z.L. Assessment of Swirl Distortion of Serpentine Inlet Based on Five-Hole Probe. Acta Aeronaut. Astronaut. Sin. 2017, 37, 121342. (In Chinese) [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Huang, H.X.; Tan, H.J.; Lin, Z.K.; Li, Z.J.; Sun, S.; Chen, H.; Xiao, Z.X. Flowfield of a Helicopter Submerged Inlet with Power Output Shaft. Acta Mech. Sin. 2021, 37, 156–168. [Google Scholar] [CrossRef]
- Cheng, D.S.; Tan, H.J.; Sun, S.; Tong, Y. Computational Study of a High-Performance Submerged Inlet with Bleeding Vortex. J. Aircr. 2012, 49, 852–860. [Google Scholar] [CrossRef]
- Zheng, G.J.; Wu, Z.L.; Tan, H.J.; Zhang, Y.; Wang, K. Design and Examination of a Turboprop Inlet with Scavenge Duct. Chin. J. Aeronaut. 2023, 36, 32–42. [Google Scholar] [CrossRef]
- Caradonna, F.X.; Tung, C.; Caradonna, F.X.; Tung, C. Experimental and Analytical Studies of a Model Helicopter Rotor in Hover. In Proceedings of the European Rotorcraft and Powered Lift Aircraft Forum, Bristol, UK, 16 September 1981. [Google Scholar]
- Doerffer, P.; Szulc, O.; Doerffer, P.; Szulc, O. Numerical Simulation of Model Helicopter Rotor in Hover. Sci. Bull. Acad. Comput. Cent. Gdan. 2008, 12, 227–236. [Google Scholar]
- Steven, R.W.; Theodore, H.O. A Study of the Compressible Flow through a Diffusing S-Duct; NASA Technical Memorandum: Washington, DC, USA, 1993; p. 106411. [Google Scholar]
- Cummings, R.M.; Forsythe, J.R.; Morton, S.A.; Squires, K.D. Computational Challenges in High Angle of Attack Flow Prediction. Prog. Aerosp. Sci. 2003, 39, 369–384. [Google Scholar] [CrossRef]
- Gao, L.; Xi, G.; Zhou, L. Experimental and Computational Investigation of Flows in a Vaned Diffuser Under Stage Environment. Acta Mech. Sin. 2005, 37, 110–119. (In Chinese) [Google Scholar]
- Civil Aeronautics Manual 0434: Airplane Airworthiness; United States Civil Aeronautics Administration: Washington, DC, USA, 1941.





| Parameter | Value |
|---|---|
| Blades | 3 |
| Diameter (m) | 7.62 |
| Chord (constant) (m) | 0.3556 |
| Twist (spinner to tip) (°) | 36° |
| Parameter | Value |
|---|---|
| Inner diameter | 0.36 D |
| Outer diameter | D (0.29 m) |
| L | 2.72 D |
| Parameter | Value |
|---|---|
| Blades | 2 |
| Radius (m) | 1.143 |
| Chord (constant) (m) | 0.05 |
| Aspect ratio | 6 |
| Twist (°) | 0 |
| Parameter | Value |
|---|---|
| Ambient pressure (Pa) | 101,325 |
| Pressure exit—engine duct (pa) | 90,000 |
| Pressure exit—scavenge duct (pa) | 94,500 |
| Ambient temperature (T) | 288.15 |
| Time step size(s) | 2.83 × 10−4 |
| Rotary velocity (rpm) | 589 |
| Gust velocity (m/s) | −12, −6, 0, 6, 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; He, X.; Zhang, Y.; Cheng, D.; Wang, Z.; Huang, Y.; Tan, H. Investigation of the Internal Flow Characteristics of a Tiltrotor Aircraft Engine Inlet in a Gust Environment. Aerospace 2024, 11, 342. https://doi.org/10.3390/aerospace11050342
Zhu H, He X, Zhang Y, Cheng D, Wang Z, Huang Y, Tan H. Investigation of the Internal Flow Characteristics of a Tiltrotor Aircraft Engine Inlet in a Gust Environment. Aerospace. 2024; 11(5):342. https://doi.org/10.3390/aerospace11050342
Chicago/Turabian StyleZhu, Haicheng, Xiaoming He, Yue Zhang, Daishu Cheng, Ziyun Wang, Yufeng Huang, and Huijun Tan. 2024. "Investigation of the Internal Flow Characteristics of a Tiltrotor Aircraft Engine Inlet in a Gust Environment" Aerospace 11, no. 5: 342. https://doi.org/10.3390/aerospace11050342
APA StyleZhu, H., He, X., Zhang, Y., Cheng, D., Wang, Z., Huang, Y., & Tan, H. (2024). Investigation of the Internal Flow Characteristics of a Tiltrotor Aircraft Engine Inlet in a Gust Environment. Aerospace, 11(5), 342. https://doi.org/10.3390/aerospace11050342