Semianalytical Research on Aerothermoelastic Behaviors of Functionally Graded Plates under Arbitrary Temperature Fields in Hypersonic Vehicles
Abstract
1. Introduction
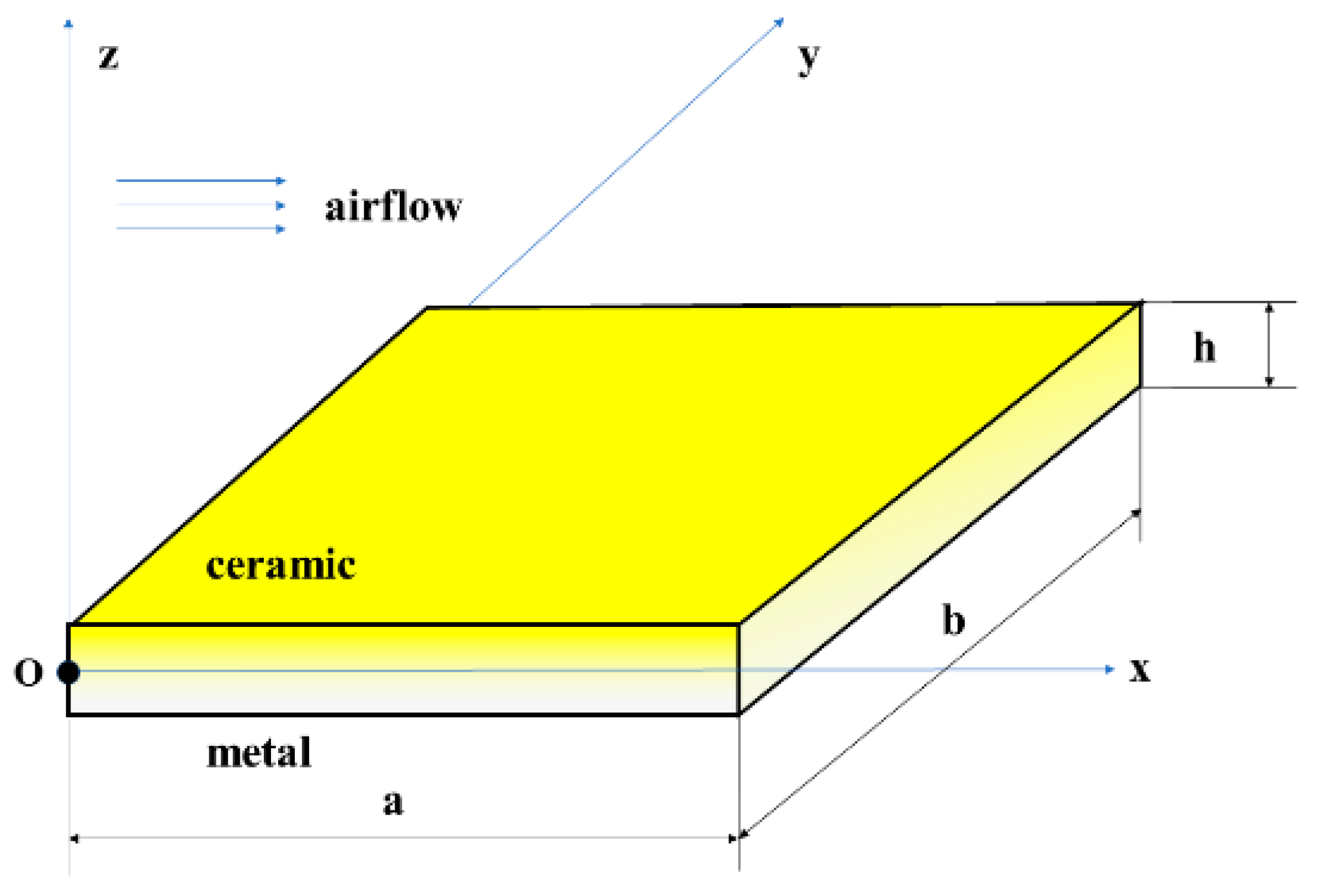
2. Methods
2.1. FGM Properties
2.2. Constitutive Relations
2.3. Thermal Effects on FGM
- (1)
- Thermal stresses related to temperature changes lower the overall structural stiffness.
- (2)
- Material properties are subject to changes in response to temperature, often resulting in a decrease in overall material performance.
2.4. Aerodynamic Modeling
2.5. Nonlinear Characterization
2.6. Static Aerothermoelastic Analysis
2.7. Linear Analysis of the Thermal Panel Flutter
2.8. Nonlinear Analysis for the Thermal Panel Flutter
3. Numerical Results of Static Aerothermoelasticity
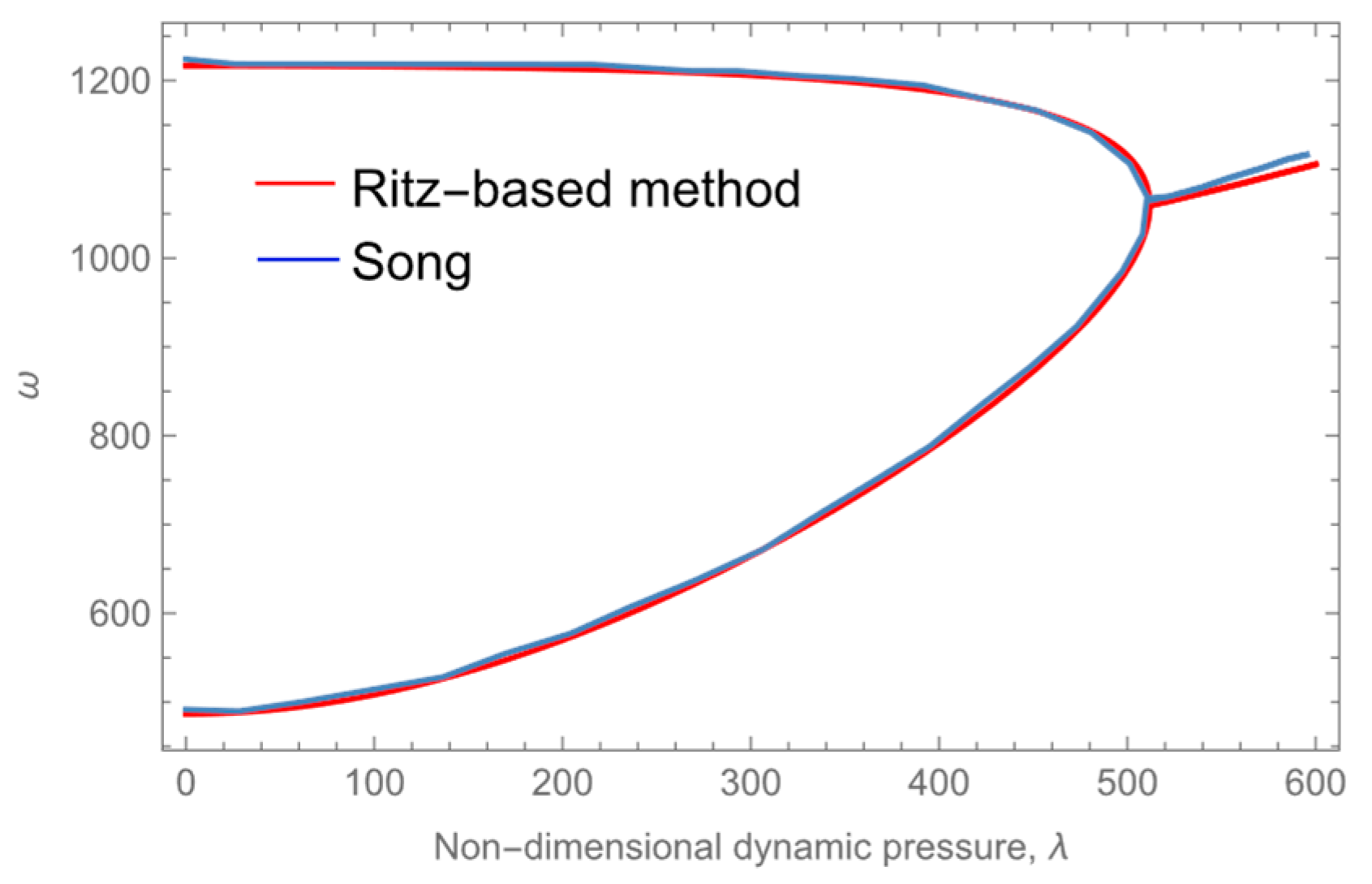
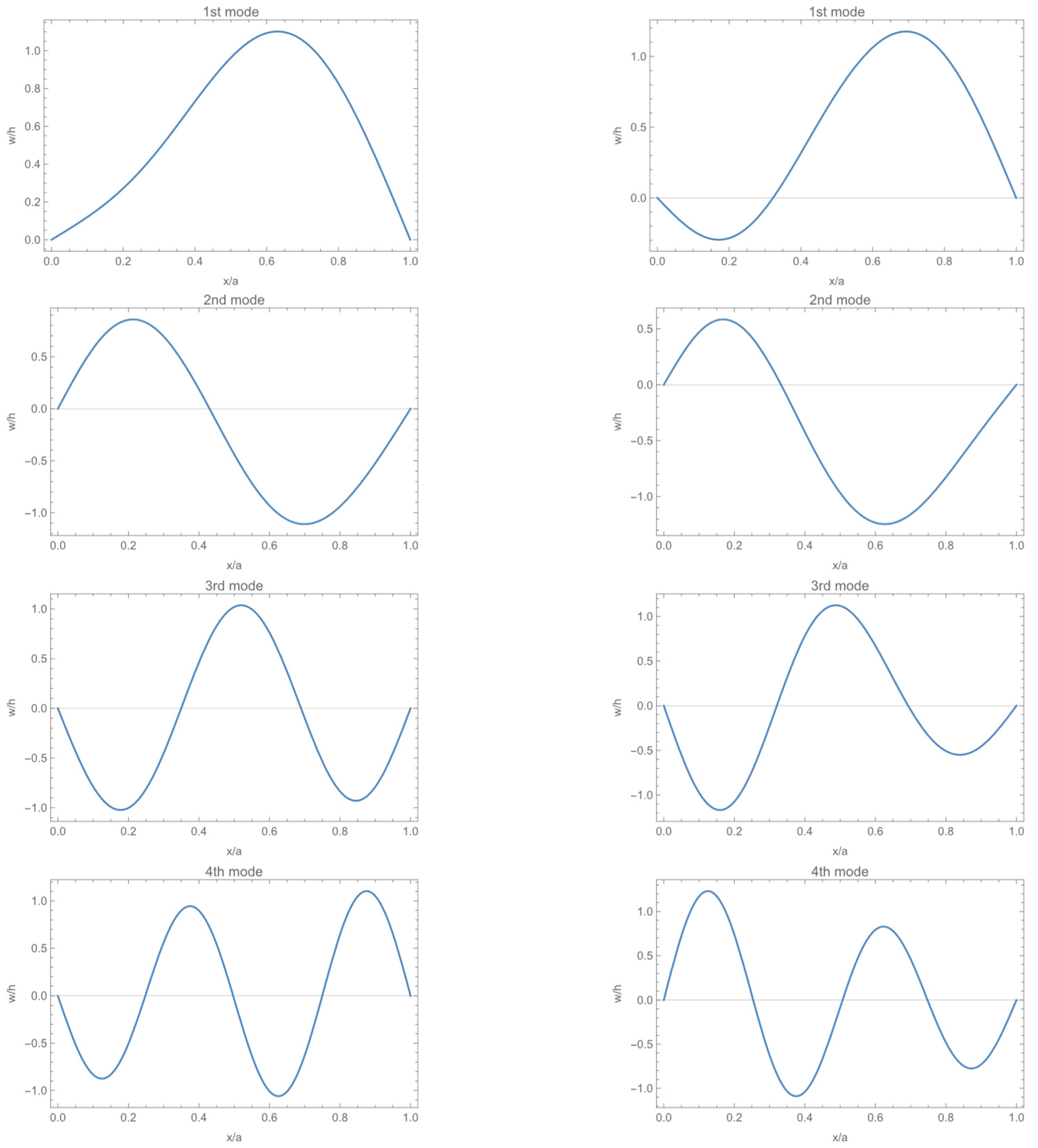
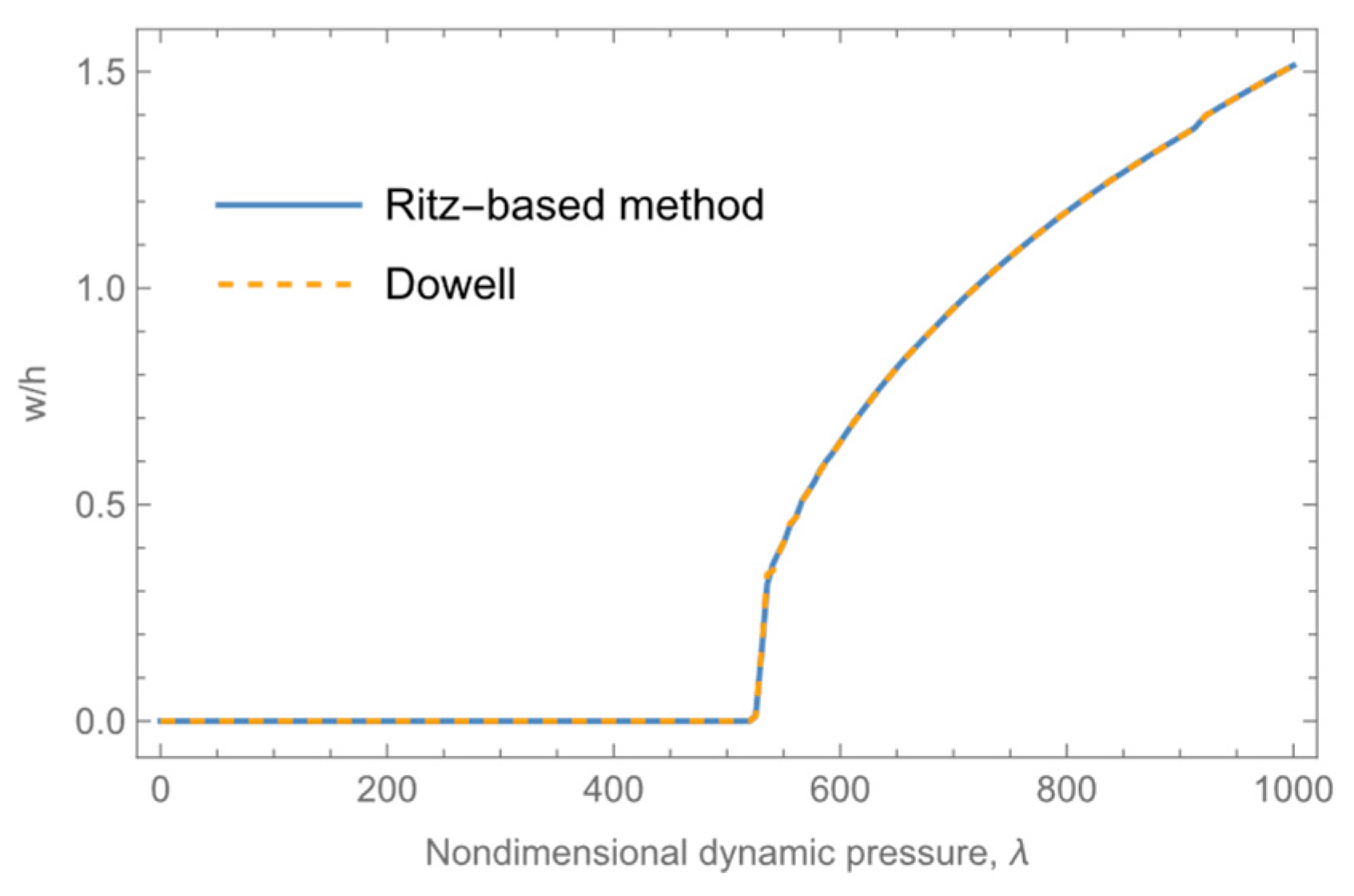
3.1. Validation
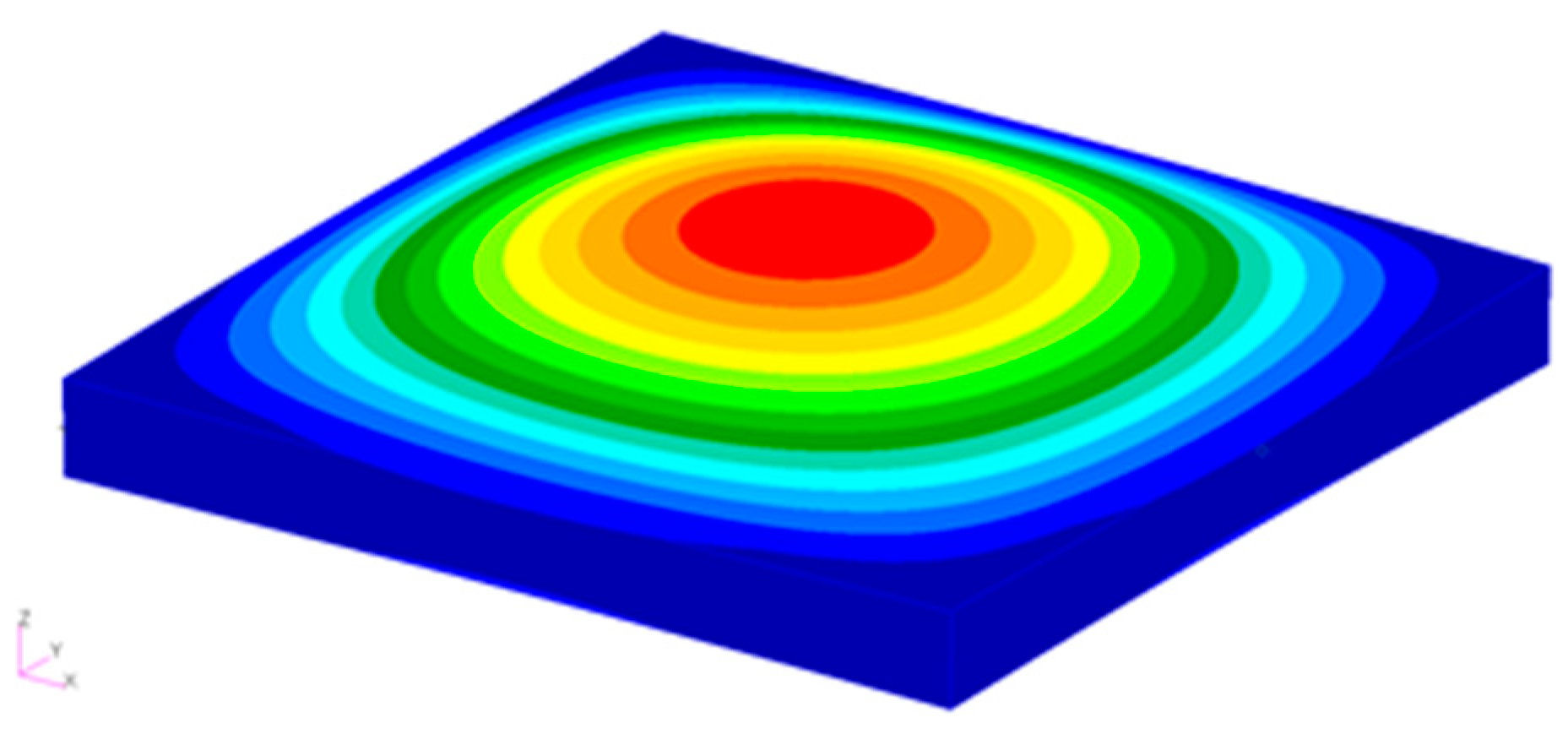
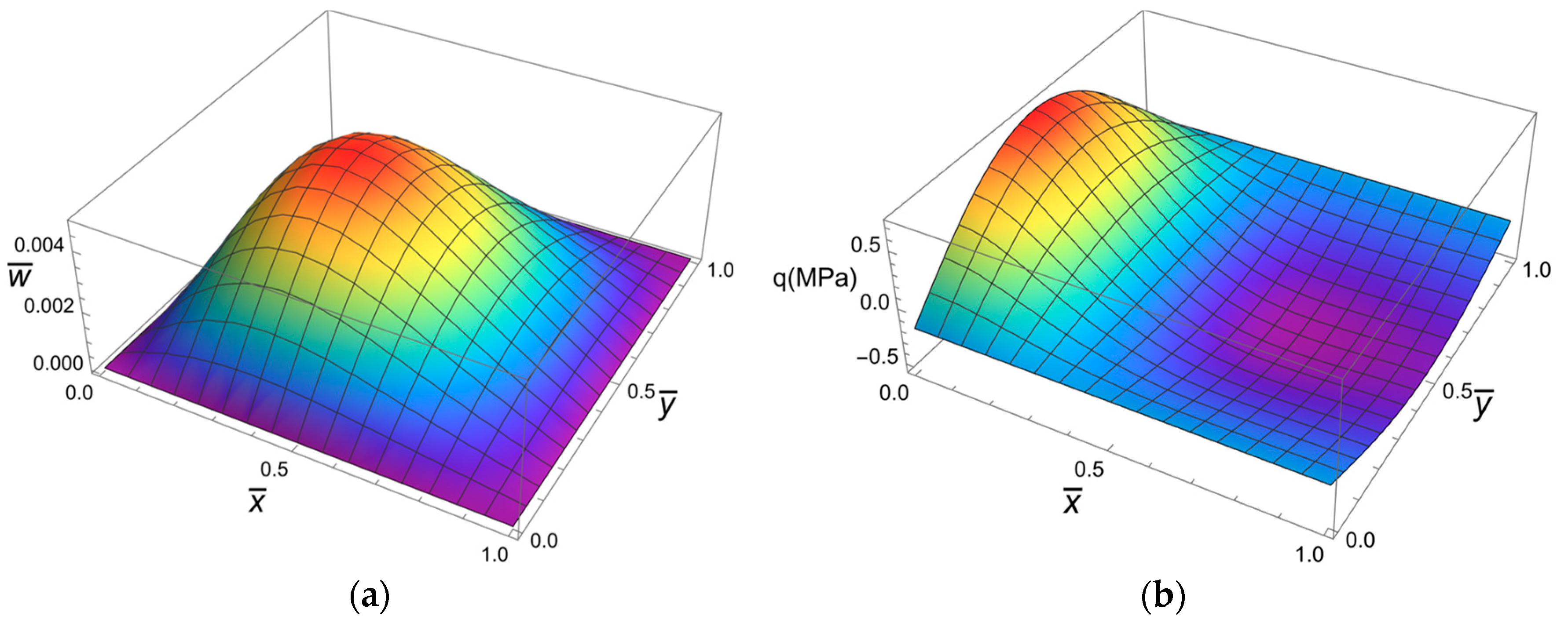
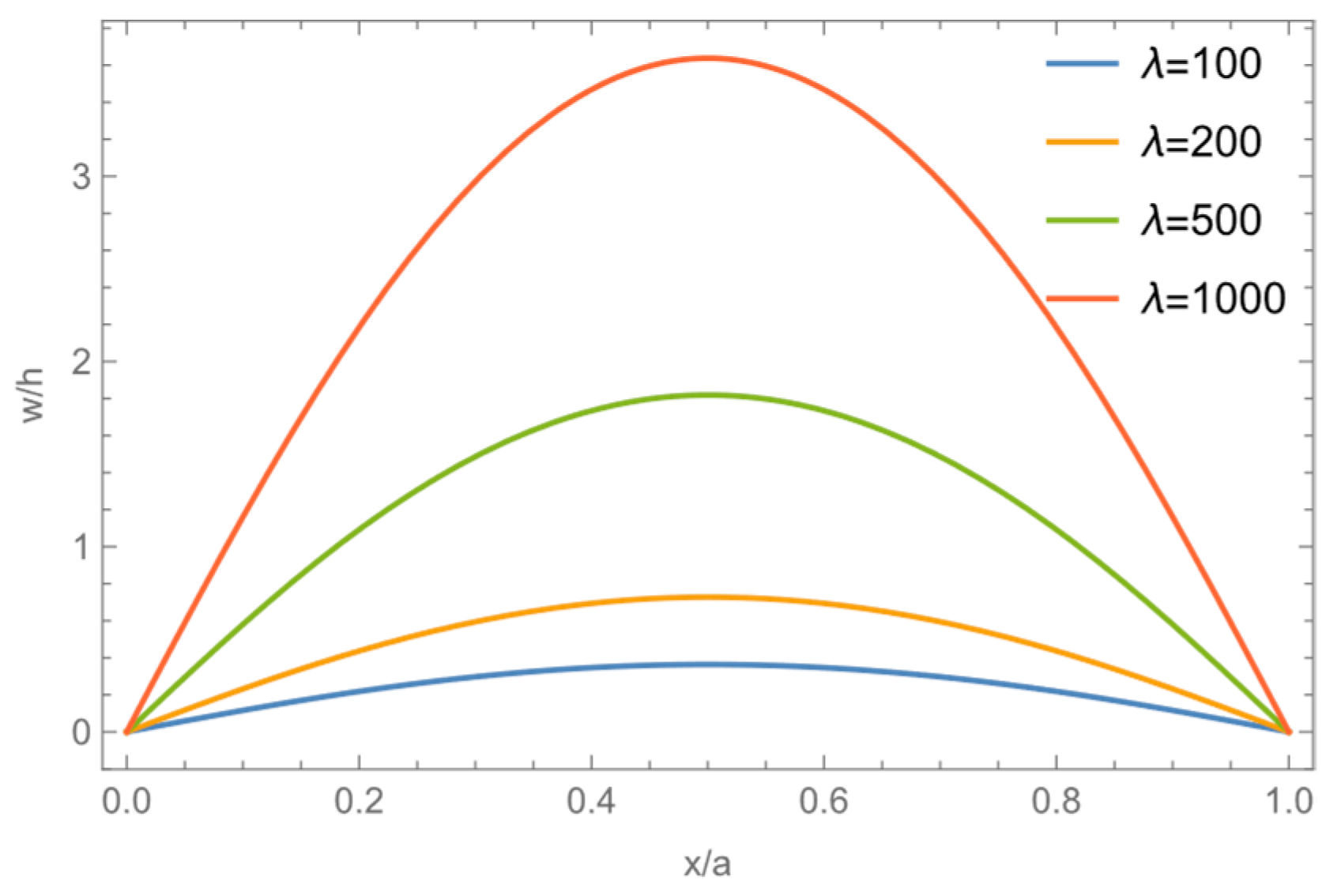
3.2. Static Aerothermoelastic Analysis
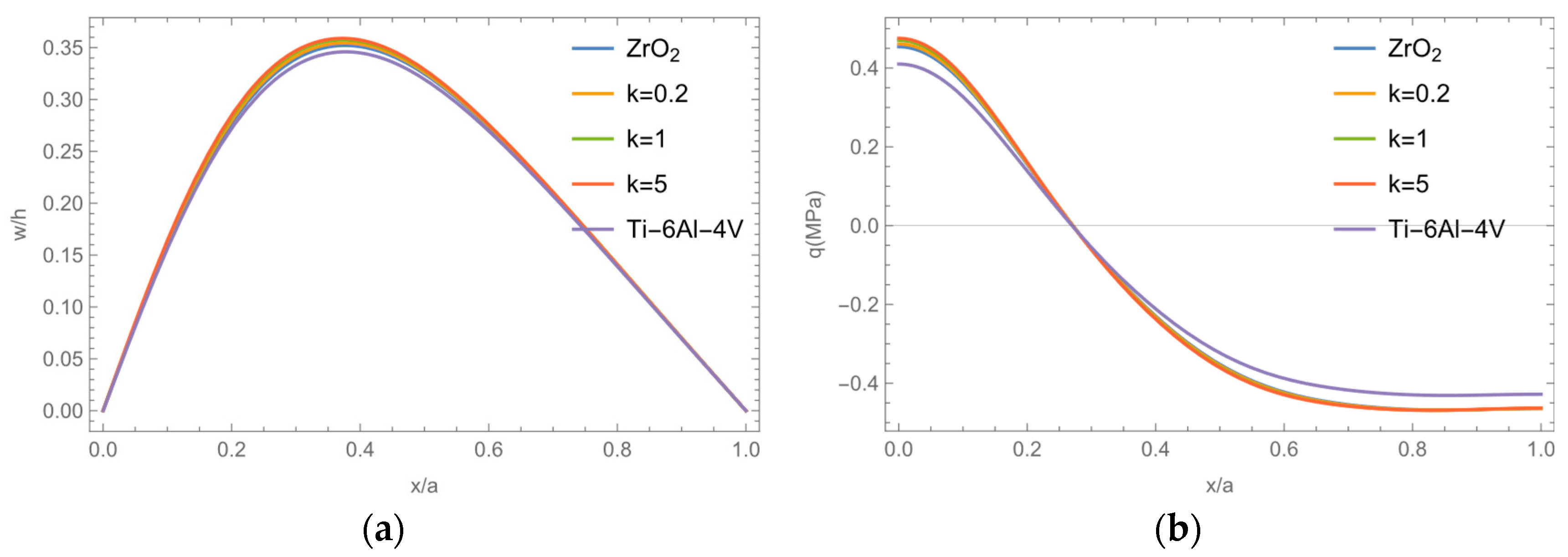
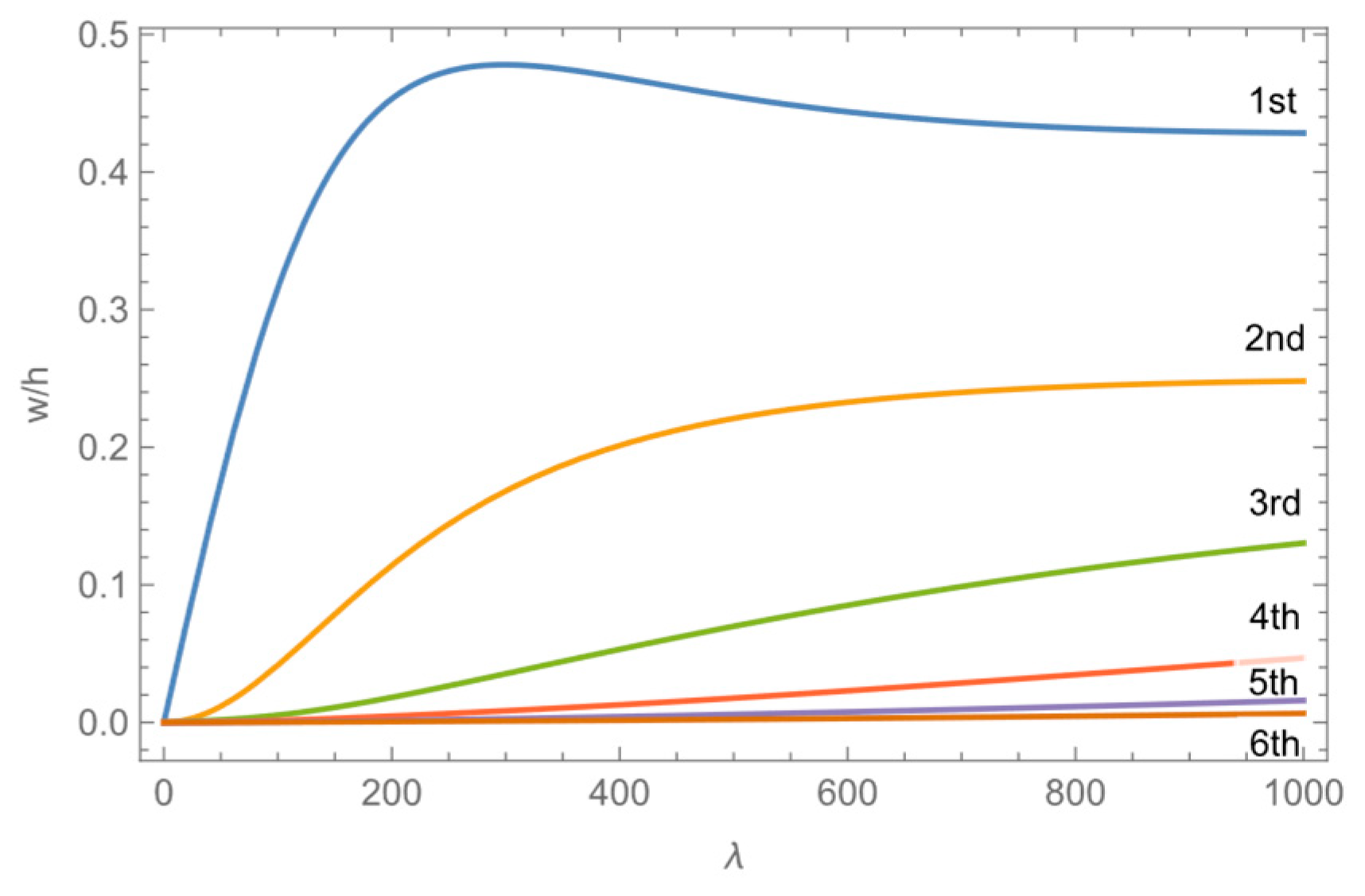
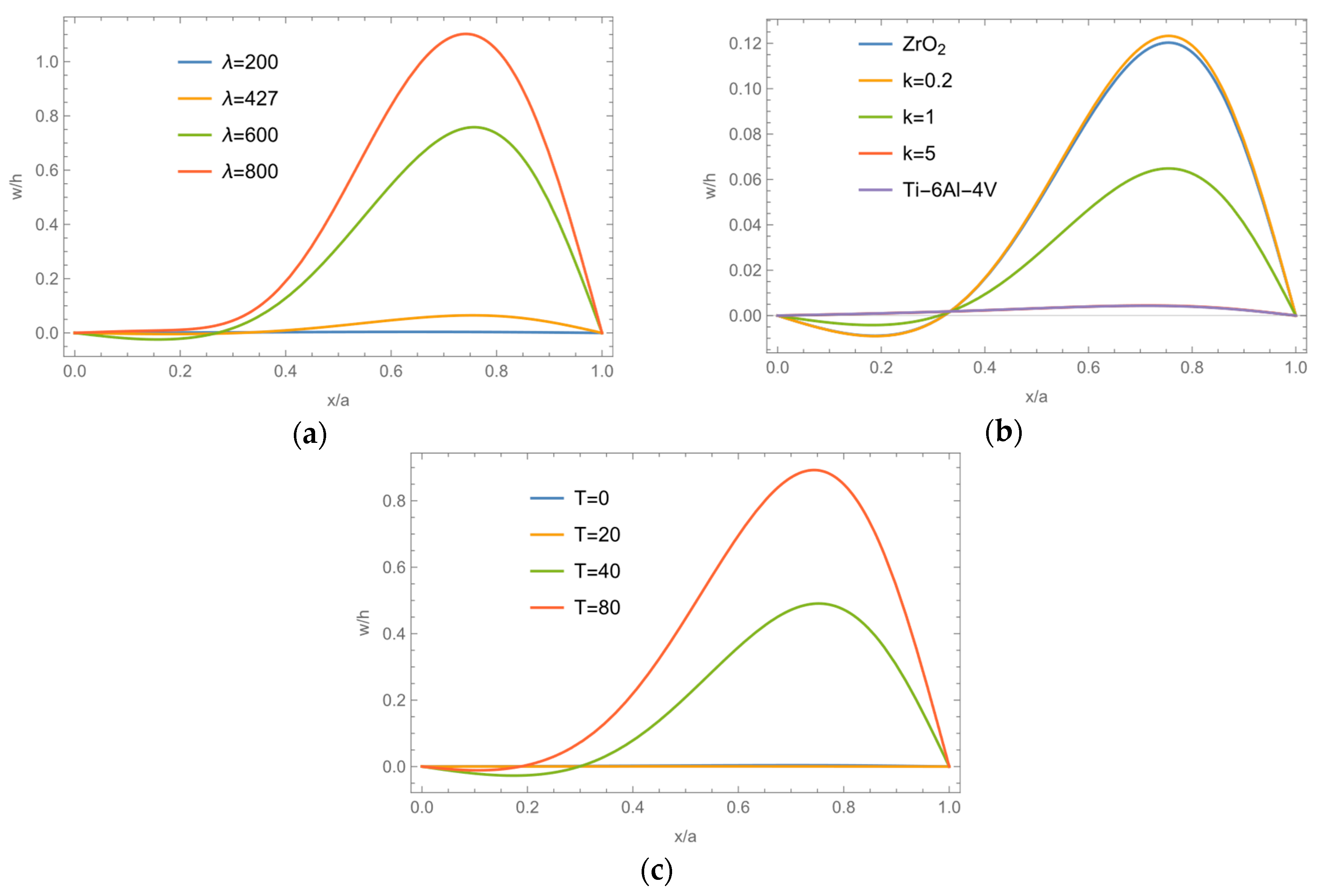
3.3. Research on Aeroelastic Effects
4. Numerical Results of Panel Flutter in Thermal Environments
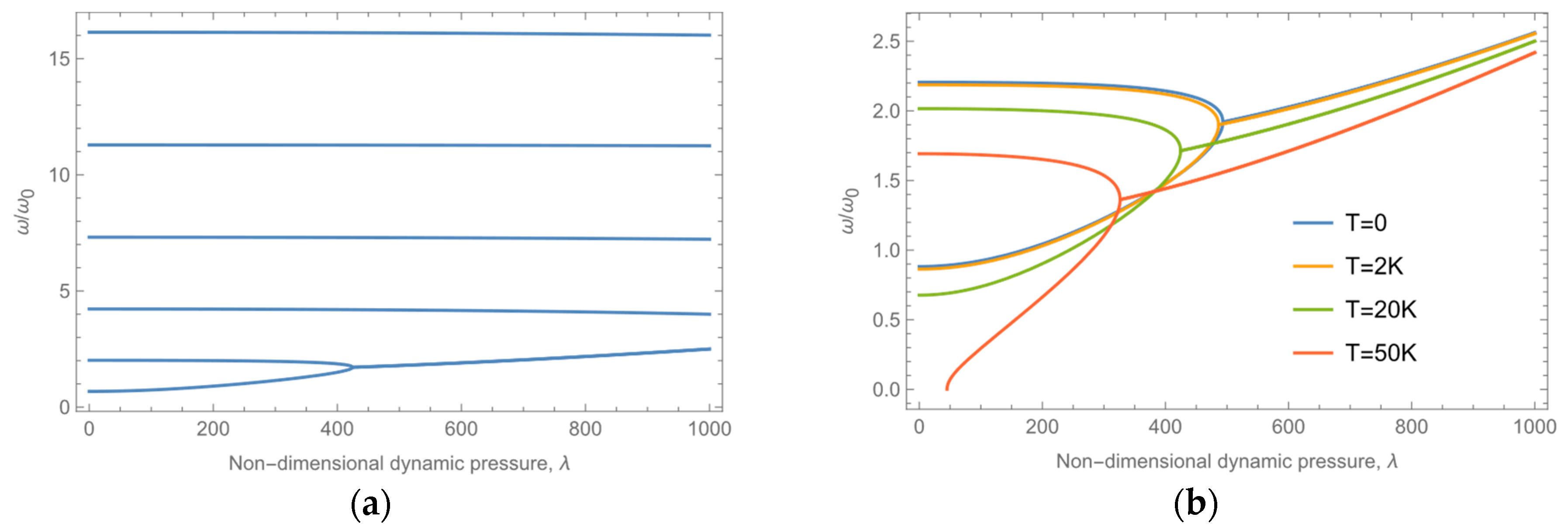
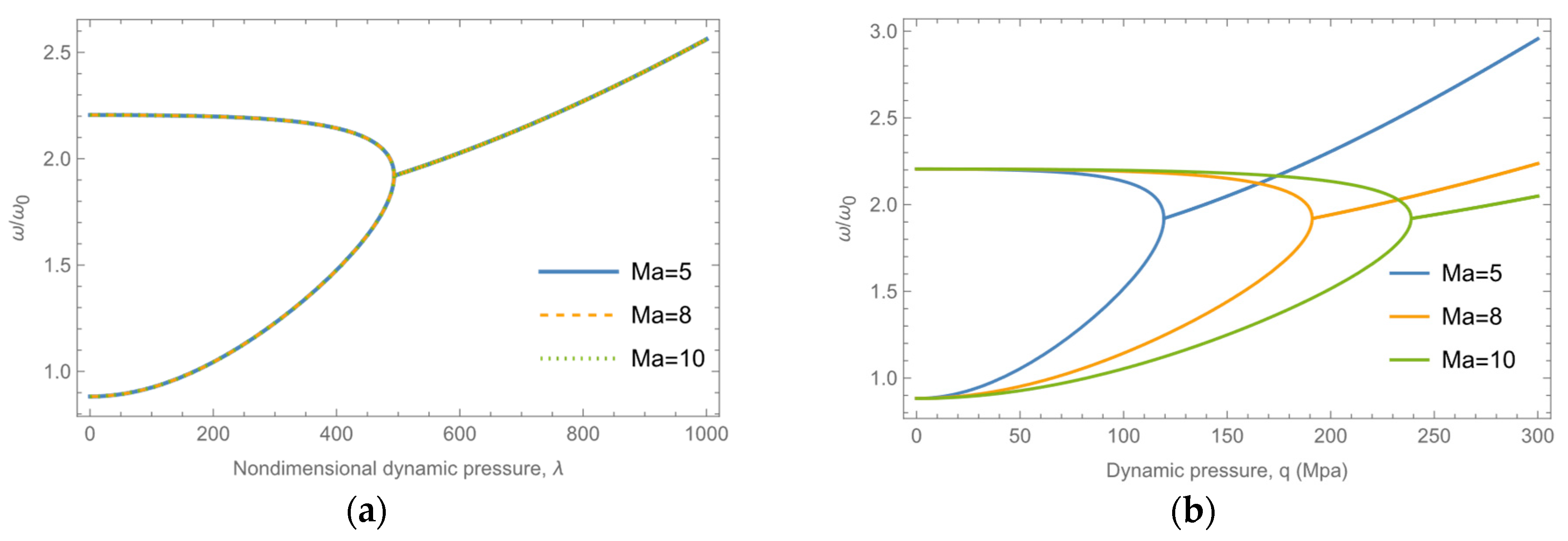
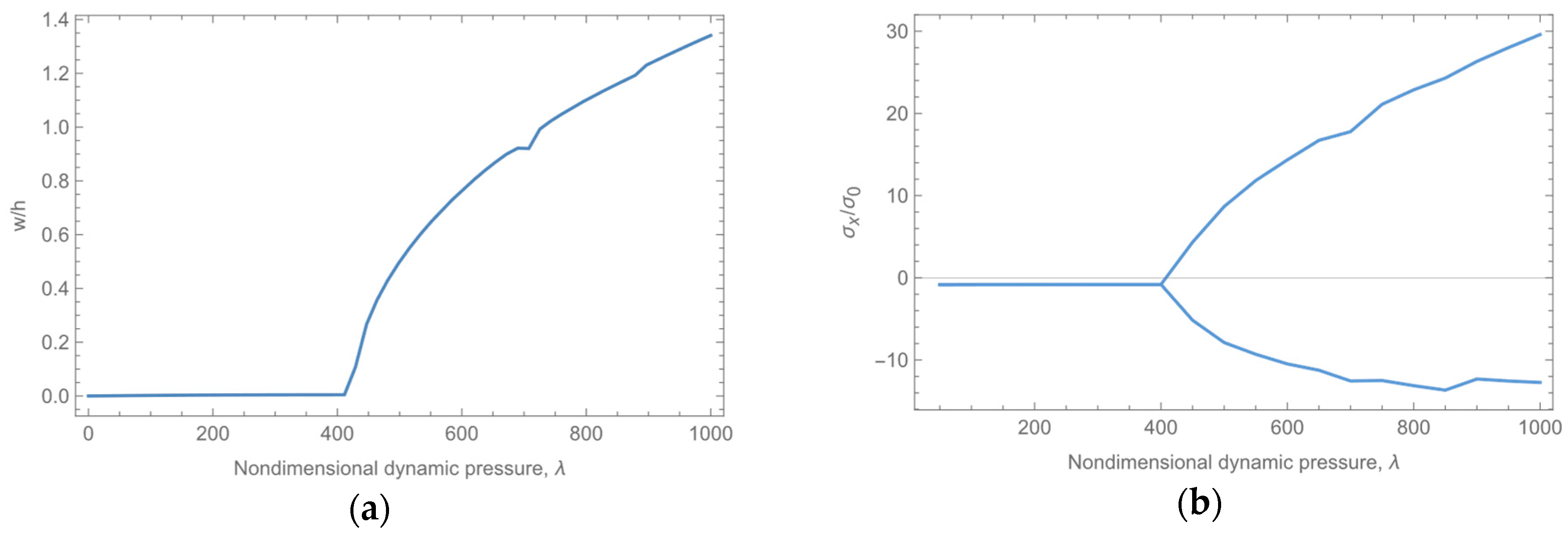
4.1. Linear Analysis
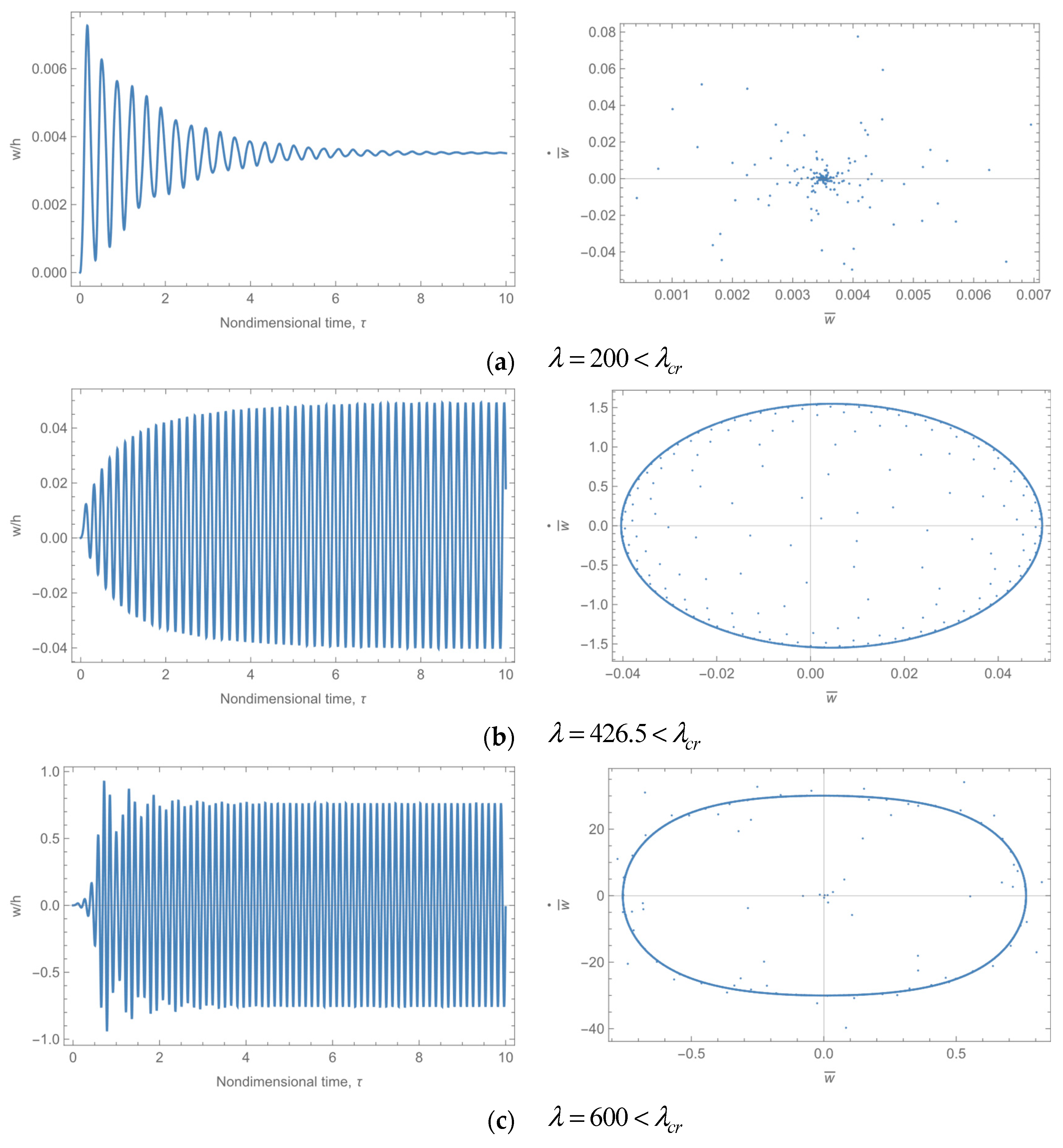
4.2. Nonlinear Analysis
5. Discussion
6. Conclusions
- (1)
- The paper presents a semianalytical analysis method for solving the unknown deflection coefficients to acquire the explicit solutions for static areothermoelastic responses and to solve the eigenvalues for the coefficient matrix and a system of ordinary differential equations in linear and nonlinear analysis for panel flutter, respectively.
- (2)
- According to the static aerothermoelastic analysis, the aeroelastic effect reduces the maximum deformation and the peak of the applied aerodynamic force. The coupling effect between the orders of aerodynamic forces shifts the deformation of the structure toward the leading edge and reduces the maximum deformation.
- (3)
- FG plates exhibit sensitivity to thermal loading, particularly concerning the correlation between stiffness and the volume fraction index. It is important to note that the ratio of mechanical stiffness to thermal stiffness was not consistent at different temperatures, as both of these stiffnesses progressively decrease with an increase in the volume fraction index despite contributing to the total stiffness in opposite directions. At lower temperatures, mechanical stiffness prevails, resulting in a decrease in total stiffness with an increase in the volume fraction index.
- (4)
- The general form of arbitrary temperature fields proposed in this paper can deal with complex thermal loads and provides a foundation for practical aerothermoelastic engineering problems. With the same temperature increase, the internal temperature of the uniform temperature field plate is the highest, while the internal temperature of the nonlinear temperature field plate is the lowest.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
References
- Hedgepeth, J.M. Flutter of Rectangular Simply Supported Panels at High Supersonic Speeds. J. Aeronaut. Sci. 1957, 24, 563–573. [Google Scholar] [CrossRef]
- Dowell, E.H. Nonlinear oscillations of a fluttering plate. AIAA J. 1966, 4, 1267–1275. [Google Scholar] [CrossRef]
- Xue, D.Y.; Mei, C. Finite element nonlinear panel flutter with arbitrary temperatures in supersonic flow. AIAA J. 1993, 31, 154–162. [Google Scholar] [CrossRef]
- Guo, X.; Mei, C. Application of aeroelastic modes on nonlinear supersonic panel flutter at elevated temperatures. Comput. Struct. 2006, 84, 1619–1628. [Google Scholar] [CrossRef]
- McNamara, J.J.; Friedmann, P.P. Aeroelastic and Aerothermoelastic Analysis in Hypersonic Flow: Past, Present, and Future. AIAA J. 2011, 49, 1089–1122. [Google Scholar] [CrossRef]
- Zhou, K.; Su, J.; Hua, H. Aero-thermo-elastic flutter analysis of supersonic moderately thick orthotropic plates with general boundary conditions. Int. J. Mech. Sci. 2018, 141, 46–57. [Google Scholar] [CrossRef]
- Quan, E.; Xu, M.; Yao, W.; Cheng, X. Analysis of the post-flutter aerothermoelastic characteristics of hypersonic skin panels using a CFD-based approach. Aerosp. Sci. Technol. 2021, 118, 107076. [Google Scholar] [CrossRef]
- Song, Z.; Chen, Y.; Li, Z.; Sha, J.; Li, F. Axially functionally graded beams and panels in supersonic airflow and their excellent capability for passive flutter suppression. Aerosp. Sci. Technol. 2019, 92, 668–675. [Google Scholar] [CrossRef]
- Wei, J.; Song, Z.; Li, F. Superior aeroelastic behaviors of axially functional graded cylindrical shells in supersonic airflow. J. Fluids Struct. 2020, 96, 103027. [Google Scholar] [CrossRef]
- Muc, A.; Flis, J. Flutter characteristics and free vibrations of rectangular functionally graded porous plates. Compos. Struct. 2020, 261, 113301. [Google Scholar] [CrossRef]
- Guo, H.; Żur, K.K.; Ouyang, X. New insights into the nonlinear stability of nanocomposite cylindrical panels under aero-thermal loads. Compos. Struct. 2023, 303, 116231. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Zhang, W. Vibration and flutter characteristics of GPL-reinforced functionally graded porous cylindrical panels subjected to supersonic flow. Acta Astronaut. 2021, 183, 89–100. [Google Scholar] [CrossRef]
- Ganapathi, M.; Aditya, S.; Shubhendu, S.; Polit, O.; Zineb, T.B. Nonlinear supersonic flutter study of porous 2D curved panels including graphene platelets reinforcement effect using trigonometric shear deformable finite element. Int. J. Non-Linear Mech. 2020, 125, 103543. [Google Scholar] [CrossRef]
- Khalafi, V.; Fazilati, J. Panel flutter analysis of cracked functionally graded plates in yawed supersonic flow with thermal effects. Appl. Math. Model. 2022, 101, 259–275. [Google Scholar] [CrossRef]
- Farsadi, T.; Rahmanian, M.; Kurtaran, H. Nonlinear stability of multilayered graphene platelet-reinforced functionally graded wing-like plates. Acta Mech. 2022, 233, 3233–3252. [Google Scholar] [CrossRef]
- Chen, J.; Han, R.; Liu, D.; Zhang, W. Active Flutter Suppression and Aeroelastic Response of Functionally Graded Multilayer Graphene Nanoplatelet Reinforced Plates with Piezoelectric Patch. Appl. Sci. 2022, 12, 1244. [Google Scholar] [CrossRef]
- Abbaslou, M.; Saidi, A.R.; Bahaadini, R. Vibration and dynamic instability analyses of functionally graded porous doubly curved panels with piezoelectric layers in supersonic airflow. Acta Mech. 2023, 234, 6131–6167. [Google Scholar] [CrossRef]
- Mahmoudkhani, S. Aerothermoelastic analysis of imperfect FG cylindrical shells in supersonic flow. Compos. Struct. 2019, 225, 111160. [Google Scholar] [CrossRef]
- Zhong, R.; Qin, B.; Wang, Q.; Shao, W.; Shuai, C. Investigation on flutter instability of magnetic-electric-thermo-elastic functionally graded plates in the supersonic airflow with any yawed angle. Int. J. Mech. Sci. 2021, 198, 106356. [Google Scholar] [CrossRef]
- Guo, H.; Li, M.; Żur, K.K.; Yuan, J.; Wu, X. Flutter of carbon-based nanohybrid composite panels. Thin-Walled Struct. 2023, 188, 110828. [Google Scholar] [CrossRef]
- Zhong, S.; Jin, G.; Ye, T.; Zhang, Q. Supersonic flutter analysis of variable thickness blades in thermal environment by using isogeometric approach. Thin-Walled Struct. 2022, 172, 108844. [Google Scholar] [CrossRef]
- Akbari, H.; Azadi, M.; Fahham, H. Flutter prediction of cylindrical sandwich panels with saturated porous core under supersonic yawed flow. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 235, 2968–2984. [Google Scholar] [CrossRef]
- Hao, Y.X.; Zhang, W.; Li, S.B.; Zhang, J.H. Nonlinear Vibrations of FGM Cylindrical Panel with Simply Supported Edges in Air Flow. Int. J. Aerosp. Eng. 2015, 2015, 246352. [Google Scholar] [CrossRef]
- Swain, P.K.; Adhikari, B.; Maiti, D.K.; Singh, B.N. Aeroelastic analysis of CNT reinforced functionally graded laminated composite plates with damage under subsonic regime. Compos. Struct. 2019, 222, 110916. [Google Scholar] [CrossRef]
- Zhou, K.; Huang, X.; Tian, J.; Hua, H. Vibration and flutter analysis of supersonic porous functionally graded material plates with temperature gradient and resting on elastic foundation. Compos. Struct. 2018, 204, 63–79. [Google Scholar] [CrossRef]
- Guo, J.; Qin, Z.; Zhang, Y. Nonlinear aerodynamic analysis of functional graded plates using an HSDT-based isogeometric approach. Thin-Walled Struct. 2023, 186, 110658. [Google Scholar] [CrossRef]
- Aditya, S.; Haboussi, M.; Shubhendu, S.; Ganapathi, M.; Polit, O. Supersonic flutter study of porous 2D curved panels reinforced with graphene platelets using an accurate shear deformable finite element procedure. Compos. Struct. 2020, 241, 112058. [Google Scholar] [CrossRef]
- Reddy, J.N.; Wang, C.M. An overview of the relationships between solutions of the classical and shear deformation plate theories. Compos. Sci. Technol. 2000, 60, 2327–2335. [Google Scholar] [CrossRef]
- Ganapathi, M.; Prakash, T.; Singha, M.K. Nonlinear Stability of Functionally Graded Plates Subjected to Aero-thermo-mechanical Loads. In Proceedings of the IUTAM Symposium on Multi-Functional Material Structures and Systems, Indian Inst Sci, Bangalore, India, 10–12 December 2010; pp. 25–33. [Google Scholar]
- Xia, W.; Zhao, X.; Li, D.; Shen, S. Nonlinear flutter response of pre-heated functionally graded panels. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 1850012. [Google Scholar] [CrossRef]
- Navazi, H.M.; Haddadpour, H. Parameter Study of Nonlinear Aero-Thermoelastic Behaviour of Functionally Graded Plates. Int. J. Struct. Stab. Dyn. 2009, 9, 285–305. [Google Scholar] [CrossRef]
- Navazi, H.M.; Haddadpour, H. Aero-thermoelastic stability of functionally graded plates. Compos. Struct. 2007, 80, 580–587. [Google Scholar] [CrossRef]
- Sator, L.; Sladek, V.; Sladek, J. A Strong Form Meshless Method for the Solution of FGM Plates. Aerospace 2022, 9, 425. [Google Scholar] [CrossRef]
- Shahverdi, H.; Khalafi, V.; Noori, S. Aerothermoelastic Analysis of Functionally Graded Plates Using Generalized Differential Quadrature Method. Lat. Am. J. Solids Struct. 2016, 13, 796–818. [Google Scholar] [CrossRef][Green Version]
- Fazilati, J.; Khalafi, V.; Shahverdi, H. Three-dimensional aero-thermo-elasticity analysis of functionally graded cylindrical shell panels. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 1715–1727. [Google Scholar] [CrossRef]
- Praveen, G.N.; Reddy, J.N. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. Int. J. Solids Struct. 1998, 35, 4457–4476. [Google Scholar] [CrossRef]
- Ibrahim, H.H.; Tawfik, M.; Al-Ajmi, M. Non-linear panel flutter for temperature-dependent functionally graded material panels. Comput. Mech. 2008, 41, 325–334. [Google Scholar] [CrossRef]
- Ibrahim, H.H.; Tawfik, M.; Al-Ajmi, M. Thermal buckling and Nonlinear flutter Behavior of functionally graded material panels. J. Aircr. 2007, 44, 1610–1618. [Google Scholar] [CrossRef]
- Ibrahim, H.H.; Yoo, H.H.; Lee, K.-S. Supersonic Flutter of Functionally Graded Panels Subject to Acoustic and Thermal Loads. J. Aircr. 2009, 46, 593–600. [Google Scholar] [CrossRef]
- Su, Z.; Wang, L.; Sun, K.; Wang, D. Vibration characteristic and flutter analysis of elastically restrained stiffened functionally graded plates in thermal environment. Int. J. Mech. Sci. 2019, 157, 872–884. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Kim, J.-H. Thermal post-buckling and snap-through instabilities of FGM panels in hypersonic flows. Aerosp. Sci. Technol. 2013, 30, 175–182. [Google Scholar] [CrossRef]
- Zhang, D.-G.; Zhou, Y.-H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Li, C.; Wan, Z.; Wang, X.; Yang, C.; Li, K. Analytical research for buckling of metal-ceramic functionally graded plates in thermal environments. J. Beijing Univ. Aeronaut. Astronaut. 2024, preprints. [Google Scholar]
- Song, Z.-G.; Li, F.-M. Investigations on the flutter properties of supersonic panels with different boundary conditions. Int. J. Dyn. Control. 2013, 2, 346–353. [Google Scholar] [CrossRef]







| Material | P0 | P1 | |
|---|---|---|---|
| E (Pa) | Ti-6Al-4V | 122.70 × 109 | −4.605 × 10−4 |
| ZrO2 | 132.20 × 109 | −3.805 × 10−4 | |
| α | Ti-6Al-4V | 7.4300 × 10−6 | 7.483 × 10−4 |
| ZrO2 | 13.300 × 10−6 | −1.421 × 10−3 | |
| ρ (kg/m3) | Ti-6Al-4V | 4429 | 0 |
| ZrO2 | 3000 | 0 | |
| λ (W/(m·K)) | Ti-6Al-4V | 7.82 | 0 |
| ZrO2 | 1.8 | 0 |
| The Type of Temperature Field | Results of the Semianalytical Method | Results of FEM | Relative Errors |
|---|---|---|---|
| Room temperature | 6.33999 | 6.28984 | 0.80% |
| Uniform (temperature-independent) | 3.92460 | 4.08109 | −3.83% |
| Uniform (temperature-independent) | 3.96067 | 4.10907 | −3.61% |
| Linear (temperature-dependent) | 5.14583 | 5.19792 | −1.00% |
| Linear (temperature-independent) | 5.16377 | 5.20979 | −0.88% |
| Nonlinear (temperature-independent) | 5.40486 | 5.45582 | −0.93% |
| Nonlinear (temperature-independent) | 5.41505 | 5.46070 | −0.84% |
| The Type of the Temperature Field | ΔT = 20 K | ΔT = 2 K | ||
|---|---|---|---|---|
| Uniform (temperature-independent) | 0.488425 | 234.952 | 0.357481 | 191.747 |
| Uniform (temperature-dependent) | 0.487631 | 233.630 | 0.357658 | 191.772 |
| Linear (temperature-independent) | 0.414324 | 184.304 | 0.352639 | 188.579 |
| Linear (temperature-dependent) | 0.413889 | 182.916 | 0.352719 | 188.538 |
| Nonlinear (temperature-independent) | 0.399063 | 174.064 | 0.351463 | 187.811 |
| Nonlinear (temperature-dependent) | 0.398896 | 172.835 | 0.351532 | 187.759 |
| The Type of the Temperature Field | Flutter Dynamic Pressure |
|---|---|
| Uniform (temperature-independent) | 424.54 |
| Uniform (temperature-dependent) | 421.85 |
| Linear (temperature-independent) | 454.93 |
| Linear (temperature-dependent) | 453.76 |
| Nonlinear (temperature-independent) | 462.50 |
| Nonlinear (temperature-dependent) | 461.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wan, Z.; Wang, X.; Yang, C.; Li, K. Semianalytical Research on Aerothermoelastic Behaviors of Functionally Graded Plates under Arbitrary Temperature Fields in Hypersonic Vehicles. Aerospace 2024, 11, 572. https://doi.org/10.3390/aerospace11070572
Li C, Wan Z, Wang X, Yang C, Li K. Semianalytical Research on Aerothermoelastic Behaviors of Functionally Graded Plates under Arbitrary Temperature Fields in Hypersonic Vehicles. Aerospace. 2024; 11(7):572. https://doi.org/10.3390/aerospace11070572
Chicago/Turabian StyleLi, Chang, Zhiqiang Wan, Xiaozhe Wang, Chao Yang, and Keyu Li. 2024. "Semianalytical Research on Aerothermoelastic Behaviors of Functionally Graded Plates under Arbitrary Temperature Fields in Hypersonic Vehicles" Aerospace 11, no. 7: 572. https://doi.org/10.3390/aerospace11070572
APA StyleLi, C., Wan, Z., Wang, X., Yang, C., & Li, K. (2024). Semianalytical Research on Aerothermoelastic Behaviors of Functionally Graded Plates under Arbitrary Temperature Fields in Hypersonic Vehicles. Aerospace, 11(7), 572. https://doi.org/10.3390/aerospace11070572







