An Advanced Control Method for Aircraft Carrier Landing of UAV Based on CAPF–NMPC

Abstract

This paper investigates a carrier landing controller for unmanned aerial vehicles (UAVs), and a nonlinear model predictive control (NMPC) approach is proposed considering a precise motion control required under dynamic landing platform and environment disturbances. The NMPC controller adopts constraint aware particle filtering (CAPF) to predict deck positions for disturbance compensation and to solve the nonlinear optimization problem, based on a model establishment of carrier motion and wind field. CAPF leverages Monte Carlo sampling to optimally estimate control variables for improved optimization, while utilizing constraint barrier functions to keep particles within a feasible domain. The controller considers constraints such as fuel optimization, control saturation, and flight safety to achieve trajectory control. The advanced control method enhances the solution, estimating optimal control sequences of UAV and forecasting deck positions within a moving visual field, with effective trajectory tracing and higher control accuracy than traditional methods, while significantly reducing single-step computation time. The simulation is carried out using UAV “Silver Fox”, considering several scenarios of different wind scales compared with traditional CAPF–NMPC and the nlmpc method. The results show that the proposed NMPC approach can effectively reduce control chattering, with a landing error in rough marine environments of around 0.08 m, and demonstrate improvements in trajectory tracking capability, constraint performance and computational efficiency.

1. Introduction

The automatic takeoff and landing of fixed-wing unmanned aerial vehicles (UAVs) on aircraft carriers has garnered widespread attention in various fields. Due to the highly nonlinear flight dynamics of UAVs and various perturbations in complex maritime environments, flight accidents are likely to occur, which necessitates the precise prediction of aircraft carrier deck motion during the final stage of UAV landing to overcome potential aerodynamic disturbances caused by the stern. Hence, this paper proposes a high-precision carrier landing controller to address these challenges.

Automatic control is a critical component of the automatic carrier landing system (ACLS) for UAVs, which has been extensively studied. The main theoretical foundations for ACLS design include classic, modern control theory, and intelligent control theory. In earlier research, researchers mostly employed PID-based classic control methods to design ACLS systems, benefiting from their simplicity and ease of implementation; considering these advantages, PID controllers have been widely applied. However, their lack of high robustness and deteriorating performance in the presence of deck random motion and stern flow disturbances during aircraft carrier landing make it challenging to meet the high precision requirements of UAV automatic landing. In response to this situation, a method called active disturbance rejection control (ADRC) was proposed in [1]. By designing a state observer to estimate and compensate for model uncertainties and external disturbances, ADRC optimizes controller parameters and demonstrates improved tracking performance and robustness in landing control. An automatic shipboard landing system using a backstepping control method that includes a deck motion prediction and compensation module is proposed in [2]. This system comprehensively considers the motion information of both aircraft and the carrier, as well as factors such as airflow disturbances and wind shear, demonstrating good efficacy in handling prediction and compensation issues. In [3,4,5,6], researchers employ sliding mode fault-tolerant control methods, which utilize an expanded state observer to accurately estimate external uncertainties and the on-board aircraft’s own faulty states in real-time, ensuring precise landing even in the presence of actuator failures and exhibiting excellent disturbance rejection capabilities. The authors of [7,8] mainly focus on the case of parameter uncertainties in UAV models and utilize adaptive nonlinear dynamic inverse control methods to achieve robust slope trajectory angle tracking, effectively reducing the impact of deck motion. Wan and Pan [9] employ an optimal controller based on the linear quadratic gaussian (LQG) method, which includes a Kalman filter, enabling precise tracking of the commanded path in the longitudinal plane despite deck motion and airflow disturbances. The classic control methods mentioned in the above references can reduce model errors and external disturbance effects during the automatic landing process. However, they cannot handle complex constraints that may exist during flight, leading to control saturation or exceeding limits of flight attitude, which will impact control accuracy and flight safety and increase landing risk factors.

Model predictive control (MPC) is a control algorithm that predicts the future response of a system using an explicit state-space model [10]. With the development of computer technology, MPC has been widely applied in various fields such as industrial production, automotives, and aerospace. For aircraft carrier takeoff and landing control, MPC can track trajectories by solving the optimal control problem based on a cost function, while also incorporating state and control constraints to limit unsafe actuator states. MPC is well suited for high-precision control in the complex environment of an aircraft carrier, but it relies on the accuracy of the system model. Tang and Wang [11] adopt a linearized small perturbation model to design a landing guidance law that suppresses the influence of stern flow disturbances. Cui and Han [12] adopt a novel anti-time-delay MPC method, which compared to traditional model predictive control, estimates and suppresses the disturbance of the air wake through the symplectic pseudospectral (SP) method and proposes the prediction error method with a particle swarm optimization (PE-PSO) delay algorithm to estimate the unknown delay parameters in the equivalent control model; this method ensures the control accuracy of aircraft landing. When external disturbances are too large, the robustness of the system may be compromised due to its neglect of high-order terms during model linearization. In contrast, nonlinear predictive control (nonlinear model predictive control, NMPC) has attracted attention from many researchers as it describes the system using a nonlinear model, leading to higher accuracy and reduced prediction errors in the MPC process. Kang and Hedrick [13] establish a simplified three-dimensional nonlinear particle model for unmanned aerial vehicles, utilizing the NMPC method to solve discrete optimization problems; this control method exhibits fast convergence and minimal overshoot. When dealing with large-scale optimization problems or highly nonlinear scenarios, the computational efficiency of NMPC needs careful consideration.

In a complex nonlinear environment such as fixed-wing UAV landing, in order to solve the problem of long computation time for NMPC, Basescu M [14] proposes a method to achieve the precise post-stall landing of a medium-sized unmanned aerial vehicle (UAV) using nonlinear model predictive control (NMPC) and learned aerodynamic coefficients. Based on a simplified model and a ‘warm-starting’ approach, NMPC can generate the entire post-stall landing trajectory in real-time at a 5 Hz frequency and follow it using TVLQR as a single trajectory tracker. Although this method can guarantee real-time performance, the simplified model and hierarchically designed controller may reduce the accuracy, and the method is less resistant to tail winds. Mathisen S [15] presents an accurate deep stall landing method for fixed-wing UAVs based on nonlinear model predictive control (NMPC). This NMPC uses a real-time iteration (RTI)-based NMPC algorithm, which is able to obtain a sufficiently converged solution within a limited computation time to satisfy the requirements of real-time control. The final simulation validates this NMPC control method, and the results show that the method can accurately guide the UAV to perform a deep stall landing and maintain a low landing speed.

Traditional NMPC approaches transform the optimal control problem into an online numerical optimization solution, explicitly considering various control input and state constraints, and implementing control inputs in a rolling manner. However, these methods require a high level of system model accuracy. In situations where the model is inaccurate or unknown factors exist, the control performance may be suboptimal. Additionally, ensuring real-time computation is challenging for numerical optimization methods. Hence, this paper proposes an NMPC approach that incorporates the Bayesian optimal estimation concept to solve nonlinear optimization problems through sampling, and it allows for the consideration of nonlinear system dynamic characteristics and constraints.

This paper addresses the issue of autonomous landing for UAV and establishes a dynamics model of the UAV and carrier. Compared with existing studies, ref. [3] does not include the parts of the wind disturbance modeling and deck prediction, and integrates the deck prediction module into the model predictive control; additionally, the ACLS system involves adaptive law, RBF neural network and sliding mode control methods, while this paper uses particle filtering and nonlinear model predictive control with high precision. The linearized model utilized in ref. [16] may potentially result in a reduction in the model’s accuracy, which could ultimately lead to the controller’s failure in practical applications. From the perspective of the ACLS system’s design, it solely considers the presence of longitudinal deck motions, whereas this paper incorporates a comprehensive modeling of the diverse perturbations. In this paper, a variety of nonlinear constraints are considered, landing problems can be solved in a predetermined time, and various safety flight constraints during the landing process are taken in account for safe landing, including input saturation, velocity constraints, and attitude angle constraints.

An improved constraint-aware particle-filtering nonlinear model predictive control method (CAPF–NMPC) is proposed as the UAV’s final approach landing controller. This method can predict the future motion of both the UAV and the carrier based on optimal estimation methods, considering carrier motion, air turbulence, and carrier air wake. It then calculates the optimal control inputs for the descent process. Finally, simulation results verify the effectiveness of the proposed controller.

The paper is organized as follows. In Section 2, the main problems of autonomous landing are described, and the models of UAV, aircraft carrier and disturbance are established. In Section 3, an ACLS framework for the carrier-based UAVs is developed, and the optimal control model with constraints is constructed. In Section 4, an improved CAPF–NMPC method is described. In Section 5, the simulation results verify the desired system performance. In Section 6, we summarize our findings with conclusions.

2. Problem Formulation

When UAVs land on the deck of an aircraft carrier on a glide trajectory, due to effects of wind disturbance and wake turbulence, coupled with the large heaving motion of the carrier itself, this may result in landing failure. Thus, it is necessary to consider the problem of predicting and resisting complex perturbations. In this section, a longitudinal dynamic model of UAV and carrier is established, and the disturbance models are described.

In this problem, three reference frames are defined as shown in Figure 1, including an inertial and two body-fixed coordinates. The inertial frame $F_0=\left\{o_i{x}_i{y}_i{z}_i\right\}$ is fixed to the Earth. $F_1=\left\{o_b{x}_b{y}_b{z}_b\right\}$ is the body-fixed frame of UAV, where the coordinate origin $o_b$ is located in the center of mass, the $x$-axis is aligned with the UAV’s body axis, pointing towards the UAV’s head, the $y$-axis points towards the UAV’s right wing, and the $z$-axis points towards the UAV’s belly. $F_2=\left\{o_a{x}_a{y}_a{z}_a\right\}$ is the airflow coordinate system, which is generated by $F_1$ rotation, the $x$-axis is rotated by an attack angle $\alpha$, and the $y$-axis is rotated by a sideslip angle $\beta$, so that the $x$-axis aligned with the airspeed vector.

To simplify the research, this paper makes the following assumptions:

Assumption 1.

The rotation of the Earth is ignored, and a point on the ground is selected as the origin to establish the inertial coordinate system. Moreover, the Earth’s horizontal plane is always flat during flight.

Assumption 2.

The aircraft carrier keeps static in the horizontal direction and has no lateral attitude change, and only moves up and down with the sea surface in the vertical direction.

Assumption 3.

The communication link between the UAV and the aircraft carrier is intact, and the UAV can obtain its own position and orientation information and the movement information of the aircraft carrier in real time.

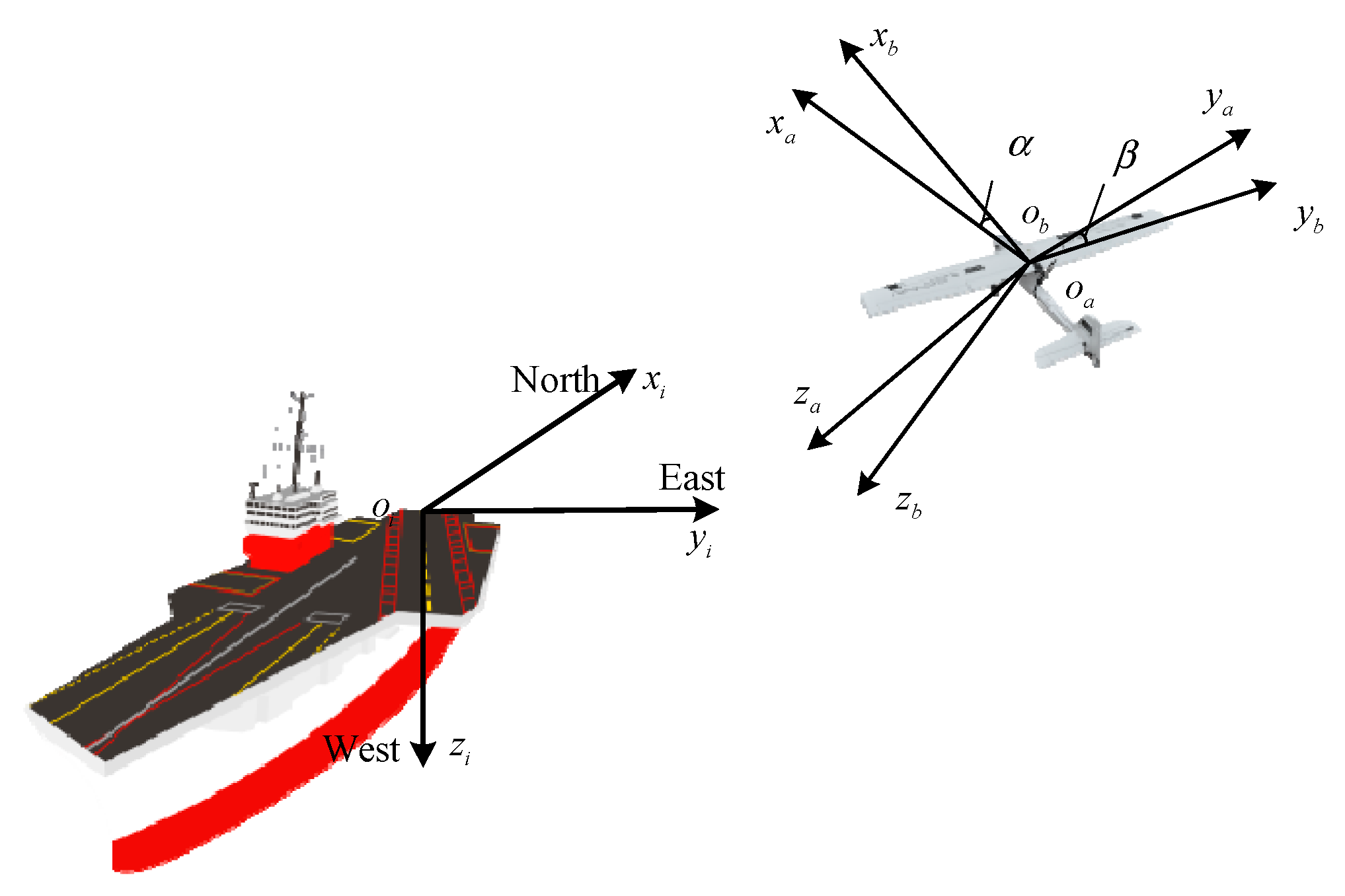
2.1. The Nonlinear Dynamic Model of UAV

This research exclusively focuses on the longitudinal motion of UAVs during landing. While it is true that longitudinal and lateral motions are coupled, the extent of coupling effects is relatively minimal. Hence, it is viable to decouple the dynamics and analyze them separately as longitudinal and lateral motions. By considering full-state nonlinear dynamic equations [17,18,19,20], and assuming all lateral state variables to be zero, the following longitudinal dynamic equations can be derived as Equation (1).

$$\left\{\begin{array}{l}\dot{x}=u\cos \theta +\omega \sin \theta \\ \dot{h}=u\sin \theta -\omega \cos \theta \\ \dot{u}=-qw-g\sin \theta +{\displaystyle \frac{\rho V_a^{2}S}{2m}}\left[C_{\chi }(\alpha )+C_{{\chi }_q}(\alpha ){\displaystyle \frac{c}{2V_a}}q+C_{{\chi }_{{\delta }_e}}(\alpha ){\delta }_e\right]+{\displaystyle \frac{\rho S_{prop}{C}_{prop}}{2m}}\left[{\left(k_{motor}{\delta }_t\right)}^2-V_a^2\right]\\ \dot{\omega }=qu+g\cos \theta +{\displaystyle \frac{\rho V_a^{2}S}{2m}}\left[C_Z(\alpha )+C_{Z_q}(\alpha ){\displaystyle \frac{c}{2V_a}}q+C_{Z_{{\delta }_e}}(\alpha ){\delta }_e\right]\\ \dot{\theta }=q\\ \dot{q}={\displaystyle \frac{\rho V_a^{2}Sc}{2J_y}}[C_m+C_{m_{\alpha }}\alpha +C_{m_q}{\displaystyle \frac{c}{2V_a}}q+C_{m_{{\delta }_e}}{\delta }_e]\end{array}\right.$$

(1)

In this equation, $x$ represents UAV position along the $x$-axis in the inertial frame, $h$ represents UAV altitude in the inertial frame, $u$ and $\omega$ represents UAV velocity along $x$ and $z$ axes in the body frame, while $\theta$ and $q$, respectively, represent the pitch angle and pitch rate of the UAV. The variables ${\delta }_e$ and ${\delta }_t$ correspond to the elevator and propulsion control surfaces of the UAV, expressed in radians and dimensionless coefficients, respectively. Additionally, $C_X$, $C_Z$, and $C_m$ are aerodynamic coefficients, and $C_X(\alpha )$ and $C_Z(\alpha )$ are presented as a nonlinear function of the angle of attack, where the subscripts $q$, $\alpha$ and ${\delta }_e$ indicate their dependence on it. $\rho$ signifies the air density, $S$ represents the area of the wing, $c$ denotes the average wing chord of the UAV, and $S_{prop}$ is the area swept by the propulsion system.

According to Equation (1), the longitudinal nonlinear dynamics model of UAV can be established.

$$\dot{X}=f\left(X,u\right)$$

(2)

where the state vector is $X={\left[\begin{array}{cccccc}x& h& u& \omega & \theta & q\end{array}\right]}^T$, and the control vector is $u={\left[\begin{array}{cc}{\delta }_e& {\delta }_t\end{array}\right]}^T$.

2.2. Aircraft Carrier Motion Model

The longitudinal motion of an aircraft carrier in this paper is considered, and a shaping filter with white noise input can be used to describe its motion. Based on extensive experimental data [16], the transfer function of the filter can be represented as follows:

$$G_s\left(s\right)=gs/\left(s^2+as+d\right)$$

(3)

where $g=0.6$, $a=0.06$, and $d=0.36$.

The state vector of the aircraft carrier is set as $X_d^T=[\begin{array}{cc}{z}_d& {\dot{z}}_d\end{array}]$, representing the movement of the aircraft carrier along the vertical axis, and the form of state space is expressed by the following formula:

$${\dot{X}}_d=A{X}_d+B{u}_d$$

(4)

where $A=\left[\begin{array}{cc}0& 1\\ -d& -a\end{array}\right]$, $B=\left[\begin{array}{c}g\\ -ga\end{array}\right]$, $u_d$ is the control variable generated by random numbers.

The longitudinal motion of the carrier deck with respect to the sea waves is illustrated in Figure 2.

2.3. Disturbance Model of Wind Field

The precision landing process of UAV on the aircraft carrier is significantly affected by atmospheric and airflow disturbances encountered after the carrier. It is crucial to accurately model and analyze this process. Atmospheric disturbances encompass various irregular and random meteorological phenomena, including fluctuations in wind speed, pressure, and temperature. Moreover, the airflow emanating from the carrier’s engine nozzle further exacerbates the challenges in UAV landing. These disturbances introduce deviations in attitude, fluctuations in height, and lateral drift during the landing process.

Different approaches have their own merits and applicability. Navier–Stokes equations are often used to describe the motion of a viscous incompressible or compressible fluid with conserved momentum, especially for incompressible flows; Navier–Stokes equations are nonlinear vector equations. However, these make the wind field model very complex, which is not conducive to the subsequent design. The Dryden wind model is specifically designed to describe the effects of atmospheric turbulence on aircraft through a statistical approach, and it is suitable for engineering applications and real-time simulations [21]. According to the Dryden wind speed model, atmospheric disturbances are typically classified as stable wind, atmospheric turbulence, and wind gusts. Firstly, the wind speed is decomposed based on the inertial coordinate system.

$$\begin{array}{l}{\Phi }_u\left(w\right)={\displaystyle \frac{2{\sigma }_u^2{L}_u}{\pi V}}\cdot {\displaystyle \frac{1}{1+{\left(L_u\frac{w}{v}\right)}^2}}\\ {\Phi }_v\left(w\right)={\displaystyle \frac{{\sigma }_v^2{L}_v}{\pi V}}\cdot {\displaystyle \frac{1+3{\left(L_u\frac{w}{v}\right)}^2}{{\left[1+{\left(L_u\frac{w}{v}\right)}^2\right]}^2}}\\ {\Phi }_w\left(w\right)={\displaystyle \frac{{\sigma }_w^2{L}_w}{\pi V}}\cdot {\displaystyle \frac{1+3{\left(L_w\frac{w}{v}\right)}^2}{{\left[1+{\left(L_w\frac{w}{v}\right)}^2\right]}^2}}\end{array}$$

(5)

The atmospheric disturbances in this paper use the model shown in Equation (5), where $L_u,L_v,L_w$ is the spatial wavelength and ${\sigma }_u,{\sigma }_v,{\sigma }_w$ is the intensity of interference of each axis of the system, which is related to the altitude.

In the range of 800 m from the stern of the aircraft carrier, the wake turbulence from the carrier’s stern can be divided into four parts according to the MIL-F-8785C military specification [22]:

• The free atmospheric turbulence component: $u_1$, $v_1$, $w_1$;
• Steady-state component of wake flow: $u_2$, $w_2$;
• Wake periodic component: $u_3$, $w_3$;
• Wake random component $u_4$, $v_4$, $w_4$;

At the same time, the wake turbulence is decomposed in longitudinal $u_g$, lateral $v_g$, and vertical wake turbulence $w_g$, as shown in Equation (6):

$$\left\{\begin{array}{l}{u}_g=u_1+u_2+u_3+u_4\\ v_g=v_1+v_4\\ w_g=w_1+w_2+w_3+w_4\end{array}\right.$$

(6)

The oscillating motion of the aircraft carrier with the sea waves and the disturbance caused by the wind field of the stern mentioned above can lead to a reduction in landing accuracy and may even result in failed landings or serious accidents. Therefore, in order to achieve a safe and stable landing, it is necessary to accurately predict the influence of the disturbance and solve the optimal control law that meets complex constraints during the landing process. This will reduce the impact of disturbances and eliminate tracking errors, ensuring the successful landing of the UAV.

3. Automatic Carrier Landing System

Section 2 provides a detailed construction of the motion model and disturbance model. In this section, these models are applied to predict deck movement, which will serve as input for adjusting the reference trajectory. Based on this, the tracking controller as well as its objective function and constraints are designed.

3.1. Prediction of the Deck Motion

Due to the complex sea conditions during landing, the deck motion caused by waves and wind disturbances, as described in Equations (4) and (5), exhibits significant randomness. This randomness can potentially lead to landing failures. Therefore, it is essential to accurately predict the deck’s movement, which serves as an input for the reference trajectory module. In this study, the deck motion prediction problem is described as follows: Assume that at time $k$, there are noisy observations of the deck position. Using the system’s dynamic model, recursively predict the state for future time steps $k:k+H$, where $H$ is the prediction horizon of MPC. The particle filter method in CAPF–NMPC is used for deck motion prediction, which will be described in Section 4.

Compared to traditional methods such as the extended Kalman filter (EKF) and auto-regressive (AR) prediction algorithms, particle filtering offers higher accuracy and better convergence speed. Additionally, it does not require the linearity and Gaussian noise assumptions for the state transition and observation functions. In this research, the deck motion model is incorporated into the deck motion prediction module. Unlike conventional particle filtering, to obtain the deck motion sequence within the prediction horizon, the recursive process of particle filtering is modified to extend from $k-1$ to $k+H$, and the sequence’s weight is evaluated based on the observation at time $k$. This approach allows the UAV to use a smaller number of deck position observations to correct the reference trajectory’s error, thereby ensuring the precision of the landing.

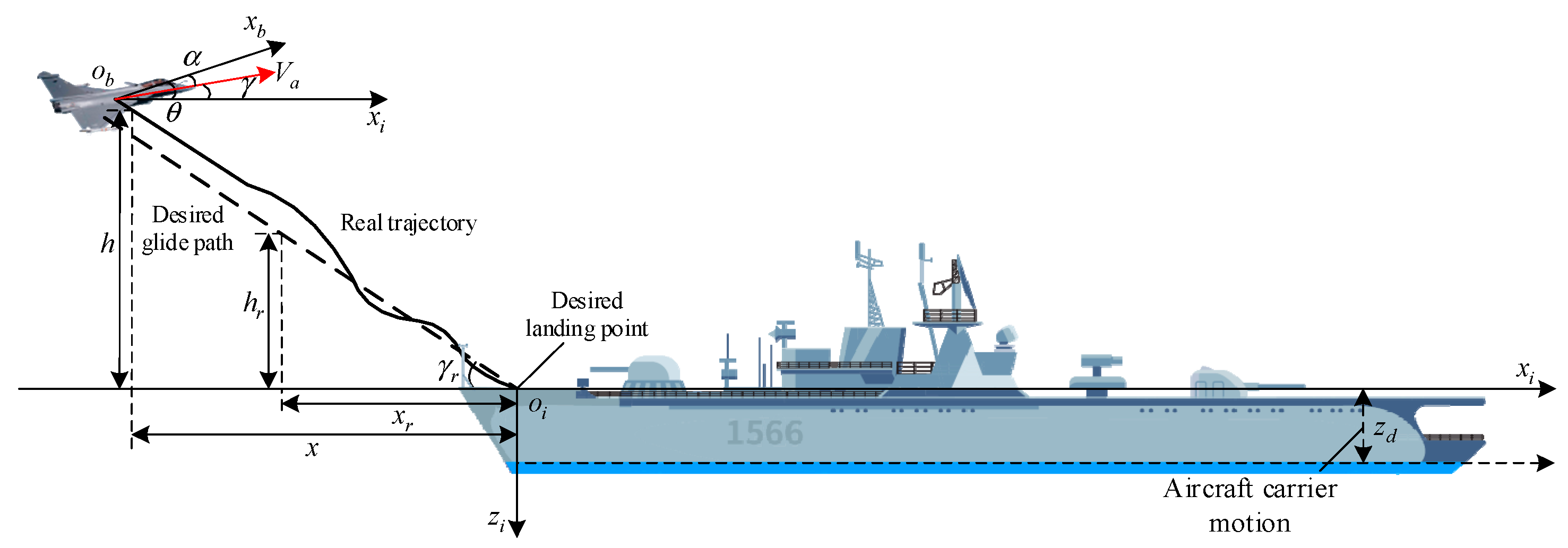
3.2. Design of Aircraft Reference Trajectory

The control system of an automatic landing system for UAV on a carrier-based platform relies on model predictive control based on a designed glide slope reference. Therefore, it is necessary to design the following glide slope reference trajectory, which serves as an input to the control system. Let $r_k=\left[\begin{array}{cc}x& h\end{array}\right]$ denote the position vector of the UAV, where the current expected position of the ship’s reference point is $r_d=\left[\begin{array}{cc}{x}_d& z_d\end{array}\right]$, and $z_d$ is obtained from the deck prediction. The reference glide slope point is denoted as $r_g=\left[\begin{array}{cc}{x}_r& h_r\end{array}\right]$.

Figure 3 shows the final descent phase glide slope as the UAV approaches the ship. The reference glide slope is fixed on the carrier deck, with a tilt angle ${\gamma }_r=-{3.5}^{\circ }$. As the ship moves vertically due to sea motion, the actual height adjustment needs to account for this movement. The distance between the UAV and the ship’s reference point is $R=x-x_d$, and the height of the reference glide slope above the deck is $h_r^{\prime }=R\cdot \tan {\gamma }_r=h_r+z_d$. Thus, the height of the reference glide slope in the absolute coordinate system is

$$h_r=\left(x-x_d\right)\cdot \tan {\gamma }_r-z_d$$

(7)

3.3. Design of the Optimal Controller

When a UAV enters the glide slope range, the NMPC is used to control the UAV in real time considering the motion of the carrier. The NMPC will propagate the states of both UAV and carrier within the $N$ step prediction horizon, solving the optimal control problem to obtain the control inputs for the UAV. Then, the first control input will be implemented at the current time step. In NMPC, an objective function needs to be designed to minimize the sum of errors between the UAV and the current reference trajectory within the prediction horizon.

In this paper, a constrained perception particle filtering approach based on the concept of Bayesian optimal estimation is proposed to solve the optimal control problem. This method interprets the NMPC problem as an estimation problem of future states and control inputs within $N$ time steps based on virtual observations. The architecture of the aircraft carrier autonomous landing system based on the CAPF–NMPC method is shown in Figure 4; the system is composed of the reference trajectory generation module and the improved CAPF–NMPC subsystem.

The reference trajectory generation module is composed of a deck motion prediction module and a glide slope calculation module. The deck motion prediction module is designed based on a particle filter algorithm, which is used to predict the deck motion under the influence of ocean waves, and this interference factor is input into the glide path calculation module. The glide slope calculation module is used to provide a reference trajectory for the controller. The CAPF–NMPC controller uses particle-filter technology to predict the future motion trajectory in the time domain, and calculates the optimal control quantity based on it.

The particle filtering itself is well-suited for nonlinear system environments and can incorporate the objective function in the weight calculation to evaluate the errors between each particle and the reference trajectory, estimating the optimal control sequence through weighted averaging. The constrained perception function adds constraint conditions to the system’s inputs and outputs, ensuring that the thrusters and control surfaces can meet complex constraints during maneuvering flight and that the flight attitude does not undergo excessive variations. The above-mentioned issues directly relate to the safety of UAV landing.

In practical problems, measurements and control are implemented in a discrete manner. The established nonlinear system of the UAV is discretized as follows:

$$X_{k+1}=f(X_k,u_k)$$

(8)

At time $k$, there are corresponding state vector $X_k$ and control vector $u_k$.

In order to implement the measurement process of particle filtering, Equation (8) is rewritten. Let the state vector at time $k$ be denoted as $Z_k={\left[\begin{array}{cc}{X}_k^T& u_k^T\end{array}\right]}^T$, the measurement value as $Y=M{X}_k+V_k$, and the measurement matrix as $M$. For the horizon within $t=k,\dots ,k+H$, the system equation can be expressed as follows:

$$\left\{\begin{array}{l}{Z}_{t+1}=f\left(Z_t\right)+W_t\\ Y_t=M{X}_t+V_t\end{array}\right.$$

(9)

In this equation, the control inputs are generated by a stochastic signal, and $W_t$ and $V_t$ represent additive disturbances. Through Equation (9), the combined state vector $Z_t$ within the current time domain can be estimated using a rolling horizon estimation approach, known as moving horizon estimation (MHE).

The key of the tracking control problem is to determine the optimal control input for the controlled system under a given trajectory. In this context, the control objective is to minimize the difference of $Y_k$ and the reference input $Y_R$. To address this, the NMPC optimization problem can be formulated as:

$$\begin{array}{l}\underset{u_{k:k+H}}{\min }{\displaystyle \sum _{t=k}^{k+H}{‖Y_k-Y_R‖}_Q^2}+{‖u_k‖}_R^2\\ s.t.X_{k+1}=f(X_k,u_k)\\ g_j(X_t,u_t)\le 0\forall j=1,\dots ,m,\\ t=k,\dots ,k+H,\end{array}$$

(10)

where $H$ is the prediction horizon of NMPC, $u_{k:k+H}=\left\{u_k,u_{k+1},\dots ,u_{k+H}\right\}$ is the control input sequence, $Q$ and $R$ are the weighting matrix, and $X_k$ is state vector in current time. $Q$ and $R$ extract the corresponding quantities from the combined state $Z_t$, and are given as follows:

$$\overline{Q}=\left[\begin{array}{ccc}{Q}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & Q_H\end{array}\right]Q_i=\mathrm{diag}\left[\begin{array}{cccc}{q}_1& q_2& \dots & q_n\end{array}\right]$$

(11)

$$\overline{R}=\left[\begin{array}{ccc}{R}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & R_H\end{array}\right]R_i=\mathrm{diag}\left[\begin{array}{cccc}{r}_1& r_2& \dots & r_n\end{array}\right]$$

(12)

Here, $n$ represents the number of state variables in $Z_k$.

The formulated problem seeks to determine the optimal control input sequence $u_{k:k+H}$ to minimize the objective function, which is the weighted quadratic sum of the control cost and tracking error of the next $H$ steps, under the premise of dynamic constraints and state variable constraints. The literature usually adopts numerical optimization methods to calculate $u_{k:k+H}$. Once the optimization is complete, the first element of $u_{k:k+H}$ and $u_k$ is applied to control the system, and this optimization and control is repeated periodically, which is called a rolling optimization process.

During the actual landing process of UAVs, the thrust magnitude of the propulsion system and the deflection angle of the control surfaces are subject to limitations imposed by actuator mechanisms. Therefore, when solving the control variables, it is necessary to limit the input range with constraints to ensure the stability of UAV flight. Specifically, the control variable saturation constraint can be expressed as follows:

$$u_{\min }\le u_k\le u_{\max }$$

(13)

Among them, the elevator angle has a range limit and is measured in radians. The propulsion system has a limit on the magnitude of thrust, which is represented by dimensionless coefficients.

Furthermore, in order to reduce the occurrence of chattering during the control process, it is necessary to increase the constraints on the control increment. This can ensure that the change rate of the UAV actuator remains within a certain range, so as to ensure the smoothness and stability of the control process. The formula for controlling incremental constraints is as follows:

$${‖\Delta u_k‖}_{\infty }\le {\tau }_{\max }$$

(14)

where ${\tau }_{\max }$ represents the maximum rate of change of the UAV actuator.

For the UAV landing mission, in addition to accurately controlling the touchdown point, it is also necessary to ensure that the speed and attitude angle do not change significantly during the landing process; otherwise, flight safety incidents are likely to occur. Therefore, the following constraints are imposed on the state variables:

$$X_{\min }\le X_k\le X_{\max }$$

(15)

The velocity constraint is described as follows:

$$\left\{\begin{array}{c}\left|u\right|\le u_{\max }\\ \left|\omega \right|\le {\omega }_{\max }\end{array}\right.$$

(16)

where $u_{\max }$ and ${\omega }_{\max }$ represent the maximum velocity components in the $x$ and $z$ directions of the body coordinate system. The equation is expressed as follows:

$$M{Z}_k\le V_{\max }$$

(17)

where

$$M=\left[\begin{array}{ccc}{0}_{2\times 2}& I_2& 0_{2\times 4}\\ 0_{2\times 2}& -I_2& 0_{2\times 4}\end{array}\right]$$

(18)

$$V_{\max }={\left[\begin{array}{cccc}{u}_{\max }& {\omega }_{\max }& u_{\max }& {\omega }_{\max }\end{array}\right]}^T$$

(19)

where $0_{m\times n}$ represents a zero matrix of dimension $m\times n$.

In this paper, the attitude constraint is described by the angle of attack, denoted as $\alpha$. Due to $\alpha =\arctan \left({\displaystyle \frac{\omega }{u}}\right)$, the constraint is formulated as follows:

$${\alpha }_{\min }\le \arctan \left({\displaystyle \frac{\omega }{u}}\right)\le {\alpha }_{\max }$$

(20)

In Equation (20), ${\alpha }_{\min }$ and ${\alpha }_{\max }$ indicate the permissible range of the UAV’s angle of attack. The equation is expressed as follows:

$$\Gamma Z_k\le A_{\max }$$

(21)

where

$$\Gamma =\left[\begin{array}{cccc}{0}_{1\times 2}& -\tan \left({\alpha }_{\max }\right)& 1& 0_{1\times 4}\\ 0_{1\times 2}& \tan \left({\alpha }_{\min }\right)& -1& 0_{1\times 4}\end{array}\right]$$

(22)

$$A_{\max }=0_{2\times 1}$$

(23)

where $0_{m\times n}$ represents a zero matrix of dimension $m\times n$.

4. Improved CAPF–NMPC Method

In Section 3, the optimization model of the real-time control process has been constructed according to the NMPC method, but it is a big problem to solve the optimization model. In the literature [23], the CAPF method has been used to solve this problem, but there were some shortcomings such as solver output chattering and poor soft constraint performance. Therefore, the improvement in its sampling and constraint way in this section can alleviate the chattering caused by this method to some extent.

4.1. CAPF–NMPC Algorithm

Standard particle filtering for optimization can be described as importance sampling, constraint awareness, resampling, and backward smoothing; we used the CAPF–NMPC method to solve the above optimal procedure and make improvements.

Importance sampling is based on the theory of Bayesian optimal estimation. It estimates the optimal state $Z_{k:k+H}$ from a virtual measurement value $Y_{k:k+H}$. At each time step, $N$ particles are randomly generated, and their weights are calculated based on the importance distribution, with distribution $q\left(\left.{\overline{Z}}_t^i\right|{\overline{Z}}_{t-1}^i,Y_{k:t}\right)=p\left(\left.{\overline{Z}}_t\right|\begin{array}{c}{\overline{Z}}_{t-1}\end{array}\right)$ being selected, $i=1,\dots ,N$. The approximate value $p\left(\left.{\overline{Z}}_{k:t}\right|\begin{array}{c}{Y}_{k:t}\end{array}\right)$ is calculated by weighted summation, where the weight and normalization calculation formula are given by:

$$W_t^i={\displaystyle \frac{p\left(\left.{\overline{Z}}_{k:t}\right|\begin{array}{c}{Y}_{k:t}\end{array}\right)}{q\left(\left.{\overline{Z}}_{k:t}\right|\begin{array}{c}{Y}_{k:t}\end{array}\right)}}={\displaystyle \frac{p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)p\left(\left.{\overline{Z}}_t^i\right|\begin{array}{c}{\overline{Z}}_{t-1}^i\end{array}\right)}{q\left(\left.{\overline{Z}}_t^i\right|{\overline{Z}}_{t-1}^i,Y_{k:t}\right)}}{W}_{t-1}^i$$

(24)

$$W_t^i={\displaystyle \frac{p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)}{{\displaystyle \sum _{j=1}^{N}p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)}}}$$

(25)

Reverse recursion means that when solving the optimal control problem, only the first or first several quantities of the optimal control sequence need to be input, and the desired optimal control variable can be obtained through reverse recursion by calculating $p\left(\left.{\overline{Z}}_k\right|\begin{array}{c}{Y}_{k:k+H}\end{array}\right)$. The reverse recursion process is expressed in the following form:

$$p\left(\left.{\overline{Z}}_k\right|\begin{array}{c}{Y}_{k:k+H}\end{array}\right)=p\left(\left.{\overline{Z}}_k\right|\begin{array}{c}{Y}_{k:t}\end{array}\right){\displaystyle \int \frac{p\left(\left.{\overline{Z}}_{t+1}\right|\begin{array}{c}{\overline{Z}}_t\end{array}\right)}{{\displaystyle \int p\left(\left.{\overline{Z}}_{t+1}\right|\begin{array}{c}{\overline{Z}}_t\end{array}\right)p\left(\left.{\overline{Z}}_t\right|Y_{k:t}\right)d{\overline{Z}}_t}}}\times p\left(\left.{\overline{Z}}_{t+1}\right|Y_{k:k+H}\right)d{\overline{Z}}_{t+1}$$

(26)

Since $p\left(\left.{\overline{Z}}_{t+1}\right|Y_{k:t}\right)={\displaystyle \int p\left(\left.{\overline{Z}}_{t+1}\right|\begin{array}{c}{\overline{Z}}_t\end{array}\right)p\left(\left.{\overline{Z}}_t\right|Y_{k:t}\right)d{\overline{Z}}_t}$, and by approximating the above relationship with the sample probability distribution in the filtering process, the sample can be recursively reweighted:

$$W_{\left.t\right|\begin{array}{c}k+H\end{array}}^i={\displaystyle \sum _{j=1}^N{W}_{\left.t+1\right|\begin{array}{c}k+H\end{array}}^i}{\displaystyle \frac{W_t^{i}p\left(\left.{\overline{Z}}_{t+1}^j\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)}{{\displaystyle \sum _{l=1}^N{W}_t^{l}p\left(\left.{\overline{Z}}_{t+1}^j\right|\begin{array}{c}{\overline{Z}}_t^l\end{array}\right)}}}$$

(27)

$$p\left(\left.{\overline{Z}}_k\right|Y_{k:k+H}\right)\approx {\displaystyle \sum _{i=1}^N{W}_{\left.k\right|\begin{array}{c}k+H\end{array}}^i\delta \left({\overline{Z}}_k-{\overline{Z}}_k^i\right)}$$

(28)

Therefore, the optimal estimate of ${\overline{Z}}_k$ based on $Y_{k:k+H}$ is:

$${\widehat{\overline{Z}}}_k^{\ast }={\displaystyle \sum _{i=1}^N{W}_{\left.k\right|\begin{array}{c}k+H\end{array}}^i{\overline{Z}}_k^i}$$

(29)

4.2. Incremental Importance Sampling

In the standard importance sampling, the sampling process of control vector $u_k$ is an independent random process, and each iteration will be re-sampled, which will lead to the chattering problem of the control variable. In order to alleviate the chattering problem of the control system caused by the solution of the random sampling process, this paper improved the sampling method while keeping the algorithm unchanged. The optimal control variable of the previous time is considered as the mean value, and the mean square error of sampling is restricted. The new sampling distribution could be obtained as follows:

$$q\left(u_k\right)=N\left(u_{k-1},{\tau }_{\max }^2\right)$$

(30)

where $u_{k-1}$ is the optimal control variable at the previous time, and ${\tau }_{\max }$ is the constraint of the increment of the control variable.

Therefore, the weight calculation Equation (25) is rewritten as follows:

$$W_t^i={\displaystyle \frac{p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i,u_{k-1}\end{array}\right)}{{\displaystyle \sum _{j=1}^{N}p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i,u_{k-1}\end{array}\right)}}}$$

(31)

where ${\widehat{u}}_k$ is the increment of the control variable obtained by sampling, and the control vector at the next moment is calculated by:

$$u_k={\widehat{u}}_k+u_{k-1}$$

(32)

4.3. Hybrid Constraint Method

In order to confine the generated particles and ensure that both the state and control variables remain within a reasonable range, it is essential to employ a constraint perception method to evaluate whether they exceed the constraints of the optimization problem construction. However, different penalties apply for violating constraints in relation to different state quantities. For instance, the state variable may not need to strictly adhere to the constraints, while the control variable must adhere strictly to the control saturation constraints. In light of this consideration, the constraint perception method is further enhanced, and a hybrid constraint perception method incorporating soft and hard constraints is adopted to ensure the optimization of approximate solution, and ensure it meets the requisite criteria.

For quantities of states that do not require strict constraints, a penalty function of the probability of the particle state relative to the constraint can be added to the weight to punish particles that exceed the constraint. The penalty function is expressed as follows:

$$\varphi \left(s\right)={\displaystyle \frac{1}{\alpha }}\ln \left(1+\exp \left(\beta \cdot s\right)\right)$$

(33)

In the formula, parameters $\alpha$ and $\beta$ are used to adjust the influence of the particle exceeding the constraint on the weight. When the particle satisfies the constraint, the output result of the function is close to zero.

At the same time, the perception variable ${\sigma }_t$ of whether the particle satisfies the constraint at time $t$ is constructed, as shown in the following equation:

$${\sigma }_t=\varphi \left(g\left({\overline{Z}}_t\right)\right)+{\eta }_t$$

(34)

where $g$ is the constrained set, ${\eta }_t$ is the additive noise, and by calculating the probability of particle relative to the measured value, the weight changes. The calculation formula of weight at time $t$ can be rewritten as:

$$W_t^i={\displaystyle \frac{p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i,u_{k-1}\end{array}\right)p\left(\left.{\sigma }_t\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)}{{\displaystyle \sum _{j=1}^{N}p\left(\left.Y_t\right|\begin{array}{c}{\overline{Z}}_t^i,u_{k-1}\end{array}\right)p\left(\left.{\sigma }_t\right|\begin{array}{c}{\overline{Z}}_t^i\end{array}\right)}}}$$

(35)

For the situations in which the actuator of a fixed wing UAV needs to strictly meet complex constraints, such as thrust saturation constraints, upper and lower limits of rudder yaw angle, etc., it is difficult to make the soft constraint processing method mentioned above completely limit the solved control variable within the constraints. Therefore, this paper adopts a hard constraint processing method based on the projection Newton method to optimize the control variable. An approximate solution satisfying the constraints is obtained.

For the above constraint $g_j(X_t,u_t)\le 0$, each particle that violates the constraint is projected, and the optimization problem of the projection Newton method is expressed as follows:

$$\begin{array}{l}\min {‖u_t-u_{t,proj}‖}^2\\ s.t.g(u_{t,proj})\le 0\end{array}$$

(36)

where $u_{t,proj}$ is the solution after projection, and $‖u_t-u_{t,proj}‖$ represents the Euclidean distance between the solution after projection and the original solution. The objective of the optimization problem is to find a $u_{t,proj}$ that satisfies the constraint conditions so that the distance between the adjusted solution and the original solution is minimal.

Finally, the projected solution is used to replace the original solution, and then Equation (35) is used to calculate the weight of the particle. This method can ensure that the generated particles in each step fully conform to the constraints, but it may also mean that the solution is not globally optimal, and it only applies to the simple constraint domain, and the constraint function must be convex and smooth.

The algorithm flow of the improved CAPF–NMPC method based on a constrained sensing particle filter is shown in Algorithm 1.

Algorithm 1: NMPC Based on Improved Constraint-Aware Particle Filtering/Smoothing.

1: Initialize CAPF–NMPC parameters

2: Create a standard glide slope with sea wave motion

3: for $k=1,\dots ,T$ do

Forward filtering

4:     for $t=k,\dots ,k+H$ do

5:      Sample based on the previous time by Equation (30)

6:      Kinetic equation recursion each particle by Equation (9) 7:      Constrain the control vector by Equation (36)

8:      Evaluate sample weights by Equation (35)

9:      Do resampling based on the weights

10:   end for

Backward smoothing 11: end for

12: Compute the optimal estimation of ${\widehat{\overline{Z}}}_k^{*}$ by Equation (20) 13: Export $u_k^{*}$, and apply it to the system Equation (1)

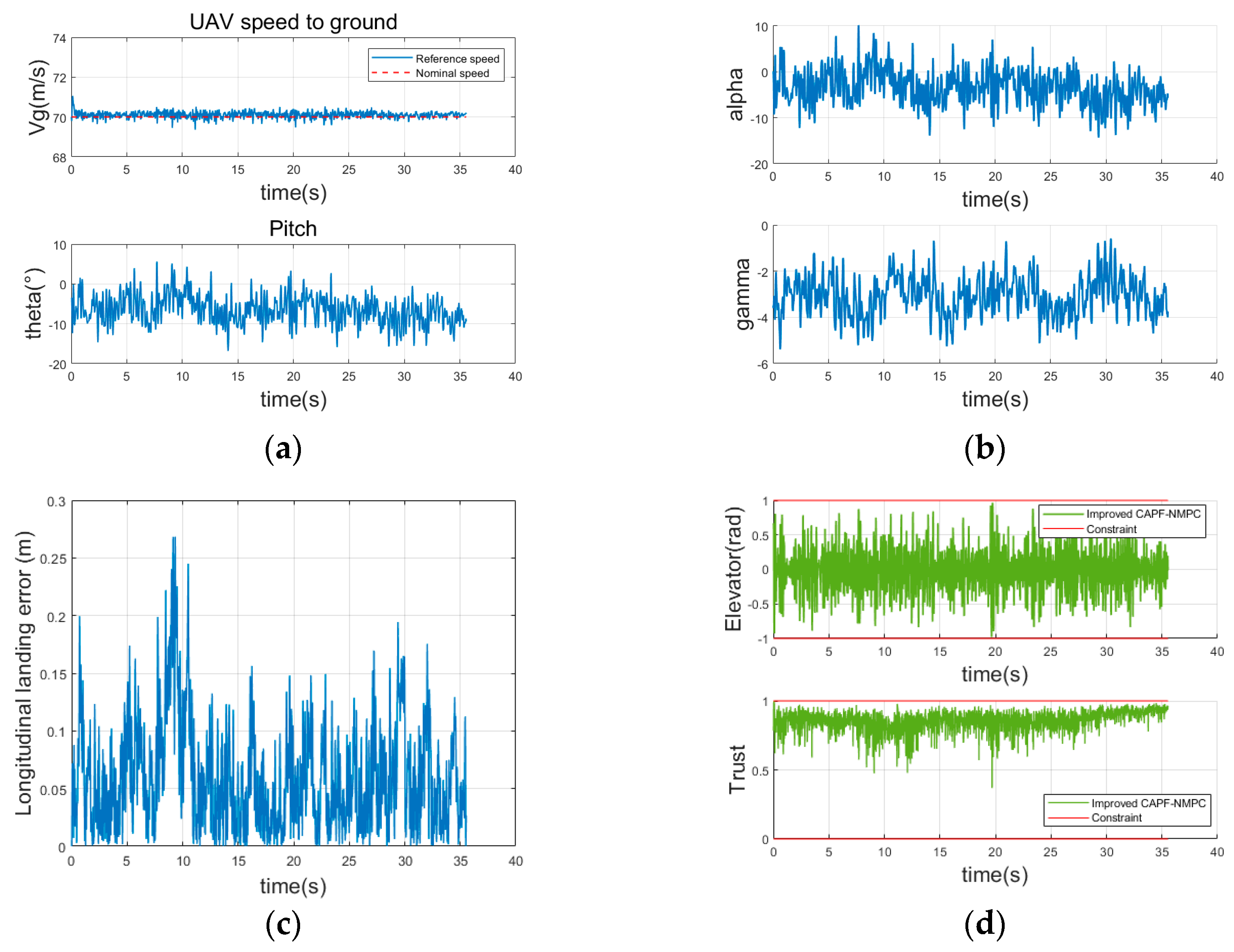
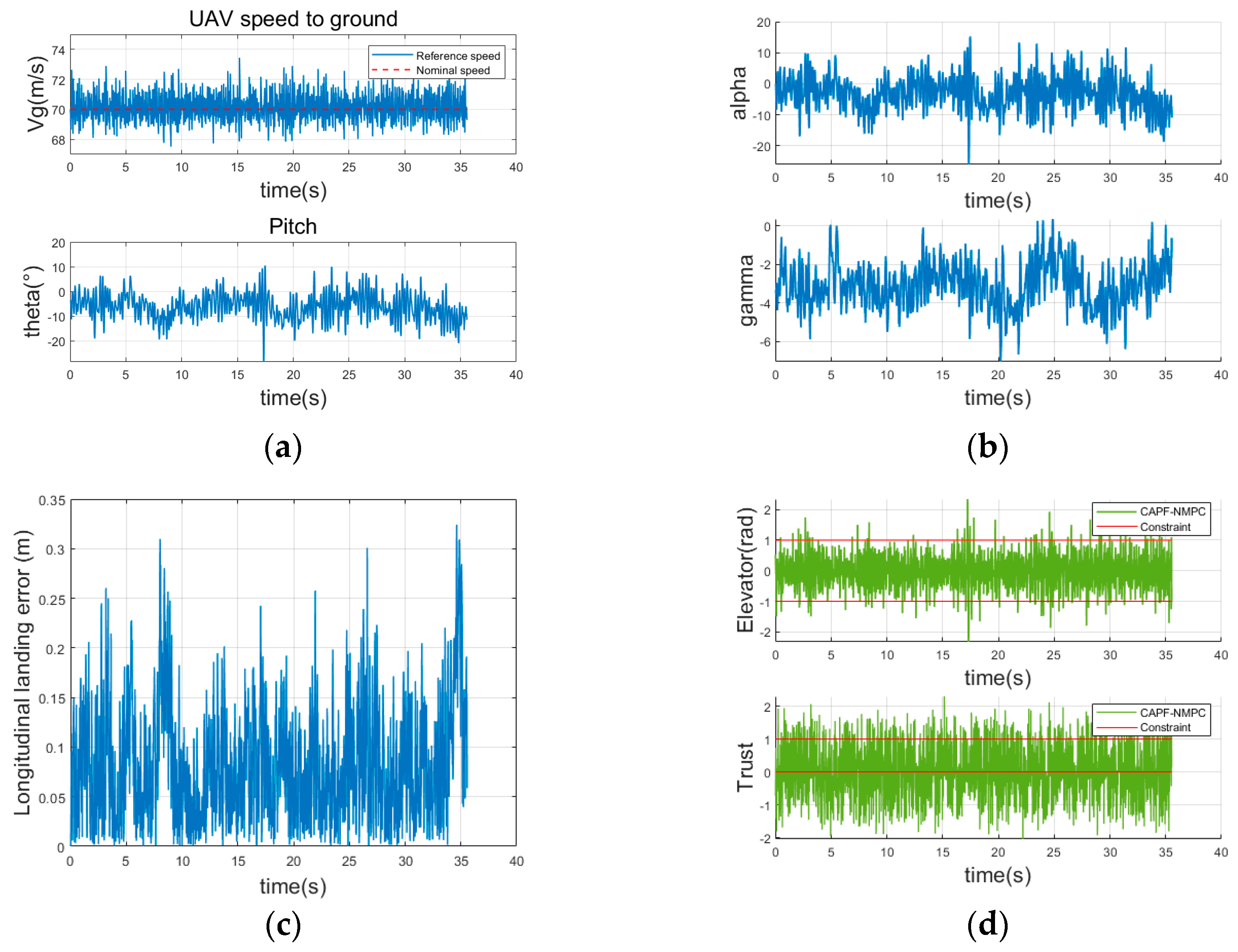
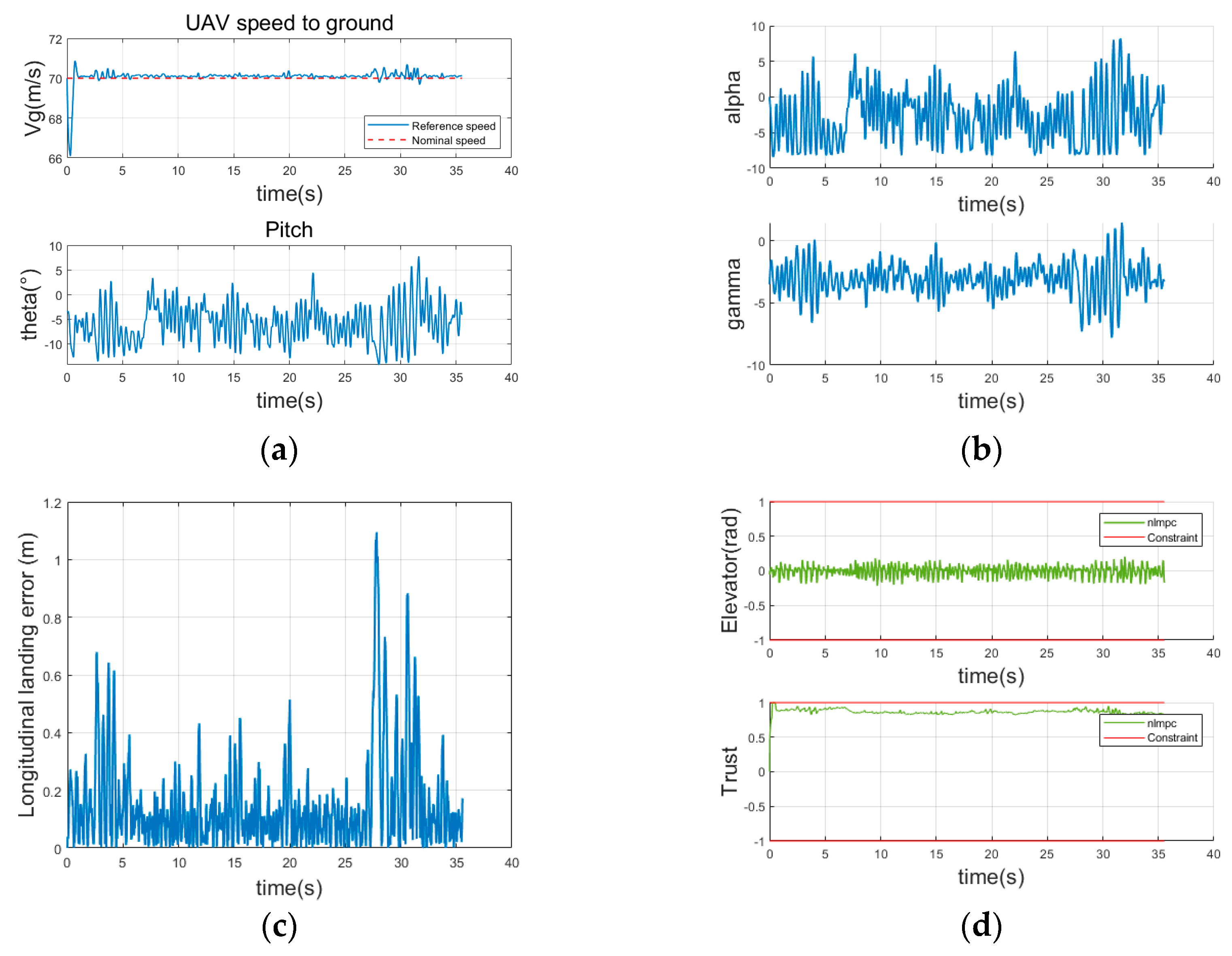
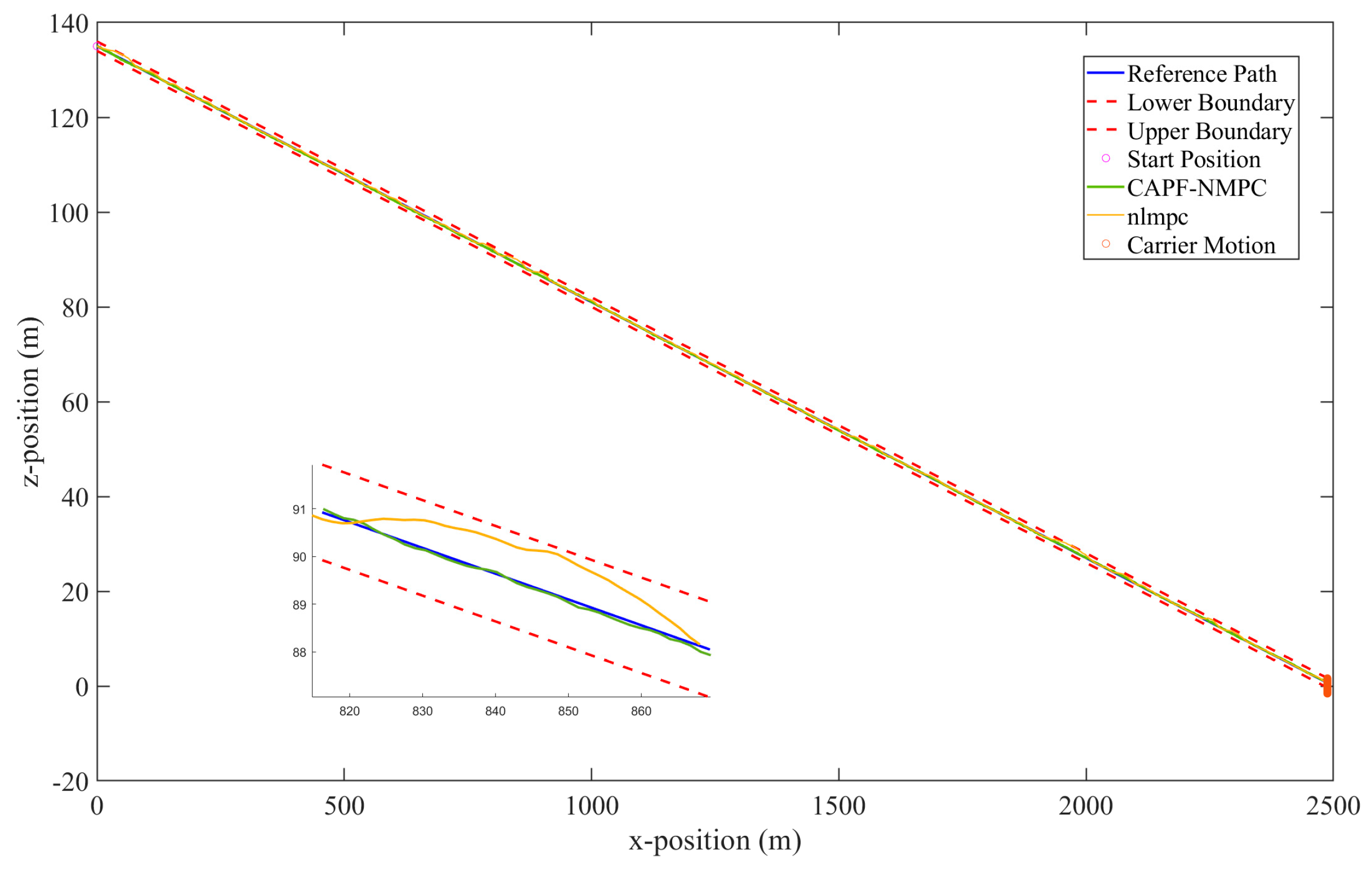
5. Numerical Simulations

5.1. Scenario Description

In this section, the carrier landing of a UAV using a CAPF–NMPC method is simulated in different sea conditions. At the same time, the classic controller nlmpc of MATLAB is used to compare with the proposed CAPF–NMPC method. It is assumed that the UAV has entered the approach position of the landing carrier. The altitude is 135 m and the initial state variable of the UAV is $X_0^T=\left[\begin{array}{cccccc}-2500& -135& 0& 70& -3.5& 0\end{array}\right]$. The initial position of the aircraft carrier is $X_d^T=\left[\begin{array}{cc}0& 0\end{array}\right]$, and the UAV is required to carry out the landing on the carrier with the reference glide slope of $\gamma =-{3.5}^{\circ }$.

The simulations were performed in several wind scales, light, moderate and severe. With light wind, it is assumed that there are small waves in the sea and a slight motion of the carrier, and there is a steady wind component at the stern. With moderate wind, it is assumed that the aircraft carrier has a moderate motion, and there is a moderate stable wind, turbulent flow and air flow. Severe wind requires high precision of the controller and was used to verify the multi-constraint processing ability and robustness of the controller, as well as the prediction ability of the deck and UAV states. The wind scale and specific parameters are shown in

Table 1. Parameters of different wind scales.

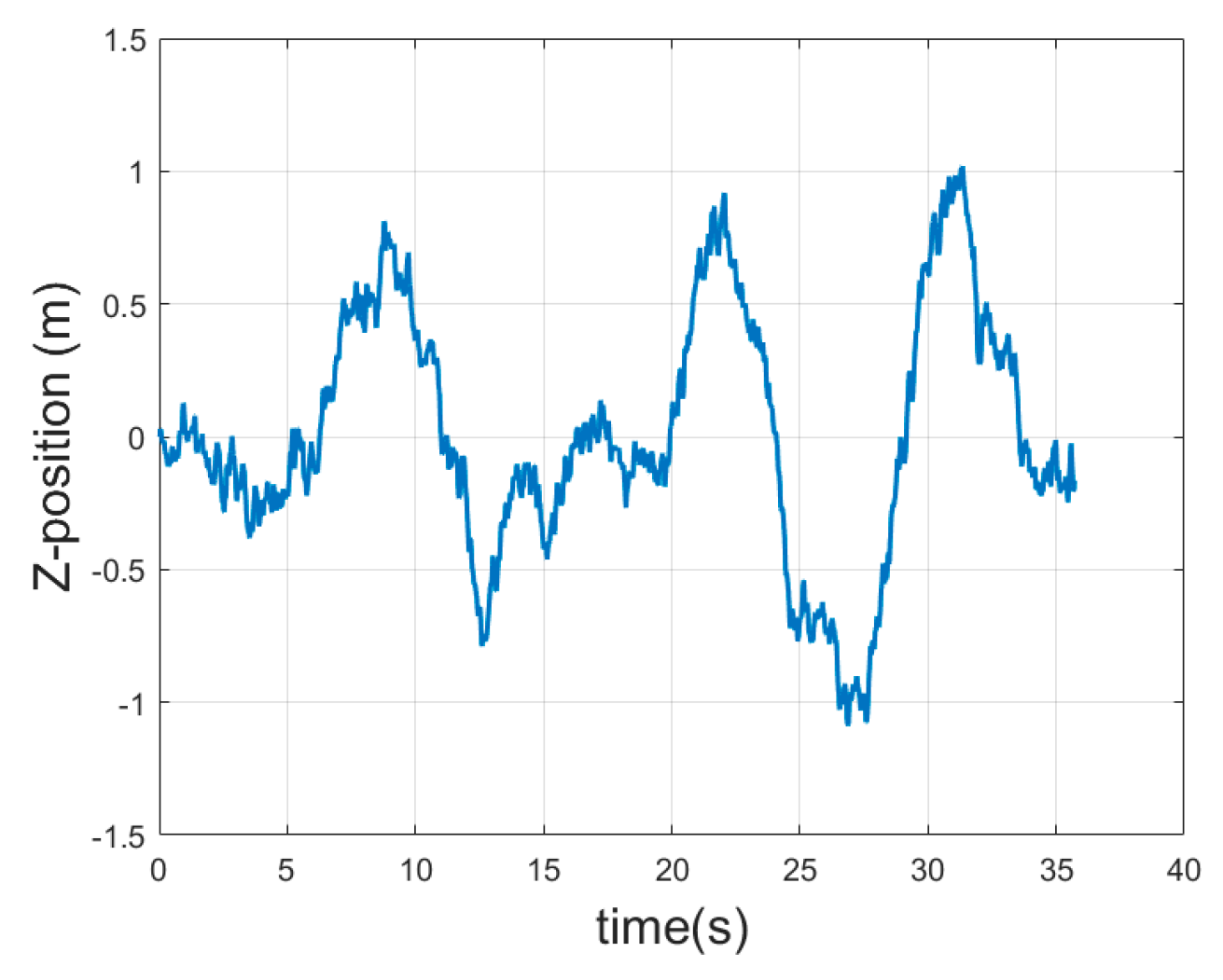
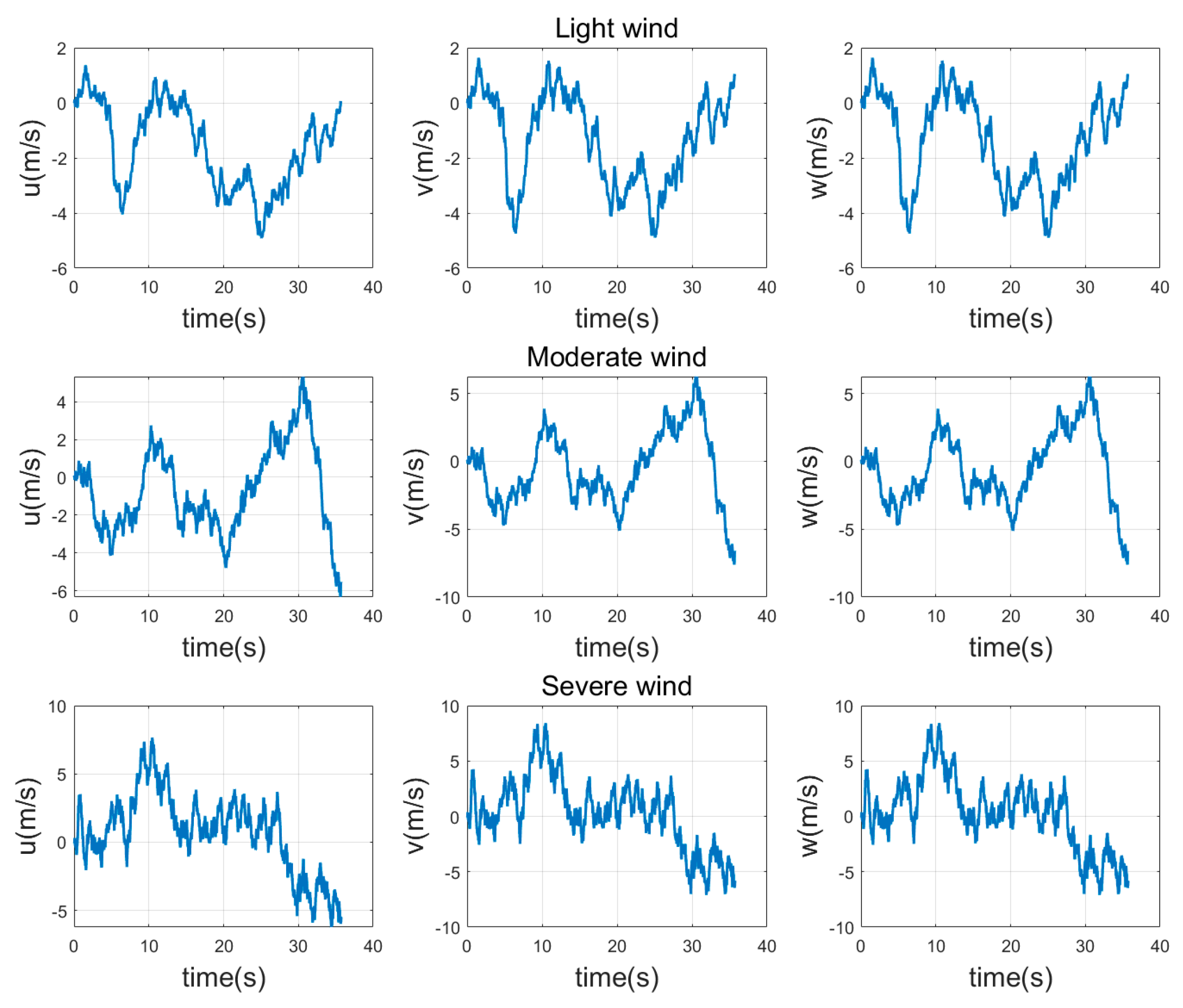
Wind Scale	Name	Wind Speed (m/s)	Wave Height (m)	Highest Wave (m)
0	Calm wind	0.0–0.2	0.0	0.0
1	Light wind	1.6–3.3	0.2	0.3
2	Moderate wind	5.5–7.9	1.0	1.5
3	Severe wind	10.8–13.8	3.0	4.0

.

In the actual landing environment, it is necessary to consider the aerodynamic influence of the UAV. In this paper, the aerodynamic parameters of the UAV “Silver Fox” are used for simulation, as shown in

Table 2. Parameters of UAV “Silver Fox”.

Parameters	Value	Unit
Thrust coefficient $C_T$	40.5	N
Elevator Ratio $C_{{\delta }_e}$	−2.021	Dimensionless
Lift coefficient $C_l$	0.228	Dimensionless
Drag coefficient $C_d$	0.0191	Dimensionless
Pitch moment coefficient $C_m$	0.107	Dimensionless
Aircraft weight $m$	9	$\mathrm{kg}$
Air density $\rho$	1.29	$\mathrm{kg}/{\mathrm{m}}^3$
Wing area $s$	0.743	${\mathrm{m}}^2$
Chord length $c$	0.305	$\mathrm{m}$
Pitch moment of inertia $I_{yy}$	0.868	$\mathrm{kg}/{\mathrm{m}}^2$

.

The restrictions of its actuator mechanism are considered, as follows:

$$\left\{\begin{array}{l}-1\le {\delta }_e\le 1\\ 0\le {\delta }_t\le 1\\ -0.3\le \Delta \delta \le 0.3\end{array}\right.$$

(37)

Here, ${\delta }_e$ represents the rudder angle of the lifting wing, and ${\delta }_t$ represents the thrust size, which is fed in the form of a dimensionless coefficient, and its increment is also limited to a certain range.

The parameters of NMPC and particle-filter method were set as shown in

Table 3. NMPC simulation parameters.

Parameters	Value	Unit
Sampling time $T_s$	0.02	s
Prediction horizon $H_p$	8	step
Control horizon $H_c$	1	step
Particle number $N$	50	dimensionless
Simulation time	40	s
Reference speed	69.69	m/s
Reference path angle	−3.5	degree

, which mainly include prediction horizon, control horizon, initial particle number, etc.

5.2. Analysis of Simulation Results

The simulation was carried out on a 64-bit Windows 11 operating system with an Intel^® Core™ i9-12900H CPU at 2.50 GHz and a RAM of 16.0 GB. Using the proposed CAPF–NMPC method, the traditional CAPF–NMPC method and the nlmpc, simulation results in serval scenarios were obtained.

The simulation results are presented in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 5 illustrates the motion of the deck with waves for three wind forces. Figure 6 depicts the air wake and wind disturbances. Figure 7, Figure 8 and Figure 9 demonstrate the simulation results of the improved CAPF–NMPC method, the CAPF–NMPC method, and the classic nlmpc method in the severe wind scenario, respectively. Figure 10 also depicts the trajectories of the UAV and the aircraft carrier during the landing process.

As illustrated in Figure 5 and Figure 6, the alterations in wind and wave during the simulation align with the outcomes presented in Table 1, thereby substantiating the precision of the carrier deck motion model and the disturbance modeling approach. This latter approach incorporates three distinct components of wind disturbance in three scenarios, designated as u, v, and w.

Figure 7a depicts the ground speed and pitch angle. It can be observed that the speed increases at the beginning and then remains at a value close to the target. This indicates that the controller is highly effective in regulating the speed. Additionally, Figure 7b illustrates the angle of attack and the track angle. It is essential that the track angle remains at around −3.5°. In the event of wind disturbance, the simulation outcomes demonstrate that the track angle exhibits minimal fluctuations. Furthermore, the error curve in Figure 7c illustrates that the controller’s position error is relatively minimal, indicating its effective landing performance. The control quantities in Figure 7d also demonstrate stability with lesser chattering and within the constraints.

A comparison of the traditional CAPF–NMPC method with the improved incremental importance sampling and constraints method reveals that the latter exhibits superior dynamic performance. Additionally, the control quantities are effectively constrained, and the presence of only minimal oscillations indicates that the method is capable of meeting actuator constraints in the field of UAV landing control.

In comparison with the classic nlmpc method in Figure 9, under sea condition in severe wind, longitudinal control error is within 0.3 m, and the velocity deviation is within 0.2 m/s, but the classic control method exhibits a longitudinal control error of about 1 m. These results demonstrate a significant improvement in precision with the CAPF–NMPC method compared to the nlmpc method, and indicate that the nlmpc exhibits a lack of resistance to wind disturbances. Additionally, the longitudinal control error exceeds 1 m on multiple occasions in Figure 10, indicating that the controller’s regulatory performance is insufficient; a quantitative comparison is detailed in

Table 4. The error distribution of the landing points.

Index	nlmpc Method			CAPF–NMPC Method			Improved CAPF–NMPC Method
	Light	Moderate	Severe	Light	Moderate	Severe	Light	Moderate	Severe
Landing error	0.104 m	0.0984 m	0.129 m	0.046 m	0.072 m	0.058 m	0.014 m	0.0632 m	0.026 m
RMSE	0.0988 m	0.1594 m	0.373 m	0.0384 m	0.0677 m	0.1017 m	0.0294 m	0.0619 m	0.0758 m

.

The results demonstrate the impact of varying wind disturbances on the performance of each controller. Among them, nlmpc is particularly susceptible to wind and wave effects, exhibiting a notable increase in RMSE with rising wind speeds and altered wave heights. Indeed, there may even be a reduction in the error as the wind speed increases; because of that, the single landings exhibit a normal distribution around the mean. However, in general, the standard deviation of the improved method is slightly smaller, and the success rate of the landings is higher; in other words, the improved CAPF–NMPC displays a more pronounced response, yet maintains a high degree of landing accuracy despite the intensification of wind and wave conditions.

In addition, compared with the classic nlmpc method, the average single-step calculation time of CAPF–NMPC is 0.2 s, while the average single-step calculation time of MATLAB toolbox is 0.25 s, and the calculation time required for optimization will be higher in some moments with large perturbations, so it can be proved that sampling NMPC execution control is more advantageous than numerical optimization in complex systems.

There are limitations of the proposed methodology in few cases: (1) the dynamic performance of the improved method can be further optimized through the incorporation of constraints, but the fixed solution time may result in suboptimal solutions if the constraints are excessively strict; (2) as particle filtering employs a probability density approach to evaluate trajectory quality, the CAPF–NMPC method may encounter difficulties in generating control quantities when the UAV is situated at a considerable distance from the reference trajectory.

6. Conclusions

In this paper, a carrier landing control method based on a novel NMPC for fixed-wing UAV is proposed to address the problem of stable landing. This method is integrated into the automatic control system, which considers various disturbances, such as carrier heaving motion, wind shears, atmospheric turbulence, and wind gusts, that the UAV may encounter during landing. An ACLS architecture is considered in the design module of the system, the deck motion prediction module uses a particle-filtering method for high accuracy prediction, and the reference trajectory generation module introduces deck motion for compensation. The control module employs an improved CAPF method to solve the nonlinear optimization problems and achieve high-precision tracking. The NMPC method takes into account complex constraints including control input saturation, speed limitations, and the flight safety of UAVs. Furthermore, incremental importance sampling and a hybrid constraint method were designed to improve CAPF–NMPC. Finally, the effectiveness and robustness of the developed controller were evaluated in different sea conditions. Simulation results demonstrate that the improved CAPF–NMPC control method exhibits high adaptation to strong nonlinear systems, meets real time control requirements, and successfully enables aircraft carrier landing at the ideal landing point. Compared with the traditional CAPF–NMPC method, it has the advantages of high accuracy and fast calculation speed, control chattering is well reduced, and the constraints are strictly satisfied.