The Determination of Criticality for Ice Shapes Based on CCAR-25
Abstract
:1. Introduction
- (1)
- Although the above advisory circulars have given a detailed explanation and analysis of the definition and application principles of critical ice shapes, while the aerodynamic effects of various ice shapes have been revealed in available literature [17], the applicable criterion of determining the critical ice shapes in terms of geometric characteristics has not been clearly given out, namely, how to determine the criticality for ice shapes with certain and limited geometric parameters from a variety of effect factors. Moreover, the previous works mainly focused on the selection of the critical icing conditions [18], where the aerodynamic effects are usually ignored, though it is the final step of the entire process.
- (2)
- According to the latest version of CCAR-25 and AC 20-73A, the determination of criticality for ice shapes should be performed under different flight phases, including takeoff, holding, en route, etc., instead of the previous requirement of only holding. According to the available results of aerodynamic performance after icing, even for the same flight phase, the corresponding critical ice shapes may be diverse for different configurations and components of aircraft; however, both the current airworthiness regulations and the related advisory circulars do not give corresponding guidance or suggestions about the geometric definition of critical ice shapes, which increases the complexity of the problem [19,20,21].
2. The Classification of Ice Shapes According to the Airworthiness Regulations
3. The Criticality of Ice Shapes with Different Geometric Characteristics
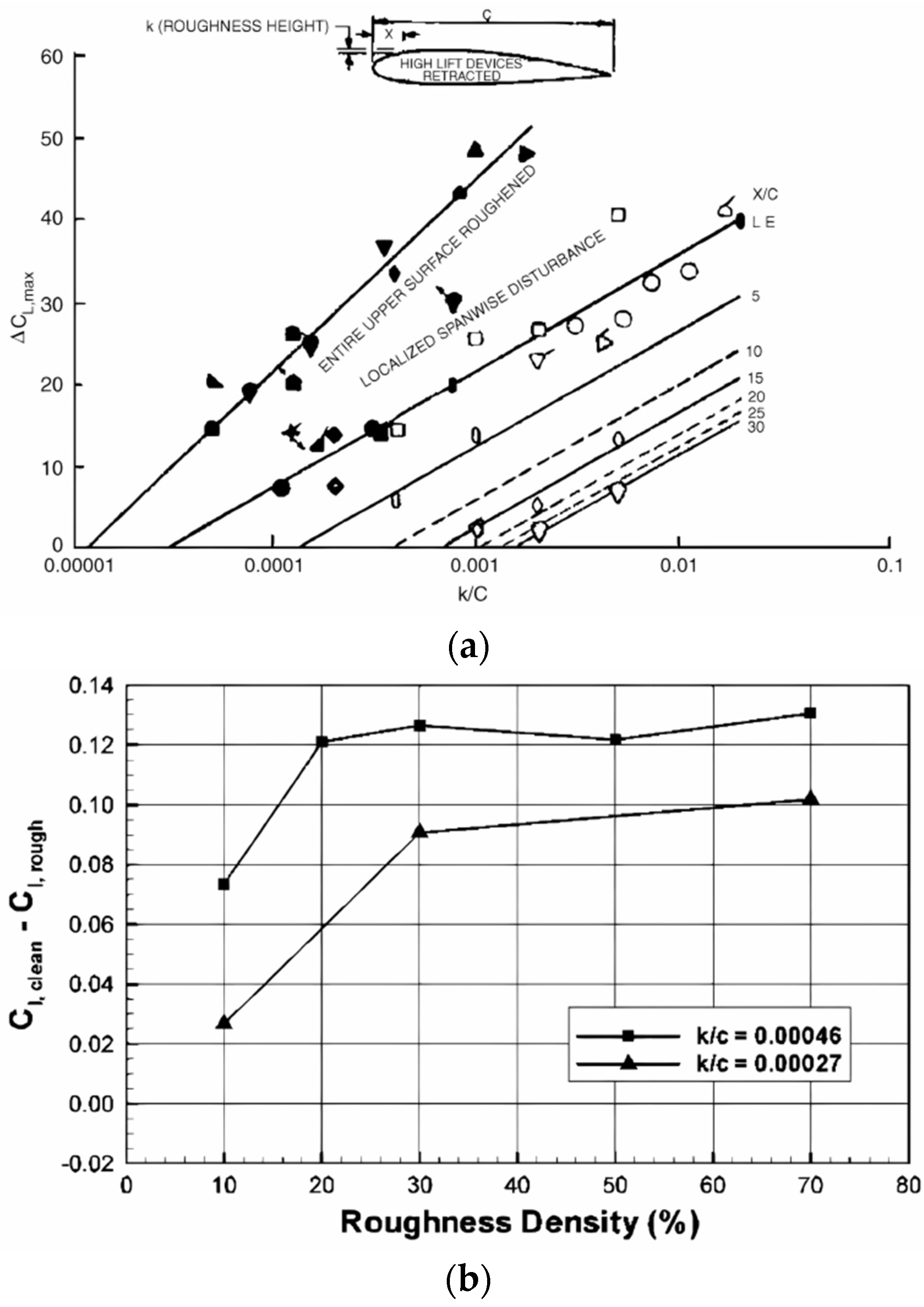
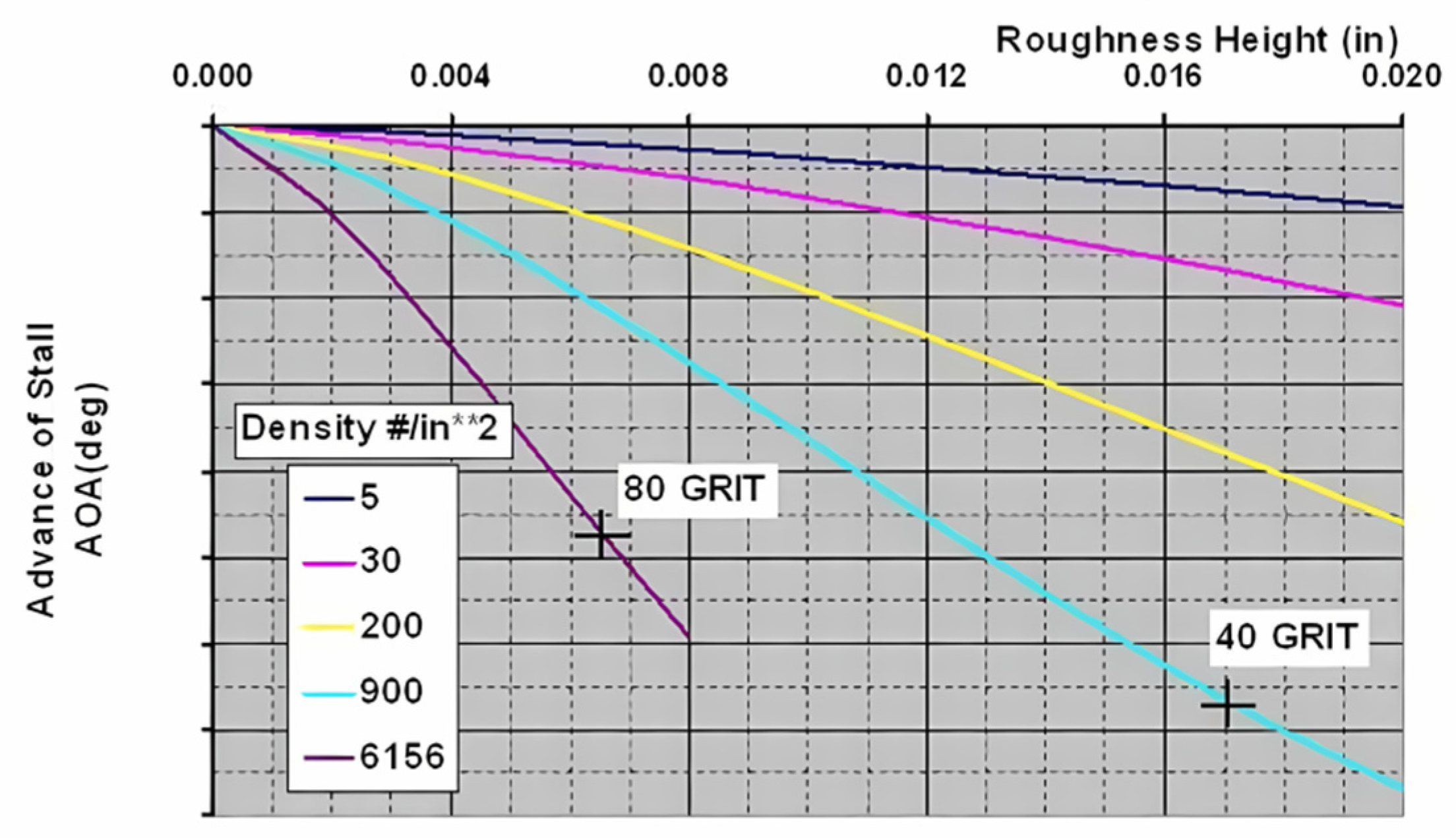
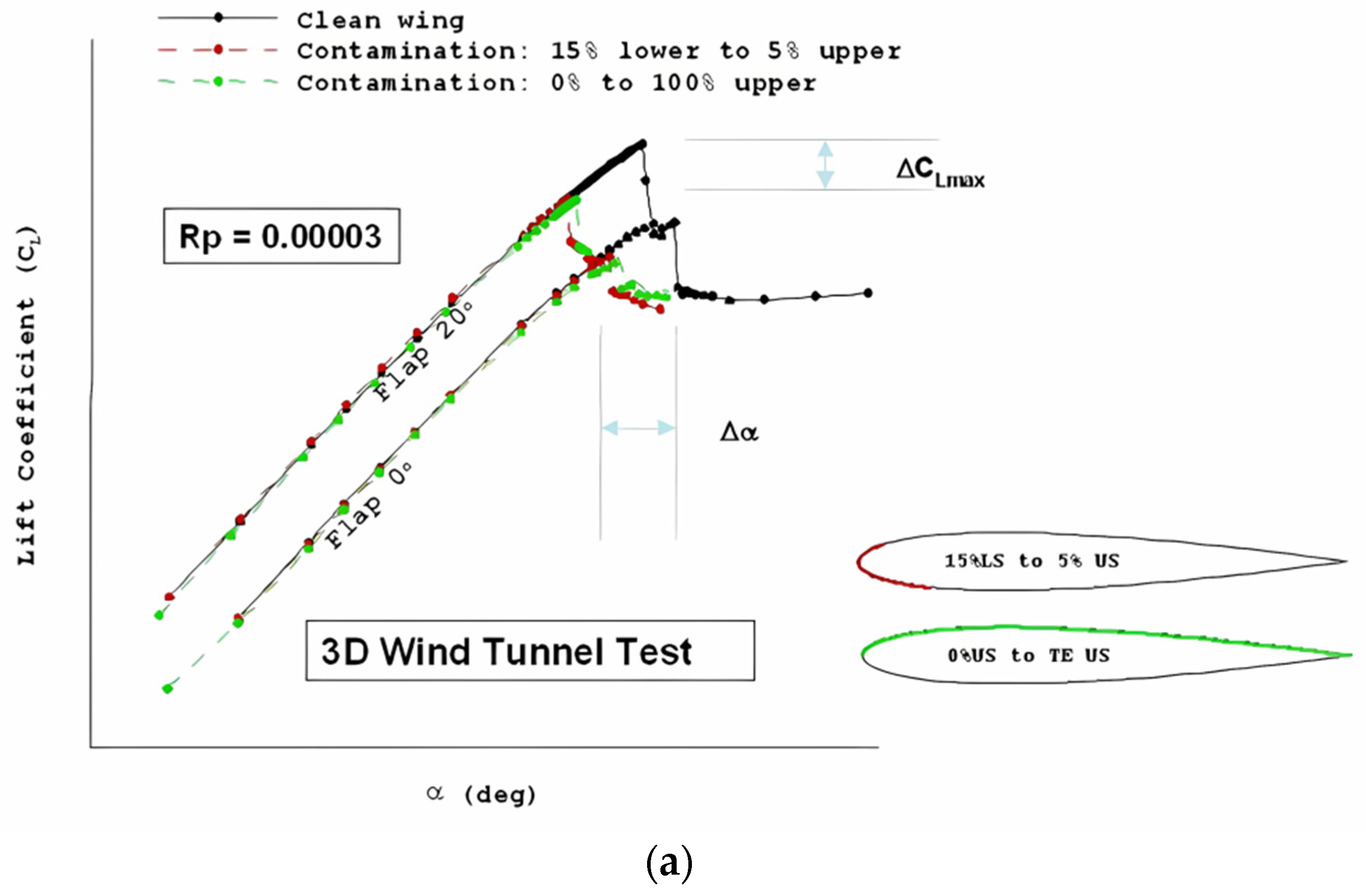
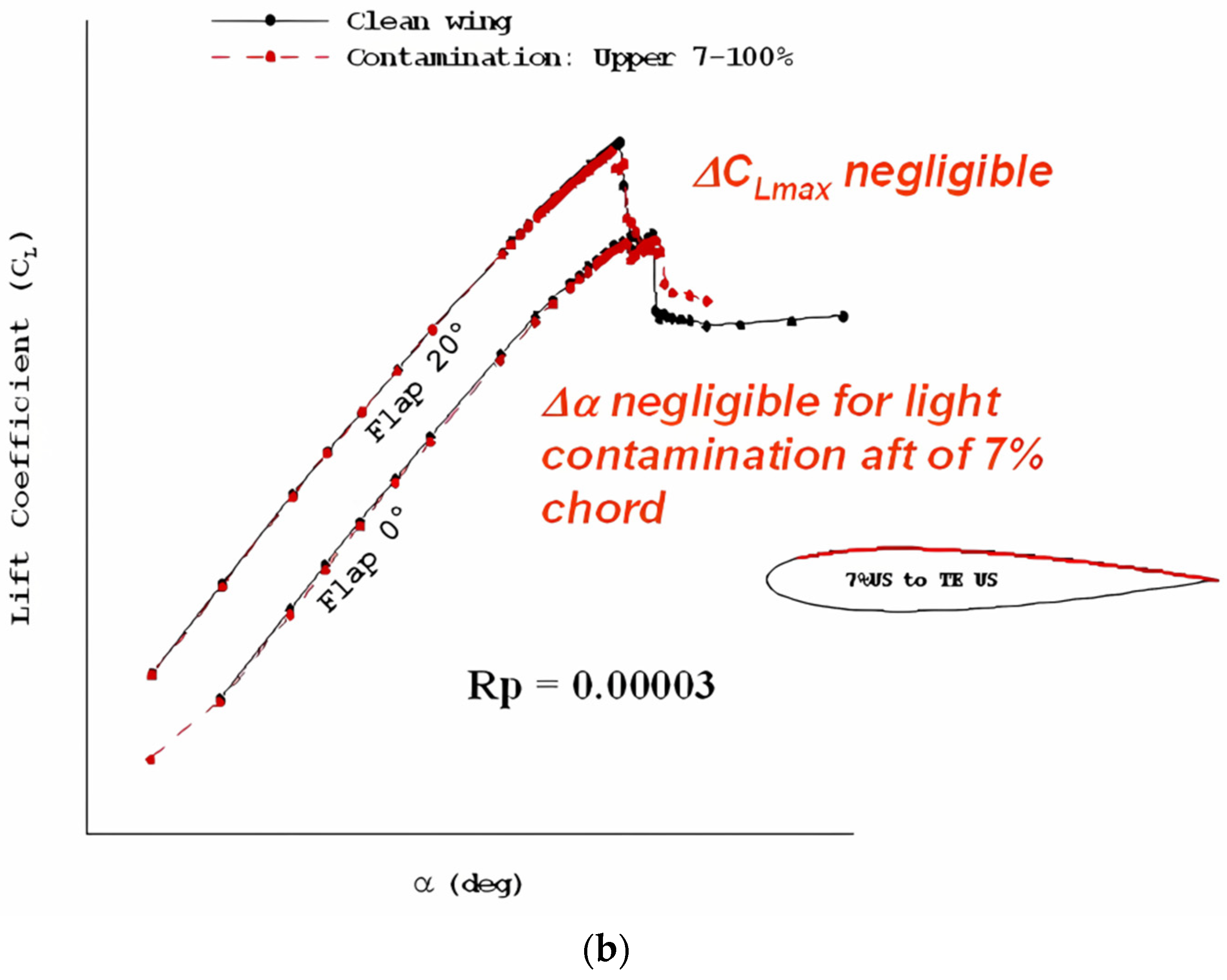
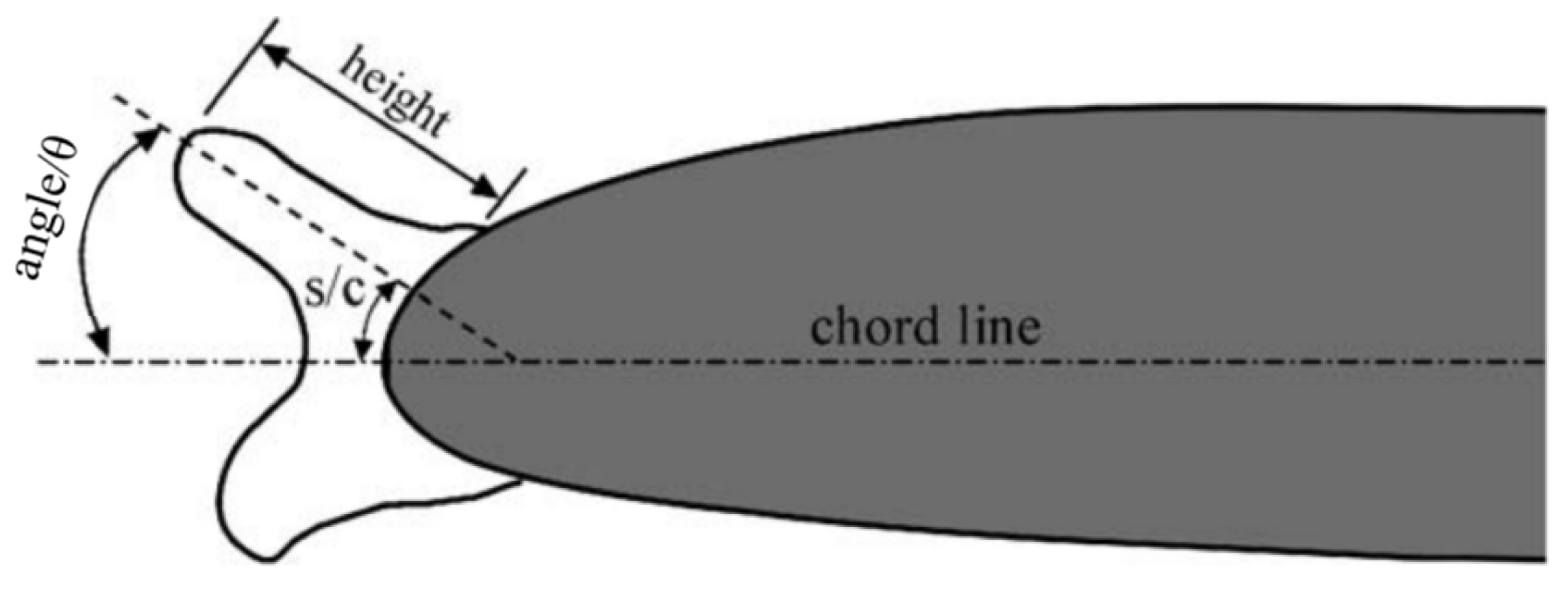
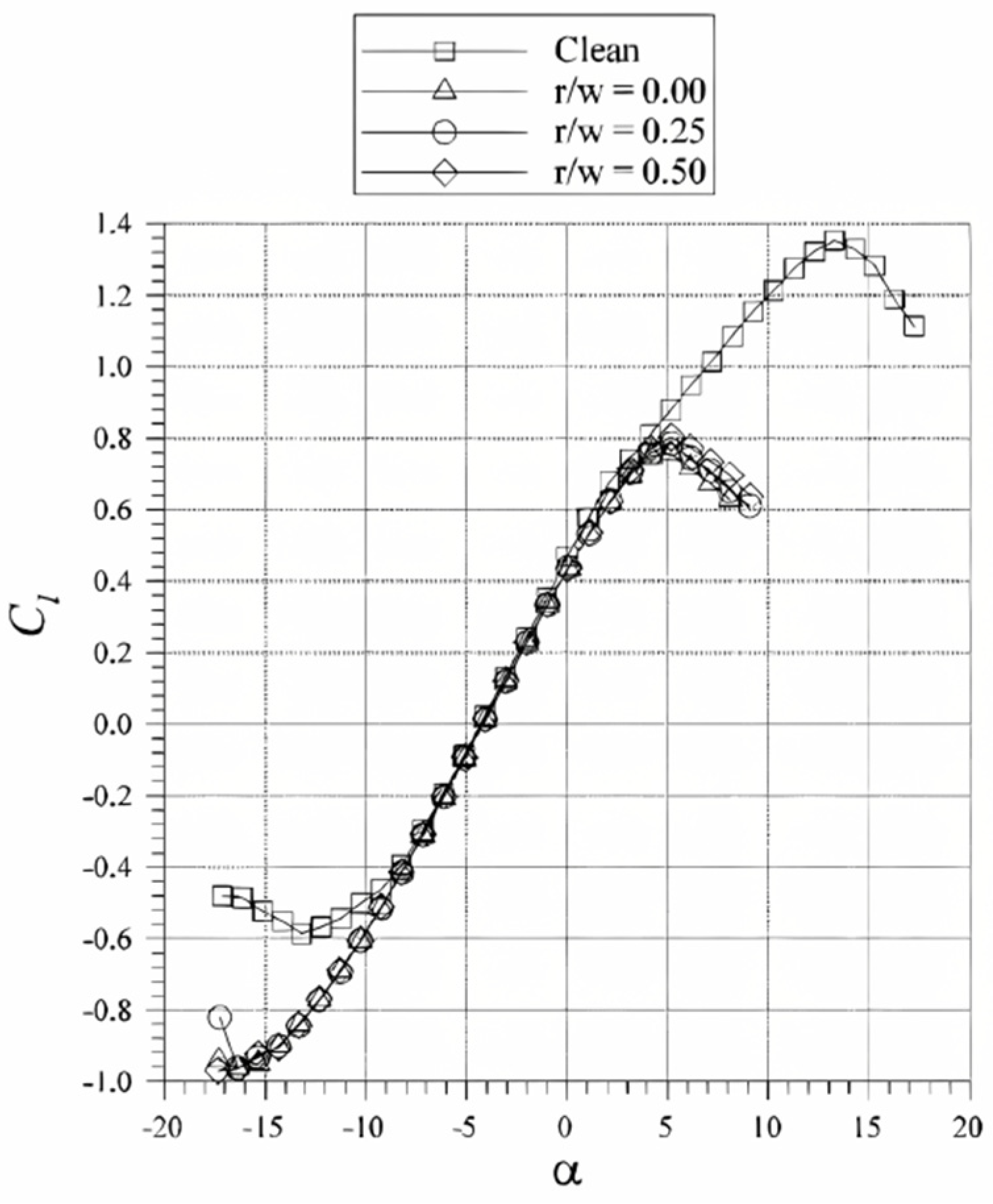
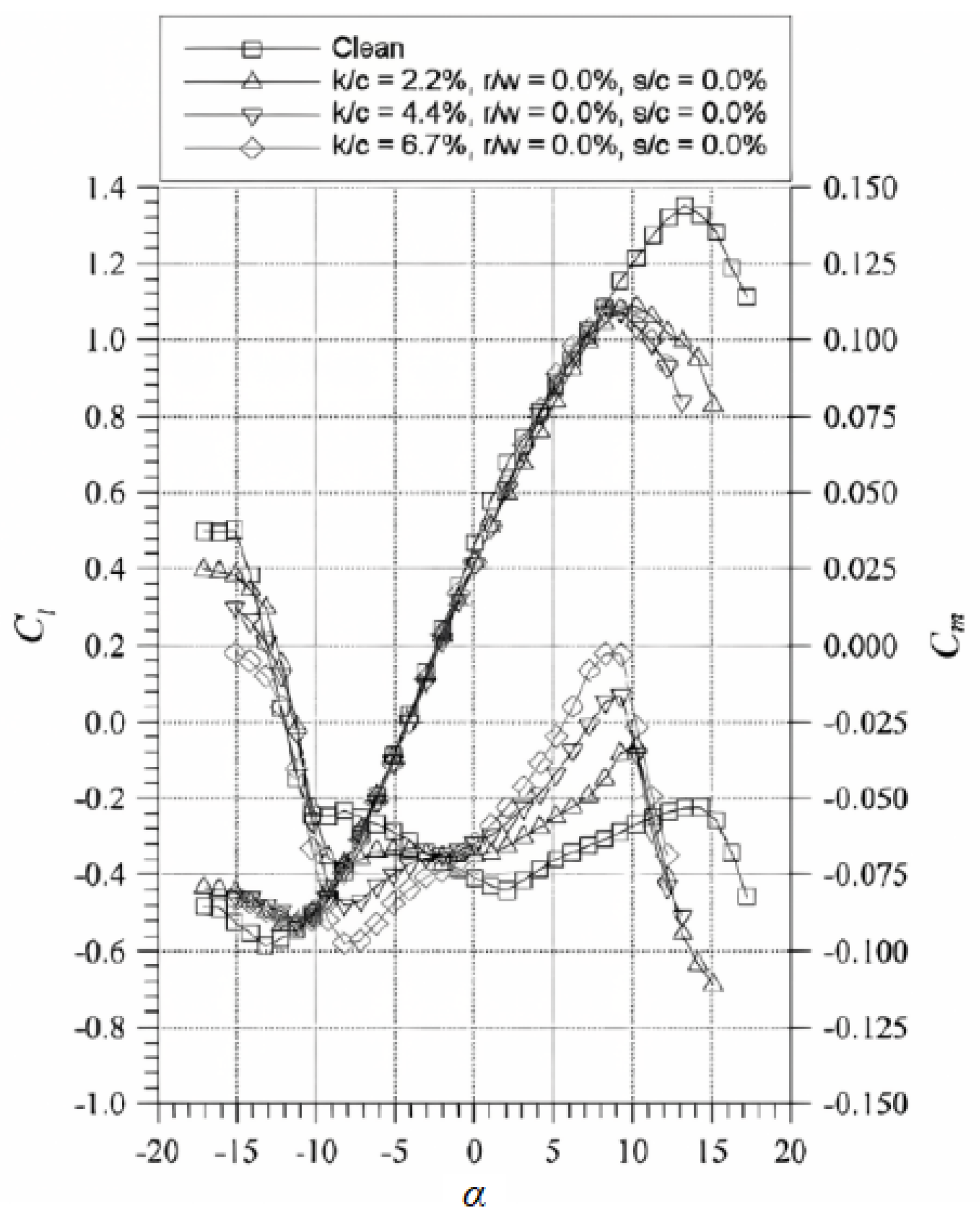
3.1. The Roughness of the Ice
- (a)
- The larger the roughness height, the more critical the effect on the aerodynamic performance of the airfoil will be. The effect will no longer increase after the roughness density reaches 30%.
- (b)
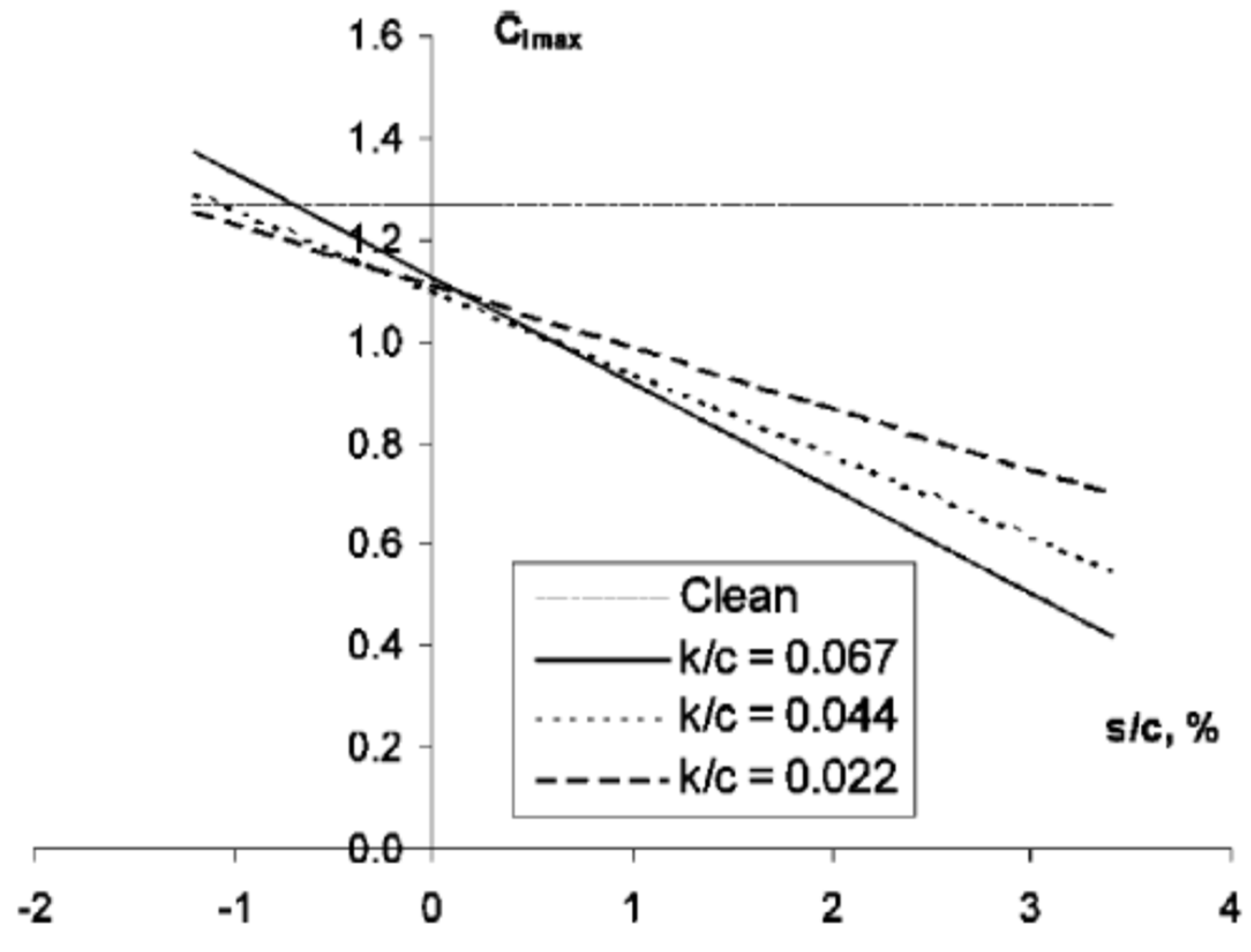
- The effect of roughness on the stall AOA and the maximum lift is most critical within 5% of the chord direction of the upper surface of the airfoil, and the wider the distribution range, the more critical it is. Thus, the geometric parameters to determine the criticality of the roughness of the ice can be defined as the roughness height and range.
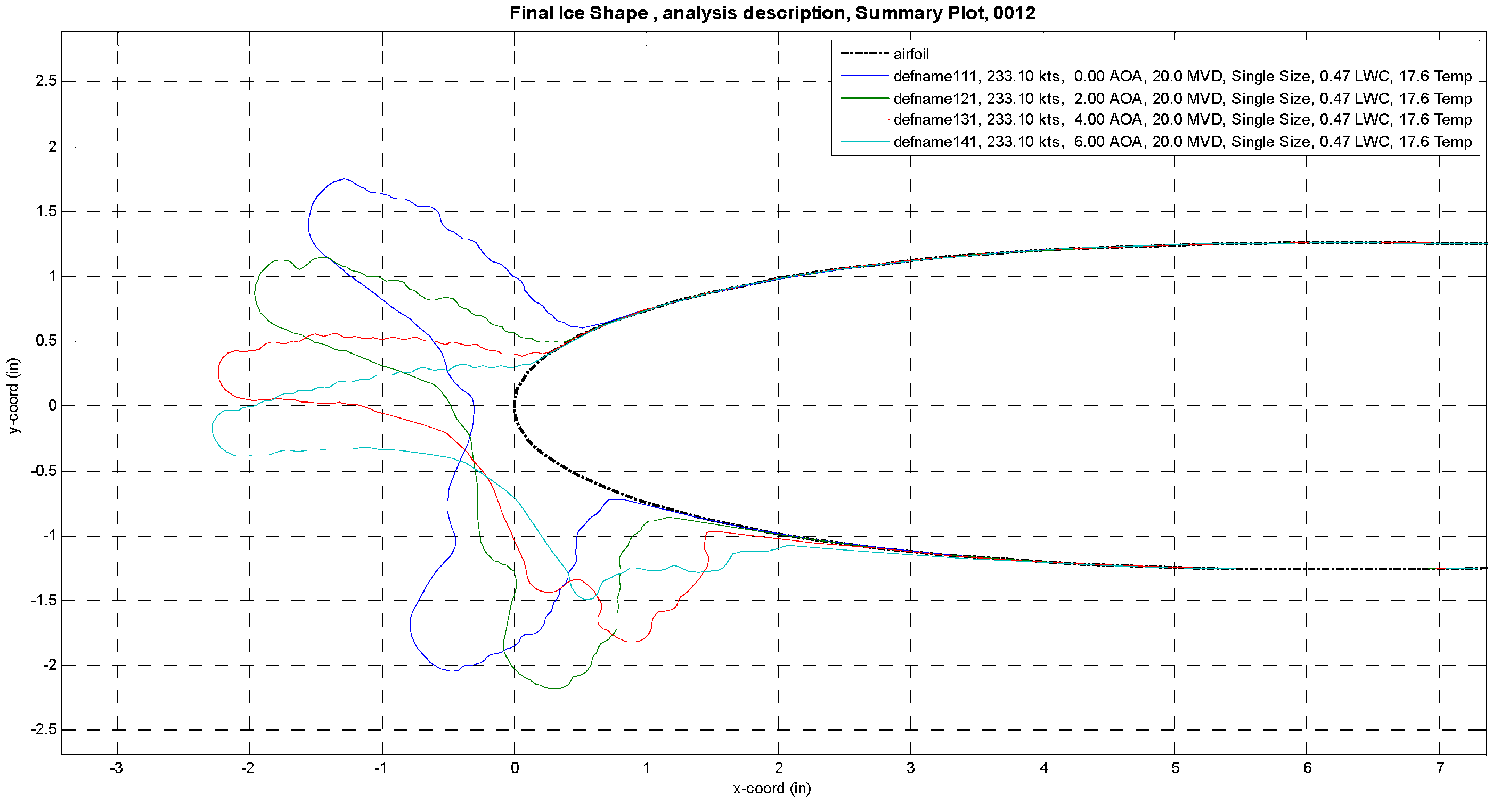
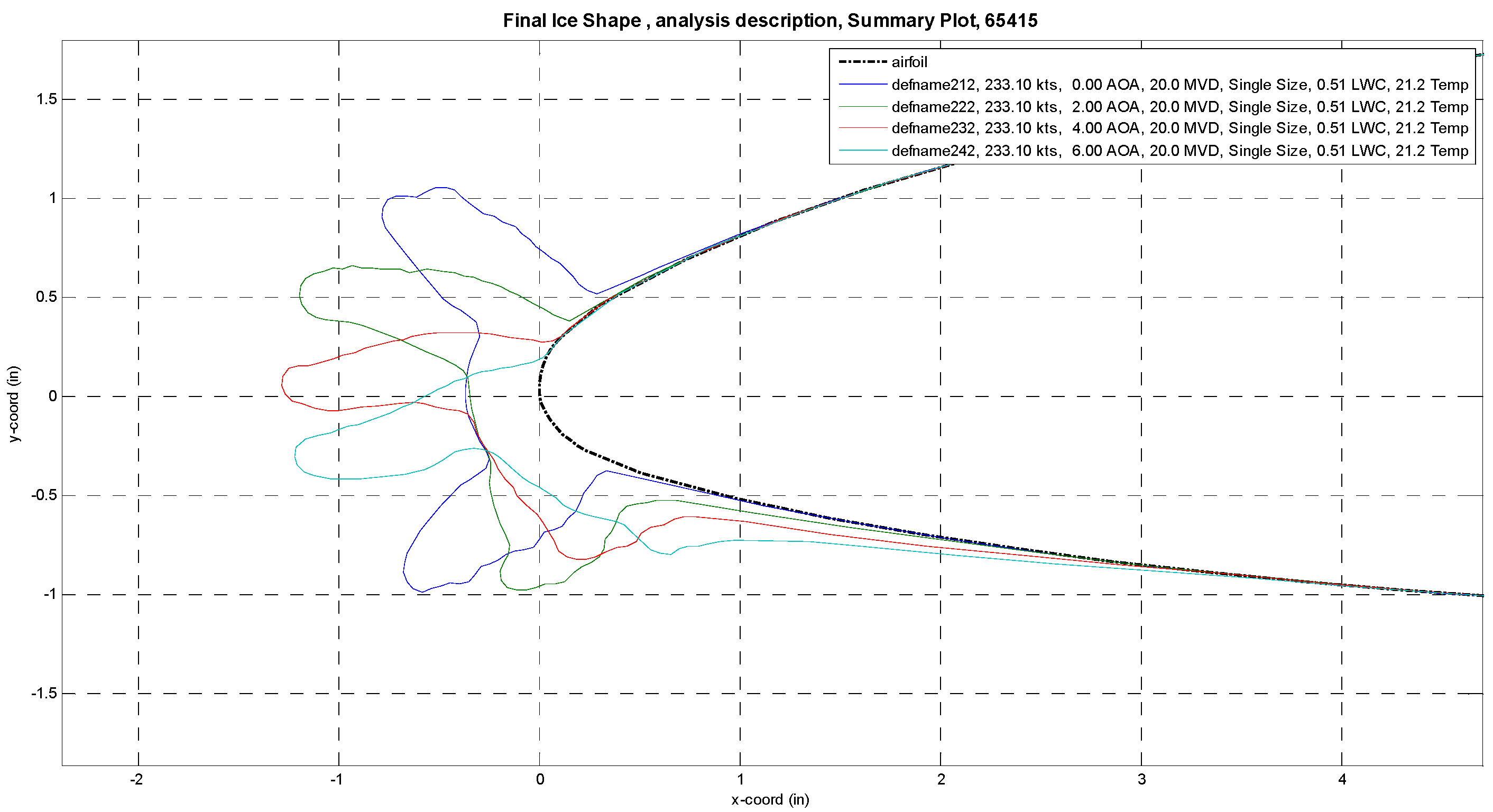
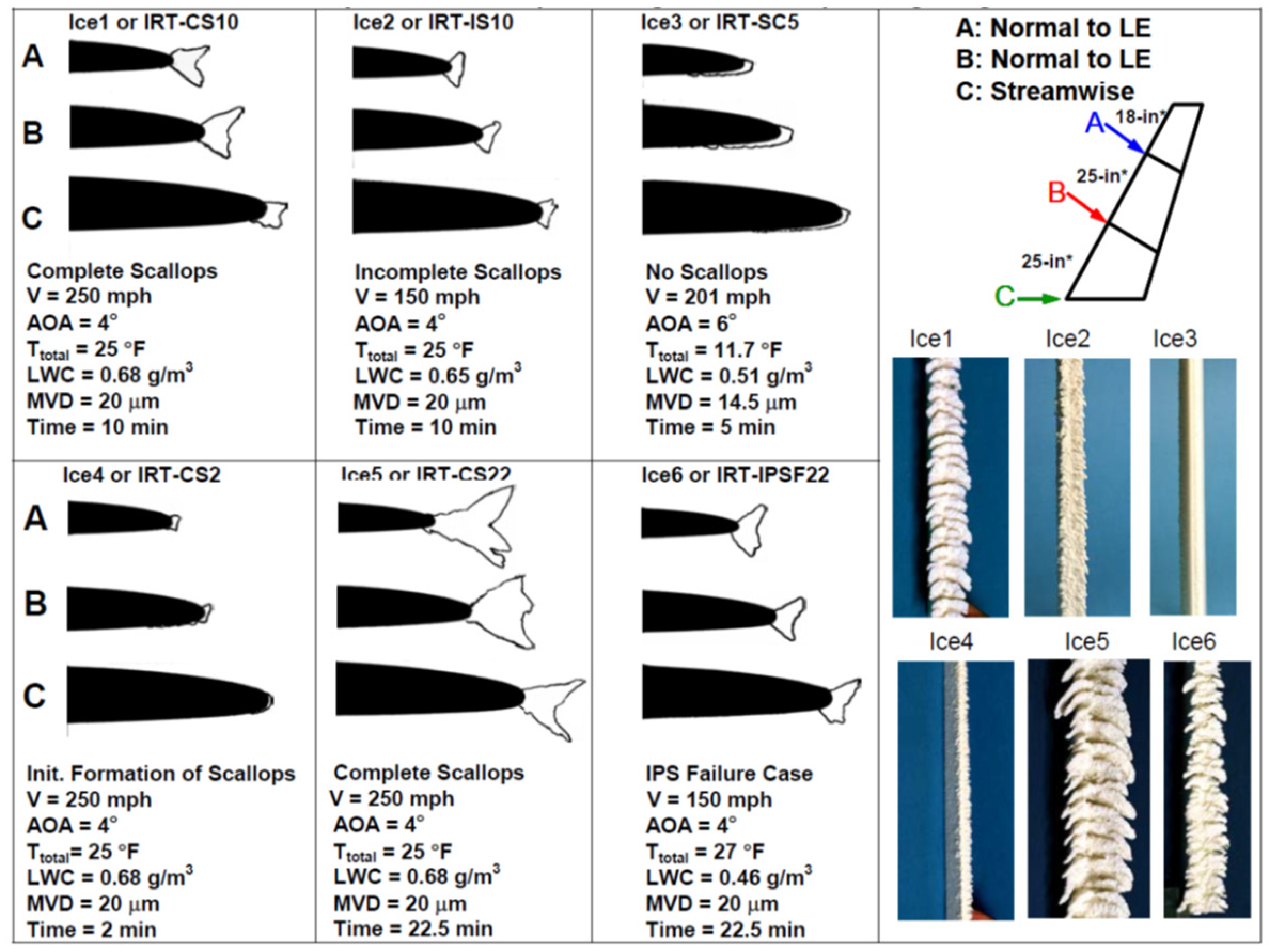
3.2. The Horn Ice
- (a)
- The height and angle of the horn are the main factors affecting the aerodynamic performance of iced airfoils. With a certain horn angle, the amount of effect increases with the height, but the correlation is non-linear. With a certain height, the amount of loss at the maximum lift is basically linearly related to the angle of the horn.
- (b)
- The larger the distance of the highest point of the horn from the chord line of the airfoil on the positive lift surface, the more critical the effect on the aerodynamic performance will be, i.e., the larger the height of the projection of the horn in the direction of lift, the more critical the effect on the aerodynamic performance will be. Thus, the geometric parameter to determine the criticality can be defined as the total projection height in the direction of lift for the horn ice.
- (c)
- The lower horn has a large effect on the drag of the airfoil but does not affect the stall performance. For the specified aircraft, flight envelope, and icing envelope, the maximum lift, stall AOA, and drag effects of double-horn ice are the most critical.
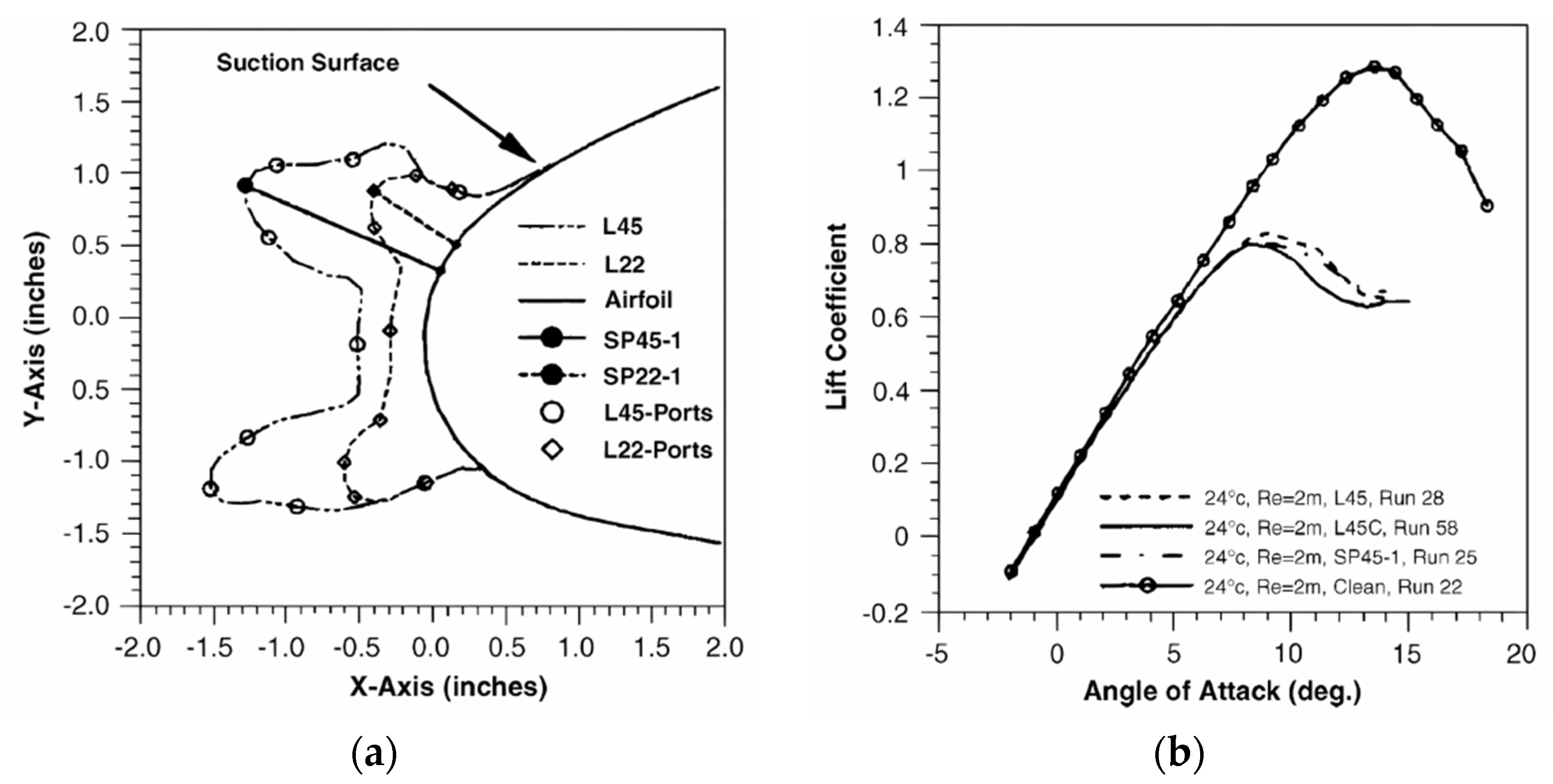
3.3. The Streamwise Ice
3.4. The Three-Dimensional Shrimp-Tail Ice
3.5. The Comparison of the Criticality of Different Ice Shapes
- (a)
- For the leading edge roughness ice, the larger the roughness height and the larger the distribution range near the leading edge on the upper surface, the more critical it will be.
- (b)
- For the leading edge horn ice, the larger the height of the upper horn and the further downstream it is, the more critical the effect on the maximum lift of the drag and the stall AOA will be. The larger the height of the projection of the lower horn in the opposite direction of the lifting force, the more critical the effect on the drag will be, which can be summarized as the larger the total height of the projection of the horn in the direction of the lifting force, the more critical it will be.
- (c)
- The effect of leading edge horn ice on the maximum lift and stall angle is greater than that of roughness ice and streamwise ice. For a given aircraft configuration, flight envelope, and icing condition, if the double-horn ice is generated, the corresponding effect on the maximum lift, the stall AOA, and the drag is the most critical.
4. The Determination of Criticality for Ice Shapes According to Flight Phases and Aircraft Components
4.1. The Determination of Criticality for Ice Shapes According to Flight Phases
4.2. The Determination of Criticality for Ice Shapes According to Aircraft Components
- (1)
- For the regulation at 25.103 of stall speed, the main verification is the stall speed, and the corresponding aerodynamic parameters are the maximum lift and the stall AOA. According to the law of the effect of ice shapes on stall performance, the conclusion can be drawn as follows:
- (a)
- For the roughness ice of takeoff, whether for protected or unprotected areas, from the leading-edge stationing point of each component, the larger the distribution range of roughness ice on the positive lift surface, the more critical it will be.
- (b)
- For the ice of the take-off final stage, if it is roughness ice, the criterion is the same as (a). If other factors such as minimum overrun capability are taken into consideration, resulting in longer flight time to reach the maximum level altitude and obvious ice accretion having already been generated on the wing surface, according to the criterion of the criticality of horn ice, the larger the projection height of the horn in the direction of the positive lift, the more critical it will be.
- (c)
- For the en route ice and the holding ice, if obvious ice accretion has already been generated, the same as in the second case of (b), at this time, the larger the projected height of the horn on the positive lift surface is, the more critical it will be.
- (2)
- For the regulation at 25.111 of the takeoff path, the main verification is the effect of the change in drag on the takeoff path after icing, and the corresponding aerodynamic parameters are drag and lift-to-drag ratio. For the takeoff ice, the criterion of roughness can be applied. For the takeoff ice of the final stage, and the total projected height should be confirmed.
- (3)
- For the performance regulations at 25.119, 25.121, 25.123, and 25.125, the main aerodynamic parameter to be examined is the lift-to-drag ratio, and for the takeoff ice of the final stage, route ice and holding ice, the icing time is long, thus the critical ice is generally horn-like, thus the criterion of horn ice can be applied.
- (4)
- For the controllability regulations at 25.143, 25.145, 25.147, and 25.161, as well as the stability regulations at 25.171, 25.175, 25.177, and 25.181, the criticality of ice can be determined according to the focus performance of components. For the fixed lift components, the ice shape, which leads to a decrease in the maximum lift coefficient and stall AOA, is the most critical. For the movable lift components, besides the above mentioned, the decrease in the efficiency of the control surface and the increase in trailing edge separation are taken into consideration. For the horizontal tail, the ice accretion mainly affects the pitching moment and controls surface efficiency. The criticality can be determined by the decrease in trimming capability. For the vertical tail, the icing effect on side force and rudder efficiency is the most concerning. Since these characteristics are all directly related to the stall performance or separation characteristics of each component, the determination of the criticality of different components is consistent, i.e., the criterion of roughness ice and horn ice can be applied based on the required icing condition.
5. Conclusions
- (1)
- Different from the previous study, which mainly focused on the ice shapes and effects of the holding flight phase, according to the aerodynamic performance required to be examined and the icing definition of each flight phase in the latest version of CCAR-25, the classification of the ice shapes in view of geometry characteristics and the corresponding aerodynamic performance to be examined is performed with the factors to be considered in the advisory circulars.
- (2)
- Based on the aerodynamic effect of ice shapes with different characteristics, the correlation between the geometric parameters and the criticality of ice shapes is clarified. According to the possible ice shapes in different flight phases, the criteria for determining the criticality of ice shapes corresponding to each flight phase and aircraft component are summarized.
- (3)
- The most critical geometry among various ice shapes is identified. For the specified aircraft, flight envelope, and icing envelope, the maximum lift, stall AOA, and drag effects of double-horn ice are the most critical. The conclusion of determining the critical ice shapes based on the 2D profiles is still applicable for the 3D swept-back wing.
- (4)
- The dominant geometric parameters to determine the criticality for typical ice shapes are defined. For the roughness of the ice, the larger the roughness height near the leading edge, the more critical it will be. For the horn ice, the larger the total height of the projection of the horn in the direction of the lifting force, the more critical it will be.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| The definition of acronyms | |
| CCAR-25 | the part 25 of China civil aviation regulation |
| NTSB | national transportation safety board |
| ASRS | aviation safety reporting system |
| AC | advisory circular |
| DTO | delayed turn on |
| NASA | National Aeronautics and Space Administration |
| AOA | angle of attack |
| Cl | coefficient of lift |
| Clmax | maximum coefficient of lift |
| Cd | coefficient of drag |
| L/D | lift to drag ratio |
| αst | AOA at stall |
| Cn | yaw moment coefficient |
| Cm | pitching moment coefficient |
| Eff | control effectiveness |
| Stab | longitudinal and lateral directional stability |
| GLC305 | Gates Learjet Corporation-305 |
| NLF414 | Natural Laminar Flow-414 |
| LWC | liquid water contents |
| MVD | median volume diameter |
| ICTS | ice-contaminated tailplane stall |
| SLD | supercooled large droplets |
References
- Cebeci, T.; Kafyeke, F. Aircraft icing. Annu. Rev. Fluid Mech. 2003, 35, 11–21. [Google Scholar] [CrossRef]
- Cao, Y.H.; Tan, W.; Wu, Z.L. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Appiah-Kubi, P. US Inflight Icing Accidents and Incidents, 2006 to 2010; The University of Tennessee: Knoxville, TN, USA, 2011. [Google Scholar]
- Aviation Safety Network (ASN) Database. Available online: https://asn.flightsafety.org/database/ (accessed on 1 August 2024).
- Joint Aviation Requirements (JAR)-25: Large Aeroplanes; Joint Aviation Authorities: Schiphol-Rijk, The Netherlands, 2022.
- Federal Aviation Regulations (FAR) Part 25: Airworthiness Standards Transport Category Aircrafts; Federal Aviation Administration: Washington, DC, USA, 2022.
- CCAR-25-R4; Airworthiness Standards: Transport Category Airplanes. China Civil Aviation Regulations: Beijing, China, 2016.
- AC25.1419; Certification of Transport Category Airplanes for Flight in Icing Conditions. Federal Aviation Administration: Washington, DC, USA, 1999.
- AC20-73A; Protection Aircraft Ice. Federal Aviation Administration: Washington, DC, USA, 2006.
- AC25-25; Performance and Handling Characteristics in the Icing Conditions Specified in Part 25. Federal Aviation Administration: Washington, DC, USA, 2007.
- Broeren, A.P.; Addy, H.E., Jr.; Bragg, M.B.; Busch, G.T.; Montreuil, E. Aerodynamic Simulation of Ice Accretion on Airfoils; NASA/TP-2011-216929; Glenn Research Center: Sandusky, OH, USA, 2011.
- Cao, Y.H.; Yuan, K.; Li, G. Effects of ice geometry on airfoil performance using neural networks prediction. Aircr. Eng. Aerosp. Technol. 2011, 83, 266–274. [Google Scholar] [CrossRef]
- Hu, T.; Lv, H.; Tian, B.; Su, D. Choosing critical ice shapes on airfoil surface for the icing certification of aircraft. Procedia Eng. 2014, 80, 456–466. [Google Scholar] [CrossRef]
- Raj, L.P.; Yee, K.; Myong, R.S. Sensitivity of ice accretion and aerodynamic performance degradation to critical physical and modeling parameters affecting airfoil icing. Aerosp. Sci. Technol. 2020, 98, 105659. [Google Scholar]
- Oztekin, E.S.; Riley, J.T.; Pellicano, P. A parametric study on the aerodynamics of ice accretions on surfaces with anti/de-icing systems. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual Event, 15–19 June 2020; p. 2844. [Google Scholar]
- Nath, P.; Lokanathan, N.; Wang, J.; Benmeddour, A.; Nichman, L.; Ranjbar, K.; Hickey, J.P. Parametric investigation of aerodynamic performance degradation due to icing on a symmetrical airfoil. Phys. Fluids 2024, 36, 75117. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Parkins, D. Developing critical ice shapes for use in aircraft development and certification. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8–11 January 2007; p. 91. [Google Scholar]
- Zhou, F.; Feng, L.; Xu, C.; Zhao, K.; Han, Z. Determination and verification of critical ice shape for the certification of civil aircraft. J. Exp. Fluid Mech. 2016, 30, 8–13. [Google Scholar]
- Dongyu, Z.; Fukun, Z.; Runan, P.; Yuan, W.; Lei, Y.; Yijun, N.; Jun, D. Research on critical ice shape determination and its effects on aerodynamics. Acta Aerodyn. Sin. 2016, 34, 714–720. [Google Scholar]
- Zhang, Q. Determination method of critical ice shapes for large civil aircraft. Civ. Aircr. Des. Res. 2019, 1, 53–58. [Google Scholar]
- Lynch, F.T.; Khodadoust, A. Effects of ice accretions on aircraft aerodynamics. Prog. Aerosp. Sci. 2001, 37, 669–767. [Google Scholar] [CrossRef]
- Gent, R.W.; Dart, N.P.; Cansdale, J.T. Aircraft icing. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Eng. Sci. 2000, 358, 2873–2911. [Google Scholar] [CrossRef]
- Shin, J. Characteristics of surface roughness associated with leading-edge ice accretion. J. Aircr. 1996, 33, 316–321. [Google Scholar] [CrossRef]
- Tanner, C.E. The effect of wing leading edge contamination on the stall characteristics of aircraft. SAE Trans. 2007, 116, 576–588. [Google Scholar]
- Bowden, D.T. Effect of Pneumatic De-Icers and Ice Formations on Aerodynamic Characteristics of an Airfoil; National Advisory Committee for Aeronautics: Washington, DC, USA, 1956.
- Kim, H.; Bragg, M.B. Effects of leading-edge ice accretion geometry on airfoil performance. In Proceedings of the 17th Applied Aerodynamics Conference, Norfolk, VA, USA, 28 June–1 July 1999; p. 3150. [Google Scholar]
- Wright, W. User’s Manual for LEWICE Version 3.2; NASA E-15537; Glenn Research Center: Sandusky, OH, USA, 2008.
- Addy, H.E. Ice Accretions and Icing Effects for Modern Airfoils; National Aeronautics Administration, Glenn Research Center: Sandusky, OH, USA, 2000.
- Bragg, M.B.; Khodadoust, A. Experimental measurements in a large separation bubble due to a simulated glaze ice shape. NASA 19880034853. In Proceedings of the 26th Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1988. [Google Scholar]
- Papadakis, M.; Gile Laflin, B.; Youssef, G.; Ratvasky, T. Aerodynamic scaling experiments with simulated ice accretions. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 833. [Google Scholar]
- Papadakis, M.; Yeong, H.W.; Vargas, M.; Potapczuk, M. Aerodynamic performance of a swept wing with ice accretions. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 731. [Google Scholar]
- Shin, J.; Bond, T.H. Experimental and computational ice shapes and resulting drag increase for a NACA 0012 airfoil. In Proceedings of the California State Univ., The Fifth Symposium on Numerical and Physical Aspects of Aerodynamic Flows, Long Beach, CA, USA, 13–15 January 1992. [Google Scholar]


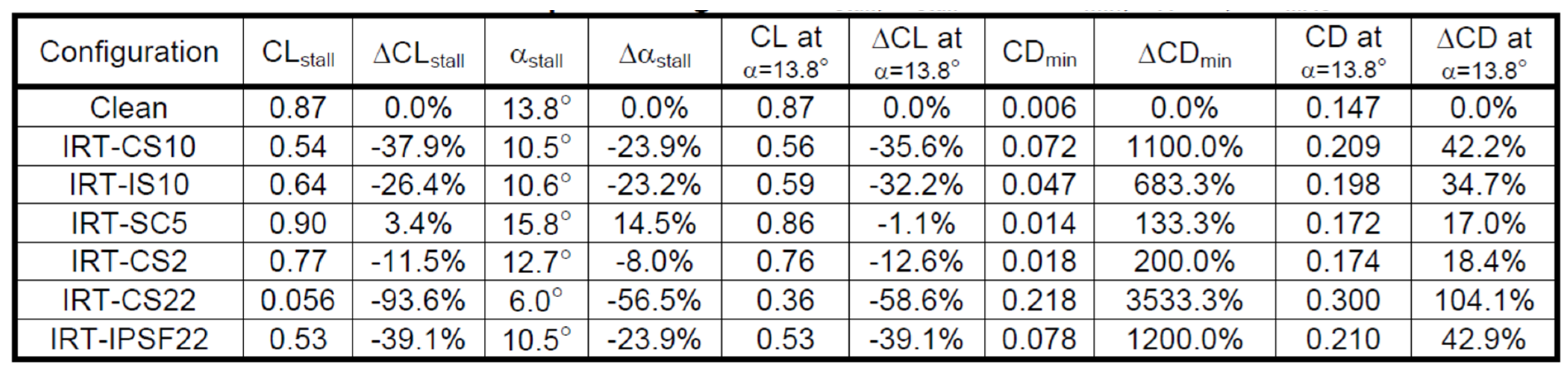
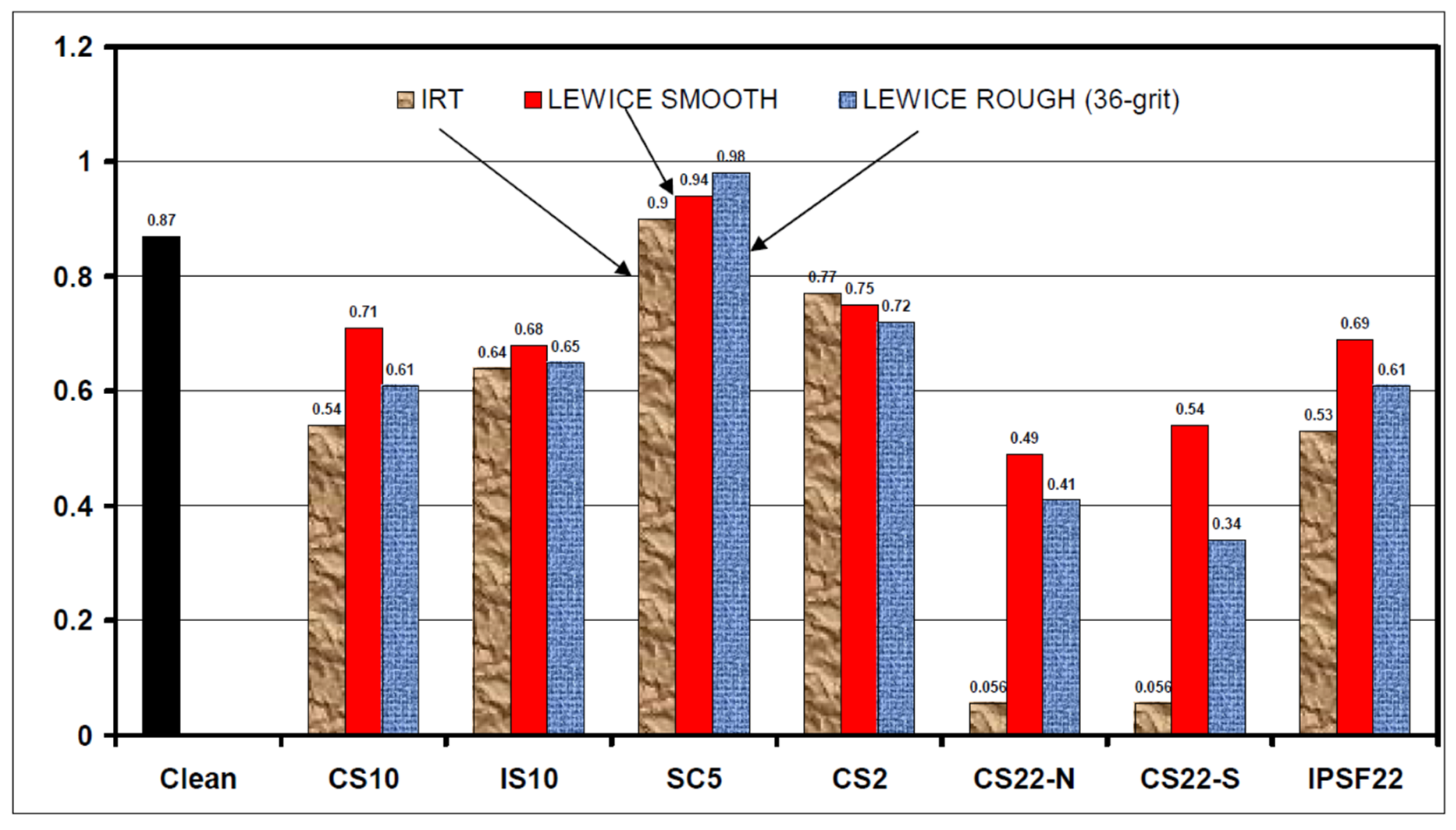
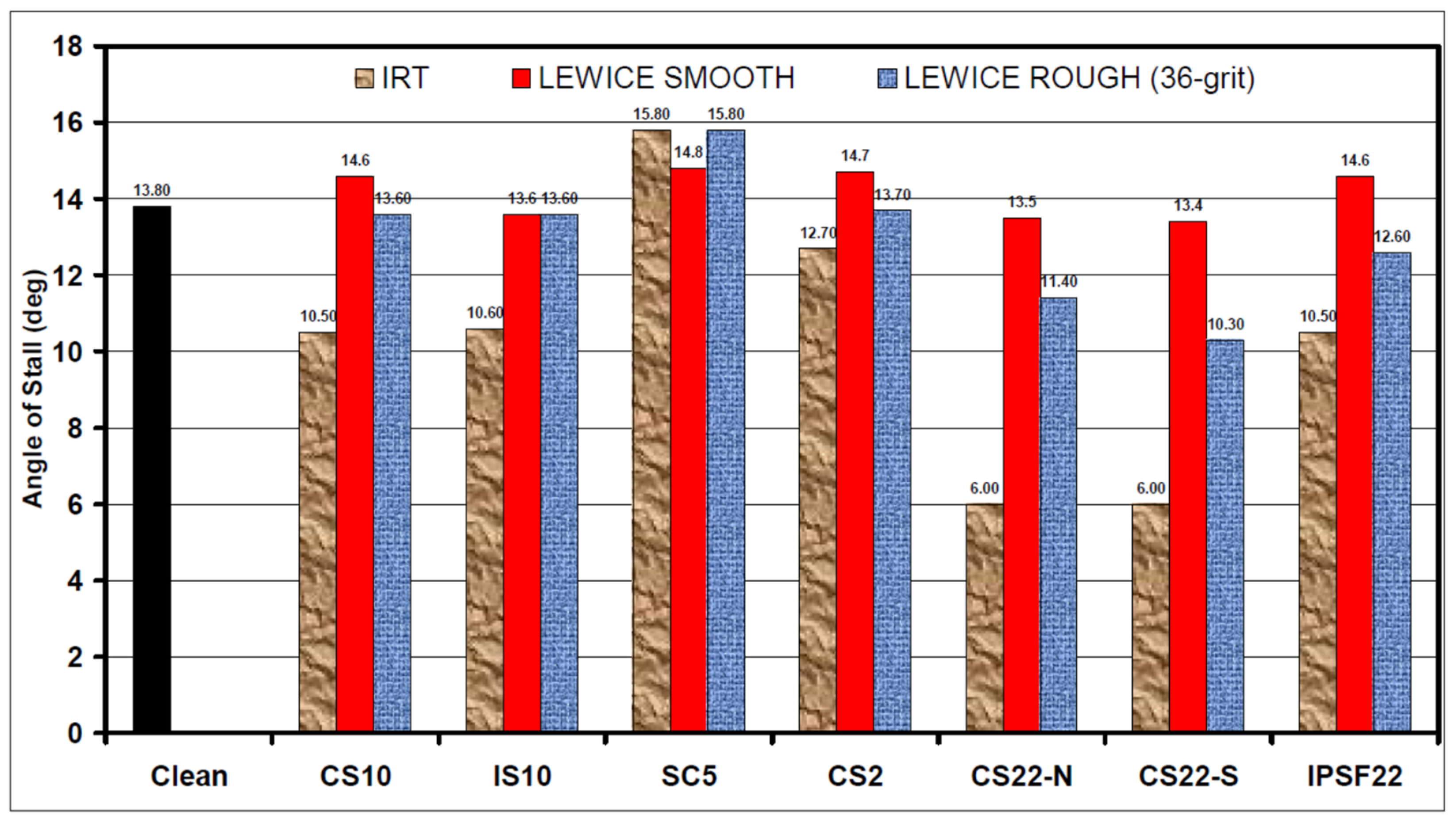


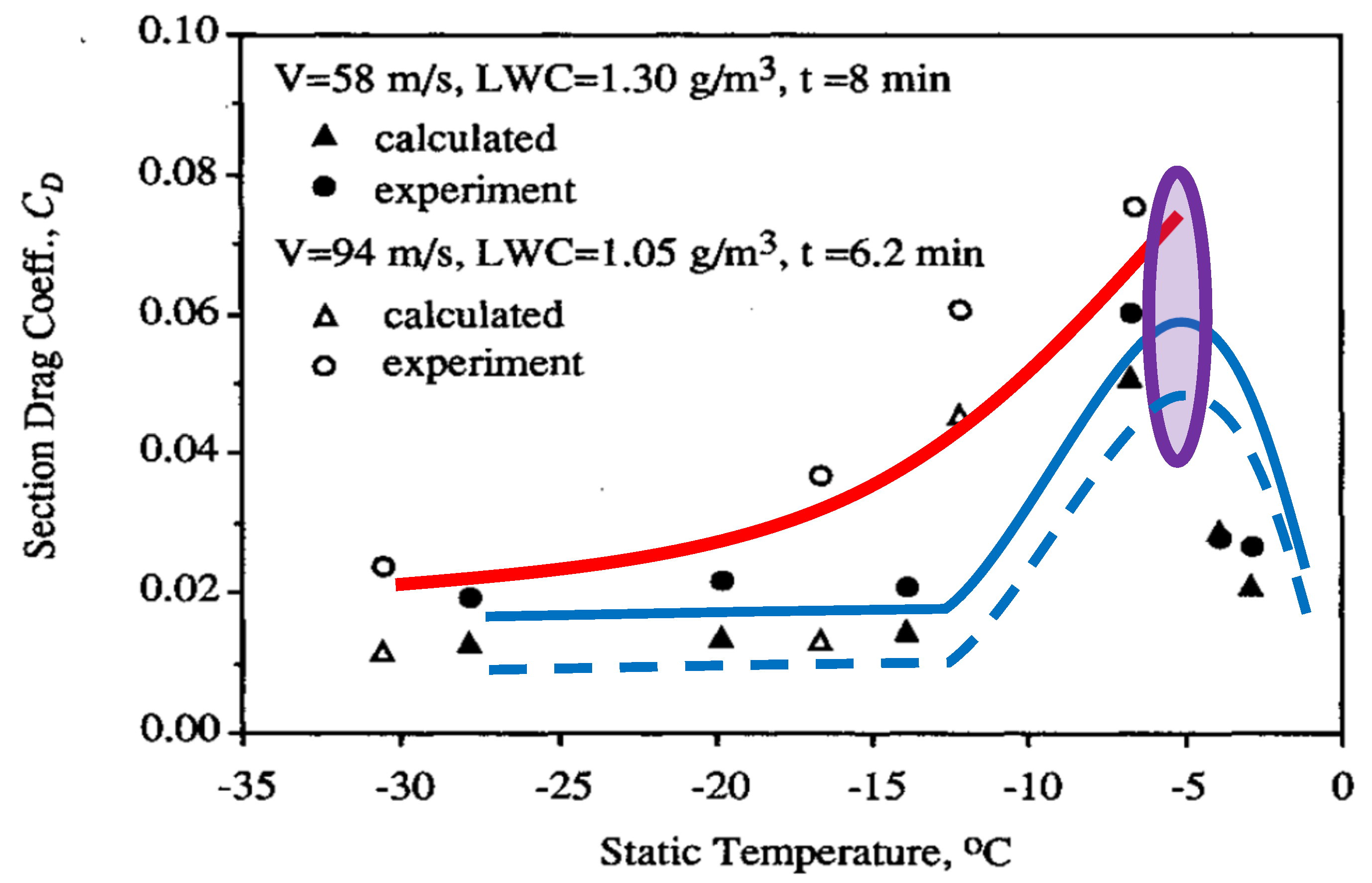
| Chapters | Contents | Recommended Ice Shapes | Aerodynamic Performance | ||||||||
| Performance | Clmax | Cd | L/D | αst | Cl | Cm | Eff | Stab | Cn | ||
| 25.103 | Stall speed | Takeoff ice | ● | ● | |||||||
| Final takeoff ice | |||||||||||
| En route ice | |||||||||||
| Holding ice | |||||||||||
| 25.111 | Takeoff Path | Takeoff ice | ● | ● | |||||||
| 25.119 | Landing Climb: all-Engines-Operating | Holding ice | ● | ||||||||
| 25.121 | Climb: one-engine-inoperative | Final takeoff ice | ● | ||||||||
| 25.123 | En route flight paths | En route ice | ● | ||||||||
| 25.125 | Landing | Holding ice | ● | ● | |||||||
| Maneuverability and Stability | Clmax | Cd | L/D | αst | Cl | Cm | Eff | Stab | Cn | ||
| 25.143 | Control ability and maneuverability—general | Holding ice | ● | ● | ● | ● | ● | ||||
| i(2) | Roughness | ● | ● | ● | ● | ● | |||||
| j | DTO | ● | ● | ● | ● | ● | |||||
| 25.145 | Longitudinal control | Holding ice | ● | ● | ● | ● | |||||
| 25.147 | Directional and lateral control | Holding ice | ● | ● | ● | ● | ● | ||||
| 25.161 | Trim | Holding ice | ● | ● | ● | ● | |||||
| 25.171 | Stability—general | ● | ● | ● | ● | ||||||
| 25.175 | Demonstration of static longitudinal stability | Holding ice | ● | ● | ● | ● | |||||
| 25.177 | Static lateral—directional stability | Holding ice | ● | ● | ● | ● | |||||
| Stall | Clmax | Cd | L/D | αst | Cl | Cm | Eff | Stab | Cn | ||
| 25.201 25.203 | Stall demonstration Stall characteristics | Holding ice | ● | ● | ● | ● | ● | ● | |||
| 25.207 | Stall warning | Holding ice | ● | ● | ● | ● | ● | ● | |||
| DTO | ● | ● | ● | ● | ● | ● | |||||
| Failure ice | ● | ● | ● | ● | ● | ● | |||||
| 25.237 | Wind velocities | Landing ice | ● | ● | ● | ||||||
| 25.251 | Vibration and buffeting | Residual ice | ● | ● | ● | ||||||
| 25.1309 | Failure conditions | Failure ice | ● | ● | ● | ● | ● | ● | |||
| Flight Phase | Classification by the Geometry of Ice |
|---|---|
| Takeoff | Roughness ice |
| Final takeoff | Roughness ice |
| Small-size horn ice | |
| Holding | Large-size horn ice |
| En route | Small-size horn ice |
| DTO | Roughness ice |
| Failure | Large-size horn ice |
| Ice Shape | Reduction of Maximum Lift | Reduction of Stall AOA |
|---|---|---|
| Roughness ice | 0.13 | 2° |
| Horn ice | 0.64 | 8° |
| Streamwise ice | 0.32 | 3° |
| Flight Phase | Classification by Ice Geometry | Criterion of Criticality |
|---|---|---|
| Takeoff | Roughness ice | The larger the roughness height and the larger the distribution range (impact limit) of ice near the leading edge on the upper surface, the more critical it will be. |
| Final takeoff | Roughness ice | Same as the takeoff. |
| Small-size horn ice | 1. The larger the height of the upper horn and the further downstream, the more critical it will be. 2. The larger the total height of the projection of the horn in the direction of the lifting force, the more critical it will be. | |
| Holding | Large-size horn ice | Same as the second case of final takeoff. |
| En route | Small-size horn ice | Same as the second case of final takeoff. |
| DTO | Roughness ice | Same as the takeoff. |
| Failure | Large-size horn ice | Same as the second case of final takeoff. |
| Flight Phase | Protected Area of Slat | Unprotected Area of Slat | Horizontal Tail | Vertical Tail |
|---|---|---|---|---|
| Takeoff | The larger the upper impact limit and the roughness height, the more critical it will be. | The larger the lower impact limit and the roughness height, the more critical it will be. | The larger the impact limit, the more critical it will be. | |
| DTO | Same as takeoff | |||
| Final takeoff | Same as takeoff | |||
| The larger the total height of the projection of the horn in the direction of the lifting force, the more critical it will be. | The larger the total height of the projection of the horn in the direction of the trimming lifting force, the more critical it will be. | The larger the total height of the projection of the horn in the direction of the side force, the more critical it will be. | ||
| Holding | Same as the second case of final takeoff. | |||
| En route | Same as the second case of final takeoff. | |||
| Failure | Same as the second case of final takeoff. | |||
| ICTS | None | Same as the second case of final takeoff | None | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Qu, S.; Zhang, H.; Zhou, F.; Chen, Y. The Determination of Criticality for Ice Shapes Based on CCAR-25. Aerospace 2024, 11, 710. https://doi.org/10.3390/aerospace11090710
Huang X, Qu S, Zhang H, Zhou F, Chen Y. The Determination of Criticality for Ice Shapes Based on CCAR-25. Aerospace. 2024; 11(9):710. https://doi.org/10.3390/aerospace11090710
Chicago/Turabian StyleHuang, Xiong, Shiru Qu, Heng Zhang, Feng Zhou, and Yong Chen. 2024. "The Determination of Criticality for Ice Shapes Based on CCAR-25" Aerospace 11, no. 9: 710. https://doi.org/10.3390/aerospace11090710
APA StyleHuang, X., Qu, S., Zhang, H., Zhou, F., & Chen, Y. (2024). The Determination of Criticality for Ice Shapes Based on CCAR-25. Aerospace, 11(9), 710. https://doi.org/10.3390/aerospace11090710






