Progress of Experimental Studies on Oblique Detonation Waves Induced by Hyper-Velocity Projectiles
Abstract
1. Introduction
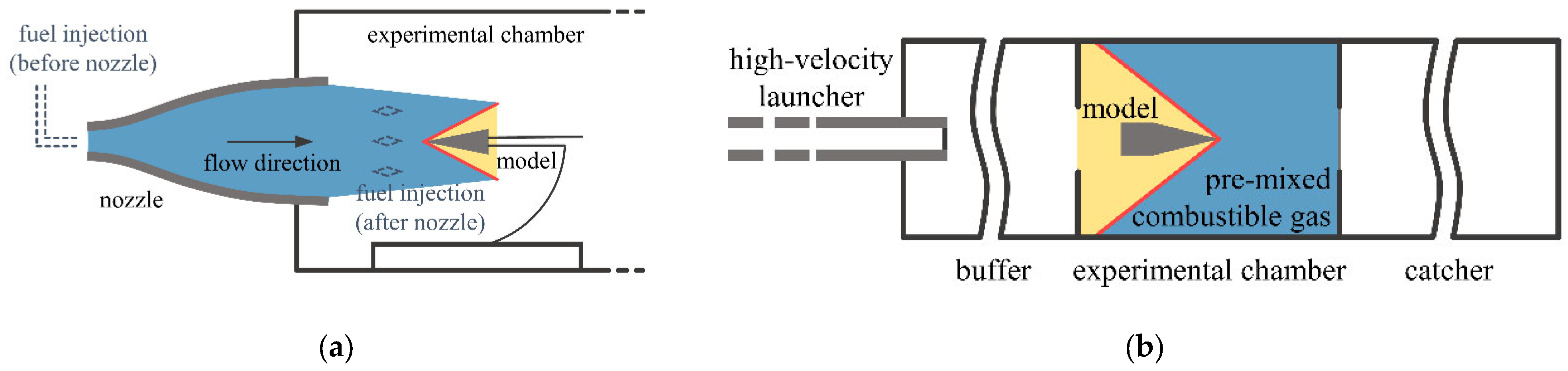
2. Experimental Method for Inducing ODWs Using Hyper-Velocity Projectiles
- (1)
- High-velocity launcher: This component accelerates the model to a predetermined velocity. Existing studies have employed either light gas guns or smoothbore powder guns. Powder guns feature mature technology and larger calibers; however, their maximum firing speed is limited by the sound speed of the gunpowder gas. In contrast, light gas guns can achieve higher firing speeds to meet their experimental requirements, making them more widely used in recent research.
- (2)
- Experimental section: This section includes a buffer chamber, an experimental chamber, and a catcher. After the model is launched, the high-temperature and high-pressure driving gas is also expelled from the muzzle. The buffer chamber mitigates its impact on the oblique detonation experiments. It is typically filled with low-pressure gases (e.g., N2 or CO2) that do not react with the driving gas. The experimental chamber is pre-filled with the experimental gases, and the model breaks through a diaphragm to initiate the ODW. The catcher stops the model after it exits the experimental chamber.
- (3)
- A timing control system regulates signal generation for the measurement apparatus to precisely gather and record experimental data. Trigger timing typically hinges on methods like pressure sensor signals, laser–photodiode signals, changes in magnetic field strength from model-mounted magnets, and the impact line method, used to measure the model’s position or velocity.
- (4)
- A measurement system typically incorporates optical, pressure, and optical signal measurements. Optical techniques such as schlieren and shadowgraph are predominantly used, while pressure and optical signals effectively discern the occurrence of chemical reactions following a shock wave.

3. Progress in Experimental Studies on ODW
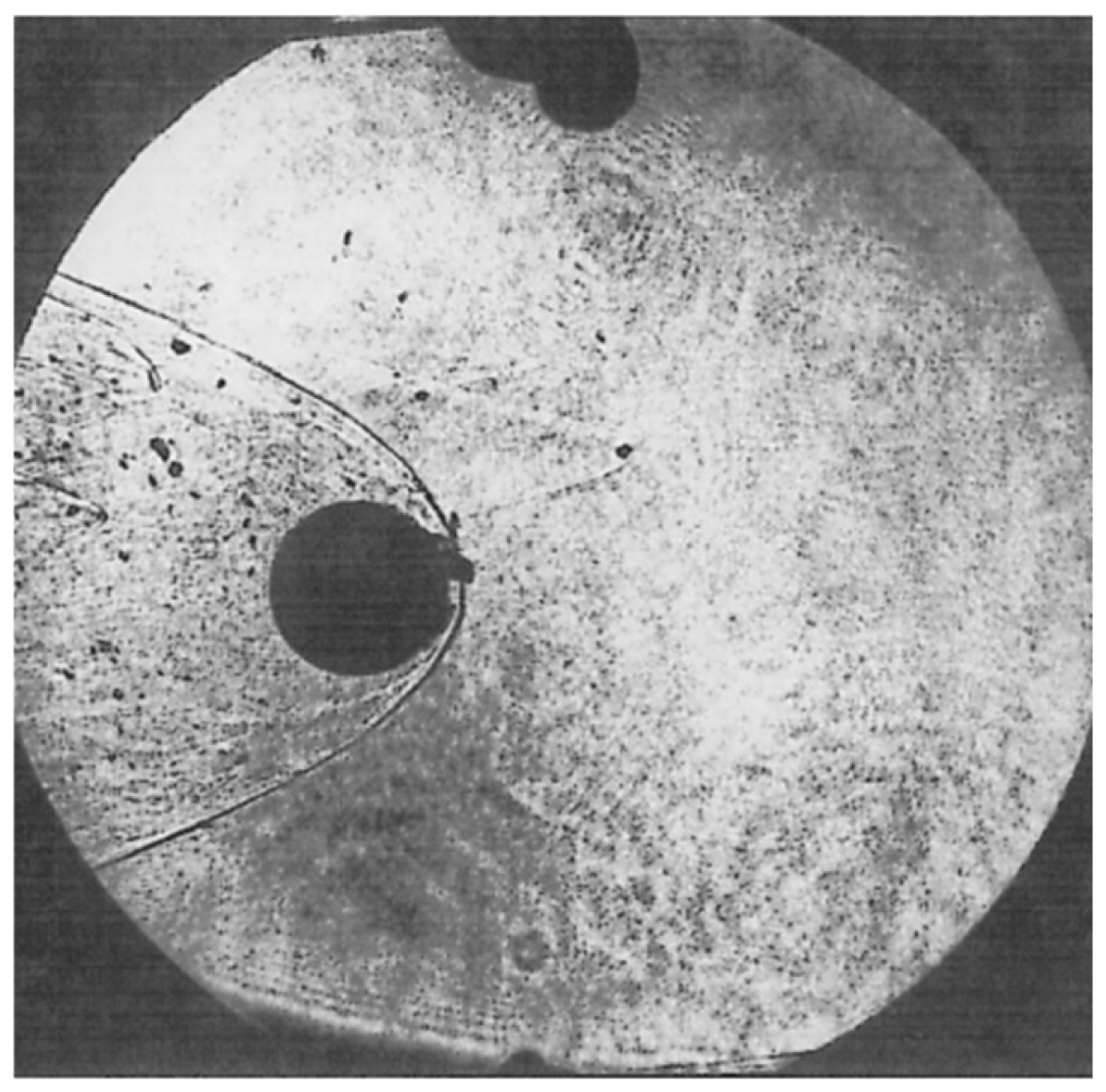
3.1. Overview of Typical Oblique Detonation Experiments
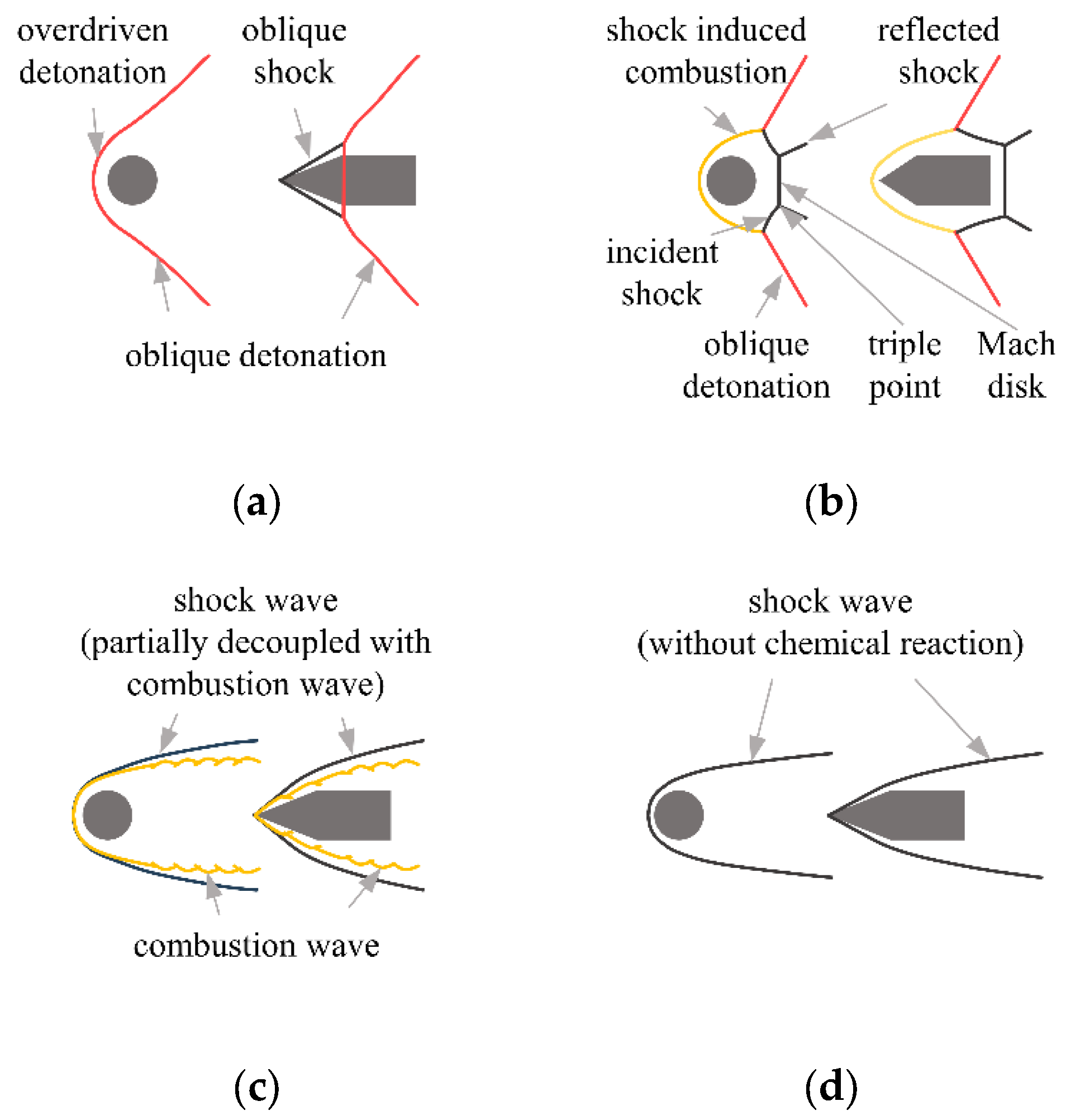
3.2. Shock Structures of the ODW Induced by Projectile
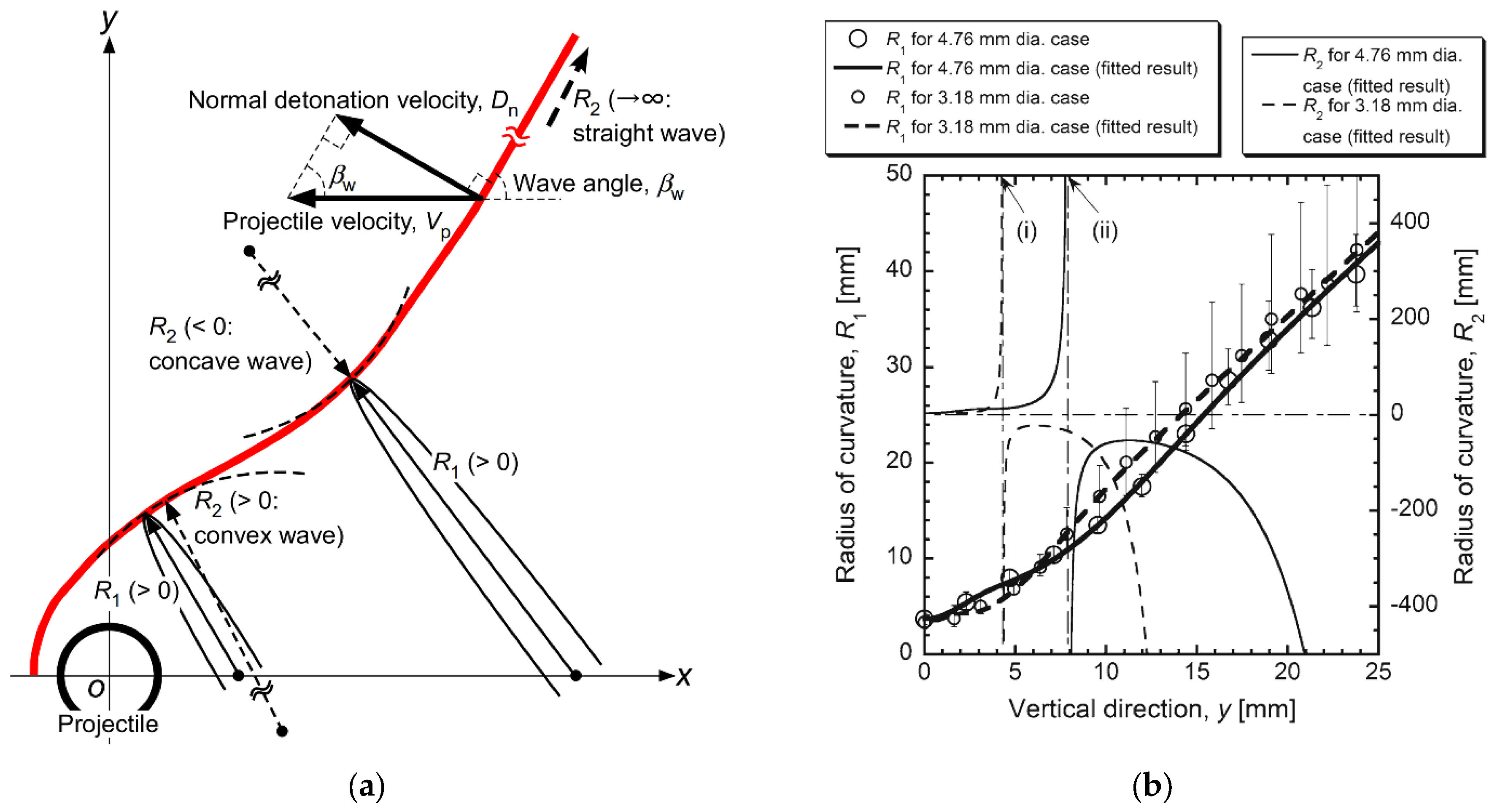
3.3. Wave Surface of the ODW
3.3.1. Propagation Velocity of the ODW
3.3.2. Wave Surface Structure of Self-Sustaining Propagation in ODW
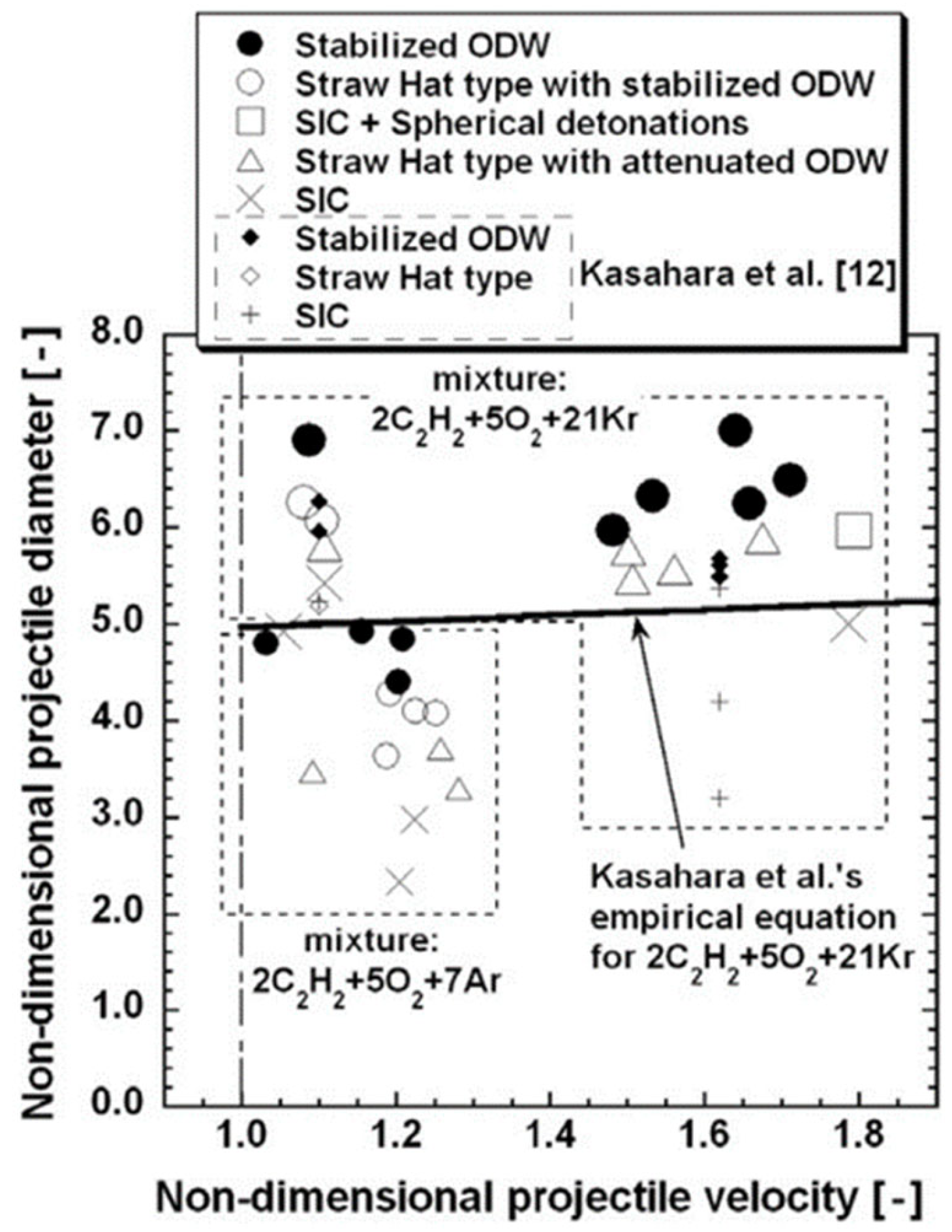
3.4. Investigation of the Initiation Characteristics of ODW Induced by High-Velocity Projectiles
4. Conclusions
- (1)
- To advance the understanding and control of oblique detonation, it is imperative to undertake an experimental investigation into the unsteady process of high-velocity models traversing combustible gaseous mixtures and inducing various shock wave structures. Previous experimental observations of ODWs have documented diverse shock wave phenomena, including inert shock, shock-induced combustion, straw-hat-type ODWs, and stabilized ODWs. While these studies provide insights into the flow processes of stabilized ODWs, they often lack in-depth analyses of propagation mechanisms and unsteady flow dynamics due to the limitations of optical measurement techniques. Additionally, there is a lack of experimental research on the formation processes of different shock wave structures, particularly concerning the unsteady initiation processes near the critical state. To enhance our comprehension of the oblique detonation mechanisms, future experimental studies should focus on elucidating the initiation processes and characterizing unsteady flow dynamics. Establishing a clear linkage between the flow processes and detonation wave criteria will be essential for advancing our understanding and control of oblique detonation phenomena.
- (2)
- To comprehensively understand ODWs, it is essential to conduct experimental observations and measurements focusing on the fine flow structure and chemical reaction processes involved. ODWs exhibit complex, unsteady behaviors, even when relatively stationary, with respect to the model. This complexity encompasses the surface wave structure of ODWs and the initiation of hot spots by combustion waves following the shock wave, which are crucial for sustaining detonation wave propagation. Current experimental findings on flow processes at the wave primarily rely on high-velocity schlieren and OH chemiluminescence images, which are limited by three-dimensional effects. As a result, these methods do not facilitate quantitative analysis of the ODW structure and post-ODW flow processes. Therefore, there is a critical need to design tailored optical measurement systems and employ advanced combustion diagnostic techniques capable of capturing three-dimensional flow fields and chemical reaction processes. Such advancements are pivotal for advancing our understanding of oblique detonation propagation mechanisms.
- (3)
- Developing robust criteria for ODWs is crucial for advancing our understanding and control of their initiation processes. Current studies predominantly rely on the energy limit theory, which focuses on the aerodynamic work of the model relative to the critical energy required for detonation in the experimental mixture. This theory includes non-dimensional projectile diameter measurements, integrated as part of the energy limit theory, which assesses the ratio of model aerodynamic work to critical detonation energy. However, the energy limit theory has notable limitations. It often uses experimentally derived cell sizes based on semi-empirical formulas or theories, which may not fully capture all physical nuances. Additionally, kinetic limits have been proposed to address specific flow process variations, but these are not universally applicable across all initiation scenarios. To overcome these drawbacks, a generalized criteria theory for ODWs should be developed. This theory should consider a broader range of factors, including physical and chemical characteristics of the experimental mixture, chemical reaction dynamics, and detailed flow processes. By incorporating these elements, a more comprehensive understanding of ODW initiation can be achieved. Furthermore, refining and supplementing existing ODW initiation theories with experimental data is essential. Experimental validation will provide insights into the mechanisms underlying ODW initiation and aid in developing effective control strategies. This approach will ultimately contribute to advancing the field of oblique detonation wave propulsion technology.
- (4)
- Integrating combustion diagnostic methods with new facilities. Advanced optical observation methods play a crucial role in the study of oblique detonation mechanisms. Early detonation diagnostic techniques primarily used the smoked foil method and high-speed cameras. Integrating more testing techniques could further advance the observation of detonation propagation characteristics. Possible testing techniques include OH-PLIF, CH-PLIF, chemiluminescence combustion diagnostics, 3D-CTC, et al. Furthermore, this paper focuses on experimental work conducted in high-speed launching devices, which have their own limitations. Integrating different experimental platforms, such as direct-connected supersonic combustion facilities, pulse wind tunnels, or expansion tunnels, and collaborating to enhance these facilities’ capabilities continuously is one of the future directions. Additionally, rapid advancements in numerical simulation technology have empowered researchers in combustion and detonation to conduct extensive studies. This technology facilitates the creation of detailed combustion process models, enabling controlled and repeatable analyses. Thus, the integration of combustion diagnostic methods with different facilities, coupled with the rapid development of numerical simulation and computer technologies, will significantly contribute to the advancement of oblique detonation propulsion technology.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, P.; Zhang, Z.; Yang, R.; Teng, H.; Jiang, Z. Theorical study on propulsive performance of oblique detonation engine. Chin. J. Theor. Appl. Mech. 2021, 53, 2853–2865. [Google Scholar]
- Bussing, T.; Pappas, G. Pulse detonation engine theory and concepts. In Developments in High-Speed-Vehicle Propulsion Systems (A 97-15029 02-07); Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1996; Volume 166, pp. 421–472. [Google Scholar]
- Rankin, B.A.; Fotia, M.L.; Naples, A.G.; Stevens, C.A.; Hoke, J.L.; Kaemming, T.A.; Theuerkauf, S.W.; Schauer, F.R. Overview of performance, application, and analysis of rotating detonation engine technologies. J. Propuls. Power 2017, 33, 131–143. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, Z.; Liu, Y.; Wang, C.; Luo, C. Criteria for hypersonic airbreathing propulsion and its experimental verification. Chin. J. Aeronaut. 2021, 34, 94–104. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, B.; Xiang, G.; Zheng, L. Numerical analysis of wedge-induced oblique detonations in two-phase kerosene-air mixtures. Proc. Combust. Inst. 2019, 37, 3637–3645. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, Y.; Ng, H.D.; Teng, H. Numerical investigation on the initiation of oblique detonation waves in stoichiometric acetylene-oxygen mixtures with high argon dilution. Combust. Flame 2019, 204, 391–396. [Google Scholar] [CrossRef]
- Xiang, G.; Li, H.; Cao, R.; Chen, X. Study of the features of oblique detonation induced by a finite wedge in hydrogen-air mixtures with varying equivalence ratios. Fuel 2020, 265, 116854. [Google Scholar] [CrossRef]
- Xiang, G.X.; Gao, X.; Tang, W.J.; Jie, X.Z.; Huang, X. Numerical study on transition structures of oblique detonations with expansion wave from finite-length cowl. Phys. Fluids 2020, 32, 0005189. [Google Scholar] [CrossRef]
- Xiang, G.; Zhang, Y.; Gao, X.; Li, H.; Huang, X. Oblique detonation waves induced by two symmetrical wedges in hydrogen-air mixtures. Fuel 2021, 295, 120615. [Google Scholar] [CrossRef]
- Guo, H.; Yang, H.; Zhao, N.; Li, S.; Zheng, H. Influence of incoming flow velocity and mixture equivalence ratio on oblique detonation characteristics. Aerosp. Sci. Technol. 2021, 119, 107088. [Google Scholar] [CrossRef]
- Rosato, D.A.; Thornton, M.; Sosa, J.; Bachman, C.; Goodwin, G.B.; Ahmed, K.A. Stabilized detonation for hypersonic propulsion. Proc. Natl. Acad. Sci. USA 2021, 118, 2102244118. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Zhou, J.; Lin, Z.-Y. Experimental investigations of detonation initiation by hot jets in supersonic premixed flows. Chin. Phys. B 2012, 21, 124702. [Google Scholar] [CrossRef]
- Zhiyong, L.I.N.; Jin, Z.; Jiye, Z.; Yu, W.; Yuhui, H. Investigation of detached detonation induced by oblique shock in premixed supersonic flow. J. Aerosp. Power 2009, 24, 50–54. [Google Scholar]
- Zhang, Z.; Wen, C.; Yuan, C.; Liu, Y.; Han, G.; Wang, C.; Jiang, Z. An experimental study of formation of stabilized oblique detonation waves in a combustor. Combust. Flame 2022, 237, 111868. [Google Scholar] [CrossRef]
- Yuan, S.-X.; Zhao, W.; Huang, Z.-C. Primary experimental observation of standing oblique detonation waves. Acta Aerodyn. Sin. 2000, 18, 473–477. [Google Scholar]
- Kamel, M.R.; Morris, C.I.; Stouklov, I.G.; Hanson, R.K. PLIF imaging of hypersonic reactive flow around blunt bodies. Symp. Int. Combust. 1996, 26, 2909–2915. [Google Scholar] [CrossRef]
- Higgins, A.; Higgins, A. The effect of confinement on detonation initiation by blunt projectiles. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997; p. 3179. [Google Scholar]
- Maeda, S.; Sumiya, S.; Kasahara, J.; Matsuo, A. Initiation and sustaining mechanisms of stabilized Oblique Detonation Waves around projectiles. Proc. Combust. Inst. 2013, 34, 1973–1980. [Google Scholar] [CrossRef]
- Chernyavskii, S.Y.; Baulin, N.N.; Mkrtumov, A.S. High-speed flow of a mixture of hydrogen and oxygen over blunt bodies. Combust. Explos. Shock. Waves 1973, 9, 687–690. [Google Scholar] [CrossRef]
- Ruegg, F.W.; Dorsey, W.W. A missile technique for the study of detonation waves. J. Res. Natl. Bur. Stand. 1963, 67, 51–58. [Google Scholar] [CrossRef]
- Behrens, H.; Struth, W.; Wecken, F. Studies of hypervelocity firings into mixtures of hydrogen with air or with oxygen. Symp. Int. Combust. 1966, 10, 245–252. [Google Scholar] [CrossRef]
- McVey, J.B.; Toong, T.Y. Mechanism of instabilities of exothermic hypersonic blunt-body flows. Combust. Sci. Technol. 1971, 3, 64–76. [Google Scholar] [CrossRef]
- Toong, T.Y. Instabilities in reacting flows. Acta Astronaut. 1974, 1, 317–344. [Google Scholar] [CrossRef]
- Powers, J.M. Oblique detonations—Theory and propulsion applications. In Combustion in High-Speed Flows; Springer: Berlin/Heidelberg, Germany, 1994; pp. 345–371. [Google Scholar]
- Pratt, D.T.; Humphrey, J.W.; Glenn, D.E. Morphology of standing oblique detonation waves. J. Propuls. Power 1991, 7, 837–845. [Google Scholar] [CrossRef]
- Vasilśev, A.A. Initiation of gaseous detonation by a high speed body. Shock. Waves 1994, 3, 321–326. [Google Scholar] [CrossRef]
- Vasilśev, A.A. Detonation combustion of gas mixtures using a hypervelocity projectile. Combust. Explos. Shock. Waves 1997, 33, 583–597. [Google Scholar] [CrossRef]
- Higgins, A.; Bruckner, A. Experimental investigation of detonation initiation by hypervelocity blunt projectiles. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; p. 342. [Google Scholar]
- Kaneshige, M.J.; Shepperd, J.E. Oblique detonation stabilized on a hypervelocity projectile. Symp. Int. Combust. 1996, 26, 3015–3022. [Google Scholar] [CrossRef]
- Kasahara, J.; Takeishi, A.; Kuroda, H.; Horiba, M.; Matsukawa, K.; Leblanc, J.; Endo, T.; Fujiwara, T. Experimental observation of oblique detonation waves around hypersonic free projectiles. In Proceedings of the Third International Workshop on Ram Accelerators, Sendai, Japan, 16–18 July 1997; pp. 264–270. [Google Scholar]
- Kasahara, J.; Endo, T.; Nishide, K.; Yahata, D.; Fujiwara, T.; Leblanc, J.E. Experimental study of interaction between oblique detonation wave and rarefaction wave around a hypersonic free projectile. J. Phys. IV 2000, 10, 109–115. [Google Scholar] [CrossRef]
- Kasahara, J.; Fujiwara, T.; Endo, T.; Arai, T. Chapman-Jouguet oblique detonation structure around hypersonic projectiles. AIAA J. 2001, 39, 1553–1561. [Google Scholar] [CrossRef]
- Kasahara, J.; Arai, T.; Matsuo, A.; Akai, N.; Takazawa, K. Critical Condition for Stabilized Chapman-Jouguet Oblique Detonation Waves Around Hypersonic Bodies. In Proceedings of the 18th Int. Colloquium on the Dynamics of Explosions and Reactive Systems, Seattle, DC, USA, 29 July–3 August 2001. [Google Scholar]
- Kasahara, J.; Arai, T.; Matsuo, A.; Akai, N.; Takazawa, K. Experimental investigations of steady-state oblique detonation waves generated around hypersonic projectiles. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001; p. 1800. [Google Scholar]
- Kasahara, J.; Arai, T.; Chiba, S.; Takazawa, K.; Tanahashi, Y.; Matsuo, A. Criticality for stabilized oblique detonation waves around spherical bodies in acetylene/oxygen/krypton mixtures. Proc. Combust. Inst. 2002, 29, 2817–2824. [Google Scholar] [CrossRef]
- Maeda, S.; Inada, R.; Kasahara, J.; Matsuo, A. Visualization of the non-steady state oblique detonation wave phenomena around hypersonic spherical projectile. Proc. Combust. Inst. 2011, 33, 2343–2349. [Google Scholar] [CrossRef]
- Maeda, S.; Inada, R.; Kasahara, J.; Matsuo, A.; Funaki, I. The stabilized oblique detonation wave and unsteady wave structure around hyper-velocity spherical projectile. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; p. 505. [Google Scholar]
- Maeda, S.; Kasahara, J.; Matsuo, A. Visualization of The Initiation and Stabilization Process of an Oblique Detonation Wave Around a Projectile. In Proceedings of the 23rd International Colloquium on the Dynamics of Explosions and Reactive Systems, Irvine, CA, USA, 24–29 July 2011; p. 116. [Google Scholar]
- Maeda, S.; Kasahara, J.; Matsuo, A. Oblique detonation wave stability around a spherical projectile by a high time resolution optical observation. Combust. Flame 2012, 159, 887–896. [Google Scholar] [CrossRef]
- Maeda, S.; Kasahara, J.; Matsuo, A. Unsteady propagation process of oblique detonation waves initiated by hypersonic spherical projectiles. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2012, 10, 1–6. [Google Scholar] [CrossRef]
- Maeda, S.; Sumiya, S.; Kasahara, J.; Matsuo, A. Scale effect of spherical projectiles for stabilization of oblique detonation waves. Shock. Waves 2015, 25, 141–150. [Google Scholar] [CrossRef]
- Uemichi, A.; Kato, S.; Kasahara, J.; Matsuo, A. Steadiness of oblique detonation waves around spherical projectiles. In Proceedings of the 22nd International Colloquium on the Dynamics of Explosions and Reactive Systems, Minsk, Belarus, 27–31 July 2009; p. 152. [Google Scholar]
- Verreault, J.; Higgins, A.J. Initiation of detonation by conical projectiles. Proc. Combust. Inst. 2011, 33, 2311–2318. [Google Scholar] [CrossRef]
- Dongming, C.; Baochun, F.; Qifeng, C. Numerical simulation and visualization od oblique detonation stabilized on a projectile. J. Ballist. 1999, 11, 63–67. [Google Scholar]
- Cui, D.; Fan, B.; Xin, X. Oblique Detonation Stabilized on a Hypervelocity Projectile. Explos. Shock. Waves 2002, 22, 264–267. [Google Scholar]
- Iwata, K.; Hanyu, N.; Maeda, S.; Obara, T. Experimental visualization of sphere-induced oblique detonation in a non-uniform mixture. Combust. Flame 2022, 244, 112253. [Google Scholar] [CrossRef]
- Shang, J.; Hu, G.; Wang, Q.; Wang, Y.; Zhang, K.; Xiang, G.; Zhao, W.; Wei, B. Experiment investigation of oblique detonation wave structure induced by hypersonic projectiles. Chin. J. Theor. Appl. Mech. 2023, 55, 309–317. [Google Scholar]
- Carlucci, D.E. Ballistics: Theory and Design of Guns and Ammunition; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Seigel, A.E. The Theory of High Speed Guns; North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development: Paris, France, 1966. [Google Scholar]
- Settles, G.S. Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Sumiya, S.; Maeda, S.; Kasahara, J.; Matsuo, A. Reflection Phenomena of oblique detonation wave around hypersonic spherical projectiles on plane plate. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 1504. [Google Scholar]
- Daimon, Y.; Matsuo, A. Three-dimensional Wave Structure of Oblique Detonation around a Blunt Body. In Proceedings of the 21st International Colloquium on the Dynamics of Explosions and Reactive Systems, Poitiers, France, 23–27 July 2007; p. 152. [Google Scholar]
- Daimon, Y.; Matsuo, A.; Kasahara, J. Wave structure and unsteadiness of stabilized oblique detonation waves around hypersonic projectile. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007; p. 1171. [Google Scholar]
- Choi, J.-Y.; Jeung, I.-S. Numerical simulation of super-detonative ram accelerator; Its shock-induced combustion and oblique detonation. In Hypervelocity Launchers; Springer: Berlin/Heidelberg, Germany, 2016; pp. 217–267. [Google Scholar]
- Muralidharan, B.; Menon, S. Numerical studies of detonation initiation by supersonic projectiles using a high-order adaptive cut-cell method. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 24–29 July 2016; p. 5106. [Google Scholar]
- Bedarev, I.A.; Temerbekov, V.M.; Fedorov, A.V. Calculation of combustion initiation by shock wave interaction with various-diameter spheres in a hydrogen-air mixture. In Proceedings of the 19th International Conference on the Methods of Aerophysical Research (ICMAR), Novosibirsk, Russia, 13–19 August 2018. [Google Scholar]
- Temerbekov, V.M. Calculation of the shock waves interaction with various diameter spheres in hydrogen-air mixture. In Proceedings of the 7th All-Russian International Scientific Conference on Current Issues of Continuum Mechanics and Celestial Mechanics, Tomsk, Russia, 26–28 November 2018. [Google Scholar]
- Bedarev, I.A.; Temerbekov, V.M.; Fedorov, A.V. Calculation of detonation initiation in a hydrogen/oxygen/argon mixture in by a small-diameter spherical projectile. In Proceedings of the 15th All-Russian Seminar on Dynamics of Multiphase Media (DMM), RAS, SB, Inst Theoret & Appl Mech, Novosibirsk, Russia, 3–5 October 2017. [Google Scholar]
- Bedarev, I.A.; Temerbekov, V.M.; Fedorov, A.V. Simulating the regimes of oblique detonation waves arising at detonation initiation by a small-diameter projectile. Thermophys. Aeromechanics 2019, 26, 59–68. [Google Scholar] [CrossRef]
- Choi, J.; Maeda, S.; Kasahara, J.; Matsuo, A. Calculation of drag coefficients for hypersonic spherical projectiles initiating oblique detonation wave or shock-induced combustion. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 983. [Google Scholar]
- Bedarev, I.; Temerbekov, V. Estimation of the energy of detonation initiation in a hydrogen-oxygen mixture by a high velocity projectile. Therm. Sci. 2021, 25, 3889–3897. [Google Scholar] [CrossRef]
- Lee, J.H. Dynamic parameters of gaseous detonations. Annu. Rev. Fluid Mech. 1984, 16, 311–336. [Google Scholar] [CrossRef]
- Lee, J. On the Initiations of Detonation by a Hypervelocity Projectile. In Advances in Combustion Science: In Honor of Ya. B. Zel’dovich; Sirignano, W.A., Merzhanov, A.G., Luca, L.D., Eds.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997; p. 199. [Google Scholar]
- Lee, J.H.S. Initiation of detonation by a hypervelocity projectile. In Advances in Combustion Science: In Honor of Ya. B. Zel’dovich (A 97-24531 05-25); Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 1997; Volume 173, pp. 293–310. [Google Scholar]
- Bedarev, I.; Temerbekov, V. Estimation of the initiation energy of detonation excited by a fast moving body. Proc. J. Phys. Conf. Ser. 2019, 1404, 012054. [Google Scholar] [CrossRef]
- Ju, Y.G.; Masuya, G.; Sasoh, A. Numerical and theoretical studies on detonation initiation by a supersonic projectile. In Proceedings of the 27th International Symposium on Combustion, Boulder, CO, USA, 2–7 August 1998; pp. 2225–2231. [Google Scholar]

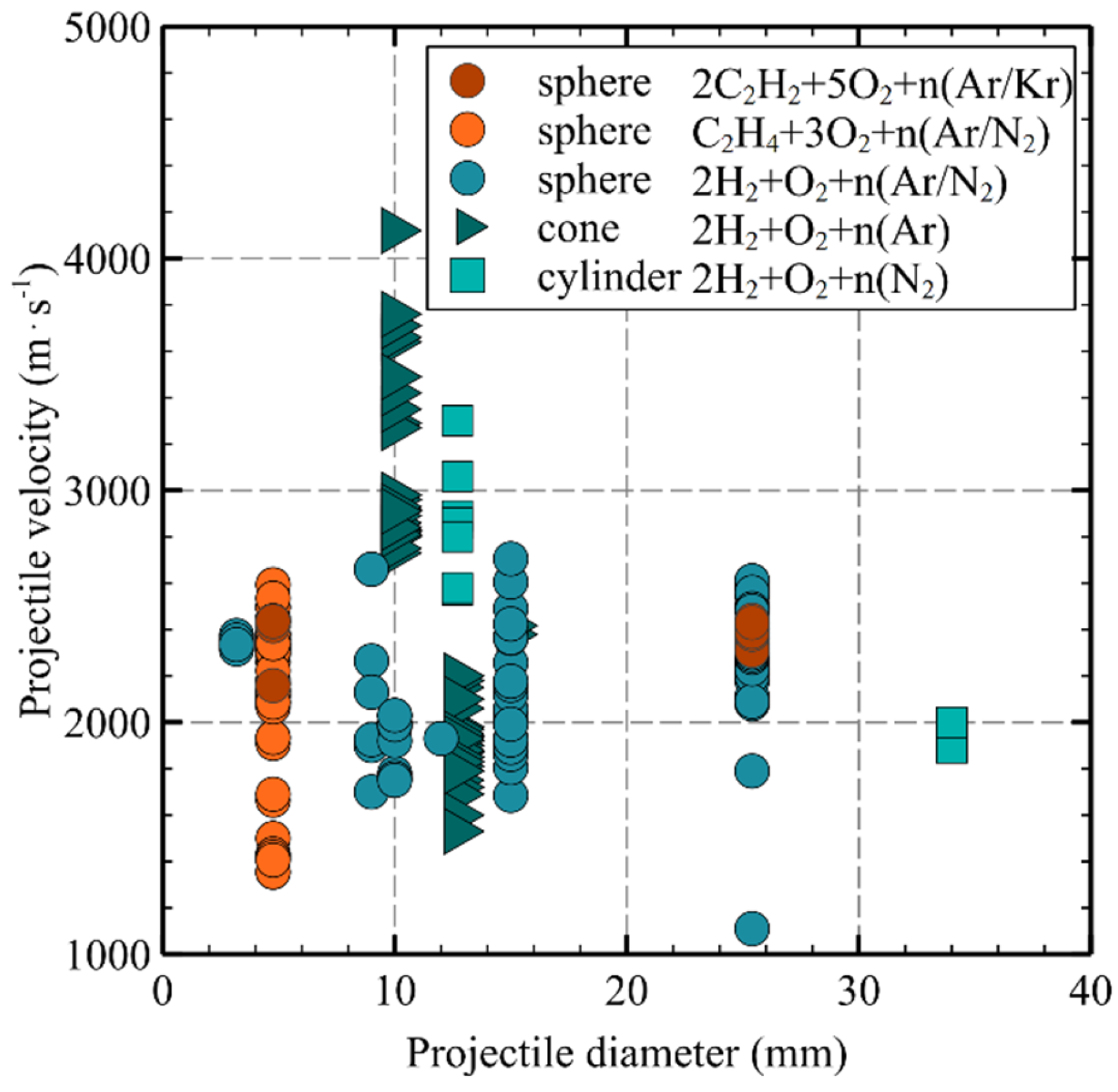



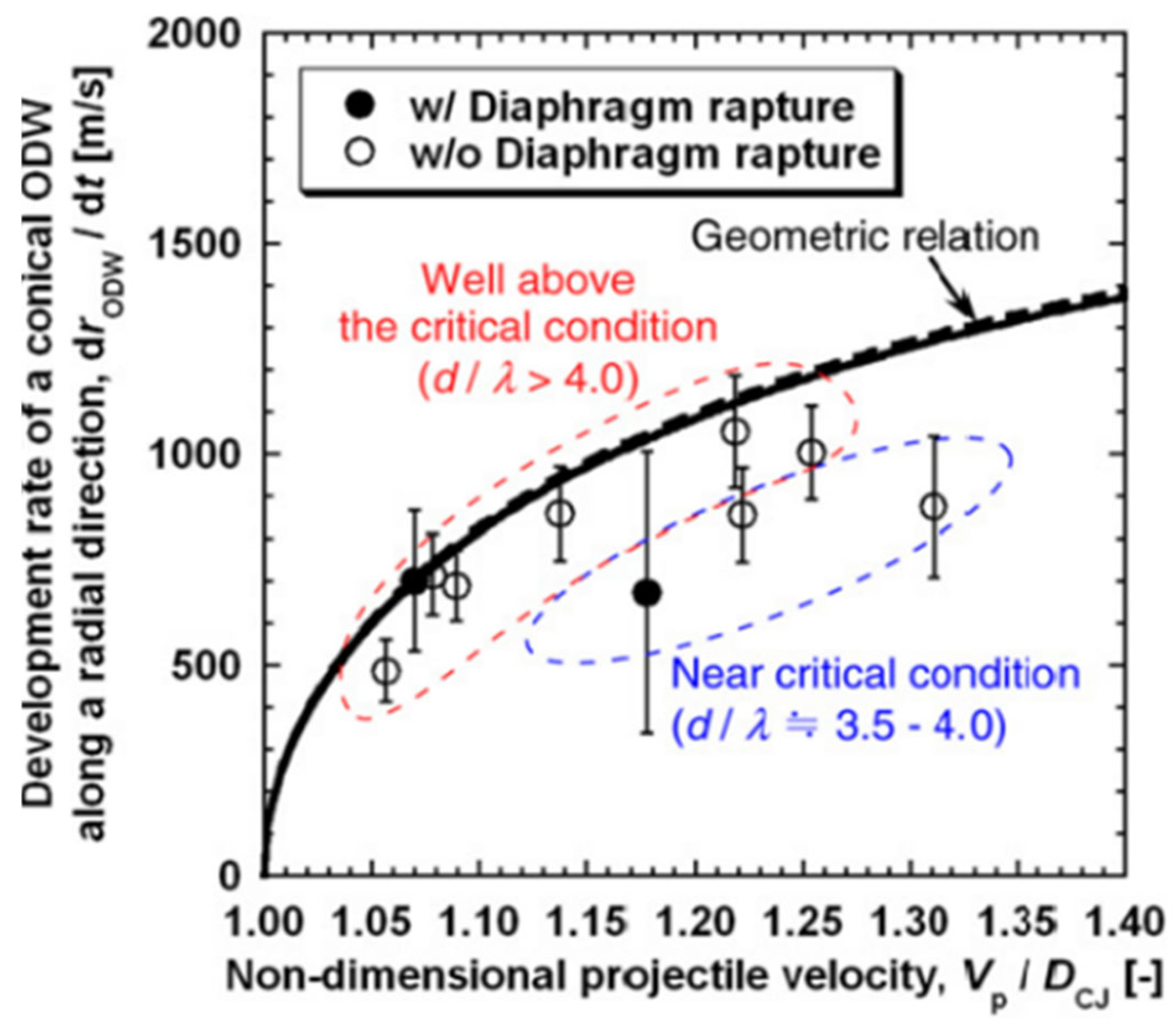
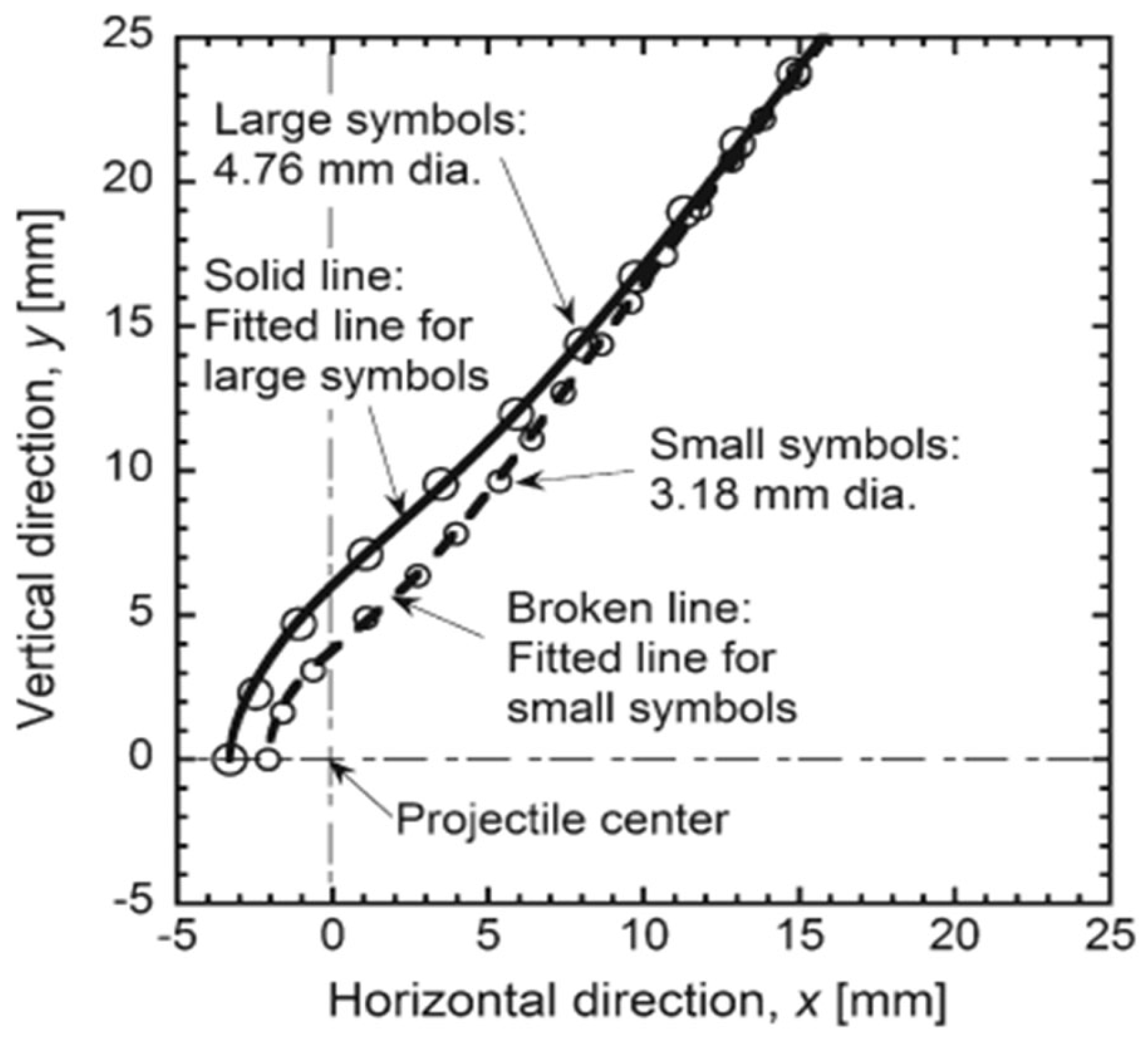
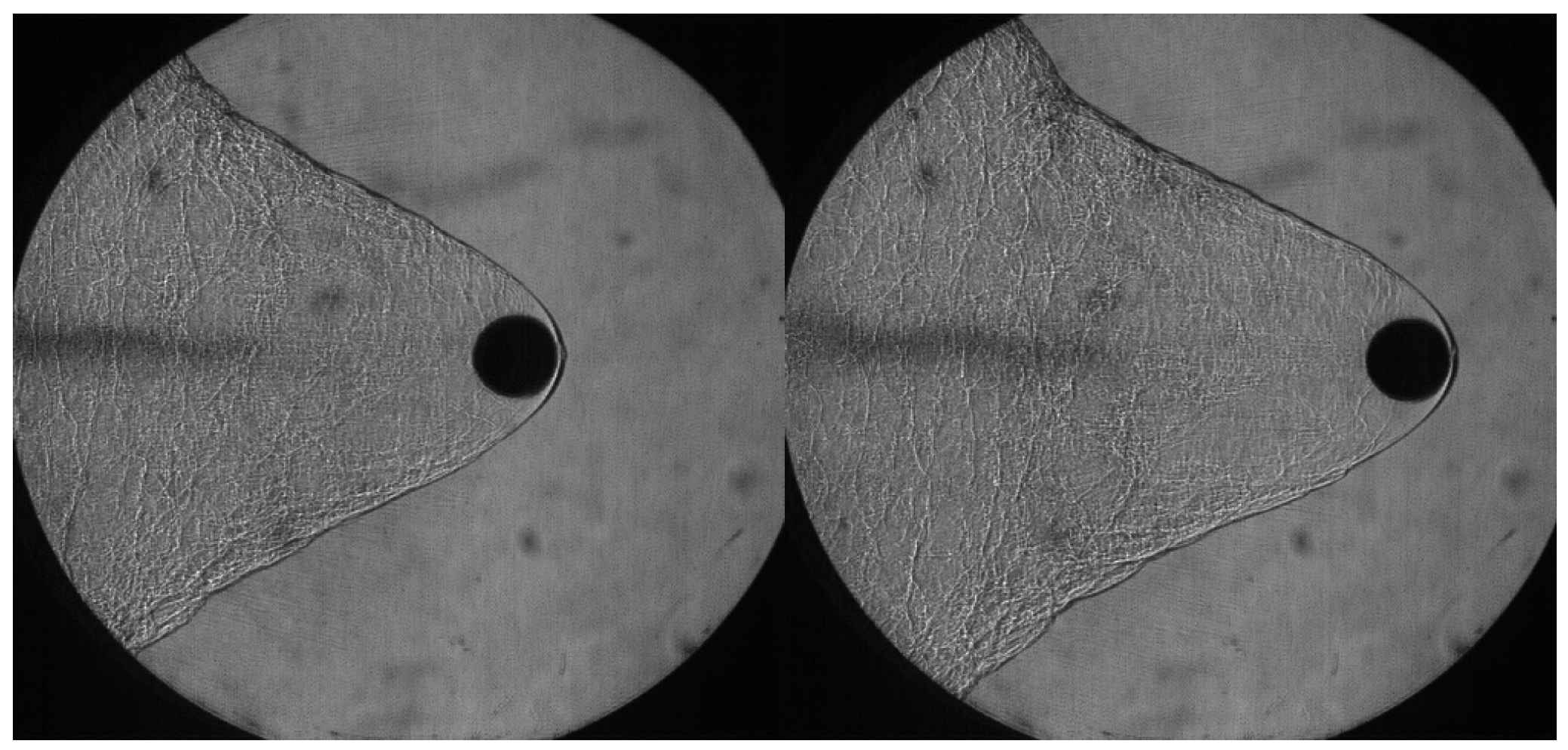

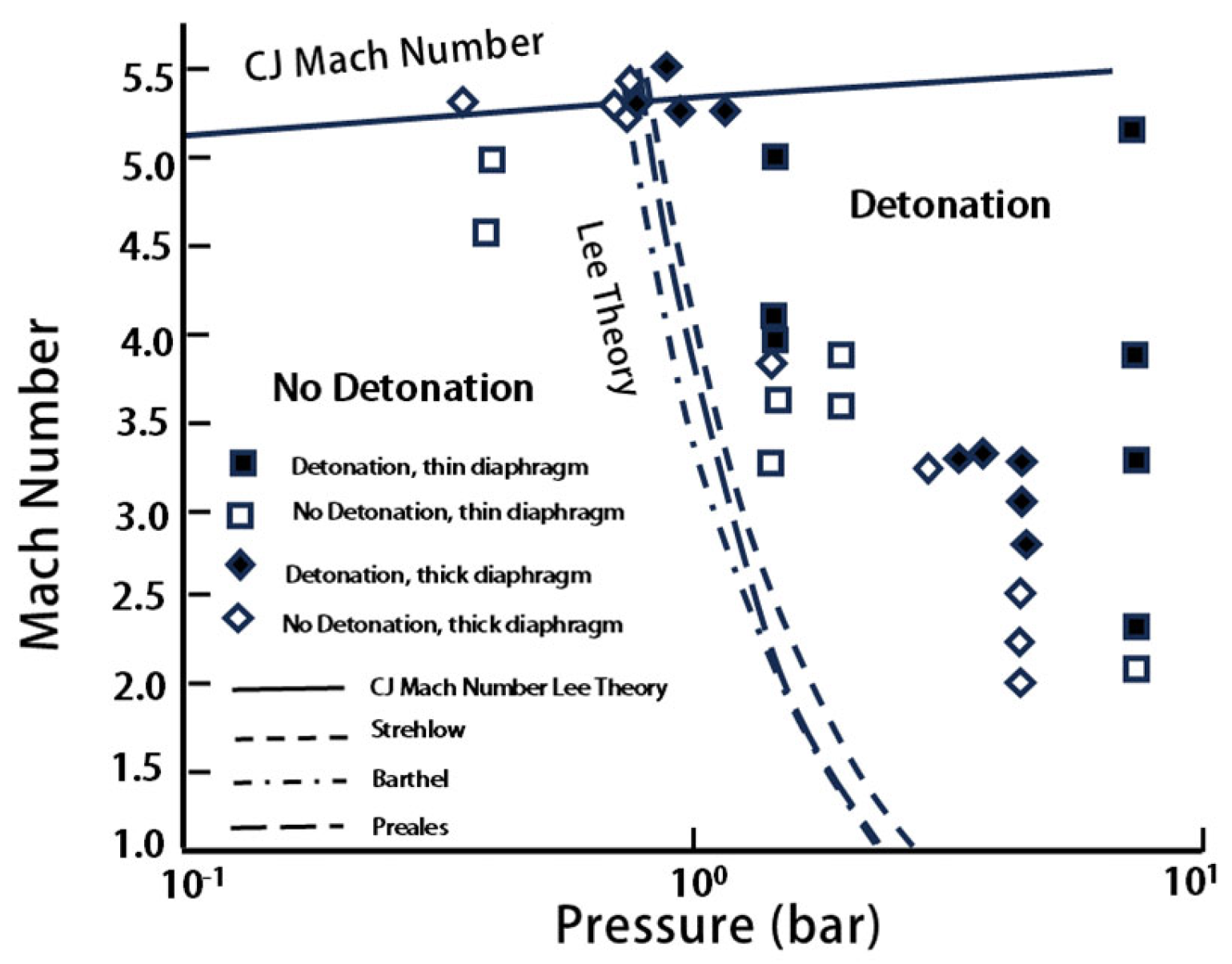


| No | Institute | Launching Device | Projectile/Diameter | Velocity (km/s) | Experimental Gases | Measurement Technique | Reference |
|---|---|---|---|---|---|---|---|
| 1 | Moscow State University, Moscow, Russian | light gas gun | blunt cylinder, 12.7 mm | 2.57~3.06 | 2H2 + O2 | schlieren | [19] |
| 2 | Siberian Division of the Russian Academy of Sciences, Siberian, Russian | smoothbore powder gun | cylinder, 7.63 mm | 0.8~1.4 | C2H2 + 2.5O2 | schlieren | [26,27] |
| 3 | University of Washington, Washington, USA | light gas gun | sphere, 4.76~25.4 mm | 0.6~2.3 | 2H2 + O2 + 7Ar | - | [17,28] |
| 4 | California Institute of Technology, California, USA | gas gun | sphere, 25 mm | 2.6~3.0 | 2H2 + O2 + N2/2H2 + O2 + 3.76N2 | shadowgraph/differential interferograms | [29] |
| 5 | Nagoya University, Nagoya, Japan | two-stage light gas gun | cone, 10 mm | 2.8~3.0 | 2H2 + O2 | schlieren | [30,31,32,33,34] |
| 6 | University of Tsukuba, Tsukuba, Japan | two-stage light gas gun | sphere, 3.18/4.76 mm | 1.3~2.5 | C2H2 + 2.5O2 + 10.5Kr/C2H2 + 2.5O2 + 3.5Ar/C2H4 + 3O2 + 4Ar/2H2 + O2 + 3Ar | schlieren/shadowgraph | [18,35,36,37,38,39,40,41,42] |
| 7 | McGill University, Montreal, Canada | one-stage light gas gun | cone, 12.7 mm | 1.7~2.2 | 2H2 + O2 + 7Ar | schlieren | [43] |
| 8 | Nanjing University of Science and Technology, Nanjing, China | smoothbore powder gun | cone, 25 mm | 1.7~2.1 | 1.4/1.0H2 + O2 | shadowgraph | [44,45] |
| 9 | Kyoto University, Kyoto, Japan | two-stage light gas gun | sphere, 9.52 mm | 1.8~2.2 | nH2 + O2 + 3Ar | shadowgraph | [46] |
| 10 | Institute of Mechanics, CAS, Beijing, China | two-stage light gas gun | blunt cylinder, 30 mm | 2.2~4.1 | 2H2 + O2 | shadowgraph | [47] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, J.; Hu, G.; Wang, Q.; Xiang, G.; Zhao, W. Progress of Experimental Studies on Oblique Detonation Waves Induced by Hyper-Velocity Projectiles. Aerospace 2024, 11, 715. https://doi.org/10.3390/aerospace11090715
Shang J, Hu G, Wang Q, Xiang G, Zhao W. Progress of Experimental Studies on Oblique Detonation Waves Induced by Hyper-Velocity Projectiles. Aerospace. 2024; 11(9):715. https://doi.org/10.3390/aerospace11090715
Chicago/Turabian StyleShang, Jiahao, Guotun Hu, Qiu Wang, Gaoxiang Xiang, and Wei Zhao. 2024. "Progress of Experimental Studies on Oblique Detonation Waves Induced by Hyper-Velocity Projectiles" Aerospace 11, no. 9: 715. https://doi.org/10.3390/aerospace11090715
APA StyleShang, J., Hu, G., Wang, Q., Xiang, G., & Zhao, W. (2024). Progress of Experimental Studies on Oblique Detonation Waves Induced by Hyper-Velocity Projectiles. Aerospace, 11(9), 715. https://doi.org/10.3390/aerospace11090715







