Large Debris Removal: Using Features of Attitude Motion for Load Factor Regulation during Re-Entry
Abstract
:1. Introduction
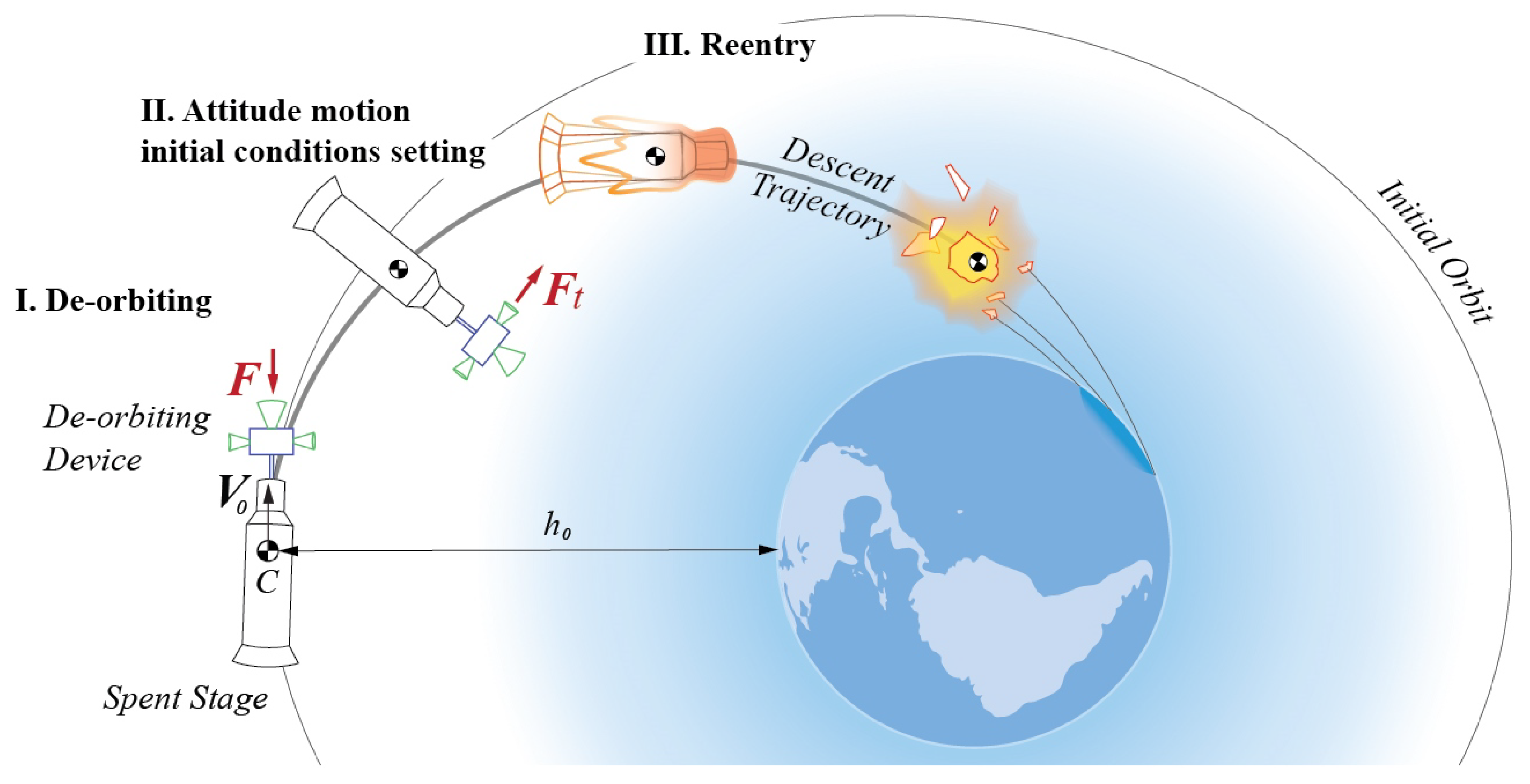
2. Spent Upper Stage Removal Mission Overview
3. Mathematical Model of Re-Entry
3.1. Key Assumptions
- During re-entry, the gravitational torque is negligibly small compared to the aerodynamic one.
- We consider only mechanical/aerodynamic loads caused by the descent.
- The density and temperature of the Earth’s atmosphere change with altitude according to the US Standard Atmosphere Model [31].
- The atmosphere is not rotating.
- The target is shaped as a body of revolution with its CoM on the longitudinal axis of symmetry and the transverse moments of inertia equal to each other.
- The target’s CoM moves in a single plane passing through the Earth’s center.
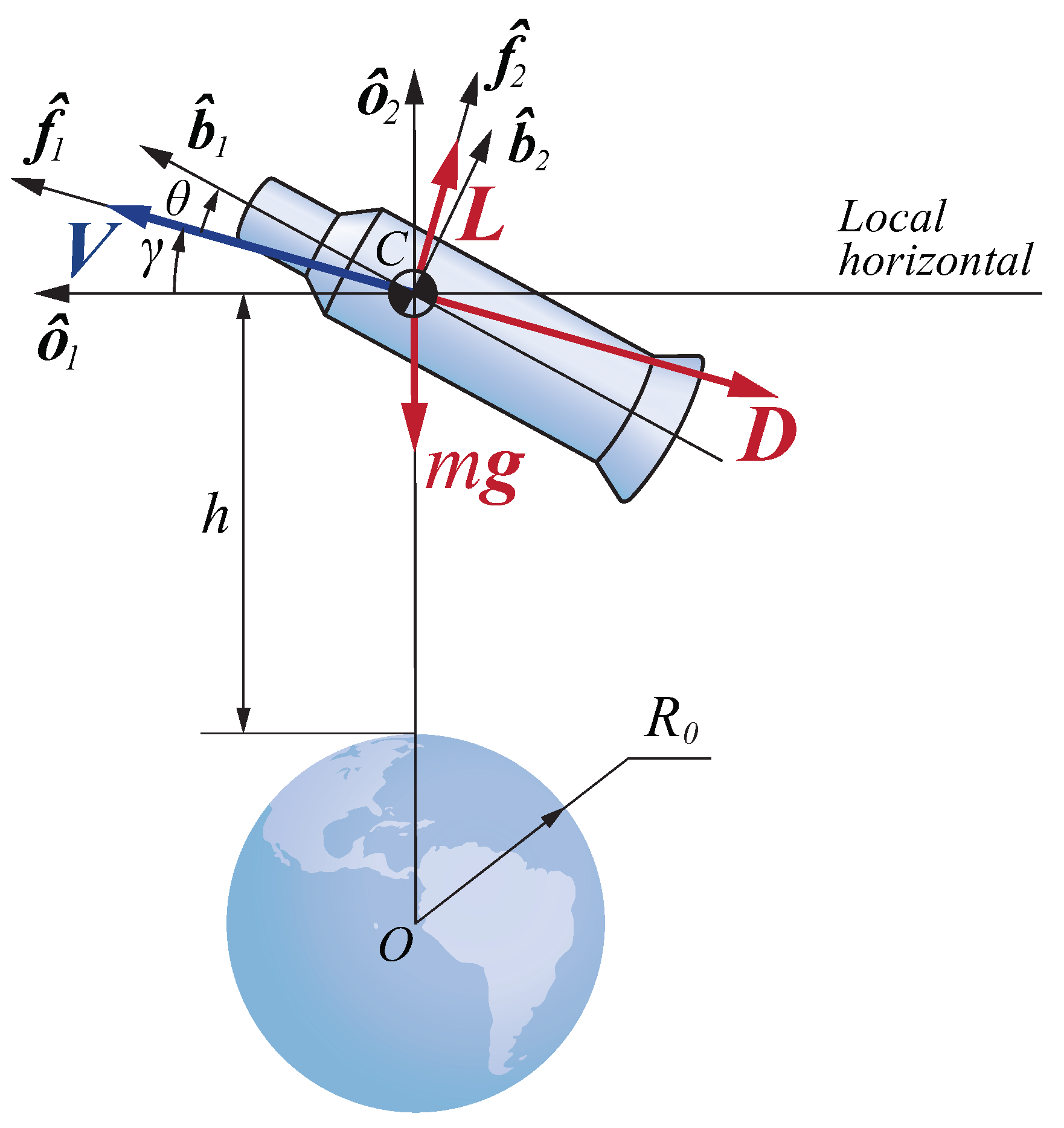
3.2. Coordinate Systems and Euler Angles
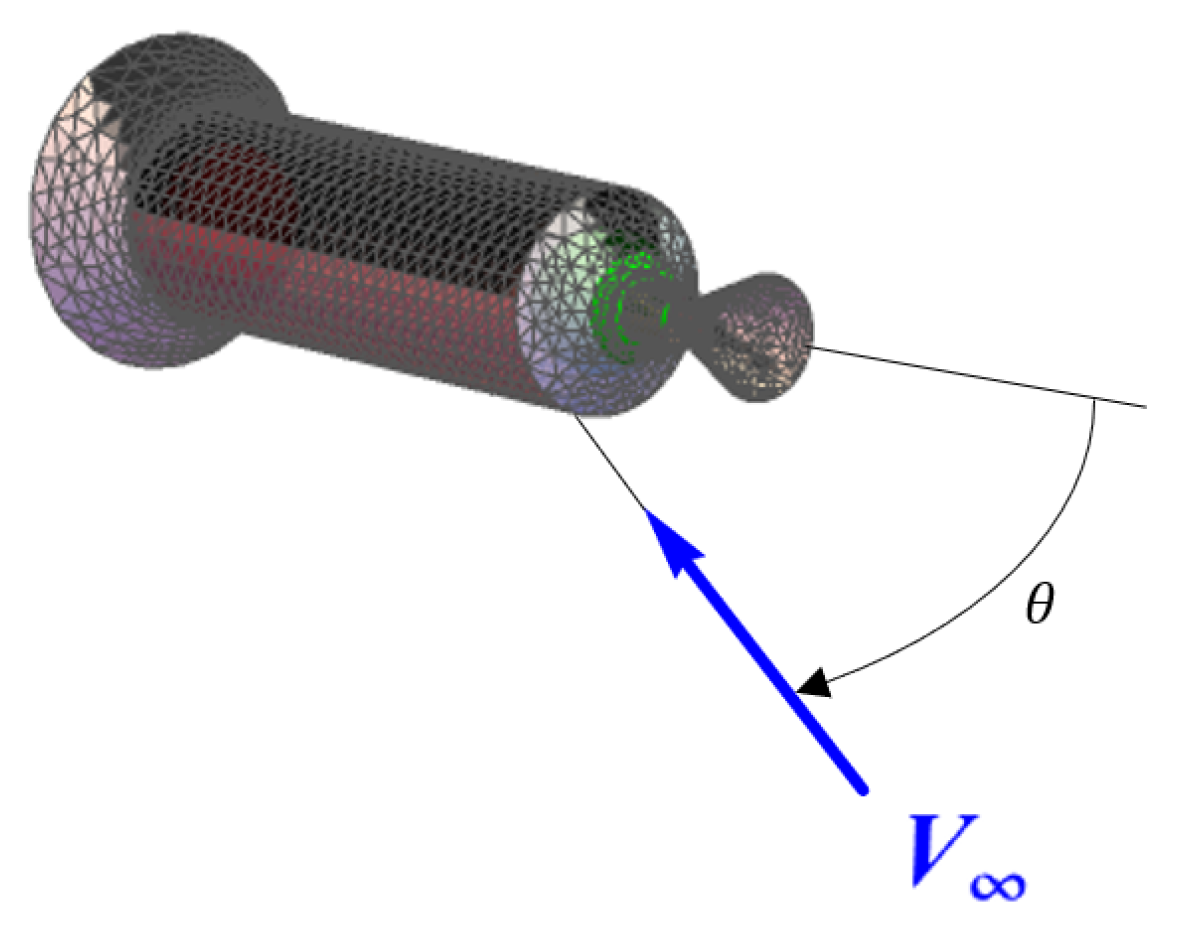
- The Local Vertical–Local Horizontal (LVLH) frame O is defined through an orthonormal right-hand set of unit vectors , , with an origin at the target’s CoM. The vector is directed along the local vertical from the center of the Earth to the CoM of the target; the vector is aligned with the local horizontal (Figure 2).
- The flight path frame F is defined through a set of unit vectors with an origin at the CoM, with the vector coinciding with the velocity of the CoM. The transformation matrix between O and F is defined bywherewhere is the flight path angle (Figure 2).
- The body-fixed frame B is defined through a set . These vectors coincide with the target’s principal axes of inertia, and the vector lies along the longitudinal axis of symmetry. The orientation of relative to is described by a symmetric set of Euler angles corresponding to three successive positive rotations: first about Axis 1 by the precession angle , then about Axis 3 by the nutation angle (angle of attack), , and finally, about Axis 1 by the spin angle , as shown in Figure 3. The transformation matrix between F and B is defined bywhere
- The intermediate frames I and are defined through unit vector sets and , respectively. The orientations of these frames relative to the orbital frame are determined by the above-mentioned rotations: a single rotation by the angle for the frame and two successive rotations by the angles and for the frame.
3.3. Equations of Motion
3.3.1. Motion of Centre of Mass
3.3.2. Attitude Motion
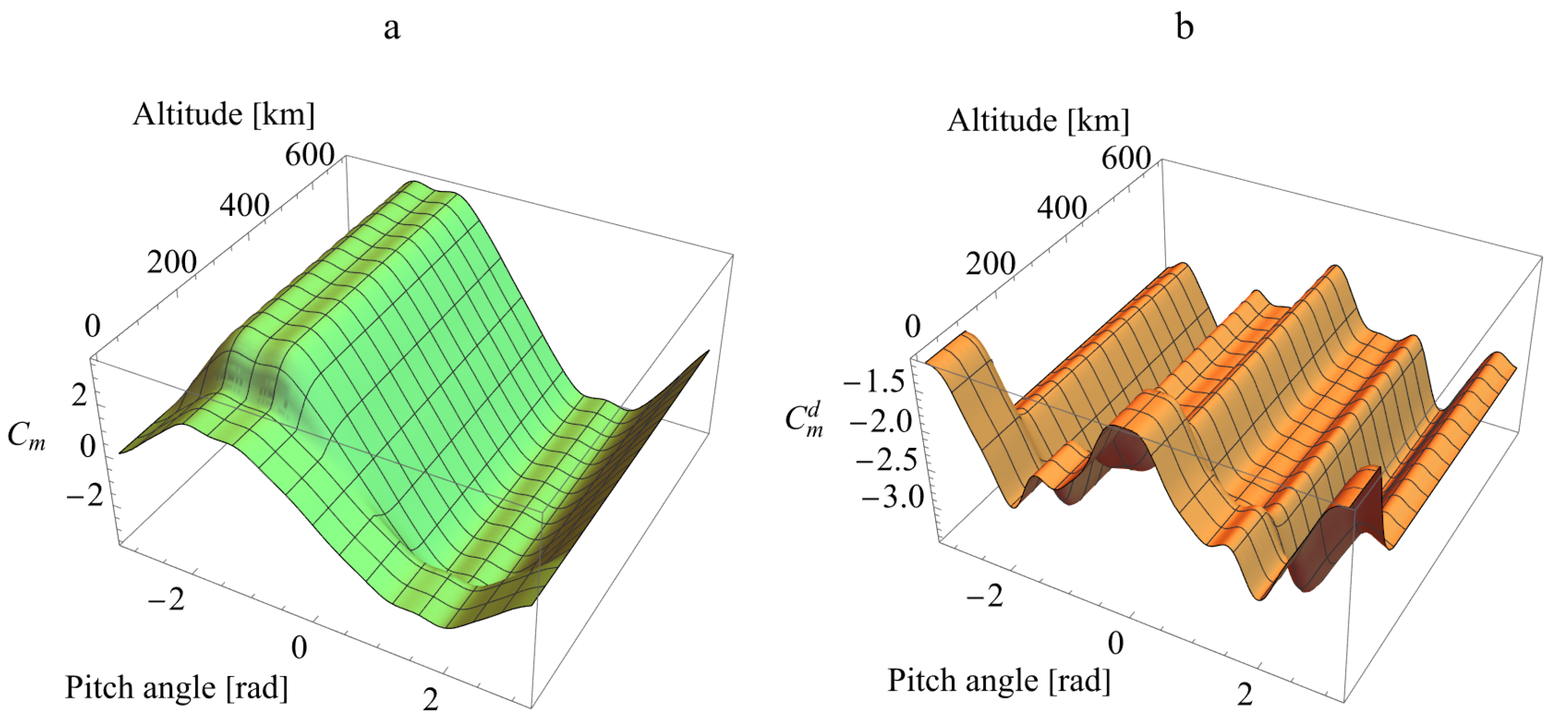
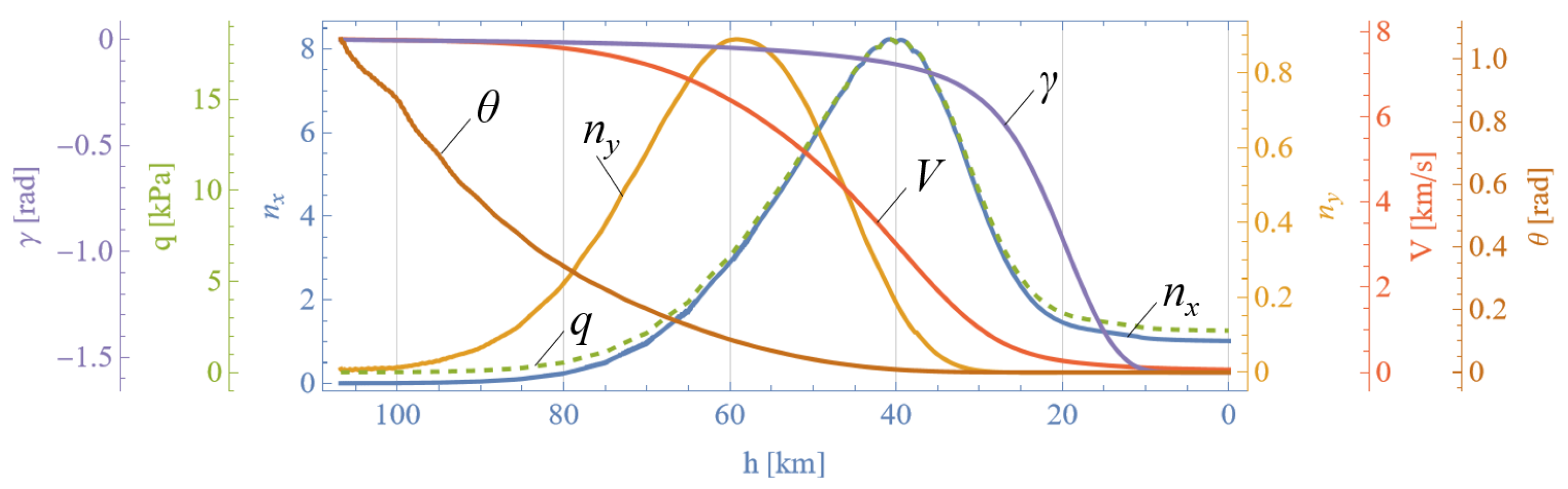
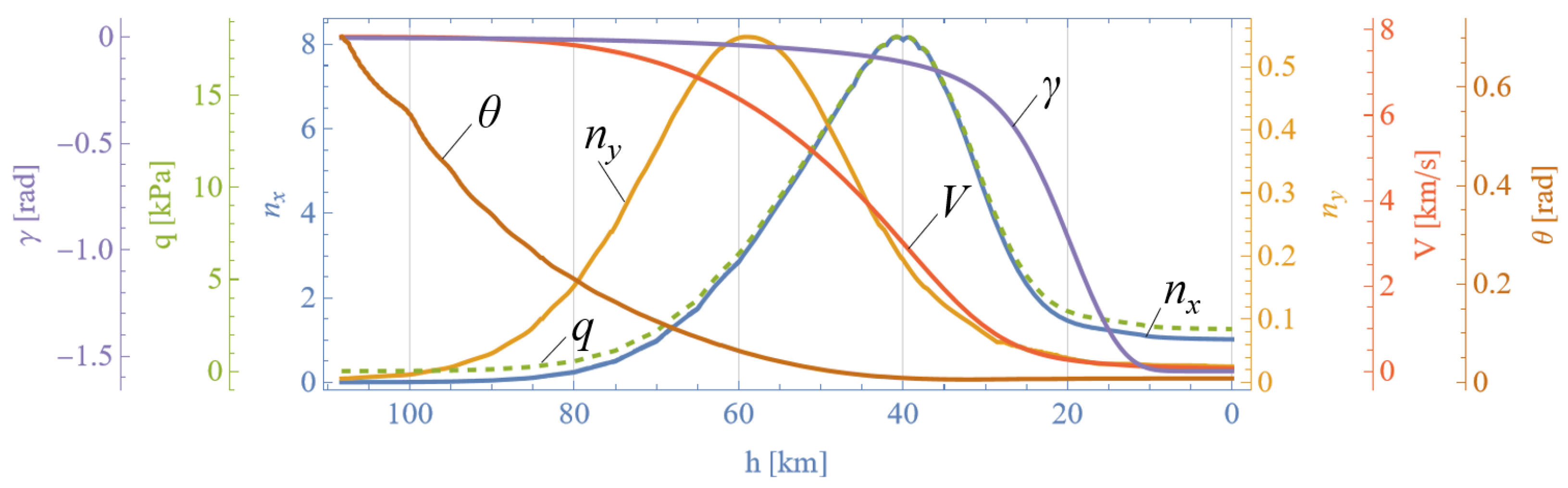
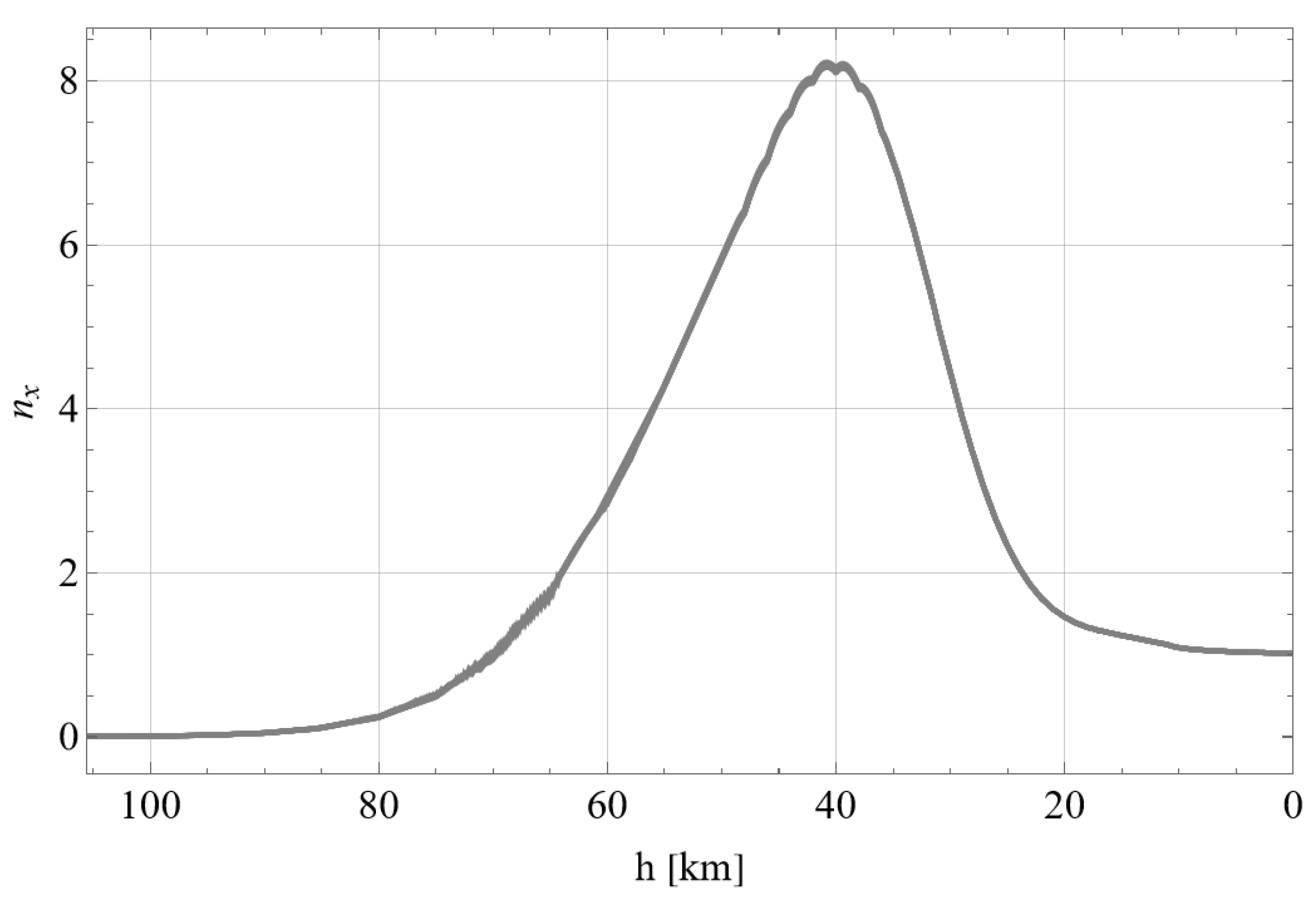
3.4. Load Factors
4. Case Study of Large Debris Re-Entry
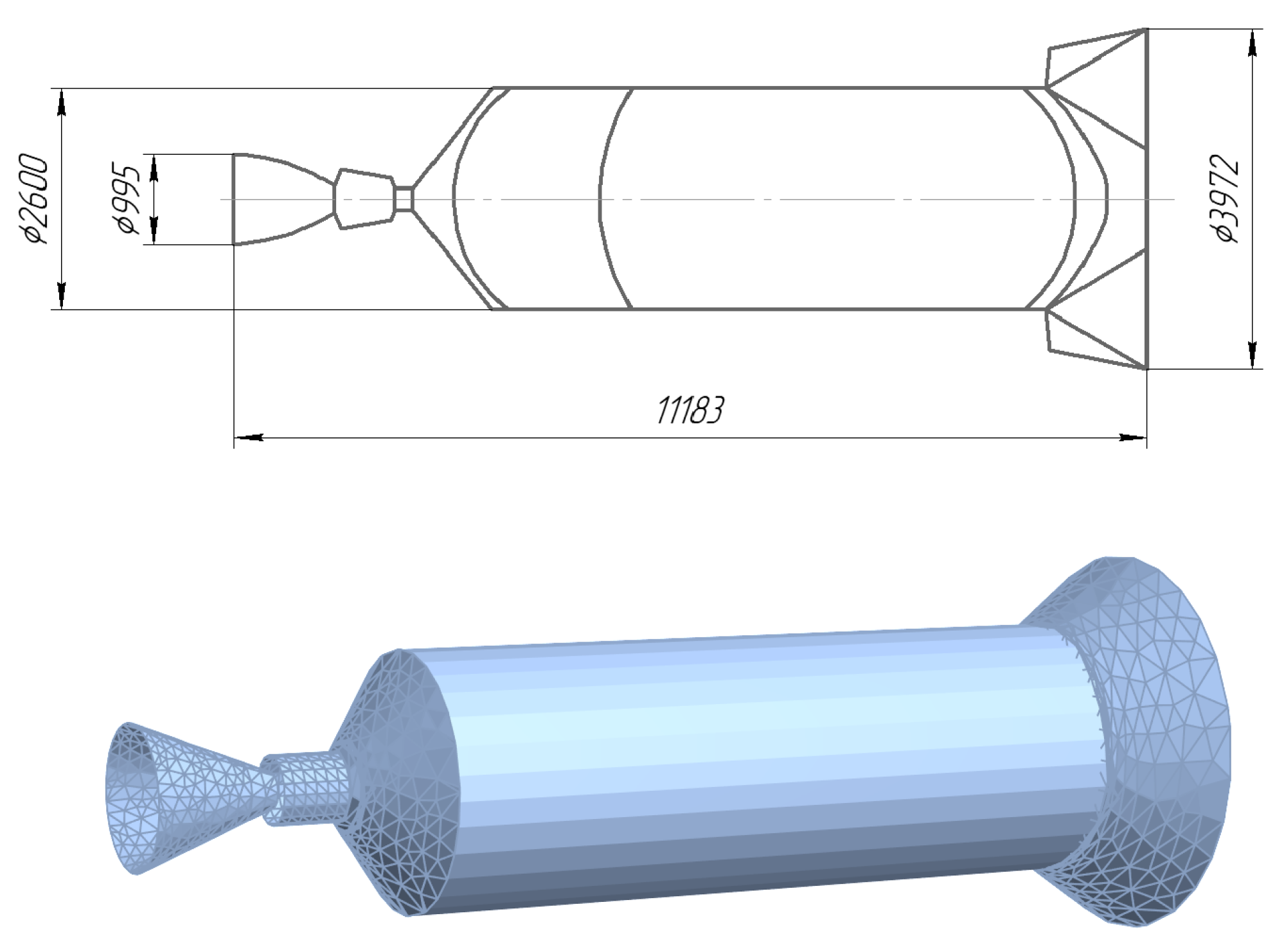
4.1. Target Upper Stage: Ariane 4 H10
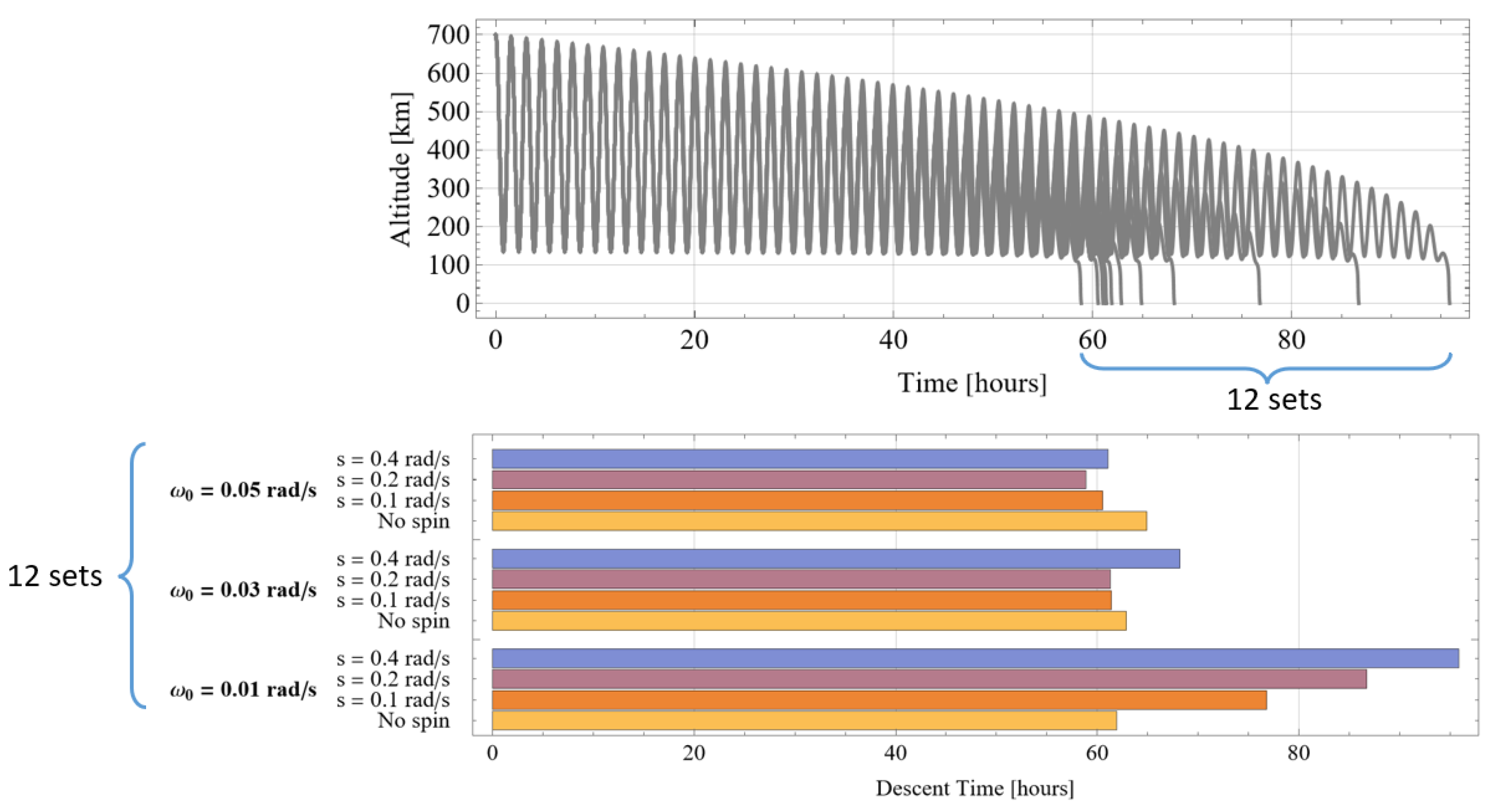
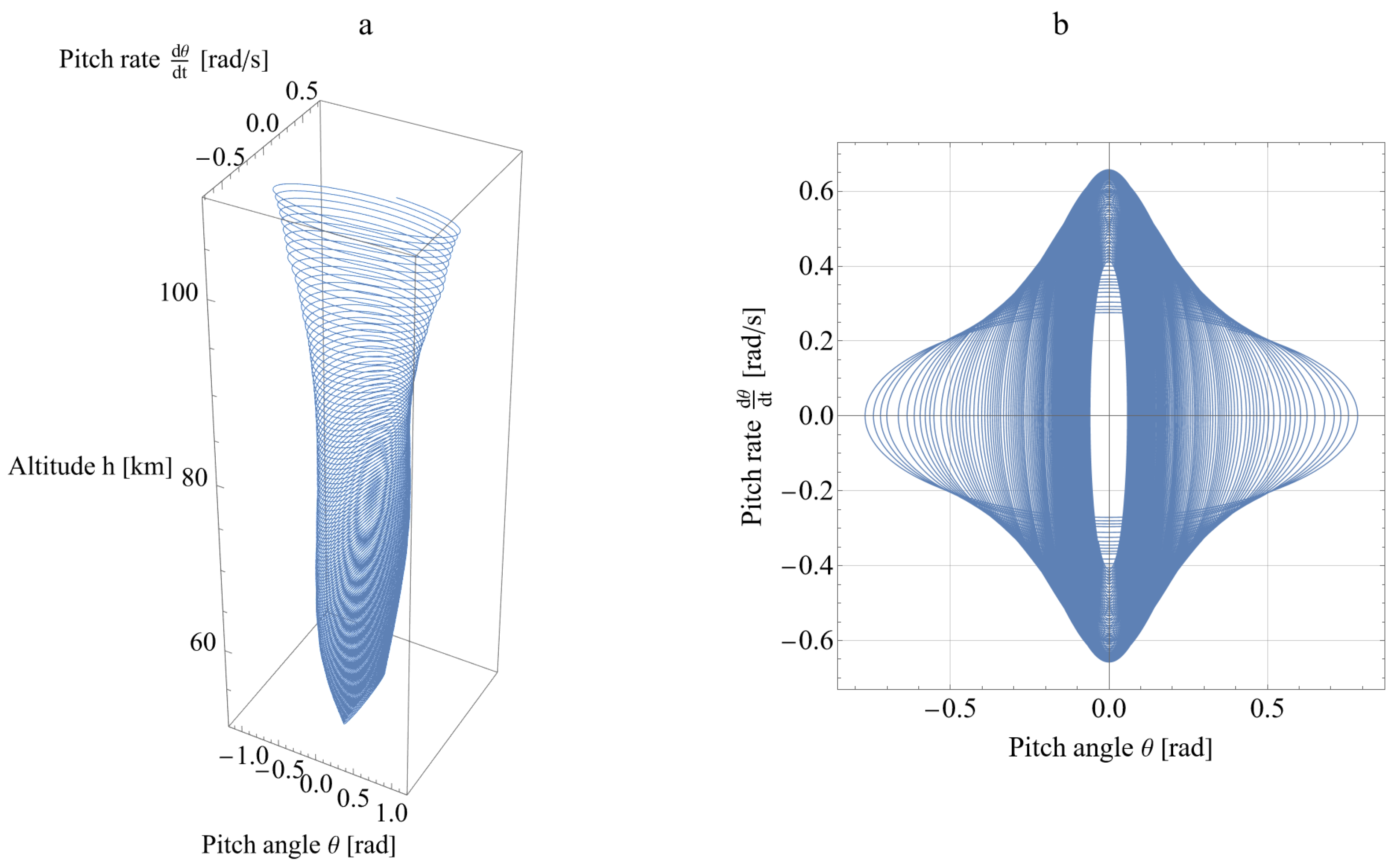
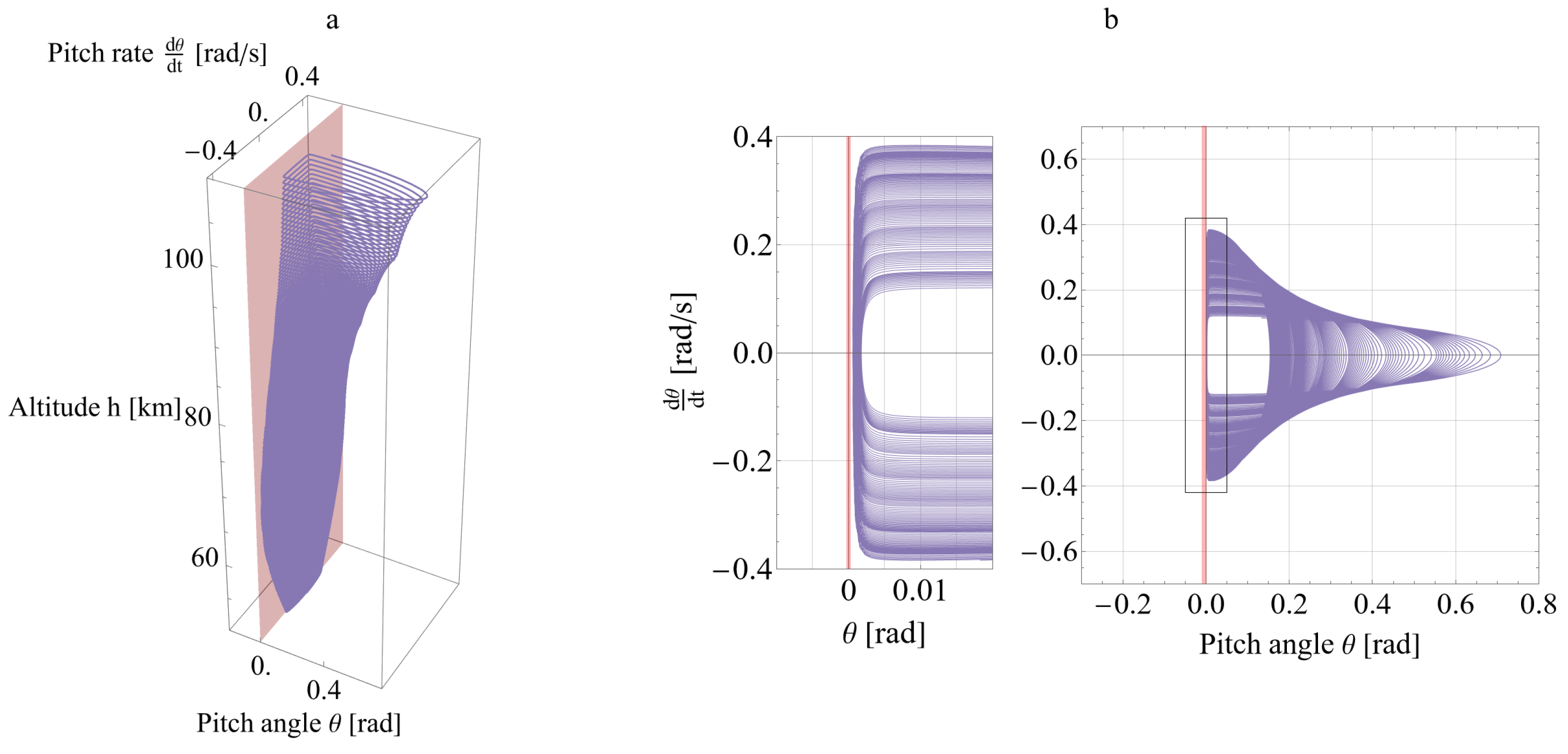
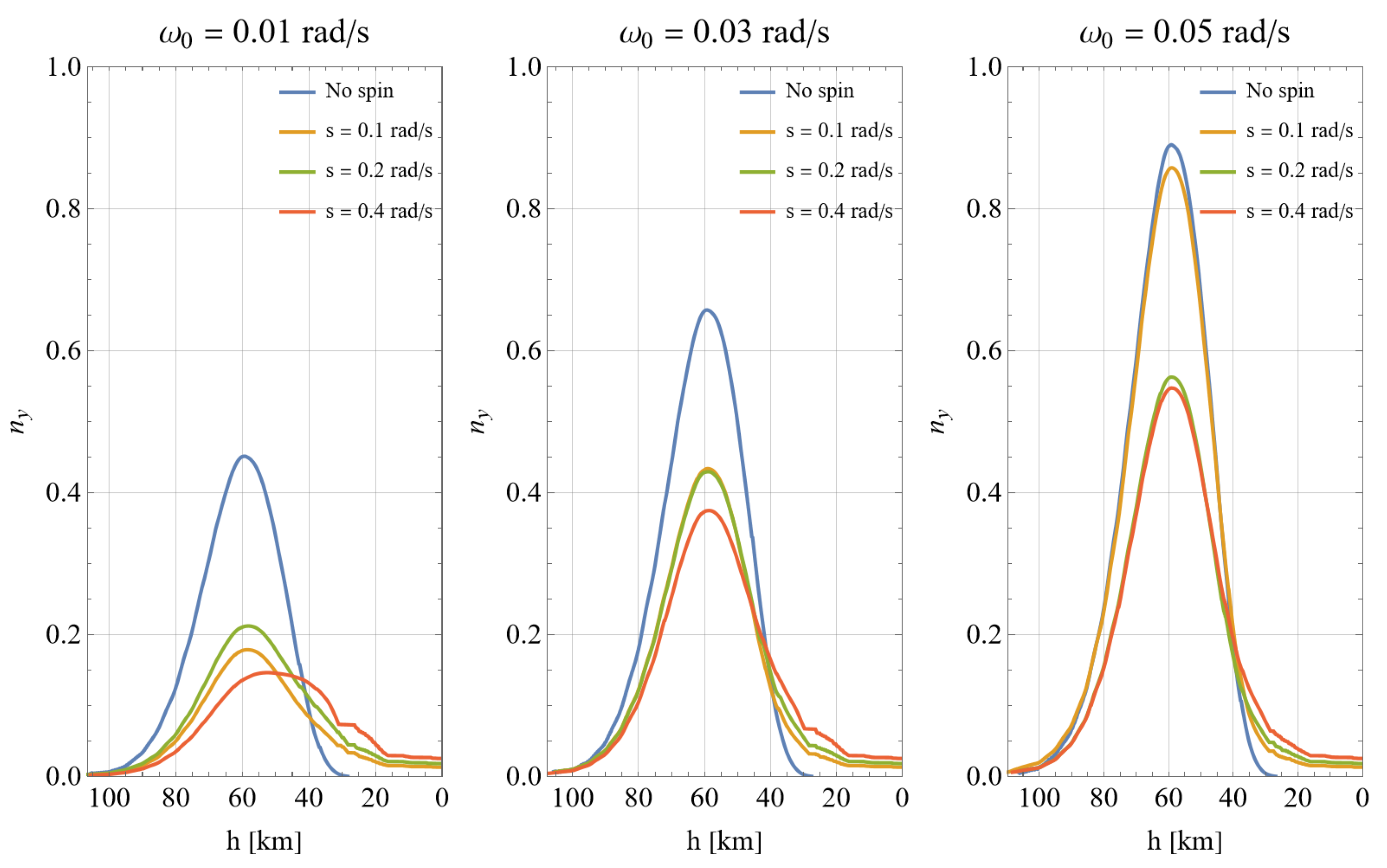
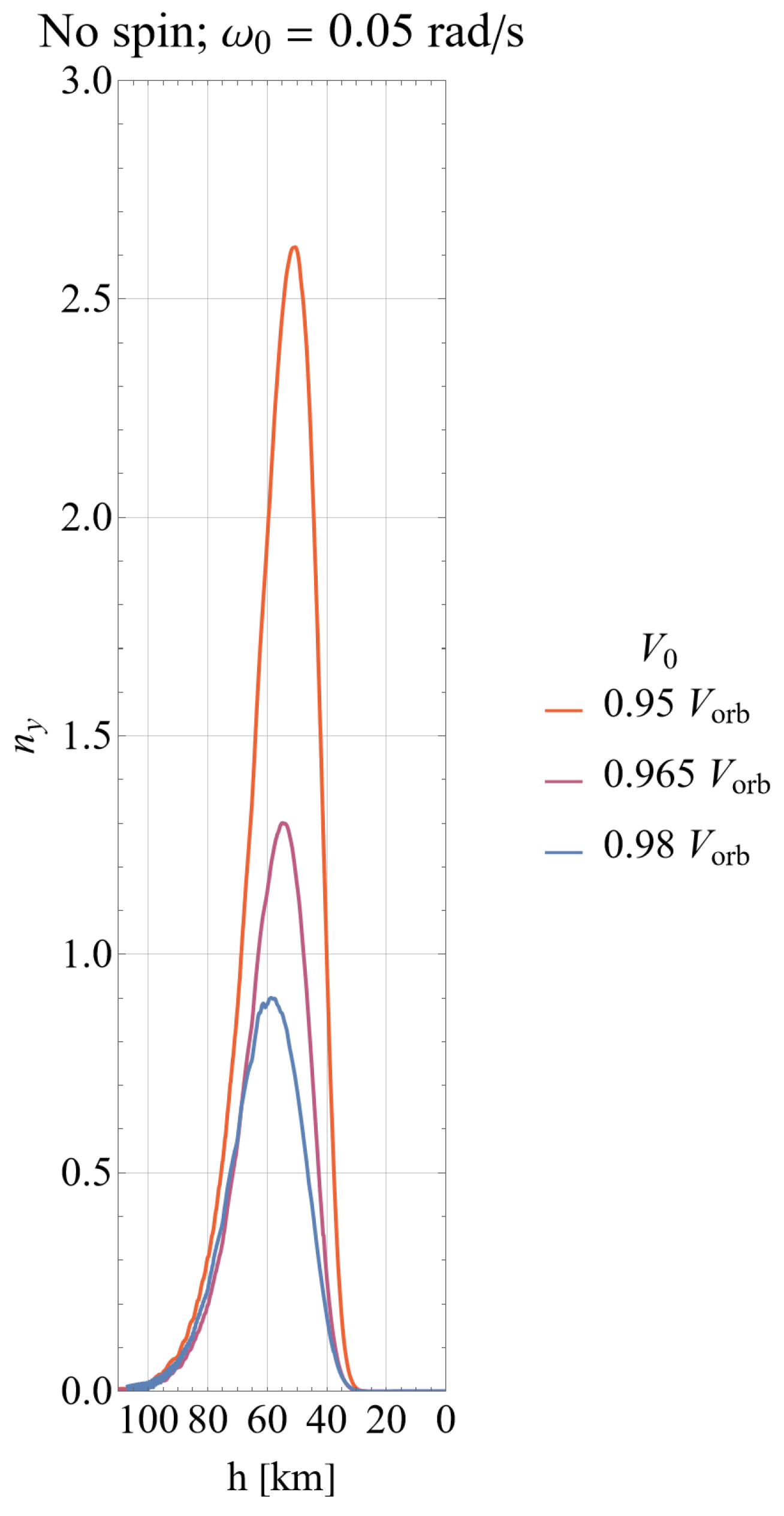
4.2. Numerical Simulations
5. Discussion: Using Features of Attitude Motion for Load Factor Regulation
5.1. Mission Scenarios Exploiting Benefits of Low and High Load Factors
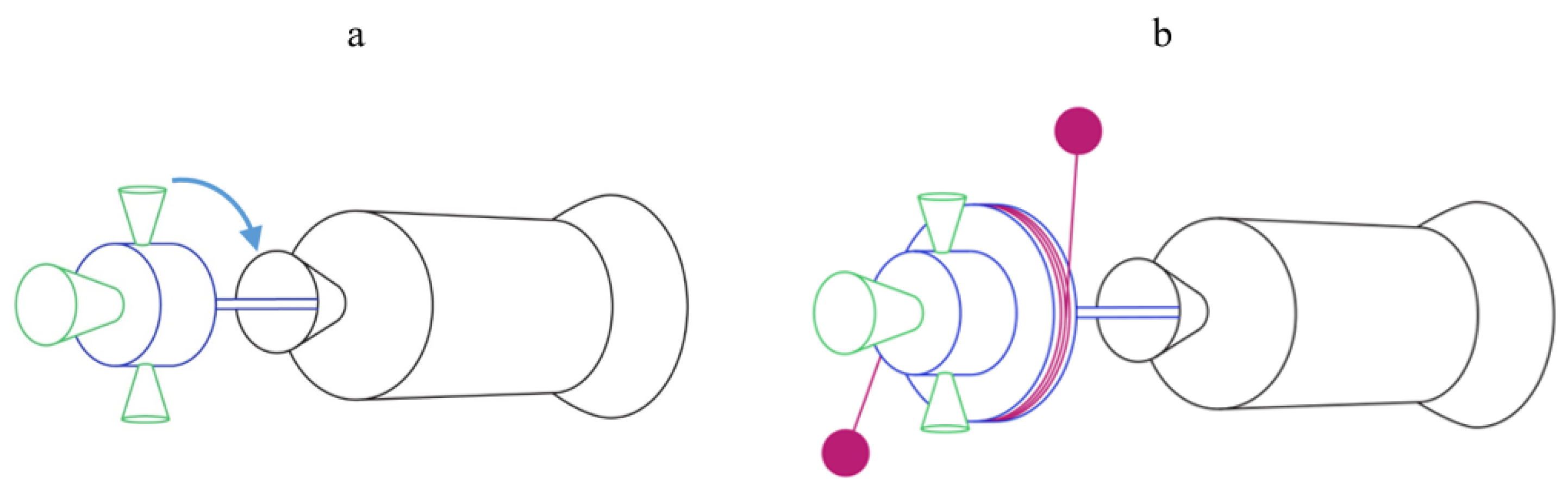
5.2. Possible De-Orbiting Devices
6. Conclusions
- Depending on the initial conditions of the descent, the character of the attitude motion can be different. Precessional motion or planar tumbling are the alternatives.
- The character of the attitude motion and its initial conditions determine the aerodynamic load factors and, thus, the breakup altitude.
- The required initial conditions can be provided by de-orbiting devices, which should be able to control both the tumbling and the spin of the target.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wright, E.; Boley, A.; Byers, M. Improving casualty risk estimates for uncontrolled rocket body reentries. J. Space Saf. Eng. 2024, 11, 74–79. [Google Scholar] [CrossRef]
- Pardini, C.; Anselmo, L. Uncontrolled re-entries of spacecraft and rocket bodies: A statistical overview over the last decade. J. Space Saf. Eng. 2019, 6, 30–47. [Google Scholar] [CrossRef]
- Salmaso, F.; Trisolini, M.; Colombo, C. A Machine Learning and Feature Engineering Approach for the Prediction of the Uncontrolled Re-Entry of Space Objects. Aerospace 2023, 10, 297. [Google Scholar] [CrossRef]
- Ledkov, A.; Aslanov, V. Review of contact and contactless active space debris removal approaches. Prog. Aerosp. Sci. 2022, 134, 100858. [Google Scholar] [CrossRef]
- Ledkov, A.; Aslanov, V. Evolution of space tethered system’s orbit during space debris towing taking into account the atmosphere influence. Nonlinear Dyn. 2019, 96, 2211–2223. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Sizov, D.A. A spent upper stage removal mission aimed to reduce debris impact footprint size. Acta Astronaut. 2020, 168, 23–30. [Google Scholar] [CrossRef]
- Endo, Y.; Kojima, H.; Trivailo, P.M. New formulation for evaluating status of space debris capture using tether-net. Adv. Space Res. 2022, 70, 2976–3002. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Ledkov, A.S. Survey of tether system technology for space debris removal missions. J. Spacecr. Rocket. 2023, 60, 1355–1371. [Google Scholar] [CrossRef]
- Bourabah, D.; Gnam, C.; Botta, E.M. Inertia tensor estimation of tethered debris through tether tracking. Acta Astronaut. 2023, 212, 643–653. [Google Scholar] [CrossRef]
- Boonrath, A.; Botta, E.M. Validation of Models for Net Deployment and Capture Simulation with Experimental Data. J. Spacecr. Rocket. 2024, 61, 181–199. [Google Scholar] [CrossRef]
- Couzin, P.; Teti, F.; Rembala, R. Active removal of large debris: System approach of deorbiting concepts and technological issues. In Proceedings of the 6th European Conference on Space Debris, Darmstadt, Germany, 22–25 April 2013. [Google Scholar]
- Sizov, D.A.; Aslanov, V.S. Space debris removal with harpoon assistance: Choice of parameters and optimization. J. Guid. Control Dyn. 2020, 44, 767–778. [Google Scholar] [CrossRef]
- Mao, L.; Zhao, W.; Pang, Z.; Gao, J.; Du, Z. Study On The Penetration Characteristics of Conical Harpoon on Rotating Space debris. Adv. Space Res. 2024, 74, 4109–4122. [Google Scholar] [CrossRef]
- Wu, C.; Yue, S.; Shi, W.; Gao, J.; Du, Z.; Zhao, Z.; Liu, Z. Research on adaptive penetration characteristics of space harpoon based on aluminum honeycomb buffer. Adv. Space Res. 2024. [Google Scholar] [CrossRef]
- Bylard, A.; MacPherson, R.; Hockman, B.; Cutkosky, M.R.; Pavone, M. Robust capture and deorbit of rocket body debris using controllable dry adhesion. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–9. [Google Scholar]
- Felicetti, L.; Sabatini, M.; Pisculli, A.; Gasbarri, P.; Palmerini, G.B. Adaptive thrust vector control during on-orbit servicing. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 10–12 September 2014; p. 4341. [Google Scholar]
- Zhang, Z.; Li, X.; Wang, X.; Zhou, X.; An, J.; Li, Y. TDE-Based Adaptive Integral Sliding Mode Control of Space Manipulator for Space-Debris Active Removal. Aerospace 2022, 9, 105. [Google Scholar] [CrossRef]
- Palma, P.; Seweryn, K.; Rybus, T. Impedance Control Using Selected Compliant Prismatic Joint in a Free-Floating Space Manipulator. Aerospace 2022, 9, 406. [Google Scholar] [CrossRef]
- Aslanov, V.S.; Yudintsev, V.V. Docking of a space tug with upper stage debris object using deployable flexible beam. In Proceedings of the International Astronautical Congress, Adelaide, Australia, 25–29 September 2017. [Google Scholar]
- Kaiser, C.; Sjöberg, F.; Delcura, J.M.; Eilertsen, B. SMART-OLEV—An orbital life extension vehicle for servicing commercial spacecrafts in GEO. Acta Astronaut. 2008, 63, 400–410. [Google Scholar] [CrossRef]
- DeLuca, L.T.; Lavagna, M.; Maggi, F.; Tadini, P.; Pardini, C.; Anselmo, L.; Grassi, M.; Tancredi, U.; Francesconi, A.; Pavarin, D.; et al. Large debris removal mission in LEO based on hybrid propulsion. Aerotec. Missili Spaz. 2014, 93, 51–58. [Google Scholar] [CrossRef]
- Takahashi, Y.; Nakasato, R.; Oshima, N. Analysis of radio frequency blackout for a blunt-body capsule in atmospheric reentry missions. Aerospace 2016, 3, 2. [Google Scholar] [CrossRef]
- Zuppardi, G.; Savino, R.; Mongelluzzo, G. Aero-thermo-dynamic analysis of a low ballistic coefficient deployable capsule in Earth re-entry. Acta Astronaut. 2016, 127, 593–602. [Google Scholar] [CrossRef]
- Carná, S.R.; Bevilacqua, R. High fidelity model for the atmospheric re-entry of CubeSats equipped with the drag de-orbit device. Acta Astronaut. 2019, 156, 134–156. [Google Scholar] [CrossRef]
- Otsu, H. Aerodynamic Characteristics of Re-Entry Capsules with Hyperbolic Contours. Aerospace 2021, 8, 287. [Google Scholar] [CrossRef]
- D’Amato, E.; Notaro, I.; Panico, G.; Blasi, L.; Mattei, M.; Nocerino, A. Trajectory Planning and Tracking for a Re-Entry Capsule with a Deployable Aero-Brake. Aerospace 2022, 9, 841. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, H.; Xu, D.; Cai, G. Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle. Aerospace 2023, 10, 310. [Google Scholar] [CrossRef]
- Otsu, H.; Nagasawa, M.; Tsujimoto, R.; Oshio, Y. Numerical Investigation of Aerodynamic Characteristics of a Re-entry Capsule with Hyperbolic Contours. J. Evol. Space Act. 2023, 1, 64. [Google Scholar]
- Peri, L.N.P.; Ingenito, A.; Teofilatto, P. Large-Eddy Simulations of a Hypersonic Re-Entry Capsule Coupled with the Supersonic Disk-Gap-Band Parachute. Aerospace 2024, 11, 94. [Google Scholar] [CrossRef]
- Hild, F.; Traub, C.; Pfeiffer, M.; Beyer, J.; Fasoulas, S. Optimisation of satellite geometries in Very Low Earth Orbits for drag minimisation and lifetime extension. Acta Astronaut. 2022, 201, 340–352. [Google Scholar] [CrossRef]
- US Standard Atmosphere; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1976.
- Aslanov, V.S. Rigid Body Dynamics for Space Applications; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Kortman, M.; Ruhl, S.; Weise, J.; Kreisel, J.; Schervan, T.; Schmidt, H.; Dafnis, A. Building block based iBoss approach: Fully modular systems with standard interface to enhance future satellites. In Proceedings of the 66th International Astronautical Congress (Jerusalem), Jerusalem, Israel, 12–16 October 2015; Volume 2, pp. 1–11. [Google Scholar]
- Gómez, N.O.; Walker, S.J. Eddy currents applied to de-tumbling of space debris: Analysis and validation of approximate proposed methods. Acta Astronaut. 2015, 114, 34–53. [Google Scholar] [CrossRef]
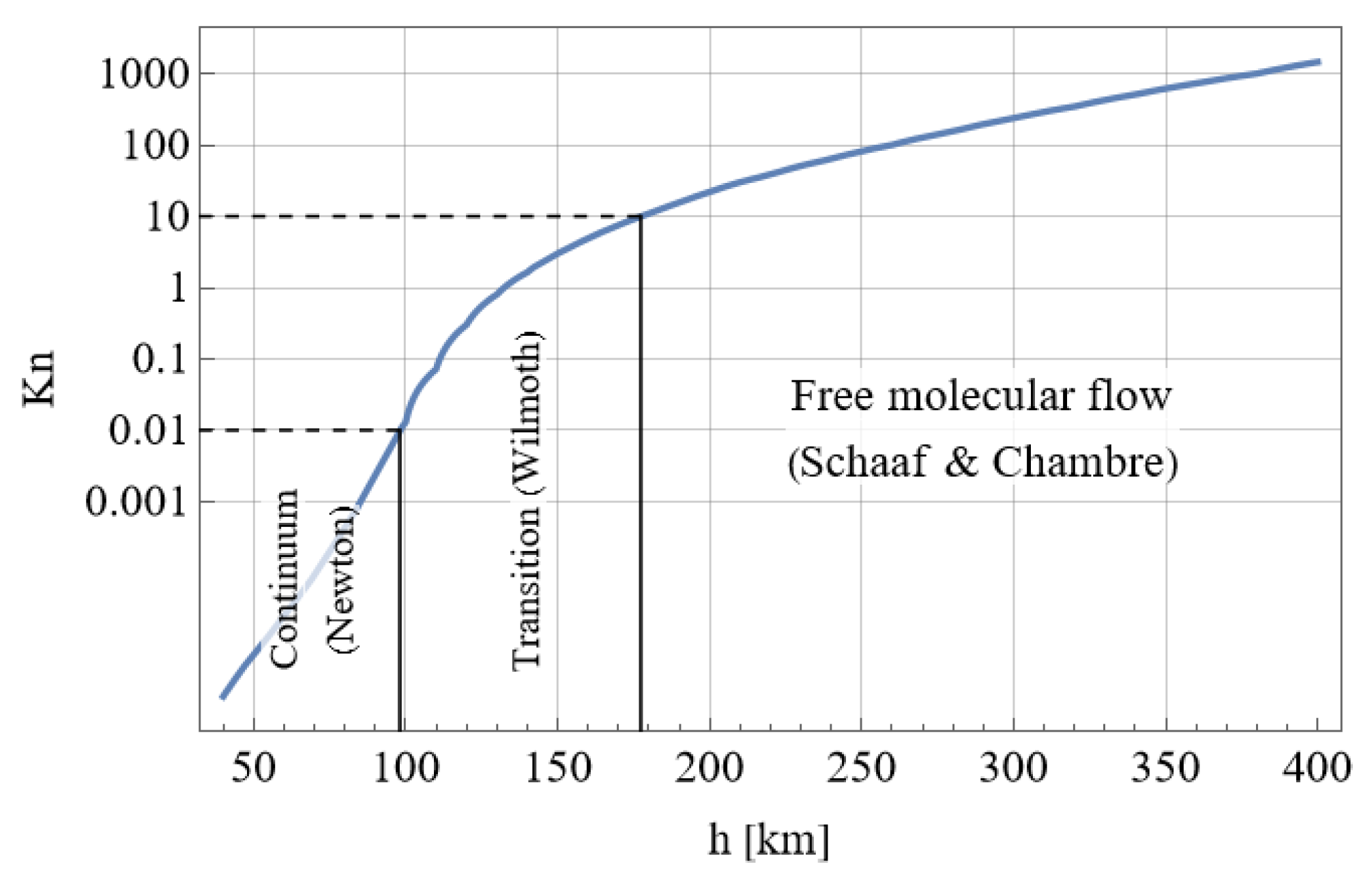
- Schaaf, S.; Chambre, P. Flow of Rarefied Gases, High Speed Aerodynamics and Jet Propulsion. In Fundamentals of Gas Dynamics; Princeton University Press NY: Princeton, NJ, USA, 1958; Volume 3. [Google Scholar]
- Gallais, P. Atmospheric Re-Entry Vehicle Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Wilmoth, R.G.; Mitcheltree, R.A.; Moss, J.N. Low-density aerodynamics of the stardust sample return capsule. J. Spacecr. Rocket. 1999, 36, 436–441. [Google Scholar] [CrossRef]
- Yudintsev, V.; Aslanov, V. Detumbling space debris using modified yo-yo mechanism. J. Guid. Control Dyn. 2017, 40, 714–721. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Mass m | 2154 kg |
| Total length = reference length | 11.183 m |
| Fuel tank diameter d | 2.6 m |
| Reference area | 5.31 |
| Longitudinal moment of inertia | 3000 kg |
| Transverse moments of inertia | 28,000 kg |
| Longitudinal shift of the CoM from the nozzle edge | m |
| Parameter | [km] | [m/s] | |||||||
| Value | 700 | 0 | 0 | 0.1 | 0 | 0 | variable (see Table 3) | ||
| Set # | Pitch Rate | Spin Rate |
|---|---|---|
| 1 | 0.05 | 0.4 |
| 2 | 0.2 | |
| 3 | 0.1 | |
| 4 | 0 | |
| 5 | 0.03 | 0.4 |
| 6 | 0.2 | |
| 7 | 0.1 | |
| 8 | 0 | |
| 9 | 0.01 | 0.4 |
| 10 | 0.2 | |
| 11 | 0.1 | |
| 12 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslanov, V.S.; Sizov, D.A. Large Debris Removal: Using Features of Attitude Motion for Load Factor Regulation during Re-Entry. Aerospace 2024, 11, 786. https://doi.org/10.3390/aerospace11090786
Aslanov VS, Sizov DA. Large Debris Removal: Using Features of Attitude Motion for Load Factor Regulation during Re-Entry. Aerospace. 2024; 11(9):786. https://doi.org/10.3390/aerospace11090786
Chicago/Turabian StyleAslanov, Vladimir S., and Dmitry A. Sizov. 2024. "Large Debris Removal: Using Features of Attitude Motion for Load Factor Regulation during Re-Entry" Aerospace 11, no. 9: 786. https://doi.org/10.3390/aerospace11090786
APA StyleAslanov, V. S., & Sizov, D. A. (2024). Large Debris Removal: Using Features of Attitude Motion for Load Factor Regulation during Re-Entry. Aerospace, 11(9), 786. https://doi.org/10.3390/aerospace11090786






