ISSA-Based Evaluation Method of Actual Navigation Performance of Rotorcraft Logistics Unmanned Aerial Vehicles
Abstract
:1. Introduction
2. Research Status of ANP
3. Optimization Model for the ANP of Rotorcraft Logistics UAVs
4. Solution Method for the ANP Optimization Model Based on ISSA
4.1. Initial Population Strategy Based on Probabilistic Decision-Making
4.2. Adaptive Dynamic Step Size Strategy
4.3. Dynamic Compression Search Strategy
| ISSA |
| Step 1: Set the population size n, number of discoverers PD, number of investigators SD, warning value R2, safety value ST, maximum number of iterations M, constant and , and control step size . Calculate the error probability Q corresponding to the ANP obtained from traditional methods. |
| Step 2: Based on Q, using the initial population strategy based on probabilistic decision-making, initialize the population, calculate the fitness value for each sparrow, and find the current optimal and worst positions. |
| Step 3: While t < M, calculate the adaptive dynamic step size according to Equation (13). |
| Step 4: Update the sparrow positions in the interval [1, PD] according to Equation (12). |
| Step 5: Update the sparrow positions in the interval [PD + 1, n] according to Equation (14). |
| Step 6: Update the sparrow positions in the interval [1, SD] according to Equation (15). |
| Step 7: Calculate the fitness value for each sparrow and find the current optimal and worst positions. Activate the dynamic compression strategy and verify if , if yes, update the sparrow positions according to Equation (16). |
| Step 8: Set t = t + 1 and return to Step 3 until the end. |
| ISSA-based real-time estimation method |
| Step 1: Calculate the variance of the position error of the navigation system and , using Equation (3), determine the lengths of the semi-major and semi-minor axes of the error ellipse. Then, calculate the ANP value using the traditional method based on Equation (3). |
| Step 2: Calculate the Q corresponding to the ANP from the traditional methods by Equations (8) and (9). Utilize the initial population strategy based on probabilistic decision-making to initialize the population. |
| Step 3: Calculate the fitness function Equation (10) using Equations (8) and (9). |
| Step 4: Execute the ISSA algorithm. |
| Step 5: Obtain the optimal ANP for the current navigation state, increment k by 1 (k = k + 1), and return to Step 1 until the end. |
5. Experiments
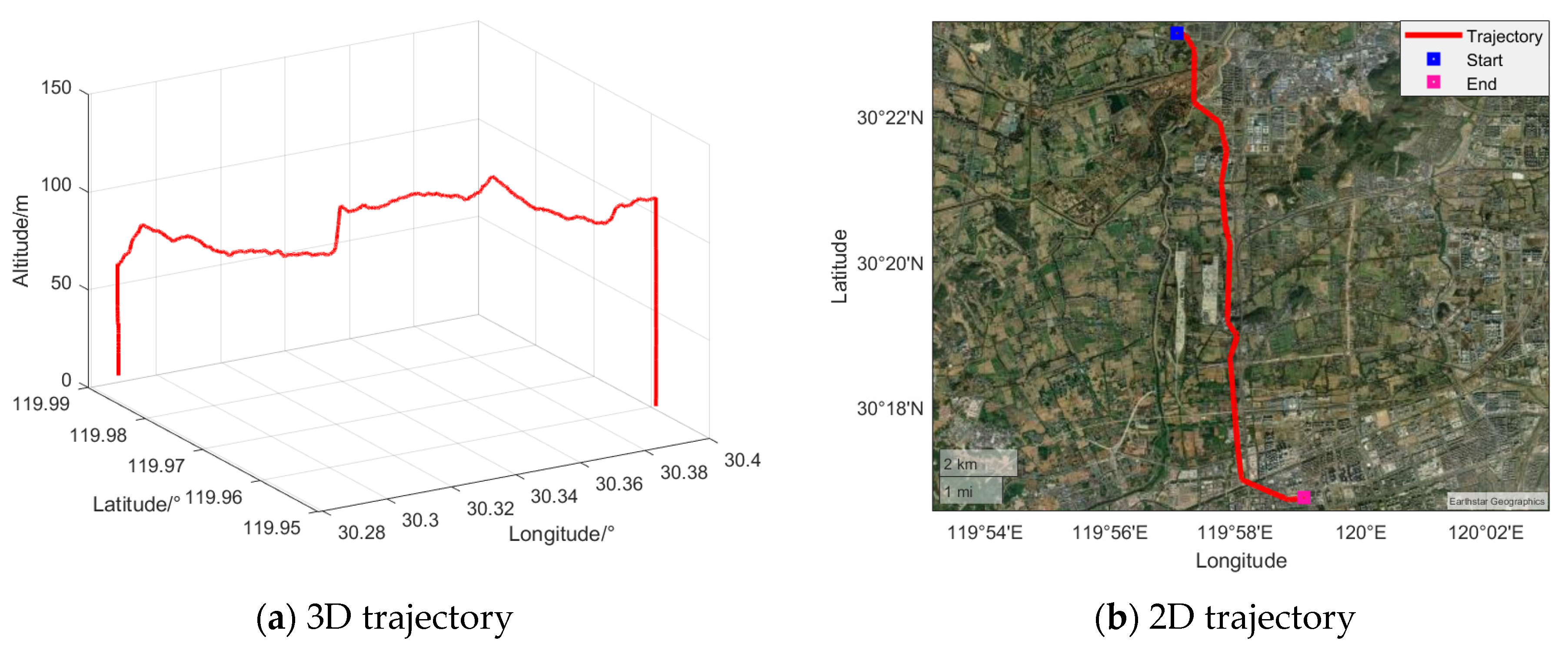
5.1. Experimental Conditions
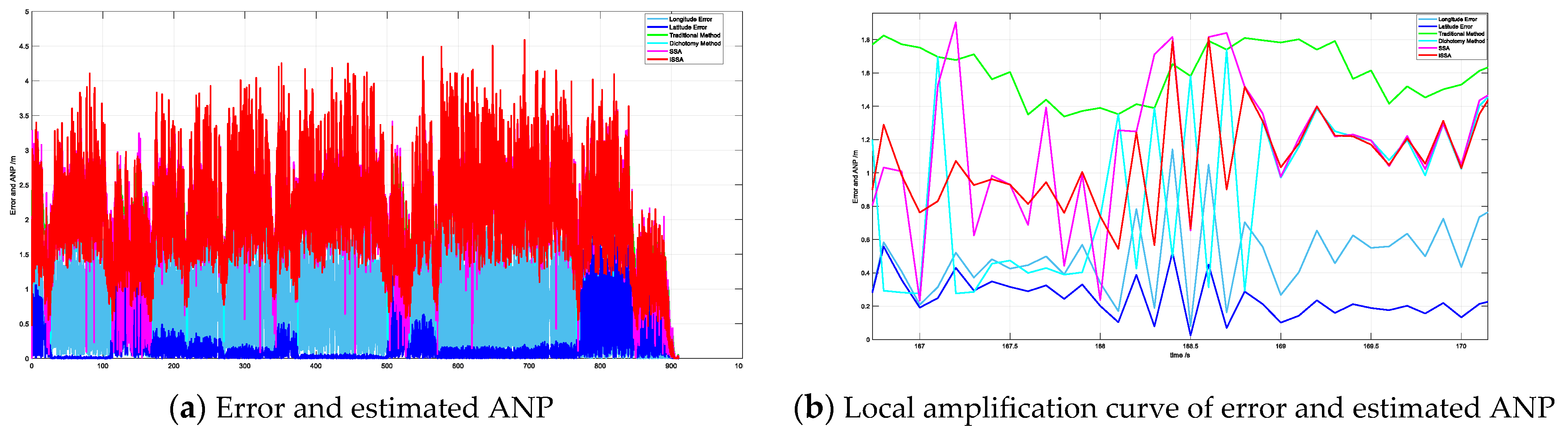
5.2. Results and Analysis
6. Conclusions
- (1)
- The experimental results validate the accuracy and feasibility of the proposed real-time ANP estimation model.
- (2)
- In urban environments, the proposed ISSA can accurately estimate ANP, with its precision surpassing that of traditional methods, the dichotomy and SSA, demonstrating that ISSA improves the optimization capability of the algorithm. The estimated ANP value corresponds to a probability of 94.99% for the UAV’s actual position falling within the error circle, meeting the PBN operational requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tedeschi, P.; Al Nuaimi, F.A.; Awad, A.I.; Natalizio, E. Privacy-aware remote identification for unmanned aerial vehicles: Current solutions, potential threats, and future directions. IEEE Trans. Ind. Inform. 2023, 20, 1069–1080. [Google Scholar] [CrossRef]
- Errico, A.; Di Vito, V. Performance-based navigation (PBN) with continuous descent operations (CDO) for efficient approach over highly protected zones. In Proceedings of the 2017 24th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 29–31 May 2017; pp. 1–8. [Google Scholar]
- Enayatollahi, F.; Atashgah, M.A.; Malaek, S.M.B.; Thulasiraman, P. PBN-based time-optimal terminal air traffic control using cellular automata. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1513–1523. [Google Scholar] [CrossRef]
- Ostroumov, I.V.; Kuzmenko, N.S. An area navigation (RNAV) system performance monitoring and alerting. In Proceedings of the 2018 IEEE First International Conference on System Analysis & Intelligent Computing (SAIC), Kyiv, Ukraine, 8–12 October 2018; pp. 1–4. [Google Scholar]
- Kallinen, V.; Martin, T.; McFadyen, A. Required navigation performance specifications for unmanned aircraft based on UTM flight trials. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 196–203. [Google Scholar]
- Bechtel, R.; Narvid, J.; Graupmann, E. Enabling Established on Required Navigation Performance Usage to Reduce Carbon Emissions. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–6. [Google Scholar]
- Dai, Y.; Lai, J.; Zhu, B.; Li, Z.; Sun, X.; Lv, P. Three-Dimensional ANP Evaluation Method Based on Spatial Position Uncertainty under RNP Operation. Aerospace 2022, 9, 703. [Google Scholar] [CrossRef]
- Wang, C.J.; Ng, E.M.; Low, K.H. Investigation and modeling of flight technical error (FTE) associated with UAS operating with and without pilot guidance. IEEE Trans. Veh. Technol. 2021, 70, 12389–12401. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, X.; Huo, H. An Actual Navigation Performance Evaluation Method Based on Efficient Numerical Integration. J. Telem. Track. Command. 2016, 37, 26–31. (In Chinese) [Google Scholar]
- Zhang, N. Research on Calculation Method of Actual Navigation Performance. Aeronaut. Comput. Tech. 2017, 47, 49–51. (In Chinese) [Google Scholar]
- Ma, H.; Wang, D.; Sun, X. DR/GPS/DME/VOR Integrated Navigation and Performance Evaluation Methods Based on RNP Operation. Command. Control Simul. 2017, 39, 123–128. (In Chinese) [Google Scholar]
- Wang, D.; Ma, H.; Sun, X. Research on the Actual Navigation Performance Evaluating Method of Ground-based Area Navigation. Avion. Technol. 2019, 49, 13–18. (In Chinese) [Google Scholar]
- Dautermann, T.; Mollwitz, V.; Többen, H.H.; Altenscheidt, M.; Bürgers, S.; Bleeker, O.; Bock-Janning, S. Design, implementation and flight testing of advanced RNP to SBAS LPV approaches in Germany. Aerosp. Sci. Technol. 2015, 47, 280–290. [Google Scholar] [CrossRef]
- Džunda, M.; Melníková, L. The Influence of Narrowband Interference on DME System Operation. Aerospace 2023, 10, 663. [Google Scholar] [CrossRef]
- Peng, X.; Zu, Z.; Zhu, C.; Qi, M. Actual navigation performance evaluation algorithm of INS/GNSS navigation system. Electron. Test 2021, 3, 41–45. (In Chinese) [Google Scholar]
- Teng, J.; Zhu, L.; Ji, Y. Real-Time Evaluation Method of Flight Error Based on Actual Navigation Performance. Mod. Navig. 2022, 13, 92–96+101. (In Chinese) [Google Scholar]
- Wang, L.; Ren, Y.; Zheng, Z. Calculation Scheme of Actual Navigation Performance of Civil Aircraft Navigation System. Ind. Control Comput. 2022, 35, 74–76+80. (In Chinese) [Google Scholar]
- Li, W.; Wang, G.G.; Gandomi, A.H. A survey of learning-based intelligent optimization algorithms. Arch. Comput. Methods Eng. 2021, 28, 3781–3799. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Lu, L.; Niu, P. Analysis and research of several new intelligent optimization algorithms. J. Front. Comput. Sci. Technol. 2022, 16, 88. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xing, Z.; Yi, C.; Lin, J.; Zhou, Q. Multi-component fault diagnosis of wheelset-bearing using shift-invariant impulsive dictionary matching pursuit and sparrow search algorithm. Measurement 2021, 178, 109375. [Google Scholar] [CrossRef]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using adaptive sparrow search algorithm. Int. J. Hydrogen Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Li, L.L.; Xiong, J.L.; Tseng, M.L.; Yan, Z.; Lim, M.K. Using multi-objective sparrow search algorithm to establish active distribution network dynamic reconfiguration integrated optimization. Expert Syst. Appl. 2022, 193, 116445. [Google Scholar] [CrossRef]
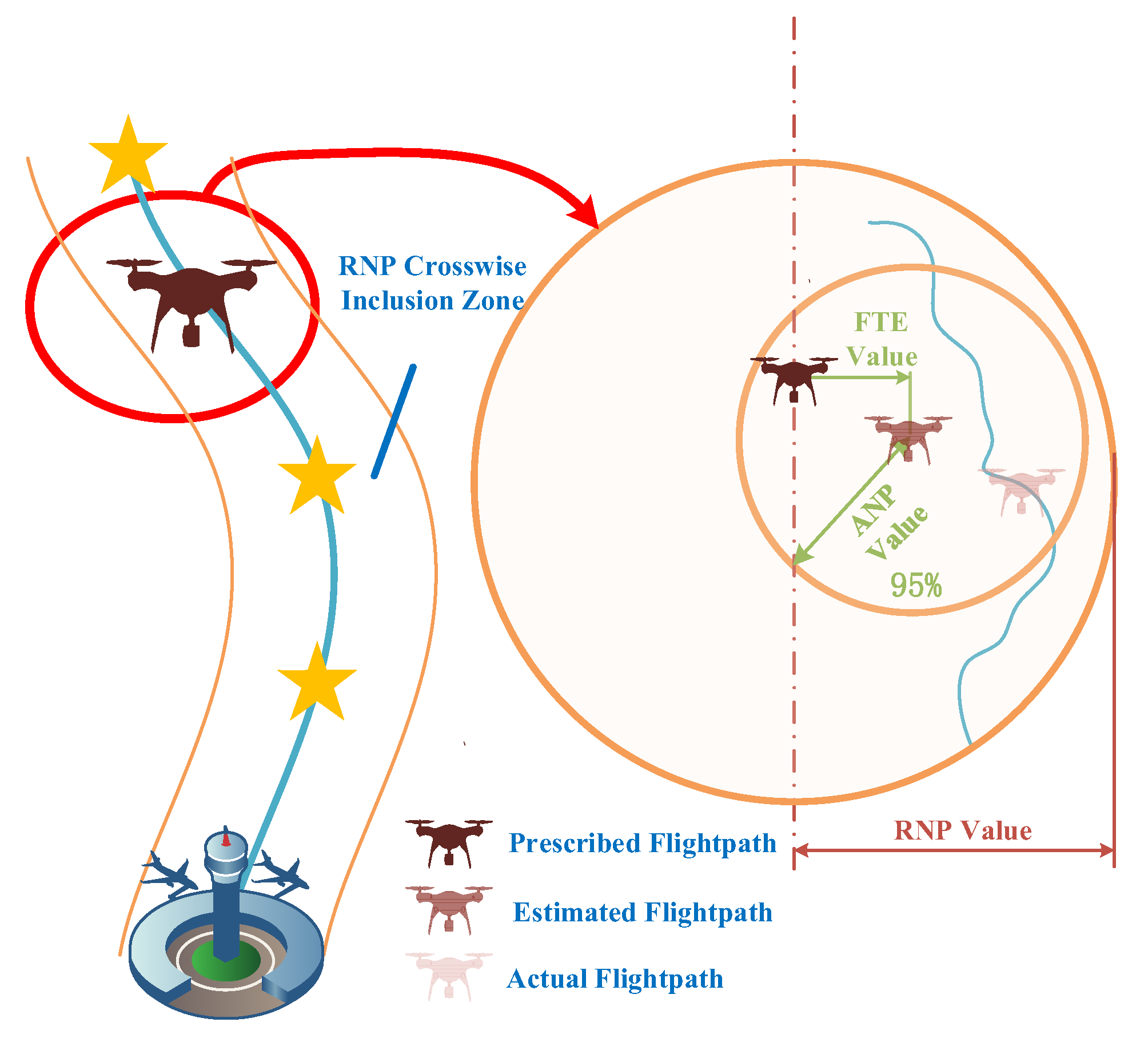
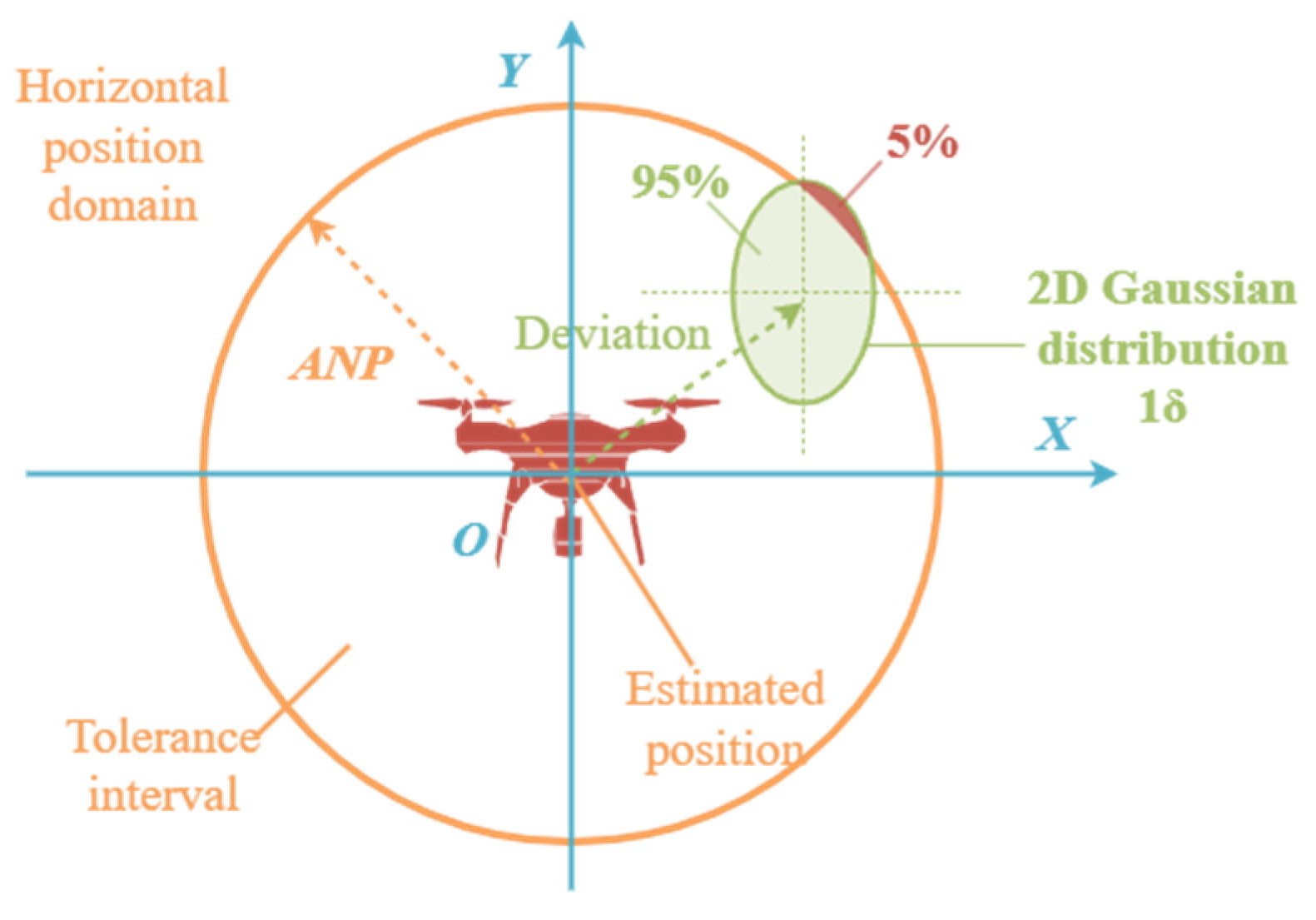

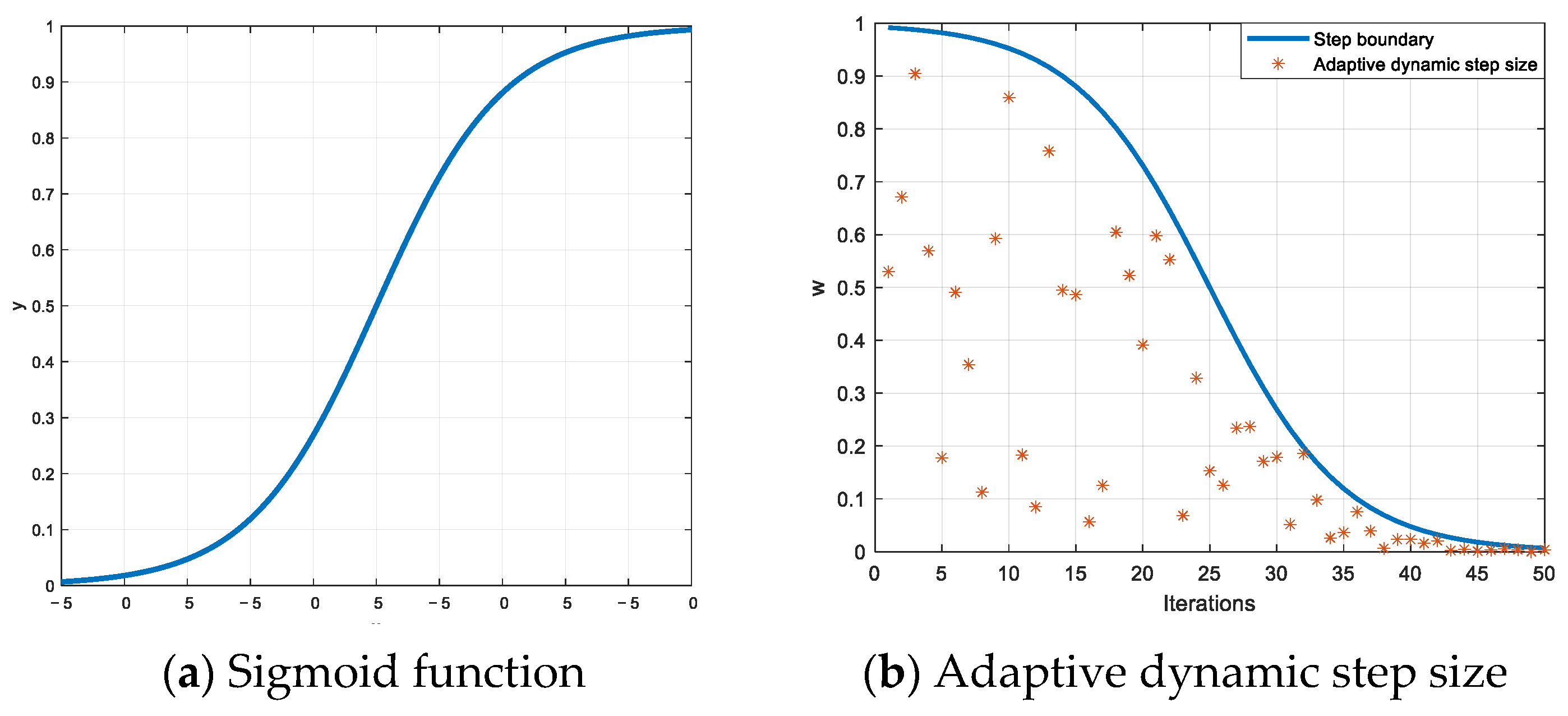
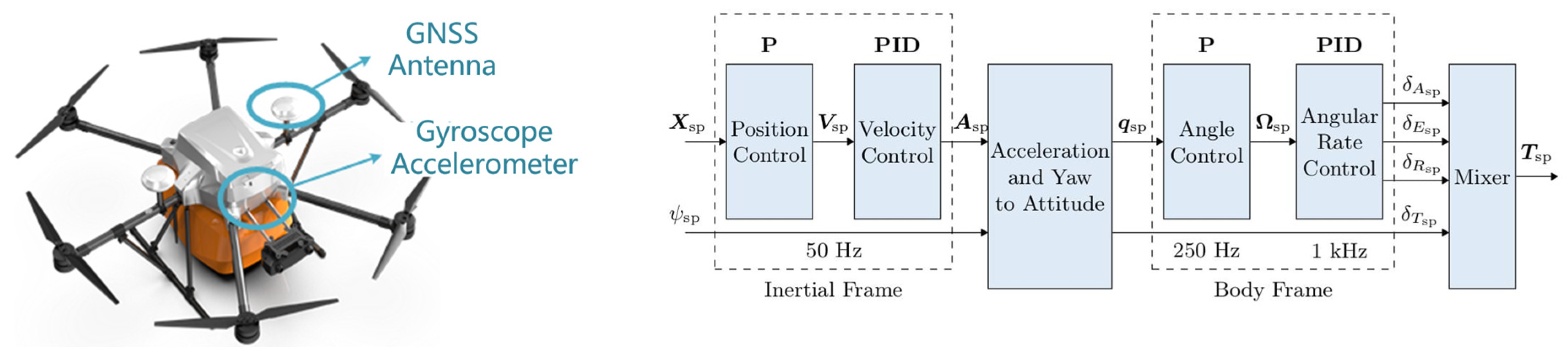



| References | Core Idea | Method Advantages | Method Disadvantages |
|---|---|---|---|
| [9] | Based on ICAO PBN requirements, ANP is solved by numerical integration method of Gauss three-point formula and complex Simpson formula. | Efficient calculation to meet the real-time requirements of civil aircraft | The influence of dynamic environmental errors (such as meteorological disturbance) on integration accuracy is not considered. |
| [10] | Aiming at the actual route, the dual mode of ANP approximation/accurate calculation is proposed | Adapted to different precision demand scenarios, with strong practicability. | The approximate calculation method has a large error in complex airspace structure. |
| [11,12] | Real-time ANP evaluation based on position covariance matrix | High-precision calculation, in line with RNP operating standards. | Strong dependence on the accuracy of the sensor error covariance matrix. |
| [13] | A new ANP computing architecture in multi-constellation GNSS environment | Support multi-system integration scenarios such as GPS/GLONASS/BDS. | The specific implementation details of the multi-constellation weight optimization algorithm are not disclosed. |
| [14] | Special ANP calculation method for land-based navigation system (such as DME/VOR) | Fill the blank of the performance evaluation of traditional navigation facilities | The mixed operation scenario with satellite-based navigation system is not considered. |
| [15] | Real-time ANP estimation of inertial/satellite integrated navigation based on two-dimensional Gaussian distribution | Low computational complexity, suitable for airborne embedded system implementation. | It is only applicable to the performance evaluation of plane navigation and lacks vertical analysis. |
| [16] | Realization of ANP dynamic verification framework on BlueSky simulation platform | Provide a standardized verification environment to support the comparability research of algorithms. | There are modeling errors between simulation environment and real flight data. |
| [17] | Hybrid ANP computing scheme in multi-navigation mode (RNAV/RNP) | Innovative Fusion Precision Factor, Error Covariance and Rayleigh Distribution | The transition algorithm for switching between different modes is not fully explained. |
| Sensor Parameters | Model | Parameters |
|---|---|---|
| Gyroscope Noise | ICM-20602 | ±4 MdPS/Z Hz |
| Accelerometer Noise | 100 μg/Hz | |
| GNSSVelocity Error | NEO 3 GNSS Module | 0.05 m/s |
| GNSS Position Error | 2.0 m |
| Methods | Traditional Methods | Dichotomy | SSA | ISSA | |
|---|---|---|---|---|---|
| Metrics | |||||
| Probability mean | 95.23% | 91.71% | 93.33% | 94.90% | |
| RMSE | 0.2181 | 3.1388 | 1.5890 | 0.0915 | |
| Upper | 95.3476% | 91.9243% | 93.5977% | 94.9371% | |
| Lower | 95.0985% | 91.4836% | 93.1369% | 94.8795% | |
| Variance | 36.7496 | 115.0108 | 125.6975 | 1.9625 | |
| Methods | Traditional Methods | Dichotomy | SSA | ISSA |
|---|---|---|---|---|
| One-step solution time (ms) | 1.1274 | 3.7528 | 8.1388 | 8.7635 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhao, L.; Wang, M.; Wu, M. ISSA-Based Evaluation Method of Actual Navigation Performance of Rotorcraft Logistics Unmanned Aerial Vehicles. Aerospace 2025, 12, 357. https://doi.org/10.3390/aerospace12040357
Liu F, Zhao L, Wang M, Wu M. ISSA-Based Evaluation Method of Actual Navigation Performance of Rotorcraft Logistics Unmanned Aerial Vehicles. Aerospace. 2025; 12(4):357. https://doi.org/10.3390/aerospace12040357
Chicago/Turabian StyleLiu, Fei, Liang Zhao, Maolin Wang, and Meiliwen Wu. 2025. "ISSA-Based Evaluation Method of Actual Navigation Performance of Rotorcraft Logistics Unmanned Aerial Vehicles" Aerospace 12, no. 4: 357. https://doi.org/10.3390/aerospace12040357
APA StyleLiu, F., Zhao, L., Wang, M., & Wu, M. (2025). ISSA-Based Evaluation Method of Actual Navigation Performance of Rotorcraft Logistics Unmanned Aerial Vehicles. Aerospace, 12(4), 357. https://doi.org/10.3390/aerospace12040357






