A Novel Ultrasonic Sampling Penetrator for Lunar Water Ice in the Lunar Permanent Shadow Exploration Mission
Abstract
1. Introduction
- (1)
- In environments exhibiting extremely low temperatures, lunar water ice demonstrates a high degree of susceptibility to disruption during the process of sampling. To maintain the integrity of the physical parameters and stratigraphic information of lunar water ice during sampling, it is essential to adhere to stringent protocols for the preservation of “in-situ quality and in-situ” [8]. The penetration coring method, a primary coring technique, is employed for the purpose of low-disturbance coring of lunar water ice. Concurrent research is underway to develop a coring method that ensures the “in-situ authenticity of lunar water ice samples”.
- (2)
- The sampling location is situated in a region of the Moon’s south pole that is perpetually shadowed. This geographical location presents challenges, as it is difficult to obtain the necessary electrical power to replenish the equipment required for the mission. This necessity for a low-power, high-efficiency penetration drive is further exacerbated by the rover’s limited energy supply. The ultrasonic sampling penetrator has the following characteristics: a compact structure, low power consumption, low drilling pressure, the absence of lubrication, and a wide range of temperature resistance (−200 °C~500 °C) [9,10], making it well suited for the penetration sampling of water ice samples from the lunar loam.
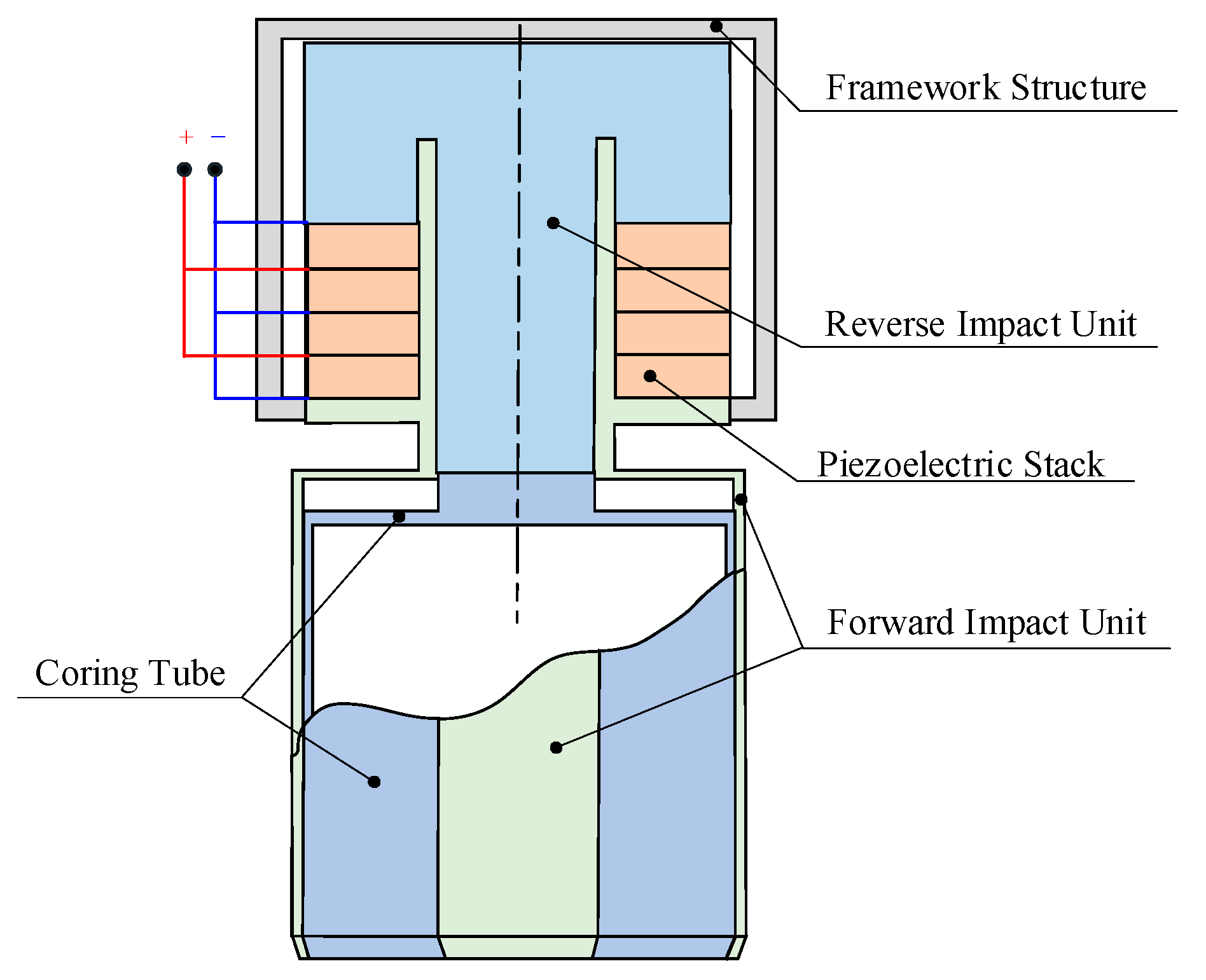
2. System Composition and Working Principle
3. Structural Design of Staggered Impact Piezoelectric Transducer
3.1. Design of Piezoelectric Transducer
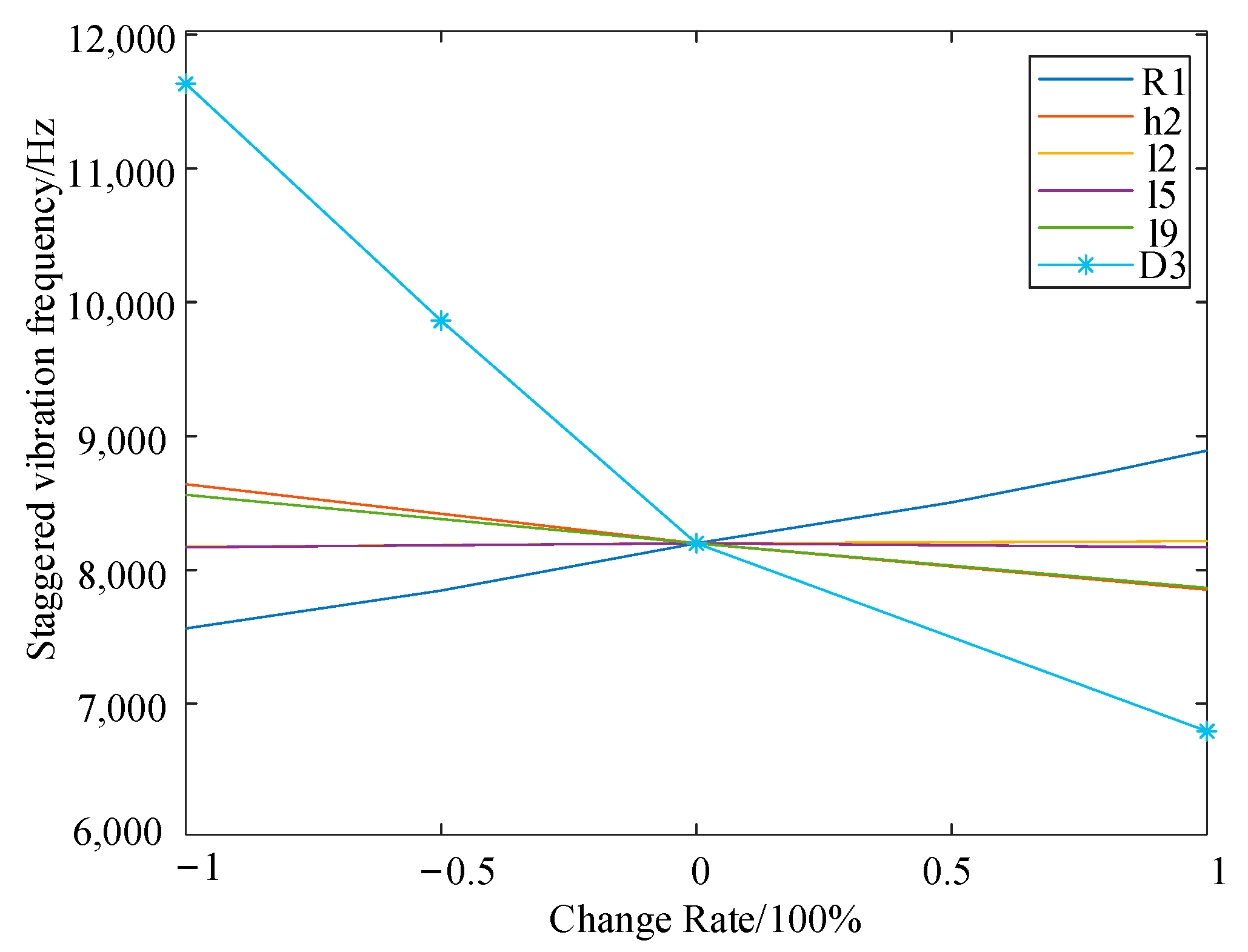
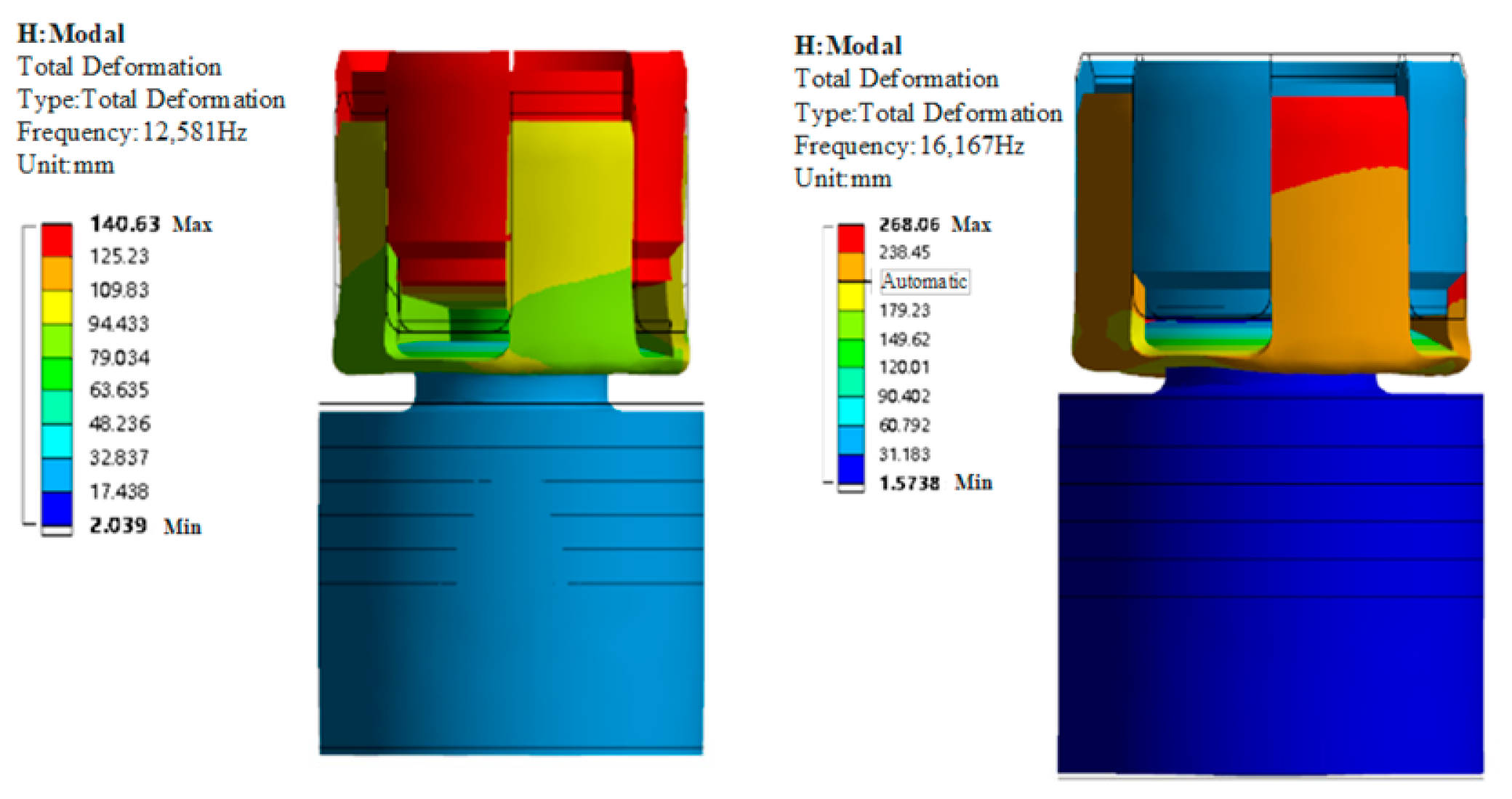
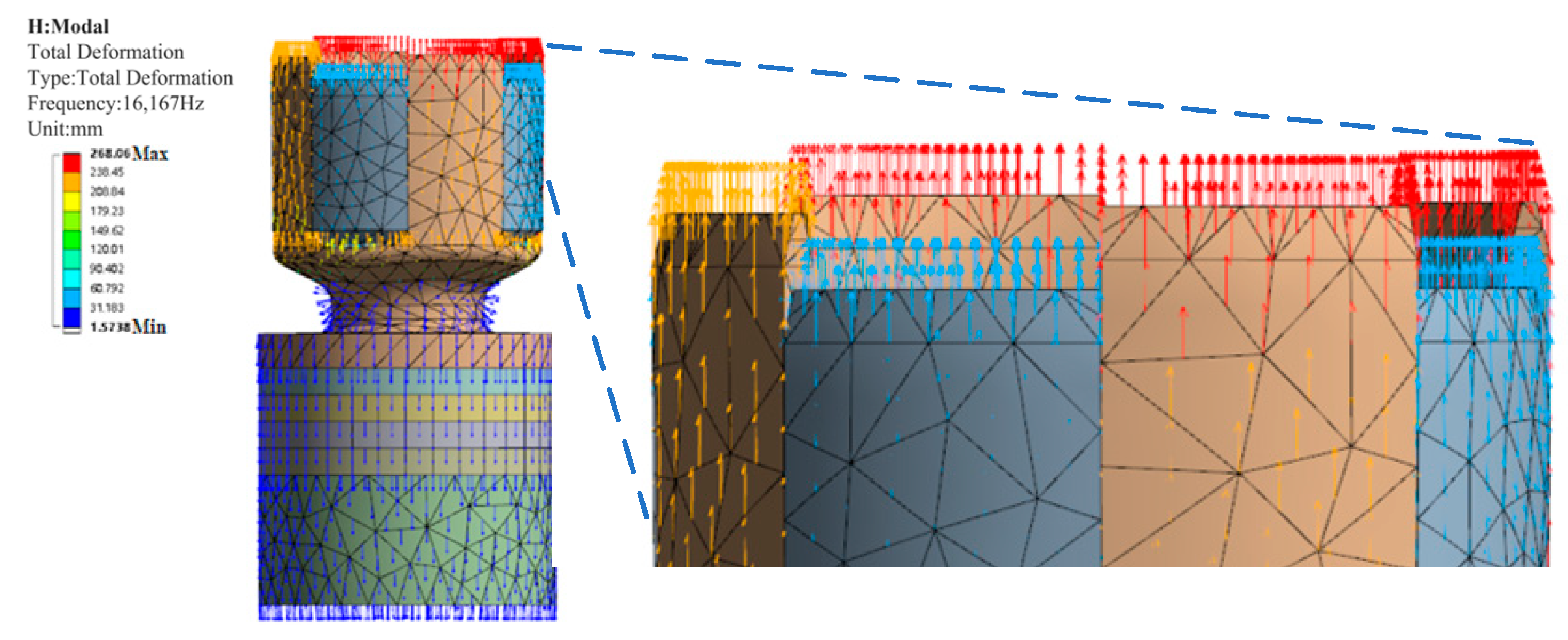
3.2. Structural Dimension Analysis of Piezoelectric Transducer
3.3. Structural Dimension Optimization of Piezoelectric Transducer
4. Piezoelectric Transducer Performance Testing
4.1. Interleaved Impact Ultrasonic Penetration Experimental Platform Prototype Development
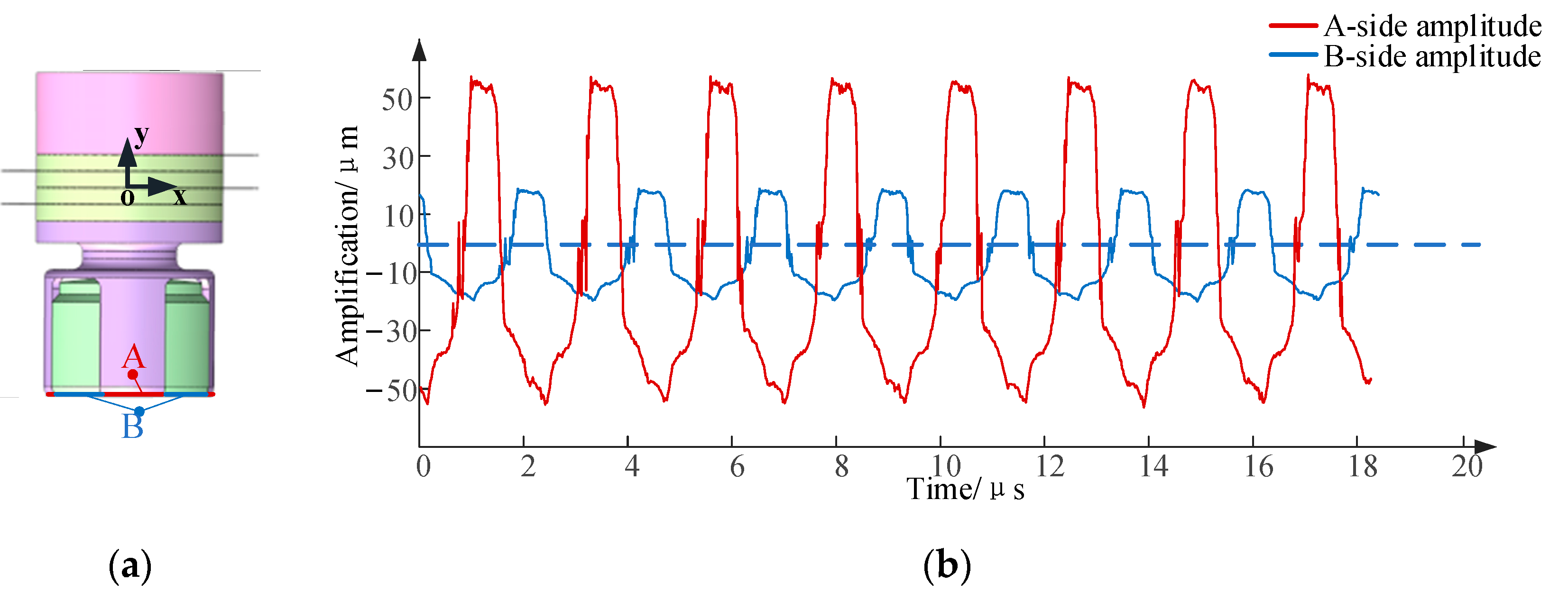
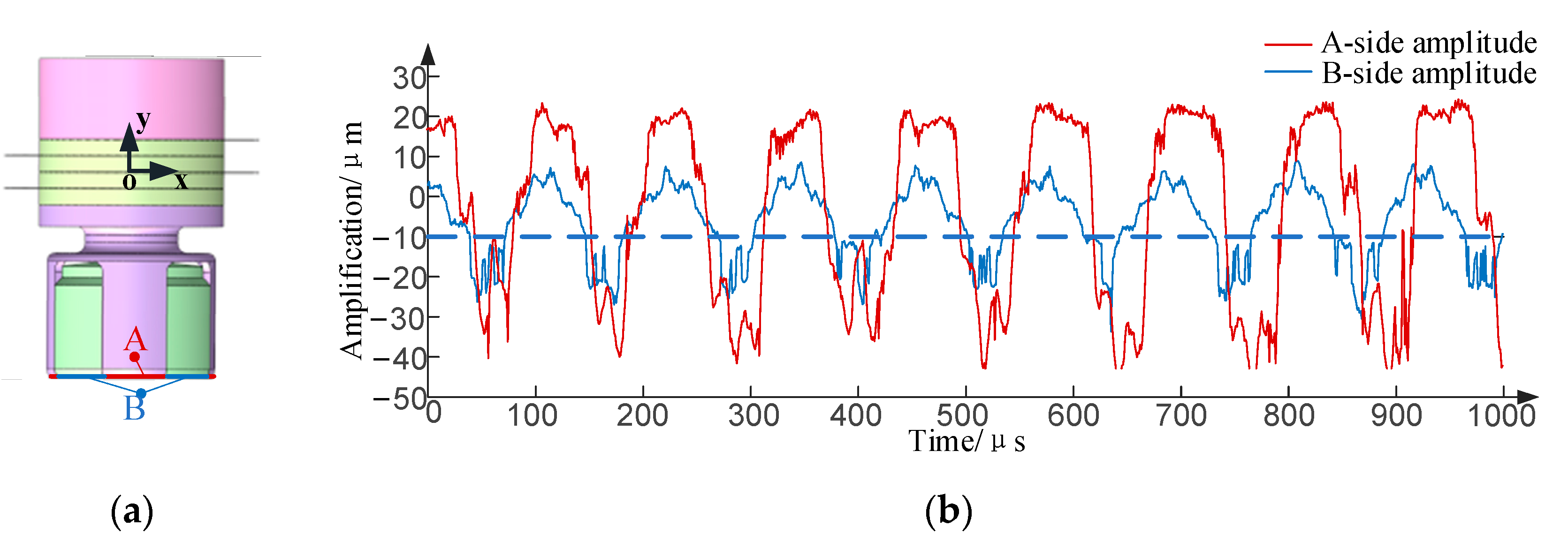
4.2. Analysis of Output Characteristics of Staggered Impact Penetrator
4.3. Experimental Study on Staggered Impact Ultrasonic Penetrator Sampler
4.3.1. Penetration Experiment with Different Moisture Contents
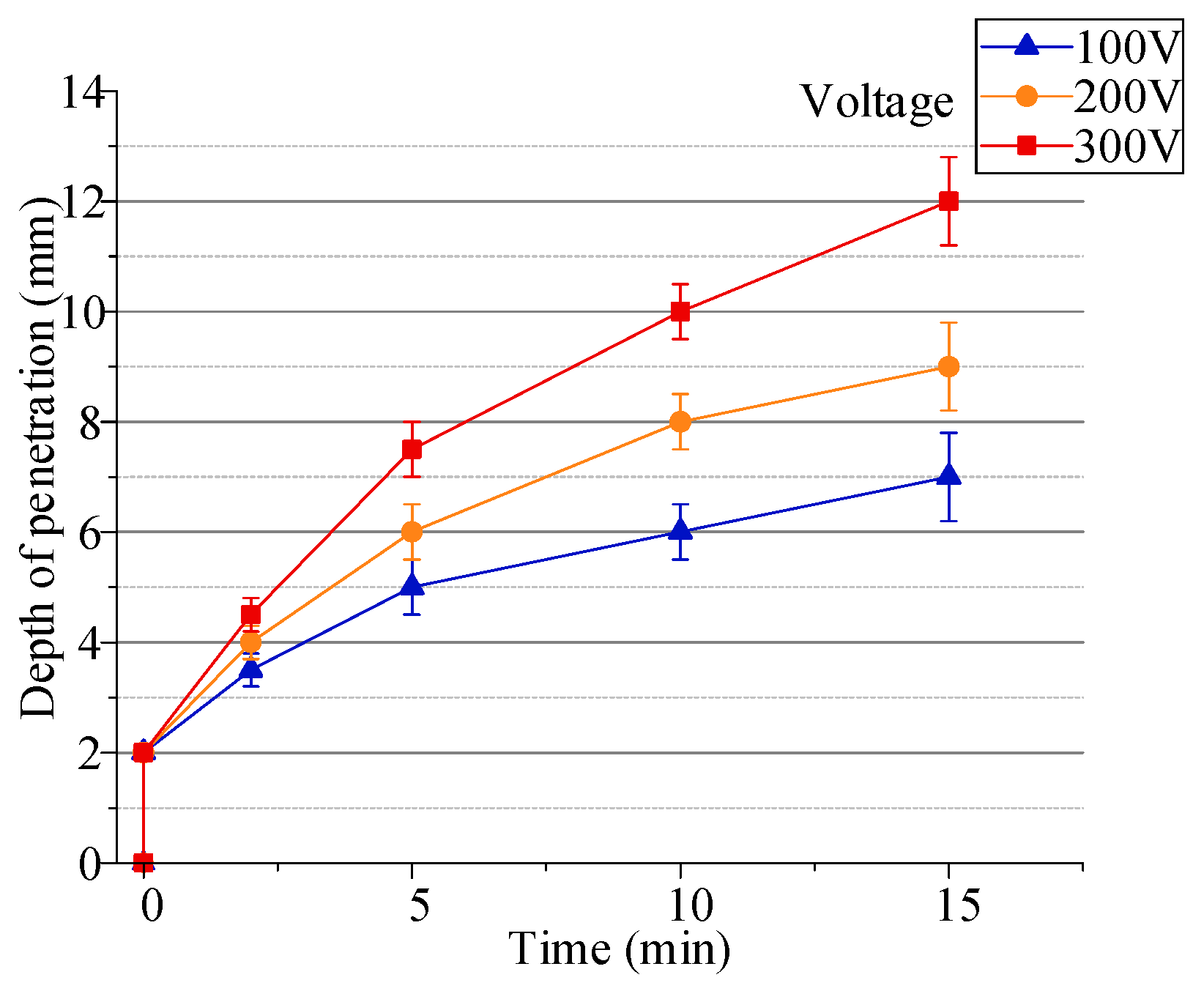
4.3.2. Penetration Experiment with Different Driving Voltages
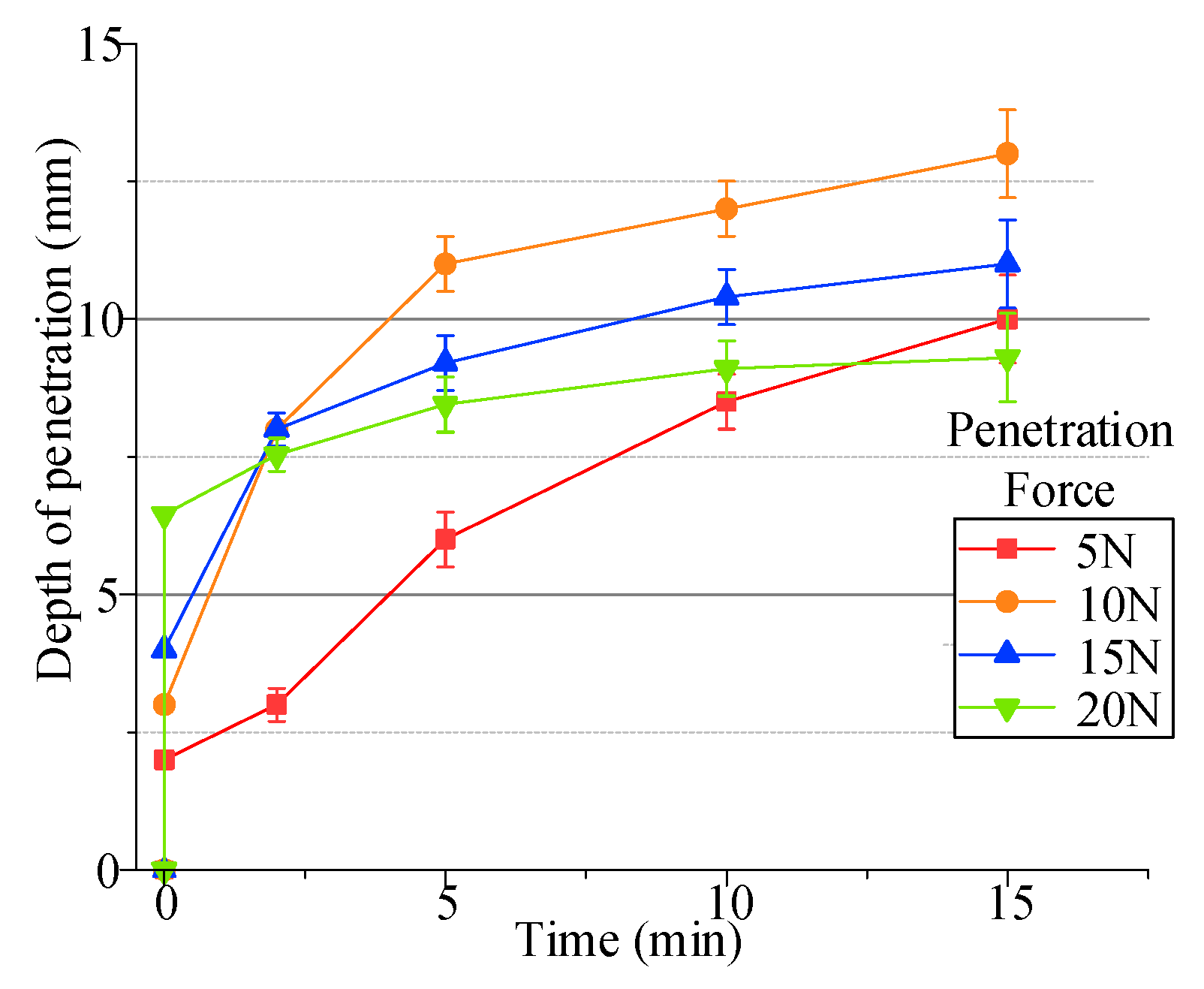
4.3.3. Penetration Experiment with Different Penetration Pressures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, Y.T.; Ouyang, Z.Y.; Xu, L.; Liu, J.J.; Xu, T. Lunar surface environmental characteristic. Quat. Sci. 2002, 06, 533–539. [Google Scholar]
- Watson, K.; Murray, B.C.; Brown, H. The behavior of volatiles on the lunar surface. J. Geophys. Res. 1961, 66, 3033–3045. [Google Scholar] [CrossRef]
- Xu, L.; Liu, J.Z.; Zou, Y.L.; Li, C.L. Detection and significance of water ice on the lunar surface. J. Space Sci. 2003, 23, 42–49. [Google Scholar]
- Li, S.; Lucey, P.G.; Milliken, R.E.; Hayne, P.O.; Fisher, E.; Williams, J.P.; Hurley, D.M.; Elphic, R.C. Direct evidence of surface exposed water ice in the lunar polar regions. Proc. Natl. Acad. Sci. USA 2018, 115, 8907. [Google Scholar] [CrossRef] [PubMed]
- Chandani, S.; Shashi, K.; Himanshu, G.; Shovan, L. Integrated Analysis of Water Ice Detection in Erlanger Crater, Lunar North Pole: Insights from Chandrayaan-1 Mini-SAR and Chandrayaan-2 DFSAR Data. Remote Sens. 2025, 17, 31. [Google Scholar]
- Wang, Y.L.; Liu, G.F.; Yang, J. Progress in lunar and deep air quantum (water ice) exploration. Nucl. Electron. Detect. Technol. 2011, 31, 614–618. [Google Scholar]
- Meng, Z.G.; Chen, S.B.; Wang, Z.J.; Cui, T.F. Study on water ice content of lunar Cabeus impact crater based on microwave radiometer data of Chang’e-1 satellite. Sci. China Phys. Mech. Astron. 2010, 40, 1363–1369. [Google Scholar]
- Xie, H.P.; Zhang, G.Q.; Luo, T.; Gao, M.Z.; Li, C.B.; Liu, T. Concept and design of lunar large-depth fidelity coring robot system. Adv. Eng. Sci. Gongcheng Kexue Yu Jishu 2020, 52, 1–9. [Google Scholar]
- Sherrit, S.; Dolgin, B.P.; Bar-Cohen, Y. Modeling of horns for sonic/ultrasonic applications. In Proceedings of the IEEE International Ultrasonics Symposium, Tahoe, NV, USA, 17–20 October 1999; Volume 1, pp. 647–651. [Google Scholar]
- Bar-Cohen, Y.; Sherrit, S.; Bao, X.Q.; Badescu, M.; Aldrich, J.; Chang, Z. Subsurface sampler and sensors platform using the ultrasonic/sonic driller/corer (USDC). Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2007, 6529, 173–180. [Google Scholar]
- Bai, D.; Deng, S.; Li, Y.; Li, H. A Novel Inchworm Piezoelectric Actuator with Rhombic Amplification Mechanism. Sens. Actuators A Phys. 2023, 360, 114515. [Google Scholar] [CrossRef]
- Bai, D.; Li, Y.; Quan, Q.; Tang, D.; Deng, Z. Development of a Rotary-Percussive Ultrasonic Drill Using a Bolt-Clamped Type Piezoelectric Actuator. Adv. Space Res. 2023, 71, 5360–5368. [Google Scholar] [CrossRef]
- Wang, Y.C.; Quan, Q.Q.; Yu, H.Y.; Li, H.; Bai, D.E.; Deng, Z.Q. Impact Dynamics of a Percussive System Based on Rotary-Percussive Ultrasonic Drill. Shock Vib. 2017, 2017, 5161870. [Google Scholar] [CrossRef]
- Li, X.; Harkness, P.; Worrall, K.; Timoney, R.; Lucas, M. A parametric study for the design of an optimized ultrasonic percussive planetary drill tool. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 64, 577–589. [Google Scholar] [CrossRef]
- Wang, Y.C.; Quan, Q.Q.; Yu, H.Y.; Li, H.; Bai, D.E.; Deng, Z.Q. A kind of rotary percussion ultrasonic drill driven by a single piezoelectric stack. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 1850–1859. [Google Scholar]
- Li, H.; Quan, Q.Q.; Wang, X.J.; Jiang, S.Y.; Deng, Z.Q. Development of a Martian rock driller based on piezoelectric drive. J. Deep Space Explor. 2016, 3, 156–161. [Google Scholar]
- Barcohen, Y.; Chang, Z.; Sherrit, S.; Badescu, M.; Bao, X. The ultrasonic/sonic driller/corer (USDC) as a subsurface drill, sampler, and lab-on-a-drill for planetary exploration applications. In Proceedings of the Smart Structures and Materials 2005: Industrial and Commercial Applications of Smart Structures Technologies, San Diego, CA, USA, 7–10 March 2005; SPIE: Bellingham, WA, USA; Volume 5762, pp. 152–159. [Google Scholar]
- Bar-Cohen, Y.; Sherrit, S.; Bao, X.; Chang, Z. Ultrasonic/sonic sampler and sensor platform for in-situ planetary exploration. In Proceedings of the International Conference on MEMS, NANO and Smart Systems, Banff, AB, Canada, 20–23 July 2003; pp. 22–31. [Google Scholar]
- Thomas, P.N.H. Magna Parva and ESA’s ultrasonic drill tool for planetary surface exploration. In Proceedings of the Earth and Space 2010: Engineering, Science, Construction, and Operations in Challenging Environments, Honolulu, HI, USA, 14–17 March 2010; pp. 1235–1245. [Google Scholar]
- Khmelev, V.N.; Khmelev, S.S.; Khmelev, M.V.; Levin, S.V.; Kuzovnikov, Y.M. Development of ultrasonic specifically drilling technology and improvement of construction of ultrasonic machine tools. In Proceedings of the IEEE International Conference & Seminar of Young Specialists on Micro/Nanotechnologies & Electron Devices, Altai, Russia, 2–6 July 2012; pp. 2–6. [Google Scholar]
- Li, H.; Wei, M.; Zhang, Z.; Shen, Y.; Aimaiti, B.; Wang, G.; Li, L.; Gao, K.; Zeng, Q. Design and Experimental Verification of an Underwater Ultrasonic Drill for Rock Exploration. Ocean Eng. 2024, 294, 116824. [Google Scholar] [CrossRef]
- Li, J.; Deng, J.; Liu, Y.X.; Yu, H.; Tian, X.; Li, K. A linear piezoelectric actuator based on working principle of three-petal mouth of a rabbit. IEEE Trans. Ind. Electron. 2022, 69, 5091–5099. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, S.; Li, C.; Chen, W.; Liu, J. A novel standing wave linear piezoelectric actuator using the longitudinal-bending coupling mode. Sens. Actuators A Phys. 2016, 251, 119–125. [Google Scholar] [CrossRef]
- Mashimo, T. Scaling of piezoelectric ultrasonic motors at submillimeter range. IEEE/ASME Trans. Mechatron. 2017, 22, 1238–1246. [Google Scholar] [CrossRef]
- Kanada, A.; Mashimo, T. Design and experiments of flexible ultrasonic motor using a coil spring slider. IEEE/ASME Trans. Mechatron. 2019, 25, 468–476. [Google Scholar] [CrossRef]
- Yu, H.P.; Quan, Q.Q.; Tian, X.Q.; Li, H. Optimization and analysis of a u-shaped linear piezoelectric ultrasonic motor using longitudinal transducers. Sensors 2018, 18, 809. [Google Scholar] [CrossRef]
- Zhang, J.T.; Zhu, H.; Zhou, S.Q.; Zhao, C.S. Optimal design of a rod shape ultrasonic motor using sequential quadratic programming and finite element method. Finite Elem. Anal. Des. 2012, 59, 11–17. [Google Scholar] [CrossRef]
- Badescu, M.; Kassab, S.; Sherrit, S.; Aldrich, J.; Bao, X.; Bar-Cohen, Y.; Chang, Z. Ultrasonic/sonic driller/corer as a hammer-rotary drill. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2007, 6529, 289–295. [Google Scholar]
- Badescu, M.; Sherrit, S.; Bao, X.; Bar-Cohen, Y.; Chen, B. Auto-Gopher a wire-line rotary-hammer ultrasonic drill. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2011, 7981, 1098–1105. [Google Scholar]
- Badescu, M.; Bar-Cohen, Y.; Sherrit, S.; Bao, X.; Chang, Z.; Donnelly, C.; Aldrich, J. Percussive augmenter of rotary drills (PARoD). Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2012, 8345, 167–174. [Google Scholar]
- Domm, L.N. Development of a Piezoelectric Rotary Hammer Drill. In NASA USRP-Internship Final Report; 2011. Available online: https://ntrs.nasa.gov/citations/20150005822 (accessed on 13 April 2025).
- Potthast, C.; Twiefel, J.; Wallaschek, J. Modelling approaches for an ultrasonic percussion drill. J. Sound Vib. 2007, 308, 405–417. [Google Scholar] [CrossRef]
- Bai, D.; Quan, Q.; Tang, D.; Deng, Z. Design and experiments of a novel rotary piezoelectric actuator using longitudinal-torsional convertors. IEEE Access 2019, 7, 22186–22195. [Google Scholar] [CrossRef]
- Neumann, N.; Sattel, T.; Wallaschek, J. On set-oriented numerical methods for global analysis of non-smooth mechanical systems. J. Vib. Control 2007, 13, 1393–1405. [Google Scholar] [CrossRef]
- Neumann, N.; Sattel, T. Set-oriented numerical analysis of a vibro-impact drilling system with several contact interfaces. J. Sound Vib. 2007, 308, 831–844. [Google Scholar] [CrossRef]












| Simulation Parameters | Value/mm | Simulation Parameters | Value/mm |
|---|---|---|---|
| D1 | 35 | l3 | 26.4 |
| D2 | 16 | l4 | 4 |
| D3 | 29 | l5 | 5 |
| D4 | 5.6 | l6 | 1.5 |
| r1 | 10.6 | l7 | 7.5 |
| r2 | 6 | l8 | 3 |
| r3 | 17.5 | l9 | 20 |
| l1 | 4 | h2 | 1.5 |
| l2 | 11 | t | 3 |
| Densities | Elastic Modulus | Particle Size Distribution | Cohesion | Ice-Cementation Strength |
|---|---|---|---|---|
| 2630 kg/m3 | 10 GPa | Basalt simulating lunar soil: 1~300 μm; Slanty plagioclase simulating lunar soil: 5~500 μm | 12.3 kPa | 8.5 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yin, Z.; Ding, C.; Liu, F.; Zhang, W.; Zu, L.; Gao, Z.; Tao, G.; Yu, S. A Novel Ultrasonic Sampling Penetrator for Lunar Water Ice in the Lunar Permanent Shadow Exploration Mission. Aerospace 2025, 12, 358. https://doi.org/10.3390/aerospace12040358
Wang Y, Yin Z, Ding C, Liu F, Zhang W, Zu L, Gao Z, Tao G, Yu S. A Novel Ultrasonic Sampling Penetrator for Lunar Water Ice in the Lunar Permanent Shadow Exploration Mission. Aerospace. 2025; 12(4):358. https://doi.org/10.3390/aerospace12040358
Chicago/Turabian StyleWang, Yinchao, Zihao Yin, Chenxu Ding, Fei Liu, Weiwei Zhang, Lin Zu, Zhaozeng Gao, Guanghong Tao, and Suyang Yu. 2025. "A Novel Ultrasonic Sampling Penetrator for Lunar Water Ice in the Lunar Permanent Shadow Exploration Mission" Aerospace 12, no. 4: 358. https://doi.org/10.3390/aerospace12040358
APA StyleWang, Y., Yin, Z., Ding, C., Liu, F., Zhang, W., Zu, L., Gao, Z., Tao, G., & Yu, S. (2025). A Novel Ultrasonic Sampling Penetrator for Lunar Water Ice in the Lunar Permanent Shadow Exploration Mission. Aerospace, 12(4), 358. https://doi.org/10.3390/aerospace12040358


_Zhu.png)



