Task Planning for Multiple-Satellite Space-Situational-Awareness Systems
Abstract
:1. Introduction
2. Problem Description
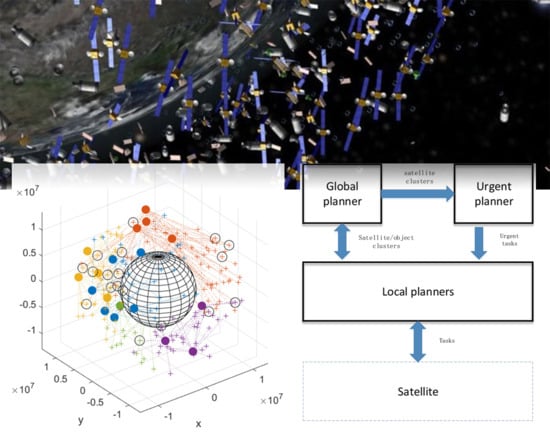
3. Task-Planning Framework
3.1. Global Task Planner
- Tender publication. The global planner broadcasts centroids of all object clusters aswhere is the global manager.
- Bidding. According to Assumption 1, one satellite from each satellite cluster bids for at least one tender on the basis of its own status and constraints once the task cluster is received. In general, the manager satellite in a cluster is selected depending on satellite ability, such as energy and computation power. Hence, the role of the manager and contractor is not fixed, and can be dynamically switched back and forth. In this paper, we assume satellites are homogeneous and select the one closest to cluster centroid as the cluster manager. The bidding can have three results: reject, not responding, and bidding. If a satellite decides to bid for a certain task cluster, the bidding can be expressed aswhere is the bidding satellite cluster, and is the cost for the i-th satellite cluster bidding for the j-th object cluster, defined as
- Task cluster allocation. When the manager receives bidding or the bidding deadline is over, task clusters are allocated to satellite clusters by minimizing the cost function (3) aswhere is the cluster tender-evaluation criterion, are average parameter values, such as centroids and mean velocities for the i-th satellite cluster and the j-th object cluster. In this paper, optimal match was obtained by developing a discrete particle swarm optimization (DPSO) algorithm [29] with task priority P embedded. Algorithmic details are given in Section 4. Lastly, we havewhere one satellite cluster is allocated with multiple object clusters, and the number of satellites and objects in each cluster is different based on clustering results.
3.2. Local Task Planner
- Tender publication. Similar to the global planner, the local planner publishes tenders to local satellites in the same cluster aswhere is the local manager.
- Bidding. This step is exactly same as Step 2 in the global planner, except that only local satellites bid for the tenders.
- Task allocation. When the local manager receives bidding or the bidding deadline is over, local tasks are allocated to satellites aswhere is the local tender-evaluation criterion, designed asUnlike cluster planning criterion (12), the local tender-evaluation criterion is a weighted combination of relative position and velocity among satellites and objects. The rationale is that a cluster centroid is a representation of multiple satellites or objects that covers a large space area; hence, the moving of satellites and objects has fewer effects on how a cluster is planned. However, on the local level, the moving of satellites and objects must be taken into account due to their high velocity in a limited space area.
- Contract signed. Similarly to the global planner, the local planner employs the iterative DPSO algorithm to obtain (10). The contract is signed, and the task-planning problem is completed.
3.3. Urgent Task Planner
- Extract priorities P of the urgent tasks.
- Decompose satellite cluster into and parts.
- Plan urgent tasks to satellites in the part following Steps 1–4 of the local planner.
4. Tender-Evaluation DPSO Algorithm
- tasks of high priorities are allocated first; and
- there is an upper bound on the maximal number of tasks with which each satellite can be allocated.
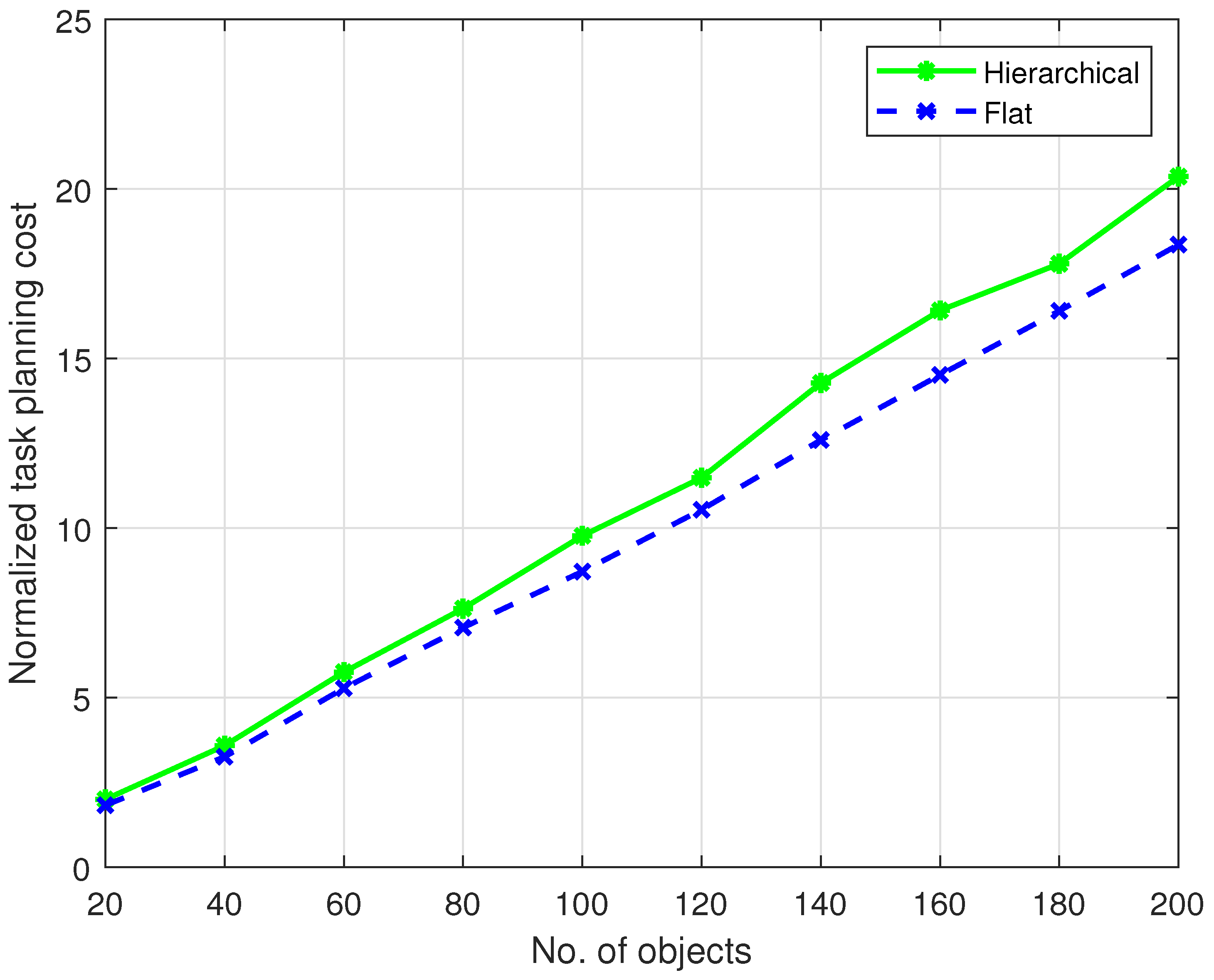
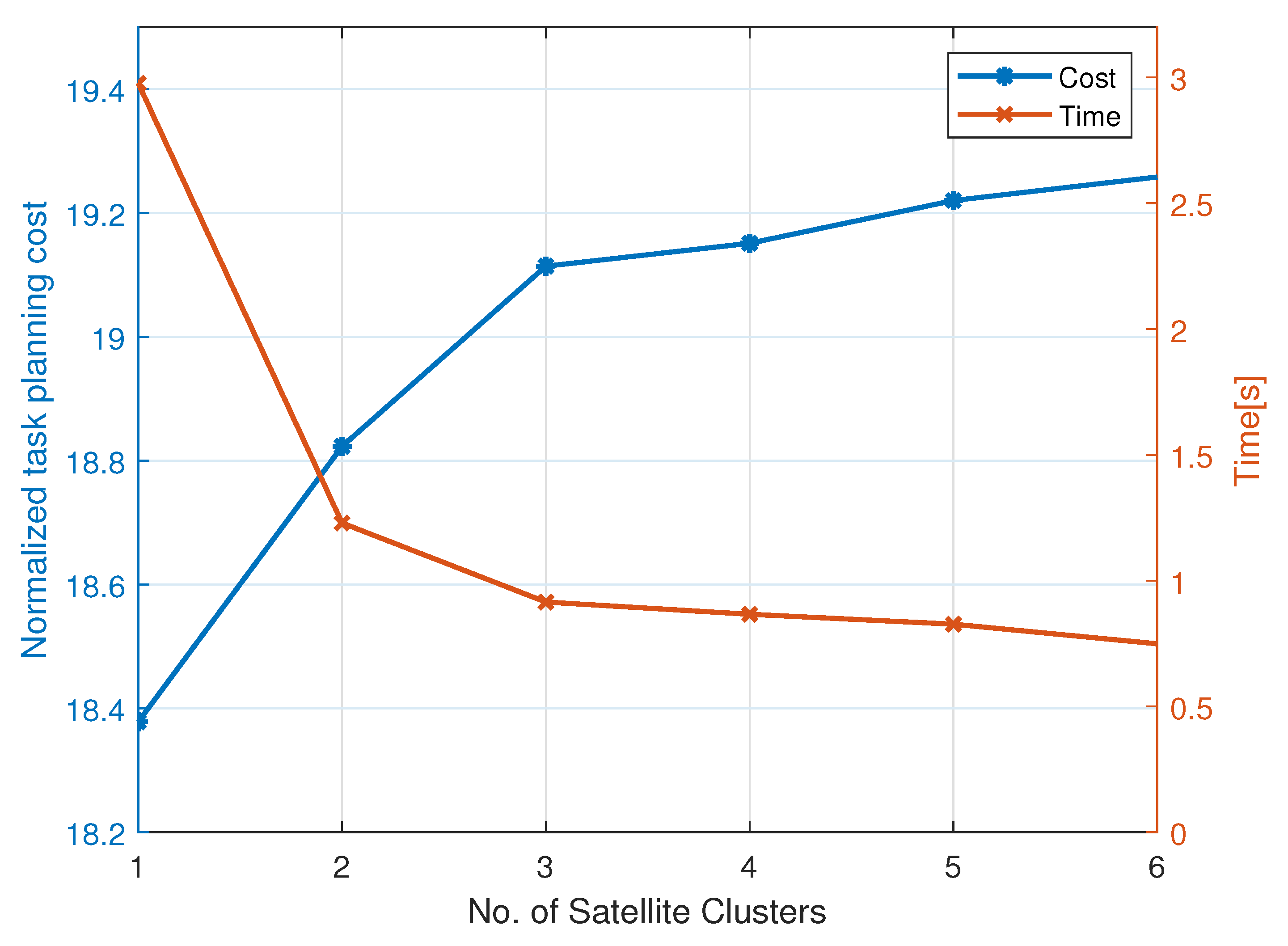
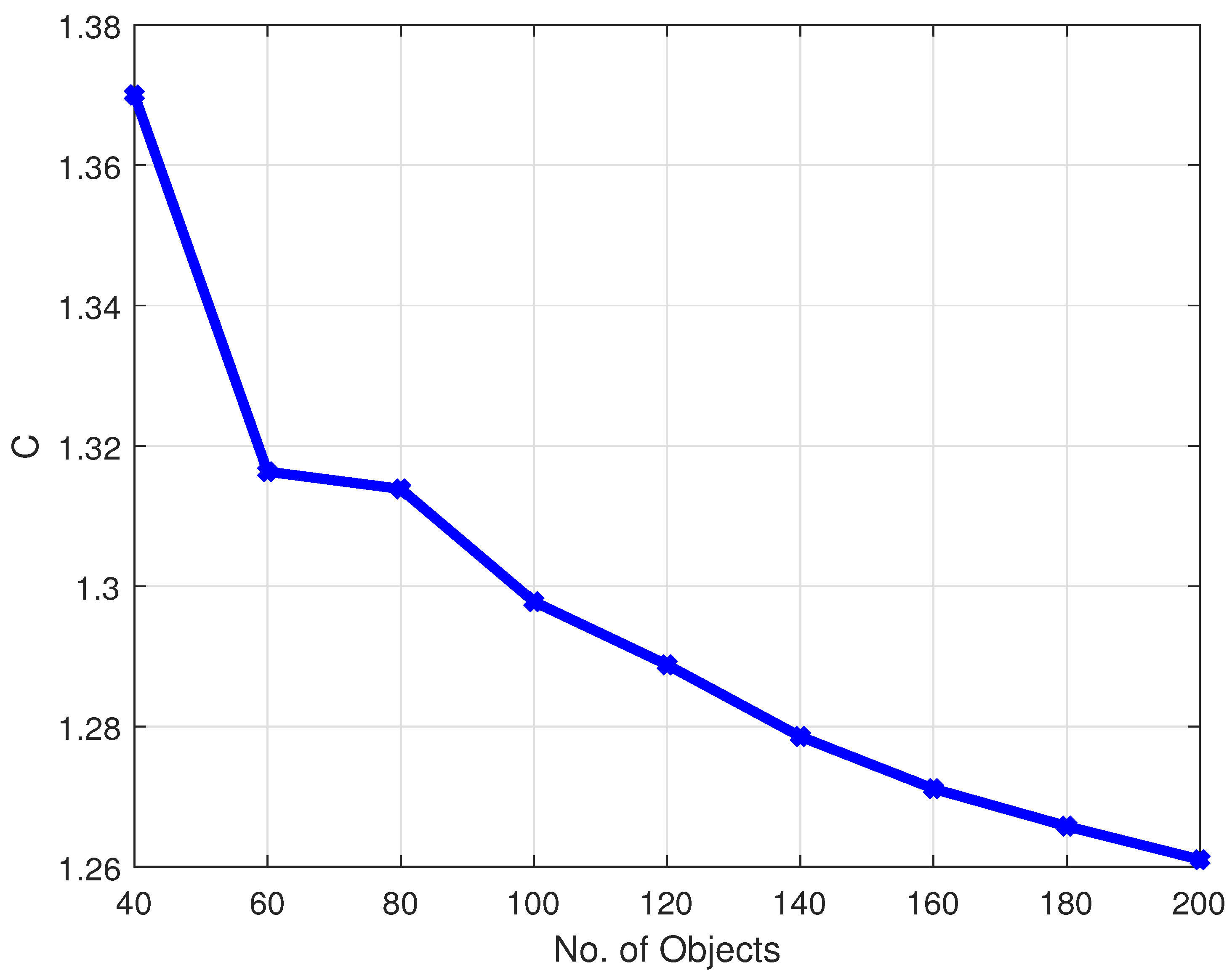
5. Simulation
5.1. Static Planning
5.2. Dynamic Planning
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kennewell, J.A.; Vo, B.N. An overview of space situational awareness. In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1029–1036. [Google Scholar]
- Jian, P.; Xiong, W.; Li, Z. Research on mission planning of space situational awareness. In Proceedings of the 4th China Conference on Command and Control, Beijing, China, 4 July 2016; pp. 520–523. [Google Scholar]
- Du, Y. Research on Key Technologies of Space Situational Awareness Based on Binocular Vision Satellite Formation. Master’s Thesis, Zhengjiang University, Hangzhou, China, 2020. [Google Scholar]
- Zheng, Z.; Guo, J.; Gill, E. Distributed onboard mission planning for multi-satellite systems. Aerosp. Sci. Technol. 2019, 89, 111–122. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. In Cooperative Robots and Sensor Networks 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 31–51. [Google Scholar]
- Lv, C. A System for Space Situational Awareness (Ssa) Based on Centralized Control. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2013. [Google Scholar]
- Zheng, Z.; Guo, J.; Gill, E. Onboard autonomous mission re-planning for multi-satellite system. Acta Astronaut. 2018, 145, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Sui, Z.; Pu, Z.; Yi, J. Optimal uavs formation transformation strategy based on task assignment and particle swarm optimization. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1804–1809. [Google Scholar]
- Miloradović, B.; Çürüklü, B.; Ekström, M.; Papadopoulos, A.V. A genetic algorithm approach to multi-agent mission planning problems. In International Conference on Operations Research and Enterprise Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 109–134. [Google Scholar]
- Afonso, R.J.; Maximo, M.R.; Galvão, R.K. Task allocation and trajectory planning for multiple agents in the presence of obstacle and connectivity constraints with mixed-integer linear programming. Int. J. Robust Nonlinear Control 2020, 30, 5464–5491. [Google Scholar] [CrossRef]
- Chang, Z.; Chen, Y.; Yang, W.; Zhou, Z. Mission planning problem for optical video satellite imaging with variable image duration: A greedy algorithm based on heuristic knowledge. Adv. Space Res. 2020, 66, 2597–2609. [Google Scholar] [CrossRef]
- Parker, L.E. Task-oriented multi-robot learning in behavior-based systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS’96, Osaka, Japan, 4–8 November 1996; Volume 3, pp. 1478–1487. [Google Scholar]
- Gage, A. Multi-Robot Task Allocation Using Affect. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2004. [Google Scholar]
- Dias, M.B.; Zlot, R.; Kalra, N.; Stentz, A. Market-based multirobot coordination: A survey and analysis. Proc. IEEE 2006, 94, 1257–1270. [Google Scholar] [CrossRef] [Green Version]
- Bogdanowicz, Z.; Coleman, N. Sensor-target and weapon-target pairings based on auction algorithm. In Proceedings of the 11th WSEAS International Conference on APPLIED MATHEMATICS, Dallas, TX, USA, 22–24 March 2007; pp. 92–96. [Google Scholar]
- Du, B.; Li, S. A new multi-satellite autonomous mission allocation and planning method. Acta Astronaut. 2019, 163, 287–298. [Google Scholar] [CrossRef]
- Dahl, T.S.; Matarić, M.; Sukhatme, G.S. Multi-robot task allocation through vacancy chain scheduling. Robot. Auton. Syst. 2009, 57, 674–687. [Google Scholar] [CrossRef]
- Dos Santos, D.S.; Bazzan, A.L. Distributed clustering for group formation and task allocation in multiagent systems: A swarm intelligence approach. Appl. Soft Comput. 2012, 12, 2123–2131. [Google Scholar] [CrossRef]
- Smith, R.G. The contract net protocol: High-level communication and control in a distributed problem solver. IEEE Trans. Comput. 1980, 12, 1104–1113. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, G.; Song, Y. Task Assignment of the Improved Contract Net Protocol under a Multi-Agent System. Algorithms 2019, 12, 70. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Wu, X.; Mao, Y.; Gao, H.; Hao, Y. Task allocation for distributed remote sensing satellites based on contract network algorithm. J. Harbin Eng. Univ. 2020, 41, 1059–1065. [Google Scholar]
- Zhou, Z.; Cheng, S.; Liu, Q. A novel contract net negotiation model based on trust mechanism. In Proceedings of the 2008 IEEE Conference on Cybernetics and Intelligent Systems, Chengdu, China, 21–24 September 2008; pp. 884–887. [Google Scholar]
- Feng, P.; Chen, H.; Peng, S.; Chen, L.; Li, L. A method of distributed multi-satellite mission scheduling based on improved contract net protocol. In Proceedings of the 2015 11th International Conference on Natural Computation (ICNC), Zhangjiajie, China, 15–17 August 2015; pp. 1062–1068. [Google Scholar]
- Song, Y.J.; Zhou, Z.Y.; Zhang, Z.S.; Yao, F.; Chen, Y.W. A framework involving MEC: Imaging satellites mission planning. Neural Comput. Appl. 2020, 32, 15329–15340. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Orbital Elements—Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/w/index.php?title=Orbital_elements&oldid=997827172 (accessed on 23 February 2021).
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Yang, M.S.; Lai, C.Y.; Lin, C.Y. A robust EM clustering algorithm for Gaussian mixture models. Pattern Recognit. 2012, 45, 3950–3961. [Google Scholar] [CrossRef]
- Zhao, Y.; Shrivastava, A.K.; Tsui, K.L. Regularized Gaussian mixture model for high-dimensional clustering. IEEE Trans. Cybern. 2018, 49, 3677–3688. [Google Scholar] [CrossRef] [PubMed]
- Clerc, M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 219–239. [Google Scholar]
- Wei, H.; Xue-qing, Z. A Multisatellite Task Planning Algorithm Based on Discrete Particle Swarm. Radio Eng. 2015, 45, 47. [Google Scholar]
- Al-Dujaili, A.; Tanweer, M.R.; Suresh, S. On the Performance of Particle Swarm Optimization Algorithms in Solving Cheap Problems. In Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015; pp. 1318–1325. [Google Scholar] [CrossRef]
- Al-Kazemi, B.S.; Habib, S.J. Complexity Analysis of Problem-Dimension Using PSO. In Proceedings of the 7th WSEAS International Conference on Evolutionary Computing, EC’06, Cavtat, Croatia, 12–14 June 2006; pp. 45–52. [Google Scholar]
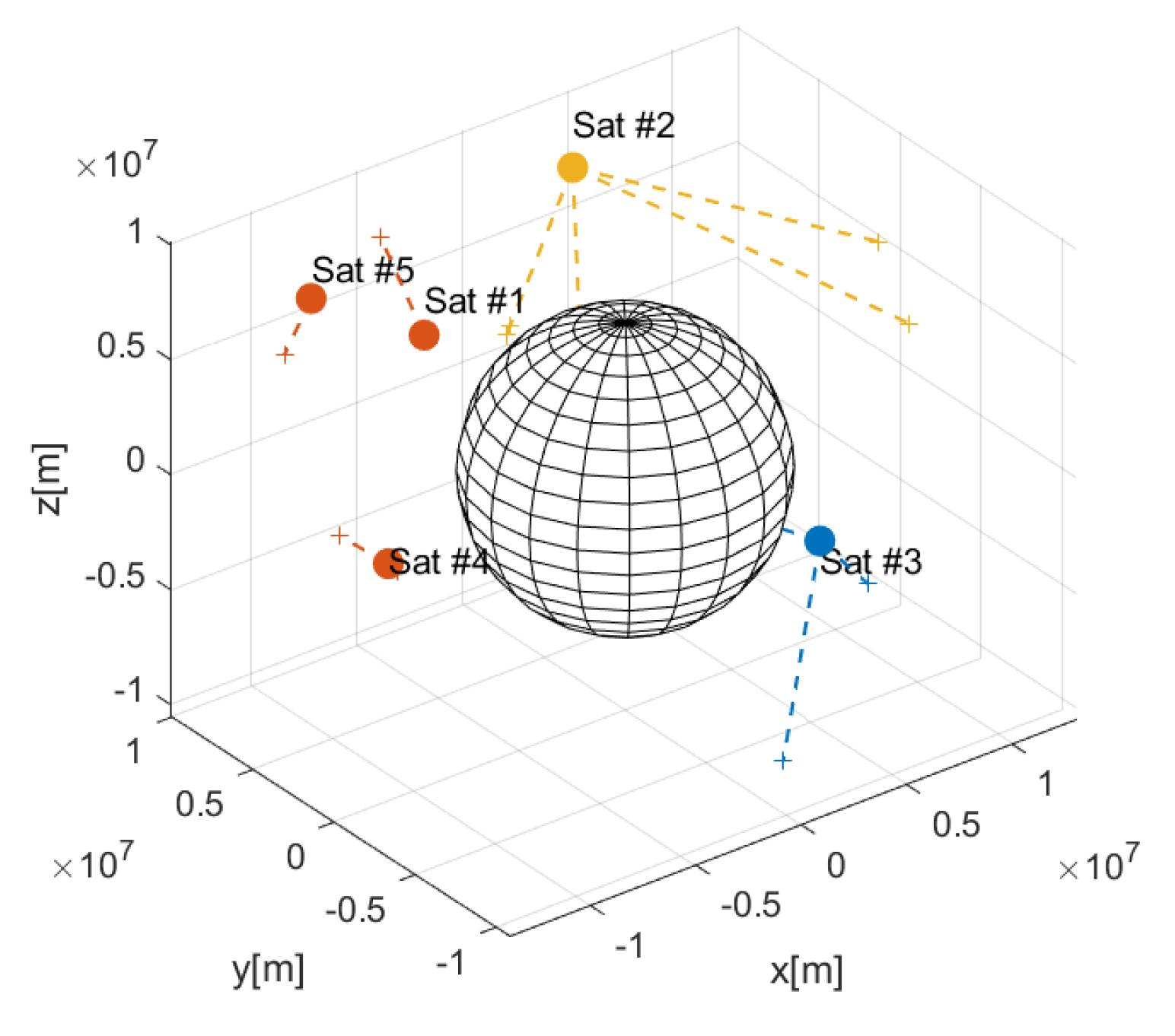
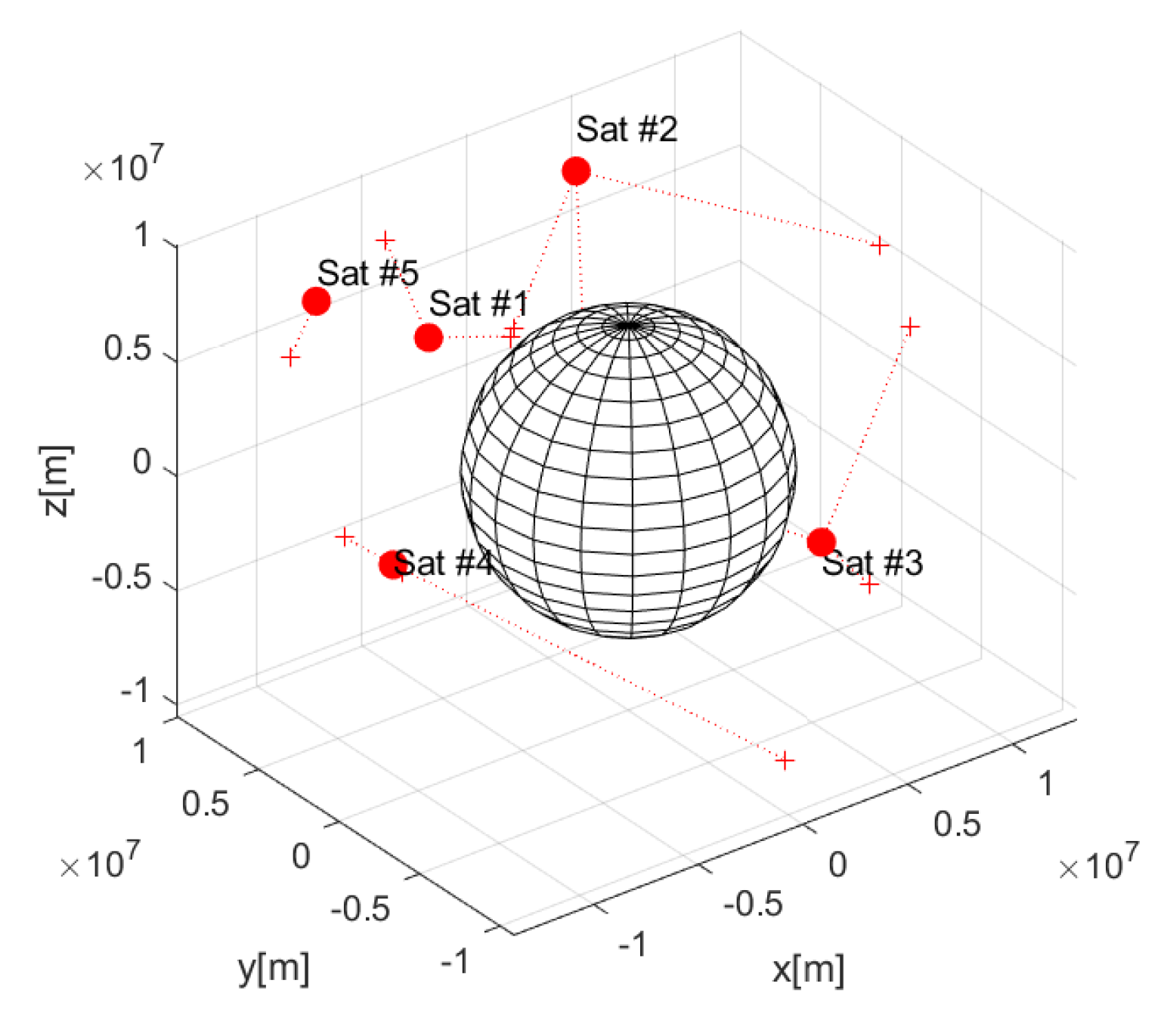
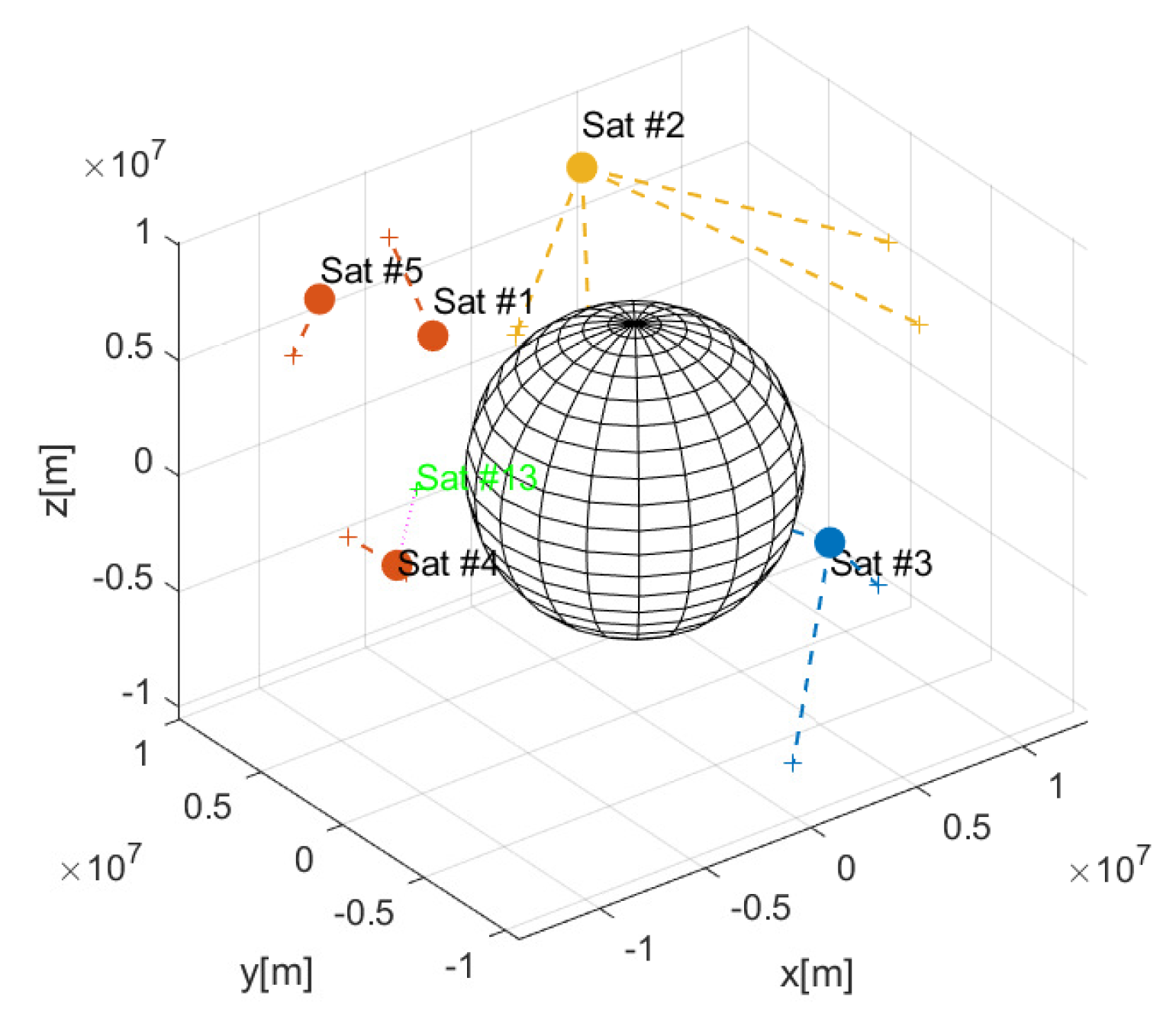

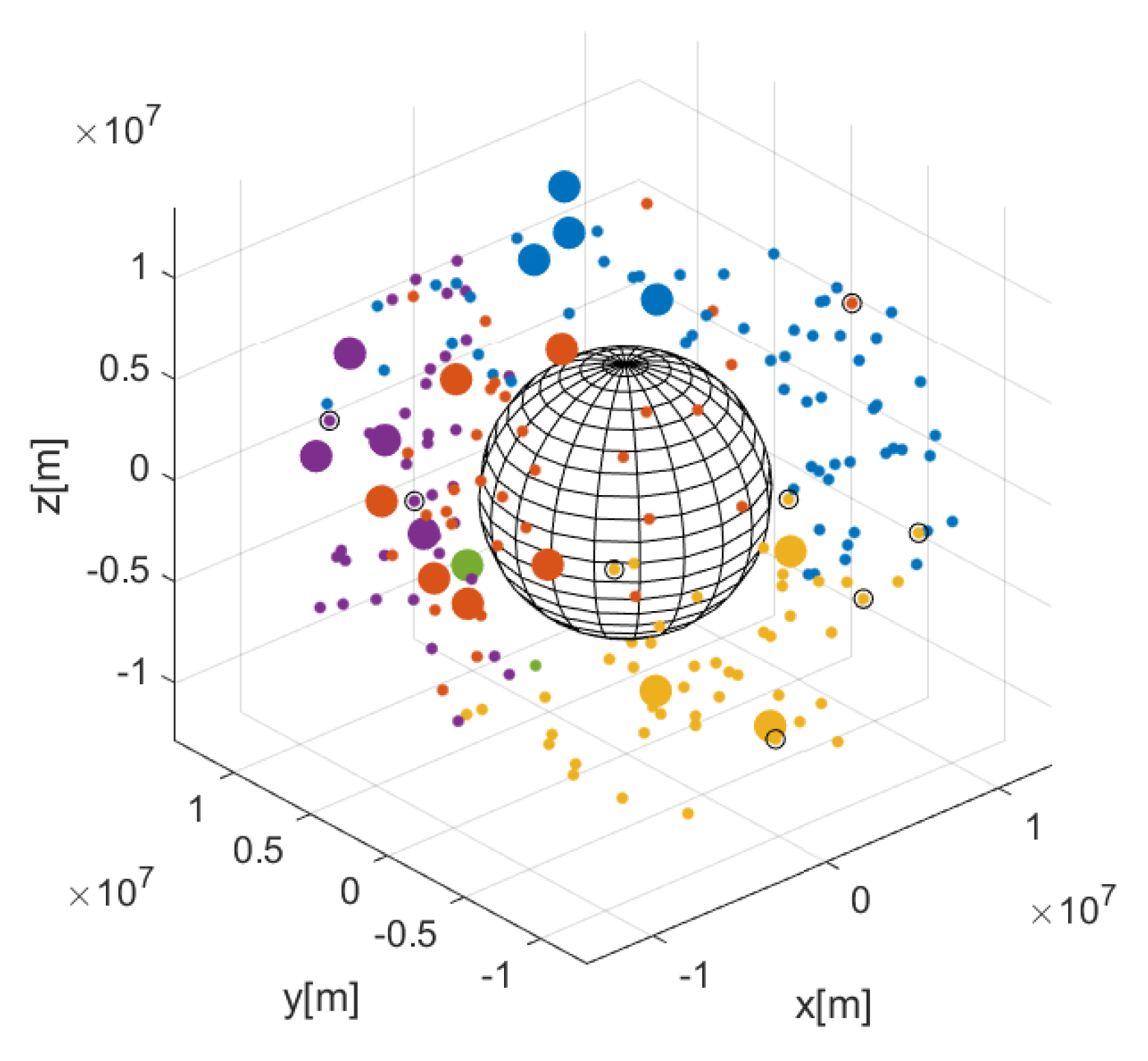


| No. | x [km] | y [km] | z [km] |
|---|---|---|---|
| Satellites: | |||
| 1 | −7883 | 2176 | 7598 |
| 2 | 2269 | 6213 | 9469 |
| 3 | 7091 | −2794 | −4344 |
| 4 | −12,203 | −1237 | 738 |
| 5 | −8294 | 8632 | 6378 |
| Objects: | |||
| 1 | −11,304 | −640 | −220 |
| 2 | −7350 | 5563 | 10,105 |
| 3 | −13,852 | −373 | 2120 |
| 4 | 4049 | 7363 | −10,494 |
| 5 | 60 | −9711 | −8224 |
| 6 | 10,512 | −1976 | 7099 |
| 7 | −9299 | 8989 | 4098 |
| 8 | 5793 | 4092 | −5105 |
| 9 | 2254 | 10,094 | 791 |
| 10 | 616 | 8124 | 1947 |
| 11 | 13,052 | −573 | 2002 |
| 12 | 3138 | −10,907 | −1095 |
| Satellite cluster no. | 1 | 2 | 3 | |||||
| Satellite no. | 2 | 3 | [1,4,5] | |||||
| Object cluster no. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Object no. | 12 | [1,3] | 4 | [2,7] | 5 | [9,10] | 8 | [6,11] |
| Satellite cluster no. | 1 | 2 | 3 |
| Object cluster no. | [3,6,8] | [1,5,7] | [2,4] |
| Cluster 1 | Cluster 2 | Cluster 3 | |||
|---|---|---|---|---|---|
| Satellite no. | 2 | 3 | 1 | 4 | 5 |
| Object no. | [4,6,9,10,11] | [5,8,12] | 3 | 1 | [2,7] |
| Cluster 1 | Cluster 2 | Cluster 3 | |||
|---|---|---|---|---|---|
| Satellite no. | 2 | 3 | 1 | 4 | 5 |
| Object no. | [4,6,9,10,11] | [5,8,12] | 3 | [1,13] | [2,7] |
| Cluster No. | 1 | 2 | 3 | 4 | 5 | Total |
|---|---|---|---|---|---|---|
| No. of Satellites | 6 | 4 | 4 | 3 | 3 | 20 |
| No. of Objects | 29 | 87 | 54 | 44 | 20 | 234 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Tian, G.; Guo, J.; Huang, J. Task Planning for Multiple-Satellite Space-Situational-Awareness Systems. Aerospace 2021, 8, 73. https://doi.org/10.3390/aerospace8030073
Chen Y, Tian G, Guo J, Huang J. Task Planning for Multiple-Satellite Space-Situational-Awareness Systems. Aerospace. 2021; 8(3):73. https://doi.org/10.3390/aerospace8030073
Chicago/Turabian StyleChen, Yutao, Guoqing Tian, Junyou Guo, and Jie Huang. 2021. "Task Planning for Multiple-Satellite Space-Situational-Awareness Systems" Aerospace 8, no. 3: 73. https://doi.org/10.3390/aerospace8030073
APA StyleChen, Y., Tian, G., Guo, J., & Huang, J. (2021). Task Planning for Multiple-Satellite Space-Situational-Awareness Systems. Aerospace, 8(3), 73. https://doi.org/10.3390/aerospace8030073