Effects of Compounds in Liquefied Methane on Rocket Engine Operation

Abstract

Methane (CH₄) is a promising rocket fuel for various future space mission scenarios. It has advantages in terms of cost, performance, and environmental friendliness. Currently, there is no clear definition on standards and specifications for liquefied methane or similar liquids such as liquefied natural gas (LNG) for their use as rocket fuel. However, those regulations are necessary for the commercial, safe, and proper operation of methane rocket engines. Composition and impurities of liquefied methane gas mixtures obtained from natural gas or biogenic sources depend on location of the natural gas source (Europe, Asia, or America), its extraction method and treatment, used cleaning methods or conditions of the gasification process, and biomass sources. In the present work, effects of impurities (N₂, CO₂, C₂H₆) within liquid natural gas/liquid methane on the methalox rocket engine operation behavior are analyzed. Regarding the cold cryogenic side, phase diagrams are discussed and critical temperatures for the fuel side are outlined. Carbon dioxide is identified as a rather problematic pollutant. The combustion processes are investigated with several numerical simulations (1D and 2D CFD). The results indicate a minor influence on the overall combustion temperature and a minor but potentially relevant influence on the pressure within the combustion chamber. Additionally, the results indicate that with respect to temperature and pressure, no complex NOx nitrogen chemistry is required.

1. Introduction

Recent advancements in the space transportation market, space technologies, and national space programs have made methane (CH₄) a promising future rocket propellant. It has advantages for various space missions in terms of performance, cost, and environmental friendliness over conventional rocket fuels such as hydrogen (H₂), kerosene, and hydrazine. Especially hydrazine was added to the candidate list of substances of very high concern (SVHC) by Europe’s Registration Evaluation Authorization and Restriction of Chemicals (REACH). Both ESA and NASA are investigating the possibilities and cost of restricting or prohibiting the use of hydrazine.

As a result, all worldwide major players in space transportation are currently developing methane rocket engines. However, no actual flying methane rocket engines exist, except from first demonstrators and first successful flight demonstrations with flight times of a few minutes.

For safe and proper operation of methane rocket engines, knowledge of technical and chemical constraints needs to be obtained to avoid accidents and other hazards to mankind and the environment on earth and in space. Therefore, standards and specifications for the use of liquefied methane (LCH₄) or similar liquids such as liquefied natural gas (LNG) as a rocket fuel must be defined in the near future.

The chemical composition and amount of different chemical compounds within liquefied methane gas mixtures obtained from natural gas or biogenic sources depends on location of the natural gas source (Europe, Asia or America), the way it is extracted and treated, as well as used cleaning methods or conditions of the gasification process, and biomass sources. Therefore, the effect of chemical compounds in small amounts, called impurities, within liquid natural gas/liquid methane on the rocket engine components and the operation of methane rocket engines is analyzed in the present work.

The combustion process of methane-air mixtures itself and the influence of impurities on formation or reduction of pollutants, such as NOx are quite well understood [1,2], However, these species with adverse health effects occur only in small concentrations and are of minor concern in rocket engine operations, due to the limited number of launches of rockets and their huge safety radius related to engine operations. Some investigations include partially oxygen-enriched combustion conditions [3], but they are still far away from the pure oxygen conditions without nitrogen in the mixture, that exist in space propulsion and result in much higher combustion temperatures. Additionally, those investigations are normally at rather low pressures compared to rocket engine pressure levels. With respect to rocket engines, there is very limited data available regarding the effects of impurities.

The effect of these impurities in liquid methane is investigated from two points of view. The first one is the influence on storage and pumping of liquid methane through the engine manifold, the fuel pump, and the cooling channels of the combustion chamber.

The second aspect considered is the investigation of the influences of small amounts of ethane (C₂H₆), carbon dioxide (CO₂), and nitrogen (N₂) on the combustion processes inside the thrust chamber.

The work is part of the interdisciplinary project “Future Fuels” [4]. The project team consists of employees of several institutes of the German Aerospace Center (DLR). It combines research on production, combustion and safe usage of synthetic renewable fuels for space, energy, transportation, and aviation. Within this project, the calculations of phase diagrams are investigated at the Institute of Combustion Technology and the flame calculations and CFD modelling are performed at the Institute of Space Propulsion.

2. Impurities in Liquefied Methane

In contrast to pure methane, liquefied natural gas often contains amounts of other low-weight hydrocarbons such as ethane (C₂H₆), propane (C₃H₈), and less or non-reactive gases such as carbon dioxide (CO₂) and nitrogen (N₂), depending on the origin of the natural gas. The purification from these impurities involves high costs due to the solubility of these substances in methane. The exact composition of liquefied natural gas depends on its source, on the used liquefying technologies, the liquefying plant, and the owner’s market strategies for the sale of separated gas components and their market values. Additionally, the composition of the LNG may change slightly during pumping, pressurizing, and long-time storage.

3. Physical–Chemical Properties, Phase Diagrams, and Their Effect on Storage and Pumping of Liquefied Methane

As a first step to investigate the effects of impurities in methane on storage and pumping behavior of liquefied methane through the rocket engine manifold, fuel pump, and cooling channels, some physical–chemical properties were collected.

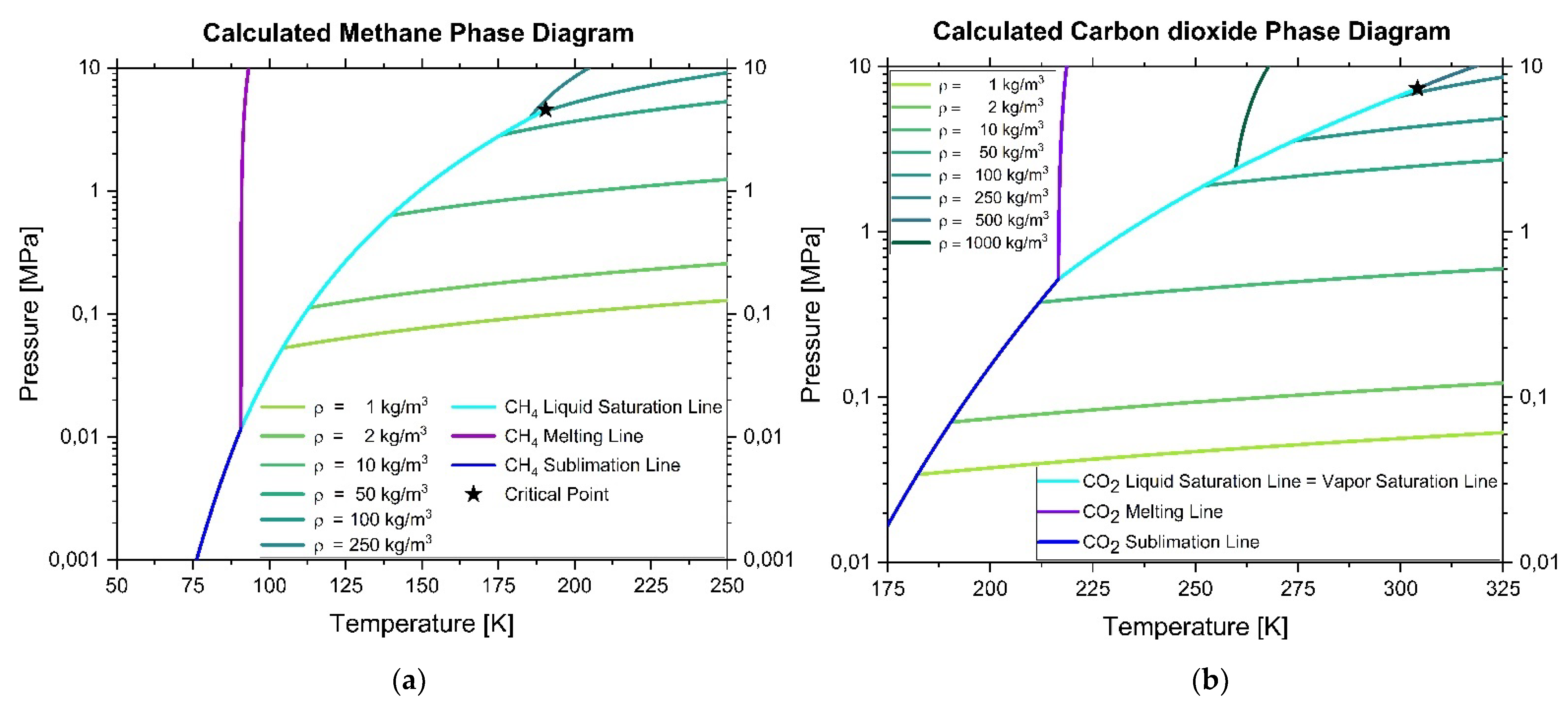
The temperatures of triple and boiling points of relevant substances available in natural gas are given in

Table 1. Temperatures of triple, normal boiling points or sublimation point of natural gas components [5].

Substance	Triple Point Temperature	Normal Boiling Point Temperature	Reference
Methane CH4	90.694 K	111.67 K	[6]
Ethane C2H6	90.368 K	184.57 K	[7]
Propane C3H8	85.525 K	231.04 K	[8]
Carbon dioxide CO2	216.59 K	(Sublimation point temperature: 194.69 K)	[9]
Nitrogen N2	63.151 K	77.355 K	[10]
Oxygen O2	54.361 K	90.188 K	[11]

, with exemption of carbon dioxide, where instead of normal boiling point temperature, sublimation point temperature is provided.

The triple point connects vapor, liquid, and solid phase boundaries and is defined by its triple point temperature and pressure. It connects the melting, vapor saturation, and sublimation lines, which have different pressure and temperature dependences. Vapor exists at pressure and temperature conditions which are below the vapor saturation line and right of the sublimation line in the pressure–temperature diagram. Liquids exist at pressure and temperature conditions which are above the vapor saturation line and right of the melting line in the pressure–temperature diagram. Above the critical point temperature and critical point pressure, the system is in a supercritical state without being in a solid state. Solids can exist at conditions which are left of the melting line and left of the sublimation line in the pressure–temperature diagram. Additionally, solids can exist at conditions which are left and above a liquid saturation line. This should be considered during design of engines and their fuel supply systems.

To get an overview of which substances are potentially problematic and should be investigated in more detail, triple point temperatures of pure natural gas components were compared.

The triple point temperature of pure methane is higher than the triple point temperatures of pure ethane, propane, and nitrogen. However, the triple point temperature of carbon dioxide and its normal sublimation temperature are much higher and, therefore, restrict the lower temperature range of safe natural gas engine operating conditions.

Therefore, in a second step, phase diagrams of pure methane and pure carbon dioxide were calculated with the NIST Reference Fluid Thermodynamic and Transport Properties database program REFPROP^® [5] for pressures up to 10 MPa.

The calculated phase diagram of pure methane for pressures between 1 kPa and 10 MPa and temperatures between 50 and 250 K is given in Figure 1a, and some of its characteristic points taken from NIST reference database are summarized in

Table 2. Characteristic points of the phase diagrams of methane [5,6] and carbon dioxide [5,9].

	Methane CH4	Carbon Dioxide CO2
CAS#:	74-82-8	124-38-9
Molar mass:	16.043 kg/kmol	44.01 kg/kmol
Triple point temperature:	90.694 K	216.59 K
Normal boiling point temperature:	111.67 K	-
Normal sublimation point temperature:	-	194.69 K
Critical point temperature:	190.56 K	304.13 K
Critical point pressure:	4.5992 MPa	7.3773 MPa
Critical point density:	162.66 kg/m3	467.6 kg/m3
Acentric factor:	0.01142	0.22394

.

For the calculation of the phase diagram of pure methane, a new reliable equation of state of Setzmann and Wagner [6] was used, which covers the range from the melting line to 625 K at pressures up to 1000 MPa. The uncertainties in calculated densities of 1, 2, 10, 50, 100 and 250 kg/m³ are 0.03% for pressures below 12 MPa and temperatures below 350 K and up to 0.07% for pressures less than 50 MPa. S.E. Quinones-Cisneros, M.L. Huber, and U.K. Deiters estimated uncertainty in viscosity, which varies from less than 0.3% between 200–400 K for pressures less than 30 MPa, to less than 2% over the rest of the fluid surface up to 100 MPa, increasing up to 5% for 100 to 500 MPa, and 10% at 500 to 1000 MPa for temperatures to 625 K. However, these uncertainties are valid only when used with the equation of state of Setzmann and Wagner [6]. The use of other equations of state may result in larger uncertainties.

For the calculation of the phase diagram of pure carbon dioxide, which is shown in Figure 1b, a new reliable equation of state of Span and Wagner [9] was used. It covers the fluid region from the triple point temperature to 1100 K at pressures up to 800 MPa. The estimated uncertainties at pressures up to 30 MPa and temperatures up to 523 K range from 0.03% to 0.05% in density, for which lines of calculated values are given for 1, 2, 10, 50, 100 and 250 kg/m³. Span and Wagner’s interest have been focused on the description of the critical region and the extrapolation behavior of the formulation of the equation of state to the limits of chemical stability. The melting line limits are 216.59 K to 1100 K and sublimation line limits are 0 K to 216.59 K. Therefore, under conditions in thermodynamic equilibrium and pressure, pure carbon dioxide exists in the solid state at pressures below its triple point pressure only at temperatures below 216.59 K. However, with increasing pressure, the freezing temperature is reached at higher values, resulting for example at pressures of 10 MPa already at a temperature of less than 220 K in frozen solid carbon dioxide. Some other characteristic points are summarized in Table 2.

The critical point of methane is lower in pressure and temperature than the critical point of carbon dioxide and lower in temperature than the triple point of carbon dioxide. Therefore, solid methane can exist only at much lower temperatures than carbon dioxide, which is limiting the low temperature side of operating conditions of a methane fuel engine with carbon dioxide impurities. However, at temperatures around and below the carbon dioxide triple point, solid carbon dioxide can exist within liquid or vapor methane, depending on the actual pressure. These conditions should be avoided completely for safety reasons.

The pitfalls of the CO₂ freezing prediction and the amount of soluble CO₂ in CH₄ were presented in 2003 by Tim Eggemann and Steve Chafin from River City Engineering Inc. Lawrence, Kansas at the 28th GPA Annual Convention [12] and published 2 years later [13]. They collected and critically evaluated experimental and calculated data of solid-liquid phase boundaries of methane carbon dioxide mixtures with several compositions and data on the solubility of CO₂ in liquid methane as well of sublimation isotherms for temperatures between 153 K and 210 K. Their CO₂ freeze utility predictions match up well with actual plant operating data.

A collection of data, whose original sources are very useful for cryogenic carbon dioxide capture from natural gas, was recently published by Babar et al. [14]. In their “review” they “reproduced” a lot of reliable available data, pictures and text, but, unfortunately, added a number of errors, such as wrong units (e.g., kPa instead of MPa, added minus sign in Figure 8 of [14]). The quality of their newer published papers, presentations, and book chapter differs extremely, and their content should be considered with care. Some lousy contributions contain, for example, no units of chemical or physical properties at all. Some phase diagrams are only overlays of different phase diagrams of pure substances, and the connecting lines therein should be used as guidelines for the eyes only and not as reliable phase boundaries. Other errors are not that obvious, e.g., in redrawn pictures or “reproduced” tables where the temperature is given in degree Celsius instead of the original temperature unit Fahrenheit, without doing the necessary recalculation. Further, the original pressure unit psi was not changed accordingly. All this results in a “bad” assessment of high-quality data or a “good” evaluation of very questionable contributions.

Considering the data at higher temperatures, liquid carbon dioxide and vapor of methane can exist together in a phase envelope area. The cricondenbar defines the point with maximal pressure in the phase envelope, and the cricondentherm on the other side defines the point with highest temperature in the phase envelope. Characteristic points of this vapor–liquid area of some mixtures of methane and carbon dioxide are given in

Table 3. Calculated characteristic points of liquid–vapor phase envelopes of some mixtures of methane and carbon dioxide [5,15].

Component	Methane/Carbon Dioxide
Mole fraction	0.99/0.01	0.98/0.02	0.95/0.05
Mass percent CH4	97.304	94.698	87.383
Mass percent CO2	2.6963	5.3017	12.617
Molar Mass	16.322 kg/kmol	16.602 kg/kmol	17.441 kg/kmol
Critical point temperature	191.56 K	192.58 K	195.78 K
Critical point pressure	4.6541 MPa	4.7124 MPa	4.9019 MPa
Critical point density	163.42 kg/m3	166.52 kg/m3	177.33 kg/m3
Cricondentherm (Point with max. temperature in phase envelope)	191.56 K, 4.6538 MPa, 158.09 kg/m3	192.61 K, 4.7113 MPa, 158.1 kg/m3	195.97 K, 4.8938 MPa, 157.44 kg/m3
Cricondenbar (Point with max. pressure in phase envelope)	191.56 K, 4.6543 MPa, 161.29 kg/m3	192.6 K, 4.713 MPa, 163.23 kg/m3	195.9 K, 4.9062 MPa, 169.94 kg/m3
Used Equation of states [15]	GERG with βT=1.0226, βV =0.99952, γT= 0.97567, γV= 1.0028, Fij =1.0

.

For the above calculation, the validated GERG-2008 wide-range equation of state for natural gases and other mixtures of Kunz and Wagner was used [15]. It is an expansion of the GERG-2004 equation of state of Kunz, Klimeck, Wagner and Jaeschke [16]. This equation was used before with an older version of the NIST program [17] to calculate phase diagrams of carbon dioxide (CO₂) with nitrogen [18], which are important for carbon dioxide capture and storage (CCS) processes.

Due to the phase boundaries around the phase envelope and the occurring change in physical properties by crossing these boundaries, e.g., densities, it is recommended to avoid this area within rocket engine operations and fuel supply systems.

The pressure–temperature diagram of a 95 mole % methane and 5 mole % carbon dioxide mixture is shown in Figure 2 as an example for pressures between 0.01 and 100 MPa and temperatures between 100 and 300 K. At temperatures and pressures near the critical point, which is marked with a black star, the properties of the mixtures, such as the density, change dramatically with small temperature and/or pressure changes.

To safely operate a rocket engine, the safe storage of liquid methane and its pumping through the engine manifold, fuel pump, and the cooling channels of the combustion chamber is necessary. In this context, carbon dioxide is the most problematic impurity due to its possibility of deposition as a solid substance at cold walls or under changing pressure conditions.

In thermodynamic equilibrium, pure carbon dioxide exists in the solid state at pressures below 10 MPa only at temperatures below circa 220 K.

However, for safety reasons, it would be advisable to ensure always a higher temperature, to make sure that at nonstationary conditions such as changing pressure conditions with the occurring Joule-Thompson effect, no carbon dioxide deposit or its solubility limit in methane is exceeded. As this is not feasible for real world rocket engines, one needs to ensure rather high purity levels with regard to carbon dioxide.

4. Effects of Impurities on the Combustion Processes

The impact of impurities in both methane and oxygen on the combustion processes in rocket engines is investigated in the following.

4.1. Hot Side—Combustion

In addition to the impact of impurities on the liquid fuels themselves, the influence of impurities within the fuel and/or oxidizer on the combustion process is investigated. The investigation is split into two parts. First, a pre-analysis is carried out, evaluating the influence of different mixture compositions on results of 1D laminar counter flow flame calculations at different pressures and strain rates. As a second step, steady-state, 2D-axisymmetric computational fluid dynamic (CFD) simulations of a generic rocket combustion chamber are performed in order to characterize the influence of the impurities on the combustion process within the chamber.

For the fuel side, three possible pollutants of the methane are considered: ethane (C₂H₆), carbon dioxide (CO₂), and nitrogen (N₂). C₂H₆ and CO₂ are primarily remnants from the extraction and/or production processes of the LNG. The third compound N₂ is a pressurizing agent used, especially at the test bench, to force the fuel from the tanks into the feed system of the engine. For the oxidizer side, only nitrogen is chosen as a possible impurity of the oxygen. It also mainly originates from the tank pressurization system, with small amounts again representing residues from the production process.

This paper investigates seven different combinations of fuel and oxidizer composition; see

Table 4. Test-case composition overview (all compositions are in mole fraction).

Test Case Name	Fuel				Oxidizer
	CH4	C2H6	CO2	N2	O2	N2
Base	1	-	-	-	1	-
C2H6	0.97	0.03	-	-	1	-
CO2	0.97	-	0.03	-	1	-
N2	0.97	-	-	0.03	1	-
ALL-F	0.91	0.03	0.03	0.03	1	-
N2inO2	1	-	-	-	0.97	0.03
ALL	0.91	0.03	0.03	0.03	0.97	0.03

.

The impact of different mixture compositions on the exhaust flow is out of the scope of the present investigation, as the calculation domain ends shortly after the nozzle throat. Regarding the NOx chemistry, several approaches of varying complexity are included. The first and simplest approach is to include the nitrogen merely as a species without it taking part in the reactions. Thus, it behaves like an inert gas, absorbing some of the energy released within the reactions, but there is no actual NOx chemistry included. Secondly, the NOx chemistry is directly included into the reaction scheme, increasing the size of the chemical mechanism. Additionally, for the CFD simulation, two different approaches on modeling the combustion are used. On the one hand a standard flamelet approach is used (see Section 4.2). Within the flamelet model, the chemistry and its effects are tabulated a priori and supplied to the CFD simulations. During the calculations only two additional transport equations for mixture fraction and its variance are solved. This is rather easy on the computational requirements but there are some downsides, especially with regard to accuracy. On the other hand, a full finite rate chemistry approach is chosen (see Section 4.3). In this case, an additional transport equation for each species is solved alongside the explicit calculation of the chemical source term for each species in each cell of the mesh.

For the current study, the kinetic mechanism C1-C4 by Zhukov [19] with 207 species and 1260 reactions forms the foundation for the most part of the investigation. The NOx additions are taken from a DLR mechanism for N₂O–ethane combustion [20]. Additionally, the GRI3.0 mechanism [21], with and without NOx chemistry, is used. The GRI-Mech 3.0 was chosen to have a medium-sized mechanism usable for the finite rate chemistry CFD simulation.

All 1D counterflow simulations are performed with the full mechanism. For the generation of the flamelet tables, minor species with a mass fraction smaller than 10⁻⁸ were excluded.

With respect to the representative operating conditions of rocket engines, four targeted pressure levels, p = 2 MPa (p02), p = 6 MPa (p06), p = 10 MPa (p10), and p = 20 MPa (p20), are chosen for this study.

4.2. One-D Counter Flow Diffusion Flames

In a first step, several 1D laminar diffusion counter flow flame simulations are performed to investigate the influences of the impurities given by the different fuel and oxidizer mixture compositions on the calculation results. The approach is chosen as it provides a more representative analysis than ignition delay times or laminar flame speed calculations. It is still a computationally simple problem and as the CFD simulations of the combustion chamber are performed using a flamelet combustion model, the flamelet solutions are a prerequisite for the flamelet table generation anyhow.

Assuming considerably faster chemistry compared to the turbulent time scales, one can derive the laminar flamelet equations (Equations (1) and (2)) in mixture fraction space [22]:

$$-\rho \frac{\chi }{2}\frac{{\partial }^2{Y}_s}{\partial Z^2}=\dot{m_s}$$

(1)

$$-\rho \frac{\chi }{2c_p}\left(\frac{{\partial }^{2}h}{\partial Z^2}-{\displaystyle \sum }_{s=1}^{N_i}{h}_s\frac{{\partial }^2{Y}_s}{\partial Z^2}\right)=-\frac{1}{C_p}{\displaystyle \sum }_s{h}_s\dot{m_s}$$

(2)

The solution of those equations is a 1D counter flow diffusion flame, and the shape is characterized by the scalar dissipation rate. The stoichiometric scalar dissipation rate χ_st is a measure for the aerodynamic strain rate at the stoichiometric point within the flame. A small χ_st represents the chemical equilibrium, whereas large χ_st (heat losses) leads to quenching of the flame. Within this approach, the combustion is modelled using a detailed Arrhenius-based finite rate chemistry model in combination with the C1-C4 mechanism by Zhukov [19]. For pure methane oxygen combustion, the stoichiometric point, where fuel and oxidizer are provided in a manner that both are fully consumed, is at an oxidizer to fuel ratio (ROF) of 4. This is equivalent to a mass fraction of 0.2. Regarding the cases of pollution, this value varies slightly as shown in

Table 5. Mixture fraction at stochiometric point for the different pollution cases.

Pollution	Mixture Fraction at Stochiometric Point [–]
Base case (no pollution)	0.2
C2H6	0.20960
CO2	0.21379
N2	0.20898
ALL-F	0.23269
N2inO2	0.19617
ALL	0.22795

.

To calculate the flamelet solutions, the software FlameMaster is used [23]. For the calculations, the assumption of Lewis number equal to one (Le = 1, diffusion and thermal conductivity are modelled to be equal) is made and only the steady burning branch (upper branch) of the S-shaped curve is considered.

Figure 3 shows the effect of different pressures on the maximum flame temperature and extinction limits and highlights the substantial differences to the common methane–air combustion at moderate pressures. Two distinct effects manifest in high pressure combustion with pure oxygen as oxidizer. Firstly, the maximum flame temperature is over 1000 K higher than the temperatures of common methane–air flames. This effect is predominantly attributed to the absence of nitrogen, which in the case of the combustion of methane and air makes up around 80% of the oxidizer mass. Nitrogen has a low reactivity due to its relative stable triple bond, therefore reactions of nitrogen with methane or oxygen do not contribute to combustion heat release. Instead, nitrogen acts mainly as an inert gas, that takes up large amounts of the released energy. Hence, the lack of nitrogen in rocket combustion strongly increases the maximum temperature. Additionally, higher pressures further increase the maximum temperature of the combustion process.

Secondly, compared to methane–air combustion, the maximum flame temperature remains constant over a large interval for an increasing scalar dissipation rate (until > 10,000 at a range of interest p > 2 MPa). This indicates that the aerodynamic strain has little to no influence on the equilibrium temperature. The diffusion-induced heat and mass transfer due to the scalar dissipation is not strong enough to substantially influence the temperature. Only at high strain rates (compared to combustion with air) a deviation from the equilibrium temperatures becomes visible. Again, the absence of nitrogen results in a considerably more reactive mixture, as no “inert” species is pulling out big amounts of the energy released by the chemical reaction. Furthermore, the extinction limits are pushed considerably higher, from a scalar dissipation at around 10² for air combustion to 10⁵ and even 10⁶ at higher pressures.

Figure 4a,b shows typical results for the upper branch of the S-shaped curve, here for base pressures of 2 MPa and 20 MPa. On a logarithmic scale only minor differences are visible. There are minor shifts with regards to the extinction limits and the maximum flame temperature (compare

Table 6. Maximum flame temperature at stoichiometric mixture fraction for different impurities of the fuel and/or the oxidizer at different pressures (counter flow diffusion flame).

	p02	p06	p10	p20
Base	3425.5 K	3579.6 K	3652.6 K	3752.7 K
C2H6	3427.9 K	3582.4 K	3655.6 K	3756.0 K
CO2	3411.5 K	3563.6 K	3635.6 K	3734.3 K
N2	3419.6 K	3572.7 K	3645.2 K	3744.6 K
ALL-F	3408.1 K	3559.5 K	3631.3 K	3729.5 K
N2inO2	3414.6 K	3566.8 K	3638.8 K	3737.4 K
ALL	3397.3 K	3546.9 K	3617.6 K	3714.4 K

). As expected, for cases with pollution the maximum temperature is slightly decreased (less than 1%), except for when ethane is included as a pollutant due to its higher heating value in comparison to methane.

Regarding an active NOx chemistry, the effect on the maximum flame temperature is minimal.

Table 7. Influence of the active NOx chemistry on the maximum flame temperature at stoichiometric mixture fraction for different impurities of the fuel and/or the oxidizer at pressures of 6 and 10 MPa. (counter flow diffusion flame).

	p06		p10
	no NOx	NOx	no NOx	NOx
Base	3579.6 K	-	3652.6 K	-
C2H6	3582.4 K	-	3655.6 K	-
CO2	3563.6 K	-	3635.6 K	-
N2	3572.7 K	3569.1 K	3645.2 K	3641.2 K
ALL-F	3559.5 K	3555.9 K	3631.3 K	3627.3 K
N2inO2	3566.8 K	3561.7 K	3638.8 K	3633.2 K
ALL	3546.9 K	3540.6 K	3617.6 K	3610.6 K

shows the respective temperatures at pressures of 6 and 10 MPa. The general influence of the NOx chemistry on the maximal flame temperature is below 0.2% and, therefore, almost negligible.

A similar behavior is observed for the influence on the extinction limits and the overall distribution of the maximum temperature over the scalar dissipation. It can be observed in Figure 5a,b that the lines are almost indistinguishable. Thus, the influence of the active NOx chemistry is almost negligible at the investigated pollution levels.

The influence on the overall species distribution is of course considerably more distinct, as only for the case with active NOx chemistry can nitrogen react and form chemical bonds with other elements. But for the overall performance levels of a rocket engine, those effects are not important. The general distribution of the species for 1-D simulations has minor expressiveness and, therefore, a more detailed look into species distribution will be conducted only for the CFD results.

4.3. CFD Simulations

The CFD simulations are performed to identify the influence of the different impurities of the oxidizer and fuel on actual combustion chamber simulations. The two main areas of interest are the temperature and the pressure distributions within the combustion chamber. The pressure represents the combustion efficiency and directly correlates to the achievable thrust. Equation (3) shows the standard thrust formula for rocket engines.

$$F=\dot{m} v_e+\left(P_e-P_a\right) A_e$$

(3)

F being the thrust, $\dot{m}$ the mass flow, $v_e$ the nozzle exit velocity, $P_e$ the pressure at the nozzle exit, $P_a$ the ambient pressure, and $A_e$ the nozzle exit area. Applying the isentropic properties and the ideal gas law one can transform the equation to show the influence of the chamber pressure $P_{cc}$ on the thrust of the rocket:

$$F=A_{th}{P}_{cc} \sqrt{\frac{2{\gamma }^2}{\gamma -1}{\left(\frac{2}{y+1}\right)}^{\frac{\gamma +1}{\gamma -1}}\left[1-{\left(\frac{P_e}{P_{cc}}\right)}^{\frac{\gamma -1}{\gamma }}\right]}+\left(P_e-P_a\right) A_e$$

(4)

Here $A_{th}$ is the throat area and $\gamma$ is the isentropic exponent. One can clearly see that the chamber pressure $P_{cc}$ has a significant influence on the achievable thrust.$\frac{P_e}{P_{cc}}$ derives from the exit velocity and is constant as an increase in $P_{cc}$ causes an equivalent increase in $P_e$. Therefore, the thrust is directly linear to the achievable chamber pressure.

Further the temperature and pressure together directly influence the wall heat flux and, therefore, determine the required cooling. Based on the heat transfer equation by Bartz [24], the wall heat flux depends on the chamber temperature $T_{cc}$ and chamber pressure $P_{cc}$ according to Equation (5), with $T_w$ being the wall temperature. As $T_w$ is determined by the chamber material and generally cannot exceed pre-defined values, the heat flux linearly correlates to $\left(T_{cc}-T_w\right)$ and, therewith, a temperature increase in the chamber.

$$\dot{q} ~ \left(T_{cc}-T_w\right), P_{cc}^{0.8}$$

(5)

The CFD investigations can be divided into two parts. For the baseline investigation, applying the flamelet model and no NOx chemistry, 28 simulations in total with 7 simulations at each of the four pressure levels for the different compositions (Table 4) are performed. Here, nitrogen only acts as an inert gas and no chemical reactions including nitrogen are considered. In the second part, the influence of different modelling approaches for the NOx chemistry is investigated. To keep the number of simulations reasonable, this investigation is only performed at a pressure level of approximately 10 MPa. Fifteen additional flamelet simulations and eleven finite-rate simulations are conducted.

4.3.1. DLR TAU Code

All CFD simulations in the framework of this paper are conducted with the DLR-TAU code [25,26]. The DLR-TAU code is a compressible finite-volume Navier–Stokes solver with second order accuracy. It can utilize structured, unstructured, and hybrid grids. The TAU Code has been used to simulate a wide variety of flows: steady and unsteady, from subsonic to supersonic, and with and without chemical reactions [27,28,29,30]. The solver uses an edge-based dual-cell approach based on a vertex-centered scheme. For time integration an explicit 3rd order Runge–Kutta scheme is used. A standard MAPS+ upwind solver [31] is used. To improve convergence, local time stepping and implicit residual smoothing algorithms are applied. The turbulence is modelled using the 2-layer k-ε model [32]. Turbulent mass diffusion fluxes and enthalpy fluxes are modelled via the turbulent Schmidt and Prandtl numbers with constant values of Sc_tr = 0.7 and Pr_tr = 0.9, respectively. The combustion is modelled using two different approaches: (a) a standard flamelet model [33] and (b) a finite rate combustion model. The flamelet tables were generated using the flamelet solutions from the previous section. For the flamelet simulations Le = 1 is assumed. The inlet conditions for the simulations are chosen at ambient temperatures, allowing use of the ideal gas equation as an equation of state and thus avoiding complex phase change or cryogenic effects.

4.3.2. Finite Rate Combustion Model

Compared to the flamelet approach, where only two additional transport equations for mass fraction and its variation are employed, the finite rate model requires a separate transport equation for each species contained within the chemical mechanism. Additionally, whereas in the flamelet model the chemical reactions and their effects on composition and temperature are pre-tabulates, the finite rate model explicitly solves the chemical source term in each step and each cell. To solve for the chemical source term the law of mass actions is applied—therefore, requiring the species composition in the cell, a set of chemical reactions, and a reaction rate constant for each reaction. The species and reactions are defined by the mechanism: in the present case of the finite rate simulations, the standard GRI3.0 mechanism. For the reaction rate a modified Arrhenius-based approach is utilized (Equation (6)):

$$k=B T^n{e}^{-\frac{E_a}{RT}}$$

(6)

In contrast to hydrogen combustion, pressure-dependent reactions are of quite some importance for methane combustion. [34] The standard Arrhenius approach is extended using the TROE [35] formulations for pressure-dependent reactions to include those effects. The pressure-dependent reaction rates of the extended Arrhenius formulations are pre-tabulated in temperature and effective particle density space to improve computational time [36].

Whilst the chemistry modeling of the finite rate model is considerably more detailed and one is especially able to also capture recombination processes, there is one big disadvantage within this approach: the turbulence/chemistry interaction is missing. Especially the combination of pressure-dependent reactions and a parabolic density function (PDF) approach for turbulent chemistry interactions is quite complicated.

4.3.3. Numerical Setup

For the CFD simulation, a generic combustion chamber design is chosen. A single shear coaxial injector element with tapering (but without recess) within a simple cylindrical combustion chamber and nozzle geometry is applied for all CFD simulations. The injector and chamber dimensions are the same for all test cases and are presented in

Table 8. Injector and chamber dimensions.

Common Design Parameters
Inner diameter of LOx post	1.80 mm
Exit diameter of LOx post	1.85 mm
Outer diameter of LOx Post	2.00 mm
Outer diameter of FUEL annulus	2.25 mm
Thickness of LOx post tip	0.15 mm
Angle of taper	10 °
Chamber diameter	15 mm

.

This setup allows for fast 2D-axisymmetric simulations. For simplification and comparability to former counter-flow simulations, and to avoid any real gas effects, both the fuel and the oxidizer are injected in gaseous state at a temperature of 300 K. The combustion is fuel-rich with a mass ratio of oxidizer to fuel (ROF) of 3.4, to be representative for rocket applications. The four targeted pressure levels are again p = 2 MPa, p = 6 MPa, p = 10 MPa, and p = 20 MPa, and these levels are labelled p02, p06, p10, and p20, respectively. In order to achieve the four different pressure levels within the combustion chamber, three different nozzle configurations and two different inlet conditions are used (see

Table 9. Mass flow and nozzle diameters for the different setups in the CFD simulations.

	Fuel Mass Flow	Oxidizer Mass Flow	Nozzle Diameter
p02	13.50 g	45.92 g	8.35 mm
p06	40 g	136 g	8.35 mm
p10	40 g	136 g	6.49 mm
p20	40 g	136 g	2.30 mm

). For the cases p06, p10, and p20, the same inlet conditions regarding mass flow rate and temperature are chosen. In order to achieve the different pressure levels inside the chamber, the nozzle diameter has been adopted accordingly. For the last configuration p02, the geometry from the p06 simulations is used and the mass flow rate is reduced to lower the chamber pressure to 2 MPa. This is necessary as otherwise the injection velocity for the p02 case would have been supersonic. The mesh is a fully structured mesh with 126,576 grid nodes and can partially be seen in Figure 6. To further simplify the test case all walls are considered to be adiabatic. As a result of that assumption, there is no heat loss over the boundary conditions (except the outflow boundary), and the entire energy released from the reactions remains within the system. Both inlets for methane and oxygen are mass flow boundaries with prescribed mass flows and their associated temperatures. The outflow boundary is a simple pressure boundary with a pressure equal to ambient conditions of 0.1 MPa.

4.3.4. CFD Results with No Active NOx Chemistry

In general, the influence on the maximum temperature within the combustion chamber and the flame shape at each pressure level are minor and are basically indistinguishable from general numerical uncertainties of the applied models (combustion model, turbulence model, etc.).

Table 10. Maximum combustion temperature for different pollutants of the fuel and/or the oxidizer at different pressure levels (CFD simulation).

	p02	p06	p10	p20
Base	3434.0 K	3579.3 K	3646.2 K	3743.4 K
C2H6	3433.8 K	3582.5 K	3651.7 K	3750.2 K
CO2	3421.9 K	3570.1 K	3639.0 K	3735.7 K
N2	3429.7 K	3577.5 K	3646.7 K	3743.2 K
ALL-F	3418.5 K	3566.1 K	3634.7 K	3731.6 K
N2inO2	3419.9 K	3566.7 K	3634.7 K	3736.4 K
ALL	3406.0 K	3553.5 K	3621.0 K	3716.3 K

shows the maximum temperature within each simulation. Within each pressure level the difference is below 0.85%, which is generally in line with the difference in maximum adiabatic flame temperature from the counter flow diffusion flame results. Figure 7 shows exemplarily the temperature within the chamber for the case with a target pressure of 6 MPa (p06) and an impurity of 0.03 mol-% of C₂H₆.

Regarding the wall temperature profile (Figure 8) one notices that with the addition of pollutants into the fuel, the recirculation zone decreases for the majority of cases. Only for the addition of ethane, the representative for higher carbons, no effect on the recirculation length is visible. On the contrary, all other pollutants which only consume energy lead to a decreased recirculation zone. Ethane, which itself contains chemical energy that is released during the combustion, shows no effect in the recirculation zone. For the other cases the temperature rises earlier in the chamber and as a result the threshold of 2500 K at the wall is reached about 10 mm upstream of the position for pollutant-free combustion. This in turn would lead to an increased heat flow towards the chamber walls into the coolant, which needs to be considered during the engine design. Although minor, the effect can also be seen in Figure 9 directly comparing the temperature filed inside the combustion chamber for the cases with no pollution (base) and all pollutants within the fuel (All-F).

In contrast, the addition of nitrogen into oxygen in contrast seems to have only a negligible effect with a minimal increase. In this case the nitrogen comprises the LOx core in the center of the chamber and, therefore, has no influence on the flow close to the wall.

With respect to the wall chamber pressure, the influence of the different impurities becomes more visible. In the p10 case the combustion pressure drop is 3.5% (0.36 MPa) between the simulation with maximum amount of pollution and the pollutant-free version.

Table 11. Pressure in [MPa] at the chamber wall (x = 0.171 m) for different pollutants of the fuel and/or the oxidizer at the four pressure levels.

	p02	p06	p10	p20
Base	2.078	6.228	10.388	20.774
C2H6	2.075 (−0.14%)	6.219 (−0.15%)	10.370 (−0.16%)	20.745 (−0.14%)
CO2	2.034 (−2.16%)	6.094 (−2.15%)	10.163 (−2.23%)	20.331 (−2.13%)
N2	2.053 (−1.22%)	6.152 (−1.21%)	10.260 (−1.25%)	20.527 (−1.19%)
ALL-F	2.007 (−3.54%)	6.014 (−3.43%)	10.029 (−3.59%)	20.065 (−3.41%)
N2inO2	2.076 (−0.10%)	6.220 (−0.12%)	10.372 (−0.16%)	20.752 (−0.11%)
ALL	2.007 (−3.54%)	6.012 (−3.46%)	10.026 (−3.62%)	20.057 (−3.45%)

shows the wall pressure at a position of x = 0.171 m from the injector. This corresponds to the spot where the pressure maximum at the chamber wall is located. Figure 10a–d shows the wall pressure profiles for the different compositions at the four respective pressure levels.

It appears that for such minor levels of pollution, the pressure influence for the case considering multiple pollutants of the fuel (ALL-F) is almost a linear combination of the cases with only a single pollutant. Furthermore, it can be said that the pollutant influence is very similar on each pressure level. Therefore, we conclude that the combustion pressure has only a minor role for the influence of the pollutants.

The species with the single most influence is carbon dioxide. Over half of the total influence (over 2% of pressure loss) at each pressure level can be associated with it. Whereas 0.03 mol-% impurity can be considered high for N₂, it is not uncommon or even low for CO_2—depending on the source of the LNG. Therefore, in order to avoid substantial losses in thrust a low tolerance for carbon dioxide is necessary. The influence of higher hydrocarbons which are represented by ethane is minimal, below 0.2%, and therefore can be tolerated in small amounts.

Although the absolute amount of nitrogen is considerably lower for the N₂ pollution of the fuel side, the effect is substantially higher (N2 curve vs. N_2inO₂ curve). Therefore, it might be advisable to use a hydrocarbon for the pressurization of the fuel system. Overall, the influence of nitrogen on the oxidizer side is very small. Therefore, it can be concluded that there is no issue with using nitrogen as a pressurizing agent for the oxygen side of the system.

As only adiabatic CFD simulations have been performed, there are no direct results regarding the effects on the wall heat flux. Using the Bartz approximation formula (Equation (5)) one can estimate the change of the wall heat flux due to the changes in pressure and maximum combustion chamber temperature (compare Equation (5)). The only additional assumption needed is a fixed wall temperature of 800 K, which is representative for cryogenically cooled rocket engines.

Table 12. Approximation of the effects on the wall heat flux due to temperature and pressure changes at 10 MPa for different pollutants (according to Bartz, Equation (5), $T_{\mathrm{wall}}$ = 800 K).

	Temperature	Pressure [MPa]	$$\begin{gathered} \dot{\mathbf{\Delta }{\mathit{h}}_{\mathit{t}\mathit{e}\mathit{m}\mathit{p}}} [–] \\ \mathbf{due} \mathbf{to} \\ \mathbf{Temperature} \end{gathered}$$	$$\begin{gathered} \dot{\mathbf{\Delta }{\mathit{h}}_{\mathit{p}}} [–] \\ \mathbf{due} \\ \mathbf{Pressure} \end{gathered}$$	$\mathbf{\Delta }\dot{{\mathit{h}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}} [–]$
Base	3646.2 K	10.388	−	−	−
C2H6	3651.7 K	10.370	0.19%	−0.14%	0.05%
CO2	3639.0 K	10.163	−0.25%	−1.74%	−1.99%
N2	3646.7 K	10.260	0.02%	−0.99%	−0.97%
ALL-F	3634.7 K	10.029	−0.40%	−2.77%	−3.18%
N2inO2	3634.7 K	10.372	−0.40%	−0.12%	−0.53%
ALL	3621.0 K	10.026	−0.89%	−2.80%	−3.68%

shows the relative changes in heat flux due to temperature and pressure changes for different pollutants at 10 MPa.

Considering the pollutant with a higher carbon amount (C₂H₆), the effects of pressure and temperature on the heat flux are counteracting each other which results in a negligible effect. For the majority of the investigated cases the effect of both temperature and pressure, on the wall heat flux lead to a decrease, enhancing each other. The maximum combined effect is predicted to be within 4% of the total heat flux.

4.3.5. CFD Results with NOx Chemistry

In a final step, the influence of various degrees of complexities for the chemical modeling is investigated. In order to keep the number of simulations at reasonable levels all simulations are performed at only one pressure, 10 MPa, as this seems to be the most appropriate for European rocket engines. In addition to the seven simulations at 10 MPa presented above, four simulations with active NOx chemistry (N2, ALL-F, N_2inO₂, ALL) are conducted using the flamelet model and the Zhukov/Kong mechanism. Further, 11 simulations using the GRI3.0 Mechanism with and without NOx chemistry and the flamelet combustion model are conducted. Finally, 11 finite rate chemistry simulations (seven without NOx chemistry and four including NOx chemistry) are performed. The FRC simulations are conducted using the GRI3.0 mechanism, as the Zhukov/Kong mechanism would have been too big to use for the complex finite rate chemistry.

Table 13. Maximum combustion temperature for different pollutants of the fuel and/or the oxidizer and different combustion modelling at 10 MPa (CFD simulation).

	Flamelet				FRC
	Z/K	Z/K NOx	GRI	GRI NOx	GRI	GRI NOx
Base	3646.2 K		3649.3 K		3872.3 K	-
C2H6	3651.7 K	-	3654.8 K	-	3874.3 K	-
CO2	3639.0 K	-	3641.4 K	-	3854.7 K	-
N2	3646.7 K	3642.0 K (−0.13 %)	3648.8 K	3644.7 K (−0.11 %)	3865.5 K	3862.1 K (−0.09 %)
ALL-F	3634.7 K	3630.5 K (−0.11 %)	3637.5 K	3633.4 K (−0.11 %)	3851.3 K	3847.2 K (−0.11 %)
N2inO2	3634.7 K	3629.3 K (−0.15 %)	3637.7 K	3632.6 K (−0.14 %)	3854.3 K	3849.1 K (−0.15 %)
ALL	3621.0 K	3613.7 K (−0.20 %)	3623.7 K	3616.6 K (−0.20 %)	3835.7 K	3828.3 K (−0.19 %)

and

Table 14. Pressure in [MPa] at the chamber wall (x = 0.171 m) for different pollutants of the fuel and/or the oxidizer and different combustion modelling at 10 MPa (CFD simulation).

	Flamelet				FRC
	Z/K	Z/K NOx	GRI	GRI NOx	GRI	GRI NOx
Base	10.388	−	10.393	−	10.642	−
C2H6	10.371	−	10.375	−	10.632 (−0.10 %)	−
CO2	10.163	−	10.171	−	10.418 (−2.16 %)	−
N2	10.261	10.257 (−0.03 %)	10.269	10.262 (−0.07 %)	10.520 (−1.16 %)	10.509 (−0.11 %)
ALL-F	10.029	10.026 (−0.04 %)	10.038	10.031 (−0.07 %)	10.281 (−3.59 %)	10.267 (−0.14 %)
N2inO2	10.372	10.366 (−0.05 %)	10.379	10.370 (−0.07 %)	10.627 (−0.14 %)	10.614 (−0.12 %)
ALL	10.026	10.017 (−0.09 %)	10.034	10.022 (−0.12 %)	10.277 (−3.55 %)	10.259 (−0.17 %)

show the pressure and the maximum temperature results from the numerical simulations for these different approaches to simulating the chemistry. The different chemical approaches are named in the following way:

• Flamelet Zhukov/Kong with (Z/K NOx) and without (Z/K) active NOx chemistry;
• Flamelet GRI with (GRI NOx) and without (GRI) active NOx chemistry;
• FRC finite rate chemistry with GRI mechanism with (GRI NOx) and without (GRI) active NOx chemistry.

The FRC approach generally predicts higher temperatures. This is not an effect specific to the NOx modeling and will, therefore, be neglected here. The relative deviations between active NOx chemistry and the usage of N₂ as a simple inert gas are almost identical between all three approaches. For the maximum temperature the difference is below 0.22% and, therefore, considered negligible.

Regarding the pressure, the FRC modeling predicts a slightly higher difference between active NOx modelling and the simpler approach of inert nitrogen. Nevertheless, the difference is identified to be below 0.2% and, therefore, within the margin of the numerical error. Overall, it can be said that, with focus on thrust, pressure, and temperature, it is not necessary to use more complex chemistry models. The approach of including nitrogen as an inert gas that does not participate in any sort of reactions seems to be sufficient. This is of course only valid as long as the NOx levels in the exhaust are of no relevance.

5. Conclusions

Investigations of the phase diagrams of carbon dioxide and methane show that typical operational conditions of methane rocket engines, by our knowledge, are planned carefully and are normally outside of critical conditions where solid parts of carbon dioxide could exist within liquid natural methane. The conditions, which should be avoided for a safe operation of a rocket engine with methane with impurities as fuel, are described.

On the hot combustion side, the influence is minor with regard to maximum temperature and flame shape. The extent of the recirculation zone is slightly decreased and, therefore, a higher heat flow can be expected. However, a drop of up to 3.5% in chamber pressure is observed, which leads to a corresponding impact on engine thrust level. A linear behavior with regard to the pressure drop between a single and multiple impurities is shown, although this should only be valid for the minor amounts of impurities investigated here.

Computational fluid dynamic (CFD) simulations show that the presence of impurities results in a slight change in the combustion chamber temperature and pressure due to the associated change in the mixture’s specific heat of combustion. With regards to the complexity of the required chemical modeling the inclusion of an active NOx chemistry in the flamelet model shows no significant impact on the results. Even the switch to a finite rate combustion model shows no relevant differences between active NOx modeling and an inert approach for nitrogen.