New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems
Abstract
:1. Introduction
2. Formulation
2.1. Governing Equations
2.2. Updating Equations of the TTBIF
2.3. Further Optimization of the TTBIF
- (1)
- for the case of 0 < γ1 < [2 ]/(1 + ρ∞), the accuracy of the TTBIF cannot be third-order, but the minimum local truncation error σ = O(τ3) can be determined by φ(γ1, ρ∞) = = 0, refer to Figure 1a;
- (2)
- for the case of γ1 > [2 + ]/(1 + ρ∞), the TTBIF can be third-order accurate, and the corresponding optimal γ1 can be determined by 1;
- (3)
- additionally, we found that γ12θ3 = 0 holds when the optimal γ1 obtained by φ(γ1, ρ∞) = 0 is adopted; then, the effective stiffness matrices of all three sub-steps are the same. This is important for linear ODEs, leading to the effective stiffness matrix being factorized only once in three sub-steps, as in single-step methods; refer to Appendix B.
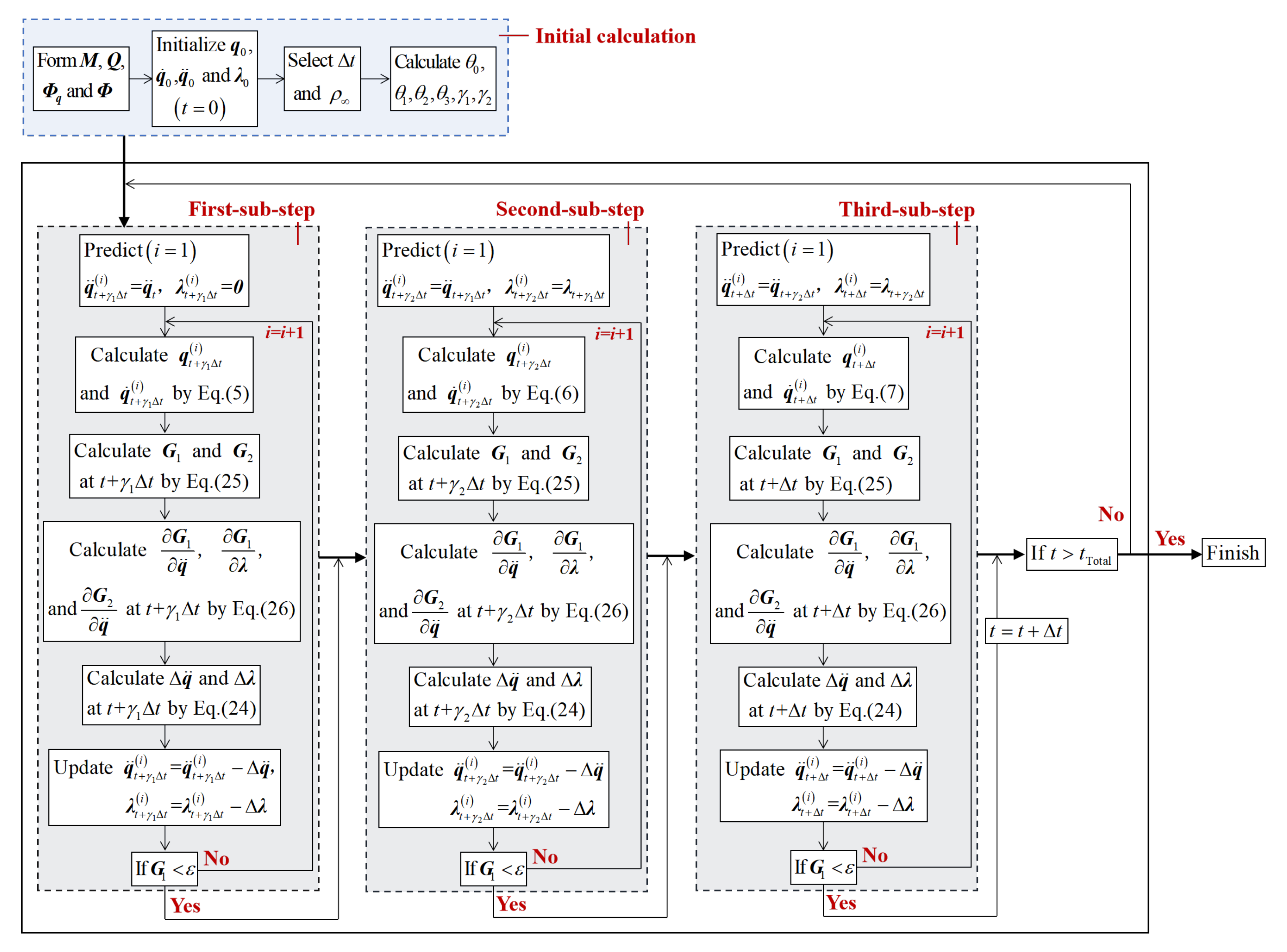
3. Implementation
4. Numerical Properties
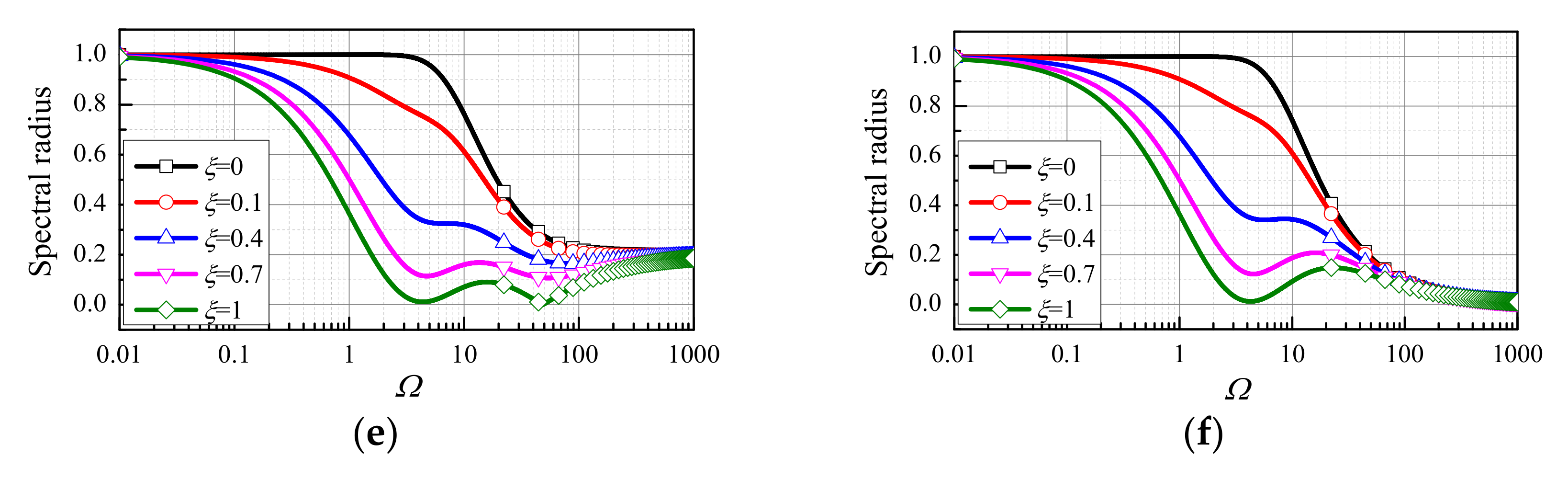
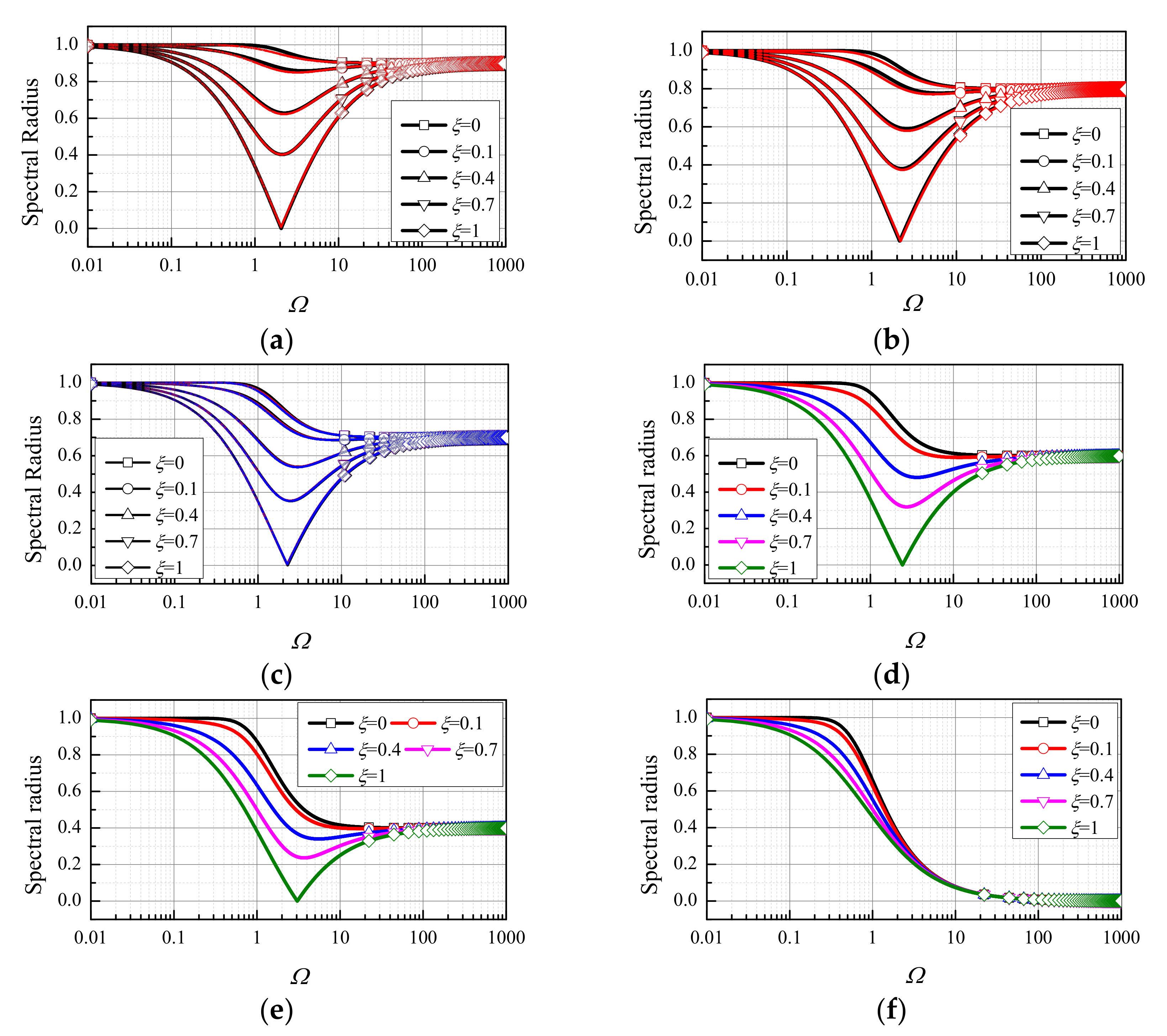
4.1. Spectral Characteristics
- (1)
- the TTBIFa and the TTBIFbn are unconditionally stable for undamped and damped systems;
- (2)
- ξ only affects ρ in the middle-frequency range;
- (3)
- if ξ = 0, the range corresponding to ρ(Ω) → 1 of the TTBIFa is wider than that of the TTBIFbn;
- (4)
- (5)
- if 0 < ξ ≤ 1, the TTBIFa and the TTBIFbn nearly have the same ρ for 0 < Ω ≤ 1.
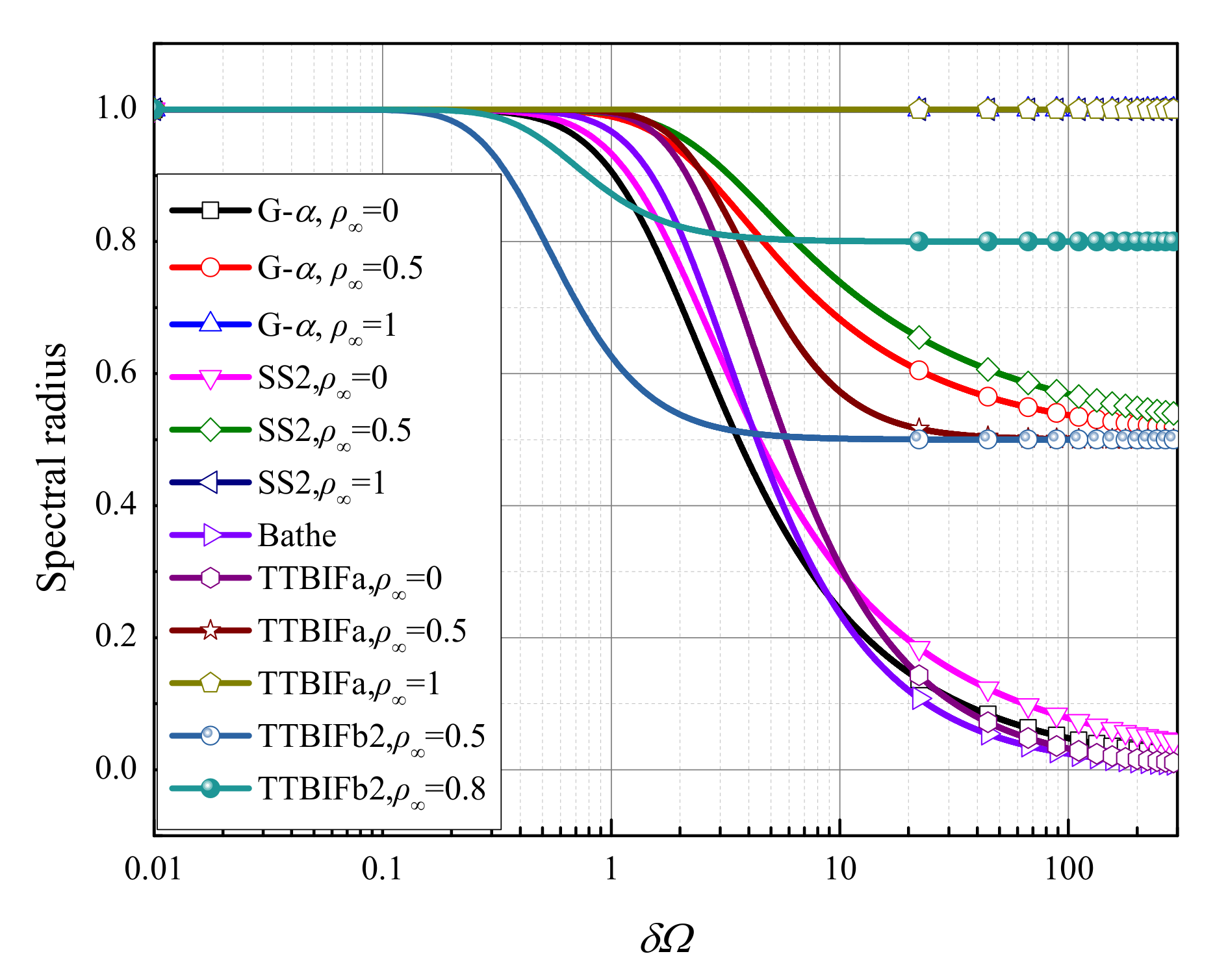
- (1)
- if ξ ≠ 0, the generalized-α method may be unstable, as ρ(Ω) > 1;
- (2)
- if ρ∞ = 1, the physical damping has no effect on the ρ of the SS2 method, and if 0 ≤ ρ∞ < 1, the ρ of the SS2 method agrees well with the exact one in the range of 0 < Ω ≤ 0.3;
- (3)
- the ρ of the Bathe method matches well with the exact one in the range of 0 < Ω ≤ 1;
- (4)
- in the range of 0 < Ω ≤ 4, the ρ of the TTBIFa agrees well with the exact one, and the ρ of the TTBIFb is consistent with the exact one in the range of 0 < Ω ≤1.
- (1)
- the TTBIFa exhibits desirable amplitude and phase accuracy for δΩ ∈ (0, 1];
- (2)
- the TTBIFb2 has considerable amplitude and phase errors in the low-frequency range, but the third-order accurate TTBIFb3 has the highest phase accuracy in the range of δΩ ∈ (0, 0.1].
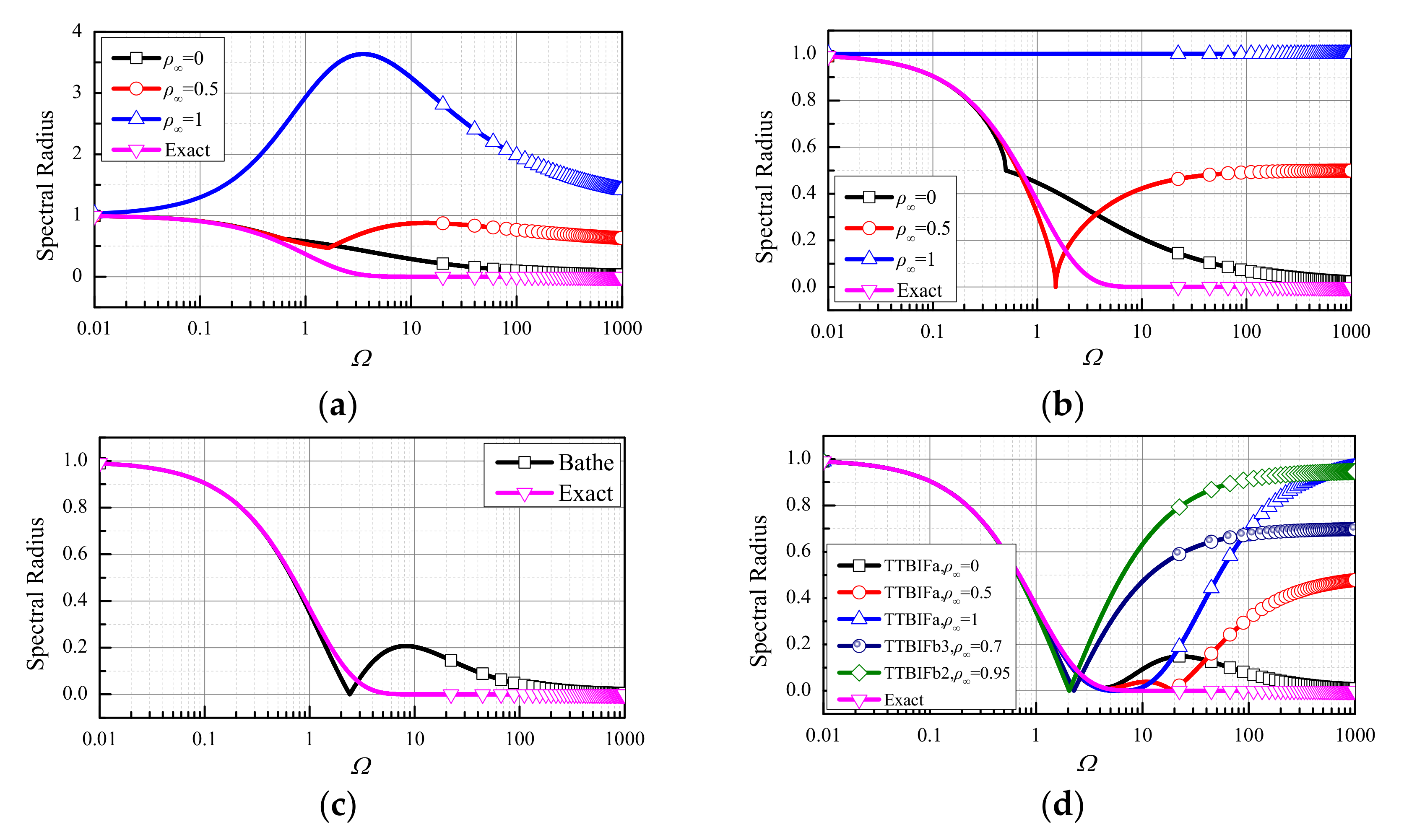
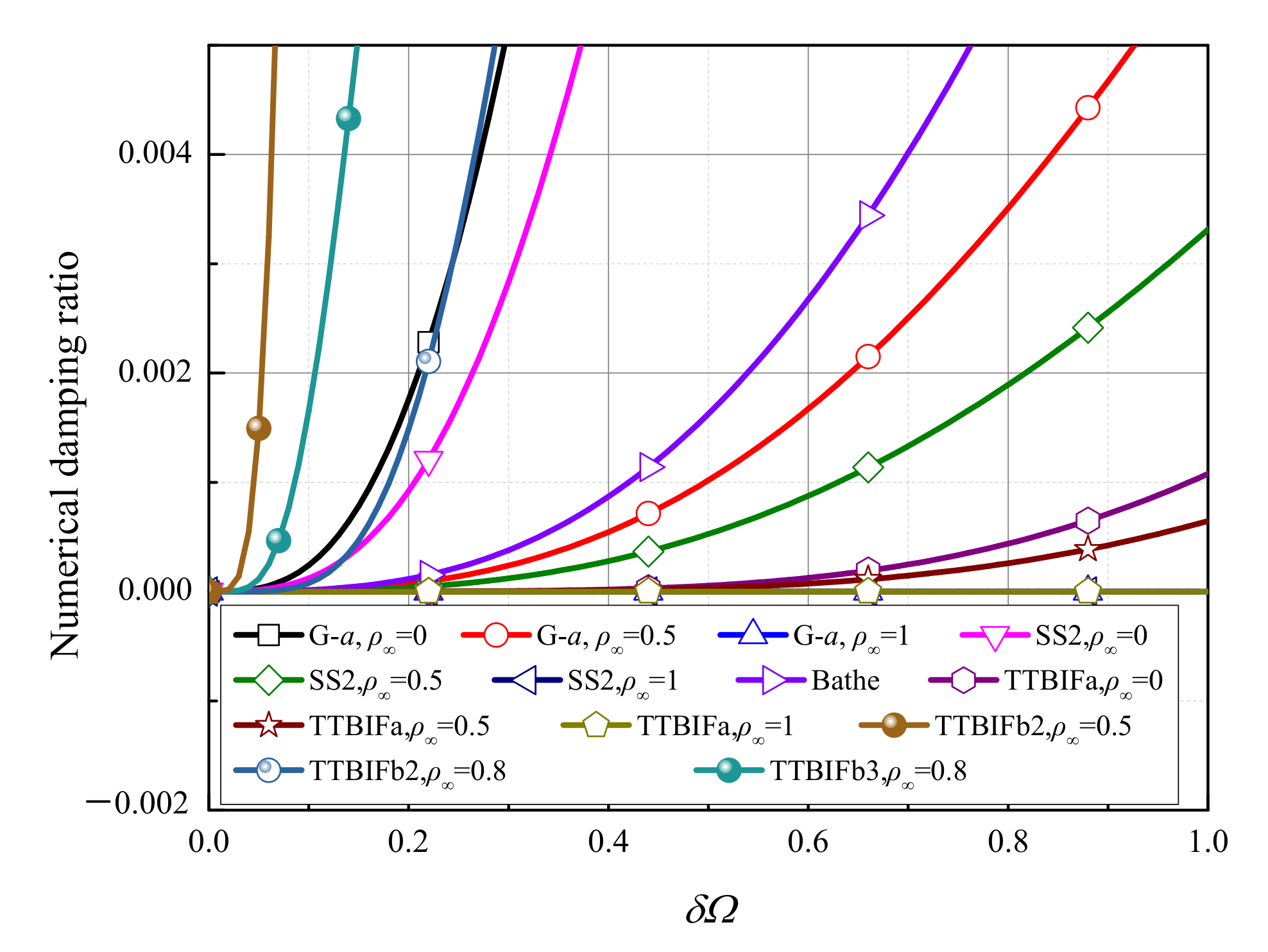
4.2. Overshoot Characteristics
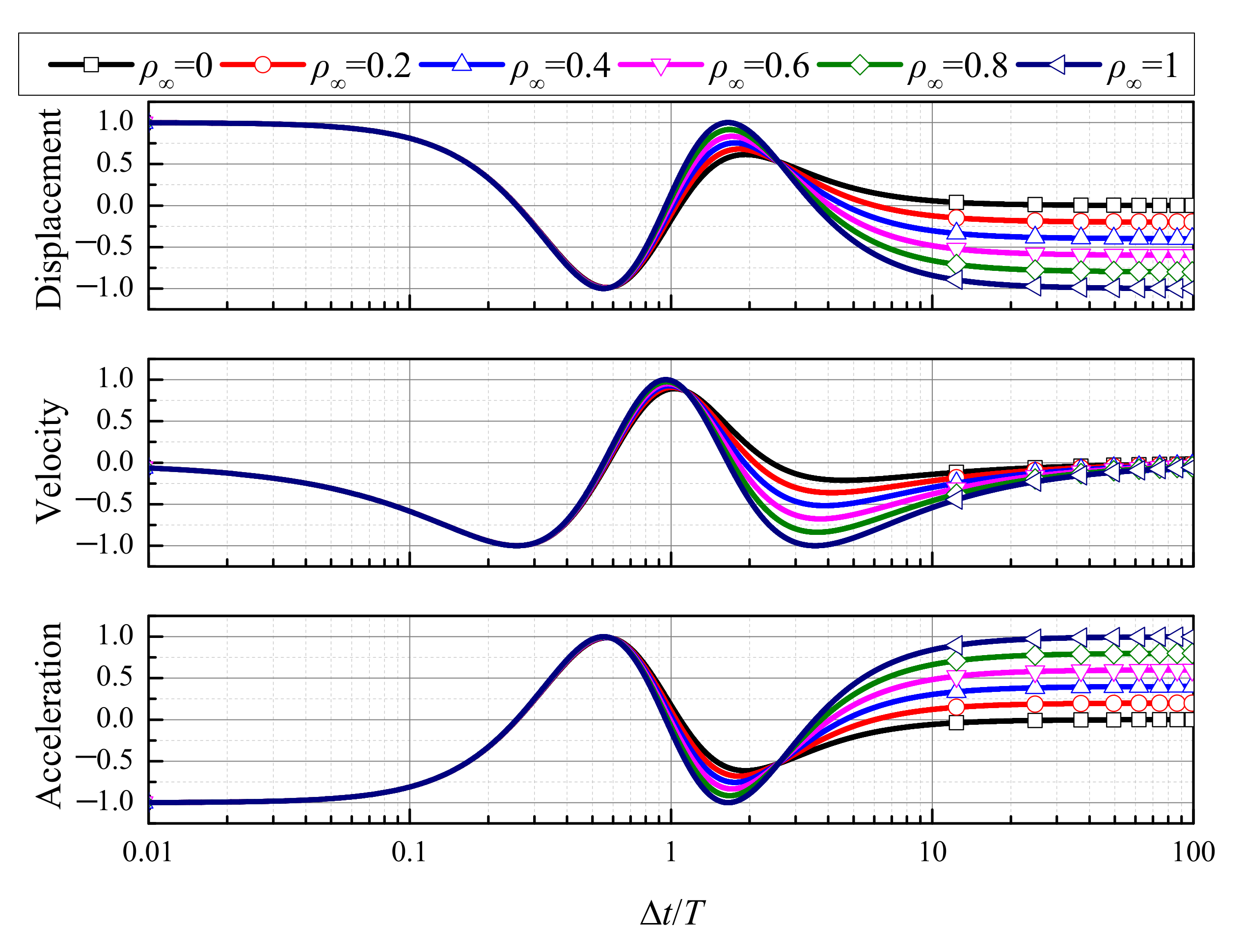
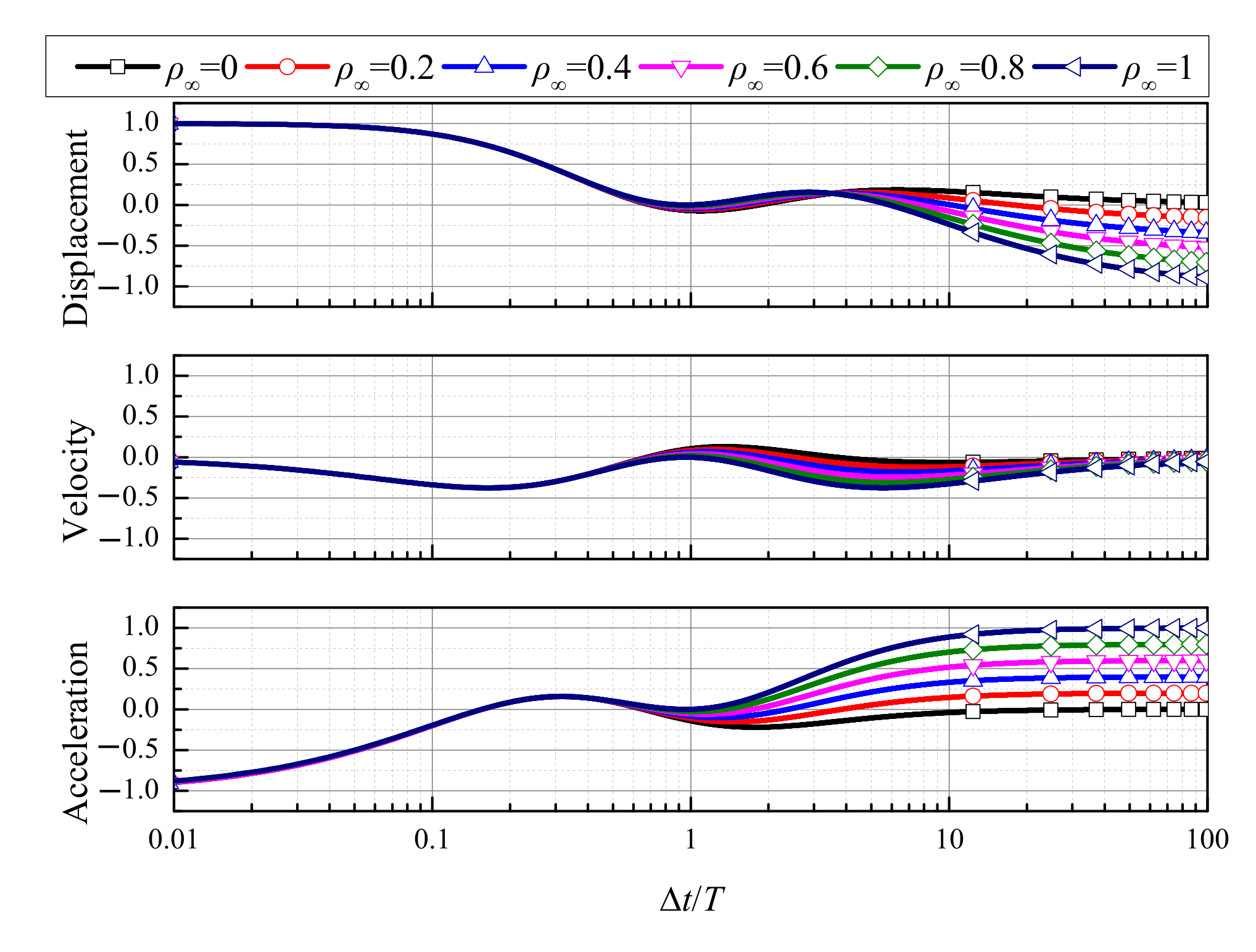
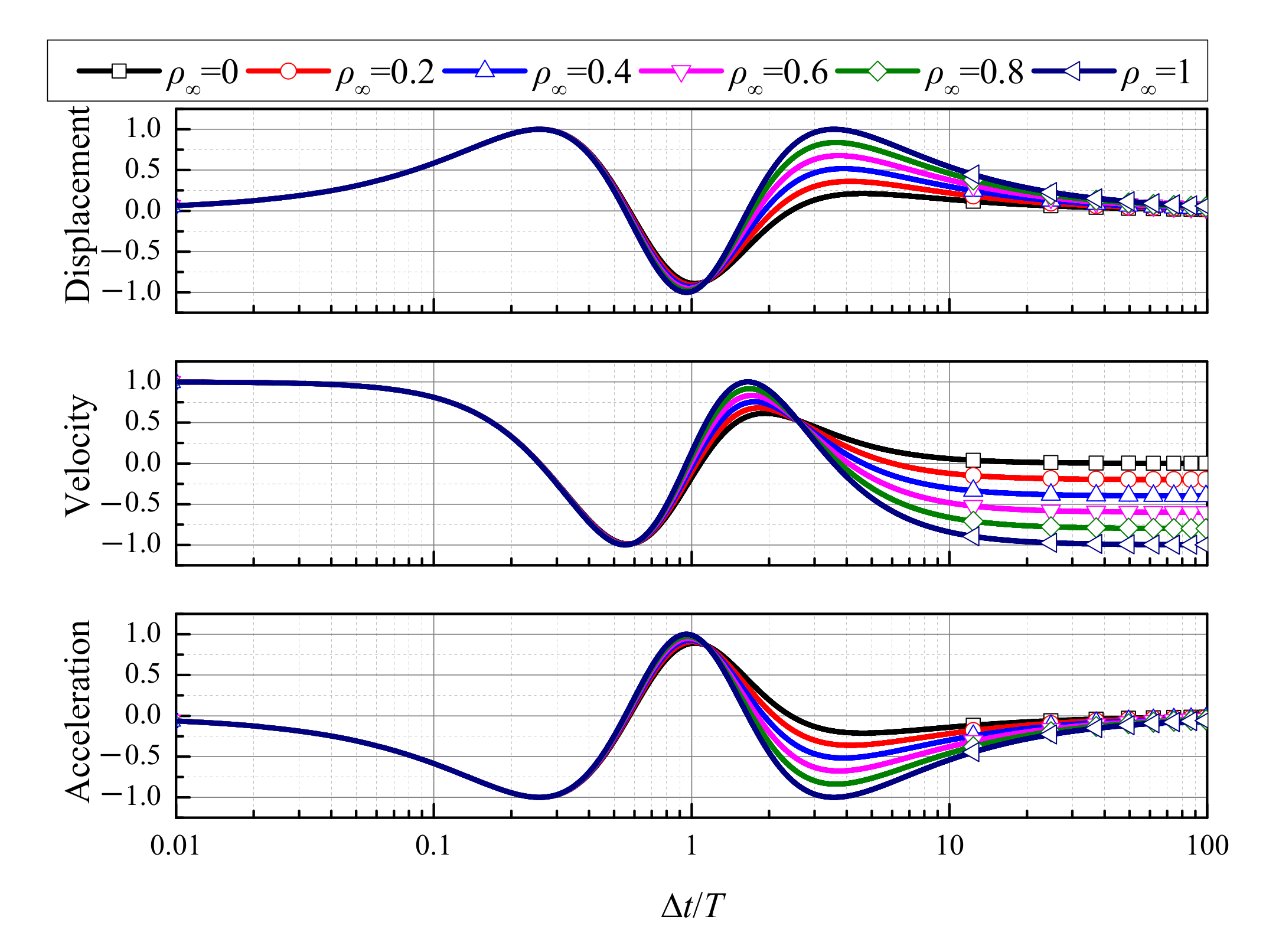
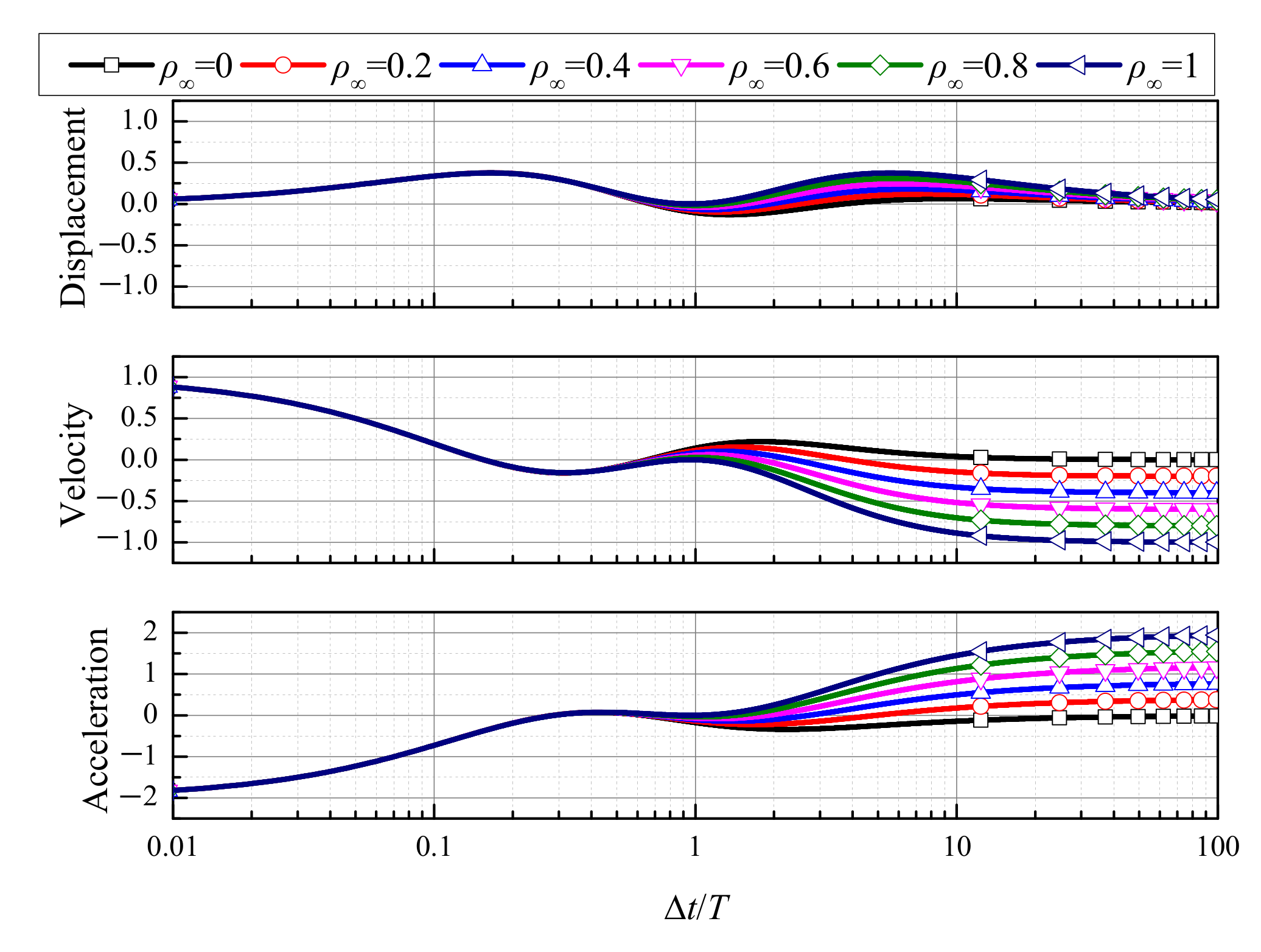
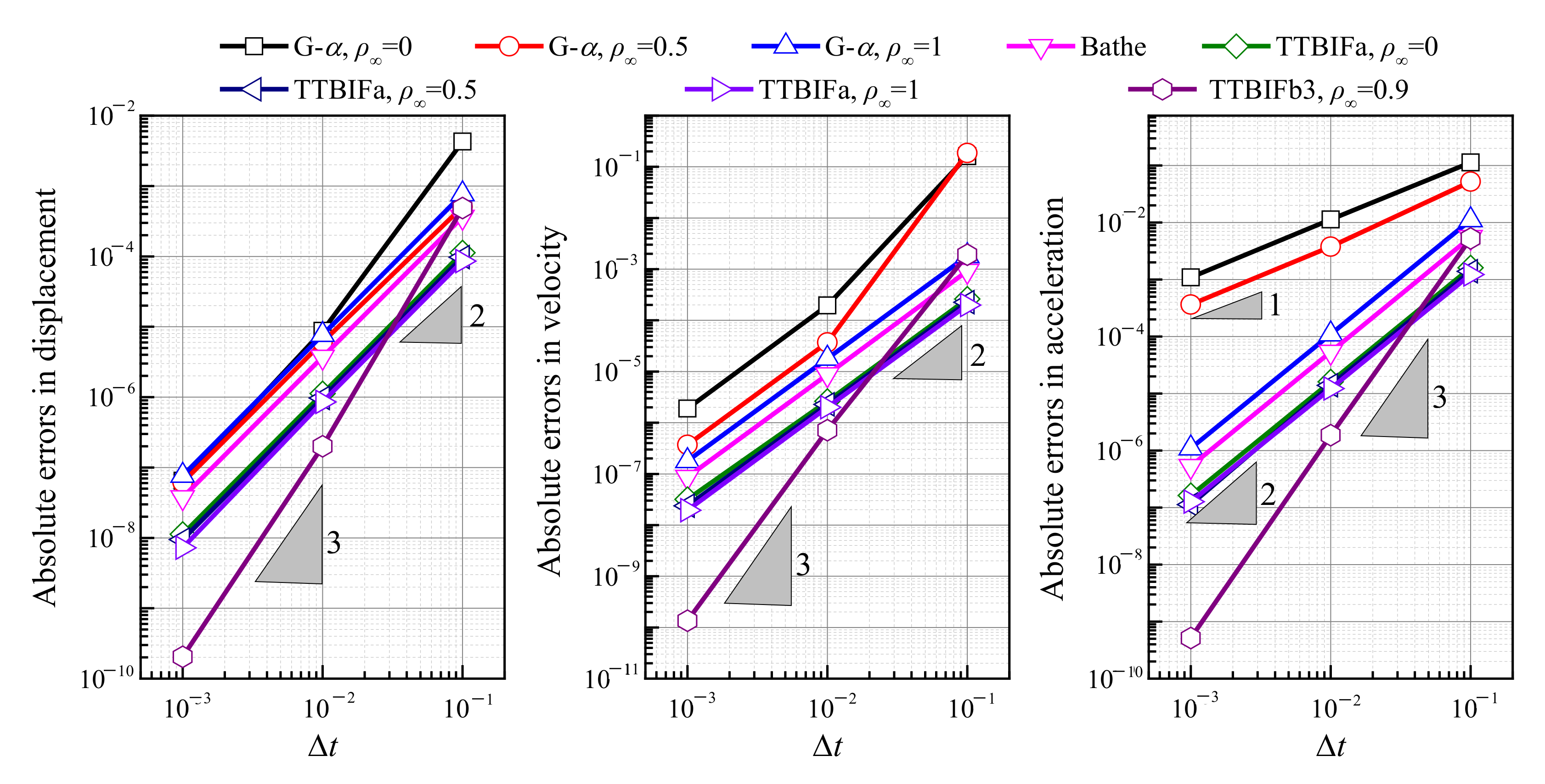
4.3. Convergence Rates
- (1)
- the TTBIFa method is strictly second-order accurate for displacement, velocity, and acceleration, and its computational accuracy can be improved with an increase in ρ∞;
- (2)
- the TTBIFb3 method can be third-order accurate for displacement, velocity, and acceleration;
- (3)
- the generalized-α method (G-α) is first-order accurate for acceleration when ρ∞ < 1.
- (1)
- the low-frequency responses of the TTBIFa are more accurate, and it has the ability to damp out high-frequency modes; therefore, the TTBIFa are applicable to conservative systems and stiff systems;
- (2)
- the low-frequency response accuracy of the TTBIFb2 is low, so the TTBIFb2 is not practical;
- (3)
- the TTBIFb3 has strong numerical dissipation and lower numerical dispersion; hence, the TTBIFb3 is more suitable for damped systems.
- (1)
- (2)
- among these methods, only TTBIF can achieve third-order accuracy for displacement, velocity, and acceleration, and it has numerical dissipation;
- (3)
- (4)
- from the values of and PE, one can see that among the second-order accurate methods, the TTBIFa’s low-frequency accuracy, including amplitude and phase, is the highest, meaning that it can give more accurate predictions when applied to dynamic problems, including structural dynamics and the multibody systems.
5. Numerical Experiments
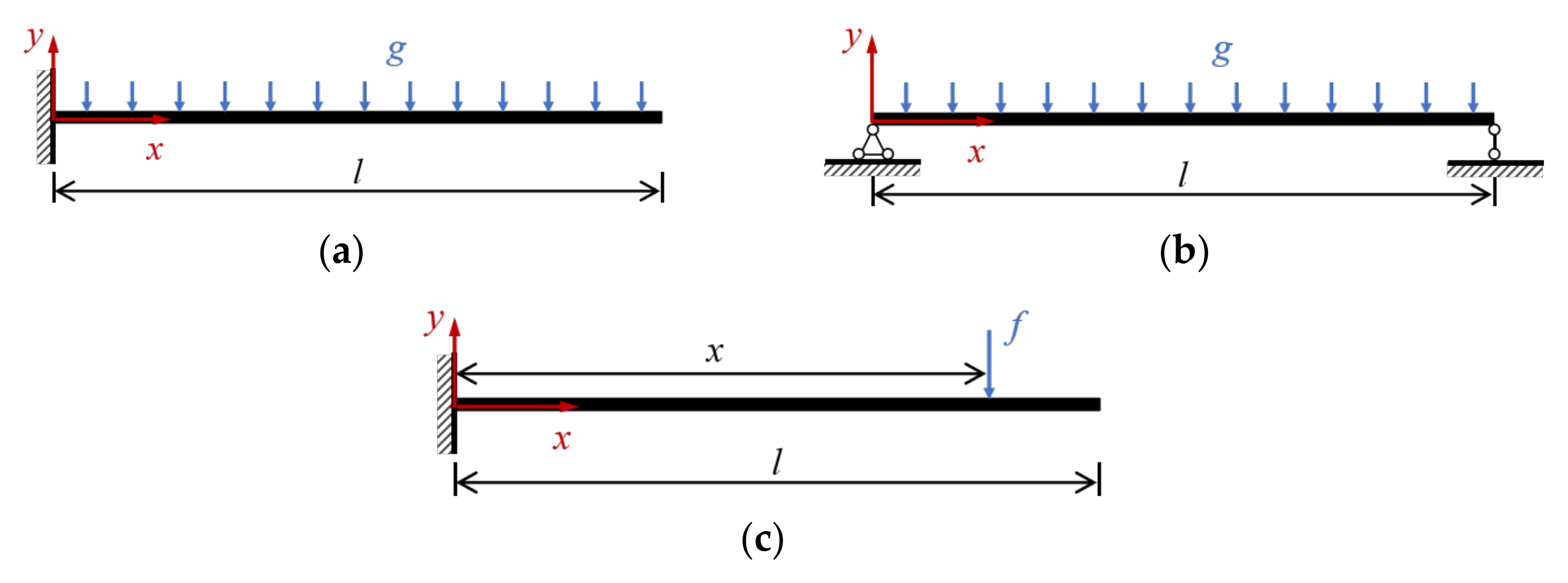
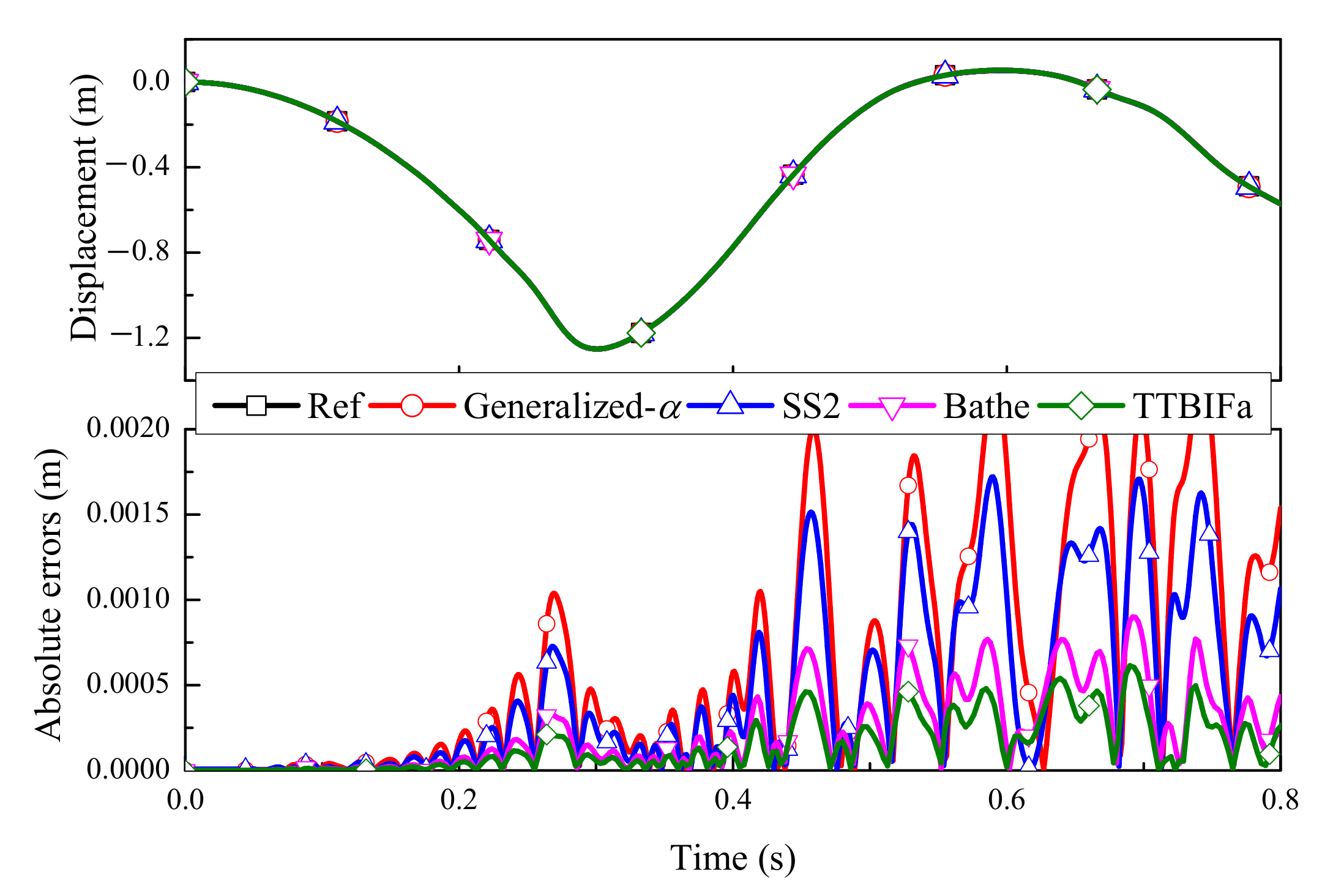
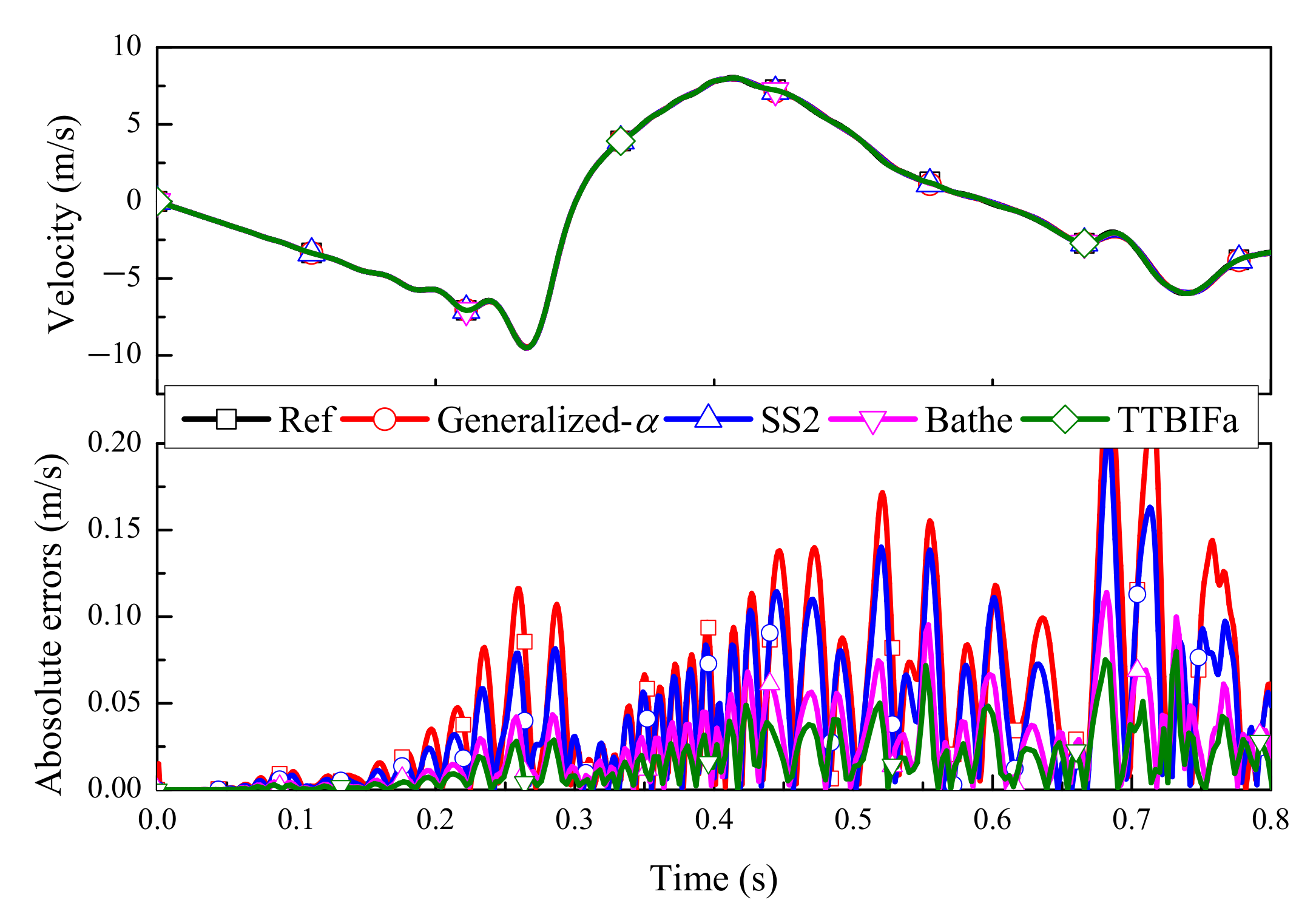
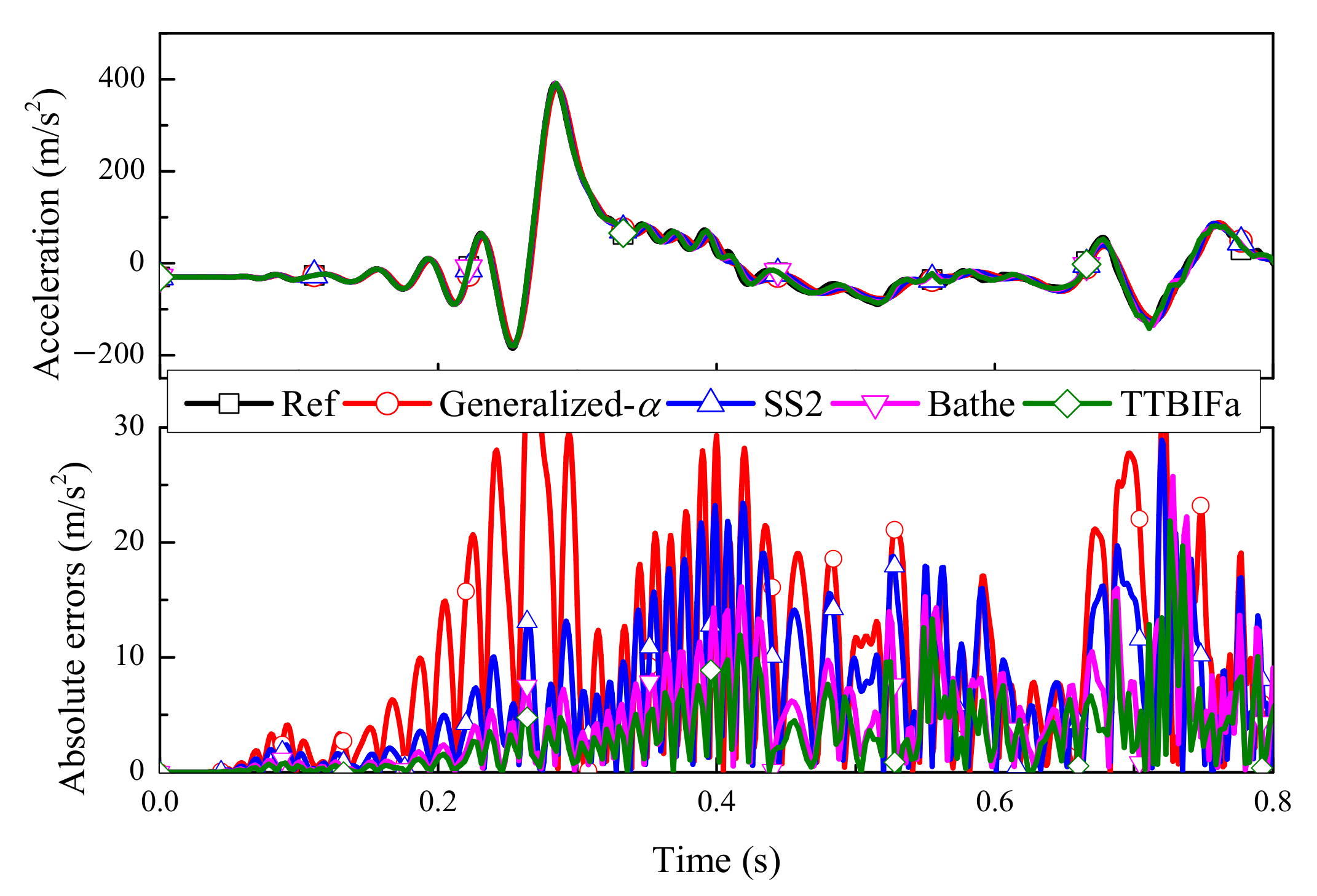
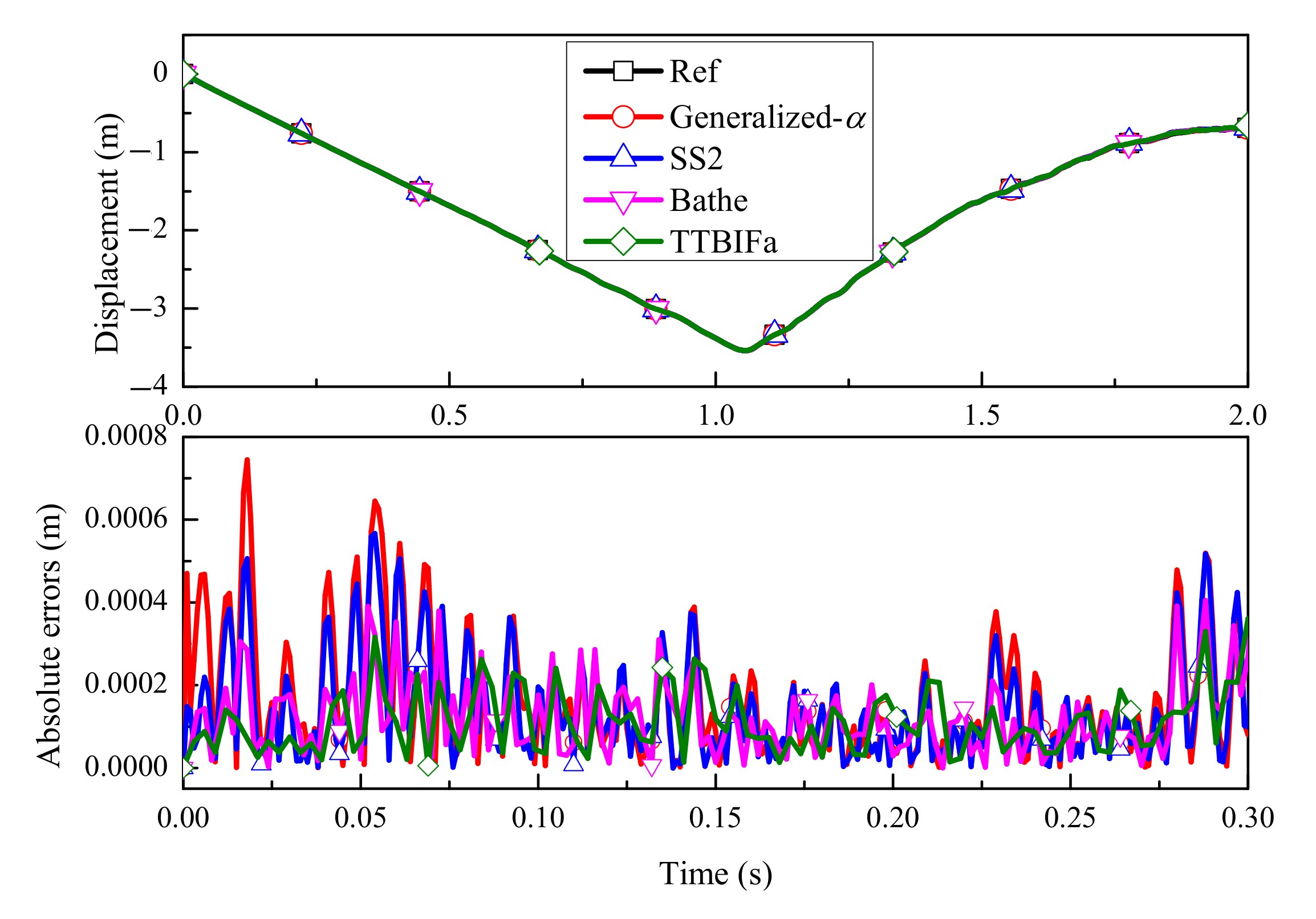
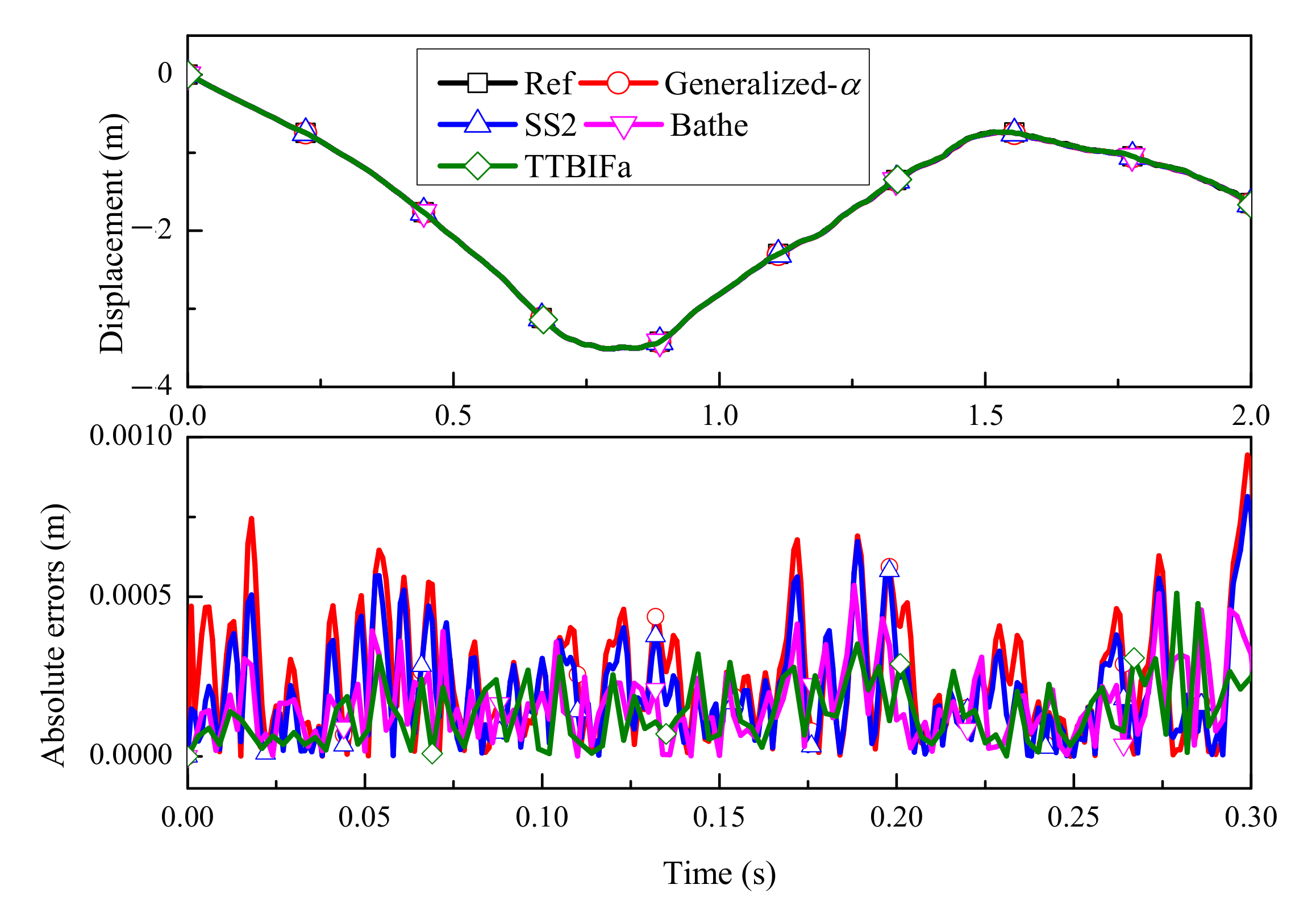
5.1. Flexible Beam
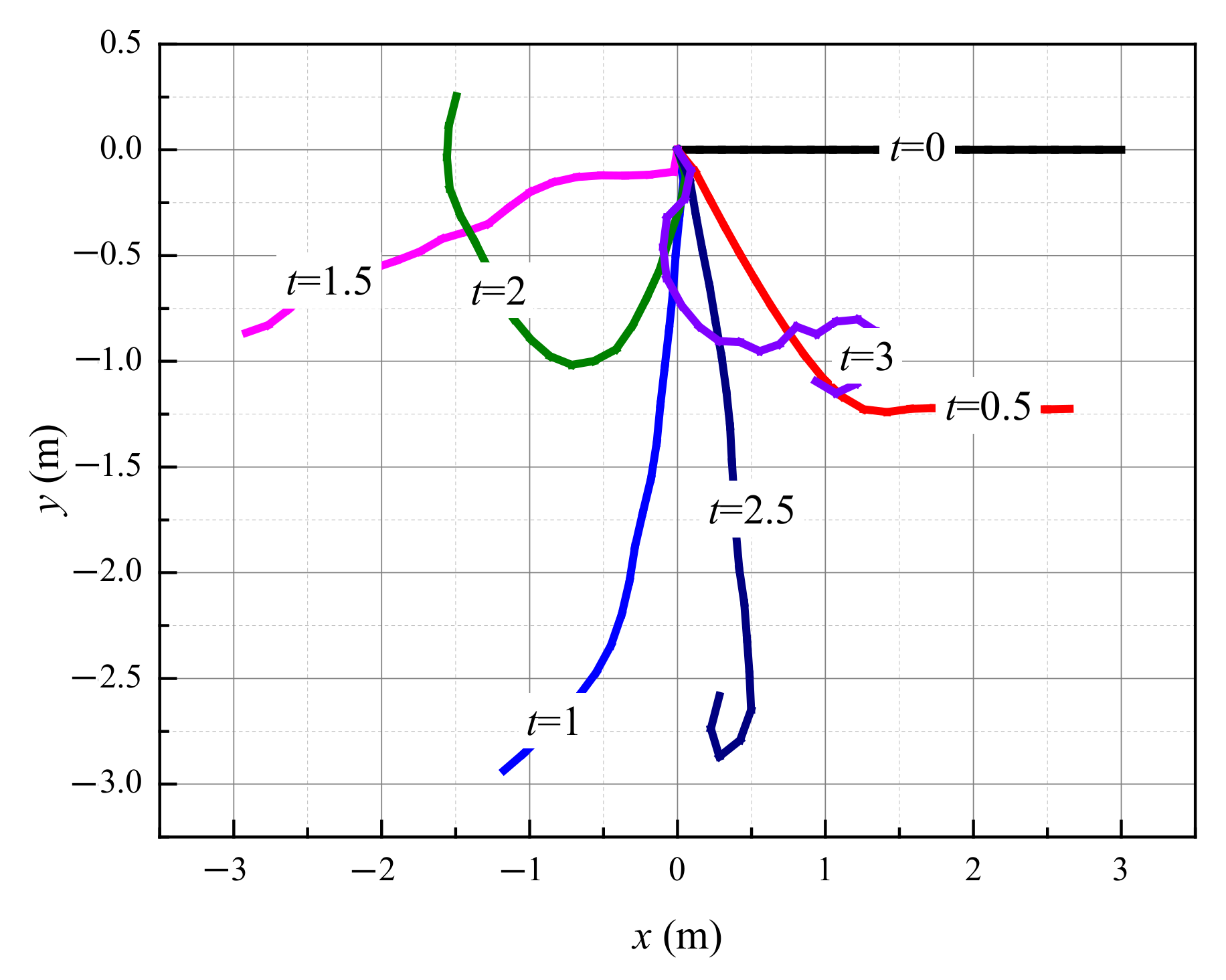
5.2. Slider–Pendulum
5.3. Moving Cable
6. Conclusions
- (1)
- The algorithmic parameter of the TTBIF (γ1) was optimized in this work to minimize local truncation error, yielding two new optimized schemes, the TTBIFa and the TTBIFbn (n = 2,3). The second-order accurate TTBIFa can accurately keep low-frequency information, and all sub-steps share the same effective stiffness matrix. The TTBIFb3 is third-order accurate, and possesses lower period errors than the second-order methods. Since the TTBIFb3 also has high dissipation capability, the TTBIFb3 is more suitable for damped systems.
- (2)
- The effects of algorithmic parameters on stability, dissipation, dispersion, overshoot, and convergence rate for damped and undamped systems were obtained in this work. The investigation is an important theoretical supplement for the TTBIF [39].
- (3)
- (4)
- The numerical experiments demonstrated that the second-order accurate, controllably dissipative, unconditionally stable TTBIFa exhibits advantages in accuracy, dissipation, stability, and energy-conservation, so it seems to be a good candidate for the response analysis of multibody systems.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivations of the Recursion Equation
Appendix B. Effective Stiffness Matrices and Load Vectors of the TTBIF
Appendix C. The Elements of the Amplification Matrix of the TTBIF
References
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Ren, H.; Zhou, P. Implementation details of DAE integrators for multibody system dynamics. J. Dyn. Control 2021, 19, 1–28. (In Chinese) [Google Scholar]
- Wei, Y.; Deng, Z.; Li, Q.; Wang, B. Projected Runge-Kutta methods for constrained Hamiltonian systems. Appl. Math. Mech. Engl. Ed. 2016, 37, 1077–1094. [Google Scholar] [CrossRef]
- Marques, F.; Souto, A.; Flores, P. On the constraints violation in forward dynamics of multibody systems. Multibody Syst. Dyn. 2017, 39, 385–419. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Chen, M. A PID type constraint stabilization method for numerical integration of multibody systems. J. Comput. Nonlinear Dyn. 2011, 6, 044501. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. Nonlinear dynamic analysis of hysteretic mechanical systems by combining a novel rate-independent model and an explicit time integration method. Nonlinear Dyn. 2019, 98, 2879–2901. [Google Scholar] [CrossRef]
- Chang, S.Y. An unusual amplitude growth property and its remedy for structure- dependent integration methods. Comput. Methods Appl. Mech. Eng. 2018, 330, 498–521. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Prentice-Hall: Englewood Cliffs, EC, USA, 1987. [Google Scholar]
- Chung, J.; Lee, J.M. A new family of explicit time integration methods for linear and nonlinear structural dynamics. Int. J. Numer. Methods Eng. 1994, 37, 3961–3976. [Google Scholar] [CrossRef]
- Kovacs, E.; Nagy, A.; Saleh, M. A new stable, explicit, third-order method for diffusion-type problems. Adv. Theory Simul. 2022, 5, 2100600. [Google Scholar] [CrossRef]
- Dong, S. BDF-like methods for nonlinear dynamic analysis. J. Comput. Phys. 2010, 229, 3019–3045. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized –α method. J. Appl. Mech. Trans. ASME 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, H.F.; Zhao, J.C.; Xu, C.Y.; Luo, Z.; Han, Q.K. Rigid-flexible coupling dynamics modeling of spatial crank-slider mechanism based on absolute node coordinate formulation. Mathematics 2022, 10, 881. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef] [Green Version]
- Noh, G.; Bathe, K.J. For direct time integrations: A comparison of the Newmark and ρ∞-Bathe schemes. Comput. Struct. 2019, 225, 106079. [Google Scholar] [CrossRef]
- Arnold, M.; Hante, S. Implementation details of a generalized –α differential-algebraic equation Lie group method. J. Comput. Nonlinear Dyn. 2017, 12, 021002. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. Implementation of HHT algorithm for numerical integration of multibody dynamics with holonomic constraints. Nonlinear Dyn. 2015, 80, 817–825. [Google Scholar] [CrossRef]
- Bruls, O.; Cardona, A.; Arnold, M. Lie group generalized–α time integration of constrained flexible multibody systems. Mech. Mach. Theory 2012, 48, 121–137. [Google Scholar] [CrossRef]
- Wang, K.; Tian, Q.; Hu, H.Y. Non-smooth spatial frictional contact dynamics of multibody systems. Multibody Syst. Dyn. 2021, 53, 1–27. [Google Scholar] [CrossRef]
- Sherif, K.; Nachbagauer, K.; Steiner, W.; Laub, T. A modified HHT method for the numerical simulation of rigid body rotations with Euler parameters. Multibody Syst. Dyn. 2019, 46, 181–202. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.M.; Xing, Y.F. A three-parameter single-step time integration method for structural dynamic analysis. Acta Mech. Sin. 2019, 35, 112–128. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Xue, T.; Tamma, K.K.; Maxam, D.; Qin, G. A three-time-level a posteriori error estimator for GS4-2 framework: Adaptive time stepping for second-order transient systems. Comput. Methods Appl. Mech. Eng. 2021, 384, 113920. [Google Scholar] [CrossRef]
- Lavrencic, M.; Brank, B. Comparison of numerically dissipative schemes for structural dynamics: Generalized- alpha vs. energy-decaying methods. Thin-Walled Struct. 2020, 157, 107075. [Google Scholar] [CrossRef]
- Zhang, H.M.; Xing, Y.F.; Ji, Y. An energy-conserving and decaying time integration method for general nonlinear dynamics. Int. J. Numer. Methods Eng. 2020, 121, 925–944. [Google Scholar] [CrossRef]
- Wu, B.; Pan, T.L.; Yang, H.W.; Xie, J.Z.; Spencer, B.F. Energy-consistent integration method and its application to hybrid testing. Earthq. Eng. Struct. Dyn. 2020, 49, 415–433. [Google Scholar] [CrossRef]
- Zhang, H.M.; Zhang, R.S.; Masarati, P. Improved second-order unconditionally stable schemes of linear multi-step and equivalent single-step integration methods. Comput. Mech. 2021, 67, 289–313. [Google Scholar] [CrossRef]
- Zhang, J. A-stable linear two-step time integration methods with consistent starting and their equivalent single-step and their equivalent single-step methods in structural dynamics analysis. Int. J. Numer. Methods Eng. 2021, 122, 2312–2359. [Google Scholar] [CrossRef]
- Zhang, H.M.; Zhang, R.S.; Zanoni, A.; Masarati, P. Performance of implicit A-stable time integration methods for multibody system dynamics. Multibody Syst. Dyn. 2022, 54, 263–301. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y.F. A two-step time integration method with desirable stability for nonlinear structural dynamics. Eur. J. Mech. A Solids 2022, 94, 104582. [Google Scholar] [CrossRef]
- Bank, R.E.; Coughran, W.M.; Fichtner, W.; Gross, E.H.; Kent, S.R.; Rose, D.J. Transient simulation of silicon devices and circuits. IEEE Trans. Electron. Devices 1985, 32, 1992–2007. [Google Scholar] [CrossRef]
- Bathe, K.J.; Baig, M.M. On a composite implicit time integration procedure for nonlinear dynamics. Comput. Struct. 2005, 83, 2513–2524. [Google Scholar] [CrossRef]
- Chandra, Y.; Zhou, Y.; Stanciulescu, I.; Eason, T.; Spottswood, S. A robust composite time integration scheme for snap-through problems. Comput. Mech. 2015, 55, 1041–1056. [Google Scholar] [CrossRef] [Green Version]
- Wen, W.B.; Wei, K.; Lei, H.S.; Duan, S.Y.; Fang, D.N. A novel sub-step composite implicit time integration scheme for structural dynamics. Comput. Struct. 2017, 182, 176–186. [Google Scholar] [CrossRef]
- Xing, Y.F.; Ji, Y.; Zhang, H.M. On the construction of a type of composite time integration methods. Comput. Struct. 2019, 221, 157–178. [Google Scholar] [CrossRef]
- Li, J.Z.; Yu, K.P. A simple truly self-starting and L-stable integration algorithm for structural dynamics. Int. J. Appl. Mech. 2020, 12, 2050119. [Google Scholar] [CrossRef]
- Malakiyeh, M.M.; Shojaee, S.; Bathe, K.J. The Bathe time integration method revisited for prescribing desired numerical dissipation. Comput. Struct. 2019, 212, 289–298. [Google Scholar] [CrossRef]
- Noh, G.; Bathe, J. The Bathe time integration method with controllable spectral radius: The ρ∞-Bathe method. Comput. Struct. 2019, 212, 299–310. [Google Scholar] [CrossRef]
- Kim, W.; Choi, S.Y. An improved implicit time integration algorithm: The generalized composite time integration algorithm. Comput. Struct. 2018, 196, 341–354. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y.F. An optimized three-sub-step composite time integration method with controllable numerical dissipation. Comput. Struct. 2020, 231, 106210. [Google Scholar] [CrossRef]
- Li, J.Z.; Zhao, R.; Yu, K.P. Directly self-starting higher-order implicit integration algorithms with flexible dissipation control for structural dynamics. Comput. Methods Appl. Mech. Eng. 2022, 389, 114274. [Google Scholar] [CrossRef]
- Liu, T.H.; Huang, F.L.; Wen, W.B.; He, X.H.; Duan, S.Y.; Fang, D.N. Further insights of a composite implicit time integration scheme and its performances on linear seismic response analysis. Eng. Struct. 2021, 241, 112490. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Lei, S.; Liu, T.H.; Zhou, D.; Wen, W.B. Performance of a three-sub-step time integration method on structural nonlinear seismic analysis. Math. Probl. Eng. 2021, 2021, 1–20. [Google Scholar]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials. Nonlinear Dyn. 2018, 93, 1647–1669. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Processing 2021, 146, 106984. [Google Scholar] [CrossRef]
- Wen, Y.K. Method for random vibration of hysteretic systems. ASCE- J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.H.; Liu, D.H. Accuracy of a composite implicit time integration scheme for structural dynamics. Int. J. Numer. Methods Eng. 2017, 109, 368–406. [Google Scholar] [CrossRef]
- Maxam, D.J.; Tamma, K.K. A re-evaluation of overshooting in time integration schemes: The neglected effect of physical damping in the starting procedure. Int. J. Numer. Methods Eng. 2022, 123, 2683–2704. [Google Scholar] [CrossRef]
- Berzeri, M.; Shabana, A.A. Development on simple models for the elastic forces in the absolute nodal co-ordinate formulation. J. Sound Vib. 2000, 235, 539–565. [Google Scholar] [CrossRef]
- Zhang, H.M.; Zhang, R.S.; Xing, Y.F.; Masarati, P. On the optimization of n-sub-step composite time integration methods. Nonlinear Dyn. 2020, 102, 1939–1962. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, J.Q.; Liu, J.P.; Ren, G.X. An efficient multibody dynamic model of arresting cable systems based on ALE formulation. Mech. Mach. Theory 2020, 151, 103892. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y.F.; Wiercigroch, M. An unconditionally stable time integration method with controllable dissipation for second-order nonlinear dynamics. Nonlinear Dyn. 2021, 53, 1951–1960. [Google Scholar] [CrossRef]
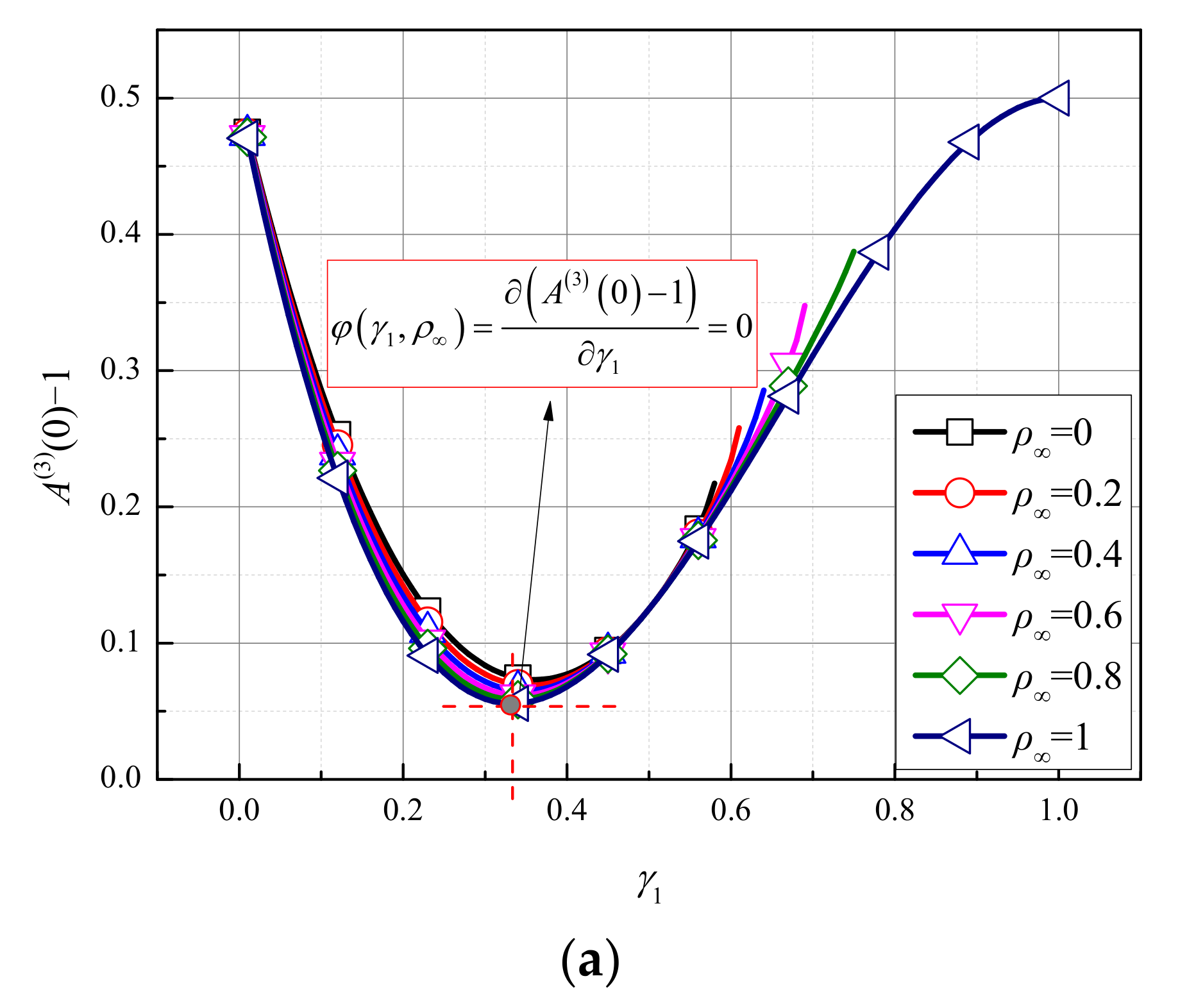
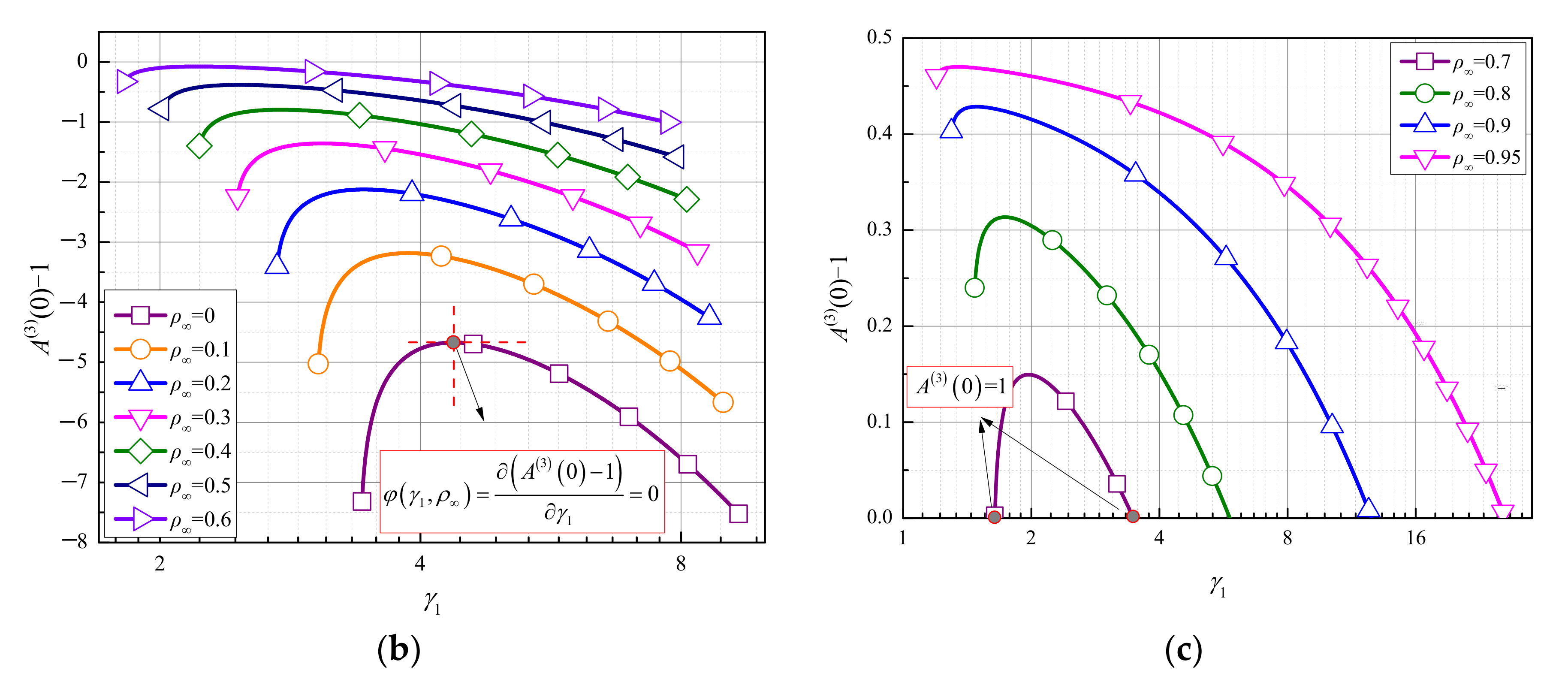



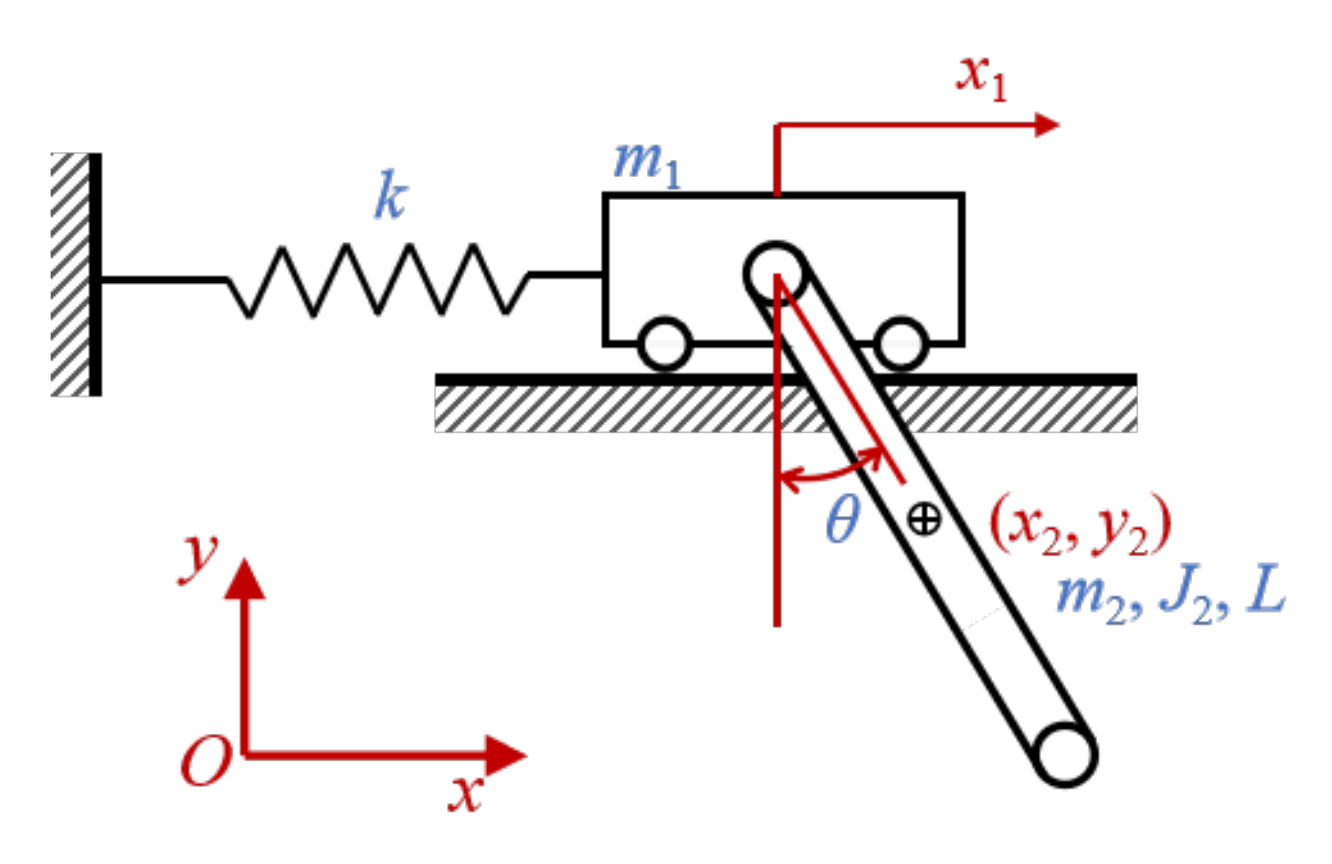
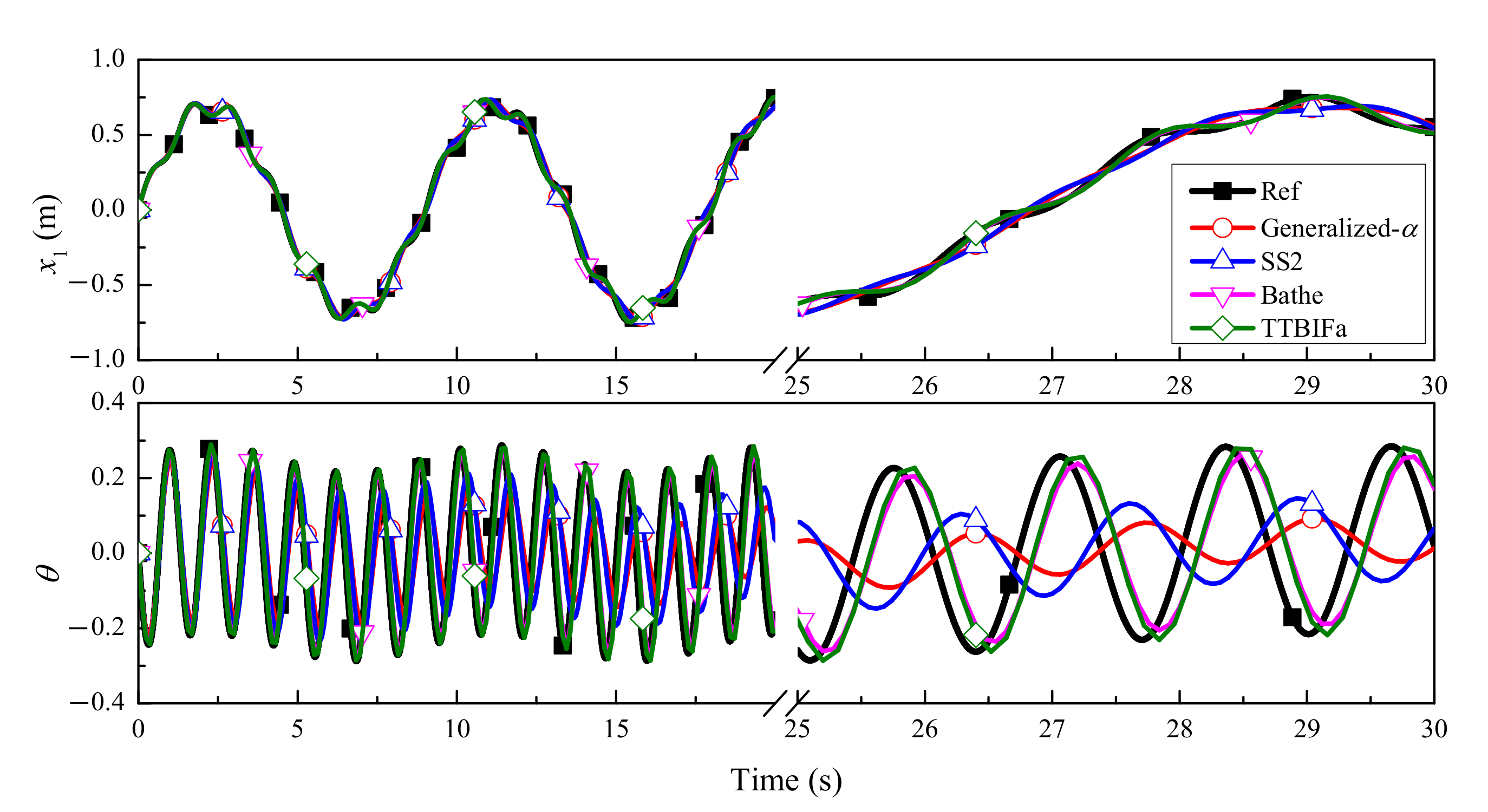
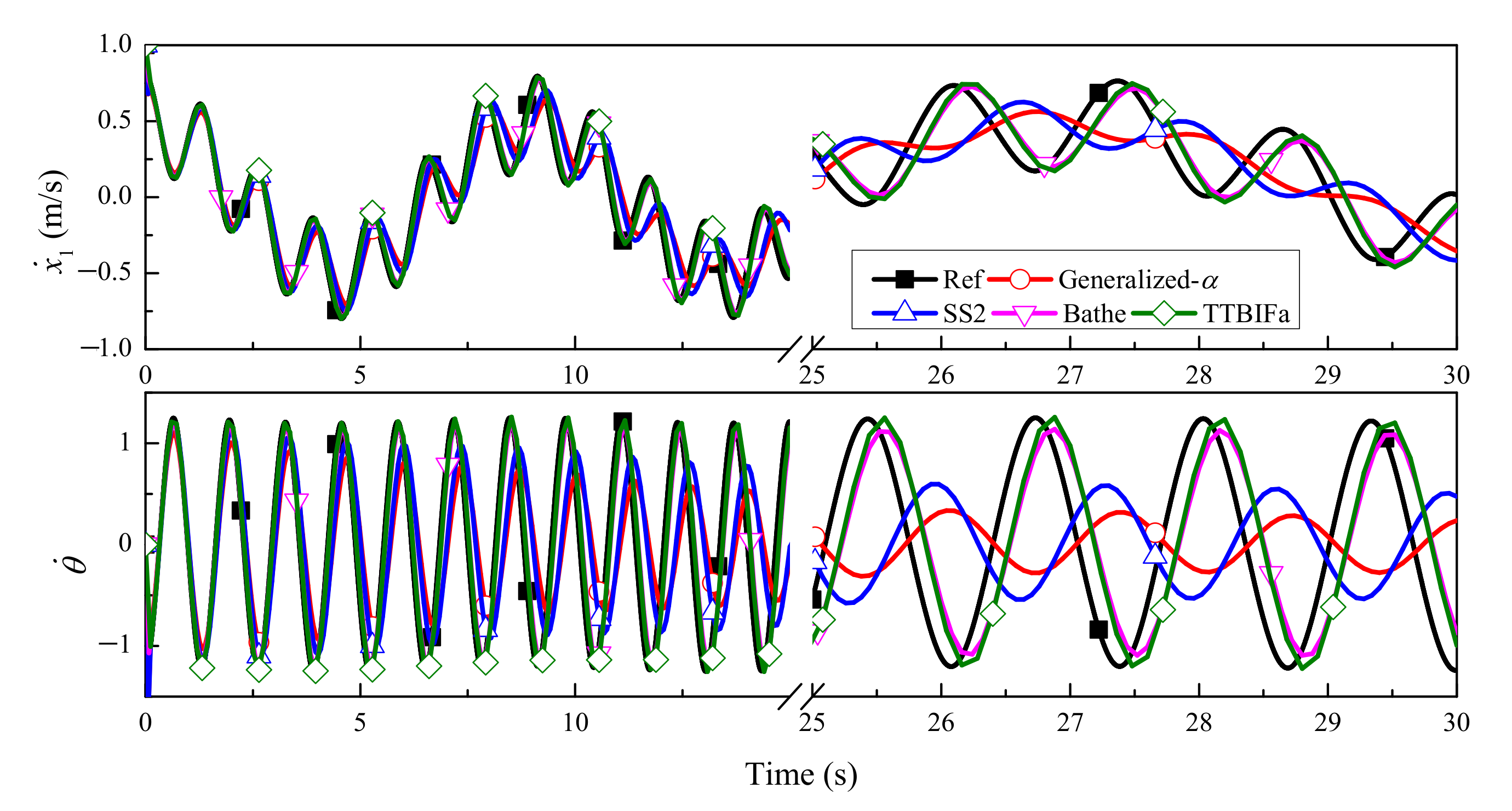
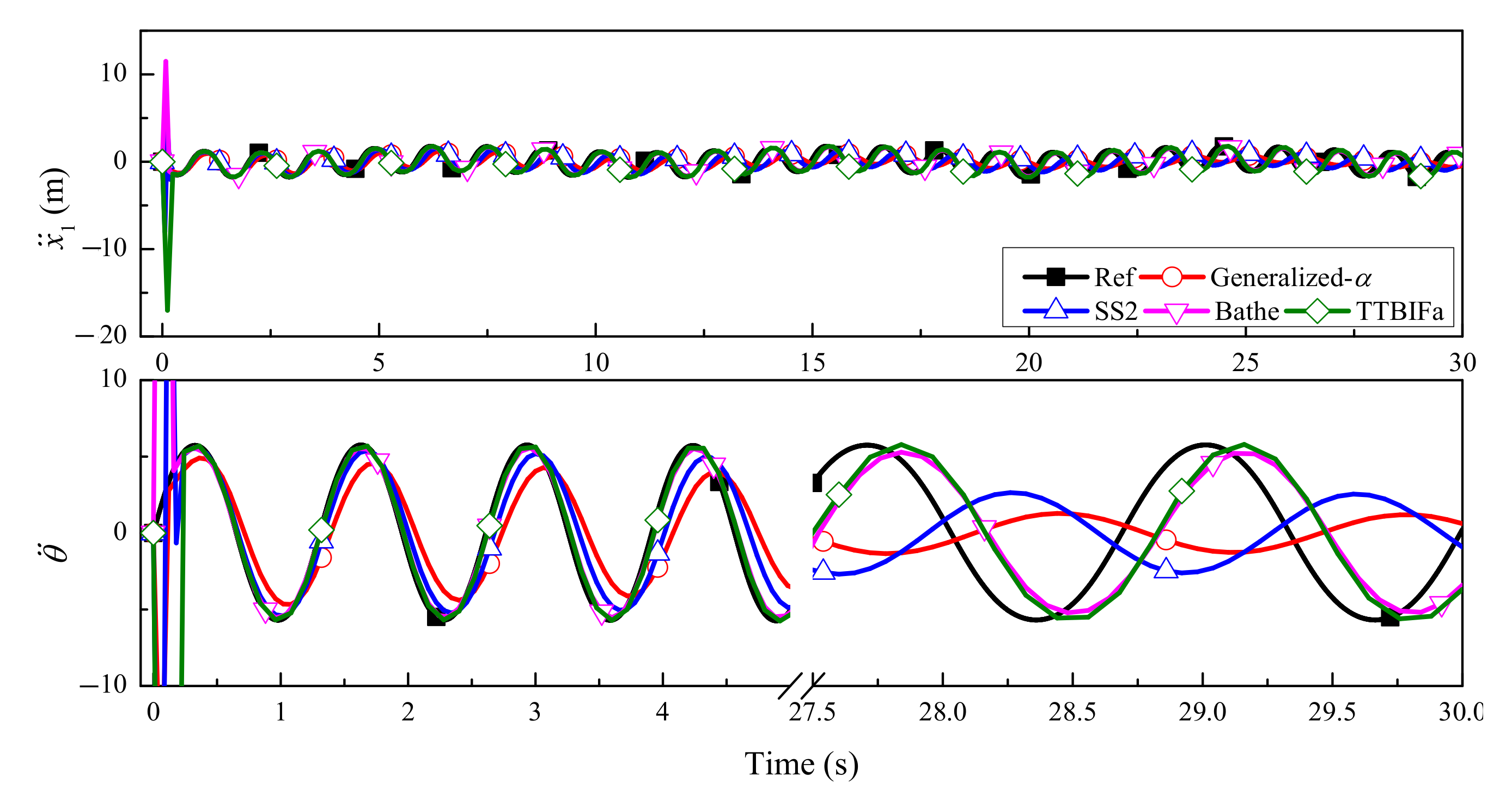


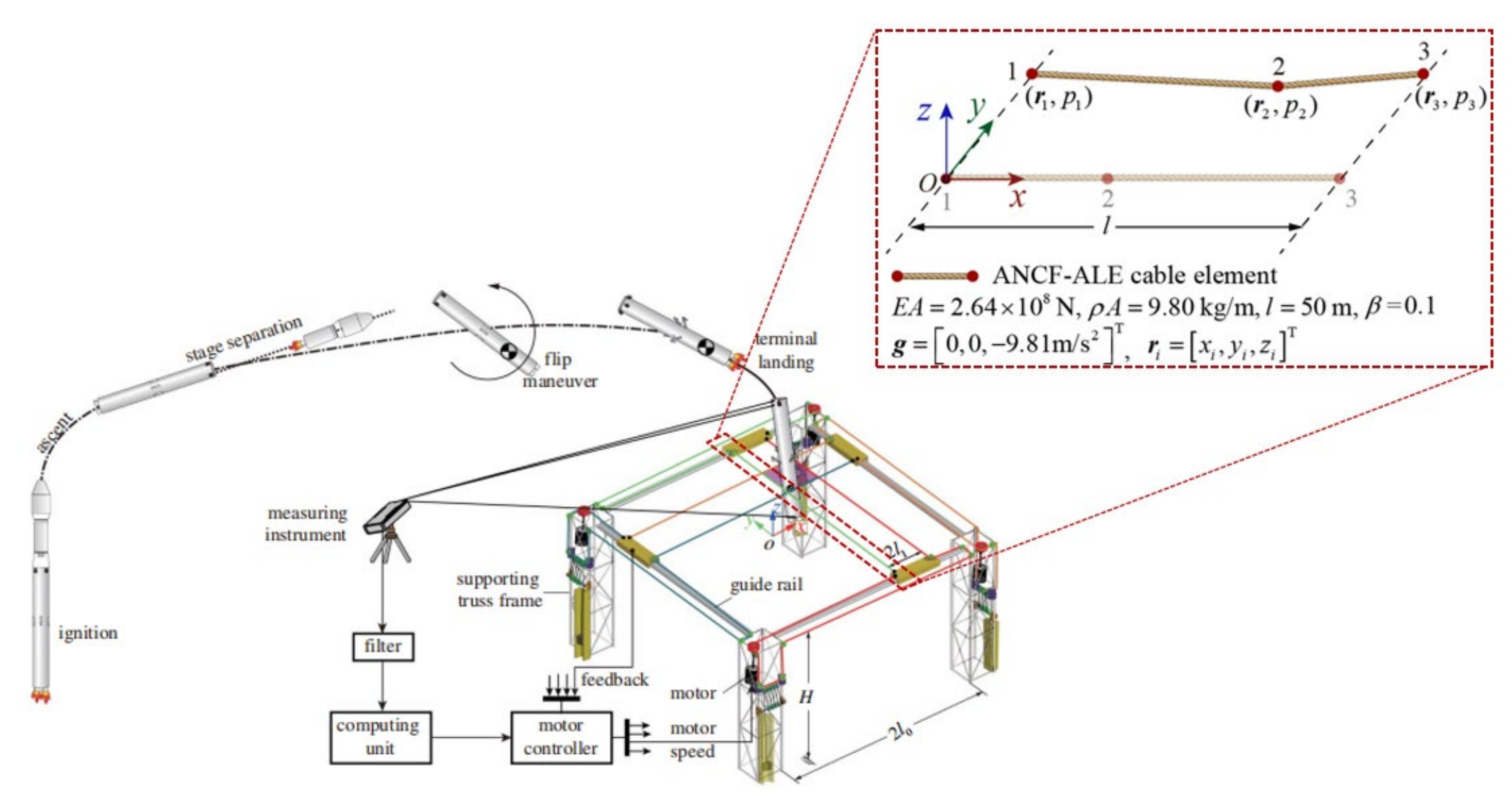
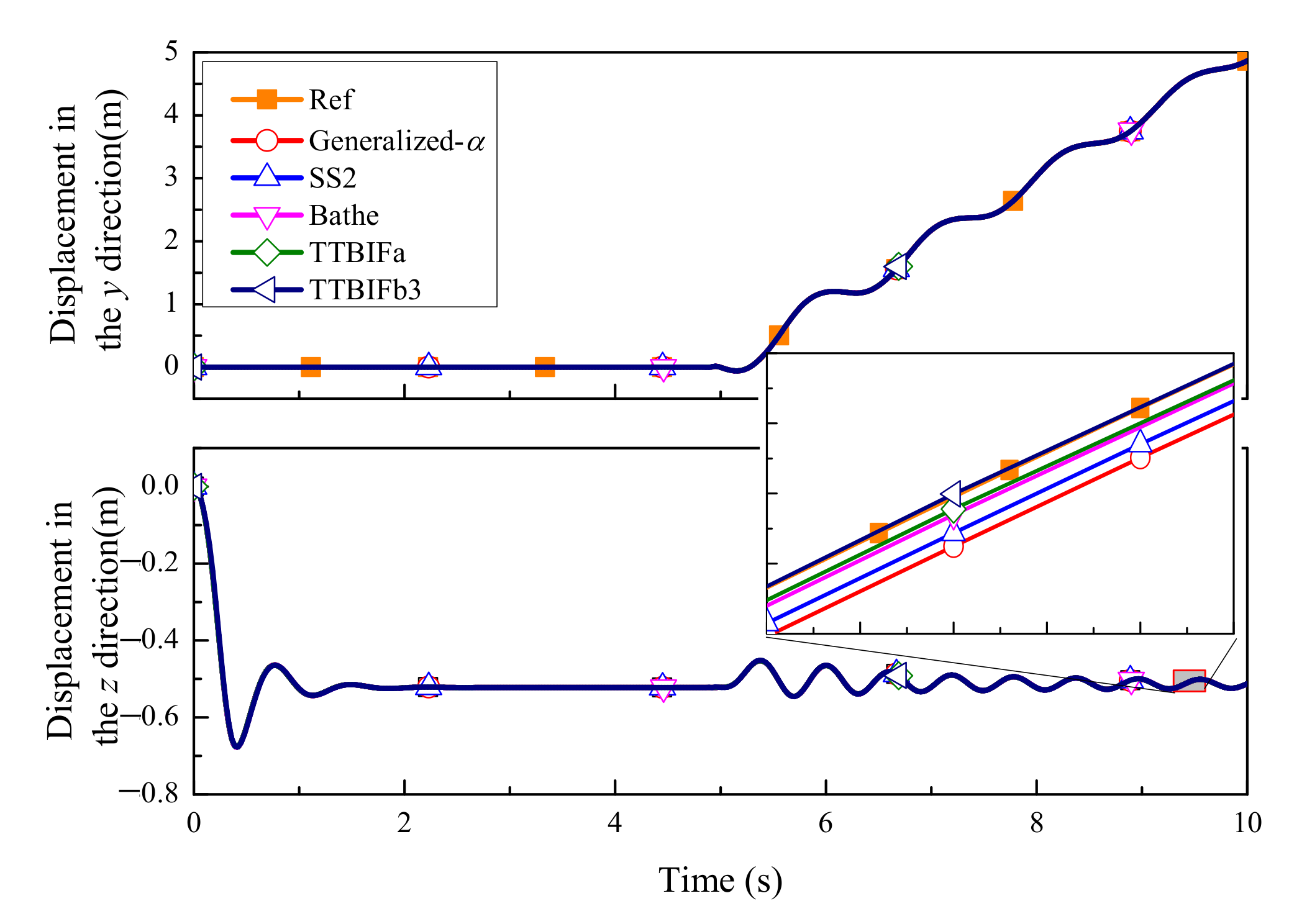
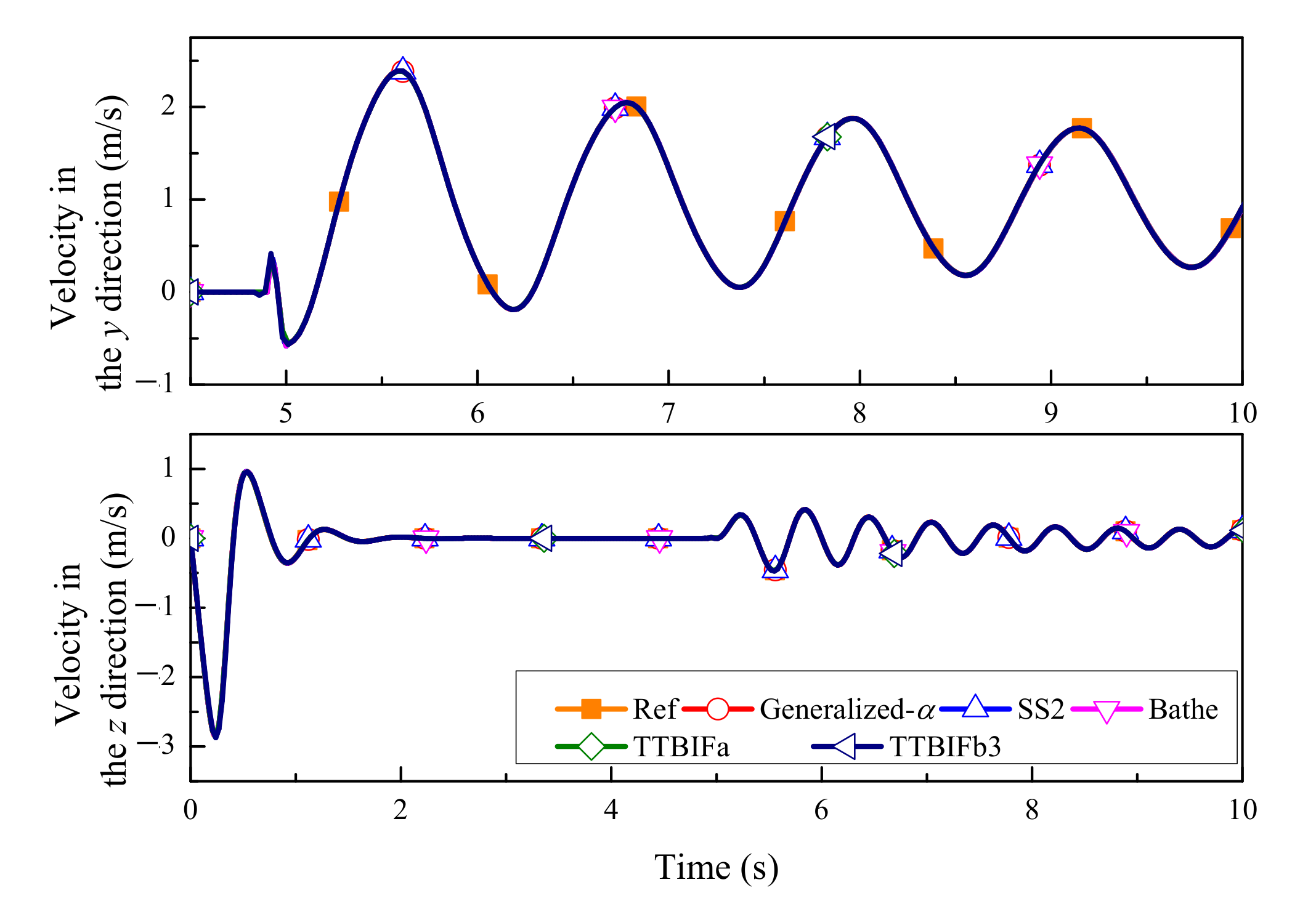
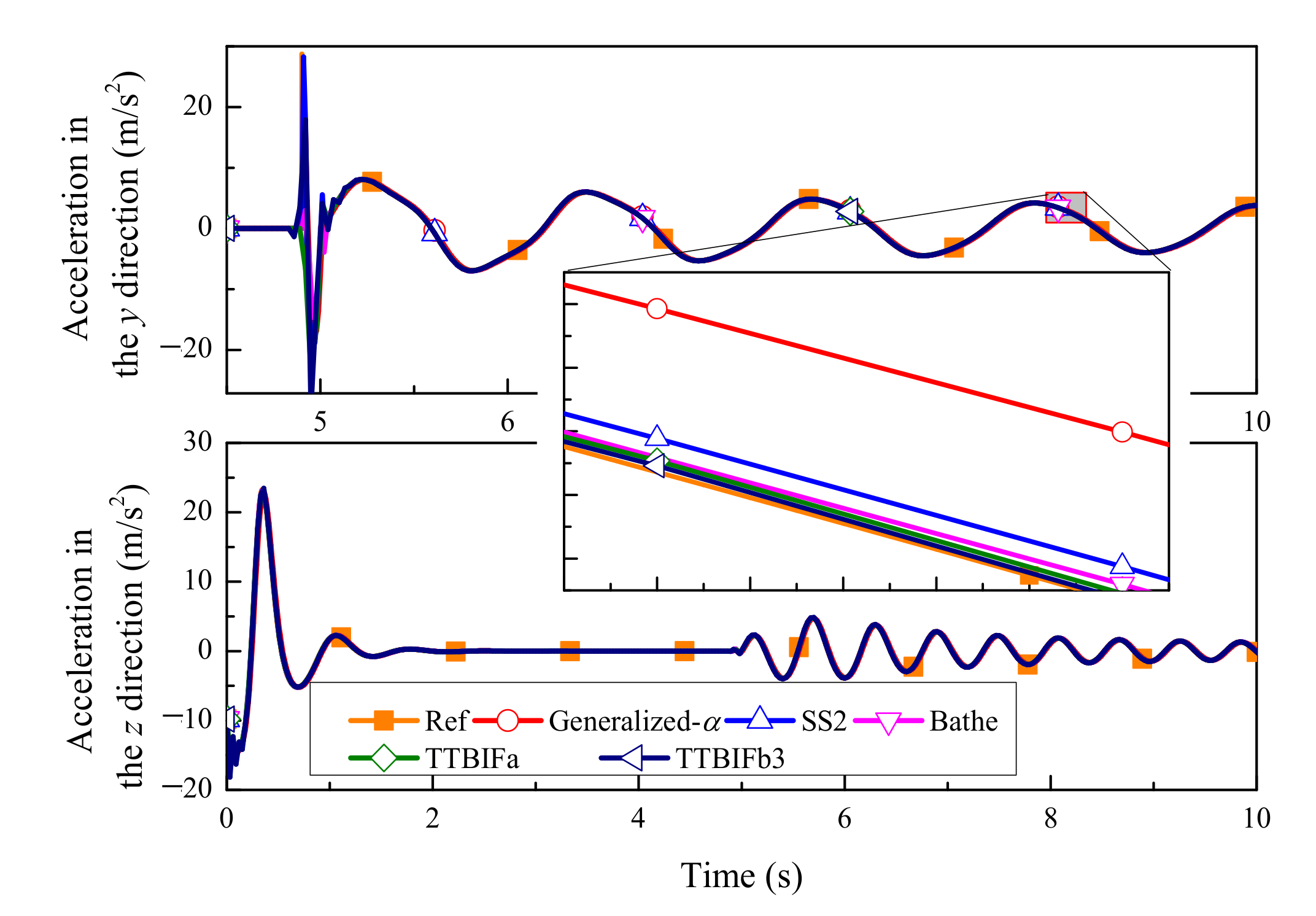
| ρ∞ | γ1 | γ1 − 2θ3 | n (Accuracy Order) | φ(γ1, ρ∞) = 0 | A(3)(0) = 1 |
|---|---|---|---|---|---|
| 0 | 0.360850612858797128269166267064 | −3.3307 × 10−16 | 2 | Yes | No |
| 0.1 | 0.357238916409318421781603138200 | 2.7756 × 10−16 | 2 | Yes | No |
| 0.2 | 0.353891613236446119002830462643 | 3.8858 × 10−16 | 2 | Yes | No |
| 0.3 | 0.350771031685691357865125234250 | −5.5511 × 10−17 | 2 | Yes | No |
| 0.4 | 0.347847215754394957955227697970 | −1.1102 × 10−16 | 2 | Yes | No |
| 0.5 | 0.345095922844178112406277539906 | 0 | 2 | Yes | No |
| 0.6 | 0.342497237181383015615320747048 | 1.6653 × 10−16 | 2 | Yes | No |
| 0.7 | 0.340034583544953015899346977758 | 1.6653 × 10−16 | 2 | Yes | No |
| 0.8 | 0.337694009358335747749068721842 | 0 | 2 | Yes | No |
| 0.9 | 0.335463651513773966300486501975 | 2.2204 × 10−16 | 2 | Yes | No |
| 1 | 1/3 | 1.6653 × 10−16 | 2 | Yes | No |
| ρ∞ | γ1 | γ1 − 2θ3 | n (Accuracy Order) | φ (γ1, ρ∞) = 0 | A(3)(0) = 1 |
|---|---|---|---|---|---|
| 0 | 4.37120019471008016525828007444 | 1.7764 × 10−15 | 2 | Yes | No |
| 0.1 | 3.86720615297079833146530716573 | 0 | 2 | Yes | No |
| 0.2 | 3.44197544571550477178258216569 | −1.7764 × 10−15 | 2 | Yes | No |
| 0.3 | 3.07637810817689875070626896811 | 3.9968 × 10−15 | 2 | Yes | No |
| 0.4 | 2.75641330487022065008264507216 | 2.6645 × 10−15 | 2 | Yes | No |
| 0.5 | 2.47130235794770540209427935717 | −7.1054 × 10−15 | 2 | Yes | No |
| 0.6 | 2.21211453543800466240456025712 | −8.8818 × 10−16 | 2 | Yes | No |
| 0.7 | 1.64139639997267794413460251235 | 9.1071 | 3 | No | Yes |
| 3.47338081413162491628554562340 | 2.1307 | 3 | No | Yes | |
| 1.97043992476900261510531844803 | 2.6645 × 10−15 | 2 | Yes | No | |
| 0.8 | 5.85462097569634387639325723285 | 4.7010 | 3 | No | Yes |
| 1.73618888723806906658432806893 | −1.7097 × 10−14 | 2 | Yes | No | |
| 0.9 | 12.6079265663953545839603975764 | 11.5479 | 3 | No | Yes |
| 1.49018874467779463098199628280 | 3.7748 × 10−15 | 2 | Yes | No | |
| 0.95 | 25.9730301544759925036487402394 | 24.9458 | 3 | No | Yes |
| 1.34386843962051960588155452569 | 3.0198 × 10−14 | 2 | Yes | No |
| Method | Number of Sub-Step | Dissipation | Accuracy (ξ ≠ 0, f ≠ 0) | Low-Frequency (ξ = 0, δΩ = 1, ρ∞ = 0) | Scope of Application | ||||
|---|---|---|---|---|---|---|---|---|---|
| Dis. | Vel. | Acc. | PE | ODEs | DAEs | ||||
| Generalized-α [12] | 1 | A-stability | 2 | 2 | 1 | 0.06118 | 0.24744 | Yes | Yes |
| Bathe [31] | 2 | L-stability | 2 | 2 | 2 | 0.01214 | 0.10516 | Yes | Yes |
| ρ∞-Bathe [37] | 2 | A-stability | 2 | 2 | 2 | 0.01214 | 0.10516 | Yes | No |
| Kim [38] | 2 | A-stability | 2 | 2 | 2 | 0.01214 | 0.10516 | Yes | No |
| TTBDF [32] | 3 | L-stability | 2 | 2 | 2 | 0.00213 | 0.11003 | Yes | No |
| TTBIFa | 3 | A-stability | 2 | 2 | 2 | 0.00108 | 0.10479 | Yes | Yes |
| TTBIFb3 | 3 | 3 | 3 | / | / | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Zhang, H.; Xing, Y. New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems. Mathematics 2022, 10, 2375. https://doi.org/10.3390/math10142375
Ji Y, Zhang H, Xing Y. New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems. Mathematics. 2022; 10(14):2375. https://doi.org/10.3390/math10142375
Chicago/Turabian StyleJi, Yi, Huan Zhang, and Yufeng Xing. 2022. "New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems" Mathematics 10, no. 14: 2375. https://doi.org/10.3390/math10142375
APA StyleJi, Y., Zhang, H., & Xing, Y. (2022). New Insights into a Three-Sub-Step Composite Method and Its Performance on Multibody Systems. Mathematics, 10(14), 2375. https://doi.org/10.3390/math10142375







