Mathematical Model and Numerical Simulation Study of the Mining Area with Multiple Air Leakage Paths
Abstract
:1. Introduction
2. Oxygen Concentration Field Model in the Mining Area
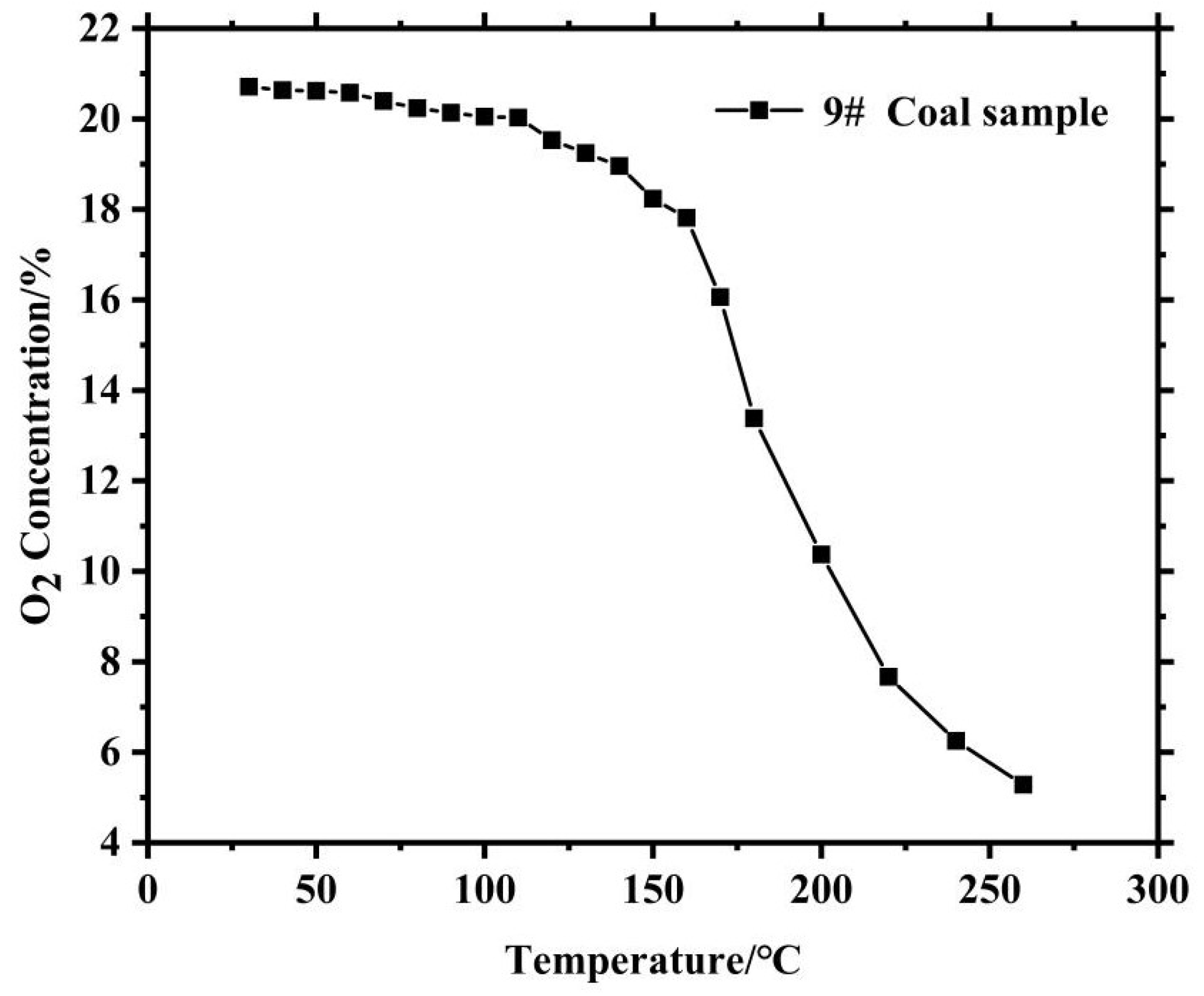
2.1. Programmed Warming Experiment and Result Analysis
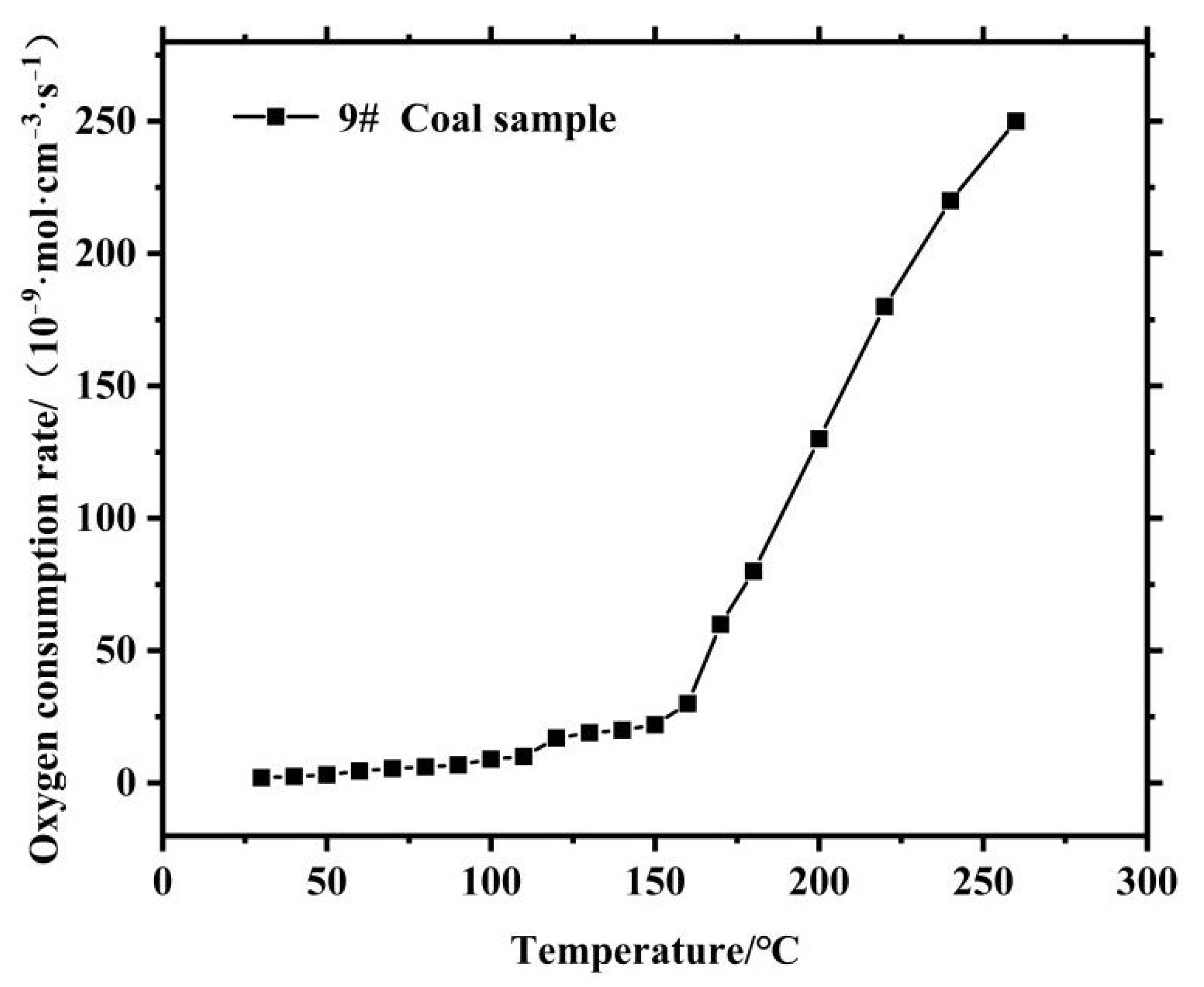
2.2. Coupled Model of Oxygen Consumption Rate of Coal Relics
- —Standard oxygen consumption rate, mol/(cm3/s);
- —Gas flow rate, cm3/min;
- —Fresh air flow oxygen concentration, 9.375 mol/m3;
- —Cross-sectional area of the coal sample tank, cm2;
- —Height of the coal sample in the coal sample tank, cm;
- , —Are the inlet and outlet oxygen concentrations of the coal sample tank, respectively, mol/m3.
- —Fresh air flow oxygen mass fraction, 23%.
3. Mathematical Model of the Flow Field in the Mining Area
- —Flow rate of fluid through the porous media area, m3/s;
- —Permeability of porous media, %;
- —Area of porous media overflow cross-section, m2;
- —Aerodynamic viscosity coefficient, Pa·s;
- —Porous media pressure gradient, Pa/m.
- , , —Distance in each direction of the coordinate axis, m;
- , , —Are the air leakage intensity in , and direction components, m3/(m2·s), respectively.
- —Pressure measuring head, m;
- , , —Are the air leakage intensity in , and direction components, m3/(m2·s), respectively.
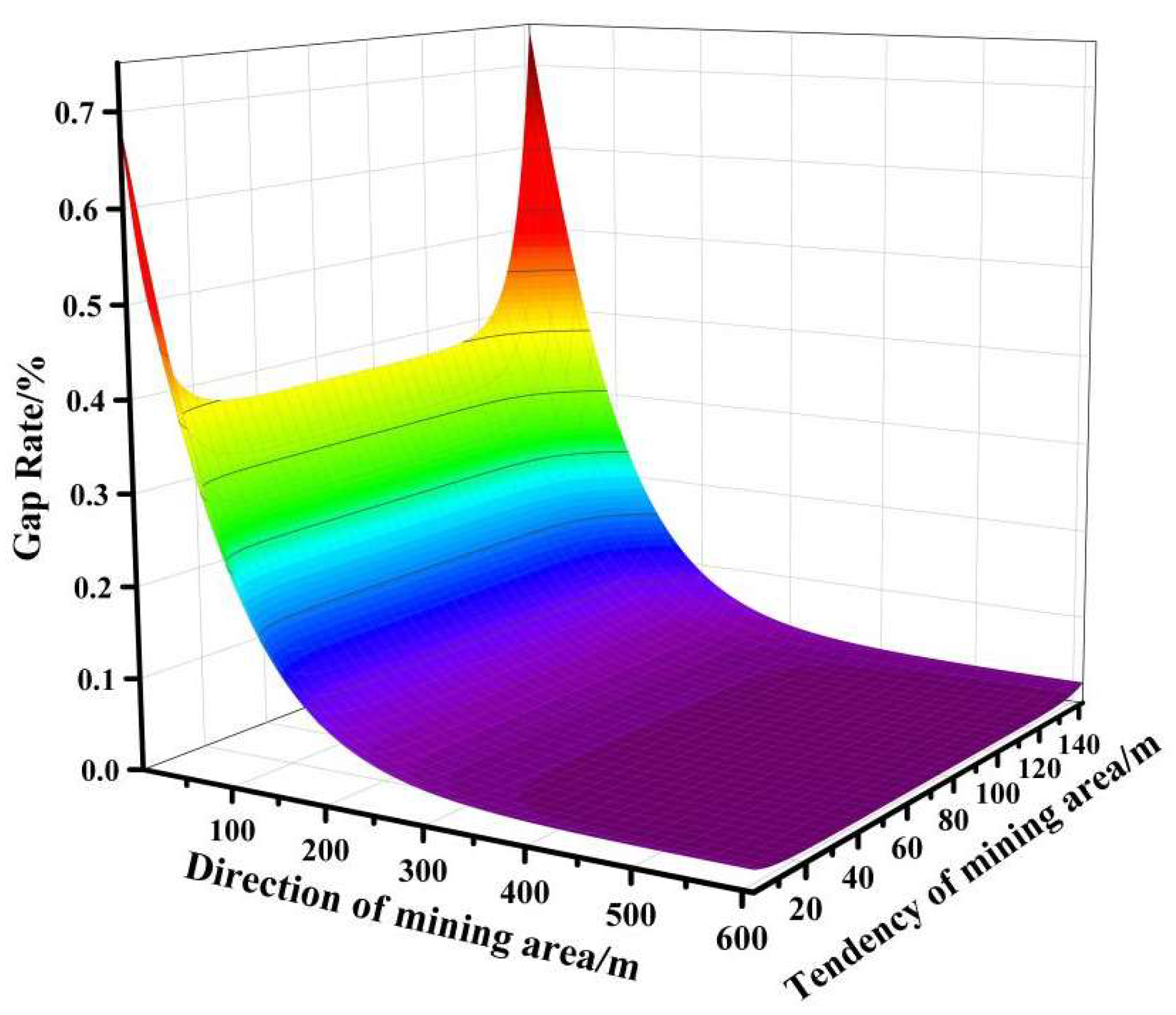
4. Three-Dimensional Distribution Model of Void Ratio in the Mining Area
- —Validity of fractured rock mass, %;
- —Fracture expansion coefficient of broken rock mass.
- —Direct top thickness, m;
- —Mining height or extraction and release height, m;
- —Residual fragmentation and swelling coefficient of the directly top broken rock mass;
- —Length of the basic top breaking rock body, m;
- —The distance towards the upper offset of the x-axis origin, m
- —Tendency distance of mining area, m;
- —Distance from the origin of the y-axis on the tendency offset, m.
- —Void ratio of loose media subjected to axial stress, %;
- —Relative axial stress, MPa;
- —Regression coefficient;
- —Vacancy of crushed rock before axial stress, %.
- —Capacity weight of rock fall, N/m3, generally 2 × 104~3 × 104 N/m3;
- —1 MPa.
- —−0.0488 when the rock fall is shale, −0.025 when the rock fall is mudstone, −0.0254 when the rock fall is sandstone;
- —Coal seam dip angle.
5. Numerical Simulation
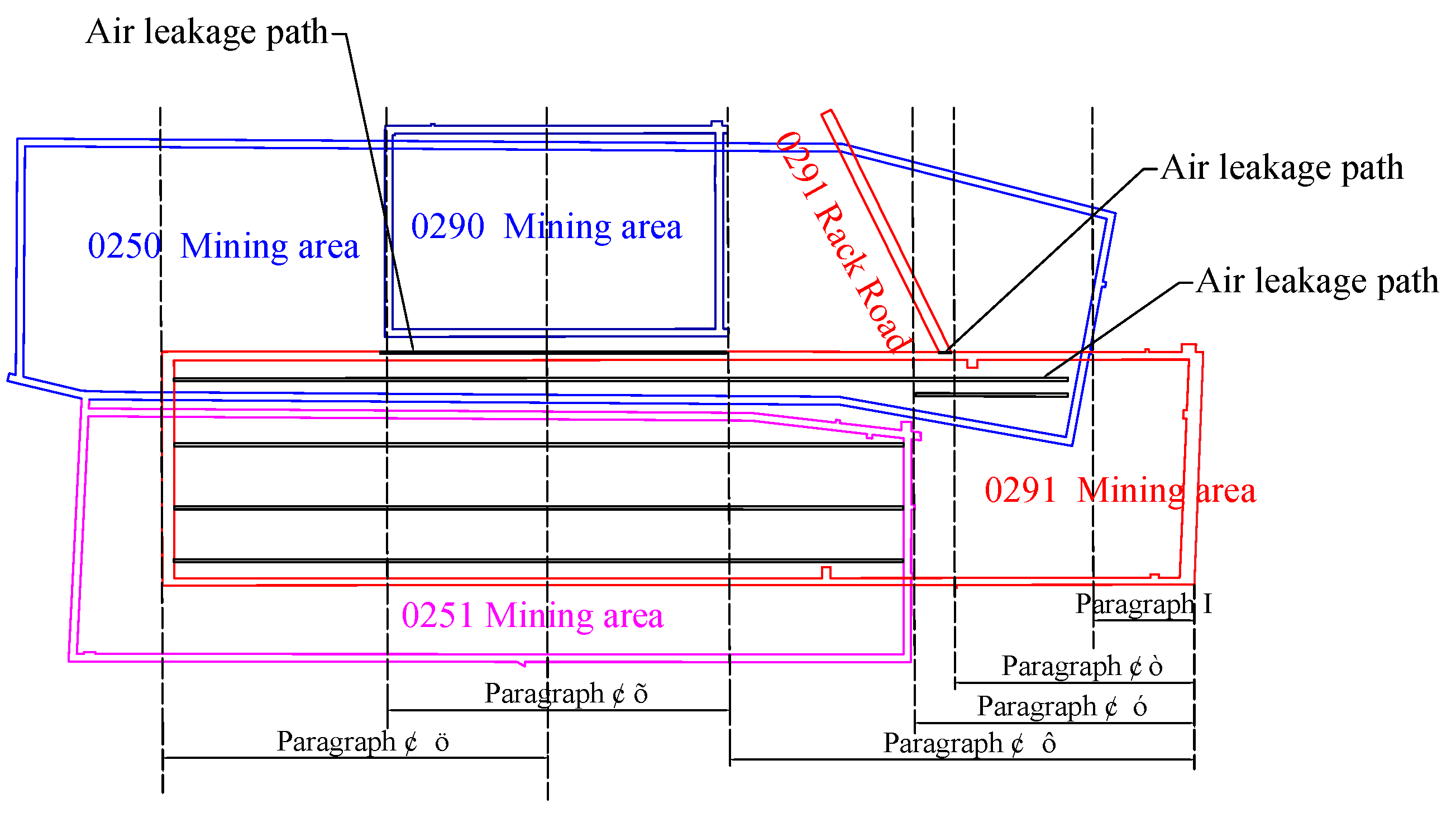
5.1. Overview of the Mine
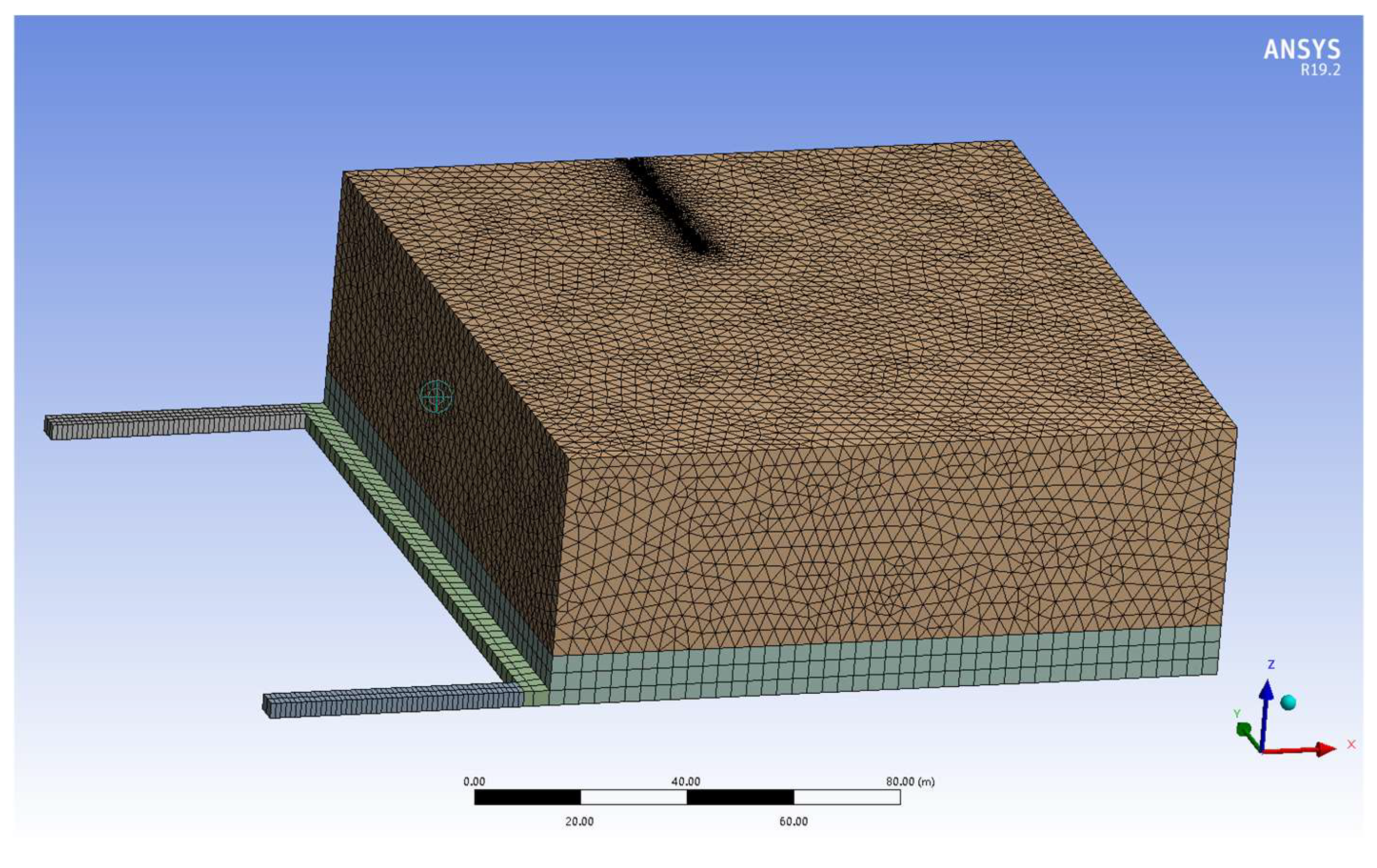
5.2. Physical Model and Boundary Condition Setting of the Mining Area
- —Height of bubble fall zone, m;
- —The working face mining height, m.
- —Height of the rift zone, m.
5.3. Numerical Simulation Results and Analysis
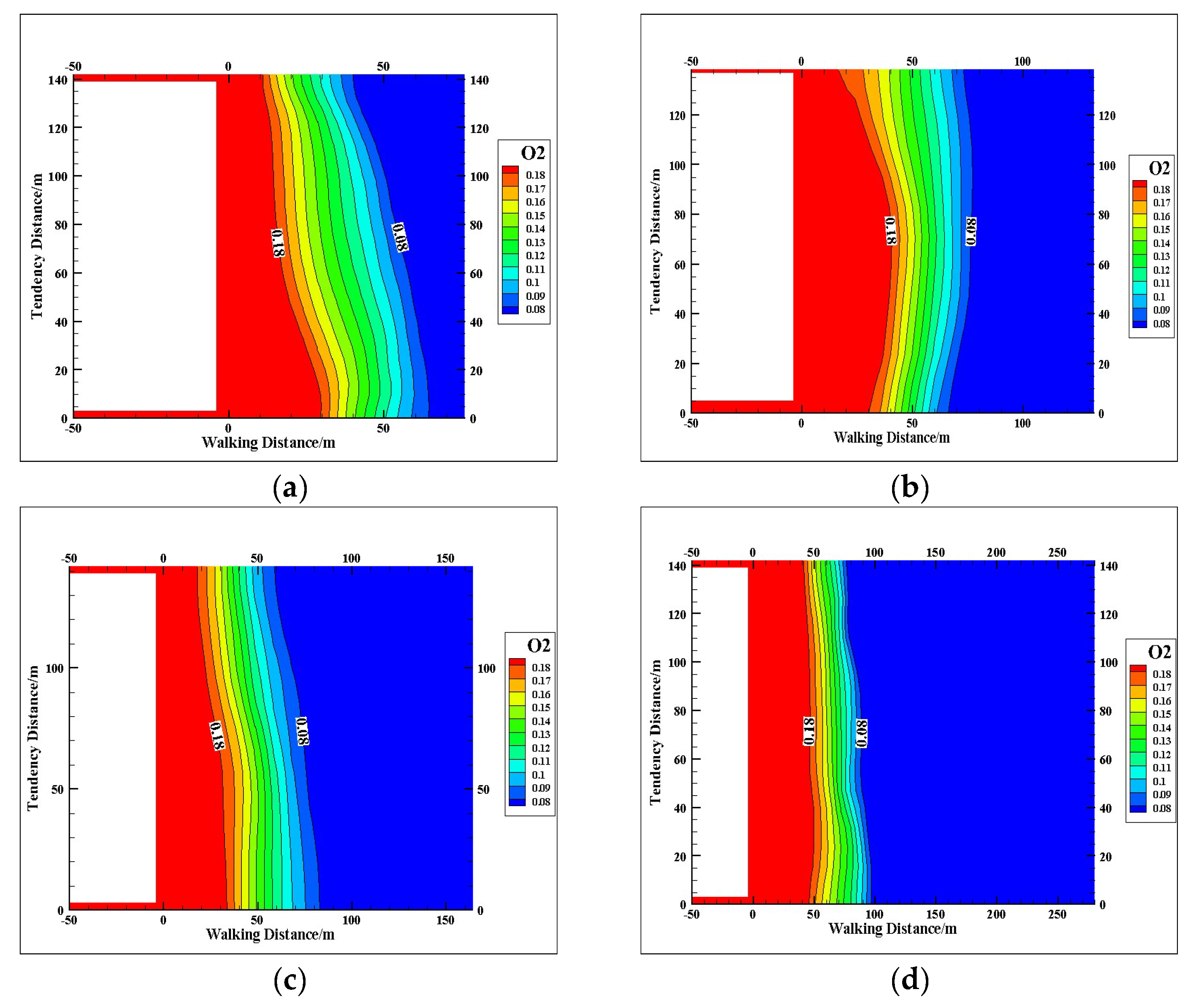
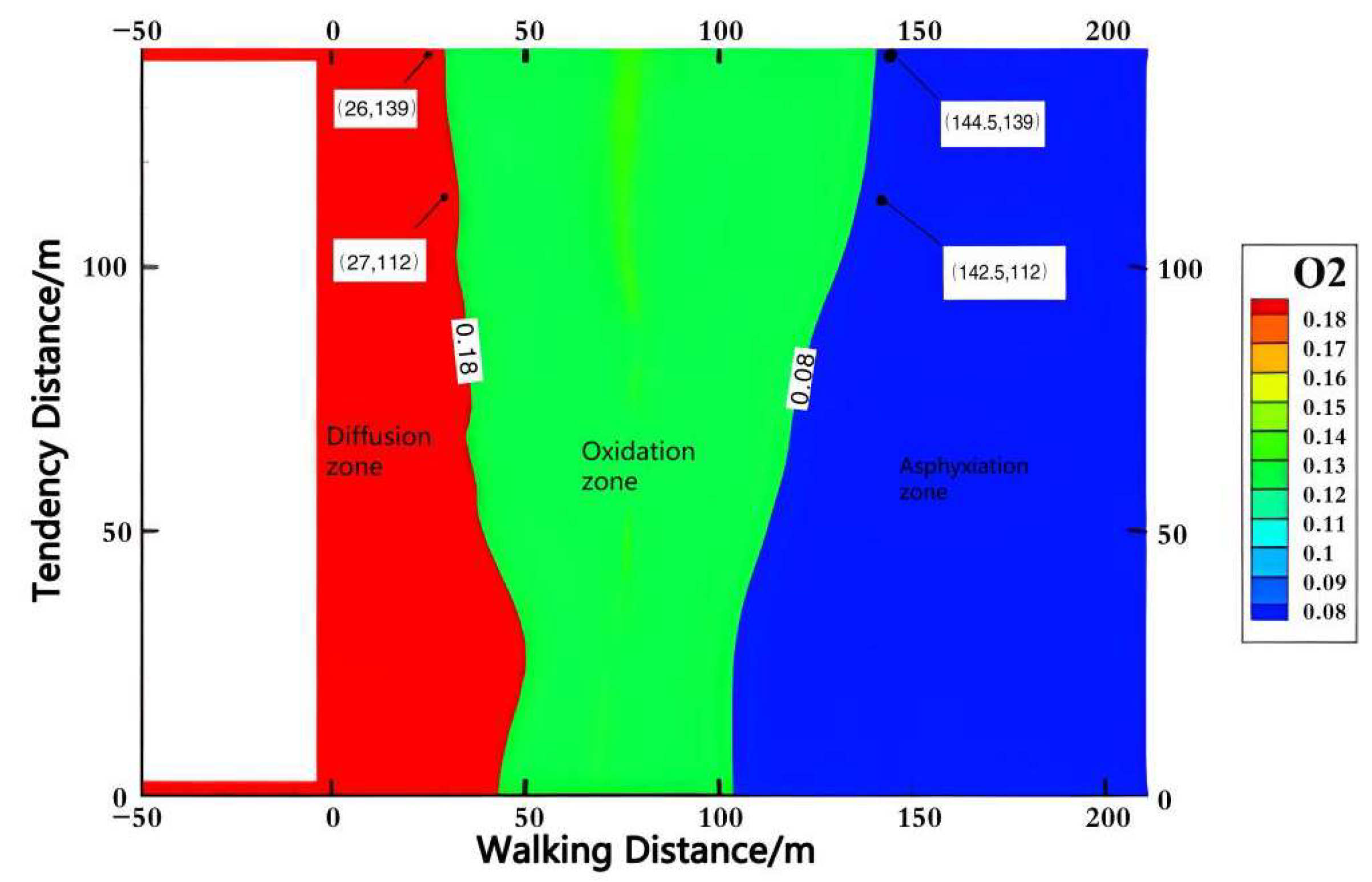
5.3.1. Stage I~IV Spontaneous Combustion “Three Belt” Distribution Law
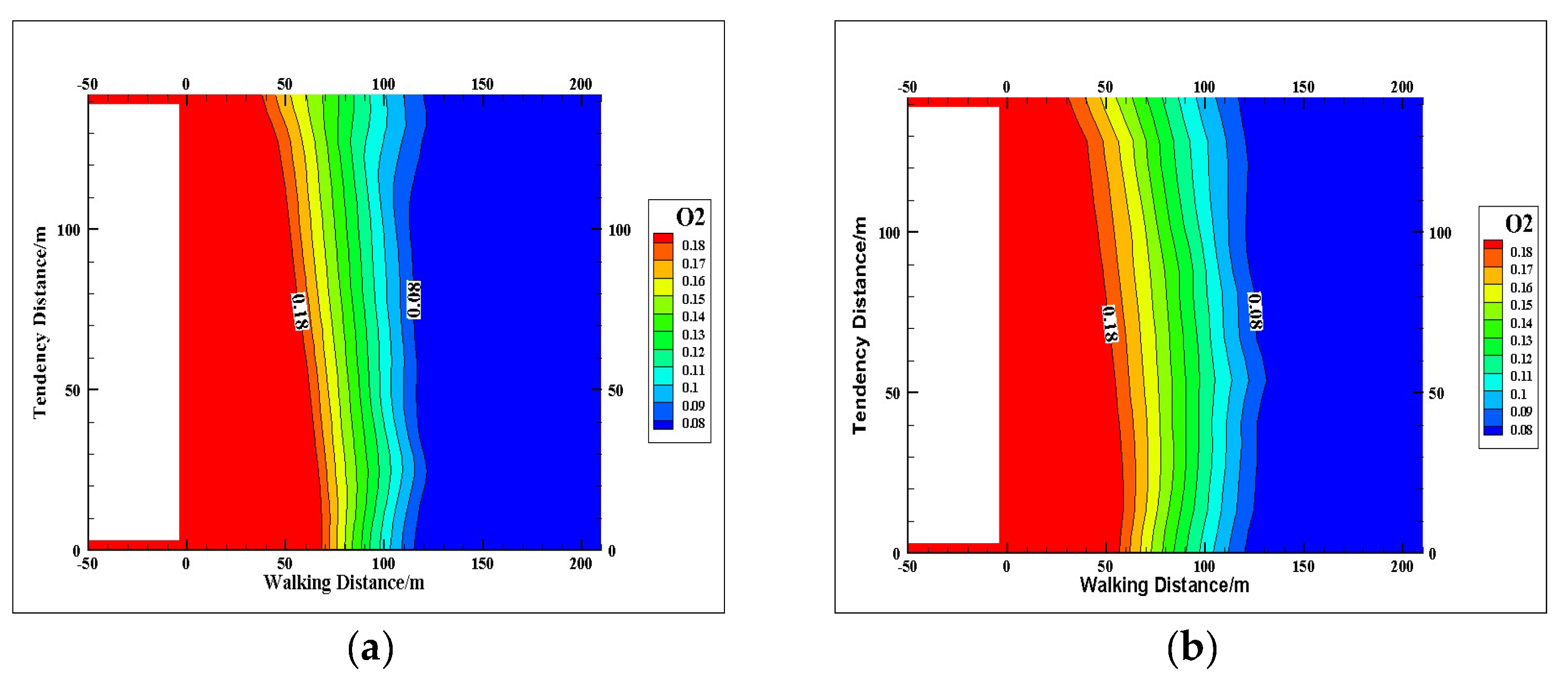
5.3.2. Stage V~VI Spontaneous Combustion “Three Belt” Distribution Law
6. Field Measurement Comparison Analysis
- —numerical simulation predicted O2 concentration, %;
- —distance, m;
- —correlation coefficient of the regression equation of the numerical simulation prediction curve.
7. Conclusions
- (1)
- The standard oxygen consumption rate is calculated through the programmed warming experiment, and the oxygen consumption rate is combined with the oxygen concentration relationship equation to establish a coupled model of the oxygen consumption rate of the legacy coal. The results show that the oxygen consumption rate of the coal body shows an approximate exponential growth trend with the increase in temperature, which is proportional to the original oxygen concentration in the environment. The percolation of porous media in the mining area is simplified to the ideal state, and the flow field model in the mining area is established according to Darcy’s law, which defines the conditions of inertial resistance, viscous resistance and permeability in the mining area. The inertial resistance, viscous resistance, permeability and other conditions of porous media in the mining area provide data support for numerical simulation according to the “O” circle theory to establish a three-dimensional distribution model of void rate in the mining area. It is found that the distribution of void rate is in the shape of a “bathtub”, the void rate in the outer area is greater than that in the inner area and the void rate in the outer area is greater than that in the inner area. The void rate in the outer area is larger than that in the inner area, the void rate along the direction of the mining area decreases logarithmically with the increase of the direction length and the proportional coupling of “double hump” changes along the tendency direction.
- (2)
- A segmented simulation method is proposed for the multiple air leakage paths mining area. According to the distribution of air leakage paths in the mining area, the mining area is divided into six stages, and each stage is set with the corresponding air leakage speed, air leakage paths and oxygen concentration according to the location relationship with the adjacent mining area. Through comparative analysis of different stages, we found that: the width of the “oxidation zone” decreases gradually along the tendency when only the working face is leaking; the leaking wind flow in the overlying mining area is smaller and the oxygen concentration is lower, which increases the width of the “oxidation zone” in the coverage area; the leaking wind in the shelf road forms an “oxidation zone” near the shelf. The air leakage from the shelf road forms an “oxidized zone” area near the entrance of the shelf road; the larger air leakage from the adjacent mining area and higher oxygen concentration increases the width of the overall “dispersal zone” and “oxidized zone”. The simulation results well reflect the change law of “three zones” of spontaneous combustion in the mining area under different conditions, which is also applicable to the conditions of buried pipe extraction and high-level drilling extraction in practical application.
- (3)
- The comparison between the downhole beam tube monitoring data and the numerical simulation results of the corresponding area reveals that the two results are basically consistent in delineating the range of the “three zones” of spontaneous combustion in the mining area, thus verifying the rationality of the mathematical model and the accuracy of the numerical simulation results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Cui, S.; Cao, J. Interference analysis of equipment installation in 8.8 m super high mining workings. Coal Eng. 2020, 52, 33–37. [Google Scholar]
- Liang, Y.; Wang, X.; Zhang, X. Analysis of anomalies in the distribution of spontaneous combustion “three zones” in the mining area of He Mo coal mine. Coal Mine Saf. 2015, 46, 166–168+172. [Google Scholar]
- Hua, H.; Liu, Z.; Si, J. Research on comprehensive fire prevention and fire suppression technology for coal pillarless mining workings in Qidong coal mine of Wanbei Coal Power. J. North China Inst. Sci. Technol. 2019, 16, 7–11. [Google Scholar]
- Zhou, X.; Jiang, Y.; Bai, G.; Li, D.; Hao, H. Experimental study on the parameters of spontaneous combustion characteristics of sulfur-containing anthracite coal affected by oxygen concentration. Coal Sci. Technol. 2022, 1–12. [Google Scholar] [CrossRef]
- Zhou, X.; Niu, Y.; Bai, G. Experimental study on the effect of air supply on the parameters of lignite spontaneous combustion characteristics. Min. Saf. Environ. Prot. 2020, 47, 31–35. [Google Scholar]
- Pan, Y.; Zhou, P.; Yan, Y.; Agrawal, A.; Wang, Y. New insights into the methods for predicting ground surface roughness in the age of digitalization. Precis. Eng. 2021, 67, 393–418. [Google Scholar] [CrossRef]
- An, J.; Zhang, J.; Ji, D.; Cai, M.; Xu, B.; Zhang, P. Study on the preferential selection of coal spontaneous combustion index gas based on segment fitting. China Sci. Technol. Saf. Prod. 2021, 17, 25–31. [Google Scholar]
- Xue, C.; Qin, R.; Zhang, S.; Dai, G.; Hou, S.; Luo, D. Experimental study on the oxidation of spontaneously combustible coal with different particle sizes at room temperature. China Saf. Prod. Sci. Technol. 2021, 17, 64–69. [Google Scholar]
- Zhang, F. Variation of spontaneous combustion limit parameters of coal relics in composite mining areas and determination of hazardous areas. Min. Saf. Environ. Prot. 2020, 47, 66–72. [Google Scholar]
- Zhang, S.; Qin, Y.; Liu, W.; Gao, P. Model analysis and numerical simulation study of flow field and oxygen concentration field in mining area. Coal Eng. 2019, 51, 104–108. [Google Scholar]
- Yang, Z. Research on Multifield Coupled Three-Dimensional Dynamic Numerical Solution Model of Mining Area Based on Flow Pipe. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2017. [Google Scholar]
- Du, Y. Research on the Characteristics of Air Leakage in the Mining Area under the Y-Shaped Ventilation Mode of the Top-Cutting and Pressure-Relief Stay Lane. Master’s Thesis, Henan University of Technology, Zhengzhou, China, 2018. [Google Scholar]
- Xu, C.; Cao, M.; Li, X.; Sun, H.; Yan, Z. Gas transport and enrichment patterns in mining areas based on three-dimensional void rate model. Coal Mine Saf. 2021, 52, 7–13. [Google Scholar]
- Wang, Z. Study on the Evolution of Permeability Law of Overburden Rock in Lao San Gou Coal Mine with Extra-Thick Coal Seam Mining. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2017. [Google Scholar]
- Liu, K.; Jin, S.; Rui, Y.; Huang, J.; Zhou, Z. Effect of Lithology on Mechanical and Damage Behaviors of Concrete in Concrete-Rock Combined Specimen. Mathematics 2022, 10, 727. [Google Scholar] [CrossRef]
- Li, C.; Xu, Z. Numerical Modeling and Investigation of Fault-Induced Water Inrush Hazard under Different Mining Advancing Directions. Mathematics 2022, 10, 1561. [Google Scholar] [CrossRef]
- Xuan, D.; Shen, C.; Li, X. Exploration of coal mine re-mining. Min. Technol. 2008, 23–24. [Google Scholar] [CrossRef]
- Li, Z.; Xuan, P.; Guo, Y. Analysis of the mechanism of coal spontaneous combustion phenomenon and prevention means. Inn. Mong. Coal Econ. 2021, 86–87. [Google Scholar] [CrossRef]
- Wan, L.; Sun, M.; Zhao, J.; Cai, D.; Ma, S. Research on wind leakage pattern and prevention and control technology in complex mining area of close coal seam. China Min. Ind. 2022, 31, 114–120. [Google Scholar]
- Zhao, W.; Zhang, W.; Liu, H.; Shi, X.; Wang, Z.; Li, Z. Study on the distribution law of three-dimensional spontaneous combustion zone in different stages of mining area of coal release from header mining. Min. Res. Dev. 2021, 41, 44–51. [Google Scholar]
- Wang, Y. Study on the distribution of “three zones” of spontaneous combustion in the shallow buried deep inclined workings. Coal Technol. 2021, 40, 110–114. [Google Scholar]
- Shen, Y.; Zhang, J.; Wu, J.; Feng, P.; Shen, Y. Numerical simulation of fire source temperature distribution law in mining area under different wind speeds. J. North China Univ. Technol. Nat. Sci. Ed. 2021, 43, 134–140. [Google Scholar]
- Wen, H.; Cheng, X.; Xu, Y.; Fan, S.; Hu, W.; Liu, H.; Guo, J. Influence of different air leakage source locations on the distribution of spontaneous combustion zone in the heaving working face of extra-thick coal seam. Coal Mine Saf. 2018, 49, 138–142. [Google Scholar]
- Liu, W.; Qin, Y.; Qiao, S.; Ma, B. Calculation and experimental demonstration of oxygen consumption rate and CO generation rate of coal. J. China Univ. Min. Technol. 2016, 45, 1141–1147. [Google Scholar]
- Si, J.; Cheng, G.; Zhu, J.; Chu, T. Three-dimensional modeling and application of permeability characteristics of non-homogeneous porous media in mining areas. Coal Sci. Technol. 2019, 47, 220–224. [Google Scholar]
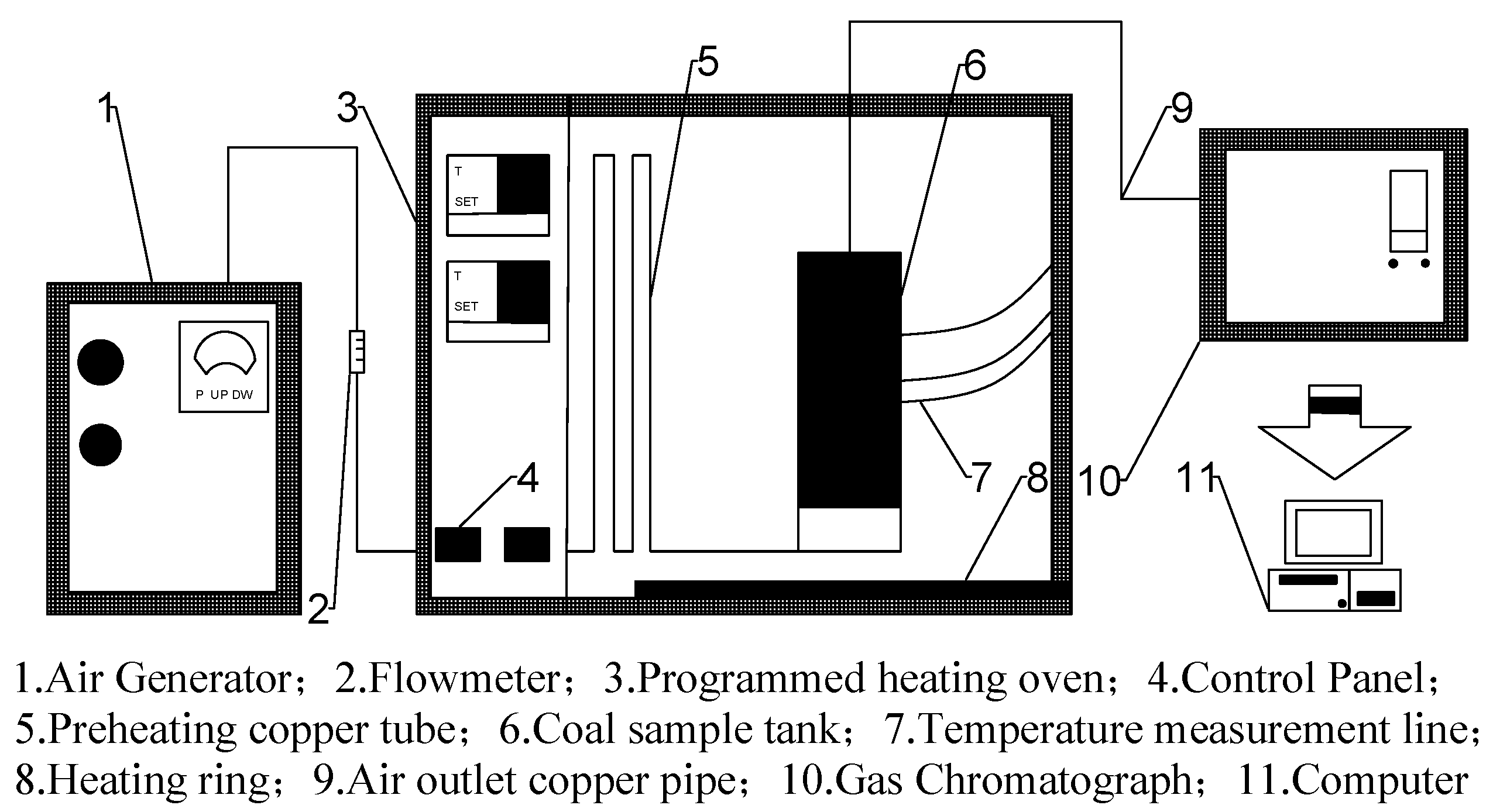

| Coal Sample Name | Moisture/% | Ash Content/% | Volatile Fraction/% | Fixed Carbon/% | C/% | H/% | O/% | N/% | S/% | True Density/(g/cm3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 9# mine | 0.95 | 14.66 | 23.54 | 61.43 | 75.72 | 4.21 | 7.02 | 1.51 | 0.46 | 1.56 |
| Boundary Conditions | Options | Parameters |
|---|---|---|
| Air inlet | Velocity-inlet | 2.5 m/s |
| Return air outlet | Outlet | Outflow |
| Regional Interfaces | Interior | |
| Regional Boundaries | Wall | |
| Gas volume fraction | O2 | 21% |
| Distance/m | 25 | 26 | 27 | 28 | 29 | 138.8 | 140 | 142.5 | 144.5 | 146 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1# Oxygen concentration/% | 18.1 | 18.0 | 17.8 | 17.6 | 17.3 | 8.5 | 8.3 | 8.3 | 8.0 | 7.8 |
| 2# Oxygen concentration/% | 18.5 | 18.3 | 18.0 | 17.6 | 16.5 | 8.2 | 8.2 | 8.0 | 7.8 | 7.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Ruan, G.; Bai, Y.; Ning, T. Mathematical Model and Numerical Simulation Study of the Mining Area with Multiple Air Leakage Paths. Mathematics 2022, 10, 2484. https://doi.org/10.3390/math10142484
Zhang J, Ruan G, Bai Y, Ning T. Mathematical Model and Numerical Simulation Study of the Mining Area with Multiple Air Leakage Paths. Mathematics. 2022; 10(14):2484. https://doi.org/10.3390/math10142484
Chicago/Turabian StyleZhang, Jiuling, Gaoyang Ruan, Yang Bai, and Tao Ning. 2022. "Mathematical Model and Numerical Simulation Study of the Mining Area with Multiple Air Leakage Paths" Mathematics 10, no. 14: 2484. https://doi.org/10.3390/math10142484
APA StyleZhang, J., Ruan, G., Bai, Y., & Ning, T. (2022). Mathematical Model and Numerical Simulation Study of the Mining Area with Multiple Air Leakage Paths. Mathematics, 10(14), 2484. https://doi.org/10.3390/math10142484





