FEM-Based Simulative Study for Multi-Response Optimization of Powder Bed Fusion Process
Abstract
:1. Introduction
2. Methods and Materials
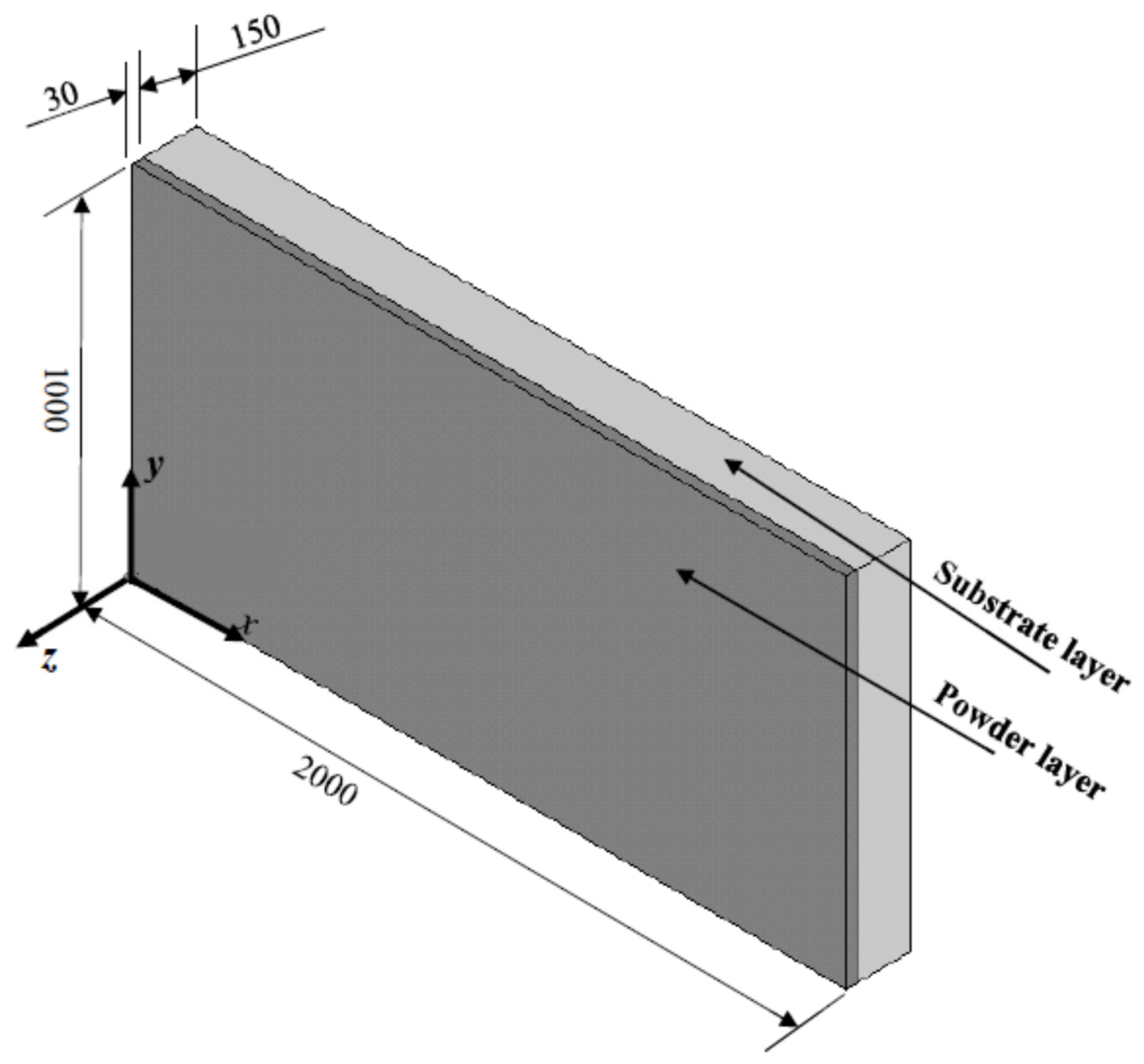
- The present study intends to understand the physics of the process by incorporating changes in the process parameters of interest. Thus, freeform or complicated geometries are neglected to reduce the complexity of the simulation. The part created is a rectangular prism situated in a three-dimensional space.
- In the LPBF process, powder particles are small and closely packed. While spreading the powder, the re-coater blade or roller vibrates to tap the spread powder, increasing the packing density. Hence, the problem of discrete particle analysis can be simplified by considering the continuous domain of analysis. On the other hand, the effect of bed porosity is not neglected completely, and is incorporated by considering material properties of interest as a function of powder bed porosity.
- Three heat transfer modes are involved in the process, namely conduction, convection, and radiation. Powder particles are closely packed, and their change in state from powder to the liquid and finally to solid takes place in a minimal time interval. Therefore, this time gap mode of heat transfer within the part by convection and radiation can be considered negligible.
- Free convection is the only mode of heat loss to the surrounding, and any radiation loss is negligible. This is a fair assumption for the LPBF process, which takes place in an inert environment. The inert gas surrounding the part allows for the convective cooling of the surface of the build and becomes a dominant cause for heat dissipation.
- Any mode of mass transfer is neglected. Therefore, heat transfer through melt mass transport is not directly simulated in this study.
- The properties, namely thermal conductivity, specific heat capacity, and density used in this study, are temperature- and powder bed porosity-dependent, but their spatial variation is neglected. Any other material properties are constant, and are not temperature-, porosity-, or position-dependent.
- Composition and, hence, material property change due to constituent vaporization is not considered.
- The process is assumed to be continuous without a break, so the cooling period is neglected.
- Build chamber temperature is assumed constant even in the vicinity of the part.
- Changes in dimensions due to temperature-induced differences in density, phase changes, or cooling-induced shrinkage are neglected.
2.1. Geometric Part Model
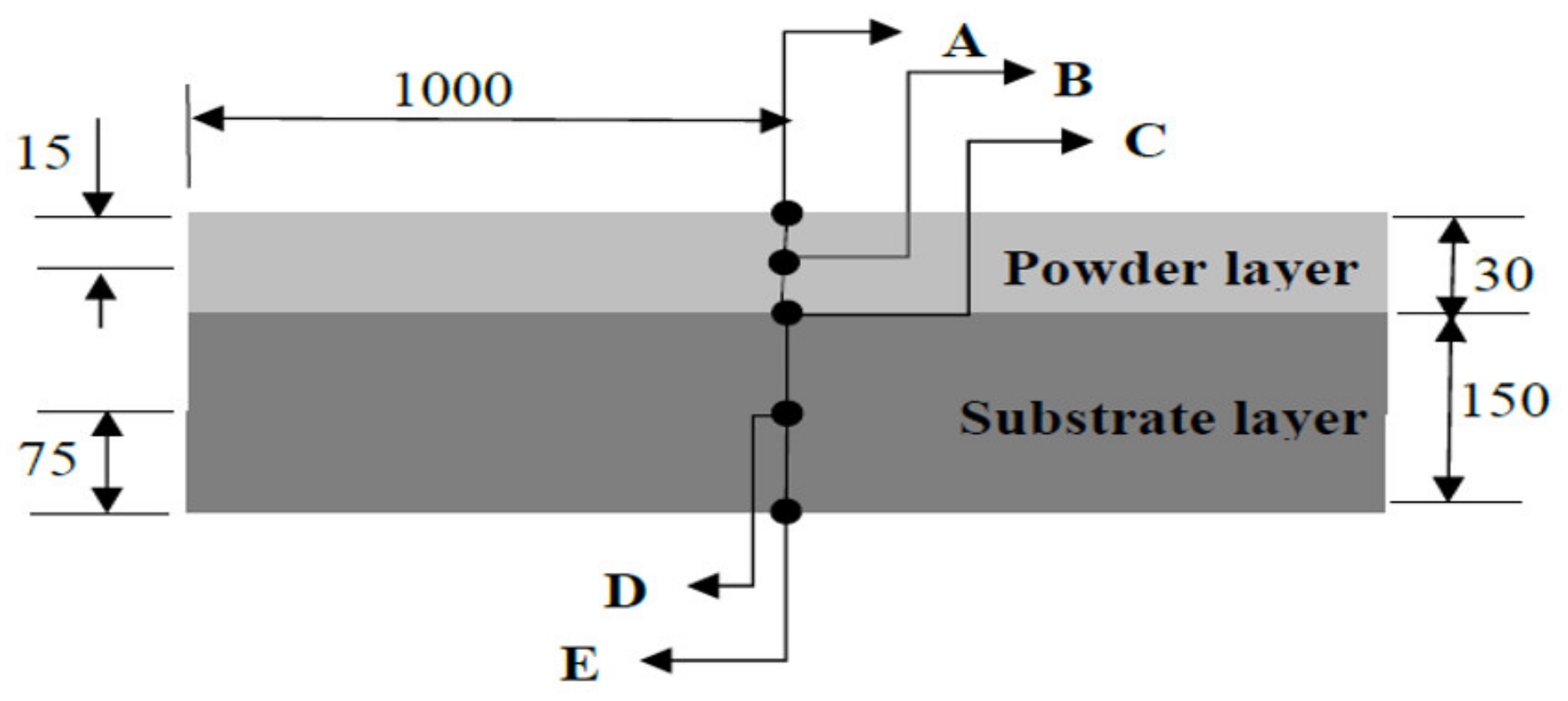
2.2. Part Mesh Model
2.3. Material Model
2.4. Heat Source Model
2.5. Thermal Model
2.6. Simulation
3. Results and Discussion
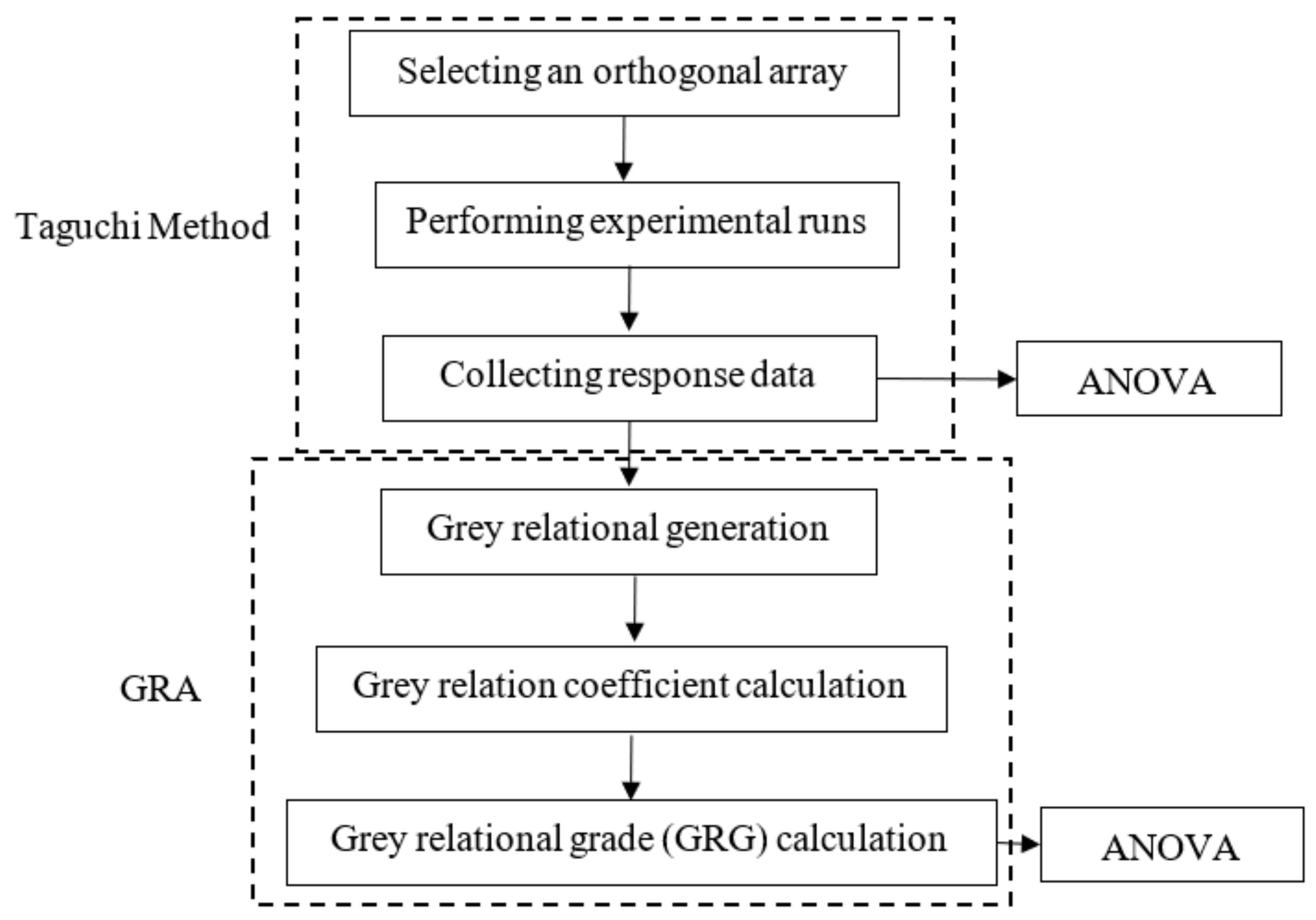
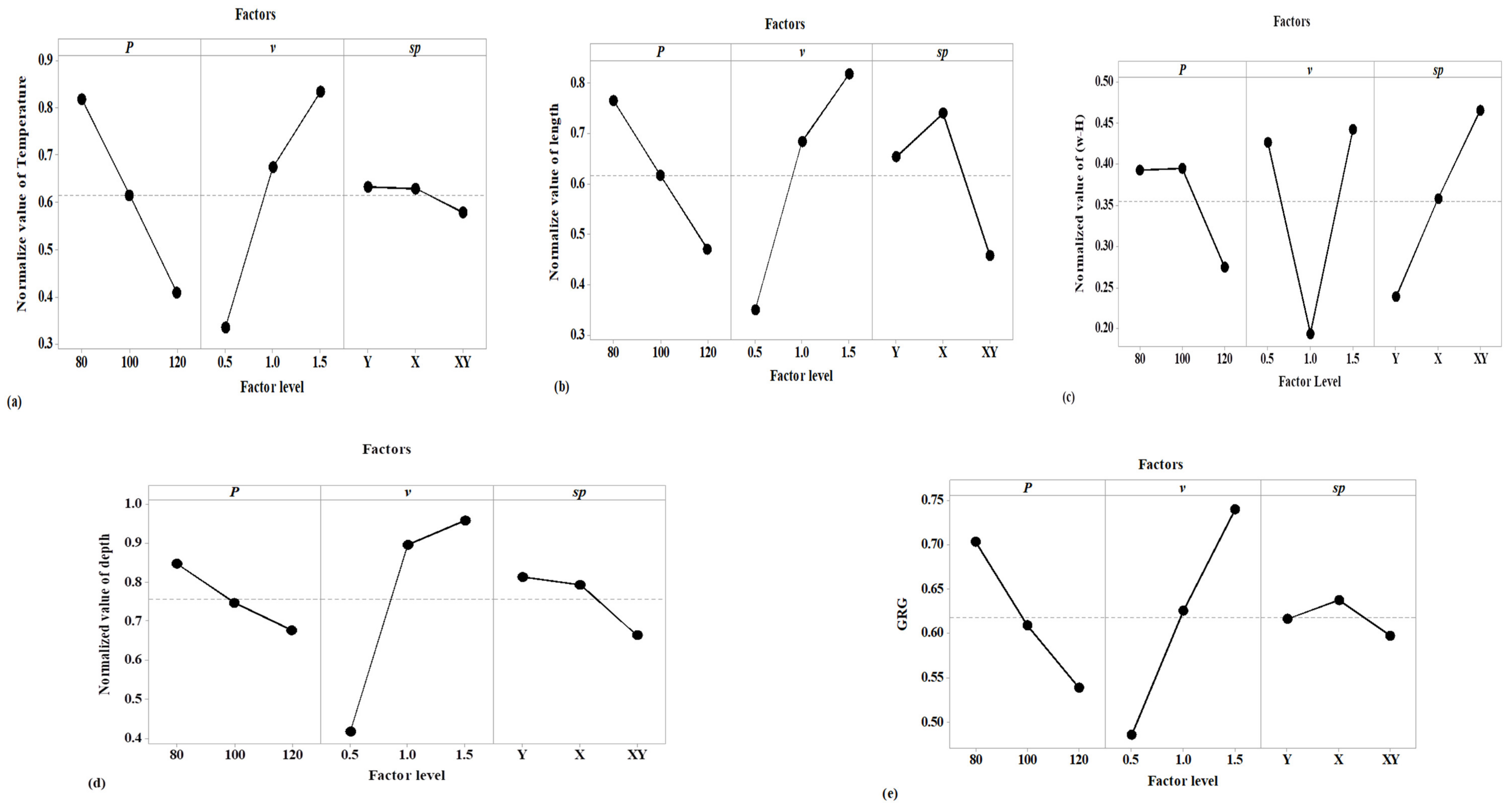
Grey-Taguchi Results
4. Conclusions
- ⮚
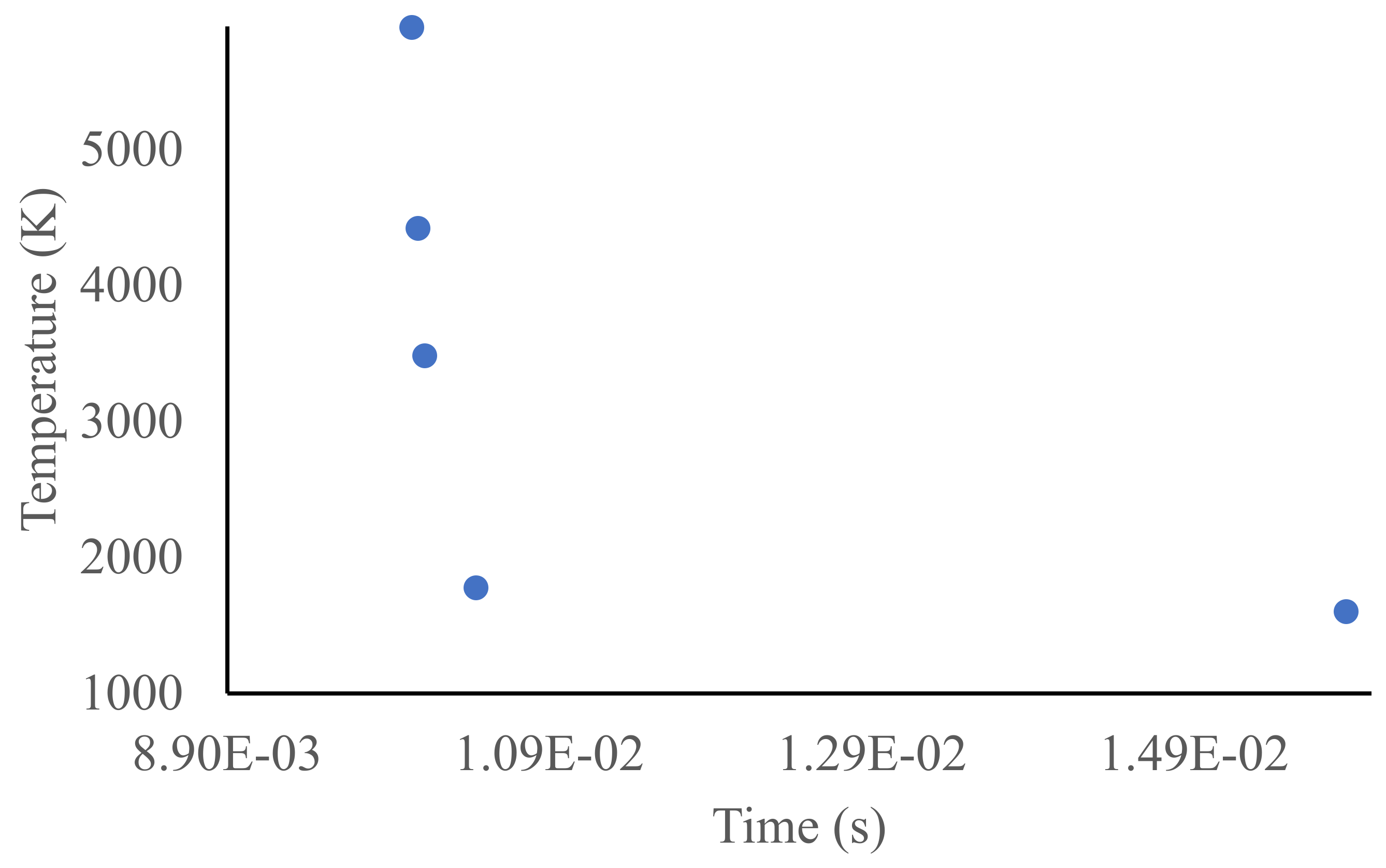
- The temperature at various locations in the layer keeps on changing with time. This is because it depends on the location of the point concerning the laser position at that particular moment.
- ⮚
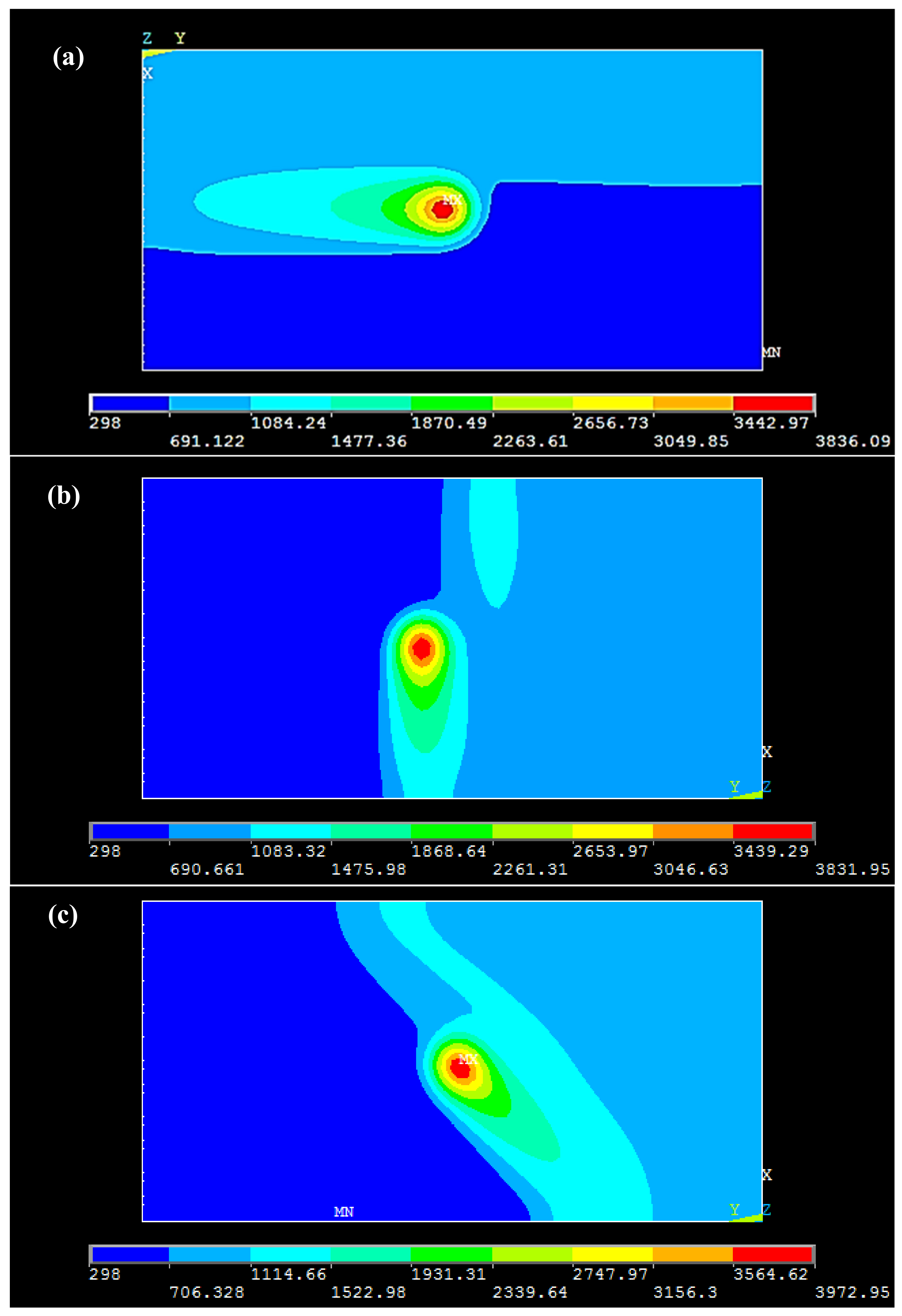
- The powder has a poor heat dissipation capacity compared to the solid phase of the same material, which results in excessive temperature near the powder phase compared to the solidified portion.
- ⮚
- The temperature variation within the melt pool along the three principal directions considered, namely length, width and depth, is not uniform, and depends on the material phase in the vicinity of the melt pool.
- ⮚
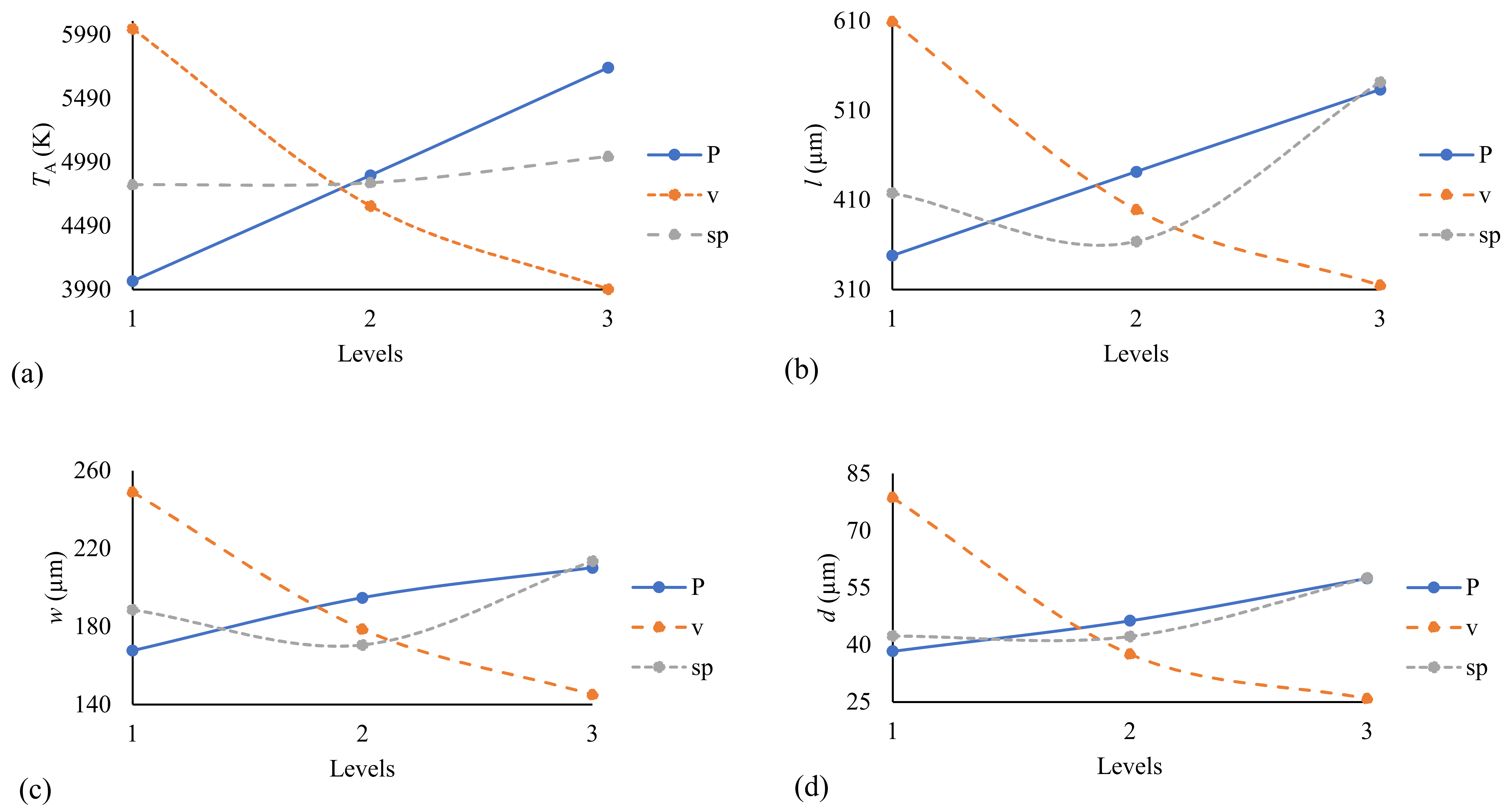
- There may be a different set of significant process parameters for different types of responses considered. Therefore, it is difficult to have a single parameter setting that enables each response to achieve its best value.
- ⮚
- Scan velocity is the most influential parameter of all the process parameters. Therefore, an optimum scan velocity is recommended to prevent over melting and an excessive temperature gradient in the melt pool or part.
- ⮚
- The root cause of all the AM problems is excessive energy input into the system. The property of the fabricated part can be improved by inputting low energy density with a good scan pattern.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Equbal, A.; Equbal, I.; Sood, A.K. An investigation on the feasibility of fused deposition modelling process in EDM electrode manufacturing. CIRP J. Manuf. Sci. Technol. 2019, 26, 10–25. [Google Scholar] [CrossRef]
- Acanfora, V.; Castaldo, R.; Riccio, A. On the Effects of Core Microstructure on Energy Absorbing Capabilities of Sandwich Panels Intended for Additive Manufacturing. Materials 2022, 15, 1291. [Google Scholar] [CrossRef] [PubMed]
- King, W.E.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A.; Rubenchik, A.M. Laser powder bed fusion additive manufacturing of metals: Physics, computational, and materials challenges. Appl. Phys. Rev. 2015, 2, 041304. [Google Scholar] [CrossRef]
- Zhechao, F.; Hongwei, F. Study on selective laser melting and heat treatment of Ti-6Al-4V alloy. Results Phys. 2018, 10, 660–664. [Google Scholar]
- Caiazzo, F.; Alfieri, V.; Argenio, P.; Sergi, V. Additive manufacturing by means of laser-aided directed metal deposition of 2024 aluminium powder: Investigation and optimization. Adv. Mech. Eng. 2017, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Romano, J.; Ladani, L.; Sadowski, M. Temperature distribution and melt geometry in laser and electron-beam melting processes—A comparison among common materials. Addit. Manuf. 2015, 8, 1–11. [Google Scholar] [CrossRef]
- King, W.E.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mater. Process. Technol. 2014, 214, 2915–2925. [Google Scholar] [CrossRef]
- Gu, D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- Pasquale, G.D.; Luceri, F.; Riccio, M. Experimental evaluation of selective laser melting process for optimized lattice structures. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2018, 233, 763–775. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Starr, T.; Stucker, B. Analysis of defect generation in Ti–6Al–4V parts made using powder bed fusion additive manufacturing processes. Addit. Manuf. 2014, 1–4, 87–98. [Google Scholar] [CrossRef]
- Hooper, P.A. Melt pool temperature and cooling rates in laser powder bed fusion. Addit. Manuf. 2018, 22, 548–559. [Google Scholar] [CrossRef]
- Narr, S.P.; Scime, L.; Beuth, J. Integrated Control of Melt Pool Geometry and Microstructure in Laser Powder Bed Fusion of AlSi10Mg. Metall. Mater. Trans. A 2018, 49, 5097–5106. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhou, X.; Shen, Z.; Liu, W. Microstructure of selective laser melted AlSi10Mg alloy. Mater. Des. 2019, 168, 107677. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Z.; Tse, Y.; Huang, C. Optimization of processing parameters and establishment of a relationship between microstructure and mechanical properties of SLM titanium alloy. Opt. Lasers Technol. 2019, 112, 159–167. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Shi, Y.; Wang, L.; Jiang, W. Balling behaviour of stainless steel and nickel powder during selective laser melting process. Int. J. Adv. Manuf. Technol. 2012, 59, 1025–1035. [Google Scholar] [CrossRef]
- Khorasani, A.; Gibson, I.; Awan, U.S.; Ghaderi, A. The effect of SLM process parameters on density, hardness, tensile strength and surface quality of Ti-6Al-4V. Addit. Manuf. 2019, 25, 176–186. [Google Scholar] [CrossRef]
- Malekipour, E.; El-Mounayri, H. Common defects and contributing parameters in powder bed fusion AM process and their classification for online monitoring and control: A review. Int. J. Adv. Manuf. Technol. 2018, 95, 527–550. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stravroulakis, P.; Leacha, R.K.; Clarea, A.T. Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Gockel, J.; Sheridan, L.; Koerper, B.; Whip, B. The influence of additive manufacturing processing parameters on surface roughness and fatigue life. Int. J. Fatigue 2019, 124, 380–388. [Google Scholar] [CrossRef]
- Luo, Z.; Zhao, Y. A survey of finite element analysis of temperature and thermal stress fields in powder bed fusion additive manufacturing. Addit. Manuf. 2018, 21, 318–332. [Google Scholar] [CrossRef] [Green Version]
- Paul, R.; Anand, S.; Gerner, F. Effect of Thermal Deformation on Part Errors in Metal Powder Based Additive Manufacturing Processes. J. Manuf. Sci. Eng. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Vastola, G.; Zhang, G.; Pei, Q.X.; Zhang, Y.-W. Controlling of residual stress in additive manufacturing of Ti6Al4V by finite element modelling. Addit. Manuf. 2016, 12, 231–239. [Google Scholar]
- Irwin, J. Modeling Microstructure of AM Processes Using the FE Method. In Thermo-Mechanical Modeling of Additive Manufacturing; Gouge, M., Michaleris, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 117–135. [Google Scholar]
- Arrizubieta, J.I.; Lamikiz, A.; Klocke, F.; Martínez, S.; Arntz, K.; Ukar, E. Evaluation of the relevance of melt pool dynamics in Laser Material Deposition process modelling. Int. J. Heat Mass Transfer 2017, 115, 80–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Y.; Kasinathan, A.R.; Shahabad, S.I.; Ali, U.; Mahmoodkhani, Y.; Toyserkani, E. 3-Dimensional heat transfer modeling for laser powder-bed fusion additive manufacturing with volumetric heat sources based on varied thermal conductivity and absorptivity. Opt. Lasers Technol. 2019, 109, 297–312. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Ross, P.J. Taguchi Techniques for Quality Engineering; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2005. [Google Scholar]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Parametric appraisal of fused deposition modelling process using the grey Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 135–145. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to Grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Liu, S.; Forrest, J.; Yang, Y. A brief introduction to grey systems theory. Grey Syst. Theory Appl. 2012, 2, 89–104. [Google Scholar] [CrossRef]
- Uzun, G. Analysis of grey relational method of the effects on machinability performance on austempered vermicular graphite cast irons. Measurement 2019, 142, 122–130. [Google Scholar] [CrossRef]
- Prabakaran, M.P.; Kannan, G.R. Optimization of laser welding process parameters in dissimilar joint of stainless steel AISI316/AISI1018 low carbon steel to attain the maximum level of mechanical properties through PWHT. Opt. Lasers Technol. 2019, 112, 314–322. [Google Scholar] [CrossRef]
- Krishnan, M.; Subramaniam, S. Multi-response optimization of friction stir corner welding of dissimilar thickness AA5086 and AA6061 aluminum alloys by Taguchi grey relational analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 3733–3742. [Google Scholar] [CrossRef]
- Solati, A.; Arab, N.B.M.; Mohammadi-Ahmar, A. Multi-criteria optimization of weld bead in pulsed Nd: YAG laser welding of stainless steel 316. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2019, 233, 151. [Google Scholar] [CrossRef]
- Ansys. ANSYS Mechanical APDL Element Reference, ANSYS, Inc. Release 15.0 South pointe 275 Technology Drive Canonsburg, PA 15317. 2013. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwi57dKc0db4AhVoUPUHHa3UAzkQFnoECAUQAQ&url=https%3A%2F%2Fwww.researchgate.net%2Ffile.PostFileLoader.html%3Fid%3D567c42a25f7f71f83b8b4567%26assetKey%3DAS%253A310263939567616%25401450984095215&usg=AOvVaw02rQ3lgSaKOTh3lDTHtPh2 (accessed on 11 May 2022).
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing Limited: Cambridge, UK, 2002. [Google Scholar]
- Fu, G.; Zhang, D.Z.; He, A.N.; Mao, Z.; Zhang, K. Finite Element Analysis of Interaction of Laser Beam with Material in Laser Metal Powder Bed Fusion Process. Materials 2018, 11, 765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cengel, Y.A. Heat Transfer: A Practical Approach; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2002. [Google Scholar]
- Fan, Z.; Liou, F. Numerical modeling of the additive manufacturing (AM) processes of titanium alloy. In Towards Achieving Enhanced Properties for Diversified Applications; Amin, A.K.M.N., Ed.; Intech: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Tang, M.; Pistorius, P.C.; Beuth, J.L. Prediction of lack of fusion porosity for powder bed fusion. Addit. Manuf. 2017, 14, 39–48. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y. Finite element simulation of thermal behaviour in single track multiple layers thin wall without support during selective laser melting. J. Manuf. Processes 2019, 42, 139–148. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Craeghs, T.; Heulens, J.; Pandelaers, L. A pragmatic model for selective laser melting with evaporation. Acta Mater. 2009, 57, 6006–6012. [Google Scholar] [CrossRef]
- Ali, H.; Ghadbeigi, H.; Mumtaz, K. Effect of scanning strategies on residual stress and mechanical properties of Selective Laser Melted Ti6Al4V. Mater. Sci. Eng. A 2018, 712, 175–187. [Google Scholar] [CrossRef]



| Factor | Symbol | Unit | Level | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| Laser power | P | W | 80 | 100 | 120 |
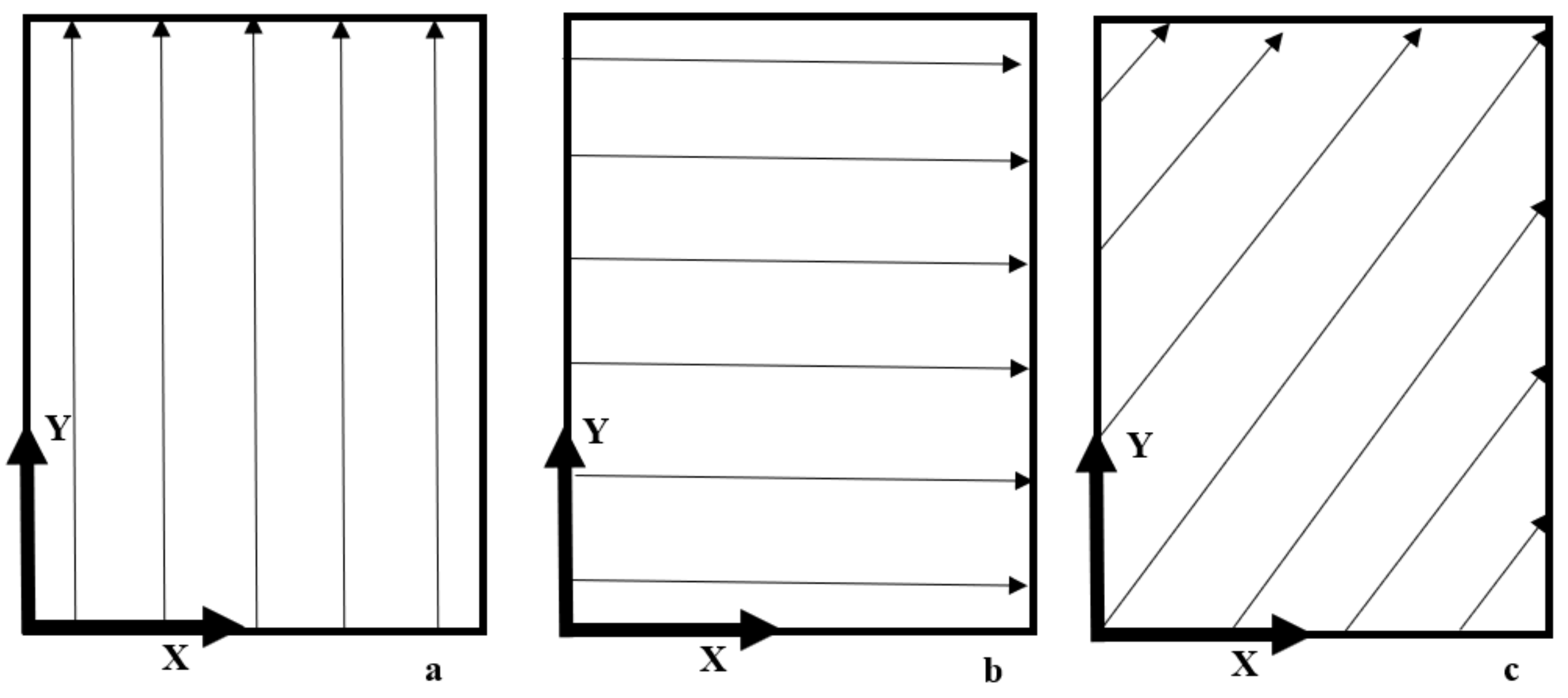
| Scan pattern | sp | --- | Y | X | XY |
| Scan speed | v | m/s | 0.5 | 1.0 | 1.5 |
| Exp. No. | Factors | Response | |||||
|---|---|---|---|---|---|---|---|
| P | sp | V | TA | L | W | d | |
| (W) | --- | (ms−1) | (K) | (µm) | (µm) | (µm) | |
| 1 | 80 | Y | 0.5 | 4864 | 400 | 210 | 60 |
| 2 | 80 | X | 0.5 | 4887 | 350 | 175 | 55 |
| 3 | 80 | XY | 0.5 | 5140 | 778 | 264 | 74 |
| 4 | 80 | Y | 1.0 | 3812 | 300 | 180 | 30 |
| 5 | 80 | X | 1.0 | 3820 | 275 | 150 | 28 |
| 6 | 80 | XY | 1.0 | 3954 | 330 | 160 | 33 |
| 7 | 80 | Y | 1.5 | 3318 | 230 | 130 | 22 |
| 8 | 80 | X | 1.5 | 3315 | 200 | 130 | 19 |
| 9 | 80 | XY | 1.5 | 3414 | 270 | 110 | 24 |
| 10 | 100 | Y | 0.5 | 5903 | 550 | 247 | 65 |
| 11 | 100 | X | 0.5 | 5922 | 450 | 225 | 70 |
| 12 | 100 | XY | 0.5 | 6256 | 800 | 321 | 90 |
| 13 | 100 | Y | 1.0 | 4582 | 400 | 180 | 35 |
| 14 | 100 | X | 1.0 | 4595 | 325 | 150 | 36 |
| 15 | 100 | XY | 1.0 | 4752 | 498 | 204 | 44 |
| 16 | 100 | Y | 1.5 | 3943 | 300 | 150 | 25 |
| 17 | 100 | X | 1.5 | 3955 | 300 | 130 | 24 |
| 18 | 100 | XY | 1.5 | 4071 | 352 | 146 | 28 |
| 19 | 120 | Y | 0.5 | 6962 | 725 | 225 | 74 |
| 20 | 120 | X | 0.5 | 6994 | 600 | 250 | 80 |
| 21 | 120 | XY | 0.5 | 7410 | 830 | 324 | 140 |
| 22 | 120 | Y | 1.0 | 5361 | 455 | 200 | 42 |
| 23 | 120 | X | 1.0 | 5377 | 425 | 175 | 40 |
| 24 | 120 | XY | 1.0 | 5574 | 584 | 208 | 50 |
| 25 | 120 | Y | 1.5 | 4580 | 400 | 175 | 28 |
| 26 | 120 | X | 1.5 | 4592 | 350 | 150 | 28 |
| 27 | 120 | XY | 1.5 | 4749 | 432 | 185 | 35 |
| Properties | Symbol | Value | Unit |
|---|---|---|---|
| Liquidus temperature | 1923 | K | |
| Solidus temperature | 1877 | K | |
| Evaporation temperature | 3533 | K | |
| Latent heat of fusion | J kg−1 | ||
| Latent heat of evaporation | J kg−1 | ||
| Laser absorption coefficient | A | 0.7 | --- |
| Ambient temperature | To | 300 | K |
| Laser spot radius | ro | 100 | µm |
| Hatch spacing | H | 200 | µm |
| Convective coefficient | H | 10 | W m−2 K−1 |
| TA | L | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | DF | SS | V | F | p | SS | V | F | p |
| P | 2 | 1.2 × 107 | 6,239,436 | 552,797 | 0.000 | 171,511 | 85,755 | 96.72 | 0.000 |
| v | 2 | 2 × 107 | 9,815,951 | 869,666 | 0.000 | 409,790 | 204,895 | 231.08 | 0.000 |
| sp | 2 | 277,745 | 138,872 | 12,303.7 | 0.000 | 156,908 | 78,454 | 88.48 | 0.000 |
| P × v | 4 | 544,599 | 136,150 | 12,062.5 | 0.000 | 7752 | 1938 | 2.19 | 0.161 |
| P × sp | 4 | 5157 | 1289 | 114.23 | 0.000 | 1260 | 315 | 0.36 | 0.834 |
| v × sp | 4 | 55,199 | 13,800 | 1222.63 | 0.000 | 62,137 | 15,534 | 17.52 | 0.001 |
| Error | 8 | 90 | 11 | 7093 | 887 | ||||
| Total | 26 | 3.3 × 107 | 816,451 | ||||||
| W | D | ||||||||
| Source | DF | SS | V | F | p | SS | VV | F | p |
| P | 2 | 7790 | 3895.1 | 33.42 | 0.000 | 855.4 | 427.7 | 144.8 | 0.000 |
| v | 2 | 48,895 | 24,447.4 | 209.75 | 0.000 | 10,680 | 5339.81 | 1807.84 | 0.000 |
| sp | 2 | 9021 | 4510.3 | 38.7 | 0.000 | 692.5 | 346.26 | 117.23 | 0.000 |
| P × v | 4 | 1301 | 325.2 | 2.79 | 0.101 | 451.3 | 112.81 | 38.19 | 0.000 |
| P × sp | 4 | 1221 | 305.3 | 2.62 | 0.115 | 93.7 | 23.43 | 7.93 | 0.007 |
| v × sp | 4 | 7510 | 1877.4 | 16.11 | 0.001 | 560.1 | 140.04 | 47.41 | 0.000 |
| Error | 8 | 932.4 | 116.6 | 23.6 | 2.95 | ||||
| Total | 26 | 76,670 | 13,356 | ||||||
| Exp. No. | GRG | ||||
|---|---|---|---|---|---|
| 1 | 0.621734 | 0.759036 | 0.912281 | 1.000000 | 0.737137 |
| 2 | 0.616117 | 0.819277 | 0.832215 | 0.941176 | 0.681326 |
| 3 | 0.554335 | 0.303614 | 0.584416 | 0.787879 | 0.475345 |
| 4 | 0.878632 | 0.879518 | 0.861111 | 0.727273 | 0.696903 |
| 5 | 0.876679 | 0.909639 | 0.712644 | 0.714286 | 0.662073 |
| 6 | 0.843956 | 0.843373 | 0.756098 | 0.747664 | 0.645013 |
| 7 | 0.999267 | 0.963855 | 0.639175 | 0.677966 | 0.715869 |
| 8 | 1.000000 | 1.000000 | 0.639175 | 0.661157 | 0.734794 |
| 9 | 0.975824 | 0.915663 | 0.579439 | 0.689655 | 0.673935 |
| 10 | 0.368010 | 0.578313 | 0.656934 | 0.933333 | 0.551352 |
| 11 | 0.363370 | 0.698795 | 0.782609 | 0.857143 | 0.566747 |
| 12 | 0.281807 | 0.277108 | 0.42654 | 0.577465 | 0.382324 |
| 13 | 0.690598 | 0.759036 | 0.861111 | 0.761905 | 0.621665 |
| 14 | 0.687424 | 0.849398 | 0.712644 | 0.769231 | 0.605546 |
| 15 | 0.649084 | 0.640964 | 0.966667 | 0.833333 | 0.665777 |
| 16 | 0.846642 | 0.879518 | 0.712644 | 0.695652 | 0.636754 |
| 17 | 0.843712 | 0.879518 | 0.639175 | 0.689655 | 0.620508 |
| 18 | 0.815385 | 0.816867 | 0.696629 | 0.714286 | 0.607436 |
| 19 | 0.109402 | 0.36747 | 0.782609 | 0.787879 | 0.478752 |
| 20 | 0.101587 | 0.518072 | 0.642857 | 0.672131 | 0.437012 |
| 21 | 0.000000 | 0.240964 | 0.420561 | 0.338843 | 0.333333 |
| 22 | 0.500366 | 0.692771 | 1.000000 | 0.816327 | 0.673912 |
| 23 | 0.496459 | 0.728916 | 0.832215 | 0.800000 | 0.584471 |
| 24 | 0.448352 | 0.537349 | 0.931034 | 0.888889 | 0.620564 |
| 25 | 0.691087 | 0.759036 | 0.832215 | 0.714286 | 0.599856 |
| 26 | 0.688156 | 0.819277 | 0.712644 | 0.714286 | 0.582937 |
| 27 | 0.649817 | 0.720482 | 0.892086 | 0.761905 | 0.618475 |
| Source | DF | SS | V | F | P | %c | SS | V | F | P | %c |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P | 2 | 0.75966 | 0.379832 | 552,796.6 | 0.000 | 37.82 | 0.35714 | 0.178571 | 96.74 | 0.000 | 21.01 |
| v | 2 | 1.19511 | 0.597557 | 869,665.9 | 0.000 | 59.5 | 0.85337 | 0.426683 | 231.16 | 0.000 | 50.20 |
| sp | 2 | 0.01691 | 0.008454 | 12,303.71 | 0.000 | 0.84 | 0.32668 | 0.163341 | 88.49 | 0.000 | 19.22 |
| P × v | 4 | 0.03315 | 0.008288 | 12,062.48 | 0.000 | 1.65 | 0.01613 | 0.004032 | 2.18 | 0.161 | 0.95 |
| P × sp | 4 | 0.00031 | 0.000078 | 114.23 | 0.000 | 0.02 | 0.00262 | 0.000656 | 0.36 | 0.834 | 0.15 |
| v × sp | 4 | 0.00336 | 0.00084 | 1222.63 | 0.000 | 0.17 | 0.12938 | 0.032346 | 17.52 | 0.001 | 7.61 |
| Error | 8 | 0.00001 | 0.000001 | 0.01477 | 0.001846 | ||||||
| Total | 26 | 2.00852 | 1.70009 | ||||||||
| Source | DF | SS | V | F | P | %c | SS | V | F | P | %c |
| P | 2 | 0.08522 | 0.042609 | 2.22 | 0.171 | 4.85 | 0.13072 | 0.06536 | 48.16 | 0.000 | 6.51 |
| v | 2 | 0.34716 | 0.173578 | 9.06 | 0.009 | 19.76 | 1.56634 | 0.783172 | 577.03 | 0.000 | 77.99 |
| sp | 2 | 0.23152 | 0.115758 | 6.04 | 0.025 | 13.18 | 0.1186 | 0.059299 | 43.69 | 0.000 | 5.91 |
| P × v | 4 | 0.31109 | 0.077772 | 4.06 | 0.044 | 17.71 | 0.08152 | 0.020381 | 15.02 | 0.001 | 4.06 |
| P × sp | 4 | 0.01005 | 0.002513 | 0.13 | 0.967 | 0.57 | 0.00522 | 0.001306 | 0.96 | 0.478 | 0.26 |
| v × sp | 4 | 0.61822 | 0.154555 | 8.07 | 0.007 | 35.20 | 0.09514 | 0.023786 | 17.53 | 0.001 | 4.74 |
| Error | 8 | 0.15326 | 0.019158 | 0.01086 | 0.001357 | ||||||
| Total | 26 | 1.75651 | 2.00841 | ||||||||
| Term | ||||
|---|---|---|---|---|
| P | 80 W | 80 W | 100 W | 80 W |
| v | 1.5 m/s | 1.5 m/s | 1.5 m/s | 1.5 m/s |
| Sp | Y | X | XY | Y |
| Significant factors and interactions | P, v, sp P × v, P × sp, v × sp | P, v, sp v × sp | v, sp P × v, v × sp | P, v, sp v × sp |
| Source | DF | SS | V | F | p | %c |
|---|---|---|---|---|---|---|
| P | 2 | 0.123268 | 0.061634 | 51.08 | 0.000 | 6.51 |
| v | 2 | 0.292462 | 0.146231 | 121.2 | 0.000 | 77.99 |
| sp | 2 | 0.007342 | 0.003671 | 3.04 | 0.104 | 5.91 |
| P × v | 4 | 0.015329 | 0.003832 | 3.18 | 0.077 | 4.06 |
| P × sp | 4 | 0.002688 | 0.000672 | 0.56 | 0.700 | 0.26 |
| v × sp | 4 | 0.009645 | 0.002411 | 2.00 | 0.188 | 4.74 |
| Error | 8 | 0.009653 | 0.001207 | |||
| Total | 26 | 0.460386 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sood, A.K.; Equbal, A.; Khan, Z.A.; Badruddin, I.A.; Hussien, M. FEM-Based Simulative Study for Multi-Response Optimization of Powder Bed Fusion Process. Mathematics 2022, 10, 2505. https://doi.org/10.3390/math10142505
Sood AK, Equbal A, Khan ZA, Badruddin IA, Hussien M. FEM-Based Simulative Study for Multi-Response Optimization of Powder Bed Fusion Process. Mathematics. 2022; 10(14):2505. https://doi.org/10.3390/math10142505
Chicago/Turabian StyleSood, Anoop Kumar, Azhar Equbal, Zahid A. Khan, Irfan Anjum Badruddin, and Mohamed Hussien. 2022. "FEM-Based Simulative Study for Multi-Response Optimization of Powder Bed Fusion Process" Mathematics 10, no. 14: 2505. https://doi.org/10.3390/math10142505
APA StyleSood, A. K., Equbal, A., Khan, Z. A., Badruddin, I. A., & Hussien, M. (2022). FEM-Based Simulative Study for Multi-Response Optimization of Powder Bed Fusion Process. Mathematics, 10(14), 2505. https://doi.org/10.3390/math10142505






