Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis
Abstract
:1. Introduction
2. Convective Magnetic Dynamo: Equations and Numerical Methods
2.1. Statement of the Problem
2.2. Numerical Techniques
2.3. Symmetries
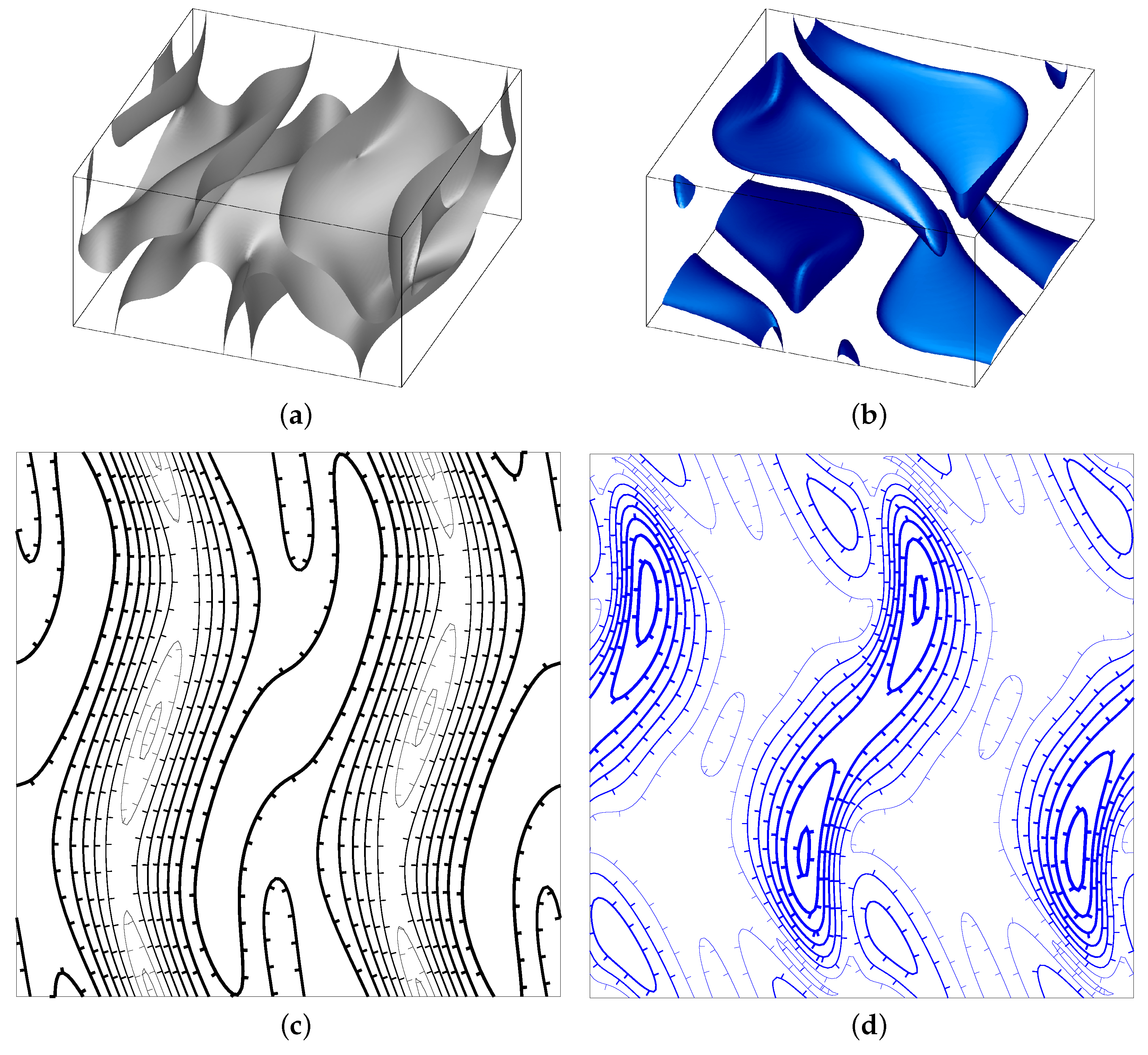
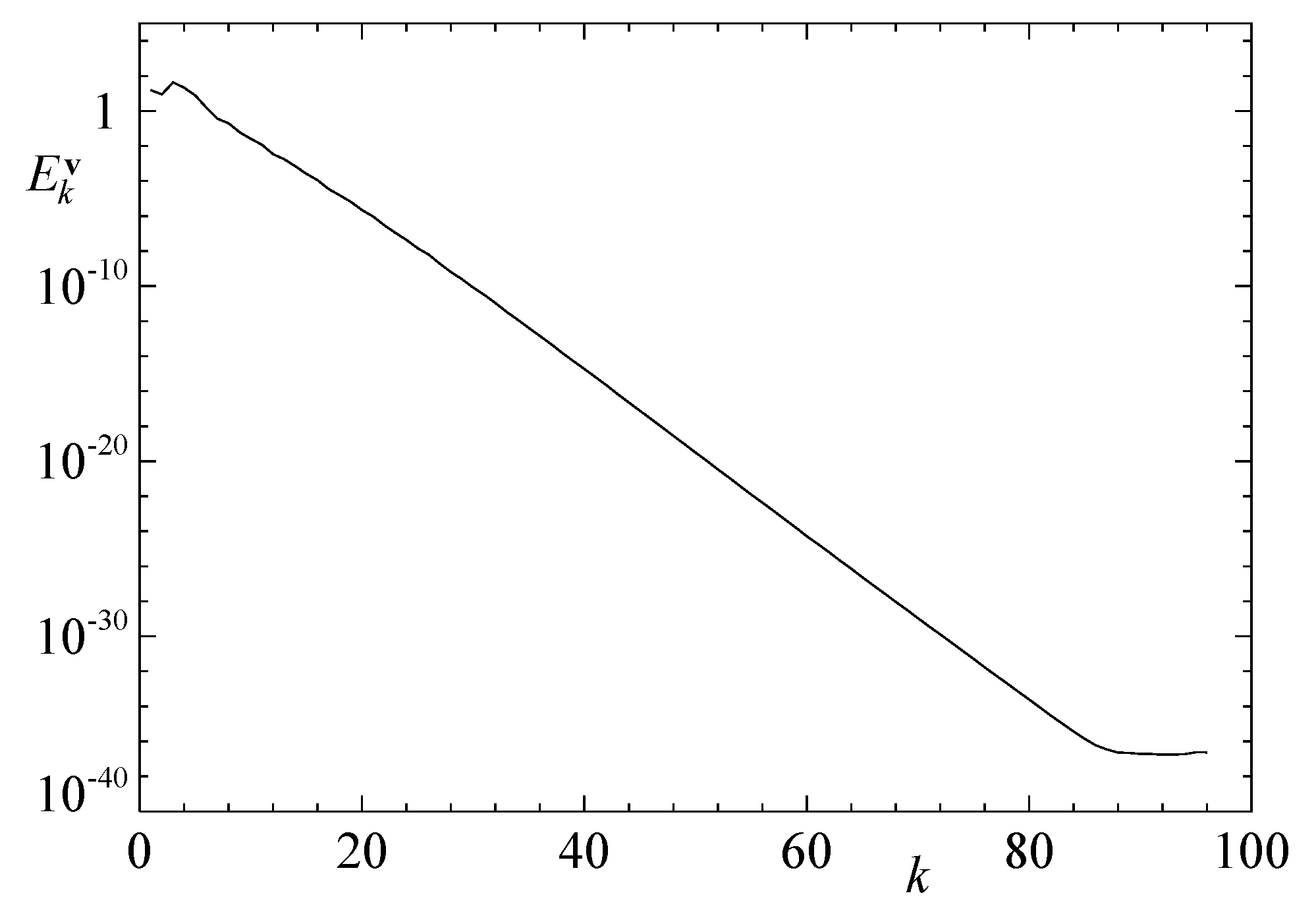
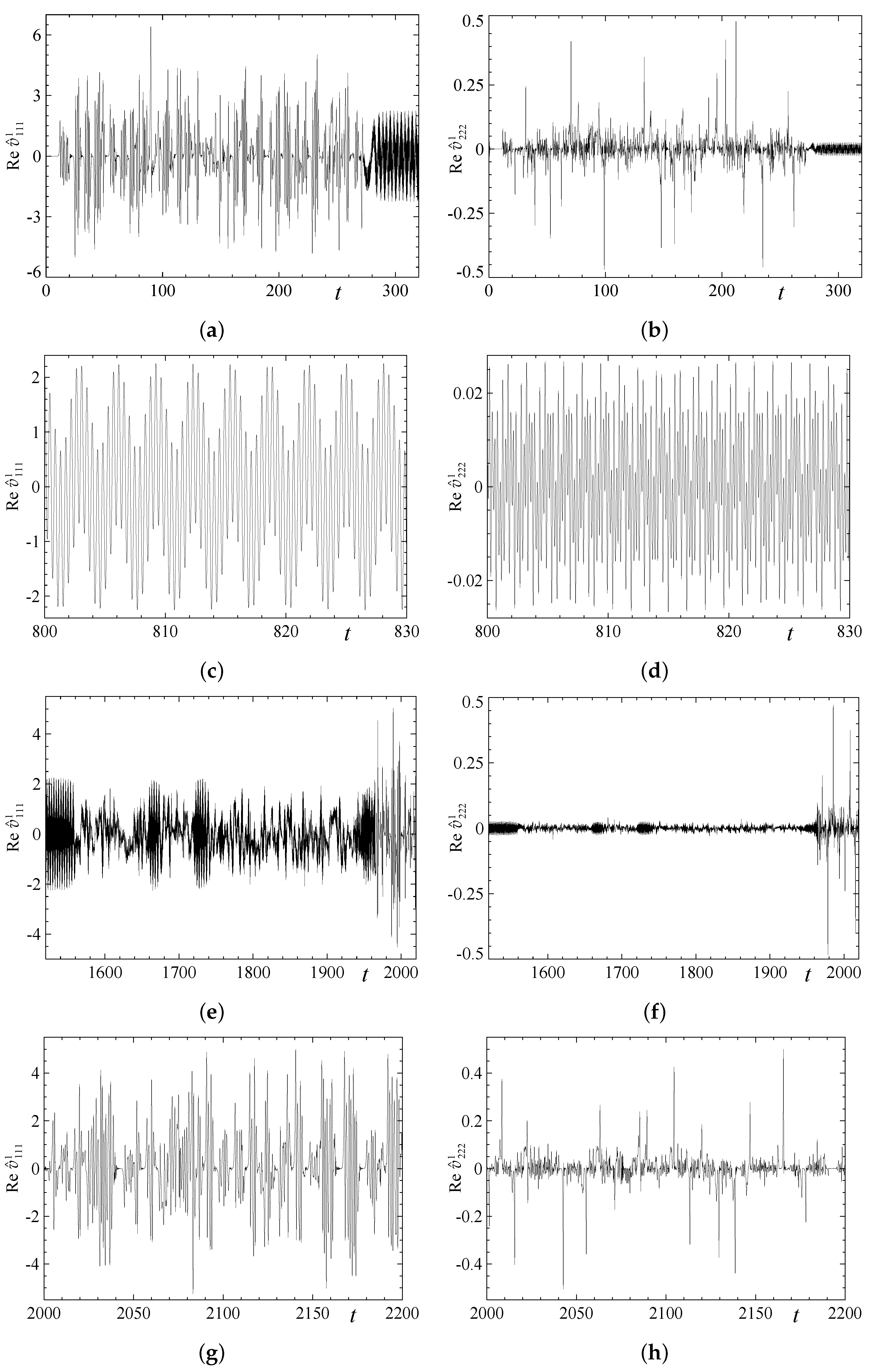
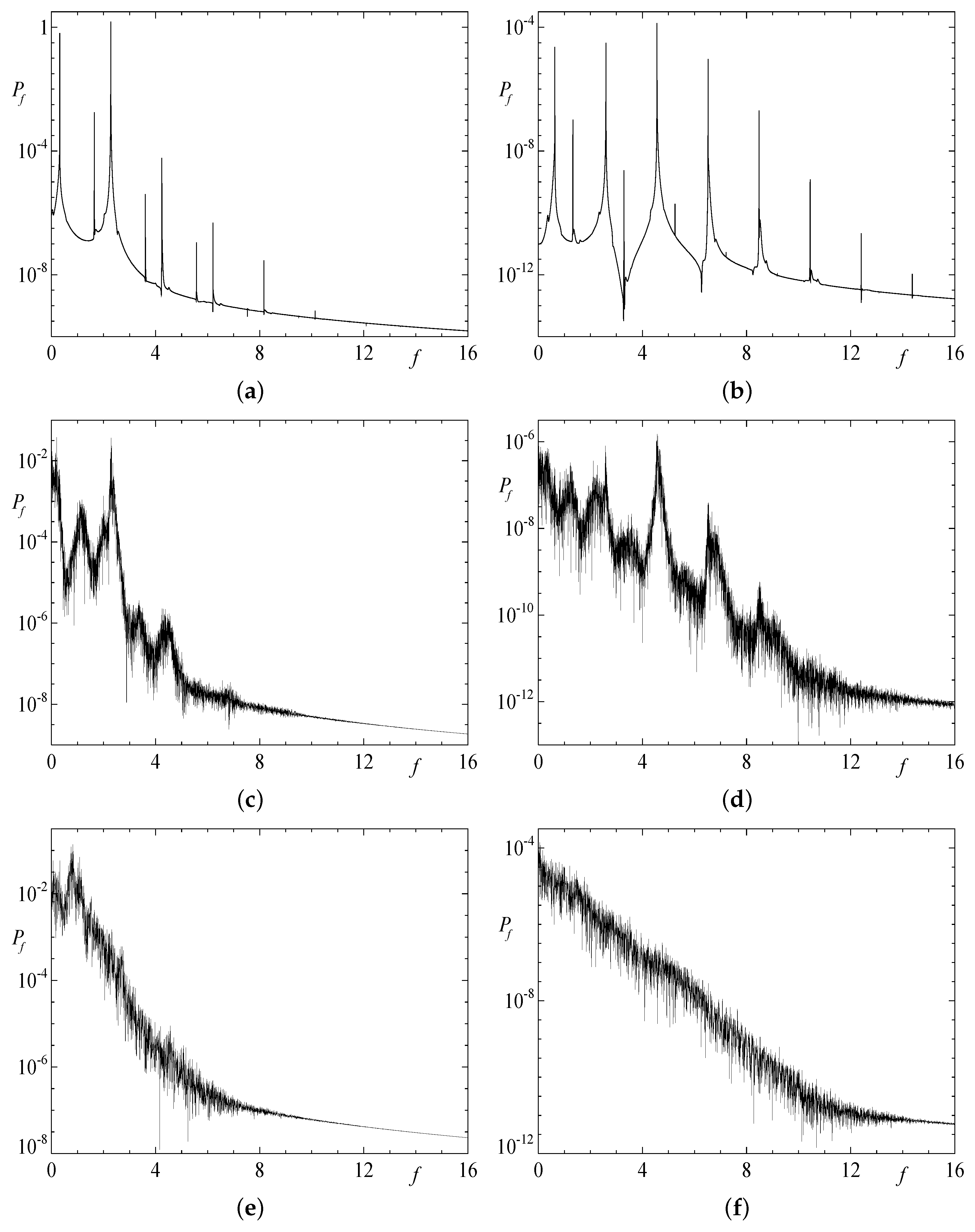
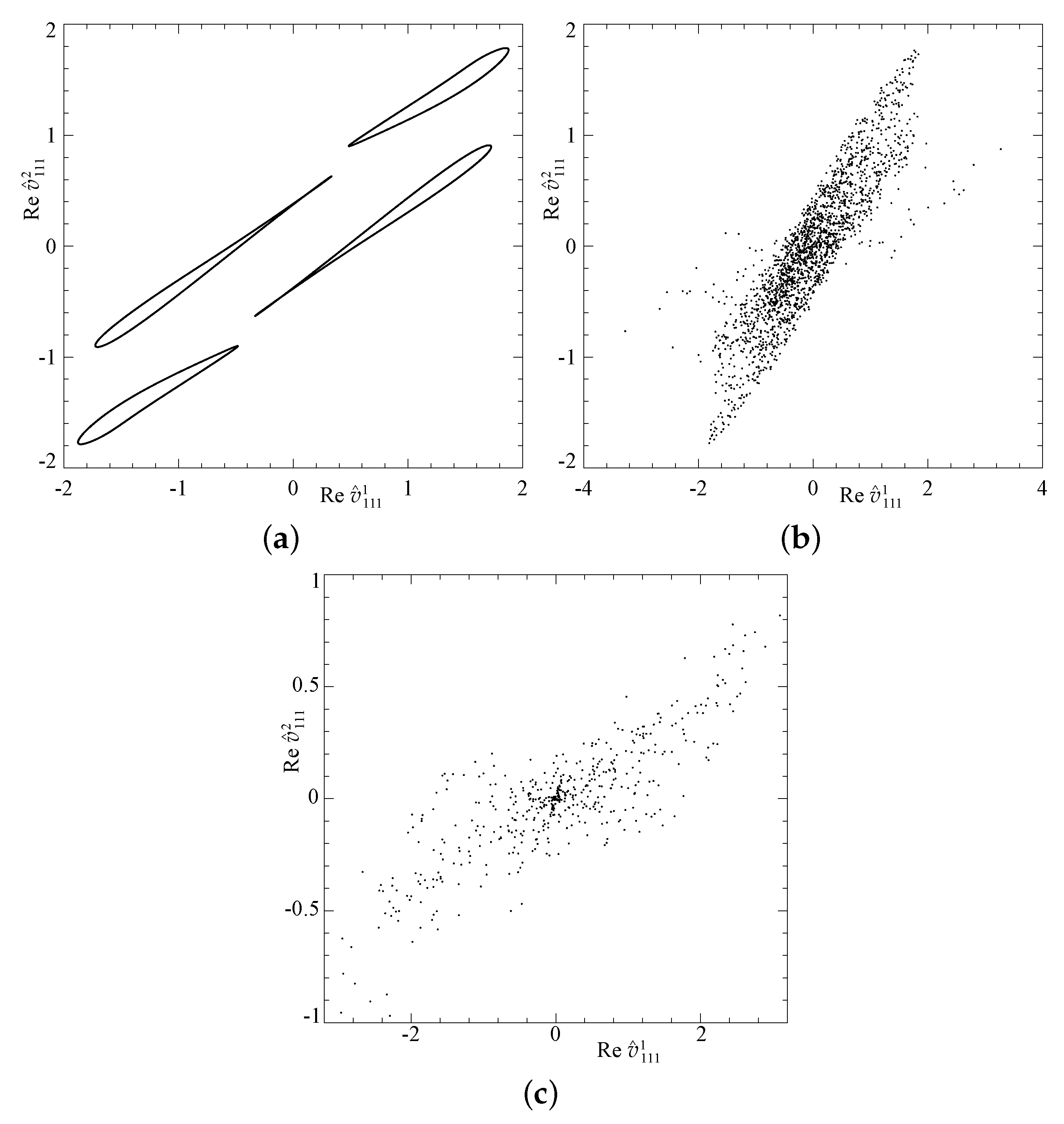
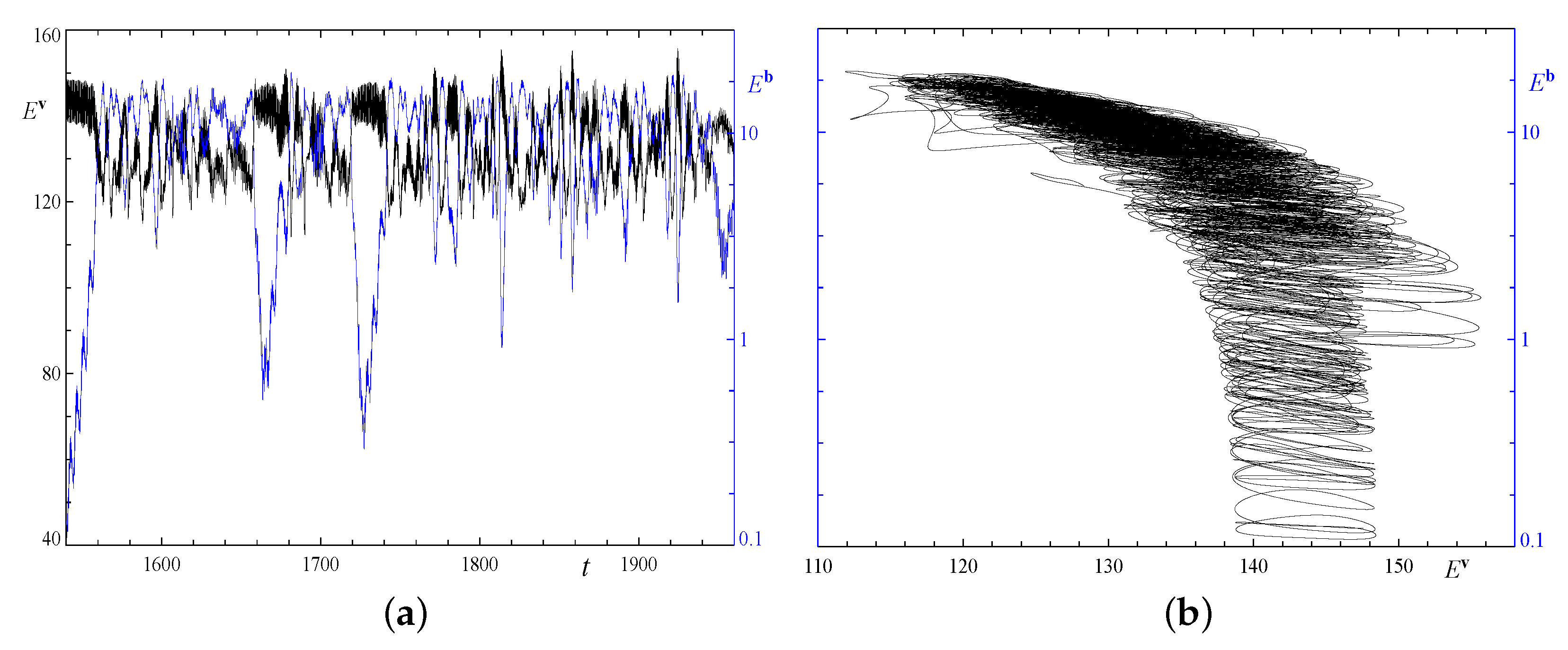
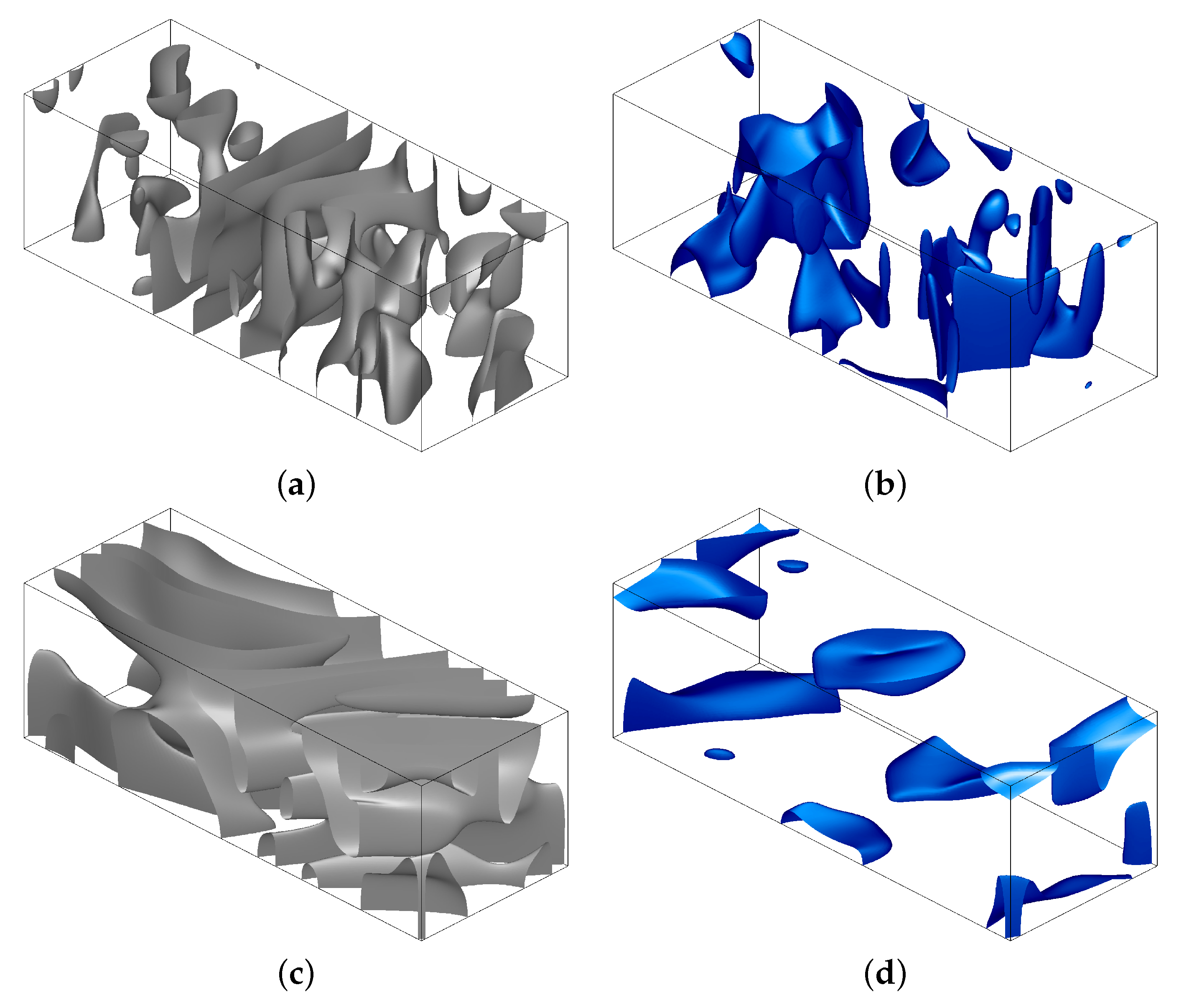
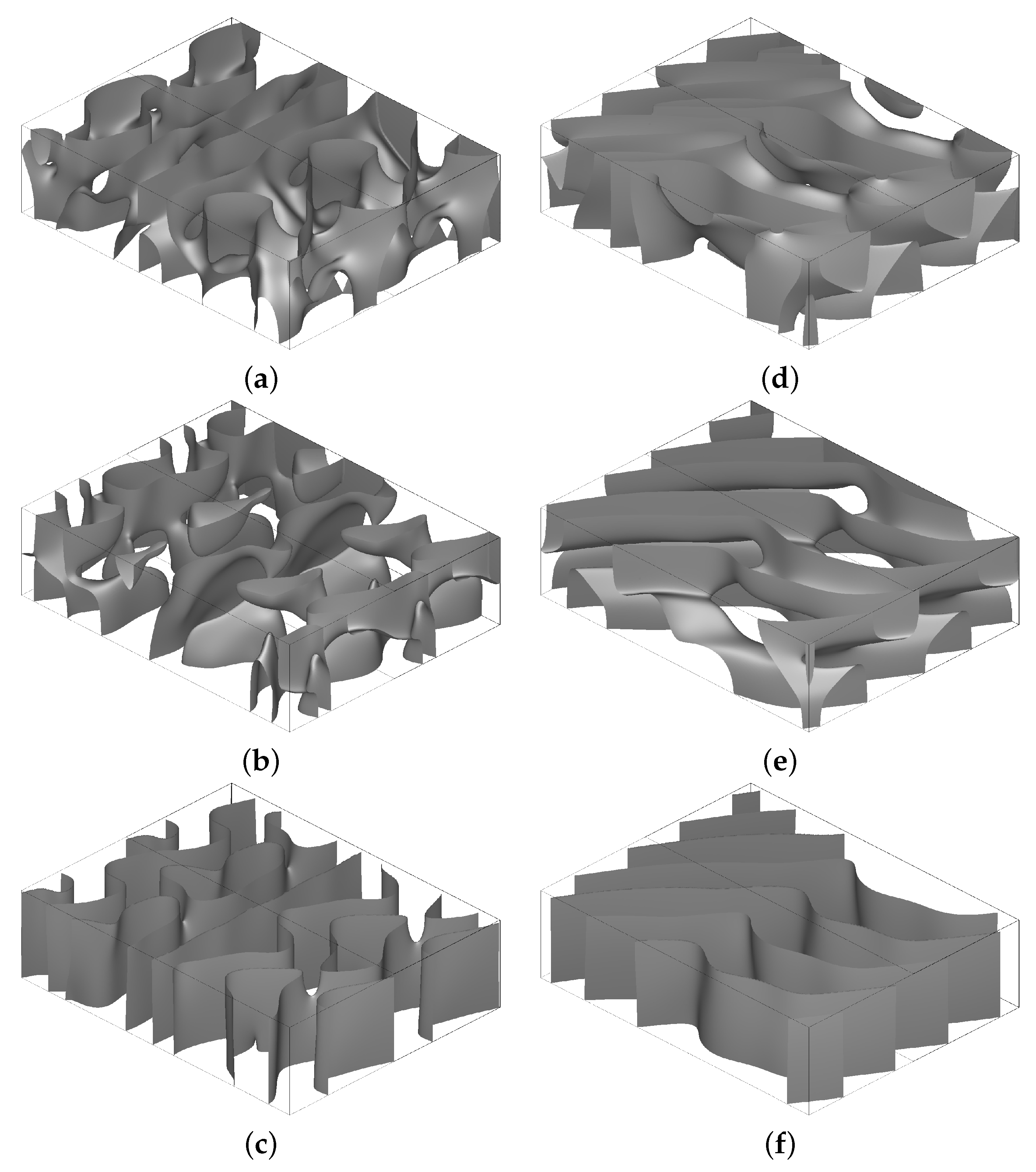
3. Results of Simulation
3.1. Regimes in the Elongated Boxes with the Periodicities 1x2/2x1
- All of them are quasiperiodic hydrodynamic travelling waves.
- The energy ranges and mean (over time) energies coincide.
- The basic frequencies are identical.
- The ranges of the magnetic Reynolds number estimates Rm and Rm and their mean (over time) values coincide.
- The ranges of the kinetic helicity and its temporal mean values are the same.
- The growth rates of the dominant magnetic modes are also equal.
- The flows have the symmetry in the 1x2 cell and in the 2x1 cell.
- Independence of (the energy of the discrepancy averaged over the periodicity cell, equal to the mean energy of the harmonics associated with wave vectors with a non-zero second component, is below 0.25 in the saturated regime for ; it shows the tendency to increase towards the ends of the intervals of almost regular helicity behaviour).
- (for , the mean energy of the discrepancy is below 24.0).
- (for , the mean energy of the discrepancy is below 14.4).
- The flow is approximately 1x1-periodic (for , the spatially averaged mean energy of the discrepancy, equal to the mean energy of the harmonics associated with wave vectors, whose first component is odd, is below 6.1).
- We have performed a hydrodynamic run (the magnetic field being set to zero at each step) in a 2x1-periodic fluid box for an initial condition that is the 2x1.1 flow at (close to the local minimum of the magnetic energy), where the -dependence is suppressed by setting to zero all harmonics associated with wave vectors, whose second component is non-zero. This run has converged fast (in roughly 15 time units) to the double-replicated R, the energy of discrepancy decreasing below .
- The energy of the discrepancies between the 2x1.1 flow at and the flows of the MHD steady states R, S and S is 0.2, 0.2 and 16.1, respectively.
3.2. Regimes in the Elongated Cells with the Periodicities 1x3/3x1
3.3. Regimes in the Elongated Cells with the Periodicities 1x4/4x1
3.4. Regimes in the -Periodicity Cells for
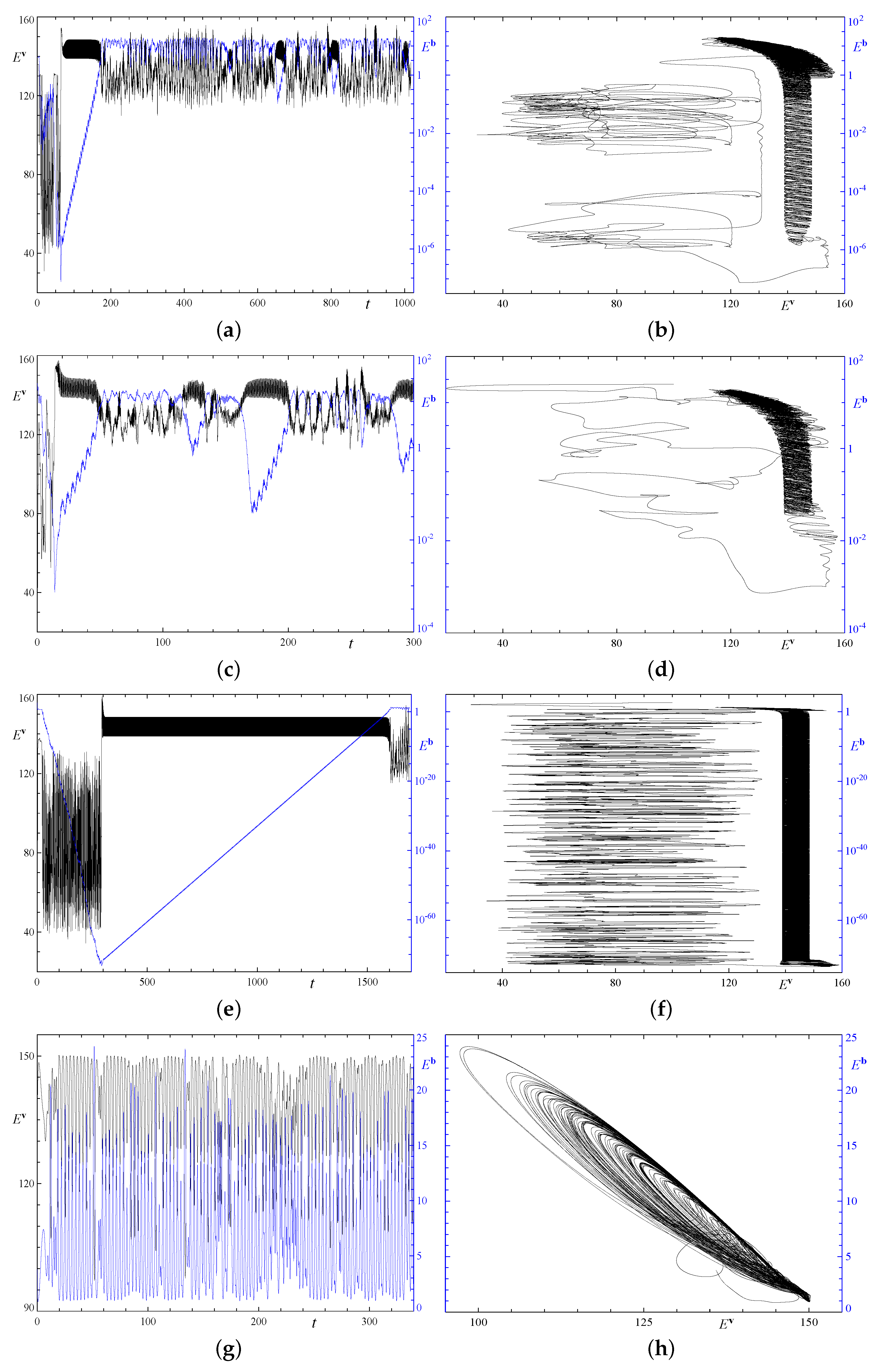
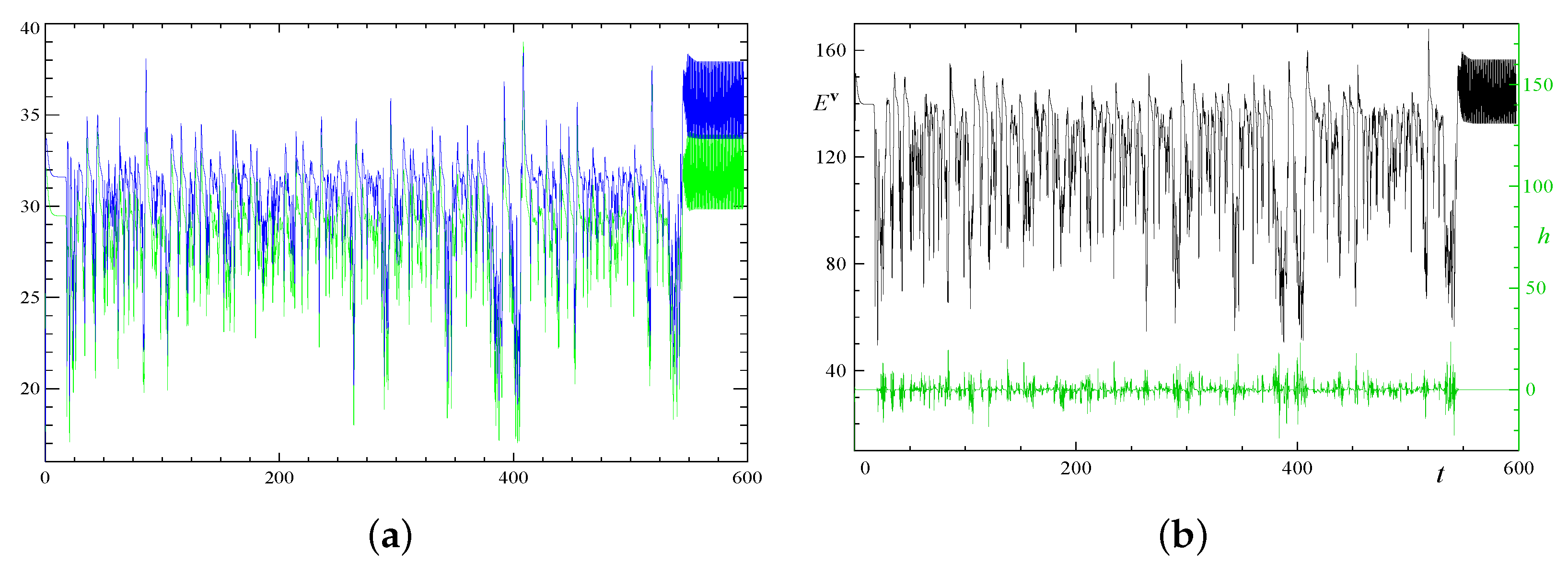
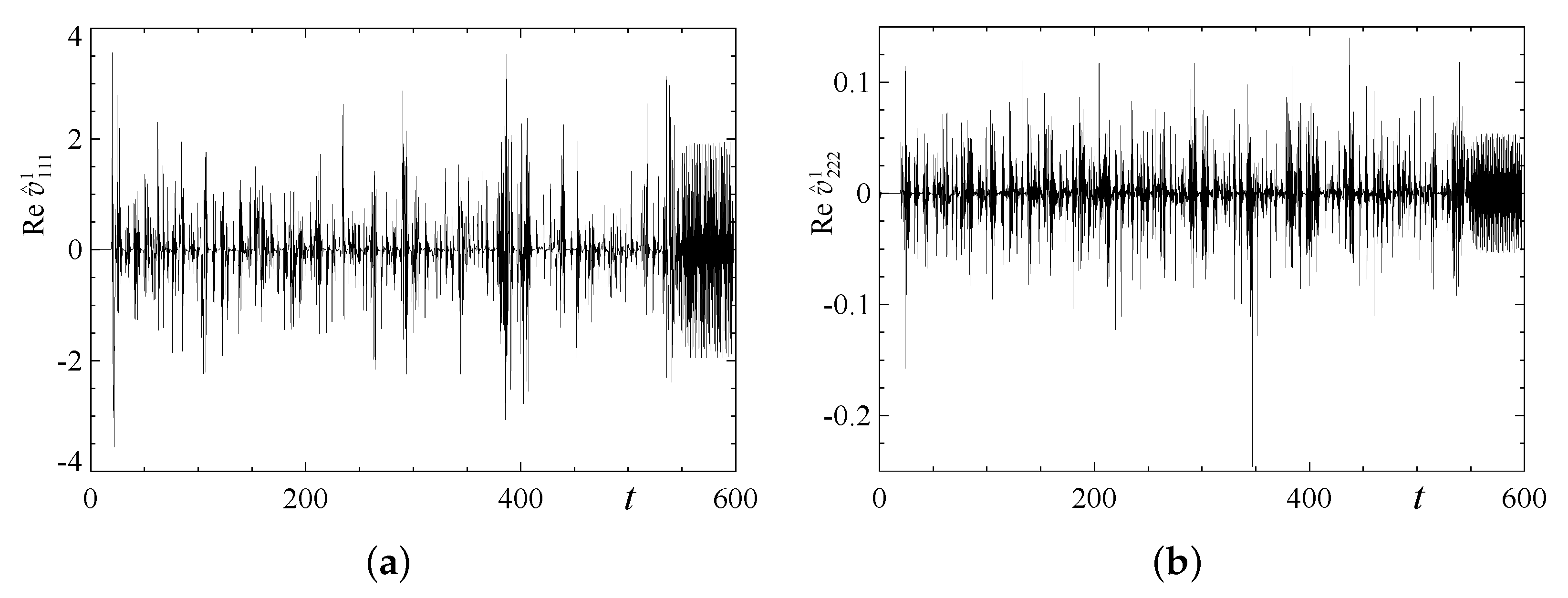
3.5. Videos of the Kinetic and Magnetic Energy Evolution
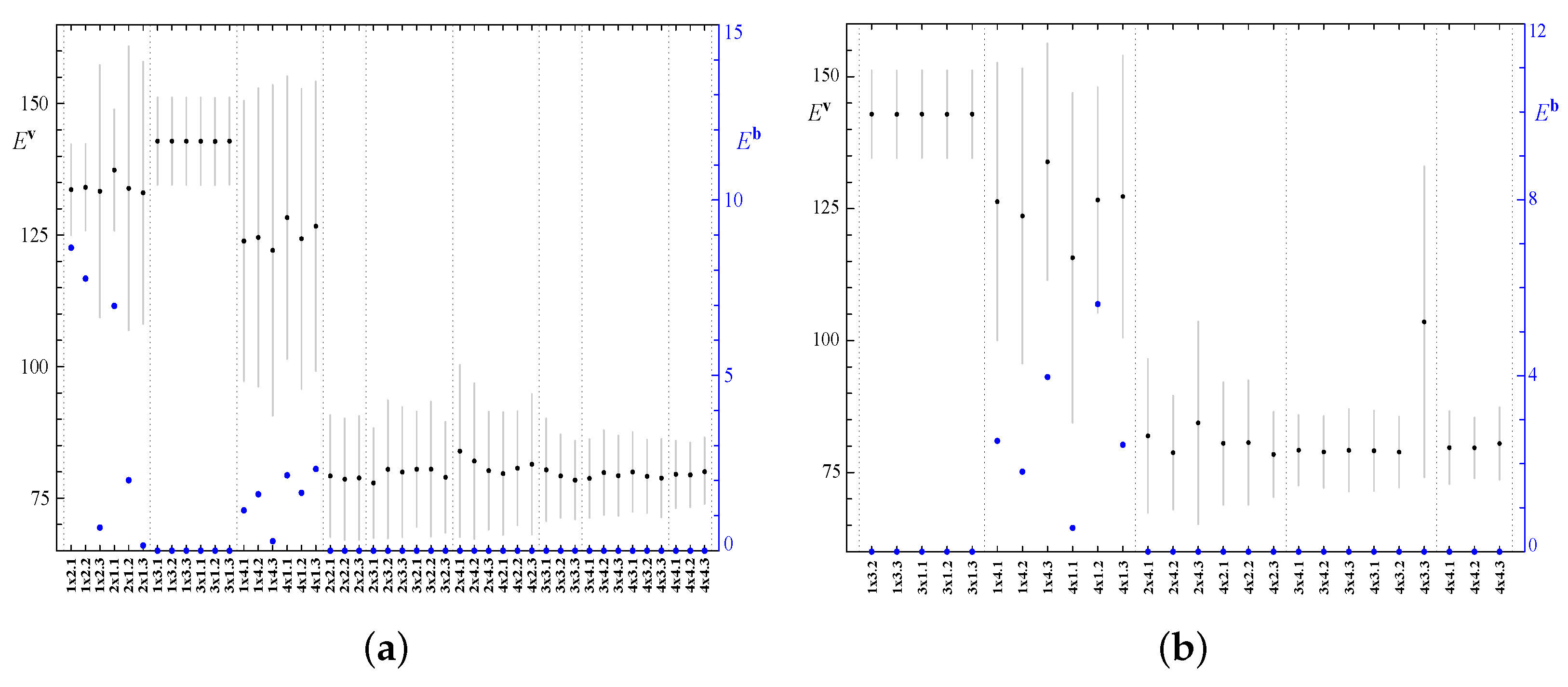
3.6. Analysis of Integral Parameters of the Regimes
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gilbert, W. De Magnete; Gilbert Club Revised English Translation, 1900; Chiswick Press: London, UK, 1600. [Google Scholar]
- Schuster, A. A critical examination of the possible causes of terrestrial magnetism. Proc. Phys. Soc. Lond. 1911, 24, 121–137. [Google Scholar] [CrossRef]
- Larmor, J. How could a rotating body such as the Sun become a magnet? In A Source Book in Astronomy and Astrophysics; Harvard University Press: Cambridge, MA, USA, 1900–1975; pp. 106–107. [Google Scholar]
- Larmor, J. Possible rotational origin of magnetic fields of Sun and Earth. Electr. Rev. 1919, 85, 412. [Google Scholar]
- Moffatt, H.K. Magnetic Field Generation in Electrically Conducting Fluids; CUP: Cambridge, UK, 1978. [Google Scholar]
- Moffatt, H.K.; Dormy, E. Self-Exciting Fluid Dynamos; CUP: Cambridge, UK, 2019. [Google Scholar]
- Priest, E.R. Solar Magnetohydrodynamics; D. Reidel: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Mestel, L. Stellar Magnetism; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Ruzmaikin, A.A.; Shukurov, A.M.; Sokoloff, D.D. Magnetic Fields of Galaxies; Kluwer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Soward, A.M.; Jones, C.A.; Hughes, D.W.; Weiss, N.O. (Eds.) Fluid Dynamics and Dynamos in Astrophysics and Geophysics; CRC Press: London, UK, 2005. [Google Scholar]
- Vainshtein, S.I.; Zeldovich, Y.; Ruzmaikin, A.A. The Turbulent Dynamo in Astrophysics; Nauka: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Jacobs, J.A. Reversals of the Earth’s Magnetic Field, 2nd ed.; CUP: Cambridge, UK, 1994. [Google Scholar]
- Ueda, S. The New View of the Earth: Moving Continents and Moving Oceans; WH Freeman: San Francisco, CA, USA, 1978. [Google Scholar]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle. Phys. Earth Planet. Inter. 1995, 91, 63–75. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 1995, 377, 203–209. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. An anelastic evolutionary geodynamo simulation driven by compositional and thermal convection. Phys. D Nonlinear Phenom. 1996, 97, 81–94. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. Rotation and magnetism of Earth’s inner core. Science 1996, 274, 1887–1891. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. Simulating the geodynamo. Contemp. Phys. 1997, 38, 269–288. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Coe, R.S.; Hongre, L.; Roberts, P.H. The role of the Earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 1999, 401, 885–890. [Google Scholar] [CrossRef]
- Roberts, P.H.; Glatzmaier, G.A. The geodynamo, past, present and future. Geophys. Astrophys. Fluid Dyn. 2001, 94, 47–84. [Google Scholar] [CrossRef]
- Parker, E.N. Hydrodynamic dynamo models. Astrophys. J. 1955, 122, 293–314. [Google Scholar] [CrossRef]
- Parker, E.N. Cosmical Magnetic Fields: Their Origin and Their Activity; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Braginsky, S.I. Self excitation of a magnetic field during the motion of a highly conducting fluid. J. Exper. Theor. Phys. 1964, 20, 726–735. [Google Scholar]
- Braginsky, S.I. Theory of the hydromagnetic dynamo. J. Exper. Theor. Phys. 1964, 47, 2178–2193. [Google Scholar]
- Braginsky, S.I. Kinematic models of the Earth’s hydromagnetic dynamo. Geomagn. Aeron. 1964, 4, 732–747. [Google Scholar]
- Braginsky, S.I. Magnetohydrodynamics of the Earth’s core. Geomagn. Aeron. 1964, 4, 898–916. [Google Scholar]
- Braginsky, S.I. Nearly axially symmetric model of the hydromagnetic dynamo of the Earth, I. Geomagn. Aeron. 1975, 15, 149–156. [Google Scholar]
- Braginsky, S.I. Nearly axially symmetric model of the hydromagnetic dynamo of the Earth, II. Geomagn. Aeron. 1978, 18, 340–351. [Google Scholar]
- Krause, F.; Rädler, K.-H. Mean-Field Magnetohydrodynamics and Dynamo Theory; Academic-Verlag: Berlin, Germany, 1980. [Google Scholar]
- Steenbeck, M.; Krause, F.; Rädler, K.-H. A calculation of the mean electromotive force in an electrically conducting fluid in turbulent motion, under the influence of Coriolis forces. Z. Naturforsch A 1966, 21, 369–376. [Google Scholar] [CrossRef]
- Rädler, K.-H. Mean-field dynamo theory: Early ideas and today’s problems. In Magnetohydrodynamics. Historical Evolution and Trends; Molokov, S., Moreau, R., Moffatt, K., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 55–72. [Google Scholar]
- Dubrulle, B.; Frisch, U. Eddy viscosity of parity-invariant flow. Phys. Rev. A 1991, 43, 5355–5364. [Google Scholar] [CrossRef]
- Zheligovsky, V.A. On the linear stability of steady space-periodic magnetohydrodynamic systems to large-scale perturbations. Phys. Solid Earth 2003, 39, 409–418. [Google Scholar]
- Zheligovsky, V.A. Large-scale perturbations of magnetohydrodynamic regimes: Linear and weakly nonlinear stability theory. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 829. [Google Scholar]
- Lanotte, A.; Noullez, A.; Vergassola, M.; Wirth, A. Large-scale dynamo by negative magnetic eddy diffusivities. Geophys. Astrophys. Fluid Dyn. 1999, 91, 131–146. [Google Scholar] [CrossRef]
- Vishik, M.M. Periodic dynamo. In Mathematical Methods in Seismology and Geodynamics; Keilis-Borok, V.I., Levshin, A.L., Eds.; Nauka: Moscow, Russia, 1986; pp. 186–215. (In Russian) [Google Scholar]
- Vishik, M.M. Periodic dynamo. II. In Numerical Modelling and Analysis of Geophysical Processes; Keilis-Borok, V.I., Levshin, A.L., Eds.; Nauka: Moscow, Russia, 1987; pp. 12–22. [Google Scholar]
- Zheligovsky, V.A.; Podvigina, O.M.; Frisch, U. Dynamo effect in parity-invariant flow with large and moderate separation of scales. Geophys. Astrophys. Fluid Dyn. 2001, 95, 227–268. [Google Scholar] [CrossRef]
- Gama, S.; Chaves, M. Time evolution of the eddy viscosity in two-dimensional Navier–Stokes flow. Phys. Rev. Lett. 2000, 61, 2118–2120. [Google Scholar]
- Gama, S.; Vergassola, M.; Frisch, U. Negative eddy viscosity in isotropically forced two-dimensional flow: Linear and nonlinear dynamics. J. Fluid Mech. 1994, 260, 95–126. [Google Scholar] [CrossRef]
- Wirth, A.; Gama, S.; Frisch, U. Eddy viscosity of three-dimensional flow. J. Fluid Mech. 1995, 288, 249–264. [Google Scholar] [CrossRef]
- Roberts, G.O. Spatially periodic dynamos. Phil. Trans. Roy. Soc. Lond. A 1970, 266, 535–558. [Google Scholar]
- Roberts, G.O. Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. Roy. Soc. Lond. A 1972, 271, 411–454. [Google Scholar]
- Chertovskih, R.A.; Zheligovsky, V.A. Linear perturbations of the Bloch type of space-periodic magnetohydrodynamic steady states. 2022. manuscript in preparation. [Google Scholar]
- Zheligovsky, V.A.; Chertovskih, R.A. On kinematic generation of magnetic modes of the Bloch type. Phys. Solid Earth 2020, 56, 104–117. [Google Scholar] [CrossRef]
- Meneguzzi, M.; Pouquet, A. Turbulent dynamos driven by convection. J. Fluid Mech. 1989, 205, 297–318. [Google Scholar] [CrossRef]
- Demircan, A.; Seehafer, N. Dynamo in asymmetric square convection. Geophys. Astrophys. Fluid Dyn. 2002, 96, 461–479. [Google Scholar] [CrossRef]
- Matthews, P.C. Dynamo action in simple convective flows. Proc. R. Soc. Lond. A 1999, 455, 1829–1840. [Google Scholar] [CrossRef]
- Chertovskih, R.; Gama, S.M.A.; Podvigina, O.; Zheligovsky, V. Dependence of magnetic field generation by thermal convection on the rotation rate: A case study. Phys. D 2010, 239, 1188–1209. [Google Scholar] [CrossRef]
- Gertsenshtein, S.Y.; Zheligovsky, V.A.; Podvigina, O.M.; Chertovskih, R.A. On magnetic field generation by three-dimensional convective flows of conducting fluid in a rotating horizontal layer. Dokl. Akad. Nauk. 2007, 417, 613–615. [Google Scholar] [CrossRef]
- Gertsenshtein, S.Y.; Chertovskikh, R.A. Generation of a magnetic field by convective flows in a rotating horizontal layer. Fluid Dyn. 2008, 43, 248–256. [Google Scholar] [CrossRef]
- Zheligovsky, V.A. Amplitude equations for weakly nonlinear two-scale perturbations of free hydromagnetic convective regimes in a rotating layer. Geophys. Astrophys. Fluid Dyn. 2009, 103, 397–420. [Google Scholar] [CrossRef]
- Chertovskih, R.; Zheligovsky, V. Large-scale weakly nonlinear perturbations of convective magnetic dynamos in a rotating layer. Physica D 2015, 313, 99–116. [Google Scholar] [CrossRef]
- Donzis, D.A.; Gibbon, J.D.; Gupta, A.; Kerr, R.M.; Pandit, R.; Vincenzi, D. Vorticity moments in four numerical simulations of the 3D Navier—Stokes equations. J. Fluid Mech. 2013, 732, 316–331. [Google Scholar] [CrossRef]
- Podvigina, O.M. Magnetic field generation by convective flows in a plane layer. Eur. Phys. J. B 2006, 50, 639–652. [Google Scholar] [CrossRef]
- Podvigina, O.M. Magnetic field generation by convective flows in a plane layer: The dependence on the Prandtl number. Geophys. Astrophys. Fluid Dyn. 2008, 102, 409–433. [Google Scholar] [CrossRef]
- Chertovskih, R.; Rempel, E.L.; Chimanski, E.V. Magnetic field generation by intermittent convection. Phys. Lett. A 2017, 381, 3300–3306. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Dover: Mineola, NY, 2001. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Peyret, R. Spectral Methods for Incompressible Viscous Flow; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Cox, S.M.; Matthews, P.C. Exponential time differencing for stiff systems. J. Comput. Phys. 2002, 176, 430–455. [Google Scholar] [CrossRef]
- Chertovskih, R.; Chimanski, E.V.; Rempel, E.L. Route to hyperchaos in Rayleigh–Bénard convection. Europhysics Lett. 2015, 112, 14001. [Google Scholar] [CrossRef]
- Hutt, A.; Graben, P. Sequences by metastable attractors: Interweaving dynamical systems and experimental data. Front. Appl. Math. Stat. 2017, 3, 11. [Google Scholar] [CrossRef]
- Doering, C.R.; Gibbon, J.D. Applied Analysis of the Navier–Stokes Equations; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Arnold, V.I.; Korkina, E.I. The growth of a magnetic field in a three-dimensional incompressible flow. Vestnik Moscow State Univ. Ser. Math. 1983, 3, 43–46. (In Russian) [Google Scholar]
- Zheligovsky, V.A. A kinematic magnetic dynamo sustained by a Beltrami flow in a sphere. Geophys. Astrophys. Fluid Dyn. 1993, 73, 217–254. [Google Scholar] [CrossRef]
- Zheligovsky, V.A.; Galloway, D.J. Dynamo action in Christopherson hexagonal flow. Geophys. Astrophys. Fluid Dyn. 1998, 88, 277–293. [Google Scholar] [CrossRef]
- Kosobokov, V.G. On a regularity in the sequence of the Earth’s magnetic field reversals. Earth Sci. Sect. 1996, 345, 128–132. [Google Scholar]
- Rasskazov, A.; Chertovskih, R.; Zheligovsky, V. Magnetic field generation by pointwise zero-helicity three-dimensional steady flow of incompressible electrically conducting fluid. Phys. Rev. E 2018, 97, 043201. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. The magnetic field in the two-dimensional motion of a conducting turbulent fluid. J. Exper. Theor. Phys. 1957, 4, 460–462. [Google Scholar]
- Zheligovsky, V. Space analyticity and bounds for derivatives of solutions to the evolutionary equations of diffusive magnetohydrodynamics. Mathematics 2021, 9, 1789. [Google Scholar] [CrossRef]
- Foias, C.; Guillopé, C.; Temam, R. New a priori estimates for Navier–Stokes equations in dimension 3. Comm. Partial. Diff. Equations 1981, 6, 329–359. [Google Scholar] [CrossRef]
- Gibbon, J.D. Weak and strong solutions of the 3D Navier–Stokes equations and their relation to a chessboard of convergent inverse length scales. J. Nonlin. Sci. 2019, 29, 215–228. [Google Scholar] [CrossRef]
- Gibbon, J.D. Regularity and singularity in solutions of the three-dimensional Navier–Stokes equations. Proc. R. Soc. A 2010, 466, 2587–2604. [Google Scholar] [CrossRef]
- Gibbon, J.D. A hierarchy of length scales for weak solutions of the three-dimensional Navier–Stokes equations. Comm. Math. Sci. 2011, 10, 131–136. [Google Scholar] [CrossRef]
- Gibbon, J.D. Conditional regularity of solutions of the three-dimensional Navier–Stokes equations and implications for intermittency. J. Math. Phys. 2012, 53, 115608. [Google Scholar] [CrossRef]






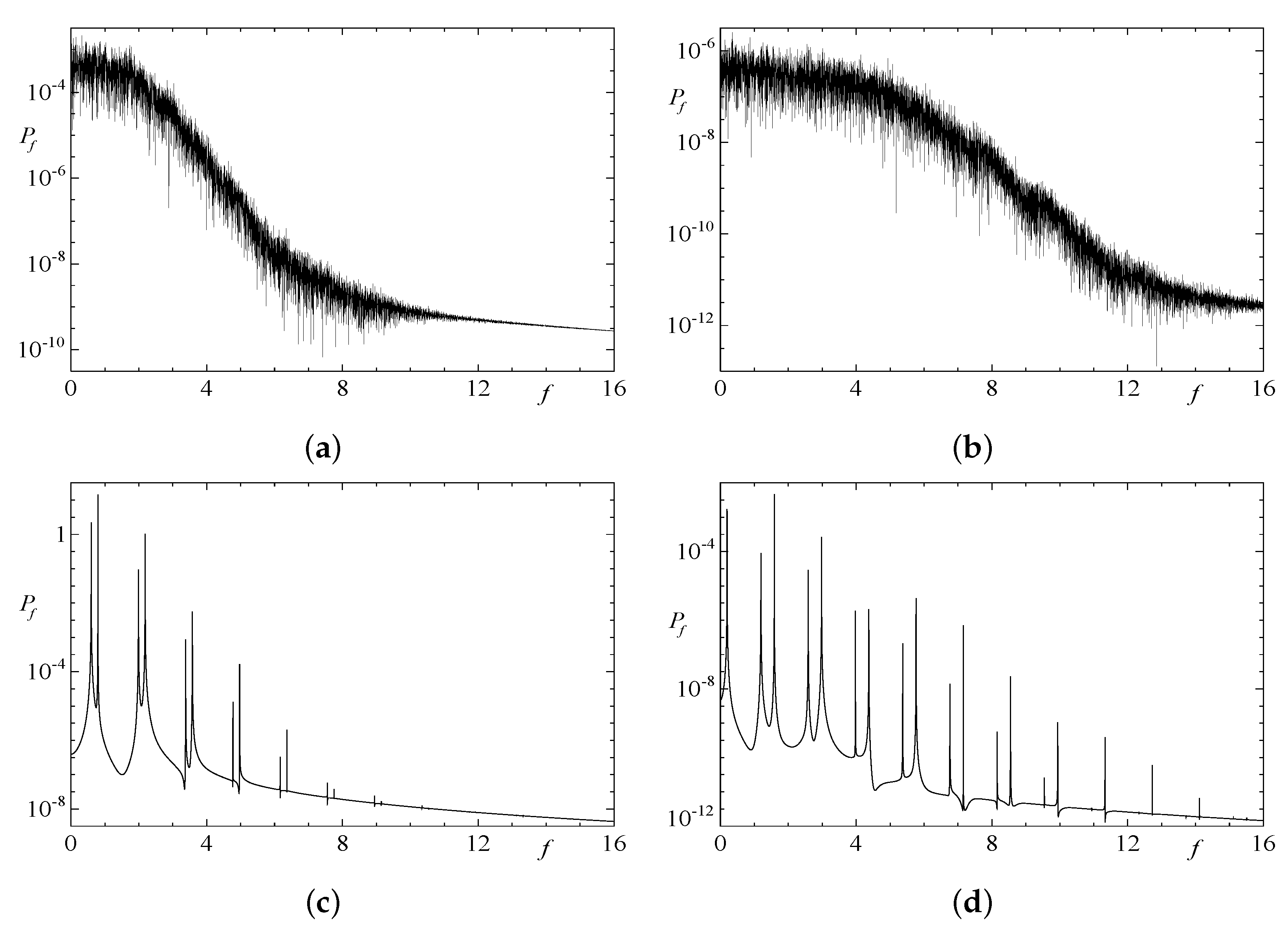
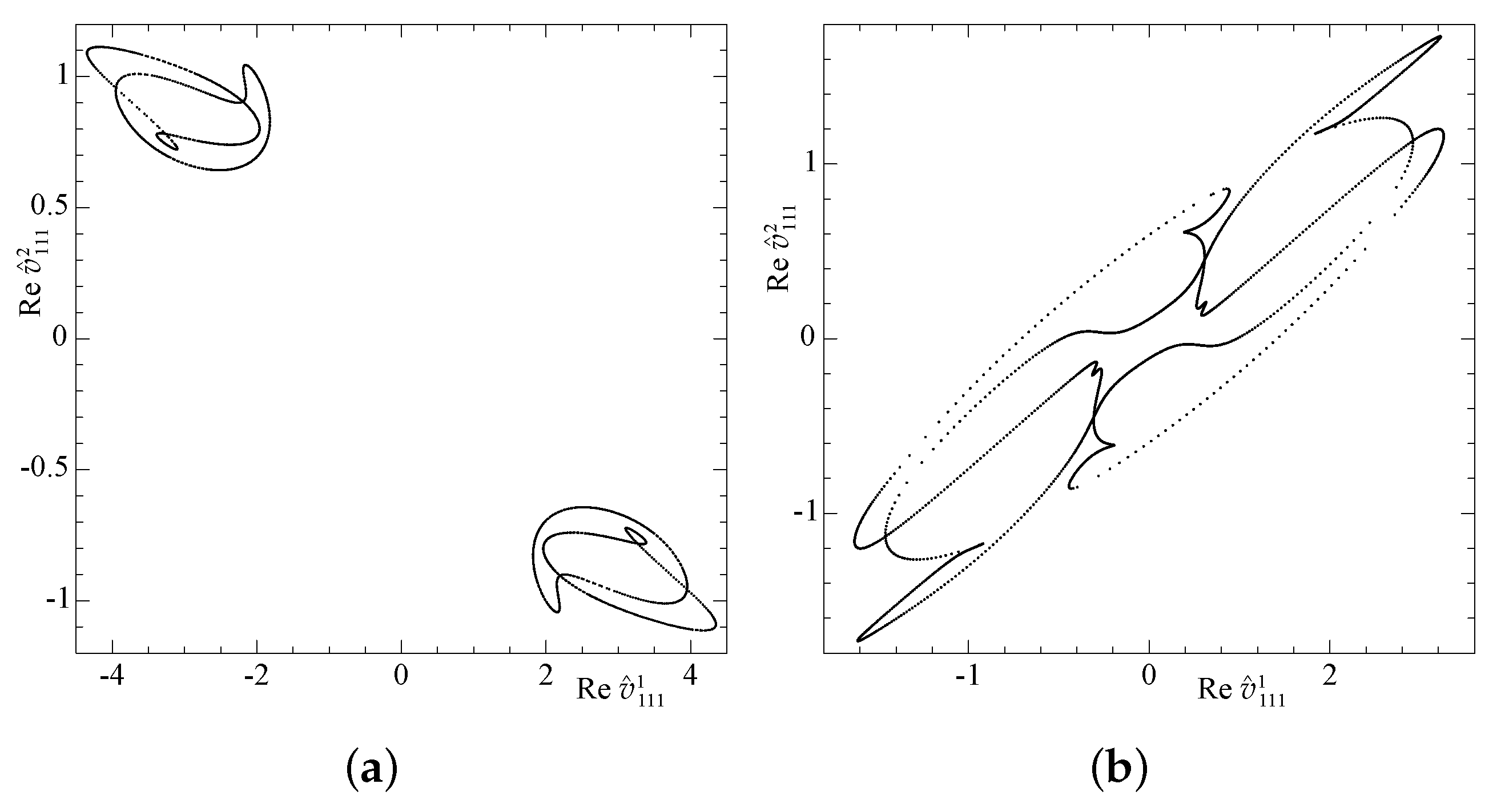

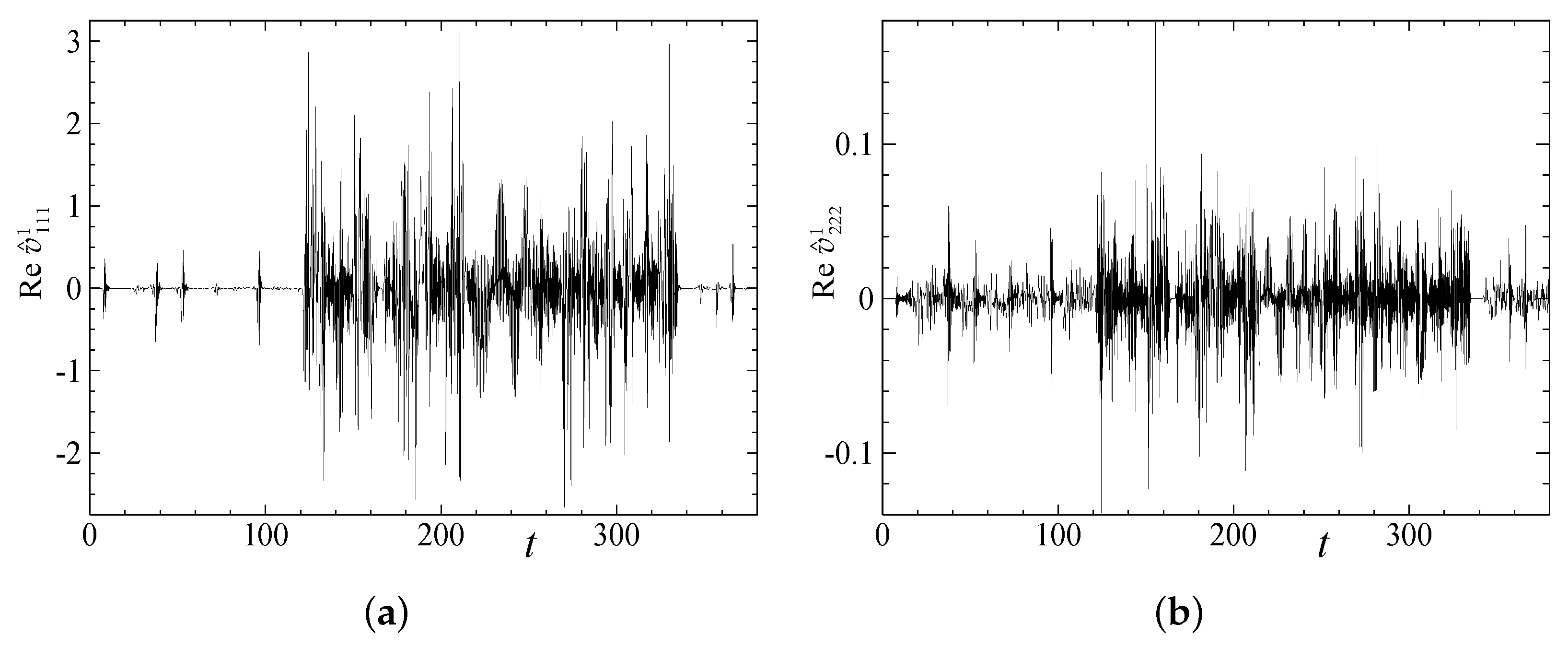
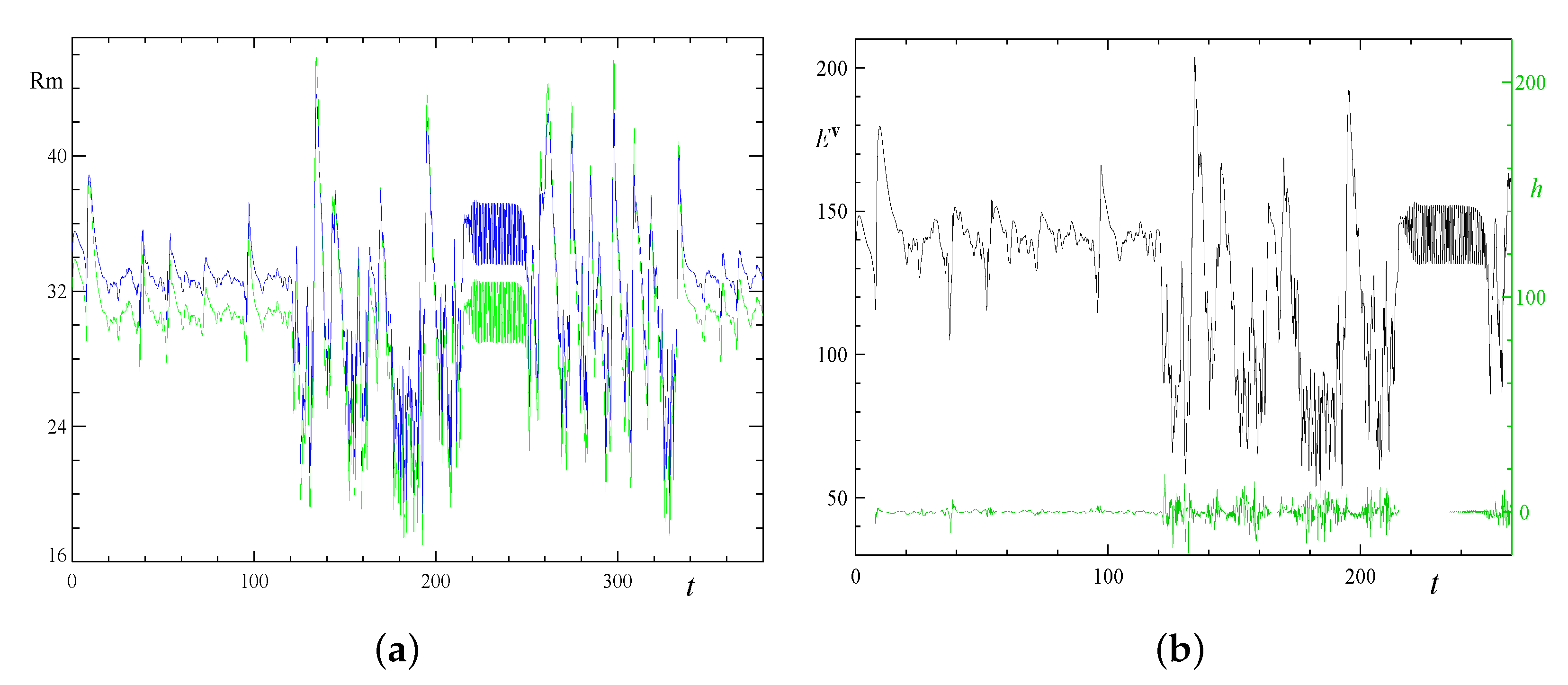
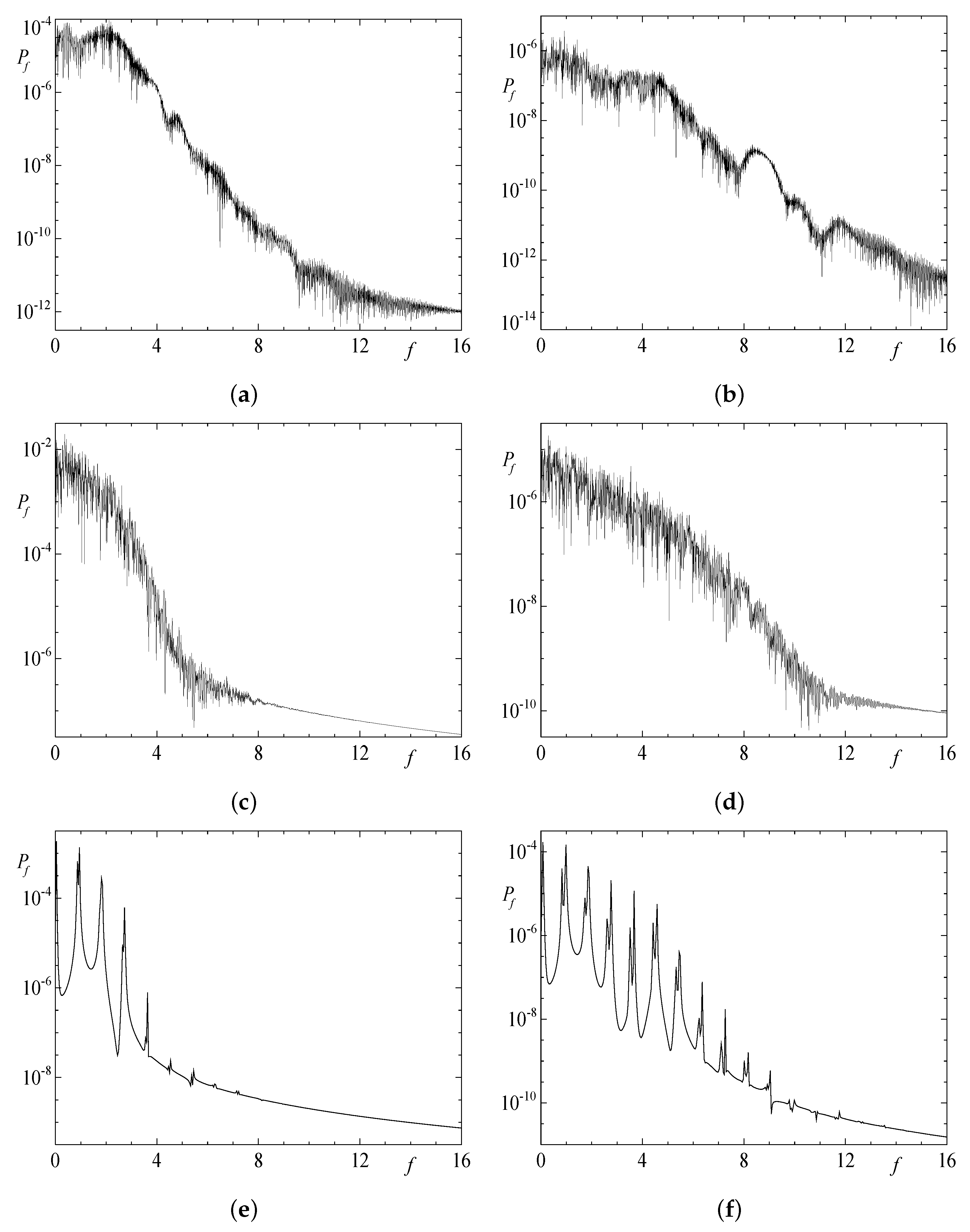
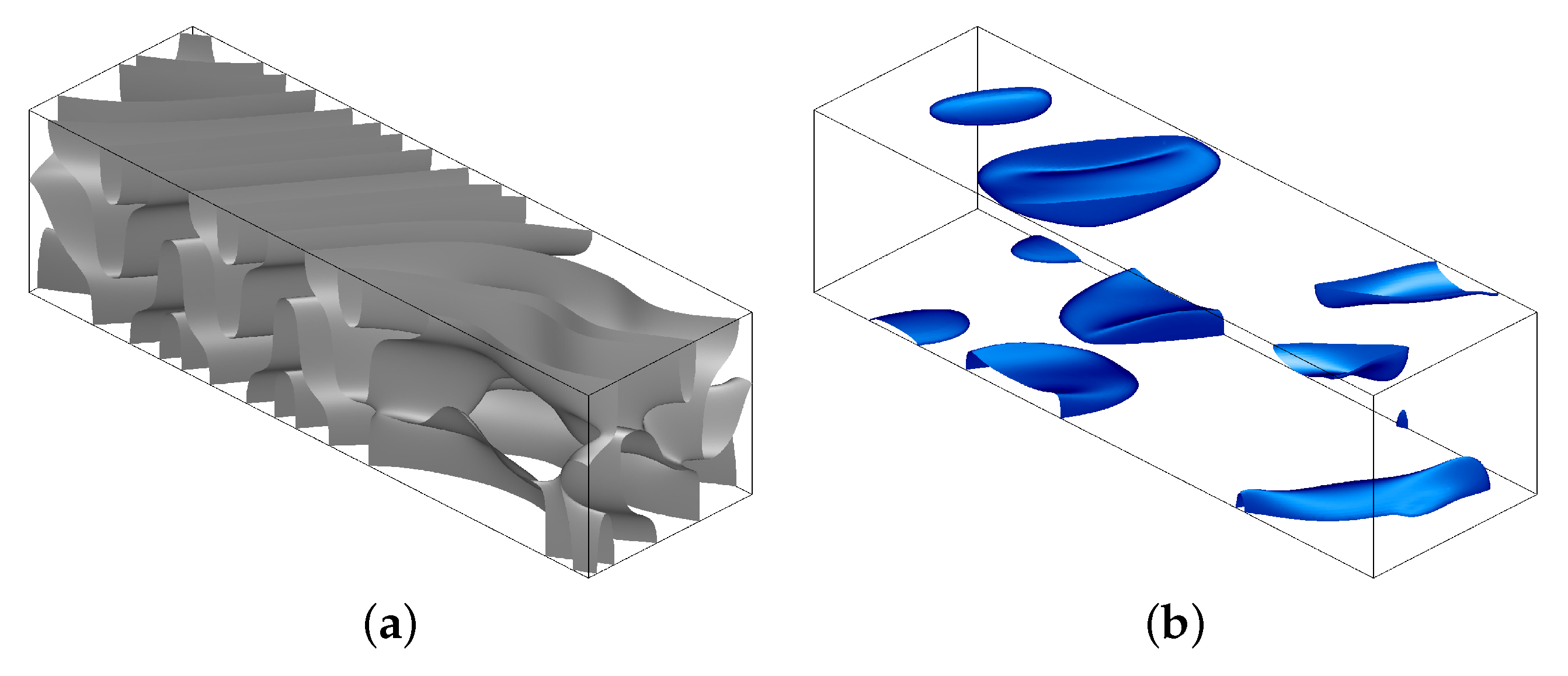

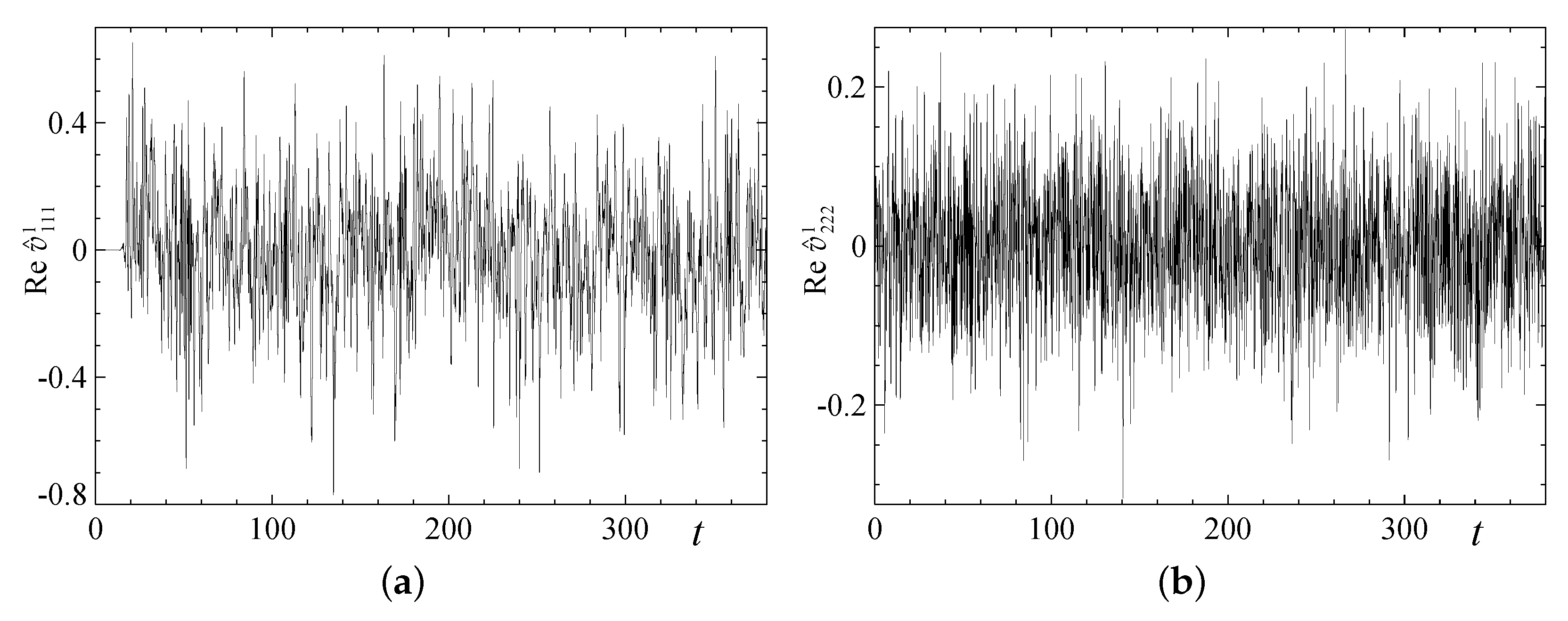


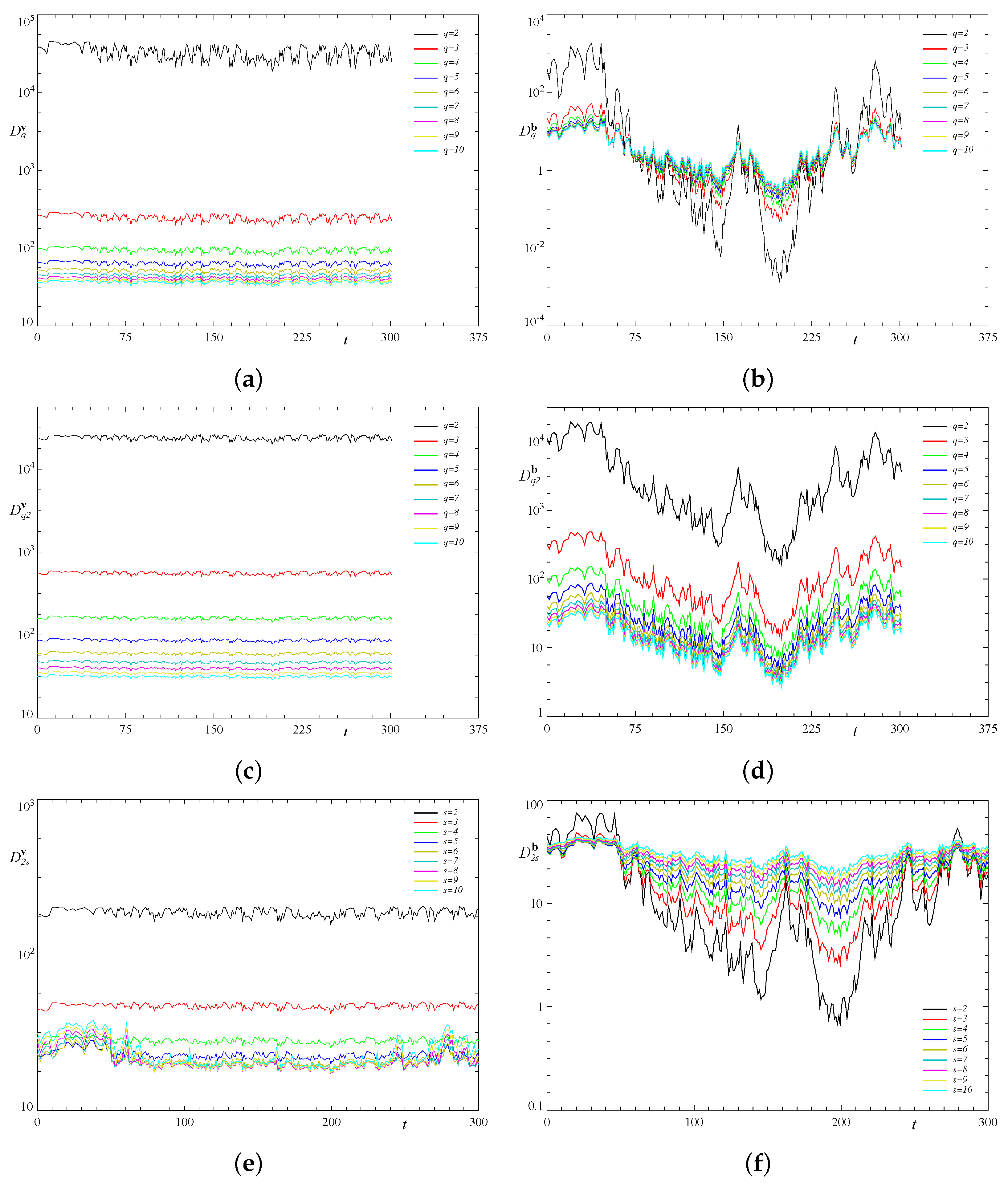
| 1 | 2 | 3 | 4 | |
| 1 | 15.8,9.6,21.8 | 21.4,8.0,24.6 | 7.8/11.7,4.3/7.2,12.7/17.6 | |
| 15.2,12.2,21.7 | 9.9/13.4,6.3/10.5,15.9/18.8 | 7.2/11.6,4.3/6.3,12.0/16.8 | ||
| 17.1,9.6,23.4 | 11.1/13.6,6.0/13.0,16.0/19.6 | 9.5/11.0,4.2/6.8,13.6/16.2 | ||
| 2 | 16.2,11.4,21.8 | 36.0,14.1,38.0 | 25.3,9.0,27.3 | 18.8/12.2,6.5/7.7,20.8/17.1 |
| 15.0,8.5,20.5 | 37.8,15.0,38.1 | 24.6,7.9,26.3 | 18.3/11.2,6.5/7.6,20.0/15.7 | |
| 25.0,9.0,27.2 | 36.9,14.6,38.0 | 24.9,8.5,26.5 | 18.6/10.9,5.9/7.2,20.2/15.7 | |
| 3 | 9.8/14.9,5.7/12.1,14.7/20.9 | 25.1,8.2,26.6 | 24.7,8.8,27.1 | 18.4/11.8,6.4/7.2,20.9/17.17 |
| 9.4/14.1,5.6/11.4,14.7/20.1 | 25.0,8.7,26.9 | 19.7,8.4,25.3 | 18.2/10.2,6.1/7.6,20.3/15.6 | |
| 10.0/13.9,5.8/11.0,15.1/19.2 | 25.2,8.8,27.2 | 18.9,8.3,24.6 | 18.1/10.4,6.1/7.3,20.6/15.2 | |
| 4 | 7.4/11.6,4.0/6.9,13.1/16.7 | 18.4/12.6,5.9/7.3,20.7/17.5 | 18.0/23.8,6.3/7.5,20.4/26.2 | 14.1/24.4,6.1/7.9,19.5/26.5 |
| 7.3/10.8,4.2/7.3,13.2/16.3 | 18.8/11.4,6.0/7.5,20.5/16.6 | 18.6/11.0,6.0/6.9,20.3/14.6 | 18.1/10.8,5.6/6.8,20.5/15.5 | |
| 7.2/11.3,4.1/7.2,12.9/15.7 | 18.5/10.6,6.3/7.5,20.6/16.1 | 18.6/10.8,6.2/7.6,20.9/15.7 | 10.7/10.2,5.7/7.2,16.1/15.4 |
| Run | A/MS | Time | Type | Symmetries | ||||
| 1x2.1 | A | 135.92 | 109.88 | 133.34 | 156.64 | [75:1016.90] | MHD | |
| 4 | 4.22 | 8.64 | 20.11 | |||||
| 0.0476 | 0.0392 | 0.0452 | 0.05 | |||||
| MS | 138.66 | 143.55 | 148.48 | [85:152], | HD | |||
| 1.54 | 0.012 | 0.13 | [655:663], | Q | ||||
| 0.0441 | 0.0451 | 0.0464 | [805:812] | TW | ||||
| MS | 130.80 | 130.87 | 130.93 | [48:50.5] | HD | |||
| 2.09 | 1.63 | 5.57 | S | |||||
| 0.0446 | 0.0446 | 0.0460 | ||||||
| 1x2.2 | A | 100 | 112.36 | 134.09 | 154.22 | [20:300.08] | MHD | |
| 25 | 0.0350 | 7.76 | 19.27 | |||||
| 0.01 | 0.0413 | 0.0451 | 0.0493 | |||||
| MS | 138.04 | 143.32 | 148.73 | [24:38], | HD | |||
| 0.0602 | 0.21 | 0.55 | [120:128], | Q | ||||
| 0.0441 | 0.0451 | 0.0477 | [170:190] | TW | ||||
| 1x2.3 | A | 100 | 34.38 | 133.34 | 158.94 | [40:1691.82] | MHD | |
| 400 | 4.42 | 0.66 | 19.65 | |||||
| 0.01 | 0.0115 | 0.0426 | 0.0506 | |||||
| MS | 138.84 | 143.56 | 148.48 | [325:1560] | HD | |||
| 4.60 | 5.44 | 1.23 | Q | |||||
| 0.0441 | 0.0451 | 0.0464 | TW | |||||
| MS | 34.38 | 82.10 | 143.21 | [40:293] | HD | |||
| 5.97 | 4.06 | 8.07 | C | |||||
| 0.0115 | 0.0291 | 0.0478 | ||||||
| 2x1.1 | A | 135.92 | 97.18 | 137.37 | 150.22 | [40:341.81] | MHD | |
| 3.76 | 0.91 | 6.98 | 23.93 | C | ||||
| 0.0476 | 0.0381 | 0.0475 | 0.0501 | |||||
| MS | 150.14 | 150.19 | 150.22 | [62.8:63.25] | HD | |||
| 0.96 | 1.19 | 1.45 | [182.4:182.7] | S2 | ||||
| 0.0498 | 0.0499 | 0.0500 | [298.8:299.1] | R1 | ||||
| 2x1.2 | A | 100 | 34.03 | 133.89 | 159.26 | [40:2218.50] | MHD | |
| 25 | 1.61 | 2.01 | 19.70 | |||||
| 0.01 | 0.0109 | 0.0432 | 0.0505 | |||||
| MS | 138.85 | 143.56 | 148.48 | [300:1500], | HD | |||
| 3.99 | 5.83 | 1.32 | [1661:1678], | Q | ||||
| 0.0441 | 0.0451 | 0.464 | [1723:1740] | TW | ||||
| MS | 34.03 | 83.34 | 133.71 | [40:270], | HD | |||
| 3.14 | 5.28 | 1.12 | [2000:2218] | C | ||||
| 0.0109 | 0.0294 | 0.0445 | ||||||
| 2x1.3 | A | 1 | 33.85 | 133.05 | 158.90 | [40:3505.05] | MHD | |
| 400 | 1.71 | 0.15 | 18.76 | |||||
| 0.01 | 0.0110 | 0.0424 | 0.0505 | |||||
| MS | 138.85 | 143.56 | 148.48 | [670:3400] | HD | |||
| 1.66 | 3.04 | 1.18 | Q | |||||
| 0.0441 | 0.0451 | 0.0464 | TW | |||||
| MS | 33.85 | 82.71 | 153.46 | [40:633.2] | HD | |||
| 1.83 | 7.26 | 5.66 | C | |||||
| 0.0110 | 0.0292 | 0.0504 | ||||||
| 1x3.1 | A | 135.92 | 132.64 | 142.87 | 156.49 | [25:483.79] | HD | |
| 4 | 1.34 | 6.34 | 5.03 | Q | ||||
| 0.0476 | 0.0435 | 0.0453 | 0.0476 | TW | ||||
| 1x3.2 | A | 100 | 132.58 | 142.87 | 156.50 | [100:558.16] | HD | |
| 25 | 7.25 | 5.26 | 0.0512 | Q | ||||
| 0.01 | 0.0435 | 0.0453 | 0.0477 | TW | ||||
| 1x3.3 | A | 1 | 132.64 | 142.87 | 156.46 | [85:1992.79] | HD | |
| 400 | 3.78 | 1.86 | 6.68 | Q | ||||
| 0.01 | 0.0435 | 0.0453 | 0.0476 | TW | ||||
| 3x1.1 | A | 135.92 | 132.59 | 142.85 | 156.49 | [1275:1348.48] | HD | |
| 3.76 | 3.06 | 2.71 | 0.0432 | Q | ||||
| 0.0476 | 0.0435 | 0.0453 | 0.0477 | TW | ||||
| 3x1.2 | A | 100 | 132.64 | 142.80 | 156.46 | [560:597.69] | HD | |
| 25 | 5.42 | 2.25 | 1.76 | Q | ||||
| 0.01 | 0.0435 | 0.0453 | 0.0476 | TW | ||||
| MS | 139.71 | 139.73 | 139.85 | [8:16] | HD | |||
| 3.60 | 1.38 | 5.35 | S2 | |||||
| 0.0468 | 0.0468 | 0.0468 | ||||||
| 3x1.3 | A | 100 | 132.51 | 142.87 | 156.63 | [160:561.06] | HD | |
| 400 | 2.54 | 1.79 | 0.0991 | Q | ||||
| 0.01 | 0.0435 | 0.0453 | 0.0477 | TW | ||||
| MS | 139.71 | 139.72 | 139.74 | [10:15.5] | HD | |||
| 5.84 | 2.84 | 1.27 | S2 | |||||
| 0.0468 | 0.0468 | 0.0468 | ||||||
| 1x4.1 | A | 135.92 | 56.81 | 123.87 | 183.43 | [50:202.18] | MHD | |
| 4 | 1.92 | 1.15 | 14.76 | C | ||||
| 0.0476 | 0.0180 | 0.0359 | 0.0487 | |||||
| MS | 131.67 | 142.41 | 151.88 | [115:121], | HD | |||
| 1.92 | 8.71 | 3.95 | [9:15.5] | Q | ||||
| 0.0439 | 0.0460 | 0.0478 | ||||||
| 1x4.2 | A | 100 | 53.62 | 128.35 | 215.63 | [50:200.89] | MHD | |
| 25 | 3.88 | 3.21 | 17.27 | C | ||||
| 0.01 | 0.0183 | 0.0389 | 0.05 | |||||
| 1x4.3 | A | 1 | 43.52 | 122.10 | 200.92 | [50:211.14] | MHD | |
| 400 | 3.01 | 0.27 | 2.92 | C | ||||
| 0.01 | 0.0136 | 0.0330 | 0.0485 | |||||
| 4x1.1 | A | 135.92 | 49.93 | 128.33 | 203.82 | [15:381.79] | MHD | |
| 4 | 1.77 | 2.15 | 16.71 | C | ||||
| 0.0476 | 0.0168 | 0.0391 | 0.0487 | |||||
| MS | 131.45 | 142.83 | 152.27 | [223:242] | HD | |||
| 1.92 | 4.22 | 8.51 | Q | |||||
| 0.0444 | 0.0462 | 0.0476 | TW | |||||
| 4x1.2 | A | 100 | 51.86 | 124.30 | 205.75 | [50:310.23] | MHD | |
| 25 | 3.60 | 1.65 | 16.04 | C | ||||
| 0.01 | 0.0172 | 0.0358 | 0.0499 | |||||
| MS | 146.06 | 147.19 | 147.87 | [246:247.75] | HD | |||
| 7.85 | 0.0799 | 0.30 | S2 | |||||
| 0.0484 | 0.0486 | 0.0487 | ||||||
| 4x1.3 | A | 100 | 51.20 | 126.69 | 187.53 | [25:286.47] | MHD | |
| 900 | 9.13 | 2.33 | 15.10 | C | ||||
| 0.01 | 0.0179 | 0.0388 | 0.0487 | |||||
| MS | 130.19 | 143.60 | 151.34 | [46:51.5] | HD | |||
| 8.92 | 1.78 | 3.03 | Q | |||||
| 0.0441 | 0.0466 | 0.0483 | ||||||
| MS | 122.37 | 123.00 | 123.76 | [12.5:15] | HD | |||
| 0.47 | 0.89 | 1.50 | S2 | |||||
| 0.0419 | 0.0419 | 0.0419 | ||||||
| 2x2.1 | A | 135.92 | 47.29 | 79.2 | 131.63 | [40:1001.34] | HD | |
| 4 | 9.49 | 2.01 | 6.90 | C | ||||
| 0.0476 | 0.0160 | 0.0267 | 0.0393 | |||||
| 2x2.2 | A | 100 | 48.34 | 78.59 | 118.35 | [40:331.19] | HD | |
| 25 | 1.77 | 3.59 | 4.69 | C | ||||
| 0.01 | 0.0166 | 0.0265 | 0.0373 | |||||
| 2x2.3 | A | 1 | 46.40 | 78.83 | 135.50 | [40:409.44] | HD | |
| 1225 | 4.30 | 1.18 | 1.98 | C | ||||
| 0.01 | 0.0171 | 0.0265 | 0.0399 | |||||
| 2x3.1 | A | 135.92 | 55.55 | 77.88 | 135.61 | [40:204.50] | HD | |
| 4 | 1.06 | 3.82 | 1.60 | C | ||||
| 0.0476 | 0.0176 | 0.0258 | 0.0358 | |||||
| 2x3.2 | A | 100 | 53.37 | 80.47 | 159.21 | [40:540.45] | HD | |
| 25 | 8.70 | 1.47 | 7.92 | C | ||||
| 0.01 | 0.0177 | 0.0263 | 0.0413 | |||||
| 2x3.3 | A | 1 | 47.40 | 79.94 | 149.96 | [40:417.59] | HD | |
| 400 | 8.98 | 1.51 | 2.21 | C | ||||
| 0.01 | 0.0161 | 0.0263 | 0.04 | |||||
| 3x2.1 | A | 135.92 | 55.47 | 80.48 | 136.12 | [40:318.22] | HD | |
| 4 | 1.56 | 4.52 | 1.16 | C | ||||
| 0.0476 | 0.0174 | 0.0264 | 0.0395 | |||||
| 3x2.2 | A | 100 | 53.78 | 80.50 | 149.84 | [40:364.87] | HD | |
| 25 | 1.79 | 1.12 | 2.41 | C | ||||
| 0.01 | 0.0188 | 0.0263 | 0.0394 | |||||
| 3x2.3 | A | 100 | 54.77 | 78.96 | 146.56 | [40:363.77] | HD | |
| 400 | 1.61 | 1.10 | 2.59 | C | ||||
| 0.01 | 0.0183 | 0.0261 | 0.0382 | |||||
| 2x4.1 | A | 135.92 | 56.35 | 83.93 | 165.97 | [40:244.38] | HD | |
| 4 | 1.25 | 1.77 | 2.77 | C | ||||
| 0.0476 | 0.0171 | 0.0263 | 0.0382 | |||||
| 2x4.2 | A | 100 | 54.33 | 82.05 | 159.80 | [40:381.79] | HD | |
| 25 | 1.94 | 9.28 | 1.62 | C | ||||
| 0.01 | 0.0196 | 0.0262 | 0.0375 | |||||
| 2x4.3 | A | 100 | 57.54 | 80.22 | 152.08 | [40:326.87] | HD | |
| 400 | 6.23 | 1.55 | 1.46 | C | ||||
| 0.01 | 0.0188 | 0.0259 | 0.0348 | |||||
| 4x2.1 | A | 135.92 | 56.54 | 79.66 | 153.39 | [40:290.67] | HD | |
| 4 | 6.00 | 1.60 | 8.01 | C | ||||
| 0.0476 | 0.0194 | 0.0261 | 0.0355 | |||||
| 4x2.2 | A | 225 | 55.31 | 80.67 | 146.53 | [40:366.17] | HD | |
| 25 | 1.49 | 7.81 | 1.50 | C | ||||
| 0.01 | 0.0194 | 0.0260 | 0.0349 | |||||
| 4x2.3 | A | 1 | 52.71 | 81.42 | 164.80 | [40:391.69] | HD | |
| 100 | 1.88 | 6.09 | 7.67 | C | ||||
| 0.01 | 0.0161 | 0.0260 | 0.0379 | |||||
| 3x3.1 | A | 135.92 | 59.34 | 80.38 | 133.18 | [40:201.10] | HD | |
| 4 | 4.48 | 6.42 | 5.76 | C | ||||
| 0.0476 | 0.0195 | 0.0262 | 0.0354 | |||||
| 3x3.2 | A | 100 | 55.04 | 79.20 | 108.71 | [40:321.50] | HD | |
| 25 | 9.71 | 4.57 | 4.75 | C | ||||
| 0.01 | 0.0186 | 0.0259 | 0.0327 | |||||
| 3x3.3 | A | 100 | 56.12 | 78.41 | 106.72 | [40:312.34] | HD | |
| 400 | 3.92 | 2.25 | 2.38 | C | ||||
| 0.01 | 0.0182 | 0.0259 | 0.0334 | |||||
| 3x4.1 | A | 135.92 | 60.18 | 78.74 | 120.72 | [40:200.17] | HD | |
| 4 | 6.08 | 3.19 | 3.62 | C | ||||
| 0.0476 | 0.0197 | 0.0256 | 0.0319 | |||||
| 3x4.2 | A | 225 | 63.75 | 79.86 | 121.48 | [40:295.39] | HD | |
| 100 | 1.11 | 1.20 | 8.99 | C | ||||
| 0.01 | 0.0203 | 0.0259 | 0.0323 | |||||
| 3x4.3 | A | 1 | 62.18 | 79.26 | 117.60 | [40:285.44] | HD | |
| 900 | 5.22 | 7.20 | 5.29 | C | ||||
| 0.01 | 0.0206 | 0.0258 | 0.0327 | |||||
| 4x3.1 | A | 135.92 | 60.75 | 79.99 | 112.65 | [40:200.01] | HD | |
| 4 | 6.26 | 1.07 | 5.83 | C | ||||
| 0.0476 | 0.0190 | 0.0259 | 0.0338 | |||||
| 4x3.2 | A | 225 | 59.81 | 79.15 | 110.28 | [40:337.28] | HD | |
| 100 | 2.34 | 7.68 | 5.46 | C | ||||
| 0.01 | 0.0202 | 0.0258 | 0.0321 | |||||
| 4x3.3 | A | 100 | 53.78 | 78.80 | 109.92 | [40:296.86] | HD | |
| 400 | 1.44 | 6.20 | 5.71 | C | ||||
| 0.01 | 0.0183 | 0.0257 | 0.0324 | |||||
| 4x4.1 | A | 135.92 | 65.55 | 79.53 | 106.56 | [40:200.51] | HD | |
| 4 | 5.33 | 1.03 | 7.88 | C | ||||
| 0.0476 | 0.0212 | 0.0257 | 0.0313 | |||||
| 4x4.2 | A | 225 | 61.65 | 79.41 | 105.68 | [40:528.55] | HD | |
| 100 | 8.18 | 3.14 | 5.88 | C | ||||
| 0.01 | 0.0201 | 0.0258 | 0.0333 | |||||
| 4x4.3 | A | 100 | 62.51 | 80.20 | 113.30 | [40:342.84] | HD | |
| 400 | 1.16 | 2.58 | 2.61 | C | ||||
| 0.01 | 0.0210 | 0.0259 | 0.0319 |
| Run | G | Interval | Rm | Rm | Rm | Rm | |||||
| 4x4.2 | 51–528.55 | 0.223 | 22.413 | 0.223 | 22.416 | 0.206 | 20.722 | 0.206 | 20.720 | 12.58 | |
| 4x2.1 | 232.40–290.65 | 0.219 | 21.769 | 0.219 | 21.770 | 0.241 | 23.988 | 0.241 | 23.983 | 12.43 | |
| 3x3.3 | 220.46–312.34 | 0.220 | 21.843 | 0.220 | 21.842 | 0.241 | 24.011 | 0.241 | 24.004 | 12.43 | |
| 2x2.3 | 310.15–409.44 | 0.219 | 21.879 | 0.220 | 21.885 | 0.242 | 24.115 | 0.242 | 24.103 | 12.46 | |
| 2x3.1 | 100–204.50 | 0.219 | 21.920 | 0.219 | 21.923 | 0.241 | 24.113 | 0.241 | 24.108 | 12.50 | |
| 4x3.3 | 223.17–296.86 | 0.221 | 22.050 | 0.221 | 22.047 | 0.242 | 24.176 | 0.242 | 24.167 | 12.48 | |
| 2x3.2 | 505.52–540.45 | 0.220 | 22.092 | 0.220 | 22.101 | 0.242 | 24.280 | 0.242 | 24.278 | 12.53 | |
| 3x2.3 | 251.39–363.77 | 0.221 | 22.183 | 0.221 | 22.190 | 0.243 | 24.365 | 0.242 | 24.358 | 12.55 | |
| 3x4.1 | 42.18–200.17 | 0.222 | 22.273 | 0.222 | 22.277 | 0.243 | 24.377 | 0.243 | 24.369 | 12.55 | |
| 3x4.3 | 219.42–295.39 | 0.221 | 22.281 | 0.221 | 22.283 | 0.243 | 24.400 | 0.242 | 24.393 | 12.57 | |
| 4x3.2 | 290.74–337.38 | 0.222 | 22.337 | 0.222 | 22.332 | 0.243 | 24.414 | 0.243 | 24.406 | 12.56 | |
| 4x4.3 | 201–336 | 0.223 | 22.385 | 0.223 | 22.385 | 0.243 | 24.439 | 0.243 | 24.436 | 12.56 | |
| 4x3.1 | 42–200.02 | 0.223 | 22.396 | 0.223 | 22.397 | 0.243 | 24.481 | 0.243 | 24.480 | 12.57 | |
| 3x4.2 | 246.87–285.44 | 0.223 | 22.454 | 0.223 | 22.446 | 0.243 | 24.497 | 0.243 | 24.486 | 12.57 | |
| 3x3.2 | 278.28–321 | 0.224 | 22.467 | 0.223 | 22.459 | 0.244 | 24.533 | 0.244 | 24.518 | 12.56 | |
| 2x3.3 | 309.16–417.59 | 0.221 | 22.382 | 0.221 | 22.415 | 0.243 | 24.554 | 0.243 | 24.560 | 12.65 | |
| 3x3.1 | 42.91–201.10 | 0.222 | 22.468 | 0.222 | 22.473 | 0.243 | 24.574 | 0.243 | 24.568 | 12.62 | |
| 2x2.2 | 200–331.19 | 0.221 | 22.333 | 0.221 | 22.356 | 0.245 | 24.698 | 0.244 | 24.680 | 12.62 | |
| 4x4.1 | 100–200.51 | 0.223 | 22.619 | 0.224 | 22.623 | 0.244 | 24.689 | 0.244 | 24.685 | 12.65 | |
| 2x2.1 | 719.70–800.70 | 0.221 | 22.484 | 0.221 | 22.502 | 0.243 | 24.788 | 0.243 | 24.779 | 12.73 | |
| 2x4.2 | 317.09–381 | 0.223 | 22.741 | 0.224 | 22.784 | 0.243 | 24.795 | 0.243 | 24.810 | 12.73 | |
| 2x4.3 | 223.93–326 | 0.224 | 22.806 | 0.224 | 22.816 | 0.244 | 24.850 | 0.244 | 24.846 | 12.72 | |
| 3x2.1 | 231.77–318 | 0.223 | 22.723 | 0.223 | 22.728 | 0.244 | 24.863 | 0.244 | 24.857 | 12.72 | |
| 4x2.3 | 268.69–366.17 | 0.224 | 22.855 | 0.224 | 22.860 | 0.244 | 24.902 | 0.244 | 24.895 | 12.73 | |
| 2x4.1 | 102–207.69 | 0.225 | 22.959 | 0.226 | 22.973 | 0.245 | 24.954 | 0.245 | 24.961 | 12.73 | |
| 3x2.2 | 304.32–364 | 0.223 | 22.978 | 0.224 | 23.022 | 0.244 | 25.093 | 0.244 | 25.104 | 12.86 | |
| 4x2.2 | 334.41–391.69 | 0.225 | 23.106 | 0.226 | 23.135 | 0.245 | 25.106 | 0.245 | 25.113 | 12.81 | |
| 3x1.1 | 100–249.39 | 0.227 | 27.379 | 0.227 | 27.279 | 0.247 | 29.761 | 0.246 | 29.608 | 15.04 | |
| 2x1.2 | M | 1946.90–1980.90 | 0.227 | 26.638 | 0.228 | 26.815 | 0.254 | 29.868 | 0.255 | 29.949 | 14.68 |
| 3x1.2 | 285.85–377.67 | 0.227 | 28.423 | 0.226 | 28.342 | 0.245 | 30.675 | 0.244 | 30.537 | 15.65 | |
| 1x4.3 | M | 130–211.14 | 0.242 | 29.726 | 0.243 | 29.786 | 0.254 | 31.235 | 0.254 | 31.163 | 15.34 |
| 4x1.3 | M | 108.81–241.99 | 0.233 | 29.797 | 0.233 | 29.727 | 0.248 | 31.701 | 0.247 | 31.589 | 15.96 |
| 4x1.2 | M | 200–310.23 | 0.238 | 30.258 | 0.238 | 30.170 | 0.253 | 32.107 | 0.252 | 31.986 | 15.85 |
| 4x1.1 | M | 168–330 | 0.238 | 29.814 | 0.238 | 29.770 | 0.256 | 32.060 | 0.256 | 32.015 | 15.65 |
| 1x4.1 | M | 140–192 | 0.242 | 30.969 | 0.241 | 30.894 | 0.252 | 32.300 | 0.251 | 32.165 | 16.00 |
| 1x4.2 | M | 120–200 | 0.237 | 31.140 | 0.236 | 31.098 | 0.259 | 34.047 | 0.257 | 33.888 | 16.45 |
| 1x2.1 | M | 185–245 | 0.238 | 30.339 | 0.238 | 30.333 | 0.267 | 34.018 | 0.267 | 34.003 | 15.92 |
| 1x2.3 | M | 1606–1691 | 0.238 | 30.534 | 0.238 | 30.526 | 0.267 | 34.206 | 0.267 | 34.181 | 16.01 |
| 2x1.3 | M | 3460–3505.05 | 0.239 | 30.794 | 0.238 | 30.787 | 0.266 | 34.407 | 0.266 | 34.383 | 16.13 |
| 1x2.2 | M | 50–300 | 0.239 | 31.193 | 0.239 | 31.188 | 0.266 | 34.715 | 0.266 | 34.684 | 16.32 |
| 2x1.1 | M | 152–277.81 | 0.248 | 33.000 | 0.248 | 32.987 | 0.261 | 34.777 | 0.261 | 34.739 | 16.64 |
| 1x3.3 | 50–354.35 | 0.234 | 31.566 | 0.234 | 31.568 | 0.263 | 35.499 | 0.263 | 35.483 | 16.87 | |
| 1x3.1 | 25–487.12 | 0.234 | 31.668 | 0.234 | 31.659 | 0.263 | 35.589 | 0.263 | 35.566 | 16.90 | |
| 1x3.2 | 83–558.16 | 0.234 | 31.669 | 0.234 | 31.660 | 0.263 | 35.590 | 0.263 | 35.567 | 16.90 | |
| 3x1.3 | 330.20–365.60 | 0.234 | 31.676 | 0.234 | 31.667 | 0.263 | 35.597 | 0.263 | 35.574 | 16.90 |
| Run | Phase | Interval | Rm | Rm | Rm | Rm | |||||
| 1x2.1 | T | 10–65 | 0.215 | 22.690 | 0.214 | 22.615 | 0.249 | 26.325 | 0.249 | 26.265 | 13.20 |
| G | 75–170 | 0.240 | 32.566 | 0.240 | 32.553 | 0.263 | 35.653 | 0.263 | 35.638 | 16.93 | |
| S | 185–250 | 0.238 | 30.425 | 0.238 | 30.418 | 0.267 | 34.099 | 0.267 | 34.083 | 15.96 | |
| 1x2.2 | T | 0–13.8 | 0.220 | 24.205 | 0.220 | 24.172 | 0.245 | 26.928 | 0.244 | 26.765 | 13.72 |
| G | 20–40 | 0.240 | 32.557 | 0.240 | 32.543 | 0.263 | 35.665 | 0.263 | 35.648 | 16.93 | |
| S | 50–115 | 0.238 | 30.439 | 0.238 | 30.432 | 0.267 | 34.165 | 0.267 | 34.151 | 15.98 | |
| 1x2.3 | D | 10–293 | 0.214 | 22.367 | 0.214 | 22.350 | 0.246 | 25.699 | 0.246 | 25.627 | 13.03 |
| G | 300–1597 | 0.240 | 32.584 | 0.240 | 32.571 | 0.263 | 35.667 | 0.263 | 35.653 | 16.94 | |
| S | 1606–1691.82 | 0.238 | 30.534 | 0.238 | 30.526 | 0.267 | 34.206 | 0.267 | 34.181 | 16.01 | |
| 2x1.1 | T | 0–8 | 0.244 | 32.150 | 0.244 | 32.151 | 0.260 | 34.363 | 0.260 | 34.362 | 16.50 |
| S | 12–277.81 | 0.248 | 33.010 | 0.248 | 32.993 | 0.261 | 34.789 | 0.261 | 34.737 | 16.65 | |
| 2x1.2 | D | 40–270 | 0.216 | 22.533 | 0.214 | 22.374 | 0.246 | 25.743 | 0.245 | 25.585 | 13.06 |
| G | 285–1555 | 0.241 | 32.658 | 0.240 | 32.621 | 0.263 | 35.727 | 0.263 | 35.699 | 16.95 | |
| S | 1570–1962 | 0.239 | 31.254 | 0.239 | 31.170 | 0.266 | 34.814 | 0.266 | 34.743 | 16.33 | |
| 2x1.3 | D | 40–633.2 | 0.215 | 22.265 | 0.214 | 22.161 | 0.246 | 25.559 | 0.245 | 25.448 | 12.97 |
| G | 646–3445 | 0.240 | 32.611 | 0.240 | 32.579 | 0.263 | 35.686 | 0.263 | 35.662 | 16.95 | |
| S | 3460–3505.05 | 0.239 | 30.794 | 0.238 | 30.787 | 0.266 | 34.407 | 0.266 | 34.383 | 16.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeyabalan, S.R.; Chertovskih, R.; Gama, S.; Zheligovsky, V. Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis. Mathematics 2022, 10, 2957. https://doi.org/10.3390/math10162957
Jeyabalan SR, Chertovskih R, Gama S, Zheligovsky V. Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis. Mathematics. 2022; 10(16):2957. https://doi.org/10.3390/math10162957
Chicago/Turabian StyleJeyabalan, Simon Ranjith, Roman Chertovskih, Sílvio Gama, and Vladislav Zheligovsky. 2022. "Nonlinear Large-Scale Perturbations of Steady Thermal Convective Dynamo Regimes in a Plane Layer of Electrically Conducting Fluid Rotating about the Vertical Axis" Mathematics 10, no. 16: 2957. https://doi.org/10.3390/math10162957







