New Class of Unit-Power-Skew-Normal Distribution and Its Associated Regression Model for Bounded Responses
Abstract
:1. Introduction
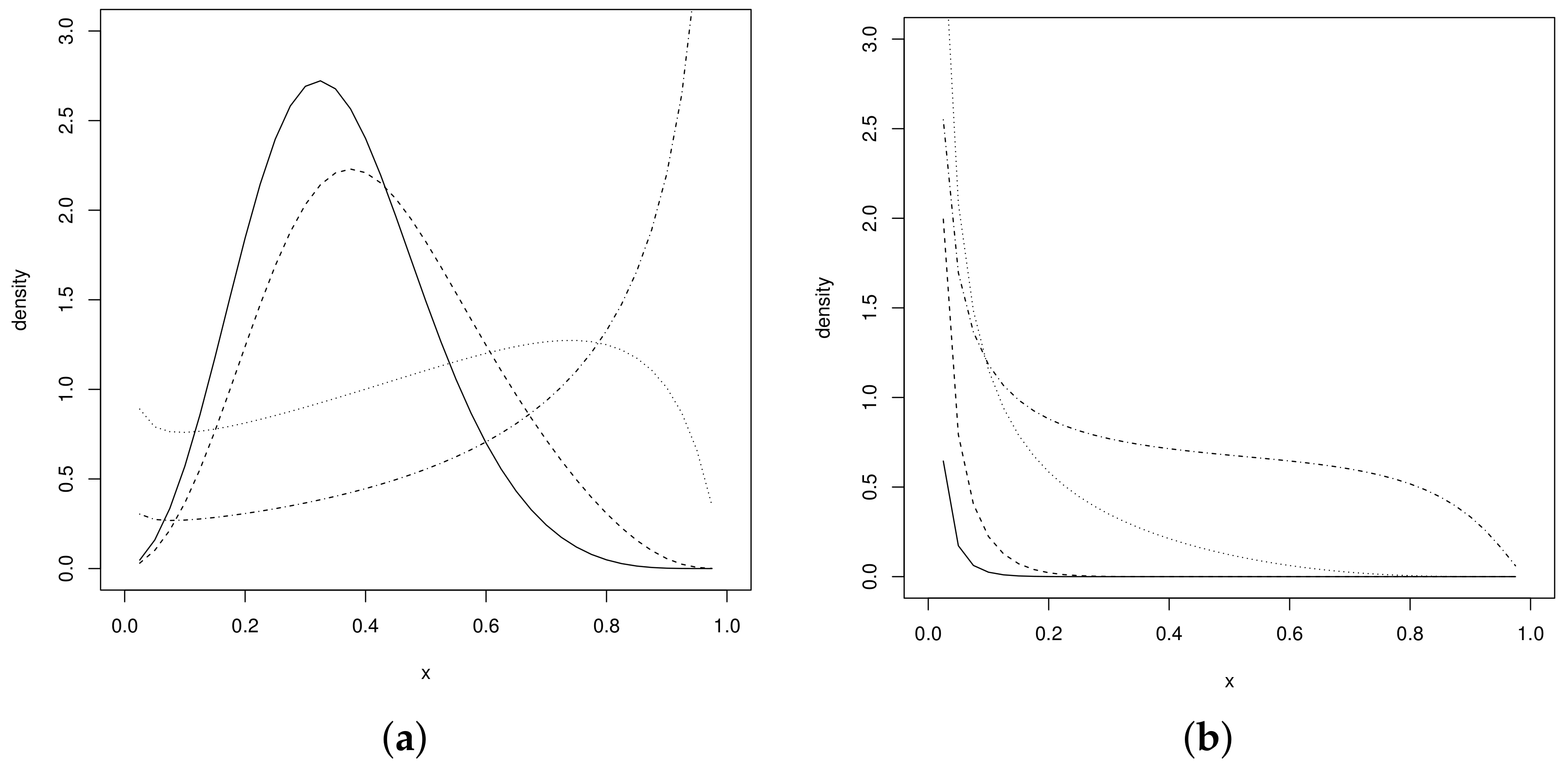
2. The Unit–Power–Skew–Normal Distribution
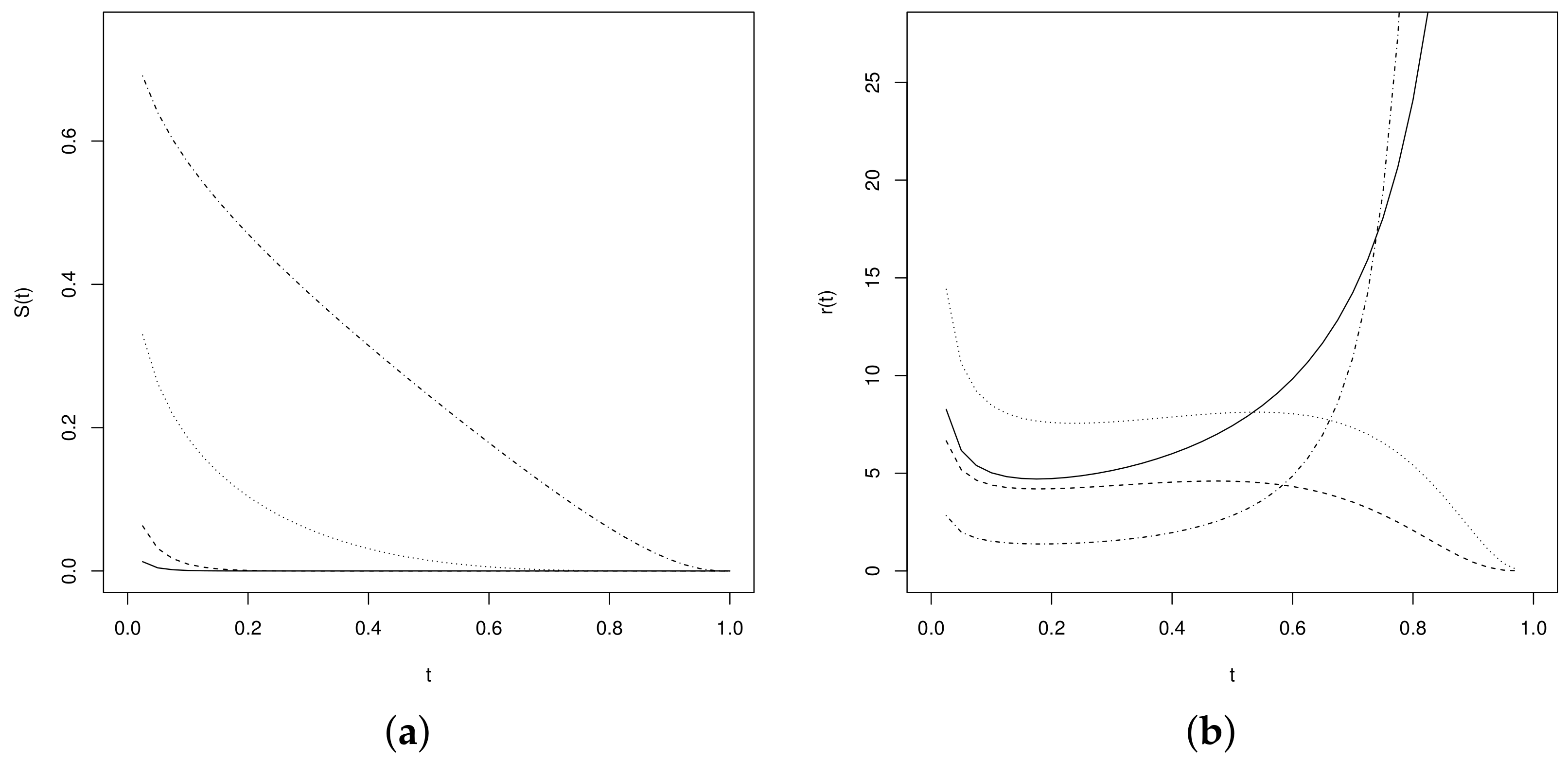
2.1. Properties
2.2. Moments
2.3. Statistical Inference
3. The USPN Regression Model
4. Simulation Study
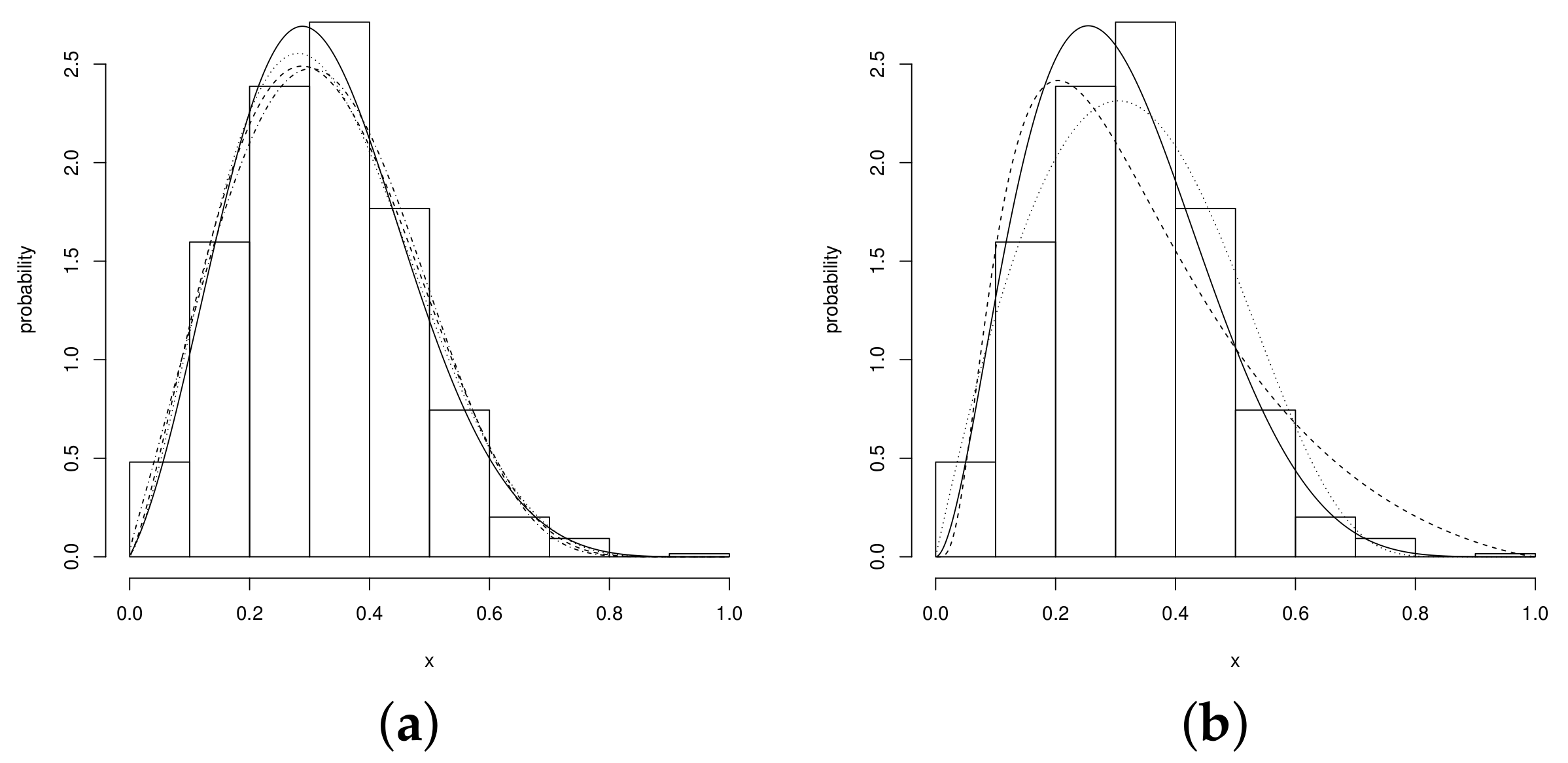
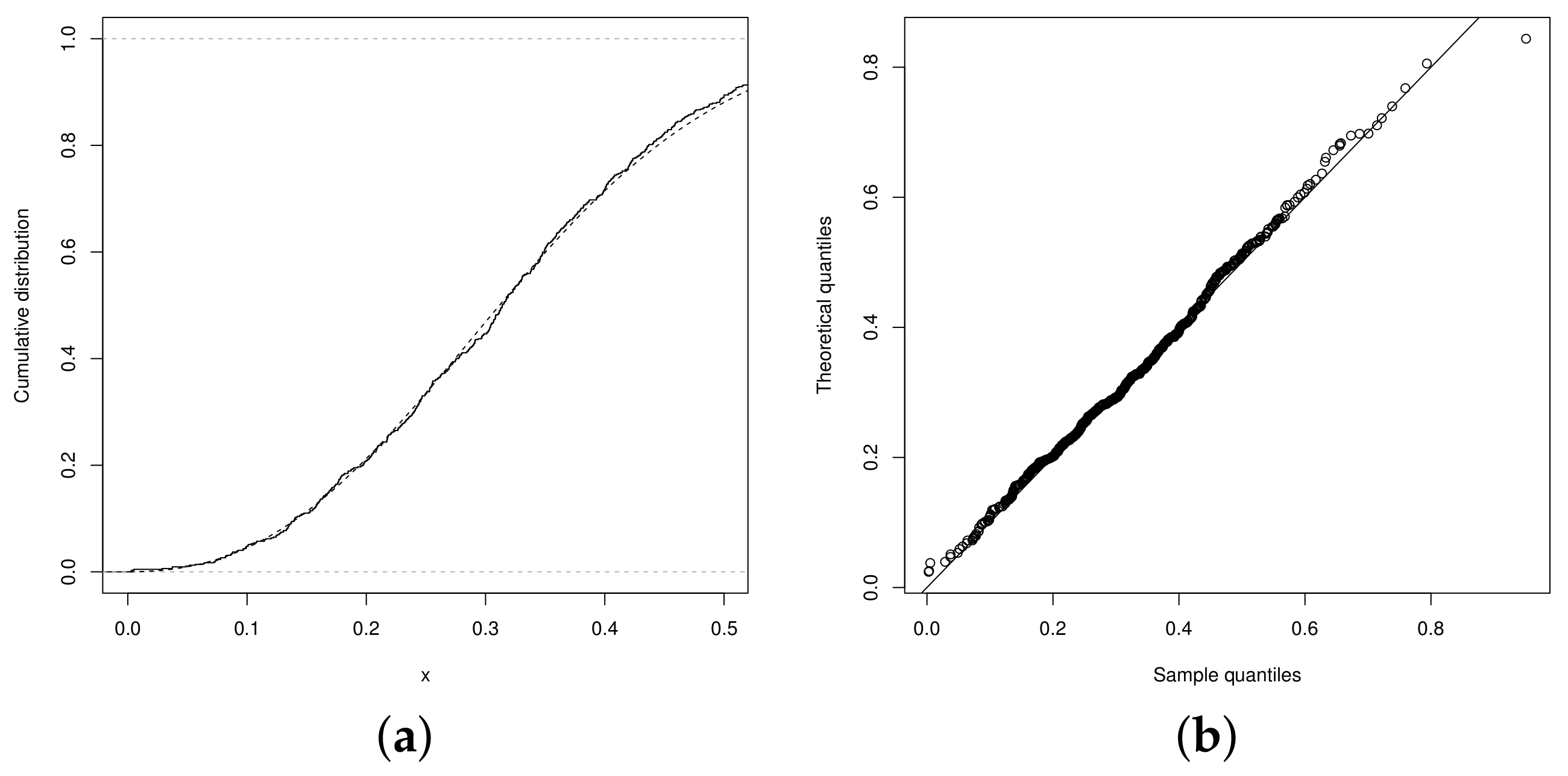
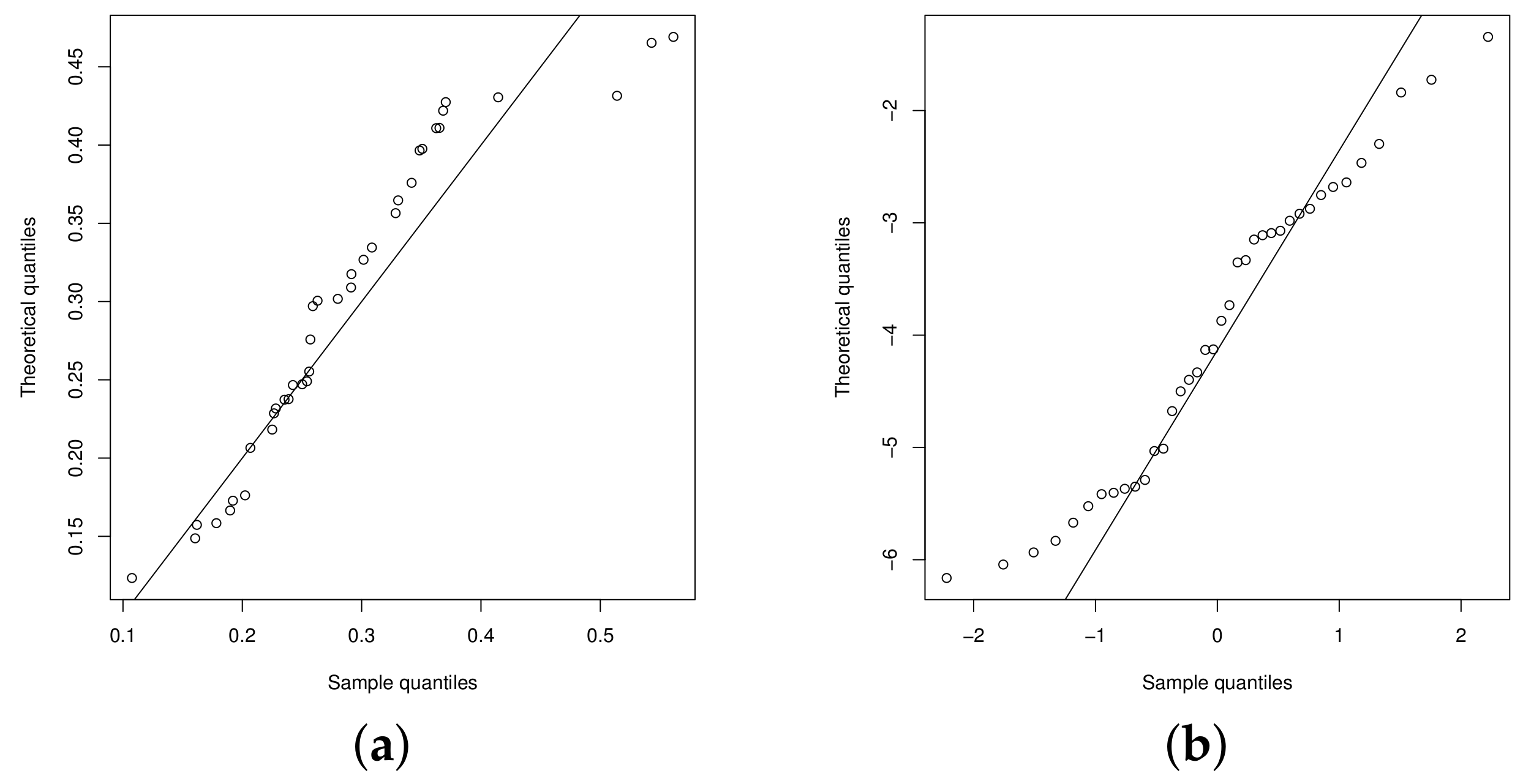
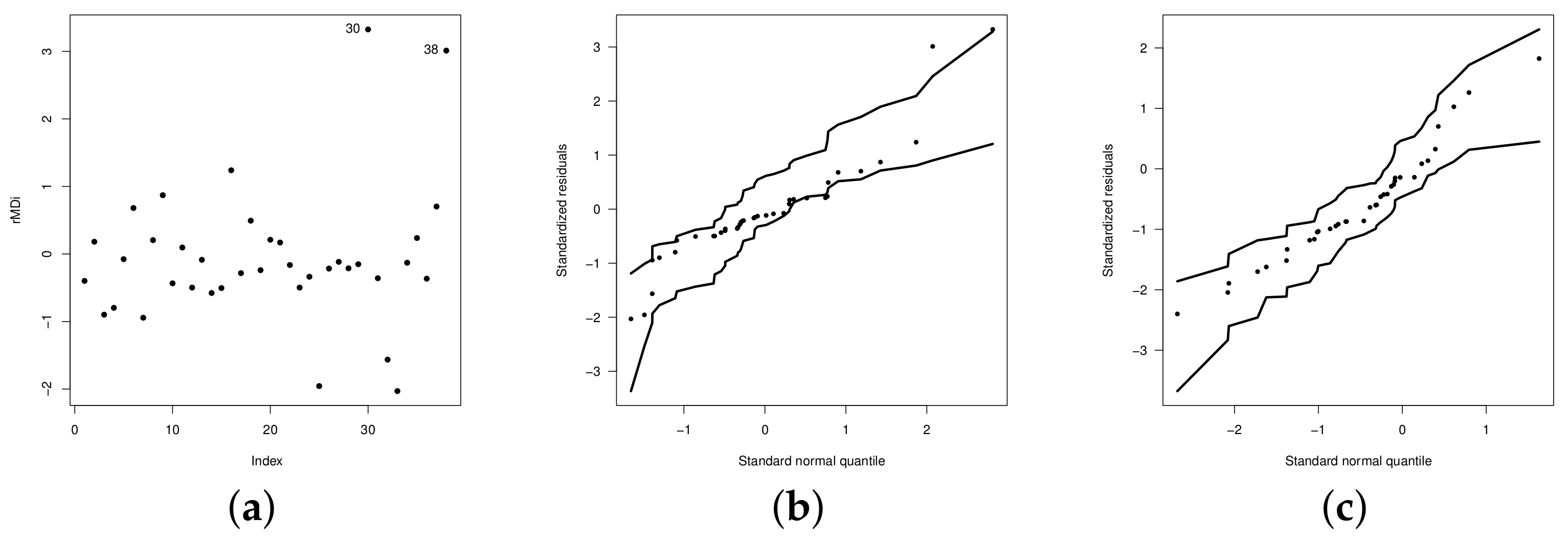
5. Illustrations
5.1. Model without Covariates
5.2. Model with Covariates
6. Bivariate Extension of the UPSN Distribution
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Elements of the Observed Information Matrix
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Pewsey, A.; Gómez, H.; Bolfarine, H. Likelihood-based inference for power distributions. Test 2012, 21, 775–789. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Power-models for proportions with zero/one excess. Appl. Math. Inf. Sci. 2012, 12, 293–303. [Google Scholar] [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Ghitany, M.E. The unit-Weibull distribution and associated inference. J. Appl. Probab. Stat. 2018, 13, 1–22. [Google Scholar]
- Mazucheli, J.; Menezes, A.; Dey, S. The unit-Birnbaum-Saunders distribution with applications. Chil. J. Stat. 2018, 9, 47–57. [Google Scholar]
- Mazucheli, J.; Menezes, A.F.B.; Chakraborty, S. On the one parameter unit-Lindley distribution and its associated regression model for proportion data. J. Appl. Stat. 2019, 49, 700–714. [Google Scholar] [CrossRef]
- Bhatti, F.A.; Ali, A.; Hamedani, G.; Korkmaz, M.Ç.; Ahmad, M. The unit Generalized Log Burr XII Distribution: Properties and Application. In Mathematical and Statistical Science Faculty Research and Publications; 2021; Volume 81, Available online: https://epublications.marquette.edu/math_fac/81 (accessed on 25 July 2022).
- Korkmaz, M.Ç.; Korkmaz, Z.S. The unit log–log distribution: A new unit distribution with alternative quantile regression modeling and educational measurements applications. J. Appl. Stat. 2021, 1–20. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. The Unit Folded Normal Distribution: A New Unit Probability Distribution with the Estimation Procedures, Quantile Regression Modeling and Educational Attainment Applications. J. Reliab. Stat. Stud. 2022, 15, 165–186. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Ospina, R.; Ferrari, S.L.P. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1623. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Doubly censored power-normal regression models with inflation. Test 2014, 24, 265–286. [Google Scholar] [CrossRef]
- Korkmaz, M.Ç.; Chesneau, C.; Korkmaz, Z.S. A new alternative quantile regression model for the bounded response with educational measurements applications of OECD countries. J. Appl. Stat. 2021, 1–24. [Google Scholar] [CrossRef]
- Mazucheli, J.; Alves, B.; Korkmaz, M.Ç.; Leiva, V. Vasicek Quantile and Mean Regression Models for Bounded Data: New Formulation, Mathematical Derivations, and Numerical Applications. Mathematics 2022, 10, 1389. [Google Scholar] [CrossRef]
- Mazucheli, J.; Korkmaz, M.Ç.; Menezes, A.F.B.; Leiva, V. The unit generalized half-normal quantile regression model: Formulation, estimation, diagnostics, and numerical applications. Soft Comput. 2022, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Owen, D.B. Tables for computing bi-variate normal probabilities. Ann. Math. Stat. 1956, 27, 1075–1090. [Google Scholar] [CrossRef]
- Salinas, H.S.; Gómez, H.W.; Martínez-Flórez, G.; Bolfarine, H. Skew-normal alpha-power model [Statistics 48(2014) 1414–1428]. Statistics 2018, 52, 950–953. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. Power-normal distribution. Statistics 2013, 47, 110–125. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Tovar-Falón, R.; Elal-Olivero, D. Some new flexible classes of normal distribution for fitting multimodal data. Statistics 2022, 56, 182–205. [Google Scholar] [CrossRef]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: http://www.R-project.org (accessed on 31 January 2022).
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. The alpha–power tobit model. Commun. Stat. Theory Methods 2013, 42, 633–643. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1974, AU-19, 716–722. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Schwarz, G. Further analysis of the data by akaike’s information criterion and the finite corrections. Commun. Stat. Theory Methods 1978, 7, 13–26. [Google Scholar]
- Hannan, E.J.; Quinn, B.G. The Determination of the order of an autoregression. J. R. Stat. Soc. Ser. B 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Griffiths, W.E.; Hill, R.C.; Judge, G.G. Learning and Practicing Econometrics; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Cribari-Neto, F.; Zeileis, A. Beta Regression in R. J. Stat. Softw. 2010, 34, 1–24. Available online: https://www.jstatsoft.org/article/view/v034i02 (accessed on 31 January 2022). [CrossRef]
- Barros, M.; Galea, M.; González, M.; Leiva, V. Influence diagnostics in the tobit censored response model. Stat. Methods Appl. 2010, 19, 379–397. [Google Scholar] [CrossRef]
- Ortega, E.M.; Bolfarine, H.; Paulda, G.A. Influence diagnostics in generalized log-gamma regression models. Comput. Stat. Data Anal. 2003, 42, 165–186. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Moreno-Arenas, G. On a multivariate regression model for rates and proportions. J. Appl. Stat. 2019, 46, 1084–1106. [Google Scholar] [CrossRef]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally specified distributions. In Lecture Notes in Statistics; Berger, J., Fienberg, J., Gani, J., Krickeberg, I., Singer, B., Eds.; Springer: New York, NY, USA, 1992; Volume 73. [Google Scholar]
- Arnold, B.C.; Castillo, E.; Sarabia, J.M. Conditionally Specification of Statistical Models; Springer Series in Statistics; Springer: New York, NY, USA, 1999. [Google Scholar]
- Martínez-Flórez, G.; Arnold, B.C.; Bolfarine, H.; Gómez, H.W. The multivariate alpha-power model. J. Stat. Plan. Inference 2013, 143, 1244–1255. [Google Scholar] [CrossRef]
- Arnold, B.C.; Strauss, D. Bivariate distributions with conditionals in prescribed exponential families. J. R. Stat. Soc. Ser. B 1991, 53, 365–375. [Google Scholar] [CrossRef]


| 0.25 | 0.75 | 0.4012 | 0.2382 | 0.0773 | 0.1536 | 1.8059 |
| 1.75 | 0.2102 | 0.0842 | 0.0400 | 0.9118 | 2.9505 | |
| 2.75 | 0.1331 | 0.0399 | 0.0222 | 1.3673 | 4.3927 | |
| 1.50 | 0.75 | 0.2506 | 0.1043 | 0.0415 | 0.618 | 2.4429 |
| 1.75 | 0.1159 | 0.0289 | 0.0154 | 1.3217 | 4.3589 | |
| 2.75 | 0.0691 | 0.0121 | 0.0073 | 1.7686 | 6.3217 | |
| 2.75 | 0.75 | 0.2113 | 0.0712 | 0.0265 | 0.531 | 2.4116 |
| 1.75 | 0.1026 | 0.0213 | 0.0108 | 1.136 | 3.7371 | |
| 2.75 | 0.0630 | 0.0095 | 0.0055 | 1.5536 | 5.2632 |
| , | , | , | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | AVB | RMSE | Mean | AVB | RMSE | Mean | AVB | RMSE | ||
| 30 | 0.6506 | 0.1506 | 0.4237 | 0.6768 | 0.1768 | 0.4078 | 0.6597 | 0.1597 | 0.4037 | |
| 0.4440 | 0.0560 | 0.1567 | 0.4299 | 0.0701 | 0.1804 | 0.4332 | 0.0668 | 0.1769 | ||
| 0.8910 | 0.1410 | 0.6898 | 0.9203 | 0.1703 | 0.5639 | 0.3099 | 0.4401 | 0.5298 | ||
| 0.3984 | 0.1016 | 0.5215 | 1.2813 | 0.2187 | 0.6199 | 3.1366 | 0.6366 | 1.4737 | ||
| 60 | 0.6406 | 0.1406 | 0.4039 | 0.6515 | 0.1515 | 0.3674 | 0.6468 | 0.1468 | 0.3756 | |
| 0.4459 | 0.0541 | 0.1495 | 0.4389 | 0.0611 | 0.1655 | 0.4396 | 0.0604 | 0.1679 | ||
| 0.6253 | 0.1247 | 0.6437 | 0.5848 | 0.1652 | 0.5464 | 0.3305 | 0.4195 | 0.5056 | ||
| 0.4110 | 0.0890 | 0.4748 | 1.2823 | 0.2177 | 0.5985 | 2.9701 | 0.4701 | 1.4212 | ||
| 100 | 0.6385 | 0.1385 | 0.3692 | 0.5879 | 0.0879 | 0.2940 | 0.6029 | 0.1029 | 0.2887 | |
| 0.4478 | 0.0522 | 0.1352 | 0.4622 | 0.0378 | 0.1218 | 0.4495 | 0.0505 | 0.1352 | ||
| 0.6670 | 0.0830 | 0.5847 | 0.8580 | 0.1080 | 0.5392 | 0.4133 | 0.3367 | 0.4972 | ||
| 0.4118 | 0.0882 | 0.3813 | 1.6264 | 0.1264 | 0.4824 | 2.8683 | 0.3683 | 1.2378 | ||
| 200 | 0.5877 | 0.0877 | 0.3138 | 0.5645 | 0.0645 | 0.2211 | 0.5635 | 0.0635 | 0.2175 | |
| 0.4706 | 0.0294 | 0.1167 | 0.4681 | 0.0319 | 0.1038 | 0.4529 | 0.0471 | 0.1118 | ||
| 0.8229 | 0.0729 | 0.4998 | 0.8210 | 0.0710 | 0.4885 | 0.5241 | 0.2259 | 0.4776 | ||
| 0.5583 | 0.0583 | 0.2650 | 1.5756 | 0.0756 | 0.3926 | 2.6427 | 0.1427 | 0.5351 | ||
| 500 | 0.5696 | 0.0696 | 0.2446 | 0.5163 | 0.0163 | 0.2096 | 0.5580 | 0.0580 | 0.1957 | |
| 0.4761 | 0.0239 | 0.0909 | 0.4763 | 0.0237 | 0.0751 | 0.4603 | 0.0397 | 0.0851 | ||
| 0.8119 | 0.0619 | 0.3837 | 0.8101 | 0.0601 | 0.4085 | 0.5558 | 0.1942 | 0.4038 | ||
| 0.5218 | 0.0218 | 0.1911 | 1.4280 | 0.0720 | 0.3156 | 2.6220 | 0.1220 | 0.4011 | ||
| 1000 | 0.5409 | 0.0409 | 0.2006 | 0.5141 | 0.0141 | 0.1644 | 0.5137 | 0.0137 | 0.1691 | |
| 0.4817 | 0.0183 | 0.0755 | 0.4794 | 0.0206 | 0.0701 | 0.4661 | 0.0339 | 0.0789 | ||
| 0.7166 | 0.0334 | 0.3332 | 0.7222 | 0.0278 | 0.3480 | 0.6104 | 0.1396 | 0.3183 | ||
| 0.4842 | 0.0158 | 0.1550 | 1.4566 | 0.0434 | 0.2120 | 2.4661 | 0.0339 | 0.3358 | ||
| , | , | , | ||||||||
| Mean | AVB | RMSE | Mean | AVB | RMSE | Mean | AVB | RMSE | ||
| 30 | 0.5896 | 0.0896 | 0.3380 | 0.5723 | 0.0723 | 0.3102 | 0.5496 | 0.0496 | 0.1738 | |
| 0.4339 | 0.0661 | 0.1531 | 0.4362 | 0.0638 | 0.1041 | 0.4273 | 0.0727 | 0.0967 | ||
| 1.5976 | 0.1524 | 0.9985 | 1.3001 | 0.4499 | 0.9439 | 1.1366 | 0.6134 | 0.9404 | ||
| 0.7603 | 0.2603 | 0.6934 | 1.7636 | 0.2636 | 1.0633 | 3.2798 | 0.7798 | 1.7809 | ||
| 60 | 0.5454 | 0.0454 | 0.3287 | 0.5701 | 0.0701 | 0.1902 | 0.5470 | 0.0470 | 0.1571 | |
| 0.4606 | 0.0394 | 0.1280 | 0.4549 | 0.0451 | 0.0847 | 0.4431 | 0.0569 | 0.0802 | ||
| 1.6007 | 0.1493 | 0.9031 | 1.4843 | 0.2657 | 0.8709 | 1.3276 | 0.4224 | 0.9213 | ||
| 0.6992 | 0.1992 | 0.6830 | 1.7410 | 0.2410 | 1.0213 | 2.9975 | 0.4975 | 1.3429 | ||
| 100 | 0.4647 | 0.0353 | 0.3202 | 0.5457 | 0.0457 | 0.1627 | 0.5431 | 0.0431 | 0.1472 | |
| 0.4731 | 0.0269 | 0.1150 | 0.4636 | 0.0364 | 0.0716 | 0.4477 | 0.0523 | 0.0756 | ||
| 1.6283 | 0.1217 | 0.8332 | 1.6066 | 0.1434 | 0.7931 | 1.3702 | 0.3798 | 0.8113 | ||
| 0.6892 | 0.1892 | 0.6424 | 1.6735 | 0.1735 | 0.8120 | 2.8614 | 0.3614 | 1.1754 | ||
| 200 | 0.4688 | 0.0312 | 0.2901 | 0.5430 | 0.0430 | 0.1490 | 0.5269 | 0.0269 | 0.1195 | |
| 0.4892 | 0.0108 | 0.0857 | 0.4647 | 0.0353 | 0.0648 | 0.4654 | 0.0346 | 0.0583 | ||
| 1.6442 | 0.1058 | 0.6433 | 1.6129 | 0.1371 | 0.6854 | 1.4212 | 0.3288 | 0.7109 | ||
| 0.6569 | 0.1569 | 0.5690 | 1.6657 | 0.1657 | 0.6672 | 2.6302 | 0.1302 | 0.7226 | ||
| 500 | 0.4740 | 0.0260 | 0.2329 | 0.5357 | 0.0357 | 0.1236 | 0.5222 | 0.0222 | 0.1099 | |
| 0.4900 | 0.0100 | 0.0598 | 0.4659 | 0.0341 | 0.0494 | 0.4754 | 0.0246 | 0.0527 | ||
| 1.6586 | 0.0914 | 0.4897 | 1.6325 | 0.1175 | 0.4413 | 1.5372 | 0.2128 | 0.5628 | ||
| 0.6379 | 0.1379 | 0.3211 | 1.5969 | 0.0969 | 0.4985 | 2.5863 | 0.0863 | 0.5885 | ||
| 1000 | 0.5159 | 0.0159 | 0.1810 | 0.5342 | 0.0342 | 0.1111 | 0.5184 | 0.0184 | 0.1083 | |
| 0.4910 | 0.0090 | 0.0437 | 0.4704 | 0.0296 | 0.0458 | 0.4795 | 0.0205 | 0.0413 | ||
| 1.6688 | 0.0812 | 0.3953 | 1.6650 | 0.0850 | 0.2996 | 1.5617 | 0.1883 | 0.4205 | ||
| 0.5945 | 0.0945 | 0.1736 | 1.4568 | 0.0432 | 0.3738 | 2.5172 | 0.0172 | 0.4406 | ||
| , | , | , | ||||||||
| Mean | AVB | RMSE | Mean | AVB | RMSE | Mean | AVB | RMSE | ||
| 30 | 0.5737 | 0.5737 | 0.6592 | 0.5661 | 0.5645 | 0.6358 | 0.4793 | 0.4793 | 0.6734 | |
| 0.5968 | 0.4032 | 0.4357 | 0.6872 | 0.3128 | 0.4435 | 0.6703 | 0.3297 | 0.3509 | ||
| 1.0611 | 0.3111 | 0.5648 | 0.9955 | 0.2455 | 0.5976 | 1.1023 | 0.3523 | 0.5404 | ||
| 0.1375 | 0.3625 | 0.3916 | 1.1393 | 0.3607 | 0.5370 | 3.1742 | 0.6742 | 1.5315 | ||
| 60 | 0.4343 | 0.4343 | 0.5254 | 0.4231 | 0.4231 | 0.5391 | 0.3144 | 0.3144 | 0.5439 | |
| 0.6806 | 0.3133 | 0.3272 | 0.7931 | 0.2069 | 0.3615 | 0.7054 | 0.2946 | 0.3164 | ||
| 0.8679 | 0.1179 | 0.5093 | 0.9029 | 0.1529 | 0.5193 | 1.0026 | 0.2526 | 0.5291 | ||
| 0.1515 | 0.3485 | 0.3508 | 1.1894 | 0.3106 | 0.3882 | 3.0385 | 0.5385 | 1.3574 | ||
| 100 | 0.2642 | 0.2642 | 0.3248 | 0.2971 | 0.2971 | 0.4935 | 0.2814 | 0.2814 | 0.4957 | |
| 0.7550 | 0.2450 | 0.2623 | 0.8172 | 0.1828 | 0.2664 | 0.7765 | 0.2235 | 0.2470 | ||
| 0.8274 | 0.0774 | 0.4850 | 0.8551 | 0.1051 | 0.4881 | 0.8792 | 0.1292 | 0.4937 | ||
| 0.2171 | 0.2829 | 0.3239 | 1.2403 | 0.2597 | 0.3478 | 2.9743 | 0.4743 | 1.1732 | ||
| 200 | 0.1635 | 0.1635 | 0.1749 | 0.2306 | 0.2306 | 0.2583 | 0.2119 | 0.2119 | 0.2984 | |
| 0.8887 | 0.1113 | 0.1701 | 0.8748 | 0.1252 | 0.1915 | 0.8091 | 0.1909 | 0.2197 | ||
| 0.8144 | 0.0644 | 0.3377 | 0.843 | 0.0930 | 0.3463 | 0.8427 | 0.0927 | 0.3148 | ||
| 0.3005 | 0.1995 | 0.2270 | 1.3985 | 0.1015 | 0.2628 | 2.8337 | 0.3337 | 0.8188 | ||
| 500 | 0.0788 | 0.0788 | 0.1596 | 0.0979 | 0.0979 | 0.1691 | 0.1698 | 0.1698 | 0.1924 | |
| 0.9040 | 0.0960 | 0.1038 | 0.8846 | 0.1154 | 0.1363 | 0.8569 | 0.1431 | 0.1621 | ||
| 0.8109 | 0.0609 | 0.2538 | 0.8333 | 0.0833 | 0.2643 | 0.8232 | 0.0732 | 0.2447 | ||
| 0.3745 | 0.1255 | 0.1429 | 1.4101 | 0.0899 | 0.1516 | 2.6476 | 0.1476 | 0.6138 | ||
| 1000 | 0.0290 | 0.0290 | 0.0917 | 0.0326 | 0.0326 | 0.0954 | 0.0863 | 0.0863 | 0.1001 | |
| 0.9762 | 0.0238 | 0.0935 | 0.9192 | 0.0808 | 0.1004 | 0.9417 | 0.0583 | 0.1189 | ||
| 0.8056 | 0.0556 | 0.1314 | 0.7877 | 0.0377 | 0.1278 | 0.8032 | 0.0532 | 0.1336 | ||
| 0.4697 | 0.0303 | 0.0938 | 1.5201 | 0.0201 | 0.0822 | 2.4629 | 0.0371 | 0.3673 | ||
| , | , | , | ||||||||
| Mean | AVB | RMSE | Mean | AVB | RMSE | Mean | AVB | RMSE | ||
| 30 | 0.1971 | 0.1971 | 0.4550 | 0.1850 | 0.1850 | 0.3728 | 0.1604 | 0.1604 | 0.2049 | |
| 0.8510 | 0.1490 | 0.1777 | 0.8728 | 0.1272 | 0.2246 | 0.8671 | 0.1329 | 0.1539 | ||
| 1.5506 | 0.1994 | 1.0690 | 1.2949 | 0.4551 | 1.0988 | 0.9859 | 0.7641 | 0.9582 | ||
| 0.6483 | 0.1483 | 0.7022 | 1.3317 | 0.1683 | 1.1201 | 3.3513 | 0.8513 | 1.8968 | ||
| 60 | 0.1421 | 0.1421 | 0.3338 | 0.1517 | 0.1717 | 0.3036 | 0.1331 | 0.1331 | 0.1760 | |
| 0.8978 | 0.1022 | 0.1452 | 0.9093 | 0.0907 | 0.1322 | 0.8926 | 0.1074 | 0.1230 | ||
| 0.9620 | 0.1680 | 0.9952 | 1.4597 | 0.2903 | 0.9984 | 0.9859 | 0.5675 | 0.8969 | ||
| 0.6336 | 0.1336 | 0.4824 | 1.3353 | 0.1647 | 1.0635 | 3.0780 | 0.5780 | 1.3369 | ||
| 100 | 0.0828 | 0.0828 | 0.2756 | 0.1082 | 0.1082 | 0.2617 | 0.0948 | 0.0948 | 0.1644 | |
| 0.9196 | 0.0804 | 0.1106 | 0.9135 | 0.0865 | 0.1124 | 0.9142 | 0.0858 | 0.1073 | ||
| 1.5820 | 0.1366 | 0.7072 | 1.5925 | 0.1575 | 0.8673 | 1.3115 | 0.4385 | 0.6356 | ||
| 0.6052 | 0.1052 | 0.4096 | 1.3815 | 0.1185 | 0.7321 | 2.8817 | 0.3817 | 1.1426 | ||
| 200 | 0.0698 | 0.0698 | 0.2390 | 0.0713 | 0.0713 | 0.2451 | 0.0649 | 0.0649 | 0.1240 | |
| 0.9212 | 0.0788 | 0.1038 | 0.9274 | 0.0726 | 0.1013 | 0.9236 | 0.0764 | 0.0993 | ||
| 1.6134 | 0.1250 | 0.4245 | 1.6446 | 0.1054 | 0.6505 | 1.3652 | 0.3848 | 0.4241 | ||
| 0.5840 | 0.0840 | 0.3182 | 1.4345 | 0.0655 | 0.5670 | 2.7755 | 0.2755 | 0.8005 | ||
| 500 | 0.0495 | 0.0495 | 0.2003 | 0.0625 | 0.0625 | 0.1807 | 0.0531 | 0.0531 | 0.1033 | |
| 0.9608 | 0.0410 | 0.0917 | 0.9576 | 0.0424 | 0.0627 | 0.9461 | 0.0539 | 0.0721 | ||
| 1.6437 | 0.1063 | 0.3592 | 1.6579 | 0.0921 | 0.4748 | 1.5415 | 0.2085 | 0.3599 | ||
| 0.5387 | 0.0387 | 0.2247 | 1.4589 | 0.0411 | 0.4683 | 2.6394 | 0.1394 | 0.6031 | ||
| 1000 | 0.0236 | 0.0236 | 0.1513 | 0.0366 | 0.0366 | 0.1060 | 0.0309 | 0.0309 | 0.0964 | |
| 0.9608 | 0.0392 | 0.0501 | 0.9586 | 0.0414 | 0.0525 | 0.9633 | 0.0367 | 0.0499 | ||
| 1.6734 | 0.0766 | 0.2748 | 1.6754 | 0.0746 | 0.3082 | 1.6455 | 0.1045 | 0.3042 | ||
| 0.5155 | 0.0155 | 0.1770 | 1.4725 | 0.0275 | 0.3470 | 2.5846 | 0.0846 | 0.3987 | ||
| , | , | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Mean | AVB | RMSE | Mean | AVB | RMSE | |
| 50 | 0.6175 | 0.1175 | 0.6485 | 0.4611 | 0.0389 | 0.4966 | |
| −0.2482 | 0.0018 | 0.0275 | −0.2492 | 0.0008 | 0.0224 | ||
| 0.4877 | 0.0123 | 0.2282 | 0.4935 | 0.0065 | 0.1729 | ||
| 0.8919 | 0.1419 | 0.7919 | 1.7263 | 0.2263 | 1.0481 | ||
| 0.6024 | 0.1024 | 0.8522 | 0.7327 | 0.2327 | 0.9243 | ||
| 100 | 0.6036 | 0.1036 | 0.4774 | 0.4704 | 0.0296 | 0.4174 | |
| −0.2490 | 0.0010 | 0.0190 | −0.2492 | 0.0008 | 0.0154 | ||
| 0.4764 | 0.0236 | 0.1648 | 0.5001 | 0.0054 | 0.1332 | ||
| 0.8450 | 0.0950 | 0.5350 | 1.6721 | 0.1721 | 0.7987 | ||
| 0.5823 | 0.0823 | 0.5159 | 0.6850 | 0.1850 | 0.6117 | ||
| 200 | 0.5800 | 0.0800 | 0.3833 | 0.4770 | 0.0230 | 0.3589 | |
| −0.2497 | 0.0003 | 0.0135 | 0.2497 | 0.0003 | 0.0110 | ||
| 0.4833 | 0.0167 | 0.1254 | 0.5062 | 0.0062 | 0.1052 | ||
| 0.8202 | 0.0702 | 0.4365 | 1.5804 | 0.0804 | 0.6419 | ||
| 0.5684 | 0.0684 | 0.4232 | 0.6554 | 0.1554 | 0.5388 | ||
| 500 | 0.5605 | 0.0605 | 0.2543 | 0.4807 | 0.0193 | 0.2709 | |
| −0.2497 | 0.0003 | 0.0084 | −0.2497 | 0.0003 | 0.0068 | ||
| 0.4861 | 0.0139 | 0.0822 | 0.5051 | 0.0051 | 0.0690 | ||
| 0.7286 | 0.0214 | 0.3298 | 1.5286 | 0.0286 | 0.4120 | ||
| 0.5186 | 0.0186 | 0.2752 | 0.6060 | 0.1060 | 0.4932 | ||
| 1000 | 0.5517 | 0.0517 | 0.1775 | 0.5014 | 0.0014 | 0.2268 | |
| −0.2499 | 0.0001 | 0.0061 | −0.2500 | 0.0000 | 0.0050 | ||
| 0.4889 | 0.0111 | 0.0572 | 0.5037 | 0.0037 | 0.0504 | ||
| 0.7692 | 0.0192 | 0.3008 | 1.5071 | 0.0071 | 0.1944 | ||
| 0.5165 | 0.0165 | 0.1679 | 0.5988 | 0.0988 | 0.3594 | ||
| , | , | ||||||
| Parameter | Mean | AVB | RMSE | Mean | AVB | RMSE | |
| 50 | 0.7776 | 0.2776 | 0.5389 | 0.7434 | 0.2434 | 0.4115 | |
| −0.2493 | 0.0007 | 0.0168 | −0.2495 | 0.0005 | 0.0160 | ||
| 0.4480 | 0.0520 | 0.1452 | 0.4482 | 0.0518 | 0.1151 | ||
| 1.0718 | 0.3218 | 0.8425 | 1.8451 | 0.3451 | 1.1519 | ||
| 2.2659 | 0.2341 | 1.5676 | 2.0723 | 0.4277 | 1.7081 | ||
| 100 | 0.6693 | 0.1693 | 0.4420 | 0.6672 | 0.1672 | 0.3362 | |
| −0.2497 | 0.0003 | 0.0121 | −0.2498 | 0.0002 | 0.0107 | ||
| 0.4755 | 0.0245 | 0.1146 | 0.4650 | 0.0350 | 0.0825 | ||
| 1.0339 | 0.2839 | 0.6331 | 1.7549 | 0.2549 | 0.8520 | ||
| 2.3699 | 0.1301 | 1.2486 | 2.3240 | 0.1760 | 1.1974 | ||
| 200 | 0.6480 | 0.1480 | 0.3686 | 0.5925 | 0.0925 | 0.2727 | |
| −0.2499 | 0.0001 | 0.0086 | −0.2496 | 0.0004 | 0.0076 | ||
| 0.4781 | 0.0219 | 0.0906 | 0.4799 | 0.0201 | 0.0674 | ||
| 0.8652 | 0.1152 | 0.4715 | 1.6440 | 0.1440 | 0.7637 | ||
| 2.4300 | 0.0700 | 0.8364 | 2.3895 | 0.1105 | 0.9520 | ||
| 500 | 0.5848 | 0.0848 | 0.2614 | 0.5323 | 0.0323 | 0.2302 | |
| −0.2500 | 0.0000 | 0.0057 | −0.2497 | 0.0003 | 0.0049 | ||
| 0.4869 | 0.0131 | 0.0630 | 0.4935 | 0.0065 | 0.0497 | ||
| 0.7307 | 0.0193 | 0.3958 | 1.5929 | 0.0929 | 0.5241 | ||
| 2.4326 | 0.0674 | 0.6236 | 2.4007 | 0.0993 | 0.7516 | ||
| 1000 | 0.5615 | 0.0615 | 0.1929 | 0.5194 | 0.0194 | 0.1965 | |
| −0.2498 | 0.0002 | 0.0037 | −0.2500 | 0.0000 | 0.0034 | ||
| 0.4891 | 0.0109 | 0.0476 | 0.4942 | 0.0058 | 0.0417 | ||
| 0.7647 | 0.0147 | 0.2799 | 1.5553 | 0.0553 | 0.2087 | ||
| 2.5099 | 0.0099 | 0.3908 | 2.4265 | 0.0735 | 0.4818 | ||
| , | , | ||||||
| Parameter | Mean | AVB | RMSE | Mean | AVB | RMSE | |
| 50 | 1.1623 | 0.3377 | 0.6241 | 1.2291 | 0.2709 | 1.6432 | |
| −1.2188 | 0.0312 | 0.0503 | −1.1914 | 0.0586 | 0.0797 | ||
| 1.2412 | 0.2412 | 1.1329 | 1.3723 | 0.3723 | 1.4677 | ||
| −1.2501 | 0.2501 | 1.2071 | −1.6629 | 0.6629 | 1.2754 | ||
| 2.4308 | 0.4308 | 1.2951 | 2.9961 | 0.9961 | 1.0634 | ||
| 100 | 1.2536 | 0.2464 | 0.5187 | 1.2683 | 0.2317 | 0.9353 | |
| −1.2189 | 0.0311 | 0.0410 | −1.1922 | 0.0578 | 0.0688 | ||
| 1.1736 | 0.1736 | 0.8932 | 1.2712 | 0.2712 | 1.1367 | ||
| −1.0871 | 0.0871 | 1.0619 | −1.4176 | 0.4176 | 0.8482 | ||
| 2.3665 | 0.3665 | 1.0342 | 2.5931 | 0.5931 | 0.7679 | ||
| 200 | 1.3286 | 0.1714 | 0.3911 | 1.3558 | 0.1442 | 0.6150 | |
| −1.2193 | 0.0307 | 0.0357 | −1.1924 | 0.0576 | 0.0633 | ||
| 1.1380 | 0.1380 | 0.7142 | 1.2128 | 0.2128 | 0.9740 | ||
| −1.0575 | 0.0575 | 0.8866 | −1.1219 | 0.1219 | 0.4114 | ||
| 2.1937 | 0.1937 | 0.6706 | 2.2563 | 0.2563 | 0.5772 | ||
| 500 | 1.3859 | 0.1141 | 0.3370 | 1.4233 | 0.0767 | 0.4100 | |
| −1.2195 | 0.0305 | 0.0335 | −1.2027 | 0.0473 | 0.0609 | ||
| 1.0777 | 0.0777 | 0.5193 | 1.0905 | 0.0905 | 0.6165 | ||
| −1.0125 | 0.0125 | 0.5773 | −0.9892 | 0.0108 | 0.2880 | ||
| 2.1253 | 0.1253 | 0.4165 | 2.1159 | 0.1159 | 0.3816 | ||
| 1000 | 1.4333 | 0.0667 | 0.1833 | 1.4479 | 0.0521 | 0.1916 | |
| −1.2350 | 0.0150 | 0.0245 | −1.2188 | 0.0312 | 0.0513 | ||
| 1.0605 | 0.0605 | 0.3021 | 1.0523 | 0.0523 | 0.3285 | ||
| −1.0089 | 0.0089 | 0.2698 | −1.1000 | 0.1000 | 0.1516 | ||
| 2.0652 | 0.0652 | 0.3773 | 2.0609 | 0.0609 | 0.2671 | ||
| Distribution | Parameters | |
|---|---|---|
| Beta | , | |
| UBS | ||
| UW | ||
| UN | , | |
| USN | , | |
| UPN | , | |
| UPSN | , |
| Estimator | Beta | UBS | UW | USN | UN | UPN | UPSN |
|---|---|---|---|---|---|---|---|
| 0.3204 | 0.4919 | 0.1406 | 0.3835 | 0.2759 | |||
| (0.0266) | (0.0428) | (0.0174) | (0.1061) | (0.0641) | |||
| 8.9858 | |||||||
| (0.4789) | |||||||
| 0.5657 | 0.4437 | 0.3566 | 1.7801 | ||||
| (0.0310) | (0.0123) | (0.0396) | (0.5384) | ||||
| 0.4742 | 2.1965 | 0.5088 | 6.2984 | ||||
| (0.0132) | (0.0574) | (0.1650) | (2.5197) | ||||
| 1.1364 | 1.4266 | ||||||
| (0.0206) | (0.0271) | ||||||
| −1.262 | −4.249 | ||||||
| (0.2160) | (1.3631) | ||||||
| 341.40 | 306.49 | 283.63 | 341.01 | 334.72 | 336.94 | 347.98 | |
| AIC | −678.80 | −608.98 | −563.26 | −676.03 | −665.45 | −667.89 | −687.95 |
| BIC | −669.86 | −600.04 | −554.32 | −662.65 | −656.51 | −654.48 | −670.07 |
| AICc | −678.78 | −608.96 | −563.24 | −675.99 | −665.43 | −667.85 | −687.88 |
| HQC | −675.33 | −605.51 | −559.79 | −670.82 | −661.98 | −662.68 | −681.01 |
| AD | 4.6189 | 3.6969 | 11.133 | 1.0053 | 1.3967 | 1.2588 | 0.3915 |
| (p-Value) | (0.0043) | (0.0122) | (0.0000) | (0.3545) | (0.2032) | (0.2462) | (0.8571) |
| Estimator | Beta | UN | USN | UPN | UPSN |
|---|---|---|---|---|---|
| −0.6225 | 0.0646 | −0.1296 | 0.1462 | 0.3107 | |
| (0.2238) | (0.1414) | (0.1412) | (0.1250) | (0.0778) | |
| −0.0122 | 0.0070 | 0.0072 | −0.0677 | −0.0533 | |
| (0.0030) | (0.0016) | (0.0016) | (0.0145) | (0.0035) | |
| 0.1184 | −0.0715 | −0.0900 | 0.0130 | 0.0128 | |
| (0.0353) | (0.0219) | (0.0191) | (0.0029) | (0.0012) | |
| 35.610 | 0.2274 | 0.3345 | 0.2809 | 0.4971 | |
| (8.080) | (0.0260) | (0.0590) | (0.1440) | (0.2396) | |
| 2.9405 | −4.4582 | ||||
| (1.7310) | (1.1941) | ||||
| 9.8208 | 7.1738 | ||||
| (1.6700) | (3.2247) | ||||
| 45.33 | 44.77 | 46.11 | 54.11 | 69.77 | |
| AIC | −82.66 | −81.54 | −82.23 | −98.22 | −127.54 |
| BIC | −76.10 | −74.99 | −74.04 | −90.03 | −117.12 |
| AICc | −81.44 | −80.32 | −80.35 | −96.34 | −124.83 |
| BIC | −80.32 | −79.20 | −79.31 | −95.30 | −124.04 |
| 0.1692 | −0.0460 | 0.0127 | 0.2919 | −3.8809 | 9.7419 |
| (0.0410) | (0.0025) | (0.0007) | (0.0699) | (0.1632) | (2.2619) |
| AIC | BIC | AICC | HQC | SW | KS | AD | |
|---|---|---|---|---|---|---|---|
| 77.1739 | −142.34 | −132.84 | −139.44 | −139.03 | 0.9746 | 0.1141 | 0.3418 |
| (0.5653) | (0.6934) | (0.9031) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Flórez, G.; Azevedo-Farias, R.B.; Tovar-Falón, R. New Class of Unit-Power-Skew-Normal Distribution and Its Associated Regression Model for Bounded Responses. Mathematics 2022, 10, 3035. https://doi.org/10.3390/math10173035
Martínez-Flórez G, Azevedo-Farias RB, Tovar-Falón R. New Class of Unit-Power-Skew-Normal Distribution and Its Associated Regression Model for Bounded Responses. Mathematics. 2022; 10(17):3035. https://doi.org/10.3390/math10173035
Chicago/Turabian StyleMartínez-Flórez, Guillermo, Rafael B. Azevedo-Farias, and Roger Tovar-Falón. 2022. "New Class of Unit-Power-Skew-Normal Distribution and Its Associated Regression Model for Bounded Responses" Mathematics 10, no. 17: 3035. https://doi.org/10.3390/math10173035
APA StyleMartínez-Flórez, G., Azevedo-Farias, R. B., & Tovar-Falón, R. (2022). New Class of Unit-Power-Skew-Normal Distribution and Its Associated Regression Model for Bounded Responses. Mathematics, 10(17), 3035. https://doi.org/10.3390/math10173035






