The Shortest-Edge Duplication of Triangles

Abstract

We introduce a new triangle transformation, the shortest-edge (SE) duplication, as a natural way of mesh derefinement suitable to those meshes obtained by iterative application of longest-edge bisection refinement. Metric properties of the SE duplication of a triangle in the region of normalised triangles endowed with the Poincare hyperbolic metric are studied. The self-improvement of this transformation is easily proven, as well as the minimum angle condition. We give a lower bound for the maximum of the smallest angles of the triangles produced by the iterative SE duplication $\alpha =\frac{\pi }{6}$. This bound does not depend on the shape of the initial triangle.

1. Introduction

Adaptive meshing is a fundamental component of adaptive finite element methods. This includes refining and coarsening meshes locally [1,2]. As the mesh is enriched through the refinement process, the solution on a given mesh provides an accurate starting iterate for the next mesh. Frequently, it is needed not only to enrich the mesh but also to coarsen it by some derefinement or coarsening strategy [3,4] in such a way that the nodes are located in the places where it is necessary for a more accurate solution while the number of unknowns remains bound. Mesh coarsening and mesh refinement are usually combined to provide a flexible approach for the adaptation of time-dependent problems [5].

In the context of adaptive finite element methods, both in two and three dimensions, longest-edge bisection-based algorithms have been largely studied in the last years [6,7,8]. These algorithms guarantee the construction of high-quality triangulations [9,10], assuring the maximum angle condition [11] and the non-degeneracy of the obtained meshes [10]. Non-degeneracy of the meshes means that the minimum angle generated is bounded away from zero, and it is closely related to the finite number of similarly different triangles or tetrahedra generated. Further, some longest-edge bisection-based partitions show a mesh quality improvement property, meaning that the generated meshes not only do not degenerate but also present better quality than the previously obtained mesh as the refinement is applied.

For coarsening a refined mesh, we may consider different approaches, such as removing nodes, swapping edges, or amplifying elements [2]. Here we study the shortest-edge duplication of a triangle as a simple procedure to be applied to those triangles for coarsening a triangular mesh that has been obtained by the iterative application of local refinements based on longest-edge bisection. This method shows to be effective at coarsening meshes while improving the smallest angle. On the other hand, if it is desired to maintain the resolution of the mesh while improving the smallest angles, the method can be combined with a local refinement strategy to improve high-order mesh quality while maintaining sufficient resolution, for example, by the self-similar refinement scheme [2,12], albeit this issue will not be tackled in this paper. It should be underlined, however, that there have been recent approaches, such as the $hr$-adaptivity, which are able to address this problem [13].

Our goal in the paper is to study the metric properties of the shortest-edge duplication, in the sequel SE duplication, of a triangle. To this end, we will employ the results of hyperbolic geometry and particularly the Poincare half-plane model, which has demonstrated its utility in similar triangle partitions [14,15].

Given an initial triangle, a new triangle is obtained by doubling the shortest edge, maintaining the longest edge as unaltered. The SE duplication will be explicitly set up in the next definition.

Definition 1.

Let $t_0(A,B,C)$ denote triangle $t_0$ with vertices A, B and C. Let us assume that the shortest edge of $t_0$ is edge $AB$, while the longest one is edge $BC$. Then, the SE SE duplication of $t_0$ is $t_1(A_1,B,C)$, where $A_1=B+2\overrightarrow{BA}$.

Notice that the SE duplication is a transformation of triangles that may be applied recursively. For example, and continuing with the triangle in Definition 1, if the shortest-edge of triangle $t_1$ is $A_{1}B$, and the longest one is $BC$, the SE duplication of $t_1$ is triangle $t_2(A_2,B,C)$, where $A_2=B+2\overrightarrow{B{A}_1}$. See Figure 1.

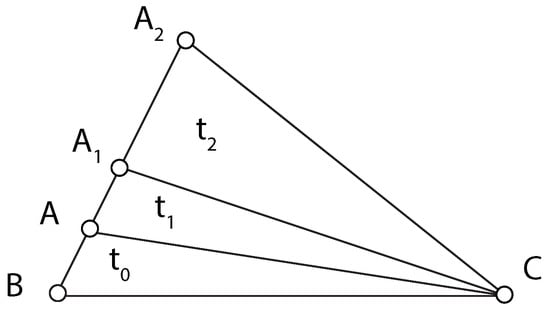
Figure 1. First SE duplications of triangle $t_0$.

It is clear that by the SE duplication of a triangle, the two shortest edges of the triangle increase, while the longest edge remains unaltered.

Let $\tau$ be a locally refined triangular mesh obtained by a longest-edge bisection-based refinement. One could apply the SE duplication of some triangles in order to coarsen the mesh. This procedure consists of locally changing a triangle by SE duplication. As a matter of example, Figure 2 shows the application of SE duplication to a refined mesh obtained by the longest-edge bisection so that a derefined mesh appears.

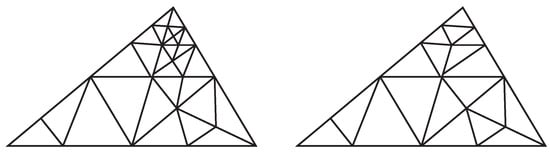
Figure 2. SE duplication procedure as a derefinement process.

2. Normalised Region for Triangles and Piecewise Function for the SE Duplication

For any arbitrary triangle, a similar triangle can be found by performing suitable symmetries, scaling, translations and rotations such that the normalised triangle has the longest edge with vertices $(0,0)$ and $(1,0)$, and the opposite vertex, z, in the upper plane at the left of the vertical line $x=\frac{1}{2}$; that is, with the shortest edge to the left with vertices $(0,0)$ and z [12]. Using this procedure, all similar triangles are represented by a unique complex number $z\in \Sigma$, where $\Sigma$ is the set of the complex plane ${\displaystyle \Sigma =\{z/\mathrm{Im}z>0,\mathrm{Re}z\le \frac{1}{2},|z-1|\le 1\}}$. $\Sigma$ is called the space of triangular shapes. See Figure 3, where $\Sigma$ is in grey.

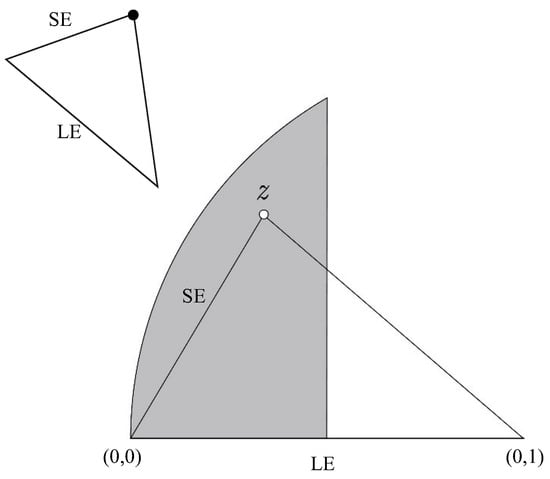
Figure 3. Normalised triangle and normalised region $\Sigma =\{z/\mathrm{Im}z>0,\mathrm{Re}z\le \frac{1}{2},|z-1|\le 1\}$.

For any point $z\in \Sigma$, let $w\left(z\right)$ be its image in $\Sigma$ by the shortest-edge duplication transformation. $w\left(z\right)$ is a piecewise function that depends on the location of z in $\Sigma$. Explicitly, function $w\left(z\right)$ is defined as follows, depending on which subregion point z is in according to the subregions in Figure 4.

$$w\left(z\right)=\left\{\begin{array}{cc}{w}_V\left(z\right)=2z\hfill & \mathrm{if}z\in V,\hfill \\ w_{VI}\left(z\right)=1-2\overline{z}\hfill & \mathrm{if}z\in VI,\hfill \\ {\displaystyle w_{III}\left(z\right)=\frac{2\overline{z}}{2\overline{z}-1}}\hfill & \mathrm{if}z\in III,\hfill \\ {\displaystyle w_{IV}\left(z\right)=\frac{2z-1}{2z}}\hfill & \mathrm{if}z\in IV,\hfill \\ {\displaystyle w_{II}\left(z\right)=\frac{1}{1-2z}}\hfill & \mathrm{if}z\in II,\hfill \\ {\displaystyle w_I\left(z\right)=\frac{1}{2\overline{z}}}\hfill & \mathrm{if}z\in I.\hfill \end{array}\right.$$

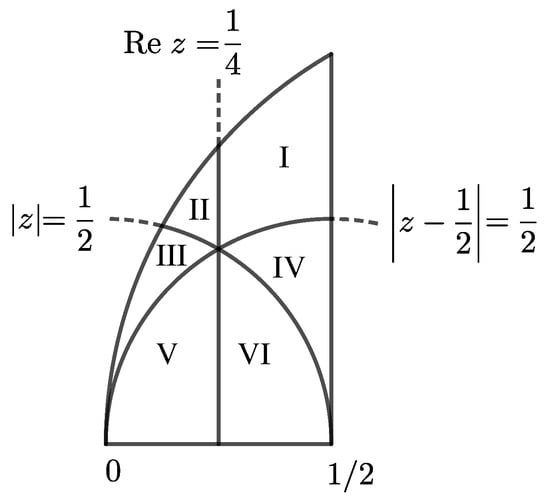
Figure 4. Circles and straight lines defining the subregions for the piecewise function w.

Figure 4 shows the subdomains in $\Sigma$ needed to define function $w\left(z\right)$.

The values of function w, depending on the position of point z in each sub-region, may be easily deduced. As a matter of example, Figure 5 shows the definition of function $w\left(z\right)$ for z in the first two lower subregions of the space of triangular shapes. Similar figures may be found for the other subregions. In Figure 5 right, $w\left(z\right)=2z$, while in Figure 5 left, $w\left(z\right)=1-2\overline{z}$ in order to normalise the triangle to have its shortest edge on the left side, so that $w\left(z\right)$ belongs to $\Sigma$.

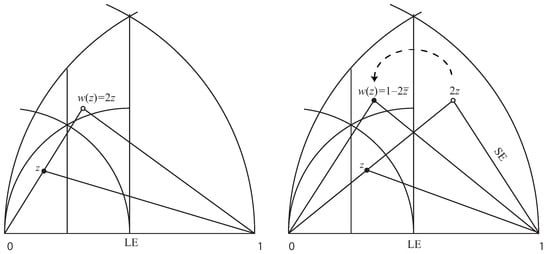
Figure 5. Definition of w for $z\in V$ on the left, and for $z\in VI$ on the right.

Using hyperbolic geometry, such as the Poincare half-plane model, see [14,15,16,17], the circumferences and straight lines in the definition of the piecewise function w are orthogonal to $\mathrm{Im}z=0$ and, therefore, are geodesics in the Poincare half-plane. The expressions for function w are isometries in the half-plane hyperbolic model because they have the form ${\displaystyle \frac{az+b}{cz+d}}$ or ${\displaystyle \frac{a\left(\overline{z}\right)+b}{c\left(\overline{z}\right)+d}}$ with real coefficients $ad-bc>0$. Function w is invariant with respect to the inversion of the circumferences $\left|z\right|=1/2$ and $|z-1/2|=1/2$, and under symmetry with respect to the straight line $\mathrm{Re} z=1/2$. We recall here the expression of these transformations in [18]. Let K be an arbitrary circle with centre q and radius R. Then the inversion in K, written $z\mapsto \tilde{z}={\mathcal{I}}_K\left(z\right)$, is equal to

$${\mathcal{I}}_K\left(z\right)=\frac{R^2}{\overline{z}-\overline{q}}+q=\frac{q\overline{z}+(R^2-{\left|q\right|}^2)}{\overline{z}-\overline{q}}.$$

In particular, for $K_1$, circle $\left|z\right|=1/2$, we have ${\displaystyle {\mathcal{I}}_{K_1}\left(z\right)=\frac{1}{4\overline{z}}}$, while for $K_2$, circle $|z-1/2|=1/2$, we have ${\displaystyle {\mathcal{I}}_{K_2}\left(z\right)=\frac{\overline{z}}{2\overline{z}-1}}$.

On the other hand, ff $\overline{\alpha }z+\alpha \overline{z}=r$ is a line in the complex plane such that $z_1$ is the reflection of $z_2$ in the given line, then $r=\overline{z_1}\alpha +z_2\overline{\alpha }$. In particular, for the straight line L with equation $\mathrm{Re}z=1/2$, the expression of the reflection in line L, say ${\mathcal{R}}_L\left(z\right)$, is ${\mathcal{R}}_L\left(z\right)=\frac{1}{2}-\overline{z}$.

Theorem 1.

Function w is invariant with respect to the inversion of the two circumferences, $|z-1/2|=1/2$ and $\left|z\right|=1/2$, and under symmetry with respect to the straight line $Rez=1/2$ that appears in its definition.

Proof. 

The proof follows easily by checking that

$$\left\{\begin{array}{cc}{w}_I\left({\mathcal{R}}_L\left(z\right)\right)=w_{II}\left(z\right)\forall z\in II,\hfill & w_{II}\left({\mathcal{R}}_L\left(z\right)\right)=w_I\left(z\right)\forall z\in I,\hfill \\ w_{III}\left({\mathcal{R}}_L\left(z\right)\right)=w_{IV}\left(z\right)\forall z\in IV,\hfill & w_{IV}\left({\mathcal{R}}_L\left(z\right)\right)=w_{III}\left(z\right)\forall z\in III,\hfill \\ w_V\left({\mathcal{R}}_L\left(z\right)\right)=w_{VI}\left(z\right)\forall z\in VI,\hfill & w_{VI}\left({\mathcal{R}}_L\left(z\right)\right)=w_V\left(z\right)\forall z\in V.\hfill \end{array}\right.$$

Similarly, for inversions ${\mathcal{I}}_{K_i}\left(z\right)$, with $i=1,2$, it holds, in closed form, that

$$w_J\left({\mathcal{I}}_{K_i}\left(z\right)\right)=w_{{\mathcal{I}}_{K_i}\left(J\right)}\left(z\right)\forall z\in {\mathcal{I}}_{K_i}\left(z\right)$$

where J represents any subregion in the definition of function w.    □

If $z_1$ and $z_2$ are such that $\mathrm{Im}{z}_i>0$, then the hyperbolic distance d between $z_1$ and $z_2$, $d(z_1,z_2)$, is

$$d(z_1,z_2)={cosh}^{-1}\left({\displaystyle 1+\frac{\left|z_1-z_2\right|}{2\mathrm{Im}{z}_1\mathrm{Im}{z}_2}}\right).$$

On the other hand, if $\mathrm{Re}{z}_1=\mathrm{Re}{z}_2$, then

$$d(z_1,z_2)=\left|ln\left(\frac{\mathrm{Im}{z}_1}{\mathrm{Im}{z}_2}\right)\right|.$$

Let $z_1$ and $z_2$ be points in a geodesic circumference, and $z_2$ be the upper point located over the centre of the circumference, the hyperbolic length of the segment in the geodesic from $z_1$ to $z_2$, say l, verifies

$$\theta =2arctan\left(e^{-l}\right)$$

where $\theta$ is the difference between $\pi /2$ and the central angle is determined by the segment from $z_1$ to $z_2$ over the geodesic. See Figure 6.

Definition 2.

A region $\Omega \subset \Sigma$ is called a closed region for SE duplication if $w\left(z\right)\in \Omega \forall z\in \Omega$.

Lemma 1

(non-increasing property). If $z_1,z_2\in \Sigma$, then $d(w\left(z_1\right),w\left(z_2\right))\le d(z_1,z_2)$.

Proof. 

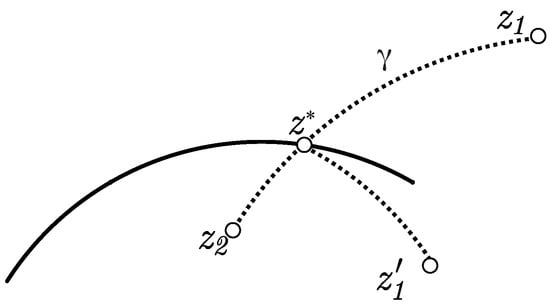
Let us first assume that $z_1$ and $z_2$ are in a region with the same definition of w, then $d(z_1,z_2)=d(w\left(z_1\right),w\left(z_2\right))$. This may be checked easily and also follows because w is an isometry in $\Sigma$.

Suppose now that $z_1$ and $z_2$ are not in a region with the same definition of w. $z_1$ and $z_2$ may be in two regions sharing a common boundary. In this case, there is $z_1^{\prime }$ in the region of $z_2$ with $w\left(z_1\right)=w\left(z_1^{\prime }\right)$ because of the symmetry of w with respect to the boundary. Let $\gamma$ be the geodesic line that joins $z_1$ and $z_2$. $\gamma$ intersects the boundary at a point, say $z^{*}$. Then, since points $z_1$, $z^{*}$ and $z_2$ are in the same geodesic, $d(z_1,z_2)=d(z_1,z^{*})+d(z^{*},z_2)$. Further, $d(z_1,z^{*})=d(z_1^{\prime },z^{*})$ because $z_1$ and $z_1^{\prime }$ are symmetrical points with respect to the boundary containing $z^{*}$. See Figure 7.

Figure 7. The geodesic line joining $z_1$ and $z^{*}$ is an image by reflection of the segment joining $z_1^{\prime }$ with $z^{*}$, and so $d(z_1,z^{*})=d(z_1^{\prime },z^{*})$.

Therefore, by the triangular inequality,

$$d(z_1,z_2)=d(z_1,z^{*})+d(z^{*},z_2)=d(z_1^{\prime },z^{*})+d(z^{*},z_2)>d(z_1^{\prime },z_2).$$

Thus, $d(w\left(z_1\right),w\left(z_2\right))=d(w\left(z_1^{\prime }\right),w\left(z_2\right))=d(z_1^{\prime },z_2)<d(z_1,z_2)$.

If, $z_1$ and $z_2$ are in different regions not sharing a common boundary, we may apply the previous process to bring both $z_1$ and $z_2$ into the same region and the proof is finished.    □

Definition 3.

Let z be in Σ. The orbit of z by the SE duplication, $\Gamma \left(z\right)$, is the set as ${\displaystyle \Gamma \left(z\right)={\cup }_{n\ge 0}{w}^{\left(n\right)}\left(z\right)}$, where $w^{\left(0\right)}\left(z\right)=z$, and $w^{\left(n\right)}\left(z\right)=w\left(w^{(n-1)}\left(z\right)\right)$.

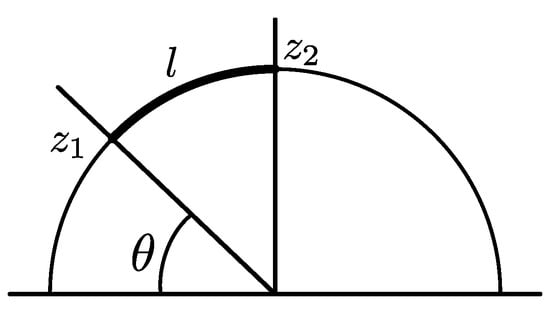
Figure 6. Hyperbolic length l from $z_1$ to $z_2$ verifies $\theta =2arctan\left(e^{-l}\right)$.

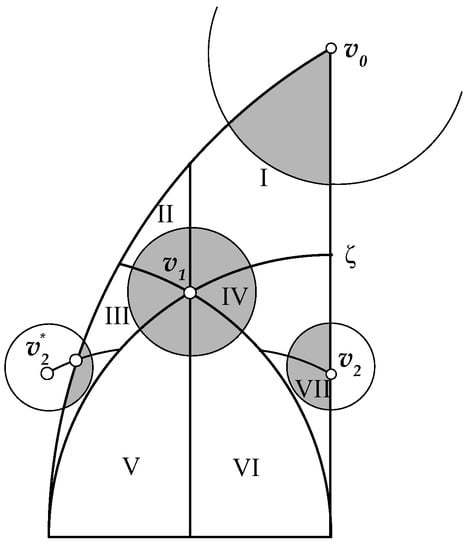
For $\zeta =\frac{1}{2}+\frac{1}{2}i$, $\Gamma \left(\zeta \right)=\left\{\zeta \right\}$, since $w\left(\zeta \right)=\zeta$. Other fixed points for w are $x_1=\frac{1}{4}+\frac{\sqrt{7}}{4}i$ and $q_1=\frac{3}{8}+\frac{\sqrt{23}}{8}i$. In sub-region I, as denoted in Figure 8, $w\left(z\right)=\frac{1}{2\overline{z}}$, which is an inversion with respect to the circumference of equation $\left|z\right|=\frac{\sqrt{2}}{2}$, or $x^2+y^2=\frac{1}{2}$. Therefore, for z in the arc of that circumference which is in region I, ${\displaystyle \left|\Gamma \left(z\right)\right|=1}$. It may be easily verified that these are the only fixed points for $w\in \Sigma$. Notice that although $(0,0)$ is another fixed point, that triangle is invalid and does not belong to the space of triangular shapes $\Sigma$ where it is required $\mathrm{Im}z>0$. Further, it follows that for $z\in I$, ${\displaystyle \left|\Gamma \left(z\right)\right|\le 2}$. For example, for $v_0=\frac{1}{2}+\frac{\sqrt{3}i}{2}$, which corresponds to the equilateral triangle, then $\Gamma \left(v_0\right)=\left\{v_0,v_1\right\}$, where $v_1=\frac{1}{4}+\frac{\sqrt{3}}{4}i$.

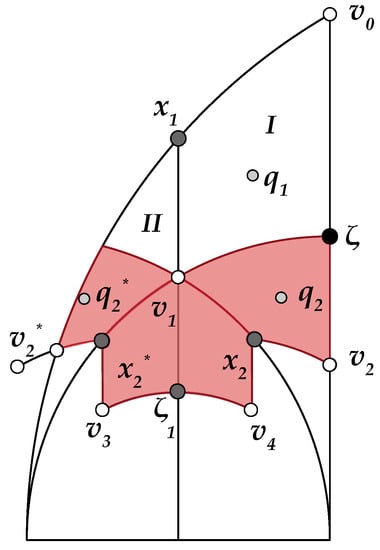
Figure 8. Regions for Lemma 2.

In order to prove that the orbit for any point z is finite, we will use the division of the normalised region is shown in Figure 8. We consider the sets $w_J^{-1}\left(I\right)$, with $J=III,V,VI,IV$, where $w_J^{-1}\left(I\right)=\left\{w_J^{-1}\left(z\right)\mathrm{for}z\in I\right\}$. It is clear that $w_J^{-1}\left(I\right)\subset J$. These sets are the coloured subsets in Figure 8. The points labelled in the figure are $x_1=\frac{1}{4}+\frac{\sqrt{7}}{4}i$, $x_2=\frac{3}{8}+\frac{\sqrt{7}}{8}i$ and $x_2^{*}=\frac{1}{8}+\frac{\sqrt{7}}{8}i$ are pre-images of $x_1$. Similarly, $v_1=w^{-1}\left(v_0\right)$, $v_2=w_{IV}^{-1}\left(v_1\right)$, $v_2^{*}=w_{III}^{-1}\left(v_1\right)$, $v_3=w_V^{-1}\left(v_1\right)$, and $v_4=w_{VI}^{-1}\left(v_1\right)$. Further, $q_2$ is the pre-image of $q_1$ in region $IV$; that is, $q_2=\frac{5}{12}+\frac{\sqrt{23}}{12}i$, while $q_2^{*}=\frac{1}{12}+\frac{\sqrt{23}}{12}i=w_{III}^{-1}\left(q_1\right)$.

Lemma 2.

$S=I\cup II\cup w_{III}^{-1}\left(I\right)\cup w_V^{-1}\left(I\right)\cup w_{VI}^{-1}\left(I\right)\cup w_{IV}^{-1}\left(I\right)$ is a closed region. Further, if $z\in S$, then $\left|\Gamma \left(z\right)\right|\le 3.$

Proof. 

Let $z\in S$. If $z\in I$, $w\left(z\right)=w_I\left(z\right)=\frac{1}{2\overline{z}}$ is an inversion with respect to the circumference of equation $\left|z\right|=\frac{\sqrt{2}}{2}$, then $w(z\in I)=z^{\prime }\in I$. Therefore, for $z\in I$, $\left|\Gamma \left(z\right)\right|\le 2$. Further, by construction, $w\left(w_J^{-1}\left(I\right)\right)\subset I$, with $J=III,V,VI,IV$, so $\left|\Gamma \left(z\right)\right|\le 3$ for $z\in w_{III}^{-1}\left(I\right)\cup w_V^{-1}\left(I\right)\cup w_{VI}^{-1}\left(I\right)\cup w_{IV}^{-1}\left(I\right)$. Finally, by the symmetry of function w about line $\mathrm{Re}z=\frac{1}{4}$, then for $z\in II$, $w\left(z\right)=\frac{-1}{2z-1}\in I$, and, therefore, $\left|\Gamma \left(z\right)\right|\le 3$ for $z\in II$.    □

The argument of the last lemma may be applied recursively, considering each of the pre-images of the last sets by $w_J$, with $J=III,V,VI,IV$. In that way, since the pre-images of the lowest vertices considered tend to the horizontal line $\mathrm{Im}\left(z\right)=0$, it follows that $\left|\Gamma \left(z\right)\right|<\infty$, $\forall z\in \Sigma$. This fact will also be shown experimentally by a Monte Carlo experiment later.

Lemma 3.

There is ${\epsilon }^{\prime }>0$ such that for every $z\in \Sigma$ such that the hyperbolic distance to any of the points $v_0$, $v_1$, $v_2$ or $v_2^{*}$ is less than or equal to ${\epsilon }^{\prime }$ then $\left|\Gamma \left(z\right)\right|<\infty .$

Proof. 

Notice that ${\epsilon }^{\prime }$ may be chosen such that every hyperbolic circle with centre $v_0$, $v_1$, $v_2$ or $v_2^{*}$ and radius ${\epsilon }^{\prime }$ intersects only the geodesic lines defining w that pass through their centres, as Figure 9 shows.

Figure 9. ${\epsilon }^{\prime }$ is such that every hyperbolic circle with a centre at $v_0$, $v_1$ and $v_2$ intersects only with the geodesic lines in the definition of $w\left(z\right)$ passing through its centres.

Let us first suppose that $z\in \Sigma$ with $d(z,v_0)\le {\epsilon }^{\prime }$. In that case, $z\in I$ so $\left|\Gamma \left(z\right)\right|\le 2.$

On the other hand, if $d(z,v_1)\le {\epsilon }^{\prime }$, $w\left(z\right)\in I$, so $\left|\Gamma \left(z\right)\right|\le 3.$ Finally, if $d(z,v_2)\le {\epsilon }^{\prime }$ or $d(z,v_2^{*})\le {\epsilon }^{\prime }$, then $d(w\left(z\right),v_1)\le {\epsilon }^{\prime }$, so it is reduced to the previous case.     □

Lemma 4.

Let $q_1=\frac{3}{8}+\frac{\sqrt{23}}{8}i$ and $r=d(q_1,v_1)$. Then there exists $\epsilon >0$ such that for every $z\in \Sigma$ with $d(q_1,z)\le r+\epsilon$, then $\left|\Gamma \left(z\right)\right|<\infty .$

Proof. 

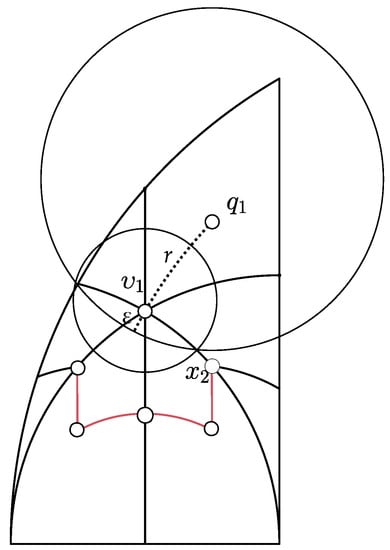
Let us consider that $\epsilon >0$ is small enough so that the hyperbolic circle with a centre at $q_1$ and radius $r+\epsilon$ does not intersect with region $VII$. This is possible because $d(q_1,v_1)<d(q_1,x_2)$, as it is shown in Figure 10. With such a $\epsilon$, we may assure that the region of z such that $d(q_1,z)\le r+\epsilon$ is contained in $I\cup IV$ along with a small hyperbolic circle with its centre at $v_1$, so it is inside region S from Lemma 2. It follows that $\left|\Gamma \left(z\right)\right|<\infty .$ □

Figure 10. For a suitable $\epsilon$, a circle with its centre at $q_1$ and radius $d(q_1,v_1)+\epsilon$ is in region S from Lemma 2.

Lemma 5.

Let $\epsilon >0$ as in the previous lemma, and $r=d(q_1,v_1)$. Let K be a compact set contained in the normalised region $\Sigma$ such that for every $z\in K$ it holds that $d(z,q_1)>r+\epsilon$. Then, there exists a value A, where $0<A<1$ such that for every $z\in K$, $d(w\left(z\right),q_1)<A·d(z,q_1)$.

Proof. 

Function

$${\displaystyle \varphi \left(z\right)=\frac{d(w\left(z\right),q_1)}{d(z,q_1)}}$$

is continuous in K. Since K is compact, there exists A, the maximum value of $\varphi \left(z\right)$ in K. By not increasing the distance and since $w\left(q_1\right)=q_1$, then $d(w\left(z\right),q_1)\le d(z,q_1)$. In addition, if $z\in K$, z is not in region I, and the inequality between the distances is strict. In particular, this happens for the value of $z\in K$ in where the maximum is attained, where $A<1$.    □

Theorem 2.

If $z\in \Sigma$, then $\left|\Gamma \left(z\right)\right|<\infty .$

Proof. 

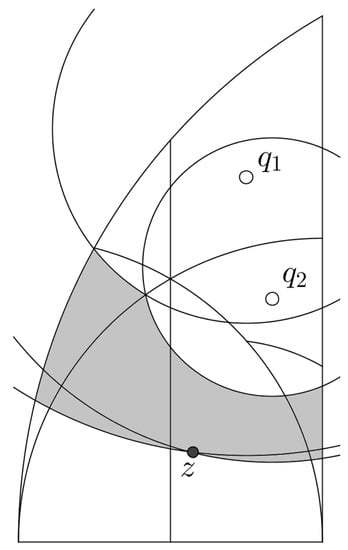
Let r and $\epsilon$ be as in the previous lemmas. If $d(z,q_1)\le r+\epsilon$, then $\left|\Gamma \left(z\right)\right|<\infty$, by Lemma 5. Let us suppose, therefore, that $d(z,q_1)>r+\epsilon$. Let K be the compact set given by the points $u\in \Sigma$ such that $d(u,q_1)\le d(z,q_1)$ with $d(u,q_1)\ge r+\epsilon$, and also $d(u,q_2)\le d(z,q_2)$ with $d(u,q_2)\ge r+\epsilon$. In Figure 11, K is grey. By Lemma 5, there exists A such that for every $u\in K$, $d(w\left(u\right),q_1)\le A·d(u,q_1)$. Therefore, $d(w\left(z\right),q_1)\le A·d(z,q_1)$ with $A<1$. By the non-increasing property, $d(w\left(z\right),q_2)\le A·d(z,q_2)$. Therefore, either $w\left(z\right)\in K$ or the orbit $\left|\Gamma \left(w\right(z\left)\right)\right|<\infty .$ By iterating this process, the orbit $\left|\Gamma \left(z\right)\right|$ is described as a finite set and a finite number of finite orbits of points with a distance to $q_1$ of less than or equal to $r+\epsilon$. Therefore, by Lemma 4 these orbits are also finite.    □

Figure 11. In grey are the points $u\in \Sigma$ with $d(u,q_i)\le d(z,q_i)$ and $d(u,q_i)\ge r+\epsilon$, for $i=1,2$.

3. Classes of Triangles

Here, we focus on the number of dissimilar triangles that are produced in the SE duplication scheme. Our goal in this section is to study the number of dissimilar triangles so that we can get a classification of the triangles. Let class $C_n$ be the set of triangles for which the SE duplication produces exactly n dissimilar triangles.

We develop a Monte Carlo experiment that can be used to visually represent the classes of triangles according to the number of dissimilar triangles generated.

The process can be described in three phases: (1) Pick a point within the mapping domain defined by the horizontal base and by the two bounding exterior circular arcs. This point $z=(x,y)$ is the apex of a target triangle. (2) Apply SE duplication to the triangle defined by z and its successors and stop when no new shapes appear. (3) The number of steps until termination defines the number of dissimilar triangles for z. This process is recursively applied to a large sample of triangles uniformly over the domain. The output of the experiment is a graph where all of the dissimilar triangles are represented using a colour map to obtain the result in Figure 12.

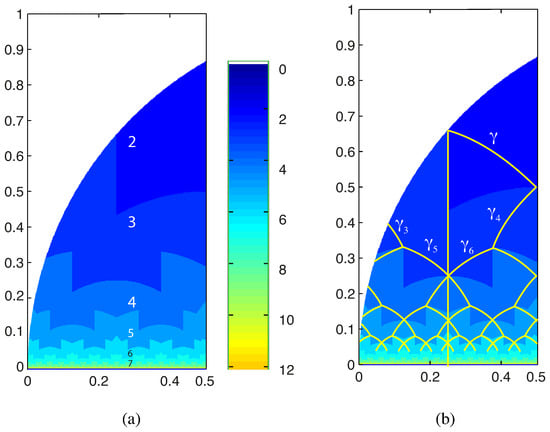
Figure 12. (a) Dissimilar triangle classes generated by a Monte Carlo computational experiment for the SE duplication. (b) Lines inside each $n^{\mathrm{th}}$ triangle class with $\Gamma \left(z\right)=n-1$.

Note that the number of dissimilar triangles has been drawn within several coloured regions. For instance, label 2 stands for the two dissimilar triangles and is associated with the targeted triangles within the region above the pair of arcs that intersect on the vertical line of symmetry near the point $y=0.3$. Label 3 is in the region below for the 3 dissimilar triangles. A graph is then constructed in this manner that fills a completely coloured diagram. It should be noted that triangles with needle-like shapes located close to the baseline will require a higher number of SE duplications until new dissimilar triangles no longer appear.

Note that the region where all the trajectories end in the diagram is located at the dark blue region. Therefore, we can determine a lower bound of the maximum of the smallest angles for the last generated triangles of $\alpha ={30}^{\circ }$, which are related to the apex with $\mathrm{Re}z=1/4$. It can be seen that the smallest angle in each of the regions generated by duplicating its shortest edge is bounded from below with total independence of the initial point of the respective trajectories. This is a salient property in comparison with the evolution of the angles in other longest-edge schemes, for example, in the 4T-LE partition. In the case of 4T-LE partition, these lower bounds depend on the geometry of the initial triangle. See [9,10] for details on the evolution properties of the angles when the 4T-LE partition is recursively applied. In Table 1, the minimum angles generated in the process are listed.

Table 1. Sequences of dissimilar triangles obtained by SE duplication.

	Triangle 1			Triangle 2
	# of Dissimilar Triangles 7			# of Dissimilar Triangles 8
It. n	${\gamma }_n$	${\beta }_n$	${\alpha }_n$	${\gamma }_n$	${\beta }_n$	${\alpha }_n$
0	145.455	32.595	1.950	173.972	5.423	0.605
1	143.291	32.595	4.114	173.216	5.423	1.361
2	138.199	32.595	9.206	170.950	5.423	3.627
3	123.933	32.595	23.472	153.690	20.887	5.423
4	77.683	69.722	32.595	144.929	20.887	14.184
5	69.722	59.153	51.126	102.859	56.254	20.887
6	84.036	59.153	36.811	78.056	56.254	45.690
7	69.722	59.153	51.126	81.241	56.254	42.504
8				78.056	56.254	45.690
	Triangle 3			Triangle 4
	# of Dissimilar Triangles 7			# of Dissimilar Triangles 4
It. n	${\gamma }_n$	${\beta }_n$	${\alpha }_n$	${\gamma }_n$	${\beta }_n$	${\alpha }_n$
0	169.900	8.572	1.528	114.624	54.900	10.475
1	167.719	8.572	3.708	102.074	54.900	23.025
2	158.613	12.814	8.572	74.625	54.900	50.475
3	125.395	41.790	12.814	86.502	54.900	38.598
4	106.818	41.790	31.390	74.625	54.900	50.475
5	75.424	62.784	41.790
6	73.181	62.784	44.033
7	75.424	62.784	41.790

In addition, we may find curves inside each coloured region that appear from the trajectories of the triangles in the diagram. Figure 12b shows some of these curves of interest as follows.

It has already been proven that for $z\in I$, $\Gamma \left(z\right)\le 2$. In this sub-region, $w\left(z\right)=\frac{1}{2\overline{z}}$ is an inversion with respect to the circumference of $\left|z\right|=\frac{\sqrt{2}}{2}$, or $x^2+y^2=\frac{1}{2}$. Therefore, for z in the arc of circumference $w\left(z\right)=z$ so $\left|\Gamma \left(z\right)\right|=1$.

Similarly to the points in region I, where $\left|\Gamma \left(z\right)\right|=1$, there exist points in lower regions such that $\left|\Gamma \left(z\right)\right|=2$. These points will be those where $w\left(z\right)$ is precisely in the arc of circumference, say $\gamma$, of equation $\left|z\right|=\frac{\sqrt{2}}{2}$. That is, by studying the pre-images of w for $z\in \gamma$, the corresponding arcs in lower regions of $\sigma$ may be found as follows

• If $z\in II$, $w\left(z\right)=\frac{-1}{2z-1}$. If $w\left(z\right)\in \gamma$, then $\left|z-\frac{1}{2}\right|=\frac{\sqrt{2}}{2}$, which is the arc of a circumference with centre $(\frac{1}{2},0)$ and radius $\frac{\sqrt{2}}{2}$. Notice that this circumference is out of $\Sigma$, and, therefore, there is no point in region $II$ where $\left|\Gamma \left(z\right)\right|=2$.
• If $z\in III$, $w\left(z\right)=\frac{2\overline{z}}{2\overline{z}-1}$. If $w\left(z\right)\in \gamma$, then $\left|\frac{2\overline{z}}{2\overline{z}-1}\right|=\frac{1}{\sqrt{2}}$. If $z=(x,y)$, we have ${(x+\frac{1}{2})}^2+y^2=\frac{1}{2}$, which is the arc of a circumference with centre $(-\frac{1}{2},0)$ and radius $\frac{\sqrt{2}}{2}$, arc ${\gamma }_3$ in the figure.
• If $z\in IV$, $w\left(z\right)=\frac{2z-1}{2z}$. If $w\left(z\right)\in \gamma$, then $\left|\frac{2z-1}{2z}\right|=\frac{1}{\sqrt{2}}$. If $z=(x,y)$, ${\left(x-1\right)}^2+y^2=\frac{1}{2}$, which is the arc of a circumference with centre $(1,0)$ and radius $\frac{\sqrt{2}}{2}$, arc ${\gamma }_4$ in the figure.
• If $z\in V$, $w\left(z\right)=2z$. If $w\left(z\right)\in \gamma$, then $\left|z\right|=\frac{\sqrt{2}}{4}$, which is a circumference with centre $(0,0)$ and radius $\frac{\sqrt{2}}{4}$, arc ${\gamma }_5$ in the figure.
• If $z\in VI$, $w\left(z\right)=1-2\overline{z}$. If $w\left(z\right)\in \gamma$, then $\left|1-2\overline{z}\right|=\frac{1}{\sqrt{2}}$, so $\left|z-\frac{1}{2}\right|=\frac{\sqrt{2}}{4}$, arc of a circumference with centre $(\frac{1}{2},0)$ and radius $\frac{\sqrt{2}}{4}$, arc ${\gamma }_6$ in the figure.

The analysis of subsequent lines where ${\displaystyle \left|\Gamma \left(z\right)\right|=n}$, for $n\ge 3$ is analogous to those already carried out by considering the pre-images of the circular arcs already studied. The first of these arcs is depicted in Figure 12b.

It is worth noting here that the fractal appearance of these arcs, in the diagram of triangular shapes is similar to that of the fractal appearance of the boundary of the regions depending on the number of dissimilar triangles generated by SE duplication.

4. Improvement Properties

The non-degeneracy property has been very relevant in the approximation properties of finite element spaces and the convergence issues of multigrid and multilevel algorithms [19]. The non-degeneracy is held when the interior angles of all elements are bounded uniformly away from zero. This property should be assured in refinement and remeshing strategies. It is well-known that the longest-edge bisection algorithms guarantee the construction of high-quality triangulations [10,15].

However, the most interesting property of SE duplication is the self-improvement property, as the following theorem establishes.

Theorem 3

(self-improvement property). Let $t_0$ be an initial obtuse triangle in which SE duplication is iteratively applied. Then a (finite) sequence of dissimilar triangles, one per iteration, is obtained: $\left\{t_0,t_1,\dots t_{N-1},t_N,\dots t_{N+M}\right\}$, where triangles $t_0,t_1,t_2,\dots ,t_{N-1}$ are obtuse, triangle $t_N$ is nonobtuse, and the SE duplication of $t_N$ produces a finite number of new, not obtuse triangles $t_{N+1}$ and $t_{N+M}$.

The iterative SE duplication transformation applied to an initial obtuse triangle produces a finite sequence of ‘better’ triangles in the sense that the new triangle is ‘less obtuse’ than the previous one, and its minimum angle is greater than the minimum angle of the previous triangle, until triangle $t_N$ becomes nonobtuse.

This process results in one of the situations illustrated in the next diagram:

(1)	$t_{N-1}$	→	$t_N⥀$
	obtuse		nonobtuse
(2)	$t_{N-1}$	→	$t_N$	⇌	$t_{N+1}$
	obtuse		nonobtuse		nonobtuse
(3)	$t_{N-1}$	→	$t_N$	$\to \cdots$	$t_{N+M-1}$	⇌	$t_{N+M}$
	obtuse		nonobtuse		nonobtuse		nonobtuse
The three endings to an orbit by the SE duplication.

The first situation corresponds to the orbit ending in a fixed point for the SE duplication. In the other two possibilities, the orbit also ends in region I but not at a fixed point of w. Since function $w\left(z\right)$ is an inversion in I$w^2\left(z\right)=z$. The only difference between the two last scenarios is that in (2), the first nonobutse triangle is in I, while in (3), it is not in I. See Figure 8 and Figure 12. We will show some examples in the next section.

5. Numerical Examples

In this section, we present the evolution of the iterative application of the SE duplication to some initial test triangles. The first four initial triangles were also chosen and studied by Rivara and Iribarren in [9] and Plaza et al. in [10] in the context of the 4-triangle longest-edge partition. Table 1 shows the different-shaped triangles obtained by SE duplication of these triangles. The evolution of the generated triangles is visible at a glance in Figure 13.

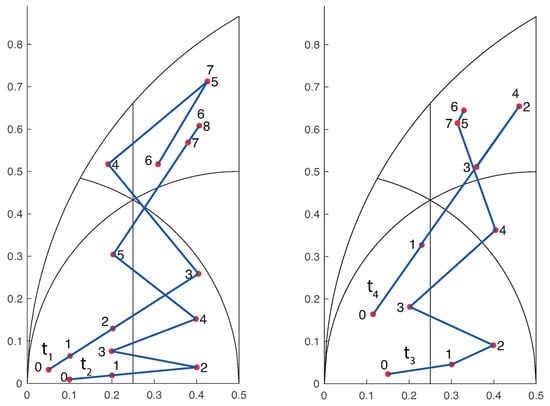
Figure 13. Evolution of SE duplication for the four different triangles in Table 1.

Table 2 shows the evolution by the SE duplication applied to four more triangles sharing the same minimum angle, $5^{\circ }$. It should be noted that, as before, the generated triangles are better shaped than the previous ones until the respective orbit ends in subregion $I\%$. We observe that triangle 8 is an acute isosceles, and all triangles of its orbit are acute.

Table 2. Sequences of triangles obtained by SE duplication from initial triangles with the same minimum angle ${\alpha }_0$.

	Triangle 5			Triangle 6
	# of Dissimilar Triangles 6			# of Dissimilar Triangles 5
It. n	${\gamma }_n$	${\beta }_n$	${\alpha }_n$	${\gamma }_n$	${\beta }_n$	${\alpha }_n$
0	146.875	28.125	5.000	123.75	51.250	5.000
1	140.057	28.125	11.817	118.092	51.250	10.658
2	117.363	34.512	28.125	104.840	51.250	23.910
3	78.236	67.252	34.512	74.750	54.002	51.25
4	67.252	62.637	50.111	87.821	54.002	38.177
5	80.958	62.637	36.405	74.750	54.002	51.25
6	67.252	62.784	50.111
	Triangle 7			Triangle 8
	# of Dissimilar Triangles 4			# of Dissimilar Triangles 4
It. n	${\gamma }_n$	${\beta }_n$	${\alpha }_n$	${\gamma }_n$	${\beta }_n$	${\alpha }_n$
0	100.625	74.375	5.000	87.500	87.500	5.000
1	95.456	74.375	10.169	87.500	82.538	9.962
2	84.935	74.375	20.690	82.538	77.685	19.777
3	74.375	65.442	40.183	77.685	64.346	37.968
4	70.022	65.442	44.537	68.170	64.346	47.483
5	74.375	65.442	40.183	77.685	64.346	37.968

The evolution of the generated triangles is visible at a glance in Figure 14. Notice that once a nonobtuse triangle appears in the sequence all its sucessors in orbit are also nonobtuse.

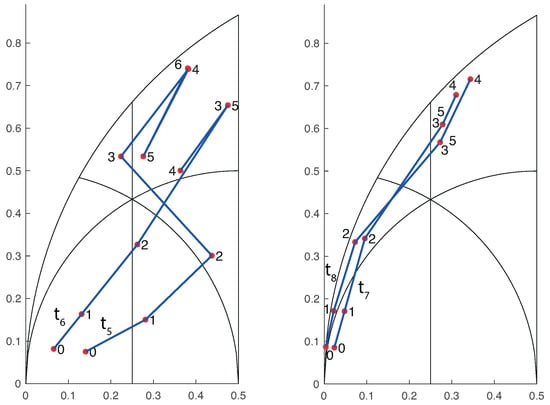
Figure 14. Evolution of SE duplication for the four different triangles in Table 2.

6. Conclusions

In this paper, a new triangle transformation, the shortest-edge duplication of triangles, has been defined. This transformation may be seen as the natural counterpart of the longest-edge partition of a triangle. Metric properties of the SE duplication of a triangle in the region of normalised triangles endowed with the Poincare hyperbolic metric have been studied. The self-improvement of this transformation has been easily proven, as well as the minimum angle condition. A lower bound for the maximum of the smallest angles of the triangles obtained by iterative SE duplication has been obtained with the value $\alpha =\frac{\pi }{6}$. This value does not depend on the shape of the initial triangle. Finally, some numerical examples have been shown to be in total agreement with the mathematical analysis.