Stochastic Analysis of a Hantavirus Infection Model
Abstract
1. Introduction
2. Hantavirus Model
3. Dynamics of the Stochastic Model
- there is a positive number such that
- there exists a nonnegative function V such that is negative on
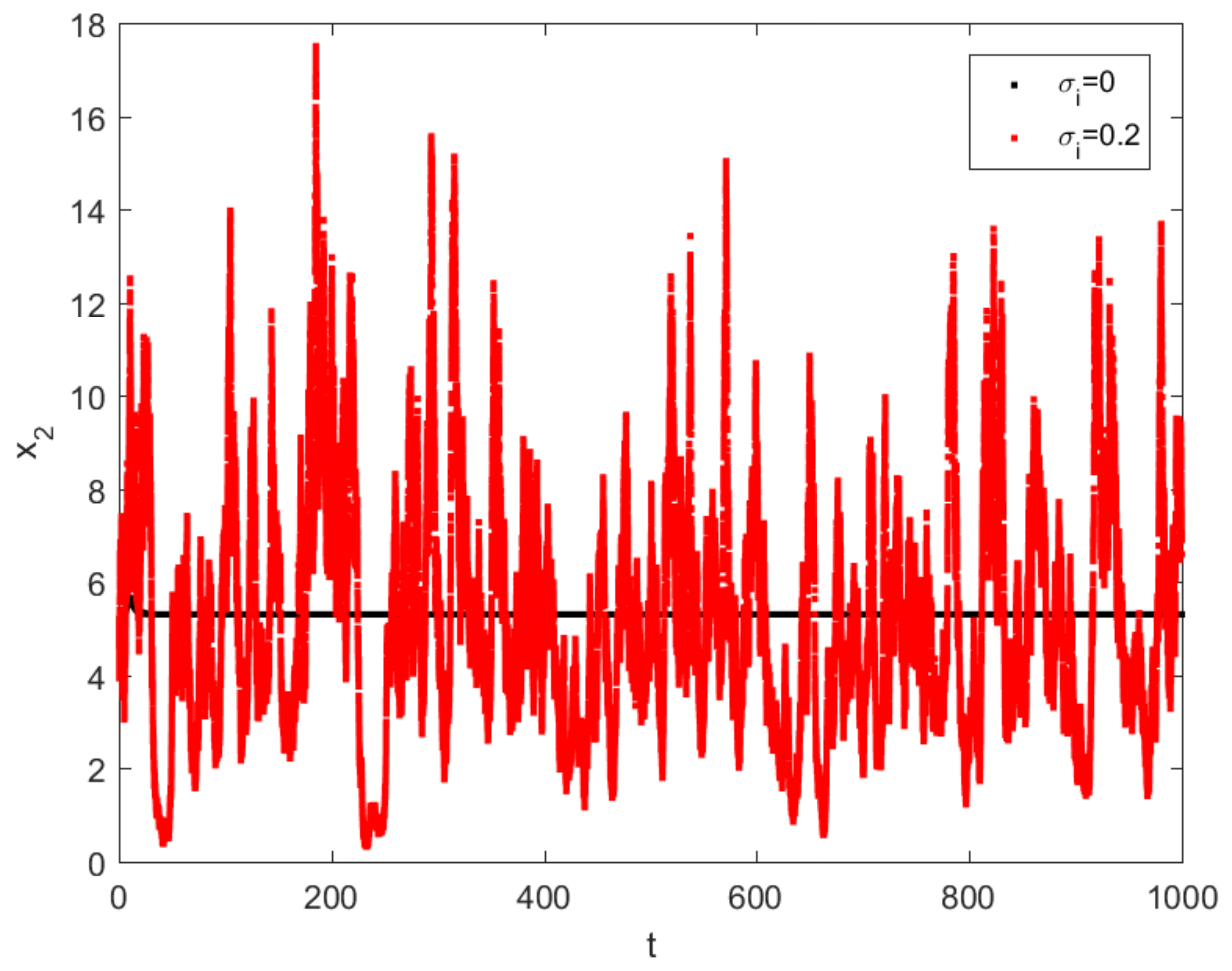
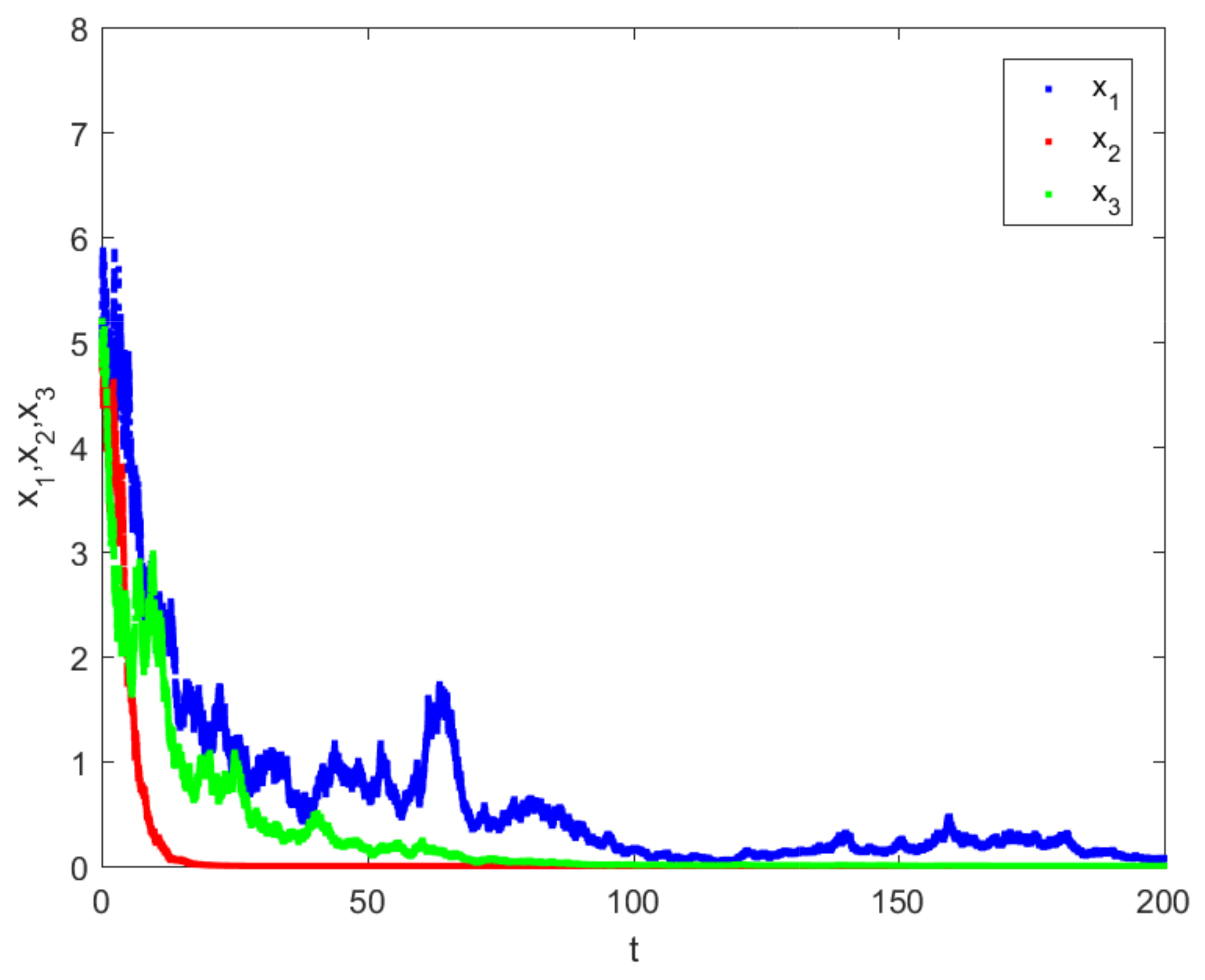
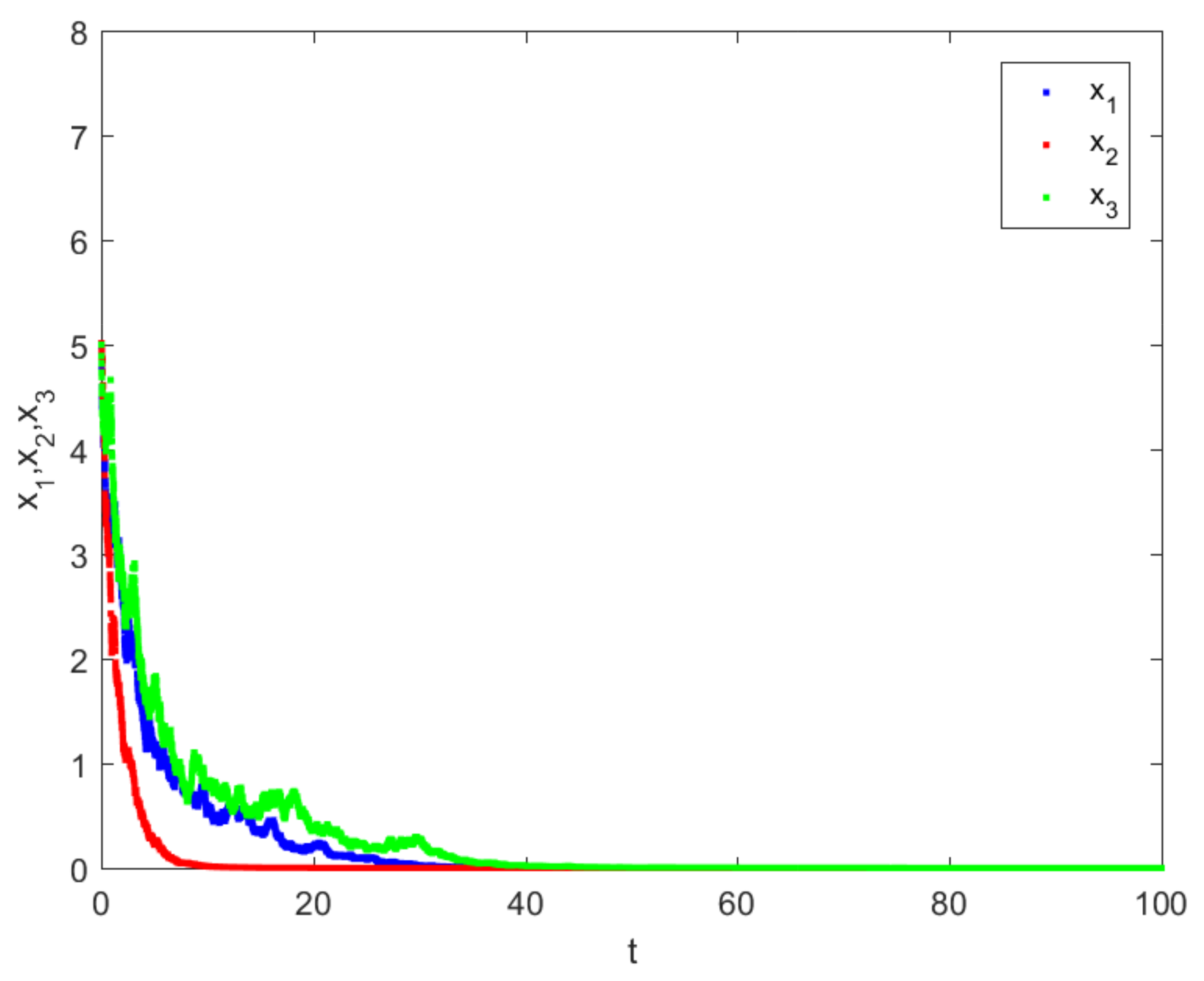
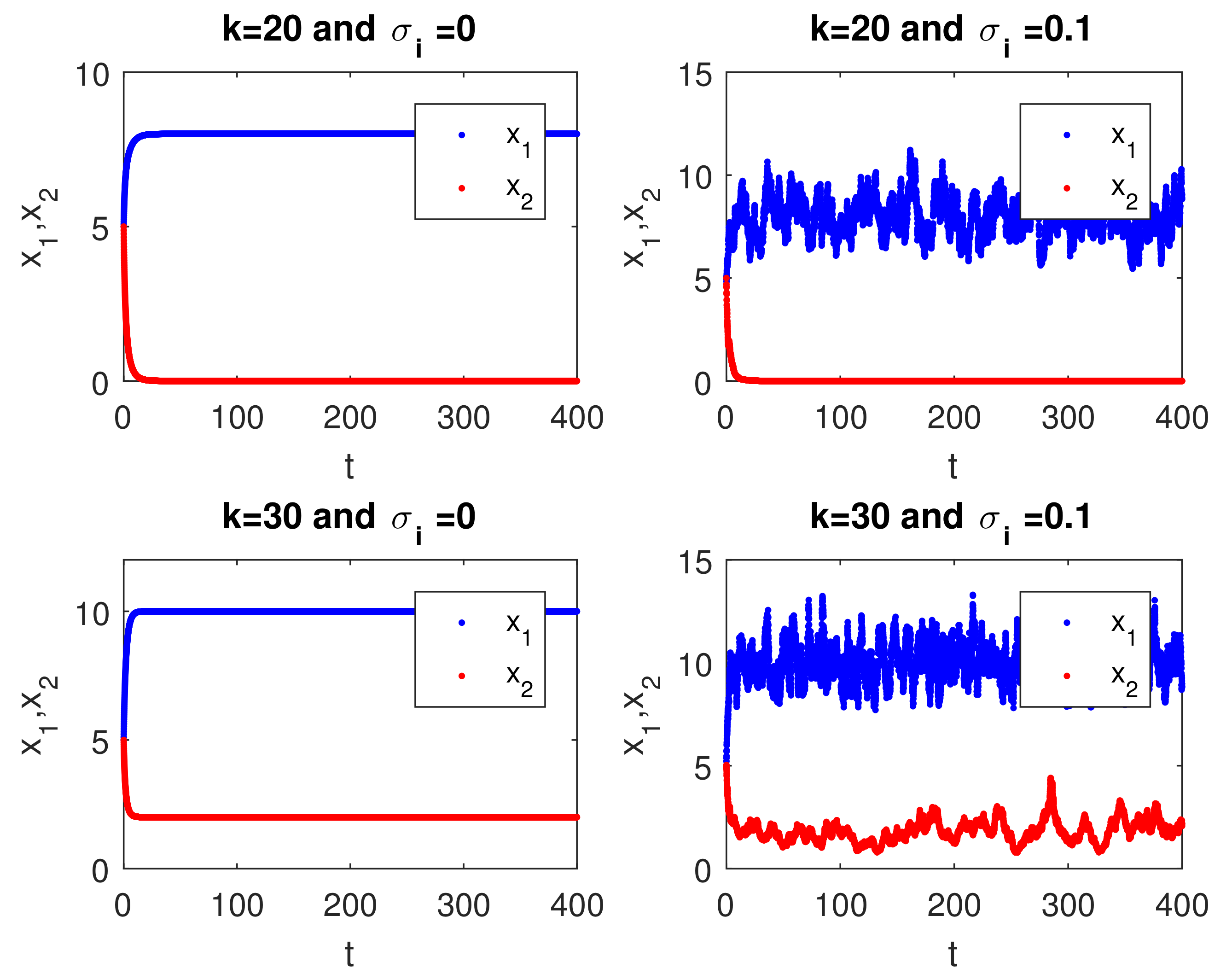
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abramson, G.; Kenkre, V.M. Spatiotemporal patterns in the Hantavirus infection. Phys. Rev. E 2002, 66, 011912. [Google Scholar] [CrossRef] [PubMed]
- Peixoto, I.D.; Abramson, G. The effect of biodiversity on the Hantavirus epizootic. Ecology 2006, 87, 873–879. [Google Scholar] [CrossRef]
- Solomon, E.; Berg, L.; Martin, D.W. Biology; Cengage Learning: Boston, MA, USA, 2010. [Google Scholar]
- Yusof, F.M.; Mohd, M.H.; Yatim, Y.M.; Ismail, A.I.M. Effects of Biotic Interactions, Abiotic Environments and Harvesting on the Spread of Hantavirus Infection. MATEMATIKA Malays. J. Ind. Appl. Math. 2020, 36, 1–14. [Google Scholar]
- Abdullah, F.A.; Ismail, A.I. Simulations of the spread of the Hantavirus using fractional differential equations. Matematika 2011, 27, 149–158. [Google Scholar]
- Chen, M.; Clemence, D.P. Analysis of and numerical schemes for a mouse population model in Hantavirus epidemics. J. Differ. Equ. Appl. 2006, 12, 887–899. [Google Scholar] [CrossRef]
- Gedeon, T.; Bodelón, C.; Kuenzi, A. Hantavirus transmission in sylvan and peridomestic environments. Bull. Math. Biol. 2010, 72, 541–564. [Google Scholar] [CrossRef]
- Allen, L.J.S.; Wesley, C.L.; Owen, R.D.; Goodin, D.G.; Koch, D.; Jonsson, C.B.; Chu, Y.; Hutchinson, J.M.S.; Paige, R.L. A habitat-based model for the spread of Hantavirus between reservoir and spillover species. J. Theor. Biol. 2009, 260, 510–522. [Google Scholar] [CrossRef]
- Rida, S.Z.; Abd-elradi, A.S.; Arafa, A.; Khalil, M. The effect of the environmental parameter on the Hantavirus infection through a fractional-order SI model. Int. J. Basic Appl. Sci. 2012, 1, 88–99. [Google Scholar] [CrossRef]
- Aguirre, M.A.; Abramson, G.; Bishop, A.R.; Kenkre, V.M. Simulations in the mathematical modeling of the spread of the Hantavirus. Phys. Rev. E 2002, 66, 041908. [Google Scholar] [CrossRef]
- Buceta, J.; Escudero, C.; Rubia, F.J.; Lindenberg, K. Outbreaks of Hantavirus induced by seasonality. Phys. Rev. E 2004, 69, 021906. [Google Scholar] [CrossRef]
- Karim, M.F.A.; Ismail, A.I.M.; Ching, H.B. Cellular automata modelling of Hantarvirus infection. Chaos Solitons Fractals 2009, 41, 2847–2853. [Google Scholar] [CrossRef]
- Abramson, G. The criticality of the Hantavirus infected phase at Zuni. arXiv 2004, arXiv:q-bio/0407003. [Google Scholar]
- Goh, S.M.; Ismail, A.I.M.; Noorani, M.S.M.; Hashim, I. Dynamics of the Hantavirus infection through variational iteration method. Nonlinear Anal. Real World Appl. 2009, 10, 2171–2176. [Google Scholar] [CrossRef]
- Yusof, F.M.; Abdullah, F.A.; Ismail, A.I. Modeling and optimal control on the spread of Hantavirus infection. Mathematics 2019, 7, 1192. [Google Scholar] [CrossRef]
- Moustafa, M.; Mohd, M.H.; Ismail, A.I.; Abdullah, F.A. Dynamical Analysis of a Fractional-Order Hantavirus Infection Model. Int. J. Nonlinear Sci. Numer. Simul. 2019, 21, 171–181. [Google Scholar] [CrossRef]
- Moustafa, M.; Abdullah, F.A.; Shafie, S.; Ismail, Z. Dynamical behavior of a fractional-order Hantavirus infection model incorporating harvesting. Alex. Eng. J. 2022, 61, 11301–11312. [Google Scholar] [CrossRef]
- Wei, C.; Liu, J.; Zhang, S. Analysis of a stochastic eco-epidemiological model with modified Leslie-Gower functional response. Adv. Differ. Equ. 2018, 2018, 119. [Google Scholar] [CrossRef]
- May, R.M. Stability and complexity in model ecosystems. In Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Liu, M.; Wang, K.; Wu, Q. Survival analysis of stochastic competitive models in a polluted environment and stochastic competitive exclusion principle. Bull. Math. Biol. 2011, 73, 1969–2012. [Google Scholar] [CrossRef]
- Xu, C.; Ren, G.; Yu, Y. Extinction analysis of stochastic predator-prey system with stage structure and crowley-martin functional response. Entropy 2019, 21, 252. [Google Scholar] [CrossRef]
- Song, G. Dynamics of a stochastic population model with predation effects in polluted environments. Adv. Differ. Equ. 2021, 2021, 189. [Google Scholar] [CrossRef]
- Mu, Y.; Lo, W.C. Stochastic dynamics of populations with refuge in polluted turbidostat. Chaos Solitons Fractals 2021, 147, 110963. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, M.; Liu, M. Stationary distribution of a stochastic ratio-dependent predator-prey system with regime-switching. Chaos Solitons Fractals 2021, 142, 110462. [Google Scholar] [CrossRef]
- Salman, S.; Yousef, A.; Elsadany, A. Dynamic behavior and bifurcation analysis of a deterministic and stochastic coupled logistic map system. Int. J. Dyn. Control 2022, 10, 69–85. [Google Scholar] [CrossRef]
- Lei, Q.; Yang, Z. Dynamical behaviors of a stochastic SIRI epidemic model. Appl. Anal. 2017, 96, 2758–2770. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmad, B. A stochastic SIRS epidemic model with logistic growth and general nonlinear incidence rate. Phys. A Stat. Mech. Its Appl. 2020, 551, 124152. [Google Scholar] [CrossRef]
- Li, Q.; Cong, F.; Liu, T.; Zhou, Y. Stationary distribution of a stochastic HIV model with two infective stages. Phys. A Stat. Mech. Its Appl. 2020, 554, 124686. [Google Scholar] [CrossRef]
- Khan, A.; Hussain, G.; Yusuf, A.; Usman, A.H.; Humphries, U.W. A hepatitis stochastic epidemic model with acute and chronic stages. Adv. Differ. Equ. 2021, 2021, 181. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Wang, K. Extinction and persistence of a stochastic SICA epidemic model with standard incidence rate for HIV transmission. Adv. Differ. Equ. 2021, 2021, 260. [Google Scholar]
- Wang, X.; Tan, Y.; Cai, Y.; Wang, K.; Wang, W. Dynamics of a stochastic HBV infection model with cell-to-cell transmission and immune response. Math. Biosci. Eng. 2021, 18, 616–642. [Google Scholar] [CrossRef]
- Lan, G.; Yuan, S.; Song, B. The impact of hospital resources and environmental perturbations to the dynamics of SIRS model. J. Frankl. Inst. 2021, 358, 2405–2433. [Google Scholar] [CrossRef]
- Ikram, R.; Khan, A.; Zahri, M.; Saeed, A.; Yavuz, M.; Kumam, P. Extinction and stationary distribution of a stochastic COVID-19 epidemic model with time-delay. Comput. Biol. Med. 2022, 141, 105115. [Google Scholar] [CrossRef]
- Johari, A.; Khodaparast, A. Analytical stochastic analysis of seismic stability of infinite slope. Soil Dyn. Earthq. Eng. 2015, 79, 17–21. [Google Scholar] [CrossRef]
- Gholampour, A.; Johari, A. Reliability analysis of a vertical cut in unsaturated soil using sequential Gaussian simulation. Sci. Iran. 2019, 26, 1214–1231. [Google Scholar] [CrossRef]
- Hu, C.; Song, D.; Chen, Z. Analytical stochastic analysis of rock wedge stability using a JDRV method considering the residual factor as a random variable. Geomat. Nat. Hazards Risk 2020, 11, 2079–2094. [Google Scholar] [CrossRef]
- Li, L.; Zhao, W. Deterministic and stochastic dynamics of a modified Leslie-Gower prey-predator system with simplified Holling-type IV scheme. Math. Biosci. Eng. 2021, 18, 2813–2831. [Google Scholar] [CrossRef]
- Li, J.; Shan, M.; Banerjee, M.; Wang, W. Stochastic dynamics of feline immunodeficiency virus within cat populations. J. Frankl. Inst. 2016, 353, 4191–4212. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Arnold, L. Stochastic Differential Equations; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 66. [Google Scholar]
- Caraballo, T.; Kloeden, P.E. The persistence of synchronization under environmental noise. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2257–2267. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D.; Liu, H.; Yang, Q. Existence, uniqueness and ergodicity of positive solution of mutualism system with stochastic perturbation. Math. Probl. Eng. 2010, 2010, 684926. [Google Scholar] [CrossRef]
- Phan, T.A.; Tian, J.P.; Wang, B. Dynamics of cholera epidemic models in fluctuating environments. Stochastics Dyn. 2021, 21, 2150011. [Google Scholar] [CrossRef]
- Li, S.; Wang, X. Analysis of a stochastic predator-prey model with disease in the predator and Beddington-DeAngelis functional response. Adv. Differ. Equ. 2015, 2015, 224. [Google Scholar] [CrossRef]
- Huang, Y.; Shi, W.; Wei, C.; Zhang, S. A stochastic predator-prey model with Holling II increasing function in the predator. J. Biol. Dyn. 2021, 15, 1–18. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, W. Dynamical analysis of a stochastic SIRS epidemic model with saturating contact rate. Math. Biosci. Eng. 2020, 17, 5925–5943. [Google Scholar] [CrossRef]
- Liu, M.; Wang, K. Stationary distribution, ergodicity and extinction of a stochastic generalized logistic system. Appl. Math. Lett. 2012, 25, 1980–1985. [Google Scholar] [CrossRef]
- Alvarez, L.H.; Shepp, L.A. Optimal harvesting of stochastically fluctuating populations. J. Math. Biol. 1998, 37, 155–177. [Google Scholar] [CrossRef]
- Lv, J.; Wang, K. Almost sure permanence of stochastic single species models. J. Math. Anal. Appl. 2015, 422, 675–683. [Google Scholar] [CrossRef]
- Yusof, F.; Ismail, A.; Ali, N. Effect of predators on the spread of hantavirus infection. Sains Malays. 2014, 43, 1045–1051. [Google Scholar]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Alnafisah, Y. The implementation of Milstein scheme in two-dimensional SDEs using the Fourier method. In Abstract and Applied Analysis; Hindawi: London, UK, 2018; Volume 2018. [Google Scholar]
- Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Oussaeif, T.E.; Momani, S. A Novel Fractional-Order Discrete SIR Model for Predicting COVID-19 Behavior. Mathematics 2022, 10, 2224. [Google Scholar] [CrossRef]
- Hening, A.; Nguyen, D.H. Coexistence and extinction for stochastic Kolmogorov systems. Ann. Appl. Probab. 2018, 28, 1893–1942. [Google Scholar] [CrossRef]
- Benaim, M. Stochastic persistence. arXiv 2018, arXiv:1806.08450. [Google Scholar]
- Phan, T.A.; Tian, J.P. Basic stochastic model for tumor virotherapy. Math. Biosci. Eng. 2020, 17, 4271–4294. [Google Scholar] [CrossRef] [PubMed]
- Phan, T.A. Stochastic Modeling for Some Biological and Medical Problems. Ph.D. Thesis, New Mexico State University, Las Cruces, NM, USA, 2020. [Google Scholar]
- Phan, T.A.; Tian, J.P. Hopf bifurcation without parameters in deterministic and stochastic modeling of cancer virotherapy, part I. J. Math. Anal. Appl. 2022, 514, 126278. [Google Scholar] [CrossRef]
- Phan, T.A.; Tian, J.P. Hopf bifurcation without parameters in deterministic and stochastic modeling of cancer virotherapy, part II. J. Math. Anal. Appl. 2022, 515, 126444. [Google Scholar] [CrossRef]
- Phan, T.A.; Wang, S.; Tian, J.P. Analysis of a new stochastic Gompertz diffusion model for untreated human glioblastomas. Stochastics Dyn. 2022, 2022, 2250019. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnafisah, Y.; El-Shahed, M. Stochastic Analysis of a Hantavirus Infection Model. Mathematics 2022, 10, 3756. https://doi.org/10.3390/math10203756
Alnafisah Y, El-Shahed M. Stochastic Analysis of a Hantavirus Infection Model. Mathematics. 2022; 10(20):3756. https://doi.org/10.3390/math10203756
Chicago/Turabian StyleAlnafisah, Yousef, and Moustafa El-Shahed. 2022. "Stochastic Analysis of a Hantavirus Infection Model" Mathematics 10, no. 20: 3756. https://doi.org/10.3390/math10203756
APA StyleAlnafisah, Y., & El-Shahed, M. (2022). Stochastic Analysis of a Hantavirus Infection Model. Mathematics, 10(20), 3756. https://doi.org/10.3390/math10203756





