Smooth, Singularity-Free, Finite-Time Tracking Control for Euler–Lagrange Systems
Abstract
:1. Introduction
- A new constrained sliding surface with finite-time convergence is proposed that possesses two important properties. (1) Compared to the existing nonsingular finite-time SMC controls for the EL systems [42,43], the proposed control strategy has no need for a piecewise continuous function, and a non-singular property is directly achieved that streamlines the stability analysis. (2) Unlike the existing constrained controls for the EL systems using the PPC concept [31,32,33,34,35,36,37,38,39,40,41], the constraint on the system output is considered into the sliding surface as a time-varying gain.
- To deal with the undesired chattering phenomenon as a result of discontinuous sign function, the upper bound of the square of the lumped uncertainty is estimated by the adaptive scheme. Therefore, the discontinuous sign function is effectively removed and a smooth control is achieved.
2. Problem Formulation and Preliminaries
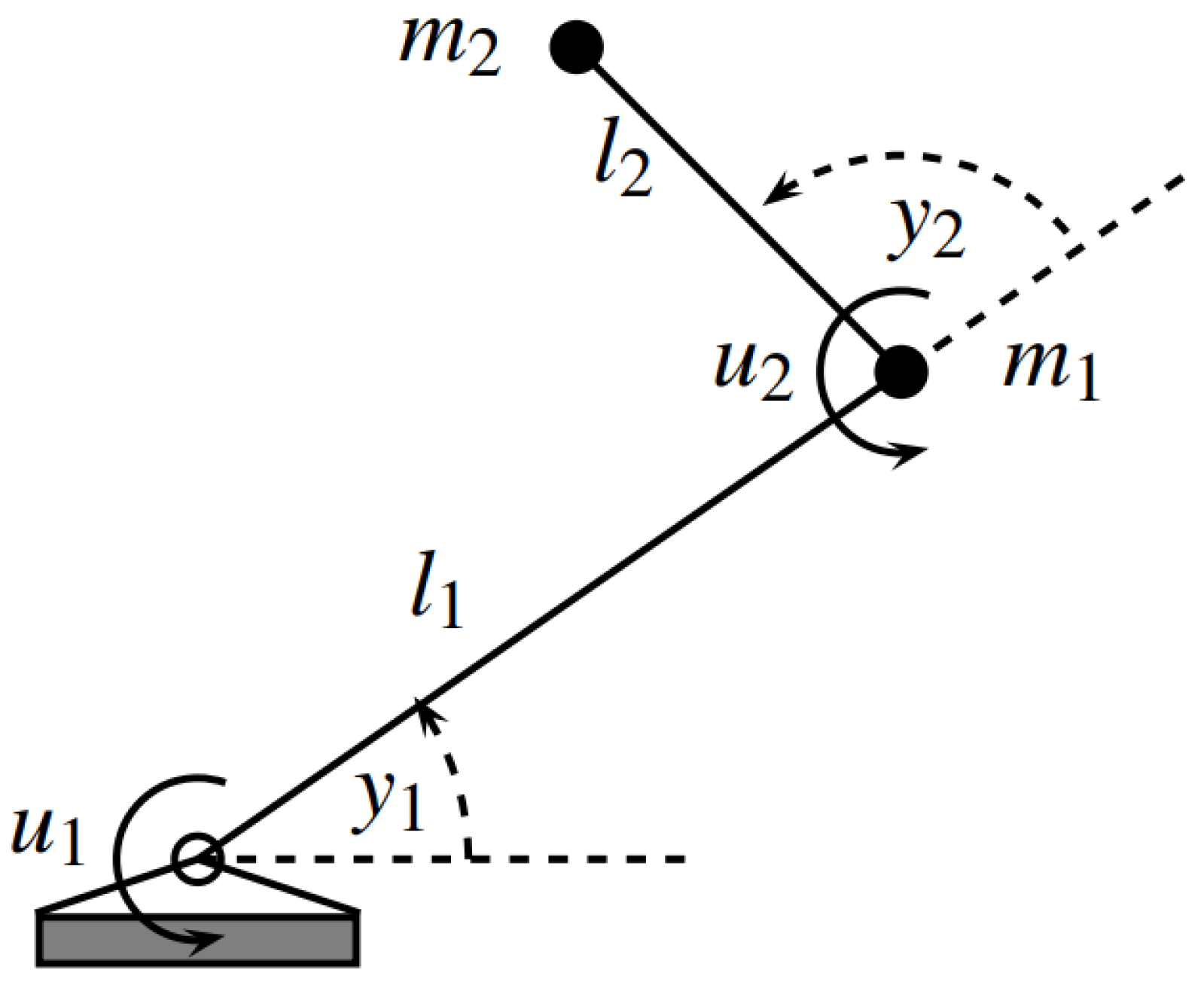
2.1. Dynamics
2.2. Preliminaries
2.3. Control Objective
- 1.
- The system output follows the reference trajectory within a finite time.
- 2.
- The prescribed performance of the system output is obtained via a performance function in which neither complicated terms nor tedious control parameters regulation are required.
3. Main Results
3.1. Nonsingular Fast Constrained Terminal Sliding Manifold (NFCTSM)
3.2. Finite-Time Tracking Control
- Larger makes the system states converge to the origin with a faster convergence rate; however, it can result in a large overshoot and more control energy consumption. Therefore, we need to make a compromise between the control effort and convergence rate.
- According to the concept of finite-time stability, the smaller value of leads to a faster and more accurate convergence. Nevertheless, the required control energy will be increased and the trade-off should be considered.
- To achieve high pointing accuracy, the value of parameter ε in the control law (12) should be selected small enough. However, it can be seen that this parameter appears in the denominator of the control law; then, the small value of ε corresponds to a more control effort. Similar to the other parameters, a comparison between control effort and control accuracy needs to be made.
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Lu, P.; Huang, W.; Xiao, J.; Zhou, F.; Hu, W. Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient. Mathematics 2021, 9, 2055. [Google Scholar] [CrossRef]
- Gao, J.; Fu, Z.; Zhang, S. Adaptive fixed-time attitude tracking control for rigid spacecraft with actuator faults. IEEE Trans. Ind. Electron. 2018, 66, 7141–7149. [Google Scholar] [CrossRef]
- Zakeri, E.; Farahat, S.; Moezi, S.A.; Zare, A. Robust sliding-mode control of a mini unmanned underwater vehicle equipped with a new arrangement of water jet propulsions: Simulation and experimental study. Appl. Ocean Res. 2016, 59, 521–542. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, D.; Zhang, Z.; Liu, J. An IDRA approach for modeling helicopter based on Lagrange dynamics. Appl. Math. Comput. 2015, 265, 733–747. [Google Scholar] [CrossRef]
- Liang, C.D.; Ge, M.F.; Liu, Z.W.; Ling, G.; Zhao, X.W. A novel sliding surface design for predefined-time stabilization of Euler–Lagrange systems. Nonlinear Dyn. 2021, 106, 445–458. [Google Scholar] [CrossRef]
- Shao, K.; Tang, R.; Xu, F.; Wang, X.; Zheng, J. Adaptive sliding-mode control for uncertain Euler–Lagrange systems with input saturation. J. Frankl. Inst. 2021, 358, 8356–8376. [Google Scholar] [CrossRef]
- Deng, Q.; Peng, Y.; Han, T.; Qu, D. Event-triggered bipartite consensus in networked Euler–Lagrange systems with external disturbance. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2870–2874. [Google Scholar] [CrossRef]
- Liu, H.; Gao, Z.; Cao, L.; Jiang, Z.; Zhang, J.; Song, Y. Tracking control of uncertain Euler–Lagrange systems with fading and saturating actuations: A low-cost neuroadaptive proportional-integral-derivative approach. Int. J. Robust Nonlinear Control 2022, 32, 2705–2721. [Google Scholar] [CrossRef]
- Zhang, G.; Cheng, D. Adaptive fault-tolerant guaranteed performance control for Euler–Lagrange systems with its application to a 2-link robotic manipulator. IEEE Access 2020, 8, 184160–184171. [Google Scholar] [CrossRef]
- Hu, Q.; Xiao, B.; Shi, P. Tracking control of uncertain Euler–Lagrange systems with finite-time convergence. Int. J. Robust Nonlinear Control 2015, 25, 3299–3315. [Google Scholar] [CrossRef]
- Islam, S.; Liu, X.P. Robust sliding-mode control for robot manipulators. IEEE Trans. Ind. Electron. 2010, 58, 2444–2453. [Google Scholar] [CrossRef]
- Pereira, A.R.; Hsu, L.; Ortega, R. Globally stable adaptive formation control of Euler–Lagrange agents via potential functions. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10 July 2009; pp. 2606–2611. [Google Scholar]
- Hong, Y.; Xu, Y.; Huang, J. Finite-time control for robot manipulators. Syst. Control Lett. 2002, 46, 243–253. [Google Scholar] [CrossRef]
- Zhao, Y.; Duan, Z.; Wen, G. Distributed finite-time tracking of multiple Euler–Lagrange systems without velocity measurements. Int. J. Robust Nonlinear Control 2015, 25, 1688–1703. [Google Scholar] [CrossRef]
- Hu, H.X.; Wen, G.; Yu, W.; Cao, J.; Huang, T. Finite-time coordination behavior of multiple Euler–Lagrange systems in cooperation-competition networks. IEEE Trans. Cybern. 2019, 49, 2967–2979. [Google Scholar] [CrossRef]
- Huang, X.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Mung, N.X.; Thanh Ha, L.N.N.; Huynh, T.T.; Hong, S.K. Finite-time attitude fault tolerant control of quadcopter system via neural networks. Mathematics 2020, 8, 1541. [Google Scholar] [CrossRef]
- Galicki, M. Finite-time control of robotic manipulators. Automatica 2015, 51, 49–54. [Google Scholar] [CrossRef]
- Yao, Q.; Jahanshahi, H. Novel finite-time adaptive sliding mode tracking control for disturbed mechanical systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236. [Google Scholar] [CrossRef]
- Luan, F.; Na, J.; Huang, Y.; Gao, G. Adaptive neural network control for robotic manipulators with guaranteed finite-time convergence. Neurocomputing 2019, 337, 153–164. [Google Scholar] [CrossRef]
- He, W.; Xu, C.; Han, Q.L.; Qian, F.; Lang, Z. Finite-Time L2 Leader–Follower Consensus of Networked Euler–Lagrange Systems With External Disturbances. IEEE Trans. Syst. Man, Cybern. Syst. 2017, 48, 1920–1928. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, S.; He, Y.; Wang, B.; Deng, Z. Finite-time anti-saturation control for Euler–Lagrange systems with actuator failures. ISA Trans. 2022, 124, 468–477. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Yang, L.; Chen, Y.; Lai, G. Adaptive sliding-mode control of Robot Manipulators with System Failures. Mathematics 2022, 10, 339. [Google Scholar] [CrossRef]
- Wang, D.; Liu, S.; He, Y.; Shen, J. Barrier Lyapunov function-based adaptive back-stepping control for electronic throttle control system. Mathematics 2021, 9, 326. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoo, S.J. Adaptive event-triggered control strategy for ensuring predefined three-dimensional tracking performance of uncertain nonlinear underactuated underwater vehicles. Mathematics 2021, 9, 137. [Google Scholar] [CrossRef]
- He, W.; Huang, H.; Ge, S.S. Adaptive neural network control of a robotic manipulator with time-varying output constraints. IEEE Trans. Cybern. 2017, 47, 3136–3147. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Non-singular terminal sliding-mode control for a manipulator robot using a barrier Lyapunov function. ISA Trans. 2022, 121, 268–283. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, Y.; Yang, C.; Wang, M.; Annamalai, A. An improved adaptive online neural control for robot manipulator systems using integral Barrier Lyapunov functions. Int. J. Syst. Sci. 2019, 50, 638–651. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Wang, Z.; Che, W. Adaptive Sliding Mode Attitude-Tracking Control of Spacecraft with Prescribed Time Performance. Mathematics 2022, 10, 401. [Google Scholar] [CrossRef]
- Hua, C.; Chen, J.; Li, Y.; Li, L. Adaptive prescribed performance control of half-car active suspension system with unknown dead-zone input. Mech. Syst. Signal Process. 2018, 111, 135–148. [Google Scholar] [CrossRef]
- Gao, S.; Liu, X.; Jing, Y.; Dimirovski, G.M. Finite-time prescribed performance control for spacecraft attitude tracking. IEEE/ASME Trans. Mechatron. 2021. [Google Scholar] [CrossRef]
- Golestani, M.; Zhang, W.; Yang, Y.; Xuan-Mung, N. Disturbance observer-based constrained attitude control for flexible spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Dai, S.L.; He, S.; Ma, Y.; Yuan, C. Cooperative learning-based formation control of autonomous marine surface vessels with prescribed performance. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 52, 2565–2577. [Google Scholar] [CrossRef]
- Huang, S.; Wang, J.; Xiong, L.; Liu, J.; Li, P.; Wang, Z. Distributed Predefined-Time Fractional-Order sliding-mode control for Power System With Prescribed Tracking Performance. IEEE Trans. Power Syst. 2022, 37, 2233–2246. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Fault-tolerant output-constrained control of unknown Euler–Lagrange systems with prescribed tracking accuracy. Automatica 2020, 111, 108606. [Google Scholar] [CrossRef]
- Yin, Z.; Luo, J.; Wei, C. Robust prescribed performance control for Euler–Lagrange systems with practically finite-time stability. Eur. J. Control 2020, 52, 1–10. [Google Scholar] [CrossRef]
- Wang, M.; Yang, A. Dynamic learning from adaptive neural control of robot manipulators with prescribed performance. IEEE Trans. Syst. Man, Cybern. Syst. 2017, 47, 2244–2255. [Google Scholar] [CrossRef]
- Yao, Q. Robust adaptive finite-time prescribed performance attitude tracking control of spacecraft. Int. J. Aeronaut. Space Sci. 2021, 22, 1183–1193. [Google Scholar] [CrossRef]
- Jing, C.; Xu, H.; Niu, X. Adaptive sliding mode disturbance rejection control with prescribed performance for robotic manipulators. ISA Trans. 2019, 91, 41–51. [Google Scholar] [CrossRef]
- Lyu, W.; Zhai, D.H.; Xiong, Y.; Xia, Y. Predefined performance adaptive control of robotic manipulators with dynamic uncertainties and input saturation constraints. J. Frankl. Inst. 2021, 358, 7142–7169. [Google Scholar] [CrossRef]
- Liu, H.; Tian, X.; Wang, G.; Zhang, T. Finite-time H∞ control for high-precision tracking in robotic manipulators using backstepping control. IEEE Trans. Ind. Electron. 2016, 63, 5501–5513. [Google Scholar] [CrossRef]
- Song, Z.; Duan, C.; Wang, J.; Wu, Q. Chattering-free full-order recursive sliding-mode control for finite-time attitude synchronization of rigid spacecraft. J. Frankl. Inst. 2019, 356, 998–1020. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Golestani, M.; Esmailzadeh, M.; Mobayen, S. Constrained attitude control for flexible spacecraft: Attitude pointing accuracy and pointing stability improvement. IEEE Trans. Syst. Man, Cybern. Syst. 2022. [Google Scholar] [CrossRef]
- Cao, L.; Xiao, B.; Golestani, M. Robust fixed-time attitude stabilization control of flexible spacecraft with actuator uncertainty. Nonlinear Dyn. 2020, 100, 2505–2519. [Google Scholar] [CrossRef]
- Berger, T.; Lê, H.H.; Reis, T. Funnel control for nonlinear systems with known strict relative degree. Automatica 2018, 87, 345–357. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xuan-Mung, N.; Golestani, M. Smooth, Singularity-Free, Finite-Time Tracking Control for Euler–Lagrange Systems. Mathematics 2022, 10, 3850. https://doi.org/10.3390/math10203850
Xuan-Mung N, Golestani M. Smooth, Singularity-Free, Finite-Time Tracking Control for Euler–Lagrange Systems. Mathematics. 2022; 10(20):3850. https://doi.org/10.3390/math10203850
Chicago/Turabian StyleXuan-Mung, Nguyen, and Mehdi Golestani. 2022. "Smooth, Singularity-Free, Finite-Time Tracking Control for Euler–Lagrange Systems" Mathematics 10, no. 20: 3850. https://doi.org/10.3390/math10203850
APA StyleXuan-Mung, N., & Golestani, M. (2022). Smooth, Singularity-Free, Finite-Time Tracking Control for Euler–Lagrange Systems. Mathematics, 10(20), 3850. https://doi.org/10.3390/math10203850






