Data-Driven Event-Triggered Platoon Control under Denial-of-Service Attacks

Abstract

This paper proposes an event-triggered model-free adaptive platoon control (MFAPC) solution for non-linear vehicle systems under denial-of-service (DoS) attacks. First, the non-linear vehicle system is transformed into an equivalent linear data model using the dynamic linearization technique. Second, to save limited communication resources and reduce the influence of cyber attacks, a novel event-triggered mechanism and attack compensation method are designed. Then, based on the equivalent linear data model, a new resilient event-triggered MFAPC algorithm is developed to achieve the vehicle platoon control objective under DoS attacks. Finally, the effectiveness of the proposed control scheme is verified using an example.

1. Introduction

With the rapid development of human society and the economy, automobiles have become increasingly widely used and important in our lives. However, the increased number of cars inevitably brings with it a variety of problems, such as environmental pollution, energy shortages, traffic congestion, traffic accidents and so on, which have a serious impact on the development of society. In recent years, various intelligent traffic control methods have been applied to vehicle systems aiming to solve these problems. For example, longitudinal dynamics control for autonomous driving of intelligent vehicles using a sliding mode controller based on a radial basis function neural network was investigated in [1]. In [2], a new application framework for intelligent transportation systems (ITS) based on 5G network slicing was proposed. In [3], an intelligent traffic control scheme using cloud computing and big-data mining for ITS was developed.

Vehicle platoon control, as an intelligent control method, has been applied in vehicle systems. In [4], the vehicle platoon control problem of linear heterogeneous vehicle systems subject to disturbances was investigated and an $H_{\infty }$ control scheme was developed to guarantee the string stability of the platoon. Under the condition of input saturation, the vehicle platoon control problem was examined using a variable time headway strategy in [5]. In [6], the vehicular platoon control problem was investigated, with an event-triggered distributed adaptive observer used to ensure that the platoon achieved a stable state asymptotically. The authors of [7] proposed a longitudinal platoon controller for connected vehicles. In [8], a distributed consensus platooning problem affected by time-varying, heterogeneous and wireless communication delays was discussed. It is worth noting that the above studies are based on system models. However, many system models cannot be accurately applied in real scenarios. Thus, data-based control methods have been developed to address vehicle platoon control problems. A vehicle platoon control strategy to reduce energy consumption based on a reinforcement learning algorithm was proposed in [9]. The cooperative adaptive cruise control (CACC) problem was examined in [10]. In addition, the vehicle eco-adaptive cruise control problem was examined in [11] and an optimal control scheme to ensure the safe distance of the vehicles was proposed using a reinforcement learning method.

Model-free adaptive control (MFAC), as a kind of data-driven method, was first proposed in 1994 and has been widely applied [12,13,14,15,16,17,18,19,20]. The main feature of the MFAC method is that the plant can achieve its control objective based on measurement data for the system inputs/outputs. In [13], a dynamic linearization technique for single-input and single-output (SISO) non-linear discrete-time systems was proposed. In [14], a brief overview of the MFAC was presented. The data-driven MFAC problem for multiple-input and multiple-output (MIMO) non-linear discrete-time systems was discussed in [15]. In [17], the MFAC problem was solved using a full-form dynamic linearization technique. The MFAC problem for MIMO non-affine systems with unknown non-linear dynamics was investigated, and verified experimentally, in [18]. In [20], a model-free adaptive integral sliding mode controller was devised for non-linear discrete-time systems. In addition, in recent years, MFAC methods have been applied to vehicle systems. In [21], the model-free adaptive integral sliding-mode-constrained-control problem of autonomous vehicle parking systems was investigated. A novel dual successive projection-based MFAC approach was proposed and applied to autonomous cars in [22]. In [23,24], the heading control of unmanned surface vehicles was investigated using the MFAC method.

It should be noted that network communication resources are limited. To save resources, an event-triggered control scheme has been proposed for the controller design. There has been some research on event-triggered model-free adaptive control. The design problem of an event-triggered MFAC controller was studied in [25,26]. An event-triggered disturbance observer was designed to estimate the disturbance using intermittent system information in [27]. Additionally, the event-triggered model-free adaptive iterative learning control problem was investigated in [28]. It should be pointed out, however, that the event-triggered conditions under which results to date have been obtained [25,26,27,28] are complexed, which leads to an increase in computational costs. Therefore, it is necessary to design a simple event-triggered condition, which is a primary purpose of this paper.

With the development of networked communication technology, increasing attention has been paid to networked control systems [29,30,31,32,33]. In networked control systems, the system states measured by sensors are transmitted to the controller via a wireless network. Some network effects may occur during data transmission, such as time-delays, packet dropouts and malicious attacks, etc., which will degrade, or even destroy, system performance [34,35]. Consequently, some work has been carried out to solve these problems. In [36], the distributed consensus tracking problem under malicious denial-of-service (DoS) attacks was investigated. In [37], a class of networked non-linear systems affected by packet disorder and network-induced delay was discussed; [38] extended the result to the two-channel packet dropout case. In addition, the MFAC problem of non-linear systems suffering from fading measurements was studied in [39]. It is noted that cyber attacks are inevitable, threatening system safety and performance. There have been some investigations focusing on network attacks in relation to the MFAC problem. A resilient control scheme for non-linear systems suffering from fading measurements was designed in [40]. In [41], an MFAC scheme based on an attack predictor was devised against jamming attacks for non-linear cyber-physical systems. In [42], the data-based MFAC problem for non-linear cyber-physical systems with event-triggered communication scheduling was investigated. However, in [41,42], the time-varying parameters used to estimate the non-linear characteristics were assumed not to be attacked, which is a strong assumption. Therefore, it is worth exploring how this assumption might be avoided.

Motivated by the above analyses, the event-triggered model-free adaptive platoon control (MFAPC) problem of non-linear vehicle systems under DoS attacks was investigated in this paper. First, the non-linear vehicle systems were transformed into a linear data model via linearization. Then, a resilient event-triggered MFAPC scheme was designed to achieve the vehicle platoon control target under DoS attacks. The contributions of this paper are as follows:

(1) In contrast to existing MFAC-based vehicle control methods [21,22,23,24], a novel MFAC framework for vehicle platoon control under DoS attacks is established. To mitigate the effects of DoS attacks, a new attack compensation mechanism is proposed using the latest available data. Then, a resilient event-triggered MFAPC algorithm is designed to enable simultaneous velocity and path tracking.

(2) Compared with existing event-triggered MFAC results reported in [26,28], where the event-triggered condition requires an additional tracking error trigger condition, the proposed event-triggered condition removes additional conditions, so that the event-triggered design is less conservative.

The remainder of this paper is arranged as follows: The MFAPC framework and formulation of the problem are described in Section 2. The security analysis undertaken and the control algorithm design are described in Section 3. The simulation results and conclusions are presented in Section 4 and Section 5, respectively.

2. MFAPC Framework and Problem Formulation

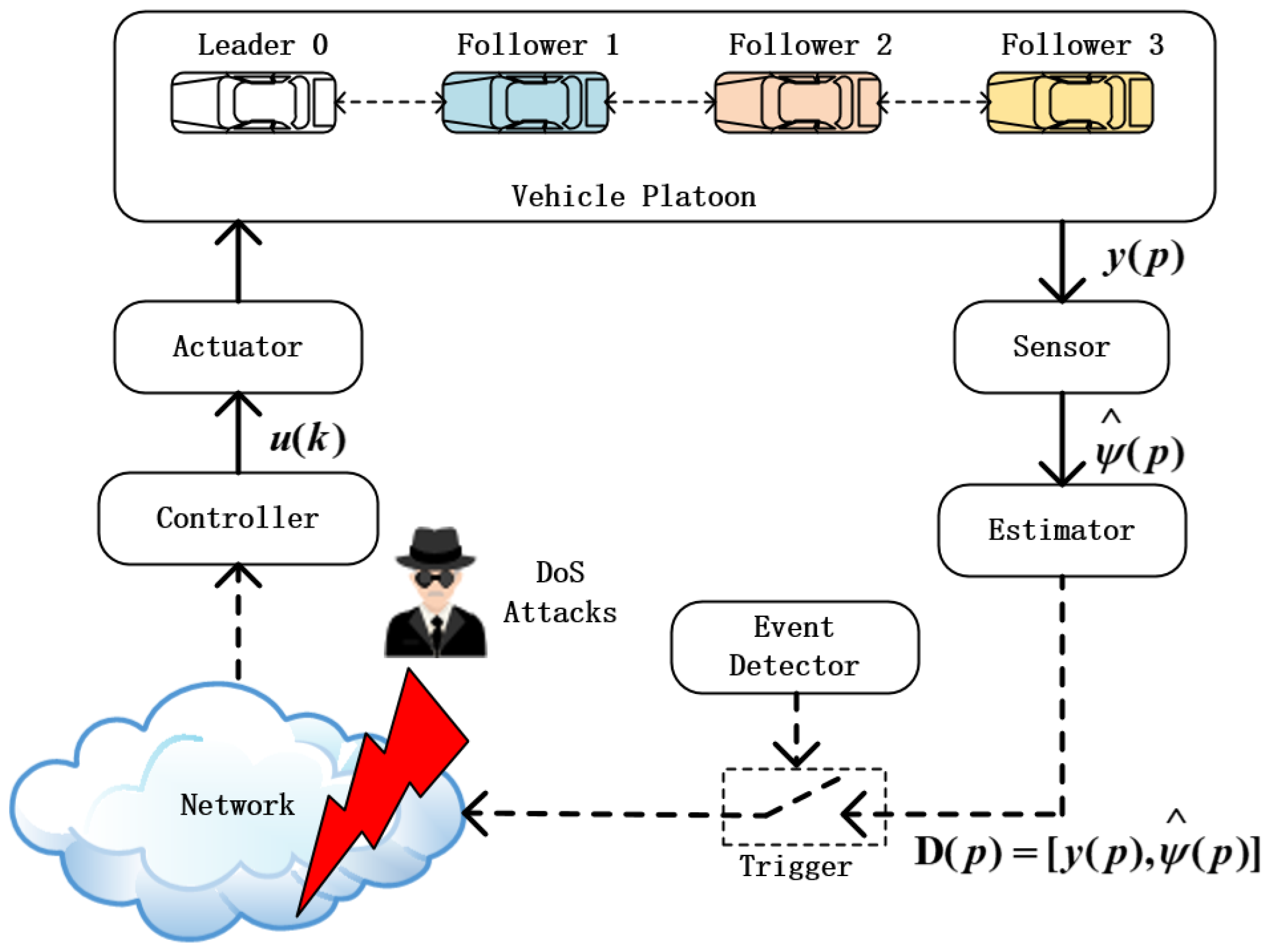
The system framework for a non-linear vehicle system under DoS attacks is illustrated in Figure 1. The sensor measures the system output, i.e., the position and velocity of the vehicle. The estimator is used to estimate the adaptive parameter. The system outputs $y\left(p\right)$ and estimated adaptive parameter $\widehat{\psi }\left(p\right)$ are packaged and transmitted to the controller via a wireless network that may be attacked.

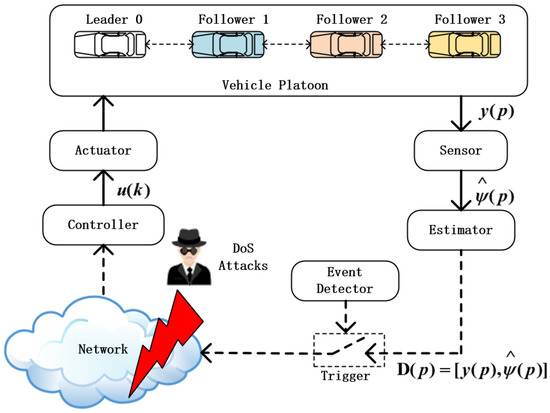
Figure 1. System framework with DoS attacks.

2.1. Vehicle System Modeling

Considering the platoon control problem for vehicles moving along the road, the dynamic model of the ith vehicle is described by

$$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& v_i\left(t\right),\hfill \\ \hfill {\dot{v}}_i\left(t\right)& =& u_i\left(t\right)+f_i(x_i\left(t\right),v_i\left(t\right)),i\in N,\hfill \end{array}$$

(1)

where $x_i\left(t\right)\in \mathbb{R}$, $v_i\left(t\right)\in \mathbb{R}$ and $u_i\left(t\right)\in \mathbb{R}$ represent the position, velocity and control input of the ith vehicle, respectively. $f_i(·,·)\in {\mathbb{R}}^2\mapsto \mathbb{R}$ is an unknown non-linear function.

Convert (1) to the following discrete-time system [23,43]:

$$\begin{array}{ccc}\hfill x_i(p+1)& =& x_i\left(p\right)+T{v}_i\left(p\right),\hfill \\ \hfill v_i(p+1)& =& v_i\left(p\right)+T{u}_i\left(p\right)+T{f}_i(x_i\left(p\right),v_i\left(p\right)),\hfill \end{array}$$

(2)

where T denotes the sampling time.

The leading vehicle is described as

$$\begin{array}{cc}\hfill x_0(k+1)& =x_0\left(k\right)+T{v}_0\left(k\right),\hfill \\ \hfill v_0(k+1)& =v_0\left(k\right)+T{f}_0(x_0\left(k\right),v_0\left(k\right)).\hfill \end{array}$$

(3)

Remark 1.

The leading vehicle provides reference signals to the following vehicle. Therefore, the control input of the leading vehicle is not considered in this paper. Moreover, it is assumed that the information for the leading vehicle is not affected by network attacks.

The following assumptions and lemmas are used:

Assumption 1.

The partial derivative of $f_i(·,·)$ with respect to $u_i\left(p\right)$ is continuous [14].

Assumption 2.

The non-linear systems satisfy the generalized Lipschitz condition that the output changes $|\Delta y_i(p+1)|\le k_i|\Delta u_i\left(p\right)|$ with $\Delta y_i(p+1)=y_i(p+1)-y_i\left(p\right)$, $\Delta u_i\left(p\right)=u_i\left(p\right)-u_i(p-1)$, and $k_i>0$ is a constant [14].

Lemma 1.

For non-linear systems that satisfy Assumptions 1, 2 and $|\Delta u_i\left(p\right)|\ne 0$ for all p, there exists a time-varying pseudo-partial derivative (PPD) parameter ${\psi }_i\left(p\right)$ such that the non-linear systems can be converted to the following compact-form dynamic linearization data model [15]:

$$\begin{array}{c}\hfill \Delta y_i(p+1)={\psi }_i\left(p\right)\Delta u_i\left(p\right),\end{array}$$

(4)

where ${\psi }_i\left(p\right)$ is bounded and satisfies $|{\psi }_i\left(p\right)|\le k_i$, with $k_i$ being a constant. If $\Delta u_i\left(p\right)=0$, then define $\Delta y_i(p+1)=0$.

Assumption 3.

The sign of the PPD parameter ${\psi }_i\left(p\right)$ remains unchanged for all p and satisfies ${\psi }_i\left(p\right)>{\sigma }_i>0$ or ${\psi }_i\left(p\right)<-{\sigma }_i$ for all p, where ${\sigma }_i$ is a constant.

For the purpose of studying the vehicle platoon control problem, redefine the output of the vehicle platoon system (2) as $y_i(p+1)=x_i(p+1)+K_i{v}_i(p+1)$ with $K_i>0$ being determined later, then the increment form $\Delta y_i(p+1)$ is calculated as $\Delta y_i(p+1)=\Delta x_i(p+1)+K_i\Delta v_i(p+1)$. According to (2), we can get $\Delta x_i(p+1)=\Delta x_i\left(p\right)+T\Delta v_i\left(p\right)$ and $\Delta v_i(p+1)=\Delta v_i\left(p\right)+T\Delta u_i\left(p\right)+T\Delta f_i(x_i\left(p\right),v_i\left(p\right))$. Then, we have

$$\begin{array}{ccc}\hfill \Delta y_i(p+1)& =& \Delta x_i(p+1)+K_i\Delta v_i(p+1)\hfill \\ \hfill & =& \Delta x_i\left(p\right)+T\Delta v_i\left(p\right)+K_i[\Delta v_i\left(p\right)+T\Delta u_i\left(p\right)+T\Delta f_i(x_i\left(p\right),v_i\left(p\right))]\hfill \\ \hfill & =& \left[\frac{\Delta x_i\left(p\right)+T\Delta v_i\left(p\right)}{\Delta u_i\left(p\right)}\right]\Delta u_i\left(p\right)+K_i\left[\frac{\Delta v_i\left(p\right)+T\Delta f_i(x_i\left(p\right),v_i\left(p\right))}{\Delta u_i\left(p\right)}+T\right]\Delta u_i\left(p\right)\hfill \\ \hfill & =& {\psi }_i\left(p\right)\Delta u_i\left(p\right),\hfill \end{array}$$

(5)

with ${\psi }_i\left(p\right)=K_i\left[\frac{\Delta v_i\left(p\right)+T\Delta f_i(x_i\left(p\right),v_i\left(p\right))}{\Delta u_i\left(p\right)}+T\right]+\left[\frac{\Delta x_i\left(p\right)+T\Delta v_i\left(p\right)}{\Delta u_i\left(p\right)}\right]$, $\Delta x_i(p+1)=x_i(p+1)-x_i\left(p\right)$, $\Delta v_i(p+1)=v_i(p+1)-v_i\left(p\right)$. Similar to [23,24], and according to Lemma 1 and Assumptions 2 and 3, one has ${\psi }_i\left(p\right)>0$ and $|{\psi }_i\left(p\right)|<k_i$.

2.2. MFAPC Algorithm Design

The actual value ${\psi }_i\left(p\right)$ is generally difficult to obtain. Therefore, an estimator is designed to estimate ${\psi }_i\left(p\right)$ to solve this problem. Then, the performance function is defined as follows:

$$\begin{array}{c}\hfill J_1\left[{\psi }_i\left(p\right)\right]={[\Delta y_i\left(p\right)-{\psi }_i\left(p\right)\Delta u_i(p-1)]}^2+\mu {[{\psi }_i\left(p\right)-{\widehat{\psi }}_i(p-1)]}^2,\end{array}$$

(6)

where ${\widehat{\psi }}_i\left(p\right)$ is the estimated value of ${\psi }_i\left(p\right)$ and $\mu$ is a weighting constant.

Taking the derivative of $J_1\left[{\widehat{\psi }}_i\left(p\right)\right]$ with respect to ${\widehat{\psi }}_i\left(p\right)$ and letting the result equal 0, one gets

$$\begin{array}{ccc}\hfill {\widehat{\psi }}_i\left(p\right)& =& {\widehat{\psi }}_i(p-1)+\frac{\eta [\Delta y_i\left(p\right)-{\widehat{\psi }}_i(p-1)\Delta u_i(p-1)]\Delta u_i(p-1)}{\Delta u_i^2(p-1)+\mu }\hfill \end{array}$$

(7)

with the step factor $\eta \in (0,1]$ being introduced to make algorithm (7) more flexible and general.

To accomplish the vehicle platoon control task, the performance function with respect to $u_i\left(p\right)$ is defined as follows:

$$\begin{array}{c}\hfill J_2\left[u_i\left(p\right)\right]={[y_0(p+1)-y_i(p+1)+d_{i0}]}^2+\lambda {[u_i\left(p\right)-u_i(p-1)]}^2,\end{array}$$

(8)

where $y_0(p+1)=x_0(p+1)+v_0(p+1)$ is a given reference output according to (3). $\lambda$ is a weighting constant. $d_{i0}>0$ represents the safety distance between the ith vehicle and the leading vehicle.

Minimizing the performance function (8) with respect to $u_i\left(p\right)$, one gets

$$\begin{array}{c}\hfill u_i\left(p\right)=u_i(p-1)+\frac{\rho {\psi }_i\left(p\right)}{{\psi }_i^2\left(p\right)+\lambda }[y_0(p+1)+d_{i0}-y_i\left(p\right)],\end{array}$$

(9)

where the role of $\rho$ is the same as $\eta$ in (7).

Remark 2.

In this controller, the distances $d_{i0}$ are assumed to be available, which can also be obtained using between-vehicle sensing distances via $d_{i0}=d_{i,i-1}+d_{i-1,i-2}+\cdots +d_{2,1}+d_{1,0}$. Moreover, this controller is a theoretical formulation. In practice, the “future” data $y_0(k+1)$ can be obtained via estimation techniques, possibly with acceptable small errors.

2.3. Event-Triggered Mechanism Design

The MFAC scheme devised above communicates continuously, which wastes network communication resources. To save network resources, event-triggered control is used. Assuming that the set of the event-triggered instants is determined as $\{k_i,i=0,1,\dots \}$, then, the event-triggered mechanism is designed as follows:

$$\left\{\begin{array}{cc}\hfill & {{\rm Y}}_i\left(p\right)=|m_i\left(p\right)|-{\zeta }_i\left|e_i\left(p\right)\right|\hfill \\ & {\Psi }_i\left(p\right)=|n_i\left(p\right)|-{\xi }_i|\Delta y_i\left(p\right)|\hfill \end{array}\right\}$$

(10)

where ${\zeta }_i>0$ and ${\xi }_i>0$ are the event-triggered thresholds. $m_i\left(p\right)=y_i\left(p\right)-y_i\left(p_i\right)$ and $n_i\left(p\right)=\Delta y_i\left(p\right)-\Delta y_i\left(p_i\right)$ with $\Delta y_i\left(p_i\right)=y_i\left(p_i\right)-y_i\left(p_{i-1}\right)$ are the measurement errors. $e_i\left(p\right)=y_i^{*}\left(p\right)-y_i\left(p\right)$ is the tracking error.

The controller receives packets at the event-triggered instant $\{p_i,i=0,1,\dots \}$, which is generated by the following event-triggered condition:

$$\begin{array}{c}\hfill p_{i+1}=inf\{p\in \mathbb{N}|p>p_i,{{\rm Y}}_i\left(p\right)>0\mathrm{or}{\Psi }_i\left(p\right)>0\}.\end{array}$$

(11)

Then, the control input $u_i\left(p\right)$ is updated as follows:

$$u_i\left(p\right)=u_i(p-1)+\frac{\rho {\psi }_i\left(p_i\right)}{{\psi }_i^2\left(p_i\right)+\lambda }[y_0(p+1)+d_{i0}-y_i\left(p_i\right)].$$

(12)

2.4. MFAPC Modeling under DoS Attacks

For a system framework under DoS attacks, we know that the DoS attacks intend to destroy system performance by blocking the data packets $D\left(p\right)$ transmitted between the controller and the sensor/estimator. If the wireless network is attacked, the controller will not receive the data packets $D\left(p\right)$, i.e., $D\left(p\right)=0$. Otherwise, the data packets $D\left(p\right)$ can be received by the controller. When DoS attacks occur, the redefined system $y_i\left(p_i\right)$ will be converted to the following form:

$$\begin{array}{c}\hfill y_{ai}\left(p_i\right)={\theta }_i\left(p_i\right)y_i\left(p_i\right),\end{array}$$

(13)

where ${\theta }_i\left(p_i\right)$ is an indicator function that represents the consequence of DoS attacks in the communication network, with ${\theta }_i\left(p_i\right)=0$ indicating that the DoS attacks to the communication are completely successful, and ${\theta }_i\left(p_i\right)=1$ otherwise. Assume that ${\theta }_i\left(p_i\right)$ conforms to the Bernoulli distribution, with probabilities of the successful and the failing DoS attacks being $\mathbb{P}\{{\theta }_i\left(p_i\right)=0\}={\theta }_i$ and $\mathbb{P}\{{\theta }_i\left(p_i\right)=1\}=1-{\theta }_i$, respectively.

An attack compensation mechanism is proposed as

$$\begin{array}{c}\hfill y_{ai}\left(p_i\right)={\theta }_i\left(p_i\right)y_i\left(p_i\right)+[1-{\theta }_i\left(p_i\right)]y_i\left(p_{i-1}\right).\end{array}$$

(14)

Remark 3.

The compensation mechanism can reduce the impact of DoS attacks. When there are DoS attacks in communication networks, the indicator function ${\theta }_i\left(p_i\right)=0$ and $y_{ai}\left(p_i\right)=y_i\left(p_{i-1}\right)$; that is, using the latest received system output $y_i\left(p_{i-1}\right)$ stored in the buffer, the impacts of DoS attacks will be compensated for. The sensor measures the vehicle output $y\left(p\right)$ and the estimator estimates the time-varying parameter based on $y\left(p\right)$ to obtain $\widehat{\psi }\left(p\right)$. Then, the system output $y\left(p\right)$ and estimated time-varying parameter $\widehat{\psi }\left(p\right)$ are packaged and transmitted to the controller via an event detector and the wireless network that may be attacked. The buffer is embedded into the controller as an attack compensator to reduce the influence of network attacks. Once the packets are transmitted to the buffer they will be stored and used to compensate for lost packets during network attacks.

According to the above analysis, the designed MFAPC algorithm is given as follows:

$$\left\{\begin{array}{c}{\widehat{\psi }}_i\left(p\right)={\widehat{\psi }}_i(p-1)+\frac{\eta \Delta y_i\left(p\right)\Delta u_i(p-1)}{\Delta u_i^2(p-1)+\mu }-\frac{\eta {\widehat{\psi }}_i(p-1)\Delta u_i^2(p-1)}{\Delta u_i^2(p-1)+\mu };\mathrm{others}\hfill \\ {\widehat{\psi }}_i\left(p\right)={\widehat{\psi }}_i\left(0\right),\mathrm{if}|{\widehat{\psi }}_i\left(p\right)|\le {\sigma }_i\mathrm{or}|\Delta u_i(p-1)|\le {\sigma }_i\mathrm{or}sign\left({\widehat{\psi }}_i\left(p\right)\right)\ne sign\left({\widehat{\psi }}_i\left(0\right)\right)\hfill \end{array}\right.$$

(15)

$$\begin{array}{c}\hfill u_i\left(p\right)=u_i(p-1)+\frac{\rho {\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }[y_0(p+1)+d_{i0}-y_{ai}\left(p_i\right)],\end{array}$$

(16)

where ${\sigma }_i>0$ represents a small constant.

Remark 4.

The designed algorithm includes two aspects: the estimation algorithm and the reset algorithm (15), and the control algorithm (16). First, the estimation algorithm calculates the estimated PPD parameter ${\widehat{\psi }}_i\left(p\right)$ and the reset algorithm (15) is used to reset ${\widehat{\psi }}_i\left(p\right)={\widehat{\psi }}_i\left(0\right)$ if the reset condition is satisfied. Then, the control algorithm (16) calculates the control input based on the estimated PPD parameter, system output and the reference output.

Remark 5.

The proposed control strategy does not require a system model and only uses the inputs/outputs data of the closed-loop system in the design of the controller. This represents a necessary supplement to the model-based method when the dynamic model is difficult and inaccurate to obtain.

Problem 1.

For a non-linear vehicle system (2) under DoS attacks, the goal is to devise a resilient MFAPC scheme to accomplish the vehicle platoon task in the mean square sense, i.e., $e_i\left(p\right)=y_0\left(p\right)+d_{i0}-y_i\left(p\right)$ converges into the following small bounded set:

$$\begin{array}{c}\hfill \{e_i\left(p\right)\left|\mathbb{E}\right\{|e_i\left(p\right)\left|\right\}\le {ϵ}_i\},\end{array}$$

(17)

where ${ϵ}_i$ is the upper bound of the tracking error.

3. Security Analysis

An analysis is presented below of the stability of the vehicle platoon system and determination of the control algorithm parameters.

Theorem 1.

If Assumptions 1–3 are satisfied, then Problem 1 can be solved using the MFAPC scheme (15) and (16) for some parameters $\lambda >{\lambda }_{min}>0$, $\rho \in (0,1]$, $\eta \in (0,1]$, $\mu >0$, ${\zeta }_i>0$ and ${\xi }_i\in (0,M)$ with $M\in (0,1)$.

Proof. 

The proof consists of two parts. First, the estimation error of the PPD parameter is uniformly bounded. Then, based on the boundedness of the estimated PPD parameter, the tracking error is uniformly bounded in the mean square sense.

$\left(1\right)$ Defining $e_{{\psi }_i}\left(p\right)={\widehat{\psi }}_i\left(p\right)-{\psi }_i\left(p\right)$, and subtracting the PPD parameter ${\psi }_i\left(p\right)$ from both sides of Equation (15), we get

$$\begin{array}{c}\hfill e_{{\psi }_i}\left(p\right)=e_{{\psi }_i}(p-1)-\frac{\eta e_{{\psi }_i}(p-1)\Delta u_i^2(p-1)}{\Delta u_i^2(p-1)+\mu }+{\psi }_i(p-1)-{\psi }_i\left(p\right).\end{array}$$

(18)

Then, taking the absolute value of (18),

$$\begin{array}{c}\hfill |e_{{\psi }_i}\left(p\right)|\le \left|1-\frac{\eta \Delta u_i^2(p-1)}{\Delta u_i^2(p-1)+\mu }\right||e_{{\psi }_i}(p-1)|+|{\psi }_i(p-1)-{\psi }_i\left(p\right)|.\end{array}$$

(19)

It is clear that $\frac{\eta \Delta u_i^2(p-1)}{\Delta u_i^2(p-1)+\mu }$ is monotonically increasing for $\Delta u_i^2(p-1)$ and its minimum value is $\frac{\eta {\sigma }_i^2}{\mu +{\sigma }_i^2}$ according to (15). Then, the following inequality holds for $0<\eta \le 1$ and $\mu >0$:

$$\begin{array}{c}\hfill \left|1-\frac{\eta \Delta u_i^2(p-1)}{\Delta u_i^2(p-1)+\mu }\right|\le 1-\frac{\eta {\sigma }_i^2}{\mu +{\sigma }_i^2}\triangleq d_1<1,\end{array}$$

(20)

where $d_1$ is a constant. According to Lemma 1, one has $|{\psi }_i\left(p\right)|\le k_i$. Thus, $|{\psi }_i(p-1)-{\psi }_i\left(p\right)|\le 2k_i$. Then, according to (20), (19) is rewritten as

$$\begin{array}{ccc}\hfill |e_{{\psi }_i}\left(p\right)|& \le & d_1\left|e_{{\psi }_i}(p-1)\right|+2k_i\hfill \\ & \le & d_1^2\left|e_{{\psi }_i}(p-2)\right|+2d_1{k}_i+2k_i\hfill \\ & \le & \dots \hfill \\ & \le & d_1^p\left|e_{{\psi }_i}\left(0\right)\right|+\frac{2k_i(1-d_1^p)}{1-d_1}.\hfill \end{array}$$

Therefore, the estimation error $e_{{\psi }_i}\left(p\right)$ is uniformly bounded. Since ${\psi }_i\left(p\right)$ is bounded, ${\widehat{\psi }}_i\left(p\right)$ is bounded.

$\left(2\right)$ Substituting control input (16) into $\Delta y_i(p+1)={\psi }_i\left(p\right)\Delta u_i\left(p\right)$, obtained from (5), leads to

$$\begin{array}{c}\hfill y_i(p+1)=y_i\left(p\right)+\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }[y_0(p+1)+d_{i0}-y_{ai}\left(p_i\right)].\end{array}$$

(21)

Then, the error system is obtained as

$$\begin{array}{ccc}\hfill e_i(p+1)& =& y_0(p+1)+d_{i0}-y_i\left(p\right)-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }[y_0(p+1)+d_{i0}-y_{ai}\left(p_i\right)]\hfill \\ & =& \Delta y_0(p+1)+e_i\left(p\right)-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }[\Delta y_0(p+1)+e_i\left(p\right)\hfill \\ & & -({\theta }_i\left(p_i\right)-1){\psi }_i(p-1)\Delta u_i(p-1)+({\theta }_i\left(p_i\right)-1)n_i\left(p\right)+m_i\left(p\right)],\hfill \end{array}$$

(22)

where the following transformation is used:

$$\begin{array}{ccc}\hfill y_0(p+1)+d_{i0}-y_{ai}\left(p_i\right)& =& \Delta y_0(p+1)+y_0\left(p\right)+d_{i0}-{\theta }_i\left(p_i\right)y_i\left(p_i\right)-[1-{\theta }_i\left(p_i\right)]y_i\left(p_{i-1}\right)\hfill \\ \hfill & =& \Delta y_0(p+1)+y_0\left(p\right)+d_{i0}-[{\theta }_i\left(p_i\right)\Delta y_i\left(p_i\right)-\Delta y_i\left(p_i\right)+y_i\left(p_i\right)]\hfill \\ \hfill & =& \Delta y_0(p+1)+y_0\left(p\right)+d_{i0}-[({\theta }_i\left(p_i\right)-1)\Delta y_i\left(p_i\right)+y_i\left(p_i\right)]\hfill \\ \hfill & =& \Delta y_0(p+1)-({\theta }_i\left(p_i\right)-1)\Delta y_i\left(p\right)+({\theta }_i\left(p_i\right)-1)n_i\left(p\right)-y_i\left(p_i\right)+m_i\left(p\right)\hfill \\ \hfill & =& \Delta y_0(p+1)+e_i\left(p\right)-({\theta }_i\left(p_i\right)-1){\psi }_i(p-1)\Delta u_i(p-1)\hfill \\ \hfill & & +({\theta }_i\left(p_i\right)-1)n_i\left(p\right)+m_i\left(p\right),\hfill \end{array}$$

(23)

with $\Delta y_i\left(p\right)={\psi }_i(p-1)\Delta u_i(p-1)$ obtained from (5).

Then, taking the absolute value and expectation of (22), one has

$$\begin{array}{ccc}\hfill \mathbb{E}\left\{\right|e_i(p+1)\left|\right\}& \le & \left|1-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\left[\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}+|\Delta y_0(p+1)|\right]\hfill \\ & & +\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|{\psi }_i(p-1)\left|\right|\Delta u_i(p-1)|\hfill \\ & & +\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|n_i\left(p\right)|+\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\left|m_i\left(p\right)\right|.\hfill \end{array}$$

(24)

According to the event-triggered condition, one gets

$$\begin{array}{ccc}\hfill \mathbb{E}\left\{\right|e_i(p+1)\left|\right\}& \le & \left|1-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\left[\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}+|\Delta y_0(p+1)|\right]\hfill \\ & & +\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|{\psi }_i(p-1)\left|\right|\Delta u_i(p-1)|\hfill \\ & & +{\xi }_i\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|\Delta y_i\left(p\right)|+{\zeta }_i\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}& \le & \left|1-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\left[\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}+|\Delta y_0(p+1)|\right]\hfill \\ & & +\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|{\psi }_i(p-1)\left|\right|\Delta u_i(p-1)|\hfill \\ & & +{\xi }_i\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|{\psi }_i(p-1)\left|\right|\Delta u_i(p-1)|\hfill \\ & & +{\zeta }_i\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}.\hfill \end{array}$$

(26)

Consequently, ${\psi }_i\left(p\right)>0$ and $|{\psi }_i\left(p\right)|\le k_i$. According to Lemma 1 and Assumption 3, there exists a positive constant $0<M_i<1$ such that

$$\begin{array}{c}\hfill 0<M_i\le \frac{{\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{\lambda +{\widehat{\psi }}_i^2\left(p_i\right)}\le \frac{k_i{\widehat{\psi }}_i\left(p_i\right)}{\lambda +{\widehat{\psi }}_i^2\left(p_i\right)}\le \frac{k_i{\widehat{\psi }}_i\left(p_i\right)}{2\sqrt{\lambda }{\widehat{\psi }}_i\left(p_i\right)}.\end{array}$$

(27)

Letting ${\lambda }_{min}=\frac{k_i^2}{4}$, the following inequality holds for all $\lambda >{\lambda }_{min}$:

$$\begin{array}{c}\hfill \frac{k_i{\widehat{\psi }}_i\left(p_i\right)}{2\sqrt{\lambda }{\widehat{\psi }}_i\left(p_i\right)}<\frac{k_i}{2\sqrt{{\lambda }_{min}}}=1.\end{array}$$

(28)

Then, one can get

$$\begin{array}{c}\hfill \left|1-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|=1-\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\le 1-\rho M_i\triangleq d_2<1,\end{array}$$

(29)

where $d_2$ is a constant. Since the control input cannot change too fast in the actual system, the increment of the control input $\Delta u_i\left(p\right)$ should be bounded, denoted as $|\Delta u_i\left(p\right)|<{\epsilon }_i$ for all p with ${\epsilon }_i>0$ being a constant. Then, one gets

$$\begin{array}{c}\hfill (1+{\xi }_i)\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|{\psi }_i(p-1)\left|\right|\Delta u_i(p-1)|\le (1+{\xi }_i)\rho k_i{\epsilon }_i\triangleq d_3,\end{array}$$

(30)

where $d_3$ is a constant. Additionally, the increment of the desired output $\Delta y_0(p+1)$ should be bounded, denoted as $|\Delta y_0(p+1)|<d_4$, where $d_4$ is a constant. Then, (25) can be converted to the following inequality:

$$\begin{array}{c}\hfill \mathbb{E}\left\{\right|e_i(p+1)\left|\right\}\le (1-M+{\zeta }_i)\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}+d_2{d}_4+d_3.\end{array}$$

(31)

Additionally, the following inequality can be obtained if $0<{\zeta }_i<M$:

$$\begin{array}{c}\hfill 1-M+{\zeta }_i=1-(M-{\zeta }_i)\triangleq d_5<1.\end{array}$$

(32)

Then, it follows from (31) that

$$\begin{array}{ccc}\hfill \mathbb{E}\left\{\right|e_i(p+1)\left|\right\}& \le & d_5\mathbb{E}\left\{\right|e_i\left(p\right)\left|\right\}+d_2{d}_4+d_3\hfill \\ & \le & d_5^2\mathbb{E}\left\{\right|e_i(p-1)\left|\right\}+d_5(d_2{d}_4+d_3)+d_2{d}_4+d_3\hfill \\ & \le & \dots \hfill \\ & \le & d_5^{p+1}\mathbb{E}\left\{\right|e_i\left(0\right)\left|\right\}+\frac{(d_2{d}_4+d_3)(1-d_5^{p+1})}{1-d_5}.\hfill \end{array}$$

(33)

Therefore, the tracking error is uniformly bounded in the mean square sense, i.e., $e_i\left(p\right)$ converges to the following set:

$$\left\{e_i\left(p\right)\left|\mathbb{E}\right\{|e_i\left(p\right)\left|\right\}\le \frac{d_2{d}_4+d_3}{1-d_5}\right\}.$$

□

Remark 6.

In contrast to the stability analysis of the data-driven platoon control scheme for non-linear vehicles [44], in the error system (22), the introduction of the measurement errors $m_i\left(p\right)$ and $n_i\left(p\right)$ caused by the event-triggered mechanism will make the stability analysis more complicated. Specifically, compared with the traditional control scheme where ${\psi }_i\left(p\right)$ and $y_i\left(p\right)$ are used in the controller, the trigger instant values ${\psi }_i\left(p_i\right)$ and $y_i\left(p_i\right)$ are used in the event-triggered control scheme (16). Then, by introducing the measurement error $m_i\left(p\right)=y_i\left(p\right)-y_i\left(p_i\right)$ and $n_i\left(p\right)=\Delta y_i\left(p\right)-\Delta y_i\left(p_i\right)$, ${\psi }_i\left(p_i\right)$ is replaced by ${\psi }_i\left(p\right)$ and $m_i\left(p\right)$, and $y_i\left(p_i\right)$ is replaced by $y_i\left(p\right)$ and $n_i\left(p\right)$. This transformation will lead to additional terms $\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right||{\theta }_i-1\left|\right|n_i\left(p\right)|+\left|\frac{\rho {\psi }_i\left(p\right){\widehat{\psi }}_i\left(p_i\right)}{{\widehat{\psi }}_i^2\left(p_i\right)+\lambda }\right|\left|m_i\left(p\right)\right|$ appearing. To handle these two terms, the event-triggered condition (11) is designed. Then, the main difficulty is how to design its trigger condition. If the event-triggered condition with the additional term cannot be solved, this will affect the stability analysis.

4. Simulation and Experimental Results

An example is provided to test the effectiveness of the proposed control algorithm.

Consider the following vehicle platoon system:

$$\begin{array}{ccc}\hfill {\dot{x}}_i\left(t\right)& =& v_i\left(t\right),\hfill \\ \hfill {\dot{v}}_i\left(t\right)& =& u_i\left(t\right)-3v_i^3\left(t\right)+0.1x_i\left(t\right),i\in N.\hfill \end{array}$$

The dynamic model of the leading vehicle is considered as

$$\begin{array}{ccc}\hfill {\dot{x}}_0\left(t\right)& =& v_0\left(t\right),\hfill \\ \hfill {\dot{v}}_0\left(t\right)& =& -3v_0^3\left(t\right)+0.1x_0\left(t\right).\hfill \end{array}$$

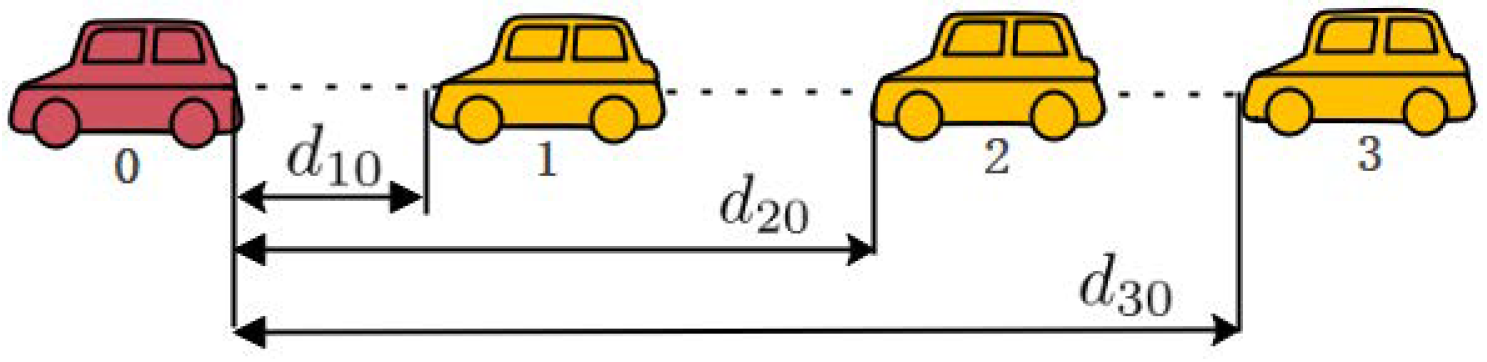
The vehicle platoon control scheme is presented in Figure 2. The distances between the ith vehicle and the leading vehicle are $d_{10}=1$ metre, $d_{20}=3$ metre and $d_{30}=5$ metre, respectively, and the initial values are $x_i\left(0\right)=0.1$, $v_i\left(0\right)=0$, $u_i\left(0\right)=0$ and ${\widehat{\psi }}_i\left(0\right)={[0.5,0.5]}^T(i=1,2,3)$. By Theorem 1, the control parameters are $\mu =50$, $\eta =1$, $\rho =0.35$, $\lambda =5$ and $K_i=1$. The sampling period is $T=0.005$ and the probability of successful DoS attacks is ${\theta }_i=0.6$. The parameters of the event-triggered mechanism are selected as ${\zeta }_i=0.2$ and ${\xi }_i=0.1$.

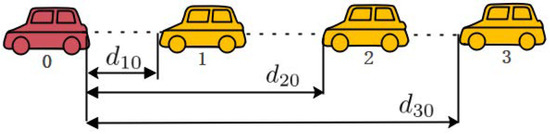
Figure 2. The vehicle platoon control scheme.

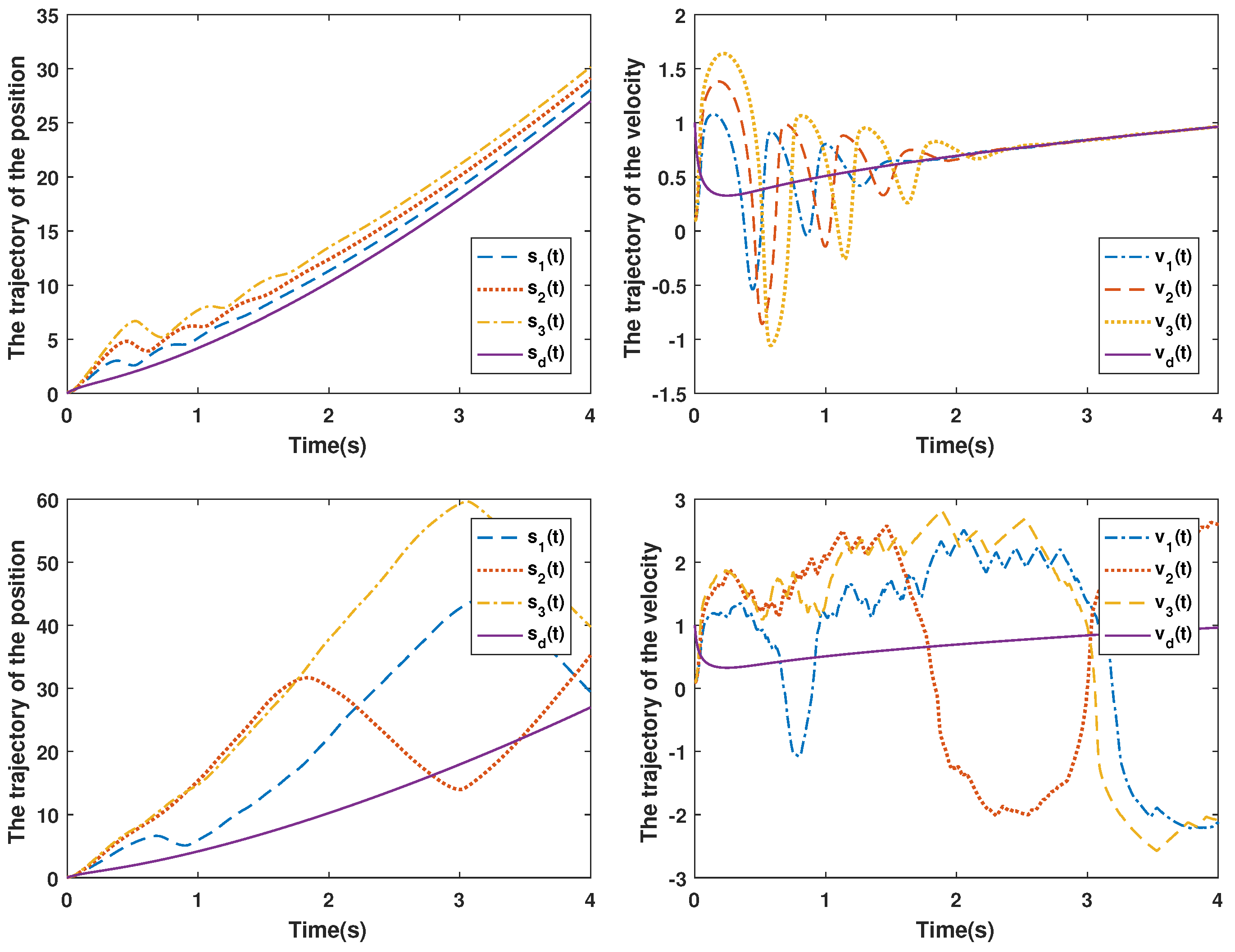
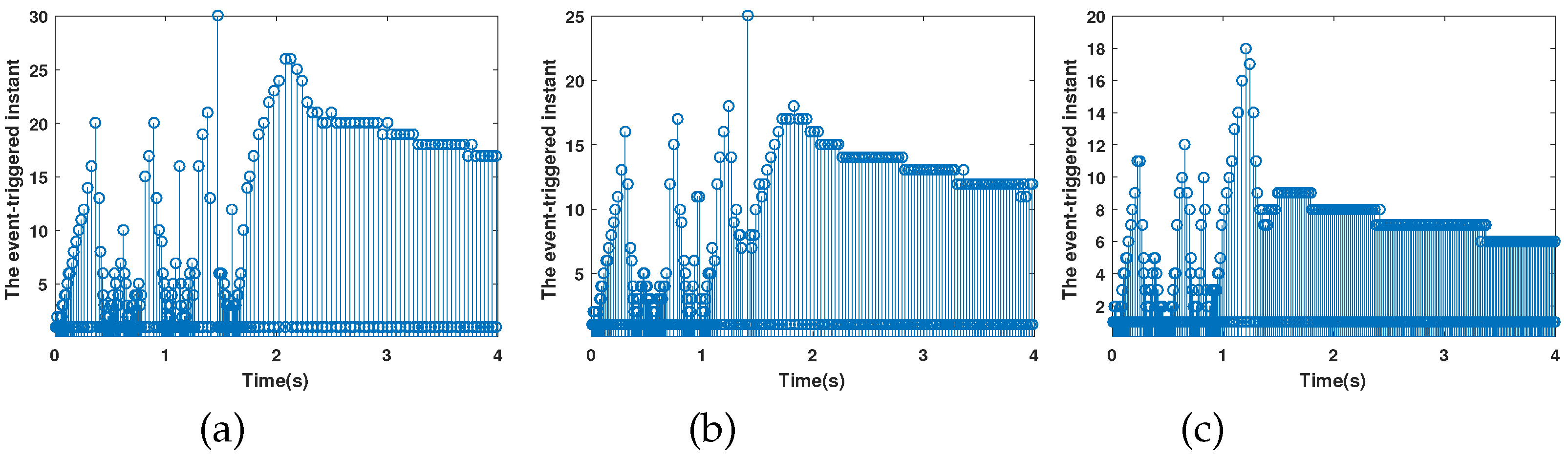
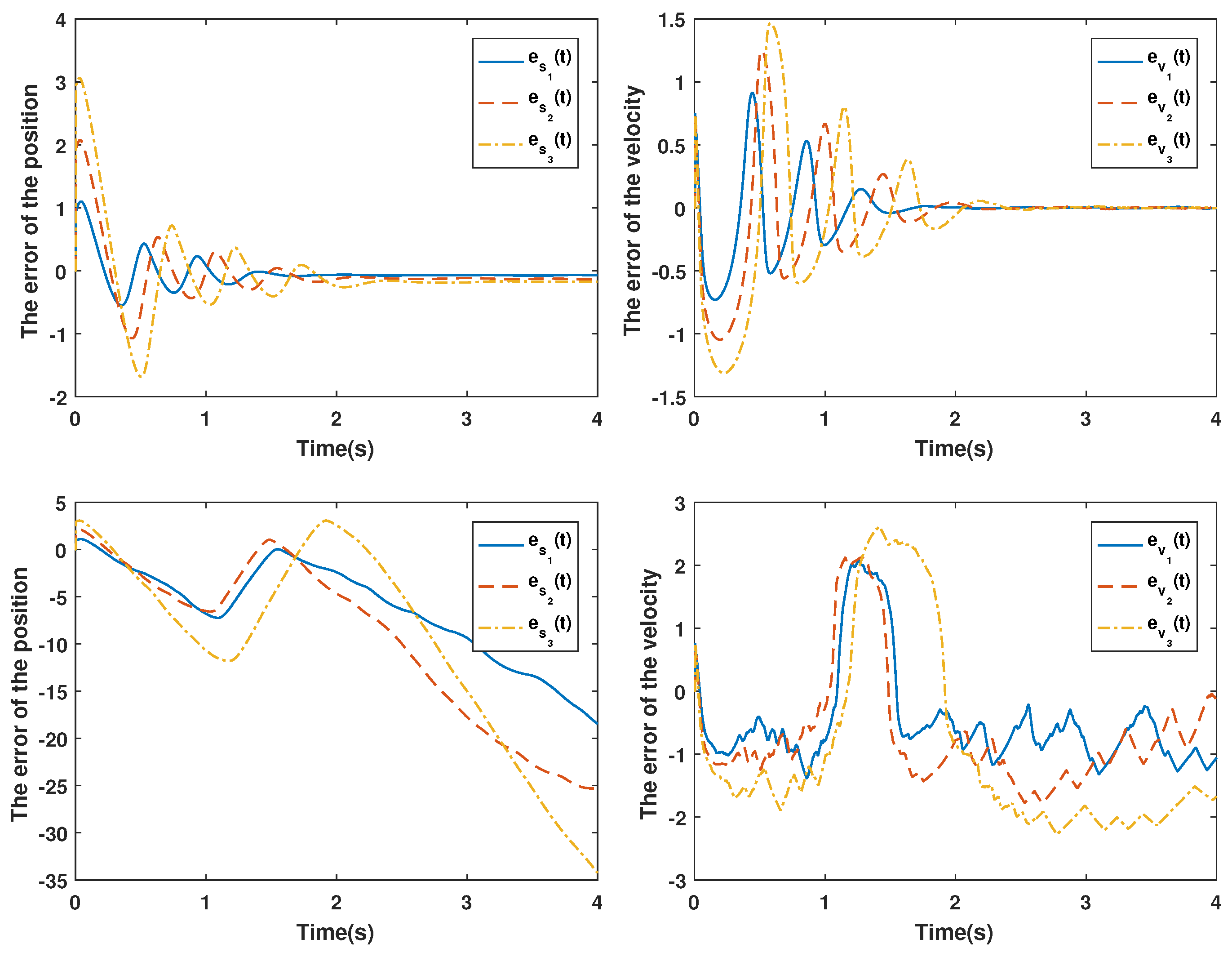
Figure 3 shows a comparison of the control scheme proposed here and in [13]. The vehicular platoon control objective is achieved using the proposed method under DoS attacks; that is, there is a safety distance between the following vehicles and the leading vehicle, and the velocity of the following vehicles can track the velocity of the leading vehicle at the same time. However, the vehicular control objective cannot be achieved using the control method designed in [13] under DoS attacks. The event-triggered instants of all vehicles are illustrated in Figure 4; Figure 4a–c denote the event-triggered instants for vehicle 1, 2 and 3. By calculation, the number of communication packets of vehicles 1, 2 and 3 are 598, 433 and 393 (number of communication packets under time-triggered: 2000), respectively, which implies that the packet transmission rate is reduced by $70.1\%$, $78.35\%$ and $80.35\%$, respectively. Therefore, the designed event-triggered mechanism can effectively reduce the network communication.

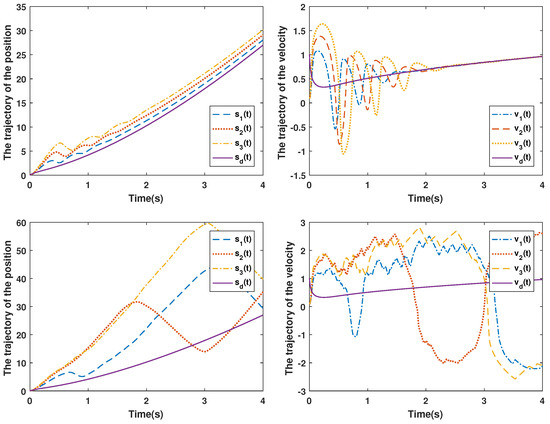
Figure 3. The trajectories of the position and velocity of the vehicular platoon system between the proposed method (up) and the method in [13] (down).

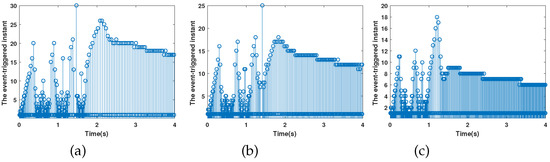
Figure 4. The event-triggered instant. (a–c) denote the event-triggered instants for vehicle 1, 2 and 3.

In contrast to the existing vehicle platoon control result [44], the event-triggered mechanism is introduced into the vehicle platoon control scheme to save the limited network communication resources. By simulation, the number of communication packets without using the event-triggered mechanism [44] were 2000, 2000, 2000 (i.e., time-trigger) for vehicles 1, 2 and 3, but the number of communication packets for vehicles 1, 2 and 3 using the proposed event-triggered mechanism were 598, 433 and 393. Therefore, compared with the vehicle platoon control scheme without considering the event-triggered mechanism [44], the proposed event-triggered vehicle platoon control scheme can achieve the control task with limited network communication resources.

The effectiveness of the proposed method is more clearly illustrated in Figure 5. The 2-norms of the errors between the method proposed and [13] are shown in Table 1, where $\parallel e_{v_i}\left(k\right)\parallel$ and $\parallel e_{x_i}\left(k\right)\parallel$ are the 2-norms of the tracking errors of the velocity and position in the ith vehicle, respectively.

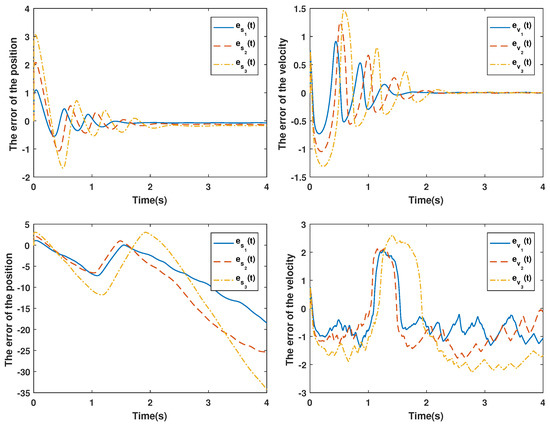
Figure 5. The errors of the position and velocity for the vehicular platoon system between the proposed method (up) and the method in [13] (down).

Table 1. The 2-norms of the tracking errors of the position and velocity.

	This Paper	[13]
$\parallel e_{x_1}\left(t\right)\parallel$	26.18	1.33 $\times {10}^3$
$\parallel e_{x_2}\left(t\right)\parallel$	58.83	1.48 $\times {10}^3$
$\parallel e_{x_3}\left(t\right)\parallel$	98.72	2 $\times {10}^3$
$\parallel e_{v_1}\left(t\right)\parallel$	25.77	75.96
$\parallel e_{v_2}\left(t\right)\parallel$	46.04	119.80
$\parallel e_{v_3}\left(t\right)\parallel$	67.34	176.21

5. Conclusions

The data-driven event-triggered platoon control problem was addressed for non-linear vehicle systems under DoS attacks. The input-output equivalent linear data model for a non-linear vehicle system was established using a dynamic linearization technique and the event trigger mechanism was used to save communication resources. Then, a novel resilient control scheme was developed to resist DoS attacks. In this scheme, a new attack compensation mechanism was designed to reduce the impact of DoS attacks based on the latest received system information. The simulation results show that the algorithm was able to achieve the platoon control target under DoS attacks well and save communication resources effectively. Future work will mainly focus on the dynamic event-triggered platoon control problem under a class of aperiodic DoS attacks.