Bayesian Estimation of a Transmuted Topp-Leone Length Biased Exponential Model Based on Competing Risk with the Application of Electrical Appliances

Abstract

Competing risk ($C_{o}R$) models are frequently disregarded in failure rate analysis, and traditional statistical approaches are used to study the event of interest. In this paper, we proposed a new lifetime distribution by generalizing the length biased exponential (LBE) distribution using the transmuted Topp-Leone-G ($T{T}_L$-G) family of distributions. The new three parameter model is called the transmuted Topp-Leone length biased exponential ($T{T}_{L}LBE$) distribution. A comprehensive account of various mathematical features of the $T{T}_{L}LBE$ model are derived. The unknown parameters of the proposed distribution are estimated by six classical approaches: the maximum likelihood (ML) approach, maximum product spacing (MPS) approach, least square (LS) approach, Weighted LS (WLS) approach, Cramér-Von Mises (CVN) approach, Anderson–Darling (AD) approach, and Bayesian approach. The stability of the model parameters is examined through the simulation study. The applications of our proposed distribution are explained through real data and its performance is illustrated through its comparison with the competent existing distributions. The $T{T}_{L}LBE$ model depend on the $C_{o}R$ model has been obtained and estimated parameter of this model by ML and Bayesian estimation approaches. In electrical appliances, we found two main causes of failure, and the data of electrical appliances are fitted to our model. Therefore, we analyzed the $T{T}_{L}LBE$ model depend on the $C_{o}R$ model to obtain the strong cause of failure.

1. Introduction

Lifetime data models have garnered statisticians’ attention in the area of statistical inference. These models have a wide range of applications, including management, public health, biology, engineering, and medicine. Recently, by employing multiple transformation techniques, several authors suggested several ways of generating new families of statistical models in the literature on statistics. One frequent strategy is to add one or more additional parameters to a regular probability distribution to both theoretically and practically increase its capacity to match various lifetime data, for example, the Kumaraswamy- G by [1], Type I half logistic Burr X-G by [2], Topp-Leone-G ($T_L$-G) by [3], odd Perks-G by [4], the Weibull-G by [5], sine $T_L$-G by [6], type II power $T_L$-G by [7], X-Gamma Lomax by [8] and a new Power $T_L$ -G by [9], among others.

The $T_L$ distribution is a simple bounded J-shaped distribution that has grabbed the interest of statisticians as a viable alternative to the beta distribution. The $T_L$-G family proposed by [3] has the next cumulative distribution function (cdf) as below

$$F_{TL-G}(x;\alpha )=G{\left(x\right)}^{\alpha }{(2-G\left(x\right))}^{\alpha },\alpha >0,x\in R,$$

where $\alpha$ is the positive shape parameter. The corresponding probability density function (pdf) is provided via

$$f_{TL-G}(x;\alpha )=2\alpha g\left(x\right)\overline{G}\left(x\right)G{\left(x\right)}^{\alpha -1}{(2-G\left(x\right))}^{\alpha -1},$$

where $G\left(x\right)$ is the baseline distribution function, $\overline{G}\left(x\right)$ is the parent survival function and $g\left(x\right)$ is the parent pdf. Ref. [10] proposed the $T{T}_L-G$ family of continuous distributions, which expands the transmuted class established by [11]. Because its hazard rate forms can be rising, decreasing, J, reversed-J, bathtub, and upside-down bathtub shaped, this family is adaptable. The cdf and pdf of the proposed family are, respectively, given by

$$\begin{array}{cc}\hfill F_{{}_{T{T}_L-G}}(x,\lambda ,\alpha )& =(1+\lambda ){\left(1-{\overline{G}}^2\left(x\right)\right)}^{\alpha }-\lambda {\left(1-{\overline{G}}^2\left(x\right)\right)}^{2\alpha }\hfill \\ & ={\left(1-{\overline{G}}^2\left(x\right)\right)}^{\alpha }\left[1+\lambda -\lambda {\left(1-{\overline{G}}^2\left(x\right)\right)}^{\alpha }\right],\alpha >0,\mid \lambda \mid \le 1,x\in R,\hfill \end{array}$$

(1)

and

$$f_{{}_{T{T}_L-G}}(x,\lambda ,\alpha )=2\alpha g\left(x\right)\overline{G}\left(x\right){\left(1-{\overline{G}}^2\left(x\right)\right)}^{\alpha -1}\left[1+\lambda -2\lambda {\left(1-{\overline{G}}^2\left(x\right)\right)}^{\alpha }\right].$$

(2)

According to the notion of Fisher, [12] proposed the LBE distribution by adding weight to the exponential distribution. They demonstrated that the LBE has greater flexibility than the exponential distribution. The cdf and pdf of LBE distribution are provided via

$$G_{{}_{LBE}}(x,\beta )=1-(1+\frac{x}{\beta })e^{-\frac{x}{\beta }},x>0;\beta >0,$$

(3)

and

$$g_{{}_{LBE}}(x,\beta )=\frac{x}{{\beta }^2}{e}^{-\frac{x}{\beta }},$$

(4)

respectively, where $\beta$ is a scale parameter.

Many authors looked at the burr extensions model as: [13,14,15], etc. Many authors looked at the burr family of statistical models as: [16], etc.

It is quite common in survival analysis studies to point to one objective (system) while also pointing to several causes of failure. It is frequently significant that an investigator must evaluate a particular danger in the presence of multiple risk variables. In the statistical literature, this method is known as the $C_{o}R$ model. In theory, data consisting of a failure period and an indicator indicating the cause of failure are assumed by comparing risk models. Many authors looked at the comparing risk model as: [17,18,19,20,21], etc. They thought that every individual in a target population died of a particular cause, such as cancer or other causes. They held the opinion that everyone in the target group passes away from a particular disease, such as cancer or another disease. They specifically took into account the next two possibilities:

• The system failed for a specified reason, and both the failure time and the failure cause are documented.
• Both the failure time and the failure cause are recorded, and the system failed for a defined failure reason.

The paper has more contributions as follows:

• Introducing the $T{T}_{L}LBE$ distribution.
• Obtaining moments ($M_{o}s$), $M_o$ generating function ($M_{o}GF$), conditional $M_o$ ($C{M}_o$) and entropy ($E_N$) are derived for $T{T}_{L}LBE$ distribution.
• Estimating parameters of $T{T}_{L}LBE$ distribution six classical estimation methods.
• Finding the estimated parameters when the parameters have prior distribution (Bayesian estimation).
• Comparison between six classical estimation approaches as; ML, MPS, LS, WLS, CVN, AD and Bayesian estimation.
• Modeling the $C_{o}R$ to the $T{T}_{L}LBE$ distribution.
• Fitting precipitation data and times of receiving an analgesic by $T{T}_{L}LBE$ distribution.
• Analyzing of causes risk for electrical appliances by $T{T}_{L}LBE$ depend on $C_{o}R$ model.

The main purpose of the paper is to find a new interested extension of the LBE distribution named the $T{T}_{L}LBE$ distribution. The statistical inferences for a $C_{o}R$ model when risks are in the $T{T}_{L}LBE$ distribution are discussed in this work. In actuality, the $T{T}_{L}LBE$ model is created by the $T{T}_L$ class of distributions and it is a very popular and wider applicability in a lot of fields, such as industrial reliability, engineering, and biomedical studies. Furthermore, we obtain the relative risks of $C_{o}R$ model when risks in the $T{T}_{L}LBE$ distribution.

The remainder of the paper proceeds as follows: We define the $T{T}_{L}LBE$ distribution in Section 2. Section 3 derives the main mathematical properties of the proposed model. Bayesian and six classical estimation methods of the model parameters are addressed in Section 4. Section 5 discusses the simulation’s results. We use a real data set in Section 6 and Section 8 to illustrate the importance of the new proposed model. The $C_{o}R$ model of the proposed model is discussed in Section 7. Finally, some closing remarks are provided in Section 9.

2. The New Model

The cdf and pdf of $T{T}_{L}LBE$ model, respectively, can be defined by inserting Equations (3) and (4) in Equations (1) and (2), where

$$F_{{}_{T{T}_{L}LBE}}(x,\lambda ,\alpha ,\beta )=(1+\lambda ){\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\alpha }-\lambda {\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{2\alpha },\alpha ,\beta >0,\mid \lambda \mid \le 1,x>0,$$

(5)

and

$$\begin{array}{cc}\hfill f_{{}_{T{T}_{L}LBE}}(x,\lambda ,\alpha ,\beta )& =\frac{2\alpha x}{{\beta }^2}(1+\frac{x}{\beta })e^{-\frac{2x}{\beta }}{\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\alpha -1}\hfill \\ & \times \left[1+\lambda -2\lambda {\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\alpha }\right],\alpha ,\beta >0,\mid \lambda \mid \le 1,x>0.\hfill \end{array}$$

(6)

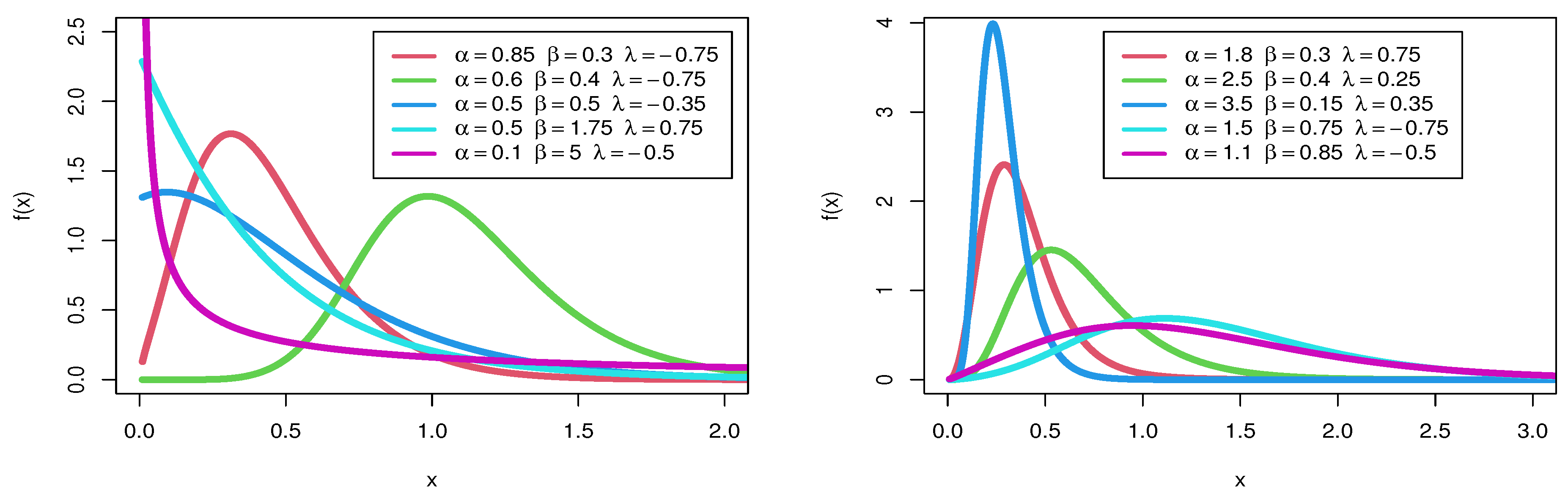
Depending on the values of its parameters, Figure 1 shows some conceivable shapes of the $T{T}_{L}LBE$ pdf. The $T{T}_{L}LBE$ pdf can be take the following forms of a symmetrical, unimodal, asymmetrical, decreasing, right skewness and left skewness shape.

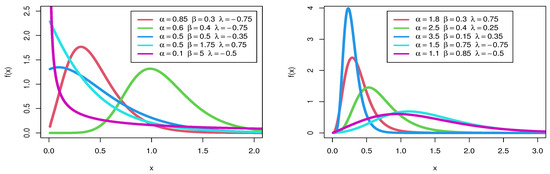
Figure 1. pdf of $T{T}_{L}LBE$ distribution.

The survival function (sf) and the hazard or failure rate function (hrf) can indeed be expressed as

$${\overline{F}}_{{}_{T{T}_{L}LB}}(x,\lambda ,\alpha ,\beta )=1-\left\{(1+\lambda ){\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\alpha }-\lambda {\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{2\alpha }\right\}$$

(7)

and

$$\begin{array}{cc}\hfill {\tau }_{{}_{T{T}_{L}LBE}}(x,\lambda ,\alpha ,\beta )=& \frac{2\alpha x}{{\beta }^2}(1+\frac{x}{\beta })e^{-\frac{2x}{\beta }}{\left(1-w_{\beta }\left(x\right)\right)}^{\alpha -1}\left[1+\lambda -2\lambda {\left(1-w_{\beta }\left(x\right)\right)}^{\alpha }\right]\hfill \\ & \frac{1}{1-\left\{(1+\lambda ){\left(1-w_{\beta }\left(x\right)\right)}^{\alpha }-\lambda {\left(1-w_{\beta }\left(x\right)\right)}^{2\alpha }\right\}}\hfill \end{array}$$

where, $w_{\beta }\left(x\right)={(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}.$

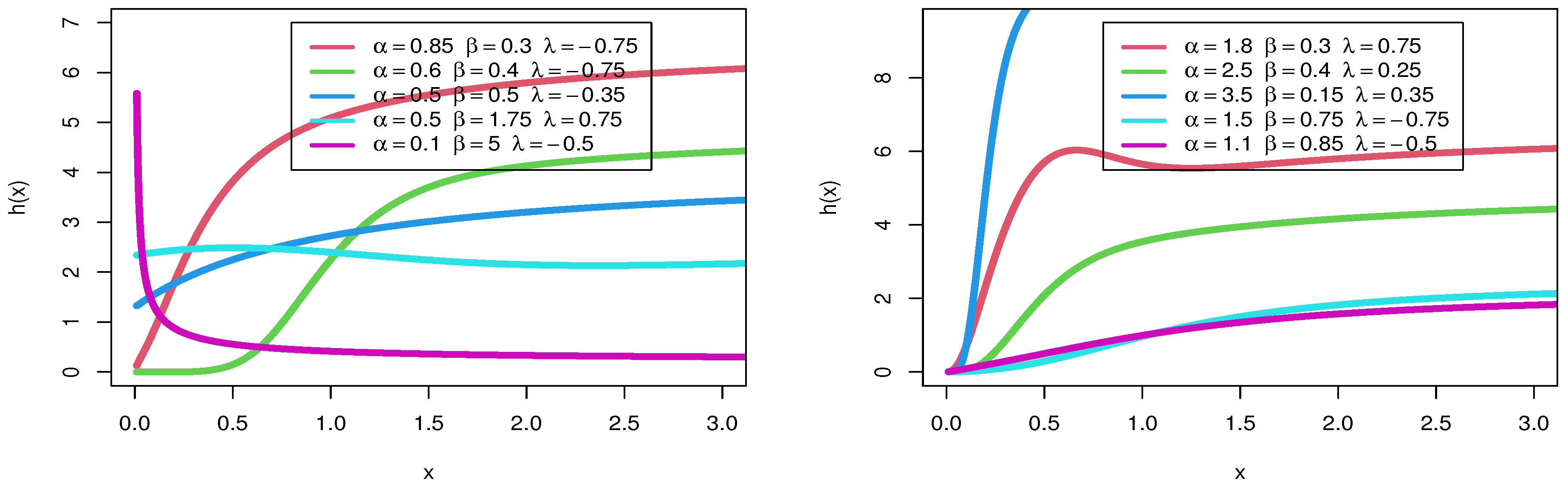
The $T{T}_{L}LBE$ model’s hazard rate plots are shown in Figure 2. The hrf can be take the following forms: J shape, unimodal, a constant shape, and decreasing and increasing shape.

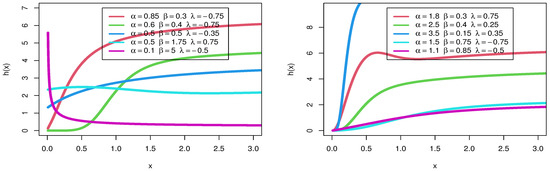
Figure 2. hrf of $T{T}_{L}LBE$ distribution.

If $b>0$ positive real non-integer and $\mid z\mid <1,$ then the binomial series expansion given by

$${(1-z)}^{b-1}=\sum _{j=0}^{\infty }{(-1)}^j\left(\genfrac{}{}{0pt}{}{b-1}{j}\right)z^j$$

(8)

If $\mid {(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\mid <1$. Then, the pdf of Equation (6) can be represented linearly in a convenient way by

$$\begin{array}{cc}\hfill f_{{}_{T{T}_{L}LBE}}(x,\lambda ,\alpha ,\beta )& =\frac{2\alpha }{{\beta }^2}\left\{(1+\lambda )\sum _{i,j=0}^{\infty }{(-1)}^i\left(\genfrac{}{}{0pt}{}{\alpha -1}{i}\right)\left(\genfrac{}{}{0pt}{}{2i+1}{j}\right)\frac{x^{j+1}}{{\beta }^j}{e}^{-\frac{2(i+1)x}{\beta }}-2\lambda \sum _{i,j=0}^{\infty }{(-1)}^i\left(\genfrac{}{}{0pt}{}{2\alpha -1}{i}\right)\left(\genfrac{}{}{0pt}{}{2i+1}{j}\right)\frac{x^{j+1}}{{\beta }^j}{e}^{-\frac{2(i+1)x}{\beta }}\right\}\hfill \\ & =\sum _{i,j=0}^{\infty }{\varpi }_{i,j}{x}^{j+1}{e}^{-\frac{2(i+1)x}{\beta }},\alpha ,\beta >0,\mid \lambda \mid \le 1,x>0\hfill \end{array}$$

(9)

where

$${\varpi }_{i,j}={(-1)}^i\frac{2\alpha }{{\beta }^{2+j}}\left[(1+\lambda )\left(\genfrac{}{}{0pt}{}{\alpha -1}{i}\right)-2\lambda \left(\genfrac{}{}{0pt}{}{2\alpha -1}{i}\right)\right]\left(\genfrac{}{}{0pt}{}{2i+1}{j}\right)$$

3. Mathematical Properties

Here, some fundamental mathematical aspects of $T{T}_{L}LBE$ distribution such as, $M_{o}s$, $M_{o}GF$, $C{M}_o$, and $E_N$ for $T{T}_{L}LBE$ are discussed.

3.1. Ordinary Moments and Moment Generating Functions

$M_{o}s$ are crucial in any statistical analysis and are valuable for quantifying skewness and kurtosis as well as for illuminating the distribution’s shape. If X has pdf (9) then the $r_{th}$$M_o$ of X is given by

$${\mu }_r^{{}^{\prime }}\left(x\right)={\int }_0^{\infty }{x}^{r}f\left(x\right)dx=\sum _{i,j=0}^{\infty }{\varpi }_{i,j}{\int }_0^{\infty }{x}^{r+j+1}{e}^{-\frac{2(i+1)x}{\beta }}dx.$$

Setting $t=\frac{2(i+1)x}{\beta }$ and after some algebra, $r_{th}$$M_o$ can indeed be expressed as

$${\mu }_r^{/}\left(x\right)=\sum _{i,j=0}^{\infty }{\varpi }_{i,j}{\left[\frac{\beta }{2(i+1)}\right]}^{r+j+2}\Gamma (r+j+2).$$

(10)

There are relationships between the behavior of a distribution’s $M_{o}GF$ and distribution features such as the occurrence of moments. The $M_{o}GF$$M_X\left(t\right)$ of X may be obtained as follows from (9):

$$\begin{array}{cc}\hfill M_X\left(t\right)& =E\left(e^{tX}\right)=\sum _{r=0}^{\infty }\frac{t^r}{r!}{\mu }_r^{/}\hfill \\ & =\sum _{r=0}^{\infty }\sum _{i,j=0}^{\infty }\frac{t^r}{r!}{\varpi }_{i,j}{\left[\frac{\beta }{2(i+1)}\right]}^{r+j+2}\Gamma (r+j+2).\hfill \end{array}$$

(11)

3.2. Conditional Moments

The $s_{th}$ upper incomplete (UI) $M_o$ of $T{T}_{L}LBE$ distribution is provided via

$$\begin{array}{cc}\hfill {\Psi }_s\left(t\right)& ={\int }_t^{\infty }{x}^{s}f\left(x\right)dx\hfill \\ & =\sum _{i,j=0}^{\infty }{\varpi }_{i,j}{\left[\frac{\beta }{2(i+1)}\right]}^{s+j+2}\Gamma (s+j+2,\frac{2(i+1)t}{\beta }).\hfill \end{array}$$

(12)

where $\Gamma (s,t)={\int }_t^{\infty }{x}^{s-1}{e}^{-x}dx$ is the “UI gamma function”. In the same way, the $s_{th}$ lower incomplete (LI) $M_{o}s$ of $T{T}_{L}LBE$ distribution is denoted by

$$\begin{array}{cc}\hfill {\Omega }_s\left(t\right)& ={\int }_0^t{x}^{s}f\left(x\right)dx\hfill \\ \hfill & =\sum _{i,j=0}^{\infty }{\varpi }_{i,j}{\left[\frac{\beta }{2(i+1)}\right]}^{s+j+2}\gamma (s+j+2,\frac{2(i+1)t}{\beta })\hfill \end{array}$$

(13)

where $\gamma (s,t)={\int }_0^t{x}^{s-1}{e}^{-x}dx$ is the “LI gamma function”.

3.3. Entropy

After taking into consideration observable macroscopic variables such as temperature, pressure, and volume, the Rényi $E_N$ represents the level of uncertainty that remains regarding a system. For the density function $f\left(x\right)$, the Rényi $E_N$ is characterized with ($\rho >0,\rho \ne 1)$

$$I_R\left(\rho \right)=\frac{1}{1-\rho }log\left[{\int }_0^{\infty }{f}^{\rho }\left(x\right)dx\right]$$

(14)

From (6), we have

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{f}^{\delta }\left(x\right)dx& ={\left(\frac{2\alpha }{{\beta }^2}\right)}^{\rho }{\int }_0^{\infty }{x}^{\rho }{(1+\frac{x}{\beta })}^{\rho }{e}^{-\frac{2\rho x}{\beta }}{\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\rho (\alpha -1)}\hfill \\ & \times {\left[1+\lambda -2\lambda {\left(1-{(1+\frac{x}{\beta })}^2{e}^{-\frac{2x}{\beta }}\right)}^{\alpha }\right]}^{\rho }.\hfill \end{array}$$

(15)

using (8) and after a few computations, we acquire

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{f}^{\delta }\left(x\right)dx& ={\left(\frac{2(1+\lambda )\alpha }{{\beta }^2}\right)}^{\rho }\sum _{i,j,k=0}^{\infty }{(-1)}^{i+j+k}{\left(\frac{2\lambda }{\lambda +1}\right)}^i\frac{\left(\genfrac{}{}{0pt}{}{\rho }{i}\right)\left(\genfrac{}{}{0pt}{}{\alpha (\rho +i)-\rho }{j}\right)\left(\genfrac{}{}{0pt}{}{2j+\rho }{k}\right)}{{\beta }^k}\hfill \\ \hfill {\left(\frac{\beta }{2(\rho +j)}\right)}^k& \times \Gamma (\rho +k+1).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill I_R\left(\rho \right)& =\frac{1}{1-\rho }log\left\{{\left(\frac{2(1+\lambda )\alpha }{{\beta }^2}\right)}^{\rho }\sum _{i,j,k=0}^{\infty }{(-1)}^{i+j+k}{\left(\frac{2\lambda }{\lambda +1}\right)}^i\frac{\left(\genfrac{}{}{0pt}{}{\rho }{i}\right)\left(\genfrac{}{}{0pt}{}{\alpha (\rho +i)-\rho }{j}\right)\left(\genfrac{}{}{0pt}{}{2j+\rho }{k}\right)}{{\beta }^k}\right.\hfill \\ \hfill & \times \left.{\left(\frac{\beta }{2(\rho +j)}\right)}^k\times \Gamma (\rho +k+1)\right\}.\hfill \end{array}$$

(16)

4. Bayesian and Classical Estimation Methods

We discussed the Bayesian and classical methods for unknown parameters of $T{T}_{L}LBE$ distribution.

4.1. Classical Methods

We investigated six classical estimation methods for unknown parameters of $T{T}_{L}LBE$ distribution.

4.1.1. Likelihood Estimation

The most common statistical inference technique is known as the ML estimates (MLEs) method. Consider a $x_1,\dots ,x_n$ random sample ($R_S$) of size n drawn from the $T{T}_{L}LBE$ distribution, and let $\varphi =(\lambda ,\alpha ,\beta )$. The log-likelihood of $T{T}_{L}LBE$ with $\varphi$ is given by

$$\begin{array}{cc}\hfill L_n& =nlog\left(2\right)+nlog\left(\alpha \right)-2nlog\left(\beta \right)+\sum _{i=1}^{n}log\left(x_i\right)-\frac{2}{\beta }\sum _{i=1}^n{x}_i+\sum _{i=1}^{n}log(1+\frac{x_i}{\beta })\hfill \\ & +(\alpha -1)\sum _{i=1}^{n}log\left[1-t_i\left(\beta \right)\right]+\sum _{i=1}^{n}log\left\{1+\lambda -2\lambda {\left(1-t_i\left(\beta \right)\right)}^{\alpha }\right\}\hfill \end{array}$$

(17)

where $t_i\left(\beta \right)={(1+\frac{x_i}{\beta })}^2{e}^{-\frac{2x_i}{\beta }}.$ Now computing the first partial derivatives of (17), we have

$$\frac{\partial L_n}{\partial \lambda }=\sum _{i=1}^n\frac{1-2{\left(1-t_i\left(\beta \right)\right)}^{\alpha }}{1+\lambda -2\lambda {\left(1-t_i\left(\beta \right)\right)}^{\alpha }},$$

(18)

$$\frac{\partial L_n}{\partial \alpha }=\frac{n}{\alpha }+\sum _{i=1}^{n}log\left[1-t_i\left(\beta \right)\right])-2\lambda \sum _{i=1}^n\frac{{\left(1-t_i\left(\beta \right)\right)}^{\alpha }log\left(1-t_i\left(\beta \right)\right)}{1+\lambda -2\lambda {\left(1-t_i\left(\beta \right)\right)}^{\alpha }},$$

(19)

and

$$\begin{array}{cc}\hfill \frac{\partial L_n}{\partial \beta }=& \frac{-2n}{\beta }+\frac{2}{{\beta }^2}\sum _{i=1}^n{x}_i-\sum _{i=1}^n\frac{x_i}{{\beta }^2(1+\frac{x_i}{\beta })}-2(\alpha -1)\sum _{i=1}^n\frac{x_i^2(1+\frac{x_i}{\beta })e^{-\frac{2x_i}{\beta }}}{{\beta }^3(1-t_i\left(\beta \right))}\hfill \\ & +2\lambda \alpha \sum _{i=1}^n\frac{{\left(1-t_i\left(\beta \right)\right)}^{\alpha -1}{x}_i^2(1+\frac{x_i}{\beta })e^{-\frac{2x_i}{\beta }}}{{\beta }^3\left[1+\lambda -2\lambda {\left(1-t_i\left(\beta \right)\right)}^{\alpha }\right]}.\hfill \end{array}$$

(20)

The MLEs $\widehat{\varphi }$ of $\varphi$ are computed by setting Equations (18)–(20) to 0 and solving them jointly.

4.1.2. Maximum Product Spacing (MPS) Estimators

The MPS technique was obtained by [22] as an alternative to the MLE technique. If the order statistics of a $R_S$n from $T{T}_{L}LBE$$\left(\varphi \right)$ are denoted by $X_{\left(1\right)}<X_{\left(2\right)}<\cdots <X_{\left(n\right)}$, the MPS function of $T{T}_{L}LBE$ can be defined as follows:

$${\Delta }_i\left(\varphi \right)=F_{{}_{T{T}_{L}LBE}}(x_i,\varphi )-F_{{}_{T{T}_{L}LBE}}(x_{i-1},\varphi ),$$

(21)

such that ${\sum }_{i=1}^{n+1}{\Delta }_i\left(\varphi \right)$. According to [22], the MPSEs of unknown parameters are computed through maximization of the next formula.

$$MPS\left(\varphi \right)=\frac{1}{n+1}\sum _{i=1}^{n+1}ln\left[{\Delta }_i\left(\varphi \right)\right].$$

(22)

Then, the MPS of $T{T}_{L}LBE$ distribution is

$$\begin{array}{cc}\hfill MPS\left(\varphi \right)=& \frac{1}{n+1}\sum _{i=1}^{n+1}ln\left\{(1+\lambda )\left({\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{\alpha }-{\left[1-{\left(1+\frac{x_{i-1}}{\beta }\right)}^2{e}^{-\frac{2x_{i-1}}{\beta }}\right]}^{\alpha }\right)\right.\hfill \\ & \left.+\lambda \left({\left[1-{\left(1+\frac{x_{i-1}}{\beta }\right)}^2{e}^{-\frac{2x_{i-1}}{\beta }}\right]}^{2\alpha }-{\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{2\alpha }\right)\right\}\hfill \end{array}$$

(23)

Because the partial derivatives of MPS with regard to unknown parameters cannot be computed directly in closed mathematical formulas, we derive the MPS estimators using numerical approaches such as Newton–Raphson algorithms. For more information about and examples of this method see [23,24,25].

4.1.3. Least Square (LS) and Weighted Least Square (WLS) Estimation

The LS and WLS estimate methods were presented by [26]. Let $X_{\left(1\right)}<X_{\left(2\right)}<\cdots <X_{\left(n\right)}$ denote the order statistics of a $R_S$ of size n from $T{T}_{L}LBE$$\left(\varphi \right)$. The LS estimations (LSE), and the Weighted LSE (WLSE) of the unknown parameters $\varphi$ and denoted by $\widehat{\varphi }$ and $\widehat{\lambda }$ can be derived via

$$\begin{array}{cc}\hfill WLSE\left(\varphi \right)& =\sum _{i=1}^n{\Omega }_i{\left[F_{{}_{T{T}_{L}LB}}(x_i,\varphi )-\frac{i}{n+1}\right]}^2\hfill \\ & =\sum _{i=1}^n{\Omega }_i{\left[(1+\lambda ){\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{\alpha }-\lambda {\left(1-{(1+\frac{x_i}{\beta })}^2{e}^{-\frac{2x_i}{\beta }}\right)}^{2\alpha }-\frac{i}{n+1}\right]}^2,\hfill \end{array}$$

(24)

where ${\Omega }_i=\frac{{(n+1)}^2(n+2)}{i(n-i+1)}$. We obtained the LSE of the unknown parameters $\varphi$ when the ${\Omega }_i=1$. Using partial derivatives of WLSE with regard to unknown parameters which these cannot be computed directly in closed mathematical formal, we derive the WLSE estimators using numerical approaches such as iterative algorithms. For more examples see [27].

4.1.4. Cramér-Von Mises Estimation

The CVN method of estimation was established by [28,29] to estimate the unknown parameters and indicated by $\varphi$ are computed by $\widehat{\varphi }$ minimizing of goodness-of-fit statistic. Assume $X_{\left(1\right)}<X_{\left(2\right)}<\cdots <X_{\left(n\right)}$ simplify the order statistics of a $R_S$ of size n from $T{T}_{L}LBE$$\left(\varphi \right)$, then, the CVN estimators can be obtained as follows:

$$\begin{array}{cc}\hfill CVN\left(\varphi \right)& =\frac{1}{12n}+\sum _{i=1}^n{\left[F_{{}_{T{T}_{L}LB}}(x_i,\varphi )-\frac{2(n-i)+1}{2n}\right]}^2\hfill \\ & =\frac{1}{12n}+\sum _{i=1}^n{\left[(1+\lambda ){\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{\alpha }-\lambda {\left(1-{(1+\frac{x_i}{\beta })}^2{e}^{-\frac{2x_i}{\beta }}\right)}^{2\alpha }-\frac{2(n-i)+1}{2n}\right]}^2.\hfill \end{array}$$

(25)

By using partial derivatives of CVN estimators with respect to unknown parameters $\varphi$ which these cannot be computed directly in closed mathematical formal, we derive the CVN estimators using numerical approaches such as iterative algorithms.

4.1.5. Anderson-Darling Estimation

AD estimate (ADE) is another sort of minimal distance estimator that is obtained by minimizing AD statistics. Ref. [30] proposed right-tail AD estimation as a refinement to the AD statistics. The ADE of the unknown parameters, represented by $\varphi$ are produced by minimizing the next formula with $\widehat{\varphi }$.

$$\begin{array}{cc}\hfill ADE\left(\varphi \right)& =-n-\frac{1}{n}+\sum _{i=1}^n(2i-1)\left[ln\left(F_{{}_{T{T}_{L}LB}}(x_i,\lambda ,\alpha ,\beta )\right)-ln\left(1-F_{{}_{T{T}_{L}LB}}(x_{n+1-i},\lambda ,\alpha ,\beta )\right)\right]\hfill \\ & =-n-\frac{1}{n}+\sum _{i=1}^n(2i-1)\left\{ln\left((1+\lambda ){\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{\alpha }-\lambda {\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{2\alpha }\right)\right.\hfill \\ & \left.+ln\left(1-(1+\lambda ){\left[1-{\left(1+\frac{x_{n+1-i}}{\beta }\right)}^2{e}^{-\frac{2x_{n+1-i}}{\beta }}\right]}^{\alpha }+\lambda {\left[1-{\left(1+\frac{x_{n+1-i}}{\beta }\right)}^2{e}^{-\frac{2x_{n+1-i}}{\beta }}\right]}^{2\alpha }\right)\right\}.\hfill \end{array}$$

(26)

By using partial derivatives of ADE with respect to unknown parameters $\varphi$ which these cannot be computed directly in closed mathematical formal, we derive the ADE using numerical approaches such as iterative algorithms.

4.2. Bayesian Estimation

In a Bayesian framework, unknown parameters in any model are handled as random variables rather than fixed constants. This is a reasonable assumption because the parameters of any population cannot remain constant throughout the research. By assuming prior distributions of unknown parameters, variance in the parameters can be accounted for. The parameters $\alpha$ and $\beta$ are assumed to follow independent gamma prior distributions of the following forms:

$$\mathbb{C}\left(\alpha \right)\propto {\alpha }^{w_1-1}exp\{-\alpha {\mathcal{q}}_1)\},\alpha >0,{\mathcal{q}}_1,w_1>0;j=1.$$

(27)

and

$$\mathbb{C}\left(\beta \right)\propto {\beta }^{w_2-1}exp\{-\beta {\mathcal{q}}_2\},\beta >0,{\mathcal{q}}_2,w_2>0;j=1,2.$$

(28)

where ${\mathcal{q}}_1,{\mathcal{q}}_2,w_1$, and $w_2$ are called hyper-parameters. While the parameter $\lambda$, we employ a uniform prior as a non-informative prior that expresses only a little bit of information about the parameters. To define prior distribution of $\lambda$ as uniform prior with interval −1 to 1. The density of uniform distribution is $\frac{1}{b-a};a<x<b$. If $b=1$, and $a=-1$ then the prior distribution of $\lambda$ is $\frac{1}{2}$. The joint prior distribution of $\varphi$ is provided via

$$\mathbb{C}\left(\varphi \right)\propto {\beta }^{w_2-1}{\alpha }^{w_1-1}exp\{-(\beta {\mathcal{q}}_2+\alpha {\mathcal{q}}_1)\},\beta ,\alpha >0,{\mathcal{q}}_j,w_j>0;j=1,2.$$

(29)

The joint posteriors distribution of $\varphi$ is obtained as follows:

$$\begin{array}{cc}\hfill \pi \left(\varphi \right|x)\propto & e^{-\beta \left({\mathcal{q}}_2+{\sum }_{i=1}^n\frac{2x_i}{{\beta }^2}\right)}\prod _{i=1}^n\left(1+\frac{x_i}{\beta }\right){\left[1-{\left(1+\frac{x_i}{\beta }\right)}^2{e}^{-\frac{2x_i}{\beta }}\right]}^{\alpha -1}\hfill \\ & \times \prod _{i=1}^n\left[1+\lambda -2\lambda {\left(1-{(1+\frac{x_i}{\beta })}^2{e}^{-\frac{2x_i}{\beta }}\right)}^{\alpha }\right]{\beta }^{w_2-2n-1}{\alpha }^{n+w_1-1}{e}^{-\alpha {\mathcal{q}}_1}.\hfill \end{array}$$

(30)

The means of their respective marginal posteriors are Bayesian estimates (BEs) of the parameters under the squared error loss. As a result, the Bayesian estimators for $\varphi$ are:

$$\begin{array}{cc}\hfill & \tilde{\alpha }={\int }_0^{\infty }{\int }_0^{\infty }{\int }_{-1}^1\alpha \pi \left(\varphi \right|x)d\alpha d\beta d\lambda \hfill \\ & \tilde{\beta }={\int }_0^{\infty }{\int }_0^{\infty }{\int }_{-1}^1\beta \pi \left(\varphi \right|x)d\alpha d\beta d\lambda \hfill \\ & \tilde{\lambda }={\int }_0^{\infty }{\int }_0^{\infty }{\int }_{-1}^1\lambda \pi \left(\varphi \right|x)d\alpha d\beta d\lambda .\hfill \end{array}$$

(31)

By using Markov chain Monte Carlo (MCMC) techniques to derive Bayes estimates for the parameters because the above formulas are difficult to calculate analytically. For information about MCMC see [31,32]. The R programming language software is used to obtain the numerical results for the six methods of estimation.

5. Numerical Outcomes

The performance of the classical estimation methods and Bayesian method of the parameters $\varphi$ of the $T{T}_{L}LBE$ distribution in terms of relative bias ($R_{E}B$), and mean square errors ($MSE$) are evaluated in this section. We take into account the values 30, 80, and 150 for a sample size of n. We generate random sample of $T{T}_{L}LBE$ distribution by using numerical analysis, where we used “uniroot” function in R package after equating the CDF with the uniform distribution with n sample size and range 0 to 1. The following possibilities are taken into account for the parameters $\alpha ,\beta$: Case I: $\alpha =1.5,\beta =1.5$, Case II: $\alpha =0.5,\beta =1.5$, Case III: $\alpha =0.85,\beta =0.7$, Case IV: $\alpha =3;\beta =1.5$, Case V: $\alpha =3;\beta =3$ and Case VI: $\alpha =1.5,\beta =3$. The $\lambda$ has been change from −0.5 to 0.7. we take replicating the process 5000 iterations. the $R_{E}B$ of the 160 estimations of the related $MSE$ are obtained in each configuration. These numerical outcomes are displayed in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6. In Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we conclude these points:

Table 1. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case I.

$\mathit{\alpha }=1.5,\mathit{\beta }=1.5$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.1149	0.3790	−0.0066	0.4685	−0.0058	0.3858	−0.1152	0.2472	0.1042	0.7527	0.0063	0.3256	−0.0112	0.0282
		$\beta$	0.1705	0.0844	0.1153	0.1583	0.1029	0.1406	0.1718	0.2000	0.0502	0.1119	0.0796	0.1139	0.0058	0.0155
		$\lambda$	−0.2568	0.2541	−0.1937	0.4160	−0.1845	0.3676	−0.2607	0.4914	−0.0889	0.3883	−0.1455	0.3752	0.0087	0.0267
	80	$\alpha$	−0.0746	0.1628	0.0192	0.1288	0.0141	0.1198	−0.0748	0.1372	0.0666	0.1616	0.0216	0.1120	0.0012	0.0141
		$\beta$	0.1095	0.0420	0.0692	0.0611	0.0587	0.0514	0.1095	0.0838	0.0449	0.0499	0.0545	0.0509	0.0003	0.0068
		$\lambda$	−0.2787	0.2286	−0.3059	0.2402	−0.2630	0.2273	−0.2776	0.2953	−0.2859	0.2329	−0.2665	0.2299	0.0007	0.0152
	150	$\alpha$	−0.0593	0.1237	0.0109	0.0868	0.0267	0.0915	−0.0590	0.1142	0.0417	0.0953	0.0318	0.0912	0.0003	0.0069
		$\beta$	0.0774	0.0304	0.0483	0.0342	0.0434	0.0300	0.0775	0.0525	0.0359	0.0300	0.0435	0.0300	−0.0020	0.0033
		$\lambda$	−0.1799	0.1966	−0.2166	0.1896	−0.2533	0.1846	−0.1814	0.2334	−0.2281	0.1849	−0.2700	0.1931	0.0020	0.0063
0.7	30	$\alpha$	−0.1695	0.1487	−0.0319	0.2496	−0.0273	0.1800	−0.1670	0.1550	0.0629	0.3629	−0.0180	0.1422	−0.0157	0.0212
		$\beta$	0.2735	0.0898	0.1343	0.4206	0.0995	0.2444	0.2681	0.3423	0.1153	0.4064	0.1103	0.2273	0.0030	0.0256
		$\lambda$	0.2485	0.1299	0.0138	0.2845	0.0081	0.2138	0.2428	0.2052	0.1424	0.2630	0.1247	0.2003	0.0265	0.0315
	80	$\alpha$	−0.0821	0.0781	−0.0214	0.1101	−0.0128	0.0899	−0.0818	0.0744	0.0117	0.1222	−0.0062	0.0840	0.0005	0.0204
		$\beta$	0.1125	0.0593	0.0643	0.1685	0.0460	0.1202	0.1122	0.1296	0.0425	0.1548	0.0399	0.1091	−0.0017	0.0101
		$\lambda$	0.0728	0.1146	0.0194	0.1335	−0.0020	0.0982	0.0721	0.0755	0.0205	0.1453	0.0067	0.0937	−0.0079	0.0142
	150	$\alpha$	−0.0514	0.0408	−0.0103	0.0623	−0.0017	0.0511	−0.0516	0.0403	0.0080	0.0668	0.0007	0.0460	−0.0050	0.0070
		$\beta$	0.0732	0.0483	0.0372	0.0969	0.0253	0.0720	0.0732	0.0781	0.0222	0.0948	0.0200	0.0612	0.0041	0.0046
		$\lambda$	0.0335	0.0955	−0.0219	0.0943	−0.0291	0.0695	0.0339	0.0557	−0.0371	0.1074	−0.0295	0.0662	−0.0033	0.0075

Table 2. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case II.

$\mathit{\alpha }=0.5,\mathit{\beta }=1.5$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.0376	0.0532	0.0130	0.0375	0.0225	0.0273	−0.0395	0.0271	0.1405	0.0483	0.0801	0.0316	0.0471	0.0102
		$\beta$	0.2052	0.0896	0.1371	0.2078	0.1340	0.1862	0.2020	0.2352	0.0643	0.1542	0.1102	0.1787	−0.0056	0.0205
		$\lambda$	−0.3249	0.2273	−0.0751	0.2548	−0.2132	0.2627	−0.3114	0.3207	−0.2017	0.2416	−0.2922	0.3006	−0.0228	0.0266
	80	$\alpha$	−0.0359	0.0219	0.0873	0.0167	0.0627	0.0162	−0.0377	0.0183	0.0967	0.0195	0.0602	0.0162	−0.0030	0.0040
		$\beta$	0.1227	0.0443	0.0822	0.0797	0.0695	0.0740	0.1215	0.1413	0.0470	0.0635	0.0516	0.0593	0.0054	0.0120
		$\lambda$	−0.2553	0.2045	−0.4739	0.2656	−0.3782	0.2576	−0.2480	0.2842	−0.3619	0.2419	−0.3168	0.2226	−0.0360	0.0170
	150	$\alpha$	−0.0176	0.0162	0.0662	0.0122	0.0833	0.0122	−0.0178	0.0135	0.0964	0.0138	0.0708	0.0119	0.0064	0.0025
		$\beta$	0.0826	0.0407	0.0530	0.0490	0.0510	0.0524	0.0831	0.0788	0.0398	0.0443	0.0381	0.0404	0.0032	0.0048
		$\lambda$	−0.1894	0.1937	−0.3135	0.1715	−0.3759	0.1892	−0.1893	0.2154	−0.3497	0.1741	−0.2982	0.1601	−0.0128	0.0072
0.7	30	$\alpha$	−0.1050	0.0105	0.0747	0.0210	0.0481	0.0150	−0.1048	0.0088	0.1432	0.0268	0.0410	0.0107	0.0197	0.0044
		$\beta$	0.4285	0.0857	0.0103	0.2200	0.1281	0.4462	0.4174	2.4423	−0.0116	0.3800	0.1881	0.8247	0.0417	0.0423
		$\lambda$	0.1472	0.1940	−0.0210	0.1157	0.1200	0.1035	0.1561	0.2939	0.0361	0.1034	0.2174	0.1449	−0.0132	0.0231
	80	$\alpha$	−0.0957	0.0053	−0.0291	0.0060	−0.0252	0.0042	−0.0934	0.0064	−0.0050	0.0062	−0.0186	0.0043	−0.0044	0.0012
		$\beta$	0.1113	0.0857	0.0402	0.2335	0.0555	0.1663	0.1194	0.1246	−0.0172	0.1750	0.0423	0.1236	0.0162	0.0170
		$\lambda$	−0.0407	0.1825	−0.0515	0.1156	0.0085	0.0691	−0.0217	0.1429	−0.0902	0.1294	0.0165	0.0706	0.0070	0.0130
	150	$\alpha$	−0.0533	0.0033	−0.0234	0.0036	−0.0163	0.0032	−0.0461	0.0035	−0.0109	0.0036	−0.0145	0.0030	0.0112	0.0010
		$\beta$	0.1032	0.0809	0.1176	0.2587	0.0888	0.1279	0.1268	0.1293	0.0998	0.2545	0.0826	0.1110	0.0005	0.0053
		$\lambda$	0.0496	0.1033	0.0852	0.0904	0.0699	0.0582	0.0584	0.0526	0.0832	0.0965	0.0705	0.0554	0.0177	0.0059

Table 3. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case III.

$\mathit{\alpha }=0.85,\mathit{\theta }=0.7$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.0623	0.0649	−0.1031	0.0486	−0.0700	0.0364	−0.0820	0.0630	−0.0035	0.0553	0.0149	0.0599	0.0330	0.0255
		$\beta$	0.3173	0.0304	0.2288	0.0678	0.2235	0.0666	0.3150	0.1103	0.1279	0.0324	0.1848	0.0516	0.0293	0.0051
		$\lambda$	−0.8728	0.3038	−0.4305	0.2958	−0.5657	0.3615	−0.8058	0.4666	−0.3767	0.2332	−0.6773	0.3645	−0.0329	0.0179
	80	$\alpha$	−0.0719	0.0553	0.0524	0.0518	0.0647	0.0441	−0.0750	0.0491	0.1060	0.0619	0.0992	0.0451	0.0096	0.0127
		$\beta$	0.0821	0.0117	0.0689	0.0171	0.0665	0.0157	0.0836	0.0141	0.0431	0.0143	0.0698	0.0158	0.0084	0.0022
		$\lambda$	−0.0368	0.2382	−0.3075	0.2501	−0.3732	0.2532	−0.0290	0.1713	−0.3343	0.2451	−0.4874	0.2882	−0.0057	0.0172
	150	$\alpha$	−0.1239	0.0433	0.0321	0.0328	0.0039	0.0372	−0.1122	0.0352	0.0533	0.0356	0.0214	0.0345	0.0050	0.0028
		$\beta$	0.0728	0.0038	0.0985	0.0141	0.0714	0.0093	0.0737	0.0064	0.0842	0.0122	0.0643	0.0079	0.0040	0.0009
		$\lambda$	0.1236	0.1213	−0.4028	0.2751	−0.2164	0.1948	0.0930	0.1242	−0.3992	0.2715	−0.2475	0.1826	0.0009	0.0067
0.7	30	$\alpha$	−0.0727	0.0341	0.0161	0.0306	0.0185	0.0245	−0.0777	0.0230	0.1039	0.0482	0.0549	0.0277	−0.0178	0.0088
		$\beta$	0.3313	0.0253	0.0573	0.0775	0.0653	0.0814	0.3140	0.2912	−0.0164	0.0588	0.0303	0.0726	0.0285	0.0078
		$\lambda$	0.2254	0.0976	0.0415	0.1905	0.0613	0.1773	0.2184	0.3101	0.0382	0.1867	0.0498	0.1844	0.0673	0.0310
	80	$\alpha$	−0.0766	0.0153	−0.0370	0.0148	−0.0404	0.0108	−0.0849	0.0140	−0.0079	0.0153	−0.0354	0.0105	0.0113	0.0068
		$\beta$	0.0649	0.0087	−0.0104	0.0159	0.0103	0.0085	0.0763	0.0137	−0.0347	0.0165	0.0066	0.0074	−0.0218	0.0056
		$\lambda$	0.0058	0.0883	−0.0962	0.0596	−0.0256	0.0344	−0.0030	0.0246	−0.0953	0.0658	−0.0175	0.0327	0.0018	0.0147
	150	$\alpha$	−0.0622	0.0097	−0.0388	0.0142	−0.0291	0.0122	−0.0647	0.0117	−0.0243	0.0140	−0.0260	0.0112	0.0101	0.0032
		$\beta$	0.0612	0.0076	0.1253	0.0457	0.0917	0.0254	0.1271	0.0214	0.1087	0.0455	0.0776	0.0224	0.0004	0.0024
		$\lambda$	0.1194	0.0705	0.1409	0.0982	0.1061	0.0622	0.1246	0.0382	0.1320	0.1079	0.0870	0.0609	−0.0017	0.0064

Table 4. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case IV.

$\mathit{\alpha }=3,\mathit{\beta }=1.5$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.1503	1.6970	0.0508	5.5365	0.0319	4.7037	−0.1503	1.3470	0.2140	10.0191	0.0350	2.4918	−0.0021	0.0333
		$\beta$	0.1709	0.0606	0.1019	0.1342	0.0952	0.1269	0.1707	0.1752	0.0427	0.1061	0.0737	0.1018	0.0036	0.0116
		$\lambda$	−0.2708	0.2184	−0.1638	0.4286	−0.1276	0.4589	−0.2704	0.8417	−0.0353	0.4252	−0.1455	0.4311	−0.0091	0.0281
	80	$\alpha$	−0.1181	0.5155	−0.0149	0.6503	−0.0125	0.5227	−0.1183	0.5623	0.0373	0.7706	−0.0001	0.5001	0.0005	0.0179
		$\beta$	0.0983	0.0298	0.0698	0.0543	0.0572	0.0446	0.0983	0.0676	0.0484	0.0449	0.0516	0.0403	0.0056	0.0060
		$\lambda$	−0.2006	0.1795	−0.2627	0.2491	−0.2212	0.2179	−0.2000	0.2640	−0.2415	0.2439	−0.2255	0.2154	0.0047	0.0154
	150	$\alpha$	−0.0810	0.4055	−0.0093	0.3587	0.0014	0.3279	−0.0819	0.4438	0.0197	0.3935	0.0011	0.3124	−0.0007	0.0076
		$\beta$	0.0875	0.0279	0.0510	0.0299	0.0477	0.0281	0.0876	0.0552	0.0390	0.0262	0.0463	0.0276	0.0008	0.0042
		$\lambda$	−0.1930	0.1621	−0.2517	0.2090	−0.2792	0.2042	−0.2991	0.2911	−0.2385	0.2014	−0.2711	0.2060	0.0014	0.0078
0.7	30	$\alpha$	−0.1095	2.7815	0.0195	2.3716	0.0259	2.1963	−0.1094	1.5471	0.1496	3.5821	0.0585	2.1930	0.0012	0.0338
		$\beta$	0.1787	0.0676	0.0923	0.5021	0.0837	0.4213	0.1782	0.5923	0.0553	0.4968	0.0703	0.3180	0.0031	0.0284
		$\lambda$	0.0771	0.1742	−0.0310	0.4648	−0.0220	0.3950	0.0770	0.5293	0.0504	0.5678	0.0346	0.3238	−0.0212	0.0284
	80	$\alpha$	−0.0729	0.4430	−0.0093	0.4628	0.0091	0.4188	−0.0765	0.3342	0.0309	0.5217	0.0223	0.4024	−0.0078	0.0240
		$\beta$	0.0672	0.0449	0.0421	0.1158	0.0110	0.0601	0.0723	0.0581	0.0251	0.1132	−0.0039	0.0337	0.0108	0.0072
		$\lambda$	0.0511	0.0729	0.0129	0.1565	−0.0544	0.1269	0.0567	0.0462	0.0175	0.1694	−0.0682	0.1120	−0.0313	0.0196
	150	$\alpha$	−0.0439	0.3387	0.0245	0.4700	0.0236	0.3708	−0.0438	0.2737	0.0479	0.5301	0.0260	0.3449	−0.0012	0.0090
		$\beta$	0.0451	0.0385	0.0022	0.0644	0.0023	0.0474	0.0450	0.0406	−0.0052	0.0651	0.0013	0.0435	0.0031	0.0033
		$\lambda$	0.0093	0.0710	−0.0984	0.1473	−0.0717	0.1014	0.0088	0.0629	−0.0882	0.1483	−0.0615	0.0935	0.0010	0.0070

Table 5. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case V.

$\mathit{\alpha }=3;\mathit{\beta }=3$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.1621	1.6092	0.0298	3.8896	0.0169	3.3786	−0.1625	1.4882	0.1862	6.9558	0.0258	2.3133	−0.0041	0.0326
		$\beta$	0.1665	0.2383	0.1015	0.5080	0.0920	0.4424	0.1667	0.6317	0.0427	0.3620	0.0712	0.3465	−0.0009	0.0262
		$\lambda$	−0.3106	0.2255	−0.2487	0.3219	−0.1774	0.3739	−0.3101	0.4194	−0.1424	0.3270	−0.1816	0.3171	−0.0053	0.0283
	80	$\alpha$	−0.1105	0.5318	−0.0058	0.7491	−0.0066	0.6145	−0.1103	0.6595	0.0387	0.9040	0.0051	0.5715	0.0015	0.0169
		$\beta$	0.1017	0.1313	0.0648	0.2070	0.0567	0.1843	0.1016	0.2920	0.0410	0.1655	0.0512	0.1625	0.0009	0.0116
		$\lambda$	−0.2627	0.1939	−0.2770	0.2339	−0.2548	0.2279	−0.2623	0.2915	−0.2103	0.2184	−0.2618	0.2237	−0.0111	0.0149
	150	$\alpha$	−0.0887	0.3818	0.0083	0.4219	0.0038	0.3608	−0.0887	0.4627	0.0364	0.4787	0.0080	0.3579	−0.0010	0.0082
		$\beta$	0.0749	0.1035	0.0512	0.1347	0.0447	0.1182	0.0748	0.1916	0.0393	0.1239	0.0457	0.1238	0.0013	0.0061
		$\lambda$	−0.1971	0.1882	−0.3025	0.2187	−0.2652	0.2030	−0.1964	0.2463	−0.2816	0.2118	−0.2858	0.2150	−0.0009	0.0070
0.7	30	$\alpha$	−0.1368	1.9840	0.0128	1.9481	0.0141	1.7599	−0.1378	1.1393	0.1403	2.9613	0.0379	1.6846	−0.0036	0.0312
		$\beta$	0.2126	0.2651	0.0809	1.0598	0.0901	0.9971	0.2117	2.2453	0.0405	0.9890	0.0769	0.9227	−0.0039	0.0326
		$\lambda$	0.2043	0.1724	−0.0040	0.4591	0.0452	0.3101	0.1989	0.5817	0.0440	0.4282	0.0775	0.3202	−0.0163	0.0283
	80	$\alpha$	−0.0885	0.5320	−0.0165	0.7109	−0.0068	0.5603	−0.0879	0.4432	0.0259	0.8218	0.0072	0.5301	0.0000	0.0173
		$\beta$	0.0886	0.1871	0.0563	0.4739	0.0455	0.3388	0.0882	0.3448	0.0415	0.4677	0.0256	0.2752	−0.0018	0.0141
		$\lambda$	0.0526	0.1618	0.0133	0.1885	0.0246	0.1126	0.0530	0.0878	0.0292	0.1934	−0.0203	0.1252	−0.0211	0.0144
	150	$\alpha$	−0.0553	0.3157	0.0081	0.3938	0.0090	0.3190	−0.0556	0.2560	0.0302	0.4406	0.0118	0.2990	−0.0008	0.0075
		$\beta$	0.0525	0.1540	0.0123	0.2701	0.0096	0.1922	0.0527	0.1634	0.0071	0.2753	0.0071	0.1732	0.0011	0.0063
		$\lambda$	0.0293	0.1092	−0.0712	0.1356	−0.0549	0.0954	0.0295	0.0513	−0.0530	0.1328	−0.0520	0.0904	−0.0050	0.0066

Table 6. Numerical outcomes of $R_{E}B$ and $MSE$ for all estimation approaches at Case VI.

$\mathit{\alpha }=1.5,\mathit{\beta }=3$			MLE		LS		WLS		MPS		CVM		AD		Bayesian
$\lambda$	n		$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$	$R_{E}B$	$\mathit{MSE}$
−0.5	30	$\alpha$	−0.1139	0.3771	0.0202	0.5934	0.0163	0.4443	−0.1140	0.2899	0.1768	0.9519	0.0435	0.4066	−0.0086	0.0304
		$\beta$	0.1757	0.3426	0.1164	0.6465	0.1068	0.5714	0.1756	0.7781	0.0545	0.4746	0.0870	0.4604	0.0001	0.0273
		$\lambda$	−0.2802	0.2642	−0.1936	0.3798	−0.2459	0.3479	−0.2798	0.3704	−0.2540	0.3543	−0.2602	0.3532	0.0063	0.0271
	80	$\alpha$	−0.0504	0.1887	0.0441	0.1928	0.0667	0.1916	−0.0517	0.1554	0.1198	0.2141	0.0627	0.1947	−0.0045	0.0123
		$\beta$	0.0824	0.1339	0.0592	0.2532	0.0429	0.1903	0.0830	0.2488	0.0431	0.2447	0.0339	0.1696	−0.0002	0.0118
		$\lambda$	−0.2016	0.1822	−0.2502	0.2465	−0.2778	0.2032	−0.2079	0.2417	−0.3838	0.2601	−0.2112	0.1870	0.0025	0.0140
	150	$\alpha$	−0.0693	0.1259	0.0498	0.1105	0.0503	0.1089	−0.0694	0.1124	0.0718	0.1287	0.0444	0.1038	−0.0050	0.0061
		$\beta$	0.0900	0.1050	0.0627	0.1613	0.0569	0.1422	0.0895	0.2373	0.0484	0.1350	0.0551	0.1387	0.0005	0.0065
		$\lambda$	−0.1921	0.1797	−0.3914	0.2301	−0.3803	0.2260	−0.2076	0.2676	−0.3609	0.2194	−0.3560	0.2273	−0.0009	0.0066
0.7	30	$\alpha$	−0.1122	0.3166	0.0053	0.4028	0.0006	0.3608	−0.1154	0.2216	0.1079	0.5628	0.0336	0.3718	−0.0121	0.0417
		$\beta$	0.2474	0.3556	0.1011	1.5254	0.1115	1.3143	0.2453	2.6929	0.0598	1.2684	0.1006	1.4671	0.0028	0.0315
		$\lambda$	0.1303	0.1928	−0.0499	0.2957	0.0036	0.2213	0.1169	0.3175	0.0185	0.2905	0.0407	0.2462	−0.0270	0.0248
	80	$\alpha$	−0.0694	0.0934	0.0101	0.1198	0.0095	0.1060	−0.0717	0.0749	0.0455	0.1406	0.0154	0.0991	0.0072	0.0296
		$\beta$	0.0848	0.2430	0.0482	0.5647	0.0409	0.4298	0.0871	0.3336	0.0377	0.6026	0.0255	0.3585	0.0020	0.0161
		$\lambda$	0.0127	0.1133	0.0171	0.1348	0.0129	0.0917	0.0169	0.0693	0.0430	0.1385	−0.0160	0.0975	−0.0076	0.0109
	150	$\alpha$	−0.0543	0.0433	−0.0111	0.0666	−0.0046	0.0522	−0.0542	0.0420	0.0066	0.0715	−0.0031	0.0489	−0.0011	0.0059
		$\beta$	0.0772	0.2120	0.0453	0.4245	0.0339	0.3004	0.0771	0.2581	0.0371	0.4292	0.0333	0.2695	0.0011	0.0070
		$\lambda$	0.0672	0.0995	0.0152	0.1124	0.0101	0.0750	0.0670	0.0499	0.0231	0.1170	0.0216	0.0679	−0.0053	0.0067

• In each case, the MSEs fall as the n rises.
• Additionally, the $R_{E}B$ of estimates goes to zero values as sample size increases.
• These results indicate that the classical estimation methods as ML, LS, WLS, CVN, and AD estimation approaches of the parameters $\varphi$, are asymptotically unbiased and consistent.
• As anticipated, performance metrics show that estimates made using the Bayesian estimating approach outperform those made using the conventional estimation methods.
• Bayesian estimators obtained under the assumption of the gamma priors are obtained for $\varphi$ has non-informative priors.

6. Application of Real Data

This section uses two actual data sets to examine the adaptability and potential of the $T{T}_{L}LBE$ distribution. We offer a $T{T}_{L}LBE$ distribution application.

For the comparison of the models, We used different measures as the values of the Akaike information criterion (VAIC), Hannan Quinn information criterion (VHQIC), statistics of the Kolmogorov–Smirnov test (SKS), the statistics Anderson-Darling test (SAD), and the statistics Cramer-von Mises test (SCVM). Thus, the $T{T}_{L}LBE$ distribution is compared with the transmuted Topp-Leone exponential ($T{T}_{L}E$) [10], Marshall-Olkin LBE (MOLBE) [33], the extention generalization of LBE (EGLBE) [34], Marshal-Olkin Kumaraswamy moment exponential (MOKwME) [35], and Gompertz Lomax (GL) [36] distributions.

6.1. Precipitation Data

The March precipitation data set is given by [37] which consists of 30 observations of the March precipitation (in inches) in Minneapolis/St Paul. The data are as follows: ‘0.77, 1.74, 0.81, 2.10, 0.52, 1.62, 1.31, 0.32, 0.59, 0.81, 2.81, 1.87, 1.20, 1.95, 1.20, 0.47, 1.43, 3.37, 2.20, 3.00, 3.09, 1.51, 1.18, 1.35, 4.75, 2.48, 0.96, 1.89, 0.90, 2.05’.

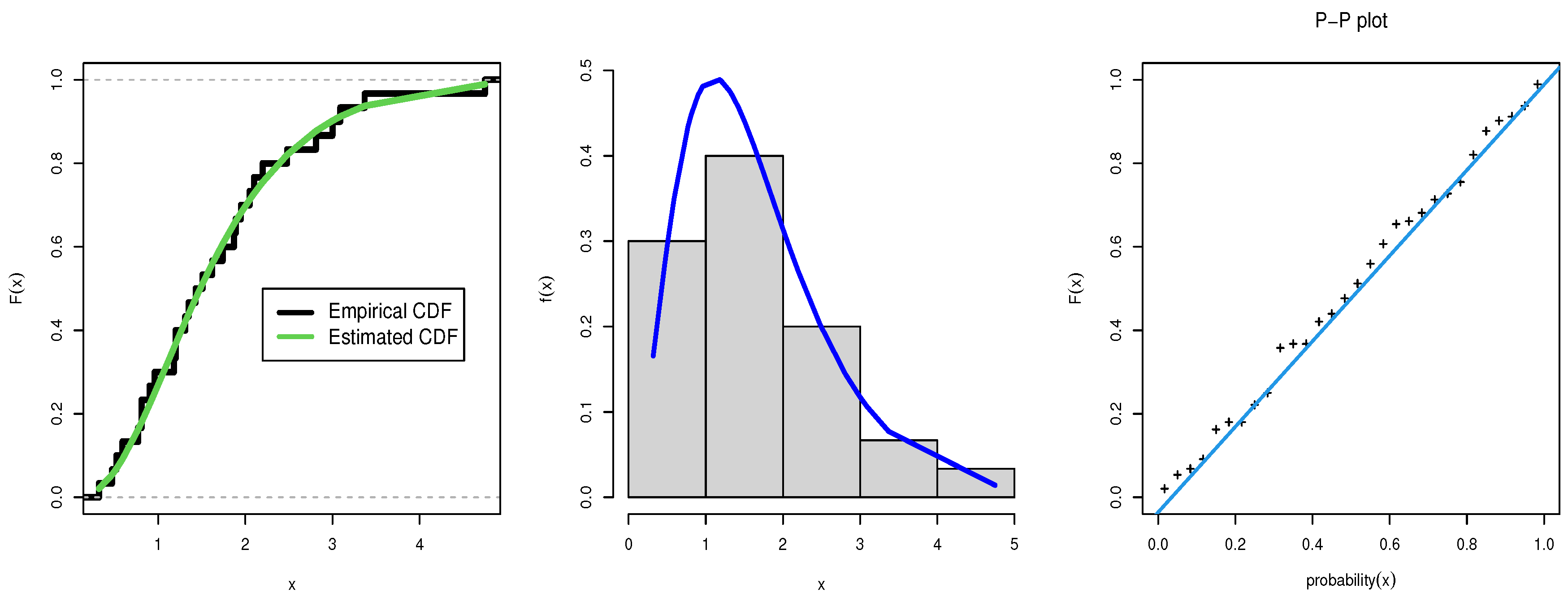
Figure 3 shows the estimated cdf with empirical cdf, probability of estimated pdf with histogram of data, and PP-plot for first data. In Table 7, the $T{T}_{L}LBE$ model has the largest p-value and the lowest SKS for first data.

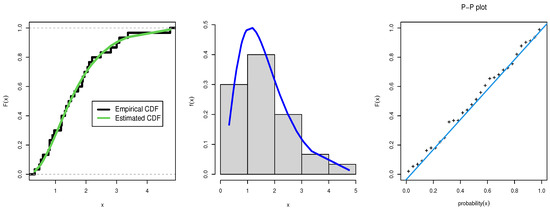
Figure 3. Estimated CDF, empirical CDF, estimated PDF with histogram, and P-P plot for the TTLLE distribution for data set 1.

Table 7. MLE with SE, SKS test with p-value and different measures for data set I.

Models		Estimates	SE	SKS	p-Value	VAIC	VHQIC	SCVM	SAD
$T{T}_{L}LBE$	$\alpha$	1.4194	0.4107	0.0578	0.99996	82.2233	83.5681	0.0138	0.1034
	$\beta$	1.1978	0.4041
	$\lambda$	0.1611	1.0324
$T{T}_{L}E$	$\alpha$	0.5988	0.1559	0.0624	0.9998	82.2741	83.5885	0.0145	0.1050
	$\beta$	3.3904	1.2811
	$\lambda$	−0.1098	0.8904
MOLBE	$\alpha$	0.6043	0.1506	0.0579	0.99996	82.2313	83.6024	0.0189	0.1447
	$\beta$	2.4960	1.8145
EGLBE	$\alpha$	0.1555	0.9366	0.0678	0.9991	82.3118	83.6273	0.0154	0.1088
	$\beta$	0.1886	1.2049
	$\lambda$	2.2532	3.0254
MOKwME	$\alpha$	0.3154	0.4032	0.0744	0.9963	84.0541	85.8471	0.0142	0.1036
	$\beta$	2.0811	1.6355
	$\lambda$	0.4209	0.6408
	$\theta$	1.4901	1.3657
GL	$\alpha$	4.9941	5.5811	0.0930	0.9576	88.3289	90.1219	0.0482	0.3452
	$\beta$	0.5928	0.6892
	$\lambda$	0.5456	0.5533
	$\theta$	0.6572	0.9295

6.2. Times of Receiving an Analgesic

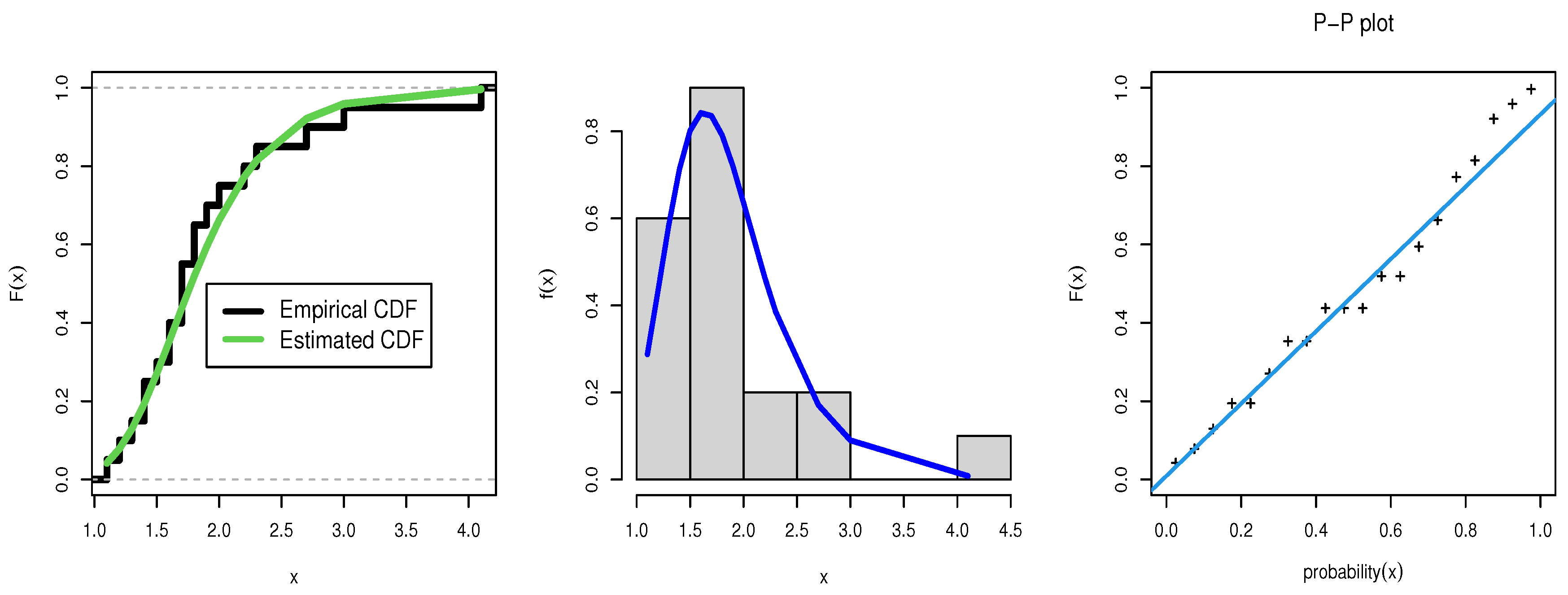
Data set II: 1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3.0, 1.7, 2.3, 1.6, 2.0. these data discussed times of twenty patients receiving an analgesic which has used [38] to fit the inverse power Lindley distribution. The fit of the empirical CDF, histogram, and PP-plot for data II were obtained in Figure 4. The Bayesian estimates for the both data are provided in Table 8. More ever the has the highest p-value and the lowest SKS for $T{T}_{L}LBE$ model have shown in Table 9.

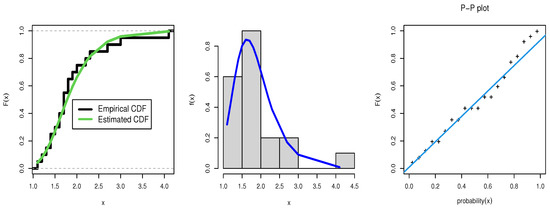
Figure 4. Estimated CDF, empirical CDF, estimated PDF with histogram, and P-P plot for the TTLLE distribution for data set 2.

Table 8. Bayesian estimation of $T{T}_{L}LBE$ model for each data sets.

Data	I		II
	Estimates	SE	Estimates	SE
$\alpha$	1.3454	0.4903	9.1389	3.0120
$\beta$	1.1636	0.2529	0.7522	0.1265
$\lambda$	−0.2383	0.3810	0.2836	0.4769

Table 9. MLE with SE, SKS test with p-value and different measures for data set II.

Models		Estimates	SE	SKS	p-Value	VAIC	VHQIC	SCVM	SAD
$T{T}_{L}LBE$	$\alpha$	9.0477	5.3782	0.1311	0.88214	38.7326	39.3157	0.0559	0.3303
	$\beta$	0.7504	0.1701
	$\lambda$	0.4773	0.4946
MOLBE	$\alpha$	0.3095	0.0618	0.1464	0.7844	42.8262	43.2149	0.1458	0.8539
	$\beta$	47.5854	49.4063
EGLBE	$\alpha$	0.5368	0.9421	0.1453	0.7923	39.3908	39.9740	0.0693	0.4093
	$\beta$	1.3652	3.0292
	$\lambda$	8.5877	6.0111
MOKwME	$\alpha$	4.4174	NA	0.1767	0.5601	48.8709	49.6484	0.1691	0.9863
	$\beta$	0.8183	NA
	$\lambda$	22.0862	NA
	$\theta$	10.1276	9.0612
GL	$\alpha$	5.3446	4.0238	0.1849	0.5011	50.2548	51.0323	0.1994	1.1707
	$\beta$	0.5673	0.4276
	$\lambda$	4.0823	2.3902
	$\theta$	0.0054	0.0041

7. Competing Risks

Competing risks are frequent in time-to-event data, and regression analysis of such data has lately seen important methodological breakthroughs. In recent years, models were developed to estimate the lifespan of certain risks in the presence of other risk variables. The data for these "competing risk models" are the failure period and an indicator variable indicating the particular reason for the failure of the individual or item. It is possible to presume that the causes of failure are either independent or dependent. In most cases, the analysis of competing risk data presupposes that failures have separate causes. Despite the fact that the assumption of dependence is more realistic, there is some concern regarding the underlying model’s identifiability. Therefore, we introduced an alternative model based on competing risks. In this section, we consider the first type of data when there are $k=2$ causes of failure for the $T{T}_{L}LBE$ distribution.

The likelihood function of the $T{T}_{L}LBE$ based on competing risk model is

$$\begin{array}{cc}\hfill L(\Omega )=& \prod _{i=1}^N{\left[\frac{\frac{2{\alpha }_1{x}_i}{{\beta }_1^2}(1+\frac{x_i}{{\beta }_1})e^{-\frac{2x_i}{{\beta }_1}}{\left(1-w_{{\beta }_1}\left(x_i\right)\right)}^{{\alpha }_1-1}\left[1+{\lambda }_1-2{\lambda }_1{\left(1-w_{{\beta }_1}\left(x_i\right)\right)}^{{\alpha }_1}\right]}{1-\left\{(1+{\lambda }_1){\left(1-w_{{\beta }_1}\left(x_i\right)\right)}^{{\alpha }_1}-{\lambda }_1{\left(1-w_{{\beta }_1}\left(x_i\right)\right)}^{2{\alpha }_1}\right\}}\right]}^{I({\delta }_i=1)}\hfill \\ & \prod _{i=1}^N{\left[\frac{\frac{2{\alpha }_2{x}_i}{{\beta }_2^2}(1+\frac{x_i}{{\beta }_2})e^{-\frac{2x_i}{{\beta }_2}}{\left(1-w_{{\beta }_2}\left(x_i\right)\right)}^{{\alpha }_2-1}\left[1+{\lambda }_2-2{\lambda }_2{\left(1-w_{{\beta }_2}\left(x_i\right)\right)}^{{\alpha }_2}\right]}{1-\left\{(1+{\lambda }_2){\left(1-w_{{\beta }_2}\left(x_i\right)\right)}^{{\alpha }_2}-{\lambda }_2{\left(1-w_{{\beta }_2}\left(x_i\right)\right)}^{2{\alpha }_2}\right\}}\right]}^{I({\delta }_i=2)}\hfill \\ & \prod _{i=1}^N{\left[1-\left\{(1+{\lambda }_1){\left(1-{(1+\frac{x_i}{{\beta }_1})}^2{e}^{-\frac{2x_i}{{\beta }_1}}\right)}^{{\alpha }_1}-{\lambda }_1{\left(1-{(1+\frac{x_i}{{\beta }_1})}^2{e}^{-\frac{2x_i}{{\beta }_1}}\right)}^{2{\alpha }_1}\right\}\right]}^{I({\delta }_i=0)}\hfill \\ & \prod _{i=1}^N{\left[1-\left\{(1+{\lambda }_2){\left(1-{(1+\frac{x_i}{{\beta }_2})}^2{e}^{-\frac{2x_i}{{\beta }_2}}\right)}^{{\alpha }_2}-{\lambda }_2{\left(1-{(1+\frac{x_i}{{\beta }_2})}^2{e}^{-\frac{2x_i}{{\beta }_2}}\right)}^{2{\alpha }_2}\right\}\right]}^{I({\delta }_i=0)}\hfill \end{array}$$

(32)

where $\Omega =({\alpha }_1,{\beta }_1,{\lambda }_1,{\alpha }_2,{\beta }_2,{\lambda }_2)$, and ${\delta }_i$ denoted two causes of failure, and N is a sample size of two causes of failure, with ${\delta }_i=1$ indicating that the cause of failure of $i^{th}$ item is due to the first cause, ${\delta }_i=2$ indicating that the cause of failure of $i^{th}$ item is due to the second cause, and ${\delta }_i=0$ indicating that the cause of failure of $i^{th}$ unit is unknown, indicating that we do not know the real cause of failure for a test.

Using the first partial derivatives of log-likelihood of $T{T}_{L}LBE$ based on competing risk model with respect to ${\alpha }_1,{\beta }_1,{\lambda }_1,{\alpha }_2,{\beta }_2$, and ${\lambda }_2$.To calculate the MLE ${\widehat{\alpha }}_1,{\widehat{\beta }}_1,{\widehat{\lambda }}_1,{\widehat{\alpha }}_2,{\widehat{\beta }}_2$, and ${\widehat{\lambda }}_2$ from the nonlinear Equation (32),we use the Newton–Raphson iterative method by substituting first partial derivatives of log-likelihood.

Furthermore, we compute the failure probability distribution of each failure cause in the presence of all others and the risk due to a particular failure cause.

The risk ${\pi }_j$ due to cause j:

$${\pi }_j={\int }_0^{\infty }{\tau }_j(x,{\lambda }_j,{\alpha }_j,{\beta }_j){\overline{F}}_1(x,{\lambda }_1,{\alpha }_1,{\beta }_1){\overline{F}}_2(x,{\lambda }_2,{\alpha }_2,{\beta }_2)dx,$$

(33)

where j = 1 and 2.

When the integrated function in Equation (33) is evaluated at the highest likelihood estimates of the parameters, the maximum likelihood estimate of ${\pi }_j$ can be determined via numerical integration using the invariant condition. In order to create random draws from the posterior distribution of j for Bayesian analysis, we will combine the random draw from the joint distribution with the integral above, which we will then use to any Bayesian analysis we want on ${\pi }_j$; $j=$ 1 and 2.

8. Analysis of Electrical Appliances with Two Causes of Failure

In this section, a real-life data set is explored (Lawless, [39], p. 441). An automatic life test was performed on the 36 small electronic components. There are 18 main categories of failure. However, we discovered that only 7 of the 33 failure modes were represented and that only modes 6–9 occurred more than twice. Failure mode 9 is highly regarded. As a result, the data set contains two failure modes: = 1 (failure mode 9) and = 2 (all other failure modes) (failure time is censored). As a result, the following data shows the failure times in order, as well as the cause of each failure, if accessible. The following displays the data set: In first causes: 1167, 1925, 1990, 2223, 2400, 2471, 2551, 2568, 2694, 3034, 3112, 3214, 3478, 3504, 4329, 6976, 7846.

In second causes: 11, 35, 49, 170, 329, 381, 708, 958, 1062, 1594, 2327, 2451, 2702, 2761, 2831, 3059.

In cause of failure is unknown: 2565, 13403, 6367.

Table 10 show MLE with SE for each causes failure and SKS test with p-value. Therefore, we note that this model is good fit of this data where p-value is more than 0.05.

Table 10. MLE with SE and SKS test with p-value.

Causes Failure	First		Second
	Estimates	SE	Estimates	SE
$\alpha$	3.089413	1.402801	0.298247	0.133408
$\beta$	1829.698	450.3735	1833.448	433.3706
$\lambda$	0.533473	0.420962	−0.32047	0.325272
SKS	0.1581		0.19124
p-Value	0.732		0.5397

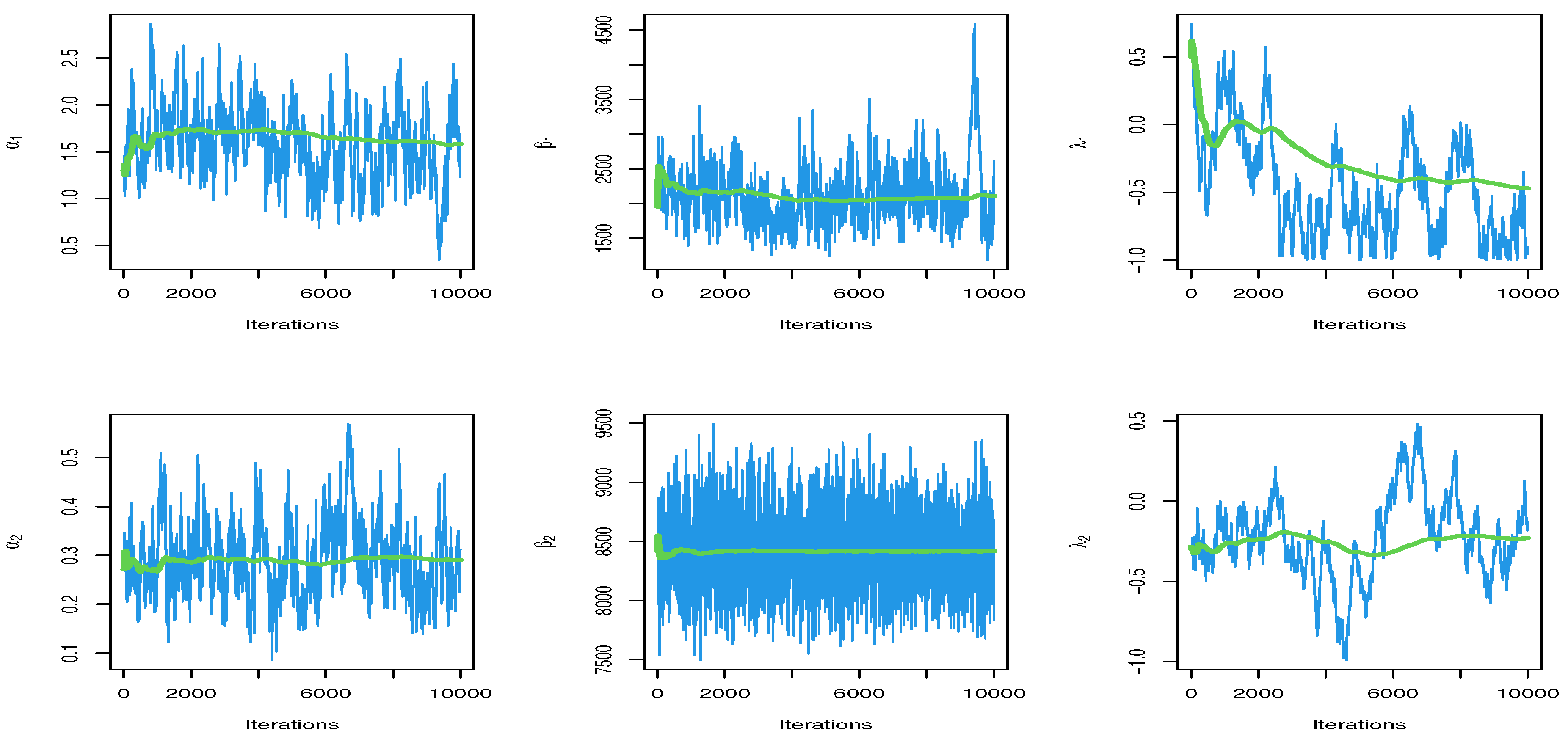
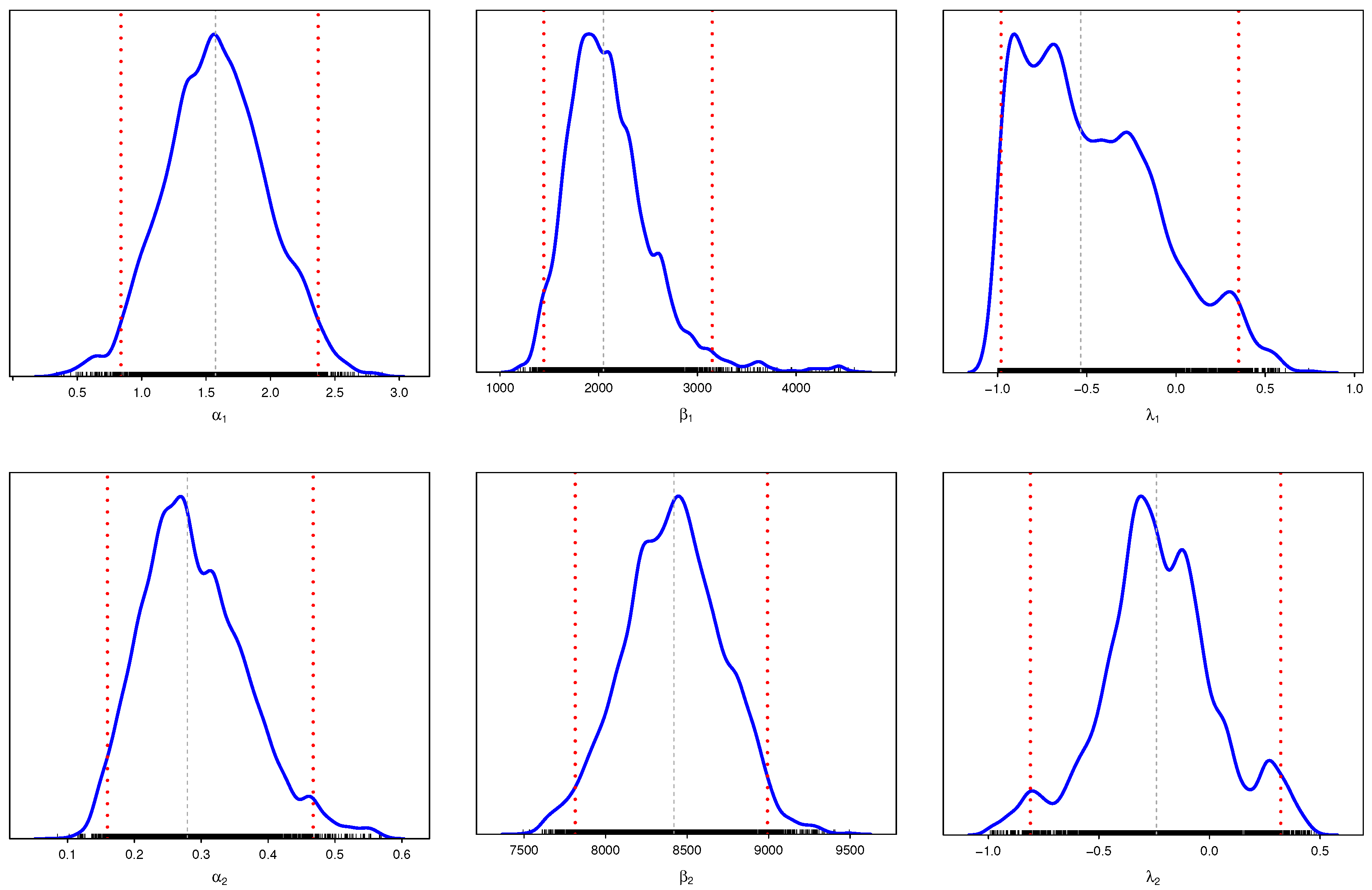
In order to examine the data, Table 11 shows the MLE and BEs of the competing risk of $T{T}_{L}LBE$ model with six parameters. Figure 5 and Figure 6 show the trace plots and marginal posterior density functions of parameters of the $T{T}_{L}LBE$ distribution under competing risks produced using the Bayesian estimation approach, respectively.

Table 11. MLE and Bayesian estimation for competing risk model.

		${\mathit{\alpha }}_1$	${\mathit{\beta }}_1$	${\mathit{\lambda }}_1$	${\mathit{\alpha }}_2$	${\mathit{\beta }}_2$	${\mathit{\lambda }}_2$
MLE	Estimates	1.3058	1958.1421	0.5298	0.2718	8416.6265	−0.2841
	SE	0.3055	421.8051	0.4331	0.1224	209.8906	0.7158
Bayesian	Estimates	1.5829	2111.2891	−0.4708	0.2901	8418.6723	−0.2300
	SE	0.2946	412.7090	0.3758	0.0782	202.4233	0.2610

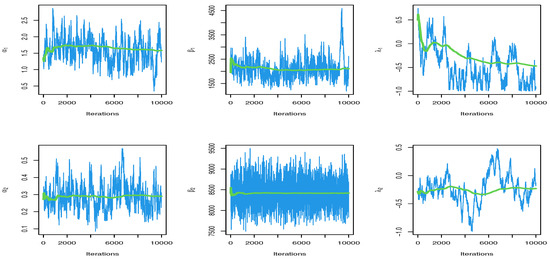
Figure 5. Trace for parameters of MCMC results.

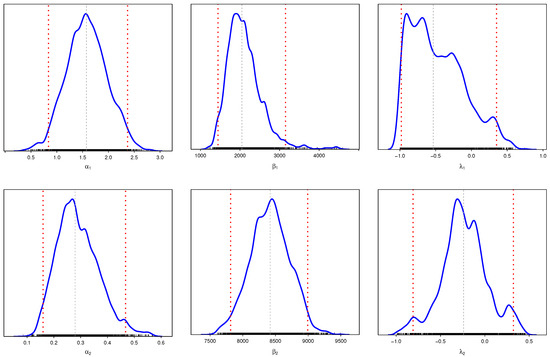
Figure 6. The posterior density for parameters of MCMC results.

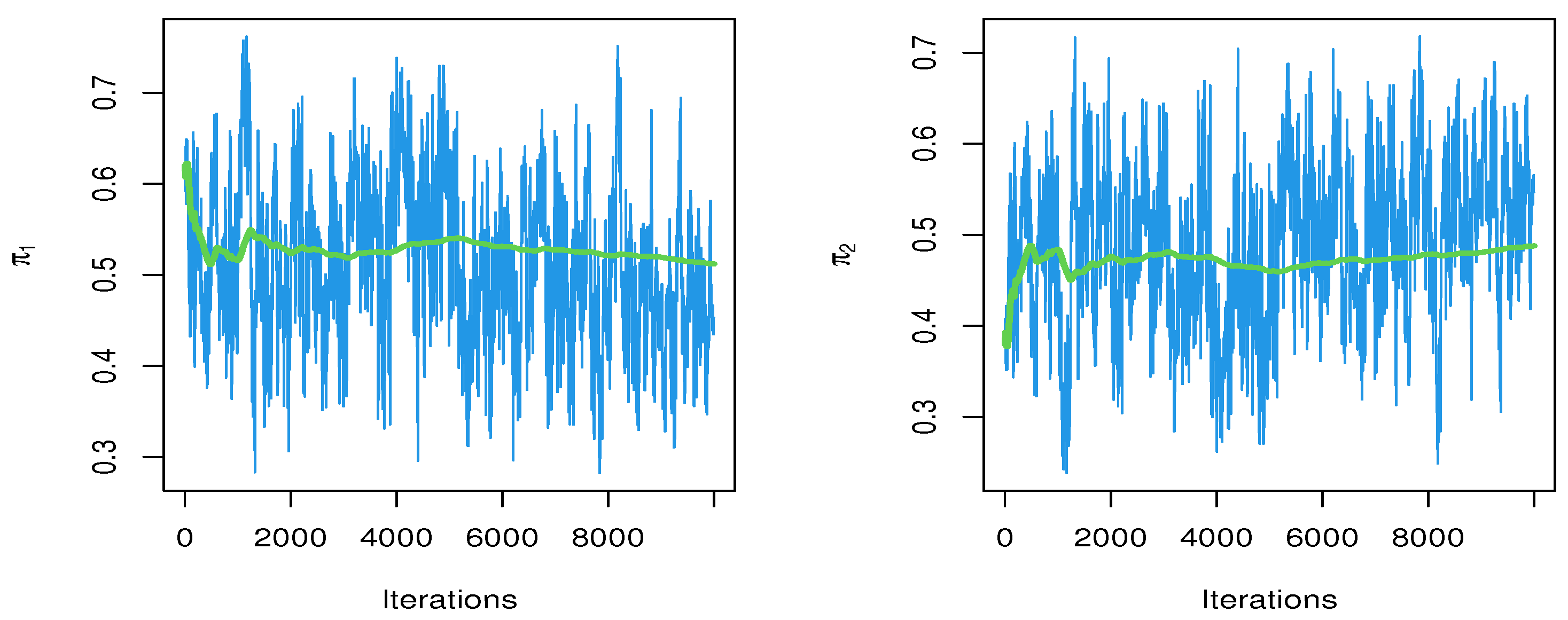
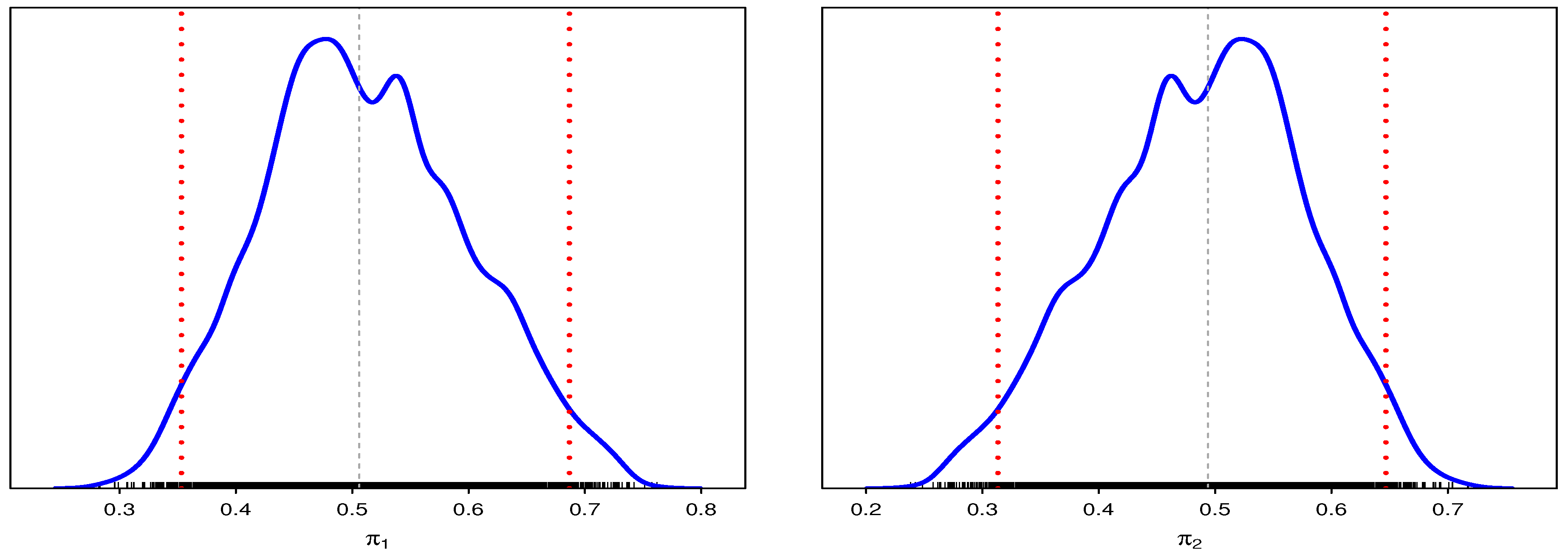
Table 12 displays the relative risks calculated for each estimation technique. The trace and convergence plots of relative risks are shown in Figure 7. Figure 8 shows that the posterior density of MCMC results for each relative risk has a symmetric normal distribution.

Table 12. Estimated relative risks for two causes.

	MLE	Bayes
$p{i}_1$	0.6220	0.5121
$p{i}_2$	0.3780	0.4879

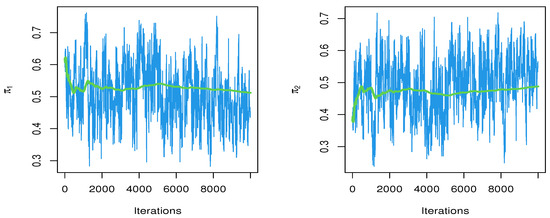
Figure 7. Trace for relative risks of MCMC results.

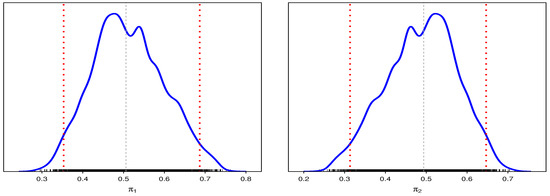
Figure 8. The posterior density for relative risks of MCMC results.

9. Conclusions

We established competing risks models with k = 2 as independent causes of failure data in this paper. When the risks follow $T{T}_{L}LBE$ distributions, we computed the model’s likelihood equation and used it to derive the likelihood function. We wrote about how to achieve maximum likelihood and BEs for model parameters. For all unknown parameters with elective hyper parameters, we employed the gamma prior distribution in Bayesian analysis, and the parameter ${\lambda }_j$ has uniform distribution with interval −1 to 1, and we used MCMC to generate random draws from the joint posterior distribution function. Farther more, we obtained different estimation method as six estimations for classical estimation methods and Bayesian estimation for parameter of $T{T}_{L}LBE$. We conclude that Bayesian estimation is better than classical estimation methods. Using data analysis, we conclude that the $T{T}_{L}LBE$ distribution is more efficient than other models, such as TTLE, MOLBE, EGLBE, MOKwME, and GL distributions. While in analysis of electrical appliances with two causes of failure, the cause of failure is probably due to the first cause as shown in the previous results.