Homogeneity Test of Multi-Sample Covariance Matrices in High Dimensions

Abstract

In this paper, a new test statistic based on the weighted Frobenius norm of covariance matrices is proposed to test the homogeneity of multi-group population covariance matrices. The asymptotic distributions of the proposed test under the null and the alternative hypotheses are derived, respectively. Simulation results show that the proposed test procedure tends to outperform some existing test procedures.

1. Introduction

In the last thirty years, statistical methods have made great developments for high-dimensional data. One common feature of high-dimensional data is that the data dimension is larger or vastly larger than the total sample size. In high-dimensional settings, many classic methods are not well-defined or have poor performances. As a result, a great deal of statistical methods have been proposed to deal with high-dimensional data. As an important issue of statistical inference, hypothesis testing is being followed with interest by scholars. Testing the equality of several covariance matrices is a fundamental problem in multivariate statistical analysis and can be found in many relevant works, such as [1,2]. This problem will arise from the analysis of gene expression data. It was shown in [3] that many genes have different variances in gene expressions between disease states. For example, the dataset of the breast cancer of patient is classified in three groups based on their gene expression signatures: well-differentiated tumors, moderately differentiated tumors, and poorly differentiated and undifferentiated tumors. Refs. [4,5,6] respectively used artificial neural networks, feature selection and a Markov blanket-embedded genetic algorithm to investigate this dataset. This dataset includes 83 samples, which is greatly less than data dimension 2308. For this gene dataset, we are interested in checking whether the covariance matrices of the four groups are the same or not. It is noted that an important assumption for multivariate analysis of variance is that of equal covariance matrices in different groups. Therefore, testing the equality of several covariance matrices is needed. Specifically, assume ${\mathbf{X}}_{i1},\cdots ,{\mathbf{X}}_{i{n}_i}$ are independent and identically distributed (iid) with a p-dimensional distribution with mean vector ${\mathbf{\mu }}_i$ and covariance matrix ${\Sigma }_i$ for $i=1,\cdots ,k$ with $k\ge 2$. We want to test the following hypothesis

$$\begin{array}{c}\hfill H_0:{\Sigma }_1=\cdots ={\Sigma }_k\mathrm{vs}.H_1:H_0\mathrm{is}\mathrm{not}\mathrm{true}.\end{array}$$

(1)

A classical method is the likelihood ratio test proposed by [7], where the population distribution is normal. However, as the data dimension is larger or vastly larger than the sample size, the likelihood ratio test is not well-defined because of the singularity of sample covariance matrices in probability one. Thus, it is vital to propose new procedures suitable to high-dimensional data. Owing to the curse of dimensionality, it becomes more challenging in high dimensions. For the hypothesis (1), there exists some test procedures in the literature. Based on the Frobenius norm, Refs. [8,9,10,11] proposed test statistics, respectively. Ref. [12] presented a test for high-dimensional longitudinal data. Ref. [13] proposed a power-enhancement high-dimensional test when the maximum eigenvalue of ${\Sigma }_i$ is bounded or $\mathrm{tr}({\Sigma }_i^j)=O(p^j)$ for $j=1,2,3,4$. Ref. [14] presented a test based on the well-known Box’s test ([15]) for high-dimensional normal data. It is noted that [9] imposed the conditions $0<{\lim }_{p\to \infty }\mathrm{tr}({\Sigma }^i)/p<\infty$ for $i=1,\dots ,8$ to obtain the asymptotical null distribution of his test under normality, where $\Sigma$ is equal to the covariance matrix under the null hypothesis $H_0$. Under high-dimensional normal data, [10] proposed a test as $0<{\lim }_{p\to \infty }\mathrm{tr}({\Sigma }^i)/p<\infty$ for $i=1,\dots ,4$. Ref. [8] imposed $0<\mathrm{tr}({\Sigma }^2)/p<\infty$ and other conditions to build asymptotical properties of his test statistic. The test statistics in [8,9,10,13,14] imposed the condition about the relationship between the data dimension p and the sample size $n_i$ or about the normal data. These conditions restrict the application of their test procedures. Ref. [11] gave a Frobenius norm-based test, which can be seen as an extension of that in [16], where the data dimension and the sample size can change arbitrarily.

The existing Frobenius norm-based tests for the hypothesis $H_0$ were almost constructed by ${\sum }_{i<j}^k\mathrm{tr}{({\Sigma }_i-{\Sigma }_j)}^2=k{\sum }_{i=1}^k\mathrm{tr}{({\Sigma }_i-\overline{\Sigma })}^2$, where $\overline{\Sigma }={\sum }_{i=1}^k{\Sigma }_i/k$ means average covariance matrix of the population covariance matrices ${\Sigma }_1,\dots ,{\Sigma }_k$. The deviations of ${\Sigma }_i$ from overall $\overline{\Sigma }$ is weighted by all equal weight $1/k$, which, however, cannot emphasize the deviations of populations with large sample sizes. Based on this, we here construct a new test statistic by a different Frobenius norm ${\sum }_{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2$ where ${\Sigma }^{*}={\sum }_{i=1}^k{n}_i{\Sigma }_i/n$ and $n={\sum }_{i=1}^k{n}_i$. Here, ${\Sigma }^{*}$ is a weighted average of k covariance matrices, which can emphasize the deviations of populations with large sample sizes. On the other hand, it is evident that the null hypothesis $H_0$ holds if and only if ${\sum }_{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2=0$.

The main purpose of this paper is to develop a new method to test the homogeneity of k high-dimensional covariance matrices on the basis of the weighted Frobenius norm. For the hypothesis in (1), most existing methods ([8,9,10,13]) imposed normality or the explicit relationship of between the data dimension p and the sample size n, and may behave poorly under non-normal data or ultra-high dimensional data. However, our method does not require normality or an explicit relationship between p and n, which is similar with the method in [11]. Thus, our method can be applied to non-normal and ultra-high dimensional data. On the other hand, the difference of the method in [11] and ours is that we use a sample-sizes-based Frobenius norm to build test statistics so that the tests in this paper and [11] behave differently, as the sample sizes are unequal. When $k=2$, our proposed test statistic can be seen as an extension of that [16] except a constant. Hence it can also be applied to two-sample data.

Simulation results show that the proposed test behaves differently from existing tests such as the tests in [11,13,14]. We will discuss the differences between the proposed test and the competing tests through numerical comparisons in various scenarios. We observe that the proposed test outperforms the competing tests in both size and power in many cases.

The remainder of the paper is organized as follows. Section 2 first presents the statistical model and the imposed conditions in order to construct our new test. In Section 3, a new test statistic is proposed and its asymptotic properties are also given. Section 4 presents a numerical study of the proposed test to compare three competing tests. Concluding remarks are provided in Section 5. The proofs of main results are arranged in Appendix A.

2. Preliminaries

We consider the following general multivariate model that is often used in literature:

$${\mathbf{X}}_{ij}={\mathbf{\mu }}_i+{\mathsf{\Gamma }}_i{\mathbf{Z}}_{ij}$$

for $j=1,\cdots ,n_i$ and $i=1,\cdots ,k$, where ${\mathsf{\Gamma }}_i$ is a $p\times r$ matrix for some $r\ge p$ such that ${\mathsf{\Gamma }}_i{\mathsf{\Gamma }}_i^{\mathrm{T}}={\Sigma }_i$ and ${\mathbf{Z}}_{i1},\dots ,{\mathbf{Z}}_{i{n}_i}$ are r-variate iid random vectors with $\mathrm{E}({\mathbf{Z}}_{ij})=0$ and $\mathrm{Var}({\mathbf{Z}}_{i1})={\mathbf{I}}_r$. Furthermore, denote ${\mathbf{Z}}_{ij}={(z_{ij1},\cdots ,z_{ijr})}^{\mathrm{T}}$ and $z_{ij1},\cdots ,z_{ijr}$ have a finite eighth moment with $\mathrm{E}(z_{ijl}^4)={\Delta }_l$ where ${\Delta }_l$ is some constant. Moreover, for any positive integers q and ${\alpha }_v$, there has

$$\mathrm{E}(z_{ij{v}_1}^{{\alpha }_1}\cdots z_{ij{v}_q}^{{\alpha }_q})=\mathrm{E}(z_{ij{v}_1}^{{\alpha }_1})\cdots \mathrm{E}(z_{ij{v}_q}^{{\alpha }_q})$$

(2)

as ${\sum }_{v=1}^q{\alpha }_v\le 8$, where $v_1,\cdots ,v_q$ are distinct indices. It shows from (2) that $z_{ij{v}_1},\cdots ,z_{ij{v}_q}$ are pseudo-independent, which is naturally satisfied when samples are generated from normal distribution.

In order to obtain the asymptotic distributions of new test statistic, some conditions are imposed as follows:

(C1)

As $n\to \infty$, $n_i/n\to c_i\in (0,1)$ for $i=1,\dots ,k$.

(C2)

As $n\to \infty$, $p=p(n_1,\cdots ,n_k)\to \infty$ and for arbitrary $l,m,s,h\in \{1,\cdots ,k\}$, $\mathrm{tr}({\Sigma }_l{\Sigma }_m)\to \infty$ and $\mathrm{tr}\left({\Sigma }_l{\Sigma }_m{\Sigma }_s{\Sigma }_h\right]=o\left[tr({\Sigma }_l{\Sigma }_m)tr({\Sigma }_s{\Sigma }_h)\right]$.

(C1) implies that all sample sizes have the same increasing rate, except constant terms. (C2) can be seen as an extension of the condition A2 in [16] to the case of multi-groups. The two conditions are the same as those in [11]. A key aspect of (C2) is that it does not impose any explicit relationship between p and sample size n. It is noted that (C2) naturally holds when all eigenvalues of k covariance matrices are uniformly bounded. Next, we consider another set of covariance matrices satisfying (C2), namely spiked covariance structures. For convenience, we set $k=4$ and let ${\Sigma }_i=\mathrm{diag}(a_{i1}{p}^{{\delta }_{i1}},\cdots ,a_{i{m}_i}{p}^{{\delta }_{i{m}_i}},a_{i,m_i+1},$$\cdots ,a_{ip})$, where $a_{ij}$s, ${\delta }_{ij}$s and $m_i$s are fixed positive constants with ${\delta }_{i1}\ge \cdots \ge {\delta }_{i{m}_i}$ for $i=1,2,3,4$. Then, the main items of $\mathrm{tr}({\Sigma }_1{\Sigma }_2{\Sigma }_3{\Sigma }_4)$, $\mathrm{tr}({\Sigma }_1{\Sigma }_2)$ and $\mathrm{tr}({\Sigma }_3{\Sigma }_4)$ is respectively $a_{11}{a}_{21}{a}_{31}{a}_{41}{p}^{{\delta }_{11}+{\delta }_{21}+{\delta }_{31}+{\delta }_{41}}+O(p)$, $a_{11}{a}_{21}{p}^{{\delta }_{11}+{\delta }_{21}}+O(p)$ and $a_{31}{a}_{41}{p}^{{\delta }_{31}+{\delta }_{41}}+O(p)$. As a result, (C2) holds if ${\delta }_{11}+{\delta }_{21}<1$ and ${\delta }_{31}+{\delta }_{41}<1$. Let ${\lambda }_{ij}$ denote the jth largest eigenvalue of ${\Sigma }_i$, then if ${\delta }_{11},\dots ,{\delta }_{41}$ are less than 0.5, ${\lambda }_{i1}^2/\mathrm{tr}({\Sigma }_i^2)\to 0$ for $i=1,\cdots ,4$, which is called a non-strongly spiked eigenvalue (NSSE) structure in [17]. Otherwise, if there exists some ${\delta }_{i1}\ge 0.5$, then ${\lambda }_{i1}^2/\mathrm{tr}({\Sigma }_i^2)\nrightarrow 0$, which is called a strongly spiked eigenvalue (SSE) structure in [17]. Therefore, (C2) holds when all of the covariance matrices have NSSE structures, or some of the covariance matrices have SSE structures.

To propose our test statistic, the hypothesis in (1) is rewritten as the following hypothesis

$$\begin{array}{c}\hfill H_0:\sum _{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2=0\mathrm{vs}.H_1:\sum _{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2>0.\end{array}$$

(3)

Then, we can construct a new test statistic based on ${\sum }_{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2$. Note that

$$\begin{array}{c}\hfill \sum _{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2=\sum _{i=1}^k\frac{n_i(n-n_i)}{n}\mathrm{tr}({\Sigma }_i^2)-\sum _{i\ne j}^k\frac{n_i{n}_j}{n}\mathrm{tr}({\Sigma }_i{\Sigma }_j).\end{array}$$

Thus, a new test statistic can be given if unbiased estimators of $\mathrm{tr}({\Sigma }_i^2)$ and $\mathrm{tr}({\Sigma }_i{\Sigma }_j)$ are respectively obtained for $i=1,\cdots ,k$.

3. Main Results

In this section, we propose a new test statistic for the hypothesis in (1) and give its asymptotic properties under conditions (C1) and (C2). According to the equivalent hypothesis in (3), our new test statistic is given as the following

$$T:=\sum _{i=1}^k\frac{n_i(n-n_i)}{n}{A}_i-\sum _{i\ne j}^k\frac{n_i{n}_j}{n}{C}_{ij},$$

(4)

where $A_i$ and $C_{ij}$ are respectively unbiased estimators of $\mathrm{tr}({\Sigma }_i^2)$ and $\mathrm{tr}({\Sigma }_i{\Sigma }_j)$, which are given as follows

$$A_i=\frac{1}{{\left(n_i\right)}_2}\sum _{j,l}^{*}{\left({\mathbf{X}}_{ij}^{\mathrm{T}}{\mathbf{X}}_{il}\right)}^2-\frac{2}{{\left(n_i\right)}_3}\sum _{j,l,f}^{*}\left({\mathbf{X}}_{ij}^{\mathrm{T}}{\mathbf{X}}_{il}{\mathbf{X}}_{ij}^{\mathrm{T}}{\mathbf{X}}_{if}\right)+\frac{1}{{\left(n_i\right)}_4}\sum _{j,l,f,g}^{*}\left({\mathbf{X}}_{ij}^{\mathrm{T}}{\mathbf{X}}_{il}{\mathbf{X}}_{if}^{\mathrm{T}}{\mathbf{X}}_{ig}\right)$$

(5)

and

$$\begin{array}{cc}\hfill C_{ij}=& \frac{1}{n_i{n}_j}\sum _{l=1}^{n_i}\sum _{m=1}^{n_j}{\left({\mathbf{X}}_{il}^{\mathrm{T}}{\mathbf{X}}_{jm}\right)}^2-\frac{1}{n_i{\left(n_j\right)}_2}\sum _{l=1}^{n_i}\sum _{f,m}^{*}\left({\mathbf{X}}_{il}^{\mathrm{T}}{\mathbf{X}}_{jf}{\mathbf{X}}_{il}^{\mathrm{T}}{\mathbf{X}}_{jm}\right)-\frac{1}{{\left(n_i\right)}_2{n}_j}\sum _{l=1}^{n_j}\sum _{f,m}^{*}\hfill \\ \hfill & \left({\mathbf{X}}_{jl}^{\mathrm{T}}{\mathbf{X}}_{if}{\mathbf{X}}_{jl}^{\mathrm{T}}{\mathbf{X}}_{im}\right)+\frac{1}{{\left(n_i\right)}_2{\left(n_j\right)}_2}\sum _{l,m}^{*}\sum _{f,g}^{*}\left({\mathbf{X}}_{il}^{\mathrm{T}}{\mathbf{X}}_{jf}{\mathbf{X}}_{im}^{\mathrm{T}}{\mathbf{X}}_{jg}\right).\hfill \end{array}$$

(6)

Here ${\left(n_i\right)}_l=\frac{\left(n_i\right)!}{\left(n_i-l\right)!}$ and ${\sum }^{*}$ denotes the sum for all different indices. Note that T is an unbiased estimator of ${\sum }_{i=1}^k{n}_i\mathrm{tr}{({\Sigma }_i-{\Sigma }^{*})}^2$. The above two unbiased estimators are used in [11,16,18,19], respectively. It is noted that we can assume, without loss of generality, ${\mathbf{\mu }}_1={\mathbf{\mu }}_2=\cdots ={\mathbf{\mu }}_k$ because T is invariant under location transformation. Under this assumption, the leading terms in $A_i$ and $C_{ij}$ are respectively the first term since the last two terms in $A_i$ and the last three terms in $C_{ij}$ are respectively infinitesimals of higher order of the first term. As a result, we only treat the first term in $A_i$ and $C_{ij}$ to save computation time. Please see [11,18] for more details about this computation time.

It shows from conditions (C1) and (C2) that the variance of T is

$$\begin{array}{cc}\hfill {\sigma }^2=& \frac{4}{n^2}\left\{\sum _{s=1}^k\frac{n_s{(n-n_s)}^2}{(n_s-1)}{\mathrm{tr}}^2({\Sigma }_s^2)+\sum _{s\ne h}^{k}2n_s{n}_h{\mathrm{tr}}^2({\Sigma }_s{\Sigma }_h)\right\}\hfill \\ \hfill & +\frac{4}{n^2}\sum _{s=1}^k\sum _{h\ne f}^k{n}_s{n}_h{n}_f\mathrm{tr}\{{\mathsf{\Gamma }}_s^{\mathrm{T}}({\Sigma }_s-{\Sigma }_h){\mathsf{\Gamma }}_s\circ {\mathsf{\Gamma }}_s^{\mathrm{T}}({\Sigma }_s-{\Sigma }_f){\mathsf{\Gamma }}_s\}\hfill \\ \hfill & +\frac{8}{n^2}\sum _{s=1}^k\sum _{h\ne f}^k{n}_s{n}_h{n}_f\mathrm{tr}\{{\Sigma }_s({\Sigma }_s-{\Sigma }_h){\Sigma }_s({\Sigma }_s-{\Sigma }_f)\}+o\left[{\mathrm{tr}}^2({\Sigma }_s^2)\right].\hfill \end{array}$$

Then, we can obtain the following asymptotic distribution of T.

Theorem 1.

Under (C1) and (C2), as $min\{p,n\}\to \infty$, we have

$$\begin{array}{c}\hfill \frac{T-\mathrm{E}(T)}{\sigma }\stackrel{d}{⟶}N(0,1).\end{array}$$

Proof. 

See Appendix B. □

It is clear that the variance of T under the null hypothesis $H_0$ is

$${\sigma }_0^2=\frac{4}{n^2}\left\{\sum _{i=1}^k\frac{n_i{(n-n_i)}^2}{(n_i-1)}{\mathrm{tr}}^2({\Sigma }_i^2)+\sum _{i\ne j}^{k}2n_i{n}_j{\mathrm{tr}}^2({\Sigma }_i{\Sigma }_j)\right\}.$$

As a result, to formulate the test procedure, we need to give a ratio-consistent estimator of ${\sigma }_0^2$. In this paper, we use the unbiased estimators $A_i$ and $C_{ij}$ in (5) and (6) to respectively estimate $\mathrm{tr}({\Sigma }_i^2)$ and $\mathrm{tr}({\Sigma }_i{\Sigma }_j)$. The following lemma is from [11].

Lemma 1.

Under (C1) and (C2), as $min\{p,n\}\to \infty$,

$$\frac{A_i}{\mathrm{tr}({\Sigma }_i^2)}\stackrel{p}{⟶}1,\frac{C_{ij}}{\mathrm{tr}({\Sigma }_i{\Sigma }_j)}\stackrel{p}{⟶}1.$$

On the basis of Lemma 1, a ratio-consistent estimator of ${\sigma }_0$ is given by

$${\widehat{{\sigma }_0}}^2:=\frac{4}{n^2}\left\{\sum _{i=1}^k\frac{n_i{(n-n_i)}^2}{(n_i-1)}{A}_i^2+\sum _{i\ne j}^{k}2n_i{n}_j{C}_{ij}^2\right\}.$$

Then, our new test is proposed by $\widehat{T}=T/\widehat{{\sigma }_0}$. It follows from Theorem 1 and Lemma 1 that $\widehat{T}\stackrel{d}{⟶}N(\mathrm{E}(T)/{\sigma }_0,{\sigma }^2/{\sigma }_0^2)$ as $min\{p,n\}\to \infty$. We see especially that the proposed test $\widehat{T}$ is asymptotically distributed with the standard norm distribution under the null hypothesis $H_0$. As a result, we reject the null hypothesis when $\widehat{T}\ge z_{\alpha }$, where $z_{\alpha }$ is the upper $\alpha$ quantile of standard normal distribution.

The following corollary is easy to be taken, which gives the asymptotic power function under the hypothesis $H_1$.

Corollary 1.

Under (C1) and (C2), as $min\{p,n\}\to \infty$, we have

$$P(\widehat{T}\ge z_{\alpha })=\mathsf{\Phi }\left[-z_{\alpha }{\sigma }_0/\sigma +\mathrm{E}(T)/\sigma \right]+o(1).$$

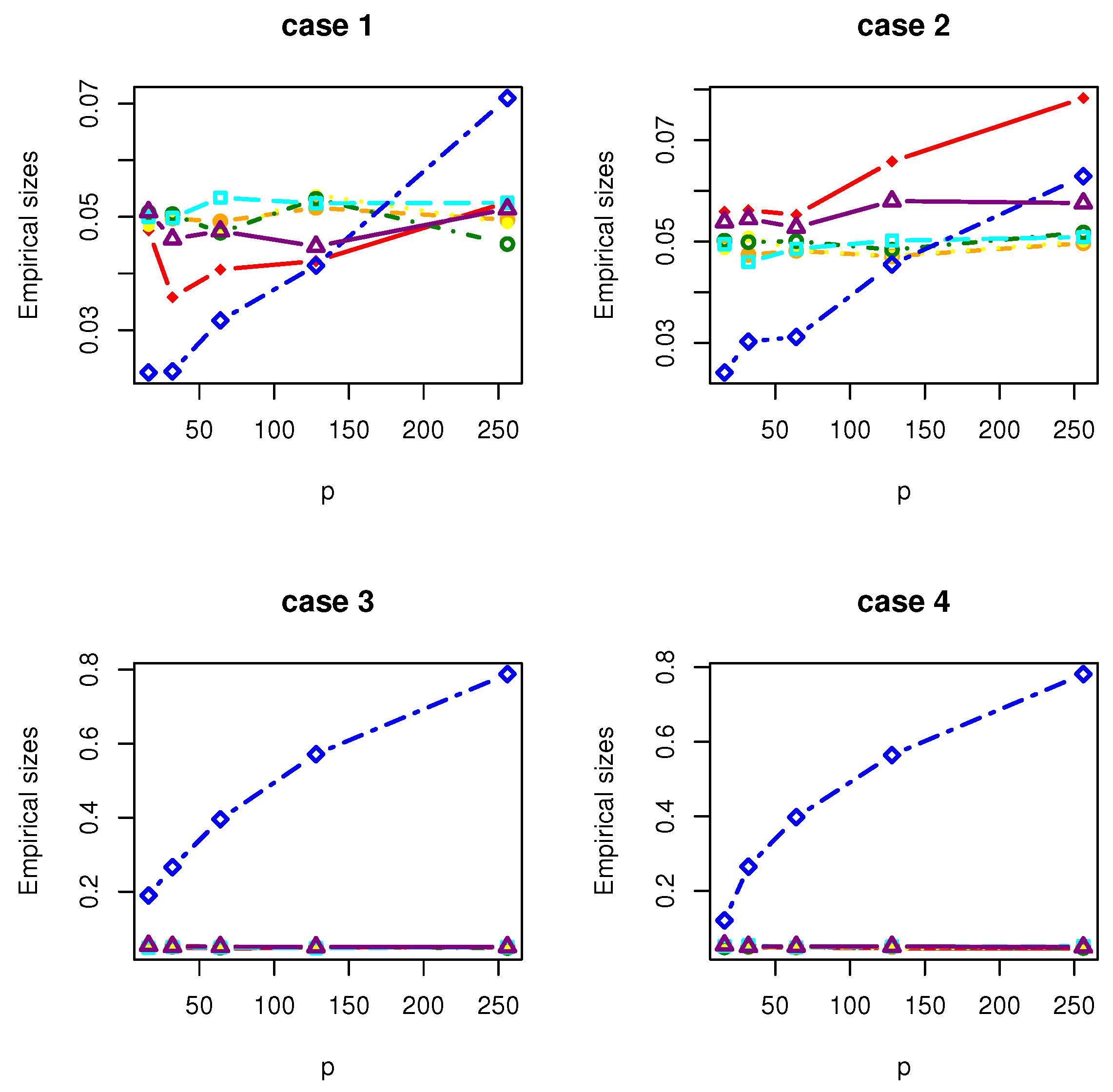
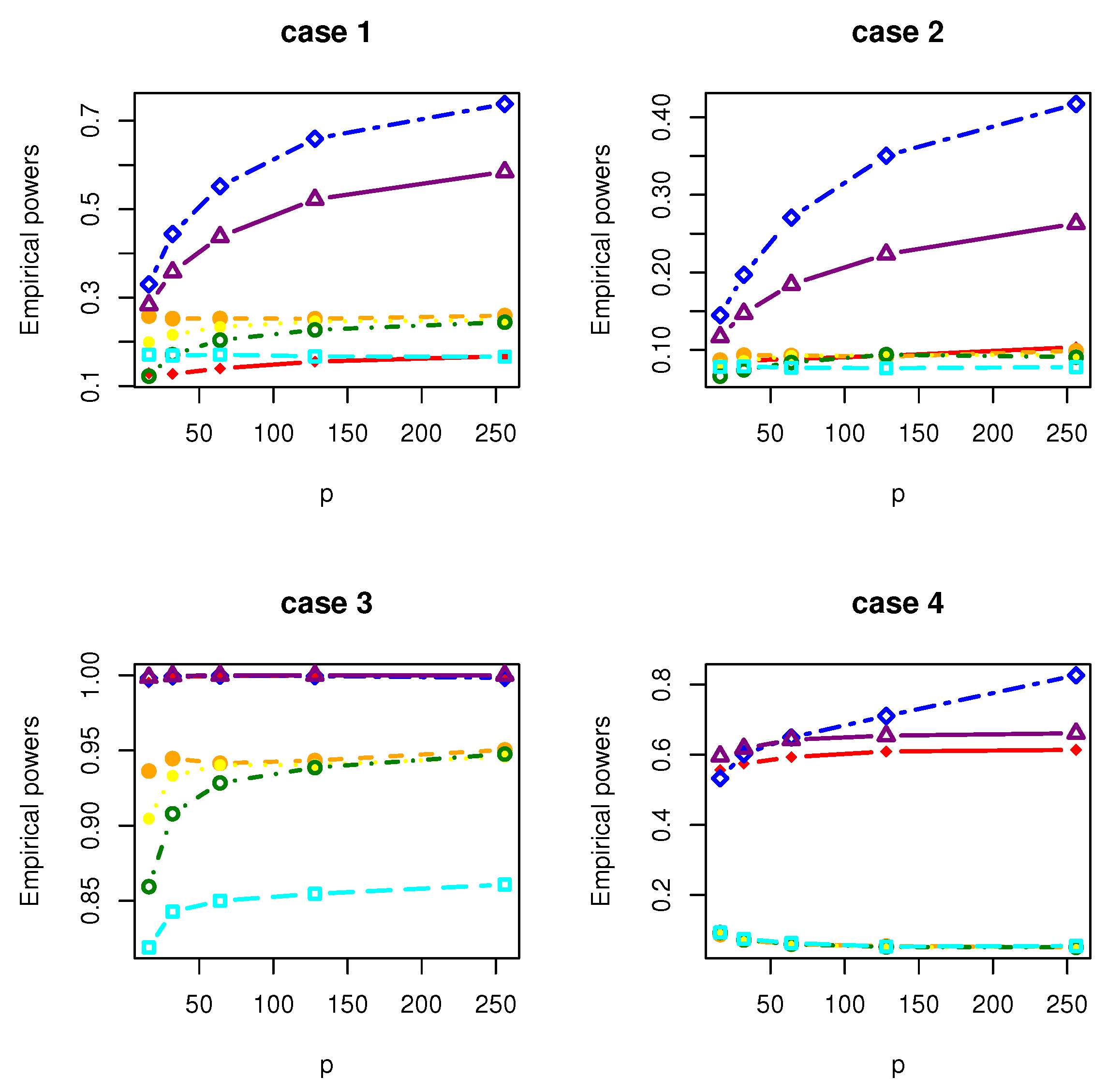
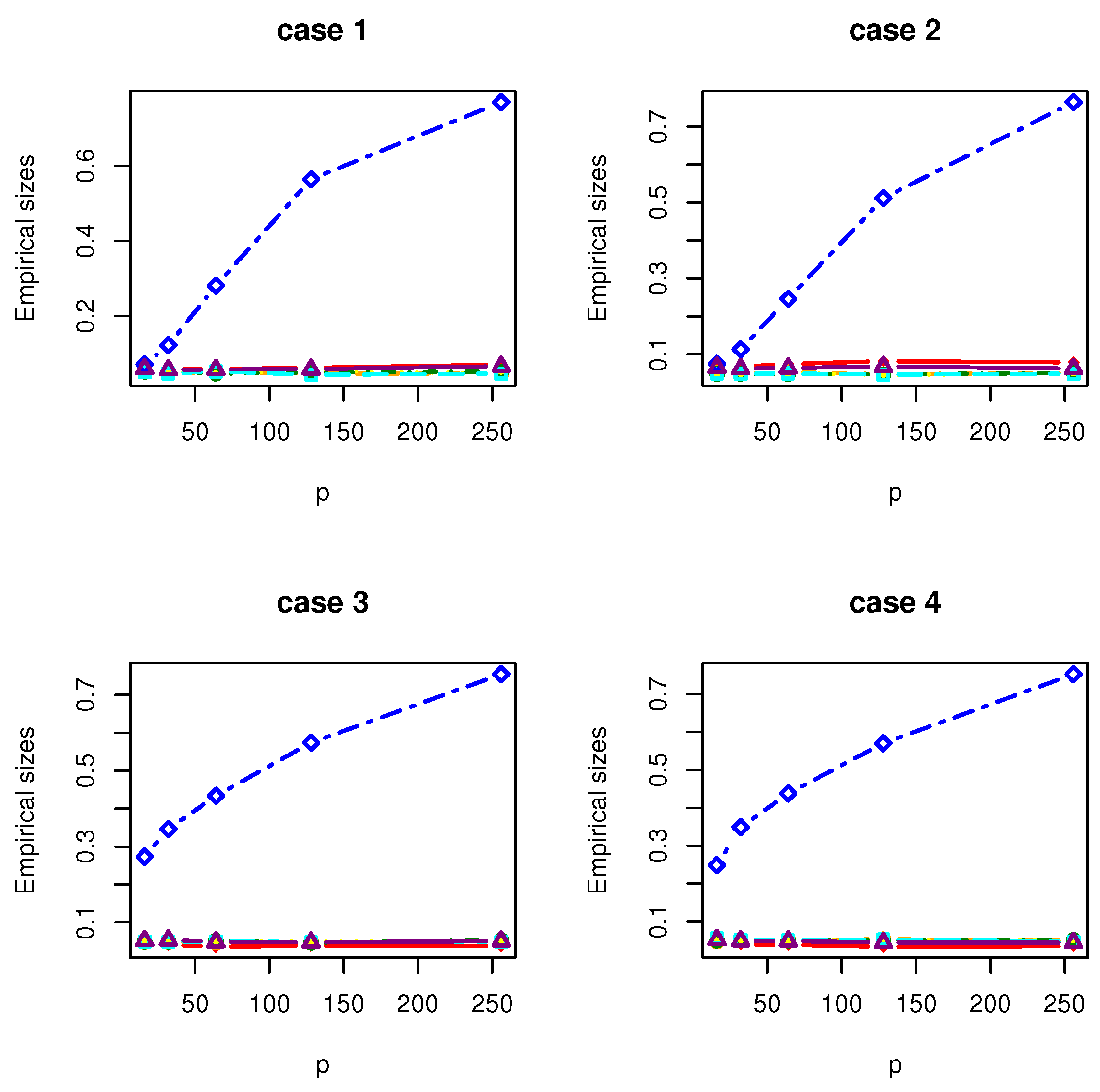
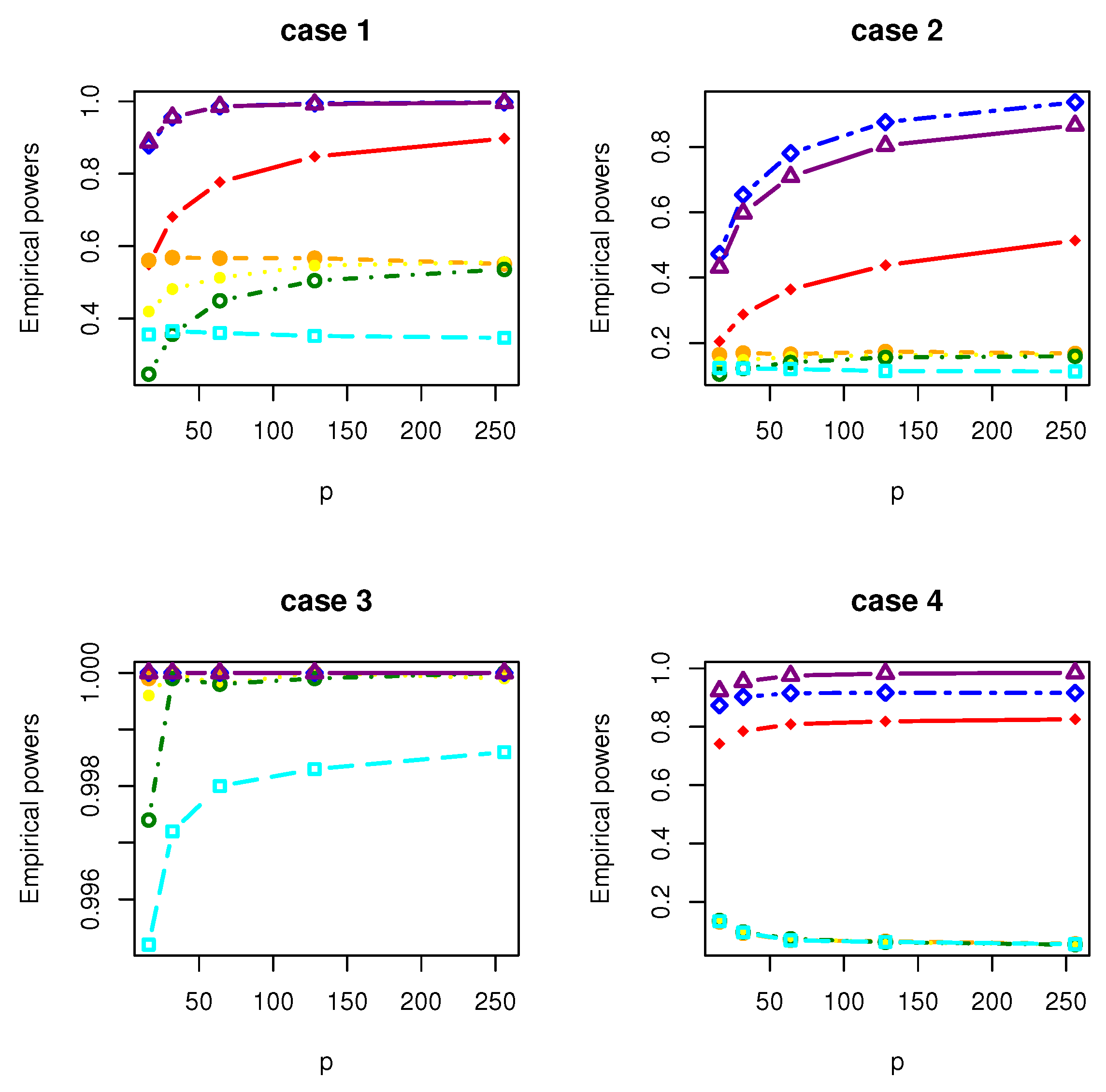
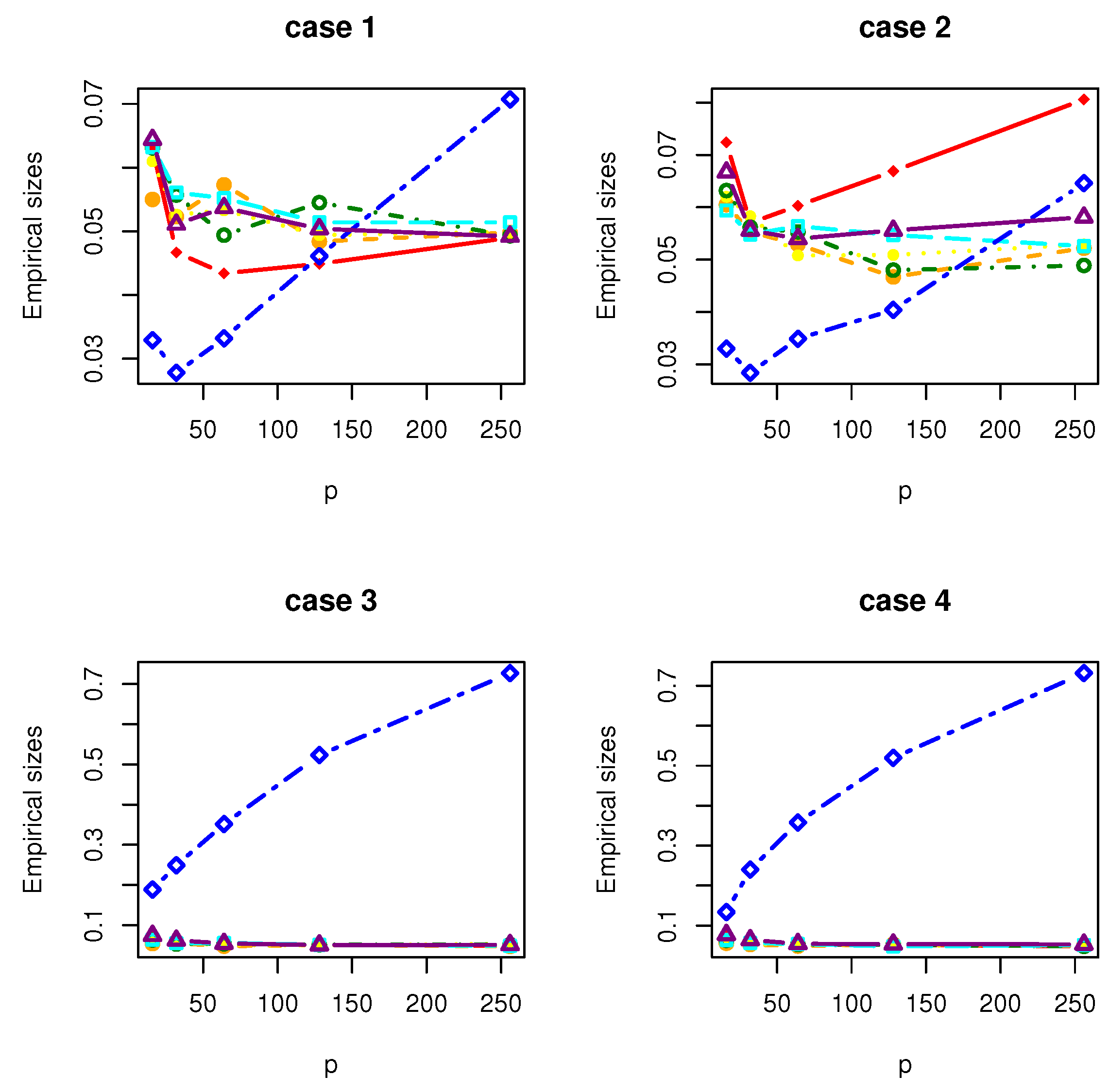
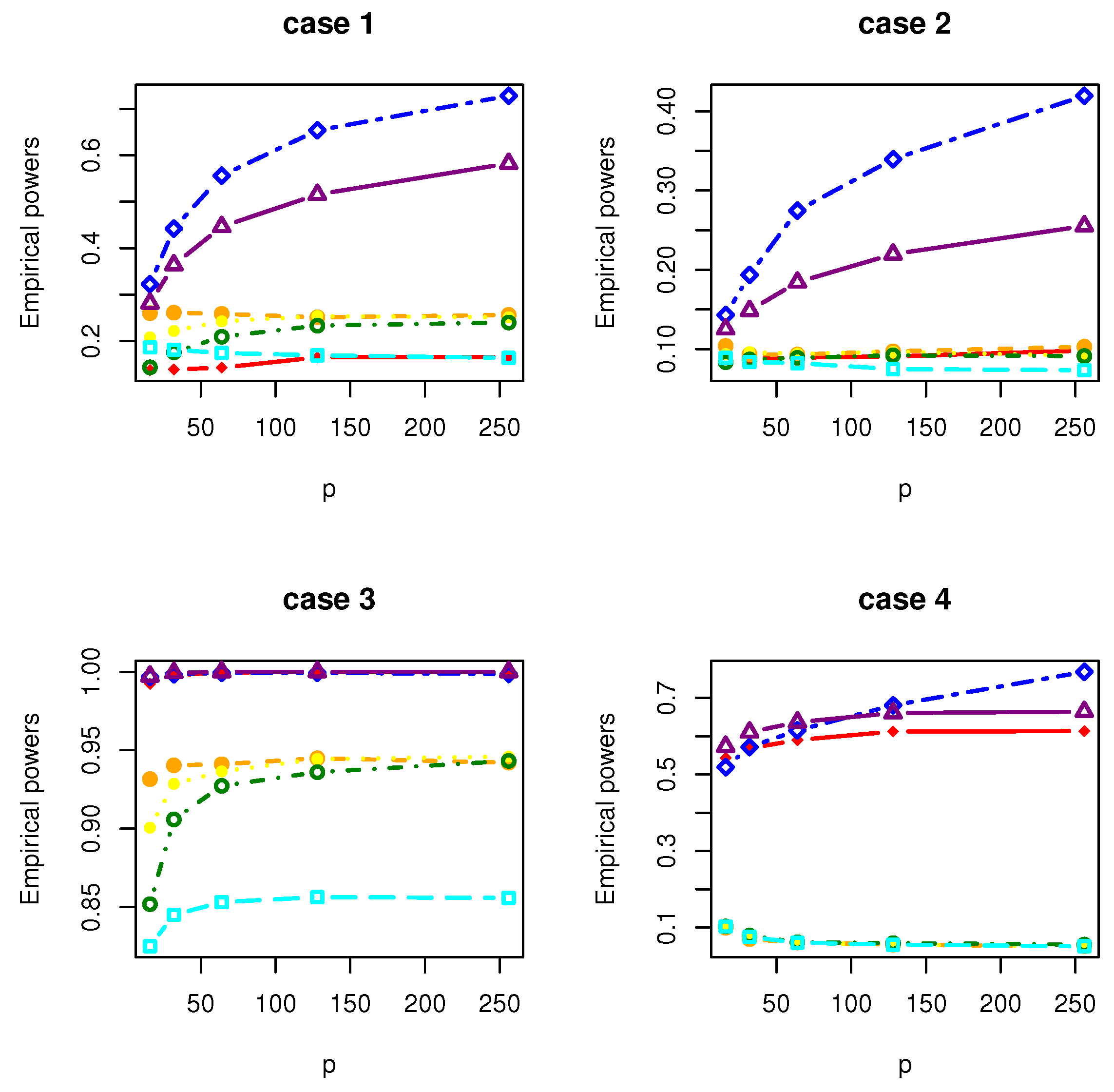
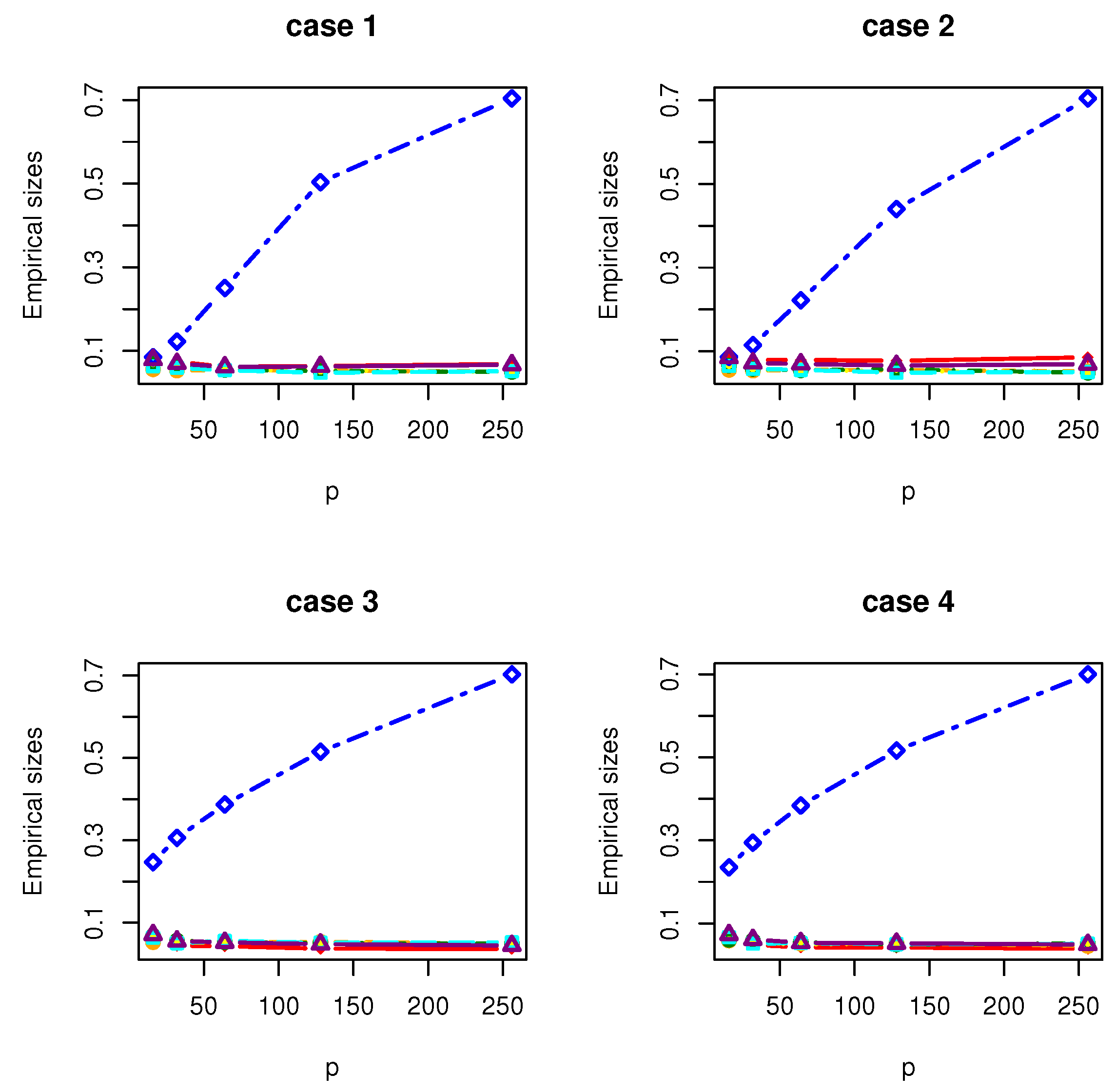
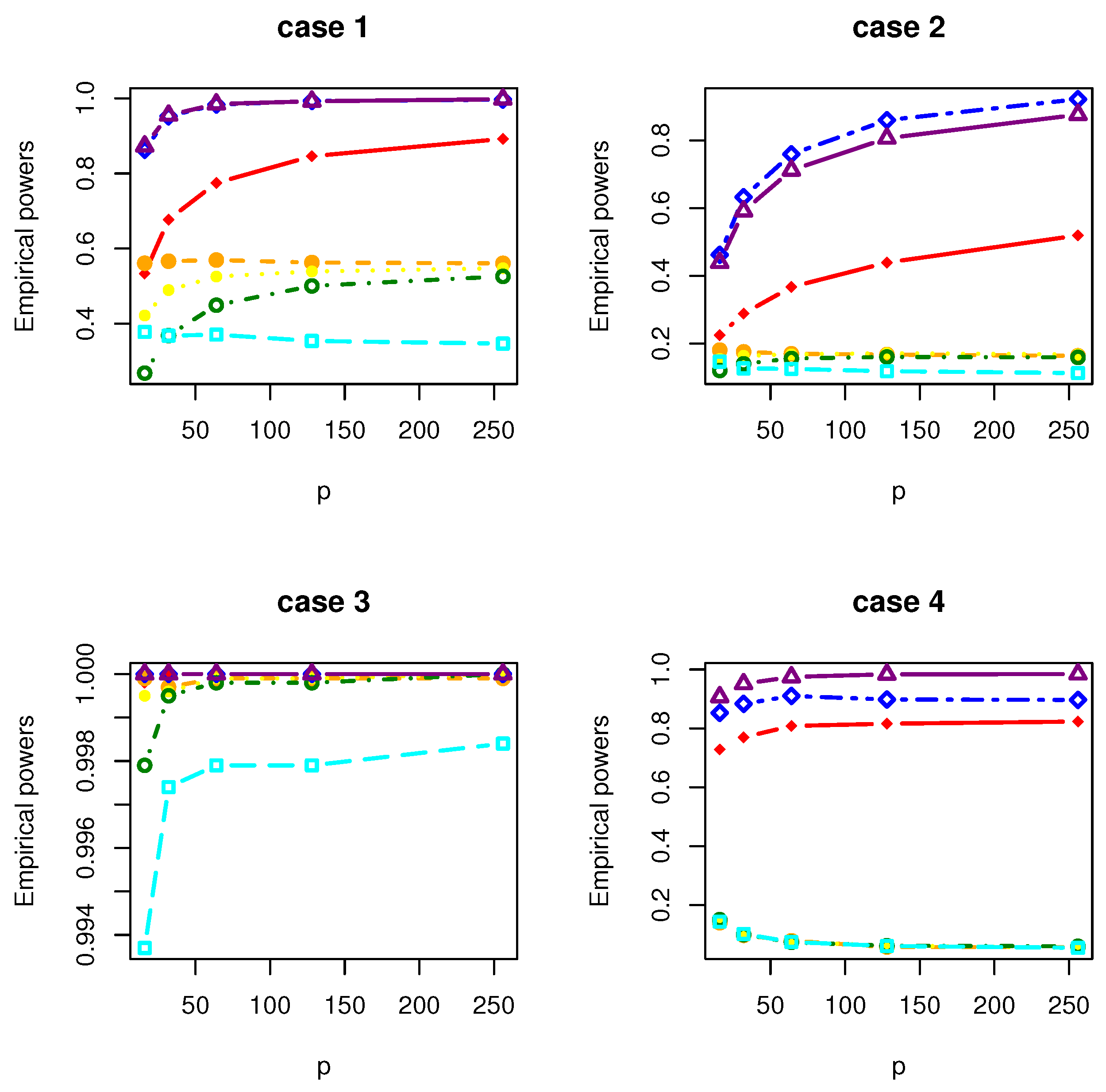
4. Simulation Studies

In this section, we compare our proposed test with four existing tests by simulation. The four competing tests are denoted by $T_{ZBHW}$, $T_{ZLGY}$ and $\rho L_k(y)$ from [11,13,14], respectively. Note that the authors used eight test statistics according to a different y in [14]. Here, we only make simulations for four test statistics to save space, namely $\rho L_k(y_i)$, $i=1,2,3$ and 4. We obtain that $z_{ijr}$s are independently generated from the standard normal distribution $N(0,1)$ and the centralized gamma distribution $Gamma(4,2)-2$, respectively, for $i=1,\dots ,k$, $j=1,\dots ,n_i$ and $r=1,\dots ,p$. We set $k=3$ and ${\mathsf{\Gamma }}_i={\Sigma }_i^{1/2}$ for i = 1, 2 and 3, where the covariance matrices are considered respectively in the following four cases:

• Case 1: $H_0:{\Sigma }_1={\Sigma }_2={\Sigma }_3=\mathsf{\Lambda }{\mathbf{U}}_0\mathsf{\Lambda }$, $H_1:{\Sigma }_i=\mathsf{\Lambda }{\mathbf{U}}_{i-1}\mathsf{\Lambda },i=1,2,3,$ where $\mathsf{\Lambda }=\mathrm{diag}({\lambda }_1,\cdots ,{\lambda }_p)$ with ${\lambda }_1,\cdots ,{\lambda }_p\stackrel{i.i.d.}{\sim }Unif(1,5)$ and ${\mathbf{U}}_{i-1}$ is a $p\times p$ matrix with the $(a,b)$th element being ${(-1)}^{a+b}{{\left(\frac{5-2^{i-1}}{6}\right)}^{|a-b|}}^{0.1}$.
• Case 2: $H_0:{\Sigma }_1={\Sigma }_2={\Sigma }_3=\mathsf{\Lambda }{\mathbf{U}}_0\mathsf{\Lambda }$, $H_1:{\Sigma }_i=\mathsf{\Lambda }{\mathbf{U}}_{i-1}\mathsf{\Lambda },i=1,2,3,$ where $\mathsf{\Lambda }=\mathrm{diag}({\lambda }_1,\cdots ,{\lambda }_p)$ with ${\lambda }_1,\cdots ,{\lambda }_p\stackrel{i.i.d.}{\sim }Unif(1,5)$ and ${\mathbf{U}}_{i-1}$ is a $p\times p$ matrix with the $(a,b)$th element being ${(-1)}^{a+b}{{\left(\frac{4-i}{5}\right)}^{|a-b|}}^{0.1}$.
• Case 3: $H_0:{\Sigma }_1={\Sigma }_2={\Sigma }_3={\mathsf{\Lambda }}_0$, $H_1:{\Sigma }_i={\Sigma }_{i-1},i=1,2,3,$ where ${\mathsf{\Lambda }}_0=\mathrm{diag}({\lambda }_1,\cdots ,{\lambda }_p)$ with ${\lambda }_1,\cdots ,{\lambda }_p\stackrel{i.i.d.}{\sim }Unif(1,5)$. ${\mathsf{\Lambda }}_1$ is a $p\times p$ symmetric matrix with the $(a,a)$th element being 1.01, the $(a,a+1)$th elements being 0.1 and the rest being 0; ${\mathsf{\Lambda }}_2$ is a $p\times p$ symmetric matrix with the $(a,a)$th element being 3, the $(a,a+1)$th elements being 2, the $(a,a+2)$th elements being 1 and the rest being 0.
• Case 4: $H_0:{\Sigma }_1={\Sigma }_2={\Sigma }_3=\mathrm{diag}({\omega }_1,\cdots ,{\omega }_p)$ where ${\omega }_1,\cdots ,{\omega }_p\stackrel{i.i.d.}{\sim }Unif(0.5,10)$, $H_1:{\Sigma }_1={\mathbf{U}}_i\mathsf{\Lambda }{\mathbf{U}}_i^{\mathrm{T}},i=1,2,3,$ where $\mathsf{\Lambda }=\mathrm{diag}({\lambda }_1,\cdots ,{\lambda }_p)$ with ${\lambda }_1,\cdots ,{\lambda }_p\stackrel{i.i.d.}{\sim }Gamma(4,0.5)$, ${\mathbf{U}}_i={({\mathbf{W}}_i^{\mathrm{T}}{\mathbf{W}}_i)}^{-1/2}{\mathbf{W}}_i^{\mathrm{T}}$ and ${\mathbf{W}}_i$ is a $p\times p$ matrix whose entries are independently generated from the normal distribution $N(0,i)$.

Without loss of generality, all the population means are chosen to be 0. The sample size and data dimension are respectively $n=45,95$ and $p=16,32,64,128,256$. Empirical sizes and powers are computed under the nominal level $\alpha =0.05$ with $10,000$ replications.

All the simulation results are reported in

Table 1. Empirical sizes and powers of seven tests under Case 1 and normal distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0476	0.0501	0.0484	0.0508	0.0500	0.0225	0.0509
n = 45	32	0.0358	0.0497	0.0507	0.0505	0.0498	0.0227	0.0461
	64	0.0407	0.0492	0.0471	0.0472	0.0534	0.0317	0.0475
	128	0.0422	0.0516	0.0539	0.0532	0.0524	0.0414	0.0448
	256	0.0526	0.0495	0.0489	0.0452	0.0525	0.0710	0.0514
n = 95	16	0.0633	0.0524	0.0535	0.0522	0.0512	0.0719	0.0601
	32	0.0584	0.0488	0.0537	0.0515	0.0479	0.1230	0.0576
	64	0.0595	0.0518	0.0499	0.0472	0.0534	0.2814	0.0582
	128	0.0628	0.0477	0.0556	0.0499	0.0445	0.5641	0.0594
	256	0.0710	0.0478	0.0477	0.0534	0.0474	0.7692	0.0669
Power	16	0.1291	0.2582	0.1991	0.1224	0.1710	0.3301	0.2837
n = 45	32	0.1273	0.2526	0.2160	0.1709	0.1691	0.4441	0.3582
	64	0.1398	0.2528	0.2337	0.2039	0.1710	0.5516	0.4377
	128	0.1552	0.2523	0.2462	0.2270	0.1671	0.6594	0.5222
	256	0.1676	0.2595	0.2490	0.2444	0.1665	0.7380	0.5847
n = 95	16	0.5490	0.5605	0.4198	0.2466	0.3561	0.8783	0.8870
	32	0.6810	0.5684	0.4816	0.3566	0.3653	0.9559	0.9563
	64	0.7771	0.5669	0.5128	0.4494	0.3603	0.9861	0.9863
	128	0.8476	0.5670	0.5465	0.5048	0.3521	0.9946	0.9924
	256	0.8974	0.5509	0.5560	0.5359	0.3469	0.9974	0.9966

,

Table 2. Empirical sizes and powers of seven tests under Case 1 and Gamma distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0630	0.0550	0.0610	0.0631	0.0632	0.0329	0.0644
n = 45	32	0.0467	0.0523	0.0526	0.0557	0.0561	0.0278	0.0511
	64	0.0434	0.0573	0.0533	0.0494	0.0552	0.0332	0.0537
	128	0.0449	0.0484	0.0494	0.0545	0.0514	0.0461	0.0504
	256	0.0490	0.0498	0.0499	0.0493	0.0514	0.0707	0.0492
n = 95	16	0.0822	0.0560	0.0657	0.0699	0.0631	0.0851	0.0789
	32	0.0741	0.0531	0.0610	0.0629	0.0594	0.1224	0.0698
	64	0.0619	0.0544	0.0535	0.0545	0.0540	0.2505	0.0617
	128	0.0638	0.0524	0.0540	0.0517	0.0477	0.5037	0.0627
	256	0.0686	0.0508	0.0493	0.0498	0.0517	0.7041	0.0668
Power	16	0.1375	0.2602	0.2085	0.1437	0.1866	0.3225	0.2815
n = 45	32	0.1392	0.2613	0.2221	0.1760	0.1815	0.4421	0.3639
	64	0.1429	0.2587	0.2427	0.2094	0.1746	0.5561	0.4463
	128	0.1652	0.2513	0.2538	0.2334	0.1695	0.6536	0.5155
	256	0.1658	0.2565	0.2514	0.2401	0.1639	0.7279	0.5824
n = 95	16	0.5336	0.5610	0.4219	0.2685	0.3780	0.8629	0.8730
	32	0.6772	0.5664	0.4895	0.3683	0.3681	0.9523	0.9551
	64	0.7749	0.5695	0.5256	0.4493	0.3709	0.9834	0.9849
	128	0.8460	0.5628	0.5391	0.5005	0.3540	0.9929	0.9923
	256	0.8922	0.5608	0.5477	0.5260	0.3470	0.9966	0.9978

,

Table 3. Empirical sizes and powers of seven tests in Case 2 and normal distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0559	0.0501	0.0485	0.0502	0.0495	0.0242	0.0539
n = 45	32	0.0562	0.0474	0.0510	0.0499	0.0460	0.0303	0.0545
	64	0.0553	0.0482	0.0483	0.0501	0.0486	0.0312	0.0528
	128	0.0658	0.0471	0.0472	0.0484	0.0502	0.0455	0.0580
	256	0.0783	0.0497	0.0500	0.0518	0.0509	0.0629	0.0576
n = 95	16	0.0724	0.0511	0.0499	0.0484	0.0494	0.0750	0.0656
	32	0.0675	0.0492	0.0497	0.0486	0.0491	0.1132	0.0624
	64	0.0747	0.0532	0.0505	0.0483	0.0498	0.2468	0.0641
	128	0.0821	0.0479	0.0465	0.0473	0.0468	0.5114	0.0680
	256	0.0790	0.0514	0.0488	0.0514	0.0492	0.7645	0.0625
Power	16	0.0838	0.0869	0.0804	0.0662	0.0781	0.1447	0.1170
n = 45	32	0.0862	0.0933	0.0858	0.0743	0.0788	0.1969	0.1471
	64	0.0883	0.0928	0.0923	0.0838	0.0771	0.2706	0.1844
	128	0.0924	0.0915	0.0933	0.0940	0.0765	0.3505	0.2235
	256	0.1035	0.0989	0.0937	0.0907	0.0779	0.4172	0.2631
n = 95	16	0.2053	0.1640	0.1405	0.1048	0.1238	0.4722	0.4314
	32	0.2877	0.1693	0.1482	0.1220	0.1225	0.6532	0.5974
	64	0.3641	0.1659	0.1569	0.1405	0.1203	0.7805	0.7090
	128	0.4380	0.1740	0.1632	0.1559	0.1143	0.8758	0.8046
	256	0.5136	0.1680	0.1651	0.1595	0.1129	0.9364	0.8659

,

Table 4. Empirical sizes and powers of seven tests in Case 2 and Gamma distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0724	0.0605	0.0620	0.0632	0.0594	0.0330	0.0667
n = 45	32	0.0570	0.0553	0.0583	0.0562	0.0548	0.0284	0.0556
	64	0.0603	0.0529	0.0508	0.0553	0.0564	0.0349	0.0540
	128	0.0669	0.0467	0.0509	0.0480	0.0547	0.0404	0.0556
	256	0.0806	0.0522	0.0529	0.0489	0.0526	0.0646	0.0581
n = 95	16	0.0886	0.0556	0.0653	0.0660	0.0649	0.0865	0.0844
	32	0.0792	0.0539	0.0554	0.0580	0.0580	0.1146	0.0718
	64	0.0794	0.0557	0.0550	0.0545	0.0555	0.2220	0.0696
	128	0.0774	0.0549	0.0524	0.0570	0.0490	0.4400	0.0658
	256	0.0855	0.0523	0.0504	0.0486	0.0505	0.7047	0.0691
Power	16	0.0976	0.1041	0.0937	0.0834	0.0889	0.1430	0.1253
n = 45	32	0.0882	0.0934	0.0961	0.0870	0.0839	0.1936	0.1486
	64	0.0893	0.0931	0.0942	0.0890	0.0823	0.2746	0.1844
	128	0.0908	0.0972	0.0965	0.0922	0.0748	0.3395	0.2197
	256	0.0982	0.1029	0.0918	0.0913	0.0734	0.4195	0.2553
n = 95	16	0.2248	0.1807	0.1547	0.1205	0.1464	0.4621	0.4391
	32	0.2886	0.1757	0.1641	0.1403	0.1267	0.6325	0.5913
	64	0.3671	0.1699	0.1681	0.1560	0.1253	0.7592	0.7119
	128	0.4392	0.1675	0.1715	0.1605	0.1184	0.8598	0.8064
	256	0.5194	0.1641	0.1682	0.1593	0.1129	0.9217	0.8760

,

Table 5. Empirical sizes and powers of seven tests in Case 3 and normal distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0530	0.0517	0.0478	0.0495	0.0484	0.1897	0.0545
n = 45	32	0.0491	0.0539	0.0513	0.0514	0.0503	0.2663	0.0517
	64	0.0463	0.0521	0.0498	0.0487	0.0491	0.3956	0.0513
	128	0.0490	0.0481	0.0503	0.0496	0.0475	0.5715	0.0508
	256	0.0492	0.0512	0.0491	0.0478	0.0501	0.7879	0.0511
n = 95	16	0.0455	0.0489	0.0516	0.0493	0.0496	0.2732	0.0520
	32	0.0407	0.0484	0.0508	0.0493	0.0493	0.3462	0.0535
	64	0.0357	0.0471	0.0501	0.0516	0.0496	0.4335	0.0483
	128	0.0386	0.0483	0.0496	0.0465	0.0483	0.5736	0.0476
	256	0.0381	0.0497	0.0501	0.0532	0.0494	0.7541	0.0506
Power	16	0.9951	0.9363	0.9047	0.8594	0.8190	0.9981	0.9986
n = 45	32	0.9988	0.9446	0.9331	0.9079	0.8428	0.9993	0.9997
	64	0.9996	0.9415	0.9403	0.9284	0.8500	0.9997	0.9999
	128	0.9998	0.9433	0.9404	0.9386	0.8547	0.9994	1.0000
	256	0.9999	0.9504	0.9458	0.9476	0.8608	0.9983	1.0000
n = 95	16	1.0000	0.9999	0.9996	0.9974	0.9952	1.0000	1.0000
	32	1.0000	1.0000	1.0000	0.9999	0.9972	1.0000	1.0000
	64	1.0000	1.0000	0.9998	0.9998	0.9980	1.0000	1.0000
	128	1.0000	1.0000	1.0000	0.9999	0.9983	1.0000	1.0000
	256	1.0000	1.0000	0.9999	1.0000	0.9986	1.0000	1.0000

,

Table 6. Empirical sizes and powers of seven tests in Case 3 and Gamma distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0743	0.0540	0.0587	0.0633	0.0637	0.1885	0.0740
n = 45	32	0.0599	0.0553	0.0544	0.0530	0.0551	0.2490	0.0622
	64	0.0532	0.0476	0.0512	0.0536	0.0557	0.3514	0.0544
	128	0.0506	0.0508	0.0494	0.0511	0.0511	0.5232	0.0503
	256	0.0493	0.0471	0.0533	0.0516	0.0487	0.7273	0.0510
n = 95	16	0.0619	0.0526	0.0614	0.0679	0.0635	0.2469	0.0709
	32	0.0441	0.0513	0.0565	0.0562	0.0501	0.3059	0.0553
	64	0.0430	0.0526	0.0537	0.0524	0.0558	0.3869	0.0521
	128	0.0368	0.0534	0.0500	0.0506	0.0511	0.5153	0.0478
	256	0.0365	0.0494	0.0463	0.0489	0.0523	0.7029	0.0445
Power	16	0.9924	0.9316	0.9007	0.8519	0.8251	0.9968	0.9972
n = 45	32	0.9978	0.9404	0.9286	0.9059	0.8451	0.9984	0.9994
	64	0.9996	0.9411	0.9365	0.9273	0.8532	0.9994	1.0000
	128	0.9999	0.9449	0.9444	0.9360	0.8564	0.9993	1.0000
	256	1.0000	0.9421	0.9459	0.9432	0.8559	0.9986	1.0000
n = 95	16	0.9998	0.9999	0.9995	0.9979	0.9937	1.0000	1.0000
	32	1.0000	0.9997	0.9996	0.9995	0.9974	1.0000	1.0000
	64	1.0000	0.9999	0.9999	0.9998	0.9979	1.0000	1.0000
	128	1.0000	0.9999	0.9999	0.9998	0.9979	1.0000	1.0000
	256	1.0000	0.9999	1.0000	1.0000	0.9984	1.0000	1.0000

,

Table 7. Empirical sizes and powers of seven tests in Case 4 and normal distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0517	0.0490	0.0514	0.0484	0.0522	0.1209	0.0548
n = 45	32	0.0481	0.0496	0.0506	0.0507	0.0541	0.2649	0.0507
	64	0.0487	0.0480	0.0495	0.0493	0.0487	0.3975	0.0512
	128	0.0459	0.0496	0.0459	0.0515	0.0510	0.5640	0.0511
	256	0.0455	0.0504	0.0483	0.0469	0.0520	0.7811	0.0493
n = 95	16	0.0450	0.0470	0.0522	0.0489	0.0550	0.2487	0.0513
	32	0.0388	0.0504	0.0511	0.0514	0.0502	0.3486	0.0484
	64	0.0381	0.0504	0.0503	0.0488	0.0502	0.4379	0.0480
	128	0.0329	0.0530	0.0511	0.0487	0.0523	0.5704	0.0441
	256	0.0348	0.0498	0.0508	0.0514	0.0462	0.7527	0.0438
Power	16	0.5566	0.0872	0.0922	0.0930	0.0933	0.5331	0.5965
n = 45	32	0.5749	0.0710	0.0698	0.0724	0.0749	0.6018	0.6180
	64	0.5935	0.0596	0.0591	0.0601	0.0633	0.6495	0.6432
	128	0.6095	0.0547	0.0507	0.0522	0.0532	0.7108	0.6546
	256	0.6142	0.0516	0.0527	0.0508	0.0552	0.8269	0.6615
n = 95	16	0.7418	0.1311	0.1361	0.1359	0.1338	0.8735	0.9232
	32	0.7846	0.0923	0.0916	0.0966	0.0953	0.9024	0.9548
	64	0.8089	0.0680	0.0738	0.0735	0.0679	0.9151	0.9753
	128	0.8184	0.0650	0.0607	0.0615	0.0626	0.9166	0.9824
	256	0.8258	0.0560	0.0548	0.0533	0.0549	0.9161	0.9849

and

Table 8. Empirical sizes and powers of seven tests in Case 4 and Gamma distribution.

	p	${\mathit{T}}_{\mathit{Z}\mathit{B}\mathit{H}\mathit{W}}$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_1)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_2)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_3)$	$\mathit{\rho }{\mathit{L}}_{\mathit{k}}({\mathit{y}}_4)$	${\mathit{T}}_{\mathit{Z}\mathit{L}\mathit{G}\mathit{Y}}$	$\widehat{\mathit{T}}$
Size	16	0.0776	0.0559	0.0589	0.0632	0.0641	0.1338	0.0773
n = 45	32	0.0634	0.0526	0.0534	0.0584	0.0567	0.2403	0.0642
	64	0.0532	0.0488	0.0527	0.0527	0.0540	0.3579	0.0546
	128	0.0520	0.0533	0.0500	0.0517	0.0480	0.5195	0.0534
	256	0.0483	0.0495	0.0506	0.0482	0.0512	0.7316	0.0530
n = 95	16	0.0674	0.0586	0.0605	0.0605	0.0668	0.2348	0.0729
	32	0.0482	0.0528	0.0530	0.0586	0.0514	0.2945	0.0613
	64	0.0425	0.0511	0.0491	0.0551	0.0525	0.3839	0.0533
	128	0.0420	0.0523	0.0522	0.0491	0.0499	0.5164	0.0520
	256	0.0388	0.0456	0.0488	0.0519	0.0511	0.6998	0.0490
Power	16	0.5435	0.0993	0.1039	0.1028	0.1026	0.5191	0.5735
n = 45	32	0.5685	0.0697	0.0741	0.0787	0.0756	0.5717	0.6106
	64	0.5901	0.0606	0.0601	0.0615	0.0602	0.6153	0.6368
	128	0.6124	0.0551	0.0552	0.0592	0.0551	0.6810	0.6606
	256	0.6133	0.0511	0.0512	0.0554	0.0510	0.7685	0.6645
n = 95	16	0.7283	0.1401	0.1468	0.1506	0.1438	0.8526	0.9070
	32	0.7695	0.0973	0.0997	0.1000	0.1019	0.8832	0.9513
	64	0.8081	0.0790	0.0745	0.0738	0.0749	0.9100	0.9746
	128	0.8158	0.0577	0.0627	0.0621	0.0611	0.8980	0.9835
	256	0.8231	0.0570	0.0545	0.0601	0.0550	0.8966	0.9843

and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figures provide intuitive observation, and tables show the simulated values. First, Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 show that the empirical sizes of the test $T_{ZLGY}$ are seriously inflated, especially when $n=95$ in all cases of simulation. For example, just as what is presented in Table 1, the empirical sizes of $T_{ZLGY}$ are respectively 0.0719, 0.1230, 0.2814, 0.5641 and 0.7692 when $n=95$ and $p=$16, 32, 64, 128, 256. Thus, $T_{ZLGY}$ cannot control the nominal size reasonably. Second, Table 1, Table 2, Table 3 and Table 4 imply that the empirical sizes of tests $\rho L_k(y_i)$, $i=1,2,3,4$, are closer to a given size than those of $T_{ZBHW}$ and $\widehat{T}$, while $T_{ZBHW}$ and $\widehat{T}$ respectively obtains about $7\%$ and $6\%$ of empirical sizes as $n=95$. Thus, $\rho L_k(y_i)$ outperforms $T_{ZBHW}$ and $\widehat{T}$ in size under Cases 1 and 2 when data are generated from standard normal distribution and gamma distribution. At the same time, our new test $\widehat{T}$ has higher empirical powers than $T_{ZBHW}$ and $\rho L_k(y_i)$. For example, as $n=95$ and $p=256$, the empirical powers of $\widehat{T}$, $T_{ZBHW}$ and $\rho L_k(y_i)$, $i=1,2,3,4$, are respectively 0.9966, 0.8974, 0.5509, 0.5560, 0.5359 and 0.3469 under Case 1 and normal distribution. Finally, Table 5, Table 6, Table 7 and Table 8 show that the six tests $T_{ZBHW}$, $\rho L_k(y_i)$, $i=1,2,3,4$, and $\widehat{T}$ have similar empirical sizes, which are all close to the nominal size. On the other hand, the six tests still have similar empirical powers under Case 3. However, under Case 4, the empirical powers of $\rho L_k(y_i)$ are extremely deflated, which are no more than 0.1600. Moreover, the empirical powers of our new test are respectively 0.04 and 0.16 more than those of $T_{ZBHW}$ when $n=45$ and 95.

In summary, our proposed test $\widehat{T}$ can control a given size reasonably and has greater powers than competing tests in all cases of our simulation whenever samples are from the normal model or the non-normal model. However, $T_{ZLGY}$ fails in controlling a given size. $\rho L_k(y_i)$, $i=1,2,3,4$, seriously deflates the empirical powers in some cases of our simulations. $T_{ZBHW}$ can slightly inflate the empirical size in some cases of our simulation.

5. Real Data Analysis

This problem will arise from the analysis of gene expression data. It was shown in [3] that many genes have different variances in gene expressions between disease states. For example, the dataset of the breast cancer of patient is classified into three groups based on their gene expression signatures: well-differentiated tumors ($n_1$ = 29), moderately differentiated tumors ($n_2$ = 136), and poorly differentiated and undifferentiated tumors ($n_3$ = 35). The breast cancer microarray data sets, including patient outcome information, were downloaded from the National Center for Biotechnology Information (NCBI) Gene Expression Omnibus (GEO) data repository and are accessible through GEO Series accession now. GSE11121 (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE11121, accessed on 26 June 2022). This dataset includes 200 samples, which is far fewer than data dimension 22,283. For this gene dataset, we are interested in checking whether the covariance matrices of the three groups are the same or not. It is noted that an important assumption for multivariate analysis of variance is that of equal covariance matrices in different groups. Therefore, testing the equality of several covariance matrices is necessary.

Since we used the raw breast cancer dataset (22,283 features), there are many features and no preprocessing. First, we preprocessed and filtered the data, including conventional preprocessing such as background adjustment, normalization, and summarization. Then, we performed feature screening, filtered out features whose coefficient of variation is out of range (0.25, 1.0) and controlled at least 5 samples to exceed 1320 count values. Finally, a data set of 200 samples and 1280 features was screened out, and then a high-dimensional hypothesis test problem was performed on the screened data set.

Compared with other methods and our method, the observed test statistics (p value) of the screened breast cancer dataset are $T_{ZBHW}(1.92,2.75\times {10}^{-2})$, $\rho L_k(y_1)(0.46,0.79)$, $\rho L_k(y_2)(0.4,0.82)$, $\rho L_k(y_3)(0.91,0.63)$, $\rho L_k(y_4)(0.27,0.69)$, $T_{ZLGY}(2.47,6.62\times {10}^{-3})$ and $\widehat{T}(1.96,2.52\times {10}^{-2})$. The p-values of the comparison method statistics $T_{ZBHW}$, $T_{ZLGY}$ and our method’s statistic are significant.

6. Concluding Remarks

In this paper, we propose a new test on the homogeneity of k-sample covariance matrices in a high-dimensional setting. The asymptotic properties of the proposed test are derived under some regularity conditions. We compare our new test with six competing tests by simulation. Numerical results show that our proposed test can control the nominal size reasonably and that it has the highest empirical powers in our simulation scenario. However, just as what we showed in Section 2, the technique condition (C2) may not hold again when covariance matrices have some spiked eigenvalues. How to obtain the theoretical results of test statistics under spiked covariance matrices structure is an interested problem. We leave this problem as a future research direction.