Application of the Generalized Bessel Function to Two-Color Phase-of-the-Phase Spectroscopy
Abstract
:1. Introduction
2. Theoretical Method
3. Derivation of RPC and PP
3.1. First Order RPC and PP
3.2. Second Order RPC and PP
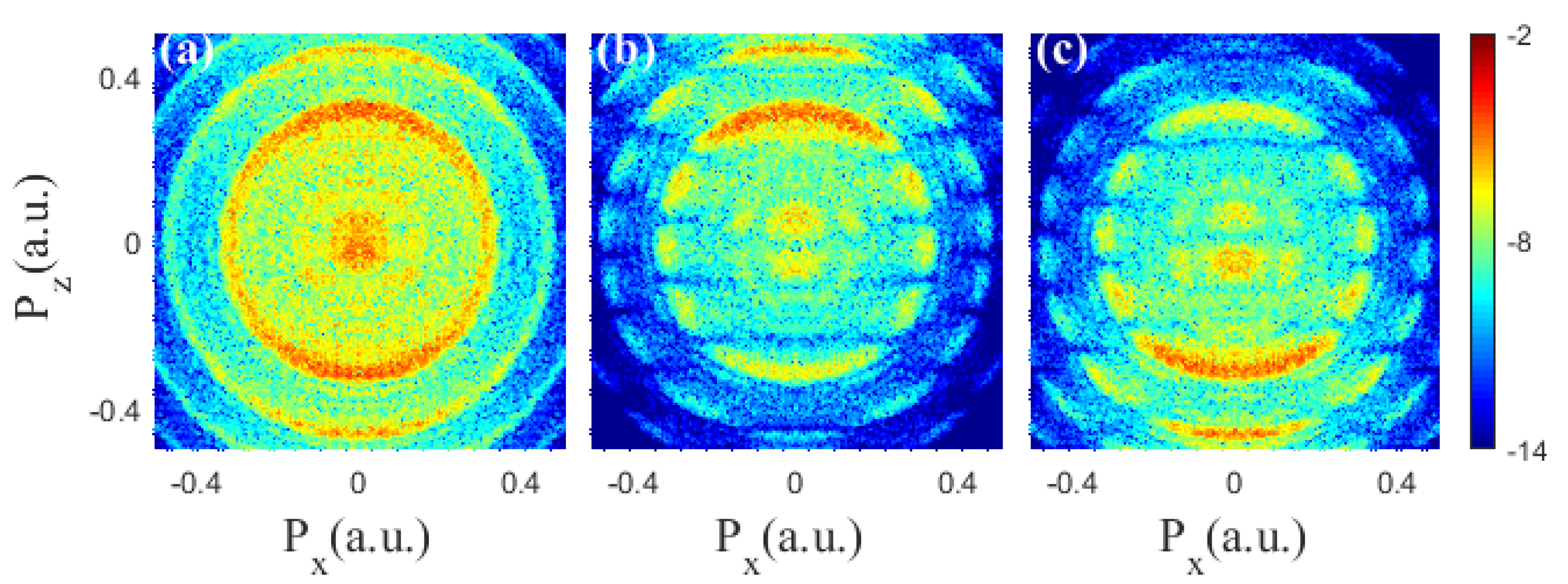
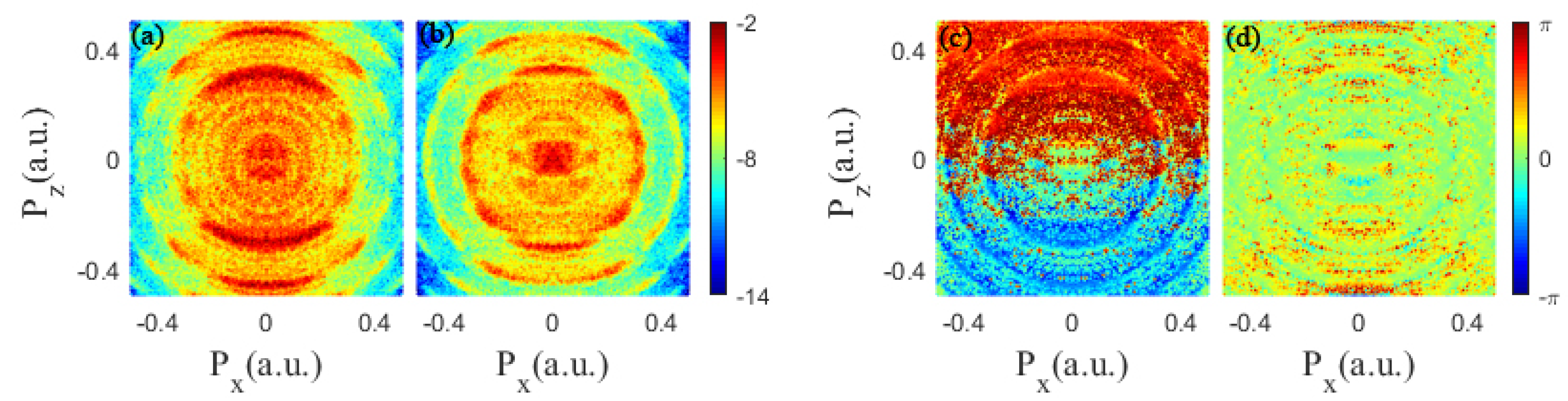
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. General Properties of the Generalized Bessel Function Jn (u,v)
References
- Huppert, M.; Jordan, I.; Baykusheva, D.; Conta, A.V.; Worner, H.J. Attosecond Delays in Molecular Photoionization. Phys. Rev. Lett. 2016, 117, 093001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locher, R.; Castiglioni, L.; Lucchini, M.; Greif, M.; Gallmann, L.; Osterwalder, J.; Hengsberger, M.; Keller, U. Energy-dependent photoemission delays from noble metal surfaces by attosecond interferometry. Optica 2015, 2, 405–410. [Google Scholar] [CrossRef] [Green Version]
- Schultze, M.; Fiess, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T. Delay in photoemission. Science 2010, 328, 1658–1662. [Google Scholar] [CrossRef]
- Muller, H.G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B 2014, 74, s17–s21. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Auge, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef]
- Itatani, J.; Quere, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond streak camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef] [Green Version]
- Zuo, R.X.; Trautmann, A.; Wang, G.; Hannes, W.R.; Yang, S.; Song, X.H.; Meier, T.; Ciappina, M.; Duc, H.T.; Yang, W.F. Mapping band structures with neighboring-atom-collisions in solid high harmonic generation. Ultrafast Sci. 2021, 2021, 9861923. [Google Scholar] [CrossRef]
- Zhang, C.J.; Yang, W.F.; Song, X.H.; Xu, Z.Z. Carrier-envelope phase dependence of the spectra of reflected few-cycle laser pulses in the presence of a static electric field. Phys. Rev. A 2009, 79, 043823. [Google Scholar]
- Yang, W.F.; Gong, S.Q.; Niu, Y.P.; Jin, S.Q.; Xu, Z.Z. Enhancement of four-wave mixing induced by interacting dark resonances. J. Phys. B At. Mol. Opt. 2005, 38, 2657. [Google Scholar]
- Song, X.H.; Gong, S.Q.; Yang, W.F.; Jin, S.Q.; Feng, X.L.; Xu, Z.Z. Coherent control of spectra effects with chirped femtosecond laser pulse. Opt. Commun. 2004, 236, 151. [Google Scholar]
- Eicke, N.; Brennecke, S.; Lein, M. Attosecond-Scale Streaking Methods for Strong-Field Ionization by Tailored Fields. Phys. Rev. Lett. 2020, 124, 043202. [Google Scholar] [CrossRef]
- Klunder, K.; Dahlstrom, J.M.; Gisselbrecht, M.; Fordell, T.; Swoboda, M.; Guenot, D.; Johnsson, P.; Caillat, J.; Mauritsson, J.; Maquet, A. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 2011, 106, 143002. [Google Scholar] [CrossRef]
- Eckle, P.; Pfeiffer, A.N.; Cirelli, C.; Staudte, A.; Dorner, R.; Muller, H.G.; Buttiker, M.; Keller, U. Attosecond lonization and Tunneling Delay Time Measurements in Helium. Science 2008, 322, 1525–1529. [Google Scholar] [CrossRef]
- Kraus, P.M.; Tolstikhin, O.I.; Baykusheva, D.; Rupenyan, A.; Schneider, J.; Bisgaard, C.Z.; Morishita, T.; Jensen, F.; Madsen, L.B.; Wörner, H.J. Observation of laser-induced electronic structure in oriented polyatomic molecules. Nat. Commun. 2015, 6, 7039. [Google Scholar] [CrossRef] [Green Version]
- Zherebtsov, S.; Süßmann, F.; Peltz, C.; Plenge, J.; Betsch, K.J.; Znakovskaya, I.; Alnaser, A.S.; Johnson, N.G.; Kübel, M.; Horn, A.; et al. Carrier–envelope phase-tagged imaging of the controlled electron acceleration from SiO2 nanospheres in intense few-cycle laser fields. New J. Phys. 2012, 14, 075010. [Google Scholar] [CrossRef]
- Neppl, S.; Ernstorfer, R.; Cavalieri, A.L.; Lemell, C.; Wachter, G.; Magerl, E.; Bothschafter, E.M.; Jobst, M.; Hofstetter, M.; Kleineberg, U.; et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 2015, 517, 342–346. [Google Scholar] [CrossRef] [Green Version]
- Würzler, D.; Eicke, N.; Möller, M.; Seipt, D.; Sayler, A.M.; Fritzsche, S.; Lein, M.; Paulus, G.G. Velocity map imaging of scattering dynamics in orthogonal two-color fields. J. Phys. B At. Opt. Phys. 2018, 5, 015001. [Google Scholar] [CrossRef]
- Zipp, L.J.; Natan, A.; Bucksbaum, P.H. Probing electron delays in above-threshold ionization. Optica 2014, 1, 361–364. [Google Scholar] [CrossRef]
- Natan, A.; Zipp, L.J.; Bucksbaum, P.H. Disentangling Ionization Processes by Two-Color Phase Contrast Strong Field Photoelectron Spectroscopy. In Proceedings of the International Conference on Ultrafast Phenomena (© OSA, 2016; p. UM2B.6.), Santa Fe, NM, USA, 17–22 July 2016. [Google Scholar]
- Skruszewicz, S.; Tiggesbaumker, J.; Meiwes-Broer, K.H.; Arbeiter, M.; Fennel, T.; Bauer, D. Two-Color Strong-Field Photoelectron Spectroscopy and the Phase of the Phase. Phys. Rev. Lett. 2015, 115, 043001. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Zhou, Y.; Xu, S.; Ke, Q.; Liang, J.; Ma, X.; Cao, W.; Li, M.; Zhang, Q.; Lu, P. Analyzing the electron trajectories in strong-field tunneling ionization with the phase-of-the-phase spectroscopy. Opt. Express 2021, 29, 37927–37944. [Google Scholar] [CrossRef]
- Tulsky, V.A.; Krebs, B.; Tiggesbäumker, J.; Bauer, D. Revealing laser-coherent electron features using phase-of-the-phase spectroscopy. J. Phys. B At. Mol. Opt. 2020, 53, 074001. [Google Scholar] [CrossRef] [Green Version]
- Henkel, J.; Lein, M. Analysis of electron trajectories with two-color strong-field ionization. Phys. Rev. A 2015, 92, 013422. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Zhou, Y.; He, M.; Chen, Y.; Ke, Q.; Liang, J.; Zhu, X.; Li, M.; Lu, P. Determination of the Ionization Time Using Attosecond Photoelectron Interferometry. Phys. Rev. Lett. 2018, 121, 253203. [Google Scholar] [CrossRef] [PubMed]
- Braß, J.; Milbradt, R.; Villalba-Chávez, S.; Paulus, G.G.; Müller, C. Two-color phase-of-the-phase spectroscopy applied to nonperturbative electron-positron pair production in strong oscillating electric fields. Phys. Rev. A 2020, 101, 043401. [Google Scholar] [CrossRef] [Green Version]
- Tulsky, V.A.; Almajid, M.A.; Bauer, D. Two-color phase-of-the-phase spectroscopy with circularly polarized laser pulses. Phys. Rev. A 2018, 98, 053433. [Google Scholar] [CrossRef] [Green Version]
- Würzler, D.; Skruszewicz, S.; Sayler, A.M.; Zille, D.; Möller, M.; Wustelt, P.; Zhang, Y.; Tiggesbäumker, J.; Paulus, G.G. Accurate retrieval of ionization times by means of the phase-of-the-phase spectroscopy, and its limits. Phys. Rev. A 2020, 101, 033416. [Google Scholar] [CrossRef]
- Tan, J.; Li, Y.; Zhou, Y.; He, M.; Chen, Y.; Li, M.; Lu, P. Identifying the contributions of multiple-returning recollision orbits in strong-field above-threshold ionization. Opt. Quantum Electron. 2018, 50, 57. [Google Scholar] [CrossRef]
- Gong, X.C.; Lin, C.; He, F.; Song, Q.Y.; Lin, K.; Ji, Q.Y.; Zhang, W.B.; Ma, J.Y.; Lu, P.F.; Liu, Y.Q.; et al. Energy-resolved ultrashort delays of photoelectron emission clocked by orthogonal two-color laser fields. Phys. Rev. Lett. 2017, 118, 143203. [Google Scholar] [CrossRef] [Green Version]
- Song, X.H.; Shi, G.L.; Zhang, G.J.; Xu, J.W.; Lin, C.; Chen, J.; Yang, W.F. Attosecond time delay of retrapped resonant ionization. Phys. Rev. Lett. 2018, 121, 103201. [Google Scholar] [CrossRef]
- Krebs, B.S.; Tulsky, V.; Kazak, L.; Zabel, M.; Bauer, D.; Tiggesbaumker, J. Phase-of-the-Phase Electron Momentum Spectroscopy on Single Metal Atoms in Helium Nanodroplets. J. Phys. Chem. Lett. 2022, 13, 1526–1532. [Google Scholar] [CrossRef]
- Liu, X.W.; Zhang, G.J.; Li, J.; Shi, G.L.; Zhou, M.Y.; Huang, B.Q.; Tang, Y.J.; Song, X.H.; Yang, W.F. Deep Learning for Feynman’s Path Integral in Strong-Field Time-Dependent Dynamics. Phys. Rev. Lett. 2020, 124, 113202. [Google Scholar] [CrossRef] [Green Version]
- Huo, X.Q.; Yang, W.F.; Dong, W.H.; Jin, F.C.; Liu, X.W.; Zhang, H.D.; Song, X.H. Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics. Chin. Phys. B 2022, 31, 033101. [Google Scholar] [CrossRef]
- Almajid, M.A.; Zabel, M.; Skruszewicz, S.; Tiggesbäumker, J.; Bauer, D. Two-color phase-of-the-phase spectroscopy in the multiphoton regime. J. Phys. B At. Mol. Opt. 2017, 50, 194001. [Google Scholar] [CrossRef]
- Bauer, D.; Milošević, D.B.; Becker, W. On the validity of the strong field approximation and simple man’s theory. J. Mod. Opt. 2006, 53, 135–147. [Google Scholar] [CrossRef]
- Bauer, D.; Milošević, D.B.; Becker, W. Strong-field approximation for intense-laser–atom processes: The choice of gauge. Phys. Rev. A 2005, 72, 023415. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Paulus, G.G.; Bauer, D.; Becker, W. Above-threshold ionization by few-cycle pulses. J. Phys. B At. Mol. Opt. Phys. 2006, 39, R203–R262. [Google Scholar] [CrossRef]
- Popruzhenko, S.V. Keldysh theory of strong field ionization: History, applications, difficulties and perspectives. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 204001. [Google Scholar] [CrossRef]
- Feng, Y.D.; Li, M.; Luo, S.Q.; Liu, K.; Du, B.J.; Zhou, Y.M.; Lu, P.X. Semiclassical analysis of photoelectron interference in a synthesized two-color laser pulse. Phys. Rev. A 2019, 100, 063411. [Google Scholar] [CrossRef] [Green Version]
- Bauer, D.; Koval, P. Qprop: A Schrödinger-solver for intense laser–atom interaction. Comput. Commun. 2006, 174, 396–421. [Google Scholar] [CrossRef] [Green Version]
- Cormier, E.; Lambropoulos, P. Above-threshold ionization spectrum of hydrogen using B-splinefunctions. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 77–91. [Google Scholar] [CrossRef]
- Mosert, V.; Bauer, D. Photoelectron spectra with Qprop and t-SURFF. Comput. Physics Commun. 2016, 207, 452–463. [Google Scholar] [CrossRef] [Green Version]
- Jašarević, A.; Hasović, E.; Kopold, R.; Becker, W.; Milošević, D.B. Application of the saddle-point method to strong-laser-field ionization. J. Phys. A Math. Theor. 2020, 53, 125201. [Google Scholar] [CrossRef]
- Bauer, J. Comment on ‘Generalized Bessel functions in tunnelling ionization’. J. Phys. A Math. Gen. 2005, 38, 521–525. [Google Scholar] [CrossRef]
- Reiss, H.R.; Krainov, V.P. Generalized Bessel functions in tunnelling ionization. J. Phys. A Math. Gen. 2003, 36, 5575–5585. [Google Scholar] [CrossRef]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. A 1980, 22, 1786–1813. [Google Scholar] [CrossRef]
- Reiss, H.R.; Krainov, V.P. Further ‘comment on ‘Generalized Bessel functions in tunnelling ionization”. J. Phys. A Math. Gen. 2005, 38, 527–529. [Google Scholar] [CrossRef]
- Vanne, Y.V.; Saenz, A. Quasistatic limit of the strong-field approximation describing atoms and molecules in intense laser fields. Phys. Rev. A 2007, 75, 063403. [Google Scholar] [CrossRef] [Green Version]
- Jin, F.C.; Tian, Y.Y.; Chen, J.; Yang, Y.J.; Liu, X.J.; Yan, Z.C.; Wang, B.B. Nonsequential double ionization of helium in IR+XUV two-color laser fields: Collision-ionization process. Phys. Rev. A 2016, 93, 043417. [Google Scholar] [CrossRef]
- Jin, F.C.; Yang, H.H.; Zhang, H.D.; Wang, B.B.; Yang, W.F. Influence of polarization directions of the IR+XUV two-color laser fields on angle-resolved photoelectron energy spectrum. Opt. Express 2021, 29, 10726–10736. [Google Scholar] [CrossRef] [PubMed]
- Long, S.; Becker, W.; McIver, J.K. Model calculations of polarization-dependent two-color high-harmonic generation. Phys. Rev. A 1995, 52, 3. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F.; McIver, J.K. Electron-atom ionizing collisions in the presence of a bichromatic laser field. Phys. Rev. A 1997, 56, 5. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. S-matrix theory of above-threshold ionization in a bichromatic laser field. J. Phys. B At. Mol. Opt. 1999, 32, 1585–1596. [Google Scholar] [CrossRef]
- Pazdzersky, V.A.; Koval’, A.V. Angular photoelectron spectra for atom ionization in an intense two-colour laser field. J. Phys. B At. Mol. Opt. 2005, 38, 3945–3952. [Google Scholar] [CrossRef]
- Al-Jarrah, A.; Dempsey, K.M.; Glasser, M.L. Generalized series of Bessel functions. J. Comput. Appl. Math. 2002, 143, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Cesarano, C.; Assante, D. A note on Generalized Bessel Functions. Int. J. Math. Model. Methods Appl. Sci. 2013, 7, 625–629. [Google Scholar]
- Dattoli, G.; Chiccoli, C.; Lorenzutta, S.; Maino, G.; Torre, A. Generalized Bessel Functions and Generalized Hermite Polynomials. J. Math. Anal. Appl. 1993, 178, 509–516. [Google Scholar] [CrossRef] [Green Version]
- Dattoli, G.; Giannessi, L.; Mezi, L.; Torre, A. Theory of Generalized Bessel Functions. Nuovo C. B 1990, 105, 327–348. [Google Scholar] [CrossRef]
- Hu, X.; Wang, H.; Guo, D.S. Phased Bessel functions. Can. J. Phys. 2008, 86, 863–870. [Google Scholar] [CrossRef]
- Korsch, H.J.; Klumpp, A.; Witthaut, D. On two-dimensional Bessel functions. J. Phys. A Math. Gen. 2006, 39, 14947–14964. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, X.; Yang, W.; Jin, F.; Ben, S.; Song, X. Application of the Generalized Bessel Function to Two-Color Phase-of-the-Phase Spectroscopy. Mathematics 2022, 10, 4642. https://doi.org/10.3390/math10244642
Huo X, Yang W, Jin F, Ben S, Song X. Application of the Generalized Bessel Function to Two-Color Phase-of-the-Phase Spectroscopy. Mathematics. 2022; 10(24):4642. https://doi.org/10.3390/math10244642
Chicago/Turabian StyleHuo, Xunqin, Weifeng Yang, Facheng Jin, Shuai Ben, and Xiaohong Song. 2022. "Application of the Generalized Bessel Function to Two-Color Phase-of-the-Phase Spectroscopy" Mathematics 10, no. 24: 4642. https://doi.org/10.3390/math10244642




