A Malware Attack Enabled an Online Energy Strategy for Dynamic Wireless EVs within Transportation Systems
Abstract
1. Introduction
- We analyzed the energy consumption of EVs using on a traffic flow-based online dynamic energy model and developed it by WSNs to control the traffic flow within a transportation system.
- We modeled a malware attack and implemented it into the WSN-based EVs with the aim of infecting the wireless sensor nodes and also proposing an effective offense–defense game strategy to deal with that.
- We presented a UT-based uncertainty method to model the high-risk energy consumption of the EVs considering the varied density rates of the traffic flow.
2. The Traffic Flow Density-Based Online Dynamic Model of the Transportation System
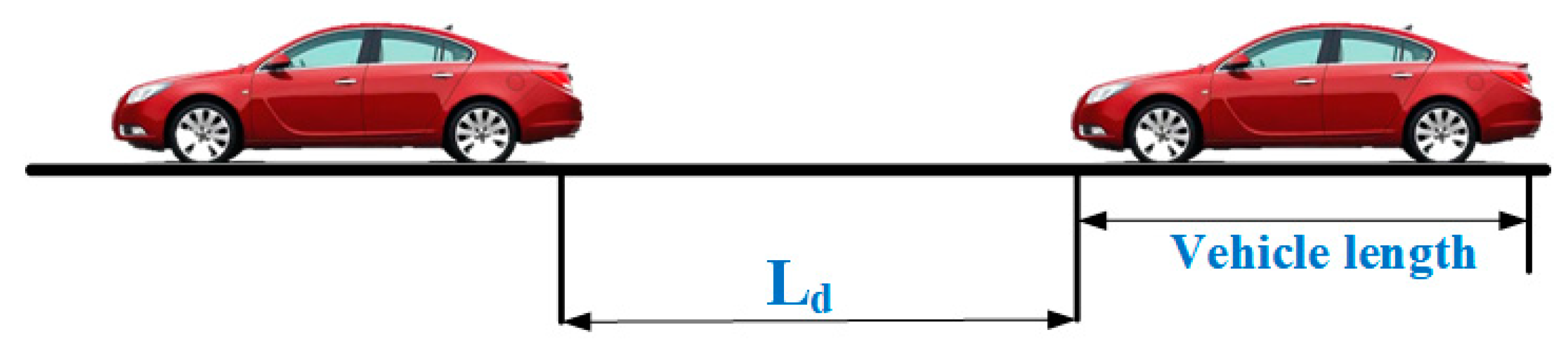
2.1. Definition of the Traffic Flow Model
2.2. The Proposed Online Dynamic Energy Management for TSs
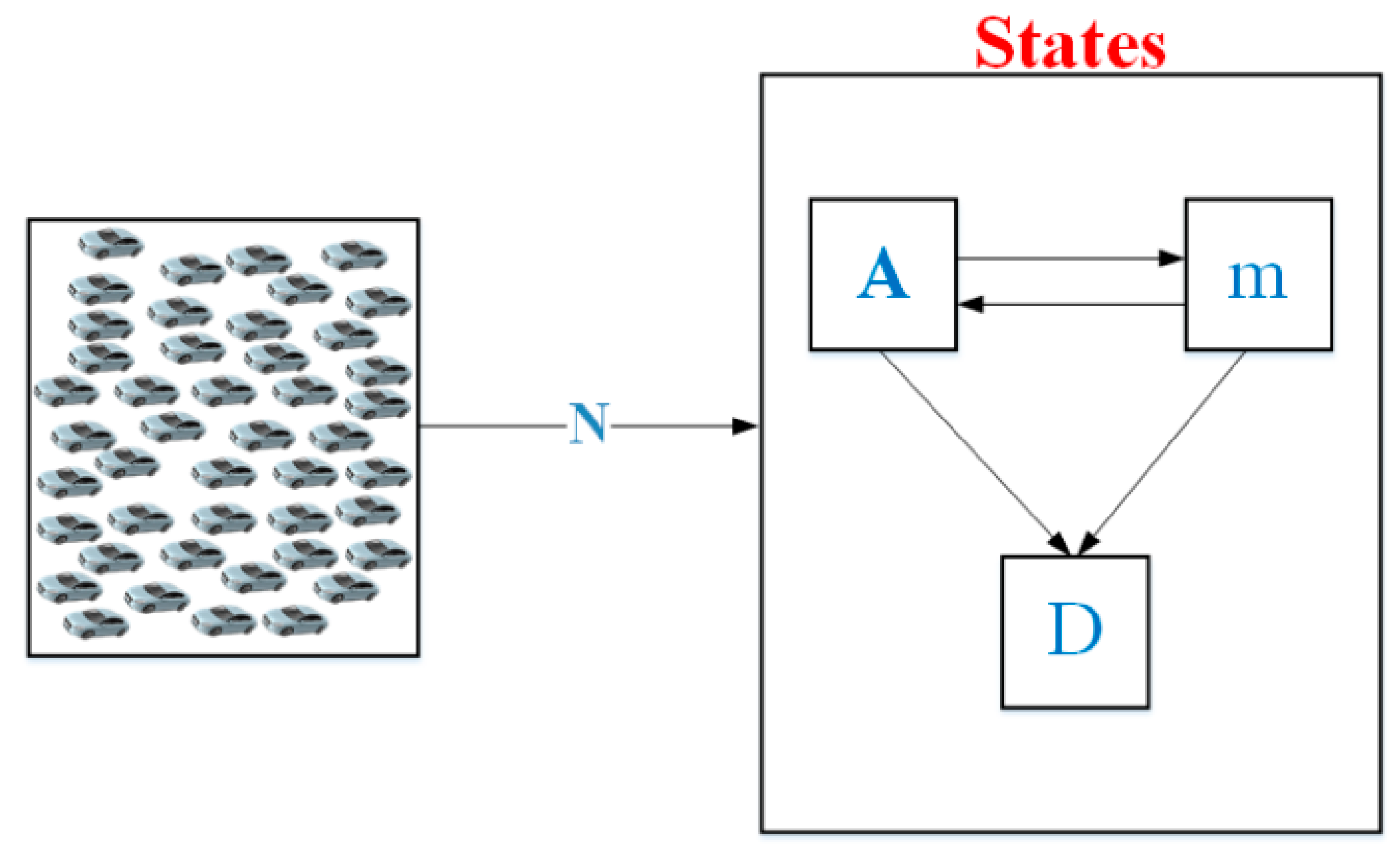
3. The Malware Attack Analysis in the Transportation System
3.1. Malware Attack Model
3.2. The Malware Attack-Based Offense–Defense Strategy
4. UT-Based Uncertainty Model
5. Emulation and Evaluation
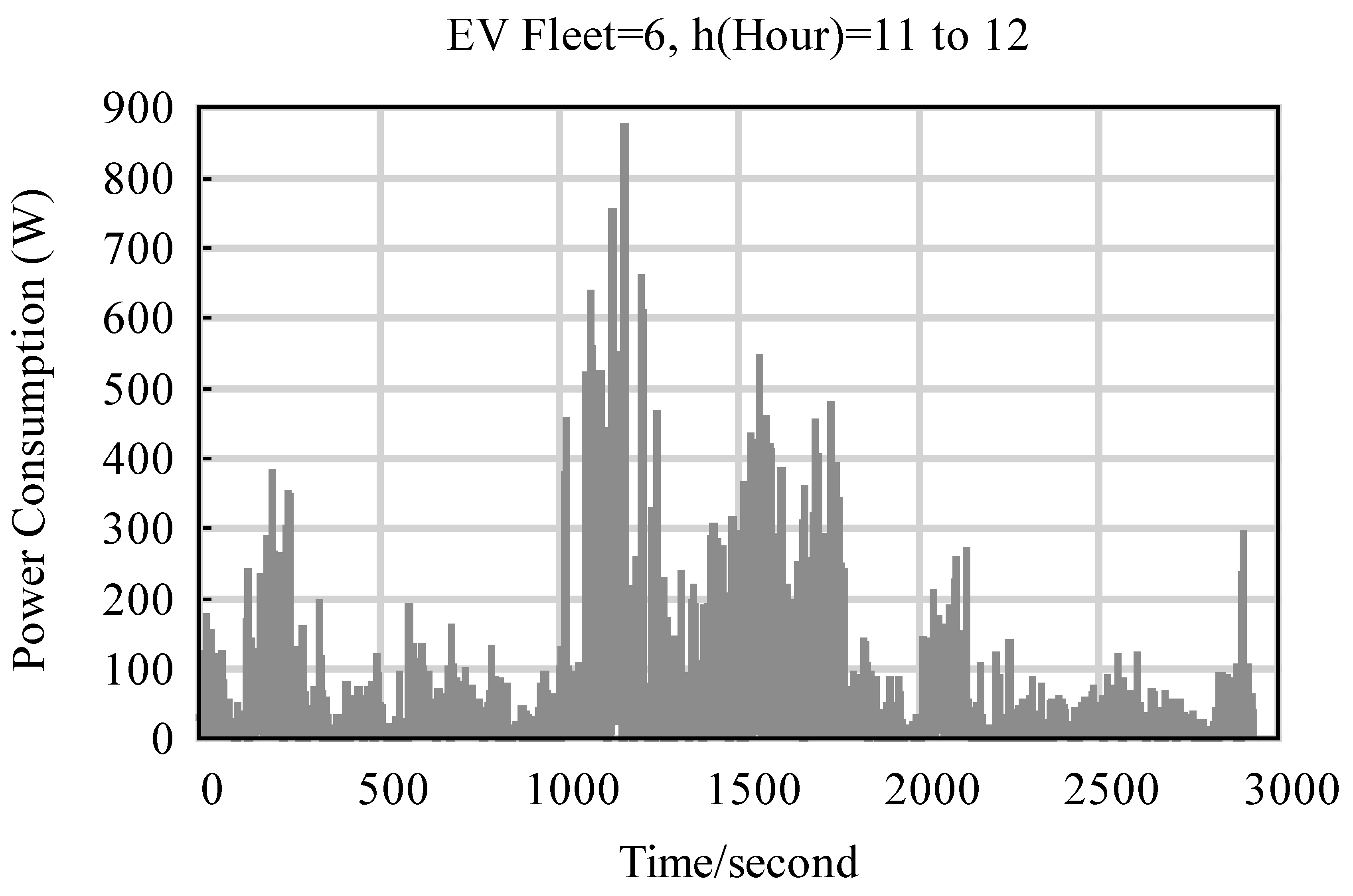
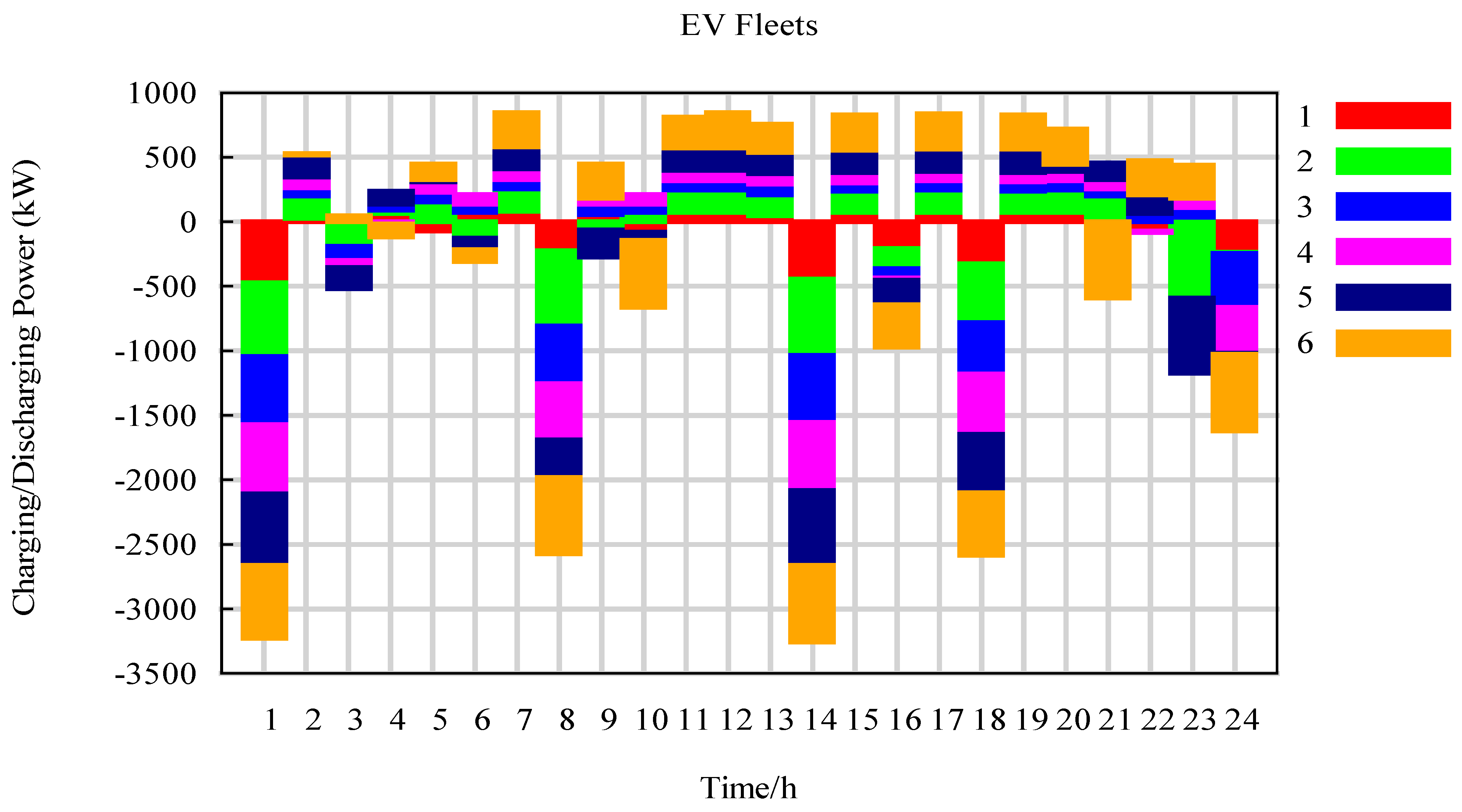
5.1. The Numerical and Dynamic Simulation of TSs
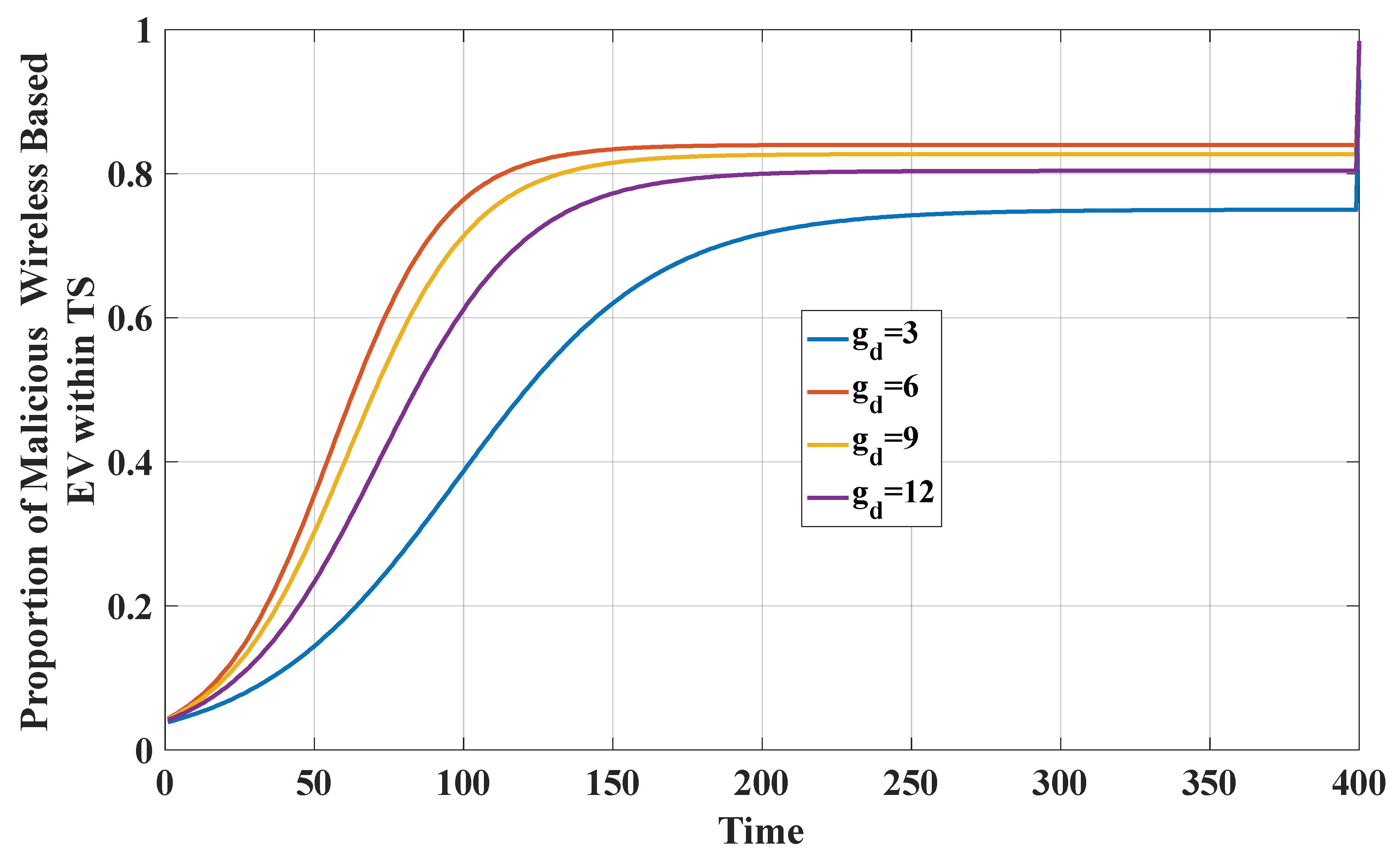
5.2. Analyzing Malware Model and Offense–Defense Strategy
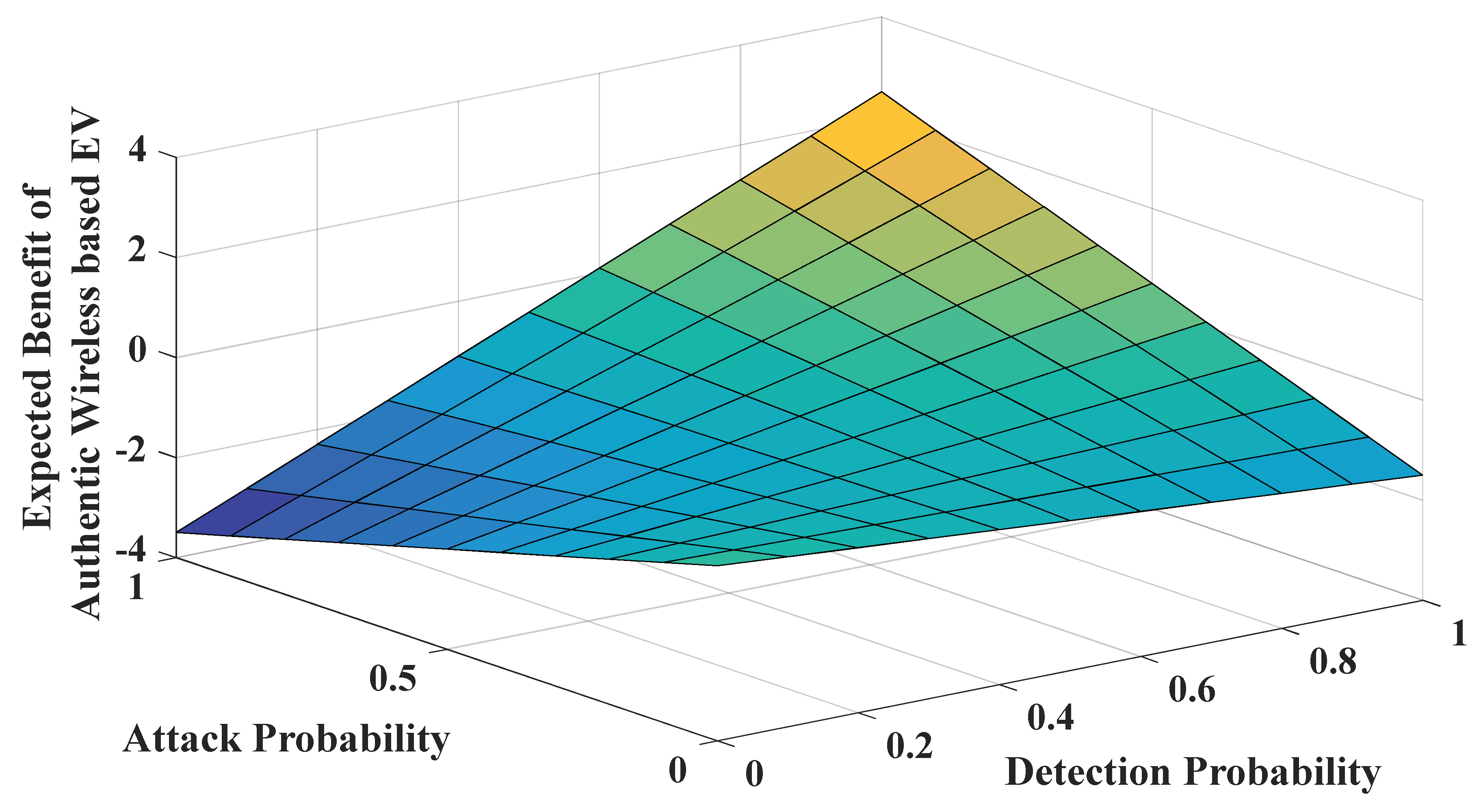
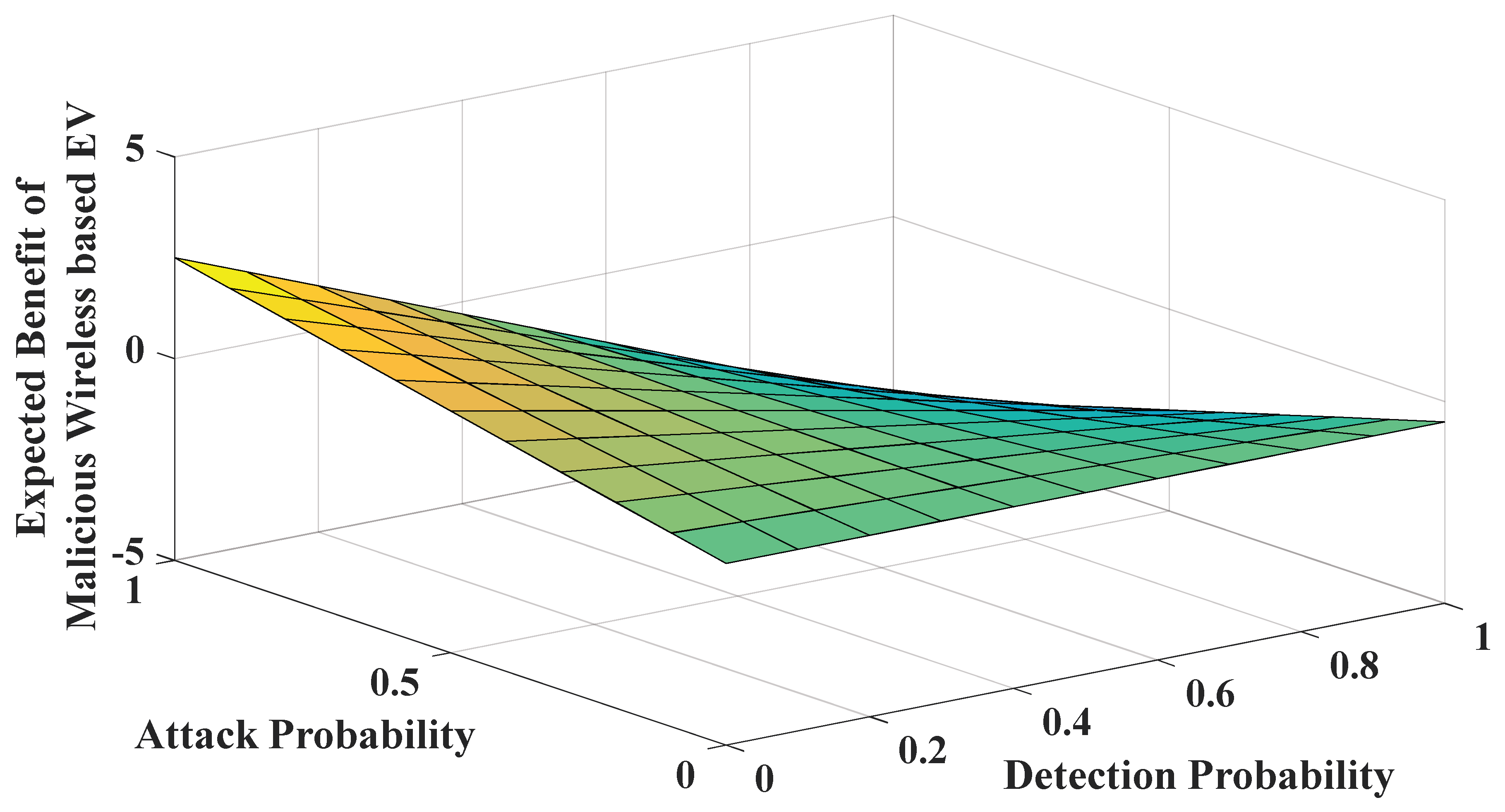
5.3. The Simulation of the Uncertainty Model Based on UT
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Sets/Indices | |
| Ωp/p | Set/index of roads. |
| Ωs/s | Set/index of stations. |
| Ωt/t | Set/index of time. |
| Ωv/v | Set/index of EVs. |
| Constants | |
| The velocity for the special values of x and t. | |
| The change in number of EVs. | |
| The density of the traffic flow. | |
| The EVs’ speed. | |
| The distance parameter. | |
| The time interval. | |
| Min/max charging/discharging powers of EV. | |
| Min/max EV battery energy. | |
| The number of authentic, malicious nodes and the total number of nodes. | |
| The proportions of the authentic and malicious nodes. | |
| Cost/benefit for the detection. | |
| The energy costs for the malicious and authentic nodes. | |
| The benefit for the successful attack, and the penalty for the attack failed. | |
| The degradation cost of EVs battery. | |
| , | Charging and discharging efficiencies, respectively. |
| Variables | |
| The consumed total energy of the EV, the EV’s wheel energy, the involved energy of air resistance, the involved energy of gradient resistance. | |
| The power consumption and the traction force. | |
| EVs, V2G and V2M energy transaction costs and degradation costss | |
| Binary variables related to the charging, and discharging of the EVs. | |
| , , | Charging/discharging powers during V2M and V2G, respectively. |
| The EV battery capacity. | |
| The removing probabilities of 𝛾1 and 𝛾2 for both authentic and malicious nodes. | |
| 𝜅, µ | The infected probability, the repairing probability. |
| The successful probabilities of authentic and malicious nodes. | |
| The generated points. | |
| The mean value. | |
| The covariance matrix. | |
| The output points of the uncertainty model. | |
References
- Wang, B.; Ma, H.; Wang, F.; Dampage, U.; Al-Dhaifallah, M.; Ali, Z.M.; Mohamed, M.A. An IoT-Enabled Stochastic Operation Management Framework for Smart Grids. IEEE Trans. Intell. Transp. Syst. 2022, 1–10. [Google Scholar] [CrossRef]
- Avatefipour, O.; Al-Sumaiti, A.S.; El-Sherbeeny, A.M.; Awwad, E.M.; Elmeligy, M.A.; Mohamed, M.A.; Malik, H. An intelligent secured framework for cyberattack detection in electric vehicles’ CAN bus using machine learning. IEEE Access 2019, 7, 127580–127592. [Google Scholar] [CrossRef]
- Batista, F.K.; del Rey, A.M.; Queiruga-Dios, A. A new individual-based model to simulate malware propagation in wireless sensor networks. Mathematics 2022, 8, 410. [Google Scholar] [CrossRef]
- Al-Mousawi, A.J.; AL-Hassani, H.K. A survey in wireless sensor network for explosives detection. Comput. Electr. Eng. 2019, 72, 682–701. [Google Scholar] [CrossRef]
- Farjamnia, G.; Gasimov, Y.; Kazimov, C. Review of the techniques against the wormhole attacks on wireless sensor networks. Wirel. Pers. Commun. 2019, 105, 1561–1584. [Google Scholar] [CrossRef]
- Jamshidi, M.; Zangeneh, E.; Esnaashari, M.; Darwesh, A.M.; Meybodi, M.R. A novel model of sybil attack in cluster-based wireless sensor networks and propose a distributed algorithm to defend it. Wirel. Pers. Commun. 2019, 105, 145–173. [Google Scholar] [CrossRef]
- Yuan, Y.; Huo, L.; Wang, Z.; Hogrefe, D. Secure APIT localization scheme against sybil attacks in distributed wireless sensor networks. IEEE Access 2018, 6, 27629–27636. [Google Scholar] [CrossRef]
- Dung, T.N.; Choe, J.; Thang, L.D.; Tai, L.D.; Zalyubovskiy, V.V.; Choo, H. Delaysensitive flooding based on expected path quality in low duty-cycled wireless sensor networks. Int. J. Distrib. Sens. Netw. 2016, 12, 15501477166642548. [Google Scholar]
- Zhang, Q.; Zhang, W. Accurate detection of selective forwarding attack in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2019, 15, 15501477188240081. [Google Scholar] [CrossRef]
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef]
- Bridge, G.; Bouzarovski, S.; Bradshaw, M.; Eyre, N. Geographies of energy transition: Space, place and the low-carbon economy. Energy Policy 2013, 53, 331–340. [Google Scholar] [CrossRef]
- Zhou, H.; Shen, S.; Liu, J. Malware propagation model in wireless sensor networks under attack–defense confrontation. Comput. Commun. 2020, 162, 51–58. [Google Scholar] [CrossRef]
- Liu, J.; Yue, G.; Shen, S.; Shang, H.; Li, H. A game-theoretic response strategy for coordinator attack in wireless sensor networks. Sci. World J. 2014, 2014, 950618. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Li, H.; Han, R.; Vasilakos, A.V.; Wang, Y.; Cao, Q. Differential game-based strategies for preventing malware propagation in wireless sensor networks. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1962–1973. [Google Scholar] [CrossRef]
- Harrison, C.; Eckman, B.; Hamilton, R.; Hartswick, P.; Kalagnanam, J.; Paraszczak, J.; Williams, P. Foundations for smarter cities. IBM J. Res. Dev. 2010, 54, 1–16. [Google Scholar] [CrossRef]
- Mohamed, M.A. A relaxed consensus plus innovation based effective negotiation approach for energy cooperation between smart grid and microgrid. Energy 2022, 252, 123996. [Google Scholar] [CrossRef]
- Yang, W.; Liu, W.; Chung, C.Y.; Wen, F. Joint planning of EV fast charging stations and power distribution systems with balanced traffic flow assignment. IEEE Trans. Ind. Inform. 2020, 17, 1795–1809. [Google Scholar] [CrossRef]
- Qian, Z.; Yi, Z.; Zhong, W.; Yue, H.; Yaojia, S. Siting and sizing of electric vehicle fast-charging station based on quasi-dynamic traffic flow. IET Renew. Power Gener. 2020, 14, 4204–4214. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X. Stochastic nonlinear complementarity problem and applications to traffic equilibrium under uncertainty. J. Optim. Theory Appl. 2018, 137, 277–295. [Google Scholar] [CrossRef]
- Lippi, M.; Bertini, M.; Frasconi, P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Trans. Intell. Transp. Syst. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Roustaei, M.; Niknam, T.; Salari, S.; Chabok, H.; Sheikh, M.; Kavousi-Fard, A.; Aghaei, J. A scenario-based approach for the design of Smart Energy and Water Hub. Energy 2020, 195, 116931. [Google Scholar] [CrossRef]
- Chabok, H.; Aghaei, J.; Sheikh, M.; Roustaei, M.; Zare, M.; Niknam, T.; Lehtonen, M.; Shafi-khah, M.; Catalão, J.P. Transmission-constrained optimal allocation of price-maker wind-storage units in electricity markets. Appl. Energy 2021, 310, 118542. [Google Scholar] [CrossRef]
- Korayem, A.H.; Khajepour, A.; Fidan, B. Vehicle-trailer lateral velocity estimation using constrained unscented transformation. Veh. Syst. Dyn. 2022, 60, 1048–1075. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, L.; Alsokhiry, F.; Mohamed, M.A. A Novel Stochastic Blockchain-Based Energy Management in Smart Cities Using V2S and V2G. IEEE Trans. Intell. Transp. Syst 2022, 1–8. [Google Scholar] [CrossRef]
- Ding, S.; Cao, Y.; Vosoogh, M.; Sheikh, M.; Almagrabi, A. A directed acyclic graph based architecture for optimal operation and management of reconfigurable distribution systems with PEVs. IEEE Trans. Ind. Appl. 2020, 1. [Google Scholar] [CrossRef]
- Zou, H.; Tao, J.; Elsayed, S.K.; Elattar, E.E.; Almalaq, A.; Mohamed, M.A. Stochastic multi-carrier energy management in the smart islands using reinforcement learning and unscented transform. Int. J. Electr. Power Energy Syst. 2021, 130, 106988. [Google Scholar] [CrossRef]
- Gong, X.; Dong, F.; Mohamed, A.M.; Abdalla, O.M.; Ali, Z.M. A secured energy management architecture for smart hybrid microgrids considering PEM-fuel cell and electric vehicles. IEEE Access 2020, 8, 47807–47823. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Zhu, C.; Yang, Y.; Abdullah, H.M.; Mohamed, M.A. Stochastic management of hybrid AC/DC microgrids considering electric vehicles charging demands. Energy Rep. 2020, 6, 1338–1352. [Google Scholar] [CrossRef]
- Almalaq, A.; Albadran, S.; Mohamed, M.A. Deep machine learning model-based cyber-attacks detection in smart power systems. Mathematics 2022, 10, 2574. [Google Scholar] [CrossRef]
- Chen, J.; Mohamed, M.A.; Dampage, U.; Rezaei, M.; Salmen, S.H.; Obaid, S.A.; Annuk, A. A multi-layer security scheme for mitigating smart grid vulnerability against faults and cyber-attacks. Appl. Sci. 2021, 11, 9972. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Abdullah, H.M.; El-Meligy, M.A.; Sharaf, M.; Soliman, A.T.; Hajjiah, A. A novel fuzzy cloud stochastic framework for energy management of renewable microgrids based on maximum deployment of electric vehicles. Int. J. Electr. Power Energy Syst. 2021, 129, 106845. [Google Scholar] [CrossRef]
- Chaudhary, R.; Jindal, A.; Aujla, G.S.; Aggarwal, S.; Kumar, N.; Choo, K.K.R. BEST: Blockchain-based secure energy trading in SDN-enabled intelligent transportation system. Comput. Secur. 2019, 85, 288–299. [Google Scholar] [CrossRef]
- Al-Saud, M.; Eltamaly, A.M.; Mohamed, M.A.; Kavousi-Fard, A. An intelligent data-driven model to secure intravehicle communications based on machine learning. IEEE Trans. Ind. Electron. 2019, 67, 5112–5119. [Google Scholar] [CrossRef]
- Tan, H.; Yan, W.; Ren, Z.; Wang, Q.; Mohamed, M.A. A robust dispatch model for integrated electricity and heat networks considering price-based integrated demand response. Energy 2022, 239, 121875. [Google Scholar] [CrossRef]
- Norouzi, M.; Aghaei, J.; Pirouzi, S.; Niknam, T.; Fotuhi-Firuzabad, M.; Shafie-khah, M. Hybrid stochastic/robust flexible and reliable scheduling of secure networked microgrids with electric springs and electric vehicles. Appl. Energy 2021, 300, 117395. [Google Scholar] [CrossRef]
- Lan, T.; Jermsittiparsert, K.; Alrashood, S.T.; Rezaei, M.; Al-Ghussain, L.; Mohamed, M.A. An advanced machine learning based energy management of renewable microgrids considering hybrid electric vehicles’ charging demand. Energies 2021, 14, 569. [Google Scholar] [CrossRef]




| Parameter Type | Macro Parameter | Micro Parameter |
|---|---|---|
| Parameters of traffic flow model | Volume or flow rate | The speed of each vehicle |
| Density | Time interval | |
| Speed | Local interval |
| Game Strategies | |||
|---|---|---|---|
| Node Type | Not-Attack | Attack | |
| Authentic node | r + CA, -Cm | gd-CA-r, -gd-Cm | Detected |
| Malicious node | -r, -Cm | -ga-r, ga-Cm | Not detected |
| Total Energy Cost (¢) | |||
|---|---|---|---|
| Studied Cases | Traffic Rate (Normal) | Traffic Rate (10%) | Traffic Rate (40%) |
| Determinacy | 1.9497 × 105 | 1.8928 × 105 | 2.0854 × 105 |
| Uncertainty | 2.2191 × 105 | 1.9511 × 105 | 2.3536 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsokhiry, F.; Annuk, A.; Kabanen, T.; Mohamed, M.A. A Malware Attack Enabled an Online Energy Strategy for Dynamic Wireless EVs within Transportation Systems. Mathematics 2022, 10, 4691. https://doi.org/10.3390/math10244691
Alsokhiry F, Annuk A, Kabanen T, Mohamed MA. A Malware Attack Enabled an Online Energy Strategy for Dynamic Wireless EVs within Transportation Systems. Mathematics. 2022; 10(24):4691. https://doi.org/10.3390/math10244691
Chicago/Turabian StyleAlsokhiry, Fahad, Andres Annuk, Toivo Kabanen, and Mohamed A. Mohamed. 2022. "A Malware Attack Enabled an Online Energy Strategy for Dynamic Wireless EVs within Transportation Systems" Mathematics 10, no. 24: 4691. https://doi.org/10.3390/math10244691
APA StyleAlsokhiry, F., Annuk, A., Kabanen, T., & Mohamed, M. A. (2022). A Malware Attack Enabled an Online Energy Strategy for Dynamic Wireless EVs within Transportation Systems. Mathematics, 10(24), 4691. https://doi.org/10.3390/math10244691








