Constructing Condition Monitoring Model of Wind Turbine Blades
Abstract
:1. Introduction
2. Related Work
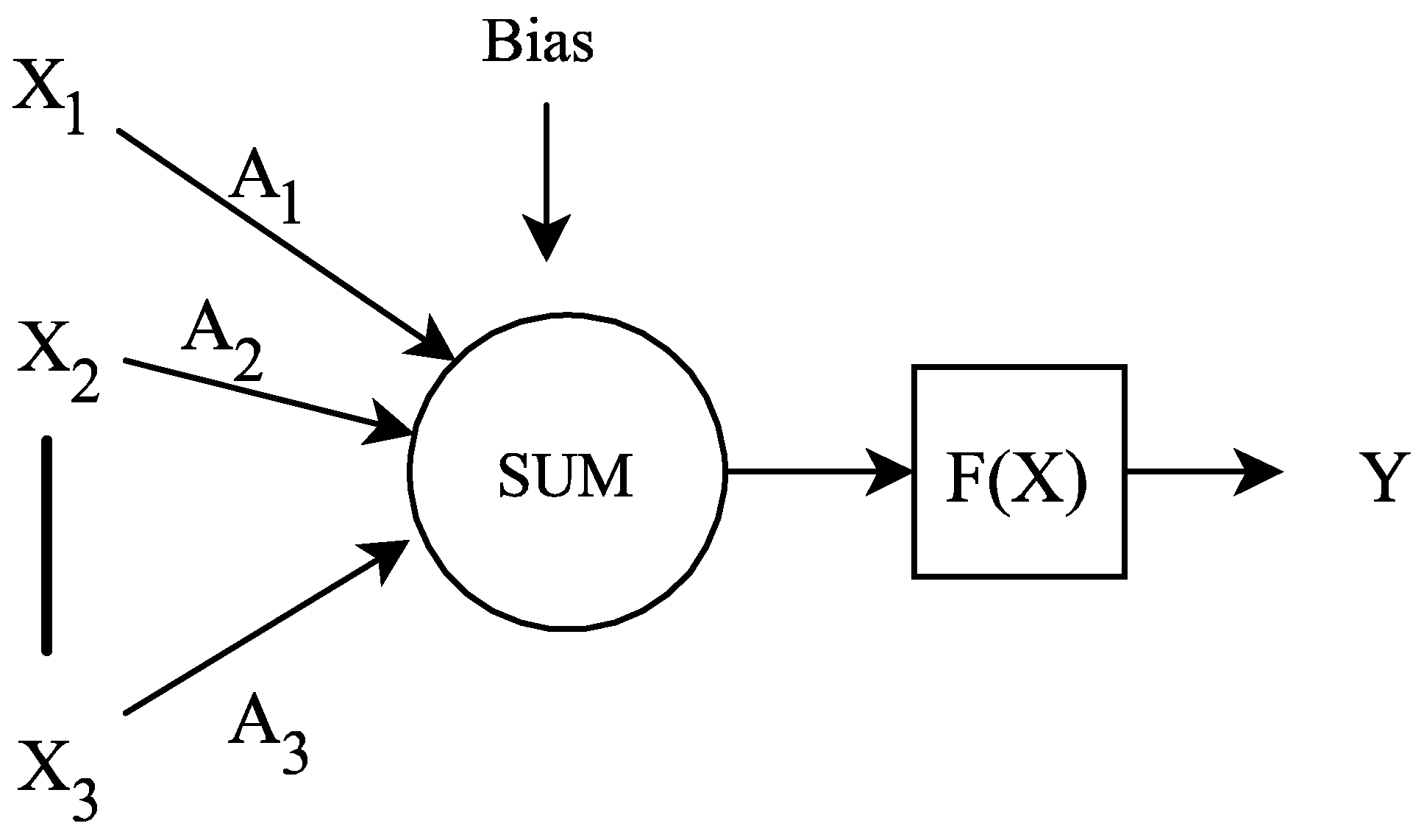
2.1. Deep Neural Network
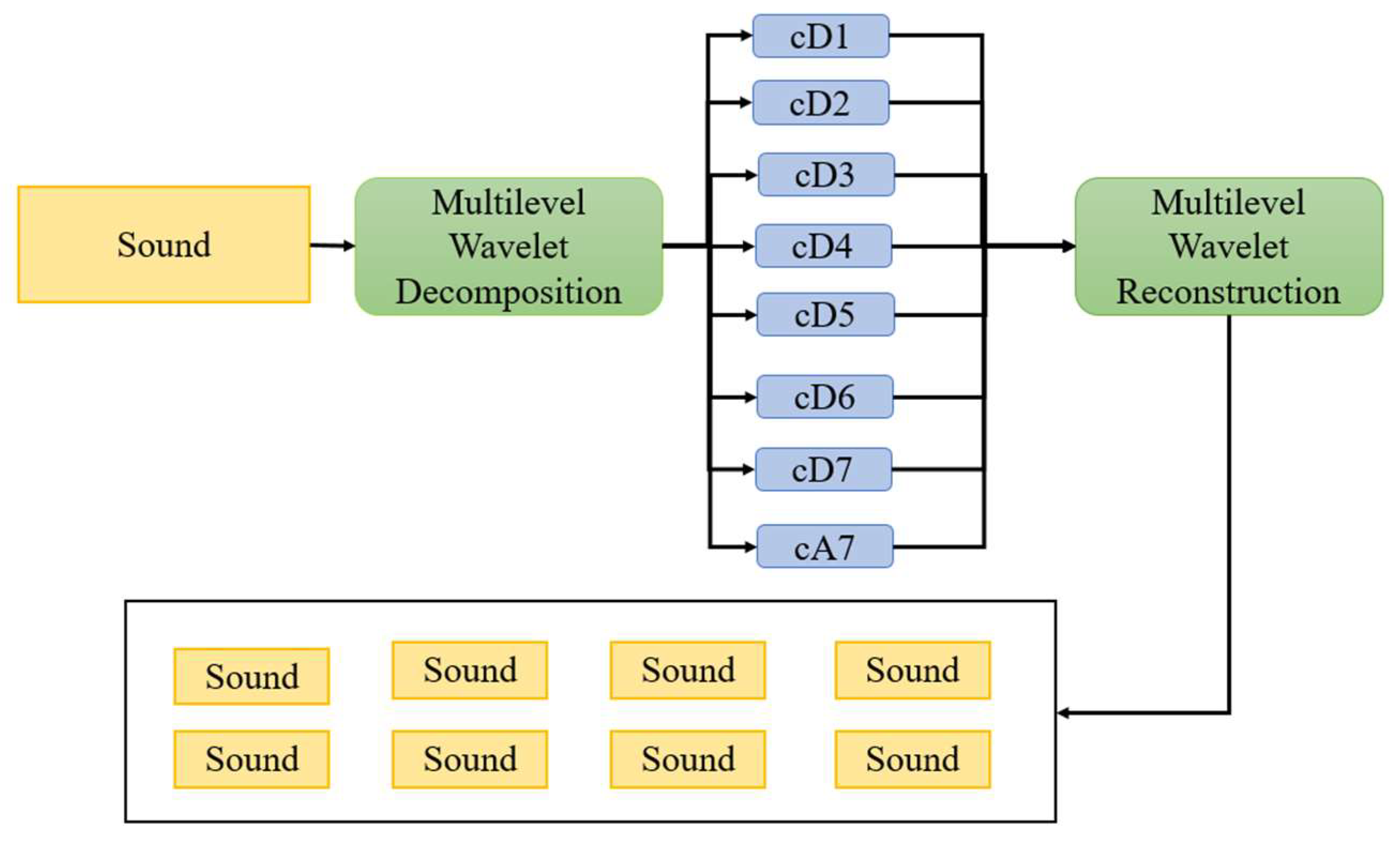
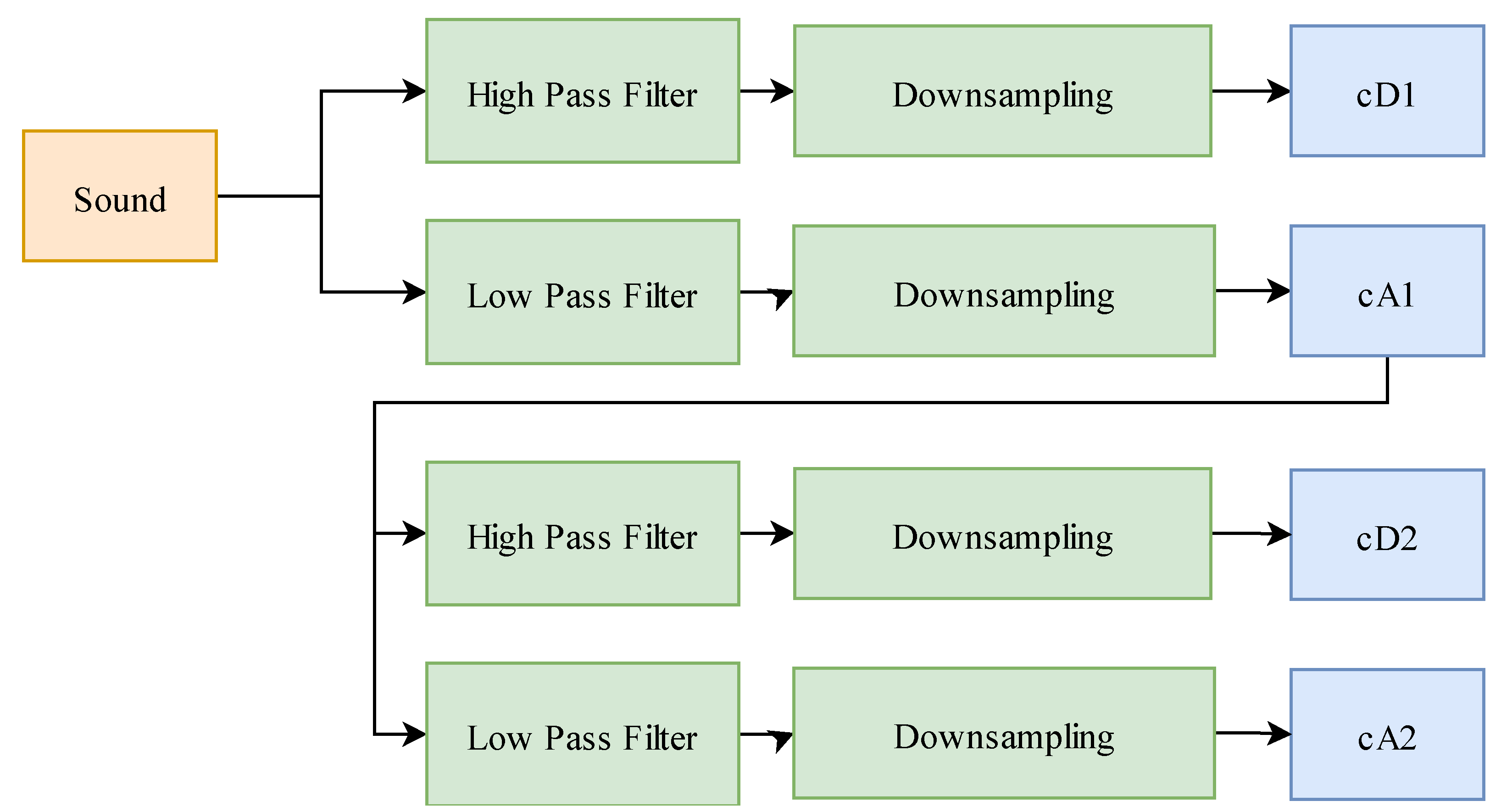
2.2. Wavelet Transform
2.3. Anomaly Detection
2.4. Structural Health Monitoring
3. The Proposed Approach
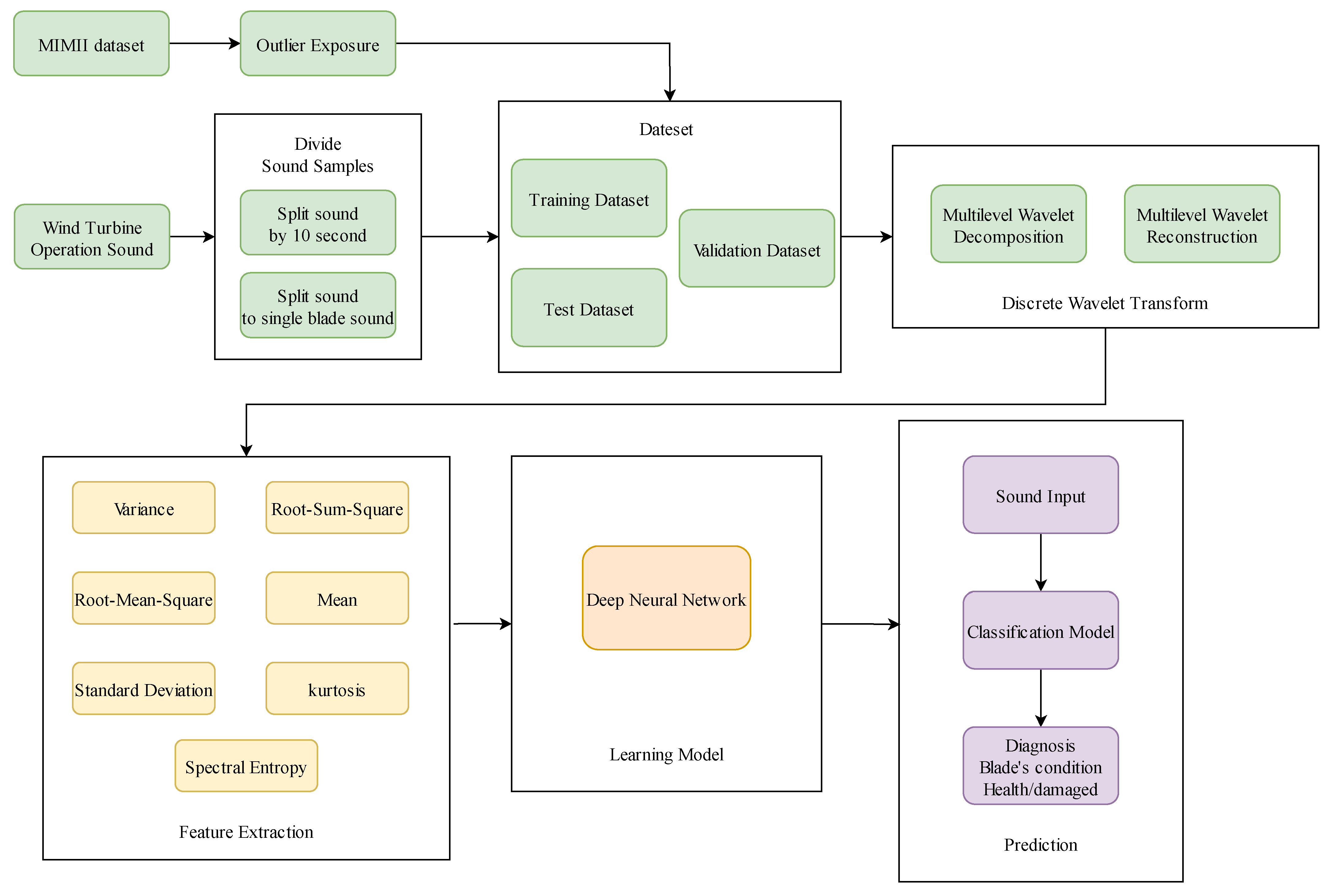
3.1. Monitor Model Architecture Diagram
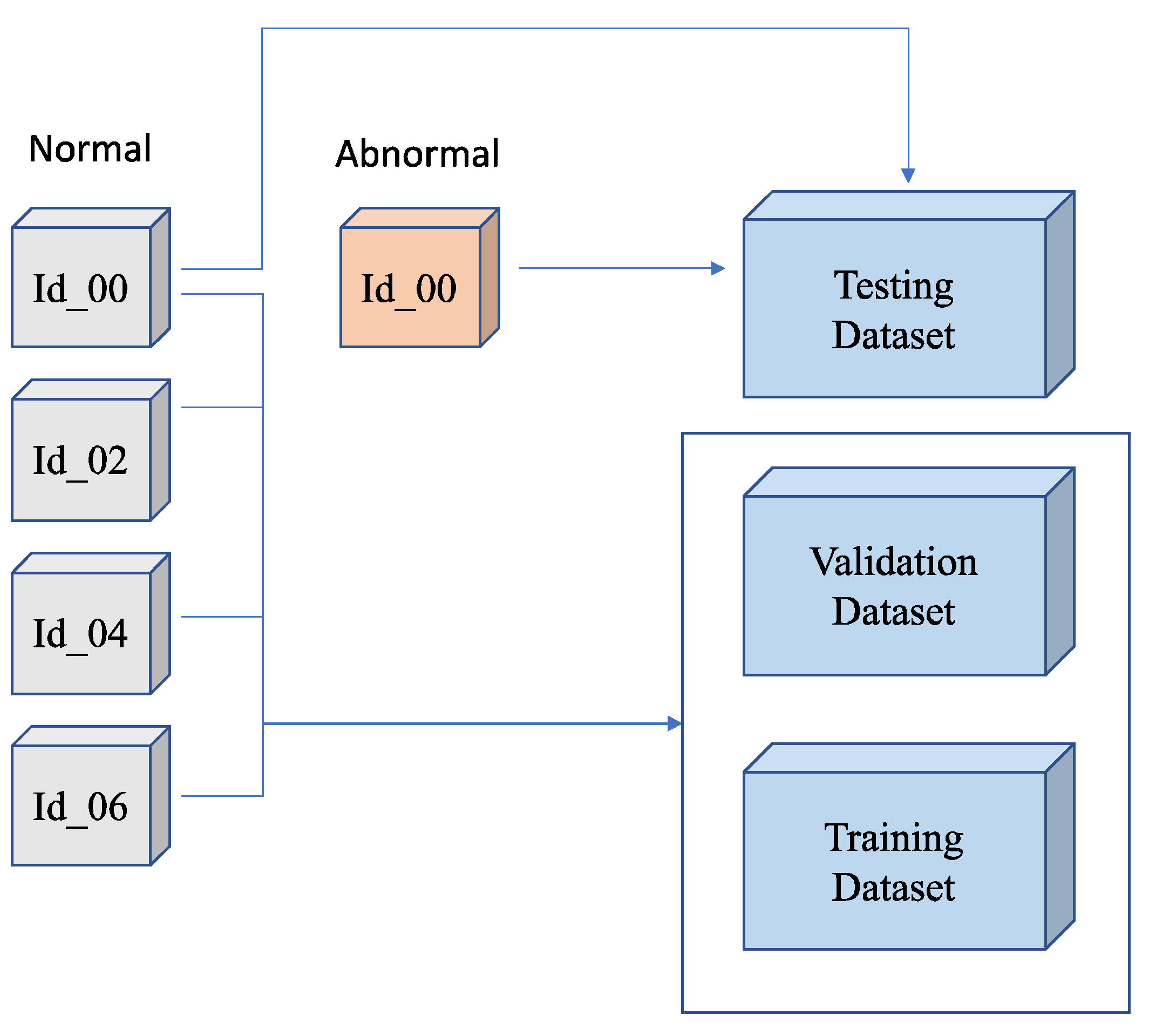
3.2. Dataset
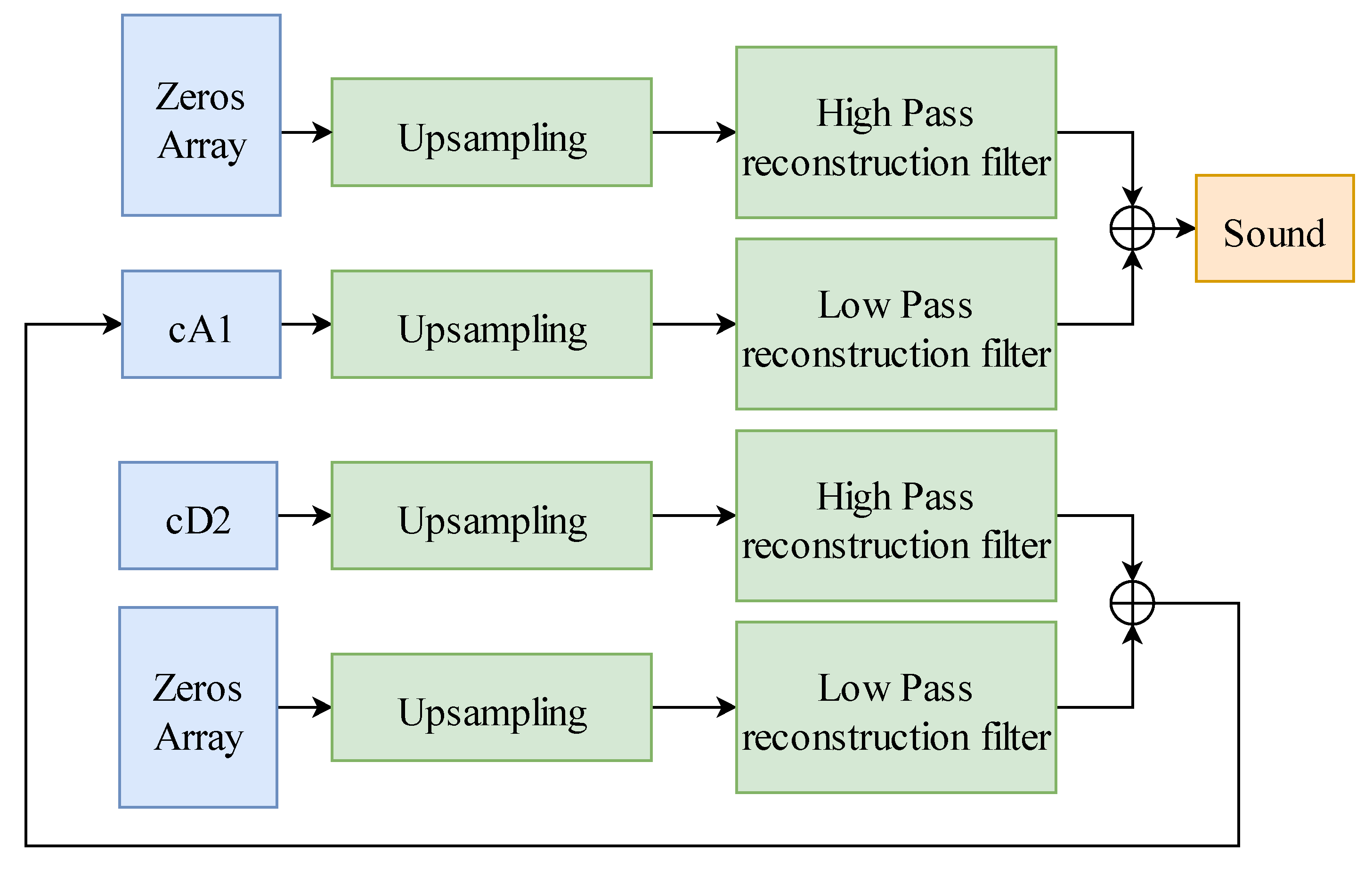
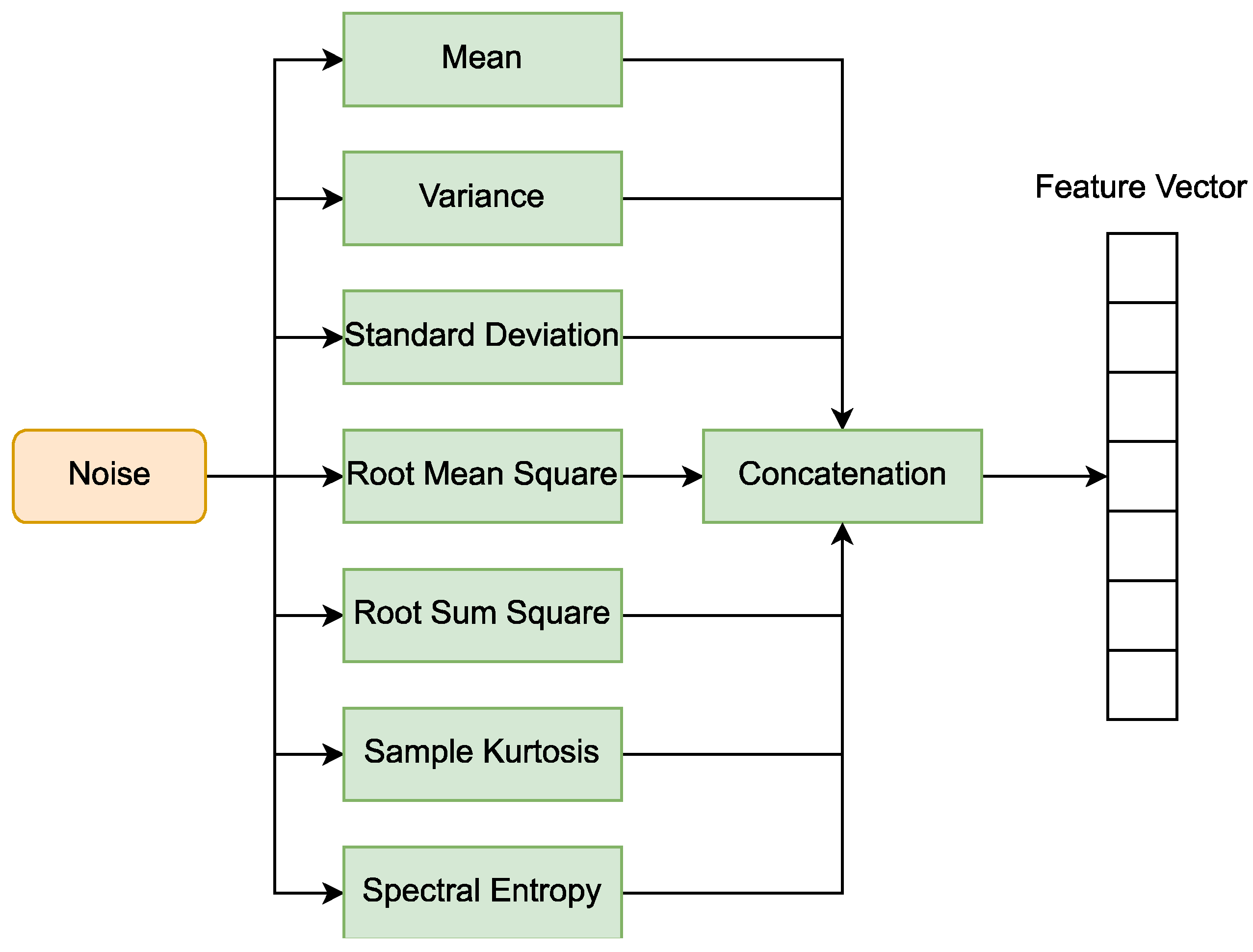
3.3. Data Preprocessing
3.4. Neural Network Architecture
4. Experiment
4.1. Experimental Process
4.2. Experimental Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Regan, T.; Beale, C.; Inalpolat, M. Wind turbine blade damage detection using supervised machine learning algorithms. J. Vib.Acoust. Trans. ASME 2017, 139, 061010. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Zhang, L. Fault Diagnosis of Industrial Wind Turbine Blade Bearing Using Acoustic Emission Analysis. IEEE Trans. Instrum. Meas. 2020, 69, 6630–6639. [Google Scholar] [CrossRef]
- Latoufis, K.; Riziotis, V.; Voutsinas, S.; Hatziargyriou, N. Effects of leading edgeerosion on the power performance and acoustic noise emissions of locally manufactured small wind turbine blades. J. Phys. Conf. Ser. 2019, 1222, 012010. [Google Scholar] [CrossRef]
- Mollasalehi, E.; Wood, D.; Sun, Q. Indicative Fault Diagnosis of Wind Turbine Generator Bearings Using Tower Sound and Vibration. Energies 2017, 10, 1853. [Google Scholar] [CrossRef] [Green Version]
- Castellani, F.; Garibaldi, L.; Daga, A.P.; Astolfi, D.; Natili, F. Diagnosis of Faulty Wind Turbine Bearings Using Tower Vibration Measurements. Energies 2020, 13, 1474. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Yang, B.; Wang, X.; Zhang, L. Acoustic Emission Analysis for Wind Turbine Blade Bearing Fault Detection Under Time-Varying Low-Speed and Heavy Blade Load Conditions. IEEE Trans. Ind. Appl. 2021, 57, 2791–2800. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Jia, W.; Shukla, R.M.; Sengupta, S. Anomaly Detection using Supervised Learning and Multiple Statistical Methods. In Proceedings of the 2019 18th IEEE International Conference On Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; Available online: https://www.researchgate.net/publication/336902630 (accessed on 18 November 2019).
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Gearbox Fault Diagnosis Using a Deep Learning Model with Limited Data Sample. IEEE Trans. Ind. Inform. 2020, 16, 6263–6271. [Google Scholar] [CrossRef]
- Yang, G.; Zhong, Y.; Yang, L.; Tao, H.; Li, J.; Du, R. Fault Diagnosis of Harmonic Drive with Imbalanced Data Using Generative Adversarial Network. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Kong, X.; Li, X.; Zhou, Q.; Hu, Z.; Shi, C. Attention Recurrent Autoencoder Hybrid Model for Early Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Ribeiro, A.; Matos, L.M.; Pereira, P.J.; Nunes, E.C.; Ferreira, A.L.; Cortez, P.; Pilastri, A. Deep Dense and Convolutional Autoencoders for Unsupervised Anomaly Detection in Machine Condition Sounds. arXiv 2020, arXiv:2006.10417. [Google Scholar]
- Hendrycks, D.; Mazeika, M.; Dietterich, T. Deep anomaly detection with outlier exposure. arXiv 2019, arXiv:1812.04606. [Google Scholar]
- Tokognon, C.A.; Gao, B.; Tian, G.Y.; Yan, Y. Structural Health Monitoring Framework Based on Internet of Things: A Survey. IEEE Internet Things J. 2017, 4, 619–635. [Google Scholar] [CrossRef]
- Kim, J.; Lee, H.; Jeong, S.; Ahn, S. Sound-based remote real-time multi-device operational monitoring system using a Convolutional Neural Network. J. Manuf. Syst. 2021, 58, 431–441. [Google Scholar] [CrossRef]
- Müller, R.; Ritz, F.; Illium, S.; Popien, C.L. Acoustic Anomaly Detection for Machine Sounds based on Image Transfer Learning. arXiv 2020, arXiv:2006.03429. [Google Scholar]
- Purohit, H.; Tanabe, R.; Ichige, T.; Endo, T.; Nikaido, Y.; Suefusa, K.; Kawaguchi, Y. MIMII Dataset: Sound Dataset for Malfunctioning Industrial Machine Investigation and Inspection. arXiv 2019, arXiv:1909.09347. [Google Scholar]
- Primus, P.; Haunschmid, V.; Praher, P.; Widmer, G. Anomalous Sound Detection as a Simple Binary Classification Problem with Careful Selection of Proxy Outlier Examples. arXiv 2020, arXiv:2011.02949. [Google Scholar]
| Normal | Abnormal | |
|---|---|---|
| The number of samples | 596 | 143 |
| Normal | Abnormal | |
|---|---|---|
| The number of samples | 539 | 221 |
| Layer | Size | Activation |
|---|---|---|
| Input | 56 | None |
| Hidden Layer | 40 | ReLU |
| BatchNormalization | None | None |
| Hidden Layer | 40 | ReLU |
| BatchNormalization | None | None |
| Hidden Layer | 30 | ReLU |
| BatchNormalization | None | None |
| Hidden Layer | 20 | ReLU |
| BatchNormalization | None | None |
| Hidden Layer | 10 | ReLU |
| Output | 1 | Sigmoid |
| This Paper | log-Mel Spectrogram +ResNet50 | log-Mel Spectrogram +ResNet18 | |
|---|---|---|---|
| fan | 0.7481 | 0.7537 | 0.6872 |
| pump | 0.7632 | 0.7282 | 0.7505 |
| slider | 0.8507 | 0.7497 | 0.8806 |
| valve | 0.9419 | 0.9406 | 0.8436 |
| average | 0.8260 | 0.7931 | 0.7905 |
| This Paper | log-Mel Spectrogram +ResNet50 | log-Mel Spectrogram +ResNet18 | |
|---|---|---|---|
| Average epoch time | 4.39 s | 24.21 s | 14.12 s |
| This Paper | Ribeiro et al. [12] | Müller et al. [16] | Purohit et al. [17] | |
|---|---|---|---|---|
| fan | 0.7481 | 0.6678 | 0.6805 | 0.6625 |
| pump | 0.7632 | 0.7207 | 0.7404 | 0.66 |
| slider | 0.8507 | 0.9177 | 0.854 | 0.7 |
| valve | 0.9419 | 0.7883 | 0.6852 | 0.555 |
| average | 0.8260 | 0.7736 | 0.7400 | 0.6443 |
| Accuracy | AUC | |
|---|---|---|
| This paper | 98.04% | 0.9932 |
| log-mel spectrogram+ResNet18 | 99.85% | 0.9894 |
| log-mel spectrogram+ResNet50 | 98.14% | 0.9980 |
| Accuracy | AUC | |
|---|---|---|
| This paper | 96.04% | 0.9664 |
| log-mel spectrogram+ResNet18 | 95.62% | 0.9650 |
| log-mel spectrogram+ResNet50 | 96.40% | 0.9720 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, J.-Y.; You, S.-Y.; Lin, H.-C.; Hsu, C.-Y.; Lei, B. Constructing Condition Monitoring Model of Wind Turbine Blades. Mathematics 2022, 10, 972. https://doi.org/10.3390/math10060972
Kuo J-Y, You S-Y, Lin H-C, Hsu C-Y, Lei B. Constructing Condition Monitoring Model of Wind Turbine Blades. Mathematics. 2022; 10(6):972. https://doi.org/10.3390/math10060972
Chicago/Turabian StyleKuo, Jong-Yih, Shang-Yi You, Hui-Chi Lin, Chao-Yang Hsu, and Baiying Lei. 2022. "Constructing Condition Monitoring Model of Wind Turbine Blades" Mathematics 10, no. 6: 972. https://doi.org/10.3390/math10060972
APA StyleKuo, J.-Y., You, S.-Y., Lin, H.-C., Hsu, C.-Y., & Lei, B. (2022). Constructing Condition Monitoring Model of Wind Turbine Blades. Mathematics, 10(6), 972. https://doi.org/10.3390/math10060972






