An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System
Abstract
:1. Introduction
2. Modeling of System
2.1. Satellite Dynamics Model
2.2. Measurements
3. Adaptive Neural Fuzzy Inference System
3.1. Fuzzy Logic
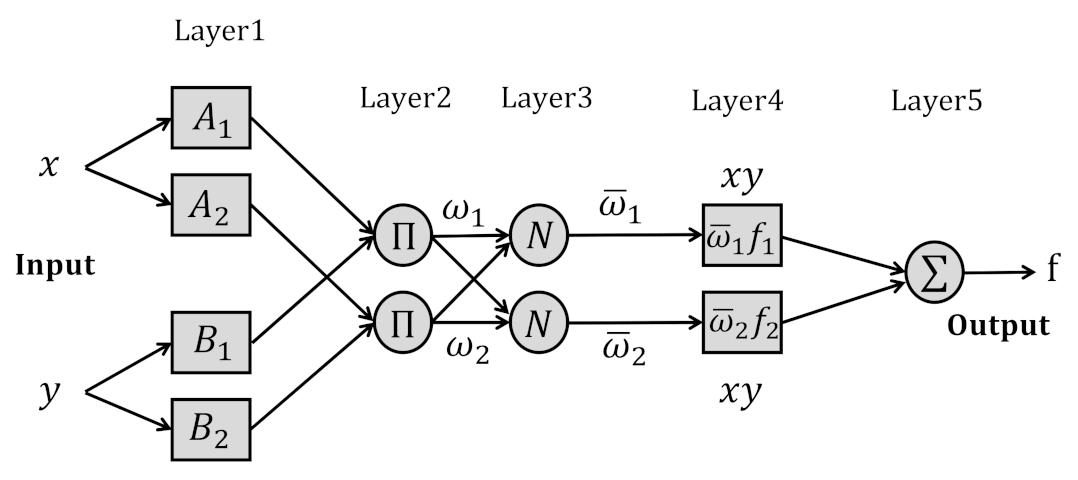
3.2. ANFIS
3.3. Hybrid Learning Algorithm
3.4. Optimal PID Controller
4. ANFIS Controller and Estimator
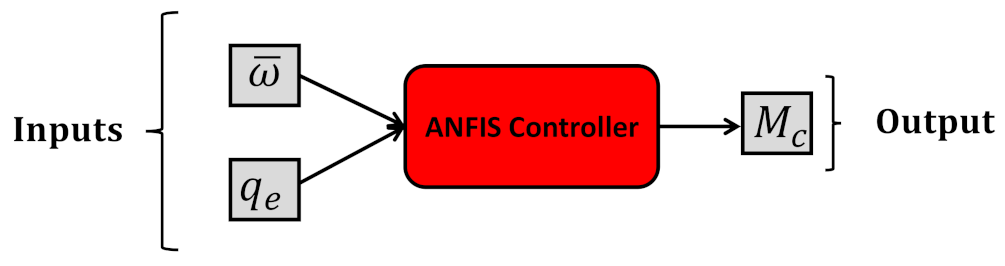
4.1. ANFIS Controller
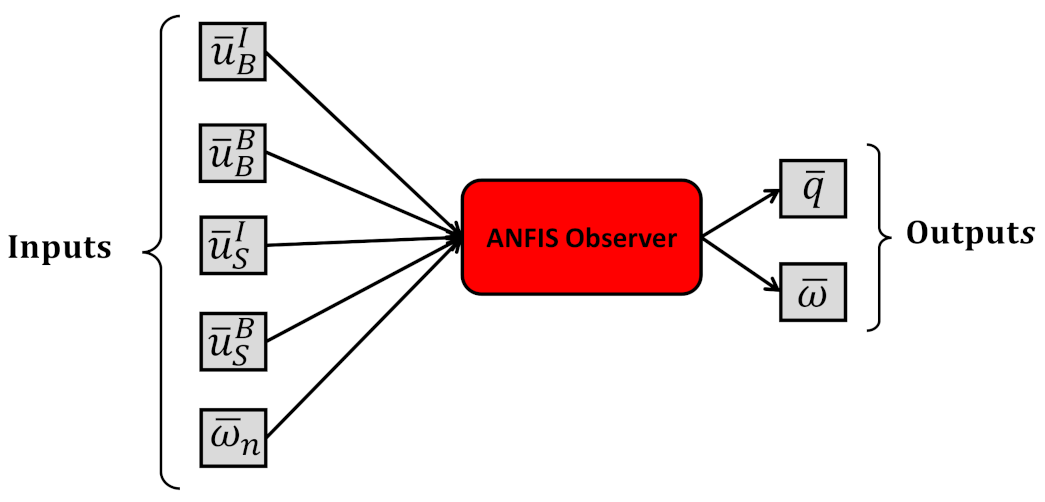
4.2. ANFIS Estimator
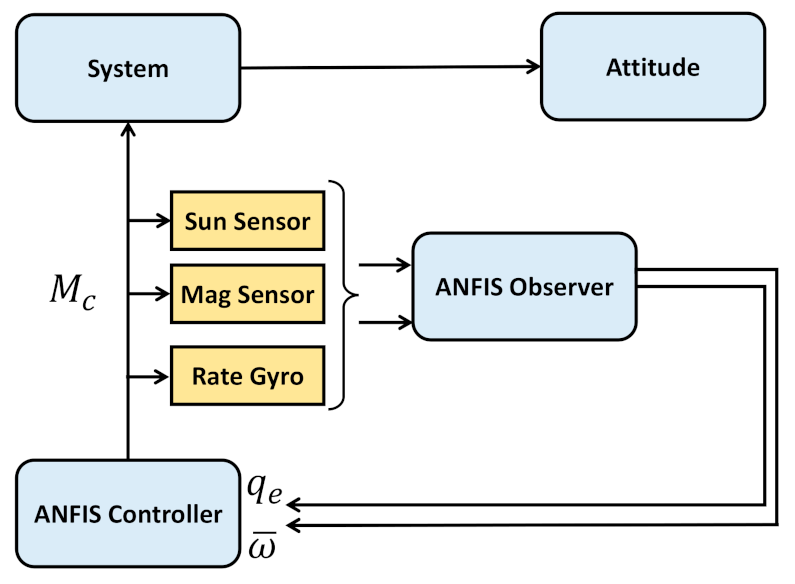
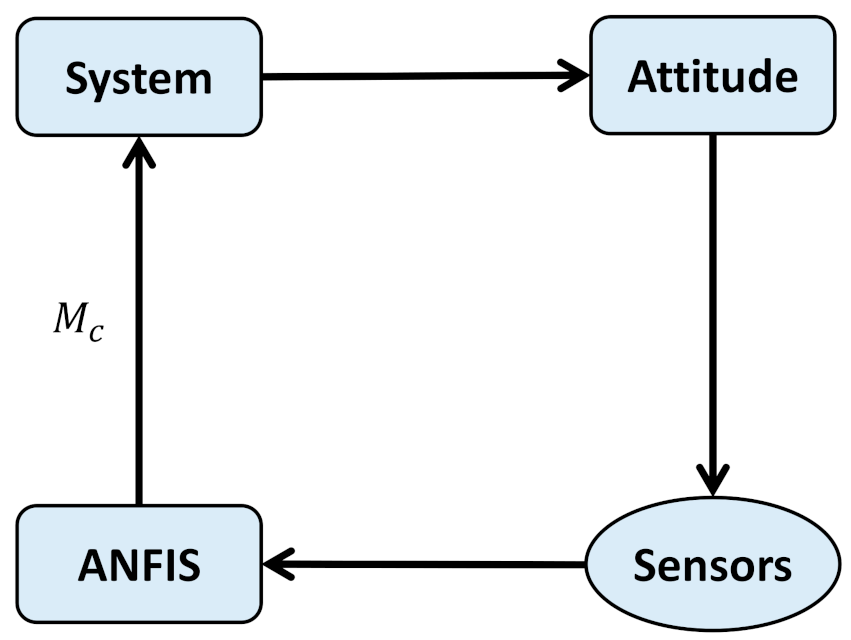
4.3. Combined Control and Estimation Using ANFIS
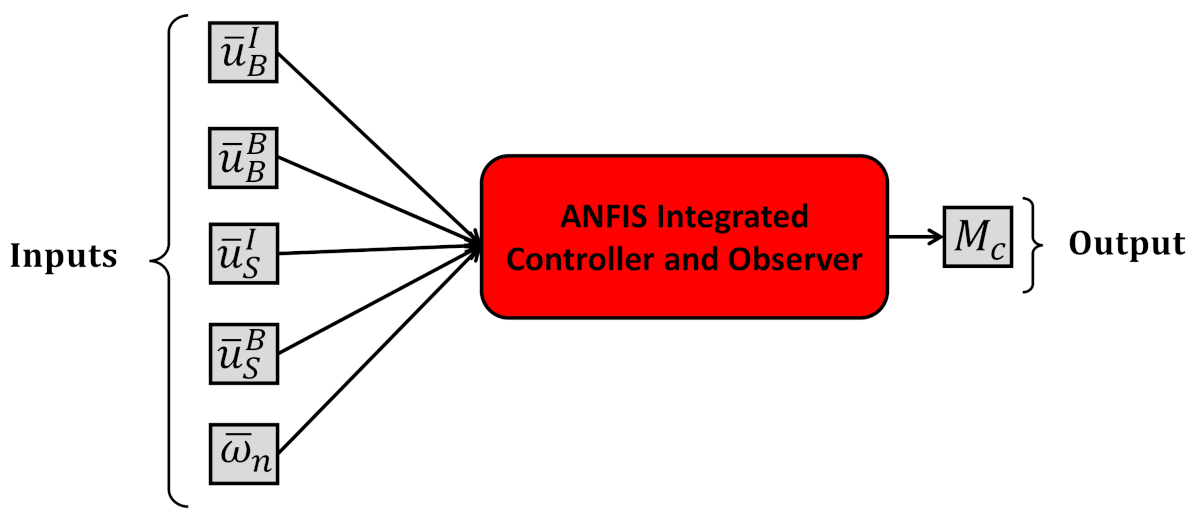
4.4. Integrated Control and Estimation Using ANFIS
5. Evaluation of ANFIS Control and Estimation
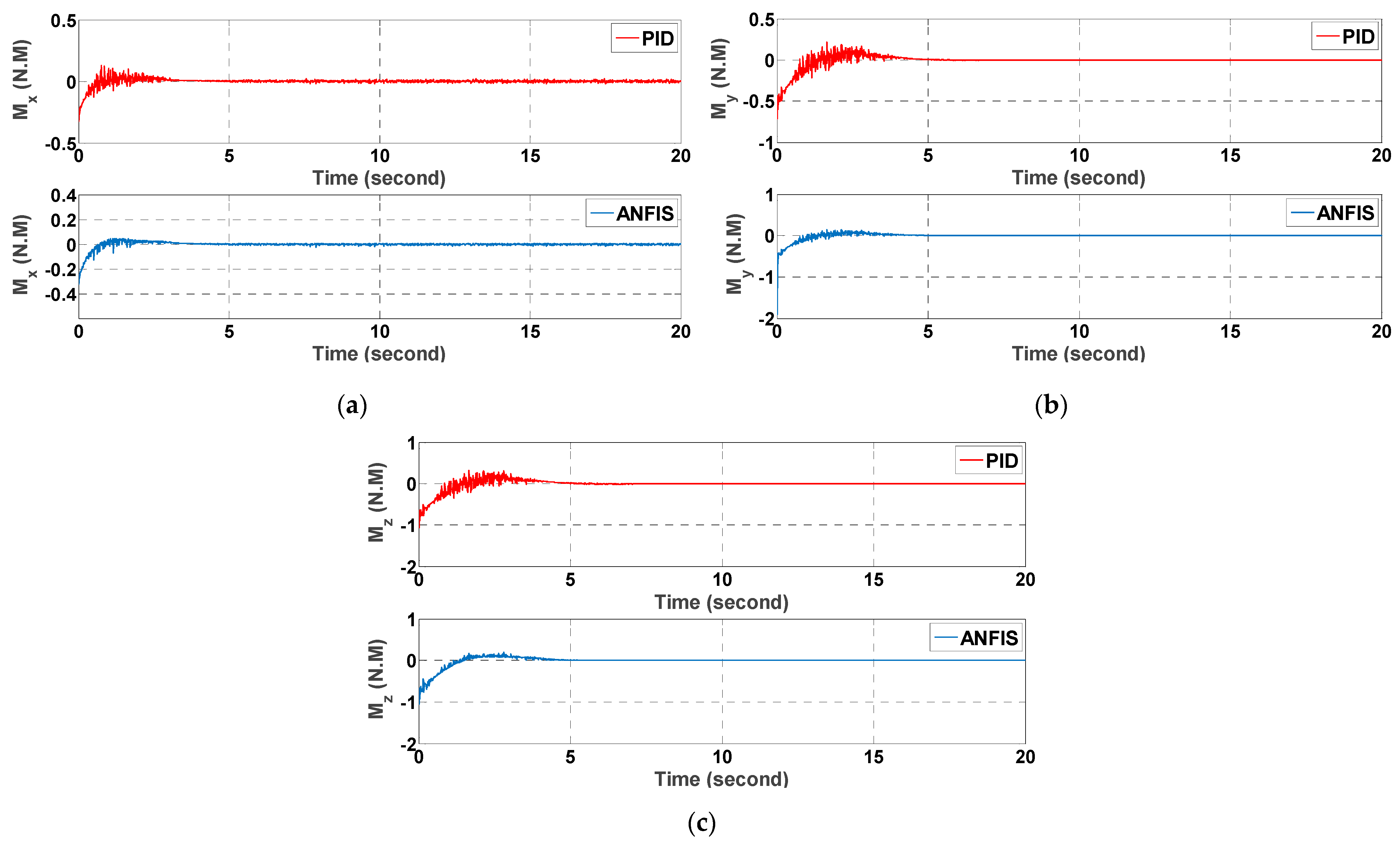
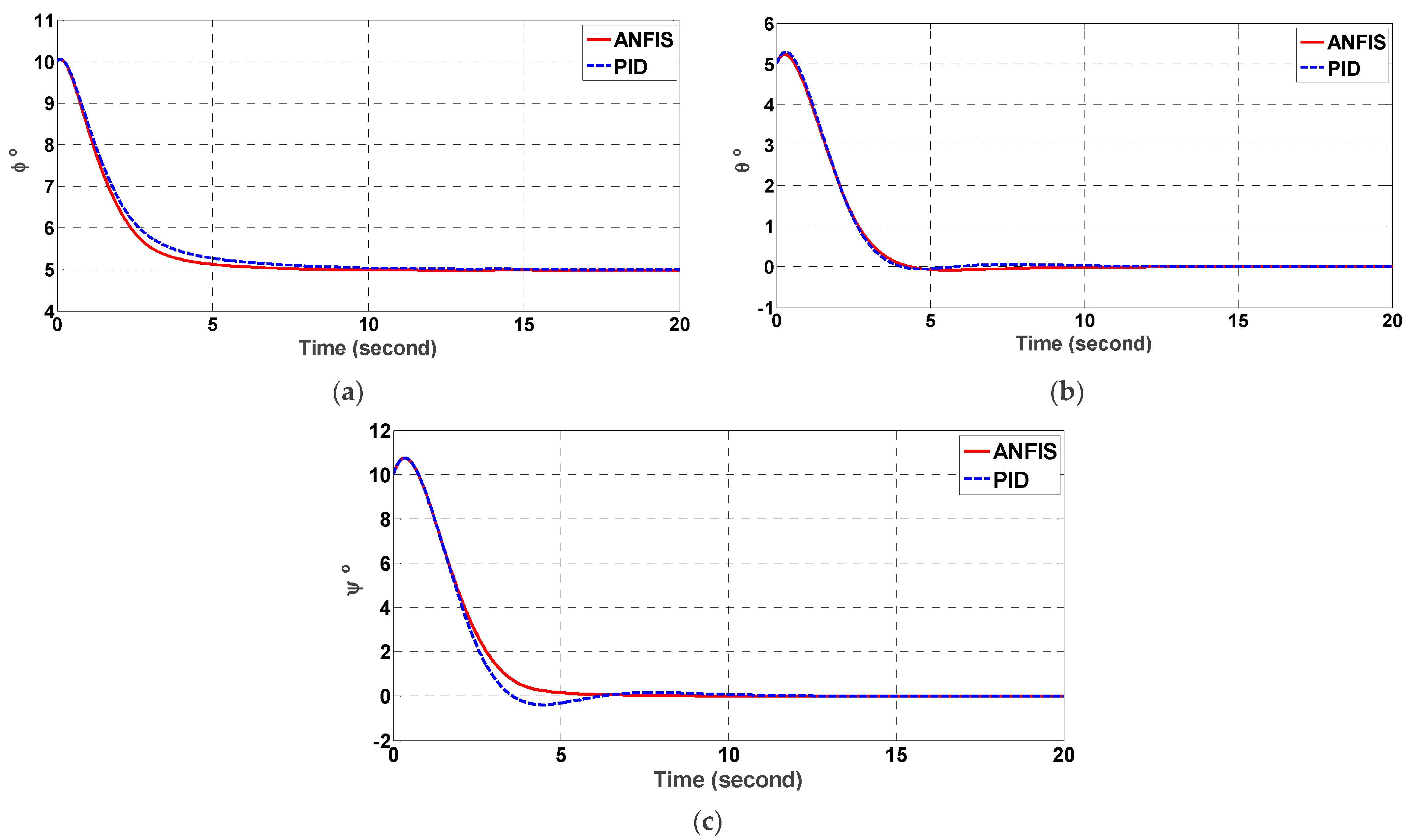
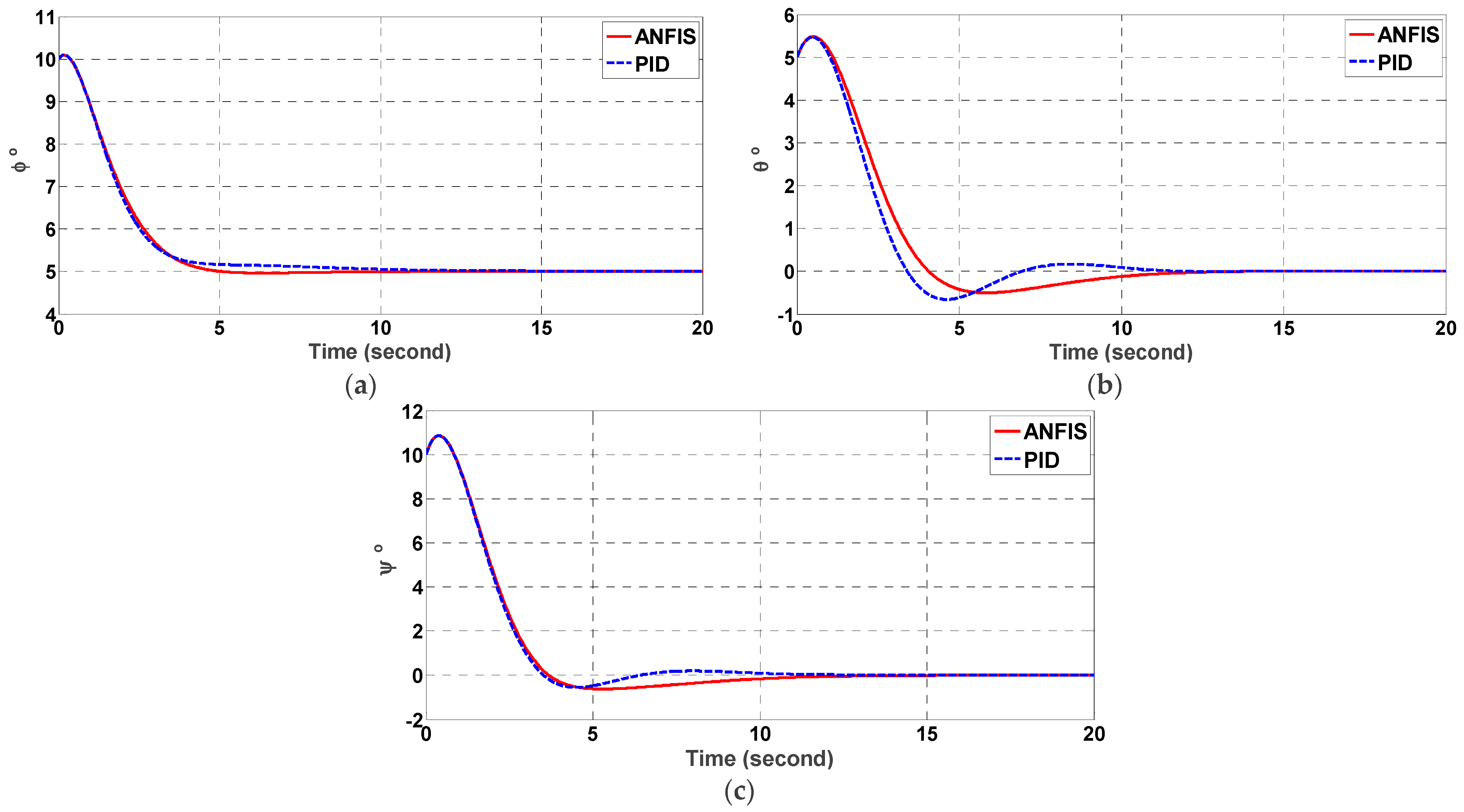
5.1. ANFIS Performance Comparison
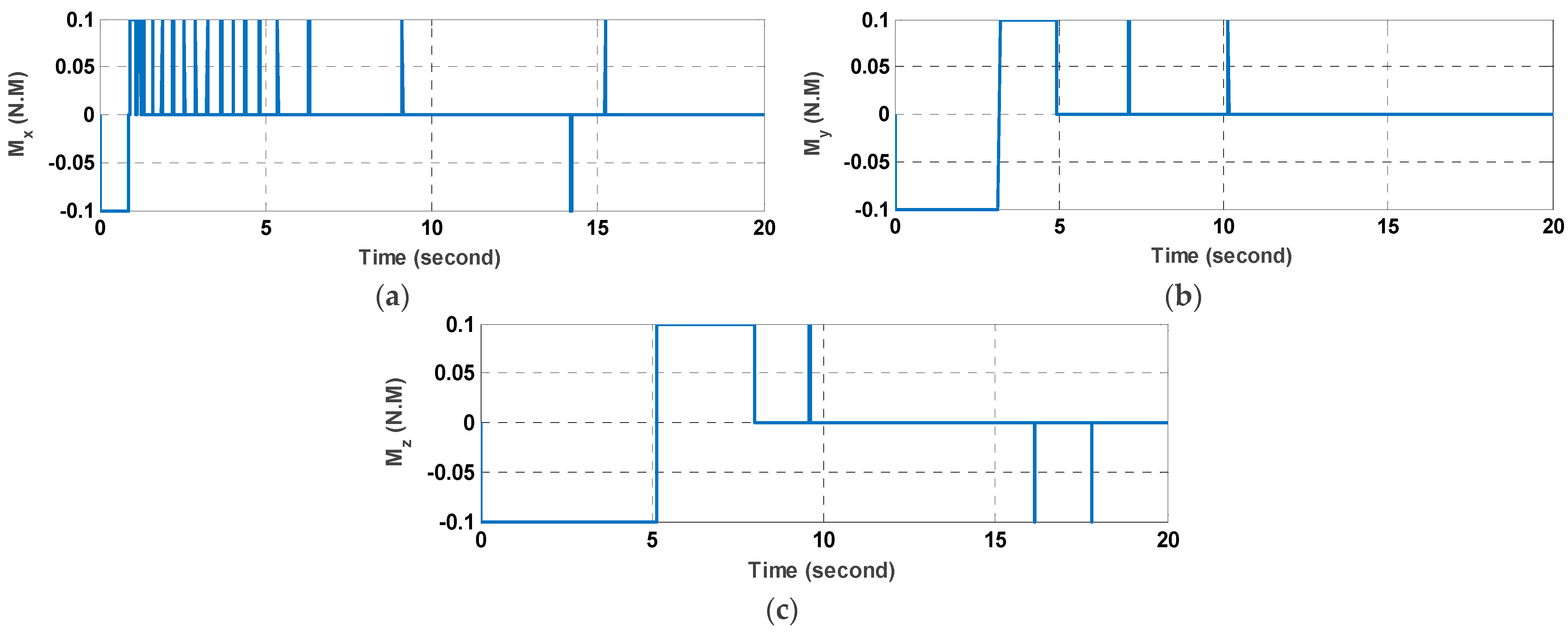
5.2. Command Modulation
5.3. Monte Carlo Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ismail, Z.; Varatharajoo, R. A study of reaction wheel configurations for a 3-axis satellite attitude control. Adv. Sp. Res. 2010, 45, 750–759. [Google Scholar] [CrossRef]
- Inamori, T.; Sako, N.; Nakasuka, S. Compensation of time-variable magnetic moments for a precise attitude control in nano- and micro-satellite missions. Adv. Sp. Res. 2011, 48, 432–440. [Google Scholar] [CrossRef]
- Siahpour, S.; Zand, M.M.; Mousavi, M. Dynamics and vibrations of particle-sensing MEMS considering thermal and electrostatic actuation. Microsyst. Technol. 2018, 24, 1545–1552. [Google Scholar] [CrossRef]
- Mousavi, M.; Rahnavard, M.; Haddad, S. Observer based fault reconstruction schemes using terminal sliding modes. Int. J. Control 2020, 93, 881–888. [Google Scholar] [CrossRef]
- Mousavi, M.; Rahnavard, M.; Yazdi, M.R.H.; Ayati, M. On the Development of Terminal Sliding Mode Observers. In Proceedings of the 26th Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018; pp. 951–956. [Google Scholar] [CrossRef]
- Mousavi, M.; Rahnavard, M.; Ayati, M.; Hairi Yazdi, M.R. Terminal sliding mode observers for uncertain linear systems with matched disturbance. Asian J. Control 2019, 21, 377–386. [Google Scholar] [CrossRef] [Green Version]
- Sajjadi, M.; Chahari, M.; Pishkenari, H.N. Imaging performance of trolling mode atomic force microscopy: Investigation of effective parameters. Arch. Appl. Mech. 2022, 2022, 1–20. [Google Scholar] [CrossRef]
- Rahnavard, M.; Ayati, M.; Hairi Yazdi, M.R.; Mousavi, M. Finite time estimation of actuator faults, states, and aerodynamic load of a realistic wind turbine. Renew. Energy 2019, 130, 256–267. [Google Scholar] [CrossRef]
- Sajjadi, M.; Pishkenari, H.N.; Vossoughi, G. Dynamic modeling of trolling-mode AFM: Considering effects of cantilever torsion, nanoneedle flexibility and liquid-nanoneedle interactions. Ultramicroscopy 2017, 182, 99–111. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control Systems. J. Guid. Control Dyn. 2002, 28, 1689–1699. [Google Scholar]
- Sajjadi, M.; Chahari, M.; Pishkenari, H.N.; Vossoughi, G. Designing nonlinear observer for topography estimation in trolling mode atomic force microscopy. J. Vib. Control 2021. [Google Scholar] [CrossRef]
- Chahari, M.; Sajjadi, M. Modeling of eccentric nanoneedle in trolling-mode atomic force microscope. Microsc. Res. Tech. 2020, 84, 639–655. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhou, Z.; Li, R.; Yang, L.; Fourati, H. Attitude determination using a single sensor observation: Analytic quaternion solutions and property discussion. IET Sci. Meas. Technol. 2017, 11, 731–739. [Google Scholar] [CrossRef]
- Abtahi, S.; Sharifi, M. Machine learning method to control and observe for treatment and monitoring of hepatitis b virus. arXiv 2020, arXiv:2004.09751. [Google Scholar]
- Kristiansen, R.; Nicklasson, P.J. Satellite attitude control by quaternion-based backstepping. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 907–912. [Google Scholar]
- Kang, J.; Zhu, Z.H.; Wang, W.; Li, A.; Wang, C. Fractional order sliding mode control for tethered satellite deployment with disturbances. Adv. Sp. Res. 2017, 59, 263–273. [Google Scholar] [CrossRef]
- Aleksandrov, A.Y.; Aleksandrova, E.B.; Tikhonov, A.A. Stabilization of a programmed rotation mode for a satellite with electrodynamic attitude control system. Adv. Sp. Res. 2018, 62, 142–151. [Google Scholar] [CrossRef]
- Li, Y.; Ye, D.; Sun, Z. Robust finite time control algorithm for satellite attitude control. Aerosp. Sci. Technol. 2017, 68, 46–57. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S.; Wu, L. A structure simple controller for satellite attitude tracking maneuver. IEEE Trans. Ind. Electron. 2016, 64, 1436–1446. [Google Scholar] [CrossRef]
- Vatankhahghadim, B.; Damaren, C.J. Magnetic attitude control with impulsive thrusting using the hybrid passivity theorem. J. Guid. Control Dyn. 2017, 40, 1860–1876. [Google Scholar] [CrossRef] [Green Version]
- Fan, Z.; Hua, S.; Chundi, M.; Yuchang, L. An optimal attitude control of small satellite with momentum wheel and magnetic torquerods. In Proceedings of the 4th World Congress on Intelligent Control and Automation (Cat. No. 02EX527), Shanghai, China, 10–14 June 2002; Volume 2, pp. 1395–1398. [Google Scholar]
- Wisniewski, R.; Markley, F.L. Optimal magnetic attitude control. IFAC Proc. Vol. 1999, 32, 7991–7996. [Google Scholar] [CrossRef]
- Arantes, G.; Martins-Filho, L.S.; Santana, A.C. Optimal on-off attitude control for the Brazilian multimission platform satellite. Math. Probl. Eng. 2009, 2009, 750945. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Yue, X.; Li, P.; Yuan, J. Fast spacecraft adaptive attitude tracking control through immersion and invariance design. Acta Astronaut. 2017, 139, 77–84. [Google Scholar] [CrossRef]
- Lee, K.W.; Singh, S.N. 1 adaptive attitude control of satellites in elliptic orbits using solar radiation pressure. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 611–626. [Google Scholar] [CrossRef]
- Lee, K.W.; Singh, S.N. Non-certainty-equivalent adaptive satellite attitude control using solar radiation pressure. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 977–988. [Google Scholar] [CrossRef]
- Zhang, J.; Swain, A.K.; Nguang, S.K. Robust sensor fault estimation scheme for satellite attitude control systems. J. Franklin Inst. 2013, 350, 2581–2604. [Google Scholar] [CrossRef]
- Cao, L.; Li, H. Unscented predictive variable structure filter for satellite attitude estimation with model errors when using low precision sensors. Acta Astronaut. 2016, 127, 505–513. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, S.; Xing, Y.; Cao, X. Robust adaptive filter for small satellite attitude estimation based on magnetometer and gyro. Abstr. Appl. Anal. 2014, 2014, 159149. [Google Scholar] [CrossRef] [Green Version]
- Kouyama, T.; Kanemura, A.; Kato, S.; Imamoglu, N.; Fukuhara, T.; Nakamura, R. Satellite attitude determination and map projection based on robust image matching. Remote Sens. 2017, 9, 90. [Google Scholar] [CrossRef] [Green Version]
- Daley, S.; Gill, K.F. A design study of a self-organizing fuzzy logic controller. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1986, 200, 59–69. [Google Scholar] [CrossRef]
- Mukherjee, B.K.; Giri, D.K.; Sinha, M. Lorentz-force-based fuzzy proportional–integral–derivative attitude control for earth-pointing satellites. J. Spacecr. Rockets 2017, 54, 1153–1160. [Google Scholar] [CrossRef]
- Huo, B.; Xia, Y.; Yin, L.; Fu, M. Fuzzy adaptive fault-tolerant output feedback attitude-tracking control of rigid spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1898–1908. [Google Scholar] [CrossRef]
- Zhong, C.; Guo, Y.; Wang, L. Fuzzy active disturbance rejection attitude control of spacecraft with unknown disturbance and parametric uncertainty. Int. J. Control Autom. 2015, 8, 233–242. [Google Scholar] [CrossRef]
- Ran, D.; Chen, X.; Sheng, T. Adaptive fuzzy fault-tolerant control for rigid spacecraft attitude maneuver with finite-time convergence. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 779–792. [Google Scholar] [CrossRef]
- Sun, G.; Chen, J.; Zhu, B. Generalized predictive control for spacecraft attitude based on adaptive fuzzy estimator. J. Aerosp. Eng. 2017, 30, 4017024. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man. Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jenkins, B.M.; Annaswamy, A.M.; Lavretsky, E.; Gibson, T.E. Convergence Properties of Adaptive Systems and the Definition of Exponential Stability. SIAM J. Control Optim. 2018, 56, 2463–2484. [Google Scholar] [CrossRef]
- Wie, B. Space Vehicle Dynamics and Control; Aiaa: Reston, VA, USA, 1998; ISBN 1563472619. [Google Scholar]
- Finlay, C.C.; Maus, S.; Beggan, C.D.; Bondar, T.N.; Chambodut, A.; Chernova, T.A.; Chulliat, A.; Golovkov, V.P.; Hamilton, B.; Hamoudi, M. International geomagnetic reference field: The eleventh generation. Geophys. J. Int. 2010, 183, 1216–1230. [Google Scholar]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 12, ISBN 0792369033. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, W.; Ma, H.; Luo, Z.; Li, X. Degradation Alignment in Remaining Useful Life Prediction Using Deep Cycle-Consistent Learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Open-Set Domain Adaptation in Machinery Fault Diagnostics Using Instance-Level Weighted Adversarial Learning. IEEE Trans. Ind. Inform. 2021, 17, 7445–7455. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man. Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man. Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Ramos-Fernández, J.C.; López-Morales, V.; Márquez-Vera, M.A.; Pérez, J.M.X.; Suarez-Cansino, J. Neuro-Fuzzy Modelling and Stable PD Controller for Angular Position in Steering Systems. Int. J. Automot. Technol. 2021, 22, 1495–1503. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Transfer learning using deep representation regularization in remaining useful life prediction across operating conditions. Reliab. Eng. Syst. Saf. 2021, 211, 107556. [Google Scholar] [CrossRef]
- Hanafy, T.O.S. Modeling and Identification of Spacecraft Systems Using Adaptive Neuro Fuzzy Inference Systems (ANFIS). IOSR J. Eng. 2014, 4, 47–59. [Google Scholar] [CrossRef]
- Gupta, A.K.; Kumar, P.; Sahoo, R.K.; Sahu, A.K.; Sarangi, S.K. Performance measurement of plate fin heat exchanger by exploration: ANN, ANFIS, GA, and SA. J. Comput. Des. Eng. 2017, 4, 60–68. [Google Scholar] [CrossRef] [Green Version]
- Ting, W.; Bo, X. ANFIS Controller for Spacecraft Formation Flying. In Proceedings of the International Conference on Computer Science Education Innovation & Technology (CSEIT), Phuket, Thailand, 28–29 October 2013; Global Science and Technology Forum: Singapore, 2013; p. 45. [Google Scholar]
- Abtahi, S.; Sharifi, M. Machine Learning Method Used to find Discrete and Predictive Treatment of Cancer. arXiv 2020, arXiv:2004.09753. [Google Scholar]



| Ix | Iy | Iz | |
|---|---|---|---|
| Moment of Inertia | 1.5 | 2.6 | 3 |
| Moments of Inertia in case of uncertainty | 2.5 | 4 | 3.3 |
| (deg) | (deg) | (deg) | ||||
|---|---|---|---|---|---|---|
| Initial condition | 0.0125 | 0.05 | 0.075 | 10 | 5 | 10 |
| Desired condition | 0 | 0 | 0 | 5 | 0 | 0 |
| X Axis | Y Axis | Z Axis | Total | |
|---|---|---|---|---|
| Without noise and uncertainty | ||||
| ANFIS | 0.1311 | 0.3956 | 0.7208 | 1.2475 |
| PID | 0.1287 | 0.4282 | 0.7485 | 1.3054 |
| Considering noise | ||||
| ANFIS | 0.1732 | 0.4117 | 0.6925 | 1.2774 |
| PID | 0.1983 | 0.4719 | 0.8126 | 1.4830 |
| Considering uncertainty | ||||
| ANFIS | 0.1910 | 0.6030 | 0.7891 | 1.5831 |
| PID | 0.1992 | 0.7048 | 0.8343 | 1.7383 |
| X Axis | Y Axis | Z Axis | |
|---|---|---|---|
| Without noise and uncertainty | |||
| ANFIS | 7.23 | 4.87 | 8.88 |
| PID | 9.62 | 8.82 | 9.51 |
| Considering noise | |||
| ANFIS | 6.4 | 6.62 | 4.94 |
| PID | 9.34 | 8.68 | 9.46 |
| Considering uncertainty | |||
| ANFIS | 4.59 | 11.38 | 10.9 |
| PID | 9.84 | 10.65 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Abtahi, S.M.; Chahari, M.; Zhao, T. An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System. Mathematics 2022, 10, 976. https://doi.org/10.3390/math10060976
Wang X, Abtahi SM, Chahari M, Zhao T. An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System. Mathematics. 2022; 10(6):976. https://doi.org/10.3390/math10060976
Chicago/Turabian StyleWang, Xin, Seyed Mehdi Abtahi, Mahmood Chahari, and Tianyu Zhao. 2022. "An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System" Mathematics 10, no. 6: 976. https://doi.org/10.3390/math10060976
APA StyleWang, X., Abtahi, S. M., Chahari, M., & Zhao, T. (2022). An Adaptive Neuro-Fuzzy Model for Attitude Estimation and Control of a 3 DOF System. Mathematics, 10(6), 976. https://doi.org/10.3390/math10060976







