Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations
Abstract
:1. Introduction
2. Basic Definitions and the Main Theorems
3. Legendre Polynomials and Numerical Scheme
3.1. The Shifted Legendre Polynomials
3.2. Convergence Analysis
3.3. Construction of the Numerical Scheme of MSFFKS and MSFFKDVE
- (1)
- We can approximate the function by taking the first terms of the sum of the shifted Legendre polynomials as follows:
- (2)
- (3)
- At points , we collocate the Equation (24) as given below:
- (4)
- By substituting from Equation (23) into the Equations (18)–(21), we obtain the following related initial and boundary conditions of this system:andWe thus get the roots and we find the solution of the following equation:and we then set it as the collocation points.
- (5)
- We solve the set of the ordinary differential Equations (25)–(28) for getting the unknowns By setting the following points and putting , we divide the interval into subintervals of equal length. Hence, clearly, the system involving the Equations (25)–(28) transforms to a set of nonlinear algebraic equations as follows:under the initial and boundary conditions given byand
- (6)
- Before applying the Newton-Raphson iteration method with , we set the system such as (30)–(33) in matrix form given bywhere and are the nonlinear terms and the inverse of the Jacobian matrix, respectively. We set and, in view of (26) and (28), we can get the initial solution .
- (a)
- (b)
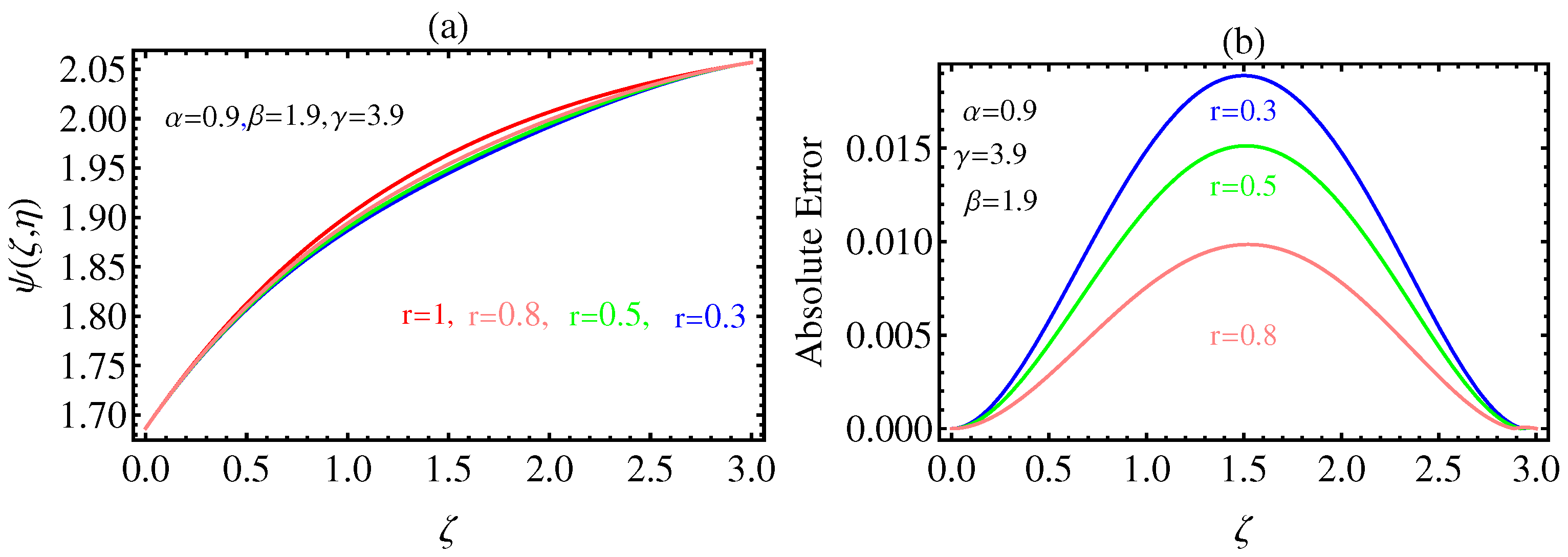
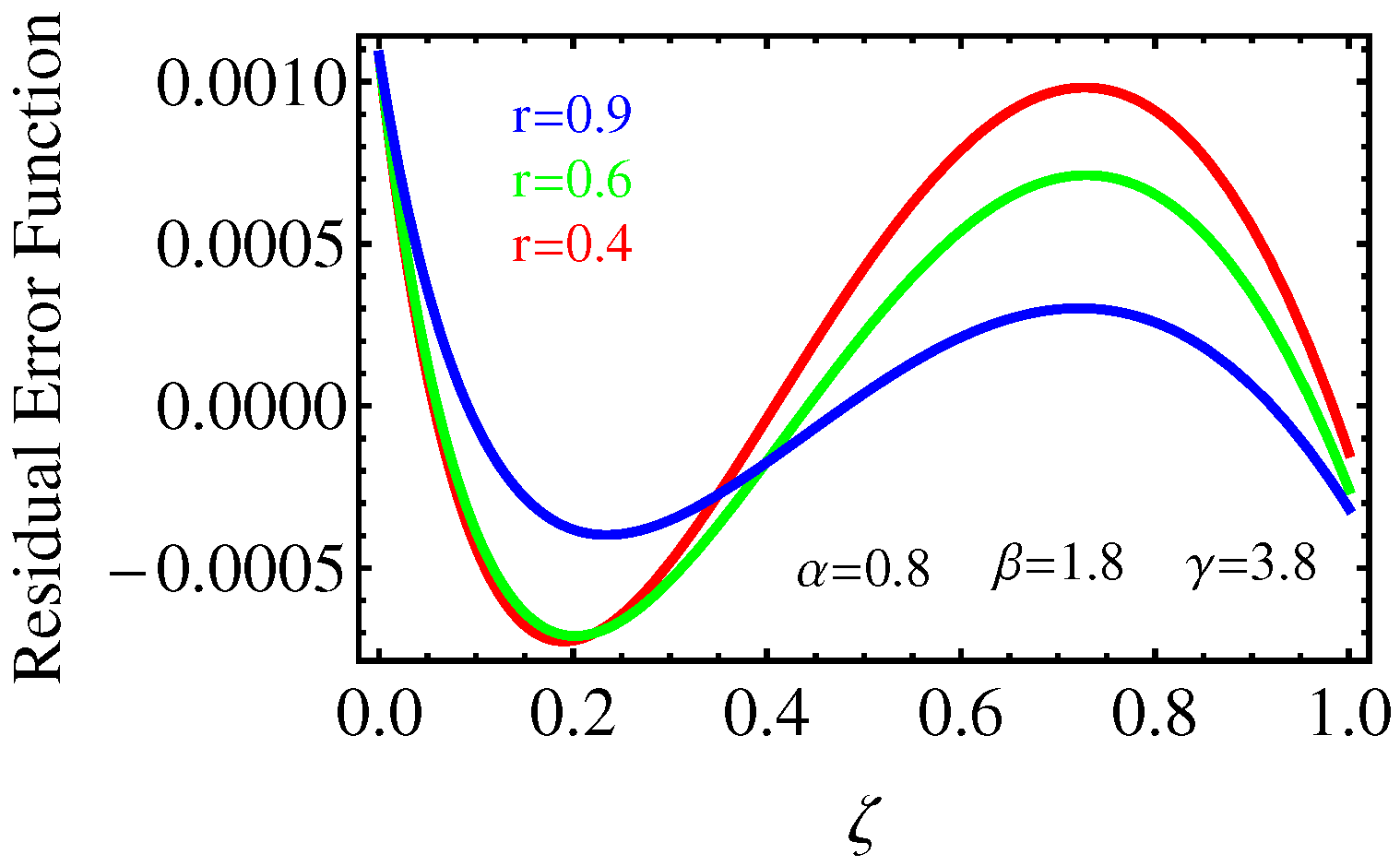
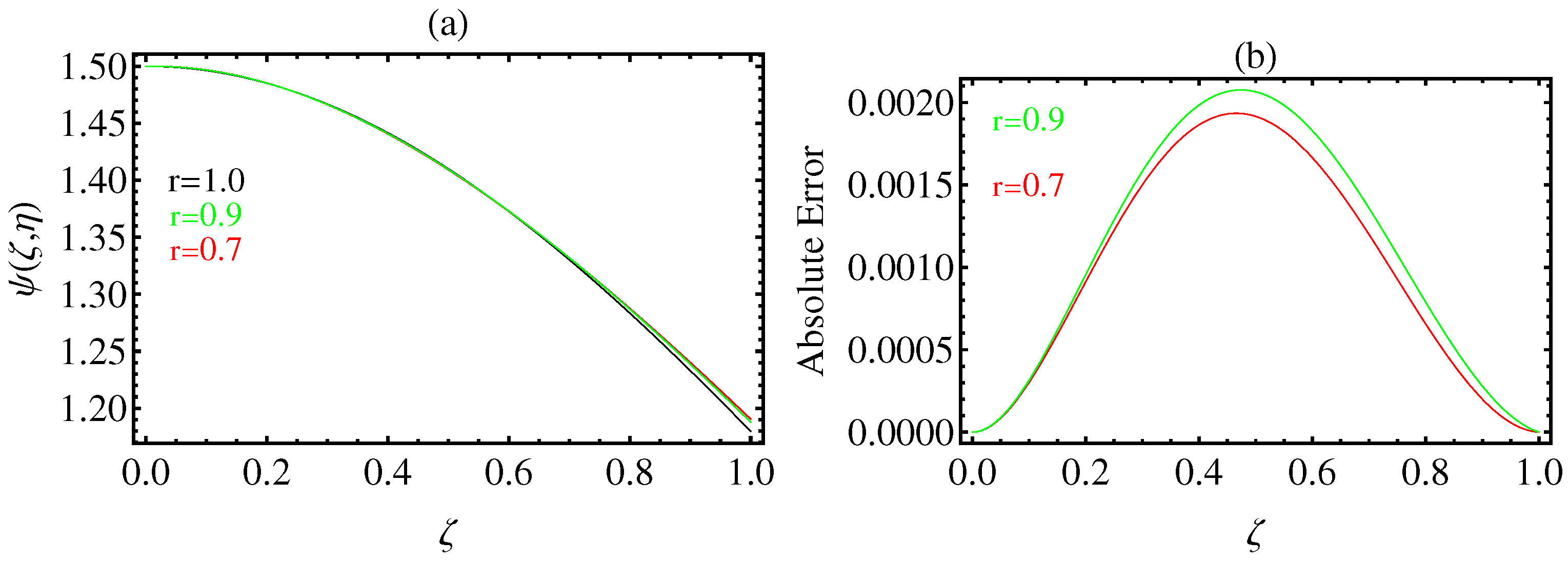
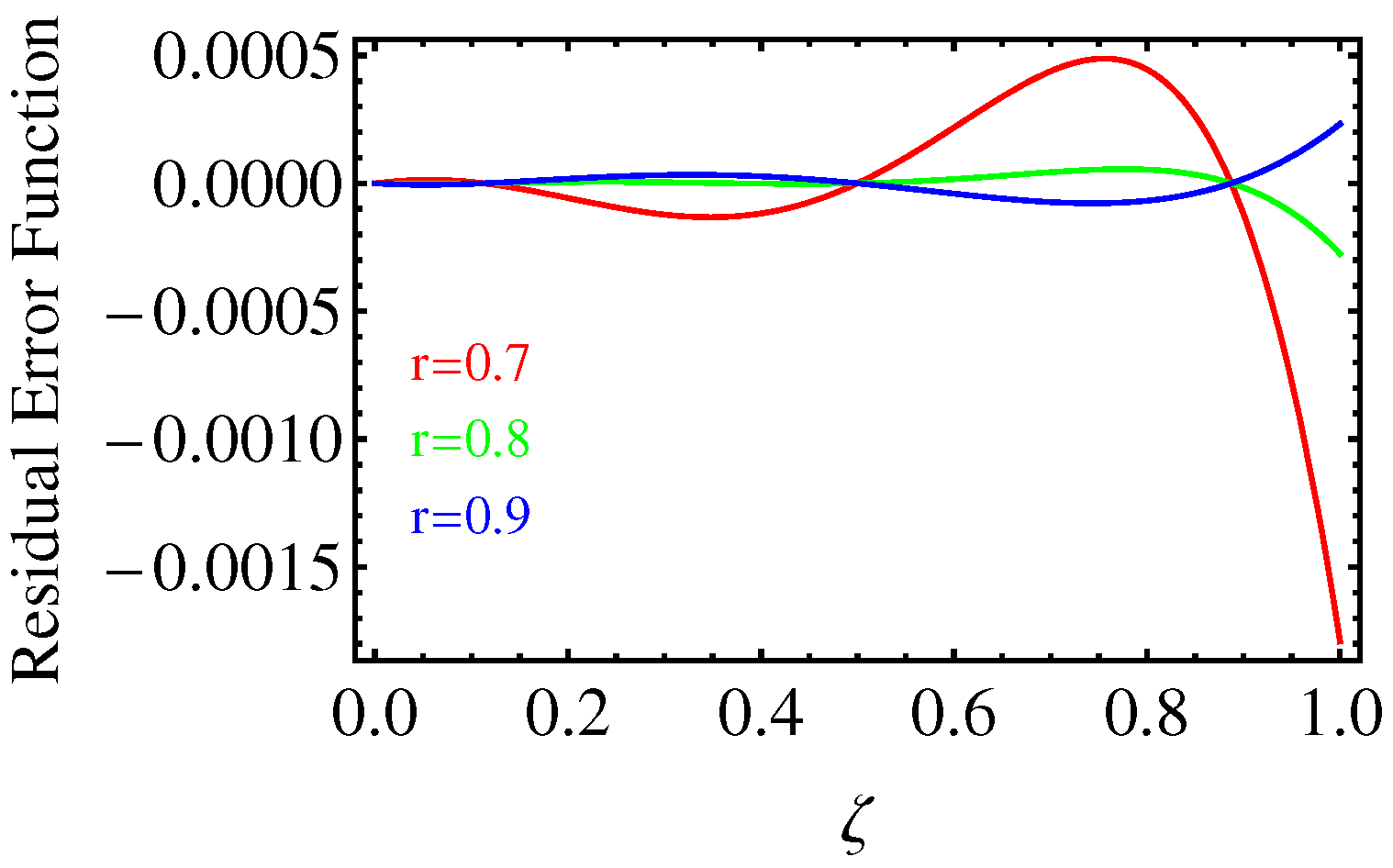
4. Numerical Results and Graphical Illustrations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1999; Volume 198. [Google Scholar]
- Srivastava, H.M. An introductory overview of fractional-calculus operators based upon the Fox-Wright and related higher transcendental functions. J. Adv. Eng. Comput. 2021, 5, 135–166. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Gómez-Aguilar, J.F.; Aly, S.; Saad, K.M. A fuzzy fractional model of coronavirus (COVID-19) and its study with Legendre spectral method. Results Phys. 2021, 21, 103773. [Google Scholar] [CrossRef] [PubMed]
- Izadi, M.; Srivastava, H.M. A novel matrix technique for multi-order pantograph differential equations of fractional order. Proc. R. Soc. A Math. Phys. Eng. Sci. 2021, 477, 2021031. [Google Scholar] [CrossRef]
- Saad, K.M.; Alqhtani, M. Numerical simulation of the fractal-fractional reaction diffusion equations with general nonlinear. AIMS Math. 2021, 6, 3788–3804. [Google Scholar] [CrossRef]
- Kumar, S.; Pandey, R.K.; Srivastava, H.M.; Singh, G.N. A convergent collocation approach for generalized fractional integro-differential equations using Jacobi poly-fractonomials. Mathematics 2021, 9, 979. [Google Scholar] [CrossRef]
- He, J.-H. Variational iteration method: A kind of nonlinear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 708–799. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Sharif, E.H.F. Analytical study for time and time-space fractional Burgers equation. Adv. Differ. Equ. 2017, 2017, 300. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.-C.; Huang, L.-L.; Zeng, Y. Fast Adomian decomposition method for the Cauchy problem of the time-fractional reaction diffusion equation. Adv. Mech. Eng. 2016, 8, 1687814016629898. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014, 54, 937954. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Yoshimoto, Y.; Suda, R. Second order accuracy finite difference methods for space-fractional partial differential equations. J. Comput. Appl. Math. 2017, 320, 101–119. [Google Scholar] [CrossRef]
- Cenesiz, Y.C.; Keskin, Y.; Kurnaz, A. The solution of the Bagley-Torvik equation with the generalized Taylor collocation method. J. Frankl. Inst. 2010, 347, 452–466. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Aomari, A.-K.N.; Saad, K.M.; Hamanah, W.M. Some dynamical models involving fractional-order derivatives with the Mittag-Leffler type kernels and their applications based upon the Legendre spectral collocation method. Fractal Fract. 2021, 5, 131. [Google Scholar] [CrossRef]
- Saad, K.M. New fractional derivative with non-singular kernel for deriving Legendre spectral collocation method. Alex. Eng. J. 2020, 59, 1909–1917. [Google Scholar] [CrossRef]
- Abdeljawad, T. A Lyapunov type inequality for fractional operators with nonsingular Mittag-Leffler kernel. J. Inequalities Appl. 2017, 2017, 130. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional diferentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal-fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Saad, K.M.; Khader, M.M.; Gómez-Aguilar, J.F.; Baleanu, D. Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 023116. [Google Scholar] [CrossRef]
- Hosseininia, M.; Heydari, M.H.; Avazzadeh, Z. The numerical treatment of nonlinear fractal-fractional 2D Emden-Fowler equation utilizing 2D Chebyshkov polynomials. Fractals 2020, 28, 2040042. [Google Scholar] [CrossRef]
- Khalil, H.; Khan, R.A.; Al-Smadi, M.H.; Freihat, A.A.; Shawagfeh, N. New operational matrix for shifted Legendre polynomials and fractional differential equations with variable coefficients. Punjab Univ. J. Math. 2015, 47, 1–23. [Google Scholar]
- Srivastava, H.M.; Saad, K.M. A comparative study of the fractional-order clock chemical model. Mathematics 2020, 8, 1436. [Google Scholar] [CrossRef]
- Lebedev, N.N. Special Functions and Their Applications; Silverman, R.A., Translator; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Khader, M.M. On the numerical solution and convergence study for system of non-linear fractional diffusion equations. Can. J. Phys. 2014, 92, 1658–1666. [Google Scholar] [CrossRef]
- Khater, A.H.; Temsah, R.S. Numerical solutions of the generalized Kuramoto-Sivashinsky equation by Chebyshev spectral collocation methods. Comput. Math. Appl. 2008, 56, 1465–1472. [Google Scholar] [CrossRef] [Green Version]
- Kuramoto, Y. Diffusion-induced chaos in reaction systems. Prog. Theor. Phys. Suppl. 1978, 64, 346–367. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. Nonlinear analysis of hydrodynamic instability in laminar flames. I. Derivation of basic equations. Acta Astronaut. 1977, 4, 1177–1206. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. On flame propagation under conditions of stoichiometry. SIAM J. Appl. Math. 1980, 39, 67–82. [Google Scholar] [CrossRef]
- Liu, X. Gevrey class regularity and approximate inertial manifolds for the Kuramoto-Sivashinsky equation. Physica D Nonlinear Phenom. 1991, 50, 135–151. [Google Scholar] [CrossRef]
- Grimshaw, R.; Hooper, A.P. The non-existence of a certain class of travelling wave solutions of the Kuramoto-Sivashinsky equation. Physica D Nonlinear Phenom. 1991, 50, 231–238. [Google Scholar] [CrossRef]
- Baldwin, D.; Goktas, U.; Hereman, W.; Hong, L.; Martino, R.S.; Miller, J.C. Symbolic computation of exact solutions expressible in hyperbolic and elliptic functions for nonlinear PDEs. J. Symb. Comput. 2004, 37, 669–705. [Google Scholar] [CrossRef] [Green Version]
- Parkes, E.J.; Duffy, B.R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 1895, 539, 422–443. [Google Scholar] [CrossRef]
- Yang, X.-J.; Hristov, J.; Srivastava, H.M.; Ahmad, B. Modelling fractal waves on shallow water surfaces via local fractional Korteweg-de Vries equation. Abstr. Appl. Anal. 2014, 2014, 278672. [Google Scholar] [CrossRef] [Green Version]
- Fung, M.-K. KdV equation as an Euler-Poincaré equation. Chin. J. Phys. 1997, 35, 789–796. [Google Scholar]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “Solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240–243. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Saad, K.M.; Hamanah, W.M. Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations. Mathematics 2022, 10, 1089. https://doi.org/10.3390/math10071089
Srivastava HM, Saad KM, Hamanah WM. Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations. Mathematics. 2022; 10(7):1089. https://doi.org/10.3390/math10071089
Chicago/Turabian StyleSrivastava, Hari M., Khaled Mohammed Saad, and Walid M. Hamanah. 2022. "Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations" Mathematics 10, no. 7: 1089. https://doi.org/10.3390/math10071089
APA StyleSrivastava, H. M., Saad, K. M., & Hamanah, W. M. (2022). Certain New Models of the Multi-Space Fractal-Fractional Kuramoto-Sivashinsky and Korteweg-de Vries Equations. Mathematics, 10(7), 1089. https://doi.org/10.3390/math10071089







