Unsupervised Fault Diagnosis of Sucker Rod Pump Using Domain Adaptation with Generated Motor Power Curves
Abstract
:1. Introduction
2. Generation of the Motor Power Curves
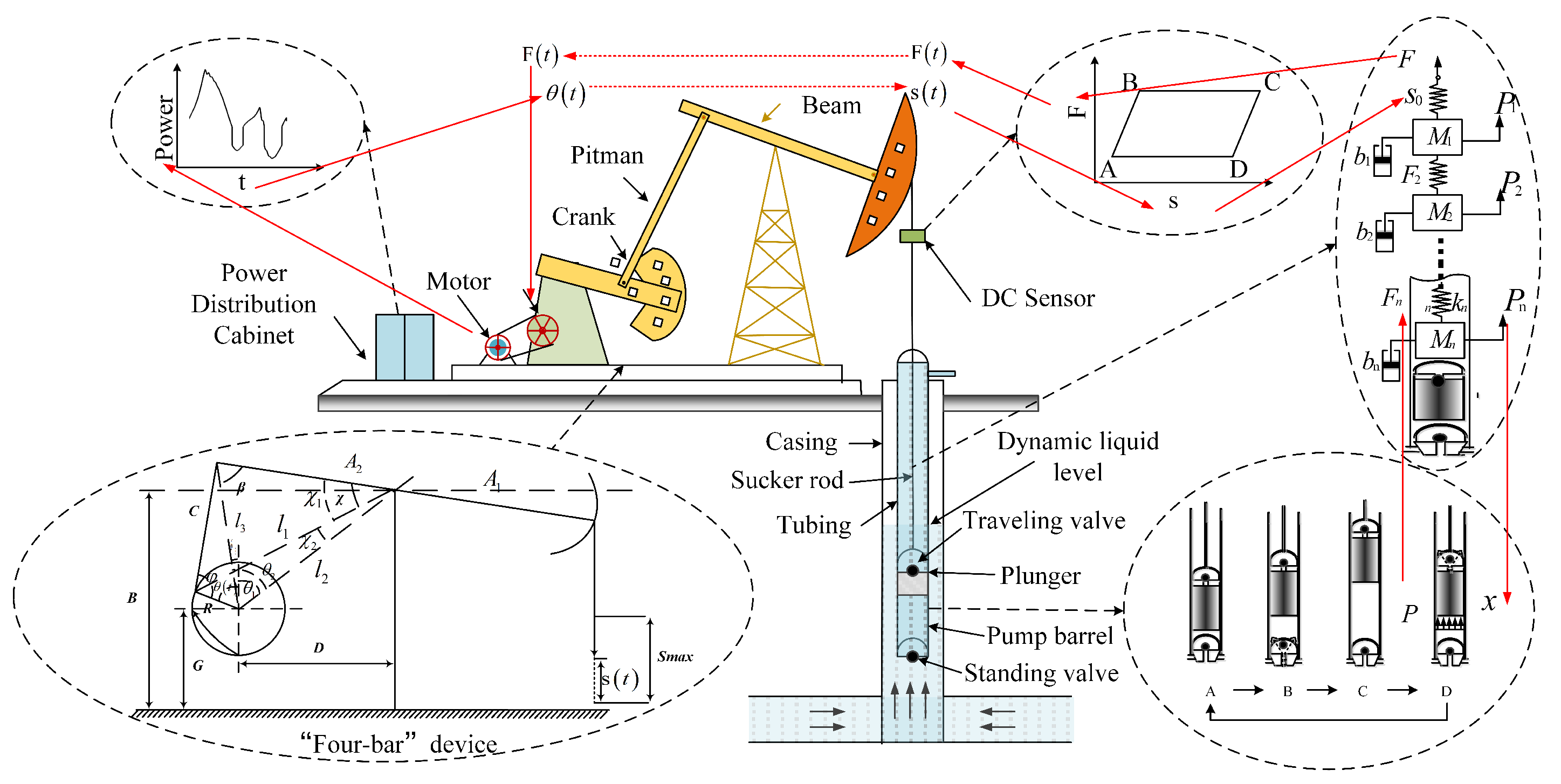
2.1. Mathematical Model of the Sucker Rod Pumping System
2.1.1. Polished Rod Motion Simulation
2.1.2. Rod String Simulation
2.1.3. Down-Hole Pump Simulation
2.1.4. Moter and Gearbox Simulation
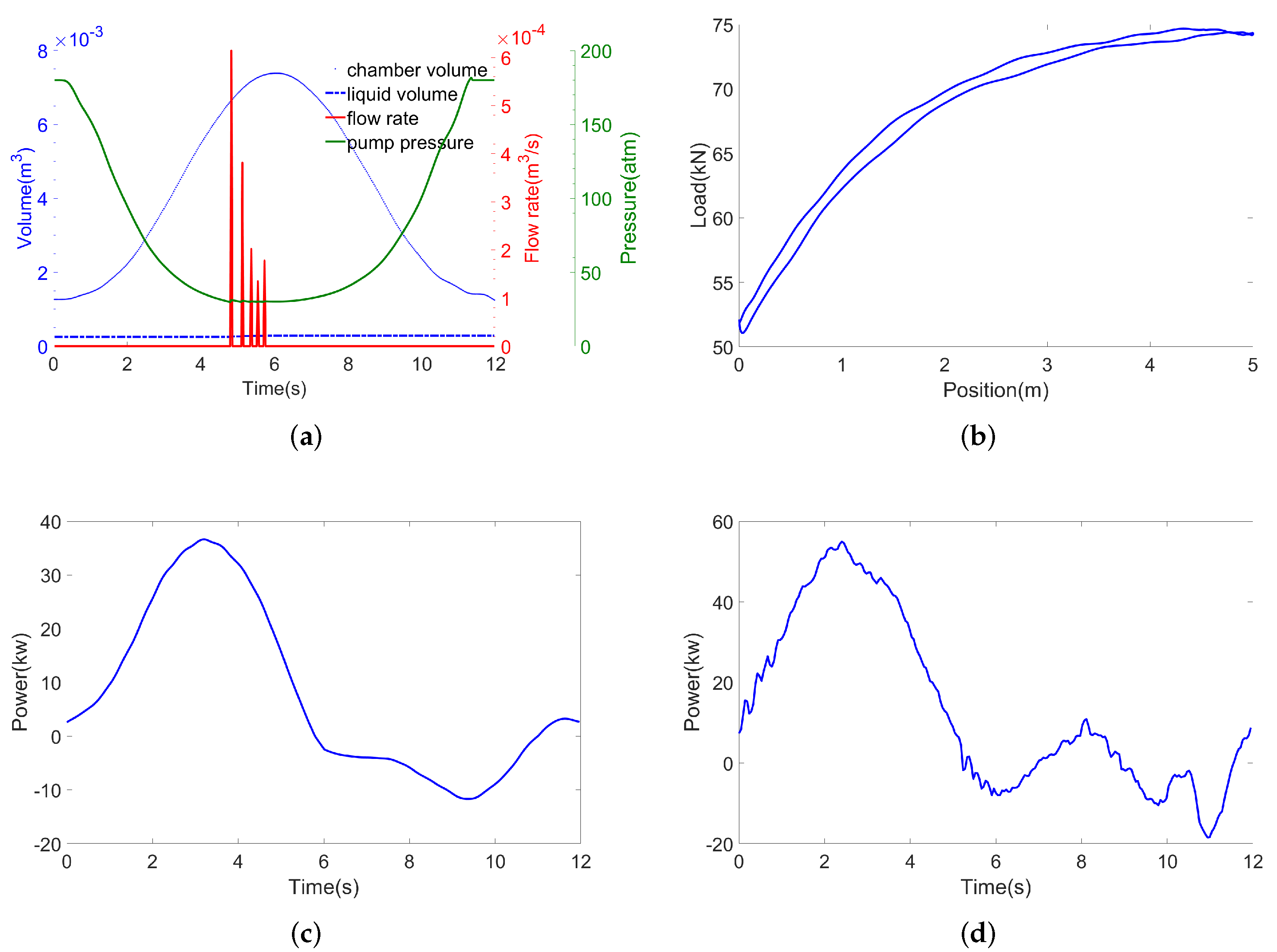
2.1.5. Dynamic Implementation of the Overall Model
| Algorithm 1: Generation of motor power waveforms. |
 |
2.2. Generation for Faulty Working States
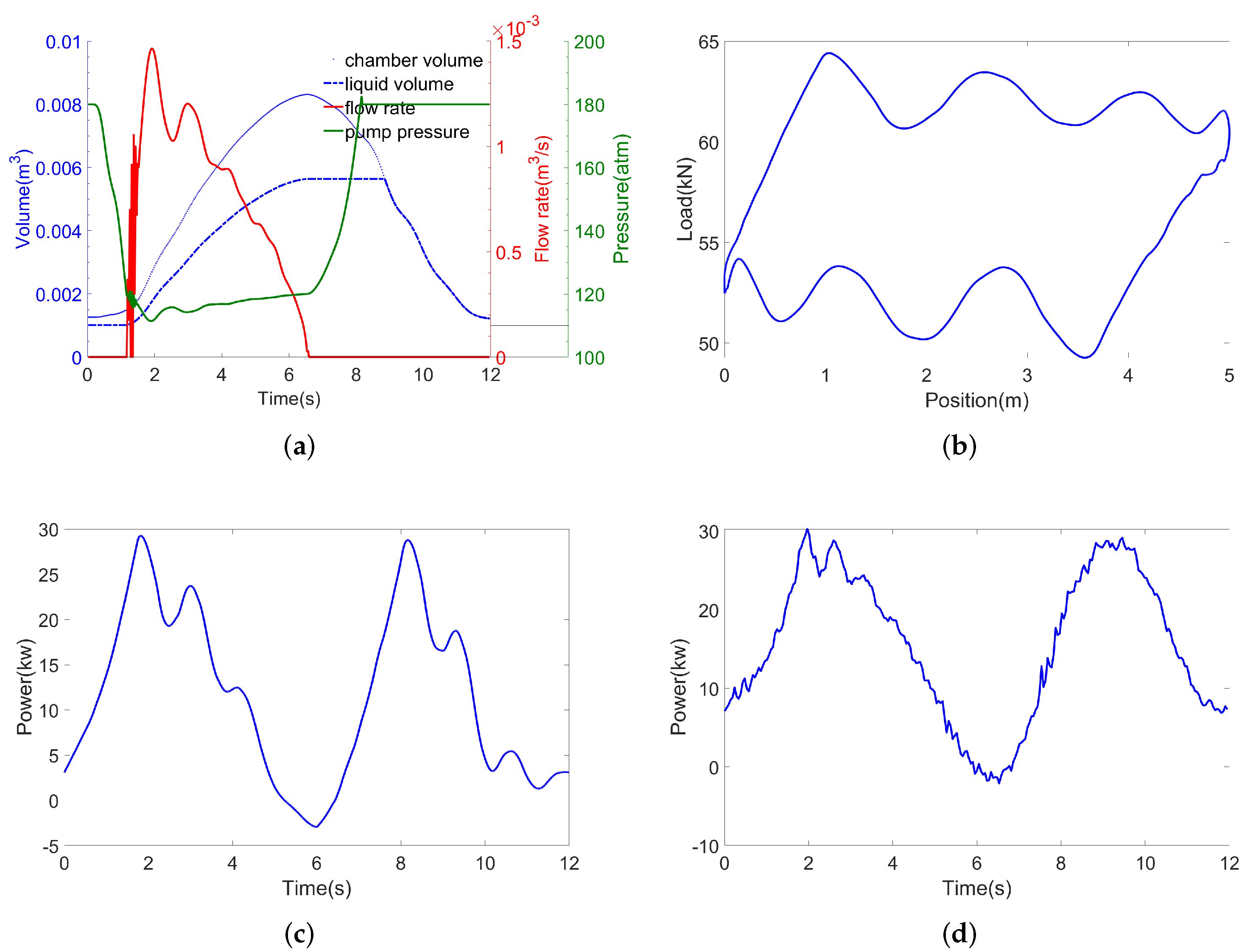
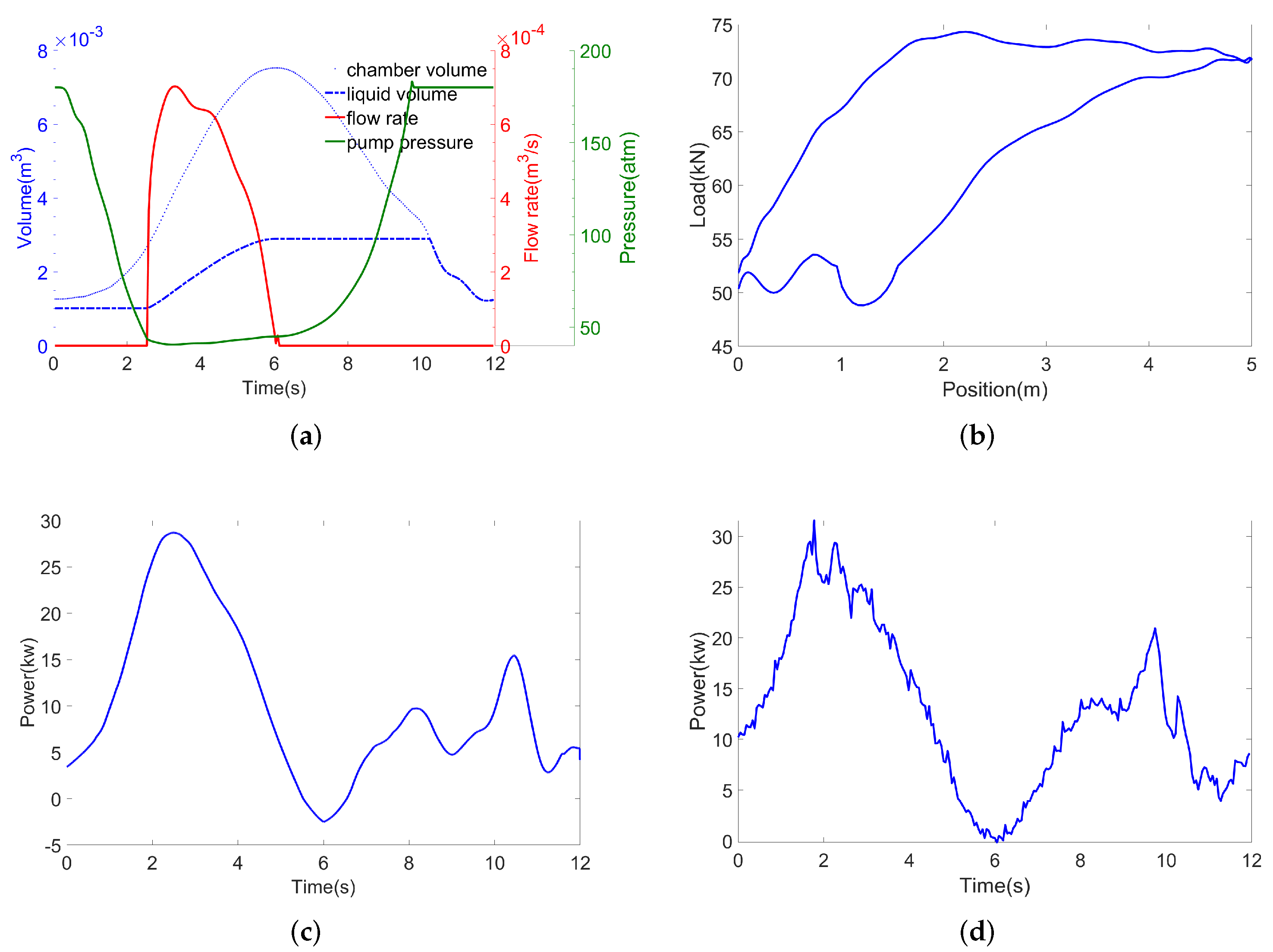
2.2.1. Traveling Valve Leakage
2.2.2. Insufficient Liquid Supply
2.2.3. Gas Affected
2.2.4. Gas Locking
2.2.5. Parting Rod
3. Domain Adaptation Based on Generated Motor Power Curves
3.1. Problem Setting
3.2. Network Architecture
3.2.1. Pseudo-Label Learning Layer
3.2.2. Feature Generator Network
3.2.3. Label Classifier
3.2.4. Domain Classifier
3.2.5. Conditional Distribution Discrepancy Metrics
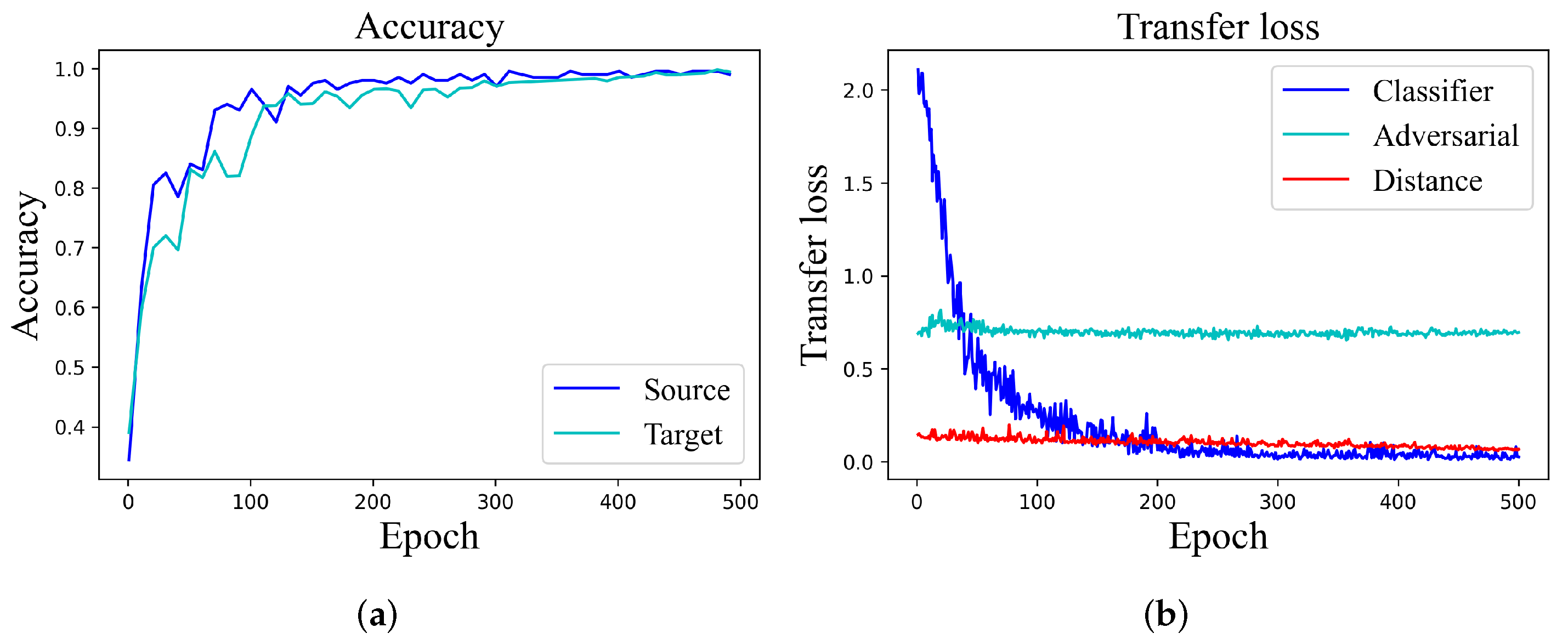
3.3. Optimization
4. Industrial Experiments
4.1. Data Collection
- Power acquisition unit: realize the motor power calculation with the help of the ATT7022B.
- Transmission unit: realize remote query and parameter adjustment on mobiles and computers.
- Human–machine interaction unit: a touch screen is equipped to facilitate parameter entry, data query, and data display.
- Data storage unit: it is used to store the collected and calculated data and parameters.
- Data processing unit: with the help of the XC7Z020CLG400 chip, it implements the core calculation, including the trained diagnostic model, device operation, etc.
4.2. Validation of the Generated Motor Power Curves
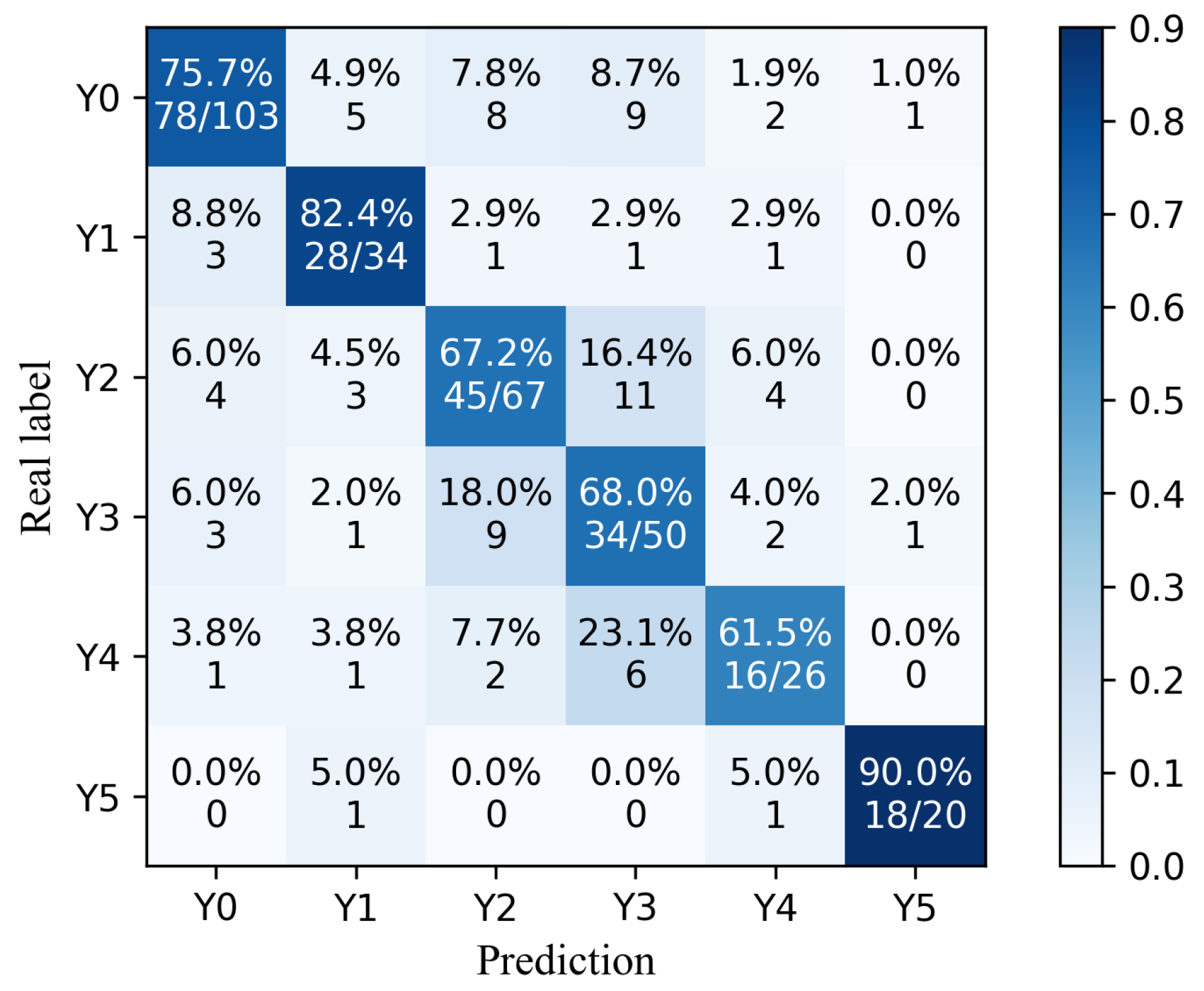
4.3. Diagnosis Based on Domain Adaptation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Damping coefficient of ith rod string | |
| Constant | |
| Henry’s law constant | |
| Perimeter of the rod string and pump | |
| Diameter of pump | |
| Diameter of sucker rod | |
| F | Polished rod load |
| Crank torque | |
| Friction coefficient of ith rod string | |
| Friction coefficient of plunger | |
| ith rod modulus of elasticity | |
| Length of ith rod string | |
| Mass of ith rod string | |
| Mass of free gas in pump | |
| Mass of whole gas in pump | |
| Mass of oil in pump | |
| Molar mass of methane | |
| Mass of water in pump | |
| n | Times of stroke |
| Motor speed | |
| Motor power | |
| Discharge pressure of the pump | |
| Load on the plunger | |
| Submergence pressure (Mpa) | |
| Q | Flow rate though standing valve |
| Weight radius of crankshaft | |
| S | Displacement of sucker rod node |
| Are of sucker rod | |
| Leaked area of traveling valve | |
| Passage area of standing valve | |
| Passage area of traveling valve | |
| Passage area of plunger | |
| Absolute temperature | |
| Torque factor | |
| Volume of oil in the pump | |
| Volume of the pump | |
| Volume of water in the pump | |
| Balanced weight of crankshaft | |
| Weight of crankshaft | |
| Counterbalance weight | |
| Gas mass ratio of produced fluid | |
| Oil mass ratio of produced fluid | |
| Water mass ratio of produced fluid | |
| Gas solubility | |
| Efficiency of four-bar linkage | |
| Efficiency of motor and reduction gearbox | |
| Gas related constant | |
| Density of produced fluid | |
| Density of oil | |
| Density of water | |
| Damping coefficient of standing valve | |
| Angular velocity of crankshaft |
References
- Lv, X.; Wang, H.; Zhang, X.; Liu, Y.; Jiang, D.; Wei, B. An evolutional SVM method based on incremental algorithm and simulated indicator diagrams for fault diagnosis in sucker rod pumping systems. J. Pet. Sci. Eng. 2021, 203, 108806. [Google Scholar] [CrossRef]
- Han, Y.; Song, X.; Li, K.; Yan, X. Hybrid modeling for submergence depth of the pumping well using stochastic configuration networks with random sampling. J. Pet. Sci. Eng. 2022, 208, 109423. [Google Scholar] [CrossRef]
- Li, K.; Han, Y.; Wang, T. A novel prediction method for down-hole working conditions of the beam pumping unit based on 8-directions chain codes and online sequential extreme learning machine. J. Pet. Sci. Eng. 2018, 160, 285–301. [Google Scholar] [CrossRef]
- Han, Y.; Li, K.; Ge, F.; Wang, Y.; Xu, W. Online fault diagnosis for sucker rod pumping well by optimized density peak clustering. ISA Trans. 2021, 120, 222–234. [Google Scholar] [CrossRef] [PubMed]
- Takacs, G.; Kis, L. A new model to find optimum counterbalancing of sucker-rod pumping units including a rigorous procedure for gearbox torque calculations. J. Pet. Sci. Eng. 2021, 205, 108792. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, X.; Pan, R. Sucker rod pump working state diagnosis using motor data and hidden conditional random fields. IEEE Trans. Ind. Electron. 2019, 67, 7919–7928. [Google Scholar] [CrossRef]
- Wei, J.; Gao, X. Fault Diagnosis of Sucker Rod Pump Based on Deep-Broad Learning Using Motor Data. IEEE Access 2020, 8, 222562–222571. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, X.; Li, X. Complete Simulation and Fault Diagnosis of Sucker-Rod Pumping. SPE Prod. Oper. 2021, 36, 277–290. [Google Scholar]
- Zheng, B.; Gao, X.; Li, X. Fault detection for sucker rod pump based on motor power. Control Eng. Pract. 2019, 86, 37–47. [Google Scholar] [CrossRef]
- Chen, L.; Gao, X.; Li, X. Using the motor power and XGBoost to diagnose working states of a sucker rod pump. J. Pet. Sci. Eng. 2021, 199, 108329. [Google Scholar] [CrossRef]
- Gibbs, S. Predicting the behavior of sucker-rod pumping systems. J. Pet. Technol. 1963, 15, 769–778. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, X.; Li, X. Diagnosis of sucker rod pump based on generating dynamometer cards. J. Process Control 2019, 77, 76–88. [Google Scholar] [CrossRef]
- Lv, X.; Wang, H.; Liu, Y.; Chen, S.; Lan, W.; Sun, B. A novel method of output metering with dynamometer card for SRPS under fault conditions. J. Pet. Sci. Eng. 2020, 192, 107098. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Q.; Yu, X.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Applications of Unsupervised Deep Transfer Learning to Intelligent Fault Diagnosis: A Survey and Comparative Study. IEEE Trans. Instrum. Meas. 2021, 70, 1–28. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Open-Set Domain Adaptation in Machinery Fault Diagnostics Using Instance-Level Weighted Adversarial Learning. IEEE Trans. Ind. Inf. 2021, 17, 7445–7455. [Google Scholar] [CrossRef]
- Ainapure, A.; Siahpour, S.; Li, X.; Majid, F.; Lee, J. Intelligent Robust Cross-Domain Fault Diagnostic Method for Rotating Machines Using Noisy Condition Labels. Mathematics 2022, 10, 455. [Google Scholar] [CrossRef]
- Zhang, H.; Ren, H.; Mu, Y.; Han, J. Optimal Consensus Control Design for Multiagent Systems with Multiple Time Delay Using Adaptive Dynamic Programming. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 136–144. [Google Scholar] [CrossRef]
- Ye, Z.; Yu, J.; Mao, L. Multisource Domain Adaption for Health Degradation Monitoring of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 7, 2279–2292. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Zhan, Z.; Wu, Q. Deep multi-scale separable convolutional network with triple attention mechanism: A novel multi-task domain adaptation method for intelligent fault diagnosis. Expert Syst. Appl. 2021, 182, 115087. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 2030–2096. [Google Scholar]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep convolutional transfer learning network: A new method for intelligent fault diagnosis of machines with unlabeled data. IEEE Trans. Ind. Electron. 2018, 66, 7316–7325. [Google Scholar] [CrossRef]
- Cheng, C.; Zhou, B.; Ma, G.; Wu, D.; Yuan, Y. Wasserstein distance based deep adversarial transfer learning for intelligent fault diagnosis with unlabeled or insufficient labeled data. Neurocomputing 2020, 409, 35–45. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, L.; Gao, H.; Lin, Z.; Liu, Y. MiDAN: A framework for cross-domain intelligent fault diagnosis with imbalanced datasets. Measurement 2021, 183, 109834. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Jia, L.; Gao, S.; Li, Q.; Qiu, M. Intelligent fault diagnosis by fusing domain adversarial training and maximum mean discrepancy via ensemble learning. IEEE Trans. Ind. Inf. 2020, 17, 2833–2841. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Deep Learning-Based Partial Domain Adaptation Method on Intelligent Machinery Fault Diagnostics. IEEE Trans. Ind. Electron. 2021, 68, 4351–4361. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ma, H.; Luo, Z.; Li, X. Universal domain adaptation in fault diagnostics with hybrid weighted deep adversarial learning. IEEE Trans. Ind. Inf. 2021, 17, 7957–7967. [Google Scholar] [CrossRef]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 2–8 December 2013; pp. 2200–2207. [Google Scholar]
- Li, X.; Zhang, W.; Xu, N.X.; Ding, Q. Deep learning-based machinery fault diagnostics with domain adaptation across sensors at different places. IEEE Trans. Ind. Electron. 2019, 67, 6785–6794. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Lu, N.; Xiao, H.; Sun, Y.; Han, M.; Wang, Y. A new method for intelligent fault diagnosis of machines based on unsupervised domain adaptation. Neurocomputing 2021, 427, 96–109. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, L.; Qiu, J.; Lu, J.; Wang, W. Unsupervised Domain Adaptation for Nonintrusive Load Monitoring Via Adversarial and Joint Adaptation Network. IEEE Trans. Ind. Inf. 2022, 18, 266–277. [Google Scholar] [CrossRef]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 1180–1189. [Google Scholar]







| Layer Type | Activation Function | Kernel Number | Kernel Size × Stride | Output Size |
|---|---|---|---|---|
| Input | / | / | / | |
| Conv1 | Relu | 16 | 64 × 1 | |
| MaxPooling1 | / | 16 | 2 × 2 | |
| Conv2 | Relu | 32 | 5 × 1 | |
| MaxPooling2 | / | 32 | 2 × 2 | |
| Conv3 | Relu | 64 | 5 × 1 | |
| MaxPooling3 | / | 64 | 2 × 2 | |
| Flatten | / | / | / | |
| FC | Relu | 1024 | / |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Well | CYJ14-5-73HB | Moter | Y250M-6 |
| /mm | 7000 | n/min | 4 |
| /mm | 3110 | /atm | 120 |
| C/mm | 5790 | /atm | 180 |
| B/mm | 7210 | :: | 0.1:0.2:0.2 |
| G/mm | 1460 | /mm | 44 |
| D/mm | 3110 | /mm | 22 |
| R/mm | 1270 | /mm | 1520 |
| /kg | 5374 | /m | 1600 |
| /kg | 5378 | /kg | 5139.2 |
| /kg | 1229 | /g·mol | 16 |
| Method | A | B | C | D | E |
|---|---|---|---|---|---|
| Collected samples | 0 | 240 | 240 | 240 | 240 |
| Generated samples | 300 | 0 | 150 | 300 | 450 |
| 1-D CNN | 0.747 | 0.863 | 0.907 | 0.933 | 0.94 |
| CNN | 0.713 | 0.843 | 0.883 | 0.90 | 0.9133 |
| MCRF | 0.733 | 0.837 | 0.883 | 0.893 | 0.9067 |
| Method | MDA | CDA | Pseudo-Labels |
|---|---|---|---|
| 1-D CNN | / | / | / |
| DANN | MMD | / | / |
| DATLN | MMD + Adversail | / | / |
| DTN | MMD | MMD | Pre-train network |
| MiDAN | Adversail | MMD | Pre-train network |
| MADAN (ours) | Adversail | MMD | Mechanism + Classifier |
| Method | Accuracy (%) | F1 (%) | MCC (%) |
|---|---|---|---|
| 1-D CNN | 83.33 | 83.25 | 79.9 |
| DANN | 91.67 | 91.38 | 89.69 |
| DATLN | 92.33 | 92.17 | 90.58 |
| DTN | 95.33 | 95.34 | 94.39 |
| MiDAN | 97 | 97.03 | 96.42 |
| MADAN (ours) | 98.33 | 98.51 | 98.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, D.; Gao, X. Unsupervised Fault Diagnosis of Sucker Rod Pump Using Domain Adaptation with Generated Motor Power Curves. Mathematics 2022, 10, 1224. https://doi.org/10.3390/math10081224
Hao D, Gao X. Unsupervised Fault Diagnosis of Sucker Rod Pump Using Domain Adaptation with Generated Motor Power Curves. Mathematics. 2022; 10(8):1224. https://doi.org/10.3390/math10081224
Chicago/Turabian StyleHao, Dezhi, and Xianwen Gao. 2022. "Unsupervised Fault Diagnosis of Sucker Rod Pump Using Domain Adaptation with Generated Motor Power Curves" Mathematics 10, no. 8: 1224. https://doi.org/10.3390/math10081224
APA StyleHao, D., & Gao, X. (2022). Unsupervised Fault Diagnosis of Sucker Rod Pump Using Domain Adaptation with Generated Motor Power Curves. Mathematics, 10(8), 1224. https://doi.org/10.3390/math10081224





