An Improved Wild Horse Optimizer for Solving Optimization Problems
Abstract
:1. Introduction
- The random running strategy is proposed to balance the exploration and exploitation phases.
- The dynamic inertia weight strategy is applied to the waterhole to achieve the optimal global solution.
- The competition for waterhole mechanism is introduced to stallion position calculations to boost exploitation behavior.
2. Wild Horse Optimizer
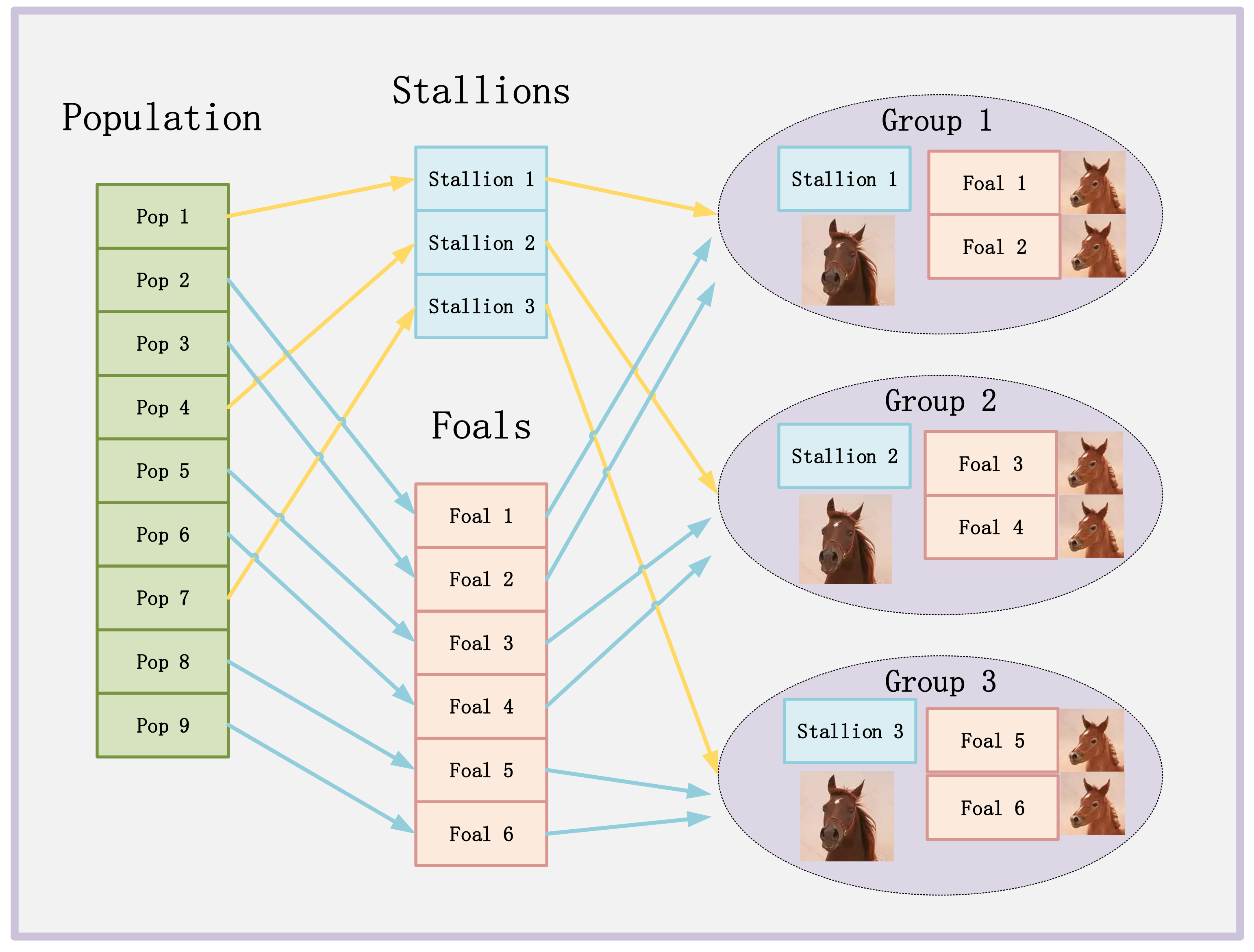
2.1. Creating Initial Populations, Horse Groups, Determining Leaders
2.2. Grazing Behavior
2.3. Horse Mating Behavior
2.4. Group Leadership
2.5. Exchange and Selection of Leaders
3. Improved Wild Horse Optimizer
3.1. Random Running Strategy (RRS)
3.2. Dynamic Inertia Weight Strategy (DIWS)
3.3. Competition for Waterhole Mechanism (CWHM)
3.4. Improved Wild Horse Optimizer
| Algorithm 1 Pseudocode of IWHO |
| Start IWHO. 1. Input IWHO parameters: PC = 0.13, PS = 0.2, wmin = 0.01, wmax = 0.99, PRR = 0.1. 2. Set population size (N) and the maximum number of iterations (T). 3. Initialize the population of horses at random. 4. Create foal groups and select stallions. 5. While (t ≤ T) 6. Calculate TDR using Equation (3). 7. Calculate Z using Equation (2). 8. For the number of stallions 9. For the number of foals 10. If rand > PC 11. Update the position of the foal using Equation (1). 12. Else if rand > PRR 13. Update the position of the foal using Equation (4). 14. Else 15. Update the position of the foal using Equation (7). 16. End 17. End for 18. If rand > PRR 19. If rand > 0.5 20. Generate the candidate position of stallion using Equation (10). 21. Else 22. Generate the candidate position of stallion using Equation (9). 23. End if 24. Else 25. Generate the candidate position of stallion using Equation (7). 26. End if 27. If the candidate position of the stallion is better 28. Replace the position of the stallion using the candidate position. 29. End if 30. End for 31. Exchange foals and stallions position using Equation (6). 32. t = t + 1 33. End While 34. Output the best solution obtained by IWHO. End IWHO. |
3.5. Analysis of Algorithm Computational Complexity
4. Experimental Study
4.1. Optimization of Functions and Parameter Settings
4.2. Analysis of Performance for the CEC 2005 Test Suite
4.3. Statistical Analysis of Performance for the CEC 2021 Test Suite
5. Real-World Applications
5.1. Welded Beam Design Problem
- Welded thickness (h)
- Bar length (l)
- Bar height (t)
- Bar thickness (b)
5.2. Tension/Compression Spring Design Problem
- Diameter of wire (d)
- Coil diameter (D)
- Active coils number (N)
5.3. Three-Bar Truss Design Problem
| Algorithm | Optimal Values for Variables | Optimum Weight | |
|---|---|---|---|
| x1 | x2 | ||
| IWHO | 0.7884 | 0.4081 | 263.8523 |
| WHO [49] | 0.7980 | 0.3816 | 263.9181 |
| HHO [71] | 0.788662816 | 0.408283133832900 | 263.8958434 |
| SSA [52] | 0.78866541 | 0.408275784 | 263.89584 |
| AOA [75] | 0.79369 | 0.39426 | 263.9154 |
| MVO [72] | 0.78860276 | 0.408453070000000 | 263.8958499 |
| MFO [51] | 0.788244771 | 0.409466905784741 | 263.8959797 |
| GOA [18] | 0.788897555578973 | 0.407619570115153 | 263.895881496069 |
5.4. Car Crashworthiness Design Problem
5.5. Speed Reducer Design Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Hassanien, A.E.; Emary, E. Swarm Intelligence: Principles, Advances, and Applications; CRC Press: Boca Raton, FL, USA, 2018; pp. 93–119. [Google Scholar]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Amin, M.; Azar, A.T. New binary whale optimization algorithm for discrete optimization problems. Eng. Optimiz. 2020, 52, 945–959. [Google Scholar] [CrossRef]
- Yang, X.S. Engineering Optimization: An Introduction with Metaheuristic Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimization problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar]
- Fathi, H.; AlSalman, H.; Gumaei, A.; Manhrawy, I.I.M.; Hussien, A.G.; El-Kafrawy, P. An Efficient Cancer Classification Model Using Microarray and High-Dimensional Data. Comput. Intel. Neurosc. 2021, 2021, 7231126. [Google Scholar] [CrossRef] [PubMed]
- Mousavi-Avval, S.H.; Rafiee, S.; Sharifi, M.; Hosseinpour, S.; Notarnicola, B.; Tassielli, G.; Renzulli, P.A. Application of multi-objective genetic algorithms for optimization of energy, economics and environmental life cycle assessment in oilseed production. J. Clean. Prod. 2017, 140, 804–815. [Google Scholar] [CrossRef]
- Abualigah, L.; Gandomi, A.H.; Elaziz, M.A.; Hussien, A.G.; Khasawneh, A.M.; Alshinwan, M.; Houssein, E.H. Nature-inspired optimization algorithms for text document clustering—A comprehensive analysis. Algorithms 2020, 13, 345. [Google Scholar] [CrossRef]
- Shamir, J.; Rosen, J.; Mahlab, U.; Caulfield, H.J. Optimization methods for pattern recognition. Int. Soc. Opt. Eng. 1992, 40, 2–24. [Google Scholar]
- Houssein, E.H.; Amin, M.; Hassanien, A.G.; Houssein, A.E. Swarming behaviour of salps algorithm for predicting chemical compound activities. In Proceedings of the 8th IEEE International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2017; pp. 315–320. [Google Scholar]
- Chou, J.S.; Pham, A.D. Nature-inspired metaheuristic optimization in least squares support vector regression for obtaining bridge scour information. Inform. Sci. 2017, 399, 64–80. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Bhattacharyya, S.; Amin, M. S-shaped Binary Whale Optimization Algorithm for Feature Selection. In Recent Trends in Signal and Image Processing; Springer: Singapore, 2019; Volume 727, pp. 79–87. [Google Scholar]
- Hussien, A.G.; Houssein, E.H.; Hassanien, A.E. A binary whale optimization algorithm with hyperbolic tangent fitness function for feature selection. In Proceedings of the 8th IEEE International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2017; pp. 166–172. [Google Scholar]
- Besnassi, M.; Neggaz, N.; Benyettou, A. Face detection based on evolutionary Haar filter. Pattern Anal. Appl. 2020, 23, 309–330. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Xing, H.L.; Li, T.R.; Yang, Y.; Qu, R.; Pan, Y. A modified ant colony optimization algorithm for network coding resource minimization. IEEE T. Evolut. Comput. 2016, 20, 325–342. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE T. Evolut. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef] [Green Version]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Kaveh, A.; Farhoudi, N. A new optimization method: Dolphin echolocation. Adv. Eng. Softw. 2013, 59, 53–70. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M. A self-adaptive Harris Hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection. Int. J. Mach. Learn. Cyb. 2022, 13, 309–336. [Google Scholar] [CrossRef]
- Hussien, A.G.; Oliva, D.; Houssein, E.H.; Juan, A.A.; Yu, X. Binary whale optimization algorithm for dimensionality reduction. Mathematics 2020, 8, 1821. [Google Scholar] [CrossRef]
- Assiri, A.S.; Hussien, A.G.; Amin, M. Ant Lion Optimization: Variants, hybrids, and applications. IEEE Access 2020, 8, 77746–77764. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M.; Wang, M.; Liang, G.; Alsanad, A.; Gumaei, A.; Chen, H. Crow Search Algorithm: Theory, Recent Advances, and Applications. IEEE Access 2020, 8, 173548–173565. [Google Scholar] [CrossRef]
- Hussien, A.G. An enhanced opposition-based Salp Swarm Algorithm for global optimization and engineering problems. J. Amb. Intel. Hum. Comp. 2021, 13, 129–150. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M.; Abd El Aziz, M. A comprehensive review of moth-flame optimisation: Variants, hybrids, and applications. J. Exp. Theor. Artif. Intell. 2020, 32, 705–725. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization Algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Hussien, A.G.; Khan, M.A.; Kadry, S.; Hashim, F. Enhanced COOT Optimization Algorithm for Dimensionality Reduction. In Proceedings of the Fifth International Conference of Women in Data Science at Prince Sultan University (WiDS PSU), Riyadh, Saudi Arabia, 28–29 March 2022. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Juste, K.; Kita, H.; Tanaka, E.; Hasegawa, J. An evolutionary programming solution to the unit commitment problem. IEEE T. Power Syst. 1999, 14, 1452–1459. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Massa, A. Differential evolution as applied to electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Contr. Syst. Mag. 2002, 22, 52–67. [Google Scholar]
- Moscato, P.; Mendes, A.; Berretta, R. Benchmarking a memetic algorithm for ordering microarray data. Biosystems 2007, 88, 56–75. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inform. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- BİRBİL, Ş.İ.; Fang, S.C. An electromagnetism-like mechanism for global optimization. J. Glob. Optim. 2003, 25, 263–282. [Google Scholar] [CrossRef]
- Javidy, B.; Hatamlou, A.; Mirjalili, S. Ions motion algorithm for solving optimization problems. Appl. Soft Comput. 2015, 32, 72–79. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Hussien, A.G.; Alsalibi, B.; Jalali, S.M.J.; Gandomi, A.H. Lightning search algorithm: A comprehensive survey. Appl. Intell. 2021, 51, 2353–2376. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex search algorithm. Inform. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Ramezani, F.; Lotfi, S. Social-based algorithm (SBA). Appl. Soft Comput. 2013, 13, 2837–2856. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE T. Evolut. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Ning, G.Y.; Cao, D.Q. Improved Whale Optimization Algorithm for Solving Constrained Optimization Problems. Discret. Dyn. Nat. Soc. 2021, 2021, 8832251. [Google Scholar] [CrossRef]
- Nautiyal, B.; Prakash, R.; Vimal, V.; Liang, G.; Chen, H. Improved Salp Swarm Algorithm with Mutation Schemes for Solving Global Optimization and Engineering Problems. Eng. Comput. 2021, 1–23. [Google Scholar] [CrossRef]
- Tubishat, M.; Idris, N.; Shuib, L.; Abushariah, M.A.M.; Mirjalili, S. Improved Salp Swarm Algorithm Based on Opposition Based Learning and Novel Local Search Algorithm for Feature Selection. Expert Syst. Appl. 2020, 145, 113122. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization Algorithm with Hybrid Search Phase. Knowl. Based Syst. 2020, 191, 105277. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Singh, N.; Kaur, J. Hybridizing sine-cosine algorithm with harmony search strategy for optimization design problems. Soft Comput. 2021, 25, 11053–11075. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Liu, J. Dynamic sine cosine algorithm for large-scale global optimization problems. Expert Syst. Appl. 2021, 177, 114950. [Google Scholar] [CrossRef]
- Wang, S.; Sun, K.; Zhang, W.; Jia, H. Multilevel thresholding using a modified ant lion optimizer with opposition-based learning for color image segmentation. Math. Biosci. Eng. 2021, 18, 3092–3143. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Chen, H.L.; Yang, C.J.; Heidari, A.A.; Zhao, X.H. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Dong, H.; Xu, Y.L.; Li, X.P.; Yang, Z.L.; Zou, C.H. An improved antlion optimizer with dynamic random walk and dynamic opposite learning. Knowl. Based Syst. 2021, 216, 106752. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report, Nanyang Technological University, Singapore and KanGAL; Kanpur Genetic Algorithms Lab.: Kanpur, India, 2005. [Google Scholar]
- Zheng, R.; Jia, H.M.; Abualigah, L.; Wang, S.; Wu, D. An improved remora optimization algorithm with autonomous foraging mechanism for global optimization problems. Math. Biosci. Eng. 2022, 19, 3994–4037. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Theodorsson-Norheim, E. Friedman and Quade tests: BASIC computer program to perform nonparametric two-way analysis of variance and multiple comparisons on ranks of several related samples. Comput. Biol. Med. 1987, 17, 85–99. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar]
- Baykasoğlu, A.; Akpinar, Ş. Weighted superposition attraction (WSA): A swarm intelligence algorithm for optimization problems–part 2: Constrained optimization. Appl. Soft Comput. 2015, 37, 396–415. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Ray, T.; Saini, P. Engineering design optimization using a swarm with an intelligent information sharing among individuals. Eng. Optimiz. 2001, 33, 735–748. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Method Appl. M. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Gu, L.; Yang, R.; Tho, C.H.; Makowskit, M.; Faruquet, O.; Li, Y.L. Optimisation and robustness for crashworthiness of side impact. Int. J. Vehicle Des. 2001, 26, 348–360. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. R. 2013, 1, 36–50. [Google Scholar] [CrossRef] [Green Version]












| Function Type | Function | D | Range | Theoretical Optimization Value |
|---|---|---|---|---|
| Unimodal test functions | F1 | 30/100/500/1000 | [−100, 100] | 0 |
| F2 | 30/100/500/1000 | [−10, 10] | 0 | |
| F3 | 30/100/500/1000 | [−100, 100] | 0 | |
| F4 | 30/100/500/1000 | [−100, 100] | 0 | |
| F5 | 30/100/500/1000 | [−30, 30] | 0 | |
| F6 | 30/100/500/1000 | [−100, 100] | 0 | |
| F7 | 30/100/500/1000 | [−1.28, 1.28] | 0 | |
| Multimodal test functions | F8 | 30/100/500/1000 | [−500, 500] | −418.9829 × D |
| F9 | 30/100/500/1000 | [−5.12, 5.12] | 0 | |
| F10 | 30/100/500/1000 | [−32, 32] | 0 | |
| F11 | 30/100/500/1000 | [−600, 600] | 0 | |
| F12 | 30/100/500/1000 | [−50, 50] | 0 | |
| F13 | 30/100/500/1000 | [−50, 50] | 0 | |
| Fixed-dimension multimodal test functions | F14 | 2 | [−65, 65] | 0.998004 |
| F15 | 4 | [−5, 5] | 0.0003075 | |
| F16 | 2 | [−5, 5] | −1.03163 | |
| F17 | 2 | [−5, 5] | 0.398 | |
| F18 | 2 | [−2, 2] | 3 | |
| F19 | 3 | [−1, 2] | −3.8628 | |
| F20 | 6 | [0, 1] | −3.3220 | |
| F21 | 4 | [0, 10] | −10.1532 | |
| F22 | 4 | [0, 10] | −10.4028 | |
| F23 | 4 | [0, 10] | −10.5363 | |
| CEC2021 unimodal test functions | CEC_01 | 20 | [−100, 100] | 100 |
| CEC2021 basic test functions | CEC_02 | 20 | [−100, 100] | 1100 |
| CEC_03 | 20 | [−100, 100] | 700 | |
| CEC_04 | 20 | [−100, 100] | 1900 | |
| CEC2021 hybrid test functions | CEC_05 | 20 | [−100, 100] | 1700 |
| CEC_06 | 20 | [−100, 100] | 1600 | |
| CEC_07 | 20 | [−100, 100] | 2100 | |
| CEC2021 composition test functions | CEC_08 | 20 | [−100, 100] | 2200 |
| CEC_09 | 20 | [−100, 100] | 2400 | |
| CEC_10 | 20 | [−100, 100] | 2500 |
| Algorithm | Parameters |
|---|---|
| IWHO | PS = 0.2; PC = 0.13; PRR = 0.1; w ∈ [0.01, 0.99] |
| WHO [49] | PS = 0.2; PC = 0.13 |
| GWO [50] | a = [2, 0] |
| MFO [51] | b = 1; t = [−1,1]; a ∈ [−1,−2] |
| SSA [52] | c1 ∈ [0, 1]; c2 ∈ [0, 1] |
| WOA [53] | a1 = [2, 0]; a2 = [−2, −1]; b = 1 |
| PSO [15] | c1 = 2; c2 = 2; W ∈ [0.2, 0.9]; vMax = 6 |
| HSCAHS [54] | a = 2; Bandwidth = 0.02 |
| DSCA [55] | w ∈ [0.1, 0.9], σ = 0.1; aend = 0; astart = 2 |
| MALO [56] | Switch possibility = 0.5 |
| Function | D | Metric | IWHO | WHO | GWO | MFO | SSA | WOA | PSO | HSCAHS | DSCA | MALO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 30 | Mean | 0 | 3.05 × 10−43 | 2.09 × 10−27 | 1.69 × 103 | 1.97 × 10−7 | 8.09 × 10−74 | 2.09 × 10−4 | 2.79 × 10−50 | 3.88 × 10−106 | 1.28 × 10−3 |
| Std | 0 | 1.57 × 10−42 | 3.99 × 10−27 | 3.83 × 103 | 3.38 × 10−7 | 2.79 × 10−73 | 3.23 × 10−4 | 1.41 × 10−49 | 2.11 × 10−105 | 1.17 × 10−3 | ||
| 200 | Mean | 0 | 4.57 × 10−32 | 9.50 × 10−8 | 2.88 × 105 | 1.69 × 104 | 5.20 × 10−70 | 3.38 × 102 | 3.46 × 10−34 | 1.34 × 10−91 | 3.95 × 104 | |
| Std | 0 | 1.81 × 10−31 | 4.45 × 10−8 | 2.81 × 104 | 2.15 × 103 | 2.84 × 10−69 | 4.88 × 101 | 8.54 × 10−34 | 7.35 × 10−91 | 9.15 × 103 | ||
| 500 | Mean | 0 | 2.96 × 10−28 | 1.63 × 10−3 | 1.16 × 106 | 9.46 × 104 | 3.14 × 10−71 | 5.85 × 103 | 4.56 × 10−29 | 1.90 × 10−78 | 2.17 × 105 | |
| Std | 0 | 1.62 × 10−27 | 5.53 × 10−4 | 3.51 × 104 | 6.80 × 103 | 8.49 × 10−71 | 4.89 × 102 | 8.10 × 10−29 | 1.04 × 10−77 | 3.75 × 104 | ||
| 1000 | Mean | 0 | 6.50 × 10−29 | 2.53 × 10−1 | 2.73 × 106 | 2.37 × 105 | 6.48 × 10−70 | 4.10 × 104 | 2.05 × 10−25 | 4.69 × 10−73 | 5.80 × 105 | |
| Std | 0 | 2.29 × 10−28 | 6.74 × 10−2 | 5.33 × 104 | 1.27 × 104 | 3.21 × 10−69 | 2.39 × 103 | 4.20 × 10−25 | 2.57 × 10−72 | 8.66 × 104 | ||
| F2 | 30 | Mean | 0 | 2.22 × 10−25 | 9.06 × 10−17 | 2.65 × 101 | 2.37 | 1.56 × 10−51 | 7.36 | 4.04 × 10−27 | 1.22 × 10−60 | 5.29 × 101 |
| Std | 0 | 7.39 × 10−25 | 6.90 × 10−17 | 2.03 × 101 | 1.73 | 4.94 × 10−51 | 1.05 × 101 | 9.46 × 10−27 | 6.65 × 10−60 | 5.31 × 101 | ||
| 200 | Mean | 0 | 6.92 × 101 | 3.14 × 10−5 | 7.55 × 102 | 1.55 × 102 | 1.18 × 10−49 | 4.76 × 102 | 1.19 × 10−18 | 1.05 × 10−51 | 3.76 × 1073 | |
| Std | 0 | 1.80 × 102 | 9.14 × 10−6 | 4.70 × 101 | 1.26 × 101 | 3.91 × 10−49 | 6.08 × 101 | 1.99 × 10−18 | 3.96 × 10−51 | 2.06 × 1074 | ||
| 500 | Mean | 0 | 6.01 × 102 | 1.09 × 10−2 | 4.30 × 10116 | 5.38 × 102 | 1.00 × 10−48 | 5.74 × 1058 | 3.84 × 10−16 | 7.18 × 10−50 | 2.31 × 10244 | |
| Std | 0 | 6.18 × 102 | 2.39 × 10−3 | 2.23 × 10117 | 2.39 × 101 | 4.88 × 10−48 | 3.14 × 1059 | 6.21 × 10−16 | 3.93 × 10−49 | Inf | ||
| 1000 | Mean | 0 | 1.43 × 103 | 8.06 × 10−1 | Inf | 1.20 × 103 | 1.30 × 10−49 | 1.40 × 103 | 5.11 × 10−15 | Inf | Inf | |
| Std | 0 | 1.37 × 103 | 9.03 × 10−1 | NaN | 3.61 × 101 | 3.29 × 10−49 | 7.08 × 101 | 1.09 × 10−14 | NaN | NaN | ||
| F3 | 30 | Mean | 0 | 3.56 × 10−26 | 6.23 × 10−6 | 2.28 × 104 | 1.74 × 103 | 4.35 × 104 | 7.36 × 101 | 1.08 × 10−48 | 2.25 × 10−57 | 4.56 × 103 |
| Std | 0 | 1.82 × 10−25 | 1.02 × 10−5 | 1.31 × 104 | 1.30 × 103 | 1.17 × 104 | 3.10 × 101 | 4.06 × 10−48 | 1.23 × 10−56 | 1.79 × 103 | ||
| 200 | Mean | 0 | 1.76 × 10−12 | 2.14 × 104 | 8.63 × 105 | 2.32 × 105 | 5.05 × 106 | 8.90 × 104 | 1.73 × 10−31 | 2.86 × 10−45 | 3.42 × 105 | |
| Std | 0 | 4.91 × 10−12 | 1.11 × 104 | 1.56 × 105 | 1.31 × 105 | 1.36 × 106 | 1.88 × 104 | 5.48 × 10−31 | 1.54 × 10−44 | 9.60 × 104 | ||
| 500 | Mean | 0 | 1.06 × 10−8 | 3.26 × 105 | 4.86 × 106 | 1.01 × 106 | 2.91 × 107 | 5.94 × 105 | 5.34 × 10−26 | 1.35 × 10−43 | 2.09 × 106 | |
| Std | 0 | 5.30 × 10−8 | 1.03 × 105 | 9.34 × 105 | 5.23 × 105 | 9.83 × 106 | 1.18 × 105 | 9.19 × 10−26 | 6.83 × 10−43 | 6.22 × 105 | ||
| 1000 | Mean | 0 | 2.36 × 10−5 | 1.52 × 106 | 1.83 × 107 | 4.24 × 106 | 1.18 × 108 | 2.47 × 106 | 5.52 × 10−23 | 1.46 × 10−35 | 7.32 × 106 | |
| Std | 0 | 1.28 × 10−4 | 2.93 × 105 | 4.06 × 106 | 1.96 × 106 | 4.57 × 107 | 6.38 × 105 | 1.12 × 10−22 | 7.85 × 10−35 | 2.30 × 106 | ||
| F4 | 30 | Mean | 1.98 × 10−320 | 1.97 × 10−17 | 7.10 × 10−7 | 6.92 × 101 | 1.05 × 101 | 5.04 × 101 | 1.04 | 9.05 × 10−26 | 5.55 × 10−48 | 1.68 × 101 |
| Std | 0 | 4.78 × 10−17 | 6.47 × 10−7 | 9.08 | 2.71 | 2.89 × 101 | 2.44 × 10−1 | 2.18 × 10−25 | 3.03 × 10−47 | 3.47 | ||
| 200 | Mean | 0 | 2.10 × 10−11 | 2.37 × 101 | 9.72 × 101 | 3.49 × 101 | 8.49 × 101 | 1.96 × 101 | 2.86 × 10−16 | 1.39 × 10−41 | 4.09 × 101 | |
| Std | 0 | 7.03 × 10−11 | 6.67 | 7.39 × 10−1 | 3.49 | 1.40 × 101 | 1.61 | 4.71 × 10−16 | 5.77 × 10−41 | 4.46 | ||
| 500 | Mean | 0 | 7.02 × 10−10 | 6.47 × 101 | 9.89 × 101 | 4.00 × 101 | 7.72 × 101 | 2.81 × 101 | 1.16 × 10−11 | 3.39 × 10−33 | 4.95 × 101 | |
| Std | 0 | 1.24 × 10−9 | 4.89 | 4.11 × 10−1 | 3.33 | 2.80 × 101 | 1.37 | 1.59 × 10−11 | 1.73 × 10−32 | 4.89 | ||
| 1000 | Mean | 0 | 2.25 × 10−9 | 7.89 × 101 | 9.95 × 101 | 4.55 × 101 | 8.43 × 101 | 3.30 × 101 | 2.50 × 10−7 | 1.97 × 10−28 | 5.30 × 101 | |
| Std | 0 | 4.00 × 10−9 | 3.18 | 1.95 × 10−1 | 3.35 | 1.85 × 101 | 1.90 | 4.41 × 10−7 | 1.08 × 10−27 | 4.17 | ||
| F5 | 30 | Mean | 4.37 | 3.58 × 101 | 2.70 × 101 | 2.68 × 106 | 2.19 × 102 | 2.79 × 101 | 3.13 × 103 | 2.88 × 101 | 2.86 × 101 | 9.77 × 10−1 |
| Std | 9.71 | 2.35 × 101 | 6.78 × 10−1 | 1.46 × 107 | 3.37 × 102 | 4.26 × 10−1 | 1.64 × 104 | 9.01 × 10−2 | 3.04 × 10−1 | 5.22 | ||
| 200 | Mean | 4.34 × 101 | 2.88 × 102 | 1.98 × 102 | 1.05 × 109 | 4.11 × 106 | 1.98 × 102 | 6.61 × 105 | 1.99 × 102 | 1.99 × 102 | 5.60 × 101 | |
| Std | 7.82 × 101 | 3.26 × 102 | 4.76 × 10−1 | 1.13 × 108 | 1.14 × 106 | 1.89 × 10−1 | 1.52 × 105 | 4.40 × 10−2 | 6.75 × 10−2 | 4.75 × 101 | ||
| 500 | Mean | 1.27 × 102 | 4.99 × 102 | 4.98 × 102 | 5.12 × 109 | 3.86 × 107 | 4.96 × 102 | 3.00 × 107 | 4.99 × 102 | 4.99 × 102 | 2.31 × 102 | |
| Std | 1.90 × 102 | 2.18 | 3.18 × 10−1 | 2.17 × 108 | 8.07 × 106 | 4.62 × 10−1 | 3.48 × 106 | 5.15 × 10−3 | 1.87 × 10−2 | 1.93 × 102 | ||
| 1000 | Mean | 1.22 × 102 | 9.98 × 102 | 1.07 × 103 | 1.24 × 1010 | 1.18 × 108 | 9.94 × 102 | 2.82 × 108 | 9.99 × 102 | 9.99 × 102 | 4.36 × 102 | |
| Std | 2.47 × 102 | 9.67 × 10−1 | 3.20 × 101 | 3.12 × 108 | 1.13 × 107 | 7.27 × 10−1 | 2.87 × 107 | 3.67 × 10−2 | 1.69 × 10−2 | 3.94 × 102 | ||
| F6 | 30 | Mean | 5.09 × 10−5 | 9.53 × 10−3 | 8.12 × 10−1 | 1.00 × 103 | 1.52 × 10−7 | 4.21 × 10−1 | 2.27 × 10−4 | 6.67 | 5.57 | 4.69 × 10−4 |
| Std | 4.64 × 10−5 | 2.92 × 10−2 | 4.15 × 10−1 | 3.04 × 103 | 1.80 × 10−7 | 2.56 × 10−1 | 3.22 × 10−4 | 1.76 × 10−1 | 3.09 × 10−1 | 3.21 × 10−4 | ||
| 200 | Mean | 2.19 | 3.58 × 101 | 2.91 × 101 | 2.88 × 105 | 1.69 × 104 | 1.07 × 101 | 3.24 × 102 | 4.92 × 101 | 4.81 × 101 | 1.56 | |
| Std | 3.26 | 3.22 × 101 | 1.58 | 2.26 × 104 | 1.84 × 103 | 2.78 | 4.57 × 101 | 2.13 × 10−1 | 3.38 × 10−1 | 6.98 × 10−1 | ||
| 500 | Mean | 1.07 × 101 | 1.10 × 102 | 9.06 × 101 | 1.18 × 106 | 9.48 × 104 | 2.84 × 101 | 5.92 × 103 | 1.24 × 102 | 1.23 × 102 | 6.01 | |
| Std | 1.34 × 101 | 3.18 × 101 | 1.89 | 2.78 × 104 | 5.33 × 103 | 8.78 | 5.16 × 102 | 2.13 × 10−1 | 3.46 × 10−1 | 2.62 | ||
| 1000 | Mean | 1.20 × 101 | 2.29 × 102 | 2.02 × 102 | 2.74 × 106 | 2.36 × 105 | 6.85 × 101 | 4.06 × 104 | 2.49 × 102 | 2.48 × 102 | 1.24 × 101 | |
| Std | 2.28 × 101 | 2.01 × 101 | 2.53 | 3.49 × 104 | 1.03 × 104 | 1.80 × 101 | 1.94 × 103 | 2.60 × 10−1 | 4.41 × 10−1 | 4.84 | ||
| F7 | 30 | Mean | 2.23 × 10−4 | 1.23 × 10−3 | 1.85 × 10−3 | 2.29 | 1.77 × 10−1 | 4.07 × 10−3 | 3.16 | 1.30 × 10−4 | 1.86 × 10−3 | 9.01 × 10−5 |
| Std | 2.05 × 10−4 | 8.00 × 10−4 | 1.19 × 10−3 | 2.96 | 7.74 × 10−2 | 5.54 × 10−3 | 4.20 | 1.92 × 10−4 | 1.88 × 10−3 | 7.28 × 10−5 | ||
| 200 | Mean | 4.58 × 10−4 | 1.62 × 10−3 | 1.70 × 10−2 | 2.99 × 103 | 1.76 × 101 | 6.24 × 10−3 | 2.92 × 103 | 1.08 × 10−4 | 2.34 × 10−3 | 7.14 × 10−5 | |
| Std | 4.58 × 10−4 | 2.22 × 10−3 | 5.45 × 10−3 | 4.19 × 102 | 3.53 | 7.00 × 10−3 | 4.63 × 102 | 9.81 × 10−5 | 2.07 × 10−3 | 5.22 × 10−5 | ||
| 500 | Mean | 5.06 × 10−4 | 1.75 × 10−3 | 5.38 × 10−2 | 3.86 × 104 | 2.72 × 102 | 3.39 × 10−3 | 4.39 × 104 | 1.13 × 10−4 | 3.77 × 10−3 | 1.03 × 10−4 | |
| Std | 6.25 × 10−4 | 1.56 × 10−3 | 1.48 × 10−2 | 1.74 × 103 | 4.13 × 101 | 3.30 × 10−3 | 5.70 × 103 | 8.65 × 10−5 | 3.35 × 10−3 | 1.10 × 10−4 | ||
| 1000 | Mean | 4.28 × 10−4 | 3.08 × 10−3 | 1.38 × 10−1 | 1.98 × 105 | 1.78 × 103 | 5.79 × 10−3 | 2.44 × 105 | 1.14 × 10−4 | 3.20 × 10−3 | 9.34 × 10−5 | |
| Std | 4.57 × 10−4 | 2.65 × 10−3 | 2.96 × 10−2 | 7.27 × 103 | 1.74 × 102 | 5.81 × 10−3 | 6.04 × 103 | 1.43 × 10−4 | 3.32 × 10−3 | 8.66 × 10−5 | ||
| F8 | 30 | Mean | −1.26 × 104 | −8.80 × 103 | −5.98 × 103 | −8.46 × 103 | −7.46 × 103 | −9.80 × 103 | −4.77 × 103 | −2.44 × 103 | −4.46 × 103 | −1.21 × 104 |
| Std | 6.64 × 10−4 | 5.09 × 102 | 6.98 × 102 | 1.19 × 103 | 7.32 × 102 | 1.57 × 103 | 1.30 × 103 | 3.14 × 102 | 3.59 × 102 | 1.08 × 103 | ||
| 200 | Mean | −8.38 × 104 | −3.48 × 104 | −2.96 × 104 | −3.70 × 104 | −3.46 × 104 | −6.87 × 104 | −1.31 × 104 | −6.34 × 103 | −1.18 × 104 | −7.52 × 104 | |
| Std | 5.24 | 3.54 × 103 | 4.82 × 103 | 2.68 × 103 | 3.14 × 103 | 1.29 × 104 | 4.80 × 103 | 9.93 × 102 | 8.64 × 102 | 9.10 × 103 | ||
| 500 | Mean | −2.09 × 105 | −6.03 × 104 | −5.72 × 104 | −6.21 × 104 | −5.99 × 104 | −1.77 × 105 | −2.40 × 104 | −1.05 × 104 | −1.91 × 104 | −1.90 × 105 | |
| Std | 3.87 × 101 | 7.66 × 103 | 4.22 × 103 | 4.14 × 103 | 4.63 × 103 | 2.92 × 104 | 8.68 × 103 | 1.56 × 103 | 2.27 × 103 | 2.43 × 104 | ||
| 1000 | Mean | −4.19 × 105 | −8.36 × 104 | −8.80 × 104 | −8.87 × 104 | −8.66 × 104 | −3.48 × 105 | −3.44 × 104 | −1.52 × 104 | −2.83 × 104 | −3.76 × 105 | |
| Std | 2.01 × 102 | 9.06 × 103 | 1.43 × 104 | 6.25 × 103 | 6.65 × 103 | 5.54 × 104 | 1.30 × 104 | 2.13 × 103 | 3.81 × 103 | 4.60 × 104 | ||
| F9 | 30 | Mean | 0 | 4.55 × 10−10 | 3.40 | 1.66 × 102 | 5.25 × 101 | 0 | 1.01 × 102 | 0 | 0 | 8.33 × 101 |
| Std | 0 | 1.74 × 10−9 | 4.19 | 3.80 × 101 | 1.57 × 101 | 0 | 3.03 × 101 | 0 | 0 | 2.80 × 101 | ||
| 200 | Mean | 0 | 0 | 2.21 × 101 | 2.22 × 103 | 8.20 × 102 | 7.58 × 10−15 | 2.03 × 103 | 0 | 0 | 1.03 × 103 | |
| Std | 0 | 0 | 9.22 | 1.11 × 102 | 8.14 × 101 | 4.15 × 10−14 | 1.45 × 102 | 0 | 0 | 8.92 × 101 | ||
| 500 | Mean | 0 | 0 | 7.71 × 101 | 6.98 × 103 | 3.15 × 103 | 0 | 6.31 × 103 | 0 | 0 | 3.74 × 103 | |
| Std | 0 | 0 | 2.84 × 101 | 1.37 × 102 | 1.38 × 102 | 0 | 1.92 × 102 | 0 | 0 | 1.88 × 102 | ||
| 1000 | Mean | 0 | 0 | 2.05 × 102 | 1.55 × 104 | 7.63 × 103 | 0 | 1.42 × 104 | 0 | 0 | 8.78 × 103 | |
| Std | 0 | 0 | 4.77 × 101 | 2.12 × 102 | 1.44 × 102 | 0 | 3.30 × 102 | 0 | 0 | 2.93 × 102 | ||
| F10 | 30 | Mean | 8.88 × 10−16 | 2.07 × 10−15 | 1.03 × 10−13 | 1.78 × 101 | 2.74 | 4.44 × 10−15 | 4.07 × 10−1 | 8.88 × 10−16 | 8.88 × 10−16 | 4.17 |
| Std | 0 | 1.70 × 10−15 | 2.27 × 10−14 | 4.32 | 7.62 × 10−1 | 1.87 × 10−15 | 6.82 × 10−1 | 0 | 0 | 2.11 | ||
| 200 | Mean | 8.88 × 10−16 | 2.66 × 10−15 | 2.40 × 10−5 | 2.00 × 101 | 1.31 × 101 | 4.44 × 10−15 | 6.57 | 8.88 × 10−16 | 8.88 × 10−16 | 1.49 × 101 | |
| Std | 0 | 5.26 × 10−15 | 4.81 × 10−6 | 7.54 × 10−2 | 6.63 × 10−1 | 2.47 × 10−15 | 3.42 × 10−1 | 0 | 0 | 8.88 × 10−1 | ||
| 500 | Mean | 8.88 × 10−16 | 1.48 × 10−15 | 1.89 × 10−3 | 2.03 × 101 | 1.42 × 101 | 5.15 × 10−15 | 1.20 × 101 | 1.24 × 10−15 | 8.88 × 10−16 | 1.60 × 101 | |
| Std | 0 | 1.35 × 10−15 | 4.06 × 10−4 | 1.17 × 10−1 | 2.52 × 10−1 | 2.86 × 10−15 | 3.13 × 10−1 | 1.08 × 10−15 | 0 | 7.80 × 10−1 | ||
| 1000 | Mean | 8.88 × 10−16 | 1.95 × 10−15 | 1.76 × 10−2 | 2.03 × 101 | 1.46 × 101 | 4.56 × 10−15 | 1.60 × 101 | 6.10 × 10−15 | 8.88 × 10−16 | 1.60 × 101 | |
| Std | 0 | 1.90 × 10−15 | 2.26 × 10−3 | 2.24 × 10−1 | 1.45 × 10−1 | 2.55 × 10−15 | 3.82 × 10−1 | 8.64 × 10−15 | 0 | 1.28 | ||
| F11 | 30 | Mean | 0 | 0 | 2.56 × 10−3 | 3.10 × 101 | 2.07 × 10−2 | 8.30 × 10−3 | 9.87 × 10−3 | 0 | 0 | 5.55 × 10−2 |
| Std | 0 | 0 | 5.97 × 10−3 | 4.92 × 101 | 1.48 × 10−2 | 3.16 × 10−2 | 1.05 × 10−2 | 0 | 0 | 2.88 × 10−2 | ||
| 200 | Mean | 0 | 0 | 5.28 × 10−3 | 2.56 × 103 | 1.57 × 102 | 0 | 1.48 | 0 | 0 | 3.74 × 102 | |
| Std | 0 | 0 | 1.37 × 10−2 | 1.65 × 102 | 2.56 × 101 | 0 | 6.05 × 10−1 | 0 | 0 | 9.11 × 101 | ||
| 500 | Mean | 0 | 0 | 2.22 × 10−2 | 1.03 × 104 | 8.55 × 102 | 3.70 × 10−18 | 8.09 × 101 | 0 | 0 | 1.96 × 103 | |
| Std | 0 | 0 | 3.95 × 10−2 | 3.03 × 102 | 5.06 × 101 | 2.03 × 10−17 | 9.46 | 0 | 0 | 3.25 × 102 | ||
| 1000 | Mean | 0 | 0 | 3.75 × 10−2 | 2.45 × 104 | 2.13 × 103 | 3.70 × 10−18 | 2.77 × 102 | 0 | 0 | 5.35 × 103 | |
| Std | 0 | 0 | 5.93 × 10−2 | 4.32 × 102 | 1.03 × 102 | 2.03 × 10−17 | 2.08 × 101 | 0 | 0 | 9.55 × 102 | ||
| F12 | 30 | Mean | 6.24 × 10−7 | 7.45 × 10−3 | 3.91 × 10−2 | 8.53 × 106 | 7.37 | 2.42 × 10−2 | 6.91 × 10−3 | 1.05 | 7.71 × 10−1 | 1.67 × 10−5 |
| Std | 1.16 × 10−6 | 2.63 × 10−2 | 1.88 × 10−2 | 4.67 × 107 | 3.37 | 2.20 × 10−2 | 2.63 × 10−2 | 4.52 × 10−2 | 7.15 × 10−2 | 1.67 × 10−5 | ||
| 200 | Mean | 9.49 × 10−4 | 3.80 × 10−1 | 5.38 × 10−1 | 2.17 × 109 | 4.93 × 103 | 7.15 × 10−2 | 3.94 × 101 | 1.19 | 1.14 | 4.62 × 10−4 | |
| Std | 1.56 × 10−3 | 1.70 × 10−1 | 4.58 × 10−2 | 2.91 × 108 | 7.29 × 103 | 3.02 × 10−2 | 1.98 × 101 | 2.79 × 10−2 | 3.13 × 10−2 | 3.36 × 10−4 | ||
| 500 | Mean | 1.44 × 10−3 | 7.45 × 10−1 | 7.46 × 10−1 | 1.19 × 1010 | 1.46 × 106 | 1.06 × 10−1 | 2.38 × 105 | 1.19 | 1.17 | 9.62 × 10−4 | |
| Std | 2.08 × 10−3 | 2.14 × 10−1 | 4.10 × 10−2 | 6.36 × 108 | 9.21 × 105 | 5.63 × 10−2 | 9.88 × 104 | 9.22 × 10−3 | 8.84 × 10−3 | 6.70 × 10−4 | ||
| 1000 | Mean | 1.00 × 10−3 | 9.73 × 10−1 | 1.20 | 3.06 × 1010 | 1.11 × 107 | 9.41 × 10−2 | 9.37 × 106 | 1.18 | 1.17 | 4.64 × 10−4 | |
| Std | 2.08 × 10−3 | 1.86 × 10−1 | 2.17 × 10−1 | 1.13 × 109 | 2.60 × 106 | 4.92 × 10−2 | 2.32 × 106 | 3.00 × 10−3 | 5.39 × 10−3 | 4.04 × 10−4 | ||
| F13 | 30 | Mean | 4.35 × 10−5 | 1.14 × 10−1 | 5.87 × 10−1 | 1.37 × 107 | 1.31 × 101 | 4.99 × 10−1 | 4.46 × 10−3 | 2.85 | 2.81 | 6.16 × 10−4 |
| Std | 1.38 × 10−4 | 2.74 × 10−1 | 2.68 × 10−1 | 7.49 × 107 | 1.48 × 101 | 2.17 × 10−1 | 8.92 × 10−3 | 3.32 × 10−2 | 4.64 × 10−2 | 2.06 × 10−3 | ||
| 200 | Mean | 1.27 × 10−1 | 1.79 × 101 | 1.69 × 101 | 4.49 × 109 | 1.33 × 106 | 6.22 | 5.70 × 103 | 1.99 × 101 | 1.99 × 101 | 9.64 × 10−2 | |
| Std | 3.60 × 10−1 | 3.27 | 6.35 × 10−1 | 4.98 × 108 | 7.44 × 105 | 2.08 | 3.07 × 103 | 3.27 × 10−2 | 5.31 × 10−2 | 6.79 × 10−2 | ||
| 500 | Mean | 2.08 × 10−1 | 5.62 × 101 | 5.05 × 101 | 2.23 × 1010 | 3.59 × 107 | 1.91 × 101 | 4.14 × 106 | 4.99 × 101 | 5.00 × 101 | 4.49 × 10−1 | |
| Std | 2.87 × 10−1 | 1.15 × 101 | 1.29 | 1.21 × 109 | 9.80 × 106 | 5.58 | 1.17 × 106 | 2.52 × 10−2 | 3.91 × 10−2 | 2.67 × 10−1 | ||
| 1000 | Mean | 7.12 × 10−1 | 1.15 × 102 | 1.25 × 102 | 5.54 × 1010 | 1.54 × 108 | 3.96 × 101 | 8.03 × 107 | 9.99 × 101 | 1.00 × 102 | 1.05 | |
| Std | 1.02 | 1.00 × 101 | 1.40 × 101 | 1.68 × 109 | 2.46 × 107 | 1.18 × 101 | 1.17 × 107 | 2.82 × 10−2 | 4.65 × 10−2 | 6.62 × 10−1 | ||
| F14 | 2 | Mean | 9.98 × 10−1 | 2.21 | 4.07 | 2.35 | 1.16 | 2.93 | 3.00 | 2.84 | 4.64 × 10−2 | 1.63 |
| Std | 1.30 × 10−16 | 2.76 | 4.00 | 2.03 | 5.87 × 10−1 | 3.07 | 2.54 | 4.52 × 10−1 | 7.05 × 10−1 | 9.20 × 10−1 | ||
| F15 | 4 | Mean | 4.48 × 10−4 | 1.39 × 10−3 | 2.48 × 10−3 | 2.78 × 10−3 | 3.48 × 10−3 | 7.32 × 10−4 | 4.94 × 10−3 | 2.40 × 10−3 | 1.31 × 10−3 | 2.15 × 10−3 |
| Std | 2.56 × 10−4 | 3.61 × 10−3 | 6.07 × 10−3 | 5.14 × 10−3 | 6.74 × 10−3 | 5.21 × 10−4 | 7.86 × 10−3 | 1.24 × 10−3 | 3.22 × 10−4 | 4.97 × 10−3 | ||
| F16 | 2 | Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.02 | −1.03 | −1.03 |
| Std | 6.05 × 10−16 | 4.97 × 10−16 | 1.95 × 10−8 | 6.78 × 10−16 | 2.74 × 10−14 | 9.52 × 10−10 | 6.25 × 10−16 | 5.56 × 10−3 | 1.83 × 10−4 | 1.28 × 10−13 | ||
| F17 | 2 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 6.76 × 10−1 | 4.00 × 10−1 | 3.98 × 10−1 |
| Std | 0 | 0 | 1.68 × 10−6 | 0 | 9.46 × 10−15 | 2.08 × 10−5 | 0 | 2.05 × 10−1 | 2.95 × 10−3 | 2.20 × 10−14 | ||
| F18 | 2 | Mean | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.01 | 3.01 | 3.00 |
| Std | 1.82 × 10−15 | 6.85 × 10−16 | 3.02 × 10−5 | 1.70 × 10−15 | 2.22 × 10−13 | 5.43 × 10−5 | 1.33 × 10−15 | 1.68 × 10−2 | 8.68 × 10−3 | 7.64 × 10−13 | ||
| F19 | 3 | Mean | −3.86 | −3.84 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.43 | −3.83 | −3.86 |
| Std | 2.52 × 10−15 | 1.41 × 10−1 | 3.59 × 10−3 | 2.71 × 10−15 | 1.38 × 10−12 | 7.94 × 10−3 | 2.65 × 10−15 | 3.26 × 10−1 | 2.73 × 10−2 | 6.35 × 10−13 | ||
| F20 | 6 | Mean | −3.26 | −3.25 | −3.27 | −3.24 | −3.23 | −3.20 | −3.22 | −1.78 | −3.01 | −3.25 |
| Std | 6.05 × 10−2 | 6.00 × 10−2 | 7.38 × 10−2 | 6.40 × 10−2 | 6.34 × 10−2 | 1.18 × 10−1 | 1.07 × 10−1 | 6.08 × 10−1 | 9.02 × 10−2 | 5.86 × 10−2 | ||
| F21 | 4 | Mean | −1.02 × 101 | −7.89 | −9.32 | −6.14 | −7.06 | −8.28 | −6.71 | −6.54 × 10−1 | −4.08 | −6.86 |
| Std | 5.49 × 10−15 | 3.12 | 2.21 | 3.45 | 3.46 | 2.73 | 3.19 | 2.50 × 10−1 | 9.62 × 10−1 | 2.59 | ||
| F22 | 4 | Mean | −1.04 × 101 | −8.51 | −1.02 × 101 | −7.36 | −9.11 | −8.18 | −8.54 | −7.37 × 10−1 | −4.48 | −6.85 |
| Std | 8.73 × 10−16 | 3.22 | 9.63 × 10−1 | 3.57 | 2.69 | 2.99 | 2.96 | 2.99 × 10−1 | 2.34 × 10−1 | 3.48 | ||
| F23 | 4 | Mean | −1.05 × 101 | −7.33 | −1.01 × 101 | −7.95 | −8.15 | −7.31 | −8.57 | −1.01 | −4.45 | −6.78 |
| Std | 2.06 × 10−15 | 3.75 | 1.75 | 3.53 | 3.26 | 3.39 | 3.11 | 3.03 × 10−1 | 1.08 | 3.64 |
| Function | D | IWHO vs. WHO | IWHO vs. GWO | IWHO vs. MFO | IWHO vs. SSA | IWHO vs. WOA | IWHO vs. PSO | IWHO vs. HSCAHS | IWHO vs. DSCA | IWHO vs. MALO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F2 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F3 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F4 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F5 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.22 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 4.21 × 10−1 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.37 × 10−2 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.37 × 10−2 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.83 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.69 × 10−1 | |
| F6 | 30 | 1.83 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 3.05 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.22 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 5.54 × 10−2 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.16 × 10−3 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 2.52 × 10−1 | |
| F7 | 30 | 1.22 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.22 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 4.27 × 10−4 | 6.10 × 10−5 |
| 200 | 3.05 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 2.62 × 10−3 | 1.22 × 10−4 | 4.79 × 10−2 | |
| 500 | 8.54 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 8.54 × 10−4 | 6.10 × 10−5 | 6.71 × 10−3 | 1.22 × 10−4 | 1.53 × 10−3 | |
| 1000 | 2.01 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 2.01 × 10−3 | 6.10 × 10−5 | 1.51 × 10−2 | 1.22 × 10−4 | 1.25 × 10−2 | |
| F8 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.83 × 10−4 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | |
| F9 | 30 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 |
| 200 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 500 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 1000 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| F10 | 30 | 1.25 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 9.77 × 10−4 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 |
| 200 | 1.25 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 3.91 × 10−3 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 500 | 6.25 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 7.81 × 10−3 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 1000 | 6.25 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.95 × 10−3 | 6.10 × 10−5 | 4.88 × 10−4 | 1.00 | 6.10 × 10−5 | |
| F11 | 30 | 1.00 | 1.25 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 5.00 × 10−1 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 |
| 200 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 500 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| 1000 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 1.00 | 1.00 | 6.10 × 10−5 | |
| F12 | 30 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 1.81 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 1.83 × 10−4 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 7.62 × 10−1 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 8.04 × 10−1 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 3.03 × 10−1 | |
| F13 | 30 | 3.36 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 5.37 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 8.33 × 10−2 |
| 200 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 2.52 × 10−1 | |
| 500 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 4.27 × 10−3 | |
| 1000 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 | 8.90 × 10−1 | |
| F14 | 2 | 7.81 × 10−3 | 6.10 × 10−5 | 1.95 × 10−3 | 1.95 × 10−3 | 6.10 × 10−5 | 9.77 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F15 | 4 | 8.36 × 10−3 | 5.54 × 10−2 | 3.66 × 10−4 | 1.51 × 10−2 | 2.29 × 10−1 | 1.22 × 10−4 | 6.10 × 10−5 | 6.10 × 10−5 | 4.27 × 10−3 |
| F16 | 2 | 1.00 | 6.10 × 10−5 | 1.00 | 1.22 × 10−4 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F17 | 2 | 1.00 | 6.10 × 10−5 | 1.00 | 4.88 × 10−4 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 1.22 × 10−4 |
| F18 | 2 | 1.95 × 10−3 | 6.10 × 10−5 | 7.54 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 3.07 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F19 | 3 | 1.00 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 1.00 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F20 | 6 | 7.66 × 10−1 | 2.56 × 10−2 | 1.56 × 10−2 | 8.54 × 10−4 | 2.52 × 10−1 | 6.27 × 10−1 | 6.10 × 10−5 | 6.10 × 10−5 | 2.01 × 10−3 |
| F21 | 4 | 3.13 × 10−2 | 6.10 × 10−5 | 3.13 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 7.81 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F22 | 4 | 6.25 × 10−2 | 6.10 × 10−5 | 6.25 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 3.91 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| F23 | 4 | 3.13 × 10−2 | 6.10 × 10−5 | 1.95 × 10−3 | 6.10 × 10−5 | 6.10 × 10−5 | 1.56 × 10−2 | 6.10 × 10−5 | 6.10 × 10−5 | 6.10 × 10−5 |
| Overall (+/=/−) | 45/17/0 | 59/3/0 | 57/5/0 | 62/0/0 | 52/10/0 | 57/5/0 | 47/11/4 | 50/12/0 | 45/12/5 | |
| Function | Metric | IWHO | WHO | GWO | MFO | SSA | WOA | PSO | HSCAHS | DSCA | MALO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CEC_01 | Mean | 2.64 × 103 | 4.54 × 103 | 8.07 × 108 | 2.13 × 109 | 2.41 × 103 | 1.44 × 109 | 1.58 × 103 | 3.25 × 1010 | 1.40 × 1010 | 1.70 × 103 |
| Std | 3.02 × 103 | 4.17 × 103 | 6.80 × 108 | 1.62 × 109 | 2.82 × 103 | 1.03 × 109 | 1.94 × 103 | 2.42 × 109 | 2.58 × 109 | 1.99 × 103 | |
| Ranking | 4 | 5 | 6 | 8 | 3 | 7 | 1 | 10 | 9 | 2 | |
| CEC_02 | Mean | 2.60 × 103 | 2.76 × 103 | 2.74 × 103 | 3.28 × 103 | 3.52 × 103 | 4.34 × 103 | 3.38 × 103 | 6.29 × 103 | 5.76 × 103 | 3.36 × 103 |
| Std | 4.49 × 102 | 4.21 × 102 | 7.65 × 102 | 7.86 × 102 | 5.76 × 102 | 6.19 × 102 | 3.65 × 102 | 2.98 × 102 | 2.33 × 102 | 6.28 × 102 | |
| Ranking | 1 | 3 | 2 | 4 | 7 | 8 | 6 | 10 | 9 | 5 | |
| CEC_03 | Mean | 7.93 × 102 | 7.92 × 102 | 7.94 × 102 | 8.37 × 102 | 8.21 × 102 | 9.68 × 102 | 7.85 × 102 | 1.06 × 103 | 9.86 × 102 | 8.61 × 102 |
| Std | 2.45 × 101 | 2.89 × 101 | 2.66 × 101 | 7.11 × 101 | 4.42 × 101 | 4.63 × 101 | 1.86 × 101 | 1.78 × 101 | 1.82 × 101 | 5.06 × 101 | |
| Ranking | 3 | 2 | 4 | 6 | 5 | 8 | 1 | 10 | 9 | 7 | |
| CEC_04 | Mean | 1.91 × 103 | 1.91 × 103 | 2.02 × 103 | 1.05 × 104 | 1.91 × 103 | 2.80 × 103 | 1.90 × 103 | 4.20 × 105 | 8.47 × 104 | 1.91 × 103 |
| Std | 3.44 | 4.80 | 2.92 × 102 | 1.22 × 104 | 2.24 | 1.81 × 103 | 1.60 | 2.13 × 105 | 4.36 × 104 | 3.19 | |
| Ranking | 3.5 | 3.5 | 6 | 8 | 3.5 | 7 | 1 | 10 | 9 | 3.5 | |
| CEC_05 | Mean | 2.26 × 105 | 2.76 × 105 | 8.21 × 105 | 2.87 × 106 | 6.26 × 105 | 2.43 × 106 | 1.92 × 105 | 6.72 × 106 | 4.43 × 106 | 2.92 × 105 |
| Std | 1.52 × 105 | 2.00 × 105 | 6.45 × 105 | 4.73 × 106 | 4.90 × 105 | 1.20 × 106 | 1.35 × 105 | 2.02 × 106 | 2.22 × 106 | 2.27 × 105 | |
| Ranking | 2 | 3 | 6 | 8 | 5 | 7 | 1 | 10 | 9 | 4 | |
| CEC_06 | Mean | 1.86 × 103 | 1.99 × 103 | 2.01 × 103 | 2.04 × 103 | 2.26 × 103 | 2.65 × 103 | 2.19 × 103 | 3.82 × 103 | 2.75 × 103 | 2.41 × 103 |
| Std | 1.53 × 102 | 1.93 × 102 | 1.69 × 102 | 2.10 × 102 | 2.30 × 102 | 3.11 × 102 | 2.35 × 102 | 2.69 × 102 | 2.10 × 102 | 2.74 × 102 | |
| Ranking | 1 | 2 | 3 | 4 | 6 | 8 | 5 | 10 | 9 | 7 | |
| CEC_07 | Mean | 1.43 × 105 | 9.90 × 104 | 3.30 × 105 | 1.07 × 106 | 2.39 × 105 | 1.34 × 106 | 1.07 × 105 | 2.78 × 106 | 2.23 × 106 | 1.30 × 105 |
| Std | 1.15 × 105 | 1.10 × 105 | 4.35 × 105 | 1.59 × 106 | 2.27 × 105 | 1.00 × 106 | 9.74 × 104 | 1.54 × 106 | 1.16 × 106 | 1.18 × 105 | |
| Ranking | 4 | 1 | 6 | 7 | 5 | 8 | 2 | 10 | 9 | 3 | |
| CEC_08 | Mean | 2.36 × 103 | 2.80 × 103 | 3.02 × 103 | 4.07 × 103 | 2.93 × 103 | 4.21 × 103 | 3.64 × 103 | 5.91 × 103 | 6.04 × 103 | 2.30 × 103 |
| Std | 3.38 × 102 | 1.03 × 103 | 9.10 × 102 | 1.32 × 103 | 1.31 × 103 | 1.92 × 103 | 1.49 × 103 | 4.45 × 102 | 8.07 × 102 | 1.15 × 101 | |
| Ranking | 2 | 3 | 5 | 7 | 4 | 8 | 6 | 9 | 10 | 1 | |
| CEC_09 | Mean | 2.88 × 103 | 2.87 × 103 | 2.87 × 103 | 2.89 × 103 | 2.86 × 103 | 3.04 × 103 | 3.06 × 103 | 3.47 × 103 | 3.02 × 103 | 2.90 × 103 |
| Std | 3.78 × 101 | 3.22 × 101 | 3.95 × 101 | 3.40 × 101 | 2.14 × 101 | 7.19 × 101 | 8.00 × 101 | 9.40 × 101 | 1.99 × 101 | 2.36 × 101 | |
| Ranking | 4 | 2.5 | 2.5 | 5 | 1 | 8 | 9 | 10 | 7 | 6 | |
| CEC_10 | Mean | 2.96 × 103 | 2.97 × 103 | 3.00 × 103 | 3.04 × 103 | 2.95 × 103 | 3.13 × 103 | 2.95 × 103 | 5.29 × 103 | 3.84 × 103 | 2.97 × 103 |
| Std | 3.77 × 101 | 3.22 × 101 | 3.95 × 101 | 1.56 × 102 | 3.29 × 101 | 7.21 × 101 | 2.97 × 101 | 2.94 × 102 | 2.42 × 102 | 2.64 × 101 | |
| Ranking | 3 | 4.5 | 6 | 7 | 1.5 | 8 | 1.5 | 10 | 9 | 4.5 | |
| Overall Ranking | 1 | 2 | 6 | 7 | 4 | 8 | 3 | 10 | 9 | 5 | |
| Algorithm | Optimal Values for Variables | Minimum Cost | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| IWHO | 0.2057 | 3.2530 | 9.0366 | 0.2057 | 1.6952 |
| WHO [49] | 0.2058 | 3.2514 | 9.0370 | 0.2058 | 1.6958 |
| GWO [50] | 0.202369 | 3.544214 | 9.048210 | 0.205723 | 1.728712 |
| MFO [51] | 0.302546 | 2.662619 | 7.262456 | 0.318524 | 1.726186 |
| WOA [53] | 0.328517 | 2.465267 | 7.046271 | 0.426580 | 1.878023 |
| SCA [65] | 0.141883 | 5.225674 | 10.00000 | 0.211640 | 1.858033 |
| ALO [66] | 0.125130 | 9.784118 | 6.522153 | 0.394937 | 1.785364 |
| DA [67] | 0.206905 | 3.314990 | 9.397212 | 0.206905 | 1.749248 |
| LSHADE [68] | 0.20573 | 3.4705 | 9.0366 | 0.20573 | 1.724852 |
| Algorithm | Optimal Values for Variables | Minimum Weight | ||
|---|---|---|---|---|
| d | D | N | ||
| IWHO | 0.0517 | 0.4155 | 7.1564 | 0.0102 |
| AO [70] | 0.0502439 | 0.35262 | 10.5425 | 0.011165 |
| HHO [71] | 0.051796393 | 0.359305355 | 11.138859 | 0.012665443 |
| SSA [52] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| WOA [53] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 |
| GWO [50] | 0.05169 | 0.356737 | 11.28885 | 0.012666 |
| PSO [15] | 0.051728 | 0.357644 | 11.244543 | 0.0126747 |
| MVO [72] | 0.05251 | 0.37602 | 10.33513 | 0.012790 |
| GA [30] | 0.051480 | 0.351661 | 11.632201 | 0.01270478 |
| HS [73] | 0.051154 | 0.349871 | 12.076432 | 0.0126706 |
| Algorithm | IWHO | GWO [50] | GOA [18] | PSO [15] | MFO [51] | SSA [52] | DSCA [55] | MALO [56] |
|---|---|---|---|---|---|---|---|---|
| x1 | 0.5000 | 0.5000 | 0.50000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 |
| x2 | 1.1186 | 1.0268 | 1.11670 | 1.1327 | 1.0946 | 1.1221 | 0.9765 | 1.2023 |
| x3 | 0.5000 | 0.5929 | 0.50000 | 0.5000 | 0.5000 | 0.5062 | 1.3381 | 0.5000 |
| x4 | 1.2982 | 1.3772 | 1.30208 | 1.2781 | 1.3461 | 1.3170 | 0.5000 | 1.2833 |
| x5 | 0.5000 | 0.5000 | 0.50000 | 0.5000 | 0.5000 | 0.5000 | 0.5214 | 0.5000 |
| x6 | 1.5000 | 1.5000 | 1.50000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.1728 |
| x7 | 0.5000 | 0.5000 | 0.50000 | 0.5000 | 0.5000 | 0.5000 | 0.6263 | 0.5000 |
| x8 | 0.3450 | 0.3450 | 0.34500 | 0.3450 | 0.3450 | 0.3136 | 0.1920 | 0.3347 |
| x9 | 0.3450 | 0.3450 | 0.19200 | 0.3450 | 0.3450 | 0.2115 | 0.3450 | 0.3096 |
| x10 | −19.1594 | −30.0000 | −19.54935 | −16.6449 | −23.4599 | −21.9139 | −30.0000 | −5.3953 |
| x11 | 0.0020 | 0.1523 | −0.00431 | 0.1076 | 0.0014 | 2.2405 | 7.8909 | 7.3999 |
| Optimal value | 22.8427 | 23.1976 | 22.84474 | 22.8556 | 22.8744 | 22.9855 | 24.9261 | 23.3406 |
| Algorithm | Optimal Values for Variables | Optimum Weight | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | ||
| IWHO | 3.4976 | 0.7 | 17 | 7.3 | 7.8 | 3.3501 | 5.2855 | 2995.43736 |
| AO [70] | 3.5021 | 0.7 | 17 | 7.3099 | 7.7476 | 3.3641 | 5.2994 | 3007.7328 |
| PSO [15] | 3.5001 | 0.7 | 17.0002 | 7.5177 | 7.7832 | 3.3508 | 5.2867 | 3145.922 |
| AOA [75] | 3.50384 | 0.7 | 17 | 7.3 | 7.72933 | 3.35649 | 5.2867 | 2997.9157 |
| MFO [51] | 3.49745 | 0.7 | 17 | 7.82775 | 7.71245 | 3.35178 | 5.28635 | 2998.9408 |
| GA [29] | 3.51025 | 0.7 | 17 | 8.35 | 7.8 | 3.36220 | 5.28772 | 3067.561 |
| SCA [65] | 3.50875 | 0.7 | 17 | 7.3 | 7.8 | 3.46102 | 5.28921 | 3030.563 |
| HS [73] | 3.52012 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.28871 | 3029.002 |
| FA [78] | 3.50749 | 0.7001 | 17 | 7.71967 | 8.08085 | 3.35151 | 5.28705 | 3010.13749 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, R.; Hussien, A.G.; Jia, H.-M.; Abualigah, L.; Wang, S.; Wu, D. An Improved Wild Horse Optimizer for Solving Optimization Problems. Mathematics 2022, 10, 1311. https://doi.org/10.3390/math10081311
Zheng R, Hussien AG, Jia H-M, Abualigah L, Wang S, Wu D. An Improved Wild Horse Optimizer for Solving Optimization Problems. Mathematics. 2022; 10(8):1311. https://doi.org/10.3390/math10081311
Chicago/Turabian StyleZheng, Rong, Abdelazim G. Hussien, He-Ming Jia, Laith Abualigah, Shuang Wang, and Di Wu. 2022. "An Improved Wild Horse Optimizer for Solving Optimization Problems" Mathematics 10, no. 8: 1311. https://doi.org/10.3390/math10081311
APA StyleZheng, R., Hussien, A. G., Jia, H.-M., Abualigah, L., Wang, S., & Wu, D. (2022). An Improved Wild Horse Optimizer for Solving Optimization Problems. Mathematics, 10(8), 1311. https://doi.org/10.3390/math10081311









