MHD Micropolar Fluid in a Porous Channel Provoked by Viscous Dissipation and Non-Linear Thermal Radiation: An Analytical Approach
Abstract
:1. Introduction
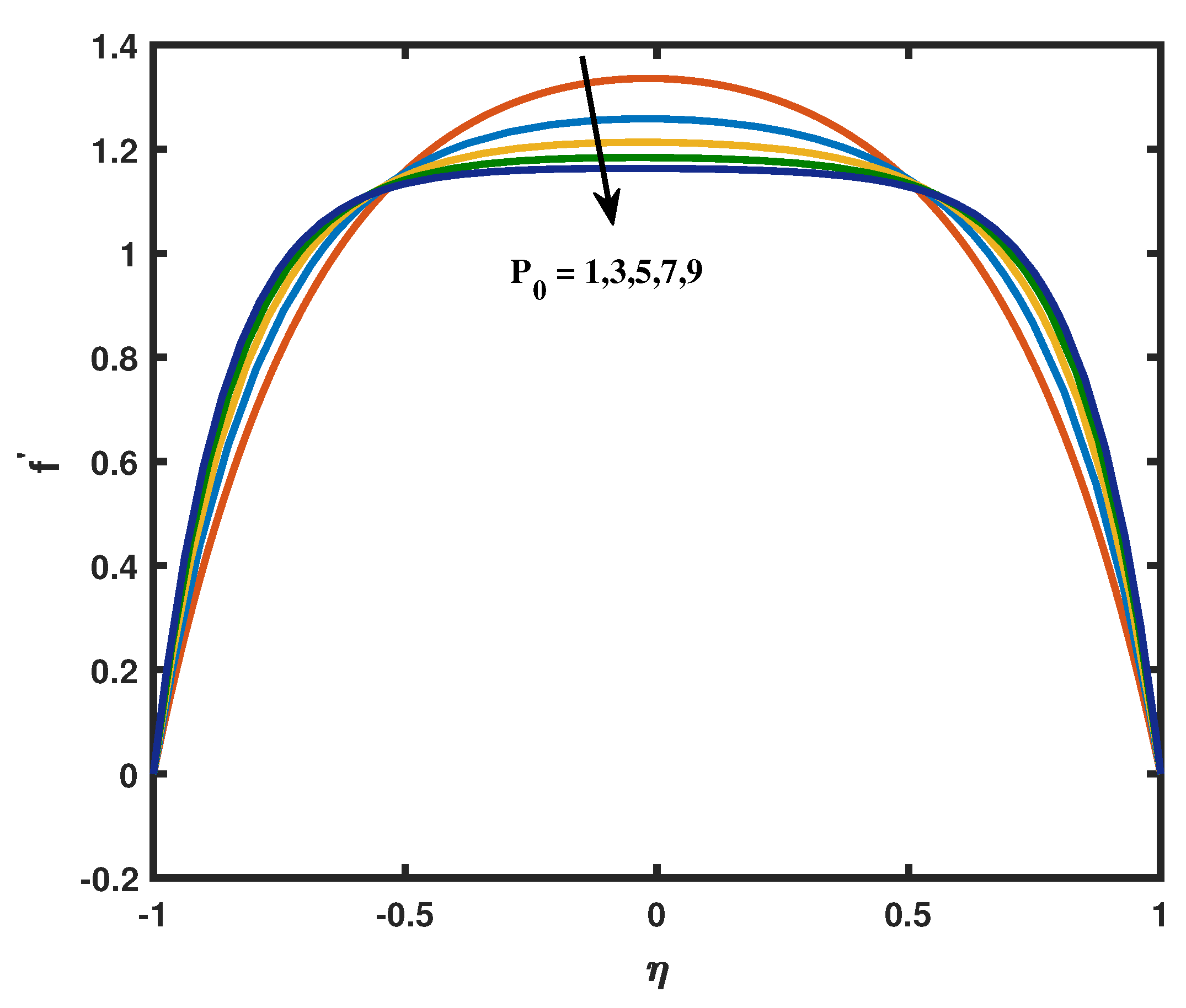
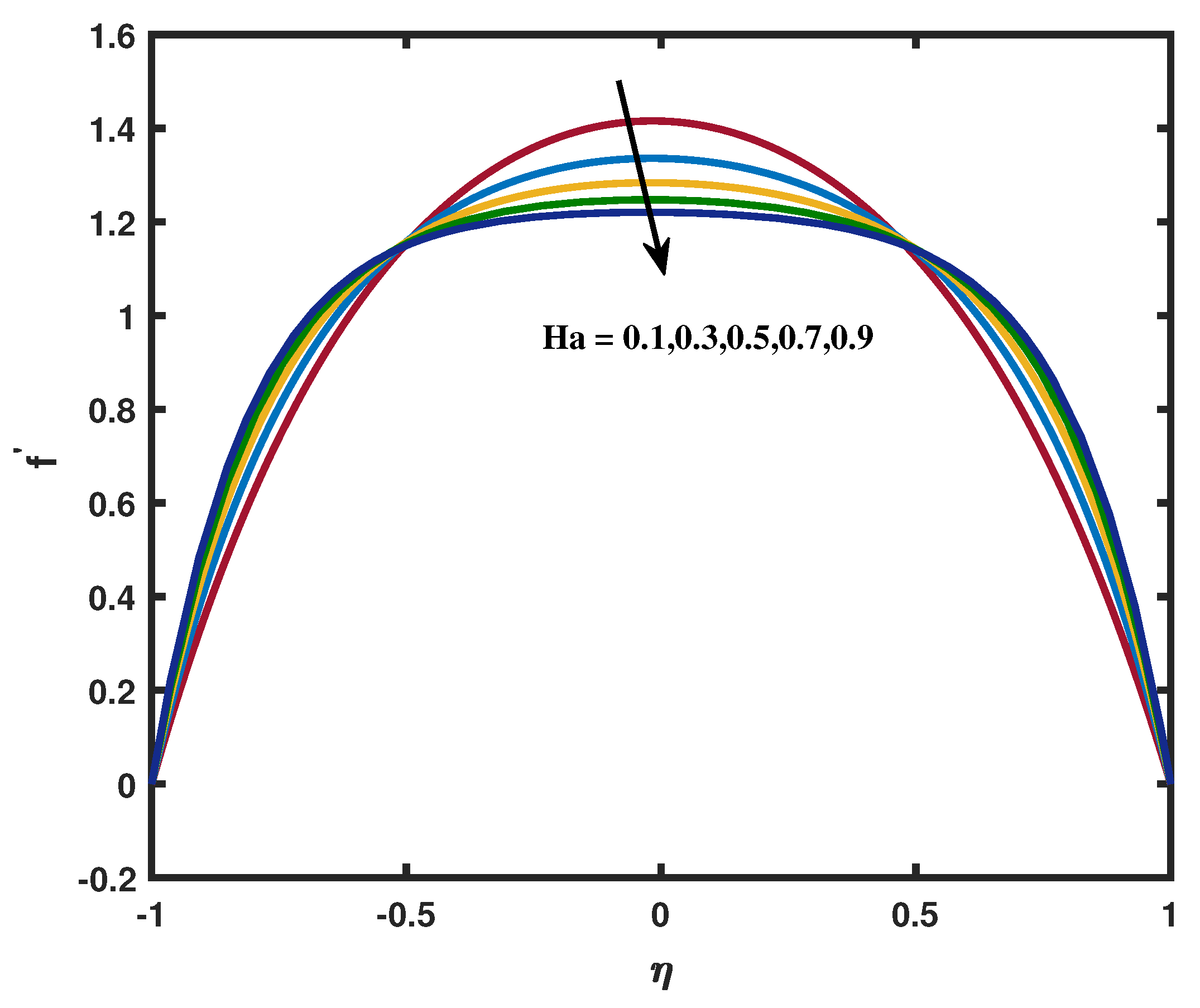
- How do the porosity parameter and magnetic number affect the velocity profile?
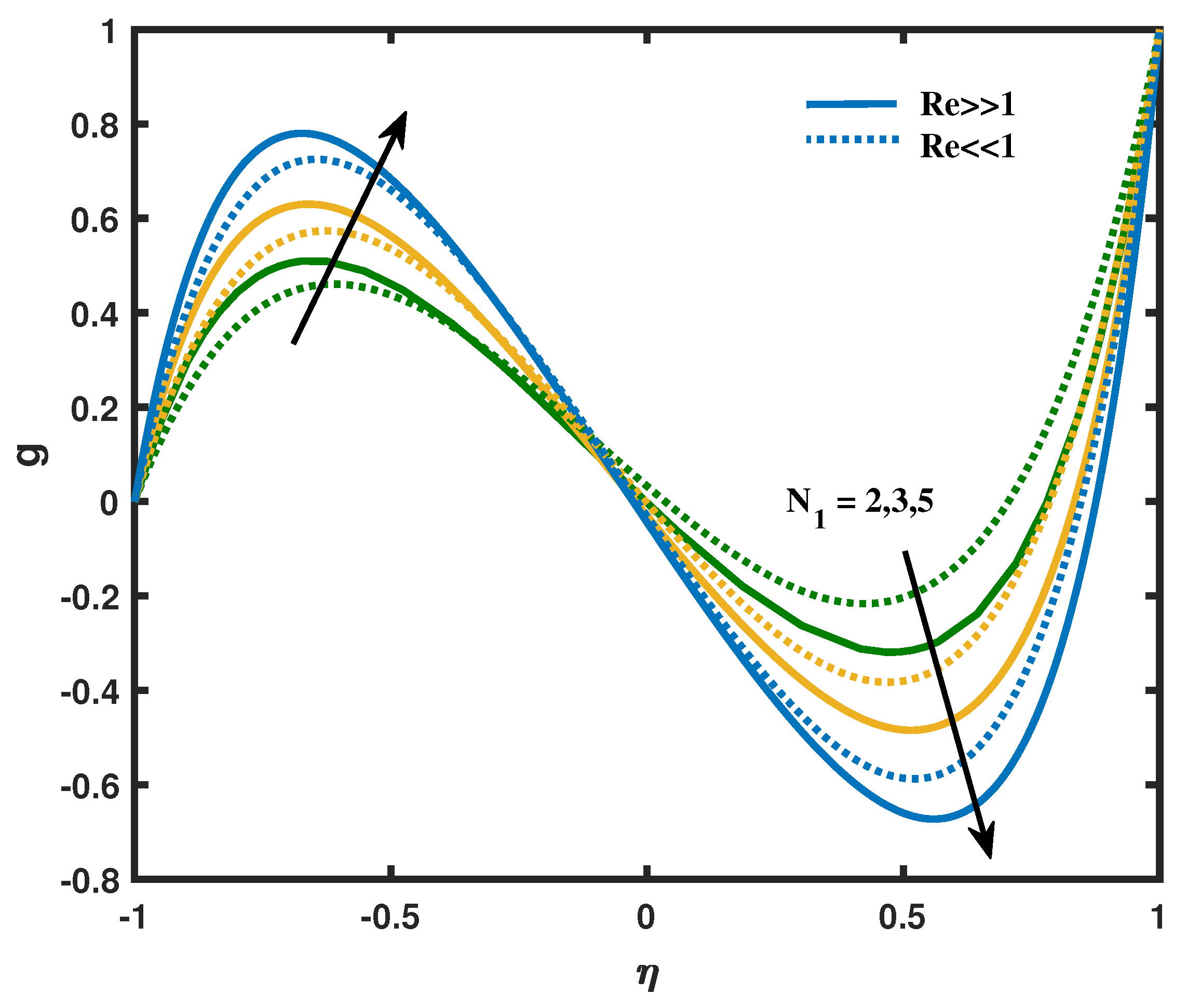
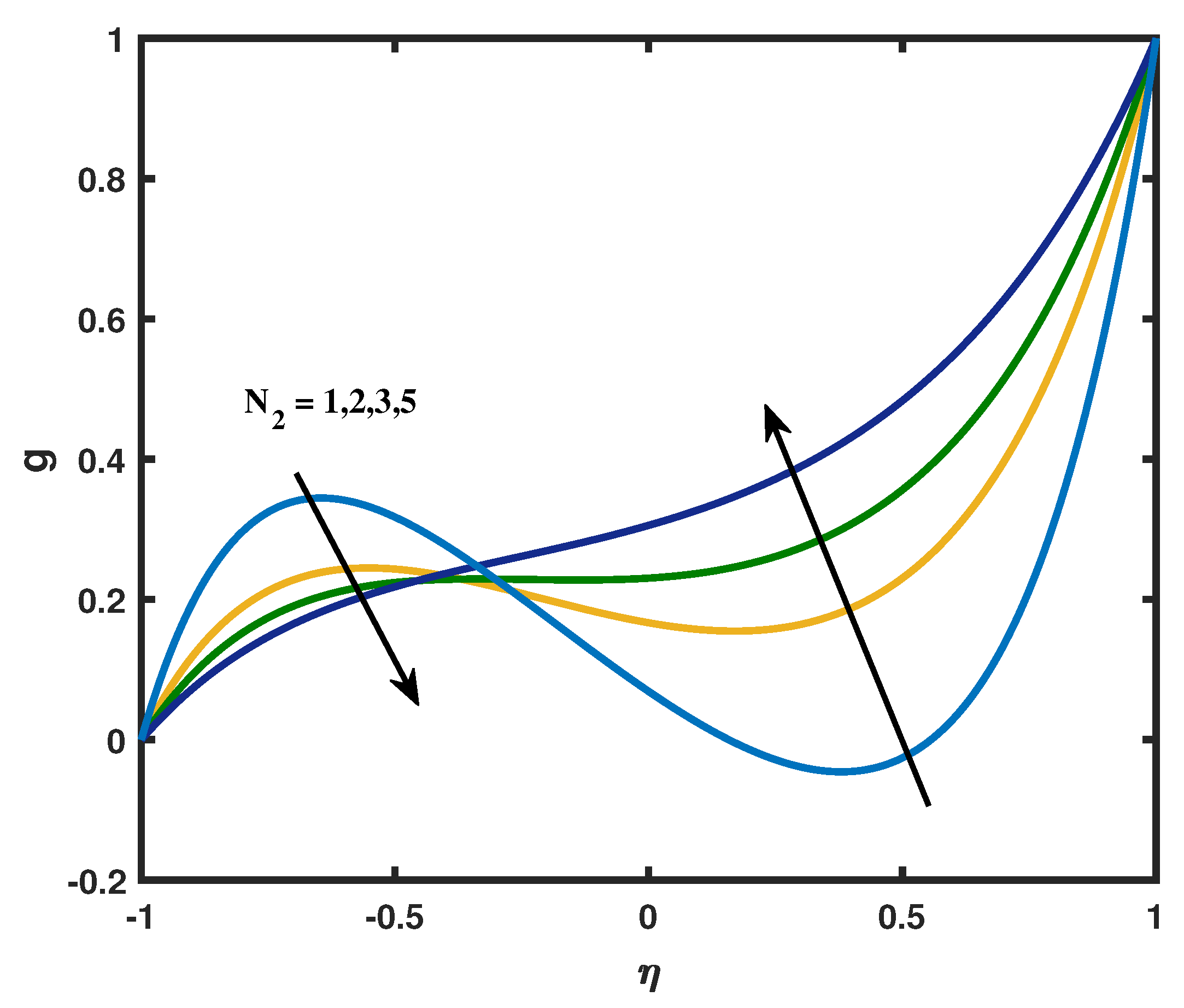
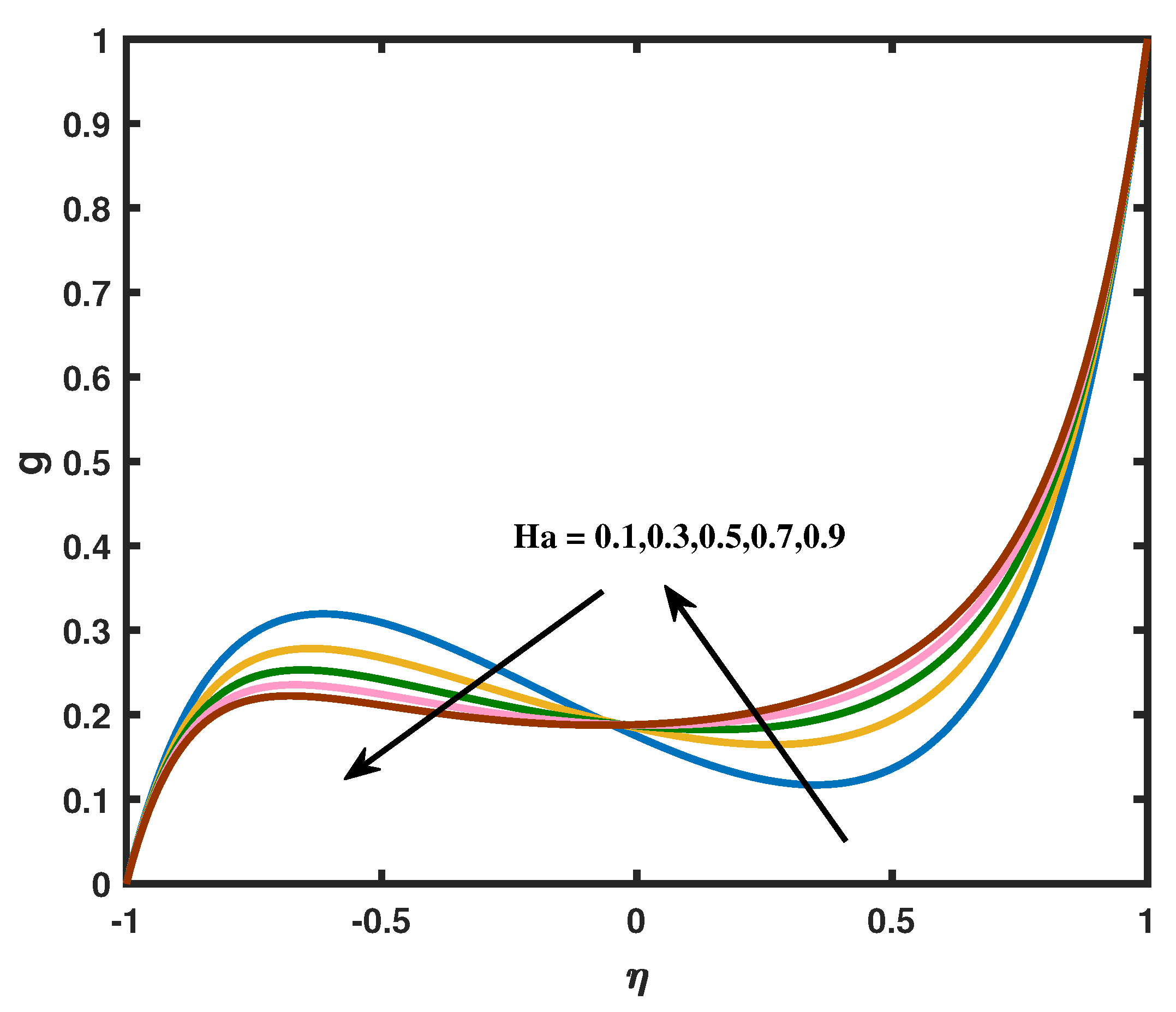
- How do the vortex viscosity parameter and magnetic parameter affects the angular velocity profile.
- Why non-linear thermal radiation is chosen to analyze the heat transfer process?
- In what way the radiation term and temperature ratio parameter affects the temperature profile?
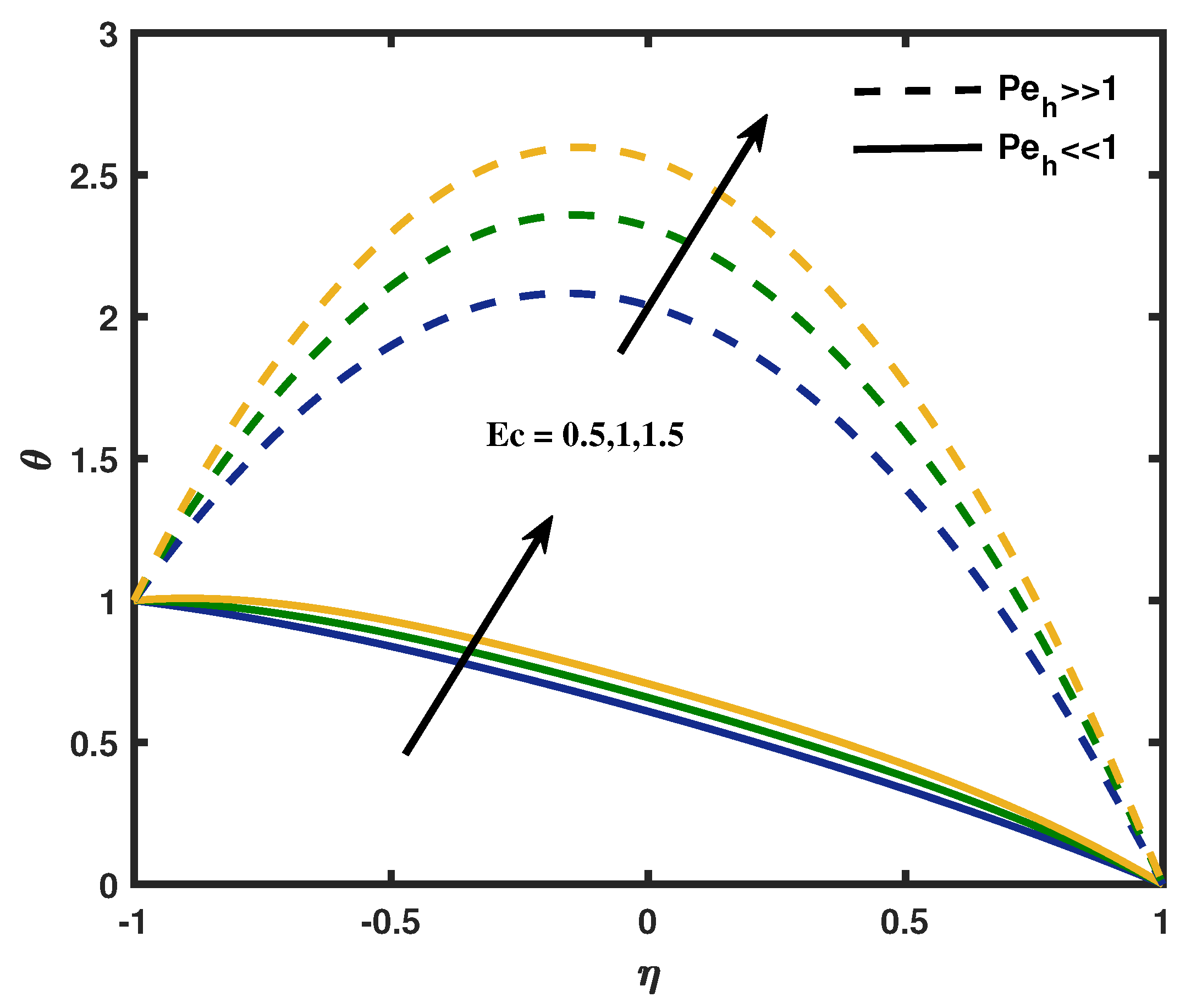
- How does the Peclet number for heat and mass transfer affect the temperature and concentration profile?
- What is the superiority of ADM and VIM compared with other analytical method?
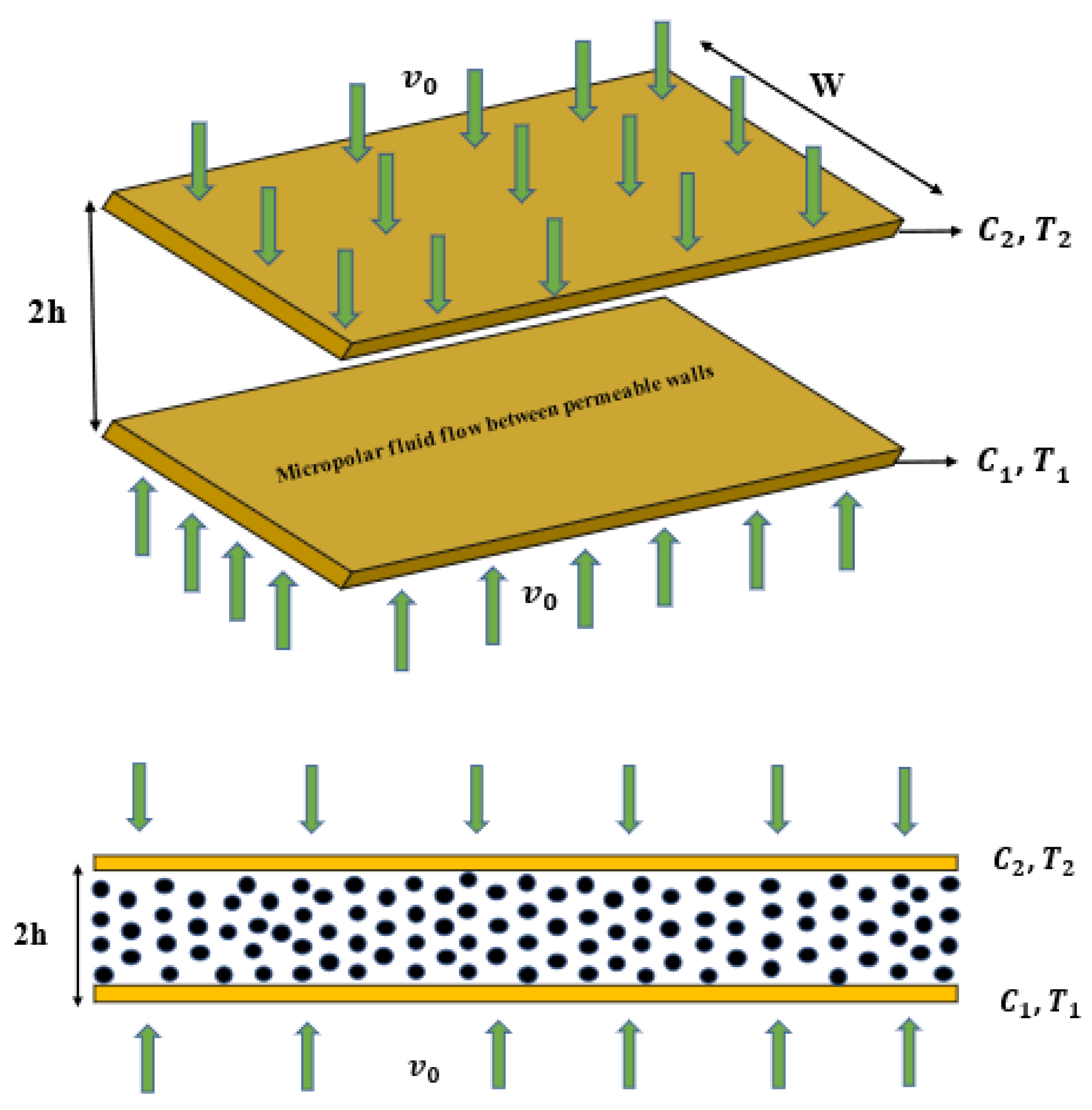
2. Problem Formulation
3. Dimensionless Formulation
4. Numerical Approach
5. Analytical Approach
5.1. Adomian Decomposition Method (ADM)
5.2. Variational Iteration Method (VIM)
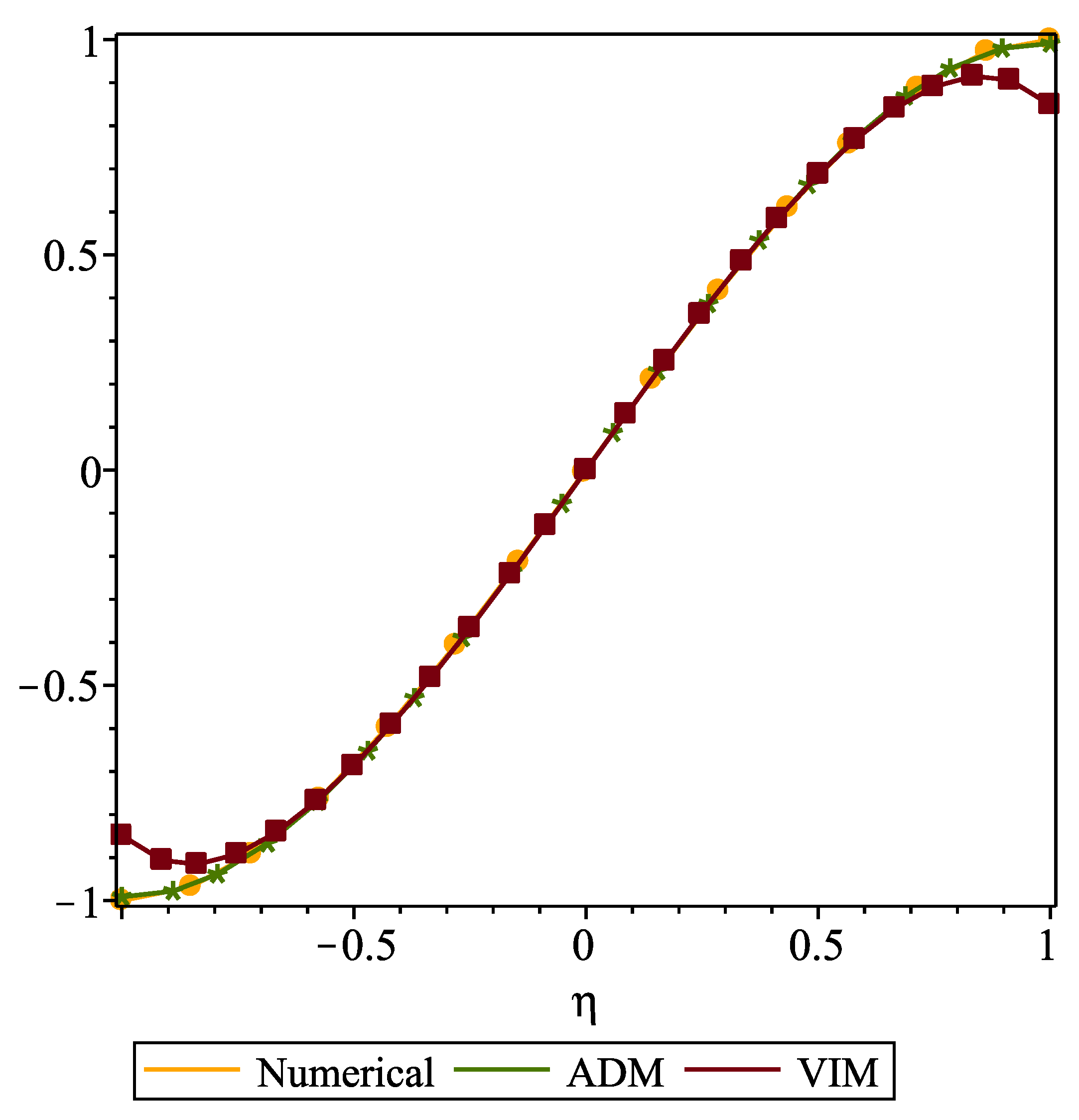
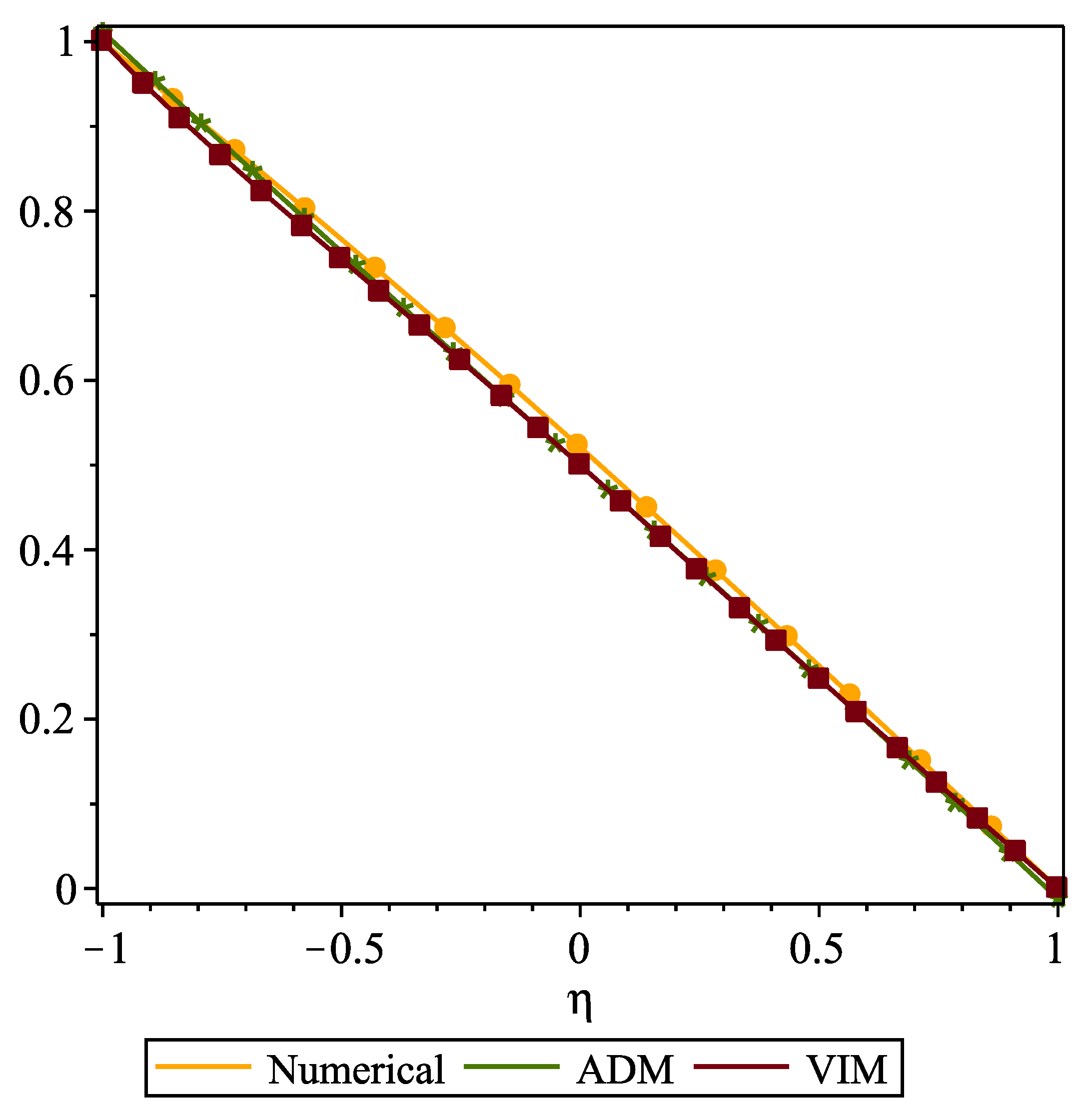
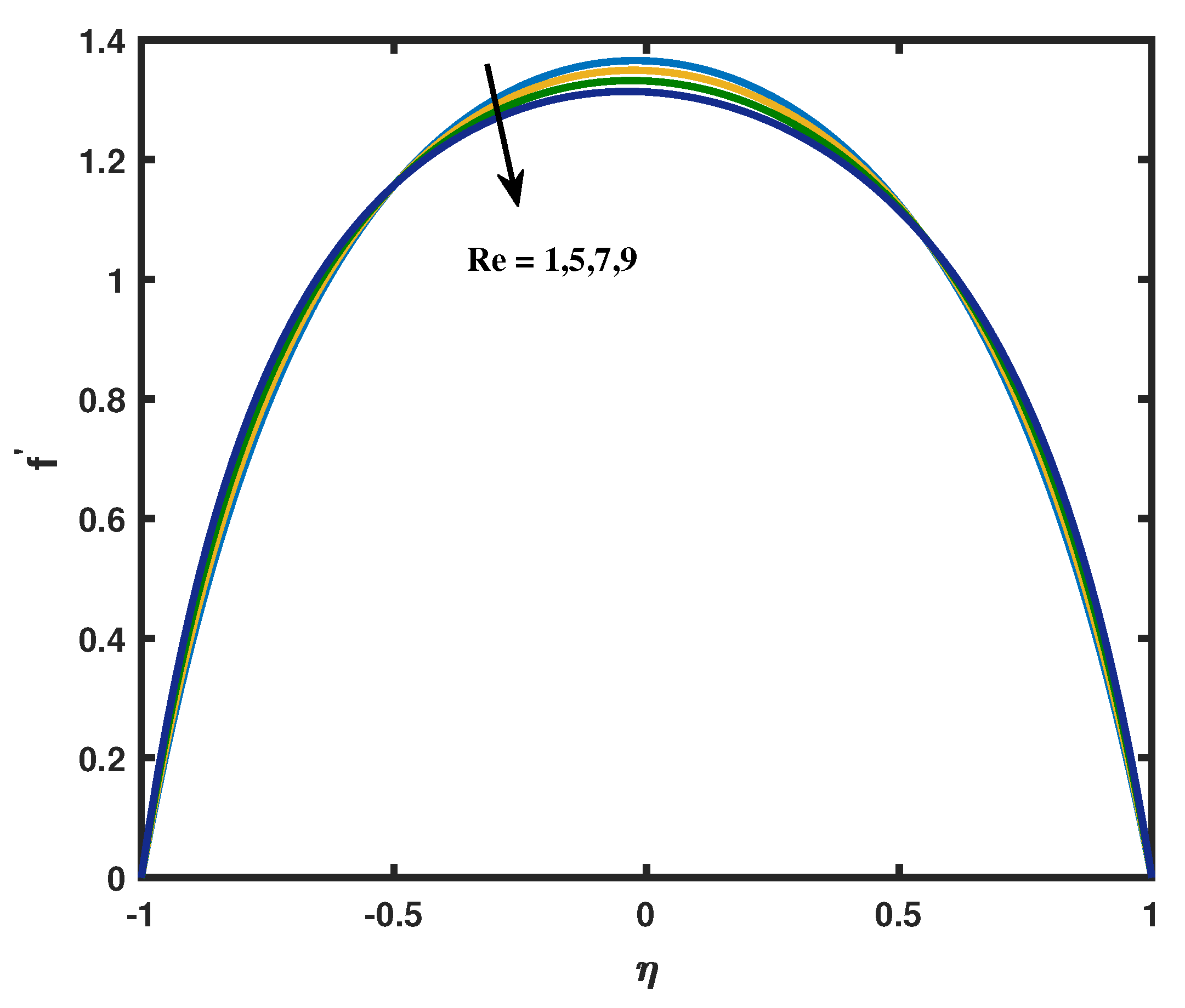
6. Results Discussion and Code Validation
7. Concluding Remarks
- The vortex viscosity parameter and spin gradient viscosity parameter shows the opposite reaction on micro-rotation profile.
- The porosity parameter increases the surface drag, while its effect reduces the mass and thermal transit rates.
- The presumptions obviously demonstrate that the micro-rotation and velocity are restrained by the porosity parameter and the Reynolds number.
- Increasing the magnetic field opposing the fluid motion.
- Increases the Eckert number rises the kinetic energy which enhances the temperature.
- The effect of viscous dissipation is to increase the heat transfer rate.
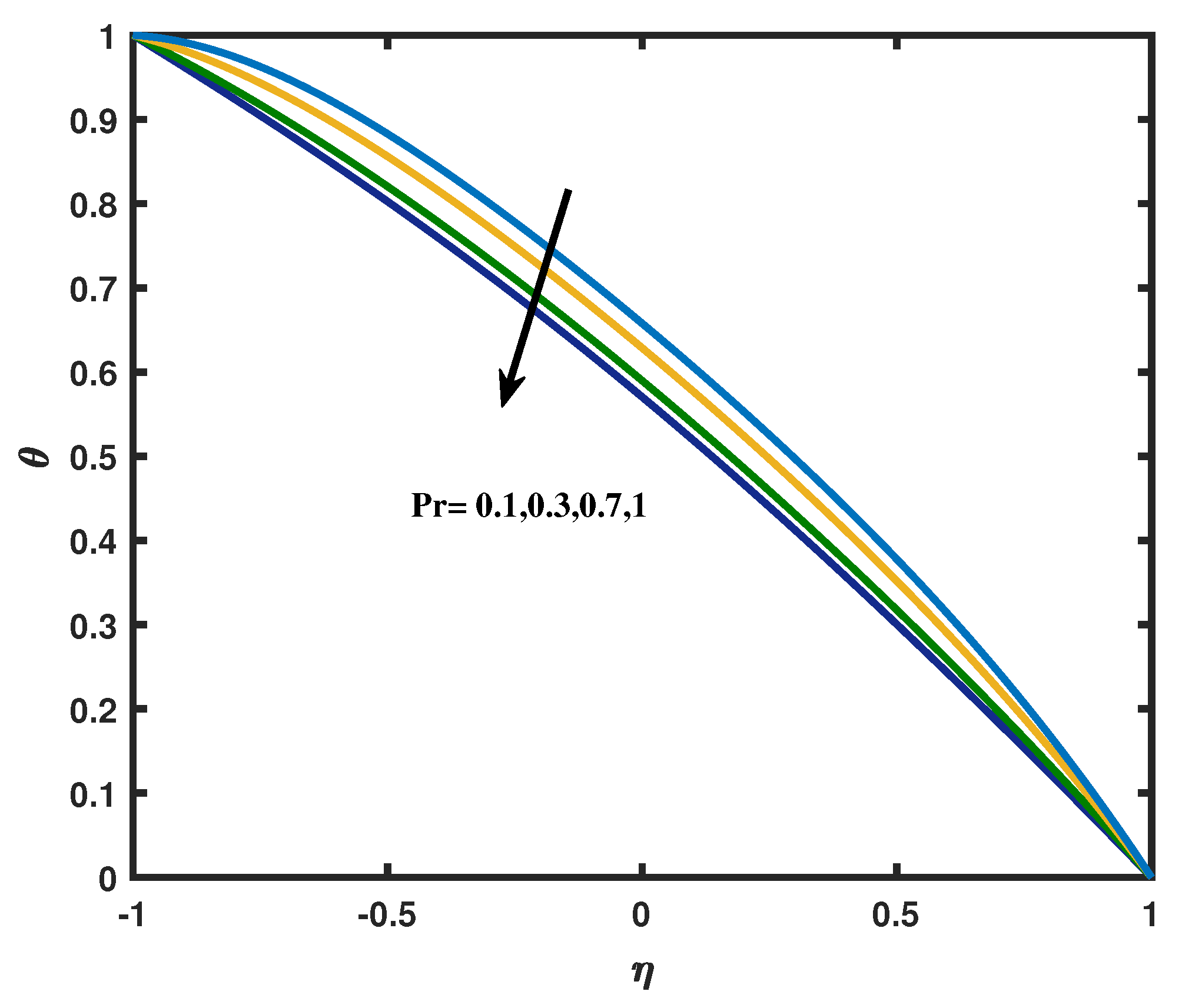
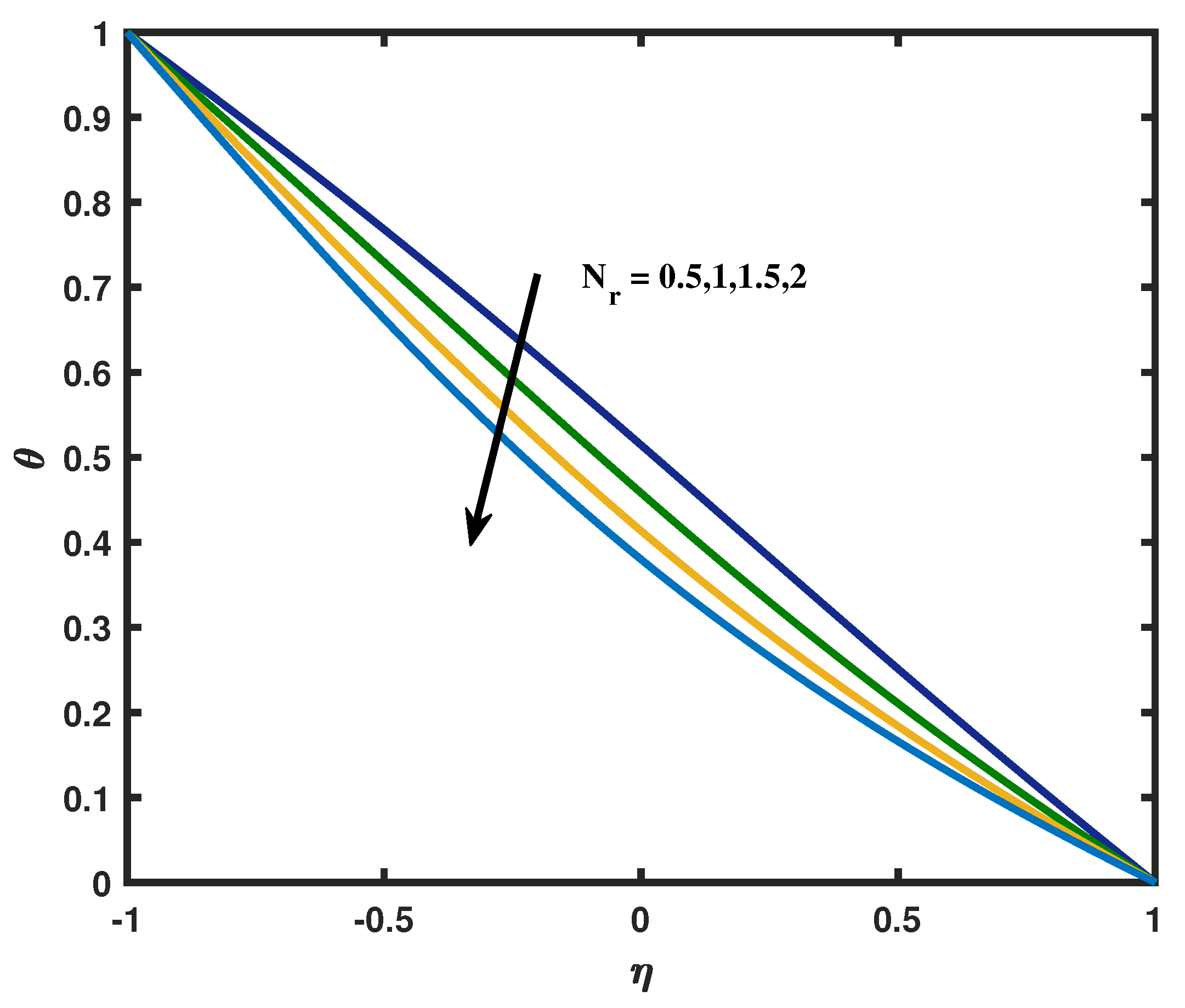
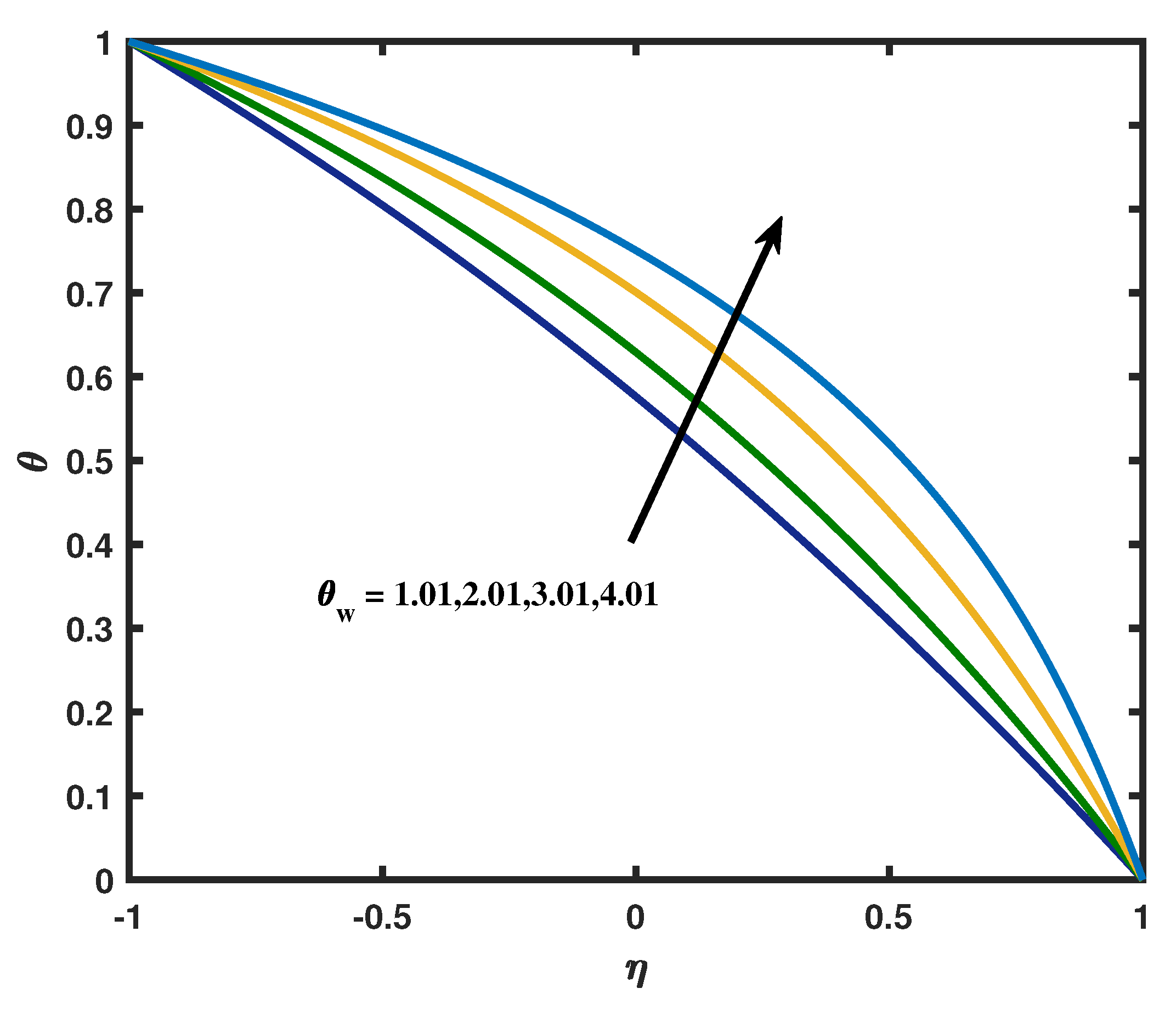
- The thermal radiation phenomena flattens the temperature and speeds up the heat transfer rate in the lower wall
- Temperature distribution upgraded with increases in the temperature ratio parameter.
- The skin friction values increases when increases the magnetic number in the lower wall whereas the reverse trend is noted in the upper wall.
- The impact of thermal rays is essential in space technology and high temperature processes. At the point when the temperature variation is very high, the linear thermal radiation causes a noticeable error. To overcome such errors, nonlinear thermal radiation is taken into account.
- VIM and ADM having high accuracy in solving nonlinear differential problems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. ADM Formulation
Appendix A.2. VIM Formulataion
References
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–8. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicrofluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef] [Green Version]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Rana, B.M.; Arifuzzaman, S.M.; Islam, S.; Reza-E-Rabbi, S.; Al-Mamun, A.; Mazumder, M.; Roy, K.C.; Khan, M.S. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid. Therm. Sci. Eng. Prog. 2021, 25, 101018. [Google Scholar] [CrossRef]
- Tetbirt, A.; Bouaziz, M.N.; Abbes, M.T. Numerical study of magnetic effect on the velocity distribution field in a macro/micro-scale of a micropolar and viscous fluid in vertical channel. J. Mol. Liq. 2016, 216, 103–110. [Google Scholar] [CrossRef]
- Pal, D.; Biswas, S. Magnetohydrodynamic convective-radiative oscillatory flow of a chemically reactive micropolar fluid in a porous medium. Propuls. Power Res. 2018, 7, 158–170. [Google Scholar] [CrossRef]
- Nisar, K.S.; Faridi, A.A.; Ahmad, S.; Khan, N.; Ali, K.; Jamshed, W.; Abdel-Aty, A.H.; Yahia, I.S. Cumulative impact of micropolar fluid and porosity on MHD channel flow: A numerical study. Coatings 2022, 12, 93. [Google Scholar] [CrossRef]
- Ashraf, M.; Kamal, M.A.; Syed, K.S. Numerical study of asymmetric laminar flow of micropolar fluids in a porous channel. Comput. Fluids 2009, 38, 1895–1902. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A note on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2014, 72, 388–391. [Google Scholar] [CrossRef]
- Cao, L.; Si, X.; Zheng, L. The flow of a micropolar fluid through a porous expanding channel: A Lie group analysis. Appl. Math. Comput. 2015, 270, 242–250. [Google Scholar] [CrossRef]
- Lu, D.; Kahshan, M.; Siddiqui, A.M. Hydrodynamical study of micropolar fluid in a porous-walled channel: Application to flat plate dialyzer. Symmetry 2019, 11, 541. [Google Scholar] [CrossRef]
- Tiwari, A.; Shah, P.D.; Chauhan, S.S. Analytical study of micropolar fluid flow through porous layered microvessels with heat transfer approach. Eur. Phys. J. Plus 2020, 135, 1–32. [Google Scholar] [CrossRef]
- Siddheshwar, P.G.; Mahabaleshwar, U.S. Analytical solution to the MHD flow of micropolar fluid over a linear stretching sheet. Int. J. Appl. Mech. Eng. 2015, 20, 397–406. [Google Scholar] [CrossRef] [Green Version]
- Nandi, S.; Kumbhakar, B. Navier’s slip effect on Carreau nanouid flow past a convectively heated wedge in the presence of nonlinear thermal radiation and magnetic field. Int. Commun. Heat Mass Transf. 2020, 118, 104813. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Kutbi, M.A. MHD three-dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 396, 31–37. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Raju, C.S.; Sandeep, N. Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alex. Eng. J. 2016, 55, 1595–1606. [Google Scholar] [CrossRef] [Green Version]
- Ramzan, M.; Chung, J.D.; Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 2017, 130, 31–40. [Google Scholar] [CrossRef]
- Patel, H.R.; Singh, R. Thermophoresis, Brownian motion and non-linear thermal radiation effects on mixed convection MHD micropolar fluid flow due to nonlinear stretched sheet in porous medium with viscous dissipation, joule heating and convective boundary condition. Int. Commun. Heat Mass Transf. 2019, 107, 68–92. [Google Scholar] [CrossRef]
- Si, X.; Zheng, L.; Lin, P.; Zhang, X.; Zhang, Y. Flow and heat transfer of a micropolar fluid in a porous channel with expanding or contracting walls. Int. J. Heat Mass Transf. 2013, 67, 885–895. [Google Scholar] [CrossRef]
- Muthuraj, R.; Srinivas, S.; Shukla, A.K.; Ramamohan, T.R. Effects of Thermal Diffusion, Diffusion Thermo, and Space Porosity on MHD Mixed Convective Flow of Micropolar Fluid in a Vertical Channel with Viscous Dissipation. Heat Transf. Asian Res. 2014, 43, 561–576. [Google Scholar] [CrossRef]
- Sheri, S.R.; Shamshuddin, M.D. Heat and mass transfer on the MHD flow of micro polar fluid in the presence of viscous dissipation and chemical reaction. Procedia Eng. 2015, 127, 885–892. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Numerical simulation of viscous dissipation in a micropolar fluid flow through a porous medium. J. Appl. Mech. Tech. Phys. 2019, 60, 996–1004. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Alrihieli, H.F.; Bilal, M.; Saeed, A.; Weera, W. Numerical approach toward ternary hybrid nanofluid flow using variable diffusion and non-Fourier’s concept. ACS Omega 2022, 7, 29380–29390. [Google Scholar] [CrossRef] [PubMed]
- Kataria, H.R.; Mistry, M.; Mittal, A. Influence of nonlinear radiation on MHD micropolar fluid flow with viscous dissipation. Heat Transf. 2022, 51, 1449–1467. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Khan, I.; Abu-Zinadah, H.; Aldahlan, M.A. Mathematical simulation of casson MHD flow through a permeable moving wedge with nonlinear chemical reaction and nonlinear thermal radiation. Materials 2022, 15, 747. [Google Scholar] [CrossRef] [PubMed]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method some recent results and new interpretations. J. Comput. Appl. Math. 2007, 207, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Lu, J. An analytical approach to the Fornberg Whitham type equations by using the variational iteration method. Comput. Math. Appl. 2011, 61, 2010–2013. [Google Scholar] [CrossRef] [Green Version]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Roy, A.; Roy, D. An adaptation of adomian decomposition for numeric analytic integration of strongly nonlinear and chaotic oscillators. Comput. Methods Appl. Mech. Eng. 2007, 196, 1133–1153. [Google Scholar] [CrossRef]
- Aski, F.S.; Nasirkhani, S.J.; Mohammadian, E.; Asgari, A. Application of Adomian decomposition method for micropolar flow in a porous channel. Propuls. Power Res. 2014, 3, 15–21. [Google Scholar] [CrossRef]
- Seny, O.; Rasmane, Y.; Loufouilou, J.M.; Pare, Y. Exact Analytical Solution of Some Volterra Second Kind Integrodifferential Equations by the Numerical Analysis Methods ADM and VIM. Adv. Dyn. Syst. Appl. (ADSA) 2021, 16, 1075–1096. [Google Scholar]
- Abed, A.M.; Younis, M.F.; Hamoud, A.A. Numerical Solutions of Nonlinear Volterra-Fredholm Integro-Differential Equations by using MADM and VIM. Nonlinear Funct. Anal. Appl. 2022, 27, 189–201. [Google Scholar]
- Pasha, P.; Nabi, H.; Peiravi, M.M.; Pourfallah, M.; Domiri Ganji, D. The application of analytical methods in the investigation effects of Magnetic parameter and Brownian motion on the fluid flow between two equal plates. Int. J. Eng. 2021, 34, 2341–2350. [Google Scholar]
- Mirzaaghaian, A.; Ganji, D.D. Application of differential transformation method in micropolar fluid flow and heat transfer through permeable walls. Alex. Eng. J. 2016, 55, 2183–2191. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ashraf, M.; Ali, K. Simulation of thermal radiation in a micropolar fluid flow through a porous medium between channel walls. J. Therm. Anal. Calorim. 2021, 144, 941–953. [Google Scholar] [CrossRef]


| Numerical Results | ||||||
|---|---|---|---|---|---|---|
| Present Results | Literature [35] | Literature [36] | Present Results | Literature [35] | Literature [36] | |
| −1 | −0.999999 | −1 | −1 | 0.999999 | 1 | 1 |
| −0.8 | −0.943910 | −0.943889 | −0.943853 | 0.909591 | 0.909562 | 0.909561 |
| −0.6 | −0.791605 | −0.791757 | −0.791599 | 0.818970 | 0.818914 | 0.818912 |
| −0.4 | −0.567102 | −0.567738 | −0.295686 | 0.726688 | 0.726610 | 0.726605 |
| −0.2 | 0.621160 | 0.621165 | 0.621160 | 0.631831 | 0.631742 | 0.631734 |
| 0 | 0.001970 | 0 | 8.14 × 10−13 | 0.533923 | 0.533835 | 0.533825 |
| 0.2 | 0.298157 | 0.295835 | 0.295686 | 0.432823 | 0.432742 | 0.432737 |
| 0.4 | 0.569915 | 0.567738 | 0.567524 | 0.328631 | 0.328571 | 0.328563 |
| 0.6 | 0.793262 | 0.791757 | 0.791599 | 0.221584 | 0.221544 | 0.221538 |
| 0.8 | 0.944445 | 0.943889 | 0.943853 | 0.111965 | 0.111945 | 0.111942 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| −1 | −1 | −0.991187 | −0.848750 |
| −0.8 | −0.942612 | −0.941534 | −0.909184 |
| −0.6 | −0.788848 | −0.791491 | −0.786459 |
| −0.4 | −0.564296 | −0.567940 | −0.567526 |
| −0.2 | −0.293073 | −0.295998 | −0.295990 |
| 0 | 0.001294 | 0 | 0 |
| 0.2 | 0.295483 | 0.295998 | 0.295990 |
| 0.4 | 0.566196 | 0.567940 | 0.567526 |
| 0.6 | 0.790007 | 0.791791 | 0.786459 |
| 0.8 | 0.943005 | 0.941531 | 0.909184 |
| 1 | 1 | 0.991187 | 0.848750 |
| −1 | 1 | 1.011693 | 1.000000 |
| −0.8 | 0.907783 | 0.906892 | 0.889632 |
| −0.6 | 0.814341 | 0.803208 | 0.790784 |
| −0.4 | 0.718910 | 0.701014 | 0.695296 |
| −0.2 | 0.621160 | 0.600131 | 0.598848 |
| 0 | 0.521108 | 0.500000 | 0.500000 |
| 0.2 | 0.419032 | 0.399868 | 0.399232 |
| 0.4 | 0.315380 | 0.298985 | 0.297984 |
| 0.6 | 0.210677 | 0.196791 | 0.197696 |
| 0.8 | 0.105425 | 0.093107 | 0.098848 |
| 1 | 0 | −0.011693 | −0.000001 |
| 0.1 | 1 | 0.1 | 0.1 | 3.03075693 | −2.9140140 |
| 0.3 | 3.05059889 | −2.9346138 | |||
| 0.5 | 3.07033151 | −2.9550899 | |||
| 1 | 0.1 | 3.20550833 | −3.09510636 | ||
| 0.3 | 3.22441278 | −3.11465427 | |||
| 0.5 | 3.24321921 | −3.13409317 | |||
| 3 | 0.1 | 0.1 | 2.96246626 | −2.61024483 | |
| 0.3 | 2.97243614 | −2.62136373 | |||
| 0.5 | 2.98237963 | −2.6324449 | |||
| 1 | 0.1 | 3.13799613 | −2.80485426 | ||
| 0.3 | 3.14751138 | −2.81533854 | |||
| 0.5 | 3.15700259 | −2.82579014 | |||
| 3 | 1 | 0.1 | 0.1 | 2.63571963 | −3.54554686 |
| 0.3 | 2.66932666 | −3.56240713 | |||
| 0.5 | 2.7023711 | −3.57937237 | |||
| 1 | 0.1 | 2.92141356 | −3.69995395 | ||
| 0.3 | 2.95109937 | −3.71734373 | |||
| 0.5 | 2.98042261 | −3.73475378 | |||
| 3 | 0.1 | 0.1 | 2.93011104 | −2.60797715 | |
| 0.3 | 2.94159375 | −2.62055067 | |||
| 0.5 | 2.95303829 | −2.6330743 | |||
| 1 | 0.1 | 3.13116496 | −2.82702306 | ||
| 0.3 | 3.14199858 | −2.83876397 | |||
| 0.5 | 3.15279838 | −2.85046238 |
| 0.5 | 0.5 | 0.1 | 0.1 | −0.52235455 | 1.12730298 |
| 0.3 | −0.56353378 | 1.15291334 | |||
| 0.5 | −0.60462149 | 1.17848312 | |||
| 1 | 0.1 | −0.50548628 | 1.11587118 | ||
| 0.3 | −0.54611874 | 1.14117643 | |||
| 0.5 | −0.58668587 | 1.16645647 | |||
| 1 | 0.1 | 0.1 | −1.28749058 | 1.60590433 | |
| 0.3 | −1.37011473 | 1.65773933 | |||
| 0.5 | −1.45254232 | 1.70946438 | |||
| 1 | 0.1 | −1.25517384 | 1.58527646 | ||
| 0.3 | −1.33669037 | 1.63646255 | |||
| 0.5 | −1.41806512 | 1.68759003 | |||
| 1.5 | 0.5 | 0.1 | 0.1 | −0.22977973 | 0.65968306 |
| 0.3 | −0.27017615 | 0.67421018 | |||
| 0.5 | −0.31053466 | 0.68873936 | |||
| 1 | 0.1 | −0.21591700 | 0.65463068 | ||
| 0.3 | −0.25575187 | 0.66899326 | |||
| 0.5 | −0.29556943 | 0.68336359 | |||
| 1 | 0.1 | 0.1 | −0.98466242 | 0.93321072 | |
| 0.3 | −1.06703783 | 0.96337151 | |||
| 0.5 | −1.10820333 | 0.97845345 | |||
| 1 | 0.1 | −0.95466686 | 0.92270556 | ||
| 0.3 | −1.03583161 | 0.95242927 | |||
| 0.5 | −1.11692093 | 0.98218711 | |||
| 2.5 | 0.5 | 0.1 | 0.1 | 0.02844384 | 0.47956902 |
| 0.3 | −0.01027970 | 0.48928915 | |||
| 0.5 | −0.04899951 | 0.49901518 | |||
| 1 | 0.1 | 0.03870808 | 0.47716153 | ||
| 0.3 | 0.00045747 | 0.48680983 | |||
| 0.5 | −0.03780857 | 0.49646556 | |||
| 1.5 | 0.1 | 0.1 | −0.69651762 | 0.66164154 | |
| 0.3 | −0.77672460 | 0.68193716 | |||
| 0.5 | −0.81684114 | 0.69210542 | |||
| 1 | 0.1 | −0.67144335 | 0.65622783 | ||
| 0.3 | −0.75038308 | 0.67625805 | |||
| 0.5 | −0.82940928 | 0.69634174 |
| M | |||||
|---|---|---|---|---|---|
| 0.5 | 0.5 | 0.1 | 1 | 0.09049591 | 1.01213098 |
| 3 | 0.09196038 | 1.00934866 | |||
| 5 | 0.09331174 | 1.00672027 | |||
| 2 | 1 | 0.09549966 | 1.00233443 | ||
| 3 | 0.09659781 | 1.00006941 | |||
| 5 | 0.09762307 | 0.99791445 | |||
| 2.5 | 0.1 | 1 | 3.18338485 | −1.4665947 | |
| 3 | 3.18830548 | −1.4828353 | |||
| 5 | 3.19322282 | −1.4986293 | |||
| 2 | 1 | 3.20203016 | −1.5259728 | ||
| 3 | 3.20688324 | −1.5405845 | |||
| 5 | 3.21169920 | −1.5548001 | |||
| 5 | 0.5 | 0.1 | 1 | 0.11605991 | 1.00085941 |
| 3 | 0.11499436 | 0.99886207 | |||
| 5 | 0.11426621. | 0.99685709 | |||
| 2 | 1 | 0.11352000 | 0.99331531 | ||
| 3 | 0.11331770 | 0.99141162 | |||
| 5 | 0.11321857 | 0.98956335 | |||
| 2.5 | 0.1 | 1 | 3.14123546 | −1.3900296 | |
| 3 | 3.15022379 | −1.4158994 | |||
| 5 | 3.15868590 | −1.4399207 | |||
| 2 | 1 | 3.17287387 | −1.4794332 | ||
| 3 | 3.18028355 | −1.4996793 | |||
| 5 | 3.18740999 | −1.5188976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saraswathy, M.; Prakash, D.; Durgaprasad, P. MHD Micropolar Fluid in a Porous Channel Provoked by Viscous Dissipation and Non-Linear Thermal Radiation: An Analytical Approach. Mathematics 2023, 11, 183. https://doi.org/10.3390/math11010183
Saraswathy M, Prakash D, Durgaprasad P. MHD Micropolar Fluid in a Porous Channel Provoked by Viscous Dissipation and Non-Linear Thermal Radiation: An Analytical Approach. Mathematics. 2023; 11(1):183. https://doi.org/10.3390/math11010183
Chicago/Turabian StyleSaraswathy, M., D. Prakash, and Putta Durgaprasad. 2023. "MHD Micropolar Fluid in a Porous Channel Provoked by Viscous Dissipation and Non-Linear Thermal Radiation: An Analytical Approach" Mathematics 11, no. 1: 183. https://doi.org/10.3390/math11010183
APA StyleSaraswathy, M., Prakash, D., & Durgaprasad, P. (2023). MHD Micropolar Fluid in a Porous Channel Provoked by Viscous Dissipation and Non-Linear Thermal Radiation: An Analytical Approach. Mathematics, 11(1), 183. https://doi.org/10.3390/math11010183






