A Lightweight Deep Learning Approach for Liver Segmentation
Abstract
1. Introduction
1.1. Liver Segmentation and Its Relevance
1.2. State of the Art on Neural Networks for Liver Segmentation
- Testing a lightweight architecture, UNeXt, in the case of liver segmentation and comparing the results with the traditional U-Net architecture.
- Empirical evaluation of two different loss functions while training the models, soft dice loss, and unified focal loss.
- Modifying the two suggested architectures, U-Net and UNeXt, with respect to activation functions by replacing the commonly used ReLU with a novel function, Funnel.
- Proposing an automatic post-processing filtering for misclassified non-liver regions.
2. Material and Methods
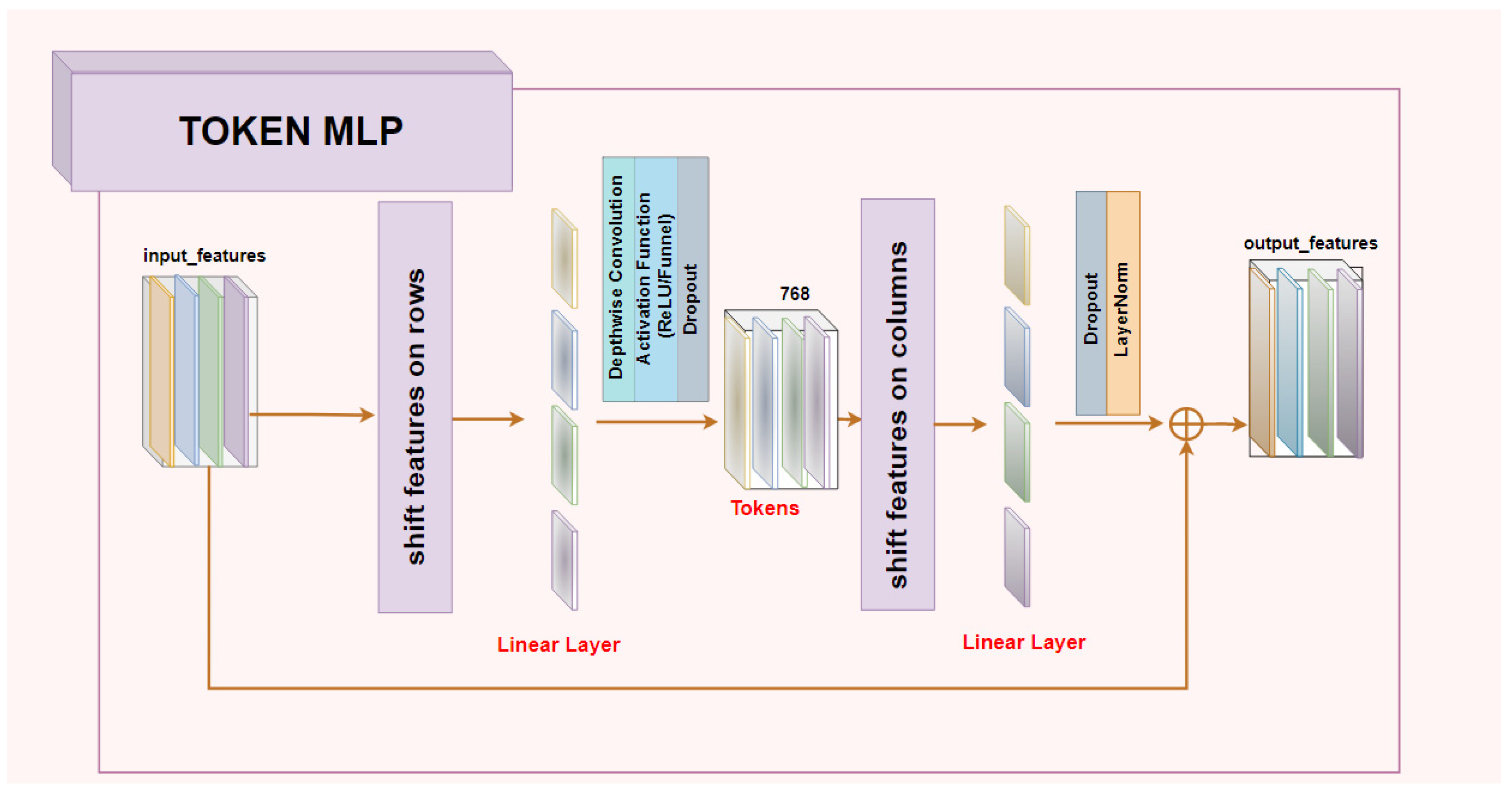
2.1. Investigated Architectures
2.2. Loss Functions
2.3. Proposed Automatic Post-Processing Filtering
3. Experimental Setup
3.1. LiTS Dataset and Pre-Processing
3.2. Train-Test Procedure
3.3. Implementation Details
3.4. Evaluation Metrics
4. Results
4.1. Pre-Processing Results
4.2. Post-Processing Results
4.3. Observations on Parameter Numbers and Inference Time
4.4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Global Cancer Observatory. Available online: https://gco.iarc.fr/ (accessed on 30 March 2021).
- Wild, C.P.; Weiderpass, E.; Stewart, B.W. (Eds.) World Cancer Report: Cancer Research for Cancer Prevention; International Agency for Research on Cancer: Lyon, France, 2020; Available online: http://publications.iarc.fr/586 (accessed on 19 November 2021).
- Koh, D.-M.; Papanikolaou, N.; Bick, U.; Illing, R.; Kahn, C.E.; Kalpathi-Cramer, J.; Matos, C.; Martí-Bonmatí, L.; Miles, A.; Mun, S.K.; et al. Artificial intelligence and machine learning in cancer imaging. Commun. Med. 2022, 2, 133. [Google Scholar] [CrossRef] [PubMed]
- Gotra, A.; Sivakumaran, L.; Chartrand, G.; Vu, K.-N.; Vandenbroucke-Menu, F.; Kauffmann, C.; Kadoury, S.; Gallix, B.; de Guise, J.A.; Tang, A. Liver segmentation: Indications, techniques and future directions. Insights Imaging 2017, 8, 377–392. [Google Scholar] [CrossRef]
- Ansari, M.Y.; Abdalla, A.; Malluhi, B.; Mohanty, S.; Mishra, S.; Singh, S.S.; Abinahed, J.; Al-Ansari, A.; Balakrishnan, S.; Dakua, S.P. Practical utility of liver segmentation methods in clinical surgeries and interventions. BMC Med. Imaging 2022, 22, 97. [Google Scholar] [CrossRef]
- Bilic, P.; Christ, P.F.; Vorontsov, E.; Chlebus, G.; Chen, H.; Dou, Q.; Fu, C.; Han, X.; Heng, P.; Hesser, J.; et al. The Liver Tumor Segmentation Benchmark (LiTS). arXiv 2019, arXiv:1901.04056. [Google Scholar] [CrossRef]
- Yuan, Y. Hierarchical Convolutional-Deconvolutional Neural Networks for Automatic Liver and Tumor Segmentation. arXiv 2017, arXiv:1710.04540. [Google Scholar]
- Li, X.; Chen, H.; Qi, X.; Dou, Q.; Fu, C.-W.; Heng, P.-A. H-DenseUNet: Hybrid Densely Connected UNet for Liver and Tumor Segmentation From CT Volumes. IEEE Trans. Med. Imaging 2018, 37, 2663–2674. [Google Scholar] [CrossRef]
- Chlebus, G.; Meine, H.; Moltz, J.H.; Schenk, A. Neural Network-Based Automatic Liver Tumor Segmentation With Random Forest-Based Candidate Filtering. arXiv 2017, arXiv:1706.00842. [Google Scholar]
- Vorontsov, E.; Tang, A.; Pal, C.; Kadoury, S. Liver lesion segmentation informed by joint liver segmentation. arXiv 2017, arXiv:1707.07734. [Google Scholar]
- Christ, P.F.; Ettlinger, F.; Grün, F.; Elshaera, M.E.A.; Lipkova, J.; Schlecht, S.; Ahmaddy, F.; Tatavarty, S.; Bickel, M.; Bilic, P.; et al. Automatic Liver and Tumor Segmentation of CT and MRI Volumes Using Cascaded Fully Convolutional Neural Networks. arXiv 2017, arXiv:1702.05970. [Google Scholar]
- Zhang, J.; Xie, Y.; Zhang, P.; Chen, H.; Xia, Y.; Shen, C. Light-Weight Hybrid Convolutional Network for Liver Tumor Segmentation. In Proceedings of the Twenty-Eighth Internationl Joint Conference on Artificial Intelligence (IJCAI-19); International Joint Conferences on Artificial Intelligence Organization, Macao, China, 10–16 August 2019; pp. 4271–4277. Available online: https://www.ijcai.org/proceedings/2019/0593.pdf (accessed on 27 December 2021).
- Xia, K.; Yin, H.; Qian, P.; Jiang, Y.; Wang, S. Liver Semantic Segmentation Algorithm Based on Improved Deep Adversarial Networks in Combination of Weighted Loss Function on Abdominal CT Images. IEEE Access 2019, 7, 96349–96358. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Y.; Zhu, Y.; Xiao, J.; Summers, R.M. E$$^2$$Net: An Edge Enhanced Network for Accurate Liver and Tumor Segmentation on CT Scans. arXiv 2020, arXiv:2007.09791. [Google Scholar]
- Lv, P.; Wang, J.; Zhang, X.; Ji, C.; Zhou, L.; Wang, H. An improved residual U-Net with morphological-based loss function for automatic liver segmentation in computed tomography. Math. Biosci. Eng. 2021, 19, 1426–1447. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, X.; Lv, P.; Zhou, L.; Wang, H. EAR-U-Net: EfficientNet and Attention-Based Residual U-Net for Automatic Liver Segmentation in CT. arXiv 2021, arXiv:2110.01014. [Google Scholar]
- Khan, R.A.; Luo, Y.; Wu, F.-X. RMS-UNet: Residual multi-scale UNet for liver and lesion segmentation. Artif. Intell. Med. 2022, 124, 102231. [Google Scholar] [CrossRef]
- Li, L.; Ma, H. RDCTrans U-Net: A Hybrid Variable Architecture for Liver CT Image Segmentation. Sensors 2022, 22, 2452. [Google Scholar] [CrossRef]
- Ansari, M.Y.; Yang, Y.; Balakrishnan, S.; Abinahed, J.; Al-Ansari, A.; Warfa, M.; Almokdad, O.; Barah, A.; Omer, A.; Singh, A.V.; et al. A lightweight neural network with multiscale feature enhancement for liver CT segmentation. Sci. Rep. 2022, 12, 14153. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Valanarasu, J.M.J.; Patel, V.M. UNeXt: MLP-Based Rapid Medical Image Segmentation Network. arXiv 2022, arXiv:2203.04967. [Google Scholar]
- Ma, N.; Zhang, X.; Sun, J. Funnel Activation for Visual Recognition. arXiv 2020, arXiv:2007.11824. [Google Scholar]
- Ma, J.; Chen, J.; Ng, M.; Huang, R.; Li, Y.; Li, C.; Yang, X.; Martel, A.L. Loss odyssey in medical image segmentation. Med. Image Anal. 2021, 71, 102035. [Google Scholar] [CrossRef] [PubMed]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Unified Focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medical image segmentation. Comput. Med. Imaging Graph. 2022, 95, 102026. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2017, arXiv:1708.02002. [Google Scholar]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. arXiv 2017, arXiv:1706.05721. [Google Scholar]
- LiTS- Liver Tumor Segmentation Challenge. Available online: https://competitions.codalab.org/competitions/17094 (accessed on 19 November 2021).
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Müller, D.; Soto-Rey, I.; Kramer, F. Towards a guideline for evaluation metrics in medical image segmentation. BMC Res. Notes 2022, 15, 210. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef]
- Zou, K.H.; Warfield, S.K.; Bharatha, A.; Tempany, C.M.C.; Kaus, M.R.; Haker, S.J.; Wells Iii, W.M.; Jolesz, F.A.; Kikinis, R.; St, F. Statistical Validation of Image Segmentation Quality Based on a Spatial Overlap Index 1: Scientific Reports; 2004; Volume 11. Available online: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1415224/ (accessed on 10 December 2022).
- Varoquaux, G.; Cheplygina, V. Machine learning for medical imaging: Methodological failures and recommendations for the future. NPJ Digit. Med. 2022, 5, 1–8. [Google Scholar] [CrossRef]
- Liver Segmentation–3D-Ircadb-01-IRCAD. Available online: https://www.ircad.fr/research/data-sets/liver-segmentation-3d-ircadb-01/ (accessed on 20 June 2022).
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. arXiv 2017. Available online: https://arxiv.org/pdf/1707.01083 (accessed on 12 December 2022).







| References | Dice Similarity Coefficient (Per Case) | Activation Functions Used in the Architecture | Loss Functions Used for Training | Datasets Used for Training | Datasets Used for Testing | Performed Post-Processing |
|---|---|---|---|---|---|---|
| Yuan et al., 2017 [8] | 0.9670 | ReLU | Function based on Jaccard Index (IoU) | LiTS train set | LiTS TEST set | Yes |
| Li et al., 2018 [9] | 0.9610 | ReLU | Weighted cross-entropy loss | LiTS train set | LiTS test set, 3DIRCADb | No |
| Chlebus et al., 2017 [10] | 0.9600 | ReLU | Dice loss | Private dataset, LiTS train set | LiTS test set | Yes |
| Vorontsov et al., 2017 [11] | 0.9510 | ReLU | Dice loss | LiTS train set | LiTS test set | No |
| Christ et al., 2017 [12] | 0.943 | ReLU | Weighted Cross-entropy loss | 3DIRCADb, private dataset | 3DIRCADb, private dataset | Yes |
| Zhang et al., 2019 [13] | 0.9650 | ReLU | Combined loss functions (dice loss, cross-entropy loss) | LiTS train set, 3DIRCADb, | LiTS test set 3DIRCADb, | No |
| Xia et al., 2019 [14] | 0.970 | ReLU | Hybrid loss function (region-based, context-based, and adversarial-based) | private dataset, LiTS train set | LiTS test set, private dataset | No |
| Tang et al., 2022 [15] | 0.968 | ReLU | Combined loss (binary cross-entropy, Jaccard index loss) | LiTS train set | LiTS test set, 3DIRCADb | No |
| Lv et al., 2021 [16] | 0.9424 | ReLU | Weighted dice loss with morphologically based loss function | LiTS train set, SLIVER07 | LiTS train set, SLIVER07 | No |
| Wang et al., 2021 [17] | 0.952 | ReLU | Combined loss function (dice loss, binary cross-entropy loss) | SLIVER07, LiTS train set | LiTS test set SLIVER07, LiTS train set | No |
| Khan et al., 2022 [18] | 0.9738 | ReLU | Combined loss function (dice loss, absolute volumetric difference loss), Binary cross-entropy | LiTS train set, chaos, SLIVER07, 3DIRCADb | LiTS test set, chaos, SLIVER07, 3DIRCADb | No |
| Li et al., 2022 [19] | 0.9338 | ReLU | Cross-entropy loss | LiTS train set | LiTS train set | No |
| Ansari et al., 2022 [20] | 0.9580 | ReLU | Modified surface loss function | Medical decathlon Train set | Medical decathlon train set | No |
| Proposed Model (Activation/Loss Function Used for Training) | Dice Similarity Coefficient | Specificity | Sensitivity | Intersection over Union (IoU) or Jaccard Index |
|---|---|---|---|---|
| UNeXt (Funnel/unified focal loss) | 0.9401 (0.0434) * | 0.9565 (0.0448) | 0.9663 (0.0135) | 0.9044 (0.0623) |
| UNeXt (ReLU/unified focal loss) | 0.9538 (0.0199) | 0.9741 (0.0198) | 0.9626 (0.0153) | 0.9236 (0.0286) |
| UNeXt (Funnel/soft dice loss) | 0.9473 (0.026) | 0.9709 (0.0263) | 0.9571 (0.0139) | 0.915 (0.0359) |
| UNeXt (ReLU/soft dice loss) | 0.9453 (0.019) | 0.9761 (0.017) | 0.9495 (0.0182) | 0.9129 (0.0256) |
| U-Net (Funnel/unified focal loss) | 0.9503 (0.0299) | 0.9761 (0.0205) | 0.9582 (0.02) | 0.9214 (0.04) |
| U-Net (ReLU/unified focal loss) | 0.9435 (0.0423) | 0.9789 (0.0207) | 0.9466 (0.0361) | 0.9143 (0.0582) |
| U-Net (Funnel/soft dice loss) | 0.9606 (0.0263) | 0.9772 (0.0204) | 0.9702 (0.0179) | 0.9358 (0.037) |
| U-Net (ReLU/soft dice loss) | 0.9570 (0.0293) | 0.9784 (0.0186) | 0.9645 (0.025) | 0.9316 (0.041) |
| Proposed Model (Activation/Loss Function Used for Training) | Dice Similarity Coefficient | Specificity | Sensitivity | Intersection over Union (IoU) or Jaccard Index |
|---|---|---|---|---|
| UNeXt (Funnel/unified focal loss) | 0.9251 (0.0136) * | 0.9613 (0.0089) | 0.9414 (0.0183) | 0.8849 (0.0187) |
| UNeXt (ReLU/unified focal loss) | 0.9307 (0.0126) | 0.9645 (0.0068) | 0.9423 (0.0134) | 0.8925 (0.0166) |
| UNeXt (Funnel/soft dice loss) | 0.932 (0.015) | 0.9670 (0.0057) | 0.9424 (0.0168) | 0.8951 (0.0195) |
| UNeXt (ReLU/soft dice loss) | 0.9243 (0.0148) | 0.9665 (0.0069) | 0.9311 (0.0148) | 0.8839 (0.0196) |
| U-Net (Funnel/unified focal loss) | 0.9201 (0.0236) | 0.9704 (0.0103) | 0.9229 (0.0246) | 0.8806 (0.0321) |
| U-Net (ReLU/unified focal loss) | 0.9298 (0.0131) | 0.9702 (0.0068) | 0.9350 (0.0148) | 0.8921 (0.0188) |
| U-Net (Funnel/soft dice loss) | 0.9343 (0.0161) | 0.9762 (0.0059) | 0.9343 (0.0201) | 0.8995 (0.0224) |
| U-Net (ReLU/soft dice loss) | 0.9331 (0.0236) | 0.9678 (0.016) | 0.9435 (0.0145) | 0.9115 (0.0267) |
| Proposed Model (Activation/Loss Function Used for Training) | Post-Processing | Dice Similarity Coefficient | Specificity | Sensitivity | Intersection over Union (IoU) or Jaccard Index |
|---|---|---|---|---|---|
| UNeXt (Funnel/unified focal loss) | Before | 0.6695 | 0.6757 | 0.9903 | 0.6615 |
| After | 0.9883 | 0.9945 | 0.9903 | 0.9803 | |
| UNeXt (ReLU/unified focal loss) | Before | 0.8786 | 0.8885 | 0.9825 | 0.8692 |
| After | 0.9874 | 0.9973 | 0.9825 | 0.978 | |
| UNeXt (Funnel/soft dice loss) | Before | 0.7277 | 0.7317 | 0.9932 | 0.7202 |
| After | 0.9902 | 0.9941 | 0.9932 | 0.9827 | |
| UNeXt (ReLU/soft dice loss) | Before | 0.9602 | 0.9741 | 0.9769 | 0.9501 |
| After | 0.9845 | 0.9985 | 0.9769 | 0.9827 | |
| U-Net (Funnel/unified focal loss) | Before | 0.9514 | 0.9583 | 0.9876 | 0.9442 |
| After | 0.9912 | 0.9979 | 0.9876 | 0.9839 | |
| U-Net (ReLU/unified focal loss) | Before | 0.9509 | 0.9572 | 0.9889 | 0.9446 |
| After | 0.9906 | 0.9969 | 0.9889 | 0.9843 | |
| U-Net Funnel/soft dice loss | Before | 0.908 | 0.9092 | 0.9974 | 0.9056 |
| After | 0.9976 | 0.9989 | 0.9974 | 0.9953 | |
| U-Net ReLU/soft dice loss | Before | 0.9799 | 0.981 | 0.9978 | 0.9778 |
| After | 0.9978 | 0.9989 | 0.9978 | 0.9957 |
| Proposed Model (Activation/Loss Function Used for Training) | RMSE— Start Index Slice | RMSE— Stop Index Slice |
|---|---|---|
| UNeXt (Funnel/unified focal loss) | 1.6 | 48.5 |
| UNeXt (ReLU/unified focal loss) | 27.1 | 9.4 |
| UNeXt (Funnel/soft dice loss) | 2.75 | 35.8 |
| UNeXt (ReLU/soft dice loss) | 5.75 | 18.85 |
| U-Net (Funnel/unified focal loss) | 3.05 | 18.15 |
| U-Net (ReLU/unified focal loss) | 10.75 | 20.05 |
| U-Net (Funnel/soft dice loss) | 2.5 | 41.05 |
| U-Net (ReLU/soft dice loss) | 5.1 | 29.25 |
| Proposed Model | Number of Learnable Parameters (M) | Inference Time —GPU(s) | Inference Time —CPU(s) | ||
|---|---|---|---|---|---|
| Without Post-Processing | With Post-Processing | Without Post-Processing | With Post-Processing | ||
| Proposed UNeXt with ReLU activation | 4.09 | 21.73 | 24.59 | 481.98 | 486.2 |
| Proposed UNeXt with Funnel activation | 4.12 | 28.95 | 31.95 | 695.92 | 700.54 |
| Proposed U-Net with ReLU activation | 59.27 | 86.04 | 88.71 | 2601.11 | 2604.88 |
| Proposed U-Net with Funnel activation | 59.4 | 109.63 | 112.43 | 3403.19 | 3407.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogoi, S.; Udrea, A. A Lightweight Deep Learning Approach for Liver Segmentation. Mathematics 2023, 11, 95. https://doi.org/10.3390/math11010095
Bogoi S, Udrea A. A Lightweight Deep Learning Approach for Liver Segmentation. Mathematics. 2023; 11(1):95. https://doi.org/10.3390/math11010095
Chicago/Turabian StyleBogoi, Smaranda, and Andreea Udrea. 2023. "A Lightweight Deep Learning Approach for Liver Segmentation" Mathematics 11, no. 1: 95. https://doi.org/10.3390/math11010095
APA StyleBogoi, S., & Udrea, A. (2023). A Lightweight Deep Learning Approach for Liver Segmentation. Mathematics, 11(1), 95. https://doi.org/10.3390/math11010095




