A Family of Multi-Step Subgradient Minimization Methods

Abstract

For solving non-smooth multidimensional optimization problems, we present a family of relaxation subgradient methods (RSMs) with a built-in algorithm for finding the descent direction that forms an acute angle with all subgradients in the neighborhood of the current minimum. Minimizing the function along the opposite direction (with a minus sign) enables the algorithm to go beyond the neighborhood of the current minimum. The family of algorithms for finding the descent direction is based on solving systems of inequalities. The finite convergence of the algorithms on separable bounded sets is proved. Algorithms for solving systems of inequalities are used to organize the RSM family. On quadratic functions, the methods of the RSM family are equivalent to the conjugate gradient method (CGM). The methods are intended for solving high-dimensional problems and are studied theoretically and numerically. Examples of solving convex and non-convex smooth and non-smooth problems of large dimensions are given.

1. Introduction

The beginning of research in the field of subgradient methods for minimizing a convex, but not necessarily differentiable, function was laid in the works [1,2], the results of which can be found in [3]. There are several directions for constructing non-smooth optimization methods. One of them [4,5,6] is based on the construction and use of function approximations. A number of effective approaches in the field of non-smooth optimization are associated with a change in the space metric as a result of space dilation operations [7,8]. Distance-to-extremum relaxation methods for minimization were first proposed in [9] and developed in [10]. The first relaxation-by-function methods were proposed in [11,12,13].

The need for methods for solving complex non-smooth high-dimensional minimization problems is constantly growing. In the case of smooth functions, the conjugate gradient method (CGM) [3] is one of the universal methods for solving ill-conditioned high-dimensional problems. The CGM is a multi-step method that is optimal in terms of the convergence rate on quadratic functions [3,14].

CGM generates search directions that are more consistent with the geometry of the minimized function. In practice, the CGM shows faster convergence rates than gradient descent algorithms, so CGM is widely used in machine learning. The original CGM, known as the Hestenes–Stiefel method [15], was introduced in 1952 for solving linear systems. There are several modifications of the Hestenes–Stiefel method, such as the Fletcher–Reeves method [16], Polak–Ribiere method [17], or Dai–Yuan method [18], which mainly differ in the way the conjugate gradient update parameter is calculated.

Fletcher and Reeves justified the convergence of the CGM for quadratic functions and generalized it for the case of non-quadratic functions. The Polak–Ribiere method is based on an exact procedure for searching along a straight line and on a more general assumption about the approximation of the objective function. At each iteration of the Polak–Ribiere or Fletcher–Reeves methods, the function and its gradient are calculated once, and the problem of one-dimensional optimization is solved. Thus, the complexity of one step of the CGM is of the same order as the complexity of the step of the steepest descent method. It was proven in [19] that the Polak–Ribiere method is also characterized by a linear convergence rate in the absence of returns to the initial iteration, but it has an advantage over the Fletcher–Reeves method in solving problems with general objective functions and is less sensitive to rounding errors when conducting a one-dimensional search. The Dai–Yuan algorithm converged globally, provided the line search made the standard Wolfe conditions hold.

Miele and Cantrell [20] generalized the approach of Fletcher and Reeves by proposing a gradient method with memory. The method is based on the use of two selectable minimization parameters in each of the search directions. This method is efficient in terms of the number of iterations required to solve the problem, but it requires more computations of the function values and gradient components than the Fletcher–Reeves method. The idea of the memory gradient method was further extended to the multi-dimensional search methods that are used mostly for unconstrained optimization in large-scale problems [21,22,23,24,25,26].

The improved CGM [27], Fletcher–Reeves (IFR), and Dai–Yuan methods mixed together with the second inequality of the strong Wolfe line search can be used to construct two new conjugate parameters. In online CGM, Xue et al. [28] combined the IFR method with the variance reduction approach [29]. This algorithm achieves a linear convergence rate under the strong Wolfe line search for the smooth and strongly convex objective function.

Dai and Liao [30] introduced CGM based on a modified conjugate gradient update parameter. Modifications of this method were later presented in [31,32,33,34].

In [35], an improved CG algorithm with a generalized Armijo search technique was proposed. A modified Fletcher–Reeves CGM for monotone nonlinear equations was described in [36]. Nonlinear CGM was considered an adaptive momentum method combined with the steepest descent along the search direction in [37]. In [38], the author used an estimate of the Hessian to approximate the optimal step size. The paper in [39] proposed a CGM on Riemannian manifolds. CG algorithms for stochastic optimization were introduced in [40,41,42]. Algorithms of this type use a small part of samples for large-scale learning problems.

Preconditioning is another technique to speed up the convergence of CG descent. The idea of preconditioning is to make a change in variables using an invertible matrix. The authors in [43] proposed a non-monotone scaled CG algorithm for solving large-scale unconstrained optimization problems, which combines the idea of a scaled memoryless Broyden–Fletcher–Goldfarb–Shanno (BFGS) method with the non-monotone technique. Inexact preconditioned CGM with an inner–outer iteration for a symmetric positive definite system was proposed in [44]. In [45], the authors developed an optimizer that uses CG with a diagonal preconditioner.

In [46], the authors combined the limited memory technique with a subspace minimization conjugate gradient method and presented a limited memory subspace minimization conjugate gradient algorithm that, by the first step, determines the search direction, and by the second step, applies the quasi-Newtonian method in the subspace to improve the orthogonality of gradients.

The idea of the spectral CG method is based on combining the idea of CG methods with spectral gradients. Li et al. [47] proposed a spectral three-term conjugate gradient method and proved the global convergence of this algorithm for uniformly convex functions. This work was further developed in [48].

The practical application of the conjugate gradient method is very wide and includes, for example, structured prediction problems and neural network learning [29], continuum mechanics [49], signal and image recovery problems [32,36], COVID-19 regression models [50], robot motion control problems [50], psychographic reconstruction [51], and molecular dynamics simulations [52].

For a more detailed review of conjugate gradient methods, see [40,53].

It seems relevant to create multi-step universal methods for solving non-smooth problems that are applicable in terms of computer memory resources for solving high-dimensional minimization problems [54,55,56,57]. In this work, we propose a family of multi-step RSMs for solving large-scale problems. With a certain organization of the methods of the family, such as the CGM, they enable us to find the minimum of a quadratic function in a finite number of iterations.

The subgradient method is an algorithm that was originally developed by Shor [1] for minimizing a non-differentiable convex function. The issue of subgradient methods is their speed, and several approaches can be used to speed them up.

Incremental subgradient methods were studied in [58,59,60,61,62]. The main difference with the standard subgradient method is that at each iteration, x is changed incrementally through a sequence of steps. In [60], a class of subgradient methods for minimizing a convex function that consists of the sum of many component functions was considered. In [63], the authors presented a family of subgradient methods that dynamically incorporate knowledge of the geometry of the data observed in earlier iterations to perform more informative gradient-based learning. An adaptive subgradient method for the split quasi-convex feasibility problems was developed in [64]. Proximal subgradient methods were presented in [65,66]. The authors in [65] proposed a model with a proximal conjugate subgradient (PCS-TT) method for solving the non-convex rank minimization problem by using properties of Moreau’s decomposition. A conjugate subgradient projection model as applied to continuous road network design problems was presented in [67]. The paper in [68] described a conjugate subgradient algorithm that minimizes a convex function containing a least squares fidelity term and an absolute value regularization term. This method can be applied to the inversion of ill-conditioned linear problems. A non-monotone conjugate subgradient type method without any line search was described in [69].

The principle of organization in a number of the RSMs [70] is that, in a particular RSM, there is an independent algorithm for finding the descent direction, which makes it possible to go beyond some neighborhood of the current minimum. In [70,71], the problem of finding the descent direction in RSM was formulated as the problem of solving systems of inequalities on separable sets. The use of a particular model of subgradient sets makes it possible to reduce the original problem to the problem of estimating the parameters of a linear function from information about subgradients obtained during the operation of the minimization algorithm, and mathematically formalize it as a problem of minimizing the quality functional. This makes it possible to use the ideas and methods of machine learning [72] to find the descent direction in RSM [70,71,73,74].

Thus, a specific new learning algorithm will be used as the basis of a new RSM method. The properties of the minimization method are determined by the learning algorithm underlying it. The aim of this work is to develop a family of methods for solving systems of inequalities (MSSIs) and, on this basis, to create a family of multi-step RSMs (MRSMs) for solving large-scale smooth and non-smooth minimization problems. Known methods [73,74] are special cases of the MRSM family presented here.

It Is proven that the algorithms of the MSSI family converge in a finite number of iterations on separable sets. On strictly convex functions, the convergence of the MRSM algorithms is theoretically substantiated. It is proven that MRSM algorithms on quadratic functions are equivalent to the CGM.

In the practical implementation of RSM, several problems arise in combining the use of information about the function, both for minimization and for the internal algorithm for finding the descent direction. If, in CGM, the goal of a one-dimensional search is high accuracy, then, in RSM, the goal is to keep the step of a one-dimensional search proportional to the distance to the extremum, which eliminates looping and enables the learning algorithm to find a way out of a wide neighborhood of the current minimum. In accordance with the noted principle, we use a one-dimensional minimization procedure in which the rate of step decrease is controlled.

The described algorithms are implemented. A numerical experiment was carried out to select efficient versions from a family of algorithms. For the selected versions, an extensive experiment was carried out to compare them on smooth functions with various versions of the CGM. It was found that, along with the CGM, the proposed algorithms can be used to minimize smooth functions. The proposed methods are studied numerically on large-scale tests for solving convex and non-convex non-smooth optimization problems.

The rest of this paper is organized as follows: In Section 2, we state the problem of our study. In Section 3, we describe the method for solving systems of inequalities. In Section 4, we present a subgradient minimization method. In Section 5, we implement the proposed minimization algorithm. In Section 6, we perform a series of experiments with the implemented method. In the last section, we provide a short conclusion of the work.

2. The Problem Formulation

Let us solve a minimization problem for a convex function f(x) in Rⁿ. In the RSM, the successive approximations are constructed according to the expressions [13]:

$$x_{k+1}=x_k-{\gamma }_k{s}_{k+1},{\gamma }_k=\arg \underset{\gamma \in R}{\min }f(x_k-\gamma s_{k+1})$$

(1)

where the descent direction s_k+1 is chosen as a solution for the system of inequalities [13]:

$$(s,g)>0,\forall g\in G$$

(2)

Here, $G={\partial }_{\epsilon }f(x_i)$ is the ε-subgradient set at point x_i. Denote by S(G) the set of solutions to (2) and the subgradient set in x by $\partial f(x)\equiv \partial f_0(x)$. Iterative methods (learning algorithms) are used to solve systems of inequalities (2) in the RSM. Since elements of the ε-subgradient set are not explicitly specified, subgradients calculated on the descent trajectory of the minimization algorithm are used instead.

The solution vector s* of the system (2) forms an acute angle with each of the subgradients of the set G. If the subgradients of some neighborhood of the current minimum of (1) act as the set G, then iteration (1) for $s_k=s^{\ast }$ provides the possibility of going beyond this neighborhood with a simultaneous decrease in the function. It seems relevant to search for efficient methods for solving (2).

In [70,71,73,74], the authors proposed the following approach to reduce the system (2) to an equivalent system of equalities. Let $G\subset R^n$ belong to some hyperplane, and its vector $\eta (G)$ closest to the origin be also the vector of the hyperplane closest to the origin. In this case, the solution of the system $(s,g)=1,\forall g\in G$ is also a solution for (2). It can be found as a solution to the system [70,71,73,74]:

$$(s,g_i)=y_i,i=0,1,\dots ,k,y_i\equiv 1.$$

(3)

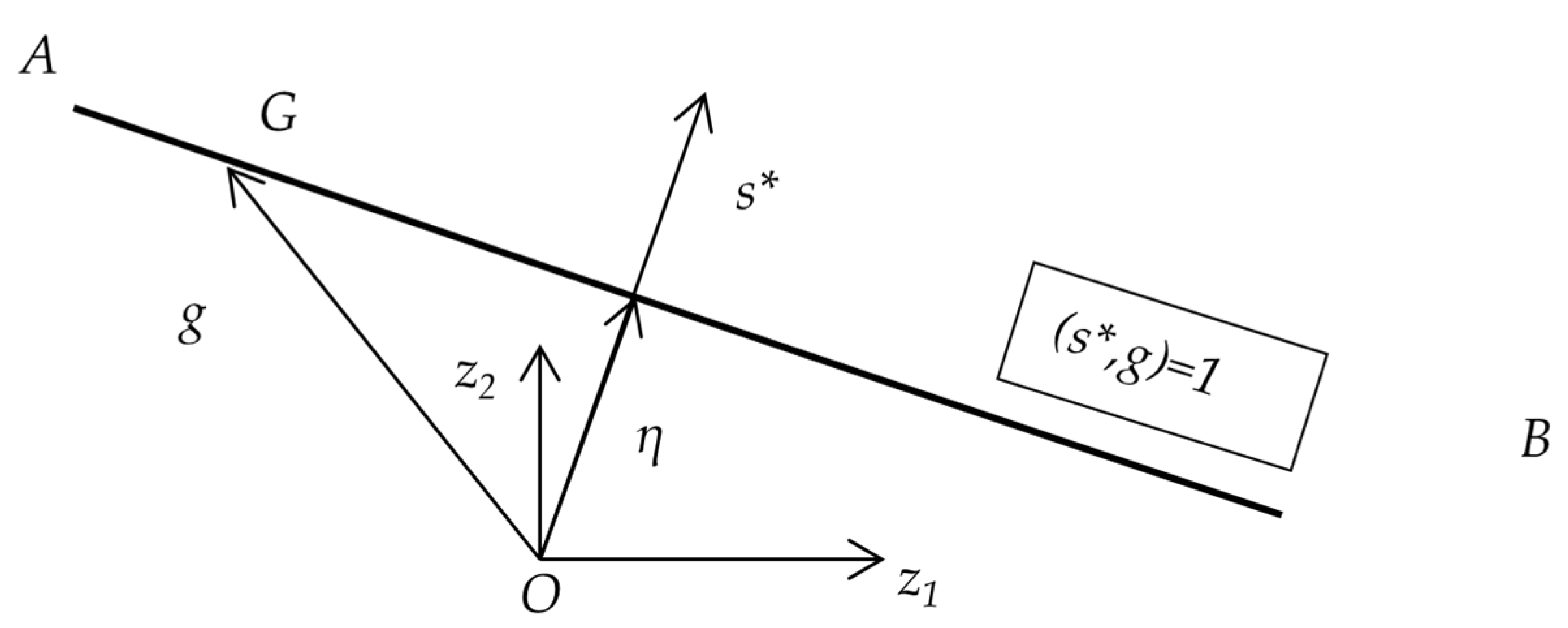
Figure 1 shows the projection of a subgradient set in the form of a segment [A,B] lying on a straight line in the plane of vectors z₁ and z₂. The vector $\eta (G)\in G$ lies in this plane and is the normal of the hyperplane (s*, g) = 1 formed by the vectors g at $s^{*}=\eta (G)/\left|\right|\eta (G)|{|}^2$.

The problem of solving the system (3) is one of the most common data analysis problems for which gradient minimization methods are used. The minimization function is formulated as:

$$F_k(s)=(y_k-(s,g_k))/2.$$

To minimize it, various gradient-type methods are used. In a similar way, a solution is sought in the problems of constructing approximations by neural networks.

In [70], for solving system (3), a gradient minimization method was proposed—the Kaczmarz algorithm [75]:

$$s_{k+1}=s_k+\frac{1-(s_k,g_k)}{(g_k,g_k)}{g}_k.$$

(4)

The method (4) provides an approximation $s_{k+1}$ that satisfies the equation $(s,g_k)=1$, i.e., the last-received training equation from (3).

Figure 2 shows iterations (4) in the plane of vectors g_k, s*, assuming that the set G represented by the segment [A,B] belongs to the hyperplane. The dashed line W_k in Figure 2 is the projection of the hyperplane $(g_k,s)=1$ for vectors s. In the case when the set G belongs to the hyperplane, the hyperplane of vectors s $(s,g)=1$ formed with some $g\in G$ contains the vector s*.

In [71], to solve the system of inequalities (2), the descent direction correction scheme was used based on the exact solution of the last two equalities from (3) for the pair of indices k−1 and k, which can be realized by correction along the vector p_k orthogonal to vector g_k−1.

$$s_{k+1}=s_k+\frac{1-\left(s_k,g_k\right)}{\left(p_k,g_k\right)}{p}_k,$$

(5)

$$p_k=g_k-{\alpha }_k\frac{(g_k,g_{k-1})}{{\Vert g_{k-1}\Vert }^2}{g}_{k-1}$$

(6)

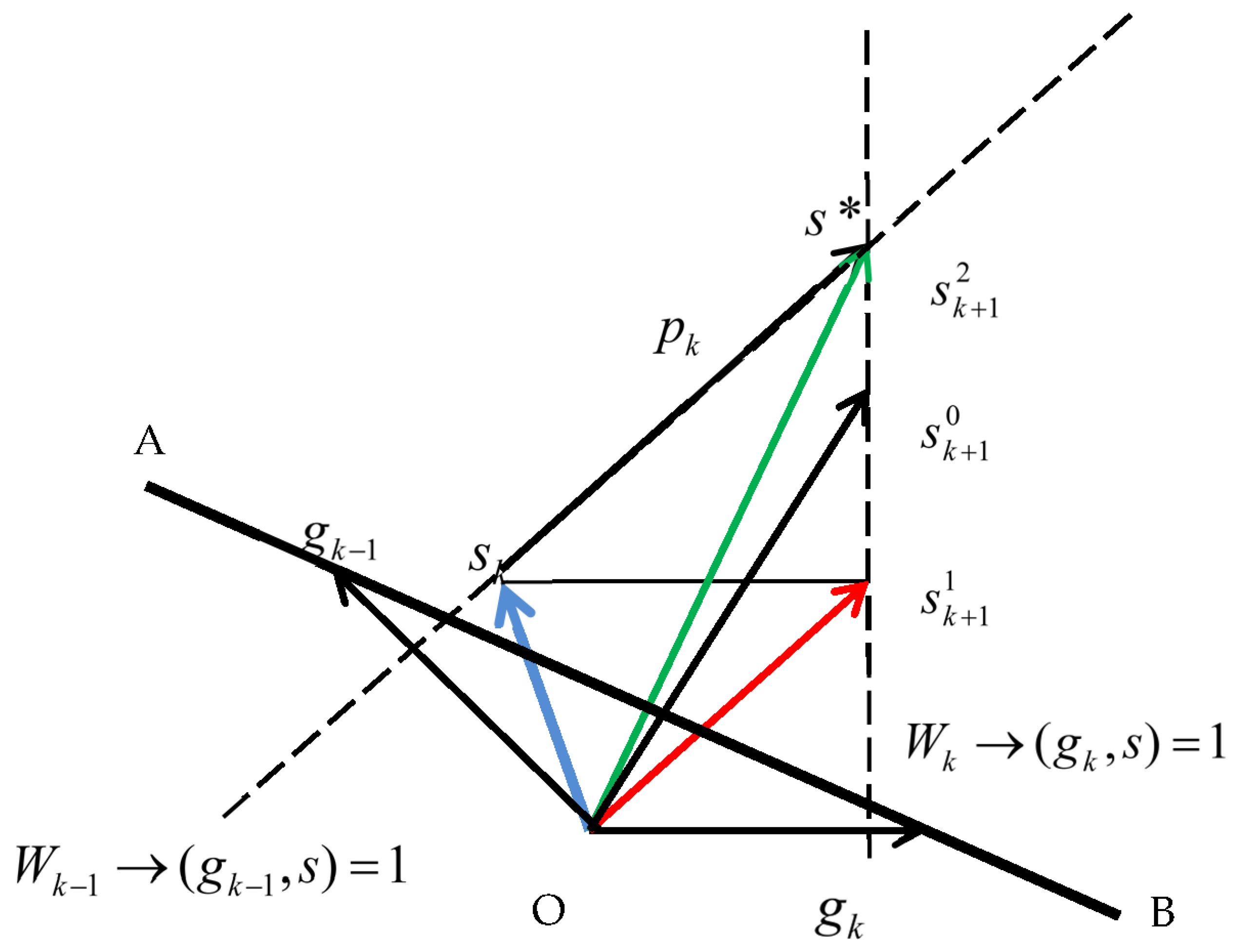
Here, α_k is the space dilation parameter. It is assumed here that before operations (5) and (6) are performed, the initial conditions $(g_{k-1},s_{k-1})=1$ and $(g_{k-1},g_k)\le 0$ are satisfied, which is shown in Figure 3.

Figure 3 shows iterations (6) and (5) in the plane of vectors g_k and g_k−1. As a result of the operation, the vector s²_k+1 will be found—the projection of the vector s* in the plane of the vectors g_k and g_k−1. The projections of the hyperplanes $(g_k,s)=1$ and $(g_{k-1},s)=1$ are shown as dashed lines W_k and W_k−1. The vector s¹_k+1 is the projection into the plane of the result of iteration (4).

On separable sets, iterations (6) and (5) lead to an acceleration in the convergence of the method for solving systems of inequalities. In the minimization method, under conditions of a rapidly changing position of the current minimum, the subgradients used in (6) and (5) in many cases do not belong to separable sets, which leads to the need to update the process (6), (5) with the loss of accumulated information.

In this paper, we consider a linear combination of solutions s¹_k+1 and s²_k+1 as a descent vector s⁰_k+1. This enables us to form a family of methods for solving systems of inequalities. On this basis, a family of subgradient MRSMs is constructed. Practical implementations with a special choice of the solution s⁰_k+1 turn out to be more efficient, capable of covering wider neighborhoods of the current approximation using a rough one-dimensional search. The wider the neighborhood is, the greater the progress towards the extremum, and the higher the stability of the method to roundoff errors, noise, and the ability to overcome small local extrema. In this regard, the minimization methods studied in this work are of particular importance, in which, unlike the method from [11] and its modification [13], the built-in algorithms for solving systems of inequalities enable us to use the subgradients of a fairly wide neighborhood of the current minimum approximation and do not require exact one-dimensional descent.

3. A Family of Methods for Solving Systems of Inequalities

In the family of algorithms presented below, successive approximations of the solution to the system of inequalities (2) are constructed by correcting the current approximation.

Let us denote the vector closest to the origin of the coordinates in the set G as: ${\eta }_G\equiv \eta (G)$, ${\rho }_G\equiv \rho (G)=\left|\right|\eta (G)\left|\right|$, ${\mu }_G=\eta (G)/\left|\right|\eta (G)\left|\right|$, $s^{\ast }={\mu }_G/{\rho }_G$, $R_G\equiv R(G)=\underset{g\in G}{\max }||g||$. Let us make an assumption concerning the set G.

 Assumption 1. 

The set G is non-empty, convex, closed, bounded $R_G<\infty$, satisfying the separability condition, i.e., ${\rho }_G>0$.

Figure 4 shows the separable set and its elements.

Under the assumption made, since the vector η_G is a vector of minimal length in G, taking into account the convexity of the set, the inequalities $({\eta }_G,g)\ge {\rho }_G^2$ and $\forall g\in G$ will hold. Under these conditions, the vectors η_G, μ_G, and s* are solutions to (2), and the vectors $g\in G$ satisfy the constraints:

$$1\le (s^{*},g)\le R_G/{\rho }_G,\forall g\in G$$

(7)

The vector s* is one of the solutions to system (2). The following algorithm searches for an approximation of s* using linear combinations of iterations (4) and (6), (5).

Algorithm 1 for α_k = 0 implements a scheme based on the Kaczmarz algorithm [73], denote it as A0. For α_k = 1, it implements an algorithm for solving systems of inequalities from [74].

Algorithm 1: A(αk).

Input: initial approximation s0 Output: solution s* 1. Assume k = 0, gk−1 = 0. 2. Choose arbitrary $g_k\in G$ so that  $$(s_k,g_k)\le 0$$ (8) If such a vector does not exist, then s* = $s_k\in S\left(G\right)$, stop the algorithm. 3. Estimate sk+1: $$s_{k+1}=s_k+\frac{1-\left(s_k,g_k\right)}{\left(p_k,g_k\right)}{p}_k,$$ (9) where the correction vector pk, taking into account the condition: $$(g_k,g_{k-1})<0$$ (10) Which is given by: $$p_k=g_k,$$ (11) if (10) does not hold, then $$p_k=g_k-{\alpha }_k\frac{(g_k,g_{k-1})}{{\Vert g_{k-1}\Vert }^2}{g}_{k-1},$$ (12) if (10) holds. The value αk is limited by: $$0\le {\alpha }_k\le 1$$ (13) 4. Assign k = k + 1. Go to step 2.

Since the algorithm is designed to find a solution to system (2) in the form of a vector s*, we will study the behavior of the residual vector ${\Delta }_k=s^{*}-s_k$.

 Lemma 1. 

Let the sequence {s_k} be obtained as a result of the use of Algorithm 1. Then, for k = 0, 1, 2,…, we have the following estimates:

$$(s_{k+1},g_k)=1,k=0,1,2,\dots$$

(14)

$$(p_k,p_k)\le (p_k,g_k)\le (g_k,g_k),k=0,1,2,\dots$$

(15)

$$({\Delta }_k,g_{k-1})\ge 0,k=0,1,2,\dots$$

(16)

$$({\Delta }_k,p_k)\ge ({\Delta }_k,g_k)\ge 1-(s_k,g_k)\ge 1,k=0,1,2,\dots$$

(17)

 Proof of Lemma 1. 

Let us prove (14). Consider the cases of transformation (9) combined with (11) and (12). According to (9) and (11)

$$(s_{k+1},g_k)=(s_k,g_k)+\frac{1-\left(s_k,g_k\right)}{\left(g_k,g_k\right)}(g_k,g_k)=1$$

According to (9), (12)

$$(s_{k+1},g_k)=(s_k,g_k)+\frac{1-\left(s_k,g_k\right)}{\left(p_k,g_k\right)}(p_k,g_k)=1$$

Thus, equality (14) always holds. In the case of transformation (12) with α_k = 1, the vectors p_k and g_k−1 are orthogonal:

$$(p_k,g_{k-1})=(g_k,g_{k-1})-\frac{(g_k,g_{k-1})}{{\Vert g_{k-1}\Vert }^2}(g_{k-1},g_{k-1})=0$$

Therefore, the equality $(s_{k+1},g_{k-1})=1$ is preserved. This case corresponds to the exact solution of the last two equalities in (3).

Let us prove (15). Inequalities (15) will hold in the case (11). In the case (12), we carry out transformations proving (15):

$$(p_k,p_k)=(g_k,g_k)-2{\alpha }_k\frac{{(g_k,g_{k-1})}^2}{{\Vert g_{k-1}\Vert }^2}+{\alpha }_k{}^2\frac{{(g_k,g_{k-1})}^2}{{\Vert g_{k-1}\Vert }^2}$$

Hence, from (13) and (12) follows:

$$(p_k,p_k)\le (g_k,g_k)-2{\alpha }_k\frac{{(g_k,g_{k-1})}^2}{{\Vert g_{k-1}\Vert }^2}+{\alpha }_k\frac{{(g_k,g_{k-1})}^2}{{\Vert g_{k-1}\Vert }^2}=(g_k,g_k)-{\alpha }_k\frac{{(g_k,g_{k-1})}^2}{{\Vert g_{k-1}\Vert }^2}=(p_k,g_k)\le (g_k,g_k)$$

Let us prove (16). For k = 0, (16) is satisfied due to g₋₁ = 0. For k > 0, (16) follows from (7) and (14):

$$({\Delta }_k,g_{k-1})=(s^{*},g_{k-1})-(s_k,g_{k-1})\ge 1-(s_k,g_{k-1})\ge 1-1=0$$

Let us prove (17). The first of the inequalities in (17) holds as an equality for (11), and in case (12), taking into account the sign under condition (10) and inequality (16), we obtain:

$$({\Delta }_k,p_k)=({\Delta }_k,g_k)-{\alpha }_k\frac{(g_k,g_{k-1})}{{\Vert g_{k-1}\Vert }^2}({\Delta }_k,g_{k-1})\ge ({\Delta }_k,g_k)$$

The second inequality in (17) follows from constraints (7). The last inequality in (17) follows from condition (8). □

The following theorem states that transformation (12) provides a direction p_k to the solution point s* with a more acute angle compared to g_k.

 Theorem 1. 

Let the sequence {s_k} be obtained as a result of the use of Algorithm 1. Then, for k = 0, 1, 2…, we have the estimate:

$$\frac{({\Delta }_k,p_k)}{{({\Delta }_k,{\Delta }_k)}^{0.5}{(p_k,p_k)}^{0.5}}\ge \frac{({\Delta }_k,g_k)}{{({\Delta }_k,{\Delta }_k)}^{0.5}{(g_k,g_k)}^{0.5}}$$

(18)

 Proof of Theorem 1. 

Consistently using (17) and (15), we obtain (18):

$$\frac{({\Delta }_k,p_k)}{{({\Delta }_k,{\Delta }_k)}^{0.5}{(p_k,p_k)}^{0.5}}\ge \frac{({\Delta }_k,g_k)}{{({\Delta }_k,{\Delta }_k)}^{0.5}{(p_k,p_k)}^{0.5}}\ge \frac{({\Delta }_k,g_k)}{{({\Delta }_k,{\Delta }_k)}^{0.5}{(g_k,g_k)}^{0.5}}$$

□

 Lemma 2. 

Let the set G satisfy Assumption 1. Then,$s_k\in S(G)$  if

$$\left|\right|{\Delta }_k\left|\right|<1/R_G$$

(19)

 Proof of Lemma 2. 

Using (19) and the scalar product property, we obtain an estimate in the form of a strict inequality for vectors from G:

$$|({\Delta }_k,g)|=|(s^{*}-s_k,g)|\le \left|\right|s^{*}-s_k\left|\right|\times \left|\right|g\left|\right|\le \left|\right|s^{*}-s_k\left|\right|\times R_G<R_G/R_G=1.$$

Hence, taking into account the constraint (7), we obtain the proof. □

The following theorem substantiates the finite convergence of Algorithm 1.

 Theorem 2. 

Let the set G satisfy Assumption 1. Then, to estimate the convergence rate of the sequence {s_k}, k = 0, 1, 2… to the point s* generated by Algorithm 1 up to the moment of stopping, the following observations are true:

$$({\Delta }_k,{\Delta }_k)\le ({\Delta }_{k-1},{\Delta }_{k-1})-\frac{1}{R_G^2}$$

(20)

$$\left|\right|{\Delta }_k|{|}^2\le {(|\left|s_0\right||+{\rho }_G{}^{-1})}^2-k/R_G^2$$

(21)

for ρ_G⁻¹ we have the estimate:

$${\rho }_G{}^{-1}\ge {({\displaystyle \sum _{j=0}^k{(g_j,g_j)}^{-1}})}^{0.5}-||s_0||\ge \frac{k^{0.5}}{R_G}-||s_0||$$

(22)

and for some value k, satisfying the inequality:

$$k\le k^{\ast }\equiv {\left(R_G^{}||s_0||+\frac{R_G^{}}{{\rho }_G}\right)}^2+1$$

we will obtain the vector $s_k\in S(G)$.

 Proof of Theorem 2. 

Using (9), we obtain an equality for the squared norm of the residual ${\Delta }_{k+1}$:

$$({\Delta }_{k+1},{\Delta }_{k+1})=({\Delta }_k,{\Delta }_k)-2({\Delta }_k,p_k)\frac{1-(s_k,g_k)}{(p_k,g_k)}+(p_k,p_k)\frac{{(1-(s_k,g_k))}^2}{{(p_k,g_k)}^2}$$

We transform the right side of the resulting expression, considering inequalities (17), replacing $({\Delta }_k,p_k)$ with $1-(s_k,g_k)$:

$$({\Delta }_{k+1},{\Delta }_{k+1})\le ({\Delta }_k,{\Delta }_k)-2\frac{{(1-(s_k,g_k))}^2}{(p_k,g_k)}+(p_k,p_k)\frac{{(1-(s_k,g_k))}^2}{{(p_k,g_k)}^2}$$

In the resulting expression, we replace the factor $(p_k,p_k)$, according to (15), by a larger value $(p_k,g_k)$. As a result, we obtain:

$$({\Delta }_{k+1},{\Delta }_{k+1})\le ({\Delta }_k,{\Delta }_k)-\frac{{(1-(s_k,g_k))}^2}{(p_k,g_k)}\le ({\Delta }_k,{\Delta }_k)-\frac{1}{(g_k,g_k)}\le ({\Delta }_k,{\Delta }_k)-\frac{1}{R_G^2}$$

Here, the last two inequalities are obtained considering (8) and the definition of R_G. With the indexing taken into account, we prove (20). Using recursively (20) and the inequality:

$$\left|\right|s^{\ast }-s_0|{|}^2\le {(|\left|s_0\right||+|\left|s^{\ast }\right||)}^2={(|\left|s_0\right||+{\rho }_G^{-1})}^2$$

which follows from the properties of the norm, we obtain estimate (21). Estimate (22) is a consequence of (21).

According to (21) $\left|\right|{\Delta }_k\left|\right|\to 0$. Therefore, at some step k, inequality (19) will be satisfied for the vector s_k, i.e., a vector $s_k\in S(G)$ will be obtained that is a solution to system (2). As an upper bound for the required number of steps, we can take k*, equal to the value k at which the right side of (21) vanishes, increased by 1. This provides an estimate for the required number of iterations k*. □

In the minimization algorithm, s₀ = 0 is set. In this case, (22) will take the form:

$${\rho }_G\le {\left({\displaystyle \sum _{j=0}^k{(g_j,g_j)}^{-1}}\right)}^{-0.5}\le \frac{R_G}{k^{0.5}}$$

(23)

Inequalities (23) will hold as long as it is possible to find a vector $g_k\in G$, satisfying the condition (8). In the minimization algorithm, under the condition of exact one-dimensional descent, there will always be g_k satisfying condition (8). Therefore, estimates (23) will be used in the rules for updating the algorithm for solving systems of inequalities in the minimization method under constraints on the parameters of subgradient sets.

4. A Family of Subgradient Minimization Methods

The idea of organizing a minimization algorithm is to construct a descent direction that provides a solution to a system of inequalities of type (2) for subgradients in the neighborhood of the current minimum. Such a solution will allow, by means of one-dimensional minimization (1), to go beyond this neighborhood, that is, to find a point with a smaller value of the function outside the neighborhood of the current minimum.

Let the function $f(x),x\in {\mathrm{R}}^n$ be convex. Denote $d(x)=\mathsf{\rho }(\partial f(x))$ as the length of the vector of the minimum length of the subgradient set at the point x, $D(z)=\{x\in {\mathrm{R}}^n|f(x)\le f(z)\}$.

 Note 1. 

For a function convex on Rⁿ, if the set D(x₀) is bounded, for points  $x^{*}\in D(x_0)$satisfying the condition $d(x^{*})<d_0$, the following estimate is correct [13]:

$$f(x^{\ast })-f^{\ast }\le D{d}_0$$

(24)

where D is the diameter of set D(x₀), d₀ is a given value, $f^{\ast }=\underset{x\in R^n}{\inf }f(x)$.

The minimization algorithm must build a sequence of approximations of which the limit points x* satisfy the condition d(x*) < d₀ for a given value of d₀. This will provide, according to (24), the specified accuracy of minimization with respect to the function. For these purposes, the parameters are set in the algorithm in such a way as to ensure the search for points x* that satisfy the condition d(x*) < d₀. The connection between d₀ and the parameters of the algorithm will be established in more detail in Theorem 3.

When solving a minimization problem with a built-in algorithm for solving systems of inequalities in an exact one-dimensional search along a direction, according to the necessary condition for the minimum of a one-dimensional function, there is always a subgradient that satisfies condition (8). Therefore, criteria for updating the method for solving systems of inequalities are necessary, sufficient, but not excessive, for convergence to limit points x* satisfying the condition $d(x^{*})<d_0$. For these purposes, relations (23) will be used, signaling the solution of a system of inequalities with given characteristics sufficient to exit the neighborhood of the current minimum.

Let us describe the minimization method with a built-in Algorithm 1 for finding points $x^{\ast }\in {\mathrm{R}}^n$ such that $d(x^{\ast })\le E_0$, where $E_0>0$.

In Algorithm 2, in steps 2, 4, and 5, there is a built-in algorithm for solving inequalities. Algorithm 2 for α_k = 0 was obtained in [73] and uses the method for solving the inequalities with the Kaczmarz Formula (4) (we denote it as M0). Algorithm 2 for α_k = 1 was obtained in [74].

Algorithm 2: MA(αk).

Input: initial approximation point x0 Output: minimum point x* 1. Set the initial approximation $x_0\in R^n$, integer k = j = 0. 2. Assign $j=j+1$, $q_j=k$, $s_k=0,$ $g_{k-1}=0$, ${\Sigma }_k=0$. 3. Set ${\epsilon }_j,m_j.$ 4. Calculate the subgradient $g_k\in \partial f(x_k)$, which satisfies $(s_k,g_k)\le 0$. If $g_k=0$, then x* = xk, stop the algorithm. 5. Obtain a new approximation $s_{k+1}=s_k+\frac{1-\left(s_k,g_k\right)}{\left(p_k,g_k\right)}{p}_k,$ where $p_k=\{\begin{array}{ll}{g}_k,& if(g_k,g_{k-1})\ge 0,\\ g_k-{\alpha }_k\frac{\left(g_k,g_{k-1}\right)}{{\Vert g_{k-1}\Vert }^2}{g}_{k-1},& if(g_k,g_{k-1})<0.\end{array}$ The value of αk is bounded $0\le {\alpha }_k\le 1$ similarly to (13). 6. Calculate a new approximation of the criterion ${\Sigma }_{k+1}={\Sigma }_k+{(g_k,g_k)}^{-1}$. 7. Calculate a new approximation of the minimum point $x_{k+1}=x_k-{\gamma }_k{s}_{k+1},{\gamma }_k=\arg \underset{\gamma \in R}{\min }f(x_k-\gamma s_{k+1}).$ 8. Set k = k + 1. 9. If $1/\sqrt{{\Sigma }_k}<{\epsilon }_j$, then go to step 2. 10. If $k-q_j>m_j$, then go to step 2; otherwise, go to step 4.

The index q_j, j = 0, 1, 2,… was introduced to denote the numbers of iterations k, at which, in step 2, when the criteria of steps 9 and 10 are met, the algorithm for solving inequalities is updated (s_k = 0, g_k−1 = 0). According to (21) and (22), the algorithm for solving the system of inequalities with s₀ = 0 has the best convergence rate estimates. Therefore, when updating in step 2 of Algorithm 2, we set s_k = 0. The need for updating arises due to the fact that as a result of the shifts in step 7, the subgradient sets in the neighborhood of the current point of the minimum are changed, which leads to the need to solve the system of inequalities based on new information.

By virtue of exact one-dimensional descent along the direction (−s_k+1) in step 7, at a new point x_k+1, the vector g_k+1 ∈ ∂f(x_k+1), such that (g_k+1,s_k+1) ≤ 0, always exists according to the necessary condition for a minimum of one-dimensional function (see [13]). Therefore, regardless of the number of iterations k, the condition (g_k,s_k) ≤ 0 of step 4 will always be satisfied.

The proof of the convergence of Algorithm 2 is based on the following lemma.

 Lemma 3 ([13]). 

Let the function f(x) be strictly convex on Rⁿ, the set D(x₀) be bounded, and the sequence ${\left\{x_k\right\}}_{k=0}^{\infty }$ be such that  $f(x_{k+1})=\underset{\alpha \in [0,1]}{\min }f(x_k+\alpha (x_{k+1}-x_k))$. Then, $\underset{k\to \infty }{\lim }||x_{k+1}-x_k||=0$.

Under the conditions of an exact one-dimensional search, the conditions of Lemma 3 will be satisfied in iterations of Algorithm 2.

Denote by $W_{\epsilon }(G)=\{z\in R^n|\Vert z-x\Vert \le \epsilon ,\forall x\in G\}$ the ε-neighborhood of the set G, by $U_{\delta }(x)=\{z\in {\mathrm{R}}^n|\left|\right|z-x\left|\right|\le \delta \}$ the δ-neighborhood of the point x, $z_j=x_{q_j},Q_j={\Sigma }_{q_j},j=1,2,\dots ,$ i.e., the points x_k and the values of the ${\Sigma }_k$, corresponding to the indices k at the time of updating in step 2 of Algorithm 2.

 Theorem 3. 

Let the function f(x) be strictly convex on Rⁿ and the set D(x₀) be bounded, and the parameters ε_j and m_j specified in step 2 of Algorithm 2 are fixed:

$${\epsilon }_j=E_0>0,m_j=M_0$$

(25)

Then, if x* is the limit point of the sequence ${\{x_{q_j}\}}_{j=1}^{\infty }$ generated by Algorithm 2; then,

$$d(x^{\ast })\le \max \{E_0,R(x_0)/\sqrt{M_0}\}\equiv d_0$$

(26)

where $R(x_0)=\underset{x\in D(x_0)}{\max }\underset{v\in \partial f(x)}{\max }||v||$. In particular, if $M_0\ge R^2(x_0)E_0^{-2}$, then $d(x^{\ast })\le E_0$.

 Proof of Theorem 3. 

Let conditions (25) be satisfied. The existence of limit points of the sequence {z_k} follows from the fact that the set D(x₀) is bounded and $z_j\in D(x_0)$. Assume that the statement of the theorem is false: suppose that the subsequence $z_{j_s}\to x^{\ast }$, but

$$d(x^{\ast })=d^{\ast }>d_0>0$$

(27)

Assume that

$$\epsilon =(d^{\ast }-d_0)/2.$$

(28)

Denote $W_{\epsilon }^{\ast }=W_{\epsilon }(\partial f(x^{\ast }))$. Choose $\delta >0$, so that

$$\partial f(x)\subset W_{\epsilon }^{\ast }\forall x\in U_{\delta }(x^{\ast })$$

(29)

Such a choice is possible due to the upper semicontinuity of the point-set mapping $\partial f(x)$ (see [13]).

Choose a number K, such that for j_s > K, the following will hold:

$$z_{j_s}\in U_{\delta /2}(x^{\ast }),x_k\in U_{\delta }(x^{\ast }),q_{j_s}\le k\le q_{j_s}+M_0$$

(30)

i.e., such a number K that the points x_k remain in the neighborhood $U_{\delta }(x^{\ast })$ for at least M₀ steps of the algorithm. Such a choice is possible due to the assumption of convergence $z_{j_s}\to x^{\ast }$ and the result of Lemma 3, the conditions of which are satisfied under the conditions of Theorem 3 and an exact one-dimensional descent in step 7 of Algorithm 2.

According to assumption (27), the choice conditions of ε in (28), δ in (29), and K, which ensures (30), for j_s > K, the inequality will hold:

$$\mathsf{\rho }(W_{\epsilon }^{\ast })\ge \mathsf{\rho }(\partial f(x^{\ast }))-\epsilon =d^{\ast }-(d^{\ast }-d_0)/2>d_0$$

(31)

For j_s > K, due to the validity of relations (30), it follows from (29): $g_k\in W_{\epsilon }^{\ast },q_{j_s}\le k\le q_{j_s}+M_0$. Algorithm 2 includes Algorithm 1. Therefore, taking into account the estimates from (23), depending on the steps of Algorithm 2 (step 9 or step 10), the update occurs at some k, and one of the inequalities will be satisfied:

$$\mathsf{\rho }(W_{\epsilon }^{\ast })\le {\sum }_k^{-0.5}\le {\epsilon }_j\le E_0\le d_0$$

(32)

$$\mathsf{\rho }(W_{\epsilon }^{\ast })\le R(x_0)/\sqrt{m_j}\le R(x_0)/\sqrt{M_0}\le d_0$$

(33)

The last transition in the inequalities follows from the definition of d₀ in (26). However, (31) contradicts both (32) and (33). The resulting contradiction proves the theorem.

According to estimate (26), for any limit point of the sequence {z_j} generated by Algorithm 2, $d(x^{\ast })<d_0$ will be satisfied, and therefore, estimate (24) will be valid. □

The following theorem defines the conditions under which Algorithm 2 generates a sequence {x_k} converging to a minimum point.

 Theorem 4. 

Let the function f(x) be strictly convex, the set D(x₀) be bounded, and

$${\epsilon }_j\to 0,m_j\to \infty$$

(34)

Then, any accumulation point of the sequence $\{x_{q_j}\}$generated by Algorithm 2 is a minimum point of the function f(x) on Rⁿ.

 Proof of Theorem 4. 

Assume that the statement of the theorem is false: suppose that the subsequence $z_{j_s}\to x^{\ast }$, but in this case, there exists d₀ > 0, such that inequality (27) is satisfied. As before, we set ε according to (28). We choose δ > 0, such that (29) will be satisfied. By virtue of conditions (34), there is K₀, such that when j > K₀, the relation will hold:

$$\max \{{\epsilon }_j,R(x_0)/\sqrt{m_j}\}\le d_0$$

(35)

Denote E₀ = d₀ and denote by M₀ the minimum value m_j with j > K₀. This renaming allows us to use the proofs of Theorem 3. Let us choose an index K > K₀, such that (30) holds for j_s > K, i.e., a number K such that the points x_k remain in neighborhood U_δ(x*) for at least M₀ steps of the algorithm. According to assumption (27), conditions for choosing ε in (28), δ in (29), and k in (30) for j_s > K inequality (31) will hold. For j_s > K, due to (30), from (29) follows $g_k\in W_{\epsilon }^{\ast },q_{j_s}\le k\le q_{j_s}+M_0$. Algorithm 2 contains Algorithm 1. Therefore, taking into account the estimates from (23), depending on the step number of Algorithm 2 (step 9 or step 10) in which the update occurs at some k, one of the inequalities (32) and (33) will be satisfied, where the last transition in inequalities follows from the definition of E₀ and M₀. However, (31) contradicts both (32) and (33). The resulting contradiction, taking into account (35) and (34), proves that the limit point can only be the minimum point. □

5. Correlation with the Conjugate Gradient Method

Let us show that the presented Algorithm 2 has the properties of the conjugate gradient method, and successive approximations of the minimum of both methods are the same on quadratic functions. Denote by $\nabla f(x)$ the gradient of a function, which, in the case of a differentiable convex function, coincides with the subgradient and is the only element of the subgradient set [13]. Denote by m a number of iterations (m ≤ n) at which the minimum point is not reached. Iterations of Algorithm 2 for k = 1, 2,…, m can be written as follows:

$$x_{k+1}=x_k-{\gamma }_k{s}_{k+1},{\gamma }_k=\arg \underset{\gamma \in R}{\min }f(x_k-\gamma s_{k+1}).$$

(36)

$$s_{k+1}=s_k+\frac{1-\left(s_k,g_k\right)}{\left(p_k,g_k\right)}{p}_k,g_k=\nabla f(x_k),g_0=0,s_1=0$$

(37)

$$p_k=\{\begin{array}{ll}{g}_k,& if(g_k,g_{k-1})\ge 0,\\ g_k-{\alpha }_k\frac{\left(g_k,g_{k-1}\right)}{{\Vert g_{k-1}\Vert }^2}{g}_{k-1},& if(g_k,g_{k-1})<0.\end{array}$$

(38)

The value of α_k is limited $0\le {\alpha }_k\le 1$.

Let us establish a connection between Algorithm 2 and the CGM, the iteration of which has the form:

$${\overline{x}}_{k+1}={\overline{x}}_k-{\overline{\gamma }}_k{\overline{s}}_{k+1},\hspace{1em}{\overline{\gamma }}_k=\underset{\overline{\gamma }}{\arg \min }f({\overline{x}}_k-\overline{\gamma }{\overline{s}}_{k+1}),k=1,\dots ,m,$$

(39)

$${\overline{s}}_2=g_1,{\overline{s}}_{k+1}={\overline{g}}_k+\frac{({\overline{g}}_k,{\overline{g}}_k)}{({\overline{g}}_{k-1},{\overline{g}}_{k-1})}{\overline{s}}_k,k=2,\dots ,m,\hspace{1em}{\overline{g}}_k=\nabla f({\overline{x}}_k)$$

(40)

 Theorem 5. 

Let the function f(x), $x\in R^n$, be quadratic, and its matrix of second derivatives is strictly positive definite; then, provided that the initial points in the algorithms (36)–(38), (39), and (40) are equal $x_1={\overline{x}}_1$, they generate an identical sequence of approximations of the minimum, and their characteristics satisfy the relations:

$$\left(\mathrm{a}\right)p_k=g_k,\left(\mathrm{b}\right)s_{k+1}={\overline{s}}_{k+1}/(g_k,g_k),\left(\mathrm{c}\right)x_{k+1}={\overline{x}}_{k+1},k=1,2,\dots ,m$$

(41)

In this case, the minimum will be found after no more than n steps.

 Proof of Theorem 5. 

We will use induction. As a result of iterations (36)–(38), for k = 1, due to g₀ = 0 and s₁ = 0, we have $p_1=g_1$ and $s_2=g_1/(g_1,g_1)$. As a result of iterations (39) and (40), for k = 1, we have ${\overline{s}}_2=g_1$. Consequently, equalities (41(a)) and (41(b)) are satisfied for k = 1. Due to the exact one-dimensional descent and the collinearity of the descent directions, equality (41(c)) will hold for k = 1.

Assume that equalities (41) are satisfied for k = 1, 2,…, l, where l > 1. Let us show that they are satisfied for k = l + 1. According to (41(a)), the gradients of the CGM algorithms (39), (40), and (36)–(38) coincide due to the identity of the points (41(c)) at which they are calculated, and the gradients used in the CGM and, hence, in (36)–(38), are mutually orthogonal [3]. Thus, in (38), for k = l + 1, as a result of the orthogonalization of vectors g_{l +1} and g_l, we obtain $p_{l+1}=g_{l+1}$. This proves (41(a)) for k = l + 1.

According to the condition of exact one-dimensional descent, the equality $(s_{l+1},g_{l+1})=0$ follows. Therefore, the transformation (37), taking into account (41(a)) for k = l + 1, (41(b)) for k = l, and (40), takes the form:

$$s_{l+2}=s_{l+1}+\frac{g_{l+1}}{(g_{l+1},g_{l+1})}=\frac{{\overline{s}}_{l+1}}{(g_l,g_l)}+\frac{g_{l+1}}{(g_{l+1},g_{l+1})}=\frac{{\overline{s}}_{l+2}}{(g_{l+1},g_{l+1})}$$

This implies (41(b)). Due to the exact one-dimensional descent and the collinearity of the descent directions, equality (41(c)) will hold for k = l + 1.

From the above proof of the equivalence of sequences generated by the CGM algorithms and (36)–(38), taking into account the property of the termination of the process of minimization by the CGM method after no more than n steps [3], the proof of the theorem follows. □

6. Implementation of the Minimization Algorithm

Algorithm 2 is implemented according to the RSM implementation technique [70,71,73,74]. Consider a version of Algorithm 2 that includes a one-dimensional minimization procedure along the direction s. This procedure: (a) constructs the current approximation of the minimum x_m; (b) constructs a point y from a neighborhood x_m such that for $g_1\in \partial f(y)$, the inequality $(s,g_1)\le 0$ holds. The subgradient g₁ is used to solve the system of inequalities. Calling the procedure will be denoted as follows:

$$OM(\{x,s,g_x,f_x,h_0\};\{{\gamma }_m,f_m,g_m,{\gamma }_1,g_1,h_1\})$$

The input parameters are the point of the current approximation of the minimum x, descent direction s, $g_x\in \partial f(x)$, $f_x=f(x)$, and the initial step h₀. It is assumed that the necessary condition $(g_x,s)>0$ for the possibility of descent in direction s is satisfied. The output parameters include γ_m, which is a step to the point of the obtained approximation of the minimum $x^{+}=x-{\gamma }_{m}s$, $f_m=f(x^{+})$, $g_m\in \partial f(x^{+})$, γ₁, which is a step along s, such that at the point $y^{+}=x-{\gamma }_{1}s$ for $g_1\in \partial f(y^{+})$, the inequality $(g_1,s)\le 0$ holds and h₁, which is an initial descent step calculated in the procedure for the next iteration. In the algorithm presented below, vectors $g_1\in \partial f(y^{+})$ are used to solve a set of inequalities, and points $x^{+}=x-{\gamma }_{m}s$ are used as points of approximations of a minimum.

Algorithm of one-dimensional descent (OM). Let it be required that to find an approximation of the minimum of the one-dimensional function $\mathsf{\varphi }(\mathsf{\beta })=f(x-\mathsf{\beta }s)$, where x is some point, and s is the descent direction. Take an ascending sequence ${\mathsf{\beta }}_0=0$ and ${\mathsf{\beta }}_i=h_0{q}_M^{i-1}$ for $i\ge 1$. Denote $z_i=x-{\mathsf{\beta }}_{i}s$, $r_i\in \partial f(z_i)$, l as the minimum number i at which the relation $(r_i,s)\le 0$ is satisfied for the first time, $i=0,1,2,\dots$. Let us set the parameters of the segment $[{\gamma }_0,{\gamma }_1]$ of localization of the one-dimensional minimum: ${\gamma }_0={\beta }_{l-1}$, $f_0=f(z_{l-1})$, $g_0=r_{l-1}$, ${\gamma }_1={\mathsf{\beta }}_l$, $f_1=f(z_l)$, $g_1=r_l$. Let us find the point of minimum γ* of the one-dimensional cubic approximation of the function on the segment of localization. Calculate:

$${\gamma }_m=\{\begin{array}{ll}{q}_{\gamma 1}{\gamma }_1,& ifl=1and{\gamma }^{\ast }\le q_{\gamma 1}{\gamma }_1,\\ {\gamma }_1,& if{\gamma }_1-{\gamma }^{\ast }\le q_{\gamma }({\gamma }_1-{\gamma }_0),\\ {\gamma }_{0,}& ifl>1and{\gamma }^{\ast }-{\gamma }_0\le q_{\gamma }({\gamma }_1-{\gamma }_0),\\ {\gamma }^{\ast },& otherwise.\end{array}$$

(42)

Calculate the initial descent step for the next iteration:

$$h_1=h_0{q}_m{({\gamma }_1/h_0)}^{1/2}$$

(43)

In (42), a rough search for the minimum on the interval is carried out, and when choosing γ₀ or γ₁ instead of γ_m, the calculation of the function and the gradient is not required. We use parameters q_γ = 0.2 and q_γ1 = 0.1 and coefficients q_M > 1 and q_m < 1.

Minimization algorithm. In the implementation of Algorithm 2 proposed below, the method for solving inequalities is not updated, and the exact one-dimensional descent is replaced by an approximate one.

Let us explain the steps of the algorithm. The OM procedure returns two subgradients ${\tilde{g}}_{k+1}$ and $g_{k+1}$. The first of them is used to solve the inequalities in step 2, and the second one is used in step 3 to correct the direction of descent using Equation (4) in order to provide the necessary condition $(s_{k+1},g_k)>0$ for the possibility of descent in the direction ($-s_{k+1}$). Iteration (4) in (45) for $({\tilde{s}}_{k+1},g_k)<1$ is a correction (4) by the Kaczmarz algorithm. This transformation is carried out in order to direct the descent according to the subgradient of the current approximation of the minimum.

Unlike the idealized case, Algorithm 3 does not provide updates. Although the rationale for the convergence of idealized versions of RSM is made under the condition of exact one-dimensional descent, the implementation of these algorithms is carried out with one-dimensional minimization procedures in which the initial step, depending on progress, can increase or decrease, which is determined by the given coefficients q_M > 1 and q_m < 1. These coefficients should be chosen so that the step length (43) decrease in the one-dimensional minimization procedure corresponds to the rate of reduction in the distance to the minimum point. The minimum iteration step cannot be less than some fraction of the initial step, the value of which is given in (42) by the parameters q_γ = 0.2 and q_γ1 = 0.1. We used these values in our calculations.

Algorithm 3: MOM(αk).

Input: initial approximation x0, initial step of one-dimensional descent h0, maximum allowed number of iterations N, argument minimization precision εx, gradient minimization precision εg Output: minimum point x* 1. Set the initial approximation $x_0\in R^n$, the initial step of one-dimensional descent h0. Set $k=0$, $g_0={\tilde{g}}_0\in \partial f(x_0)$, $g_{k-1}=0$, $f_0=f(x_0)$, $s_0={\tilde{s}}_0=0$. Set the stop parameters: maximum allowed number of iterations N, argument minimization precision εx, gradient minimization precision εg. 2. Obtain an approximation $${\tilde{s}}_{k+1}=s_k+\frac{1-\left(s_k,{\tilde{g}}_k\right)}{\left(p_k,{\tilde{g}}_k\right)}{p}_k,$$ (44) where $p_k=\{\begin{array}{c}{\tilde{g}}_k,if({\tilde{g}}_k,g_{k-1})\ge 0,\\ {\tilde{g}}_k-{\alpha }_k\frac{\left({\tilde{g}}_k,g_{k-1}\right)}{{\Vert g_{k-1}\Vert }^2}{g}_{k-1},if({\tilde{g}}_k,g_{k-1})<0.\end{array}$ 3. Obtain the descent direction  $$s_{k+1}=\{\begin{array}{l}{\tilde{s}}_{k+1},if({\tilde{s}}_{k+1},g_k)\ge 1,\\ {\tilde{s}}_{k+1}+g_k(1-({\tilde{s}}_{k+1},g_k))/(g_k,g_k),if({\tilde{s}}_{k+1},g_k)<1.\end{array}$$ (45) 4. Perform a one-dimensional descent along the normalized direction $w_{k+1}=s_{k+1}{(s_{k+1},s_{k+1})}^{-1/2}$: $$OM(\{x_k,w_{k+1},g_k,f_k,h_k\};\{{\gamma }_{k+1},f_{k+1},g_{k+1},{\tilde{\gamma }}_{k+1},{\tilde{g}}_{k+1},h_{k+1}\}).$$ 5. Calculate the minimum point approximation $x_{k+1}=x_k-{\gamma }_{k+1}{w}_{k+1}$. 6. If k > N or $\Vert x_{k+1}-x_k\Vert \le {\epsilon }_x$ or $\Vert g_{k+1}\Vert \le {\epsilon }_g$, then x* = xk+1, stop the algorithm; otherwise, k = k + 1, and go to step 2.

Consider ways to set parameters α_k. With a numerical implementation with α_k = 1, the number of iterations is either less than it is when α_k = 0, or greater. Unplanned stops often occur in (44) due to the proximity to the zero of the $\left(p_k,{\tilde{g}}_k\right)$ values. Denote by εp a value from a segment [0, 1]. In step 2 of the algorithm, we will use the following method for setting the parameter α_k:

$$\mathrm{If}(p_k,p_k)\le \epsilon p({\tilde{g}}_k,{\tilde{g}}_k),\mathrm{then}{\alpha }_k=1-\epsilon p;\mathrm{otherwise},{\alpha }_k=1$$

(46)

We also used the second choice of parameter α_k:

$$\mathrm{If}(p_k,p_k)\le \epsilon p({\tilde{g}}_k,{\tilde{g}}_k),\mathrm{then}{\alpha }_k=0;\mathrm{otherwise},\mathrm{else}{\alpha }_k=1$$

(47)

In the next section, we will select an appropriate parameter εp from the set $\epsilon p\in \{0.5;0.1;{10}^{-3};{10}^{-4};{10}^{-8};{10}^{-15}\}$, with which the main computational experiment will be carried out.

7. Numerical Experiment

In Algorithm 3, the coefficients of decrease q_m < 1 and increase q_M > 1 of the initial step of the one-dimensional descent at iteration play a key role. Values q_m close to 1 provide a low rate of step decrease and, accordingly, a low rate of method convergence. A small rate of step decrease eliminates the looping of the method due to the fact that the subgradients of the function involved in solving the inequalities are taken from a wider neighborhood. The choice of the parameter q_m must be commensurate with the possible rate of convergence of the minimization method. The higher the speed capabilities of the algorithm, the smaller this parameter can be chosen. For example, in RSM with space dilation [71,73], q_m = 0.8 is chosen. For smooth functions, the choice of this parameter is not critical and can be taken from the interval [0.8, 0.98]. The convergence rate practically does not depend on the step increase parameter, so it can be taken as $q_M\in [1.5,3]$.

The computational experiment is preceded by the choice of a parameter εp for the proposed Algorithm 3, which is used in Formulas (46) and (47). After that, we will conduct the main testing of the method with the selected parameter εp and its comparison with the known methods of conjugate gradients according to the following scheme:

• Testing on smooth and non-smooth test functions with known characteristics of level surface elongation.
• Testing on non-convex smooth and non-smooth test functions.
• Testing on known smooth test functions.

We used the following methods:

• AMMI—the distance-to-extremum relaxation method of minimization [10];
• sub—Algorithm 3 with (46);
• subm—Algorithm 3 with more precise one-dimensional descent and (46);
• subg—Algorithm 3 with (47);
• subgm—Algorithm 3 with (47) and exact one-dimensional descent;
• sub0—Algorithm 3 with α_k = 0;
• sgrFR—the conjugate gradient method (Fletcher–Reeves method [3]) with exact one-dimensional descend;
• sgr—method sgrFR with one-dimensional minimization procedure OM;
• sgrPOL—the Polak–Ribiere–Polyak method [17];
• sgrHS—the Hestenes–Stiefel method [15];
• sgrDY—the Dai–Yuan method [18].

We used the following test groups. Each group has its own stopping criterion.

The first group of tests includes smooth and non-smooth functions with a maximum ratio of level surfaces elongation along the coordinate axes equal to 100:

$$\begin{array}{c}{f}_1(x)={\displaystyle \sum _{i=1}^n{x}_i{}^2}\cdot {(1+(i-1)(100-1)/(n-1))}^2,x_{0,i}=1,x_i^{\ast }=0,i=0,1,2,\dots ,n,\epsilon ={10}^{-8}\\ f_2(x)={\displaystyle \sum _{i=1}^n\left|x_i\right|}\cdot (1+(i-1)(100-1)/(n-1)),x_{0,i}=1,x_i^{\ast }=0,i=0,1,2,\dots ,n,\epsilon ={10}^{-4}\end{array}$$

The stopping criterion is

$$f(x_k)-f*\le \epsilon$$

(48)

The second group of tests includes the Extended White and Holst function, which is not convex:

$$f_{GW}(x)={\displaystyle \sum _{i=1}^{n/2}[100{(x_{2i}^{}-x_{2i-1}^3)}^2+{(1-x_{2i-1}^{})}^2]},x_0=(-1.2,1,\dots ,-1.2,1),\epsilon ={10}^{-10}$$

The non-smooth non-convex function derived from it:

$$f_{NW}(x)={\displaystyle \sum _{i=1}^{n/2}(10|x_{2i}^{}-x_{2i-1}^3|+|1-x_{2i-1}^{}|)},x_0=(-1.2,1,\dots ,-1.2,1),\epsilon ={10}^{-4}$$

The Raydan1 function is biased to obtain a new function with a zero minimum value:

$$f_{GR}(x)={\displaystyle \sum _{i=1}^n\frac{i}{10}(\exp (x_i^{})-x_i^{}-1)},x_0=(2,2,\dots ,2),\epsilon ={10}^{-10}$$

We transform this function into a non-smooth one as follows:

$$f_{NR}(x)={\displaystyle \sum _{i=1}^n\frac{a_i^{}}{10}\max \left\{\exp (x_i^{})-1,-x_i^{}\right\}},x_0=(1,1,\dots ,1),\epsilon ={10}^{-4}$$

$$a_i^{}=1+\frac{i-1}{n-1}(a_{\max }^{}-1),a_{\max }^{}=100,i=1,2,\dots ,n$$

Here, the coefficients a_i are bounded and not equal to $\sqrt{i}$. Criterion (48) is used as a stopping criterion for these functions.

The third group of tests is composed of functions from [76]. We chose the functions that were difficult to minimize by gradient methods, which was revealed by the study in [53]. The stopping criteria:

$$\Vert \nabla f(x_k)\Vert \le {10}^{-6},\frac{|f(x_{k+1})-f(x_k)|}{1+|f(x_k)|}\le {10}^{-16}$$

(49)

Several experiments were carried out for each function. The number of iterations and the number of function and gradient calculations were counted.

Denote:

• S1 is a sum of resulting scores for dimensions 100, 200,…, and 1000;
• S2 is a sum of resulting scores for dimensions 100, 500, 1000, 2000, 3000, 5000, 7000, 8000, 10,000, and 15,000.

The results for the dimensions T_i = 100,000 × i are given separately for changing i. We will use these notations for arbitrary functions.

For the functions from [76], the following notation is used: the Diagonal 9 function: (Diagonal9); the LIARWHD function (CUTE): (LIARWHD); the Quadratic QF2 function: (QF2); the DIXON3DQ function (CUTE): (DIXON3DQ); the TRIDIA function (CUTE): (TRIDIA); the Extended White and Holst function: (WHolst); and the Raydan 1 function: (Raydan1).

As a result for the methods, we will use it—the number of iterations, nfg—the number of functions and gradient calculations necessary to solve the problem with a given stopping criterion for a specific function.

Preliminarily, based on an experiment on some of the above functions, we study the dependence of Algorithm 3 (sub, subg, and sub0), using Formulas (46) or (47), on the parameter εp chosen from the set $\epsilon p\in \{0.5;0.1;{10}^{-3};{10}^{-4};{10}^{-8};{10}^{-15}\}$. The results for the costs (nfg—the number of calculations of the function and the gradient) are given in

Table 1. Results of S1 calculations for Algorithm 3 with different values of εp parameters.

Function	Method	αk = 0	εp
			0.5	10−1	10−3	10−4	10−8	10−15
Diagonal9	sub	25,194	15,666	12,396	11,627	11,627	11,627	11,627
Diagonal9	subg	25,194	24,494	12,678	11,627	11,627	11,627	11,627
$f_1$	sub	12,451	9347	9298	9298	9298	9298	9298
$f_1$	subg	12,451	9316	9298	9298	9298	9298	9298
$f_{NR}$	sub	64,051	17,740	17,749	17,749	17,749	17,749	17,749
$f_{NR}$	subg	64,051	17,803	17,749	17,749	17,749	17,749	17,749
$f_2$	sub	291,378	103,681	103,600	103,600	103,600	103,600	103,600
$f_2$	subg	291,378	103,518	103,618	103,618	103,618	103,618	103,618

.

When α_k = 0, the methods spend significantly more computations of the function and gradient. When α_k = 1, the method is not operational due to unplanned stops. Therefore, these variants are not considered during testing. According to the results of Table 1, starting from εp = 10⁻³, the results stabilize and are almost always the best. In further studies, we used εp = 10⁻⁸, which reflects some geometric mean of the effective interval for both methods (46) and (47). Given the equivalence of the sub and subg methods, we carried out subsequent studies with only one of them for a given objective function.

The results for the first group of tests are presented in

Table 2. Results for the first group of tests (upper number is the number of iterations, lower number is the number of function and gradient evaluations).

Function	Method	S1	S2	T1	T2	T3	T4	T5
$f_1$	subg	5512 9308	6141 10,442	728 1189	747 1229	754 1268	760 1312	766 1343
$f_1$	subgm	4679 9426	5759 11,603	713 1438	730 1472	740 1492	748 1508	753 1519
$f_1$	sgrPOL	5319 10,706	5985 12,055	713 1438	730 1472	740 1492	748 1508	753 1519
$f_1$	sgrFR	4673 9414	5756 11,597	713 1438	730 1472	740 1492	748 1508	753 1519
$f_1$	sgr	-	-	1515 2373	1580 2484	1597 2525	1626 2591	1647 2624
$f_1$	AMMI	4980	6347	713	730	740	748	753
$f_2$	subg	144,036 288,123	153,651 307,413	20,148 40,345	58,196 116,463	58,978 118,043	59,758 119,604	59,481 119,063
$f_2$	AMMI	42,382	94,278	24,563	35,788	31,395	33,517	41,528

. The cell shows the number of iterations (upper number) and the number of function and gradient evaluations (lower number).

For example, part of the calculations on function f₁ was carried out for the sgr method, which is the sgrFR method with the one-dimensional OM procedure. The results here are two times worse than for sgrFR, and for other functions, it was sometimes not possible to solve the problem. This result is presented in order to emphasize the effectiveness of choosing the descent direction in the new method, where, in contrast to the CGM, it is possible to obtain a rapidly converging method for inexact one-dimensional descent, which is important when solving non-smooth minimization problems. To solve smooth problems, there are many efficient variants of the CGM.

Here, we should note the quality of the descent direction of the new method. With inexact one-dimensional descent, the subg cost is less than that of the sgrFR method. The method proposed in the paper is stable with both minimization procedures, and its results are almost equivalent to the results of the sgrFR method, which is a finite method for minimizing quadratic functions. In this case, the sgrFR method acts as a reference method. Since the results for other CGMs on this function are completely identical, we do not present them here.

On a non-smooth function, the AMMI method [10] acts as a reference, in which only one calculation of the function and gradient is required at each iteration. As follows from the results of Table 2, the number of iterations on large-dimensional functions differs insignificantly. The running cost of calculating the function and the gradient in the transition from a smooth quadratic function to a non-smooth one for functions at n = 500,000 with equal proportions of the level line elongation for these methods is 119,063/1343 = 88.65 for the subg method, and 41,528/753 = 55.15 for the AMMI method. Considering that the conditions here are ideal for the AMMI method, since the minimum value of the function and its degree of homogeneity is known, and the calculations were carried out for functions at high dimensionalities, such a result for the subg method can be considered excellent.

The minimization results for the second group of tests are given in

Table 3. Results for the second group of tests (upper number is the number of iterations, lower number is the number of function and gradient evaluations).

Function	Method	S1	S2	T1	T2	T3	T4	T5
$f_{GW}$	subg	813 2397	889 2669	102 306	112 348	177 567	224 224	134 421
$f_{GW}$	subgm	223 568	199 533,	20 51	26 71	27 73	22 60	19 49
$f_{GW}$	sgrFR	772 1643	794 1705	55 125	53 121	41 97	48 109	42 97
$f_{NW}$	subg	226,786 454,889	247,632 497,799	33,801 68,149	29,192 58,640	33,209 66,776	33,784 67,926	34,230 68,818
$f_{GR}$	subg	1365 2313	3927 6594	1823 3168	2546 4431	3318 5826	3610 6333	3883 6808
$f_{GR}$	subgm	1664 3394	4898 9879	2491 4994	3232 6674	4449 8909	4356 8725	5089 10,191
$f_{GR}$	sgrFR	1372 2803	4432 8938	2813 5637	3994 7999	4086 8003	6059 12,131	4422 8855
$f_{NR}$	subg	31,592 63,235	34,625 69,341	38,959 77,939	39,706 79,436	40,009 80,047	40,203 80,439	40,591 81,213

.

On smooth variants of functions, the subgm and subg methods are commensurate with sgrFR in terms of the cost of calculating the number of functions and gradient values. Therefore, taking into account these and previous tests, along with the CGM, when minimizing smooth functions, these methods can be used.

The subg method also handles non-smooth variants of functions (function f_NW is non-smooth and non-convex).

The minimization results for the third group of smooth test functions are given in

Table 4. Results for the third group of tests (upper number is the number of iterations, lower number is the number of function and gradient evaluations).

Function	Method	S1	S2	T1	T3	T5
Diagonal9	sgrFR	23,431 46,941	83,952 167,999	9322 18,660	31,151 62,317	48,236 97,511
Diagonal9	sgrPOL	9714 19,518	10,743 21,590	2912 5841	5805 11,626	6642 13,304
Diagonal9	sgrHS	5554 11,190	10,806 21,715	3221 6459	6396 12,812	6640 13,300
Diagonal9	sgrDY	9343 18,763	41,835 83,766	9409 18,834	20,408 40,830	NaN
Diagonal9	subm	4872 9817	9768 19,629	3931 7889	7262 14,553	10,083 20,197
Diagonal9	sub	5912 11,627	10,345 19,324	4318 7668	9214 16,589	10,866 19,781
LIARWHD	sgrFR	1244 2569	947 1996	72,001 144,015	7412 14,836	146 306
LIARWHD	sgrPOL	207 485	247 587	52 121	31 74	80 173
LIARWHD	sgrHS	166 404	183 462	32 76	21 53	17 47
LIARWHD	sgrDY	1275 2629	1069 2239	210 435	176 364	182 378
LIARWHD	subm	228 544	269 640	24 64	30 75	37 87
LIARWHD	sub	644 1325	719 1498	-	-	-
Quadratic QF2	sgrFR	14,320 28,677	28,988 58,022	11,233 22,473	13,222 26,452	29,820 59,648
Quadratic QF2	sgrPOL	2104 4246	6546 13,139	3196 6399	7056 14,120	8392 16,792
Quadratic QF2	sgrHS	2161 4359	6574 13,195	5706 11,420	6096 12,200	11,337 22,683
Quadratic QF2	sgrDY	5231 10,494	48,603 97,248	72,001 144,009	31,542 63,092	36,438 72,884
Quadratic QF2	subm	4161 8360	13,920 27,890	4687 9382	15,664 31,337	21,891 43,792
Quadratic QF2	sub	2453 4227	6656 11,227	3156 5304	4977 8247	7496 12,540
DIXON3DQ	sgrFR	2750 5538	25,800 51,645	50,001 100,008	-	-
DIXON3DQ	sgrPOL	2750 5538	25,800 51,645	50,001 100,008	-	-
DIXON3DQ	sgrHS	2750 5538	25,800 51,645	50,001 100,008	-	-
DIXON3DQ	sgrDY	2750 5538	25,800 51,645	50,001 100,008	-	-
DIXON3DQ	subm	2750 5538	25,800 51,645	50,001 100,008	-	-
DIXON3DQ	sub	13,179 22,335	249,981 417,396	NaN	-	-
TRIDIA	sgrFR	2390 4815	7190 14,424	3746 7499	6539 13,086	8470 16,949
TRIDIA	sgrPOL	2392 4819	7191 14,426	3746 7499	6539 13,086	8470 16,949
TRIDIA	sgrHS	2389 4813	7189 14,422	3746 7499	6539 13,086	8469 16,947
TRIDIA	sgrDY	2395 4825	7192 14,428	3747 7501	6539 13,086	8470 16,949
TRIDIA	subm	2397 4829	7197 14,438	3747 7501	6540 13,088	8470 16,949
TRIDIA	sub	4413 7405	16,905 28,169	11,922 19,700	23,467 38,984	32,270 53,801
WHolst	sgrFR	1429 2957	1624 3365	65 145	61 137	49 111
WHolst	sgrPOL	220 548	240 587	23 59	22 56	26 62
WHolst	sgrHS	190 483	192 485	25 64	22 58	16 43
WHolst	sgrDY	676 1461	594 1310	52 120	387 789	63 138
WHolst	subm	268 659	235 605	27 65	34 87	23 57
WHolst	sub	254 616	270 664	108 226	179 419	289 661
Raydan1	sgrFR	1708 3475	5863 11,800	4013 8037	10,548 21,109	9273 18,558
Raydan1	sgrPOL	1691 3442	4906 9887	2533 5077	4489 8989	5807 11,626
Raydan1	sgrHS	1731 3524	4871 9818	2593 5198	4501 9012	8041 16,097
Raydan1	sgrDY	2371 4803	6321 12,717	6104 12,219	NaN	NaN
Raydan1	subm	2100 4266	6475 13,033	3541 7094	6748 13,507	8101 16,215
Raydan1	sub	1722 3032	5756 9876	3153 5432	6175 10,918	9552 17,070

. A dash means that no calculations were made. The sign NaN marks the problems that could not be solved by this method.

Based on the results for this group of tests, we can conclude that subm and sub methods are applicable for minimizing smooth large-scale functions.

In general, the following conclusions can be drawn from the results of the experiment:

• The choice of the parameters of the method, which ensures its stable operation, is carried out.
• On tests with known parameters of level surface elongation, the behavior of the method and its comparison with other methods, confirming its effectiveness, were studied.
• The method was studied on non-smooth, including non-convex, functions.
• On commonly accepted tests of smooth functions, the method was compared with variants of the CGM, which enables us to conclude that it is applicable along with the CGM for minimizing smooth functions.

8. Conclusions

In our work, we proposed a family of iterative methods for solving systems of inequalities, which are generalizations of the previously proposed algorithms. The developed methods were substantiated theoretically and the estimates of their convergence rate were obtained. On this basis, a family of relaxation subgradient minimization algorithms was formulated and justified, which is applicable to solving non-convex problems as well.

According to the properties of convergence on quadratic functions of high dimension, with large spreads of eigenvalues, the developed algorithm is equivalent to the conjugate gradient method. The new method enables us to solve non-smooth non-convex large-scale minimization problems with a high degree of elongation of level surfaces.