An Optimal Opportunistic Maintenance Planning Integrating Discrete- and Continuous-State Information
Abstract
:1. Introduction
- ■
- Constructing an innovative group maintenance framework integrating both continuous and discrete health information, which dynamically integrates (a) opportunistic maintenance and (b) delayed maintenance to significantly enhance maintenance effectiveness and availability;
- ■
- Allowing defect removals to be postponed so as to (a) exploit the remaining lifetime potentials and (b) offer extra chances for the selection and implementation of cost-effectiveness opportunistic maintenance;
- ■
- Scheduling multiple types of opportunistic maintenance arising from (a) threshold-based replacement, (b) delayed replacement, and (c) corrective maintenance to sufficiently control system downtime and enhance decision-making robustness;
- ■
- Realizing the high-efficiency optimization of maintenance interaction problems via the Semi-Markov Decision Process, and demonstrating the model’s applicability through numerical experiments on a circling pump.
2. Problem Description
3. Maintenance Planning
3.1. Basic Assumptions
- (a)
- Units 1 and 2 are as good as new when initially put into use. In other words, the initial degradation accumulation of Unit 1 and the virtual age of Unit 2 are equal to 0. This is a common assumption used to simply the maintenance problem, which can be easily relaxed [26];
- (b)
- Inspections are instantaneous, non-destructive, and perfect. In other words, both the degradation severity (Unit 1) and the defective state (Unit 2) of the system can be accurately reported. This is a widely accepted setting since well-prepared inspections, in contrast to sensor-based condition monitoring, incur negligible measurement error [7];
- (c)
- Maintenance, either corrective, preventive, or opportunistic, returns the unit back to as-good-as-new status. This is equivalent to the effect of spare part replacement. In the rest of the section, we use maintenance and replacement interchangeably;
- (d)
- The time to execute maintenance activities is non-negligible, and these activities require the stoppage of the entire system, and the downtime loss cannot be ignored.
3.2. Group Maintenance Scheduling
- Regular inspection. Inspections are equally spaced within the lifetime horizon according to an interval of , with a cost per time unit. The function of inspection is twofold, (a) reporting the latest degradation magnitude of Unit 1, and (b) revealing the hidden defective state of Unit 2. Inspections are perfect and instantaneous, but require stopping the system;
- Threshold-centered replacement (TR). Upon an inspection , if the degradation of Unit 1 exceeds a pre-specified control limit , but does not yet reach the failure threshold , a TR is immediate with a cost and time ;
- Delayed replacement (DR). If Unit 2 is found defective upon an inspection, then its preventive replacement is scheduled inspection intervals later, equivalent to time units. Such replacement incurs a cost of and time ;
- Corrective replacement (CR). CR is triggered when (1) the degradation measurement of Unit 1 at an inspection exceeds the failure threshold , and (2) the defect of Unit 2 deteriorates to a complete failure. The incurred cost for each unit is and , respectively; the incurred time for each unit is and , respectively;
- Opportunistic replacement (OR). OR is available for both units, whose acceptance hinges on the entire system state. Here, two situations are possible:
- (a)
- OR of Unit 1. If Unit 2 fails unexpectedly due to defect evolution or requires replacement, Unit 1 is offered extra chances for OR. Specifically, if the degradation accumulation exceeds , the chance is accepted and a cost is incurred; otherwise, no action is taken;
- (b)
- OR of Unit 2. If the degradation of Unit 1 exceeds either the pre-set replacement threshold, while Unit 2 is waiting for DR, Unit 2 will be offered chances for OR. To be specific, if the time elapsed since the defect identification exceeds , the chance for OR is accepted and a cost is incurred; otherwise, no action is taken;
- ♦
- Remark. The sufficient interaction and integration of OR with TR and DR addressed in this maintenance policy is an effective and robust way to exploit unit dependencies (structural dependency and economy dependency), so as to enhance operational profitability by minimizing system downtime and downtime loss. For similar reasons, predictive maintenance is a cost-effective solution for multi-phase units/systems due to its nature of (a) avoiding excessive maintenance, (b) extending the remaining lifetime, (c) allowing sufficient resource preparing, and (d) offering extra chances for OR.
4. Model Formulation and Optimization
4.1. State Transition of Unit 1
4.2. State Transition of Unit 2
4.3. System Transition Probability
- System state set. Denote the system operational state as , where , . Moreover, let state sets represent the state in which Unit 1 fails while Unit 2 remains normal/defective, represent the state in which Unit 2 fails while Unit 1 remains operational, and represent that both units fail. Clearly, the entire system state set is the union of the above-mentioned scenarios, i.e., ;
- System action set. A maintenance decision is made at each inspection time . The set of maintenance actions is , where 0 means no maintenance action, 1 means corrective replacement action, 2 means preventive replacement action (including TR of Unit 1 and DR of Unit 2), and 3 means opportunistic maintenance action. Let represent the maintenance action taken for both units. For instance, when , this means both units are normally working, so no action is taken, and .
- System state transition. It is clear that the system transition probability can be derived by multiplying the transition probabilities of Unit 1 and Unit 2. For instance, we define as the transition probability from state to state when action is taken. Then, the probability is derived as
4.4. Expected Sojourn Time
- a.
- No maintenance action is taken
- b.
- Only Unit 1 is replaced
- c.
- Only Unit 2 is replaced
- d.
- Both components are replaced
4.5. Expected Cost
- a.
- No maintenance action is taken
- b.
- Only Unit 1 is replaced
- c.
- Only Unit 2 is replaced
- d.
- Both components are replaced
4.6. System Objective Function
4.7. Solution Procedure
- Step 1. Initialization parameters, including the degradation coefficients of Unit 1 and Unit 2, and the time and cost needed to execute CR, TR, DR, and OR. Initialize the ant amount , the information heuristic factor , the expectation heuristic factor , the objective function , and the iteration times . Initialize the solution set ;
- Step 2. Put the ant starting point in the current solution set. For each ant, the probability is transferred to the next point , which places the vertex in the current solution set;
- Step 3. Calculate the target value function for each ant;
- Step 4. Modify the trajectory strength by updating the process ;
- Step 5. Reduce the number of iterations by one, i.e., . If , and there is no degradation behavior, return to step 2. Otherwise, output the optimal parameters .
5. Numerical Experiment
5.1. Optimization Results
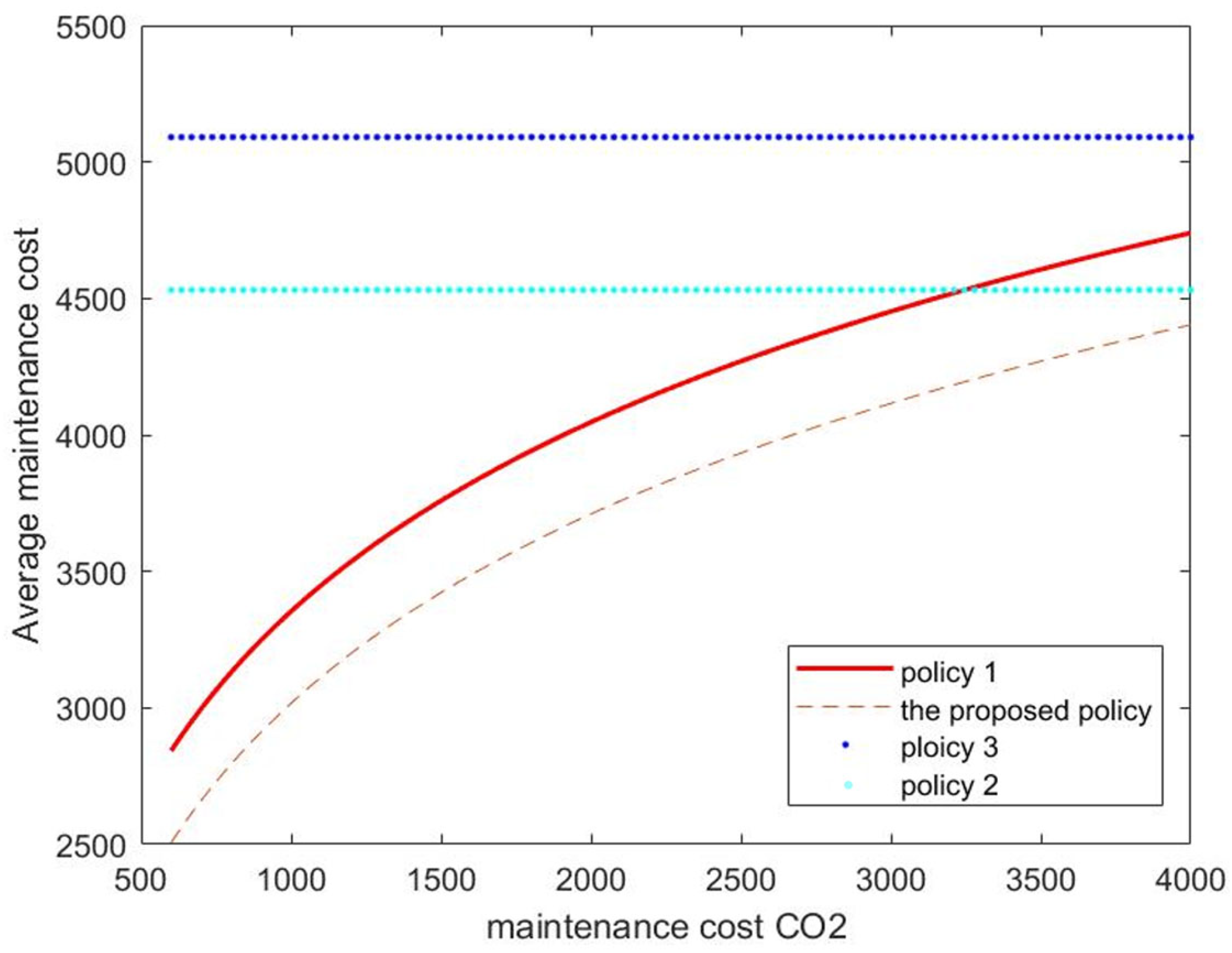
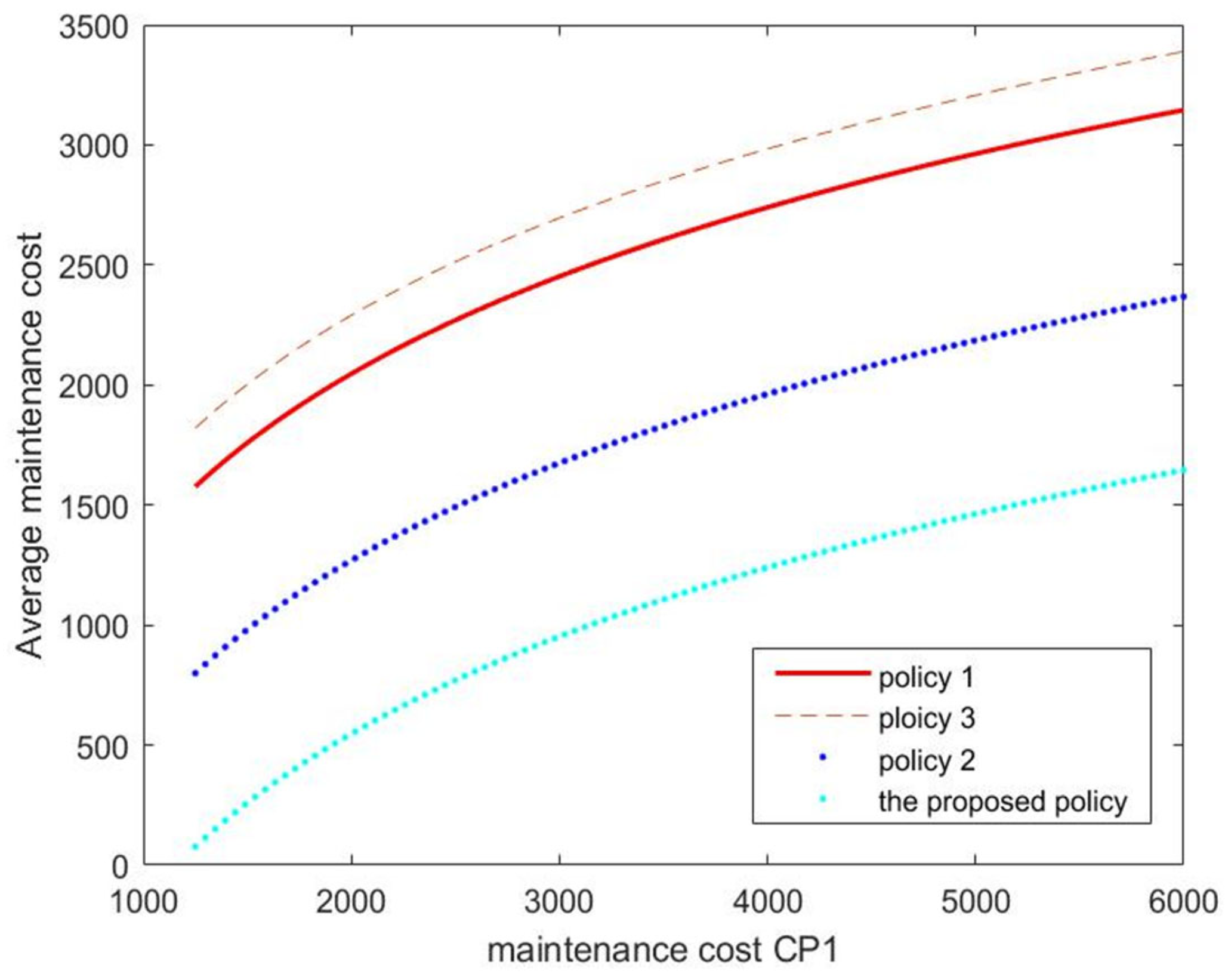
5.2. Policy Comparison
- ■
- Policy 1. TR and CR are executed for Unit 1, but OR is ignored. Unit 2 undergoes TR, DR, CR, and OR, which is aligned with the proposed policy;
- ■
- Policy 2. DR and CR are executed for Unit 2, but OR is ignored; Unit 1 remains the same as the proposed policy;
- ■
- Policy 3. Both units undergo TR, DR, and CR, and OR is omitted. Then, the policy reduces to a conventional preventive maintenance policy without considering unit dependencies.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations and Abbreviations
| CBM | Condition-based maintenance |
| CDF | Cumulative distribution function |
| Probability distribution function | |
| SMDP | Semi-Markov Decision Process |
| PM | Preventive maintenance |
| OM | Opportunistic maintenance |
| TR | Threshold-based replacement |
| DR | Delayed replacement |
| CR | Corrective replacement |
| OR | Opportunistic replacement |
| Periodic inspection interval | |
| Execution time of the k-th inspection | |
| Degradation process characterized by Wiener process | |
| Random defect initialization time of Unit 2 | |
| Random delay time of Unit 2 | |
| Failure threshold regarding degradation of Unit 1 | |
| TR threshold regarding degradation of Unit 1 | |
| OR threshold regarding degradation of Unit 1 | |
| Threshold for DR interval of Unit 2 | |
| Threshold for OR interval of Unit 2 | |
| Cost per inspection | |
| Cost per corrective replacement for Unit | |
| Cost per TR for Unit 1 and DR for Unit 2 | |
| Cost per opportunistic replacement for Unit |
References
- Yang, L.; Chen, Y.; Qiu, Q.; Wang, J. Risk Control of Mission-Critical Systems: Abort Decision-Makings Integrating Health and Age Conditions. IEEE Trans. Ind. Inform. 2022, 18, 6887–6894. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Fu, Y. Joint Optimization of Condition-Based Maintenance and Performance Control for Linear Multi-State Consecutively Connected Systems. Mathematics 2023, 11, 2724. [Google Scholar] [CrossRef]
- Qiu, Q.; Maillart, L.M.; Prokopyev, O.A.; Cui, L. Optimal condition-based mission abort decisions. IEEE Trans. Reliab. 2023, 72, 408–425. [Google Scholar] [CrossRef]
- Wu, D.; Han, R.; Ma, Y.; Yang, L.; Wei, F.; Peng, R. A two-dimensional maintenance optimization framework balancing hazard risk and energy consumption rates. Comput. Ind. Eng. 2022, 169, 108193. [Google Scholar] [CrossRef]
- Peng, R. Optimal maintenance strategy for systems with two failure modes. Reliab. Eng. Syst. Saf. 2019, 188, 624–632. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Viliam, M.; Xian, Z. Optimal condition-based and age-based opportunistic maintenance policy for a two-Unit series system. Comput. Ind. Eng. 2019, 134, 1–10. [Google Scholar] [CrossRef]
- Van, P.D.; Bérenguer, C. Condition-based maintenance with imperfect preventive repairs for a deteriorating production system. Qual. Reliab. Eng. Int. 2012, 28, 624–633. [Google Scholar] [CrossRef]
- Truong-Ba, H.; Borghesani, P.; Cholette, M.E.; Ma, L. Optimization of condition-based maintenance considering partial opportunities. Qual. Reliab. Eng. Int. 2020, 36, 529–546. [Google Scholar] [CrossRef]
- Sugumaran, V.; Ramachandran, K. Automatic rule learning using decision tree for fuzzy classifier in fault diagnosis of roller hearing. Mech. Syst. Signal Process. 2007, 21, 2237–2247. [Google Scholar] [CrossRef]
- Lei, B.; Ren, Y.; Luan, H.; Dong, R.; Wang, X.; Liao, J.; Gao, K. A Review of Optimization for System Reliability of Microgrid. Mathematics 2023, 11, 822. [Google Scholar] [CrossRef]
- Berrade, M.; Scarf, P.; Cavalcante, C. A study of postponed replacement in a delay time model. Reliab. Eng. Syst. Saf. 2017, 168, 70–79. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Sun, J.; Qiu, Q.; Chen, K. Optimal inspection and mission abort policies for systems subject to degradation. Eur. J. Oper. Res. 2021, 292, 610–621. [Google Scholar] [CrossRef]
- Kou, G.; Liu, Y.; Xiao, H.; Peng, R. Optimal Inspection Policy for a Three-Stage System Considering the Production Wait Time. IEEE Trans. Reliab. 2022. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L. Gamma process based optimal mission abort policy. Reliab. Eng. Syst. Saf. 2019, 190, 106496. [Google Scholar] [CrossRef]
- Jafari, L.; Makis, V. Optimal production and maintenance policy for a partially observable production system with stochastic demand. Int. J. Ind. Syst. Eng. 2019, 13, 449–456. [Google Scholar]
- Wang, J.; Qiu, Q.; Wang, H. Joint optimization of condition-based and age-based replacement policy and inventory policy for a two-Unit series system. Reliab. Eng. Syst. Saf. 2021, 205, 107251. [Google Scholar] [CrossRef]
- Castanier, B.; Grall, A.; Berenguer, C. A condition-based maintenance policy with non-periodic inspections for a two-Unit series system. Reliab. Eng. Syst. Saf. 2005, 87, 109–120. [Google Scholar] [CrossRef]
- Yi, K.; Xiao, H.; Kou, G.; Peng, R. Trade-off between maintenance and protection for multi-state performance sharing systems with transmission loss. Comput. Ind. Eng. 2019, 136, 305–315. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Yan, L. Degradation Models with Wiener Diffusion Processes Under Calibrations. IEEE Trans. Reliab. 2016, 65, 613–623. [Google Scholar] [CrossRef]
- Xie, M.; Cho, G.; Kong, Y.; Li, D.L.; Altamirano, F.; Luo, X.; Hill, J.A. Activation of Autophagic Flux Blunts Cardiac Ischemia/Reperfusion Injury. Circ. Res. 2021, 129, 435–450. [Google Scholar] [CrossRef]
- Wu, T.; Wei, F.; Yang, L.; Ma, X.; Hu, L. Maintenance optimization of k-out-of-n Load-Sharing Systems Under Continuous Operation. IEEE Trans. Syst. Man Cybern. Syst. 2023. [Google Scholar] [CrossRef]
- Huynh, K.; Castro, I.; Barros, A.; Bérenguer, C. On the Use of Mean Residual Life as a Condition Index for Condition-Based Maintenance Decision-Making. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 877–893. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L. Reliability modelling based on dependent two-stage virtual age processes. J. Syst. Eng. Electron. 2021, 32, 711–721. [Google Scholar]
- Yang, L.; Chen, Y.; Ma, X.; Peng, R. A Prognosis-centered Intelligent Maintenance Optimization Framework under Uncertain Failure Threshold. IEEE Trans. Reliab. 2023. [Google Scholar]
- Jardine, A.K. Optimizing condition-based maintenance decisions. In Proceedings of the Annual Reliability and Maintainability Symposium: 2002 Proceedings (Cat. No. 02CH37318), Seattle, WA, USA, 28–31 January 2002; pp. 90–97. [Google Scholar]
- Li, S.; Chu, X. New tristate fault classification model and its threshold determination. J. Nanjing Univ. Aeronaut. Astronaut. 2008, 40, 292–296. [Google Scholar]
- Gopalan, M.; Ramesh, T. Cost-benefit analysis of a one-server two-Unit system subject to shock and degradation. Microelectron. Reliab. 1986, 26, 499–518. [Google Scholar] [CrossRef]
- Malefaki, S.; Koutras, V.; Platis, A. Optimizing Availability and Performance of a Two-Unit Redundant Multi-State Deteriorating System. In Recent Advances in Multi-State Systems Reliability: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 71–105. [Google Scholar]
- Ahmad, R.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Xiang, Y. Optimal replacement and reactivation in warm standby systems performing random duration missions. Comput. Ind. Eng. 2020, 149, 106791. [Google Scholar] [CrossRef]
- Barbu, V.S.; D’Amico, G.; Gkelsinis, T. Sequential interval reliability for discrete-time homogeneous semi-Markov repairable systems. Mathematics 2021, 9, 1997. [Google Scholar] [CrossRef]
- Dekker, R.; Wildeman, R.; Schouten, F. A review of multi-component maintenance models with economic dependence. Econom. Inst. Res. Pap. 1997, 45, 411–435. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, G.; Manca, R.; Petroni, F.; Selvamuthu, D. On the computation of some interval reliability indicators for semi-Markov systems. Mathematics 2021, 9, 575. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Peng, R.; Guo, L. A delay-time-based inspection model for a two-component parallel system. In Proceedings of the 2013 Quality Reliability Risk Maintenance and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 616–619. [Google Scholar]
- Zhang, Z.; Yang, L. State-Based Opportunistic Maintenance with Multifunctional Maintenance Windows. IEEE Trans. Reliab. 2021, 70, 1481–1494. [Google Scholar] [CrossRef]
- Najafi, S.; Makis, V. Comparison of two maintenance policies for a two-unit series system considering general repair. Int. J. Ind. Manuf. Eng. 2020, 14, 618–623. [Google Scholar]
- Chen, Y.; Ma, X.; Wei, F.; Yang, L.; Qiu, Q. Dynamic scheduling of intelligent group maintenance planning under usage availability constraint. Mathematics 2022, 10, 2730. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L. Reliability evaluation based on a dependent two-stage failure process with competing failures. Appl. Math. Model. 2018, 64, 699–712. [Google Scholar] [CrossRef]
- Yang, L.; Wei, F.; Qiu, Q. Mission Risk Control via Joint Optimization of Sampling and Abort Decisions. Risk Anal. 2023. [Google Scholar] [CrossRef]
- Rafiee, K.; Feng, Q.; Coit, D.W. Reliability analysis and condition-based maintenance for failure processes with degradation-dependent hard failure threshold. Qual. Reliab. Eng. Int. 2017, 33, 1351–1366. [Google Scholar] [CrossRef]
- Xiao, H.; Yi, K.; Peng, R.; Kou, G. Reliability of a distributed computing system with performance sharing. IEEE Trans. Reliab. 2021, 71, 1555–1566. [Google Scholar] [CrossRef]
- Whitmore, G. Estimating degradation by a Wiener diffusion process subject to measurement error. Lifetime Data Anal. 1995, 1, 307–319. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Peng, R.; He, X.; Zhong, C.; Kou, G.; Xiao, H. Preventive replacement policies with time of operations, mission durations, minimal repairs and maintenance triggering approaches. J. Manuf. Syst. 2020, 220, 108310. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Xiang, Y. Optimal multiple replacement and maintenance scheduling in two-Unit systems. Reliab. Eng. Syst. Saf. 2021, 22, 107803. [Google Scholar] [CrossRef]
- Peng, R.; He, X.; Zhong, C.; Kou, G.; Xiao, H. Preventive maintenance for heterogeneous parallel systems with two failure modes. Reliab. Eng. Syst. Saf. 2022, 220, 108310. [Google Scholar] [CrossRef]
- Basri, E.I.; Razak, I.H.A.; Ab-Samat, H.; Kamaruddin, S. Preventive maintenance (PM) planning: A review. J. Qual. Maint. Eng. 2017, 23, 114–143. [Google Scholar] [CrossRef]


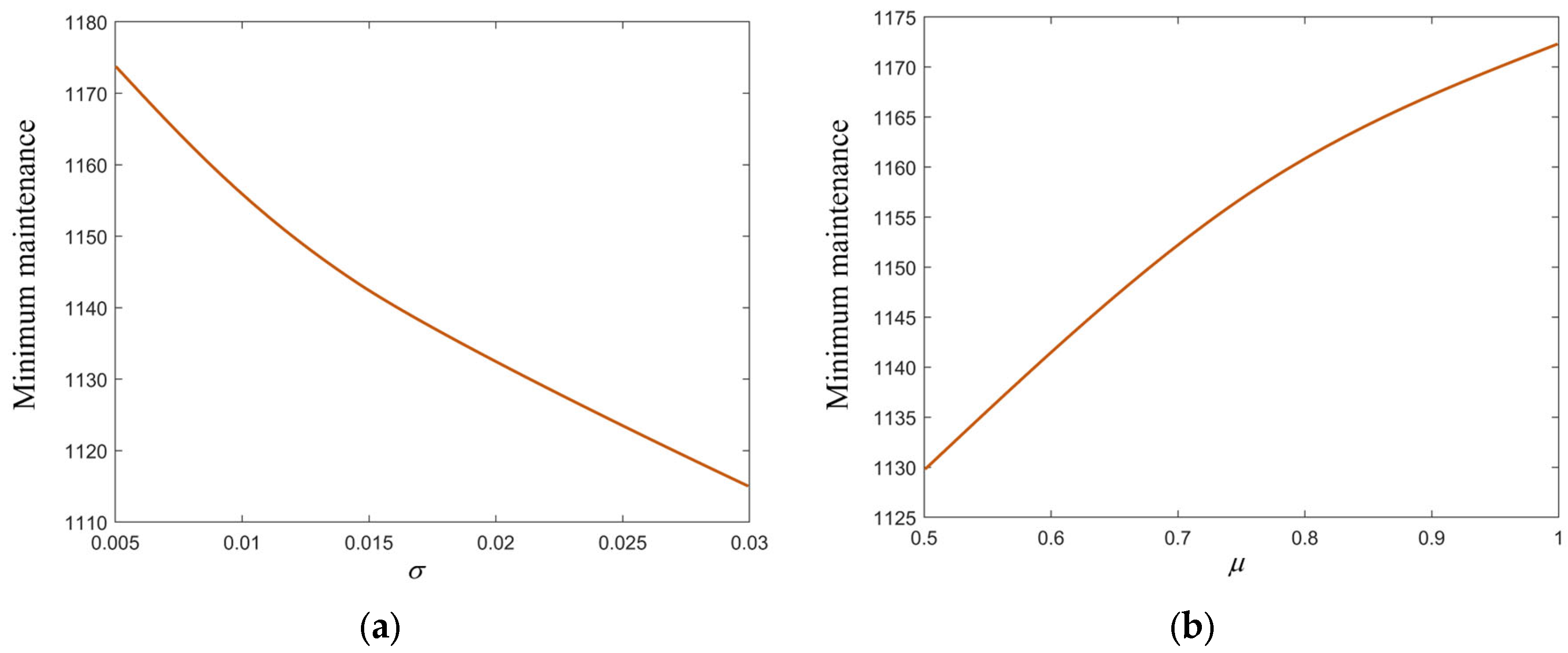
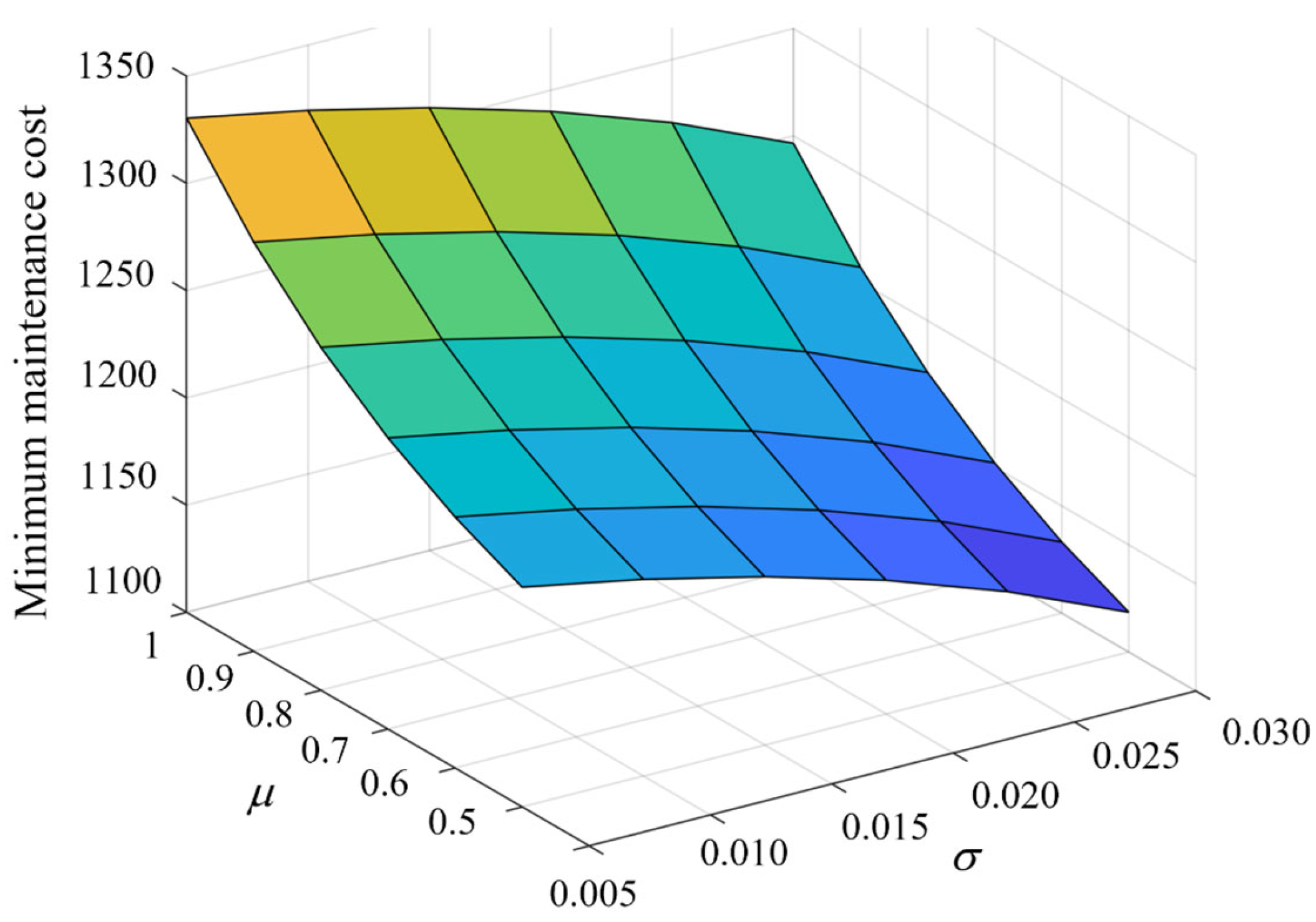
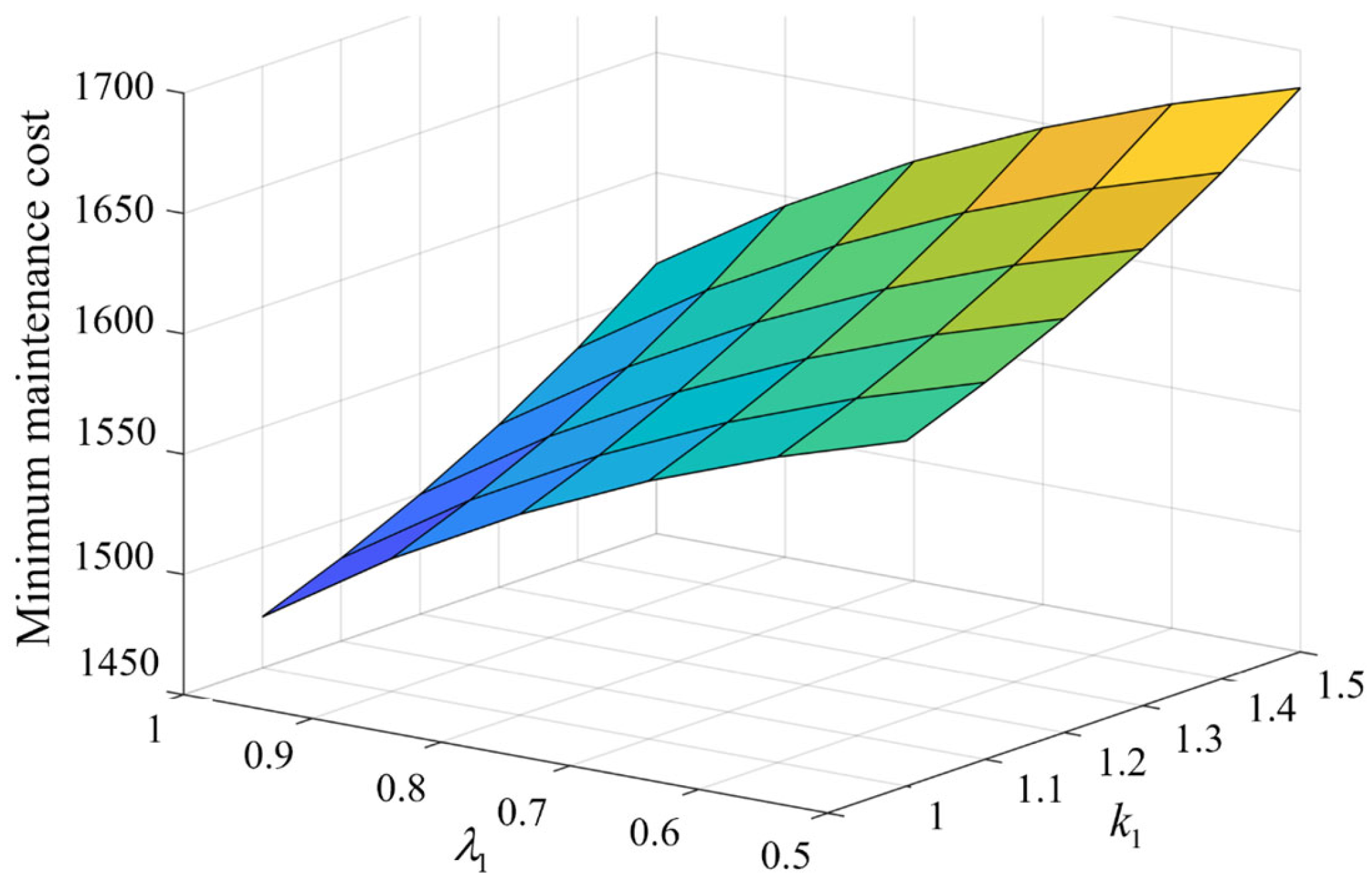
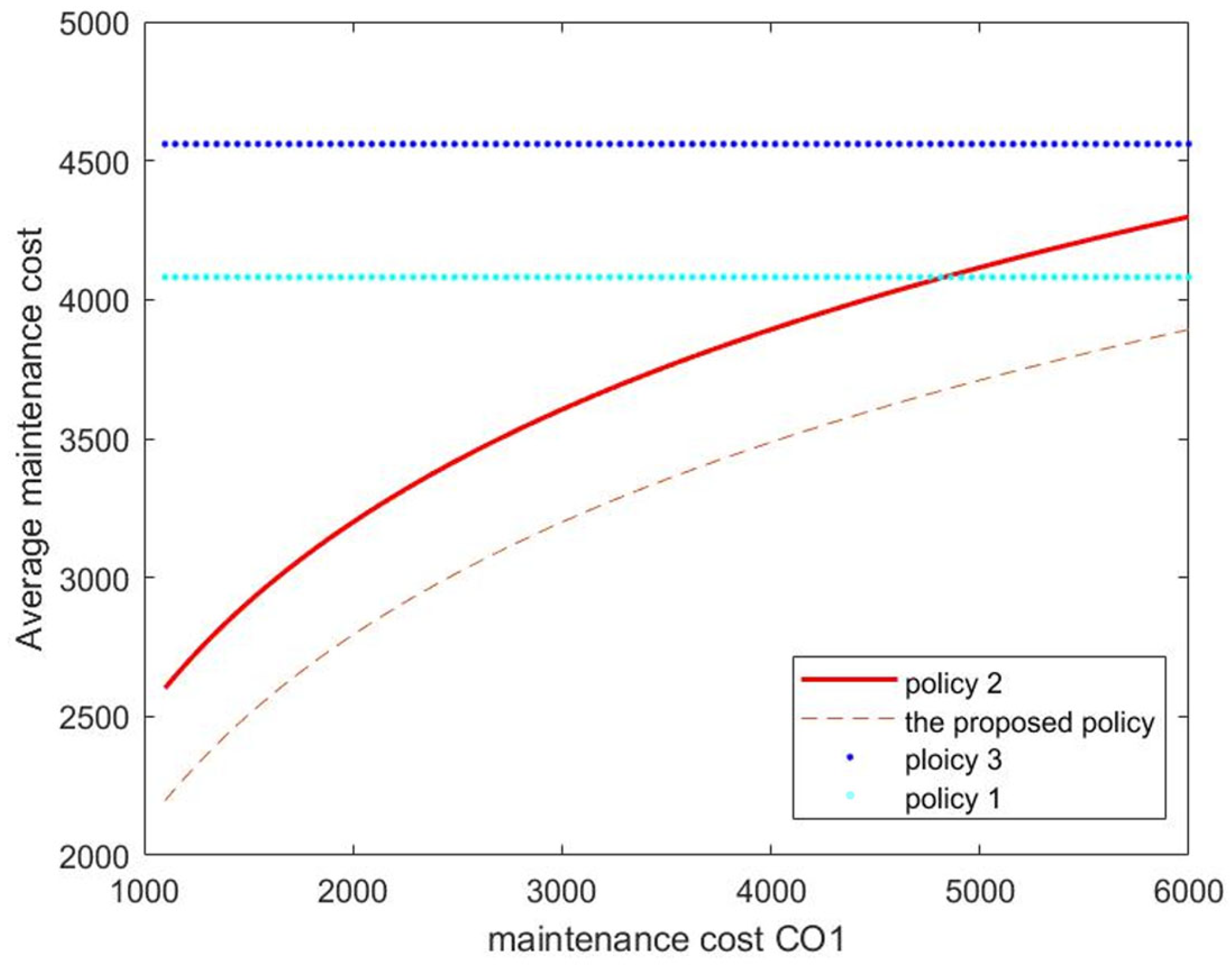
| Policies | H (Week) | V (Week) | S (mm) | L (mm) | Average Cost |
|---|---|---|---|---|---|
| Proposed policy | 12 | 9 | 17.1 | 19.6 | 2941.5 |
| Policy 1 | 12 | 9 | 16.5 | 18.4 | 3321.7 |
| Policy 2 | 10 | 8 | 15.5 | 17.6 | 3154.9 |
| Policy 3 | 9 | 7 | 15.2 | 16.8 | 3467.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, F.; Wang, J.; Ma, X.; Yang, L.; Qiu, Q. An Optimal Opportunistic Maintenance Planning Integrating Discrete- and Continuous-State Information. Mathematics 2023, 11, 3322. https://doi.org/10.3390/math11153322
Wei F, Wang J, Ma X, Yang L, Qiu Q. An Optimal Opportunistic Maintenance Planning Integrating Discrete- and Continuous-State Information. Mathematics. 2023; 11(15):3322. https://doi.org/10.3390/math11153322
Chicago/Turabian StyleWei, Fanping, Jingjing Wang, Xiaobing Ma, Li Yang, and Qingan Qiu. 2023. "An Optimal Opportunistic Maintenance Planning Integrating Discrete- and Continuous-State Information" Mathematics 11, no. 15: 3322. https://doi.org/10.3390/math11153322
APA StyleWei, F., Wang, J., Ma, X., Yang, L., & Qiu, Q. (2023). An Optimal Opportunistic Maintenance Planning Integrating Discrete- and Continuous-State Information. Mathematics, 11(15), 3322. https://doi.org/10.3390/math11153322








