Decision-Making Model of Performance Evaluation Matrix Based on Upper Confidence Limits

Abstract

A performance evaluation matrix (PEM) is an evaluation tool for assessing customer satisfaction and the importance of service items across various services. In addition, inferences based on point estimates of sample data can increase the risk of misjudgment due to sampling errors. Thus, this paper creates a decision-making model for a performance evaluation matrix based on upper confidence limits to provide various service operating systems for performance evaluation and decision making. The concept is that through the gap between customer satisfaction and the level of importance of each service item, we are able to identify critical-to-quality (CTQ) service items requiring improvement. Many studies have indicated that customer satisfaction and the importance of service items follow a beta distribution, and based on the two parameters of this distribution, the proposed indices for customer satisfaction and the importance of service items represent standardization. The vertical axis of a PEM represents the importance index; the horizontal axis represents the satisfaction index. Since these two indices have unknown parameters, this paper uses the upper confidence limit of the satisfaction index to find out the CTQ service items and the upper confidence limit of the importance index to determine the order of improvement priority for each service item. This paper then establishes a decision-making model for a PEM based on the above-mentioned decision-making rules. Since all decision-making rules proposed in this paper are established through upper confidence limits, the risk of misjudgment caused by sampling errors can be reduced. Finally, this article uses a practical example to illustrate how to use a PEM to find CTQ service items and determine the order of improvement priority for these service items that need to be improved.

1. Introduction

Many studies have indicated that the performance evaluation matrix (PEM) is an evaluation tool for customer satisfaction and the importance of service items within various service operation systems [1,2,3]. Some studies have pointed out that evaluations using sample point estimation can increase the risk of misjudgment due to sampling errors [4,5]. Therefore, this paper will create a decision-making model for a performance evaluation matrix based on upper confidence limits to provide various service operating systems for performance evaluation and decision making for improvement. The concept is that through the gap between customer satisfaction and the level of importance of each service item, we can identify critical-to-quality (CTQ) service items requiring improvement. Meanwhile, many studies have worked on the research of the PEM to evaluate various service systems to see whether the performance meets the requirements and make further decisions about a service item: whether improvements are needed, whether the status quo should be maintained, or whether resource transfer is recommended [6,7,8,9,10]. Similar to many other studies and to maintain generality, this paper assumes that there are q service items provided by a service system. Then, 2q questions are designed to conduct a survey of learners about satisfaction and importance [11]. As noted by Chen et al. [12], Lambert and Sharma [13] used the Likert scale to collect data on customer satisfaction and the importance of service items with q service items. The horizontal axis of a PEM represents customer satisfaction; the vertical axis represents the importance of service items. The PEM then is divided into three areas: improvement, maintenance, and resource transfer. Hung, Huang, and Chen [1] revised the placement of the three performance areas in the above-mentioned PEM, making the evaluation rule more reasonable. Since the value of the beta distribution falls between one and zero, based on the beta distribution, Hung et al. [1] asserted that customer satisfaction and the importance of service items should follow a beta distribution, and based on the two parameters of this distribution, they proposed indices of importance and satisfaction, which represent standardization. These two index values are both between zero and one. The index value of satisfaction ranges from zero, representing zero percent satisfaction, to one, representing one hundred percent satisfaction. Likewise, the index value of importance ranges from zero, representing zero percent importance, to one, representing one hundred percent importance.

According to Liu et al. [2], the random variable $X_h$ represents the hth service item of satisfaction and then $X_h$ is distributed as a beta distribution, denoted by $X_h~Beta\left({\alpha }_h,{\beta }_h\right)$. Similarly, let $Y_h$ indicate the hth service item of importance and then $Y_h$ is distributed as a beta distribution, denoted by $Y_h~Beta\left({\delta }_h,{\gamma }_h\right)$. Thus, these two indices can be expressed as follows:

$${\theta }_h=\frac{{\alpha }_h}{{\alpha }_h+{\beta }_h} (\mathrm{satisfaction}\mathrm{index})$$

(1)

$${\tau }_h=\frac{{\delta }_h}{{\delta }_h+{\gamma }_h} (\mathrm{importance}\mathrm{index})$$

(2)

Based on the above information, the values of these two indices are both between zero and one. Additionally:

• When ${\alpha }_h>{\beta }_h$, then ${\theta }_h>0.5$ and $p\left(X_h>50\%\right)>0.5$, which indicates that the distribution of highly satisfied customers, $p\left(X_h>50\%\right)$, is of a high proportion.
• When ${\alpha }_h={\beta }_h$, then ${\theta }_h=0.5$ and $p\left(X_h\ge 50\%\right)=p\left(X_h\le 50\%\right)=0.5$, which indicates that the distributions of highly satisfied customers, $p\left(X_h>50\%\right)$, and customers with low satisfaction, $\left(X_h<50\%\right)$, are of equal proportions.
• When ${\alpha }_h<{\beta }_h$, then ${\theta }_h<0.5$ and $p\left(X_h<50\%\right)>0.5$, which indicates that the distribution of customers with low satisfaction, $\left(X_h<50\%\right)$, is of a high proportion.

We can see that when the proportion of highly satisfied customers is higher, the value of parameter $a_l$ is higher than that of parameter $b_l$, and the value of the satisfaction index is higher as well. Likewise, when the proportion of customers with low satisfaction is higher, the value of parameter $a_l$ is lower than that of parameter $b_l$, and the value of the satisfaction index is lower. And, when the value of parameter $a_l$ is equal to that of parameter $b_l$, the value of the satisfaction index is exactly one-half. Additionally, the importance index has the same characteristic as the satisfaction index. We can see that these two indices can reasonably reflect the distributions of customer satisfaction and the importance of service items.

There are some papers that set the satisfaction index as the x-axis and the importance index as the y-axis to form the performance evaluation matrix; at the same time, based on the concepts of total quality management and a continuous improvement process, they use the mean value ${\theta }_0$ as the standard of evaluation [14,15]. Then, based on the critical value derived from the statistical test, they form the evaluation area and the evaluation rule of the PEM. The critical value is affected by sample size n and by the value of the variance of the index estimator, causing the critical values of the q service items to be different. As a result, the minimum value is chosen to represent these q-critical values. Although this method has overcome the problem of inconsistency in evaluation criteria, another problem has arisen, i.e., inconsistency in the level of significance. To tackle this issue, this paper instead uses the upper confidence limit of the satisfaction index of the q service items to test whether the value of the satisfaction index of the service items is larger than the mean value ${\theta }_0$, and then to decide whether to improve the satisfaction level of the service items. Next, we use the upper confidence limit of the importance index of q service items to test whether the value of the importance index of the service items is larger than the mean value ${\tau }_0$, and to determine the order of improvement priority. This method is based on the statistical test and hence can lower the risk of misjudgment, which can be caused by sampling errors.

The remainder of this paper is organized as follows. In Section 2, this paper will derive the 100$\left(1-\alpha \right)$% upper confidence limit of the two indices based on sample data. In Section 3, this paper allows the horizontal axis to represent the mean value of the satisfaction index ${\theta }_0$, and the vertical axis to represent the mean value of the importance index ${\tau }_0$; these two axes divide the PEM into four evaluation quadrants. Then, we use the upper confidence limits of the two indices to mark the evaluation coordinates of each service item $\left(x_h,y_h\right)$, and based on where the coordinates $\left(x_h,y_h\right)$ are located in the PEM, we can evaluate whether a service item needs improvement. When resources are limited, we can set the order of improvement priority. In Section 4, we use a case study to illustrate an application of the model proposed in this paper, showing how to establish the evaluation coordinates and identify service items requiring improvement, and when resources are limited, how to set the order of improvement priority. Section 5 presents the conclusions.

2. The 100(1 − α)% Upper Confidence Limits

As stated, as the satisfaction index and importance index possess unknown parameters, they need to be estimated from the sample data of respondents. Let $\left(X_{h,1},X_{h,2},\dots ,X_{h,n}\right)$ be a random sample of customer satisfaction with a sample size of n, where h $=$ 1, 2, …, q. Then, the unbiased estimator of the satisfaction index ${\theta }_h$ is written as follows:

$${\widehat{\theta }}_h=\frac{1}{n}\times {\displaystyle \sum _{j=1}^n{X}_{lj}}.$$

(3)

This is the expected value of ${\widehat{\theta }}_h$, which is equal to ${\theta }_h$, which is expressed as follows:

$$\begin{array}{cc}E\left[{\widehat{\theta }}_h\right]& =\frac{1}{n}{\displaystyle \sum _{j=1}^{n}E\left[X_{h,j}\right]}\hfill \\ & ={\displaystyle \underset{0}{\overset{1}{\int }}x\times Beta\left({\alpha }_h,{\beta }_h\right)d_x}\left(\frac{1}{n}\times {\displaystyle \sum _{j=1}^{n}1}\right)\hfill \\ & =\frac{\Gamma \left({\alpha }_h+{\beta }_h\right)\Gamma \left({\alpha }_h+1\right)}{\Gamma \left({\alpha }_h+{\beta }_h+1\right)\Gamma \left({\alpha }_h\right)}{\displaystyle \underset{0}{\overset{1}{\int }}Beta\left({\alpha }_h+1,{\beta }_h\right)d_x}\hfill \\ & ={\theta }_h.\hfill \end{array}$$

(4)

In addition, the sample standard deviation is written as follows:

$$S_{Xh}=\sqrt{\frac{1}{n-1}\times {\displaystyle \sum _{j=1}^n{\left(X_{h,j}-{\overline{X}}_h\right)}^2}}$$

(5)

Let the random variable $Z_l$ be written as follows:

$$Z_h=\frac{{\widehat{\theta }}_h-{\theta }_h}{S_{Xh}/\sqrt{n}}$$

(6)

Based on the Central Limit Theorem (CLT), the random variable $Z_h$ is approximately distributed as a standard normal distribution for a large sample size n [16], that is,

$$Z_h\underset{}{\overset{n\to \infty }{\to }}N\left(0,1\right)$$

(7)

Based on the above information, this paper derives the 100$\left(1-\alpha \right)$% upper confidence limit of the satisfaction index ${\theta }_h$, as follows:

$$\begin{array}{cc}1-\alpha & =p\left(Z_h\ge -z_{\alpha }\right)\hfill \\ & =p\left(\frac{{\widehat{\theta }}_h-{\theta }_h}{S_{Xh}/\sqrt{n}}\ge -z_{\alpha }\right)\hfill \\ & =p\left({\theta }_h\le {\widehat{\theta }}_h+z_{\alpha }\frac{S_{Xh}}{\sqrt{n}}\right)\hfill \end{array}$$

(8)

Therefore, the 100$\left(1-\alpha \right)$% upper confidence limit of the satisfaction index is

$$U{\theta }_h={\widehat{\theta }}_h+z_{\alpha }\frac{S_{Xh}}{\sqrt{n}}$$

(9)

where $z_{\alpha }$ is the upper $\alpha$ quantile of the standard normal distribution.

Similarly, let $\left(Y_{ h,1},Y_{ h,2},\dots ,Y_{ h,n}\right)$ be a random sample of customer importance with a sample size of n, where h $=$ 1, 2, …, q. Then, the unbiased estimator of the importance index ${\tau }_h$ is written as follows:

$${\widehat{\tau }}_h=\frac{1}{n}\times {\displaystyle \sum _{j=1}^n{Y}_{h,j}}$$

(10)

This is the expected value of ${\widehat{\tau }}_h$, which is equal to ${\tau }_h$ $\left(E\left[{\widehat{\tau }}_h\right]={\tau }_h\right)$. In addition, the sample standard deviation is written as follows:

$$S_{Yh}=\sqrt{\frac{1}{n-1}\times {\displaystyle \sum _{j=1}^n{\left(Y_{h,j}-{\overline{Y}}_h\right)}^2}}$$

(11)

Let the random variable $T_h$ be expressed as follows:

$$T_h=\frac{{\widehat{\tau }}_h-{\tau }_h}{S_{Yh}/\sqrt{n}}$$

(12)

Based on the Central Limit Theorem (CLT), the random variable $T_h$ is approximately distributed as the standard normal distribution for a large sample size n [16], that is,

$$T_h\underset{}{\overset{n\to \infty }{\to }}N\left(0,1\right)$$

(13)

Based on the above information, this paper derives the 100$\left(1-\alpha \right)$% upper confidence limit of the importance index ${\tau }_h$, as follows:

$$\begin{array}{cc}1-\alpha & =p\left(T_h\ge -z_{\alpha }\right)\hfill \\ & =p\left(\frac{{\widehat{\tau }}_h-{\tau }_h}{S_{Yh}/\sqrt{n}}\ge -z_{\alpha }\right)\hfill \\ & =p\left({\tau }_h\le {\widehat{\tau }}_h+z_{\alpha }\frac{S_{Yh}}{\sqrt{n}}\right)\hfill \end{array}$$

(14)

Therefore, the 100$\left(1-\alpha \right)$% upper confidence limit of the importance index ${\tau }_h$ is

$$U{\tau }_h={\widehat{\tau }}_h+z_{\alpha }\frac{S_{Yh}}{\sqrt{n}},$$

(15)

where $z_{\alpha }$ is the upper $\alpha$ quantile of the standard normal distribution.

3. The Decision-Making Model

As noted in some studies, the PEM is widely used to evaluate the performance level of q service items across various service systems [17,18]. Similar to these papers, the satisfaction index ${\theta }_h$ is set as the x-axis and the importance index ${\tau }_h$ is set as the y-axis to form the PEM. Let

$${\theta }_0=\frac{1}{q}{\displaystyle \sum _{h=1}^q{\widehat{\theta }}_h}$$

(16)

and

$${\tau }_0=\frac{1}{q}{\displaystyle \sum _{l=1}^q{\widehat{\tau }}_h}$$

(17)

Then, the hypothesis of the statistical test for the satisfaction index h is written as follows:

$$\mathrm{null} \mathrm{hypothesis} H_0: {\theta }_h\ge {\theta }_0$$

(18)

$$\mathrm{alternative} \mathrm{hypothesis} H_1: {\theta }_h<{\theta }_0$$

(19)

Similarly, the hypothesis of the statistical test for importance index h is written as follows:

$$\mathrm{null} \mathrm{hypothesis} H_0: {\tau }_h\ge {\tau }_0$$

(20)

$$\mathrm{alternative} \mathrm{hypothesis} H_1: {\tau }_h<{\tau }_0$$

(21)

Then, this paper uses the horizontal line $y={\tau }_0$ and the vertical line $x={\theta }_0$ to divide the performance evaluation matrix into four performance quadrants, as follows:

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{I}: Q_{\mathrm{I}}=\left\{\left(x,y\right)|{\theta }_0\le x\le 1, {\tau }_0\le y\le 1\right\}$$

(22)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{II}: Q_{\mathrm{II}}=\left\{\left(x,y\right)|0\le x\le {\theta }_0, {\tau }_0\le y\le 1\right\}$$

(23)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{III}: Q_{\mathrm{III}}=\left\{\left(x,y\right)|0\le x\le {\theta }_0, 0\le y\le {\tau }_0\right\}$$

(24)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{IV}: Q_{\mathrm{IV}}=\left\{\left(x,y\right)|{\theta }_0\le x\le 1, 0\le y\le {\tau }_0\right\}$$

(25)

According to Equations (22)–(25), the performance evaluation matrix and four performance quadrants can be depicted, as shown in Figure 1, the red dots representing items that need improvement, and the blue dots representing items that do not need improvement.

Next, this paper uses the upper confidence limits of these two indices to serve as the evaluation coordinates of each service item $\left(x_h,y_h\right)$, as follows:

$$\left(x_h,y_h\right)=\left(U{\theta }_h,U{\tau }_h\right)=\left({\widehat{\theta }}_h+z_{\alpha }\frac{S_{Xh}}{\sqrt{n}},{\widehat{\tau }}_h+z_{\alpha }\frac{S_{Yh}}{\sqrt{n}}\right)$$

(26)

For the satisfaction index ${\theta }_h$, based on the statistical test rules, the rules for whether improvements should be made are as follows:

• When the 100$\left(1-\alpha \right)$% upper confidence limit of the satisfaction index ${\theta }_h$ is greater than or equal to ${\theta }_0$, that is, $x_h=U{\theta }_h\ge {\theta }_0$, we can conclude that ${\theta }_h\ge {\theta }_0$, indicating that the value of the satisfaction level of the service item h is higher than the mean value, and thus no improvement is needed.
• When the 100$\left(1-\alpha \right)$% upper confidence limit of the satisfaction index ${\theta }_h$ is smaller than ${\theta }_0$, that is, $x_h=U{\theta }_h<{\theta }_0$, we can conclude that ${\theta }_h<{\theta }_0$, indicating that the value of the satisfaction level of the service item h is lower than the mean value, and thus improvements are needed.

For the importance index ${\tau }_h$, based on the statistical test rules, the rules for determining the order of improvement priority are written as follows:

• When the 100$\left(1-\alpha \right)$% upper confidence limit of the importance index ${\tau }_h$ is greater than or equal to ${\tau }_0$, that is, $y_h=U{\tau }_h\ge {\tau }_0$, we can conclude that ${\tau }_h\ge {\tau }_0$, indicating that the value of the importance level of the service item h is higher than the mean value, and improvements of this service item should be prioritized when resources are limited.
• When the 100$\left(1-\alpha \right)$% upper confidence limit of the importance index ${\tau }_h$ is smaller than ${\tau }_0$, that is $y_h=U{\tau }_h<{\tau }_0$ we can conclude that ${\tau }_h<{\tau }_0$, indicating that the value of the importance level of the service item h is higher than the mean value, and improvements of this service item can be made later when resources are limited.

Based on the above concept, the evaluation rules determining which service items should be improved and the order of improvement priority are established as follows:

• If the evaluation coordinates of the hth service item $\left(x_h,y_h\right)\in Q_{\mathrm{I}}$, we can conclude that ${\theta }_h\ge {\theta }_0$. Thus, service item h does not need improvements.
• If the evaluation coordinates of the hth service item $\left(x_h,y_h\right)\in Q_{\mathrm{II}}$, we can conclude that ${\theta }_h<{\theta }_0$ and ${\tau }_h\ge {\tau }_0$. Thus, service item h needs to be improved and with high priority.
• If the evaluation coordinates of the hth service item $\left(x_h,y_h\right)\in Q_{\mathrm{III}}$, we can conclude that ${\theta }_h<{\theta }_0$ and ${\tau }_h<{\tau }_0$. Thus, service item h needs to be improved and with lower priority.
• If the evaluation coordinates of the hth service item $\left(x_h,y_h\right)\in Q_{\mathrm{IV}}$, we can conclude that ${\theta }_h\ge {\theta }_0$. Thus, service item h does not need improvements.

4. Case Study

As stated, the decision-making model of the performance evaluation matrix based on upper confidence limits, developed in this paper, can assist managers of various service systems in quickly identifying CTQ service items requiring improvements and in making improvements. For example, in the field of e-learning, many researchers have been working on research about using teaching apps and computer-assisted language learning systems to increase learning effectiveness [19,20,21,22]. The proposed method can also be applied to the performance evaluation and model analysis of a real teaching setting. In technological and vocational education, students in practical courses learn through hands-on experience to combine theory and practice. So, this paper uses the case of practical courses as an example to illustrate the application of the proposed model. The questionnaires for the level of teaching satisfaction designed by Chen and Yureference Yeh et al. [23] and Yu et al. [24]. The questionnaires comprise an adequate number of questions and are quite comprehensive. Based on the version of Chen and Yu, this paper has designed a questionnaire to survey the level of satisfaction with the practical course, which includes seventeen questions and five dimensions: (1) Teaching preparation, (2) Teaching attitude, (3) Teaching ability, (4) Teaching management, and (5) Assessment. For each question, respondents are asked to provide both their level of satisfaction and the level of importance, and there are, in fact, thirty-four (q = 17, 2q = 34) questions to be answered. The questionnaire is as follows:

Dimension 1: Teaching preparation

• The degree of difficulty of the practical material prepared by the teacher is moderate.
• The learning amount of the practical material is moderate.
• The practical material is helpful in enhancing students’ practical abilities.
• The teacher is well-prepared for the practical course.

Dimension 2: Teaching attitude

5.

The teacher pays attention to students’ hands-on experience.

6.

The teacher considers students’ opinions important.

7.

The teacher maintains a good relationship with each student.

8.

The teacher is willing to assist students with problems.

9.

The teacher treats every student fairly.

Dimension 3: Teaching ability

10.

The teacher speaks clearly.

11.

The teacher speaks coherently.

Dimension 4: Teaching management

12.

The teacher implements a diversity of teaching methods in the practical course.

13.

The practical course stimulates my interest in real teaching practice.

14.

The teaching pace of the practical course is moderate.

Dimension 5: Assessment

15.

The number of assignments and examinations is adequate.

16.

The degree of difficulty of assignments and examinations is adequate.

17.

The assignments or assessments can help enhance my practical abilities.

This paper used the above-shown questionnaire to collect data on the level of satisfaction and level of importance of students participating in practical courses. The respondents were students participating in a practical course at Taiwan’s University of Technology and Science. In total, 367 questionnaires were issued and 301 were recovered (with a recall rate of 82.02%). Next, we calculated the values of the sample statistics of each service item, as follows:

According to Equations (16) and (17), we obtain

$${\theta }_0=\frac{1}{17}{\displaystyle \sum _{h=1}^{17}{\widehat{\theta }}_h}=0.7864$$

(27)

and

$${\tau }_0=\frac{1}{17}{\displaystyle \sum _{l=1}^{17}{\widehat{\tau }}_h}=0.8337$$

(28)

Then, the four performance quadrants of the performance evaluation matrix are as follows:

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{I}: Q_{\mathrm{I}}=\left\{\left(x,y\right)|0.7864\le x\le 1, 0.8337\le y\le 1\right\}$$

(29)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{II}: Q_{\mathrm{II}}=\left\{\left(x,y\right)|0\le x\le 0.7864, 0.8337\le y\le 1\right\}$$

(30)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{III}: Q_{\mathrm{III}}=\left\{\left(x,y\right)|0\le x\le 0.7864, 0\le y\le 0.8337\right\}$$

(31)

$$\mathrm{Performance} \mathrm{Quadrant} \mathrm{IV}: Q_{\mathrm{IV}}=\left\{\left(x,y\right)|0.7864\le x\le 1, 0\le y\le 0.8337\right\}$$

(32)

Based on the data from

Table 1. Sample statistics of each service item.

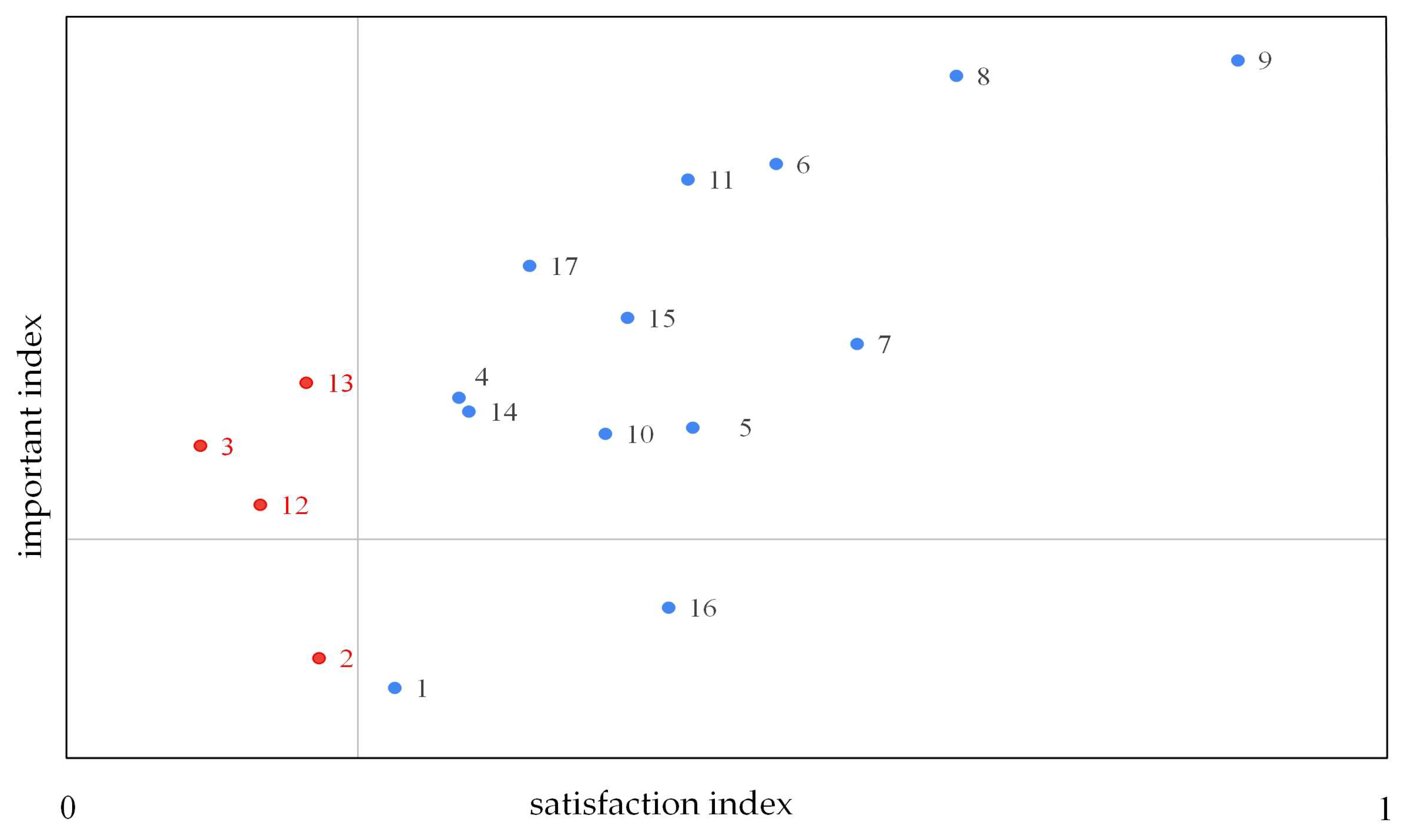
Dimensions	Item	${\widehat{\mathit{\theta }}}_{\mathit{h}}$	${\mathit{S}}_{\mathit{X}\mathit{h}}$	${\widehat{\mathit{\tau }}}_{\mathit{h}}$	${\mathit{S}}_{\mathit{Y}\mathit{h}}$	${\mathit{x}}_{\mathit{h}}=\mathit{U}{\mathit{\theta }}_{\mathit{h}}$	${\mathit{y}}_{\mathit{h}}=\mathit{U}{\mathit{\tau }}_{\mathit{h}}$	Quadrant
Dimension 1	1	0.7684	0.2255	0.7983	0.2043	0.7898	0.8176	I
	2	0.7617	0.2230	0.8023	0.1961	0.7829	0.8209	IV *
	3	0.7498	0.2352	0.8262	0.1856	0.7721	0.8438	II **
	4	0.7737	0.2310	0.8302	0.1984	0.7956	0.8490	I
Dimension 2	5	0.7963	0.2171	0.8275	0.1925	0.8169	0.8458	I
	6	0.8036	0.2199	0.8587	0.1630	0.8244	0.8742	I
	7	0.8116	0.2133	0.8375	0.1824	0.8318	0.8548	I
	8	0.8209	0.2107	0.8680	0.1650	0.8408	0.8837	I
	9	0.8474	0.2004	0.8700	0.1615	0.8664	0.8853	I
Dimension 3	10	0.7870	0.2313	0.8262	0.1995	0.8089	0.8451	I
	11	0.7956	0.2193	0.8561	0.1731	0.8164	0.8725	I
Dimension 4	12	0.7557	0.2295	0.8189	0.1956	0.7775	0.8374	II **
	13	0.7584	0.2459	0.8322	0.1942	0.7817	0.8506	II **
	14	0.7744	0.2335	0.8282	0.2037	0.7965	0.8475	I
Dimension 5	15	0.7896	0.2244	0.8401	0.1841	0.8109	0.8576	I
	16	0.7943	0.2148	0.8069	0.2047	0.8147	0.8263	I
	17	0.7810	0.2215	0.8454	0.1873	0.8020	0.8632	I

Remark: items need improvement with a high priority **; items need improvement with a low priority *.

, we plotted the 17 evaluation coordinates $\left(x_h,y_h\right)$ as dots on the PEM below:

Results and Discussion

In Figure 2, the evaluation coordinates of these 17 service items are plotted in the four evaluation quadrants, the red dots representing items that need improvement, and the blue dots representing items that do not need improvement.

Quadrant 1: items 4, 5, 6, 7, 8, 9, 10, 11, 14, 15, and 17

According to the evaluation rule determining which service items (larger than ${\theta }_0=0.7864$) should not be improved, service items 4, 5, 6, 7, 8, 9, 10, 11, 14, 15, and 17 do not need improvements.

Quadrant 2: items 3, 12, and 13

According to the evaluation rules determining which service items should be improved (smaller than ${\theta }_0=0.7864$) and the order of improvement priority (larger than ${\tau }_0=0.8337$), service items 3, 12, and 13 need improvements with a high priority.

Quadrant 3: item 2

According to the evaluation rules determining which service items should be improved (smaller than ${\theta }_0=0.7864$) and the second order of improvement priority (smaller than ${\tau }_0=0.8337$), service item 2 needs improvement with a low priority.

Quadrant 4: items 1 and 16

According to the evaluation rule determining which service items should not be improved (larger than ${\theta }_0=0.7864$) and the second order of improvement priority (smaller than ${\tau }_0=0.8337$), service items 1 and 16 do not need improvements.

Obviously, this model takes the average of the two evaluation indices as the testing standard and can improve the service direction with relatively weak performance, which is in line with the spirit of continuously improving total quality management. In addition, in the case of limited resources, priority should be given to improving service items with high importance to improve improvement efficiency. Based on this case, readers can be more aware of the application of the model proposed in this article, and it is convenient for enterprises to apply this model for evaluation and improvement.

5. Conclusions, Research Limitations, and Future Research

5.1. Conclusions

This paper has discussed the correlation between the values of the two indices and the proportion of customer satisfaction/importance of service items. We discovered that when the values of the indices are larger, the proportion of customer satisfaction/importance of service items becomes higher as well. We can see that these two indices can adequately reflect the actual distributions of customer satisfaction and the importance of service items. This paper set the mean value of the satisfaction index ${\theta }_0$ and that of the importance index ${\tau }_0$ as the horizontal line and the vertical of the PEM, which divided the matrix into four evaluation quadrants. This defined the set of these four evaluation quadrants, making this tool easy for managers to apply to their own systems. Since these two indices have unknown parameters, if the evaluation is performed directly by the point estimation, there will be a risk of misjudgment caused by sampling errors. As a result, based on the rule of using the upper confidence limits to conduct the statistical test, this paper used the upper confidence limits of the two indices as the evaluation coordinates of each service item $\left(x_h,y_h\right)$, and based on where the coordinates $\left(x_h,y_h\right)$ are located in the PEM, we can evaluate whether a service item needs improvement, and when resources are limited, we can set the order of improvement priority. Then, we used a real case to explain how to apply the model proposed in this paper, construct evaluation coordinates, identify CTQ service items, and determine the order of priority for improvements when resources are limited. We can see that this method is based on statistical tests; as a result, the risk of misjudgment caused by sampling errors can be reduced. Obviously, this rule is in line with the spirit of continuously improving total quality management. At the same time, under the condition of limited resources, prioritizing the improvement of high-importance service items can improve improvement efficiency. Based on this case, readers can be more aware of the application of the model proposed in this article, and it is convenient for enterprises to apply this model for evaluation and improvement.

5.2. Research Limitations and Future Research

Based on the recommendations of many studies, this paper uses the beta distribution as the distribution of customer importance and satisfaction. However, the statistical inference of the two indices must follow the central limit theorem, so the sample size must be large enough, which is the limitation of this study. In addition, the beta distribution is a continuous random variable. However, the collection of customer voices must be carried out through discontinuous scales. How to use the scale to make a reasonable discontinuity is the focus of future research.