Adaptive Control for an Aircraft Wing System with Hysteresis Nonlinearity
Abstract
:1. Introduction
2. Problem Statement
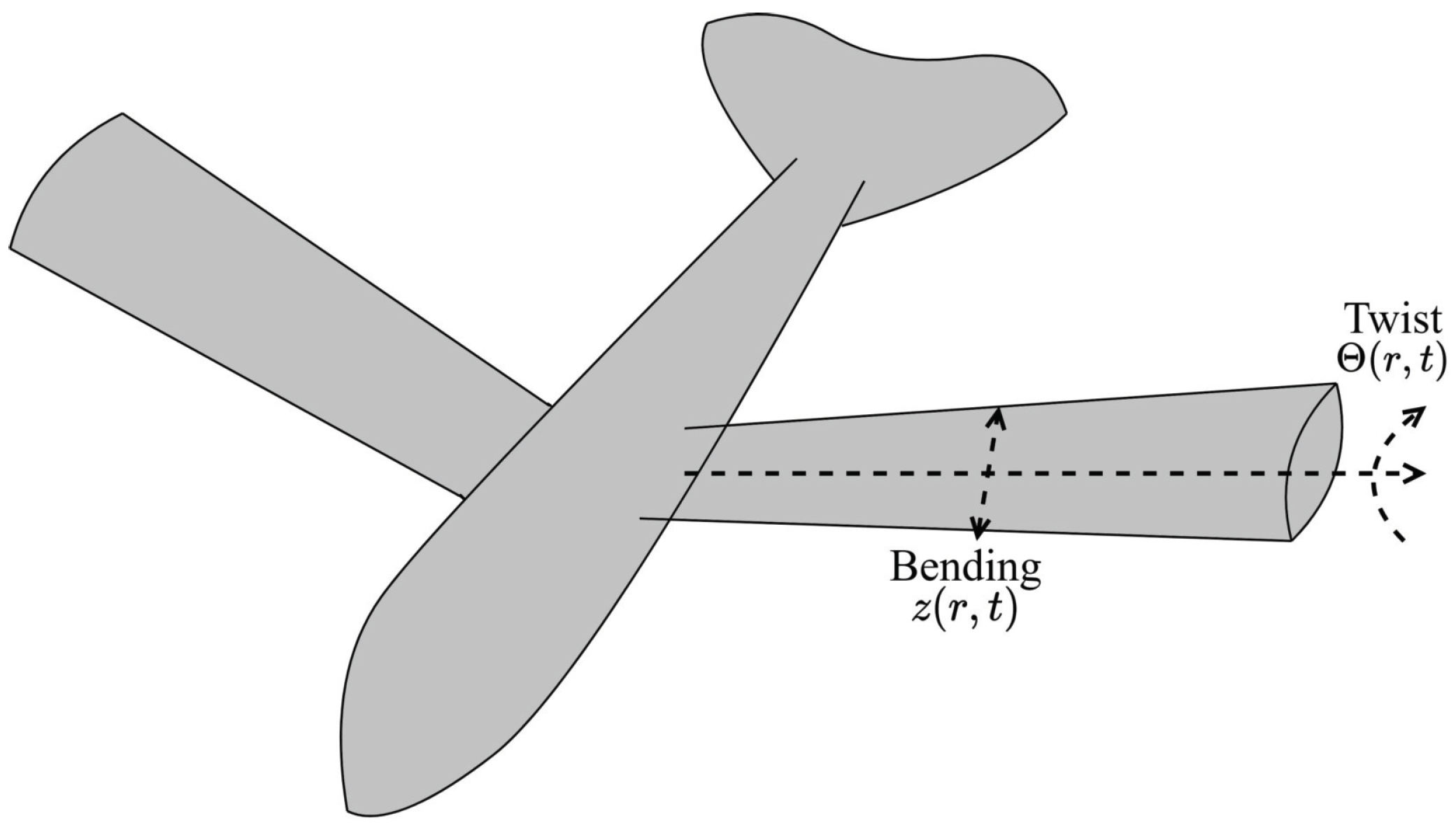
2.1. System Depiction
2.2. Hysteresis Characteristic Analysis
2.3. Preliminaries
3. Control Design
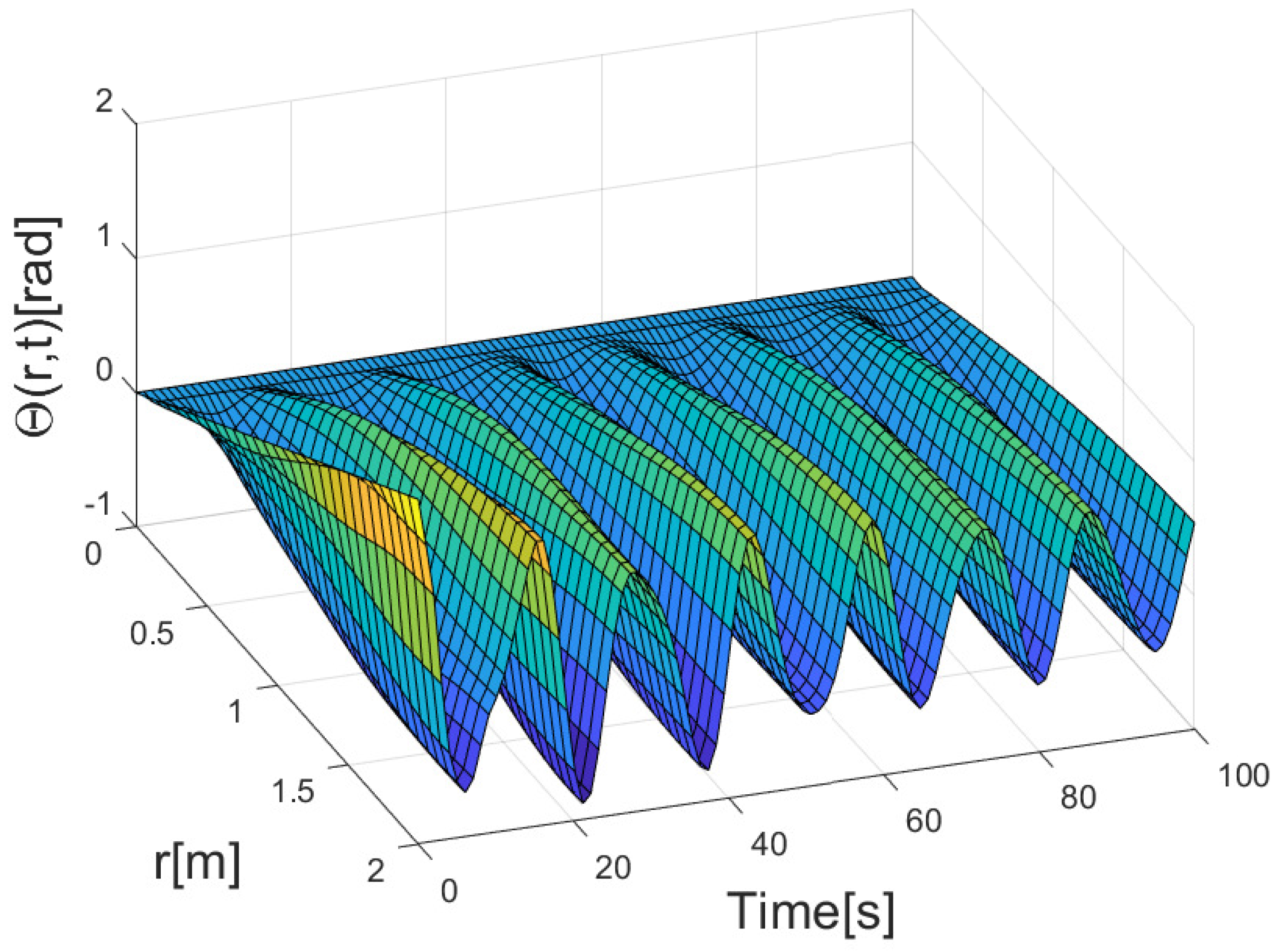
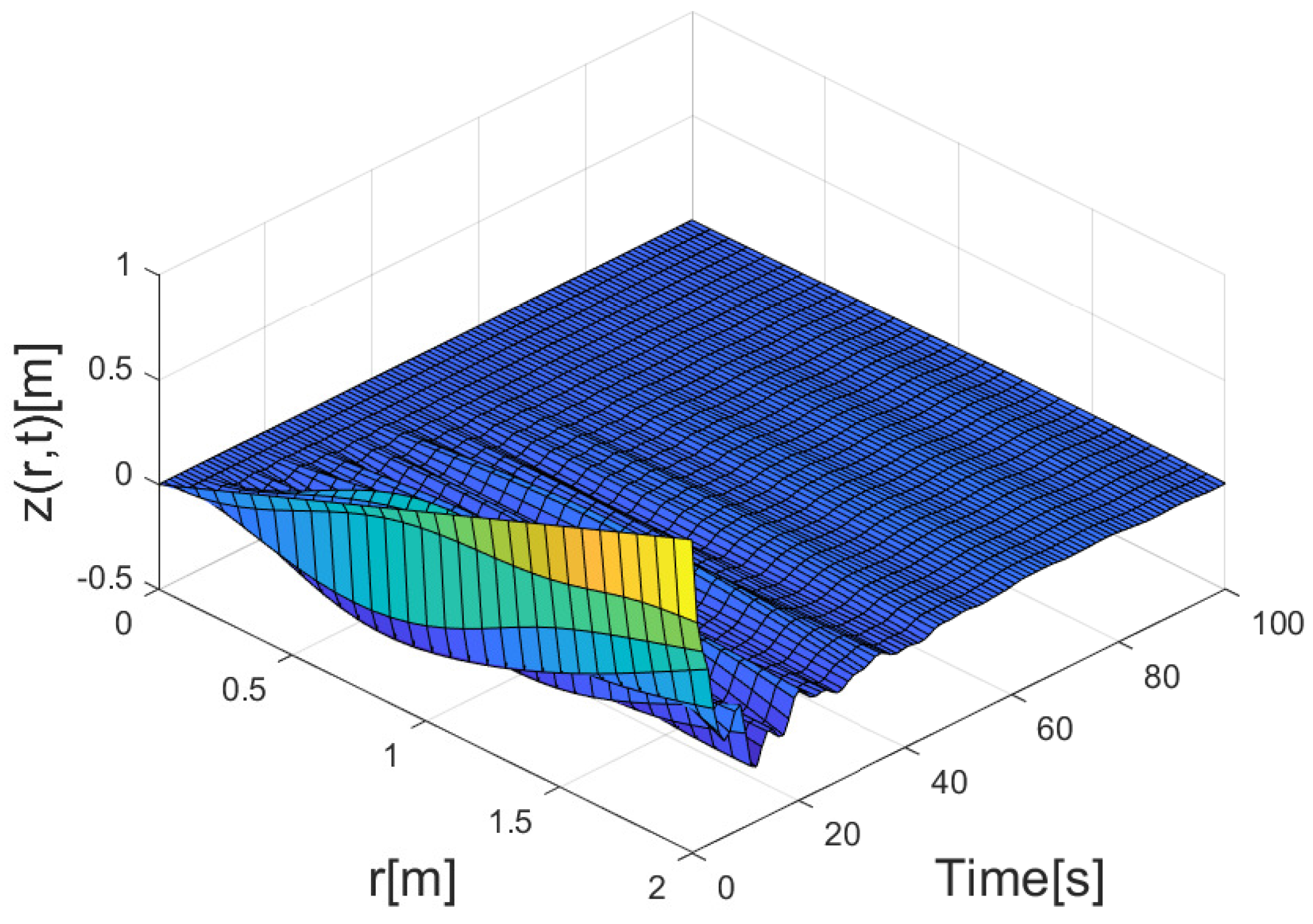
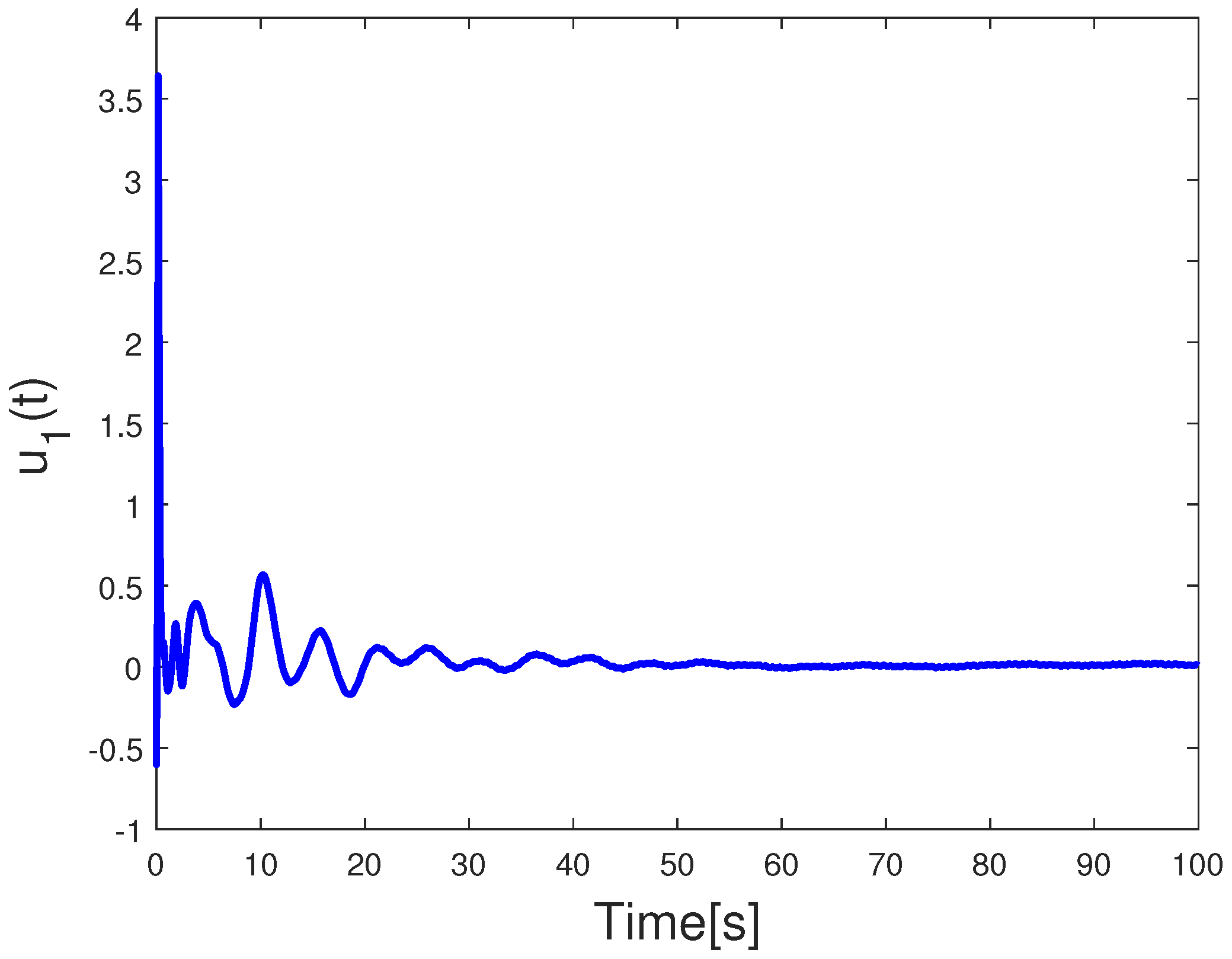
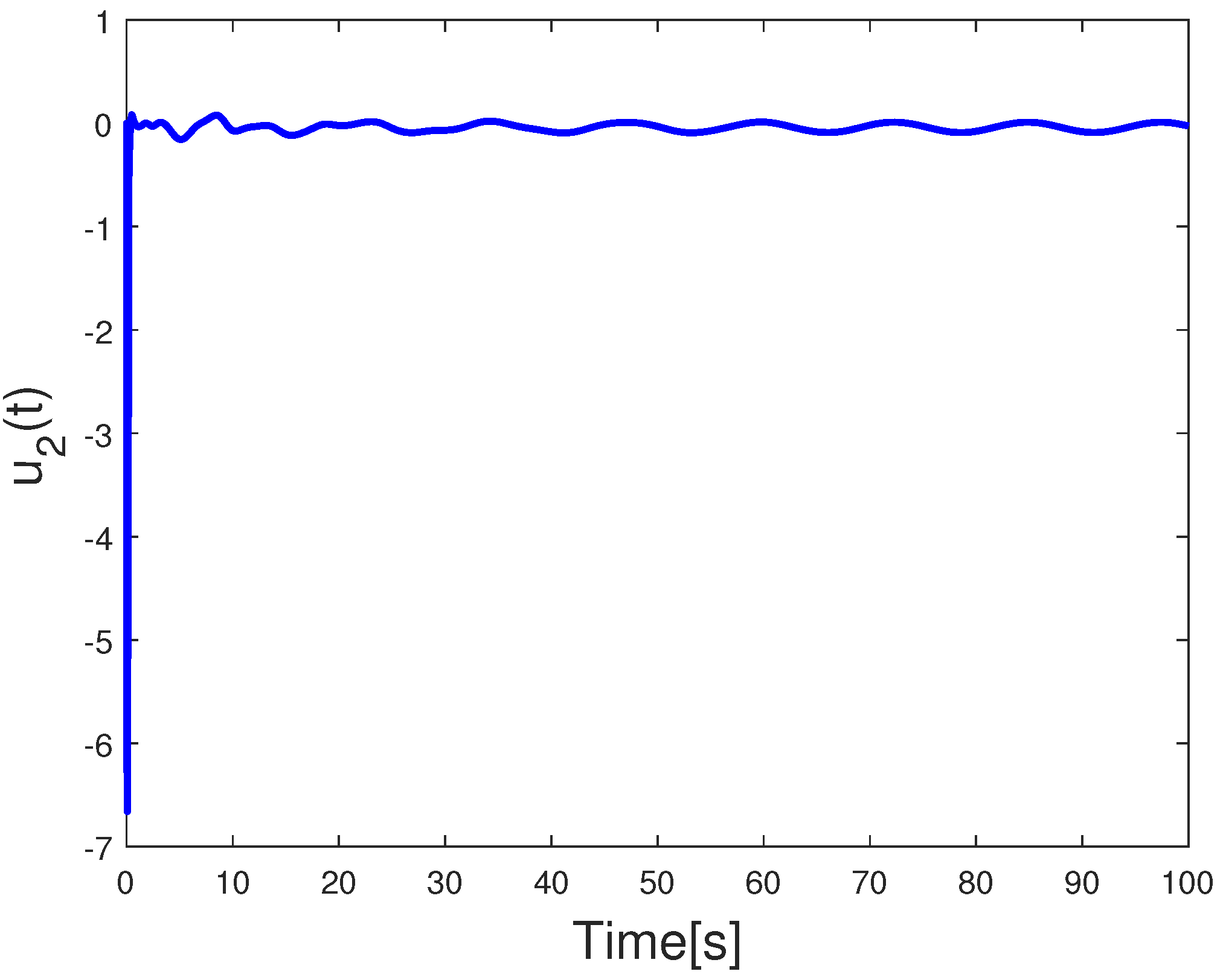
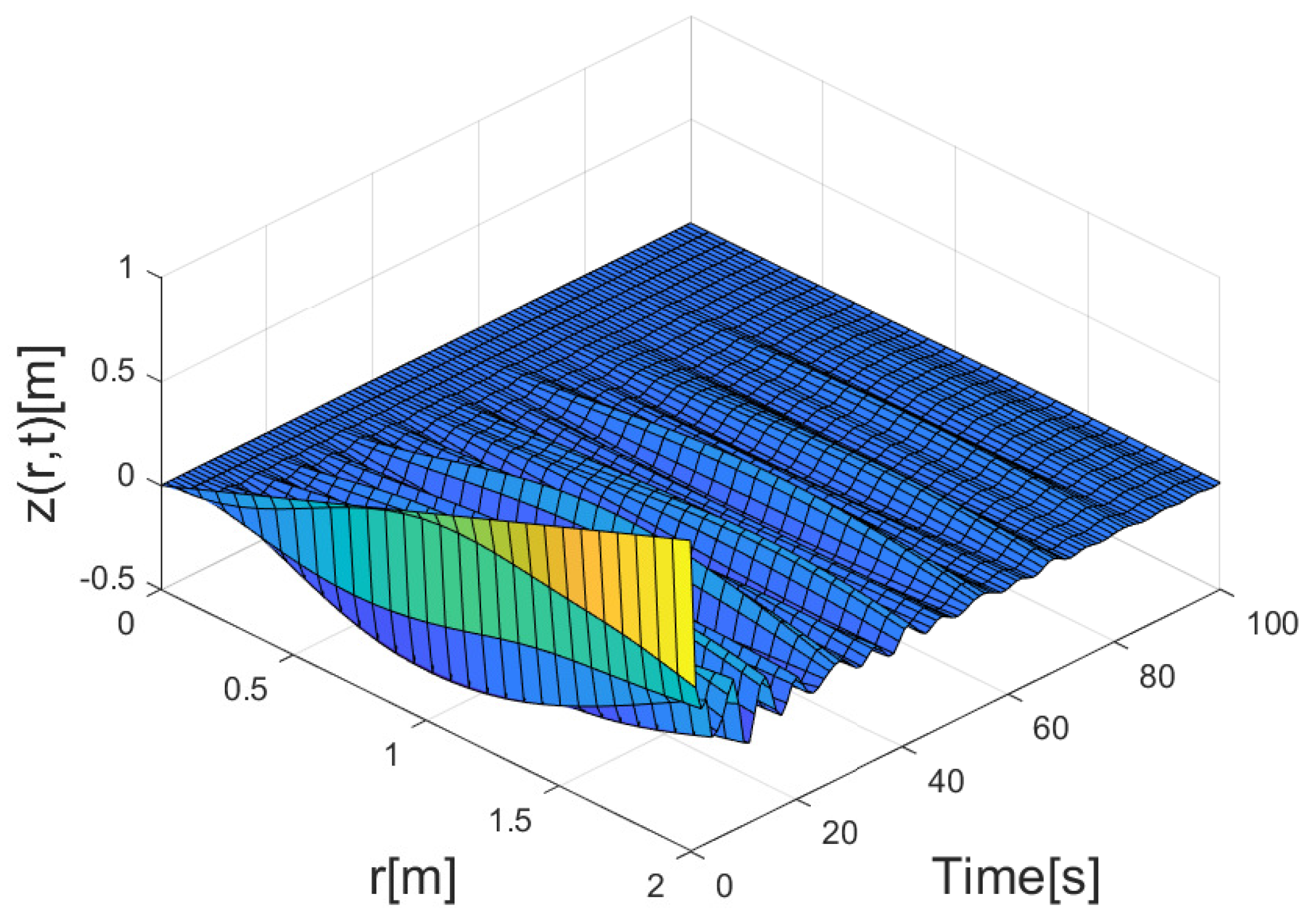
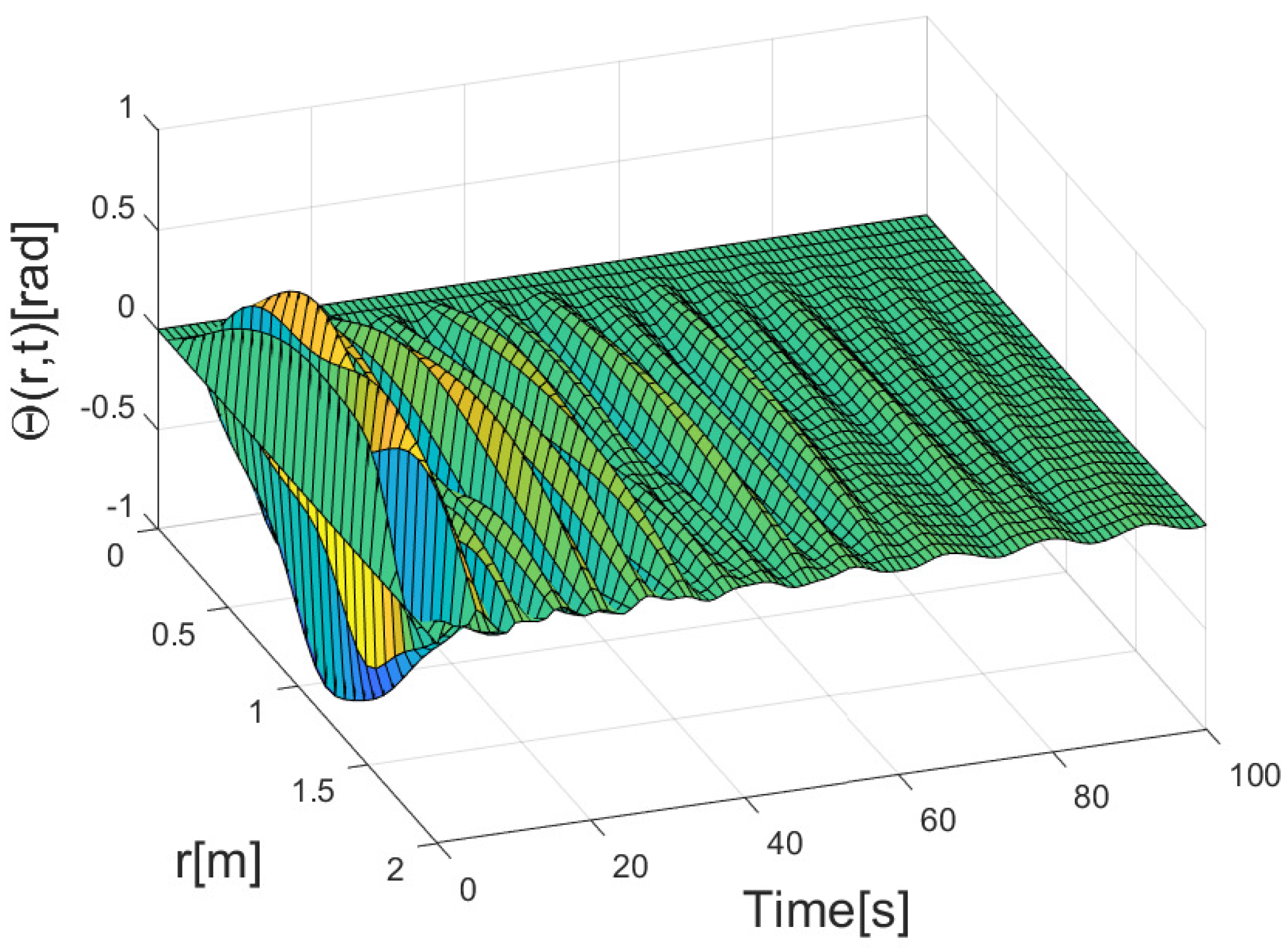
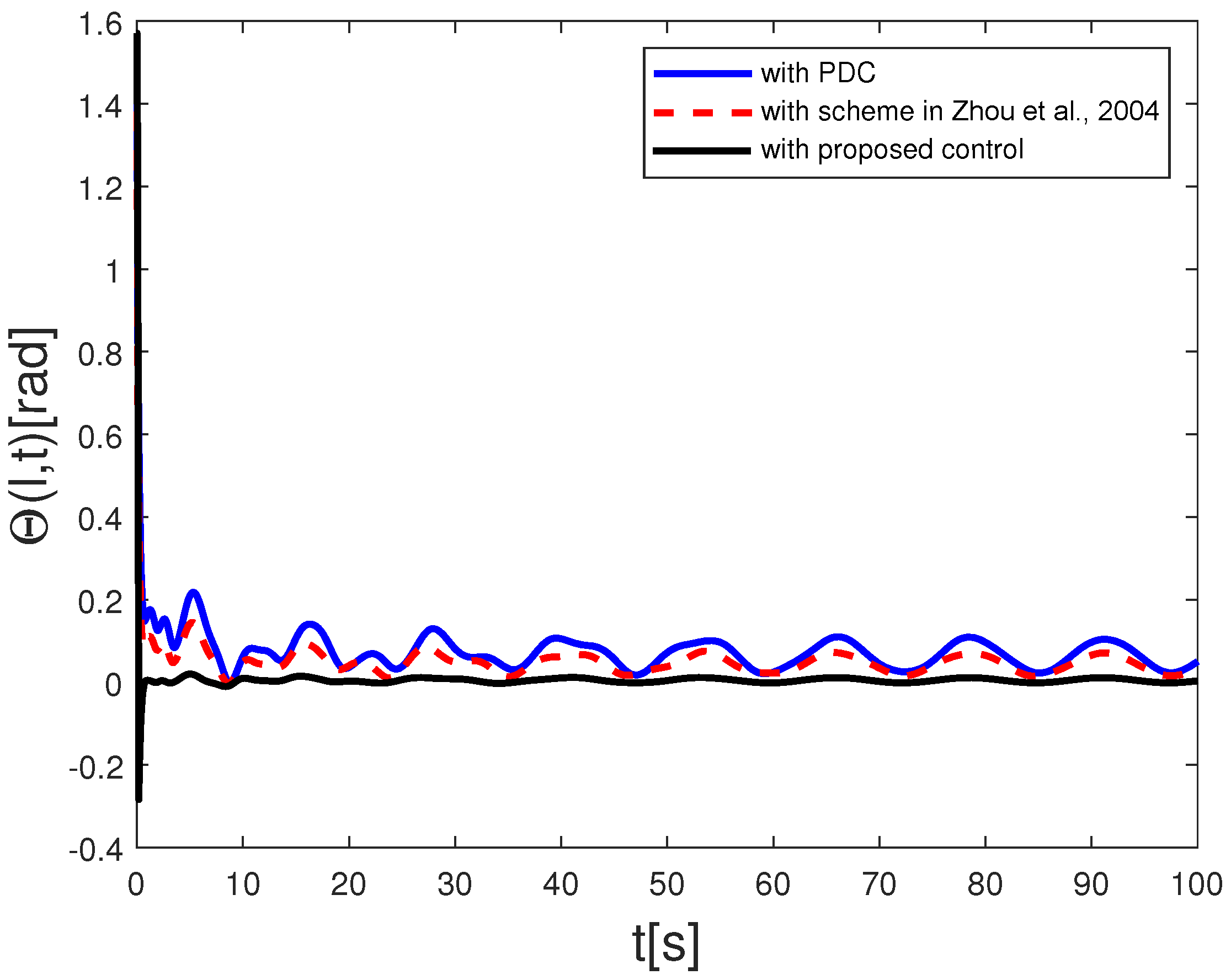
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Woo, D.; Yu, S. Virtual reality metaverse system supplementing remote education methods: Based on aircraft maintenance simulation. Appl. Sci. 2022, 12, 2667. [Google Scholar] [CrossRef]
- Barzkar, A.; Ghassemi, M. Components of electrical power systems in more and all-electric aircraft: A review. IEEE Trans. Transp. Electrif. 2022, 8, 4037–4053. [Google Scholar] [CrossRef]
- Henderson, I.L. Aviation safety regulations for unmanned aircraft operations: Perspectives from users. Transp. Policy 2022, 125, 192–206. [Google Scholar] [CrossRef]
- Cinar, G.; Cai, Y.; Bendarkar, M.V.; Burrell, A.I.; Denney, R.K.; Mavris, D.N. System analysis and design space exploration of regional aircraft with electrified powertrains. J. Aircr. 2023, 60, 382–409. [Google Scholar] [CrossRef]
- Li, Q.; Ji, A.; Shen, H.; Li, R.; Liu, K.; Zheng, X.; Shen, L.; Han, Q. Experimental study on the wing parameter optimization of flapping-wing aircraft based on the clap-and-fling mechanism. Int. J. Aeronaut. Space Sci. 2022, 23, 265–276. [Google Scholar] [CrossRef]
- Smith, M.J.C. Simulating moth wing aerodynamics-towards the development of flapping-wing technology. AIAA J. 1996, 34, 1348–1355. [Google Scholar] [CrossRef]
- Jiao, Z.; Wang, L.; Zhao, L.; Jiang, W. Hover flight control of X-shaped flapping wing aircraft considering wing–tail interactions. Aerosp. Sci. Technol. 2021, 116, 106870. [Google Scholar] [CrossRef]
- He, W.; Mu, X.; Chen, Y.; He, X.; Yu, Y. Modeling and vibration control of the flapping-wing robotic aircraft with output constraint. J. Sound Vib. 2018, 423, 472–483. [Google Scholar] [CrossRef]
- Ozaki, T.; Hamaguchi, K. Improved lift force of a resonant-driven flapping-wing micro aerial vehicle by suppressing wing–body and wing–wing vibration coupling. Extrem. Mech. Lett. 2020, 40, 100867. [Google Scholar] [CrossRef]
- He, W.; Meng, T.; He, X.; Sun, C. Iterative learning control for a flapping wing micro aerial vehicle under distributed disturbances. IEEE Trans. Cybern. 2018, 49, 1524–1535. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Z.; He, W.; Hong, K.-S.; Li, H.-X. Boundary adaptive fault-tolerant control for a flexible Timoshenko arm with backlash-like hysteresis. Automatica 2021, 130, 109690. [Google Scholar] [CrossRef]
- Bymes, C.I.; Laukó, I.G.; Gilliam, D.S.; Shubov, V.I. Output regulation for linear distributed parameter systems. IEEE Trans. Autom. Control 2000, 45, 2236–2252. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, X.; Song, S.; Stojanovic, V. Finite-Time sliding mode control for singularly perturbed PDE systems. J. Frankl. Inst. 2023, 360, 841–861. [Google Scholar] [CrossRef]
- Zhu, G.; Ge, S.S.; Lee, T.H. Simulation studies of tip tracking control of a single-link flexible robot based on a lumped model. Robotica 1999, 17, 71–78. [Google Scholar] [CrossRef]
- Ouyang, Y.; He, W.; Li, X. Reinforcement learning control of a single-link flexible robotic manipulator. IET Control. Theory Appl. 2017, 11, 1426–1433. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Z.; Li, Y.; He, W. Nonlinear disturbance observer-based direct joint control for manipulation of a flexible payload with output constraints. Int. J. Control 2023, 96, 1377–1388. [Google Scholar] [CrossRef]
- Sinclair, B.; McConnell, M.; Green, D.P. Detecting spillover effects: Design and analysis of multilevel experiments. Am. J. Political Sci. 2012, 56, 1055–1069. [Google Scholar] [CrossRef]
- Liu, Z.; Han, Z.; Zhao, Z.; He, W. Modeling and adaptive control for a spatial flexible spacecraft with unknown actuator failures. Sci. China Inf. Sci. 2021, 64, 152208. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Zou, T.; Hong, K.-S.; Li, H.-X. Robust adaptive fault-tolerant control for a riser-vessel system with input hysteresis and time-varying output constraints. IEEE Trans. Cybern. 2022, 53, 3939–3950. [Google Scholar] [CrossRef]
- Li, A.; Liu, M.; Cao, X.; Liu, R. Adaptive quantized sliding mode attitude tracking control for flexible spacecraft with input dead-zone via Takagi-Sugeno fuzzy approach. Inf. Sci. 2022, 587, 746–773. [Google Scholar] [CrossRef]
- Zhu, G.; Li, H.; Zhang, X.; Wang, C.; Su, C.-Y.; Hu, J. Adaptive consensus quantized control for a class of high-order nonlinear multi-agent systems with input hysteresis and full state constraints. IEEE/CAA J. Autom. Sin. 2022, 9, 1574–1589. [Google Scholar] [CrossRef]
- Cheng, Y.; Niu, B.; Zhao, X.; Zong, G.; Ahmad, A.M. Event-triggered adaptive decentralised control of interconnected nonlinear systems with Bouc-Wen hysteresis input. Int. J. Syst. Sci. 2023, 54, 1275–1288. [Google Scholar] [CrossRef]
- Liu, X.; Tong, D.; Chen, Q.; Zhou, W.; Shen, S. Observer-based adaptive funnel dynamic surface control for nonlinear systems with unknown control coefficients and hysteresis input. Neural Process. Lett. 2022, 54, 4681–4710. [Google Scholar] [CrossRef]
- Liao, X.; Liu, Z.; Chen, C.L.P.; Zhang, Y. Event-triggered fuzzy control for nonlinear time-delay system with full-state constraints and unknown hysteresis. J. Frankl. Inst. 2022, 359, 1582–1611. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Niu, B.; Zhao, X.; Ahmad, A.M. Adaptive neural finite-time hierarchical sliding mode control of uncertain under-actuated switched nonlinear systems with backlash-like hysteresis. Inf. Sci. 2022, 599, 147–169. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Li, T. Adaptive output feedback control of uncertain nonlinear systems with hysteresis nonlinearity. IEEE Trans. Autom. Control 2012, 57, 2627–2633. [Google Scholar] [CrossRef]
- He, W.; Meng, T. Adaptive control of a flexible string system with input hysteresis. IEEE Trans. Control Syst. Technol. 2017, 26, 693–700. [Google Scholar] [CrossRef]
- Tao, G.; Kokotovic, P.V. Adaptive control of plants with unknown hystereses. IEEE Trans. Autom. Control 1995, 40, 200–212. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Y.; Liu, J. Adaptive fault-tolerant boundary control for a flexible aircraft wing with input constraints. Aerosp. Sci. Technol. 2019, 90, 34–43. [Google Scholar] [CrossRef]
- Ren, Y.; Chen, M.; Liu, J. Bilateral coordinate boundary adaptive control for a helicopter lifting system with backlash-like hysteresis. Sci. China Inf. Sci. 2020, 63, 1–3. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Ma, G.; Hong, K.-S.; Li, H.-X. Adaptive Fuzzy Fault-Tolerant Control for a Riser-Vessel System With Unknown Backlash. IEEE Trans. Syst. Man Cybern. Syst. 2023. early access. [Google Scholar] [CrossRef]
- Zhao, Z.; Tan, Z.; Liu, Z.; Efe, M.O.; Ahn, C.K. Adaptive Inverse Compensation Fault-Tolerant Control for a Flexible Manipulator with Unknown Dead-zone and Actuator Faults. IEEE Trans. Ind. Electron. 2023, 70, 12698–12707. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Zhang, Y. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis. IEEE Trans. Autom. Control 2004, 49, 1751–1759. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Cai, S.; Li, Z.; Wang, Y.; Hong, K.-S.; Li, H.-X. Adaptive Quantized Control of Flexible Manipulators Subject to Unknown Dead Zones. IEEE Trans. Syst. Man Cybern. Syst. 2023. early access. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, J.; Liu, Z.; He, W.; Hong, K.-S. Adaptive quantized fault-tolerant control of a 2-DOF helicopter system with actuator fault and unknown dead zone. Automatica 2023, 148, 110792. [Google Scholar] [CrossRef]





| Index | Bending Deformation | |||
| Methods | PDC | Scheme in [33] | Proposed Control | |
| ITSE | - | 16.8644 | 6.3893 | 5.0516 |
| ITAE | - | 227.1647 | 114.4611 | 105.0891 |
| Index | Twist Deformation | |||
| Methods | PDC | Scheme in [33] | Proposed Control | |
| ITSE | - | 25.8436 | 11.4897 | 2.2290 |
| ITAE | - | 326.4926 | 215.9104 | 25.2367 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Guo, F.; Wang, F.; Li, X.; Hu, Y. Adaptive Control for an Aircraft Wing System with Hysteresis Nonlinearity. Mathematics 2023, 11, 3841. https://doi.org/10.3390/math11183841
Qin Y, Guo F, Wang F, Li X, Hu Y. Adaptive Control for an Aircraft Wing System with Hysteresis Nonlinearity. Mathematics. 2023; 11(18):3841. https://doi.org/10.3390/math11183841
Chicago/Turabian StyleQin, Yi, Fang Guo, Fujie Wang, Xing Li, and Yaohua Hu. 2023. "Adaptive Control for an Aircraft Wing System with Hysteresis Nonlinearity" Mathematics 11, no. 18: 3841. https://doi.org/10.3390/math11183841
APA StyleQin, Y., Guo, F., Wang, F., Li, X., & Hu, Y. (2023). Adaptive Control for an Aircraft Wing System with Hysteresis Nonlinearity. Mathematics, 11(18), 3841. https://doi.org/10.3390/math11183841







