Enhanced Whale Optimization Algorithm for Improved Transient Electromagnetic Inversion in the Presence of Induced Polarization Effects

Abstract

The transient electromagnetic (TEM) method is a non-contact technique used to identify underground structures, commonly used in mineral resource exploration. However, the induced polarization (IP) will increase the nonlinearity of TEM inversion, and it is difficult to predict the geoelectric structure from TEM response signals in conventional gradient inversion. We select a heuristic algorithm suitable for nonlinear inversion—a whale optimization algorithm to perform TEM inversion with an IP effect. The inverse framework is optimized by opposition-based learning (OBL) and an adaptive weighted factor (AWF). OBL improves initial population distribution for better global search, while the AWF replaces random operators to balance global and local search, enhancing solution accuracy and ensuring stable convergence. Tests on layered geoelectric models demonstrate that our improved WOA effectively reconstructs geoelectric structures, extracts IP information, and performs robustly in noisy environments. Compared to other nonlinear inversion methods, our proposed approach shows superior convergence and accuracy, effectively extracting IP information from TEM signals, with an error of less than 8%.

1. Introduction

The electromagnetic method in a time domain is a geophysical prospecting method that uses coils to transmits pulsed electromagnetic waves (primary field) and receive induced electromagnetic fields (secondary fields) excited by underground abnormal bodies. It offers significant benefits such as extensive detection depth, exceptional precision, cost-effectiveness, is less affected by terrain, and other advantages [1,2,3]. So far, its application has spread extensively to geological survey, mineral resource exploration, engineering survey, geological disaster survey, environmental survey, and other fields at home and abroad.

The sign inversion of the transient electromagnetic method (TEM) response has attracted the attention of many scholars [4,5,6]. After analysis and research on the cause of the sign inversion, people attribute it to the dispersion of conductivity [7,8]. Flis employed the Cole–Cole architecture to characterize the subsurface behavior of three-dimensional conductors [9]. In the transient response simulation of overlapping loops, the reversal of the sign of the induced signal is attributed to polarized bodies. Traditional inversion imaging techniques reliant on resistivity models struggle to efficiently process inversion data signals, so it is necessary to carry out time-domain electromagnetic inversion involving induced polarization (IP) effects.

One dimensional inversion method incorporating lateral constraints can address the extraction of induced polarization information from time-domain electromagnetic measurements. Study outcomes have illustrated the effectiveness of this method in accurately estimating IP parameters, particularly resistivity and susceptibility [10]. It also has very good solvability. The traditional least-squares method to solve the TEM inversion problem with the IP effect can obtain IP information, but this process is easily affected by noisy data [11].

Although it is theoretically feasible to extract IP information from TEM response signals, traditional gradient inversion heavily relies on the initial geoelectric model, and most of them are suitable for specific conditions, but not suitable for the optimization process of inversion with severe nonlinearity, especially when the induced polarization effect intensifies the nonlinearity. We must consider that an heuristic algorithm is more suitable for optimization problems with severe nonlinearity due to its excellent ability to jump out of local extreme value, and this kind of algorithm has successfully entered the actual data processing stage in the field of TEM inversion, and achieved good results. In this study, a TEM inversion framework of an heuristic algorithm is established, which can be applied to inversion difficulties caused by the excitation polarization caused by the TEM response signal change. In addition, we optimize the inversion framework in terms of population optimization and dynamic parameter selection.

2. Related Work

2.1. Inverse with IP Effect

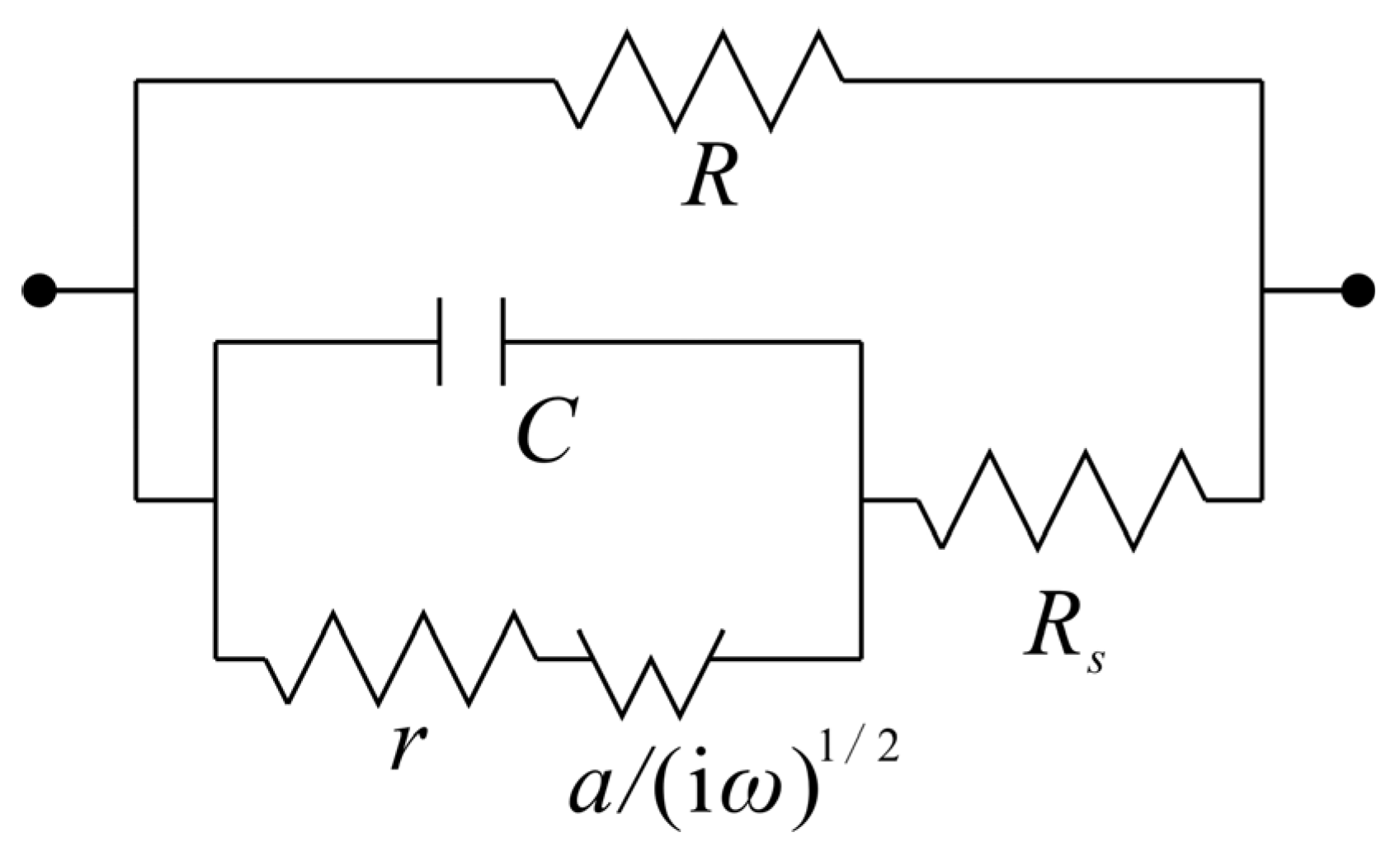
The induced polarization phenomenon in rocks arises from the interstitial electrochemical characteristics of both the rock matrix and interstitial fluids when subjected to an external electric field. In the study of rock-induced polarization, the equivalent circuit (Figure 1) is generally used to establish a model to simulate the dispersion characteristics of rock.

The IP phenomenon in rocks arises from the intricate electrochemical properties of both rocks and the interstitial fluids when subjected to an external electric field. In the investigation of rock-induced polarization, researchers often employ an equivalent circuit (Figure 1) to construct a model that simulates the dispersion characteristics exhibited by rocks.

The sign inversion of the response (TEM) caused by the IP-induced polarization effect (Figure 2a) increases the difficulty of TEM inversion optimization. The method for extracting IP utilizing the thin-plate approach was discussed; however, its applicability is confined to geological bodies with thin-plate characteristics [12]. The Cole–Cole model parameters were established by EL-Kaliouby et al., accompanied by the provision of an approximate formula for computing the maximum negative value [13]. Kozhevikov employed both single-inversion and joint-inversion techniques for the complex resistivity inversion of a two-layer model. This study demonstrated the viability of joint inversion for resolving polarized strata even without prior information [14]. Further enhancements to the algorithm based on one-dimensional lateral constraints were introduced [15]. They established a stable initial model through model space conversion, set a reasonable regularization factor, and successfully obtained resistivity and polarizability close to the true value. Although it is theoretically feasible to extract IP information from TEM response signals, most of them are applicable to specific conditions. This is because the traditional gradient inversion method heavily depends on the initial geoelectric model; it becomes challenging to fulfill the calculation requirements, especially when the induced polarization effect exacerbates the nonlinearity.

When inversion is performed using the traditional gradient class method [16,17], and when the initial geoelectric structure is a uniform half-space model, it is difficult to find the geoelectric structure that makes a TEM signal appear in the wrong direction (Figure 2a) during the inversion process, and the predicted geoelectric structure cannot be close to the preset structure (Figure 2b). The optimization process is stalled.

2.2. Machine Learning Inversion

To avoid the inversion optimization process highly dependent on the initial model, the iterative process is easy to fall into extreme values. Some nonlinear inversion methods [18], such as particle swarm optimization (PSO) [19], genetic algorithms [20], tabu search methods, ant colony optimization, artificial bee colony (ABC), whale optimization algorithm (WOA), simulated annealing [21] and artificial neural networks (ANNs) [22,23] have been proposed. Compared with ANNs, which are widely used, an heuristic algorithm does not need to prepare a large number of training samples for application scenarios, and is not only widely used in TEM inversion, but also widely used in other electromagnetic-detection problems [24,25].

As an heuristic optimization algorithm [26,27,28], WOA has been successfully used to process TEM signal features and geoelectric structure features, so we decided to develop a WOA-based heuristic TEM inversion framework. The resistivity of the polarized body is regarded as a complex function related to frequency, which aggravates the nonlinearity of TEM inversion, resulting in the optimization process of the heuristic inversion algorithm. This makes it difficult to balance its search efficiency and low computational efficiency [24,29,30]. Therefore, although the aforementioned WOA has been used for electromagnetic-data inversion, the computational efficiency of the inversion framework needs to be further improved.

By referring to the solutions of other heuristic optimization algorithms to solve engineering problems, and improving the way of evolution of heuristic algorithms, an applicable multi-threading technology can be developed based on the characteristics of the optimizer [31], and the search efficiency can be improved by optimizing the population of candidate solutions [32,33,34]. The binary scheme selector [35], the optimization strategy selector [36,37,38], and the dynamic parameter selector [36,37,39] can be used.

For this investigation, the fundamental heuristic swarm intelligence search algorithm chosen for TEM inversion was the whale optimization algorithm (WOA), which effectively combines global information interaction and local search, and adjusts the population state during the evolution process according to the worst individual information [40]. Compared with the swarm intelligence search algorithm that needs to adjust all individuals, WOA can take into account the state of the global optimum and local optimum, and has higher execution efficiency [41,42]. Not only that, through grouping operators and meme search, a opposite learning strategy is employed for enhancing the diversity of a population within the meme group, thereby boosting the algorithm’s global search capabilities; operators are employed to balance the algorithm’s ability for early-stage search and later-stage convergence; finally, an improved WOA is formed to accurately extract IP information and invert geoelectric structures based on TEM response signals.

3. TEM Forward Modeling

The Cole–Cole model initially found application in describing the dispersion effect of complex permittivity. Based on many experiments, Pelton et al. believed that the induced electrical effects of rocks are consistent with the Cole–Cole model, which serves as a descriptor for the complex resistivity as [10]

$$\rho \left(\omega \right)={\rho }_0\left(1-m\left(1-\frac{1}{1+{\left(i\omega \tau \right)}^c}\right)\right),$$

(1)

where ρ₀ represents the resistivity of rock as the angular frequency ω approaches 0, ρ(ω) signifies the complex resistivity, m stands for the polarizability, τ represents the polarization current-decay time constant, and C denotes the frequency-dependent constant. m = (ρ₀ − ρ_∞)/ρ₀, ρ_∞ is the rock resistivity when the angular frequency approaches infinity.

In addition, the Dias model is also a common model used to describe rocks and minerals with IP characteristics [43]. The complex resistivity calculation expression of the Dias model is

$$\rho \left(\omega \right)={\rho }_0\left(1-m\left(1-\frac{1}{1+i\omega {\tau }^{\prime }\left(1+\frac{1}{\mu }\right)}\right)\right),$$

(2)

where μ is defined as iωτ + (iωτ″)^1/2, and τ′ and τ″ represent the relaxation times associated with different planning mechanisms. In the equivalent circuit of the rock unit, the capacitance is C, τ′ = (R + R_s)C, τ″ = (aC)². a is a constant.

Let the TEM device be a central loop device, that is, there are two circular coils with a common center point. When the radius of the small coil is much smaller than that of the large coil, the small coil is regarded as the observation station. In the Cartesian coordinate system, the vertical z-axis is positive and negative below the ground. The vertical magnetic field z component, Hz, produced by the center loop source can be expressed as

$$H_z=\frac{Ia}{2}{\displaystyle {\int }_0^{\infty }\left[e^{-u_0(z+h)}+r_{TE}{e}^{u_0(z-h)}\right]\frac{{\lambda }^2}{u_0}{J}_1\left(\lambda a\right)\mathrm{d}\lambda },$$

(3)

where u₀ can be approximated as λ, J₁ denotes the Bessel function with the 1st order, z represents the ordinate of the observation station, h is the height of the excitation source, and for ground devices, z = 0, h = 0. I stands for the magnitude of the excitation step current, while a denotes the excitation loop radius. Bessel functions can be solved discretely using the Hankel transform [44]. r_TE is the surface reflection coefficient r_TE = (λ − u′₁)/(λ + u′₁). u′_i is obtained using the layered recursive formula [45]:

$$\begin{array}{ccc}{u^{\prime }}_i=u_i\frac{{u^{\prime }}_{i+1}+u_i\tanh (u_i{h}_i)}{u_i+{u^{\prime }}_{i+1}\tanh (u_i{h}_i)}& u_i={\left({\lambda }^2-k_i^2\right)}^{1/2}& i=1,2,\cdots ,N-1\end{array},$$

(4)

where N denotes the total stratum count of the geoelectric model, when I = N, u′_N = u_N. k is the wave number, k_i = (−iωμσ)^1/2.

The above formula can obtain the vertical component of the vertical induced magnetic field in the frequency domain, and the magnetic field response in the time domain can be obtained through the following Fourier transform:

$$B_z(t)=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }\left(\mathrm{Re}\left[B_z(\omega )\right]+\mathrm{Im}\left[B_z(\omega )\right]\right)}\frac{\cos (\omega t)-i\sin (\omega t)}{i\omega }d\omega ,$$

(5)

where the real part is an even function, the imaginary part is an odd function, and the integral of the imaginary part is zero. After simplification, when t > 0, using the symmetry property of the even function, the derivative of the magnetic field with respect to time can be obtained as

$$\frac{B_z(t)}{dt}=\frac{2}{\pi }\frac{\mathrm{Im}\left[B_z(\omega )\right]\cos (\omega t)}{i\omega }d\omega ,$$

(6)

The time-domain induced vertical magnetic field H_z(t) and induced electromotive force (EMF) ε can be transferred from frequency-domain induced magnetic-field signals [46], and be obtained using the piecewise linear approximation method as follows:

$$H_z(t)=-\frac{2}{\pi t^2}{\displaystyle {\sum }_{i=0}^{N_t}\frac{\frac{\mathrm{Im}[F\left({\omega }_{i+1}\right)]}{{\omega }_{i+1}}-\frac{\mathrm{Im}[F\left({\omega }_i\right)]}{{\omega }_i}}{{\omega }_{i+1}-{\omega }_i}}\left[\cos ({\omega }_{i}t)-\cos ({\omega }_{i+1}t)\right],$$

(7)

$$\epsilon (t)=\frac{-B_z(t)}{dt}=-\frac{2\mu }{\pi t^2}{\displaystyle {\sum }_{i=0}^{N_t}\frac{\mathrm{Re}[F\left({\omega }_{i+1}\right)]-\mathrm{Re}[F\left({\omega }_i\right)]}{{\omega }_{i+1}-{\omega }_i}}\left[\cos ({\omega }_{i}t)-\cos ({\omega }_{i+1}t)\right],$$

(8)

The TEM response data incorporating the induced polarization effect can be obtained by replacing the actual resistivity in Equation (3) with the complex resistivity from Equation (1) or (2). The TEM forward simulation process with the IP effect is as follows:

(1)

Set the model parameters (resistivity, thickness and polarizability) of the geoelectric model;

(2)

Give the IP response with the Dias model;

(3)

Replace the real resistivity ρ(ω) in the parameters of the geoelectric model with the complex resistivity ρ that varies with frequency;

(4)

Calculate the transformation impedance between adjacent layers according to the complex resistivity of each layer;

(5)

Obtain TEM response data with IP information, which are obtained by calculating the ground theoretical impedance according to the recursive formula.

4. Improved WOA Inversion

This section introduces the basic principle of WOA and how to improve WOA using OLB and AWF. Then, on this basis, the optimal framework of geoelectric structure inversion through the electromagnetic response signal is presented.

4.1. WOA Basic Theory

The mathematical formulation of the WOA involves describing the population size as P, and the initial whale population is M(0) = {M₁, M₂, $\cdots$, M_P}. In WOA, the whale population is randomly generated and uniformly distributed in the solution space, and the i-th whale position can be denoted as ${\mathit{X}}_i=\left\{X_i^1,X_i^2,\dots ,X_i^n\right\},i=\mathrm{1,2},\dots ,P$. Each whale structure contains n position information. Once the whales have secured the prey target’s position, the whales begin to constrict their search region around the target. This is achieved through two encircling strategies: shrinking and spiral. The updating of each whale’s prey position to the optimal state ${\mathit{X}}^{*}=\left\{X_1^{*},X_2^{*},\dots ,X_n^{*}\right\}$ is a necessary step. During the t-th iterative optimization, the positions of the whales undergo updates using the following procedure:

$$\mathit{X}(t+1)={\mathit{X}}^{*}(t)-\mathit{A}\times \mathit{D},$$

(9)

where the A·D that can be regarded as the update step is represented. A can be calculated as

$$\mathit{A}=2\mathit{\alpha }\times \mathit{r}-\mathit{\alpha },$$

(10)

where r represents a randomized vector in the range [0, 1], while α is vector of the same size as A with amplitude α. The optimization speed is regulated by coefficient A, which operates in conjunction with the convergence factor α.

The control of the whales’ shrinking encircling mechanism for reducing the search space is facilitated by the convergence factor α. The range of A changes within [−α, α] as α gradually decreases from 2 to 0:

$$\alpha =2-2t/t_{\max },$$

(11)

where t_max signifies the max iterations. As the number of iterations goes up, reducing α results in a smaller gap between the whale’s position and the optimal target position, accompanied by a decrease in the update step size. The step size D should be represented as

$$\mathit{D}=|2\mathit{r}\times {\mathit{X}}^{*}(t)-\mathit{X}(t)|,$$

which can be perceived as the separation between the cluster of whales and the presumed prey location. For the ${\mathit{D}}^{\prime }=\left|{\mathit{X}}^{*}\left(t\right)-\mathit{X}\left(t\right)\right|$, which represents the spiral search’s max radius, the step size D can be derived using the spiral encircling approach. Subsequently, the update for each whale’s position follows a spiral trajectory as

$$\mathit{X}(t+1)={\mathit{D}}^{\prime }\times e^{ql}\times \cos (2\pi l)+{\mathit{X}}^{*}(t),$$

(12)

where q is a fixed factor that can constrain the spiral configuration, while l denotes one value randomly chosen from the range of [−1, 1].

Supposing the likelihood of whales participating in various predatory actions is represented as p, the renewed positions of whales for each predation type should be denoted as

$$\mathit{X}(t+1)=\left\{\begin{array}{cc}{\mathit{X}}^{*}(t)-\mathit{A}\times \mathit{D}& p<0.5\\ {\mathit{D}}^{\prime }\times e^{ql}\times \cos (2\pi l)+{\mathit{X}}^{*}(t)& p\ge 0.5\end{array}\right.,$$

(13)

4.2. Improved WOA Based on OBL and AWF

The traditional WOA model excels at maintaining a balance between global and local search performance, which aids in enhancing the global optimal solution and execution efficiency [47]. However, there are defects such as the uneven distribution of the initial population, large individual differences in different sub-populations, and difficulty controlling the size of the moving step, resulting in slow convergence, low optimization precision, and premature convergence. To extract IP information more accurately from TEM signals, an improved WOA (IWOA) model based on opposition-based learning (OBL) and adaptive weighted factor (AWF) is recommended [36,48].

In the case of population initialization without prior information guidance, the randomly generated initial population is far away from the ideal solution space. The OBL generates an independent and reverse initial solution space, so that the distribution of the initial state covers a broader range, making it more feasible to cover the ideal solution space. The OBL strategy has achieved successful integration into multiple evolutionary algorithms [36,49]. To address the initial population’s non-uniform distribution, we utilized the opposite learning approach for generating the initial population. This involves two distinct population categories: a randomly generated initial population denoted as X(0) = {X₁, X₂, $\cdots$, X_P}, and an opposite population. Supposing that the opposite population is X′(0) = {X′₁, X′₂, $\cdots$, X′_P}, the sub-element should be

$${x^{\prime }}_i=x_{\max }+x_{\min }-x_i,$$

(14)

where x_max represents the upper boundary of the whale’s position x_i, and x_min represents the lower boundary. Following the combination of the initial population and the opposite population, a new population is formed by selecting individuals with comparatively lower fitness.

The inherent uncertainty associated with the rand() function fails to effectively steer the solution toward optimal outcomes. Consequently, this can lead to a propensity for converging towards local optima or bypassing the global optimum during the course of evolution [50]. In the solution update process, only with an appropriate moving step size can the algorithm have good global convergence. The incorporation of an adaptive weighted factor into the update step serves to regulate both global and local search capabilities, thereby enhancing the effectiveness of the random vector r and diminishing uncertainties. When the probability of whales engaging p < 0.5, the whale updating can be represented as

$$\begin{array}{cc}\mathit{X}(t+1)={\mathit{X}}^{*}(t)-{\omega }_1^{adap}\mathit{A}\times \mathit{D}& p<0.5\end{array},$$

(15)

When the probability of whales engaging p > 0.5, the whale positions can be updated as the following:

$$\begin{array}{cc}\begin{array}{cc}\mathit{X}(t+1)=& {\mathit{D}}^{\prime }\times e^{ql}\times \cos (2\pi l)+{\omega }_2^{adap}{\mathit{X}}^{*}(t)\end{array}& p\ge 0.5\end{array},$$

(16)

The adaptive weighted factors can be expressed as:

$${\omega }_1^{adap}=\beta \left(\cos \left(\pi \times t/t_{\max }\right)+\kappa \right),$$

(17)

$${\omega }_2^{adap}=\beta \left(\cos \left(\pi \times t/t_{\max }\right)-\kappa \right),$$

(18)

where β represents the extent of the variation range for ${\omega }_1^{adap}$ and ${\omega }_2^{adap}$, while κ defines the step size for adjusting the weights. The utilization of the cosine function aids in attenuating global search precision during the initial evolutionary stages, consequently facilitating an expansion of the optimization range [51]. During the middle and advanced phases of evolution, the amplified weight proves advantageous in enhancing global search capabilities [52].

4.3. Inversion Framework

The geoelectric model with L-strata encompasses three distinct electrical attributes for each layer: resistivity (ρ_i), thickness (h_i) and polarizability (m_ci) of the i-th layer, respectively. This geoelectric model can be formulated as m = [ρ₁, ρ₂, $\cdots$, ρ_L; m_c1, m_c2, $\cdots$, m_cL−1; h₁, h₂, $\cdots$, h_L−1]. The complete number of the layered structure parameters is 3L − 1. When the TEM forward modeling is the operator F[·], the TEM magnetic field response can be obtained by d = F[m], d = [H_z,1, H_z,2, …, H_z,it, …, H_z,Nt]; N_t represents the count of time observation windows.

The inversion process is represented by m = F⁻¹[d], where the inverse of operator F is characterized by significant nonlinearity. When performing an inverse fit by optimization, it is necessary to define an objective function for the optimization problem. When the WOA-type optimization algorithm is used, the objective function is the fitness of WOA, which can be defined as

$$Fitness=\sqrt{\frac{1}{N_t}{\displaystyle \sum _{\mathrm{i}=1}^{N_t}\frac{1}{t_i^2}{[(d_i^{obs}-d_i^{pre})/d_i^{pre}]}^2}},$$

(19)

where d^obs stands for the recorded TEM-induced response signals, while d^pred signifies the predicted TEM in the existing optimization state. The fitness is a normalized root-mean-square error. The time coefficients 1/t² can be weighted to balance early to late data with significant amplitude differences.

Here, an enhanced WOA model incorporating OLB and AWF is introduced for IP information extraction. Supposing that the lower bound (lb) and upper bound (ub) are 30% fluctuation of the electric medium parameters in the geoelectric structure. The specific sequence of steps for implementation steps is as outlined below:

for i in P: for j in range(M): x(j) = rand(lb, ub) x’(j) = lb + ub −x(j) x*(i, (j − 1) × 2) = x(j) x*(i, (j − 1) × 2 + 1) = x′(j) end for end for for t = 1: Nmax α = 2 − 2t/Nmax ω1 = 0.5(cos(π × t/Nmax) + 1) ω2 = 0.5 (cos(π × t/Nmax) − 1) for i = 1:P A = 2α × rand(0, 1) − α r = rand(0, 1) l = (−t/Nmax − 2) × rand(0, 1) + 1 p = rand(0, 1) for j = 1:M if p < 0.5 if |A| < 1 D = |2r × X′(t) −X(t)| X(i,j) =X*(j) − ω1 × A × D else: idx = int(P × rand(0, 1) + 1) Xrand=X(idx,:) D″ = |2r × Xrand(j) −X(i,j)| X(i,j) =Xrand(j) − ω1 × A × D″ end if else: D′ = |X*(j) −X(i,j)| X(i,j) =D′ × el × cos(2πl) + ω2 × X*(j) end if end for end for end for

4.4. Hyperparameter Setting

To determine the selection of hyperparameters in the proposed method and the comparison method, we used a 200 Ω·m uniform half-space geoelectric model inversion optimization to test the important parameters of each heuristic algorithm.

For the differential evolution (DE) algorithm, crossover (CR) probability is used to control the crossover probability between individuals, determining whether each individual will, with a certain probability, undergo a crossover operation with other individuals during the evolution process, thereby generating new individuals. This helps adjust the trade-off between exploration and exploitation in the DE algorithm. A higher CR value (close to 1) increases the probability of crossover, leading to more exploration of the search space, aiding global search but potentially sacrificing local search capabilities. A lower CR value (close to 0) reduces the probability of crossover, relying more on known information, aiding local search but potentially getting stuck in local optima.

We compared CR = 0.2 and CR = 0.8 in the context of testing the inversion of the uniform half-space electrical structure (Figure 3). Different population sizes were tested. The results indicate that, for our TEM inversion optimization problem, CR can only improve global search efficiency to some extent by controlling the crossover status of the population during iterations. The extent of improvement also depends on the population size.

For the ABC algorithm, the limits parameter was used to control whether the bees would abandon a certain food source (candidate solution) to explore other potential and better solutions, aiming for improved search effectiveness. If, for a consecutive number of iterations, the bees fail to find a better food source (a superior solution), they may decide to abandon the current food source and explore other possibilities. The upper limit for this consecutive iteration count is determined by the “limits” parameter. When limits is set to 500, it exceeds the iteration count of 100. This implies that the bee colony will not abandon the current candidate solution to explore other solutions during the optimization process.

From the comparative results (Figure 4), it can be observed that, for the TEM inversion optimization problem, the “limits” parameter does not have a significant impact on the optimization process. It can be set to a value greater than the number of optimization iterations. Additionally, when the population size is set to 50, the difference in optimization performance compared to a population size of 100 is not pronounced. Noticeable improvements in performance require a population size of 500, but this comes at a substantial computational cost.

For the WOA, we conducted comparisons using different probability values to determine the hunting behavior of whales (Figure 5). In each set of comparisons, the probability (p) ranged from 0.1 to 0.9. We conducted a total of three sets of experiments. It was observed that for the TEM inversion optimization problem, the optimal fitness values corresponding to different probabilities were quite similar, and the results varied each time. We decided to align our parameter selection with other research studies, choosing p = 0.5.

Similarly, we also conducted tests for the parameters β and κ in the WOA algorithm (Figure 6). The situation for these two parameters was similar to the probability (p) setting, where there was no clear trend indicating an optimal value for the TEM inversion optimization problem. We opted to align our parameter selection with other research studies.

5. Simulation Experiment

After defining the evaluation index of the inversion optimization model, we used a three-layer geoelectric model example to verify the effectiveness of the proposed method, and a four-layer geoelectric model example to highlight the advantages of the proposed method. Moreover, the proposed method was tested with noise resistance at different noise levels, and with a 3D geoelectric model.

5.1. Evaluation Indicator

This paper shows an example of extracting IP information from TEM observation signals using the improved WOA inversion method. To validate the effectiveness of the presented algorithm, three theoretical geoelectric models were designed. The algorithm simulation was executed in MATLAB R2023a to evaluate the inversion achievement of the presented algorithm on a CPU Core (TM) i7-9750 running at a frequency of 4.50 GHz and equipped with 64 GB RAM. In this study, the fitness of TEM responses and geoelectric models was assessed through the utilization of the mean-square error (MSE) and total relative error (TRE):

$$\mathrm{MSE}=\frac{1}{N_t}{\displaystyle \sum _{i=1}^{N_t}\frac{\left|d_i^{obs}{}_i-d_i^{pre}\right|}{\left|d_i^{obs}\right|}\times 100\%},$$

(20)

$$\mathrm{TRE}={\displaystyle \sum _{j=1}^{N_m}\left|\frac{m_{j,syn}-m_{j,pred}}{m_{j,pred}}\right|}\times 100\%$$

(21)

where d^pred is the vertical magnetic field response data with IP information predicted by inversion, d^obs is the observation response signals, and N_t denotes the channel count of observation windows. m_pred denotes the inverted value, and m_syn signifies the actual value of the geoelectric model, with N_m representing the count of parameters within the geoelectric model. Among the above indicators, MSE represents the prediction error and TRE represents the relative error of the geoelectric model. The smaller their values, the better the inversion performance.

5.2. Three-Strata Geoelectric Model

Considering the inversion of a three-strata geoelectric K-type Dias model, the resistivity values for each layer are as follows: ρ₁ = 50 Ω·m, ρ₂ = 200 Ω·m and ρ₃ = 10 Ω·m. Additionally, the corresponding layer thicknesses are h₁ = 100 m and h₂ = 200 m. Let the IP effect exist in different layers, and the polarization parameter m = 0.3; in this case, three sets of TEM response data can be generated. The IP information carried by each group of TEM responses is different. Through the inversion, we can analyze how each layer’s IP effect impacts the accuracy of the inversion.

In the inversion optimization, there are a total of six parameters for optimizing the position of whales, which are three parameters representing the resistivity information of each layer, two parameters representing the layer thickness information of the first two layers, and the remaining one parameter representing the polarization parameters. In inversion optimization, the number of iterations is 20. The MSE and TRE of the inversion outcomes show that the lower the three evaluation values, the better the TEM inversion fitting performance, and the less it is influenced by the induced polarization (

Table 1. TEM inversion results with IP effect for the K-type geoelectric model with three strata.

K-Type Model	MPE	TRE (%)
1st layer IP	0.17	25.43
2nd layer IP	0.21	32.21
3rd layer IP	0.12	13.50

).

From the results, it can be seen that when there is an induced polarization effect in the third layer, the geoelectric structure is most accurately restored. This is because this layer is considered as a structure that extends infinitely downwards, and multiple TEM response signals carry electrical information of this layer, which can be utilized more in the inversion optimization process. The induced polarization reduction accuracy of the first layer is higher than that of the second layer, because the electrical information of the first layer is carried in the early TEM response signal, which has a larger amplitude and occupies a greater weight in the inversion optimization process.

In the inversion outcomes for the three-stratum geoelectric model, the proposed inversion technique demonstrated reduced MSE and TRE fitting errors, regardless of the layer in which the IP effect was present. Notably, the best predictive performance in TEM inversion was observed when the IP effect existed at the lowest level; TEM inversion had the best prediction effect. When the IP effect occurred at the shallowest stratum, while the performance was relatively poorer when the IP effect existed in the middle layer. Figure 7 shows the inversion prediction geoelectric models corresponding to different polarization modes, the fitting of TEM response, and the variation of WOA fitness with iterative optimization.

For the three-strata geoelectric structure with a K-type, the proposed improved WOA can accurately predict the geoelectric structure including resistivity, thickness, and polarizability parameters (Figure 7). The TEM response signals generated by the geoelectric structure have a high fitting degree with the theoretical response data. Throughout the inversion optimization process, the iteration remains stable, minimizing the risk of converging towards local extremes. The outcomes of the inversion indicate that the enhanced WOA nonlinear optimization method, incorporating the opposition-based learning strategy and adaptive weighted factor, consistently maintains stable TEM inversion capabilities, thereby achieving accurate geoelectric structure inversion that incorporates IP information.

5.3. Four-Strata Geoelectric Model

To additionally confirm the efficacy of the introduced approach, a four-strata geoelectric model with a KH-type was established. The efficiency of the presented approach was benchmarked against the particle swarm optimization (PSO) algorithm [53,54], the artificial bee colony (ABC) algorithm [55] and the differential evolution (DE) algorithm [49]. The resistivity values for each layer were specified as follows: ρ₁ = 100 Ω·m, ρ₂ = 300 Ω·m, ρ₃ = 50 Ω·m and ρ₄ = 200 Ω·m, with the corresponding layer thicknesses as h₁ = 100 m, h₂ = 200 m, and h₃ = 400 m. The polarizability parameters m₂ and m₃ both had a value of 0.3. The initial parameters of all the heuristic biomimetic algorithms are outlined in

Table 2. Simulation parameter configurations for the four-strata geoelectric model with KH-type.

Parameter Type	Parameter Setting
PSO algorithm parameter	c1 = c2 = 2, w1 = 0.9, w2 = 0.4, P = 20, itermax = 20
DE algorithm parameter	F = 0.6, CR = 0.8, P = 20, itermax = 20
ABC algorithm parameter	limits= 50, P = 20, itermax = 20
WOA parameter	P = 20, p = 0.5, itermax = 20
Improved WOA parameter	P = 20, p = 0.5, κ = 1, β = 0.5, itermax = 20

.

The execution process of PSO was referenced from the literature [37,39,56], and specific parameter details can be found in the references [39,56]. The choice of the parameter setting was made to maintain consistency with the design of the introductory research and to avoid any misunderstandings arising from hyperparameter tuning. The parameters in WOA were selected based on the parameters in reference [24]. The parameters of DE were selected based on the parameters in reference [56]. The parameters in ABC were chosen by referencing the parameters in PSO, WOA, and DE, ensuring consistency between the population size and the number of iterations.

The IP effect was introduced into the middle stratum of the Dias geoelectric model. The fitting accuracy of the TEM response for inversion prediction and the fitting accuracy of the geoelectric model are shown in

Table 3. Inversion performance for various nonlinear inversion algorithms.

KH-Type Model	MSE (%)	TRE (%)	Cost Time
PSO	0.29	117.05	13.80 min
DE	0.25	89.35	13.56 min
ABC	1.32	194.52	15.63 min
WOA	0.13	70.84	13.88 min
Improved WOA	0.08	27.03	22.36 min

. When compared to the performance of the PSO, DE and ABC algorithms, the WOA method achieved better predictive fitting performance. This shows that the encircling prey and spiral updating strategies in WOA are helpful in handling TEM inversion with IP effects, and have better global search ability for such nonlinear optimization inversion.

The enhanced WOA exhibited notably superior inversion performance compared to the standard WOA, owing to the integration of the OBL strategy for generating the initial population. This strategy extended the search range of whales through random expansion, consequently bolstering the optimization capability. Then, adaptive weighted factors were applied to control the relationship between local optimization and global optimization. These two measures were used to improve WOA enhance global search capabilities, improve convergence performance in the IP-information search optimization, and largely prevent premature convergence.

Figure 8 illustrates the detailed fitting outcomes of the layered structure and induced TEM response signals, along with the progression of fitness changes during the optimization procedure involving diverse heuristic algorithms. In the context of the four-stratum geoelectric model, the proposed algorithm proficiently recovered parameters like resistivity, thickness, and polarizability. Moreover, the inversion data for TEM inductive Hz aligned well with the anticipated values.

The convergence behavior of various comparative methods is shown in Figure 9. These methods gradually converged after 10 iterations, and we have presented the results for 20 iterations. The accuracy of other methods did not reach the level achieved by our proposed WOA algorithm after 10 iterations, or even after 20 iterations. The above results show that the non-linear improved WOA model based on the OBL strategy and AWF has a better global search capability and higher inversion accuracy, and is suitable for IP information extraction.

5.4. Stability Test

To more effectively evaluate the practical application of the presented method in inversing measured data, the inversion stability and robustness of the algorithm for TEM data with different noise levels were compared. A five-strata HKH-type Dias geoelectric model was used to implement testing. The resistivity values for each layer were as follows: ρ₁ = 300 Ω·m, ρ₂ = 200 Ω·m, ρ₃ = 500 Ω·m, ρ₄ = 50 Ω·m and ρ₅ = 1000 Ω·m. Additionally, the corresponding layer thicknesses were h₁ = 100 m, h₂ = 200 m, h₃ = 300 m and h₄ = 500 m. The polarizability parameters m₃ and m₄ were both 0.3.

The inversion performance of the proposed algorithm on noisy TEM data under 5% and 10% noise levels were compared (

Table 4. Inversion accuracy with noise data.

HKH-Type Model	MSE (%)	TRE (%)	Cost Time
no noise	3.23	125.25	23.54 min
5% noise	9.49	150.71	27.76 min
10% noise	15.21	182.04	30.23 min

). The MSE and TRE inversion misfit increased gradually with the increase in noise, but the proposed algorithm always ensured lower inversion errors due to OBL and adaptive weighted factors that enhanced the robustness of the WOA. In addition, the calculation time of the inversion of the five-stratum model increased compared with the three-stratum and four-stratum models due to the expanded number of parameters subject to optimization.

Figure 10 displays the inversion-predicted geoelectric structure, the alignment status of the time-domain-induced signals generated by the five-stratum model, and the evolution of the WOA’s fitness during iterative optimization. For noise-free data, the proposed algorithm achieved the precise reconstruction of resistivity, thickness and induced polarized parameters for the presumed geoelectric model, yielding a predictive fitness (MSE) of 3.23%. For the data with 5% and 10% random noise, the resistivity, thickness, and polarizability parameters could be roughly characterized by basic trends, but level of precision in depicting details decreased.

5.5. SMS Model Test

We prepared a 3D simulation model of a seafloor massive sulfide (SMS) deposit. We set the resistivity of the mineral overlying layer to 10 Ω·m. SMS was formed in magmatic hydrothermal upwelling, and there were strong, medium and weak alteration regions with electrical resistivity values of 0.5, 1 and 2 Ω·m, respectively. In addition, there were also magmatic upwelling channels (yellow blocks) that were not fully in contact with the overlying layer and buried SMS sedimentary minerals (black blocks). We used the Cole–Cole model to simulate the induced polarization effect, and the m, t and c parameters were 0.3, 0.1 and 0.2, respectively. The perspective view, top view and slice of the 3D model are shown in Figure 11.

The inversion results of the proposed method were compared with those of the traditional gradient inversion method, as shown in Figure 12. The traditional inversion method of gradient class adopts OCCAM inversion; the specific implementation and inversion stopping strategy are referred to the literature. Due to the lack of a strategy for retrieving the induced polarization parameters, the inversion results of slices at y = 70 m and y = 110 m showed that the gradient inversion cannot accurately restore the preset SMS geoelectric structure. The inversion slices of the proposed IWOA showed that the basic electrical structural features of the magmatic hydrothermal upwelling channels, the alteration regions and the buried SMS minerals can be effectively characterized. This shows that the proposed TEM inversion framework based on IWOA can effectively consider the induced polarization effect in electrical media.

6. Conclusions

An inversion framework of a transient electromagnetic method based on WOA was proposed. Compared with the traditional gradient inversion method, this heuristic algorithm is more suitable for TEM inversion optimization under the IP effect. Not only that, we also upgraded the inversion framework with OLB and AWF strategies.

Three examples of geoelectric models showed that the proposed improved WOA can accurately predict the geoelectric structure and IP parameters while considering the IP effect. Comparing the fit of the geoelectric model and the variation in fitness during the optimization process revealed the enhanced accuracy and optimization capability of the proposed WOA over alternative heuristic inversion algorithms. The results showed that the initial population generated based on OBL fosters a wider search range and even distribution in the initial phase, thereby promoting population diversity and enhancing global search capabilities. And the adaptive weighted factor contributes to securing convergence speed and stability during the later stages, thereby enhancing the precision and resilience of IP information extraction.

Moreover, the TEM inversion ability of WOA was tested with the inversion optimization with 5% and 10% noise data, and the stability of TEM inversion based on WOA was verified.

Our future work will consider further combining the heuristic algorithm framework with deep neural networks. First, deep neural networks will be used to characterize electrical anomaly targets with induced polarization effects, and then heuristic algorithms will be used to accurately obtain resistivity information and induced polarization information.