An Optimized Control Method of Soft-Switching and No Backflow Power for LLC Resonant-Type Dual-Active-Bridge DC-DC Converters
Abstract
:1. Introduction
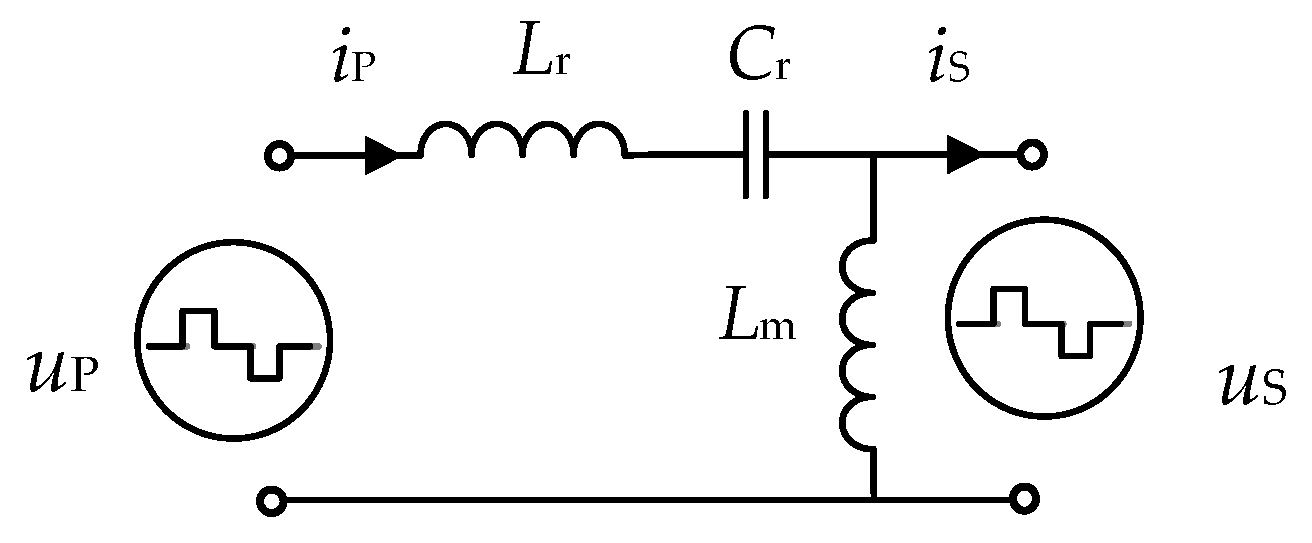
2. Principle of LLC-DAB DC-DC Converter
2.1. Principle of Power Transmission
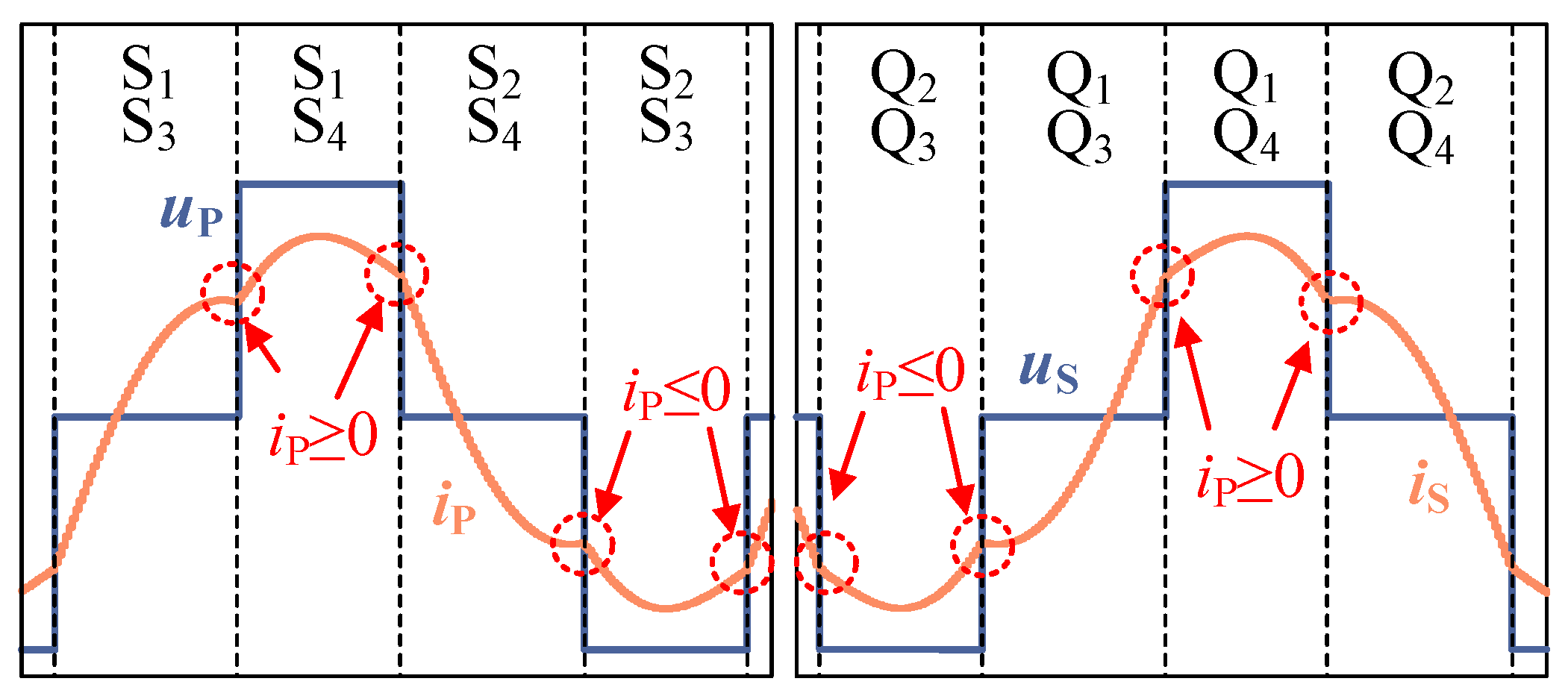
2.2. Principle of LLC-DAB Operation with DPS Modulation
3. Operating Characteristics of LLC-DAB DC-DC Converter
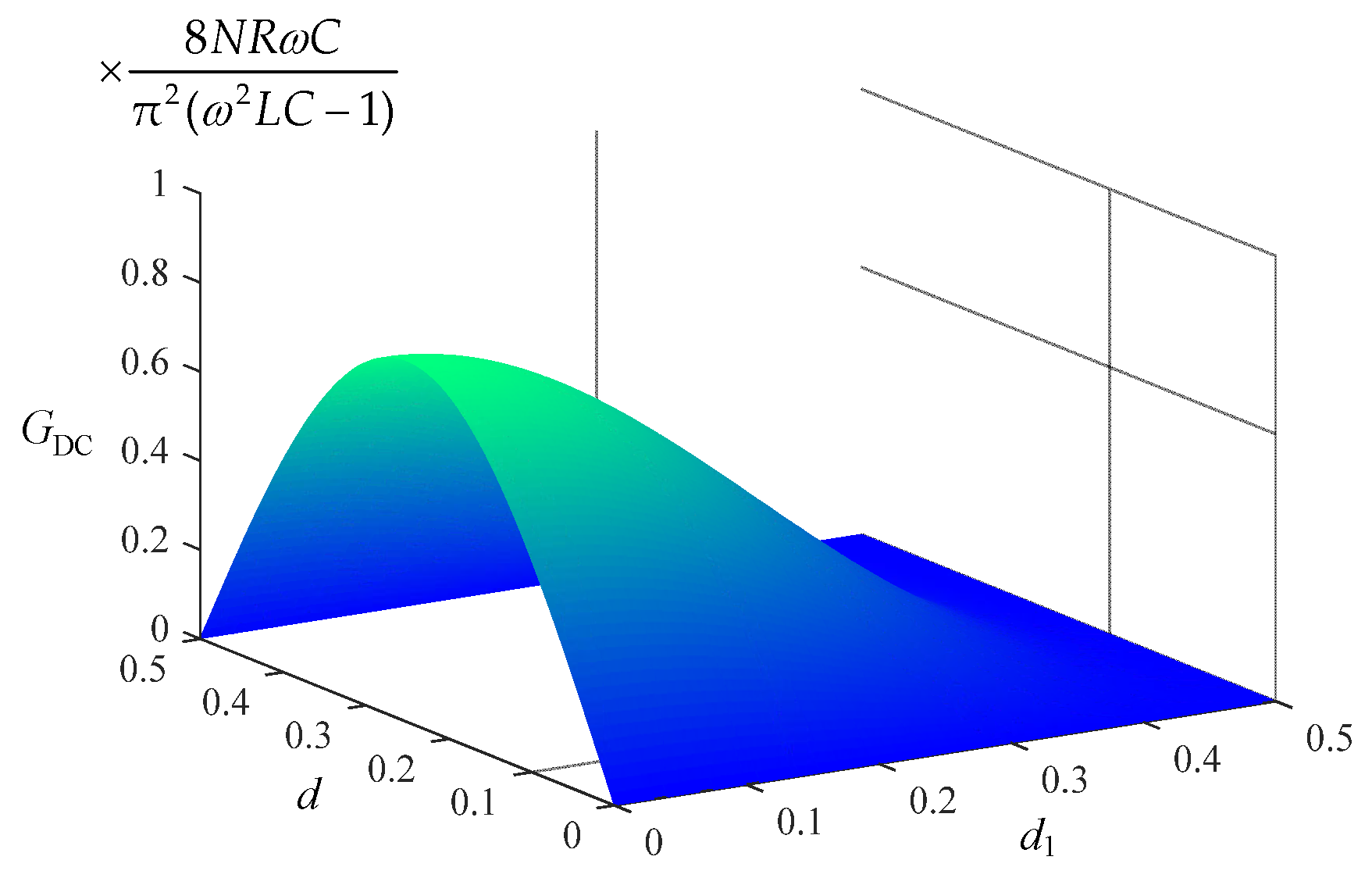
3.1. Voltage Gain Characteristics
3.2. Current Gain Characteristics
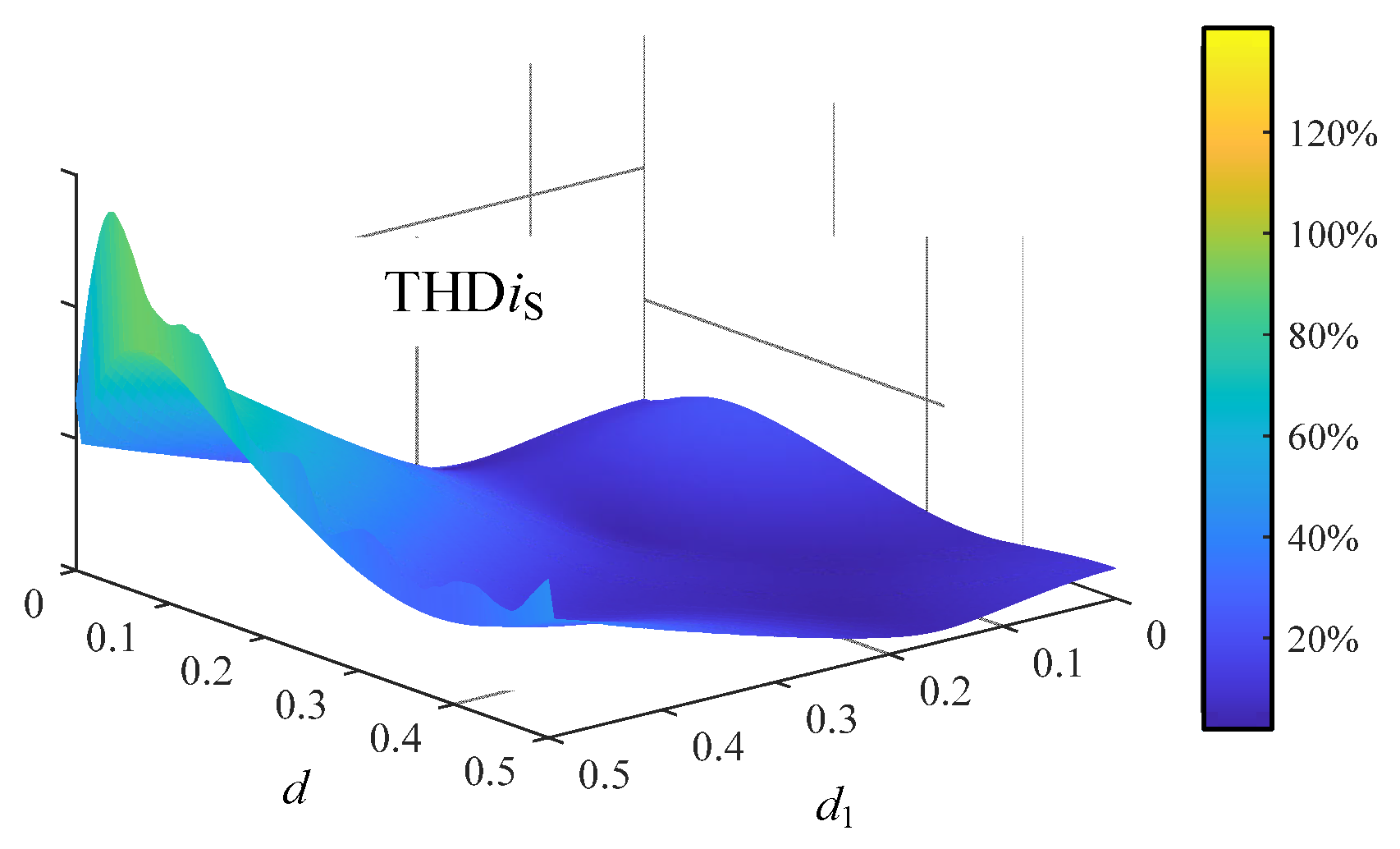
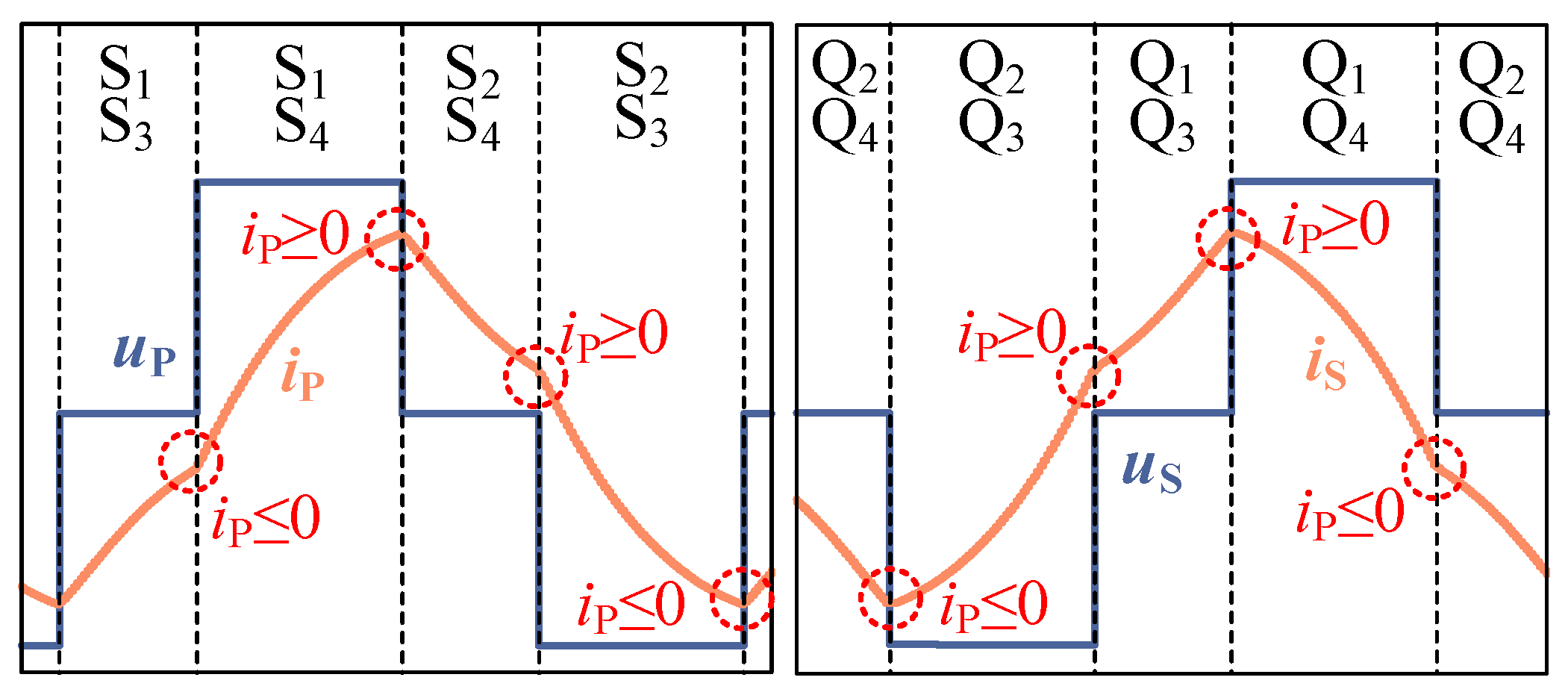
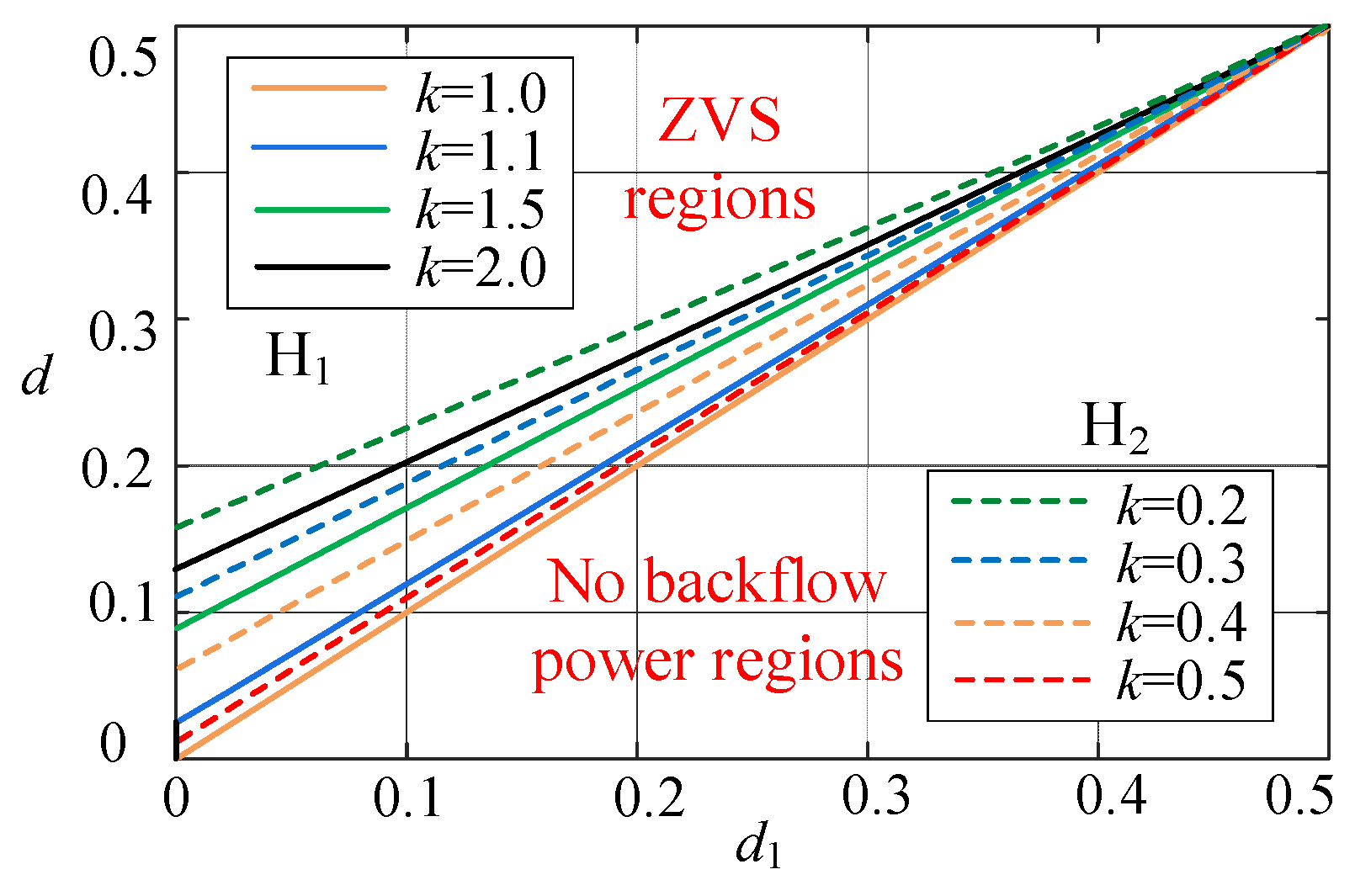
3.3. Backflow Power and Soft-Switching Characteristics
4. Soft-Switching and No Backflow Power Optimized Control Method with DPS Modulation
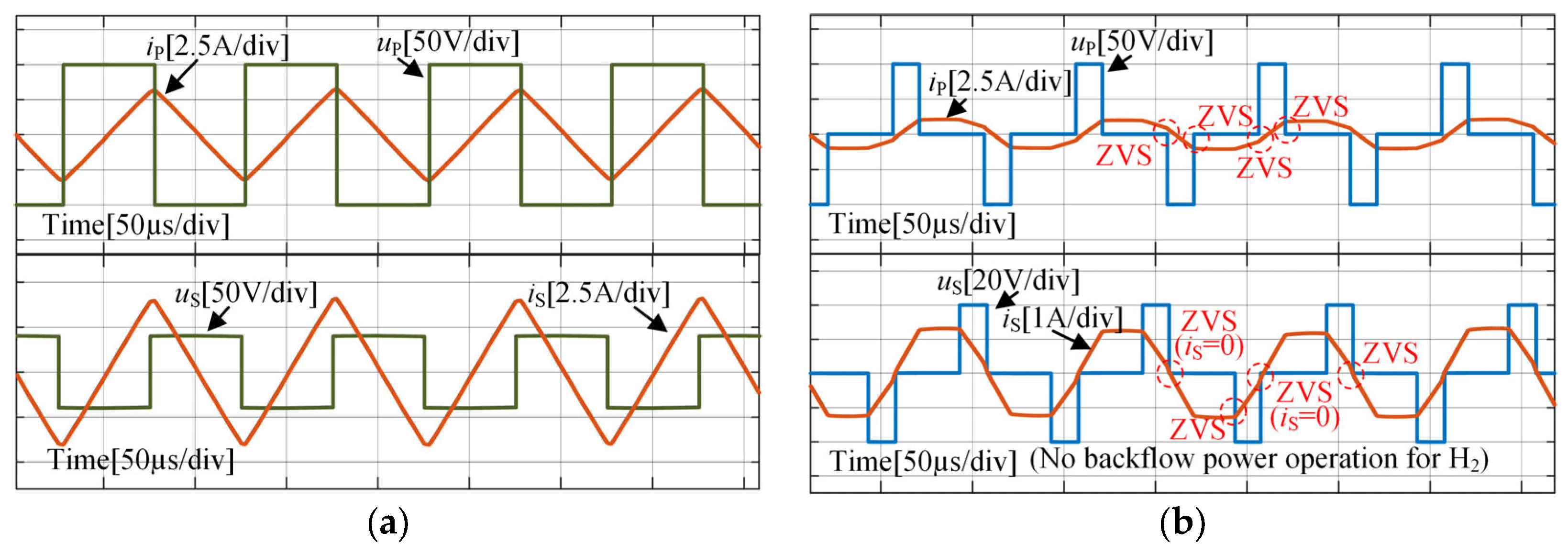
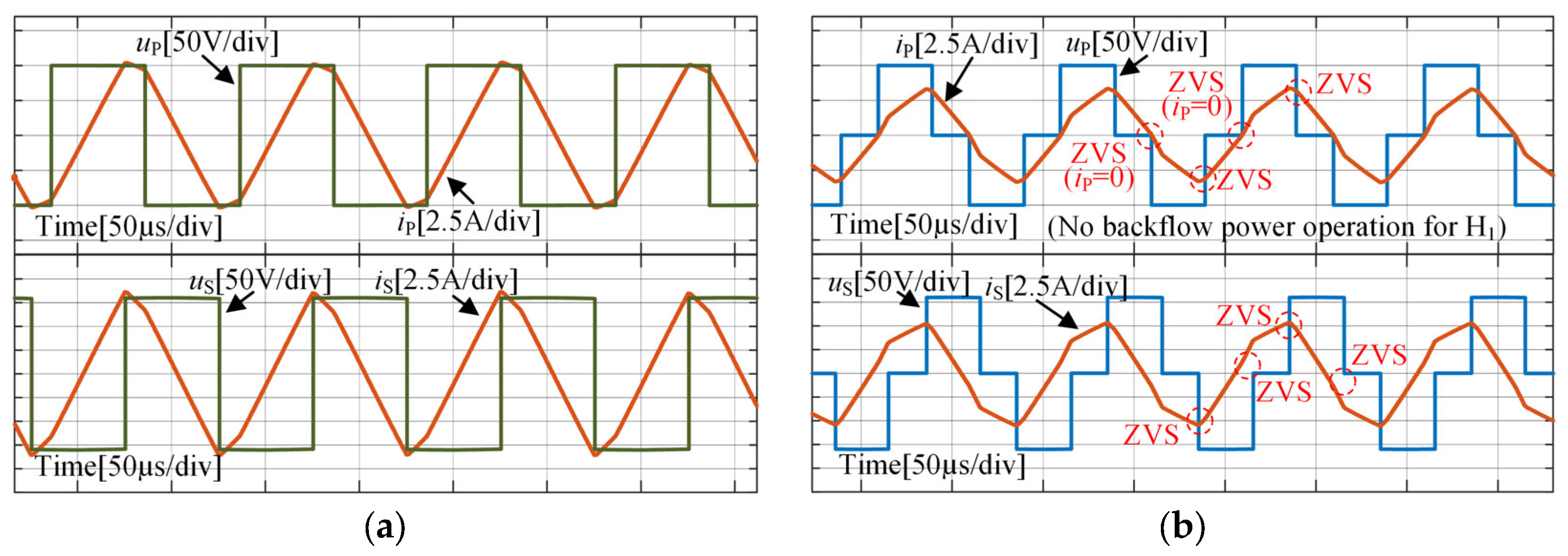
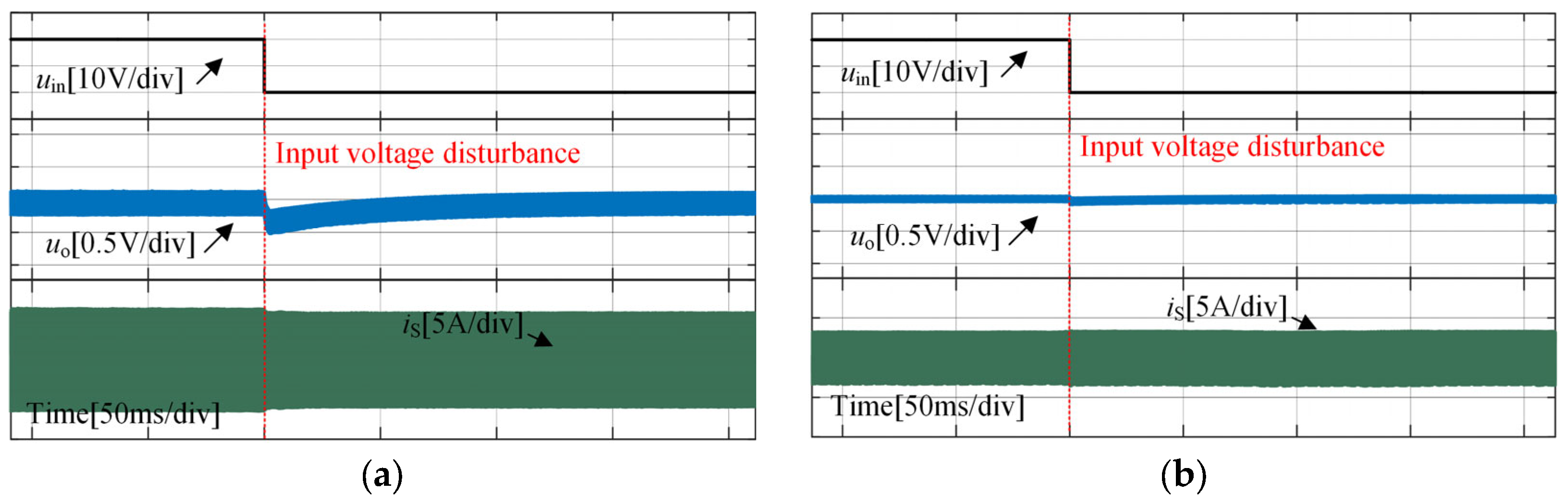
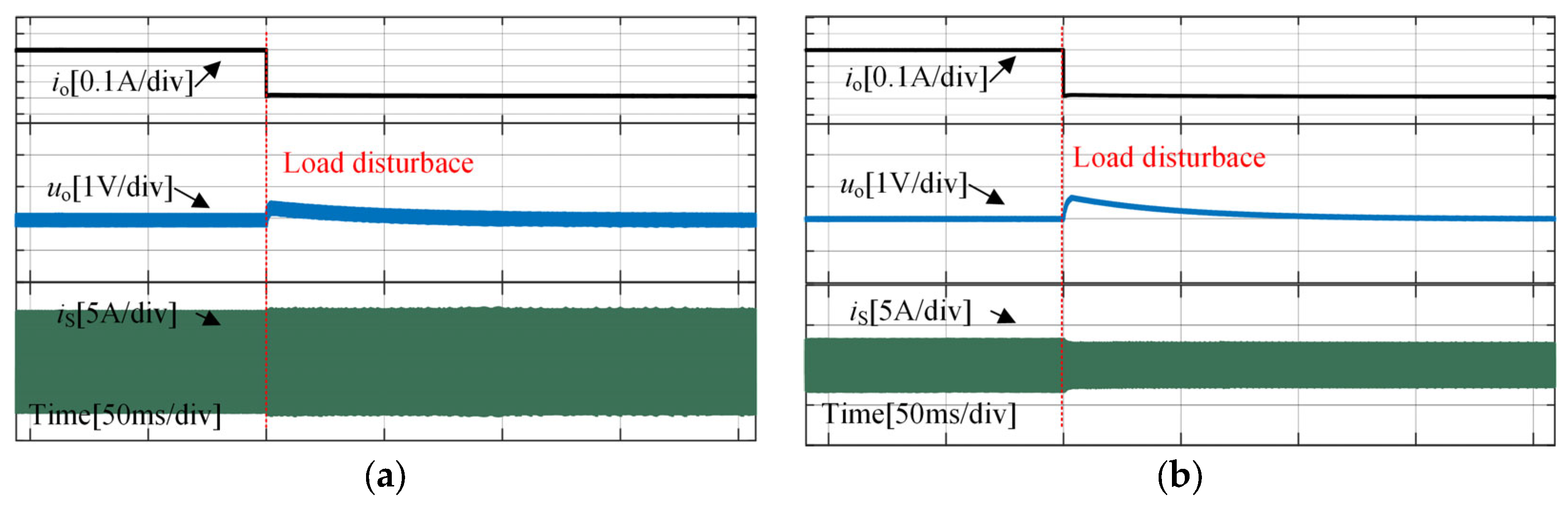
5. Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Lr, Lm | Filter inductor |
| Cr | Filter capacitor |
| N:1 | Turn ratio of the transformer |
| Uin, Uo | DC input voltage and DC output voltage |
| Cdc1, Cdc2 | DC filter capacitor |
| R | Resistance of the load |
| uP, uS | AC output voltages of the H1 bridge and H2 bridge |
| iP, iS | Currents of the inductor Lr and the primary side of the transformer |
| d | Outer phase shift ratio |
| d1 | Inner phase shift ratio |
| T | Switching period |
| fs | Switching frequency |
| ω | Resonant frequency |
| P | Transmission power |
| GDC | DC voltage gain |
| THDiP, THDiS | Total harmonic distortion of iP and iS |
References
- Inoue, S.; Akagi, H. A bi-directional isolated DC/DC converter as a core circuit of the next-generation medium-voltage power conversion system. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006. [Google Scholar] [CrossRef]
- Akagi, H.; Kinouchi, S.I.; Miyazaki, Y. Bidirectional isolated dual-active-bridge (DAB) DC-DC converters using 1.2-kV 400-A SiC-MOSFET dual modules. CPSS Trans. Power Electron. Appl. 2016, 1, 33–40. [Google Scholar] [CrossRef]
- Oswald, N.; Anthony, P.; Mcneill, N.; Stark, B.H. An Experimental Investigation of the Tradeoff between Switching Losses and EMI Generation with Hard-Switched All-Si, Si-SiC, and All-SiC Device Combinations. IEEE Trans. Power Electron. 2014, 29, 2393–2407. [Google Scholar] [CrossRef]
- Du, Y.; Lukic, S.; Jacobson, B.; Huang, A. Review of High Power Isolated Bi-directional DC-DC Converters for PHEV/EV DC Charging Infrastructure. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 31 October 2011. [Google Scholar] [CrossRef]
- Song, W.; Hou, N.; Wu, M. Virtual Direct Power Control Scheme of Dual Active Bridge DC–DC Converters for Fast Dynamic Response. IEEE Trans. Power Electron. 2017, 27, 1750–1759. [Google Scholar] [CrossRef]
- Zhao, B.; Yu, Q.; Sun, W. Extended-Phase-Shift Control of Isolated Bidirectional DC–DC Converter for Power Distribution in Microgrid. IEEE Trans. Power Electron. 2012, 27, 4667–4680. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, Z.Q.; Stone, D.A.; Foster, M.P.; Chu, W.Q.; Urquhart, I.; Greenough, J. Novel Dual Phase Shift Control with Bi-directional Inner phase shifts for Dual Active Bridge Converter Having Low Surge Current and Stable Power Control. IEEE Trans. Power Electron. 2016, 32, 4095–4106. [Google Scholar] [CrossRef]
- Wu, K.; Wdesilva, C.; Gdunford, W. Stability Analysis of Isolated Bidirectional Dual Active Full-Bridge DC–DC Converter with Triple Phase-Shift Control. IEEE Trans. Power Electron. 2012, 27, 2007–2017. [Google Scholar] [CrossRef]
- Wen, H.; Zheng, L. Minimum Backflow Power Control of Bidirectional Isolated DC-DC Converters. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems, Chennai, India, 18–21 December 2018. [Google Scholar] [CrossRef]
- Chu, Y.; Wang, S. Bi-directional isolated DC-DC converters with reactive power loss reduction for electric vehicle and grid support applications. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo, Dearborn, MI, USA, 18–20 June 2012. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H.; Hu, Y.; Jiang, L. Reactive Power Minimization in Bidirectional DC–DC Converters Using a Unified-Phasor-Based Particle Swarm Optimization. IEEE Trans. Power Electron. 2018, 33, 10990–11006. [Google Scholar] [CrossRef]
- Garcia-Bediaga, A.; Villar, I.; Rujas, A.; Mir, L. DAB modulation schema with extended ZVS region for applications with wide input/output voltage. IET Power Electron. 2018, 11, 2109–2116. [Google Scholar] [CrossRef]
- Liao, Y.; Xu, G.; Peng, T.; Sun, Y.; Liu, D.; Yang, Y.; Su, M. An LLC-DAB Bidirectional DCX Converter with Wide Load Range ZVS and Reduced Switch Count. IEEE Trans. Power Electron. 2022, 37, 2250–2263. [Google Scholar] [CrossRef]
- Wang, M.; Pan, S.; Zha, X.; Gong, J.; Lin, W.; Gao, J.; Deng, Q. Hybrid Control Strategy for an Integrated DAB-LLC-DCX DC-DC Converter to Achieve Full-Power-Range Zero-Voltage Switching. IEEE Trans. Power Electron. 2021, 36, 14383–14397. [Google Scholar] [CrossRef]
- Liu, C.; Liu, H.; Cai, G.; Cui, S.; Liu, H.; Yao, H. Novel Hybrid LLC Resonant and DAB Linear DC-DC Converter: Average Model and Experimental Verification. IEEE Trans. Ind. Electron. 2017, 64, 6970–6978. [Google Scholar] [CrossRef]
- Gopiyani, A.; Patel, V. A closed-loop control of high power LLC Resonant Converter for DC-DC applications. In Proceedings of the 2011 Nirma University International Conference on Engineering, Ahmedabad, India, 8–10 December 2011. [Google Scholar] [CrossRef]
- Liu, C.; Xing, X.; Du, C.; Zhang, B.; Zhang, C.; Blaabjerg, F. An Improved Model Predictive Control Method Using Optimized Voltage Vectors for Vienna Rectifier with Fixed Switching Frequency. IEEE Trans. Power Electron. 2023, 38, 358–371. [Google Scholar] [CrossRef]
- He, L.; Cheng, C. A Bridge Modular Switched-Capacitor-Based Multilevel Inverter with Optimized SPWM Control Method and Enhanced Power-Decoupling Ability. IEEE Trans. Ind. Electron. 2018, 65, 6140–6149. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]





| Symbol | Value | Symbol | Value |
|---|---|---|---|
| Uo(1) | 20 V | k(1) | 0.4 |
| Uo(2) | 50 V | k(2) | 1 |
| Uo(3) | 80 V | k(3) | 1.6 |
| Uin | 100 V | R | 50 Ω |
| L | 1.15 mH | N | 2 |
| C1 | 2.2 μF | fs | 10 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, M.; Zhao, Y.; Wang, Z.; Yu, D.; Xu, R. An Optimized Control Method of Soft-Switching and No Backflow Power for LLC Resonant-Type Dual-Active-Bridge DC-DC Converters. Mathematics 2023, 11, 287. https://doi.org/10.3390/math11020287
Li Z, Li M, Zhao Y, Wang Z, Yu D, Xu R. An Optimized Control Method of Soft-Switching and No Backflow Power for LLC Resonant-Type Dual-Active-Bridge DC-DC Converters. Mathematics. 2023; 11(2):287. https://doi.org/10.3390/math11020287
Chicago/Turabian StyleLi, Zimeng, Mingxue Li, Yushun Zhao, Zixiang Wang, Dongsheng Yu, and Ruidong Xu. 2023. "An Optimized Control Method of Soft-Switching and No Backflow Power for LLC Resonant-Type Dual-Active-Bridge DC-DC Converters" Mathematics 11, no. 2: 287. https://doi.org/10.3390/math11020287





