Analysis of a Multi-Server Queue with Group Service and Service Time Dependent on the Size of a Group as a Model of a Delivery System

Abstract

In this paper, we consider a multi-server queue with a finite buffer. Request arrivals are defined by the Markov arrival process. Service is provided to groups of requests. The minimal and maximal group sizes are fixed. The service time of a group has a phase-type distribution with an irreducible representation depending on the size of the group. The requests are impatient. The patience time for an arbitrary request has an exponential distribution. After this time expires, the request is lost if all servers are busy or, if some server is idle, with a certain probability, all requests staying in the buffer start their service even if their number is below the required minimum. The behavior of the system is described by a multi-dimensional continuous-time Markov chain that does not belong to the class of level-independent quasi-birth-and-death processes. The algorithm for the computation of the stationary distribution of this chain is presented, and expressions for the computation of the queuing system’s performance characteristics are derived. The description of a delivery system operation in terms of the analyzed queuing model is given, and the problem of the optimization of its operation is numerically solved. Multi-server queues with a phase-type distribution for the group service time that are dependent on the size of the group, the account of request impatience, and the correlated arrival process have not previously been analyzed in the existing literature. However, they represent a precise model of many real-world objects, including delivery systems.

1. Introduction

The problem of the optimal management of various goods and grocery delivery has become especially important due to the quick development of ordering via the Internet over the last few years. In particular, COVID-19 caused this development due to the better isolation of members of society achieved via online shopping. The business model of delivery systems suggests, as a rule, the collection of customer orders via the Internet and then the delivery of the ordered items to the customers via some transport vehicles. Typically, the size and weight of orders may not be very large, and a vehicle can deliver several orders simultaneously. Therefore, because the orders are generated at random moments, the number of orders uploaded into a vehicle is random, and the delivery times are random, adequate mathematical modeling of a delivery system can be done within the borders of the theory of queues with group service.

In this paper, we build and analyze a queuing model for a delivery system. Generally speaking, the process of providing a service to a customer in a delivery system consists of two phases. The first phase corresponds to registering the orders obtained via the Internet or phone and packing them into some containers designed for item delivery. The second phase corresponds to the delivery of these containers (throughout the paper, we call them requests) to the customers by the vehicles. A corresponding two-phase (tandem) queuing model was recently analyzed in [1]. The essential restriction of the model considered in [1] is the assumption that a single vehicle performs a delivery. This suggestion does not hold in many large real-world delivery systems. In this paper, we consider only the second phase of the delivery process, with the assumption that the fleet of available vehicles can have many items.

1.1. Short Literature Review

Queuing models with a group service have been a focus of research for about seventy years (see, e.g., the papers [2,3]). As early works, we can also mention [4,5,6,7,8]. Some surveys of relevant research can be found, e.g., in [9,10,11,12,13,14,15,16,17]. The overwhelming majority of papers devoted to queues with a group service assume that the stationary Poisson process is an arrival flow. But, this process poorly describes flows in many real-world systems. Essential restrictions of the stationary Poisson process are assumptions of a constant arrival rate that does not fluctuate during the system’s operation and has values of 1 and 0 for the coefficients of variation and correlation of the inter-arrival times, respectively. Models with an arbitrary distribution of inter-arrival times have been analyzed, e.g., in [18,19,20].

Another possibility for modeling in a more general way than the stationary Poisson arrival process is the model of the Markov arrival process ($MAP$) mentioned above, which has been known since the early 1990s. Queuing systems with the $MAP$ and group service have been considered, e.g., in papers [1,11,15,16,17,21,22,23,24,25,26,27,28,29,30,31,32].

The majority of these papers consider single-server queues. To the best of our knowledge, multi-server queues with a group service and the $MAP$ flow (or generalization of the $MAP$ to the case of batch arrivals, that is, the batch Markov arrival process) were considered only in Refs. [33,34], where systems with an infinite and a finite buffer were dealt with, respectively; Ref. [35], where the number of servers in a system from [34] can vary; Ref. [36], where a two-server queue was under study; and [12], where the retrial queuing model $BMAP/M/c$ with a constant retrial rate was considered.

1.2. Disadvantages of Previous Research

The models of multi-server queues with the $MAP$ (or $BMAP$) and group service considered in the papers [12,33,34,35,36] have some disadvantages in terms of the following aspects:

• The service time distribution is assumed to be exponential, while a more general $PH$ distribution should be considered. This would allow significantly better fitting of the actual distributions of service time in real-world systems;
• The possible impatience of requests, which is an inherent feature of many real-world systems, see, e.g., [37], is not taken into account;
• Service can only be provided to groups with fixed minimum and maximum sizes in [12,33,34,35,36]. In some real-world systems, the service of groups of sizes that are less than the fixed minimum is allowed if a request loss due to impatience can occur;
• Definitely, the service time of a group may depend on the size of the group. Such a dependence is assumed in this paper. Among the papers [12,33,34,35,36], such a dependence was considered only for a two-server queue in [36].

Due to the possible applicability of the considered queuing model to a variety of real-world systems, it is important to analyze models that are free from these disadvantages.

1.3. Aim of the Study

Taking into account the listed disadvantages, the aim of this paper is formulated as follows. We intend to analytically and numerically build and investigate a queuing model of a delivery system that satisfies the following requirements:

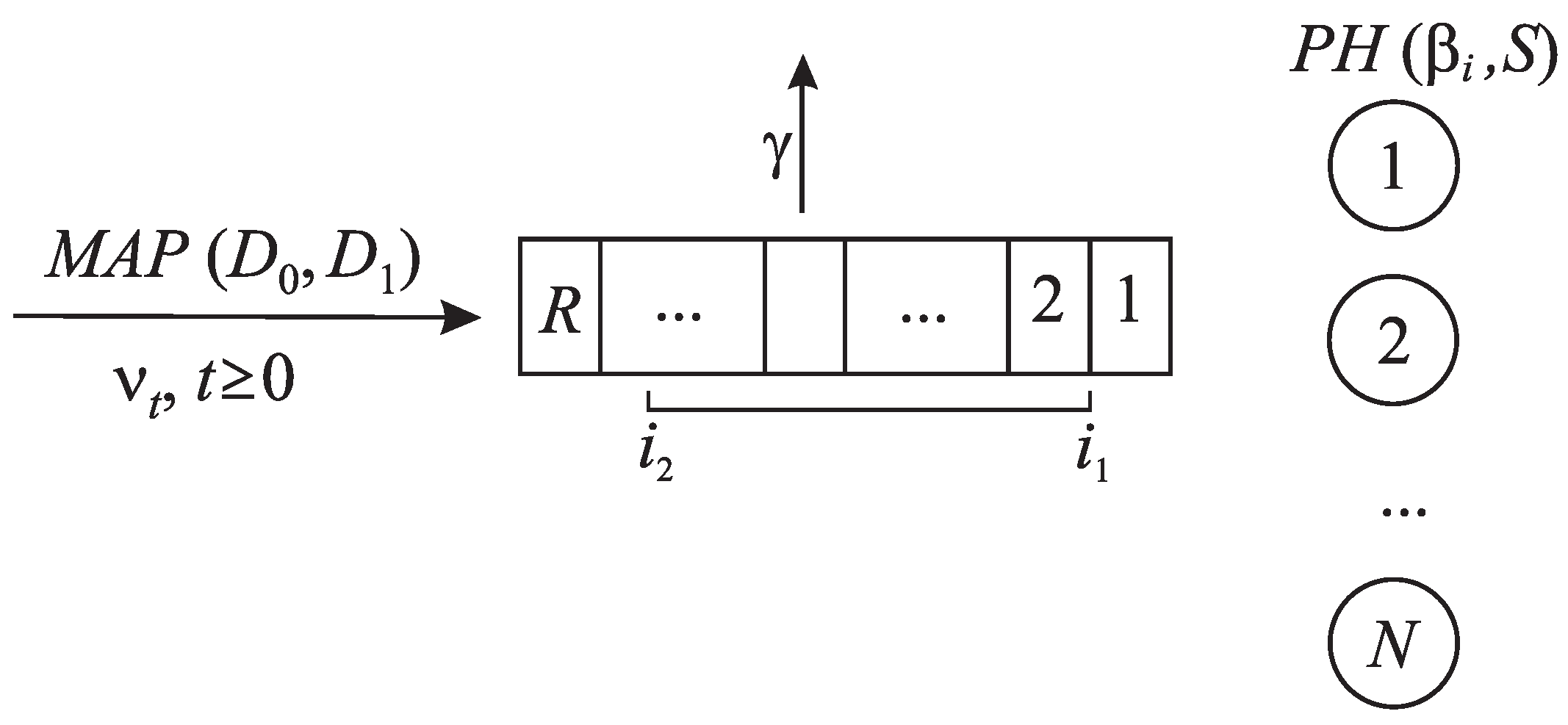
• A finite number of vehicles provide delivery, and this number can be greater than one. The minimal and maximal values of the sizes of groups to which a service can be provided are fixed;
• The process of request arrival has to take into account the typical features of real flows of orders. Namely, inter-arrival times can have a wide range of initial moments (mean value, variance, the third, fourth, etc.) and a wide range of values for the coefficient of correlation of successive inter-arrival times. The instantaneous arrival rate may essentially fluctuate during the system’s operation. This account will be done via the assumption that the requests arrive in the $MAP$. For more information about such a process, see, e.g., [38,39,40,41,42,43];
• The possible impatience (perishability, obsolescence, etc.) of requests has to be taken into account. To satisfy this requirement, we assume that after a random time interval (with an exponential distribution), the waiting request is canceled (lost) if all vehicles are busy. If at least one vehicle is idle, the system makes a randomized choice among the options to lose a request or to start the delivery process, even if the number of requests in the buffer is below the preassigned minimum;
• The delivery time of a group of requests has to depend on the number of requests in the group. Typically, the delivery of a group of requests from a warehouse to customers residing in some area consists of a permanent part, which is the transportation time between the warehouse and this area, a time for each container to upload into the vehicle, and an individual delivery time inside the area. To satisfy this requirement, we assume that the delivery (service) time has a phase-type ($PH$) distribution with an irreducible representation depending on the size of the group. For more information about the $PH$ distribution and its usefulness in stochastic modeling, see, e.g., [44];
• Algorithms for the computation of the stationary distribution of the system’s states and its main performance characteristics should provide a high computation speed for a not very large number of vehicles and buffer size. The number of vehicles (servers) and the capacity of the buffer for waiting requests should not be very small and should match the corresponding parameters of real-world systems. This requirement is explained by the necessity of using algorithms to solve various optimization problems, which require the computation of the performance measures of the system for different values of its parameters, including the capacity of the buffer and the number of servers.

1.4. Contributions of the Paper

The formulated aims are achieved, and the main contributions of the paper are as follows:

• We consider a multi-server queue with a group service of the $MAP/PH/N$ type, which allows us to model the typical bursty character of traffic in real-world systems and a wide range of service time distributions. Previously, queues with a group service, $MAP,$ and $PH$ distribution of service times were analyzed only in single-server settings;
• We account for the possible impatience of the requests waiting in the queue and apply more flexible control for the service initiation. The most common strategy of control allows the service to begin only when the number of requests in the queue is not less than a preassigned threshold. We considered the strategy that allows us to start servicing in situations where the number of requests is below this threshold, but some requests decide to leave the system without service due to impatience;
• We assume that the service time of a group depends on its size, while the majority of the papers consider a more simple case of service time that is independent of this size;
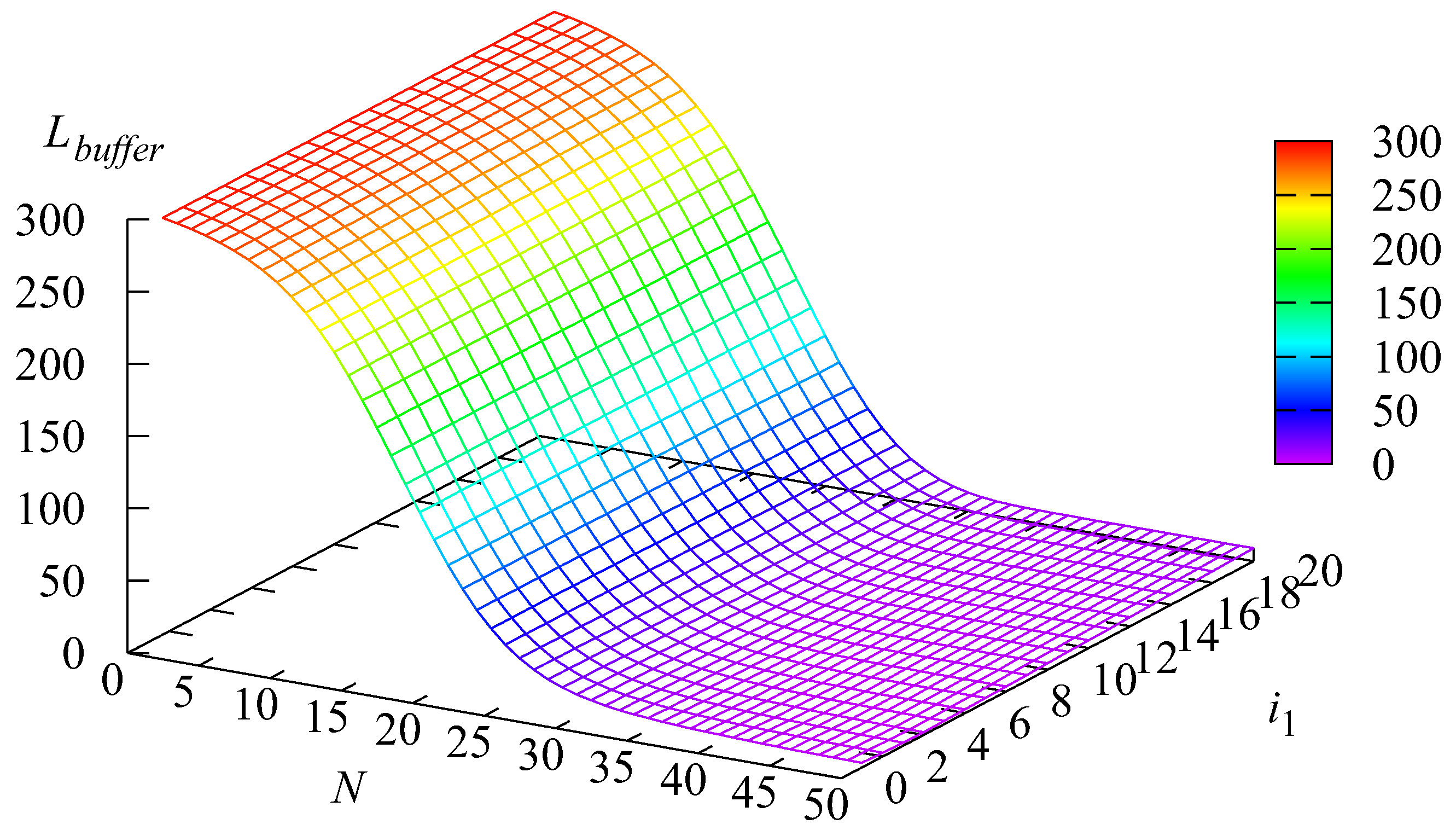
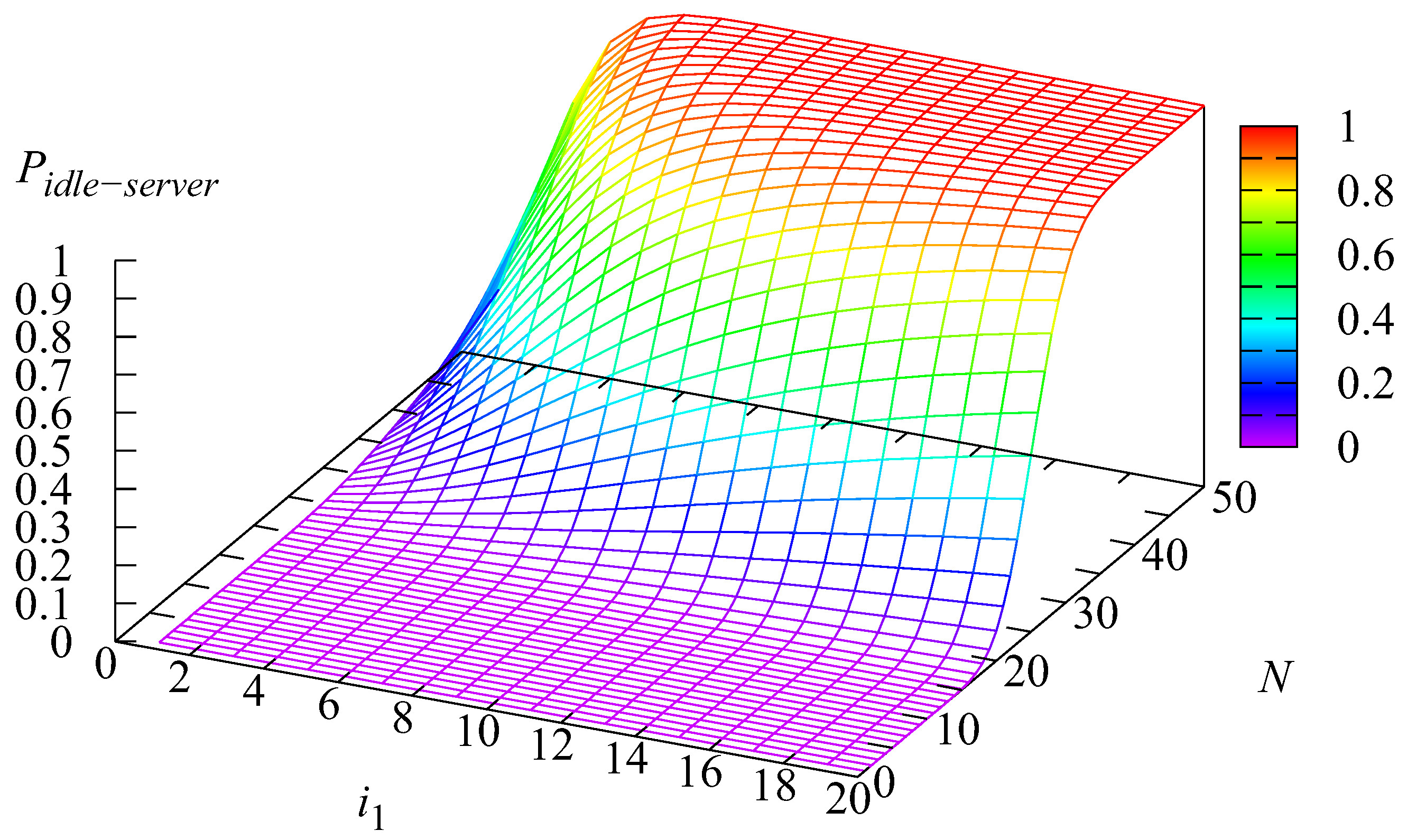
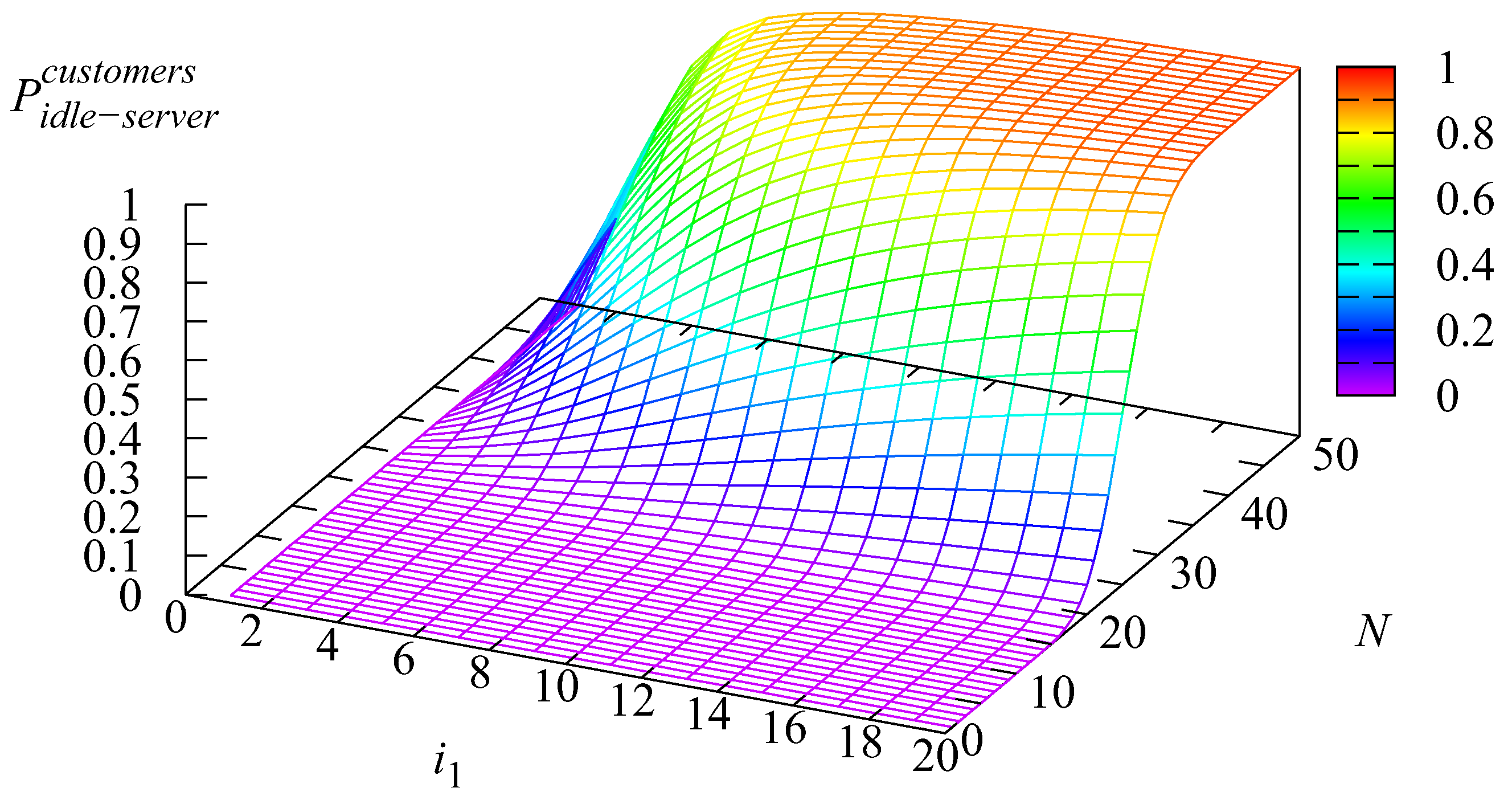
• The elaborated algorithms and software allow for the computation of the main performance measures and the solving of optimization problems for realistic system parameter values. Numerical results are presented for a system with 50 servers and a capacity of 300 for the input buffer.

1.5. Brief Outline of the Content of the Paper

Section 2 contains a mathematical description of the constructed queuing model and the necessary denotations. A multi-dimensional continuous-time Markov chain that is suitable for the description of the constructed model is defined in Section 3. The infinitesimal generator of this chain is obtained. An algorithm for the computation of its steady-state distribution is presented here. Formulas for the computation of the key performance characteristics of the system are presented in Section 4. Some numerical results that provide insight into the system’s behavior and an example of a solution to the optimization problem are given in Section 5. Section 6 concludes the paper.

2. Mathematical Model

We consider a queuing system with a finite buffer of size R with N independent identical servers. The structure of the system is shown in Figure 1.

Requests enter the system in the $MAP$ arrival flow. This flow is given by a Markov chain with continuous time ($CTMC$) ${\nu }_t,t\ge 0,$ having a state space $\{1,2,\dots ,W\}$ and matrices $D_0$ and $D_1$ of size $W.$ Here, W is a certain finite integer, and the matrix $D_1$ consists of the transition intensities of the chain ${\nu }_t$, accompanied by the arrival of a request. The non-diagonal elements of the matrix $D_0$ determine the rate of the corresponding transition of the chain ${\nu }_t$ without the arrival of a request. The modules of the negative diagonal elements determine the intensity of the exit of the process ${\nu }_t$ from the corresponding state. The matrix $D\left(1\right)=D_0+D_1$ is the generator of the $CTMC$ ${\nu }_t.$ This generator is assumed to be irreducible.

The average request arrival rate $\lambda$ is determined by the formula $\lambda =\mathit{\theta }{D}_1\mathbf{e},$ where $\mathit{\theta }$ is a row vector of stationary probabilities of the $CTMC$ ${\nu }_t.$ This vector is the only solution to the system $\mathit{\theta }D\left(1\right)=\mathbf{0},\mathit{\theta }\mathbf{e}=1$. Here and below, $\mathbf{0}$ is a row vector of an appropriate size consisting of zeros, and $\mathbf{e}$ is a column vector of an appropriate size consisting of ones.

The requests can be served in groups of varying sizes. All requests from the group accepted for service go to one server and complete their services simultaneously. We assume that if, at the service completion epoch, there are less than $i_1$ requests in the buffer, then a new service does not start. Otherwise, the server starts its service for all available requests if their number does not exceed the parameter $i_2$, such that $\max \{1,i_1-1\}<i_2\le R$. In other words, if there are more than $i_2$ requests in the buffer at the service completion epoch, then the first $i_2$ requests go for servicing, and the rest remain in the buffer. Thus, the parameters $i_1$ and $i_2,1\le i_1<i_2\le R$, determine the minimum and maximum sizes of the groups that can be taken for service.

If, at the arrival moment, the number of requests in the buffer is less than or equal to $i_1-2$, then the incoming request becomes buffered and awaits service. If the number of requests in the buffer is $i_1-1$ and there is a free server, then the entire group of size $i_1$ starts its service. If all servers are busy, the request becomes buffered to wait. If the buffer is full, the request permanently leaves the system and is lost.

It is also assumed that requests in the buffer can become impatient and try to leave the system without service at random time intervals, the lengths of which are exponentially distributed with the intensity of $\gamma$. In this case, if there is a free server with the probability $q_i$, where i is the number of requests in the buffer, all available requests go to the server and begin servicing, even though their number is less than the parameter $i_1$, and with a complimentary probability, the request leaves the system forever. If all servers are busy, the impatient request is lost.

We assume that the service time of a group has a phase-type distribution ($PH$-service). The $CTMC$ $m_t,t\ge 0,$ with transient states $\{1,2,\dots ,M\}$ and a unique absorbing state $M+1$ specify this distribution. The irreducible representation of the $CTMC$ $m_t,t\ge 0$, is given as $({\mathit{\beta }}_i,S),i=\overline{1,i_2}$, where i is the number of requests taken for service. Note that ${\mathit{\beta }}_i$ is a stochastic row vector of dimension M, and the square matrix S of dimension M is a sub-generator.

The average service time for a group of requests of size i is defined as $b_1^{\left(i\right)}={\mathit{\beta }}_i{(-S)}^{-1}\mathbf{e}$. Note that, assuming that the initial probability vector of the service time depends on the size of the group, we take into account the dependence of the service process on the size of the group.

To apply the formulated queuing model for the description and optimization of some real-world delivery system, it is necessary to determine the matrices $D_0$ and $D_1$ that define the $MAP$ of the requests and representations $({\mathit{\beta }}_i,S),i=\overline{1,i_2},$ to define the service of groups of requests.

The problem of building the matrices $D_0$ and $D_1$ based on observations of the traces of the actual arrival process (or time stamps giving the arrival epochs) is well addressed in the existing literature. For references, see, e.g., the book [45] and papers [45,46,47,48,49,50,51,52,53,54].

The problem of choosing representations $({\mathit{\beta }}_i,S),i=\overline{1,i_2,}$ to fit the known average service times of groups of different sizes can be solved, e.g., as follows:

Let the average service time of a group consisting of i requests be estimated based on the available samples as $w_i,i=\overline{1,i_2}.$ It is natural to assume that the values $w_i,i=\overline{1,i_2},$ are such that $w_1\le w_2\le \dots \le w_{i_2}$ (a larger group does not imply a shorter average service time) and $w_1\ne w_{i_2}$ (dependence of the service time on the group size exists).

The number M of transient states of the $CTMC$ $m_t,t\ge 0$, has a significant impact on the feasibility of the analysis of the $CTMC$, as shown in the next section. Thus, one should construct the irreducible representations $({\mathit{\beta }}_i,S),i=\overline{1,i_2}$, of the minimal possible size, namely, $M=2$.

It is possible to fix the sub-generator S as a diagonal matrix of size two with the diagonal entries $-w_1^{-1}$ and $-w_{i_2}^{-1}.$ It is easy to check that the desired values $w_i,i=\overline{1,i_2}$, can be achieved via the following choice of vectors ${\mathit{\beta }}_i$ of size 2,

$${\mathit{\beta }}_i=({\phi }_i,1-{\phi }_i)$$

where

$${\phi }_i=\frac{w_{i_2}-w_i}{w_{i_2}-w_1},i=\overline{1,i_2}.$$

Let us analyze the constructed queuing system under the assumption that the inter-arrival, service, and patience times are mutually independent.

3. The Process of System States and Its Stationary Distribution

Let $i_t,i_t=\overline{0,R}$, be the number of requests in the buffer; $n_t,n_t=\overline{0,N}$, be the number of busy servers; ${\nu }_t,{\nu }_t=\overline{1,W}$, be the state of the underlying process; and $MAP$, $m_t^{\left(l\right)}$ be the number of servers on the l-th service phase. $m_t^{\left(l\right)}=\overline{0,n_t},l=\overline{1,M},{\displaystyle \sum _{l=1}^M}{m}_t^{\left(l\right)}=n_t,$ at an arbitrary moment $t,t\ge 0$.

The behavior of the system under study is described by a regular irreducible $CTMC$ with continuous time

$${\xi }_t=\{i_t,n_t,{\nu }_t,m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\},t\ge 0.$$

Let us renumber the states of the $CTMC$ ${\xi }_t$ in reverse order for the components $m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}$ and in direct order for the components $n_t$ and ${\nu }_t$ and denote the set of states of the chain with the value i of the first component of the $CTMC$ as level $i,i\ge 0$.

Theorem 1.

The generator Q of the $CTMC$ ${\xi }_t,t\ge 0$, has the following lower-Hessenberg block structure:

$$Q=\left(\begin{array}{ccccccc}{Q}_{0,0}& Q_{0,1}& O& O& \dots & O& O\\ Q_{1,0}& Q_{1,1}& Q_{1,2}& O& \dots & O& O\\ Q_{2,0}& Q_{2,1}& Q_{2,2}& Q_{2,3}& \dots & O& O\\ ⋮& ⋮& ⋮& \ddots & \ddots & ⋮& ⋮\\ Q_{R-1,0}& Q_{R-1,1}& Q_{R-1,2}& Q_{R-1,3}& \dots & Q_{R-1,R-1}& Q_{R-1,R}\\ Q_{R,0}& Q_{R,1}& Q_{R,2}& Q_{R,3}& \dots & Q_{R,R-1}& Q_{R,R}\end{array}\right)$$

where the non-zero blocks $Q_{i,j},j\le i+1,$ containing the intensities of transitions from level i to level j are defined as follows:

$$Q_{i,i}=\mathrm{diag}\{D_0,D_0\oplus (A_n+{\Delta }_n),n=\overline{1,N}\}+$$

$$+{\mathrm{diag}}^{-}\{I_W\otimes L_n,n=\overline{1,N}\}-i\gamma I_{W{\displaystyle \sum _{n=0}^N}{T}_n}+$$

$$+{\delta }_{i_1,1}{\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_1\right),n=\overline{0,N-1}\},i=\overline{0,i_1-1},$$

$$Q_{i,i}=D_0\oplus (A_N+{\Delta }_N)-i\gamma I_{W{T}_N},i=\overline{i_1,R-1},$$

$$Q_{R,R}=D\left(1\right)\oplus (A_N+{\Delta }_N)-R\gamma I_{W{T}_N},$$

$$Q_{i,i+1}=\mathrm{diag}\{D_1\otimes I_{T_n},n=\overline{0,N}\},i=\overline{0,i_1-2},$$

$$Q_{i_1-1,i_1}=\left(\begin{array}{c}{O}_{W{\displaystyle \sum _{n=0}^{N-1}}{T}_n\times W{T}_N}\\ D_1\otimes I_{T_N}\end{array}\right),$$

$$Q_{i,i+1}=D_1\otimes I_{T_N},i=\overline{i_1,R-1},$$

$$Q_{1,0}=\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& \gamma I_{W{T}_N}+I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_1\right)\end{array}\right),\mathit{if}{i}_1=1,$$

$$Q_{1,0}=\gamma \mathrm{diag}\{\{(1-q_1)I_{W{T}_n},n=\overline{0,N-1}\},I_{W{T}_N}\}+$$

$$+{\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_2\right),n=\overline{0,N-1}\}+$$

$$+\gamma q_1{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_1\right),n=\overline{0,N-1}\},\mathit{if}{i}_1=2,$$

$$Q_{1,0}=\gamma \mathrm{diag}\{\{(1-q_1)I_{W{T}_n},n=\overline{0,N-1}\},I_{W{T}_N}\}+$$

$$+\gamma q_1{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_1\right),n=\overline{0,N-1}\},\mathit{if}{i}_1>2,$$

$$Q_{i,i-1}=i\gamma \mathrm{diag}\{\{(1-q_i)I_{W{T}_n},n=\overline{0,N-1}\},I_{W{T}_N}\},i=\overline{2,i_1-1},$$

$$Q_{i_1,i_1-1}=i_1\gamma \left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_{W{T}_N}\end{array}\right),i_1\ne 1,$$

$$Q_{i,i-1}=i\gamma I_{W{T}_N},i=\overline{i_1+1,R},$$

$$Q_{i,0}=i\gamma q_i{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_i\right),n=\overline{0,N-1}\},i=\overline{2,i_1-2},$$

$$Q_{i_1-1,0}={\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_{i_1}\right),n=\overline{0,N-1}\}+$$

$$+(i_1-1)\gamma q_{i_1-1}{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_{i_1-1}\right),n=\overline{0,N-1}\},i_1\ne 1,$$

$$Q_{i,0}=\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_i\right)\end{array}\right),i=\overline{i_1,i_2},\mathit{if}{i}_1\ne 1,$$

$$\mathit{and}i=\overline{i_1+1,i_2},\mathit{if}{i}_1=1,$$

$$Q_{i,i-i_2}=\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_{i_2}\right)\end{array}\right),\mathit{if}i-i_2<i_1,$$

$$Q_{i,i-i_2}=I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_{i_2}\right),\mathit{if}i-i_2\ge i_1,i=\overline{i_2+1,R}.$$

Here,

⊗ and ⊕ are the symbols of the Kronecker product and the sum of matrices (see, for example, [55]);

I is the identity matrix; O is the zero matrix, the dimension of which is indicated by a subscript if necessary;

${\delta }_{i,j}$ is the Kronecker symbol, that is, ${\delta }_{i,j}=\left\{\begin{array}{cc}1,\hfill & i=j;\hfill \\ 0,\hfill & i\ne j;\hfill \end{array}\right.$

$\mathrm{diag}\{d_1,d_2,\dots ,d_n\}$ is the diagonal matrix with the diagonal elements $d_1,d_2,\dots ,d_n;$

${\mathrm{diag}}^{+}\{d_1,d_2,\dots ,d_n\}$ is the square matrix with the non-zero overdiagonal elements $d_1,d_2,\dots ,d_n;$

${\mathrm{diag}}^{-}\{d_1,d_2,\dots ,d_n\}$ is the square matrix with the non-zero subdiagonal elements $d_1,d_2,\dots ,d_n;$ and

the number $T_n$ is equal to the cardinality of the state space of the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ when a service is simultaneously provided to n groups of requests. It is calculated as

$$T_n=\frac{(n+M-1)!}{n!(M-1)!},n=\overline{1,N}.$$

For convenience, we put $T_0=1.$

The matrix $L_n$ defines the transition intensities of the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ at the moment when service in one of n busy servers is completed, $n=\overline{1,N}.$ The matrix $A_n$ contains the transition intensities of the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ at the moment of the change in the phase of service in one of n busy servers, $n=\overline{1,N}.$ The matrix $P_n\left({\mathit{\beta }}_i\right)$ defines the transition probabilities of the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ at the moment when the group of i requests begins service in the presence of n busy servers, $n=\overline{0,N-1}.$ The diagonal elements of the diagonal matrix ${\Delta }_n$ determine the rates of the exit of the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ from the corresponding states. When the matrices $L_n$ and $A_n$ are computed, the matrices ${\Delta }_n$ are computed by the formula

$${\Delta }_n=-\mathrm{diag}\{A_n\mathbf{e}+L_n\mathbf{e}\}.$$

Detailed descriptions of the matrices $P_n\left({\mathit{\beta }}_i\right)n=\overline{0,N-1},i=\overline{1,i_2}$, $L_n$, $A_n,$ ${\Delta }_n,n=\overline{1,N},$ and algorithms for their calculation are presented in [56].

Proof. 

The proof of the theorem was carried out by analyzing the intensities of all possible transitions of the $CTMC$ ${\xi }_t$ over a time interval of infinitesimal length.

The generator has a block lower Hessenberg structure, since requests can enter the buffer strictly one at a time and leave it in groups, the size of which is up to $i_2.$

Let us explain the form of the diagonal blocks $Q_{i,i},i=\overline{0,R}.$ All diagonal elements of the block $Q_{i,i}$ are negative, and the absolute values of these elements determine the intensities of the $CTMC$ ${\xi }_t$ exiting the corresponding states. The $CTMC$ ${\xi }_t$ can exit the current state in the following cases:

a. The underlying process ${\nu }_t$ of the request arrivals leaves its current state. The corresponding transition intensities are determined up to their signs by the diagonal elements of the matrix $D_0\otimes I_{{\displaystyle \sum _{n=0}^N}{T}_n},$ if $i=\overline{0,i_1-1},$ $D_0\otimes I_{T_N}$ if $i=\overline{i_1,R-1}$, and $(D_0+D_1)\otimes I_{T_N}$ if $i=R.$

b. The service process on one of the busy servers changes its state. In this case, the transition intensities are determined by the diagonal elements of the matrices $\mathrm{diag}\{O_{W\times W},I_W\otimes {\Delta }_n,n=\overline{1,N}\}$ for $i=\overline{0,i_1-1}$ and $I_W\otimes {\Delta }_N$ for $i=\overline{i_1,R}.$

c. A request from the buffer tries to leave the system due to impatience; the corresponding intensities are specified by the matrices $i\gamma I_{W{\displaystyle \sum _{n=0}^N}{T}_n}$ if $i=\overline{0,i_1-1}$ and $i\gamma I_{W{T}_N},$ if $i=\overline{i_1,R}.$

The non-diagonal elements of the matrix $Q_{i,i}$ determine the transition intensities of the $CTMC$ ${\xi }_t$ without changing the value i of the first component. The following statements specify these transitions:

(a) For non-diagonal elements of matrices $D_0\otimes I_{{\displaystyle \sum _{n=0}^N}{T}_n}$ if $i=\overline{0,i_1-1}and$ $D_0\otimes I_{T_N}$ if $i=\overline{i_1,R}$ when the underlying process ${\nu }_t$ makes a transition without generating a request.

(b) For non-diagonal elements of the matrix $D_1\otimes I_{T_N},$ when the underlying process ${\nu }_t$ makes a transition, a generated request is lost due to the buffer being full (case $i=R$).

(c) For elements of the matrix ${\mathrm{diag}}^{-}\{I_W\otimes L_n,n=\overline{1,N}\}$, when the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ makes a transition leading to the end of the service but a new service does not start because there are fewer than $i_1$ requests in the buffer;

(d) For elements of the matrices $I_W\otimes A_n,i=\overline{0,i_1-1},$ and $I_W\otimes A_N,i=\overline{i_1,R},$ when the process $\{m_t^{\left(1\right)},\dots ,m_t^{\left(M\right)}\}$ makes a transition that does not lead to the end of the service.

(e) In the case of $i_1=1$, for the elements of the matrix ${\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_1\right),n=\overline{0,N-1}\}$, when a new request arrives and the buffer is empty. In this case, the arriving request is immediately processed for service.

As a result, we obtain blocks $Q_{i,i},i=\overline{0,R},$ presented above.

The form of the blocks $Q_{i,i+1},i=\overline{0,R}$ is explained as follows. These blocks contain the transition rates of the $CTMC$ ${\xi }_t$ as the number of requests in the buffer increases by one. This can only happen when a new request arrives in the system. The transition intensities of the process ${\nu }_t$ at the moment of the request arrival are determined by the elements of the matrix $D_1$; therefore, the blocks $Q_{i,i+1}$ are specified by the matrix $\mathrm{diag}\{D_1\otimes I_{T_n},n=\overline{0,N}\}$ if $i<i_1-1,$ the matrix $\left(\begin{array}{c}{O}_{W{\displaystyle \sum _{n=0}^{N-1}}{T}_n\times W{T}_N}\\ D_1\otimes I_{T_N}\end{array}\right)$ if there are $i_1-1$ requests in the buffer, and by the matrix $D_1\otimes I_{T_N}$ in all other cases.

Next, consider the blocks $Q_{i,j},j<i,i=\overline{1,R}.$ First, let us explain the case where $i=1.$ The form of the block $Q_{1,0}$ significantly depends on the value of the parameter $i_1$. Let us consider the following three cases:

(1) If $i_1=1$ (the server starts servicing, even if there is only one request in the buffer), then reducing the number of requests in the buffer is possible only if the service is completed (the matrix $\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_1\right)\end{array}\right)$ specifies the intensity of this event) or the request is loss due to impatience (the matrix $\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& \gamma I_{W{T}_N}\end{array}\right)$ gives the corresponding intensities).

(2) If $i_1=2$, then a decrease in the number of requests in the buffer results in (a) the loss of a request due to impatience. The intensities of this event are given by the matrix $\gamma \mathrm{diag}\{\{(1-q_1)I_{W{T}_n},n=\overline{0,N-1}\},I_{W{T}_N}\}$. Event (b) is also possible when there is a free server and a single request in the buffer. This request wants to leave the system due to impatience, but the system decides to service this single request. The corresponding intensities are given by the matrix $\gamma q_1{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_1\right),n=\overline{0,N-1}\}.$ In addition, case (c) is added. When there is a free server and a single request in the buffer, a new request arrives, and a group of two requests begins service ${\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_2\right),n=\overline{0,N-1}\}.$

(3) If $i_1>2,$ then, as in the previous case, a decrease in the number of requests in the buffer is caused by events (a), (b), and (c), which is impossible. The corresponding intensity matrices are determined in a similar way.

Then, consider the blocks $Q_{i,i-1},i=\overline{2,R}.$ The transition of $CTMC$ ${\xi }_t$ from the state with the value i for the first component in the state with a value $i-1$ for this component is possible only if the request is lost due to impatience. The corresponding intensities are given by the matrix $i\gamma \mathrm{diag}\{\{(1-q_i)I_{W{T}_n},n=\overline{0,N-1}\},I_{W{T}_N}\}$ for $i<i_1$, by the matrix $i_1\gamma \left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_{W{T}_N}\end{array}\right)$ when there are $i_1,i_1\ne 1,$ requests in the buffer, and by the matrix $i\gamma I_{W{T}_N}$ when there are more than $i_1$ requests in the buffer.

Let us explain the form of the blocks $Q_{i,0},i=\overline{2,i_2}.$ The transition of the $CTMC$ ${\xi }_t$ from the state with a value i for the first component of the chain to the state where a value of zero occurs when a group of size i is taken over for service. The following statements give the corresponding intensities:

a. For the matrix $i\gamma q_i{\mathrm{diag}}^{+}\{I_W\otimes P_n\left({\mathit{\beta }}_i\right),n=\overline{0,N-1}\},$ when there is a free server and $i,i=\overline{2,i_1-1}$ requests in the buffer, one of the requests wants to leave the buffer due to impatience, but the system decides to take all requests from the buffer for servicing, although their number is less than the minimum number allowable;

b. For the matrix ${\mathrm{diag}}^{+}\{D_1\otimes P_n\left({\mathit{\beta }}_{i_1}\right),n=\overline{0,N-1}\},$ when, at the moment of the arrival of a new request, a free server is available and $i_1-1,i_1\ne 1,$ requests are already in the buffer, and a group of $i_1$ requests is taken for servicing;

c. For the matrix $\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_i\right)\end{array}\right),$ when, at the moment when one of the busy servers is released, a group of i requests waiting for service in the buffer is taken over for service, $i=\overline{i_1,i_2}\mathit{if}{i}_1\ne 1$ and $i=\overline{i_1+1,i_2}$ if $i_1=1.$

The blocks $Q_{i,i-i_2},i=\overline{i_2+1,R},$ contain the transition intensities of the $CTMC$ ${\xi }_t$ from the state with the value i for the first component of the chain to a state with the value $i-i_2$ for this component in the case when a group of requests of size $i_2$ is taken for service at the moment of service completion on one of the busy servers. These intensities are determined by the matrix $\left(\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n}& I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_{i_2}\right)\end{array}\right)$ if the size of the group of requests remaining in the buffer does not exceed the parameter $i_1$ or the matrix $I_W\otimes L_N{P}_{N-1}\left({\mathit{\beta }}_{i_2}\right)$ otherwise.

Theorem 1 is proven.    □

Because the $CTMC$ ${\xi }_t$ is regular and irreducible and its state space is finite, the following invariant probabilities of the states of the chain exist:

$$\pi (i,n,\nu ,m^{\left(1\right)},\dots ,m^{\left(M\right)})=\underset{t\to \infty }{lim}P\{i_t=i,n_t=n,{\nu }_t=\nu ,m_t^{\left(1\right)}=m^{\left(1\right)},\dots ,m_t^{\left(M\right)}=m^{\left(M\right)}\},$$

$$i=\overline{0,R},n=\overline{0,N},\nu =\overline{1,W},m^{\left(l\right)}=\overline{0,n},l=\overline{1,M},{\displaystyle \sum _{l=1}^M}{m}^{\left(l\right)}=n.$$

Then, let us form the vectors ${\mathit{\pi }}_i,i=\overline{0,R}$ of these probabilities enumerated in the reverse order of the components $m^{\left(1\right)},\dots ,m^{\left(M\right)}$ and in the direct order of the components n and $\nu .$

It is well known that the probability vectors ${\mathit{\pi }}_i,i=\overline{0,R}$ satisfy the following system of linear algebraic equations:

$$({\mathit{\pi }}_0,{\mathit{\pi }}_1,\dots ,{\mathit{\pi }}_R)Q=\mathbf{0},({\mathit{\pi }}_0,{\mathit{\pi }}_1,\dots ,{\mathit{\pi }}_R)\mathbf{e}=1,$$

which are called an equilibrium or Chapman–Kolmogorov equations.

To solve this system, we developed the algorithm presented below Algorithm 1.

Remark 1.

Because the generator Q does not have a three-block diagonal form, the presented algorithm is not trivial. It effectively exploits the block structure of the generator. All matrices, the inversions of which are used in this algorithm, are non-singular due to O. Tausski theorem (see, e.g., [42,57]), because they are irreducible sub-generators and the diagonal entry strictly dominates in at least one row. If the matrix, say $\mathcal{A},$ is the irreducible sub-generator with the mentioned dominance, then (i) the matrix ${\mathcal{A}}^{-1}$ exists and (ii) the matrix ${(-\mathcal{A})}^{-1}$ is non-negative. Thus, the presented algorithm works with only non-negative matrices and does not use a subtraction operation. Hence, it is numerically stable. Therefore, it may be successfully exploited for the computation of the stationary distribution of the states of a variety of queuing systems with group service of requests.

Algorithm 1: Computation of the stationary probabilities

1. Calculate the matrices ${\mathcal{X}}_k^{\left(i\right)}$ by using the following formulas: $${\mathcal{X}}_k^{\left(0\right)}=\left\{\begin{array}{cc}-Q_{k,0}{Q}_{0,0}^{-1},\hfill & k=\overline{1,i_2};\hfill \\ O_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n},\hfill & k=\overline{i_2+1,R},\hfill \end{array}\right.$$ $${\mathcal{X}}_k^{\left(i\right)}=\left\{\begin{array}{cc}-({\mathcal{X}}_{i+1}^{(i-1)}{Q}_{i-1,i}+Q_{i+1,i}){(Q_{i,i}+{\mathcal{X}}_i^{(i-1)}{Q}_{i-1,i})}^{-1},\hfill & k=i+1;\hfill \\ -{\mathcal{X}}_k^{(i-1)}{Q}_{i-1,i}{(Q_{i,i}+{\mathcal{X}}_i^{(i-1)}{Q}_{i-1,i})}^{-1},\hfill & k=\overline{i+2,i_2+i-1};\hfill \\ -Q_{i_2+i,i}{(Q_{i,i}+{\mathcal{X}}_i^{(i-1)}{Q}_{i-1,i})}^{-1},\hfill & k=i_2+i;\hfill \\ \left\{\begin{array}{cc}{O}_{W{T}_N\times W{\displaystyle \sum _{n=0}^{N-1}}{T}_n},\hfill & i<i_1;\hfill \\ O_{W{T}_N\times W{T}_N},\hfill & i\ge i_1;\hfill \end{array}\right.\hfill & k=\overline{i_2+i+1,R};\hfill \end{array}\right.,$$ $$i=\overline{1,R-i_2},$$ $${\mathcal{X}}_k^{\left(i\right)}=\left\{\begin{array}{cc}-({\mathcal{X}}_{i+1}^{(i-1)}{Q}_{i-1,i}+Q_{i+1,i}){(Q_{i,i}+{\mathcal{X}}_i^{(i-1)}{Q}_{i-1,i})}^{-1},\hfill & k=i+1;\hfill \\ -{\mathcal{X}}_k^{(i-1)}{Q}_{i-1,i}{(Q_{i,i}+{\mathcal{X}}_i^{(i-1)}{Q}_{i-1,i})}^{-1},\hfill & k=\overline{i+2,R};\hfill \end{array}\right.,$$ $$i=\overline{R-i_2+1,R-2},$$ $${\mathcal{X}}_R^{(R-1)}=-({\mathcal{X}}_R^{(R-2)}{Q}_{R-2,R-1}+Q_{R,R-1}){(Q_{R-1,R-1}+{\mathcal{X}}_{R-1}^{(R-2)}{Q}_{R-2,R-1})}^{-1}.$$ 2. Calculate the matrices $Y_i$ as follows: $$Y_R=I,Y_i={\displaystyle \sum _{k=i+1}^R}{Y}_k{\mathcal{X}}_k^{\left(i\right)},i=R-1,R-2,\dots ,0.$$ 3. Find the vector ${\mathit{\pi }}_R$ as the only solution to the system $${\mathit{\pi }}_R({\mathcal{X}}_R^{(R-1)}+Q_{R,R})=\mathbf{0},$$ $${\mathit{\pi }}_R{\displaystyle \sum _{k=0}^R}{Y}_k\mathbf{e}=1.$$ 4. Calculate the vectors ${\mathit{\pi }}_i$ as ${\mathit{\pi }}_i={\mathit{\pi }}_R{Y}_i,i=\overline{0,R-1}.$

4. Performance Characteristics

Having calculated the probability vectors ${\mathit{\pi }}_i,i=\overline{0,R},$ it is possible to present the formulas for the computation of the main characteristics of the performance of the considered system.

The average number of requests in the buffer is

$$L_{buffer}={\displaystyle \sum _{i=1}^R}i{\mathit{\pi }}_i\mathbf{e}.$$

The average number of busy servers is

$$N_{serv}={\displaystyle \sum _{i=0}^{i_1-1}}{\displaystyle \sum _{n=1}^N}n\mathit{\pi }(i,n)\mathbf{e}+{\displaystyle \sum _{i=i_1}^R}N{\mathit{\pi }}_i\mathbf{e}.$$

The average intensity of the server releases is

$${\mu }_{release}={\displaystyle \sum _{i=0}^{i_1-1}}{\displaystyle \sum _{n=1}^N}\mathit{\pi }(i,n)(I_W\otimes L_n)\mathbf{e}+{\displaystyle \sum _{i=i_1}^R}{\mathit{\pi }}_i(I_W\otimes L_N)\mathbf{e}.$$

The probability that an incoming request will find the buffer full and leave the system is

$$P_{ent-loss}=\frac{1}{\lambda }{\mathit{\pi }}_R(D_1\otimes I_{T_N})\mathbf{e}.$$

The probability that a request will start its service immediately upon entering the system is

$$P_{to-serv}=\frac{1}{\lambda }{\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i_1-1,n)(D_1\otimes I_{T_n})\mathbf{e}.$$

The rate of requests entered for service is

$${\mu }_{to-serv}=i_1{\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i_1-1,n)(D_1\otimes I_{T_n})\mathbf{e}+$$

$$+{\displaystyle \sum _{i=i_1}^R}\min \{i,i_2\}{\mathit{\pi }}_i(I_W\otimes L_N)\mathbf{e}+{\displaystyle \sum _{i=1}^{i_1-1}}{i}^2{q}_i\gamma {\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}.$$

The probability of losing a request from the buffer due to impatience is

$$P_{imp-loss}=\frac{1}{\lambda }({\displaystyle \sum _{i=1}^{i_1-1}}i(1-q_i)\gamma {\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}+{\displaystyle \sum _{i=1}^{i_1-1}}i\gamma \mathit{\pi }(i,N)\mathbf{e}+{\displaystyle \sum _{i=i_1}^R}i\gamma {\mathit{\pi }}_i\mathbf{e}).$$

The average size of a group of requests taken for servicing is

$$N_{batch}=\frac{{\mu }_{to-serv}}{{\mu }_{release}}.$$

The probability of losing a request from the buffer due to impatience while there is a free server is

$$P_{idle-server}^{imp-loss}=\frac{1}{\lambda }{\displaystyle \sum _{i=1}^{i_1-1}}i\gamma (1-q_i){\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}.$$

The probability of losing a request from the buffer due to impatience at a time when all servers are busy is

$$P_{all-busy-servers}^{imp-loss}=\frac{1}{\lambda }[{\displaystyle \sum _{i=1}^{i_1-1}}i\gamma \mathit{\pi }(i,N)\mathbf{e}+{\displaystyle \sum _{i=i_1}^R}i\gamma {\mathit{\pi }}_i\mathbf{e}].$$

The probability that, at an arbitrary moment, there is at least one free server in the system is

$$P_{idle-server}={\displaystyle \sum _{i=0}^{i_1-1}}{\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}.$$

The probability that at an arbitrary moment there are requests in the buffer while there is at least one free server is

$$P_{idle-server}^{requests}={\displaystyle \sum _{i=1}^{i_1-1}}{\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}.$$

The probability of losing an arbitrary request is

$$P_{loss}=1-\frac{{\mu }_{to-serv}}{\lambda }=P_{imp-loss}+P_{ent-loss}.$$

The probability that a group with a size of less than $i_1$ undergoes servicing is

$$P_{batch<i_1}=\frac{1}{{\mu }_{release}}{\displaystyle \sum _{i=1}^{i_1-1}}i{q}_i\gamma {\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i,n)\mathbf{e}.$$

The probability that a group of the maximum size $i_2$ undergoes servicing is

$$P_{batch=i_2}=\frac{1}{{\mu }_{release}}({\displaystyle \sum _{i=i_2}^R}{\mathit{\pi }}_i(I_W\otimes L_N)\mathbf{e}+{\delta }_{i_1-i_2,0}{\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i_1-1,n)(D_1\otimes I_{T_n})\mathbf{e}).$$

The probability that a group of the maximum size from the interval $[i_1,i_2)$ undergoes servicing is

$$P_{i_1\le batch<i_2}=\frac{(1-{\delta }_{i_1-i_2,0})}{{\mu }_{release}}({\displaystyle \sum _{n=0}^{N-1}}\mathit{\pi }(i_1-1,n)(D_1\otimes I_{T_n})\mathbf{e}+{\displaystyle \sum _{i=i_1}^{i_2-1}}{\mathit{\pi }}_i(I_W\otimes L_N)\mathbf{e}).$$

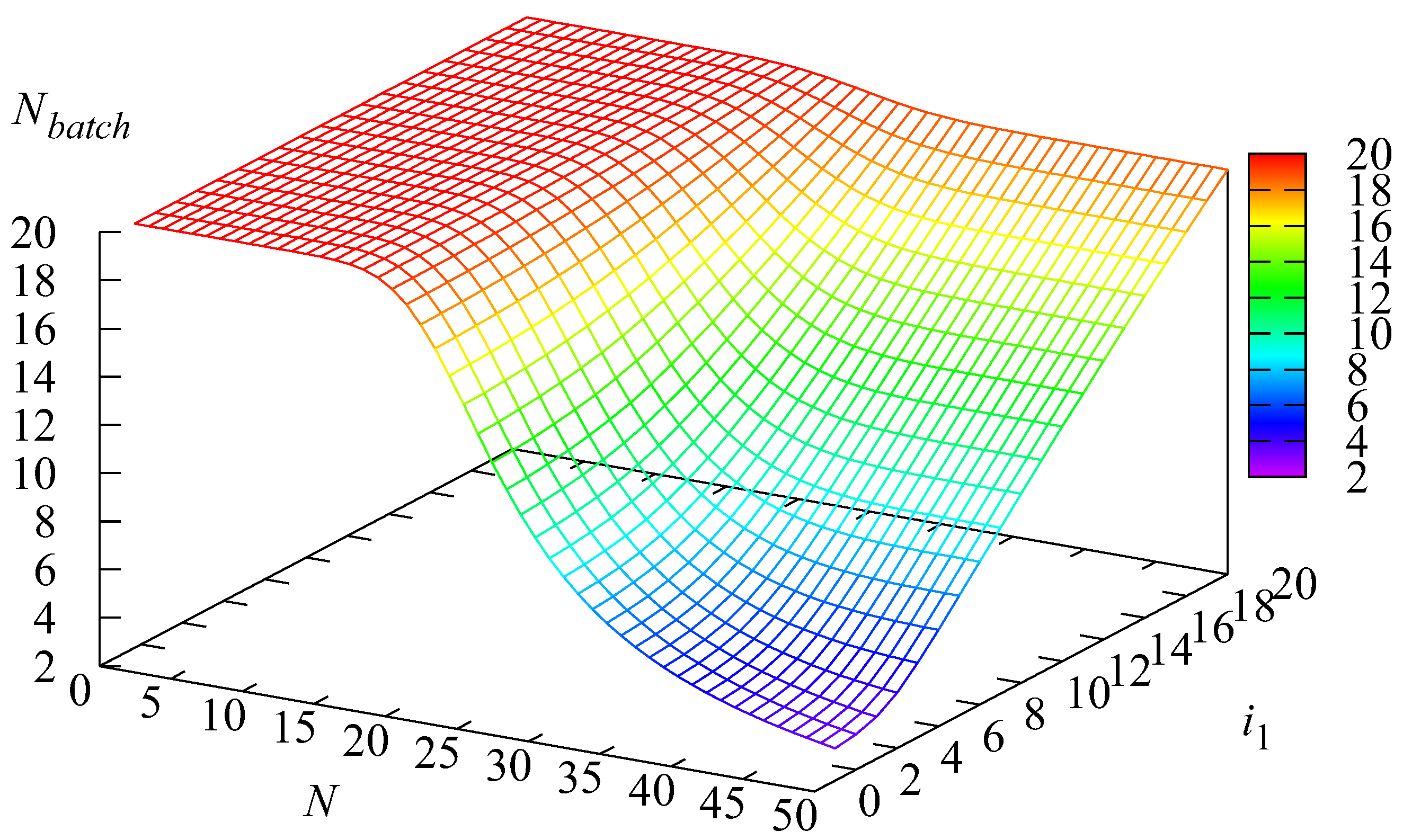
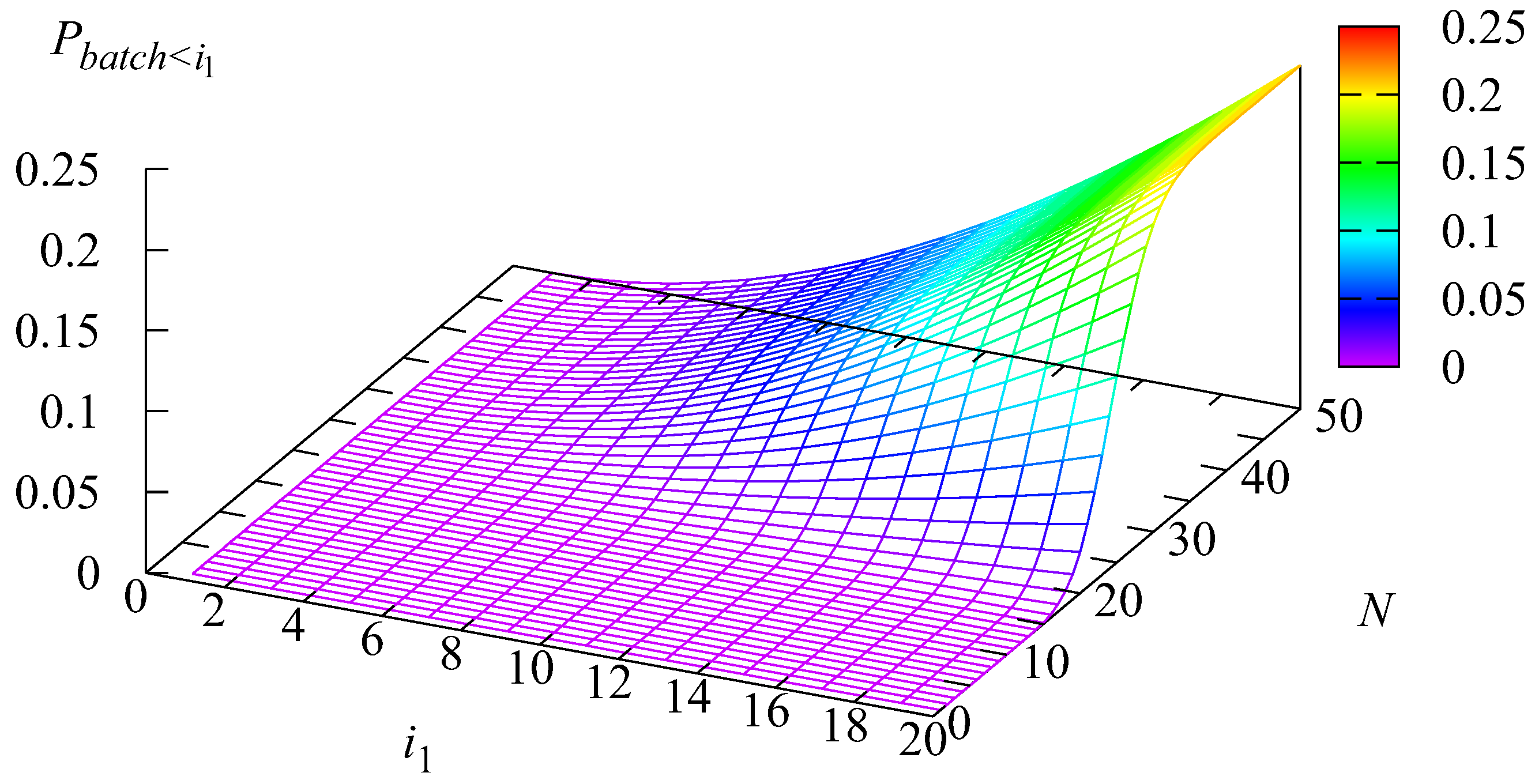
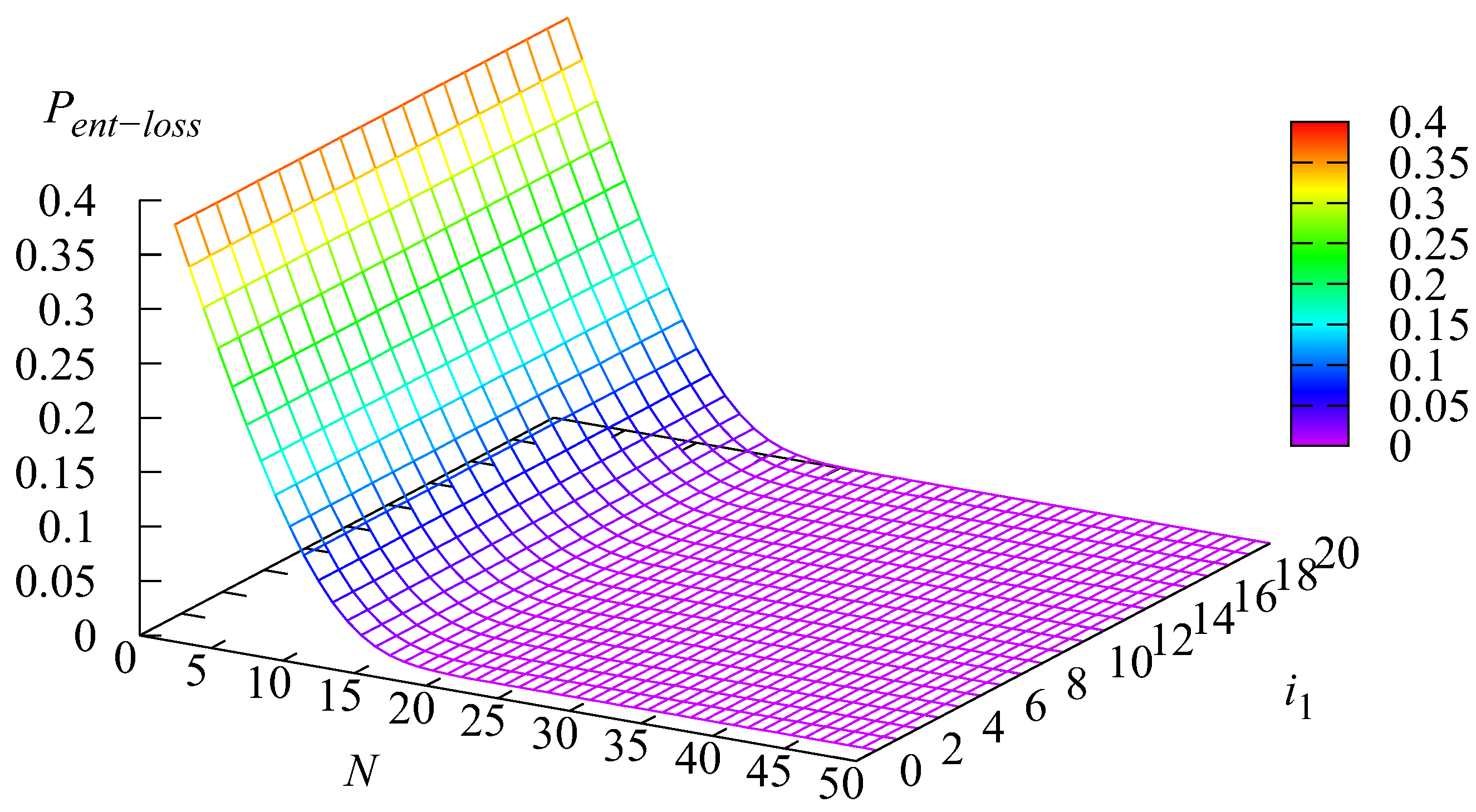
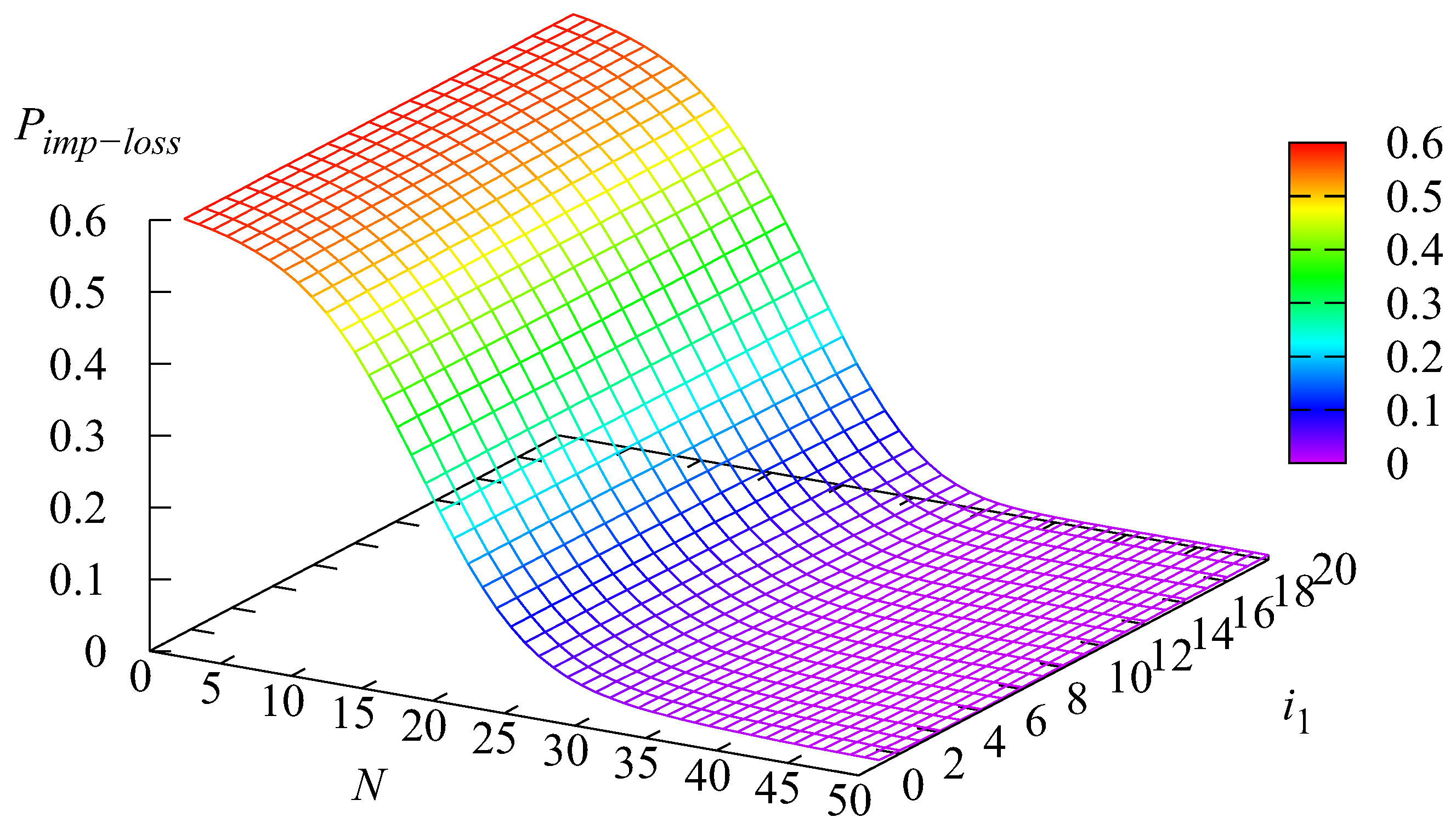
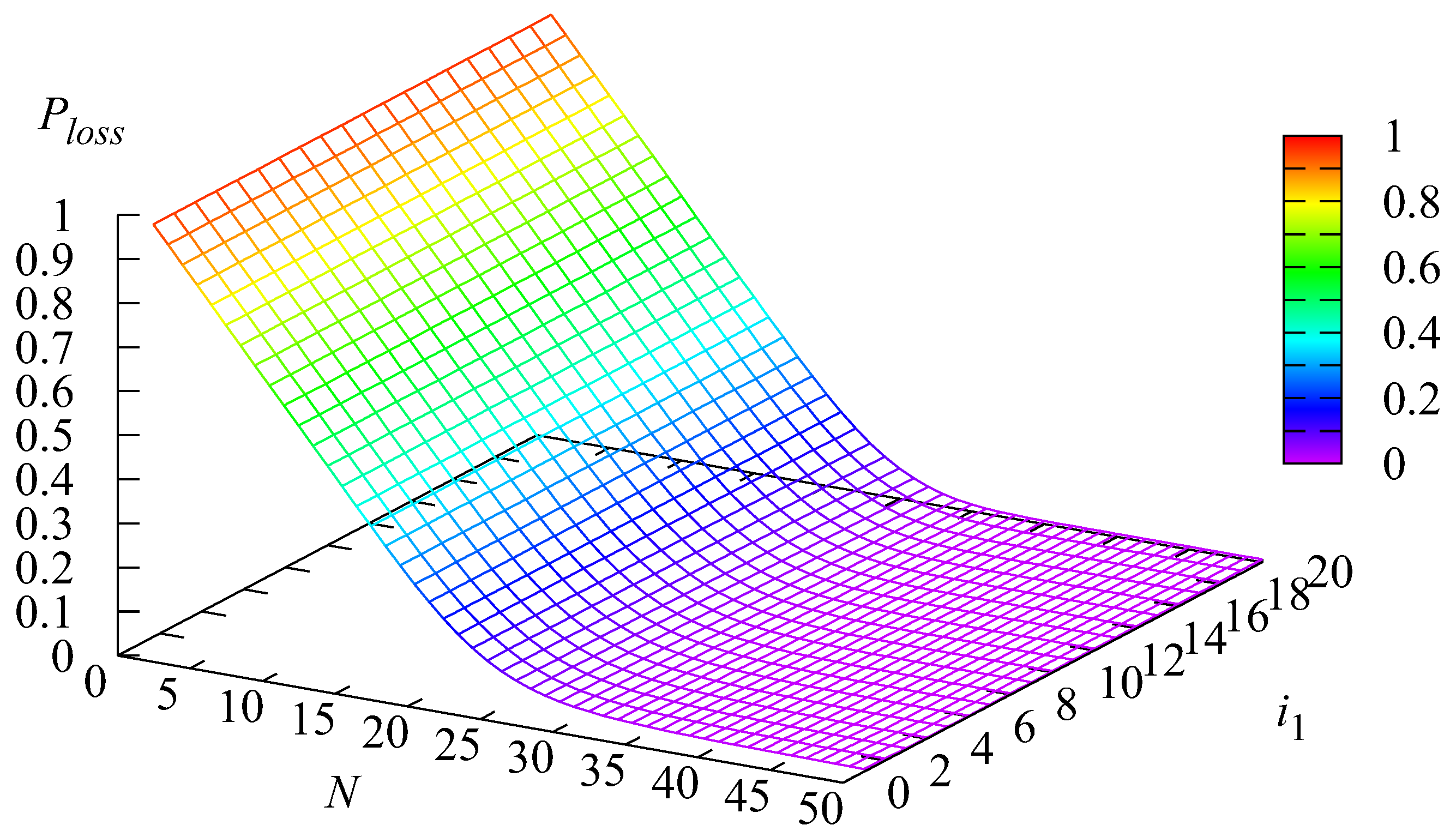
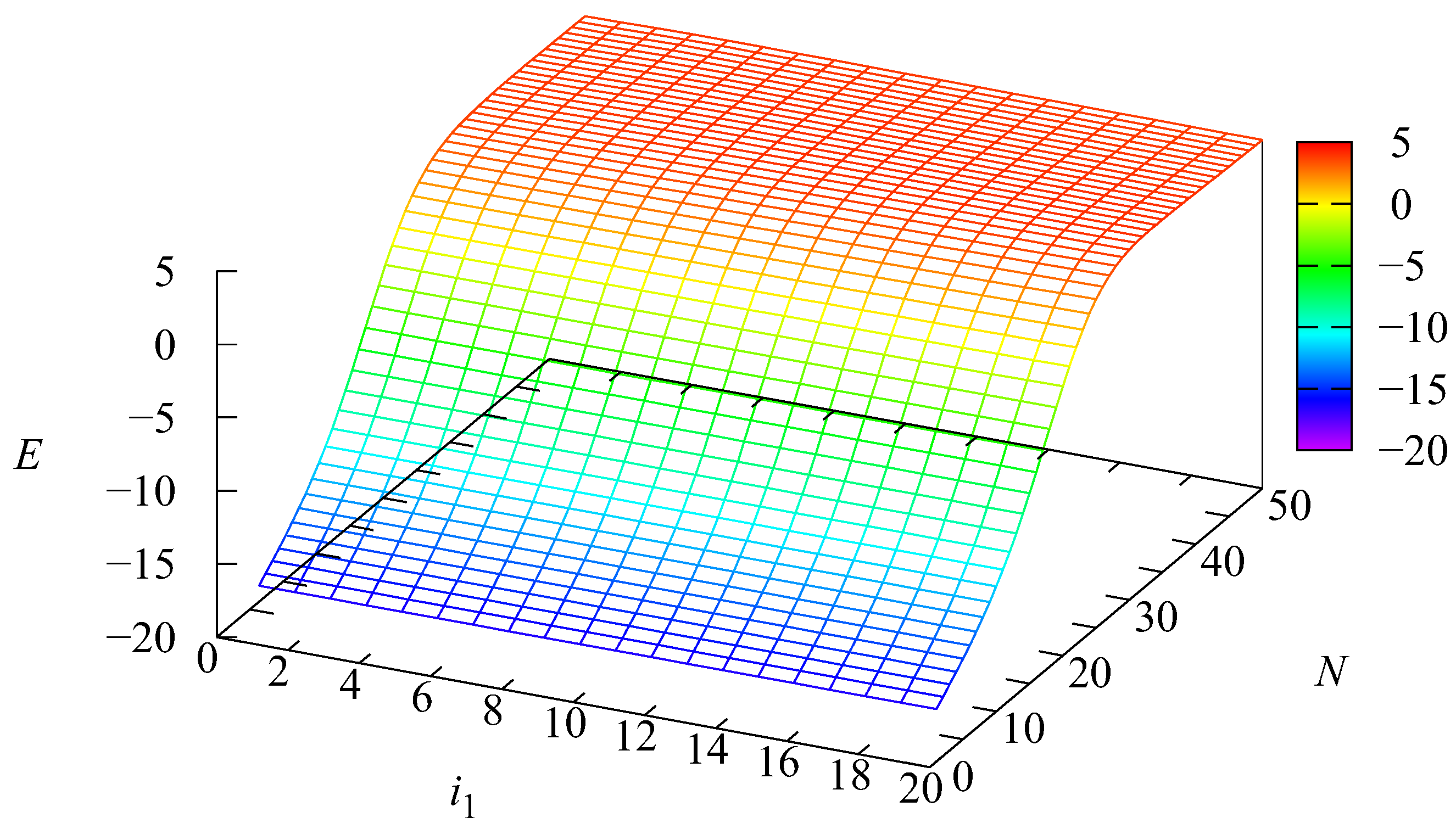
5. Numerical Examples

In this section, we consider the problem of the optimal choice of the number of required vehicles N and the value of the parameter $i_1$ that defines the minimal desirable group size for service in a delivery system.

To this end, let us consider a storehouse that can place up to $R=300$ orders for delivery. We believe that one vehicle can accommodate up to $i_2=20$ orders. Orders are received at the storehouse in accordance with the $MAP$ that is specified by the matrices

$$D_0=\left(\begin{array}{cc}-10.1599& 0.32778\\ 0.32778& -2.76287\end{array}\right),D_1=\left(\begin{array}{cc}9.44979& 0.382355\\ 0.0491604& 2.38593\end{array}\right),$$

and has an average intensity of $\lambda =5$ orders per minute as well as the coefficient of variation $c_{var}=1.8333$ and the correlation coefficient $c_{cor}=0.183092.$

The delivery time of a group consisting of i orders by one vehicle has a phase-type distribution with the parameters $({\mathit{\beta }}_i,S),$ where the matrix S has the form

$$S=\left(\begin{array}{cc}-0.01& 0\\ 0& -0.05\end{array}\right),$$

and the vector ${\mathit{\beta }}_i$ is given as

$${\mathit{\beta }}_i=(i/i_2,1-i/i_2),i=\overline{1,i_2}.$$

Thus, we assume that the average delivery time for one order is $b_1^{\left(1\right)}=24$ min, and the average delivery time for $i_2=20$ orders is $b_1^{\left(i_2\right)}=100$ min.

We assume that the intensity of impatience of orders from the buffer is determined by the parameter $\gamma =0.01.$ Thus, the average time that an arbitrary request can wait in the buffer is 100 min.

As noted earlier, the purpose of this experiment is to determine the optimal values for the parameters of the number of vehicles N and the threshold $i_1$, which defines the minimal desirable size for the group taken for service.

Let us vary the parameter N from 1 to 50 with a step of 1 and the parameter $i_1$ from 1 to $i_2=20$, also with a step of 1. We assume that the probabilities defining the tolerance to servicing a group smaller in size than the parameter $i_1$ in the case of the end of the patience time of one of the requests in the buffer are given as

$$q_i=i/i_1,i=\overline{1,i_1-1}.$$

First, let us analyze the dependence of the main characteristics of the system’s performance on the parameters N and $i_1.$ Figure 2 and Figure 3 illustrate the dependence of the average number $L_{buffer}$ of requests in the buffer and the average number $N_{serv}$ of busy servers on the parameters N and $i_1$.

Figure 4 and Figure 5 illustrate the dependence of the probabilities $P_{idle-server}$ and $P_{idle-server}^{requests}$ on the parameters N and $i_1$.

As can be seen from Figure 2, the average number $L_{buffer}$ of requests in the buffer decreases as the number of available servers increases. For small values of $N,$ the values of $L_{buffer}$ practically do not depend on the parameter $i_1$. For example, for $N=5$, $L_{buffer}=285.16345$ for $i_1=1$ and for $i_1=20.$ This is explained by the fact that, for the given system parameters, for small values of N, the probability that there will be fewer than $i_2$ requests in the buffer is negligibly small, and the servers do not stand idle but begin servicing, as follows on from Figure 4 and Figure 5, immediately after being released. For the same reason, other performance characteristics in the case under consideration also do not depend on $i_1$ for small values of $N.$ For bigger values of $N,$ in the considered case, the average number $L_{buffer}$ of requests in the buffer increases with an increase in the parameter $i_1.$ For example, for $N=50$, $L_{buffer}=3.05371$ for $i_1=1$ and $L_{buffer}=8.95773$ for $i_1=20.$

As shown in Figure 3, the average number of busy servers increases when the parameter N increases. For small values of N, the growth is linear; that is, an increase in N by one leads to an increase in $N_{serv}$ by the same unit. With a further increase in N, the dependence on N weakens, while for larger values of $i_1$, this dependence weakens earlier. As N grows, $N_{serv}$ depends on $i_1$. An increase in $i_1$ leads to a decrease in $N_{serv}$, since an increase in $i_1$ leads to an increase in the probability $P_{idle-server}$ that, at an arbitrary moment, there is at least one free server and the probability $P_{idle-server}^{requests}$ that there is at least one free server while there are requests in the buffer, which are presented in Figure 4 and Figure 5. Thus, servers are idle more often, which leads to a decrease in the average number of occupied servers.

Figure 6 and Figure 7 show the dependence of the average size $N_{batch}$ of a group of requests taken for servicing and the probability $P_{batch<i_1}$ that a group with a size of less than $i_1$ undergoes servicing on the parameters N and $i_1.$

As one can see from Figure 6, for small N values, the service is provided only for groups of requests with a maximal size of $i_2=20$. As N increases, the values of $N_{batch}$ decrease, and the rate of decrease significantly depends on the value of the parameter $i_1$: the higher $i_1$, the lower the rate of decrease of $N_{batch}$. For example, for $N=50,$ $N_{batch}=3.33746$ for $i_1=1,$ and $N_{batch}=18.78027$ for $i_1=20.$ Under the fixed value of N, the average size $N_{batch}$ of a group taken for servicing increases with an increase in $i_1.$ This is because, with an increase in $i_1$, the system tries to avoid serving small groups of requests.

The probability $P_{batch<i_1}$ that a group with a size of less than $i_1$ undergoes servicing, the shape of which is depicted in Figure 7, grows with increases in N and $i_1$. The growth of N is explained by the fact that, with an increase in N, the probability $P_{idle-server}^{requests}$ also grows (see Figure 5). Thus, when a request tries to leave the system due to impatience, a free server is more likely to be available, and the system has the possibility of providing service to a smaller group. The growth by $i_1$ can be explained by the same reasons and also by the fact that with an increase in $i_1$, the number of requests in the buffer increases, so more requests try to leave the system due to impatience.

Figure 8, Figure 9 and Figure 10 show the dependence of the probability $P_{ent-loss}$ that an arriving request will find the buffer full and leave the system, the probability $P_{imp-loss}$ of losing a request from the buffer due to impatience, and the probability $P_{loss}$ of losing an arbitrary request on the parameters N and $i_1.$

One can see from these figures that the loss probabilities essentially depend on the number of servers N. With an increase in N, all loss probabilities decrease. The impact of the parameter $i_1$ on the loss probabilities in the considered example is not so essential. This is mainly caused by the high capacity of the buffer $R=300.$ For example, to lose a request upon arrival, it is necessary to have a full buffer, and when the buffer is almost full, the service is provided to groups of the maximum possible size. Thus, we can mention that the probability $P_{ent-loss}$ increases slightly with an increase in the parameter $i_1$, since the average number of requests in the buffer grows. The dependence of the probability $P_{imp-loss}$ on $i_1$ under some fixed N can be non-monotonic. For example, for $N=50,$ $P_{imp-loss}=0.0061$ for $i_1=1$, $P_{imp-loss}=0.00195$ for $i_1=5$, and $P_{imp-loss}=0.00667$ for $i_1=20$. This can be explained by the following reasoning. For small $i_1$, the servers are more frequently utilized, and when a request shows impatience, it is possible to have no idle service at this moment, and the request will leave the system with a probability of 1. Thus, the probability $P_{imp-loss}$ should decrease with an increase in $i_1$. However, on the other hand, an increase in $i_1$ leads to an increase in the number of requests in the buffer; thus, more requests show their impatience and leave the system. So, the probability $P_{imp-loss}$ should increase with an increase in $i_1.$ All of these reasons explain the non-monotonic shape of the dependence of $P_{imp-loss}$ on $i_1$. The loss probability $P_{loss}$ is the sum of the probabilities $P_{imp-loss}$ and $P_{ent-loss}$; thus, this probability can also behave non-monotonically with an increase in $i_1$. By the way, the minimal value of the loss probability is also equal to $0.00195$, and this is reached for $N=50$ and $i_1=5$. This proves the necessity of finding the optimal values of $i_1$ to improve the system’s performance.

Looking at Figure 10, we can conclude that, for large values of N, the loss probability $P_{loss}$ becomes rather small. It is evident that the use of a server that corresponds to a vehicle in a real system costs money. It is necessary to buy vehicles, pay the costs of repairs, maintenance, and fuel, pay salaries to forwarders, etc., so it makes no sense to maintain an excessive number of vehicles. To this end, it is necessary to find the optimal number of vehicles N.

Let us assume that the quality of the system’s operation can be determined in terms of the following cost criteria:

$$E=E(N,i_1)=a{\mu }_{to-serv}-c_1\lambda P_{ent-loss}-c_2\lambda P_{imp-loss}-dN.$$

Here, a is a profit for the service of one request, $c_1$ and $c_2$ are the charges for the loss of a request at the entrance to the system and due to impatience, respectively, and d is the cost for maintaining one server per unit of time. Therefore, the criterion E determines the average system’s profit per unit of time, and our managerial goal is to obtain parameters such as N and $i_1$ under which the system’s profit is maximal.

In this numerical example, let us fix the following cost coefficients:

$$a=1,c_1=1,c_2=5,d=0.02.$$

Figure 11 shows the dependence of the cost criterion E on the parameters N and $i_1.$

As we can observe from Figure 11, the system has essential losses if the number of servers N is small. With an increase in $N,$ firstly, the system’s profit grows sharply and then starts to decrease slightly. This decrease is not essential due to the fact that we chose the small cost coefficient $d=0.02$ and the servers are cheap in the considered case. Otherwise, the decrease has to be more essential. In the considered example, the optimal value for the cost criterion is $E^{*}(N^{*},i_1^{*})=4.1125$ and it is reached for $N^{*}=36$ and $i_1^{*}=12.$ This means that it is necessary to have 36 vehicles and not start a new service after the service has been completed on some server if the number of requests in the buffer is less than 12.

If we fix $N=50$ and choose the parameter $i_1,$ then the optimal value of the cost criterion is $E^{*}(50,i_1^{*})=3.94139$ and it is reached for $i_1^{*}=5.$ Thus, for different values of N, the optimal value of $i_1$ can differ. Our results can help to determine the optimal values for the control parameters.

6. Conclusions

The mathematical model of a delivery system that acts as a multi-server queuing system with group service of requests is built. The model suggests a reasonably general $MAP$ flow for the requests and a phase-type distribution of the service time that depends on the size of the group. The possible impatience of waiting requests is taken into account. In contrast to the usual rule shown in the literature that the size of the serviced group must have values between certain fixed minimum and maximum values, it is suggested that groups of smaller size can be processed to reduce the probability of a request loss due to impatience.

The multi-dimensional $CTMC$ with a generator with the block lower Hessenberg structure describes the dynamics of the system. An effective algorithm for computing the steady-state distribution of this $CTMC$ is presented. This algorithm can be applied to the analysis of a variety of queueing models with group service of requests. Formulas for the computation of the key performance characteristics of the system were derived. The dependence of the basic performance characteristics on the number of servers and the minimum size of the group was numerically illustrated. The problems of the optimal values of the number of servers and the minimum size of the group were formulated and numerically solved.

The results can be extended in several directions, e.g., to account for the possibility of the batch arrival of the requests, the fluctuation of the number of available servers, the parameters of the service time distribution, etc. Another criterion related to the quality of the system’s operation can be considered, taking into account restrictions on the values of some characteristics of the system. The maximum size of the group can also be used as a parameter with an impact on the value of the cost criterion, and the problem of its optimization can be numerically solved.

The analyzed model has essentially wider applications than the delivery systems. Possible applications in various manufacturing systems (see, e.g., [18]) and transportation networks (see, e.g., [58]), in particular, car/ride-share systems (see, e.g., [59]) look promising. The results can be used for the optimal choice of the number of servers to provide the required quality for the requested service, the maximum capacity of the servers and their delivery speed and cost, and the economically reasonable minimum size of a group.