Evaluating Domain Randomization in Deep Reinforcement Learning Locomotion Tasks
Abstract
:1. Introduction
2. Related Works
3. Algorithms
3.1. Twin Delayed Deep Deterministic Policy Gradient (TD3)
3.2. Soft Actor–Critic (SAC)
4. Environments
- Normal Terrain (NT): The friction parameters of the environments under this terrain are kept constant with the default implementation values d from PyBullet. This implies that only the state variables are reset each time the environment is reset;
- Random Terrain (RT): In this case, each time an episode is terminated, and the environment is re-initialized (reset), the friction coefficient is sampled randomly from a k-dimensional uniform distribution (box) containing the default values d;
- Extreme Terrain (ET): Here the friction coefficient corresponding to the terrain is rest every time an episode is terminated, through uniformly sampling from one of the k-dimensional uniform distribution (box). Specifically, is sampled from the union of two intervals that straddle the corresponding interval in RT.
5. Experimental Design
Performance and Evaluation Metrics
- Default: In this scenario, each agent trained on each of NT, RT, and ET, respectively, is tested on the default environmental parameters (same as NT). This provides insight into the effects of domain randomization when compared to agents trained on default conditions;
- Interpolation: This scenario is expected to evaluate the performance of each agent on a dynamic terrain with a mild level of uncertainty. Hence, all the agents are tested based on the conditions of RT. An insight into the effect of mild-level domain randomization on the agents can be obtained by comparing results with those trained with no randomization (NT) as well as with a relatively high level of randomization (ET);
- Extrapolation: In extrapolation, ET conditions are used for the testing environment. In this test scenario, insight into the generalization effect of domain randomization to totally unseen conditions (NT) as well as partially unseen conditions (RT) during training are evaluated and compared with those trained on similar terrain conditions as the test-bed (ET).
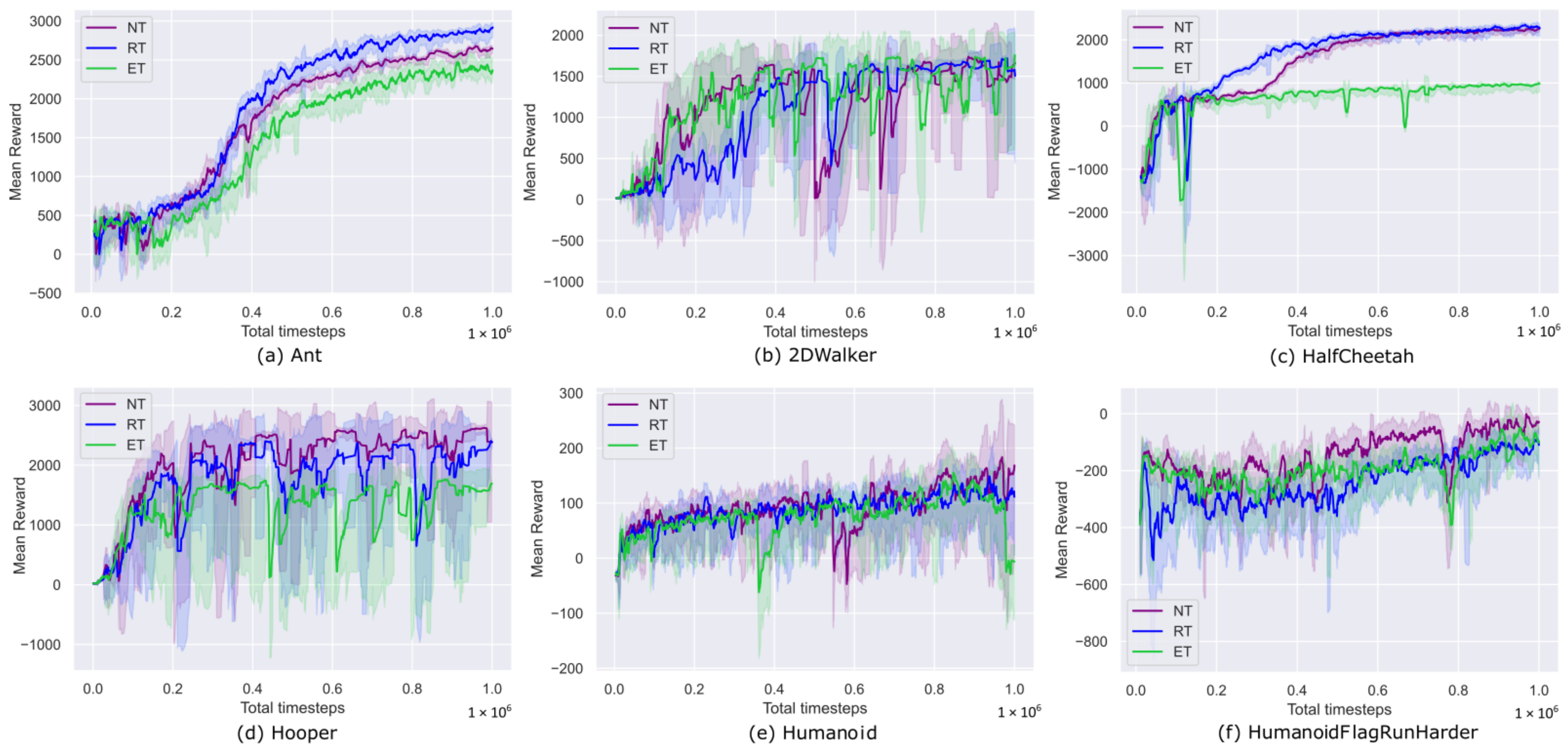
6. Results and Discussion
6.1. Training
6.2. Testing
6.2.1. Default
6.2.2. Interpolation
6.2.3. Extrapolation
6.2.4. Comparison between SAC and TD3
6.2.5. Real-World Scenario
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M.A. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Erickson, Z.M.; Gangaram, V.; Kapusta, A.; Liu, C.; Kemp, C. Assistive Gym: A Physics Simulation Framework for Assistive Robotics. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10169–10176. [Google Scholar]
- Peng, X.B.; Coumans, E.; Zhang, T.; Lee, T.; Tan, J.; Levine, S. Learning Agile Robotic Locomotion Skills by Imitating Animals. arXiv 2020, arXiv:2004.00784. [Google Scholar]
- Zhang, K.; Wang, Z.; Chen, G.; Zhang, L.; Yang, Y.; Yao, C.; Wang, J.; Yao, J. Training effective deep reinforcement learning agents for real-time life-cycle production optimization. J. Pet. Sci. Eng. 2022, 208, 109766. [Google Scholar] [CrossRef]
- Peng, Z.; Hu, J.; Shi, K.; Luo, R.; Huang, R.; Ghosh, B.K.; Huang, J. A novel optimal bipartite consensus control scheme for unknown multi-agent systems via model-free reinforcement learning. Appl. Math. Comput. 2020, 369, 124821. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Ding, Z.; Chen, J.; Luo, J.; Wang, Y.; Lu, Y. ED-DQN: An event-driven deep reinforcement learning control method for multi-zone residential buildings. Build. Environ. 2023, 242, 110546. [Google Scholar] [CrossRef]
- Ajani, O.S.; Mallipeddi, R. Adaptive evolution strategy with ensemble of mutations for reinforcement learning. Knowl.-Based Syst. 2022, 245, 108624. [Google Scholar] [CrossRef]
- Packer, C.; Gao, K.; Kos, J.; Krähenbühl, P.; Koltun, V.; Song, D. Assessing Generalization in Deep Reinforcement Learning. arXiv 2018, arXiv:1810.12282. [Google Scholar]
- Zhao, W.; Queralta, J.P.; Westerlund, T. Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: A Survey. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 737–744. [Google Scholar]
- Rajeswaran, A.; Lowrey, K.; Todorov, E.; Kakade, S. Towards Generalization and Simplicity in Continuous Control. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhang, A.; Ballas, N.; Pineau, J. A Dissection of Overfitting and Generalization in Continuous Reinforcement Learning. arXiv 2018, arXiv:1806.07937. [Google Scholar]
- Cobbe, K.; Klimov, O.; Hesse, C.; Kim, T.; Schulman, J. Quantifying Generalization in Reinforcement Learning. In Proceedings of the 2019 International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Whiteson, S.; Tanner, B.; Taylor, M.E.; Stone, P. Protecting against evaluation overfitting in empirical reinforcement learning. In Proceedings of the 2011 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL), Paris, France, 11–15 April 2011; pp. 120–127. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 2017 International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Duan, Y.; Schulman, J.; Chen, X.; Bartlett, P.; Sutskever, I.; Abbeel, P. RL2: Fast Reinforcement Learning via Slow Reinforcement Learning. arXiv 2016, arXiv:1611.02779. [Google Scholar]
- Vacaro, J.; Marques, G.; Oliveira, B.; Paz, G.; Paula, T.; Staehler, W.; Murphy, D. Sim-to-Real in Reinforcement Learning for Everyone. In Proceedings of the 2019 Latin American Robotics Symposium (LARS), 2019 Brazilian Symposium on Robotics (SBR) and 2019 Workshop on Robotics in Education (WRE), Rio Grande, Brazil, 23–25 October 2019; pp. 305–310. [Google Scholar] [CrossRef]
- Kansky, K.; Silver, T.; Mély, D.A.; Eldawy, M.; Lázaro-Gredilla, M.; Lou, X.; Dorfman, N.; Sidor, S.; Phoenix, D.; George, D. Schema Networks: Zero-shot Transfer with a Generative Causal Model of Intuitive Physics. arXiv 2017, arXiv:1706.04317. [Google Scholar]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain randomization for transferring deep neural networks from simulation to the real world. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 23–30. [Google Scholar]
- Nichol, A.; Pfau, V.; Hesse, C.; Klimov, O.; Schulman, J. Gotta Learn Fast: A New Benchmark for Generalization in RL. arXiv 2018, arXiv:1804.03720. [Google Scholar]
- Kamalaruban, P.; Huang, Y.T.; Hsieh, Y.P.; Rolland, P.; Shi, C.; Cevher, V. Robust reinforcement learning via adversarial training with Langevin dynamics. arXiv 2020, arXiv:2002.06063. [Google Scholar]
- Balaji, B.; Mallya, S.; Genc, S.; Gupta, S.; Dirac, L.; Khare, V.; Roy, G.; Sun, T.; Tao, Y.; Townsend, B.; et al. DeepRacer: Educational Autonomous Racing Platform for Experimentation with Sim2Real Reinforcement Learning. arXiv 2019, arXiv:1911.01562. [Google Scholar]
- Zhao, W.; Queralta, J.P.; Qingqing, L.; Westerlund, T. Towards Closing the Sim-to-Real Gap in Collaborative Multi-Robot Deep Reinforcement Learning. In Proceedings of the 2020 5th International Conference on Robotics and Automation Engineering (ICRAE), Singapore, 20–22 November 2020; pp. 7–12. [Google Scholar]
- Coumans, E.; Bai, Y. PyBullet, a Python Module for Physics Simulation for Games, Robotics and Machine Learning. 2016–2021. Available online: http://pybullet.org (accessed on 6 April 2021).
- Wang, J.X.; Kurth-Nelson, Z.; Soyer, H.; Leibo, J.Z.; Tirumala, D.; Munos, R.; Blundell, C.; Kumaran, D.; Botvinick, M. Learning to reinforcement learn. arXiv 2017, arXiv:1611.05763. [Google Scholar]
- Mankowitz, D.J.; Levine, N.; Jeong, R.; Abdolmaleki, A.; Springenberg, J.T.; Mann, T.; Hester, T.; Riedmiller, M.A. Robust Reinforcement Learning for Continuous Control with Model Misspecification. arXiv 2020, arXiv:1906.07516. [Google Scholar]
- Andrychowicz, O.M.; Baker, B.; Chociej, M.; Józefowicz, R.; McGrew, B.; Pachocki, J.W.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning dexterous in-hand manipulation. Int. J. Robot. Res. 2020, 39, 20–23. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 2018 International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Fujimoto, S.; Hoof, H.V.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. arXiv 2018, arXiv:1802.09477. [Google Scholar]
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. 2018. Available online: https://github.com/hill-a/stable-baselines (accessed on 27 September 2021).
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M.A. Deterministic Policy Gradient Algorithms. In Proceedings of the 2014 International Conference on Machine Learning (ICML), Beijing, China, 21–26 June 2014. [Google Scholar]
- Lillicrap, T.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2016, arXiv:1509.02971. [Google Scholar]
- Erez, T.; Tassa, Y.; Todorov, E. Infinite-Horizon Model Predictive Control for Periodic Tasks with Contacts. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Levine, S.; Koltun, V. Guided Policy Search. In Proceedings of the 2013 International Conference on Machine Learning (ICML), Atlanta, GA, USA, 17–19 June 2013. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.I.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2016, arXiv:1506.02438. [Google Scholar]
- Wawrzynski, P. Learning to Control a 6-Degree-of-Freedom Walking Robot. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 698–705. [Google Scholar] [CrossRef]
- Heess, N.M.O.; Hunt, J.J.; Lillicrap, T.P.; Silver, D. Memory-based control with recurrent neural networks. arXiv 2015, arXiv:1512.04455. [Google Scholar]
- Tassa, Y.; Erez, T.; Todorov, E. Synthesis and stabilization of complex behaviors through online trajectory optimization. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 4906–4913. [Google Scholar] [CrossRef]
- Liang, J.; Makoviychuk, V.; Handa, A.; Chentanez, N.; Macklin, M.; Fox, D. GPU-Accelerated Robotic Simulation for Distributed Reinforcement Learning. In Proceedings of the 2nd Conference on Robot Learning (CoRL 2018), Zurich, Switzerland, 29–31 October 2018. [Google Scholar]
- Miller, J.M. “Slippery” work surfaces: Towards a performance definition and quantitative coefficient of friction criteria. J. Saf. Res. 1983, 14, 145–158. [Google Scholar] [CrossRef]
- Li, K.W.; Chang, W.R.; Leamon, T.B.; Chen, C.J. Floor slipperiness measurement: Friction coefficient, roughness of floors, and subjective perception under spillage conditions. Saf. Sci. 2004, 42, 547–565. [Google Scholar] [CrossRef]




| Terrain | NT | RT | ET |
|---|---|---|---|
| Friction Coefficient | 0.8 | [0.5, 1.1] | [0.2, 0.5] ∪ [1.1, 1.4] |
| Environment | Algorithm | Reward (Mean & Std Dev) | ||
|---|---|---|---|---|
| NT | RT | ET | ||
| Ant | TD3 | 2773.37 ± 14.18 | 3009.35 ± 17.24 | 2536.21 ± 19.20 |
| SAC | 3231.36 ± 12.40 | 2960.18 ± 22.17 | 2857.20 ± 6.23 | |
| Walker2D | TD3 | 1871.02 ± 23.89 | 1788.12 ± 7.51 | 1790.57 ± 6.77 |
| SAC | 2011.16 ± 375.79 | 2130.09 ± 23.60 | 1930.08 ± 8.25 | |
| HalfCheetah | TD3 | 2353.24 ± 30.40 | 2408.77 ± 32.01 | 985.74 ± 8.71 |
| SAC | 2772.90 ± 25.19 | 2696.64 ± 13.90 | 2349.12 ± 26.31 | |
| Hopper | TD3 | 2741.39 ± 11.00 | 2526.66 ± 8.97 | 1793.55 ± 18.34 |
| SAC | 2404.11 ± 714.35 | 2526.22 ± 261.19 | 1831.47 ± 546.80 | |
| Humanoid | TD3 | 149.85 ± 62.51 | 139.39 ± 38.69 | 171.96 ± 43.16 |
| SAC | 205.75 ± 91.88 | 180.90 ± 96.46 | 157.68 ± 82.71 | |
| Humanoid Flagrun Harder | TD3 | −53.25 ± 46.76 | 18.06 ± 20.81 | −28.83 ± 15.84 |
| SAC | −0.37 ± 18.79 | −0.70 ± 24.30 | 4.54 ± 26.59 | |
| Environment | Algorithm | Reward (Mean & Std Dev) | ||
|---|---|---|---|---|
| NT | RT | ET | ||
| Ant | TD3 | 1633.09 ± 45.25 | 2999.95 ± 27.32 | 2549.26 ± 33.37 |
| SAC | 3209.12 ± 31.24 | 2952.29 ± 65.89 | 2849.54 ± 26.08 | |
| Walker2D | TD3 | 1861.79 ± 20.29 | 1792.21 ± 9.12 | 1791.41 ± 19.56 |
| SAC | 1540.25 ± 304.29 | 2005.30 ± 400.97 | 1942.19 ± 28.44 | |
| HalfCheetah | TD3 | 2285.24 ± 80.77 | 2378.99 ± 28.36 | 993.48 ± 13.68 |
| SAC | 2710.21 ± 122.65 | 2676.58 ± 80.08 | 2349.11 ± 32.35 | |
| Hopper | TD3 | 2554.05 ± 498.93 | 2420.55 ± 294.21 | 1786.45 ± 20.95 |
| SAC | 1535.22 ± 1164.44 | 1820.26 ± 952.38 | 1552.99 ± 705.53 | |
| Humanoid | TD3 | 169.09 ± 74.05 | 146.93 ± 55.99 | 158.35 ± 67.99 |
| SAC | 232.37 ± 105.32 | 165.46 ± 114.43 | 164.74 ± 98.91 | |
| Humanoid Flagrun Harder | TD3 | −50.36 ± 41.57 | −5.75 ± 22.64 | −25.36 ± 20.42 |
| SAC | −42.96 ± 31.91 | −2.59 ± 13.05 | 7.59 ± 20.38 | |
| Environment | Algorithm | Reward (Mean & Std Dev) | ||
|---|---|---|---|---|
| NT | RT | ET | ||
| Ant | TD3 | 1383.20 ± 429.61 | 2838.00 ± 232.40 | 2480.66 ± 131.91 |
| SAC | 2599.88 ± 872.06 | 2114.00 ± 1073.54 | 2797.41 ± 90.80 | |
| Walker2D | TD3 | 1117.09 ± 75.48 | 1486.92 ± 600.37 | 1741.68 ± 269.48 |
| SAC | 896.93 ± 664.27 | 1224.27 ± 849.52 | 1685.02 ± 484.83 | |
| HalfCheetah | TD3 | 1897.13 ± 309.04 | 2262.60 ± 92.93 | 1004 ± 20.63 |
| SAC | 1950.22 ± 797.80 | 2332.00 ± 203.63 | 2295.29 ± 114.13 | |
| Hopper | TD3 | 1571.73 ± 1283.61 | 1501.59 ± 1159.81 | 1780.24 ± 32.79 |
| SAC | 1613.85 ± 1234.47 | 1316.51 ± 1213.35 | 1250.74 ± 876.91 | |
| Humanoid | TD3 | 135.01 ± 62.76 | 104.25 ± 47.94 | 134.65 ± 63.33 |
| SAC | 175.89 ± 54.27 | 141.20 ± 56.02 | 199.88 ± 70.61 | |
| Humanoid Flagrun Harder | TD3 | −55.41 ± 40.60 | 5.54 ± 23.26 | −32.42 ± 25.68 |
| SAC | −44.01 ± 24.48 | −13.49 ± 15.31 | 12.94 ± 24.94 | |
| Metric | Reward | ||
|---|---|---|---|
| NT | RT | ET | |
| Win (+) | 13 | 14 | 9 |
| Loss (−) | 23 | 22 | 27 |
| Draw (≈) | – | – | – |
| Metric | Reward | ||
|---|---|---|---|
| NT | RT | ET | |
| Win (+) | 0 | 6 | 6 |
| Loss (−) | 12 | 6 | 6 |
| Draw (≈) | – | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajani, O.S.; Hur, S.-h.; Mallipeddi, R. Evaluating Domain Randomization in Deep Reinforcement Learning Locomotion Tasks. Mathematics 2023, 11, 4744. https://doi.org/10.3390/math11234744
Ajani OS, Hur S-h, Mallipeddi R. Evaluating Domain Randomization in Deep Reinforcement Learning Locomotion Tasks. Mathematics. 2023; 11(23):4744. https://doi.org/10.3390/math11234744
Chicago/Turabian StyleAjani, Oladayo S., Sung-ho Hur, and Rammohan Mallipeddi. 2023. "Evaluating Domain Randomization in Deep Reinforcement Learning Locomotion Tasks" Mathematics 11, no. 23: 4744. https://doi.org/10.3390/math11234744
APA StyleAjani, O. S., Hur, S. -h., & Mallipeddi, R. (2023). Evaluating Domain Randomization in Deep Reinforcement Learning Locomotion Tasks. Mathematics, 11(23), 4744. https://doi.org/10.3390/math11234744







